2. Potenssi ja juuri: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Potenssi ja juuri. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

2.1 Potenssifunktio ja -yhtälö: tehtäviä

Tämän kappaleen teoria.

2.1.1 Tehtävä

Yhdistä funktiot oikeisiin kuvaajiin ilman teknisiä apuvälineitä. Tehtävästä saa pisteet, kun funktion nimen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

$C(x)=x^{12}$

# t211

2.1.2 Tehtävä

Lasse on ratkaissut mielestään oikein matematiikan koetehtävän. Opettaja antoi Lasselle kuitenkin tehtävästä 3/6 pistettä. Missä virhe? Tehtävässä oli tarkoitus ratkaista potenssiyhtälö muuttujan suhteen.

# Potenssiyhtalovirhe

2.1.3 Tehtävä

Määritä juuren arvo kahden desimaalin tarkkuudella.

# MAA2potenssijajuuri1a

# MAA2potenssijajuuri1b

# MAA2potenssijajuuri1c

# MAA2potenssijajuuri1d

2.1.4 Tehtävä

Ratkaise potenssiyhtälö. Komennolla root(n)(a) saat :s juuren luvusta . Ilmoita vastaus tarkkana arvona! Yleisesti ottaen jatkossa, jos tehtävässä pyydetään ratkaisemaan yhtälö, niin vastaus tulee ilmoittaa tarkkana arvona.

# MAA2potenssijajuuri2a

# MAA2potenssijajuuri2b

# MAA2potenssijajuuri2c

# MAA2potenssijajuuri2d

2.1.5 Tehtävä

Ratkaise potenssiyhtälö.

# MAA2potenssijajuuri3a

# MAA2potenssijajuuri2a2

# MAA2potenssijajuuri3c

2.1.6 Tehtävä

Ratkaise potenssiyhtälö.

# MAA2potenssijajuuri3d

# MAA2potenssijajuuri4b

2.1.7 Tehtävä

Olli Opiskelija nosti ensimmäisenä opintovuonna $6\;000$ euron suuruisen opintolainan, joka on vuoden kuluessa kasvanut noin $6\;564$ euron suuruiseksi.

# MAA2potenssijajuuri15

2.1.8 Tehtävä

Kalle keittää kahvia neljä kertaa päivässä, aamulla, päivällä, iltapäivällä ja illalla samoista kahvipuruista. Hän arvioi, että iltakahvin voimakkuus on noin neljäsosa aamukahvin voimakkuudesta. Oletetaan, että kahvipurut suodattuvat tasaisesti. Toisin sanoen, kullakin kerralla sen hetkisestä purujen määrästä vähenee sama prosentuaalinen osuus.

# MAA2potenssijajuuri16

Vihje

Olkoon $a="\text{kahvin voimakkuus alussa}"$ ja $x="\text{suodatuksen prosenttikerroin}".$

Tällöin aamun keittämisen jälkeen kahvia on jäljellä xa,

päivällä $x\cdot xa=x^2a,$

iltapäivällä x^3a

ja illalla x^4a .

Illan määrä on neljäsosa aamun määrästä, joten muodostetaan ja ratkaistaan yhtälö

$\begin{align*} x^4a = \dfrac{1}{4}xa. \end{align*}$

Ratkaisu

$\begin{align*} x^4a &= \dfrac{1}{4}xa && ||:a\neq 0\; ^{*)} \\ x^4 &= \dfrac{1}{4}x && ||:x\neq 0 \; ^{**)} \\ x^3 &= \dfrac{1}{4} && ||\sqrt[3]{\;} \\ x &= \sqrt[3]{\dfrac{1}{4}} \approx 0,630 = 63,0 \% \end{align*}$

Kahvia suodattuu siis $100\%-63,0\% = 37,0\%$ per keittämiskerta.

$^{*)}$ Lienee turvallista olettaa, että puruja on eli $a\neq 0$ .

$^{**)}$ Vastaavasti myös voidaan olettaa, että suodatinpussi ei päästä kaikkea lävitseen. Tilannetta, jossa pussi ei suodata, vastaa x=0 . Eli aamukahvin jälkeen purujen kofeiinipitoisuus olisi nolla tai toisin sanoen, aamukahvin vahvuus olisi $100\%$ purujen vahvuudesta.

# MAA2potenssijajuuri17b

Vihje

Kun kahvia on keitetty kertaa, sitä on jäljellä ax^n .

Tutki kokeilemalla, millä muuttujan arvolla ax^n < 0,01 a . Yhtälö sievenee muotoon , missä x=0,63.

2.1.9 Tehtävä

Funktio on parillinen, jos f(x)=f(-x)

ja funktio on pariton, jos f(x)=-f(-x).

Mitkä seuraavista funktion kuvaajista ovat parillisia ja mitkä parittomia?

# Parilparit1

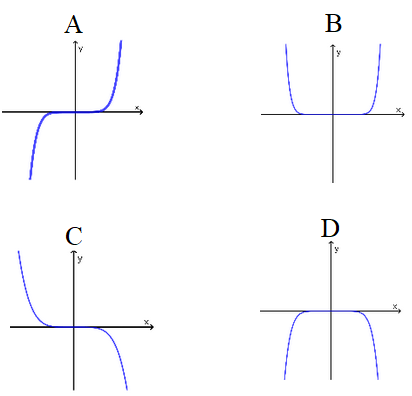
2.1.10 Tehtävä

Alapuolella on osoitettu, että jokainen parillinen potenssifunktio on parillinen funktio. Numeroi osoituksen vaiheet oikeaan järjestykseen 1-5 .

# 2110c

# 2110a

# 2110e

# 2110d

# 2110b

2.2 Juurifunktio ja -yhtälö: tehtäviä

Tämän kappaleen teoria.

2.2.1 Tehtävä

Yhdistä funktiot oikeisiin kuvaajiin ilman teknisiä apuvälineitä. Tehtävästä saa pisteet, kun funktion nimen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

$A(x)=-\sqrt[5]{x}$

$B(x)=\sqrt[9]{9x}$

$C(x)=\pi\sqrt[20]{x}$

$D(x)=-\dfrac{5}{2}\sqrt[12]{x}$

# t221

2.2.2 Tehtävä

Anne oli tehnyt läksynä tulleen juuritehtävän hieman väärin. Missä virhe? Tehtävässä oli tarkoitus ratkaista juuriyhtälö muuttujan suhteen.

# Juuriyhtalovirhe

2.2.3 Tehtävä

# p223

2.2.4 Tehtävä

Ratkaise juuriyhtälöt.

# MAA2juuriyhtalot1a

# MAA2juuriyhtalot1b

# MAA2juuriyhtalot1c

2.2.5 Tehtävä

Järjestä yhtälön $3\sqrt[8]{\dfrac{x}{2}}=6$ ratkaisun vaiheet oikeaan järjestykseen.

# 225c

# 225e

# t225a

# 225d

# 225b

2.2.6 Tehtävä

Dermatomyosiitti on on harvinaislaatuinen lihasten autoimmuuninen tulehdussairaus, joka luokitellaan reumaksi. Tiivistettynä tämä tarkoittaa sitä, että jokin laukaiseva tekijä saa elimistön immuunijärjestelmän hyökkäämään omia soluja vastaan, joka aiheuttaa lihastulehduksen. Dermatomyosiitin hoitoon kuuluu lähes poikkeuksetta kortisonilääkkeet, joiden annostusta pyritään vähentämään ajan mukaan. Lääkityksen vaikutusta voidaan mallintaa juurifunktiolla

$f(x)=1-0,1k\sqrt[5]{x},$

missä $k=\text{"päivittäinen kortisoniannostuksen määrä" (milligrammoina)}$ , $x=\text{"aika" (päivinä)}$ . Funktio f(x) ilmoittaa kuinka paljon tulehdustilan voimakkuus on alkuperäisestä tulehduksen määrästä.

# MAA2juuriyhtalotdermatomyos

Vihje

Nyt tulee ratkaista millä muuttujan arvolla $f(x)=\dfrac{1}{10}$ . Tästä saadaan juuriyhtälö

$1-0,1\cdot 5\sqrt[5]{x}=\dfrac{1}{10}.$

Ratkaisu

$\begin{align*} 1-0,1\cdot 5\sqrt[5]{x}&=\dfrac{1}{10} &&|+0,5\sqrt[5]x-0,1 \\ 0,5\sqrt[5]x&=0,9 && |:0,5 \\ \sqrt[5]x&=1,8 && |()^5 \\ x &= 18,89568... \approx 19 \end{align*}$

Lääkitystä täytyy jatkaa päivää milligramman annostuksella, että tulehdustila laskee kymmenesosaan alkuperäisestä.

2.2.7 Tehtävä (yo lyhyt/s2012)

Saksalainen tähtitieteilijä Johannes Kepler (1571-1630) keksi planeetan etäisyyden ja kiertoajan välisen yhteyden. Planeetan kiertoaikaa Auringon ympäri merkitään symbolilla ja sen etäisyyttä Auringosta symbolilla . Alla olevassa taulukossa on viiden Aurinkoa lähinnä olevan planeetan kiertoaika vuosina ja etäisyys astronomisen yksikön avulla lausuttuna.

a) Täydennä taulukkoon puuttuvat kohdat kolmen desimaalin tarkkuudella. Tehtävässä ei ole automaattitarkistusta.

# taulukko4

Open plugin

b) Päättele, mikä on Keplerin kaava etäisyydelle kiertoajan avulla lausuttuna.

# t227

Vihje

Taulukosta huomataan, että $\sqrt{y}=\sqrt[3]{x}.$ Ratkaistaan yhtälö muuttujan suhteen...

c) Saturnuksen kiertoaika on 29,457 vuotta. Mikä on sen etäisyys Auringosta?

# t227c

2.2.8 Tehtävä

Ratkaise juuriyhtälö.

# MAA2juuriyhtalot2a

# MAA2juuriyhtalot2b

2.3 Murtopotenssi: tehtäviä

Tämän kappaleen teoria.

2.3.1 Tehtävä

Ilmaise juurina potenssit. Luvun $\sqrt[n]{a}$ saa komennolla root(n)(a).

# MAA2murtopotenssi1a

# MAA2murtopotenssi1b

# MAA2murtopotenssi1c

# MAA2murtopotenssi1d

2.3.2 Tehtävä

Ilmaise potensseina juuret.

# MAA2murtopotenssi2a

# MAA2murtopotenssi2b

# MAA2murtopotenssi2c

# MAA2murtopotenssi2d

2.3.3 Tehtävä

Valitse samaa tarkoittava muoto. Oletetaan, että a>0.

# p233a

# p233b

# p233c

# p233d

2.3.4 Tehtävä

Sievennä. Kannattaa muuttaa juuret potenssimuotoon ja hyödyntää laskusääntöjä.

# MAA2murtopotenssi4a

# MAA2murtopotenssi4b

# MAA2murtopotenssi4c

# MAA2murtopotenssi4d

2.3.5 Tehtävä

Perustele omin sanoin

# murtopotenssitekaavoina

# murtopotenssitekaavoinb

2.3.6 Tehtävä

Ratkaise yhtälö. Ilmoita tarkka vastaus.

# MAA2Murtopotenssit8a

# MAA2Murtopotenssit8b

2.3.7 Tehtävä

Radioaktiivisen isotoopin määrä väheni radioaktiivisen hajoamisen seurauksena 1,5 tunnissa 5,2 milligrammasta 2,6 milligrammaan. Hajoamiselle on ominaista, että määrä pienenee samanmittaisessa ajanjaksossa aina yhtä monta prosenttia.

# MAA2murtopotenssi9

Vihje

Olkoon $p=\text{radioaktiivisuuden prosenttikerroin (per tunti)}$ . Koska aineen hajoaminen on prosentuaalisesti tasaista saamme yhtälön

$p^{1,5}\cdot 5,2 =2,6.$

Ratkaise tästä yhtälöstä .

2.3.8 Tehtävä

Olkoot a>0 sekä ja positiivisia kokonaislukuja. Alapuolella on osoitettu, että

$(\sqrt[n]{a})^m=\sqrt[n]{a^m}.$

Numeroi osoituksen vaiheet oikeaan järjestykseen 1-6 .

# 238e

# 238f

# 238a

# 238c

# 238b

# 238d