1. Polynomilaskentaa

Ensimmäinen kappale käsittelee polynomilaskentaa. Kappaleessa käydään läpi polynomien peruskäsitteitä sekä polynomeilla tehtäviä laskutoimituksia. Lopuksi käsitellään ensimmäisen asteen polynomiepäyhtälöä. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

1.1 Polynomin peruskäsitteet

MAY1-kurssilla opittiin, että merkittyä laskutoimitusta tai pelkkää lukua kutsutaan lausekkeeksi. Lausekkeita ovat esimerkiksi

$x^2,\;x+1\;\text{ja}\;8.$

Lausekkeista osa luokitellaan polynomeiksi.

Polynomi

Polynomi on muuttujista ja vakioista yhteen-, vähennys- ja kertolaskulla aikaansaatu lauseke.

Polynomin yhteenlaskettavia kutsutaan termeiksi. Jokainen termi koostuu kertoimesta ja muuttujaosasta.

Termin muuttujaosan eksponentti on termin asteluku. Jos eksponentti on nolla, niin termi on pelkkä luku eli vakiotermi. Polynomin asteluku määräytyy sen muuttujan mukaan, jolla on suurin eksponentti.

Polynomin P(x) vastapolynomi on polynomi -P(x) , joka toteuttaa ehdon P(x)+(-P(x))=0

Polynomeja luokitellaan myös termien lukumäärän mukaan:

Jos termejä on yksi, polynomia sanotaan monomiksi.
Jos termejä on kaksi, polynomia sanotaan binomiksi.
Jos termejä on kolme, polynomia sanotaan trinomiksi.

Polynomeja nimetään yleensä isoilla kirjaimilla, usein kirjaimilla tai . Kun polynomin muuttujan paikalle asetetaan jokin lukuarvo, saadaan laskettua polynomin arvo.

1.1.1 Esimerkki: polynomin peruskäsitteet

Tarkastellaan polynomia -14x^5+99x^3+x^2-12x-100.

Tarkasteltavan polynomin

kertoimia ovat , , , ja
muuttujaosia ovat , , ja
termejä ovat , , , ja vakiotermi
asteluku on , sillä se on korkeimman asteen termin muuttujaosan eksponentti
vastapolynomi on

1.1.2 Esimerkki: polynomin asteluku

Määritä polynomin asteluku.

$2x^{13}-4x^{11}+5x+11$

Ratkaisu

Asteluku on , sillä $2x^{13}$ on polynomin $2x^{13}-4x^{11}+5x+11$ korkeimman asteen termi.
Asteluku on , sillä $-7x^{2}$ on trinomin korkeimman asteen termi.
Asteluku on , sillä on binomin korkeimman asteen termin.
Asteluku on . Voidaan ajatella, että monomin muuttujaosa on , sillä .

1.1.3 Esimerkki: polynomifunktion arvo pisteessä

Laske polynomifunktion P(x)=-2x^2+1 arvo, kun

$x=-\dfrac{1}{4}$

Ratkaisu:

Polynomin arvo, kun saa jonkin arvon, saadaan sijoittamalla kyseinen arvo muuttujan paikalle ja laskemalla merkityt laskutoimitukset.

$P(1)=-2\cdot 1^2 +1 = -2+1=-1$
$P(2)=-2\cdot 2^2 +1 = -2\cdot 4+1=-7$
$P(-3)=-2\cdot(-3)^2+1=-2\cdot 9+1=-17$
$P(-\dfrac{1}{4})=-2\cdot(-\dfrac{1}{4})^2+1=-2\cdot\dfrac{1}{16}+1=-\dfrac{1}{8}+1=\dfrac{7}{8}$

Useamman muuttujan polynomi

Useamman muuttujan polynomi on lauseke, missä termit muodostuvat muuttujien ja kertoimien tulosta. Vastaavasti kuin yhden muuttujankin polynomilla, näiden termien summa muodostaa useamman muuttujan polynomin.

Useamman muuttujan asteluku määrittyy korkeimman asteen termin mukaan ja yksittäisen termin asteluku on muuttujien eksponenttien summa.

1.1.4 Esimerkki: useamman muuttujan polynomifunktion aste ja arvo pisteessä

Määritä kolmen muuttujan polynomifunktion P(x,y,z)=2xy^4z^5-2xy+3z

asteluku
arvo pisteessä

Ratkaisu:

Useamman muuttujan asteluku saadaan korkeimman asteen termin mukaan, jonka asteluku määrittyy muuttujien eksponenttien summana. Termin asteluku on , termin asteluku on ja termin asteluku on . Polynomin asteluku on siis
Sijoitetaan arvot muuttujien $x,\;y$ ja paikoille.

$P(3,1,-1)=2\cdot3\cdot1^4\cdot(-1)^5-2\cdot3\cdot 1+3\cdot(-1)=-6-6-3=-15$

Vastaus:

Polynomien peruskäsitteet: tehtäviä

1.2 Polynomien laskutoimitukset

Ennen kuin siirrymme laskemaan polynomeilla, on hyvä tiedostaa reaalilukujen laskulait (ns. reaalilukujen kunta-aksioomat), joiden mukaan reaalilukujen laskutoimitukset suoritetaan.

Reaalilukujen laskulakeja

Yhteenlaskun vaihdantalaki a+b=b+a

Yhteenlaskun liitäntälaki a+(b+c)=(a+b)+c=a+b+c

Kertolaskun vaihdantalaki $a\cdot b=b\cdot a$

Kertolaskun liitäntälaki $a\cdot (b \cdot c)=(a\cdot b)\cdot c=a \cdot b \cdot c$

Yhteen- ja kertolaskun osittelulait

$a\cdot(b+c)=a\cdot b+a\cdot c$ $(a+b)\cdot c=a\cdot c+b\cdot c$

1.2.1 Esimerkki: laskujärjestyksen muuttaminen kunta-aksioomien avulla

Yhteenlaskun vaihdantalain nojalla
Yhteenlaskun liitäntälain nojalla
Kertolaskun vaihdantalain nojalla $3 \cdot 7 = 7 \cdot 3 = 21$
Kertolaskun liitäntälain nojalla $2\cdot (3\cdot 4) = (2\cdot 3)\cdot 4 = 24$
Yhteen- ja kertolaskun liitäntälain nojalla $1\cdot(2+3)=1\cdot 2 + 1\cdot 3 = 5$
Yhteen- ja kertolaskun liitäntälain nojalla $(2+4)\cdot 7 = 2\cdot 7 + 4\cdot 7 = 42$

Suureet, joilla on sama yksikkö, voidaan laskea yhteen tai vähentää toisistaan. Esimerkiksi voidaan laskea $4\;\text{kg}-3\;\text{kg},$ mutta ei $4\;\text{kg}-3\;\text{€}$ .

Jos polynomin termien muuttujaosat ovat samat, ne voidaan yhdistää. Tällaisia termejä kutsutaan samanmuotoisiksi.

Polynomien yhteen- ja vähennyslasku

Yhteenlaskussa samanmuotoiset termit yhdistetään laskemalla termien kertoimet yhteen.

Vähennyslaskussa samanmuotoiset termit yhdistetään vähentämällä termien kertoimet toisistaan.

Muuttujaosa säilyy ennallaan.

1.2.2 Esimerkki: polynomien yhteen- ja vähennyslasku

Laske polynomien 2x^2-3x+3 ja -5x+1

summa
erotus

Ratkaisu:

$\begin{align*} &2x^2-3x+3 +(-5x+1) && \text{| avataan sulut} \\ =&\textcolor{red}{2x^2}\textcolor{green}{-3x}+\textcolor{blue}{3}\textcolor{green}{-5x}+\textcolor{blue}{1} \\ =&\textcolor{red}{2x^2}\textcolor{green}{-3x-5x}+ \textcolor{blue}{3+1} && | \text{ yhdistetään samanmuotoiset termit} \\ =&\textcolor{red}{2x^2}\textcolor{green}{-8x}+ \textcolor{blue}{4} && | \text{ järjestetään termit asteluvun mukaan} \end{align*}$

$\begin{align*} &2x^2-3x+3 - (-5x+1) && \text{| avataan sulut} \\ =&\textcolor{red}{2x^2}\textcolor{green}{-3x}+\textcolor{blue}{3}+\textcolor{green}{5x}\textcolor{blue}{-1} \\ =&\textcolor{red}{2x^2}\textcolor{green}{-3x+5x}+ \textcolor{blue}{3-1} && | \text{ yhdistetään samanmuotoiset termit} \\ =&\textcolor{red}{2x^2}+\textcolor{green}{2x}+ \textcolor{blue}{2} && | \text{ järjestetään termit asteluvun mukaan} \end{align*}$

Vastaus:

Polynomien kertolaskuissa sovelletaan vaihdanta-, liitäntä- ja osittelulakeja.

Monomilla kertominen

Kahden monomin tulossa kertoimet kerrotaan keskenään ja muuttujaosat keskenään.

Monomin ja polynomin tulossa monomilla kerrotaan jokainen polynomin termi.

Muuttujaosien kertomisessa keskenään sovelletaan samankantaisten potenssien laskusääntöjä. Samankantaisten potenssien tulossa eksponentit lasketaan yhteen.

$a^ma^n=a^{m+n}$

1.2.3 Esimerkki: kahden monomin tulo

Laske monomien ja 3x^2 tulo.

Ratkaisu:

$\begin{align*} &\textcolor{red}{2}\textcolor{green}{x}\cdot3\textcolor{green}{x^2} && |\text{Järjestetään \textcolor{red}{kerroin}- ja \textcolor{green}{muuttujaosa} erikseen}\\ =&\textcolor{red}{2}\cdot \textcolor{red}{3} \cdot \textcolor{green}{x\cdot x^2} \\ =& \textcolor{red}{6}\textcolor{green}{x^3} \end{align*}$

Vastaus: 6x^3

1.2.4 Esimerkki: monomin ja binomin tulo

Sievennä monomin ja binomin 2y+3 tulo.

Ratkaisu:

Kerrotaan jokainen binomin termi monomilla .

$\begin{align*} &\textcolor{red}{4y}\cdot({2y}+{3}) \\ =&\textcolor{red}{4y}\cdot {2y} + \textcolor{red}{4y}\cdot {3} \\ =& 8y^2+12y \end{align*}$

Vastaus: 8y^2+12y

Kahden polynomin tulo

Kahden polynomin tulossa kerrotaan kertojapolynomin jokaisella termillä kerrottavan kaikki termit ja lasketaan saadut tulot yhteen.

$(\textcolor{red}a+\textcolor{blue}b)(c+b)=\textcolor{red}ac+\textcolor{red}ad+\textcolor{blue}bc+\textcolor{blue}bd$

1.2.5 Esimerkki: binomin ja binomin tulo

Laske binomien a+3 ja a-2 tulo.

Ratkaisu:

Kerrotaan termeillä $\textcolor{green}{a}$ ja $\textcolor{red}{3}$ molemmat jälkimmäisen polynomin termit.

$\begin{align*} &(\textcolor{green}{a}+\textcolor{red}{3})\cdot({a}-{2}) \\ &=\textcolor{green}{a}\cdot({a}-{2})+\textcolor{red}{3}\cdot({a}-{2}) \\ &= \textcolor{green}{a}\cdot {a} + \textcolor{green}{a}\cdot({-2}) + \textcolor{red}{3}\cdot {a} + \textcolor{red}{3}\cdot{(-2)} \\ &= a^2-2a+3a-6 \\ &= a^2+a-6 \end{align*}$

Vastaus: a^2+a-6

1.2.6 Esimerkki: binomin ja trinomin tulo

Sievennä polynomien (3a-5) ja (2a^2-a+4) tulo.

Ratkaisu:

Kerrotaan termeillä $\textcolor{green}{3a}$ ja $\textcolor{red}{-5}$ kaikki jälkimmäisen polynomin termit.

$\begin{align*} &(\textcolor{green}{3a}\textcolor{red}{-5})\cdot(2a^2-a+4) \\ =& \textcolor{green}{3a}\cdot 2a^2 + \textcolor{green}{3a} \cdot(-a) + \textcolor{green}{3a} \cdot 4 \textcolor{red}{-5}\cdot 2a^2 \textcolor{red}{-5}\cdot(-a)\textcolor{red}{-5}\cdot 4 \\ =& 6a^3-3a^2+12a-10a^2+5a-20 \\ =& 6a^3-3a^2-10a^2+12a+5a-20 \\ =& 6a^3-13a^2+17a-20 \end{align*}$

Vastaus: 6a^3-13a^2+17a-20

1.2.7 Esimerkki: useamman binomin tulo

Sievennä (x+1)(x-2)(x+4) .

Ratkaisu:

Vaihdantalain perusteella ei ole väliä, missä järjestyksessä kertolaskut lasketaan. Valitaan, että lasketaan ensin tulo (x+1)(x-2) ja kerrotaan tällä binomi x+4 .

$\begin{align*} &\textcolor{green}{(x+1)(x-2)}(x+4) &&\\ &=\textcolor{green}{(x\cdot x+ x\cdot(-2)+1\cdot x+1\cdot(-2))}(x+4) \\ &=\textcolor{green}{(x^2-2x+x-2)}(x+4) \\ &=\textcolor{green}{(x^2-x-2)}(x+4) \\ &= \textcolor{green}{x^2}\cdot x +\textcolor{green}{x^2}\cdot 4 \textcolor{green}{-x}\cdot x \textcolor{green}{-x}\cdot 4 \textcolor{green}{-2}\cdot x \textcolor{green}{-2}\cdot 4 \\ &= x^3+4x^2-x^2-4x-2x-8 && |\text{ yhdistetään samanmuotoiset termit}\\ &= x^3+3x^2-6x-8 \end{align*}$

Tulo (x+1)(x-2) täytyy laskea sulkeiden sisällä! Jos tuloa ei merkittäisi sulkeiden sisään, niin saataisiin

$\begin{align*} &(x+1)(x-2)(x+4) \\ &=x\cdot x + x\cdot (-2)+1\cdot x + 1\cdot (-2) \cdot (x+4) \\ &=x^2-2x+x-2(x+4) \\ &=x^2-x-2x-8 \\ &=x^2-3x-8, \end{align*}$

mikä on väärin!

Vastaus: x^3+3x^2-6x-8

Polynomien laskutoimitukset: tehtäviä

1.3 Binomikaavat

Edellisessä luvussa johdettiin harjoitustehtävänä niin sanotut binomikaavat, jotka ovat varsin käyttökelpoisia työkaluja jatkossa, kun sievennetään ja ratkaistaan polynomiyhtälöitä. Käydään binomikaavat paremmin läpi tässä luvussa, missä tarkoituksena on myös hyödyntää näitä kaavoja.

Lukujen ja summan neliölle voidaan johtaa binomikaava

$\begin{align*} (a+b)^2&=(a+b)(a+b)\\ &=a^2+ab+ba+b^2 \\ &=a^2+ab+ab+b^2 \\ &=a^2+2ab+b^2. \end{align*}$

Lukujen ja summan neliö

(a+b)^2=a^2+2ab+b^2

1.3.1 Esimerkki: summan neliö

Sievennä hyödyntäen summan neliön binomikaavaa.

$(\dfrac{1}{2}a+\pi)^2$
$(\sqrt{3}r+\sqrt{3}t)^2$

Ratkaisu:

$\begin{align*} &(x+1)^2 && |a=x, b=1 \\ &=x^2+2x\cdot 1+1^2 \\ &= x^2+2x+1 \end{align*}$

$\begin{align*} &(3x+2)^2 && |a=3x, b=2 \\ &=(3x)^2+2\cdot 3x \cdot 2 + 2^2 \\ &= 9x^2+12x+4 \end{align*}$

$\begin{align*} &(\dfrac{1}{2}a+\pi)^2 && |a=\dfrac{1}{2}a, b=\pi \\ &=(\dfrac{1}{2}a)^2+2\cdot \dfrac{1}{2}a \pi + \pi^2 \\ &= \dfrac{1}{4}a^2+a\pi+\pi^2 \end{align*}$

$\begin{align*} &(\sqrt{3}r+\sqrt{3}t)^2 && |a=\sqrt{3}r, b=\sqrt{3}t \\ &=(\sqrt{3}r)^2+2\sqrt{3}r\sqrt{3}t+(\sqrt{3}t)^2 \\ &= 3r^2+6rt+3t^2 \end{align*}$

Vastaus:

$\dfrac{1}{4}a^2+a\pi+\pi^2$

Lukujen ja erotuksen neliölle voidaan johtaa binomikaava

$\begin{align*} (a-b)^2&=(a-b)(a-b)\\ &=a^2-ab-ba+b^2 \\ &=a^2-ab-ab+b^2 \\ &=a^2-2ab+b^2. \end{align*}$

Lukujen ja erotuksen neliö

(a-b)^2=a^2-2ab+b^2

1.3.2 Esimerkki: erotuksen neliö

Sievennä hyödyntäen erotuksen neliön binomikaavaa.

$(\dfrac{1}{8}x+4y)^2$
$(\sqrt{5}x^2-\sqrt{7}e^3)^2$

Ratkaisu:

$\begin{align*} &(x-1)^2 && |a=x, b=1 \\ &=x^2-2x\cdot 1+1^2 \\ &= x^2-2x+1 \end{align*}$

$\begin{align*} &(4a-3b)^2 && |a=4a, b=3b \\ &=(4a)^2-2\cdot4a \cdot 3b + (3b)^2 \\ &= 16a^2-24ab+9b^2 \end{align*}$

$\begin{align*} &(\dfrac{1}{8}x+4y)^2 && |a=\dfrac{1}{8}x, b=4y \\ &=(\dfrac{1}{8}x)^2-2\cdot \dfrac{1}{8}x \cdot 4y + (4y)^2 \\ &= \dfrac{1}{64}x^2-xy+16y^2 \end{align*}$

$\begin{align*} &(\sqrt{5}x^2-\sqrt{7}e^3)^2 && |a=\sqrt{5}x^2, b=\sqrt{7}e^3 \\ &=(\sqrt{5}x^2)^2-2\cdot \sqrt{5}x^2 \cdot \sqrt{7}e^3 + (\sqrt{7}e^3)^2 \\ &= 5x^4-2\sqrt{35}e^3x^2+7e^6 \end{align*}$

Vastaus:

$\dfrac{1}{64}x^2-xy+16y^2$
$5x^4-2\sqrt{35}e^3x^2+7e^6$

Huomio!

Periaatteessa erotuksen neliö voitaisiin laskea myös summan neliön kaavalla, sillä (a-b)^2=(a+(-b))^2=a^2+2a(-b)+b^2=a^2-2ab+b^2.

Vastaavasti summan neliö voidaan muokata laskettavaksi erotuksen neliön kaavalla, sillä (a+b)^2=(a-(-b))^2=a^2-2a(-b)+(-b)^2=a^2+2ab+b^2.

Lukujen ja summan ja erotuksen tulolle voidaan johtaa binomikaava

$\begin{align*} (a+b)(a-b)&=a^2-ab+ba-b^2 \\ &=a^2-ab+ab-b^2 \\ &=a^2-b^2. \end{align*}$

Lukujen ja summan ja erotuksen tulo

(a+b)(a-b)=a^2-b^2

1.3.3 Esimerkki: summan ja erotuksen tulo

Sievennä hyödyntäen summan ja erotuksen binomikaavaa.

$(2a-\sqrt{3}b)(2a+\sqrt{3b})$
$(\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)(-\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)$
$(\dfrac{1}{3}x+\sqrt{2}y)^2(-\dfrac{1}{3}x+\sqrt{2}y)^2$

Ratkaisu:

$\begin{align*} &(x+1)(x-1) && |a=x, b=1 \\ &= x^2-1^2 \\ &= x^2-1 \end{align*}$

$\begin{align*} &(2a-\sqrt{3}b)(2a+\sqrt{3b}) && |a=2a, b=\sqrt{3}b \\ &= (2a)^2-(\sqrt{3}b)^2 \\ &= 4a^2-3b^2 \end{align*}$

$\begin{align*} &(\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e)(-\dfrac{1}{2}\sqrt{\pi}+\sqrt{9}e) \\ &= (\sqrt{9} e+\dfrac{1}{2}\sqrt{\pi})(\sqrt{9}e-\dfrac{1}{2}\sqrt{\pi}) && |a=\sqrt{9} e, b=\dfrac{1}{2}\sqrt{\pi}\\ &= (\sqrt{9}e)^2-(\dfrac{1}{2}\sqrt{\pi})^2\\ &= 9e^2-\dfrac{1}{4}\pi \end{align*}$

$\begin{align*} &(\dfrac{1}{3}x+\sqrt{2}y)^2(-\dfrac{1}{3}x+\sqrt{2}y)^2 \\ &=(\sqrt{2}y+\dfrac{1}{3}x)^2(\sqrt{2}y-\dfrac{1}{3}x)^2 \\ &=((\sqrt{2}y+\dfrac{1}{3}x)(\sqrt{2}y-\dfrac{1}{3}x))^2 && |\textrm{summan ja erotuksen tulo: }a=\sqrt{2}y,b=\dfrac{1}{3}x \\ &=((\sqrt{2}y)^2-(\dfrac{1}{3}x)^2)^2 \\ &=(2y^2-\dfrac{1}{9}x^2)^2 && |\textrm{erotuksen neliö: }a=2y^2,b=\dfrac{1}{9}x^2 \\ &= (2y^2)^2-2\cdot2y^2 \cdot \dfrac{1}{9} x^2+(\dfrac{1}{9}x^2)^2 \\ &= 4y^4-\dfrac{4}{9}x^2y^2+\dfrac{1}{81}x^4 \end{align*}$

Vastaus:

$9e^2-\dfrac{1}{4}\pi$
$4y^4-\dfrac{4}{9}x^2y^2+\dfrac{1}{81}x^4$

1.3.4 Esimerkki: binomikaavojen perustelut GeoGebralla

Seuraavan Geogebra -simulaation on tarkoitus perustella geometrisesti binomikaavat. Etene järjestyksessä (a+b)^2, (a-b)^2 ja (a+b)(a-b) . Haluamasi simulaation saat painamalla ylhäällä olevaa painiketta.

Neliön alimmaiselta sivulta löytyy musta piste, jonka avulla voit sääätää muuttujien ja arvoa. Simulaatiossa olevan ison neliön pinta-ala vastaa lauseketta .

Säädä pituudet ja mustan pisteen avulla sellaisiksi, että .
Ison neliön pinta-alan lauseke on binomikaavan nojalla $A_{iso}=(a+b)^2=a^2+2ab+b^2$ .
Vähennä tästä kokonaispinta-alasta näiden neljän vihreän suorakaiteen pinta-alat $A_{iso}-4A_{vihre\text{ä}}$ , jolloin saat punaisen neliön pinta-ala lausekkeen $A_{punainen}=(a-b)^2$ .

Tässä simulaatiossa et voi säätää muuttujien ja arvoa, vaan ne määritellään jo edellä aiemmissa simulaatioissa. Varmista, että joko ensimmäisessä tai toisessa simulaatiossa
Voit siirtää kuvassa olevia pientä keltaista neliötä tai sinistä neliötä sekä vihreätä suorakaidetta viemällä kursorin haluttuun kuvioon.
Kuvioita voi myös kääntää valitsemalla jokin kyseisen kuvion kärkipisteistä, jonka jälkeen kuviota voi kiertää haluamaansa suuntaan.
Yritä muodostaa siirtämällä pienempien neliöiden ja suorakaiteen avulla sellainen pinta-ala, joka havainnollistaa lauseketta .

1.3.5 Esimerkki: binomikaavojen hyödyntäminen toiseen suuntaan

Ilmaise polynomi

summan ja erotuksen tulona
binomin neliönä
$\dfrac{1}{4}a^6-4a^3+64$ binomin neliönä.

Ratkaisu:

Lukujen ja summan ja erotuksen binomikaavan mukaan . Summan ja erotuksen tulona saatu polynomimme on , joten ratkaistaan luvut ja yhtälöistä

$\begin{align*} a^2&=x^2 && |\sqrt{} \\ a&=\pm x \end{align*}$

$\begin{align*} b^2&=9 && |\sqrt{} \\ b&=\pm 3. \end{align*}$

Kun a=x ja b=3 , niin x^2-9=(x+3)(x-3) .

Toisaalta myös, jos a=-x ja b=3 , niin x^2-9=(-x+3)(-x-3) .

Lukujen ja summan neliön binomikaavan mukaan . Summan neliönä saatu polynomimme on , joten ratkaistaan luvut ja yhtälöistä

$\begin{align*} a^2&=4x^2 && |\sqrt{} \\ a&=\pm 2x \end{align*}$

$\begin{align*} b^2&=y^2 && |\sqrt{} \\ b&=\pm y. \end{align*}$

Polynomissamme on myös termi 4xy=2ab , josta voimme päätellä, että lukujen ja täytyy olla samanmerkkiset. Luvut a=2x ja b=y toteuttavat keskimäisen termin $2ab=2 \cdot 2x \cdot y=4xy$ sekä luvut a=-2x ja b=-y toteuttavat keskimäisen termin $2ab=2 \cdot (-2x) \cdot (-y)=4xy$ . Eli 4x^2+4xy+y^2=(2x+y)^2 tai 4x^2+4xy+y^2=(-2x-y)^2 .

Lukujen ja erotuksen neliön binomikaavan mukaan . Erotuksen neliönä saatu polynomimme on $\dfrac{1}{4}a^6-4a^3+64$ , joten ratkaistaan luvut ja yhtälöistä

$\begin{align*} a^2&=\dfrac{1}{4}a^6 && |\sqrt{} \\ a&=\pm \dfrac{1}{2}a^3 \end{align*}$

$\begin{align*} b^2&=64 && |\sqrt{} \\ b&=\pm 8. \end{align*}$

Polynomissamme on myös termi -4a^3=2ab , josta voimme päätellä, että lukujen ja täytyy olla erimerkkiset. Eli $\dfrac{1}{4}a^6-4a^3+64=(\dfrac{1}{3}a^3-8)^2$ tai $\dfrac{1}{4}a^6-4a^3+64=(-\dfrac{1}{3}a^3+8)^2$ .

Vastaus:

tai
tai
$\dfrac{1}{4}a^6-4a^3+64=(\dfrac{1}{2}a^3-8)^2$ tai $\dfrac{1}{4}a^6-4a^3+64=(-\dfrac{1}{2}a^3+8)^2$

(2x+y)^2 =4x^2 +4xy +y^2 eikä 4x^2 + 24xy + y^2...onko virhe?

— 21 Aug 22 (edited 21 Aug 22)

Virhe korjattu.

— 22 Aug 22

1.3.6 Esimerkki: päiväkoti probleema

Päiväkodin hoitaja huomasi, että neliönmuotoiset askartelupaperit ovat liian suuria tarhalaisten askarteluun. Hoitaja päätti ottaa käyttöön suorakuolmion muotoiset askarteluarkit, joiden yksi sivu on cm pidempi ja toinen sivu cm lyhyempi kuin neliöiden sivun pituudet. Kuinka paljon pienempi on pinta-alaltaan suorakaiteen muotoinen askartelupaperi kuin neliön muotoinen askartelupaperi?

Ratkaisu:

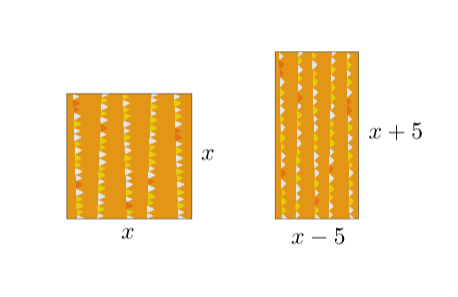
Olkoon neliön sivu. Tällöin neliön pinta-ala on $A_{1}=x^2\;(\text{cm}^2)$

Suorakulmion pinta-ala saadaan kannan ja korkeuden tulona, joten suorakulmion pinta-ala on

$\begin{align*} A_2&=(x+5)(x-5) \\ &=x^2-5^2 \\ &=x^2-25\;(\text{cm}^2) \end{align*}$

Lasketaan pinta-alojen erotus $A_1-A_2=x^2-(x^2-25)=x^2-x^2+25=25\;(\text{cm}^2)$

Vastaus: Suorakaiteen muotoinen askartelupaperi on pinta-alaltaan $25\;\text{cm}^2$ pienempi kuin neliön muotoinen askartelupaperi.

Binomikaavat: tehtäviä

1.4 Ensimmäisen asteen epäyhtälö

Reaalilukujen suurutta voidaan tutkia käyttämällä epäyhtälömerkkejä, joita ovat

$\begin{align*} &< \textrm{ pienempi kuin} \\ &\leq \textrm{ pienempi tai yhtä suuri kuin} \\ &> \textrm{ suurempi kuin} \\ &\geq \textrm{ suurempi tai yhtä suuri kuin} \end{align*}$

1.4.1 Esimerkki: muodosta luvuista epäyhtälö

Muodosta luvuista ja epäyhtälö, joka on

tosi
epätosi

Ratkaisu:

Luku on pienempi kuin , joten epäyhtälö on tosi.
Luku on pienempi tai yhtä suurikuin , joten epäyhtälö $1\leq 2$ on tosi.
Luku on suurempi kuin , joten epäyhtälö on tosi.
Luku on suurempi tai yhtä suuri kuin , joten epäyhtälö $2\geq 1$ on tosi.

Luku ei ole pienempi kuin , joten epäyhtälö on epätosi.
Luku ei ole pienempi tai yhtä suurikuin , joten epäyhtälö $2\leq 1$ on epätosi.
Luku ei ole suurempi kuin , joten epäyhtälö on epätosi.
Luku ei ole suurempi tai yhtä suuri kuin , joten epäyhtälö $1\geq 2$ on epätosi.

1.4.2 Esimerkki: epäyhtälön totuusarvo

Mikä on seuraavien väittämien totuusarvo?

$3\leq 3$
$-8\geq -8$

Ratkaisu:

Luku on suurempi kuin , joten on epätosi.
on yhtä suuri kuin , joten on epätosi.
on yhtä suuri kuin 3, joten $3\leq 3$ on tosi.
on yhtä suuri kuin , joten $-8\geq -8$ on tosi.

Ennen ensimmäisen asteen epäyhtälön käsittelyä palauta halutessassi aluksi mieleen ensimmäisen asteen yhälön teoria MAY1-kurssilta täältä.

Ensimmäisen asteen epäyhtälö

Ensimmäisen asteen epäyhtälö voidaan esittää muodossa ax+b<0,

missä on tuntematon ja a,b ovat vakioita, $a\neq0$ . Merkin tilalla voi olla myös jokin muu edellä esitetyistä neljästä epäyhtälömerkistä.

Epäyhtälön ratkaiseminen vastaa yhtälön ratkaisemista eli sallittuja operaatioita ovat puolittain luvun lisääminen ja vähentäminen. Myös puolittain kertominen ja jakaminen nollasta poikkeavalla luvulla ovat sallittua, mutta kun epäyhtälöä kerrottaan puolittain negatiivisella luvulla, niin epäyhtälömerkin suunta vaihtuu.

Perustelu

Epäyhtälömerkin suunnan vaihto voidaan perustella seuraavasti. Olkoon a>b .

$\begin{align*} a&>b && |-b \\ a-b&>0 && |\cdot c \text{, missä $c>0$}\\ c(a-b) &> c\cdot0 && \text{, sillä $c$ ja $a-b$ ovat positiivisia.} \\ ca-cb &> 0 && |+cb \\ ca &> cb \end{align*}$

Näin ollen, jos epäyhtälöä kerrotaan puolittain positiivisella luvulla , niin merkin suunta säilyy.

Jos c<0 , niin

$\begin{align*} c(a-b) &<0 && \text{, sillä negatiivisen ja positiivisen luvun tulo on negatiivinen.} \\ ca-cb &<0 && |+cb \\ ca&< cb \end{align*}$

Siispä, kun epäyhtälöä kerrotaan puolittain negatiivisella luvulla , niin merkin suunta vaihtuu.

Epäyhtälön ratkaiseminen

1) Puolittain lisääminen tai vähentäminen

$\begin{align*} 1 & < 2 && |+3 \\ 4 & < 5 && | -2 \\ 2 & < 3 \end{align*}$

$\begin{align*} -4x+3 & \geq -5x+3 && |-3 \\ -4x & \geq -5x && | +5x \\ x & \geq 0 \end{align*}$

2) Puolittain kertominen ja jakaminen nollasta eroavalla luvulla

$\begin{align*} 4 & > -4 && | :2 \\ 2 & > -2 && | \cdot (-10) \textrm{, merkin suunta vaihtuu} \\ -20 & < 20 \end{align*}$

$\begin{align*} 6x+9 & \leq 3x+9 && |:(-3) \textrm{, merkin suunta vaihtuu} \\ -2x-3 & \geq -x-3 && |\cdot (-1) \textrm{, merkin suunta vaihtuu} \\ 2x+3 & \leq x+3 \end{align*}$

3) Yhtälön puolien vaihtaminen keskenään

$\begin{align*} 2x+1 &< 4x && \;\\ 4x &> 2x+1 && \end{align*}$

1.4.3 Esimerkki: epäyhtälön ratkaiseminen algebrallisesti

Ratkaise epäyhtälö

$-3x+8\leq -1$
$-\dfrac{2}{3}x+2>-\dfrac{2}{3}x+2$
$x-1 \geq x$

Ratkaisu:

$\begin{align*} 2x+1 & <3 && | -1 \\ 2x & < 2 && | :2 \\ x & < 1 \end{align*}$

$\begin{align*} -3x+8 & \leq -1 && | -8 \\ -3x & \leq -9 && | :(-3), \textrm{ merkin suunta vaihtuu} \\ x & \geq 3 \end{align*}$

$\begin{align*} -\dfrac{2}{3}x+2 &> -\dfrac{2}{3}x+1 && | + \dfrac{2}{3}x \\ 2 &> 1 && \\ \end{align*}$

Luku on suurempi kuin luku riippumatta muuttujasta . Näin ollen epäyhtälön $-\dfrac{2}{3}x+2 > -\dfrac{2}{3}x+1$ toteuttavat kaikki reaaliluvut.

$\begin{align*} x-1 & \geq x && | -x \\ -1 \geq 0 \\ \end{align*}$

ei ole suurempi tai yhtä suuri kuin . Näin ollen yhtälöllä $x-1 \geq x$ ei ole olemassa ratkaisua.

Vastaus:

$x\geq 3$
$x \in \mathbb{R}$
Ei ratkaisua

1.4.4 Esimerkki: epäyhtälön ratkaiseminen graafisesti

Ratkaise graafisesti epäyhtälöt

$-2x+2 \leq 6x-2$
$-2x \geq -2x-1$
$4x+2 > 4x+\pi$

Ratkaisu:

Piirretään geogebralla suorat $\textcolor{red}{y_1=x+1}$ ja $\textcolor{blue}{y_2=-x-1}$ .

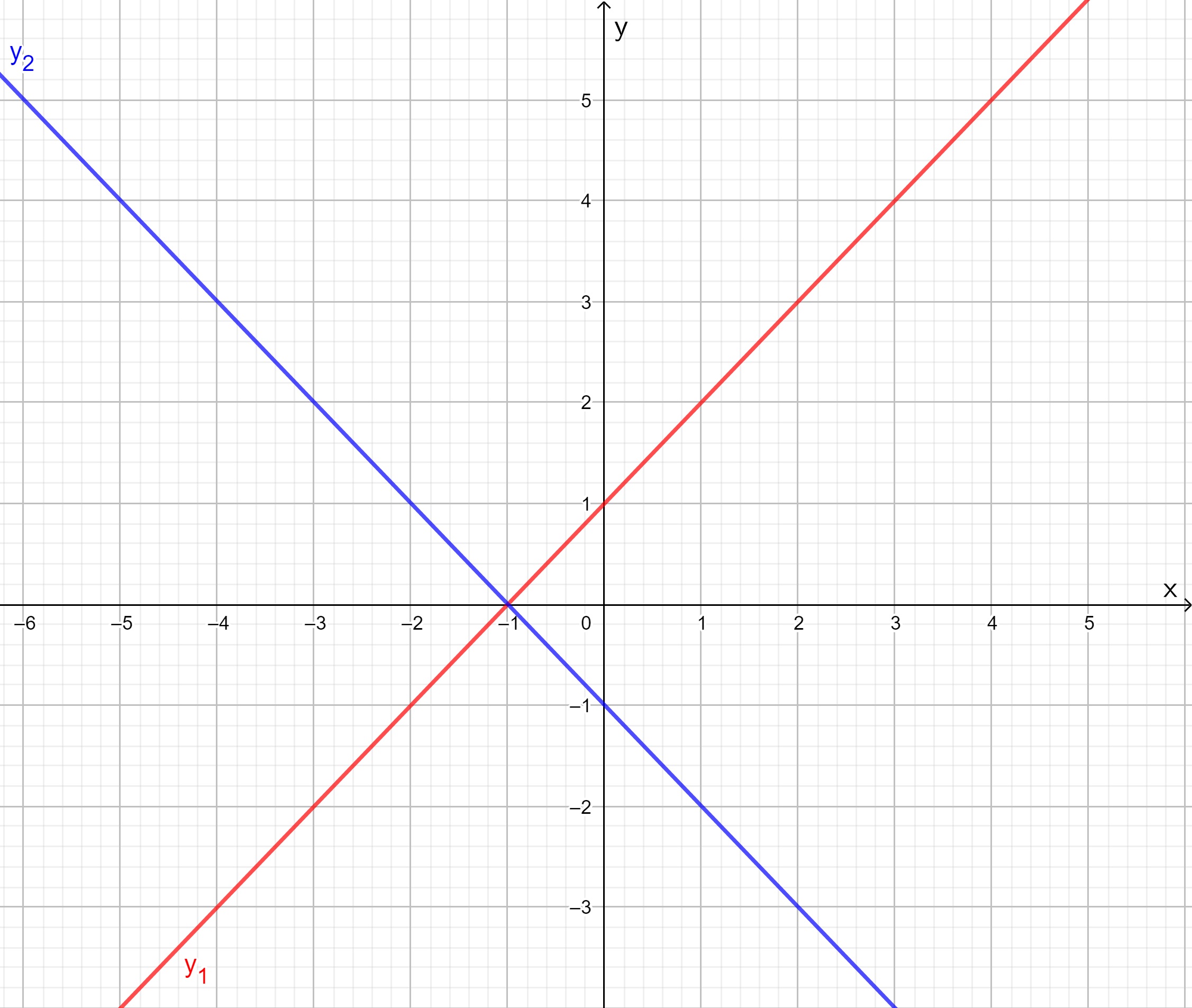
Geometrisesti tulkittuna epäyhtälö $\textcolor{red}{x+1}<\textcolor{blue}{-x-1}$ tarkoittaa niitä -tason pisteitä, missä suora $\textcolor{red}{y_1=x+1}$ saa suoraa $\textcolor{blue}{y_2=-x-1}$ pienempiä arvoja. Toisin sanoen niitä pisteitä, missä $\textcolor{red}{y_1=x+1}$ on suoran $\textcolor{blue}{y_2=-x-1}$ alapuolella.

Kuvasta huomataan, että suorat leikkaavat pisteessä (x,y)=(-1,0) mitä ennen $\textcolor{red}{y_1}$ saa suoraa $\textcolor{blue}{y_2}$ pienempiä arvoja. Vaikkakin yhden muuttujan epäyhtälö geometrisesti tulkitaankin kaksiulotteisen -avaruuden avulla, niin olemme kiinnostuneita vain suoran pisteistä. Epäyhtälön ratkaisu on siis x<-1.

Piirretään geogebralla suorat $\textcolor{red}{y_1=-2x+2}$ ja $\textcolor{blue}{y_2=6x-2}$ .

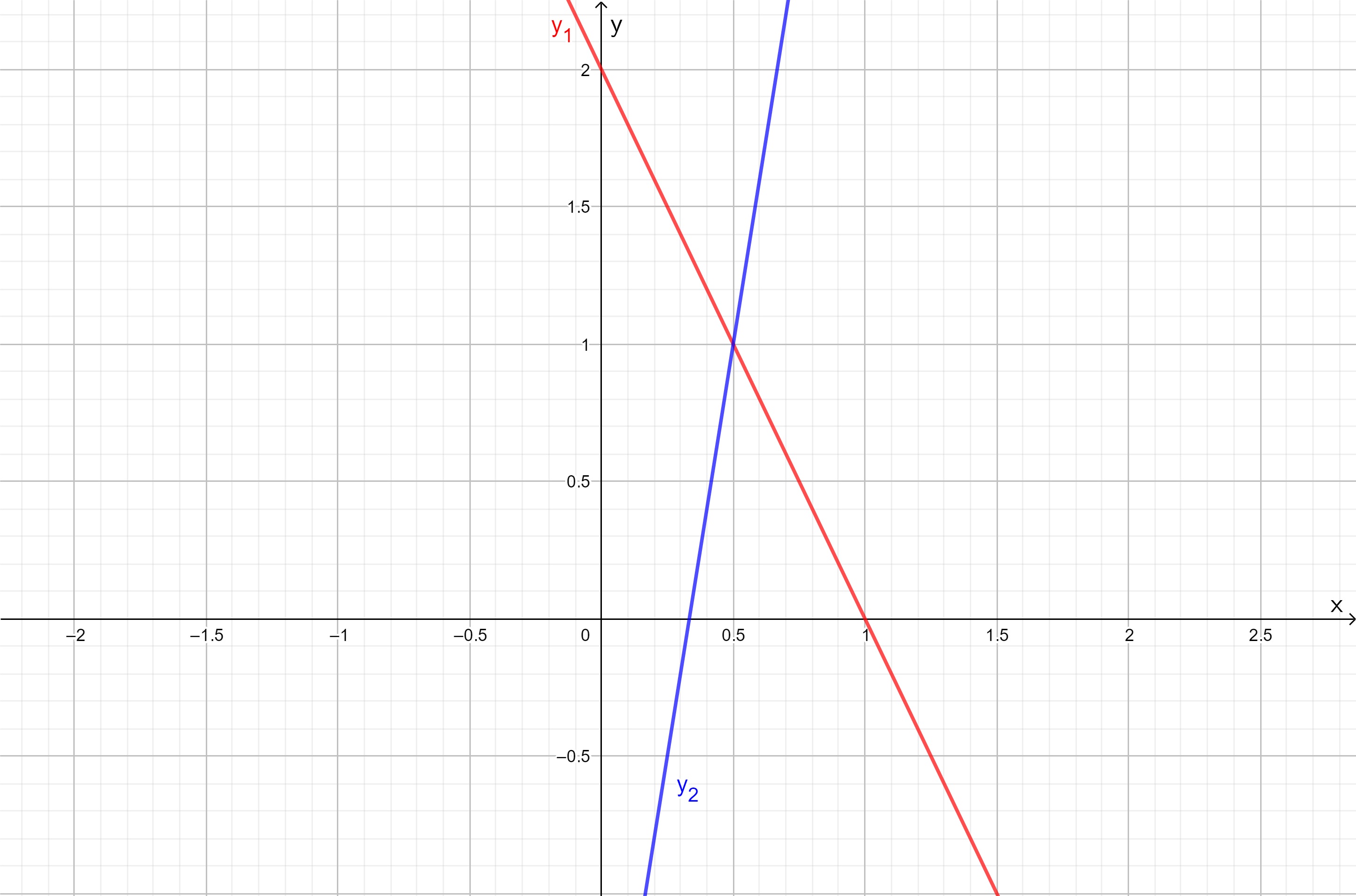
Kuvasta huomataan, että $\textcolor{red}{-2x+2} \leq \textcolor{blue}{6x-2}$ , kun $x\geq0,5$ .

Piirretään geogebralla suorat $\textcolor{red}{y_1=-2x}$ ja $\textcolor{blue}{y_2=-2x-1}$ .

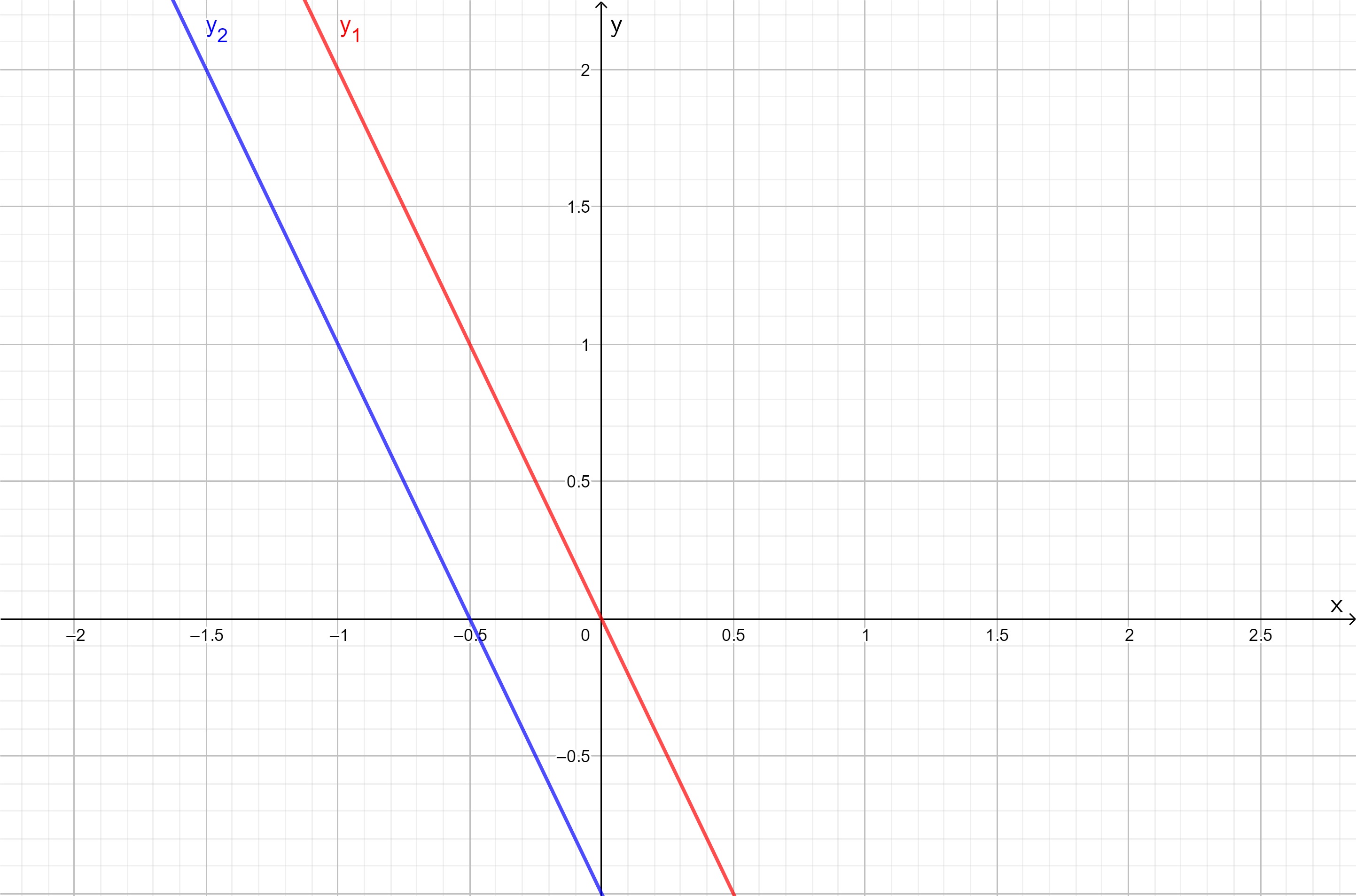
Kuvan perusteella näyttäisi siltä, että suora $\textcolor{red}{-2x}\ge \textcolor{blue}{-2x-1}$ . Tämä on odotettu tulos, sillä kyseessä ovat suorat, joilla on sama kulmakerroin. Näin ollen suorat eivät leikkaa toisansa tai ne leikkaavat äärettömän monessa pisteessä. Suorat eivät ole samat, joten $\textcolor{red}{-2x}\ge \textcolor{blue}{-2x-1}$ kaikilla $x\in \mathbb{R}$ .

Piirretään geogebralla suorat $\textcolor{red}{4x+2}$ ja $\textcolor{blue}{y_2=4x+\pi}$ .

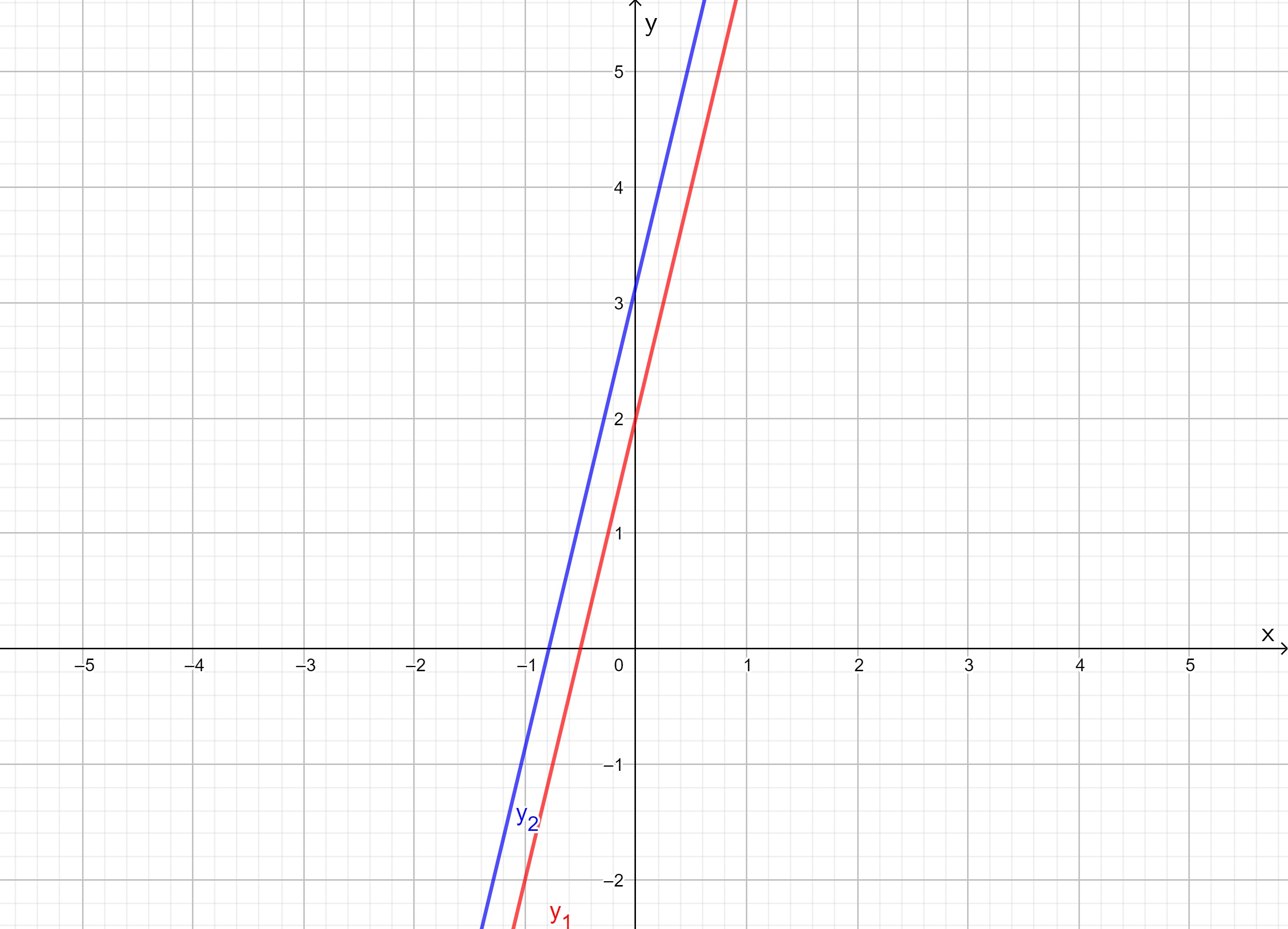
Kuvan perusteella $\textcolor{blue}{y_2}>\textcolor{red}{y_1}$ kaikilla $x\in\mathbb{R}$ . Suorilla on sama kulmakerroin, joten ne eivät leikkaa. Näin ollen epäyhtälö $\textcolor{red}{4x+2}> \textcolor{blue}{4x+\pi}$ on epätosi.

Vastaus:

$x\geq 0,5$
$x\in \mathbb{R}$
Ei ratkaisua

Merkkisääntöjä

Olkoon suora f(x)=ax+b, missä $a\neq 0$ .

Suoran nollakohta voidaan ratkaista yhtälöstä ax_0+b=0 ja saadaan $x_0=-\dfrac{b}{a}.$

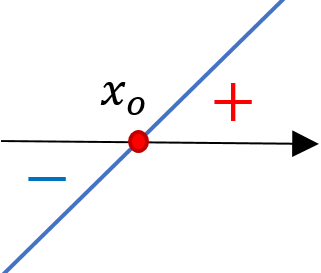
Jos suora on nouseva eli a>0 , niin suora saa positiivisia arvoja, kun x>x_0 ja negatiivisia arvoja, kun x<x_0 .

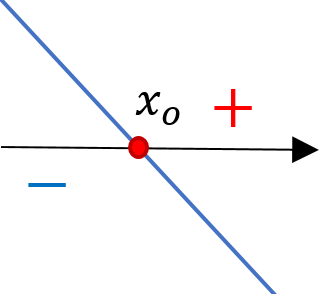
Jos suora on laskeva eli a<0 , niin suora saa negatiivisia arvoja, kun x>x_0 ja positiivisia arvoja, kun x<x_0 .

1.4.5 Esimerkki: merkkisääntöjä

Millä muuttujan arvolla

saa positiivisen arvon?
saa negatiivisen arvon?

Ratkaisu:

Ratkaistaan funktion nollakohta.

$\begin{align*} x-1 &= 0 && |+1 \\ x &= 1 \end{align*}$

Suora x-1 on nouseva suora, joten se saa positiivisia arvoja nollakohdan oikealla puolella eli kun x>-1

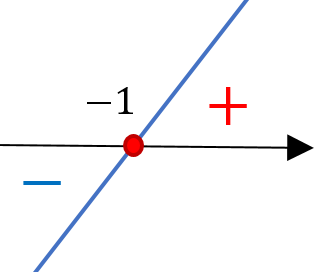
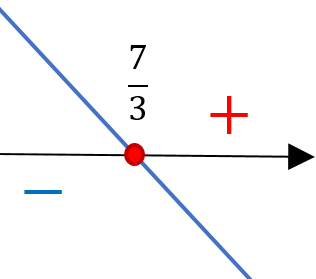
Ratkaistaan funktion nollakohta.

$\begin{align*} -3x+7 &= 0 && |-7 \\ -3x &= -7 && | :(-3) \\ x&= \dfrac{7}{3} \end{align*}$

Suora -3x+7 on laskeva suora, joten se saa negatiivisia arvoja nollakohdan oikealla puolella eli kun $x>\dfrac{7}{3}$ .

Vastaus:

$x> \dfrac{7}{3}$

1.4.6 Esimerkki: Sannin koulumatka

Eräänä päivänä Sanni kulki kotiintulo matkansa koulusta oikoreittiä ja hän huomasi, että se oli noin sekuntia nopeampi kuin hänen tavanomaisesti kulkema reittinsä. Toisena päivänä hän päätti testata toista oikoreittiä ja totesi, että aikaa kului noin puolet vähemmän verrattuna tavanomaiseen reittiin. Kuinka paljon Sannilla kuluu tavanomaisen reitin kulkemiseen, jos toinen oikoreitti on nopeampi kuin ensimmäinen oikoreitti?

Ratkaisu:

Olkoon $x=\text{"Aika, joka kuluu tavanomaisen reitin kulkemiseen" (s)}$

Näin ollen ensimmäiseen oikoreittiin kuluva aika on $x-50\;(s)$ ja toiseen $0,5x\;(s).$

Tiedämme, että toinen oikoreitti on nopeampi kuin ensimmäinen, joten voidaan muodostaa ja ratkaista epäyhtälö

$\begin{align*} 0,5x &< x-50 && |-x\\ -0,5x & < -50 && |:(-0,5)\text{, merkin suunta vaihtuu} \\ x > 100 \end{align*}$

Näin ollen Sannilla täytyy kulua enemmän kuin 100 sekuntia tavanomaiseen koulumatkaan, että toinen oikoreitti olisi nopeampi.

Vastaus: Sannilla kuluu enemmän kuin 100 sekuntia alkuperäisen koulumatkan kulkemiseen.

1.4.7 Esimerkki: itseisarvo ja epäyhtälö

Ratkaise epäyhtälö

$\mid4-x\mid>5$
$\mid 3x -2\mid< 3$
$\mid 3x -2\mid< -3$

Ratkaisu:

Itseisarvolauseke on suurempi kuin , jos itseisarvon sisällä oleva lauseke on suurempi kuin . Näin ollen muodostamme ja ratkaisemme epäyhtälön

$\begin{align*} 4-x &> 5 && |+x-5 \\ x & < -1 \end{align*}$

Toisaalta itseisarvolauseke saa lukua suuremman arvon, jos itseisarvon sisällä oleva lauseke on pienempi kuin . Muodostetaan ja ratkaistaan epäyhtälö

$\begin{align*} 4-x &< -5 && |+x+5 \\ x & > 9 \end{align*}$

Alkuperäisen itseisarvoepäyhtälö toteutuu, kun molemmat epäyhtälöt ovat tosia eli kun x<-1 ja x>9 .

Sininen väri vastaa tehtävänannon ratkaisujoukkoa ja .

x<-1 — Sininen väri vastaa tehtävänannon ratkaisujoukkoa ja .

Itseisarvolauseke on pienempi kuin , jos itseisarvon sisällä oleva lauseke on suurempi kuin ja pienempi kuin . Voitaisiin ratkaista vastaavasti kuin a)-kohdassakin jakamalla itseisarvoepäyhtälö kahdeksi epäyhtälöksi, mutta ratkaistaan tämä nyt vaihtelun vuoksi suoraan kaksoisepäyhtälön avulla.

$\begin{align*} -3 &< 3x-2 < 3 && |+2\\ -1 &< 3x < 5 && |:3\\ -\dfrac{1}{3} &< x < \dfrac{5}{3} \end{align*}$

Sininen väri vastaa tehtävänannon ratkaisujoukkoa

Heti voidaan todeta, että itseisarvo ei saa negatiivisia arvoja, joten epäyhtälöllä $\mid 3x -2\mid< -3$ ei ole ratkaisua.

Vastaus:

ja
$-\dfrac{1}{3} < x < \dfrac{5}{3}$
Ei ratkaisua

Epäyhtälöitä voidaan myös merkitä lukuvälin avulla. Oheisissa kuvissa punaisella värjätty alue kuvastaa lukuvälin reaalilukuja .

Kuva	Epäyhtälö	Lukuväli
	$a\leq x \leq b$	$\text{ }$
		$\text{ }$
	$a<x \leq b$	$\text{ }$
	$a\leq x < b$	$\text{ }$

Jos lukuväli on toisesta päästä rajoittamaton, niin voidaan lukuväli merkinnässä käyttää äärettömyyden symbolia $\infty$ .

Kuva	Epäyhtälö	Lukuväli
	$x \geq a$	$\text{ }$ $[a,\infty]$
		$\text{ }$ $]a,\infty[$
	$x\leq a$	$]-\infty,a]$
		$]-\infty,a[$

Ensimmäisen asteen epäyhtälö: tehtäviä