1. Polynomilaskentaa: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Polynomilaskentaa. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

1.1 Polynomien peruskäsitteet: tehtäviä

Tämän kappaleen teoria.

1.1.1 Tehtävä

Mitkä seuraavista lausekkeista ovat polynomeja?

# Plugin1

1.1.2 Tehtävä

Määritä polynomin $-13x^5-x^3+22x^2+x-\dfrac{1}{2}$

# seq1_1

# seq1_2

# seq1_3

# seq1_4

1.1.3 Tehtävä

Laske polynomifunktion f(x)=-2x^3+x^2+3x-2 arvo, kun

# seq2_1

# seq2_2

# seq2_3

# seq2_4

1.1.4 Tehtävä

Muodosta muuttujan viidennen asteen polynomi, jonka korkeimman asteen kerroin on $\dfrac{1}{2}$ , neljännen ja kolmannen asteen kertoimet ovat , toisen asteen kerroin on , ensimmäisen asteen kerroin on $-3\pi$ ja vakiotermi on $\sqrt{2}$ .

# seq2_5

Vihje

Viidennen asteen muuttujan polynomi on muotoa a_5z^5+a_4z^4+a_3z^3+a_2z^2+a_1z+a_0 oleva lauseke, missä a_0 on vakiotermi. Sijoita lausekkeeseen $a_5=\dfrac{1}{2}$ , a_4=0 , a_3=0 , a_2=-7 , $a_1=-3\pi$ ja $a_0=\sqrt{2}$ . Nollautuvat termit kuten 0x^4=0 voidaan luonnollisesti sievennetystä muodosta jättää pois.

1.1.5 Tehtävä

Polynomit ovat yhtä suuret täsmälleen silloin, jos niiden vastinkertoimet ovat samat. Määritä sellainen vakio , että polynomit $P(x)=ax^2-x^2+7x-\sqrt{3}$ ja $Q(x)=3x^2+7x-\sqrt{3}$ ovat samat.

# seq3_1

Vihje

Muokataan polynomi P(x) muotoon $P(x)=ax^2-x^2+7x-\sqrt{3}=(a-1)x^2+7x-\sqrt{3}$ .

Polynomien P(x) ja Q(x) kertoimien tulee olla yhtäsuuret, joten muodostetaan ja ratkaistaan yhtälöryhmä

\[\begin{cases} a-1=3\\ 7=7 \\ -\sqrt{3}=-\sqrt{3} \end{cases}\]

1.1.6 Tehtävä

Määritä kahden muuttujan polynomifunktion (ns. satulapinnan) z(x,y)=x^2-y^2

# seq4_1

Vihje

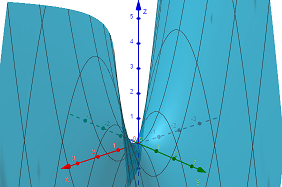
Useamman muuttujan polynomifunktion asteluku saadaan korkeimman asteen termin mukaan. Nyt polynomifunktiolla on samanasteiset termit x^2 ja -y^2 .

# seq4_2

Vihje

Sijoita $(x,y)=(2,\dfrac{5}{2})$ kahden muuttujan polynomifunktioon z(x,y)=x^2-y^2 . Eli toisin sanoen mikä on lausekkeen x^2-y^2 arvo, kun x=2 ja $y=\dfrac{5}{2}$ .

1.2 Polynomien laskutoimitukset: tehtäviä

Tämän kappaleen teoria.

Ohje tehtäviin vastaamiseen:

MathCheck ei osaa tunnistaa useamman muuttujan tuloa ilman kertomerkkiä, jonka vuoksi esimerkiksi lyhennetty merkintä muuttujien ja välisestä tulosta täytyy merkitä joko kertomerkin x*y tai välilyönnin avulla x y vastauksessa. Numeron ja muuttujan välisen tulon väliin ei tarvitse merkitä kertomerkkiä, sillä MathCheck osaa tunnistaa esimerkiksi termin tuloksi ilman tähtimerkkiä.

Ratkaisuissa MathCheck ilmoittaa useamman muuttujen välisen tulon kertomerkkien avulla lausuttuna, vaikka yleensä merkitään lyhyesti esimerkiksi $x\cdot y\cdot z=xyz$ .

1.2.1 Tehtävä

Yhdistä lausekkeisiin oikea sievennetty muoto.

# MAA5_1b

1.2.2 Tehtävä

Sievennä.

# seq5_1

# seq5_2

# seq5_3

# seq5_4

1.2.3 Tehtävä

Laske binomien 7a-1 ja -2a+3

# seq6_1

# seq6_2

Vihje

Jos ei erikseen mainita, niin laskutoimitus suoritetaan siinä järjestyksessa, kuin se on annettu. Eli esimerkiksi lukujen ja summa on lauseke a+b ja erotus a-b . Joskin yhteenlaskussa ei ole väliä laskujärjestyksellä, sillä a+b=b+a .

Kuitenkin, vähennyslaskussa eli erotuksessa laskujärjestyksen kanssa pitää olla tarkkana, sillä esimerkiksi lukujen ja erotus 4-1=3 . Toisin päin laskettuna lauseke olisi $1-4=-3\neq3$ .

Tehtävänannon mukaiset lausekkeet ovat

1.2.4 Tehtävä

Sievennä.

# seq7_1

# seq7_2

# seq7_3

# seq7_4

1.2.5 Tehtävä

Sievennä.

# pollasku1_1

# pollasku1_2

# pollasku1_3

# pollasku1_4

1.2.6 Tehtävä

Johda seuraavassa kappaleessa tulevat binomikaavat sieventämällä seuraavat lausekkeet.

# binomi1

# binomi2

# binomi3

1.2.7 Tehtävä

Sievennä.

# pollasku2_1

# pollasku2_2

# pollasku2_3

1.2.8 Tehtävä

Jääkiekkokaukalon pinta-alasta saa melko hyvän arvion, kun arvioi sen olevan suorakulmio. Vielä paremman arvion saa, kun arvioi kaukalon ulkopuolelle jäävän pinta-ala osuuksien muodostuvan kolmioista ja vähentää suorakulmion pinta-alasta.

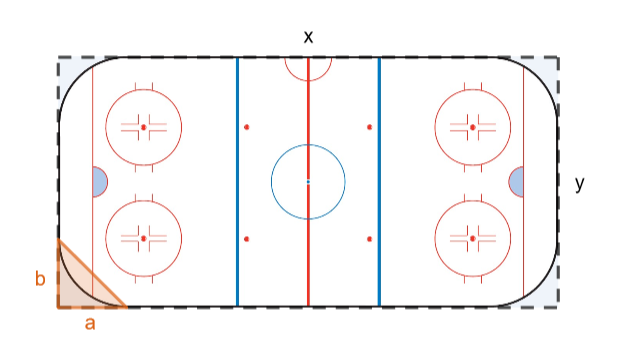
a) Muodosta jääkiekkokaukalon pinta-alan funktio A_S(x,y) , kun oletetaan jääkiekkokaukalon olevan suorakulmio.

# polkaukalo1_1

b) Muodosta ylimenevän osuuden (kaikki kolmiot!) pinta-ala funktio A_K(a,b) .

# polkaukalo1_2

c) Muodosta kaukalon pinta-alan funktio A(a,b,x,y) , kun otamme huomioon nämä ylimenevät osuudet.

# polkaukalo1_3

d) Laske Hakametsän kaukalon pinta-ala. Hakametsän kentän sivujen pituudet ovat m ja m. Lisäksi, kolmiot ovat tasakylkisiä kolmioita, joiden sivujen pituudet ovat m.

# polkaukalo1_4

1.3 Binomikaavat: tehtäviä

Tämän kappaleen teoria.

Ohje tehtäviin vastaamiseen:

Käytä tarvittaessa desimaalierottimena pistettä. Esimerkiksi 1,4=1.4.

1.3.1 Tehtävä

# Maakaksitehtavanelja

1.3.2 Tehtävä

Laske seuraavat lausekkeet lukujen ja summan ja erotuksen binomikaavalla.

# binomikaavatehtavatekaa

# binomikaavatehtavatekab

# binomikaavatehtavatekac

# binomikaavatehtavatekad

1.3.3 Tehtävä

Laske seuraavat lausekkeet summan neliön binomikaavalla.

# binomikaavatehtavattokaa

# binomikaavatehtavattokab

# binomikaavatehtavattokac

# binomikaavatehtavattokad

1.3.4 Tehtävä

Laske seuraavat lausekkeet erotuksen neliön binomikaavalla.

# binomikaavatehtavatkolmasa

# binomikaavatehtavatkolmasb

# binomikaavatehtavatkolmasc

# binomikaavatehtavatkolmasd

1.3.5 Tehtävä

Sievennä.

# binomikaavatehtavatkahdekasa

# binomikaavatehtavatkahdekasb

# binomikaavatehtavatkahdekasc

# binomikaavatehtavatkahdeksasd

1.3.6 Tehtävä

Sievennä.

# binomikaavatehtavatneljasa

# binomikaavatehtavatneljasb

# binomikaavatehtavatneljasc

# binomikaavatehtavatneljasd

1.3.7 Tehtävä

Laske binomikaavojen avulla.

# binomikaavatehtavatviidesa

Vihje

101^2=(100+1)^2

# binomikaavatehtavatviidesb

Vihje

$103\cdot97=(100+3)(100-3)$

# binomikaavatehtavatviidesc

Vihje

997^2=(1000-3)^2

# binomikaavatehtavatviidesd

Vihje

$1400^2-400^2=(1400-400)(1400+400)=1000\cdot1800$

1.3.8 Tehtävä

Janne järjesti uuden yksiönsä kunniaksi tupaantulijaiset. Hän kutsui kaveriansa, jotka väittivät, että asunnossa oli täsmälleen yksi asuinhuoneiston neliömetri vierasta kohden. Alempana on pohjapiirrustus Jannen asunnosta, missä ruskea pinta-ala A_h on huoneiston pinta-ala ja A_v vessan pinta-ala.

# binomikaavatehtavatkuudes

Vihje

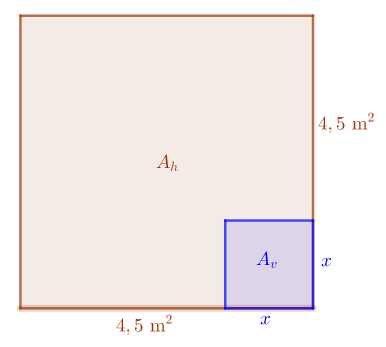
Pohjapiirrustuksen perusteella asunto on neliö, jonka sivun pituus on $4,5+x \text{ (m)}$ . Näin ollen huoneiston pinta-alalle saadaan lauseke $A_h=(4,5+x)^2-x^2 \text{ }(\text{m}^2).$ Vieraat väittivät, että asunnossa oli neliömetri vierasta kohden, joten huoneiston pinta-alan tulee olla $30\cdot 1=30\text{ }(\text{m}^2)$ .

Tästä saadaan muodostettua yhtälö A_h=30, josta voidaan ratkaista muuttuja ja sen avulla laskea kysytty pinta-ala $\dots$

1.3.9 Tehtävä

Havaitsimme kurssilla MAY1, että luvun ja yhtä pienemmän luvun neliöiden erotus on yhtä suuri kuin näiden lukujen summa. Esimerkiksi $5^2-4^2=5+4=9\;\;\;\text{ja}$ 1000^2-999^2=1000+999=1999

Alapuolella on osoitettu, että tulos pätee yleisesti reaaliluvuilla. Numeroi osoituksen vaiheet oikeaan järjestykseen 1-5 .

# 139d

# p139b

# 139e

# p139a

# p139c

1.3.10 Tehtävä

Määritä sellainen kolmannen asteen polynomi P(x) , joka toteuttaa ehdon 2P(x)-(2x+3)^2=2x^3-x^2-7x+5.

# binomikaavatehtavatseitsemass

Vihje

Kolmannen asteen polynomi on muotoa P(x)=ax^3+bx^2+cx+d . Sijoita tämä yhtälöön ja sievennä.

Ratkaisu

$\begin{align*} 2P(x)-(2x+3)^2&=2x^3-x^2-7x+5 \\ 2(ax^3+bx^2+cx+d)-(4x^2+12x+9)&=2x^3-x^2-7x+5 \\ 2ax^3+2bx^2+2cx+2d-4x^2-12x-9&= 2x^3-x^2-7x+5 \\ 2ax^3+2bx^2-4x^2+2cx-12x+2d-9 &= 2x^3-x^2-7x+5 \\ (2a)x^3+(2b-4)x^2+(2c-12)x+(2d-9) &= (2)x^3+(-1)x^2+(-7)x+(5) \end{align*}$

Polynomit ovat yhtä suuret täsmälleen silloin, kun niiden vastinkertoimet ovat yhtäsuuret. Tästä saadaan yhtälöryhmä

\[\begin{cases} 2a=2\\ 2b-4=-1 \\ 2c-12=-7 \\ 2d-9=5 \end{cases}\]

jonka ratkaisu (laskimesta) on

\[\begin{cases} a=1\\ b=\frac{3}{2} \\ \ c=\frac{5}{2} \\ d=7 \end{cases}\]

\end{cases}

Näin ollen $P(x)=x^3+\dfrac{3}{2}x^2+\dfrac{5}{2}x+7.$

1.4 Ensimmäisen asteen epäyhtälö: tehtäviä

Tämän kappaleen teoria.

Ohje tehtäviin vastaamiseen:

Suurempi tai yhtä suuri kuin merkin $\geq$ syöte vastauskentissä on .
Pienempi tai yhtä suuri kuin merkin $\leq$ syöte on .
Syötä murtoluvut murtolukumuodossa .

1.4.1 Tehtävä

# Ekanasteenepayhtalovirhe

1.4.2 Tehtävä

# MAA2_2

Vihje

Neliöjuurifunktio ei ole määritelty, kun neliöjuuren sisällä oleva lauseke saa negatiivisia arvoja. Ratkaise siis epäyhtälö $x-5\geq0$ , niin saat yhden ehdon.

Rationaalilauseke on määritelty, kun nimittäjä saa nollasta poikkeavan arvon, koska nollalla jakoa ei ole määritelty reaaliluvuilla. Eli edellisen ehdon lisäksi tulee olla voimassa $x\neq 0$ .

1.4.3 Tehtävä

Mikä on epäyhtälön totuusarvo?

# Plugin2

1.4.4 Tehtävä

Mitkä seuraavista luvuista ovat välillä $[-4,5; -\pi[$ ?

# Plugin3

1.4.5 Tehtävä

Ratkaise epäyhtälö.

# 1asteenepayhtekaa

# 1asteenepayhtekab

$-\dfrac{1}{2}x+\dfrac{1}{3}\leq -2$

# 1asteenepayhtekab2

$\dfrac{2x}{3}-\dfrac{1}{4}\leq \dfrac{x}{2}$

# 1asteenepayhtekab3

1.4.6 Tehtävä

Mikä luonnollinen luku toteuttaa molemmat epäyhtälöt 1-5n>0 ja 6+6n>4 ?

# 1asteenepayhtekab4

1.4.7 Tehtävä

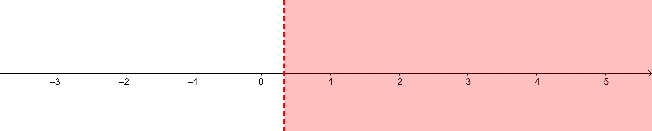
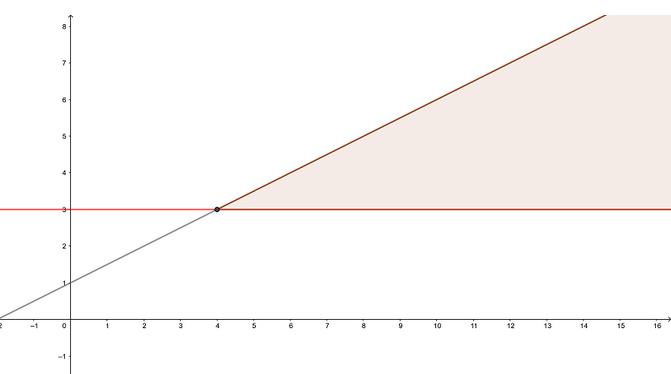
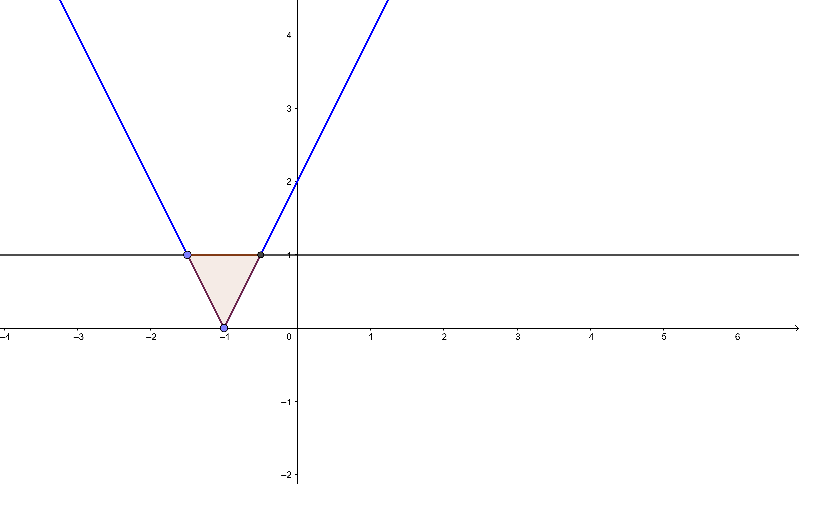
Alla on neljä epäyhtälöä sekä kolme kuviota. Kirjoita jokaisen kuvion alapuolella olevaan ruutuun sen epäyhtälön kirjain, jonka ratkaisu vastaa parhaiten kyseistä kuviota.

$\dfrac{1}{2}x+1>3$
$|-\dfrac{1}{3}x^4-2x^2-7|<0$

# 1asteenepayhtyhdistac

# 1asteenepayhtyhdistaa

# 1asteenepayhtyhdistab

1.4.8 Tehtävä

Millä vakion arvoilla epäyhtälö 4x+a<4(x+a)+1

toteutuu kaikilla muuttujan arvoilla

# 1asteenepayhtvikaa

ei toteudu millään muuttujan x arvoilla?

# 1asteenepayhtvikaa2

1.4.9 Tehtävä

Olkoon funktio f(x)=|x+3|-3 .

# epyhtalonollakohdatekaa

Vihje

Funktio f(x)=|x+3|-3 voidaan jakaa kahteen osaan itseisarvon sisällä olevan lausekkeen perusteella:

Kun $x\geq-3$ , niin f(x)=x+3-3=x .

Kun $x\leq -3$ , niin f(x)=-(x+3)-3=-x-3-3=-x-6.

Näin ollen voidaan ilmaista funktio

$\begin{align*} f(x)= \begin{cases} x,\;\;\;\;\;\;\;\;\; \text{ kun } x\geq-3\\ -x-6, \text{ kun } x\leq -3 \end{cases} \end{align*}$

Tämän jälkeen merkitään lausekkeet ja -x-6 nolliksi.

Ratkaisu

Vihjeen perusteella merkitään f(x)=0 , kun $x\leq-3$ :

$\begin{align*} -x-6&= 0 \\ x &= -6 \end{align*}$

$x=-6\leq-3$ , joten se kelpaa ratkaisuksi.

Merkitään sitten f(x)=0 , kun $x\geq-3$ :

$\begin{align*} x &= 0 \end{align*}$

$x=0\geq -3$ , joten myös se kelpaa ratkaisuksi.

# p149b

Vihje

Ratkaise epäyhtälö f(x)>0 .

Ratkaisu

Kun $x\leq -3$ , niin f(x)=-x-6 . Ratkaistaan milloin se saa negatiivisia arvoja.

$\begin{align*} -x-6 &< 0\\ x&> -6 \end{align*}$

Kun $x \geq -3$ , niin f(x)=x . Tämä saa negativiisia arvoja, kun x<0 .

Kun yhdistetään molemmat tulokset, saadaan vastaukseksi -6<x<0 .

# p149c

Vihje

Ratkaise epäyhtälö f(x)<0 tai päättele vastaus - ja -kohdan perusteella.

Ratkaisu

a)-kohdan mukaan funktion f(x) nollakohdat ovat x=0 ja x=-6 , joten näissä pisteissä f(x) ei saa positiivisia arvoja.

b)-kohdan mukaan f(x) saa negatiivisia arvoja, kun -6<x<0 .

Näin ollen f(x) saa positiivisia arvoja, kun x<-6 tai x>0 .