4. Korkeamman asteen polynomiyhtälö ja -funktio

Tässä kappaleessa siirrytään toisen asteen polynomifunktiosta yleiseen polynomifunktioon. Kappaleessa opitaan ratkaisemaan korkeamman asteen polynomiyhtälöitä sekä -epäyhtälöitä. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

4.1 Korkeamman asteen polynomifunktio ja -yhtälö

Tähän mennessä on tutustuttu ensimmäisen asteen polynomifunktioihin, jotka ovat muotoa f(x)=ax+b, ja toisen asteen polynomifunktioihin, jotka ovat muotoa f(x)=a^2+bx+c . Jos polynomin asteluku on tai enemmän, sitä kutsutaan korkemman asteen polynomiksi.

Yleinen polynomifunktio

Olkoon positiivinen kokonaisluku ja $a_n\neq0$ . Yleinen nnen asteen polynomifunktio voidaan esittää muodossa

$f(x)=a_nx^n+a_{n-1}x^{n-1}+\dots+a_1x+a_0.$

Aiemmin on havaittu, että toisen asteen polynomifunktiolla on korkeintaan kaksi ja ensimmäisen asteen polynomifunktiolla yksi nollakohta. Samoin astetta olevalla polynomifunktiolla on enintään nollakohtaa.

4.1.1 Esimerkki: polynomin asteluku

Mikä on polynomin asteluku?

Ratkaisu:

Sievennetään polynomi.

$\begin{align*} &x^6+2x^2-(3x^6-x) \\ &=x^6+2x^2-3x^6+x \\ &=-2x^6+2x^2+x \end{align*}$

Koska muuttujan suurin eksponentti on polynomin asteluku on .

Sievennetään polynomi avaamalla sulkeet.

$\begin{align*} &x^2(3x^2-4) \\ &= x^2\cdot 3x^2-x^2\cdot4 \\ &= 3x^{2+2}-4x^2 \\ &=3x^4 -4x^2 \end{align*}$

Koska muuttujan suurin eksponentti on polynomin asteluku on .

Kun tutkitaan, missä kohdassa jokin korkeamman asteen polynomifunktio saa tietyn arvon, päädytään korkeamman asteen yhtälöön. Joissakin tapauksissa korkeamman asteen yhtälö voidaan saattaa tulomuotoon erottamalla yhteinen tekijä, jolloin se saadaan ratkaistua käyttämällä tulon nollasääntöä.

4.1.2 Esimerkki: ratkaisu tulon nollasäännön avulla

Ratkaise polynomiyhtälöt tulon nollasäännön avulla.

Ratkaisu:

$\begin{align*} x^3-49x&=0 &&|\text{ erotetaan yhteinen tekijä x}\\ x(x^2-49)&=0 &&|\text{ käytetään tulon nollasääntöä}\\ x=0\;\;\;\text{tai}\;\;\;&x^2-49=0 &&|\text{ ratkaistaan x}\\ &\;\;\;\;\;\,\;\;x^2=49 \\ &\;\;\;\;\;\,\;\;\;\;x=7\;\text{tai}\;x=-7 \end{align*}$

$\begin{align*} x^3-2x^2-24x&=0 &&|\text{ erotetaan yhteinen tekijä x} \\ x(x^2-2x-24)&=0 &&|\text{ käytetään tulon nollasääntöä} \\ x=0\;\;\;\text{tai}\;\;\;&x^2-2x-24=0 &&|\text{ ratkaistaan x} \\ &x=\frac{-(-2)\pm\sqrt{(-2)^2-4\cdot1\cdot(-24)}}{2\cdot1} \\ &x=\frac{2\pm10}{2} \\ &x=6\;\text{tai}\;x=-4 \end{align*}$

Vastaus:

$x=-7,\;x=0\;\text{tai}\;x=7$
$x=-4,\;x=0\;\text{tai}\;x=6$

Joissakin tapauksissa yhteisessä tekijässä voi olla useampia termejä. Seuraavalla videolla näytetään, miten tällainen yhteinen tekijä voidaan löytää ryhmittelemällä.

4.1.3 Esimerkki: ratkaisu ryhmittelyn avulla

Ratkaise polynomiyhtälöt ryhmittelyn ja tulon nollasäännön avulla.

Ratkaisu:

Tekijä voidaan erottaa koko vasemman puolen tekijäksi.

$x^2\textcolor{red}{(x-6)}-9\textcolor{red}{(x-6)}=\textcolor{red}{(x-6)}(x^2-9)$

Nyt yhtälö voidaan ratkaista tulon nollasäännön avulla.

$\begin{align*} (x-6)(x^2-9)&=0 \\ x-6=0\;\;\;\text{tai}\;\;\;x^2-9&=0 \\ x=6\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^2&=9 \\ x&=3\;\;\text{tai}\;\;x=-3 \end{align*}$

Ensin yritetään kirjoittaa lauseke a.-kohdan lauseketta muistuttavaan muotoon.

x^3+x^2-4x-4=x^2(x+1)-4(x+1)

Tekijä (x+1) voidaan erottaa koko vasemman puolen tekijäksi.

$x^2\textcolor{red}{(x+1)}-4\textcolor{red}{(x+1)}=\textcolor{red}{(x+1)}(x^2-4)$

Nyt yhtälö voidaan ratkaista tulon nollasäännön avulla.

$\begin{align*} (x+1)(x^2-4)=0 \\ x+1=0\;\;\;\text{tai}\;\;\;x^2-4&=0 \\ x=-1\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^2&=4 \\ x&=2\;\;\text{tai}\;\;x=-2 \end{align*}$

Vastaus:

$x=-3,\;x=3\;\text{tai}\;x=6$
$x=-2,\;x=-1\;\text{tai}\;x=2$

Sellaiset neljännen asteen yhtälöt, joissa esiintyy neljännen asteen termin lisäksi vain toisen asteen termi ja vakiotermi, voidaan ratkaista soveltamalla toisen asteen yhtälön ratkaisukaavaa. Tällaista yhtälöä kutsutaan bikvadraattiseksi yhtälöksi.

4.1.4 Esimerkki: bikvadraattinen yhtälö

Ratkaise bikvadraattinen yhtälö 4x^4-25x^2+36=0 .

Ratkaisu:

Merkitään t=x^2, jolloin voidaan kirjoittaa yhtälö muodossa

4t^2-25t+36=0.

Saadaan tavallinen toisen asteen yhtälö, joka voidaan ratkaista ratkaisukaavalla.

$\begin{align*} t&=\frac{-(-25)\pm\sqrt{(-25)^2-4\cdot4\cdot36}}{2\cdot4} \\ t&=\frac{25\pm7}{8} \\ t=4\;\;&\text{tai}\;\;x=\frac{9}{4} \end{align*}$

Ratkaisusta t=4, saadaan alkuperäiselle yhtälölle kaksi ratkaisua:

$\begin{align*} x^2&=4 \\ x=2\;\;&\text{tai}\;\;x=-2 \end{align*}$

Samoin ratkaisusta $t=\dfrac{9}{4},$ saadaan alkuperäiselle yhtälölle kaksi ratkaisua:

$\begin{align*} x^2&=\frac{9}{4} \\ x=\frac{3}{2}\;\;&\text{tai}\;\;x=-\frac{3}{2} \end{align*}$

Vastaus: $x=-2,\;x=-\dfrac{3}{2},\;x=\dfrac{3}{2}\;\text{tai}\;x=2$

Edellisessä kappaleessa jaoimme toisen asteen polynomin tekijöihin polynomin nollakohtien avulla. Voit kerrata sen tarvittaessa täältä. Seuraavan lauseen mukaan vastaava tulos pätee myös korkeamman asteen polynomien tapauksessa.

Polynomin tekijä

Lauseke x-a on polynomin tekijä, jos ja vain jos x=a on polynomin nollakohta.

Jos tiedetään kaikki polynomin nollakohdat $x_1,x_2,\dots ,x_n,$ niin polynomi voidaan kirjoittaa muotoon

$a_n(x-x_1)(x-x_2)\dots(x-x_n).$

Tässä vakio a_n on polynomin korkeimman asteen termin kerroin.

4.1.5 Esimerkki: korkeamman asteen polynomin jakaminen tekijöihin

Funktiolla f(x)=3x^4+6x^3-15x^2-18x on nollakohdat x=-3, x=-1, x=0 ja x=2. Jaa polynomi nollakohtien avulla tekijöihin.

Ratkaisu:

Nollakohtaa x=-3 vastaa tekijä x-(-3)=x+3.
Nollakohtaa x=-1 vastaa tekijä x-(-1)=x+1.
Nollakohtaa x=0 vastaa tekijä x-0=x.
Nollakohtaa x=2 vastaa tekijä x-2.

Näiden tekijöiden tulo täytyy vielä kertoa polynomin korkeimman asteen termin kertoimella
Nyt saadaan

f(x)=3x^4+6x^3-15x^2-18x=3x(x+3)(x+1)(x-2)

Tarkistetaan vastaus laskimella. GeoGebralla tekijöihin jako tapahtuu käskyllä Jaa Tekijöihin.

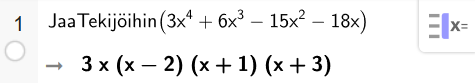
Vastaus: 3x^4+6x^3-15x^2-18x=3x(x+3)(x+1)(x-2)

4.2 Korkeamman asteen epäyhtälö

Tähän mennessä on opittu ensimmäisen asteen epäyhtälön (MAY1) sekä toisen asteen epäyhtälön ratkaisumenetelmät. Toisen asteen epäyhtälössä ratkaisun ideana oli ensin muuttaa epäyhtälö perusmuotoon, jossa yhtälön vasemmalla puolella oli polynomi ja toisella puolella nolla. Tämän jälkeen selvitettiin polynomifunktion nollakohdat ja tutkittiin funktion kulkua.

Korkeamman asteen epäyhtälöt ratkaistaan samaan tapaan. Uutena asiana tulee merkkikaavion laatiminen.

Yleisesti korkemman asteen epäyhtälön ratkaisu etenee seuraavasti:

Jaetaan polynomi tekijöihin
Ratkaistaan tekijöiden nollakohdat. Selvitetään tekijöiden merkit nollakohtien välillä.
Laaditaan merkkikaavio.
Katsotaan merkkikaaviosta välit, joilla epäyhtälö toteutuu.

4.2.1 Esimerkki: korkeamman asteen epäyhtälö

Ratkaise epäyhtälö x^3+7x^2-8x<0 .

Ratkaisu:

Jaetaan ensin polynomi tekijöihin.

x^3+7x^2-8x=x(x^2+7x-8)

Ratkaistaan tekijöiden nollakohdat ja selvitetään niiden merkit nollakohtien välillä.

Tekijä :

Nollakohta on x=0 . Tekijän kuvaaja on nouseva suora, joten sen arvo on negatiivinen, kun x<0 ja positiivinen, kun x>0 .

Tekijä :

Selvitetään tekijän nollakohdat.

$\begin{align*} &x^2+7x-8=0 \\ &x=\frac{-7\pm\sqrt{7^2-4\cdot1\cdot(-8)}}{2\cdot1}=\frac{-7\pm9}{2} \\ &x=1\;\;\text{tai}\;\;x=-8 \end{align*}$

Tekijän x^2+7x-8 kuvaaja on ylöspäin aukeva paraabeli.
Tekijän arvo on negatiivinen, kun -8<x<1 ja positiivinen,
kun x<-8 tai x>1.

Laaditaan merkkikaavio, josta tulon merkki päätellään tekijöiden merkkien avulla. Kahden positiivisen luvun tai kahden negatiivisen luvun tulo on positiivinen ja kahden erimerkkisen luvun tulo on negatiivinen.

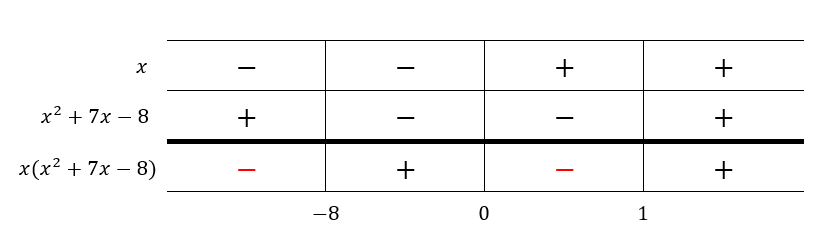
Merkkikaavion perusteella epäyhtälö x^3+7x^2-8x<0 toteutuu, kun x<-8 tai 0<x<1 .

Vastaus: x<-8 tai 0<x<1

4.2.2 Esimerkki: korkeamman asteen epäyhtälö

Ratkaise epäyhtälö $(x+5)(2x-1)(3-x)\ge0$ .

Ratkaisu:

Polynomi on valmiiksi tulomuodossa.

Tekijä :

Nollakohta on x=-5 . Tekijän x+5 kuvaaja on nouseva suora, joten sen arvo on negatiivinen, kun x<-5 ja positiivinen, kun x>-5 .

Tekijä :

Nollakohta on $x=\dfrac{1}{2}$ . Tekijän 2x-1 kuvaaja on nouseva suora, joten sen arvo on negatiivinen, kun $x<\dfrac{1}{2}$ ja positiivinen, kun $x>\dfrac{1}{2}$ .

Tekijä :

Nollakohta on x=3 . Tekijän 3-x kuvaaja on laskeva suora, joten sen arvo on positiivinen, kun x<3 ja negatiivinen, kun x>3 .

Laaditaan merkkikaavio.

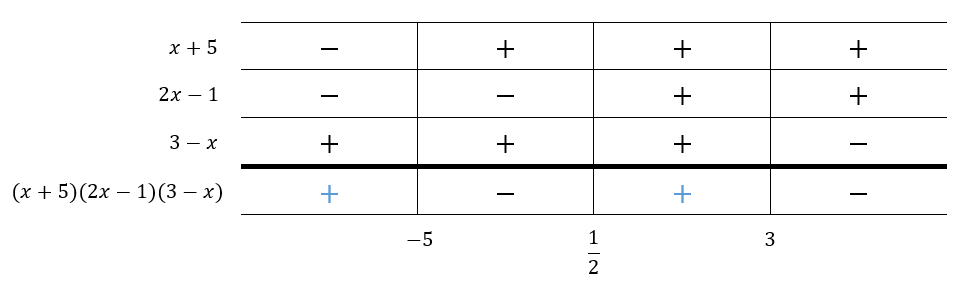
Merkkikaavion perusteella epäyhtälö $(x+5)(2x-1)(3-x)\ge0$ toteutuu, kun $x\le-5$ tai $\dfrac{1}{2}\le x\le 3$ .

Vastaus: $x\le-5$ tai $\dfrac{1}{2}\le x\le 3$