4. Korkeamman asteen polynomiyhtälö ja -funktio: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Korkeamman asteen polynomiyhtälö ja -funktio. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

4.1 Korkeamman asteen polynomifunktio ja -yhtälö

Tämän kappaleen teoria.

4.1.1 Tehtävä

Mikä on polynomin asteluku?

# t411a

# t411

# t412

4.1.2 Tehtävä

Yhdistä funktiot oikeisiin kuvaajiin ilman teknisiä apuvälineitä. Tehtävästä saa pisteet, kun funktion nimen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

$B(x)=\dfrac{1}{5}x^3-2x-1$

$D(x)=-\dfrac{1}{2}x^2+x+1$

# MAA5_1a

Vihje

Polynomifunktion asteluvun ja juurten välinen yhteys:

Astetta olevalla polynomifunktiolla on enintään nollakohtaa.

Ratkaise tehtävien 4.1.4-4.1.6 yhtälöt ilman teknisiä apuvälineitä.

4.1.3 Tehtävä

Ratkaise yhtälöt.

# p414

# p414b

4.1.4 Tehtävä

Ratkaise yhtälöt.

# p415a

# p415b

Vihje

Tekijä (x+3) voidaan erottaa vasemman puolen tekijäksi.

x^3+3x^2-4x-12=x^2(x+3)-4(x+3)

4.1.5 Tehtävä

Ratkaise bikvadraattiset yhtälöt.

# p416a

Vihje

Merkitään t=x^2, jolloin voidaan kirjoittaa yhtälö muodossa

4t^2+11t-3=0,

jolloin saadaan tavallinen toisen asteen yhtälö, joka voidaan ratkaista ratkaisukaavalla.

Huomaa, jos toisen asteen yhtälön ratkaisuksi saadaan negatiivinen n arvo, yhtällä x^2=t ei ole ratkaisua.

# p416b

Vihje

Merkitään t=x^2, jolloin voidaan kirjoittaa yhtälö muodossa

t^2-3t+2=0,

jolloin saadaan tavallinen toisen asteen yhtälö, joka voidaan ratkaista ratkaisukaavalla.

4.1.6 Tehtävä

# Plugin1

4.1.7 Tehtävä

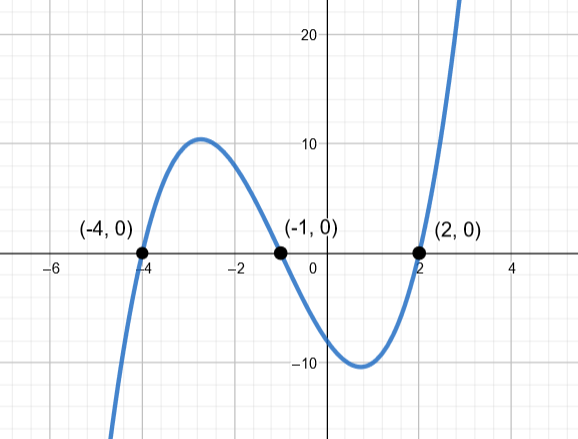
Kuvassa on kolmannen asteen polynomifunktion kuvaaja. Määritä funktion lauseke. Syötä lopullinen vastaus ei-tulomuodossa.

# p122a

Vihje

Polynomifunktion nollakohdat ovat x=-4, x=-1 ja x=2 , joten funktion tekijöitä ovat x+4, x+1 ja x-2 . Funktio on muotoa

$f(x)=(x+4)(x+1)(x-2)=\dots$

4.1.8 Tehtävä

Matti määritti funktion f(x)=2x^3-18x^2+28x+48 nollakohdiksi symbolisen laskennan ohjelmalla x=-1, x=4 ja x=6 .

# p417a

# p418b

4.1.9 Tehtävä

# RH1a

# RH1b

4.2 Korkeamman asteen epäyhtälö

Tämän kappaleen teoria.

4.2.1 Tehtävä

# p421

4.2.2 Tehtävä

Kuvassa on kolmannen asteen polynomifunktion kuvaaja.

# p422

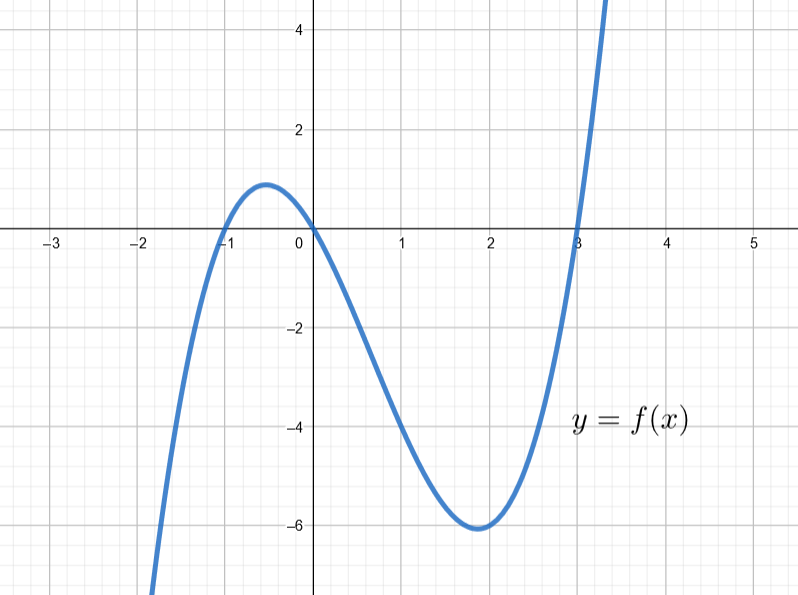
Ratkaise epäyhtälöt 4.2.3-4.2.6 ilman teknisiä apuvälineitä. Huomaa, että tehtävissä ei ole automaattitarkistusta.

4.2.3 Tehtävä

# p423a2

# p423bb

# p423c

4.2.4 Tehtävä

Ratkaise epäyhtälöt.

# p423a

# p423b

4.2.5 Tehtävä

# p426a

# p426b

4.2.6 Tehtävä

Ratkaise epäyhtälö.

# p425a

# p425b

4.2.7 Tehtävä (s2019/5)

# p4210a

# p4210

Ratkaisu

4.2.8 Tehtävä

Millä luvuilla on seuraava ominaisuus? Luku on

# MAA2427a

vihje

$x=\dfrac{x^2+x^3}{2}$

# p427b

4.2.9 Tehtävä

# p428

Vihje

$\begin{align*} ax^3+x^2+x&=0 \\ x(ax^2+x+1) &=0 \end{align*}$

Tulon nollasäännön nojalla x=0 on yhtälön yksi juuri. Yhtälöllä on siis kolme juurta, kun yhtälöllä ax^2+x+1=0 on kaksi nollasta poikkeavaa juurta.

Tutki toisen asteen yhtälön ratkasukaavan ja diskriminantin avulla yhtälöä ax^2+x+1=0 . Jos diskriminantti saa arvokseen nolla, niin mitä huomaat? Entä jos diskriminantti saa arvokseen yksi?