TIEP114 Tietokoneen rakenne ja arkkitehtuuri
Esipuhe
Tämä luentomateriaali on tehty TIEP114 Tietokoneen rakenne ja arkkitehtuuri kurssille tukemaan kurssin luentoja sekä harjoitustehtäviä.
Materiaaliin on lisätty linkkejä vanhojen luentotaltiointien kohtiin, joissa aiheita on käsitelty. Vuoden 2017 ja 2016 linkitettyjä tallenteita voi katsella ennen kuin vuoden 2018 luennoista on lisätty tallenteet. Lisäksi luennoiden painotus vaihtelee vuosittain. Syksyn 2018 kurssin luentojen jälkeen linkitetään syksyn 2018 luentotallenteet materiaaliin.
Viimeisimmät päivitykset:
- Päivitetty materiaalin loppuosaa
- Tämän materiaalin päivitys on lopetettu, uusin versio löytyy uusimmalta kurssitoteumalta.
TIM-järjestelmän käyttöohjeita löytyy esimerkiksi Ohjelmointi 1 kurssin monisteesta.
Kurssin kotisivut lukuvuosittain
Vanhojen kurssien opiskeluun liittyviä yleisiä asioita ja ohjeita löydät sen lukuvuoden kurssin kotisivulta, jolle olet korpissa ilmoittautunut.
Kurssista annetusta palautteesta olen osan koonnut palautesivulle, jossa myös vastineitani palautteisiin.
Kurssin harjoitustehtävät lukuvuosittain
TIEP114 kurssin opiskelu tehdään käytännön harjoitustehtävillä.
Kurssilla käytetyt tarkistimet
Kurssin TIM-tehtävissä on käytössä erilaisia Pythonilla kirjoitettuja tarkistimia. Jos kiinnostaa, niin niitä voinee tutkia.
- Piirikaaviotehtävien tarkistin
- Tarvittavan bittimäärän tarkistin
- Lukujärjestelmämuunnosten tarkistin
- Kahden komplementti -tehtävien tarkistin
- Reaali- ja liukulukutehtävien tarkistin
- UTF-8 tehtävien tarkistin
- Boolen algebran tehtävien tarkistin
- Binäärisen yhteenlaskun tarkistin, muuttujina merkkijonon ensimmäinen ja viimeinen kirjain
- Karnaughin kartta tehtävien tarkistin
Kurssin luentomateriaalissa on laitteistokuvauskielen tarkistin muutamalle komponentille.
Tietokoneen kokoaminen ja sen jälkeen käyttöjärjestelmän asetusten tekeminen tarkastetaan sen perusteella mitä ao. skripti antaa tulosteeksi
Kurssin esitiedoista
Kurssin opiskeleminen ei vaadi aiempaa ohjelmointiosaamista, mutta kurssin luentomateriaalissa, ja ehkä harjoitustehtävissä, käytetään apuna ja havainnollistamiseksi eri ohjelmointikieliä. Kurssissa on vapaaehtoinen lisäosa, jossa tehdään ohjelmointitehtävä, mikä vaatii kykyä itsenäiseen ohjelman tuottamiseen valitsemallaan ohjelmointikielellä.
Matemaattisesti tietokoneen prosessorin toiminta perustuu pitkälti Boolen logiikkaan. Esitietona matematiikasta riittää lukion matematiikasta potenssi- ja logaritmifunktio, sekä yksinkertaisten matemaattisten yhtälöiden sieventäminen. Boolen logiikan avulla opiskellaan se kuinka tietokoneessa kaikki 'voidaan tehdä nollilla ja ykkösillä'.
Johdantoa Boolen logiikkaan
Boolen logiikassa minkä tahansa lausekkeen arvo voi olla ainoastaan joko tosi tai epätosi, ei mitään muuta. Uusia lausekkeita voidaan muodostaa yhdistämällä lausekkeita perusoperaatioilla And, Or ja Not ja näidenkin lausekkeiden arvoksi voi tulla vain jompikumpi kahdesta arvosta tosi tai epätosi. Myöhemmin käydään läpi perusoperaatioiden määritelmät, mutta nyt riittää se että operaation englannin kielinen nimi vastaa operaation toimintaa.
Alla on esimerkkinä Python 3 kielinen ohjelma havainnollistamaan Boolen logiikkaa. Voit ajaa koodin ja halutessasi voit vaihtaa and sanan or sanaksi sekä testata vaihtaa True sanan, jommankumman tai molemmat False sanaksi. Huomaa että jos vaihdat isoja kirjaimia pieniksi tai toisin päin, niin saat tulokseksi vain virheilmoituksen. Klikkaamalla Highlight koodi näkyy korostettuna ja edellä sinisellä esitetyt sanat näkyvät koodissa sinisellä, ne kun ovat Pythonin varattuja sanoja. Klikkaamalla Tavallinen saa korostuksen pois päältä.
Ehkäpä or ehdolla kurssin pääsee läpi ja toisaalta and ehdolla saa sitten paremman arvolauseen. Esimerkin Pythonin and ja or ovat ns. Boolen operaattoreita, jotka toteuttavat Boolen logiikkaa. Tarkemmat määritelmät operaattoreille tulevat myöhemmin materiaalissa. Boolen logiikan ulostulona voi olla jompikumpi kahdesta arvosta. Edellä arvoja merkittiin termeillä True ja False. Tietokoneen toteutuksessa käytetään yleensä merkintöinä bittejä 1 ja 0.
Tietokoneen rakenne
Tietokoneen voidaan katsoa muodostuvan keskusyksiköstä (suoritin, prosessori, CPU), keskusmuistista ja I/O-komponenteista. Nämä osat on liitetty toisiinsa siten että tietokoneen perustehtävä, tietokoneohjelman suorittaminen, on mahdollista. Liitynnöistä käytetään termiä väylä, englanniksi bus. Tietokonetta voidaan karkealla tasolla kuvata edellä mainituilla osilla ja niiden keskinäisellä käyttäytymisellä.
Keskusyksikkö sisältää pienen määrän erittäin nopeaa muistia, rekisterit, joita käytetään muistiosoitteiden, väliaikaisten tulosten ja kontrollitiedon tallettamiseen. Eräs tärkeä rekisteri on ohjelmalaskuri, käskyosoitin (Program Counter, PC), joka ilmaisee mistä seuraavaksi suoritettava käsky noudetaan. Toinen tärkeä rekisteri on käskyrekisteri (Instruction Register, IR), joka sisältää kullakin hetkellä suoritettavana olevan käskyn. Keskusyksikkö sisältää myös aritmeettis-loogisen -yksikön, joka vastaa esimerkiksi laskutoimituksista.
Lähes kaikki nykyajan tietokoneet perustuvat ns. Von Neumannin arkkitehtuuriin, joka perustuu seuraaviin asioihin.
- Suoritettava ohjelma ja sen käyttämä data talletetaan samaan muistiin binäärisenä informaationa.
- Tämän muistin sisältö on osoitettavissa paikan mukaan huolimatta siitä, minkä tyyppistä tietoa sinne on talletettu.
- Ohjelman suoritus tapahtuu peräkkäin yhdestä käskystä seuraavaan paitsi, jos jostain syystä hypätään johonkin muuhun käskyyn.
Binäärinen informaatio voi olla mitä tahansa tietoa, joka on koodattu siten että tieto esitetään binäärisellä koodilla, jonka esittämiseen käytetään kahta eriarvoista merkkiä.
Binäärisen tiedon tallettaminen ja erilaisten aritmeettisten ja loogisten operaatioiden suorittaminen binäärisellä tiedolla voidaan toteuttaa pienellä määrällä muutamia loogisia peruskomponentteja.
Aloitetaan tietokoneen rakenteeseen tutustuminen lukujärjestelmistä ja siitä miten numerot, kirjaimet ja muu tieto tallennetaan binääriseen muotoon. Sen jälkeen opiskellaan perustiedot loogisista komponenteista, rakentaen simuloiden tietokoneen toteutukseen tarvittavat osat ja palataan tietokoneen rakenteeseen, arkkitehtuuriin ja organisaatioon materiaalin loppuosassa, kun tarkastellaan prosessorin toimintaa, sen sisäisiä sekä ulkoisia kytkentöjä.
Tiedon esitys tietokoneissa
Moni tieto on luonteeltaan jatkuvaa, eli se esiintyy analogisessa muodossa. Jotta analogista informaatiota voidaan käsitellä tietokoneissa, tarvitaan tiedon muuntaminen digitaaliseen muotoon. Usein joudutaan tekemään myös muunnos toiseen suuntaan, jos esimerkiksi tietoa esitetään ihmisille. Analoginen tieto on siis jatkuvaa, mutta se voidaan jakaa osiin ja määritellä eri osille erilainen digitaalinen esitystapa, koodaus.
Tiedon digitalisointi
Yksi esimerkki analogisen tiedon muuntamisesta digitaaliseksi on lukujen pyöristäminen lähimmäksi kokonaisluvuiksi. Tällöin esimerkiksi seuraavat murtoluvut pyöristetään ja
. Digitalisoitaessa voi osa informaatiosta hävitä, mutta kasvattamalla mahdollisia arvoja, joihin digitalisointi tehdään, voidaan digitalisointivirhettä pienentää. Pyöristäessä voidaan esimerkiksi pyöristää kokonaisluvun sijaan desimaaliluvuksi yhden desimaalin tarkkuudella. Aiemmat esimerkit olisivat siten
ja
.
Lisäämällä digitalisoinnin tarkkuutta saadaan analogiselle informaatiolle tarkempi digitaalinen muunnos, mutta hintana on talletuskapasiteetin kasvu. Esimerkiksi edellisissä kappaleen pyöristysesimerkeissä yhden numeron tallennustarve muuttui kahden numeron tallennustarpeeksi, kun pitää kokonaislukunumeron lisäksi tallentaa kymmenesosanumero.
Edellä digitalisointi tehtiin kahdelle yksittäiselle arvolle. Monesti digitalisoitava reaalimaailman analoginen informaatio täytyy muuttaa digitaaliseksi useana eri ajanhetkenä, esimerkiksi puheen välittäminen digitaalitekniikkaa käyttävällä matkapuhelimella. Tällöin jatkuvaa analogista informaatiota täytyy tutkia diskreetteinä ajanhetkinä, tämä tehdään ottamalla informaatiosta näytteitä tietyin väliajoin.
Alla on virtuaalinen oskilloskooppi, joka näyttää esimerkiksi tietokoneen mikrofonin kuulemaa ääntä, valitse Input lähteeksi Live Input. Live Input toimii ainakin uusimmissa Chrome selaimissa, muissa se ei näy Input-valikossa, katso tarkempia tietoja linkistä, joka löytyy oskilloskoopista. Jos Live Input ei toimi TIM-sivulla, kokeile linkin takana olevaa sivua, selain pyytää luvan käyttää tietokoneen mikrofonia. Oskilloskooppi visualisoi äänen näytöllään analogisena.
Seuraavassa kuvassa on esimerkki analogisesta äänisignaalista, josta on otettu näytteitä tasaisin väliajoin. Pystyakselilla on äänen voimakkuus, keskikohta normalisoitu arvoon nolla. Vaaka-akselilla on aika ja käyrän muoto on äänisignaalin taajuus. Pystyviivat vaaka-akselilla merkitsevät näytteenottohetket. Pystyakselilla olevat lukuarvot ja niiden kohdalla olevat viivat ovat digitalisointiin käytössä olevat arvot. Kun äänestä otetaan näyte, niin äänenvoimakkuus (punaisen viivan arvo) näytteenottohetkellä täytyy tallentaa. Koska äänenvoimakkuus on analoginen, voi se saada mitä tahansa arvoja. Nämä arvot täytyy kuitenkin digitalisointia varten pyöristää lähimpään käytössä olevaan arvoon. Tällaista pyöristämistä kutsutaan kvantisoinniksi (eng. quantization). Siniset pisteet eivät siis osu aina samalle korkeudelle punaisen viivan kanssa, vaan ne esittävät analogisen äänenvoimakkuuden näytteiden kvantisoituja digitaalia arvoja.
Jotta digitalisoidusta signaalista voidaan muodostaa alkuperäistä analogista signaalia vastaava signaali täytyy näytteenottotaajuuden olla vähintään kaksinkertainen verrattuna korkeimpaan taajuuteen, joka esiintyy alkuperäisessä signaalissa, Nyquist–Shannon-teoreema. Rekonstruoidun signaalin laatuun vaikuttaa käytetty kvantisointitarkkuus. Ylläolevassa kuvassa kvantisointi on tehty 16 eri arvoon (vaakaviivat pystyakselilla). Tarkkuutta voisi lisätä tihentämällä ja lisäämällä vaakaviivoja, eli lukuarvoja, joihin näytteenottoarvot voidaan pyöristää. Esimerkiksi CD laatuinen audio signaali generoidaan analogisesta signaalista näytteenottotaajuudella 44100 Hz, eli 44100 näytettä sekunnissa, ja kvantisointi tehdään 65536 eri arvoon. Puhelimissa riittää ihmisen puheen siirtäminen ja suurin osa ihmisten generoimasta äänistä on taajuusvälillä 100 - 3400 Hz. Yleisin puhelinliikenteessä käytetty G.711 ITU-T standardi, määrittelee mekanismin, jossa puhesignaalin näytteenottotaajuus on 8000 Hz ja kvantisointi tehdään 256 eri arvoon. Huomaa että näytteenottotaajuus on yli kaksi kertaa suurempi kuin mitä useimpien ihmisen generoimien äänien maksimitaajuus.
Pyöristysesimerkissä lukuarvoille käytetty 10-järjestelmä vaatisi tallennusmekanismin, jossa yhteen (muisti)paikkaan voidaan tallentaa 10 eri arvoa, eli arvot 0-9. Tämä ei käytännössä ole kustannustehokasta, koska tarvittaisiin hyvin tarkkoja laitteita tiedon tallentamiseen ja lukemiseen, esimerkiksi jännitettä pitäisi lukea sekä tallentaa 0.5 V tarkkuudella käytettäessä tallennukseen jänniteväliä 0 - 5 volttia. Kyseisen tarkkuuden toteuttaminen ei ole kustannustehokasta. Kun tarvitsee tallentaa vain kaksi arvoa, voi nykyisellä tekniikalla toteuttaa hyvin halpoja ja pieniä komponentteja. Esimerkiksi, tämän kurssin elektroniikkatöissä käytetään 74HC-perheen CMOS-tekniikalla toteutettuja mikropiirejä, joiden käyttämä 5 voltin jännitealue on jaettu siten että jännitealue 0 - 1.5 V vastaa loogista arvoa 0 ja jännitealue 3.5 - 5 V vastaa loogista arvoa 1. Vaihteluväli antaa turvaa sähkömagneettista kohinaa ja muita häiriöitä vastaan. Loogisten arvojen välissä oleva jännitealue 1.5 - 3.5 V on määrittelemätön ja tällöin häiriötä on niin paljon, eikä oikeaa loogista arvoa voi tietää.
Digitaalisen tiedon tallennus
Yksinkertaisin, halvin sekä helposti massatuotettava digitaalinen tallennus voidaan tehdä tallentamalla kahta eri vaihtoehtoa, jolloin riittää tutkia esimerkiksi sitä että onko jännite 0 volttia vai 5 volttia tai sitä onko jokin kytketty päälle vai eikö ole. Tällöin siis voimme tallentaa vain kahta eri vaihtoehtoa. Jos vaihtoehtoja merkitään numeroarvoilla, eli voidaan käyttää vain kahta numeroarvoa, voidaan digitaalisen informaation esittämiseen käyttää 2-järjestelmän ts. binäärijärjestelmän lukuja.
Esimerkiksi kytkin tai LED voi tallentaa kaksi eri arvoa. Alla mekaanisia kytkimiä voidaan käyttää tiedon tallentamiseen. Kytkimet on liitetty LED:eihin, jotka visualisoivat kytkimiin tallennettua arvoa.
Binäärijärjestelmässä, eli 2-järjestelmässä, on kaksi eri arvoa, näiden merkintöinä käytetään merkkejä 0 ja 1, eli kaksi ensimmäistä merkkiä 10-lukujärjestelmän ei-negatiivisista kokonaisluvuista. Merkit 0 ja 1 ovat binäärijärjestelmän numeroita, englanniksi binary digits, ja niitä kutsutaan lyhyesti termillä bitti, englanniksi bit. Kun biteistä muodostetaan useamman bitin kokonaisuuksia, niitä kutsutaan binääriluvuiksi. Kahdeksan bitin binääriluvulle on määritelty oma termi ja kahdeksan bitin binäärilukua kutsutaan tavuksi, englanniksi byte. Jotta mitä tahansa informaatiota voidaan tallentaa 2-järjestelmän lukuna, on sovittava säännöt informaation muuttamiseksi binäärijärjestelmään.
Koska 2-järjestelmässä on vain kaksi erilaista vaihtoehtoa symboliksi, täytyy esimerkiksi numeroiden ja kirjainten esittämiseen varata useita bittejä. Kun laitetaan kaksi bittiä peräkkäin, saadaan niistä neljä eri kombinaatiota 00, 01, 10 ja 11. Eli kahdella bitillä voidaan esittää neljä eri vaihtoehtoa. Yleisesti :llä bitillä voidaan esittää
erilaista binäärilukua. Täten esimerkiksi kahdeksalla bitillä voidaan esittää
eri kombinaatiota, ja jos niillä esitetään ei-negatiivisia kokonaislukuja, voidaan kahdeksalla bitillä esittää numerot välillä 0 - 255.
Esimerkki. Kuinka monta bittiä tarvitaan kaikkien välillä 0 - 999 olevien kokonaislukujen esittämiseen?
Eli tarkoitus on selvittää yhtälöstä
Kyseessä on siis binäärilukujärjestelmän kantaluvun 2 korottaminen potenssiin , eli potenssifunktio. Potenssifunktion käänteisfunktio on logaritmifunktio, tässä tapauksessa siis 2-kantainen logaritmifunktio. Jotta
saadaan ratkaistua, otetaan yhtälön molemmista puolista 2-kantainen logaritmi
ja yhtälön vasemmalla puolella käänteisfunktioiden kumotessa toisensa saadaan
Vastaukseksi ei saatu kokonaislukua, nyt vastausta lähimmät kokonaisluvut antavat , mikä ei riitä lukujen 0 - 999 esittämiseen, ja
, mikä puolestaan riittää. Eli lukujen 0 - 999 esittämiseen tarvitaan kymmenen bittiä, mutta osa bittikombinaatioista jää käyttämättä.
Yleisesti, jos meillä on erilaista elementtiä, niiden esittämiseen tarvittava minimi bittien lukumäärä on pienin kokonaisluku
, siten että
.
Tässä luentomateriaalissa ja harjoitustehtävissä käytetään matemaattisten lausekkeiden esittämiseen -ladontajärjestelmän matemaattisia symboleita. TIM-järjestelmässä on käytetty hyväksi MathJax-JavaScript kirjastoa LaTeX:in kääntämiseksi HTML-kuvauskielellä esitettäväksi. Esimerkeissä tutustutaan matemaattisten symboleiden esittämiseen LaTeX:illa sekä harjoitustehtävien tarkistinten toimintaan. Luentomateriaalin joistain esimerkeistä saatavat pisteet eivät vaikuta kurssin yhteispisteisiin, vaan ne ilmaisevat sen että esimerkki on tehty oikein.
Tehtävän vastauslaatikoissa on valmiina $$ -merkkien välissä oleva tyhjä rivi, johon vastauksesi tulee kirjoittaa. $$ -merkit ovat eräs tapa LaTeX:issa ilmaista se että näiden merkkien välissä olevat merkit tulee tulkita ja latoa matemaattisina symboleina. Näet noin sekunnin viiveellä kirjoittamaasi LaTeX:ia vastaavan matemaattisen kaavan ladottuna.
Esimerkki. Alle on kirjoitettu LaTeX:illa lauseke, joka antaa tulokseksi sen, kuinka monta eri numeroa voidaan esittää 9 bitillä. Muunna lauseke sellaiseksi että se antaa tulokseksi sen kuinka monta eri numeroa voidaan esittää 10 bitillä.
Esimerkki. Alle on kirjoitettu LaTeX:illa lauseke, joka antaa tulokseksi sen, kuinka monta bittiä tarvitaan sadan numeron esittämiseen. Muunna lauseke sellaiseksi, että se antaa tulokseksi sen kuinka monta bittiä tarvitaan tuhannen numeron esittämiseen.
Bittien ryhmittely
Ennen kuin opetellaan se miten erilaista informaatiota tallennetaan bitteihin, käydään läpi termejä ja seuraavassa luvussa mittayksiköitä, jotta opimme sen millä nimillä voidaan kutsua useampien bittien kokonaisuuksia.
Tavu
Tietokonejärjestelmissä tiedon esityksen perusyksikkö on bitti, binäärinen numero. Tavallinen nimitys 8 bitin ryhmälle on tavu, englanniksi byte, joskus käytetään myös termiä oktetti, englanniksi octet. Muun kokoisille bittiryhmille on myös nimityksiä, mutta ne eivät ole vakiintuneet ja esimerkiksi termiä sana käytetään ja on käytetty usean eri kokoisen bittiryhmän nimityksenä. Neljän bitin ryhmää kutsutaan puolitavuksi, englannin kielessä käytetään termiä nibble tai harvemmin nybble, missä y-kirjainta on käytetty linkittämään termi tavun englannin kieliseen sanaan byte.
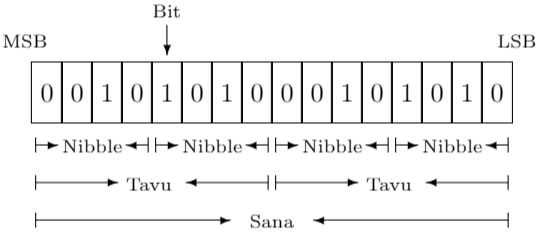
Toteutettu \(\LaTeX\) bytefield-paketilla, lähdekoodi
—Sana
Tietokoneessa käsitellään tietoa yleensä tietty bittimäärä kerrallaan. Tällaista bittimäärää kutsutaan tavallisesti sanaksi. Tietoa siirretään tietokoneessa sana kerrallaan, tietoa muokataan sana kerrallaan jne. Sanan määritys ei ole tarkka mutta yleensä se on prosessorin sisäisten rekisterien koko, eli käytännössä se määrä bittejä, joita prosessori voi yhdellä kertaa käsitellä. Sanassa olevien bittien määrää on vaihdellut hyvin paljon, mutta yleensä se on 8 bittiä, 16 bittiä, 32 bittiä tai 64 bittiä. Kuten nähdään, sanan pituus on yleensä tavun monikerta, mutta voi olla muutakin.
MSB ja LSB
Bitit sanassa ja tavussa numeroidaan yleensä oikealta vasemmalle eli oikeanpuoleisin bitti on bitti (paikassa) numero 0 ja sitä sanotaan myös vähiten merkitseväksi bitiksi, eng. Least Significant Bit (LSB). Vastaavasti vasemmanpuoleisinta bittiä sanotaan eniten merkitseväksi bitiksi, eng. Most Significant Bit (MSB). Nimitykset tulevat siitä, miten merkitsevä kyseinen bitti on binääriluvun lukuarvolle. Jos esimerkiksi binäärilukuun tulee virhe, niin virheen määrä kasvaa sitä enemmän mitä lähempänä se on MSB:tä. Alla esimerkin tarkistin antaa binäärilukua vastaava positiivisen kokonaisluvun. Kun muutat yksittäisiä nollia ykköseksi, oikealta vasemmalle, huomaat tarkistimen antavan aina vaan enemmän nollasta poikkeavia kokonaislukuarvoja.
Esimerkki. Testaa MSB ja LSB bittien muuttamisen vaikutusta binääriluvun 000000002 arvoon.
Mikroprosessoreissa käsitellään lähes aina tavun monikertoja, jota siis kutsutaan sanaksi. Muistit on kuitenkin toteutettu käytännössä siten että niiden tallennusyksikkönä on tavu, eli jokaisen osoitteen osoittama muistipaikka on tavun kokoinen. Täten sanat täytyy tallentaa useisiin muistipaikkoihin. Tietokoneen arkkitehtuurista riippuen muistia voidaan pystyä loogisesti käsittelemään sanan kokoisina paloina.
Tavujärjestys
Tietokoneen muistiin sanat talletetaan peräkkäin, mikä voidaan tehdä eri kahdella tavalla, joissa tavut ovat eri järjestyksessä. Big endian -tavassa tavut talletetaan eniten merkitsevästä tavusta vähiten merkitsevään. Little endian -tavassa tavut talletetaan päinvastaisessa järjestyksessä eli vähiten merkitsevä tavu talletetaan ensin ja sen perään toiseksi vähiten merkitsevä ja viimeiseksi eniten merkitsevä tavu. Tavujen sisällä MSB bitti on vasemmalla ja LSB bitti oikealla.
Olkoon meillä esimerkiksi seuraava 32 bittinen eli 4-tavuinen sana
10011111 00000000 10001010 11010101.
Jos tämä sana talletetaan big endian -tavalla muistiin alkaen muistipaikkatavusta, jonka osoite 100, niin osoitepaikoissa olevien tavujen 100 – 103 sisällöt ovat seuraavat
100: 10011111 101: 00000000 102: 10001010 103: 11010101
Jos tämä sana sen sijaan talletetaan little endian -tavalla alkaen tavusta, jonka osoite 100, niin tavujen 100 – 103 sisällöt ovat seuraavat
100: 11010101 101: 10001010 102: 00000000 103: 10011111
Intel x86 arkkitehtuurin prosessorit tallentavat useamman tavun tietotyypit little endian -muodossa. Toiset prosessorit, kuten Power PC prosessori tallentaa useamman tavun tietotyypit big endian -muodossa. Yleensä ohjelmoijan ei tarvitse välittää tavujärjestyksestä, eli endianness -muodosta. Tietokone, käyttöjärjestelmä tai ohjelmointikieli tekee tarvittavat muunnokset. Silloin kun siirretään tietoa erilaisten järjestelmien välillä, esimerkiksi tiedostoa tai verkkoliityntää lukiessa, voi kohde- ja lähdejärjestelmien eri endianness -muoto aiheuttaa ongelmia ja se tulisi ottaa huomioon.
Tiedonsiirrossa on määritelty käytettäväksi big endian -muotoa ja sitä usein kutsutaan myös termillä network byte order. Suurin osa tiedon siirtoon käytettävistä tietoliikenneprotokollista näin toimiikin, ei tosin kaikki. Lisäksi joidenkin protokollien määrityksissä ei kerrota kumpaa tulisi käyttää.
Tietokoneisiin liittyvät mittayksiköt
Tietokoneiden käyttäessä tiedon esittämiseen bittejä, käytetään niiden yhteydessä mittayksikkönä usein 2:n potensseja ja nimenomaan sellaisia 2:n potensseja, jotka ovat lähellä jotain 10:n potenssia, kuten esimerkiksi
- 210 = 1024,
- 220 = 1 048 576 ja
- 230 = 1 073 741 824.
Koska 210 = 1024, joka on lähellä arvoa 103 = 1000, niin molemmista käytetään termiä kilo, josta käytetään merkintää k, kun kyseessä on 1000 ja merkintää K, kun kyseessä on 1024. Sekaannusta voi aiheuttaa myös se onko yksikkönä bitti (bit) vai tavu (byte), joka on 8 bittiä. Näistä käytetään merkintää b, kun tarkoitetaan bittiä ja merkintää B, kun tarkoitetaan tavua. Sekaannusten välttämiseksi nimityksiä on standardoitu (ISO/IEC 80000) siten, että kun kyseessä on binäärinen eli kakkosen potenssi, niin symboliin lisätään i. Esimerkiksi 210 on nimeltään kibi eli kilobinary ja siitä käytetään merkintää Ki. Alla on taulukoitu SI-järjestelmän ja IEC:n standardin mukaiset etuliitteet biteille sekä tavuille.
| Value | SI | Value | IEC | ||
|---|---|---|---|---|---|
| 1000 | k | kilo | 1024 | Ki | kibi |
| 10002 | M | mega 1 | 0242 | Mi | mebi |
| 10003 | G | giga 1 | 0243 | Gi | gibi |
| 10004 | T | tera 1 | 0244 | Ti | tebi |
| 10005 | P | peta 1 | 0245 | Pi | pebi |
| 10006 | E | exa 1 | 0246 | Ei | exbi |
| 10007 | Z | zetta 1 | 0247 | Zi | zebi |
| 10008 | Y | yotta 1 | 0248 | Yi | yobi |
Standardin mukaista esitystapaa ei aina noudateta ja käytäntö vaihtelee. Tietokoneen eri osissa käytetään erilaisia esitystapoja. Lisäksi käytetään samoja esitystapoja eri tarkoituksella pääasiassa historiallisista syistä. Esimerkiksi keskusmuistin, RAM, kapasiteettia kuvatessa yksi gigatavu, GB tavanomaisesti tarkoittaa 1 073 741 824 tavua. RAM muistin tapauksessa siis standardin mukaan pitäisi käyttää lyhennettä GiB. Vastaavasti esim. prosessorin yhden megatavun (1 MB) L2 välimuisti tarkoittaa 1 048 576 tavua.
Kiintolevyjen kapasiteetit kuvataan samoin lyhentein kuin RAM muistien, mutta kiintolevyjen yhteydessä lyhenteiden tarkoitus on SI-järjestelmän mukainen. Esimerkiksi yhden teratavun, TB kiintolevyn koko on 1 000 000 000 000 tavua. Myös Flash muistilla toteutettujen SSD levyjen kapasiteetin esitys on SI-järjestelmän mukainen.
Prosessorin kellotaajuus esitetään SI-järjestelmän mukaisilla mittayksiköillä. Esimerkiksi 2 GHz kellotaajuudella toimiva prosessori vastaanottaa 2 000 000 000 kellopulssia sekunnissa.
CD ja DVD levyjen tallennuskapasiteetit käyttävät eri määrityksiä. Esimerkiksi 700 MB:n CD levyn kapasiteetti on 734 003 200 tavua, eli määritys ei ole SI-järjestelmän mukainen. DVD, Blue-ray ja useimmat muut optiset tallennusmediat käyttävät SI-järjestelmän mukaista määritystä.
Kun selvitetään esimerkiksi 700 MB CD-levylle mahtuva bittimäärä, niin ensin voi megatavut muuntaa tavuiksi ja sitten biteiksi. Tavuiksi muuntaminen tehdään kertomalla 700 MB termiä mega vastaavalla tavumäärällä, eli esimerkiksi 220 tai 10242. Koska yksi tavu vastaa kahdeksaa bittiä, tehdään biteiksi muuntaminen kertomalla tavut kahdeksalla, tai arvolla 23.
Esimerkki. Alla oleva lauseke muuntaa 700 MiB tavuiksi. Lisää lausekkeeseen vielä muunnos biteiksi.
Tiedonsiirrossa käytetään yksikkönä bittiä sekunnissa, bit/s tai bps, sekä etuliitteinä SI-järjestelmän mukaisia etuliitteitä. Esimerkiksi 1 Gbit/s nopeudella toimiva Ethernet verkkokortti siirtää siis 1 000 000 000 bittiä sekunnissa. Huomioitavaa on se, että yleensä tietoliikenteessä tiedonsiirtonopeus ilmaistaan bittien tiedonsiirtonopeutena, kun taas siirrettävä data yleensä ilmaistaan tavuina. Toisaalta esimerkiksi kiintolevylle kirjoituksen ja lukemisen tiedonsiirtonopeus ilmaistaan esimerkiksi Windows käyttöjärjestelmässä tavuina sekunnissa. Koska 1 tavu on 8 bittiä, on esimerkiksi 1 Gbit/s = 125 MB/s = 125 000 000 tavua sekunnissa. Kun tiedonsiirtonopeuden yksikkönä on tavua sekunnissa, niin tavun lyhenteenä käytetään isoa B kirjainta. Pientä b kirjainta ei tulisi käyttää kuvaamaan bittiä, tosin joskus näkee käytettävän esim. termiä Mb/s, joka ei ole virallinen termi ja voi aiheuttaa sekaannusta siitä onko kyseessä Mbit/s vai MB/s.
Moi Ari, mielenkiinnosta konvertoin gigabitit megatavuiksi oheisen ilmaisen sivun kautta (https://convertlive.com/fi/u/muuntaa/gigabitti%C3%A4/muunna/megatavua#1) ja mietin, että miksiköhän laskee 1 Gbit 128 Megatavuksi?
av: oletan, että jokin virhe toteutuksessa, ehkä mennyt sekaisin eri yksiköt
—Lukujärjestelmät
Binäärilukuja voidaan käyttää muiden lukujärjestelmien lukuarvojen tallentamiseen ja käsittelyyn. Aloitetaan ensin positiivisista kokonaisluvuista, joiden esittäminen eri lukujärjestelmissä noudattaa samanlaista mekanismia. Sen jälkee laajennetaan käsittelyä negatiiviin kokonaislukuihin ja sitten reaalilukuihin. Lopulta se miten informaatio esitetään binäärisessä muodossa on kiinni määrityksistä ja standardeista, joita on sovittu käytettäviksi tai ne ovat nousseet de facto -standardeiksi.
Kymmenjärjestelmän luvut
Kun tieto on digitaalisessa muodossa, niin se tulee esittää jonkin lukujärjestelmän mukaisesti. Tavallisesti ihmisten kesken käytetään desimaalijärjestelmää eli 10-järjestelmää (eng. decimal, lat. Decimus = "kymmenesosa"). Se perustuu kymmenen symbolin, 0, 1, 2, 3, 4, 5, 6, 7, 8 ja 9 käyttämiseen ja sanotaan että 10-järjestelmän kantaluku (eng. base) on 10. Kyseessä on paikkapohjainen järjestelmä, joka tarkoittaa sitä, että numeron paikalla on merkitystä. Esimerkiksi 7123 tarkoittaa, sitä että on 7 kappaletta tuhansia, 1 kappaletta satoja, 2 kappaletta kymmeniä ja 3 kappaletta ykkösiä eli
Luvun arvo saadaan siten, että jokainen numero kerrotaan lukujärjestelmän kantaluvulla (10), joka on korotettu numeron paikan mukaiseen potenssiin, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla. Otetaanpa vielä toinen esimerkki
Tutustutaan seuraavaksi muihin lukujärjestelmiin ja siihen kuinka niillä esitetyt luvut saadaan muutettua 10-järjestelmän luvuiksi.
Binääriluvut
Binäärijärjestelmän kantaluku on 2, jolloin binääriesityksessä käytetään vain kahta symbolia, jotka ovat 0 ja 1. Näitä kutsutaan binäärinumeroiksi (eng. Binary digits (bits) lat. bīnārius = "koostuu kahdesta"). Digitaalilaitteissa tiedon arvo esitetään lähes aina jännitteen avulla. Voidaan määritellä esimerkiksi, että jännitteen arvo alueella 0 – 0.8 V vastaa tiedon arvoa 0 ja että jännitteen arvo alueella 2.0 – 3.2 vastaa tiedon arvoa 1.
Binäärilukua vastaava 10-järjestelmän luku saadaan seuraavasti. Jokainen numero kerrotaan lukujärjestelmän kantaluvulla (2) korotettuna paikkansa mukaiseen potenssiin, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla.
Vastaavaan tapaan voidaan muodostaa myös muiden kantalukujen mukaisia lukujärjestelmiä. Tietokonemaailmassa sekä tiedonsiirrossa käytetään myös muita lukujärjestelmiä, yleensä kuvaamaan binäärilukuja kompaktimmassa muodossa. Tutustutaan seuraavaksi kahteen tällaiseen lukujärjestelmään.
Heksadesimaalijärjestelmä
Seuraavassa taulukossa lukumäärää kuvaavat pisteet on jaoteltu 4 pistettä rivilleen, kun aiemmin oli 5 pistettä rivillä. Tämä sen vuoksi että heksadesimaalilukuja käytetään usein ilmaisemaan 4 bitin joukkoja, eli puolitavuja.
Eräs tärkeä lukujärjestelmä on heksadesimaali- eli 16-järjestelmä (eng. Hexadecimal, gre. hexa + lat. dec. = 6+10 = 16). Nyt tarvitaan siis 16 symbolia heksadesimaalinumeroita varten ja tapana on käyttää symboleja 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E ja F. Aakkostosta lainataan symbolit A, B, C, D, E ja F kuvaamaan lukumääriä kymmenestä viiteentoista. Vaihtoehtoisesti symboleina käytetään myös pieniä kirjaimia a, b, c, d, e ja f.
Heksadesimaalilukua vastaava 10-järjestelmän luku saadaan seuraavasti. Summataan jokainen numero (merkki), jotka kerrotaan lukujärjestelmän kantaluvulla (16) korotettuna paikkansa mukaiseen potenssiin, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla.
Binäärijärjestelmän binääriluvut on helppo muuttaa heksadesimaalijärjestelmään. Ryhmitellään binäärinumerot neljän alkion ryhmiin oikealta alkaen. Jos vasemman puoleinen ryhmä jää vajaaksi, lisätään tarvittaessa nollia MSB biteiksi. Sitten jokainen ryhmä muutetaan vastaavaksi heksanumeroksi. Esimerkiksi
Kahdella viimeisellä rivillä on vielä heksaluvun muunnos 10-järjestelmään. Vastaavasti heksadesimaaliluvut voidaan muutta binääriluvuiksi heksanumero kerrallaan.
Oktaalijärjestelmä
Oktaalijärjestelmän kantaluku on kahdeksan ja sen mukaisissa lukujen esityksissä käytetään symboleja 0, 1, 2, 3, 4, 5, 6 ja 7. Muunnos oktaalijärjestelmän luvusta 10-järjestelmän lukuun tehdään vastaavasti kuin 16-järjestelmässä tai missä tahansa muusta järjestelmässä.
Eli oktaalijärjestelmän numerot kerrotaan lukujärjestelmän kantaluvulla (8) korotettuna paikkansa mukaiseen potenssiin, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla. Ja lopuksi summataan saadut tulokset.
Koska 8 = 23, niin yhteys binäärijärjestelmään on helppo. Ryhmitellään vain binääriluku kolmen binäärinumeron ryhminä oikealta vasemmalle ja täydennetään tarvittaessa vasemmanpuoleisin ryhmä vasemmalta nollilla. Tämän jälkeen jokainen kolmikko muutetaan vastaavaksi oktaalijärjestelmän numeroksi. Esimerkiksi
Edellä, kahdella viimeisellä rivillä, on oktaalijärjestelmän luku muutettu 10-järjestelmän luvuksi. Koska 2-järjestelmän luku on sama kuin edellä 16-järjestelmän tapauksessa, on 10-järjestelmän lukukin sama.
Oktaali- ja heksadesimaalijärjestelmien pääasiallinen tehtävä on koota pitkiä binäärimuotoisen luvun numerosarjoja paremmin hallittaviin pienempiin ryhmiin. Alla on taulukoitu edellä esitettyjen lukujärjestelmien 20 ensimmäistä lukua ja niiden vastaavuudet toisiinsa.
Kun käsitellään erilaisia lukujärjestelmiä, täytyy ne erottaa toisistaan. Jatkossa ilmaistaan käytettävän lukujärjestelmän kantaluku luvun perässä olevalla alaindeksillä, kuten edellä on tehty. On myös muita tapoja lukujärjestelmän ilmaisemiseksi, esimerkiksi ohjelmointikielissä, kun ei ole mahdollista esittää alaindeksejä.
Lukujärjestelmät ohjelmointikielissä
Kun ohjelmointikielissä käytetään 10-lukujärjestelmistä poikkeavia lukujärjestelmiä, ilmaistaan lukujärjestelmä etumerkinnällä. Esimerkiksi Java- ja C-kielessä tai
ja 10-järjestelmän luvut ilman etumerkintää, esimerkiksi
. Uusimmissa ohjelmointikielten versioissa on myös binääriluvuille vastaavanlainen merkintätapa
. Joissain yhteyksissä käytetään myös loppukirjaintunnusta
,
tai
,
.
Alla on pieni Java ohjelma, jossa käytetään binääri-, okta- ja heksalukujen etumerkintää, kun luvut sijoitetaan int tyyppiseen muuttujaan. Ajettaessa koodi, tulee tulosteeksi vastaavat 10-järjestelmän luvut. Käydään myöhemmin säännöt sille, miten lukujärjestelmien välillä tehdään muutoksia, mutta voit esimerkiksi kokeilla muuttaa lukuja siten että saat kaikista tulosteeksi saman 10-järjestelmän luvun.
Alla vastaava Python 3 ohjelma. Huomioi, että Pythonissa oktaluvun esitystapa eroaa edellisestä. Tarkista käyttämäsi ohjelmointikielen merkintätapa, jos käytät muita kuin 10-järjestelmän lukuja. Muita lukujärjestelmiä kannattaa käyttää esimerkiksi silloin, jos toteuttaa binääripohjaista tiedonsiirtoprotokollaa, jolloin informaatiota joutuu asettamaan lähetettävään pakettiin tavu tai jopa bitti kerrallaan.
Muuntaminen eri lukujärjestelmien välillä
Muuntaminen muista lukujärjestelmistä 10-järjestelmään
Edellä käytiinkin jo esimerkkien avulla läpi muuntaminen binääri-, oktaali- sekä heksadesimaalilukujärjestelmistä 10-lukujärjestelmään. Yleinen kaava kokonaislukujen muunnokselle 10-lukujärjestelmään, mistä tahansa muusta lukujärjestelmästä on
missä on siis lukujärjestelmän kanta (eli kuinka monta merkkiä on käytössä) ja alaindeksi ilmaisee merkin paikan, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla.
Muuntaminen 10-järjestelmästa muihin lukujärjestelmiin
10-lukujärjestelmän luvun muuntaminen binääriluvuksi voidaan toteuttaa jakamalla luku kahdella (binäärijärjestelmän kantaluvulla), ja sen jälkeen saatu tulos taas kahdella, tallentaen jakojäännökset, niin kauan, kunnes tulokseksi saadaan nolla.
Esim. 1 8610 muunnetaan binääriluvuksi
43 21 10 5 2 1 0
2 86 2 43 2 21 2 10 2 5 2 2 2 1
86 42 20 10 4 2 0
0 1 1 0 1 0 1
(binääriluku saadaan lukemalla jakojäännökset oikealta)
⇒ 8610 = 10101102
Jakojäännökset käänteisessä järjestyksessä on 10-järjestelmän lukua vastaava binääriluku.
Vastaavasti, kohdelukujärjestelmän kantaluvulla jakaen, voidaan 10-lukujärjestelmän lukuja muuntaa muihin lukujärjestelmiin. Alla esimerkki heksajärjestelmään muuntamisesta
Esim. 2 8610 muunnetaan heksaluvuksi
5 0
16 86 16 5
80 0
6 5
(heksadesimaaliluku saadaan lukemalla jakojäännökset oikealta)
⇒ 8610 = 5616 = 0x56
Jakolasku, sen tulokset ja jakojäännökset ilmaistaan laskettaessa 10-järjestelmän luvuilla. Kun jakojäännöksistä muodostetaan kohdejärjestelmän lukua, täytyy 10-järjestelmän luvut muuntaa kohdejärjestelmän luvuiksi.
Esim. 3 11010 muunnetaan heksaluvuksi
6 0
16 110 16 6
96 0
14(=E) 6
(heksadesimaaliluku saadaan lukemalla jakojäännökset oikealta)
⇒ 11010 = 6E16 = 0x6E
Muunnosten toteuttaminen pinon avulla
Jakojäännösten lukeminen käänteisessä järjestyksessä saadaan toteutettua esimerkiksi tallentamalla jokainen jakojäännös pinoon ja muunnoksen kohdelukujärjestelmän luku saadaan lukemalla jakojäännökset pinosta. Pino toimii LIFO (Last In, First Out) periaatteella, eli viimeisimmäksi pinoon asetettu elementti pitää ottaa ensimmäisenä pois. Alla voit tehdä muunnoksia 10-lukujärjestelmästä positiivisista kokonaisluvuista muihin lukujärjestelmiin. Funktion baseConverter ensimmäinen parametri on muutettava luku, ja toinen lukujärjestelmän kanta johon muunnetaan. Tulosteessa näkyy jakolaskut, jakojäännökset sekä pinon täyttyminen. Huomaa koodin tulosteessa, että pino täytetään vasemmalta ja tyhjennetään vasemmalta ja että pinoon tallennetaan 10-lukujärjestelmän laskutoimituksesta saatu jakojäännös muunnoksen kohteena olevan lukujärjestelmän merkkeinä.
Tietokoneet siis käsittelevät informaatiota binäärilukuina. Heksa- ja oktalukujärjestelmiä käytetään yleensä visualisoimaan binäärilukuja ihmiselle. Jotta binäärilukuja voi käyttää tietokoneissa esimerkiksi laskemiseen tulee toteuttaa logiikka (looginen piiri/komponentti), joka antaa ulostulonaan halutun laskutoimituksen.
Lukujen esitys tietokoneissa
Kun tunnetaan lukujärjestelmät, niin voidaan tarkastella lukujen tallettamista tietokoneessa. Perusideana on, että luvut talletetaan binäärimuodossa, mutta silloinkin on vielä erilaisia vaihtoehtoja. Tärkeintä on valita sellainen talletusmuoto, joka mahdollistaa tehokkaat laskennat luvuilla. Tietokoneiden (prosessorien) tärkeimpiä laskemistoimenpiteitä ovat yhteen-, vähennys-, kerto- ja jakolasku.
Laskenta tapahtuu aritmeettis-loogisessa yksikössä (eng Arithmetic Logic Unit (ALU)), ja sinne tuodaan dataa rekistereistä sekä lisäksi ohjaustietoja, jotka määrittää esim. suoritettavan laskutoimituksen. ALU palauttaa tietoja rekistereihin ja lisäksi erilaisia lipputietoja, flags, jotka talletetaan myös keskusyksikön rekistereihin.
Tietokoneissa lukuja siis talletetaan eri paikkoihin ja on tärkeää tietää, että yleensä luku talletetaan paikkaan, jonka koko on ennalta kiinnitetty, eli yhtä lukua varten on käytössä kiinteä määrä bittejä.
Binäärilukujen yhteenlasku
Binääriluku voi koostuu yhdestä tai useammasta binäärinumerosta. Binäärinumero voi saada vain kaksi arvoa, joten binäärinumeroille (1-bittinen binääriluku) on neljä erilaista yhteenlaskua, jotka on esitelty alla
Yhteenlaskun säännöt binäärinumeroille
1
0 0 1 1
+ 0 + 1 + 0 + 1
0 1 1 10
Kombinaatiologiikassa opitaan myöhemmin, kuinka yhteenlasku toteutetaan loogisilla komponenteilla.
Voit tutustua binäärilukujen yhteenlaskuun alla olevalla visualisoinnilla. Voit valita yhteenlaskettavat luvut, sekä sen kuinka monta bittiä käytetään lukujen (sekä tuloksen) esittämiseen.
Edellä olevaan yhteenlaskun visualisointiin voi antaa myös negatiivisia lukuja. Visualisoinnissa 10-järjestelmän luvut esitetään binäärilukuna ns. kahden komplementti -muodossa, joka on yleisin tietokoneiden käyttämä binäärinen esitystapa negatiivisille luvuille. Seuraavassa luvussa käydään läpi muutama erilainen tapa esittää negatiivisia lukuja binäärilukujärjestelmällä.
Negatiivisten lukujen esitys binäärilukujärjestelmässä
Se kuinka suuria 10-lukujärjestelmän lukuja voidaan tallentaa esimerkiksi ohjelmointikielen muuttujaan, riippuu mm. siitä kuinka monta bittiä on käytössä tallennukseen. Ohjelmointikielissä on erilaisia tyyppejä erilaisten lukujen käsittelemiseen ja tallentamiseen. Tähän mennessä olemme käsitelleet etumerkittömiä lukuja. Esimerkiksi C#:n tyypin (unsigned) byte koko on 8 bittiä, johon voidaan tallentaa etumerkittömiä lukuja, eli 10-järjestelmän luvut väliltä 0 - 255. Toisaalta C# -kielestä löytyy myös etumerkillinen tavu sbyte, jonka koko on myös 8 bittiä, mutta johon voi tallentaa myös negatiivisia lukuja, tällöin luvut tulee olla väliltä -128 - 127. Huomioi että eri ohjelmointikielissä tyypit voivat olla määritelty eri tavalla, vaikka niillä olisikin sama nimi. Esimerkiksi Javan tavu tyyppi - byte on etumerkillinen, eikä Javassa ole olemassa erikseen tyyppiä etumerkittömälle tavulle.
Ohjelmointikielissä on harvoin tarvetta esittää muuttujia binäärisenä, eikä niissä monesti ole metodeja, jotka tukisivat eri bittisiä positiivisten ja negatiivisten lukujen binääristen esitystapojen tulostamista. Alla muutama koodinpätkä, joilla saa tavun esitettynä 8-bittisenä binäärilukuna. Monesti muunnoksiin tarvittavat metodit käsittelevät 16-bittisiä tai suurempi bittisiä tyyppejä, eivätkä näytä haluttua bittimäärää ja ao. koodeissakin on 'virityksiä', jotta esitystavat saadaan 8-bittisiksi. On muitakin menetelmiä ja viimeisen esimerkin maskaus-menetelmä on sovellettavissa myös eri tavoin eri ohjelmointikielissä. Javalla
C# -ohjelmointikielellä, esimerkiksi
Ja Python 3
Koodeja testaamalla ja muuttujien arvoja muuntelemalla havaitaan, että negatiivilla luvuilla on vasemman puolimmainen (eniten merkitsevä, eng. MSB Most Significant Bit) bitti ykkönen. Toisaalta C#:n byte tyypissä MSB bitti on ykkönen osassa lukuja, vaikka tyyppiin ei negatiivisia lukuja voi tallentaa. Toisin sanoen sama bittikuvio voi tarkoittaa eri asiaa ja on riippuvainen mm. käytettävän muuttujan tyypistä. Onko negatiivinen versio positiivisesta binääriluvusta siis sellainen, että lisätään ykkönen MSB bitiksi? Voisi olla, mutta se ei ole kovin tehokas tapa esittää negatiivisia lukuja binäärilukuina. Negatiivisten binäärilukujen esitystavalle on useita eri menetelmiä ja käydään muutama niistä läpi jotta ymmärretään, miksi tänä päivänä käytetään kahden komplementti muotoa ja miten se määritellään.
Suora talletustapa
Tutustutaan ensin yksinkertaisimpaan menetelmään negatiivisen binääriluvun määrittämiseksi. Suorassa talletustavassa (eng. Signed magnitude representation) eniten merkitsevä bitti (MSB) vastaa etumerkkiä. Käytetään esimerkeissä 8-bittisiä binäärilukuja visuaalisuuden säilyttämiseksi, useampi bittisille luvuille pätee vastaavasti. Esimerkkinä MSB bitillä etumerkin ilmaiseminen
+6510 = 010000012
vaihdetaan MSB bitti, jotta saadaan negatiivinen
110000012 = -6510
Huonona puolena merkintätavassa on se, että nollalla kaksi merkintää, 0000000002 = +0 ja 1000000002 = -0. Tämä johtaisi tietokoneen prosessorissa siihen että aina kun prosessorin täytyy tutkia, että onko luku 0, se joutuisi tutkimaan onko luku positiivinen nolla tai onko luku negatiivinen nolla. Lisäksi huonona puolena on se, että vähennyslaskua ei voi suorittaa muuttamalla se vastaavan negatiivisen luvun yhteenlaskuksi. Eli kuten esimerkiksi koulumatematiikassa, on 7 - 5 = 2 vastaava laskutoimitus kuin 7 + (-5) = 2. Tämä ei siis onnistuisi negatiivisten lukujen suoralla talletustavalla. Jos vähennyslaskut voidaan muuttaa yhteenlaskuiksi, niin silloin prosessoriin ei tarvita erillistä komponenttia vähennyslaskulle.
Binary Decimal
Vähennyslasku
00000111 +7 Dec Bin Yhteenlasku negatiivisella luvulla
00000110 +6 111
00000101 +5 7 00000111 00000111 (+7)
00000100 +4 -5 -00000101 +10000101 +(-5)
00000011 +3 2 == 00000010 10001100 != +2
00000010 +2
00000001 +1
00000000 +0
10000000 -0
10000001 -1 Binäärisen vähennyslaskun säännöt
10000010 -2
10000011 -3
10000100 -4
10000101 -5
10000110 -6
10000111 -7
Yhden komplementtimuoto
Komplementti tarkoittaa vastalukua ja yhden komplementtimuoto negatiivisille binääriluvuille saadaan muuttamalla vastaavan positiivisen binääriluvun kaikki bitit vastaluvuikseen. Eli esimerkkinä
+6510 = 010000012
mistä saadaan luku -6510 muuttamalla kaikki bitit vastaluvuikseen
101111102 = -6510
Tässäkin muodossa vasemman puolimmainen (MSB) bitti ilmaisee etumerkin, muuten esitystapa on siis erilainen kuin suorassa talletustavassa. Yhden komplementti esitystavalla voidaan vähennyslasku muuttaa yhteenlaskuksi, kun yhteenlaskun tulokseen lisätään ylivuotobitti (ykkönen). Ylivuotobitin lisäyksestä juontuu menetelmän nimessä termi yhden. Huonona puolena menetelmässä on tarve lisätä ylivuotobitti negatiivisten lukujen yhteenlaskussa sekä se että nollalla on kaksi binääristä merkintätapaa.
Binary Decimal 00000111 +7 Yhteenlasku negatiivisilla luvuilla 00000110 +6111111100000101 +500000111(+7)00000100 +4+ 11111010+(-5)00000011 +310000000100000010 +2 | Ylivuotobitti lisätään tulokseen 00000001 +1 | 1 00000000 +0 | 00000001 11111111 -0 -->+ 111111110 -100000010== +2 11111101 -2 11111100 -3 11111011 -4 Ylivuoto bitin lisäyksestä tulee 11111010 -5 nimeen Yhden komplementti 11111001 -6 11111000 -7
Kahden komplementtimuoto
Käytännössä kaikki tietokoneet, puhelimet ja vastaavat laskutoimituksia tekevät digitaaliset laitteet käyttävät tänä päivänä negatiivisten binäärilukujen esitysmuotona ns. kahden komplementtimuotoa. Kahden komplementtimenetelmässä negatiivinen binääriluku muodostetaan seuraavasti. Ensin vastaavan positiivisen luvun binääriesityksestä muodostetaan yhden komplementti, eli muutetaan kaikki bitit vastaluvuikseen. Sen jälkeen yhden komplementtimuotoon lisätään ykkönen, mistä juontaa menetelmän nimessä termi kahden. Jatketaan yhden komplementin esimerkistä, eli luvun -6510 yhden komplementtimuoto oli
101111102(1-komplementti)
johon lisätään ykkönen, eli
101111102 + 000000012 = 101111112
ja tuloksena on siis kahden komplementtimuoto luvulle -6510
101111112(2-komplementti) = -6510
Kuten aiemmin, kahden komplementtimuodossa vasemman puolimmainen (MSB) bitti ilmaisee etumerkin. Hyötynä yhden komplementtiin verrattuna on, että nyt on vain yksi esitystapa nollalle, sekä lisäksi negatiivisten lukujen yhteenlaskun yksinkertaistuminen. Sen sijaan että ylivuotobitti tulee lisätä yhteenlaskun tulokseen, jätetään ylivuotobitti kokonaan huomioimatta. Huomaa että ylivuotobittiä tarvitaan kuitenkin informaatioksi jos esim. kahden positiivisen luvun summa ylittää esitystavan bittimäärän. Ylivuotobitti voidaan jättää negatiivisen luvun yhteenlaskussa huomioimatta, koska se on jo lisätty tehtäessä kahden komplementtimuunnos.
Binary Decimal 00000111 +7 Yhteenlasku negatiivisilla luvuilla 00000110 +61111111100000101 +5 00000111 (+7) 00000100 +4+11111011+(-5)00000011 +3 100000010 00000010 +2 00000001 +1 Ylivuotobitti yksinkertaisesti jätetään huomioimatta 00000000 +0 11111111 -1100000010 ⇒ 00000010 == +2 11111110 -2 11111101 -3 11111100 -4 11111011 -5 11111010 -6 11111001 -7 11111000 -8
Muunnos kahden komplementtimuodon negatiivisesta binääriluvusta tehdään vastaavasti, mutta käänteisessä järjestyksessä. Käydään muunnos läpi käyttämällä esimerkkinä binäärilukua
111110102(2-komplementti)
Kahden komplementtimuodon binääriluku muunnetaan ensin yhden komplementtimuotoon vähentämällä binääriluvusta yksi.
111110102 - 000000012 = 111110012
Saatu binääriluku on siis yhden komplementtimuodossa
111110012(1-komplementti)
Sen jälkeen yhden komplementtimuodon binääriluku negatoidaan, eli vaihdetaan luvun etumerkkiä, muuntamalla jokainen bitti käänteisluvukseen.
111110012 ⇒ 000001102
Muunnetaan saatu binääriluku 10-järjestelmän luvuksi
000001102 = 610
Lopuksi kumotaan aiemmin tehty etumerkin vaihto, eli vaihdetaan saadun 10-järjestelmän luvun etumerkki
610 ⇒ -610
ja tulos on siis kahden komplementtimuodon negatiivista binäärilukua 111110102 vastaava negatiivinen 10-järjestelmän luku.
Kokonaislukujen esittämiselle binäärimuodossa on myös monia muita menetelmiä, esim.
- Offset binary - "Siirretty binäärimuoto", Excess-K
- Negative base - Negatiivinen kantaluku
- Binary-coded decimal - BCD-koodi
- Gray code - Gray koodi
Tietokoneet käyttävät siis sisäisessä toteutuksessa kahden komplementtimuotoa.
Reaaliluvun muuntaminen binääriseksi
Reaaliluvun kokonaislukuosa muutetaan binääriseksi samalla tavalla kuin kokonaislukujen tapauksessa, eli jaetaan kantaluvulla niin kauan, kunnes saadaan jakolaskun tulokseksi nolla ja jakojäännöksistä saadaan käänteisessä järjestyksessä kokonaislukua vastaava binääriluku. Reaaliluvun desimaaliosa muunnetaan puolestaan kertolaskun avulla, kertomalla desimaaliosaa kantaluvulla, kunnes tulokseksi saadaan yksi, tai päädytään päättymättömään silmukkaan. Tutkitaan seuraavia esimerkkejä.
Esimerkki 6.37510 muunnetaan binääriluvuksi
3 1 0
2 6 2 3 2 1
6 2 0
0 1 1
(binääriluvun kokonaislukuosa saadaan lukemalla jakojäännökset oikealta)
⇒ 610 = 1102
Binääriluvun desimaaliosa saadaan kertolaskulla
.375*2 = 0.75 (pienempi kuin yksi → ensimmäinen bitti on 0)
.75*2 = 1.5 (suurempi kuin yksi → seuraava bitti on 1)
(huom. edeltä vain desimaaliosa otetaan mukaan seuraavaan kertolaskuun)
.5*2 = 1.0 (yhtä suuri kuin yksi → seuraava bitti on 1)
Jos saadaan tasan 1.0 ⇒ muunnos on valmis.
Desimaaliosan bitit saadaan siis laskemisjärjestyksessä ja ovat 011
Lopulta yhdistetään kokonaislukuosa ja desimaaliosa, eli saadaan
6.37510 = 110.0112
Joillain desimaaliluvuilla ei ole tarkkaa tallennusmuotoa binäärisenä, koska muunnoksessa käytetty kertolasku ei koskaan anna tulokseksi ykköstä. Esimerkiksi 0.110 on eräs desimaaliluku, josta tietokoneet eivät kykene tallentamaan tarkkaa arvoa, vaan ne tallentavat lähimmän binäärisen vastineen.
Esimerkki Olkoon meillä luku 0.110 = .1*2 = 0.2 (pienempi kuin yksi → 0) .2*2 = 0.4 (pienempi kuin yksi → 0) .4*2 = 0.8 (pienempi kuin yksi → 0) .8*2 = 1.6 (suurempi kuin yksi → 1) .6*2 = 1.2 (suurempi kuin yksi → 1) .2*2 = 0.4 (pienempi kuin yksi → 0) .4*2 = 0.8 (pienempi kuin yksi → 0) .8*2 = 1.6 (suurempi kuin yksi → 1) … = (0.00011001100110011001100110011001100110011…)2 Kertolaskut ei lopu koskaan, joten se katkaistaan, kun on saatu tarpeeksi bittejä käytettyä tallennusmenetelmää varten.
Binääriluvun muuntaminen reaaliluvuksi
Kokonaislukujen muuntamiseksi 10-järjestelmään, mistä tahansa muusta lukujärjestelmästä esitettiin aiemmin kaava
missä on siis lukujärjestelmän kanta ja alaindeksi alkoi nollasta ilmaisten merkin paikan, kun paikat lasketaan oikealta vasemmalle alkaen paikasta numero nolla. Tutkitaan nyt vain binäärilukujen muunnosta reaaliluvuiksi. Paikka numero nolla on siis ensimmäinen paikka binääripisteen, yleisesti radix-pisteen, vasemmalla puolella. Binääripisteen oikealla puolella olevat binääriosan merkkien paikat ovat siten negatiivisia, alkaen paikasta -1 aivan binääripisteen oikealla puolella.
Otetaan esimerkiksi binääriluku 110.0112, sen merkkien paikkojen indeksit ovat siten
Paikan indeksi: 2 1 0 -1 -2 -3
Vastaava merkki: 1 1 0 . 0 1 1Muunnos reaaliluvuksi tehdään vastaavasti kuin kokonaisluvuksi, eli kerrotaan jokaisessa paikassa oleva merkki lukujärjestelmän kannalla, joka on korotettu paikkansa mukaiseen potenssiin ja summataan termit, eli esimerkin tapauksessa
Pitäisikö tässä olla #- 6+(3/8) ?
—Ei tarvitse olla, \(6\frac{3}{8} = 6 + \frac{3}{8}\)
—Yleistetty kaava muunnoksille 10-järjestelmään, joka sisältää sekä kokonaisluvut että reaaliluvut, on siis
Reaalilukujen huomioiminen ohjelmoinnissa
Aina ei siis voi binääriluvuksi tallentaa tarkkaa arvoa reaaliluvusta, kuten esimerkiksi luvun 0.1 tapauksessa, koska sellaista ei ole olemassa. Yleensä ohjelmointikielet kuitenkin näyttävät tulostettaessa pyöristetyn arvon, vaikka luku on tallennettu lähimpänä approksimoituna binäärilukuna. Laskutoimituksissa kuitenkin käytetään tallennettua approksimaatiota, mistä voi tulla virheitä laskettaessa hyvin pienillä tai hyvin suurilla liukuluvuilla. Lisäksi approksimointi johtaa siihen, että kahdella reaaliluvulla voi olla sama binäärinen tallennusmuoto, jolloin ne ovat tietokoneen mielestä samat luvut. Joissain tapauksissa virhe kertaantuu ihmiselle yksinkertaisissa laskuissa, siten että saadaan vääriä vastauksia.
Edelliset esimerkit olivat Pythonilla, ja halutessasi voit tutustua tarkemmin sen liukulukujen esittämiseen ja rajoitteisiin. Liukuluku on nimitys reaaliluvusta muunnetun binääriluvun talletustavalle, johon perehdytään seuraavassa luvussa. Pythoniin löytyy laajennus jota voi käyttää silloin, jos laskennassa törmää rajoitteisiin. On tosin olemassa myös laskentaan erikoistuneita kieliä. Riippumatta käyttämästäsi ohjelmointikielestä, ota huomioon reaalilukujen rajoitetut tallennustavat digitaalisessa muodossa.
Otetaan vielä esimerkiksi reaaliluku 0.1, josta aiemmin todettiin, että sille ei ole tarkkaa binääristä esitystapaa. Tallentaessa binäärilukuja tietokoneille, käytetään erilaisia tallennustapoja, riippuen siitä kuinka suurella tarkkuudella luku halutaan tallentaa. Seuraavassa luvussa käydään tallennustapoja tarkemmin läpi mutta alla voit nähdä reaalilukua 0.1 vastaavan erään tallennustavan binäärisen muodon.
Alla oleva, artikkelista lainattu, DoubleConverter luokka tulostaa C#:ssa double:na talletetun desimaalilukua vastaavan tallennetun binääriluvun tarkan lukuarvon desimaaliluvuksi muutettuna.
Reaalilukujen esittäminen liukulukuina
Reaaliluvut esitetään tietokoneissa liukulukuina (eng. floating point numbers, joskus suomeksi liukuvan pilkun/pisteen luvut), joka on kaavamainen esitystapa reaaliluvuille. Liukuluvut approksimoivat reaaliluvun todellista arvoa. Yleensä kun käsitellään esimerkiksi hyvin suuria lukuja, mutta tarvitaan vain muutaman merkitsevän kymmenlukujärjestelmän merkin tarkkuutta, voidaan luvut tallentaa pienempään tilaan liukulukuna kuin kokonaislukuna, voidaan valita pieni tallennustila esitystarkkuuden sijaan. Reaaliluvuilla laskettaessa tulee varautua hyvin suurien ja hyvin pienien lukujen tapauksiin, koska niitä laskettaessa approksimaatioista tuleva virhe kasvaa.
Nykyään liukulukujen laskemiseen on tietokoneiden prosessoreissa yksi tai useampia matematiikkayksiköitä (eng. FPU, Floating Point Unit). Aiemmin (ennen 1990 lukua) tietokoneissa oli erillinen FPU yksikkö, tai liukulukulaskenta toteutettiin ohjelmallisesti. Tänä päivänä esim. sulautettujen järjestelmien suorittimet voi olla toteutettu ilman integroitua FPU yksikköä.
Merkitseviä numeroita kutsutaan liukulukujen yhteydessä mantissaksi (eng. mantissa, myös significand tai coefficient). Liukuluku esitetään mantissan ja lukujärjestelmän kannan eksponentin tulona, yleisesti
Digitaalisissa järjestelmissä kantalukuna on 2. Yleisesti mantissa ja eksponentti ovat etumerkillisiä, mutta esim. tietokoneiden käyttämissä esitystavoissa eksponentti biasoidaan positiiviseksi.
Termi liukuluku tulee siitä, että numeron desimaalipiste (eng. decimal point, yleisemmin lukujärjestelmille eng. radix point - 'kantalukupiste') tai binäärilukujen tapauksessa binääripiste voi 'liukua'. Eli piste voidaan asettaa mihin tahansa kohtaan suhteessa luvun merkitseviin numeroihin. Tämä paikka osoitetaan liukuluvun eksponenttiosalla. Liukuluvun esitystapaa voidaan pitää eräänlaisena tieteellisenä merkintätapana.
Tietokoneissa on ollut käytössä useita erilaisia liukuluvun esitystapoja. Vuonna 1985 IEEE (Institute of Electrical and Electronics Engineers) -organisaatio julkaisi standardin IEEE Standard 754, jota on päivitetty 2008, jonka mukaisia liukulukujen esitystapoja suurin osa tietokoneista käyttää tänä päivänä. Alkuperäinen standardi määritteli kaksi tallennusmuotoa binääriselle liukuluvulle
joista Single precision määritelmää käytetään usein "C-kieliperheen" ohjelmointikielissä float tyypille ja Double precision määritelmää käytetään usein "C-kieliperheen" ohjelmointikielissä double tyypille. Laajennettu vuoden 2008 standardi määrittelee mm. lisää tallennusmuotoja.
Jos käytetään esimerkiksi IEEE 754 single precision tallennustapaa, niin reaaliluvut saadaan tallennettua binäärisenä noin 7 desimaalinumeron tarkkuudella. Käytettäessä double precision tallennustapaa saadaan reaaliluvut tallennettua noin 16 desimaalinumeron tarkkuudella.
Koska tietokoneet tallentavat luvut aina binäärisenä, ei tietoa kannasta tarvitse tallentaa, kanta on aina 2. Riittää tallentaa mantissa ja eksponentti, ottaen huomioon niiden etumerkit. Standardeissa on varattu yksi bitti mantissan etumerkille. Eksponentti puolestaan tallennetaan aina positiivisena kokonaislukuna, siten että eksponentin arvoon lisätään biasointiarvo. Biasointiarvot eri talletusmuodoille on määritelty IEEE 754 standardissa. Biasoinnilla saadaan negatiiviset eksponentit muutettua positiivisiksi tallennusta varten, täten eksponentin etumerkille ei tarvitse varata erillistä etumerkkibittiä.
Esimerkiksi 32-bittisessä Single precision -tallennusmuodossa on yksi bitti mantissan etumerkille (MSB bitti), seuraavat 8 bittiä on varattu eksponentille ja loput 23 bittiä on varattu mantissalle. Eksponentin arvoon lisätään tallennettaessa aina biasointiarvo, joka Single precision -tallennustavalle on 127, näin ollen tallennettavalla lukuvälillä eksponentti voidaan aina tallentaa etumerkittömänä lukuna. Alla on visualisointi desimaaliluvun 0.15625 tallentamisesta binäärisenä 32-bittiseen Single precision -tallennusmuotoon.

Viimeisen bitin pyöristäminen
IEEE754 Single precision Standardi, ja muut vastaavasti, määrittelee erilaisia pyöristyksiä sellaiseen tapauksiin, kun muunnos ei mene tasan. Esimerkiksi desimaaliluvun 0.1 muunnoksessa binääriseksi viimeisen bitin vaihtaminen ykköseksi tehdään pyöristyksen vuoksi. Viimeisen bitin (LSB) ollessa 1, on tallennettu binääriluvun arvo lähempänä arvoa 0.1, kuin jos viimeinen bitti olisi 0. Voi vaikka itse kokeilla tehtävien tarkistimen vastauksista antamilla desimaaliluvuilla katsoa kuinka paljon ne eroavat arvosta 0.1.
Tietokone, tai oikeastaan ohjelmistot ja ohjelmointikielet, osaavat pyöristämisen, kun niihin on määritelty standardin mukaiset säännöt binäärilukujen tallentamiseen eri formaateissa.
Reaaliluvun muunnos liukuluvuksi
Käydään seuraavaksi läpi desimaaliluvun muunnos liukuluvuksi esimerkin avulla. Olkoon meillä 10-järjestelmän reaaliluku 0.1562510 ja muunnetaan se IEEE 754 Single precision muotoon. Ensin muunnetaan reaaliluku binääriseksi. Kokonailukuosa on nolla, joten tarkastellaan vain desimaaliosaa.
Esimerkki 0.1562510 muunnetaan binääriluvuksi Binääriluvun desimaaliosa saadaan kertolaskulla .15625*2 = 0.3125 (pienempi kuin yksi → ensimmäinen bitti on 0) .3125*2 = 0.625 (pienempi kuin yksi → seuraava bitti on 0) .625*2 = 1.25 (suurempi kuin yksi → seuraava bitti on 1) .25*2 = 0.5 (pienempi kuin yksi → seuraava bitti on 0) .5*2 = 1.0 (yhtä suuri kuin yksi → viimeinen bitti on 1 ⇒ muunnos valmis) Desimaaliosan bitit saadaan siis laskemisjärjestyksessä ja ovat 00101 Lopulta yhdistetään kokonaislukuosa ja desimaaliosa, eli saadaan 0.1562510 = 0.001012
.625*2-kohdassa pitäisi lukea suurempi kuin yksi, ei pienempi
—Korjattu
—Reaaliluku 0.1562510 on binäärisenä 0.001012.
Tallennusta varten muutetaan binääriluku tieteellistä muotoa vastaavaan muotoon (normalisoidaan mantissa), missä siis on yksi merkitsevä numero binääripisteen vasemmalla puolella.
0.001012 ⇒ 1.012 × 2-3
Koska aina tehdään vastaava mantissan normalisointi, on tallennettavan liukuluvun binääripisteen vasemmalla puolella aina arvo 1. Tämä jätetään tallennettaessa pois, eli säästetään yksi bittipositio, millä saadaan 'ilmaiseksi' yhden bitin verran lisää tarkkuutta. Eli binääripisteen oikealla puolella olevat bitit tallennetaan mantissaan (joskus käytetään myös termiä eng. fraction). Tarpeen mukaan lisätään nollia biasoidun eksponentin binääriesityksen vasemmalle puolelle. Nyt muunnettava luku on positiivinen, joten etumerkkibitti on 0.
Eksponentti -3 biasoidaan lisäämällä siihen luku 127
-3 + 127 = 124
joka muutetaan etumerkittömäksi binääriluvuksi
124 ⇒ 01111100
joka sitten tallennetaan eksponentille varattuihin bittipositioihin.
Kun yhdistetään etumerkkibitti 0, eksponenttibitit 01111100, binäärimuunnoksesta saadut binääripisteen oikealla puolella olevat bitit 01 ja ylimääräiset nollat 32:een bittiin asti 000000000000000000000, saadaan
00111110001000000000000000000000
Liukuluvun muunnos desimaaliluvuksi
Liukuluvun muuntaminen desimaaliluvuksi tehdään käänteisesti edellisessä luvussa esitettyyn menetelmään verrattuna. Otetaan tarkasteltavaksi desimaaliluvun 0.1562510 32-bittinen Single precision liukulukumuoto
001111100010000000000000000000002
Otetaan ensin käsiteltäväksi eksponentti 011111002 = 12410 ja vähennetään siitä Single precision -muodon eksponentin biasointiarvo 127, eli 124 - 127 = -3. Sitten otetaan mantissan bitit binääriluvun desimaaliosaksi ja lisätään aina kokonaislukuosaksi 1, koska tallennettu mantissa on normalisoitu.
1.010000000000000000000002
Lopuksi binäärilukuun lisätään normalisoinnin seurauksena saatu eksponentti, eli kerrotaan binääriluku kantaluvulla, joka on korotettu eksponentin mukaiseen potenssiin.
1.010000000000000000000002 × 2-3
Seuraavaksi poistetaan normalisointi, eli siirretään desimaalipistettä eksponentin verran, vasempaan jos eksponentti on negatiivinen ja oikeaan jos eksponentti on positiivinen
0.001010000000000000000002
Poistetaan oikealta ylimääräiset nollat
0.001012
minkä jälkeen binääriluku muutetaan desimaaliluvuksi. Koska etumerkkibitti oli 0 on saatu desimaaliluku positiivinen.
0.001012 = 1 × 2-3 + 1 × 2-5 = 1/8 + 1/32 = 5/32 = 0.15625
IEEE 754 standardin talletusmuodot johtavat siihen, että nollalle on kaksi binääristä merkintää, negatiivinen ja positiivinen nolla. Lisäksi on varattu erityiset bittikombinaatiot negatiiviselle ja positiiviselle äärettömyydelle sekä 'epänumeroille' (eng. Not a Number - NaN). Standardi myös määrittää laskutoimitukset edellisille.
Merkistöt
Numeroiden lisäksi tietokoneet tallentavat myös monenlaista muuta informaatiota. Merkkitieto on esimerkiksi kirjainten, numeroiden sekä erikoismerkkien esittämistä. Myös merkit esitetään ja tallennetaan bittien avulla, joten täytyy olla säännöt sille minkälainen bittijono tarkoittaa mitäkin merkkiä, eli minkälaista merkistökoodausta käytetään. Tänä päivänä käytetään vielä useita erilaisia merkistökoodauksia. Voit esimerkiksi valita joissain tekstieditoreissa sen millä merkistökoodauksella tallennus tehdään. Lisäksi aina editorit eivät kykene tulkitsemaan kaikkia merkistökoodauksia.
ASCII
ASCII-merkistökoodaus kehitettiin 1960 luvulla kirjainten esitystavaksi sekä tietokoneissa että tiedonsiirrossa. Kuten muutkin merkistökoodausmenetelmät, ASCII määrittelee merkkien ja bittikuvioiden, eli binäärilukujen, vastaavuuden. ASCII bittikuvion pituudeksi määritettiin 7 bittiä, koska se riitti ilmaisemaan samat merkit, kuin mitä sitä ennen käytössä olleet merkistökoodaukset pystyivät esittämään, lähinnä englannin kielessä käytetyt aakkoset, numerot 0-9 ja muutamia graafisia symboleita. Pohdinnassa oli myös 8 bitin käyttö, mutta päädyttiin käyttämään seitsemää bittiä. Koska kahdeksas bitti ei olisi sisältänyt informaatiota, ajateltiin säästää tiedonsiirtokapasiteettia silloin, kun ASCII merkkejä siirretään tietokoneelta toiselle.
Kokeile alle 8-bittisiä binäärilukuja, joiden MSB on 0. Tarkistin on tehty UTF-8:lle, joten se ei hyväksy 7-bittisiä binäärilukuja. Jos bittikuvio on tulostettava ASCII merkki, tulostuu se vääräksi vastaukseksi. Tulostettavat ASCII-merkit ovat alueella 2016 - 7E16. Muut 7-bittiset arvot ova kontrollimerkkejä, jotka suunniteltiin esimerkiksi printtereiden ohjaamiseen, niiden tulostaessa ASCII-merkkejä. "Oikea" vastaus tähän esimerkkiin on binääriluku merkille: ~
Kun tallennukseen käytettiin kuitenkin yleensä 8-bitin kerrannaisia, moni laite- ja ohjelmistovalmistaja otti kahdeksannen bitin käyttöön esittääkseen muun muassa englannin kielen aakkostoa poikkeavia merkkejä. Kahdeksannen bitin käyttö ei ollut yhtenäistä eikä standardoitua, joten laitteistojen, ohjelmistojen sekä käyttöjärjestelmien välillä oli yhteensopimattomuutta. Lisäksi tiedonsiirrossa osa laitevalmistajista otti kahdeksannen bitin virheentarkistukseen pariteettibitiksi.
Seitsemän bitin käyttö ASCII:ssa juonti myös sähköpostiohjelmien hankaluuksiin esittää esim. skandinaavista merkistöä, ja 2000 luvun alkupuolille asti olikin tapana suomen kielisissä sähköposteissa korvata ä -kirjain a -kirjaimella ja ö -kirjain o -kirjaimella, postin luettavuuden parantamiseksi.
Sähköpostin siirtoon vielä tänäkin päivänä käytettävän SMTP protokollan Internet standardi RCF 821 määritteli, että sähköpostit pitää lähettää käyttäen 7-bittistä ASCII merkistökoodausta ja jos tiedonsiirtokanava tukee 8-bittisiä lähetyksiä, niin se kahdeksas bitti (eli MSB) pitää olla nolla. Tämä 7-bitin rajoite on vieläkin voimassa, tosin uusimmat SMTP protokollan laajennoksista, joihin viitataan uusimmassa SMTP protokollan RFC dokumentissa, RCF 5321, mahdollistavat 8-bittiset MIME (Multipurpose Internet Mail Extensions) -laajennokset. Useat MIME RFC dokumentit määrittelevät kuinka esimerkiksi skandinaaviset merkit, kuvat ja muu kuin tekstuaalinen informaatio lähetetään sähköpostin viesti-osiossa. MIME laajennoksissa määritellään myös se kuinka otsikkokenttien arvoja voidaan esittää muilla kuin 7-bittisillä ASCII merkeillä. 8-bittiset otsikkokentät tulee kuitenkin muuntaa tiedonsiirron ajaksi 7-bittisiksi ASCII merkeiksi ja sitten takaisin 8-bittisiksi vastaanottajalla. Muunnoksiin käytettävät algoritmit on määritelty MIME laajennoksissa.
RFC821 on vanhentunut standardi, nykyinen on https://tools.ietf.org/html/rfc5321 joka sallii laajennuksella 8-bittisen merkit viestissä, mutta otsikoissa (header, ei subject) pitää olla ASCII.
—Päivitin ja tarkensin tekstiä
—Koodipiste
Merkkejä vastaavaa bittikuviota kutsutaan 'koodipisteeksi' (eng. code point) ja koska bittikuvio voidaan tulkita myös numeroksi, merkitään koodipisteitä usein kymmen- tai heksalukujärjestelmän numeroilla. Kokeile laittaa alla heittomerkkien (') väliin näppäimistöltäsi löytyviä merkkejä, yksi kerrallaan.
Esimerkiksi ASCII-merkeille koodipisteen arvo muunnettuna 7-bittiseksi binääriluvuksi on suoraan ASCII-merkin binäärinen esitystapa tai tallennusmuoto. Näin ei kuitenkaan ole yleisesti, vaan koodipisteen arvoa vastaava binääriesitys riippuu merkistökoodausmenetelmästä.
Unicode
ASCII-järjestelmän jälkeen on kehitetty ja standardoitu useita erilaisia merkistökoodauksia, mutta ne eivät ole olleet yhteensopivia toistensa kanssa. Unicode on standardi jota on alun perin suunniteltu ja kehitetty, jotta saataisiin maailman kaikille kirjoitusjärjestelmille yhtenäiset koodaus-, esitys- sekä käsittelymenetelmät. Ensimmäinen versio standardista julkaistiin 1991 ja uusien versioiden myötä Unicode:en tukemien merkkien, kielten ja symbolien määrää on lisätty. Kesäkuussa 2018 julkaistu standardin versio 11.0 sisältää yli 137000 kirjoitusmerkkiä 146:sta nykyisestä ja historiallisesta kirjoitusjärjestelmästä, sekä useita symbolijoukkoja. Vuodesta 2014 alkaen standardista on julkaistu uusi versio vuosittain.
Tietotekniikkateollisuuden kehittämä Unicode on kasvattanut suosiotaan ja se on toteutettuna nykyään useissa eri teknologioissa ja ohjelmistoissa, esimerkiksi käyttöjärjestelmissä sekä ohjelmointikielissä.
Unicode standardi määrittelee kaksi merkistöjen kuvausmenetelmää: UTF (Unicode Transformation Format) -koodausmenetelmät sekä UCS (Universal Coded Character Set) -koodausmenetelmät. Unicode standardin määrittelemät merkit voidaan implementoida erilaisilla UTF- tai UCS-merkistökoodauksilla, joista yleisimmin on käytössä UTF-8 ja UTF-16. UTF-16 on vanhentuneen Unicode merkistökoodausmenetelmän UCS-2 laajennus, joka kehitettiin, kun havaittiin että UCS-2 menetelmän kiinteät 16-bittiset koodausyksilöt eivät riittäisi. UTF-16 menetelmässä merkit koodataan joko 16-bittisenä tai 32-bittisenä koodiyksikkönä (eng. code unit). Myöhemmin kehitettiin myös kiinteitä 32-bittisiä koodiyksiköitä käyttävät menetelmät UTF-32 ja USC-4, jotka ovat käytännössä samat, mutta joiden käyttö ei ole kovin yleistä. Koska ASCII merkistökoodaus on 7-bittinen, tai 8-bittinen, jos lisätään 0 MSB bitiksi, ei UTF-16 tai UTF-32 menetelmä ole suoraan yhteensopiva ASCII-järjestelmän kanssa. UTF-8 merkistökoodausmenetelmä on yhteensopiva ASCII-järjestelmän kanssa ja siinä käytetään 8-, 16- sekä 32-bittisiä koodiyksiköitä.
UTF-16 menetelmää käytetään pääasiassa sisäisesti mm. Windows-käyttöjärjestelmässä ja Java sekä Javascript ohjelmointikielissä. Useat tekstinkäsittelyohjelmat Windows-järjestelmässä käyttävät myös UTF-16 merkistökoodausmenetelmää, tosin ASCII yhteensopivuuden vuoksi käytetään myös paljon esimerkiksi ASCII, ANSI (Windows:in 8-bittinen ASCII laajennos Windows 1252) tai ISO 8859-1 -merkistökoodausmenetelmiä. Muissa käyttöjärjestelmissä UTF-16 on hyvin harvoin käytössä tekstinkäsittelyohjelmissa. UTF-16 ei ole kuitenkaan saanut suosiota järjestelmien välisessä kommunikaatiossa, vaikka sitä käytettäisiinkin järjestelmässä sisäisesti. Internetissä sähköpostissa suositetaan käytettäväksi UTF-8:aa, sekä W3C suosittelee käytettävän UTF-8 koodausta oletuksena HTML ja XML kuvauskielissä. Suurin osa www-sivuista (87.5% 31.8.2016, 90.1% 1.11.2017, 92.5% 1.11.2018) käyttää nykyään UTF-8 merkistökoodausta.
UTF-8
Merkistökoodausmenetelmä UTF-8 kehitettiin yhteensopivaksi ASCII-järjestelmän kanssa. UTF-8 menetelmässä merkit koodataan 8-, 16-, 24- tai 32- bittisiksi, eli 1-4 tavuisiksi koodiyksiköiksi. Yhden tavun koodiyksiköissä on määritelty, että MSB bitti pitää aina olla 0, jolloin loput 7 bittiä ovat yhteensopivia ASCII-järjestelmän kanssa. Tämä mahdollistaa sen, että UTF-8 järjestelmät kykenevät tulkitsemaan ASCII-koodauksen. Tavujen ensimmäisiä bittejä käytetään UTF-8 menetelmässä tunnistamaan se kuinka monta tavua koodiyksikköön kuuluu. Jokaisen koodiyksikön ensimmäiselle tavulle on määritelty se millä bittikuviolla sen täytyy alkaa, lisäksi useampi tavuisten koodiyksiköiden ensimmäistä tavua seuraavien tavujen ensimmäiset bitit on määritelty. Näin esimerkiksi ASCII koodeja vastaavaa bittikuviota ei voi esiintyä missään useampi tavuisen koodiyksikön koodauksen tuloksena. Yleisimmin käytetyt merkit koodataan pienemmällä tavumäärällä.
UTF-8 merkistökoodauksen tavut ja MSB bitit, jotka määrittelevät sen mikä tavu on kyseessä.
Tarkastellaan merkkiä ä. Jos aiempana olevaan koodipiste-esimerkkiin annetaan kirjaimeksi 'ä', niin tulosteena saadaan Unicode standardin mukainen koodipisteen arvo 22810 = E416 = 111001002 (koodipisteet ovat etumerkittömiä lukuja), jonka merkintätapa Unicode standardin mukaan on U+00E4. Tämä Unicode arvo voidaan koodata binääriseksi siis eri menetelmillä. UTF-8 merkistökoodauksen tapauksessa, koska luku on suurempi kuin 12710 (U+007F) ja pienempi kuin 2 tavuisen UTF-8 koodipisteen arvon yläraja U+07FF, koodataan se UTF-8 menetelmällä kahden tavun kokoiseksi. Jälkimmäiseen tavuun, Tavuun 2, mahtuu 6 oikean puoleisinta, eli LSB, bittiä, alla väri sininen, joten tässä tapauksessa kaksi koodipisteen MSB bittiä, väri punainen, tallennetaan ensimmäiseen tavuun, Tavuun 1.
ä (U+00E4) = 22810 = 111001002
kun binääriluku tallennetaan UTF-8 muotoon, niin se asetetaan tavuihin
11000011 10100100
missä tavun tunnistamisbitit on violetilla ja täytteenä käytetyt nolla-bitit harmaalla.
Kun koodipistettä vastaava merkki muunnetaan binäärimuotoon, tehdään muunnos siis jollain merkistökoodauksella. Muodosta seuraavaan tehtävään merkin å UTF-8 binääriesitys.
Alla voit tutkia eri merkkien binäärisiä UTF-8 ja UTF-16 muotoja, niiden tavut tulostettuna taulukon alkioina Pythonilla.
Pythonin saa tulostamaan Unicode-merkkejä antamalla koodipisteen parametriksi print-funktiolle. Listauksia Unicode merkeistä löytyy internetistä. Pythonille esimerkiksi koodipiste U+262F annetaan muodossa \u262F.
Unicode koodipisteen arvot on toteutettu myös HTML-kuvauskieleen. Alla voit kokeilla Unicode merkkejä HTML-kuvauskielessä. Esimerkiksi koodipiste U+262F kirjoitetaan HTML-kuvauskielellä muodossa ☯
Byte order mark
Byte order mark (BOM), U+FEFF, on Unicode merkki, jota voidaan käyttää tiedostojen, pääasiassa tekstitiedostojen, alussa. BOM kertoo sen onko teksti tallennettu big vai little endian muodossa ja lisäksi on vihje siitä että tiedosto noudattaa Unicode standardia sekä kertoo mitä merkistökoodausta on tiedostossa on käytetty. BOM-merkin käyttöä ei ole määritelty pakolliseksi, joten sen käyttö saattaa sekoittaa ohjelmistoja, jotka eivät odota löytävänsä ASCII-merkeistä poikkeavia merkkejä tiedoston alusta.
Alla olevissa tehtävissä voit tutkia kahden tiedoston sisältöä tavuina. Kokeile vaikka ihan ensin kopioimalla opettajan tekemät tiedostojen linkit tehtäviin. Linkin
http://users.jyu.fi/~arjuvi/tunnus.txt
tiedostossa on sana tunnus tallennettuna UTF-8 merkistökoodauksella. Kopioi linkki alle, niin näet kirjaimia vastaavat tavut sekä heksalukuina että vastaavina positiivisina kokonaislukuina.
Linkin
http://users.jyu.fi/~arjuvi/bomtunnus.txt
tiedostossa on sana tunnus tallennettuna UTF-8-BOM merkistökoodauksella. Kopioi linkki alle, niin näet eron edellisen kohdan tulosteeseen. Nyt UTF-8 merkistökoodausta käyttävän tiedoston alussa on siis BOM-merkki, eli Unicode koodipiste U+FEFF.
En ole varma menikö nämä oikein, mutta ainakin “Pisteet 0.1” näyttäisi olevan tekstiboxissa. Points: “0/0.1” näkyy kuitenkin pisteissä. Pitikö näistä kahdesta tehtävästä tulla pisteet normaalisti?
—No pitäisi, oli näköjään määritelty vääränlainen piste-funktio. Nyt antaa pisteet molemmat
—Text-tulosteissa näkyvä b-kirjain tarkoittaa Pythonissa että tulostettu teksti on tallennettu tavuina. Kun tavuja printataan, niin jos tavua vastaa tulostettava merkki, niin se tulostetaan näyttöön, muutoin tulostetaan tavua vastaava heksaluku, kuten BOM:in tapauksessa kolme tavua, jotka Pythonin tulosteessa esitetään muodossa \xef \xbb \xbf.
Voit kokeilla vastaavien tiedoston tekoa itse. Tätä varten sinulla täytyy olla käytössä Kotisivutila (users.jyu.fi), jonka saa käyttöön Jyväskylän yliopiston OMA-palvelusta https://sso.jyu.fi/. Tarvittaessa klikkaa Alusta, niin saat sinun kotisivujen linkin takaisin vastauslaatikkoon. Tarkistin antaa 0.1 pistettä jos tiedostossa on käyttäjätunnuksesi ja se on tallennettu oikealla merkistökoodauksella.
Luo esimerkiksi Notepad++ tekstieditorilla tiedosto, kirjoita tiedostoon käyttäjätunnuksesi Anonymous, valitse tiedoston merkistökoodaukseksi UTF-8 (Encoding-menuvalikko), tallenna tiedosto, anna sille nimeksi tunnus.txt ja siirrä se W: asemallesi juurihakemistoon.
Tee toinen tiedosto vastaavasti, mutta valitse tiedoston merkistökoodaukseksi UTF-8-BOM ja tiedoston nimeksi bomtunnus.txt.
Sitten tallenna edellisiin vastauslaatikoihin linkki tekemiisi tiedostoihin ja tutki tulosteita.
Merkistökoodausesimerkki HTML-tiedostolla
Koska tänä päivänä kaikki järjestelmät eivät käytä yhtä ja samaa merkistökoodausta, syntyy paljon yhteensopivuusongelmia, kun tietoa, esimerkiksi ääkkösiä sisältävää tekstiä, siirretään esimerkiksi eri ohjelmistojen, käyttöjärjestelmien tai ohjelmointikielten välillä, muun muassa tiedostojen tai verkon välityksellä. ANSI-koodaus on yksi pääasiassa Windows-käyttöjärjestelmissä käytetty ASCII-järjestelmän 8-bittinen laajennus, joka tukee skandinaavisia merkkejä. Alla on esimerkkinä havainnollistettuna neljä linkkiä HTML-tiedostoihin, joissa on teksti Ääkkösiä:
- Notepad++ ohjelmalla tallennettu ANSI merkistökoodauksella
- Notepad++ ohjelmalla tallennettu UTF-8 merkistökoodauksella
- Notepad++ ohjelmalla tallennettu ANSI merkistökoodauksella
- ja tiedostoon on lisätty HTML tagi
<meta charset="UTF-8">
- ja tiedostoon on lisätty HTML tagi
- Notepad++ ohjelmalla tallennettu UTF-8 merkistökoodauksella
- ja tiedostoon on lisätty HTML tagi
<meta charset="UTF-8">
- ja tiedostoon on lisätty HTML tagi
Vaikka selain osaisikin näyttää oikein ANSI muotoon tallennetun tiedoston skandinaaviset merkit, ei sitä tulisi käyttää, koska se ei todennäköisesti ole yhteensopiva esimerkiksi eri käyttöjärjestelmien välillä. Toisaalta, jos tallentaa UTF-8 muodossa ja unohtaa kertoa HTML-sivulla sen millä merkistökoodauksella tiedosto on tallennettu, niin selain ei osaa näyttää ääkkösiä. Jos taas tallennetaan ANSI-merkistökoodauksella ja väitetään selaimelle HTML otsikko -tagilla että tiedosto on tallennettu UTF-8:na, niin ääkköset korvataan Unicoden merkillä, joka kertoo ettei ääkköselle käytetty merkki ollut Unicode määritysten mukainen. Eli HTML tiedostot tulee tallentaa UTF-8 merkistökoodauksella, ja lisäksi pitää HTML:n <head></head> osuudessa määritellään käytetty merkistökoodaus.
Informaation tallennus visuaaliseen muotoon
Informaatiota voidaan muuttaa myös visuaaliseen muotoon, kuten esimerkiksi viivakoodiksi tai QR-koodi. Tällöin pienen informaatiomäärän optinen tulkitseminen koneellisesti on helppoa.
Loogiset portit ja funktiot
Kaikki tietokoneen käsittelemä ja tallentama tieto koostuu biteistä. Bitti tarkoittaa ns. binäärijärjestelmän eli kaksijärjestelmän lukua 0 tai 1. Vaikka binäärijärjestelmä sisältää vain kaksi merkkiä, voidaan sillä esittää kaikki luvut ja kirjaimet, määrittelemällä niille kullekin niitä vastaava bittijono. Binäärijärjestelmällä voidaan esittää myös esimerkiksi kuvia, musiikkia ja videoita. Tietokoneen keskusyksikön loogiset piirit käsittelevät ja muokkaavat tietoa esittäviä bittijonoja.
Loogiset funktiot tai operaattorit toteuttavat jonkin loogisen operaation lukujärjestelmän merkeille. Boolen funktioiden tai operaattorien tapauksessa merkkejä on kaksi kappaletta, jatkossa tässä materiaalissa ne ovat 0 ja 1. Voidaan kuitenkin ajatella että 0 vastaa arvoa epätosi ja 1 arvoa tosi.
Yksi esimerkki Boolen funktiosta on AND-funktio, tai suomeksi JA-funktio. Jatkossa materiaalissa käytetään englanninkielisiä termejä, niitä usein käytetään myös suomenkielisissä teksteissä. Olkoon meillä kaksi kytkintä ja yksi ledi. Jokainen näistä voi olla kahdessa eri tilassa:
0tai epätosi vastaa sitä että laite ei ole päällä1tai tosi vastaa sitä että laite on päällä
missä laite on tässä siis kytkin tai ledi. AND-funktiota voi havainnollistaa näillä siten että kytkimillä ja ledillä on suhde siten että ledi on päällä vain silloin kun molemmat kytkimet ovat päällä. Jos kytkimet nimetään A ja B, niin ledi on päällä siis vain silloin kuin A on päällä JA B on päällä.
Boolen loogiset funktiot voidaan toteuttaa mekaanisten kytkinten lisäksi myös elektronisilla komponenteilla, sähköisinä kytkiminä toimivilla transistoreilla. Tällaista loogisen funktion elektronista toteutusta kutsutaan usein loogiseksi portiksi. Loogisista porteista rakennettuja kokonaisuuksia kutsutaan loogisiksi piireiksi.
Loogiset portit
Loogiset piirit voidaan rakentaa hyvin pienestä joukosta erilaisia loogisia portteja, jotka valmistetaan transistoreista. Seuraavassa tarkastellaan neljää erilaista loogista porttia: AND, OR, XOR ja NOT. Loogisilla porteilla on sekä sisäänmenoja (joita yleensä merkitään kirjaimilla, esim. A ja B) että ulostulo. Alla loogisten porttien ulostuloarvon riippuminen sisäänmenojen arvoista on esitelty sekä sanallisesti että totuustauluissa.
AND-, OR-, XOR- ja NOT-portit
AND-portin ulostulon arvo on 1, jos sen molemmissa sisäänmenoissa A ja B on arvo 1. Jos vähintään toinen sisäänmenoista on 0, niin ulostulo on myös 0.
| A | B | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR-portin ulostulon arvo on 1, jos ainakin toisen sisäänmenon arvo on 1. Ulostulon arvo on 0 vain, jos molemmat sisäänmenot A ja B ovat 0.
| A | B | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR-portin ulostulon arvo on 1, jos sen sisäänmenot A ja B ovat eriarvoisia. Jos sisäänmenot ovat samat, niin ulostulo on 0.
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOT-portin ulostulon arvo on ainoan sisäänmenon negaatio. Jos sisäänmenon A arvo on 0, niin ulostulon arvo on 1. Vastaavasti, jos sisäänmenon A arvo on 1, niin ulostulon arvo on 0
| A | NOT |
|---|---|
| 0 | 1 |
| 1 | 0 |
Loogisia piirejä suunniteltaessa piirretään yleensä piirikaavioita. Tätä varten loogisilla porteilla pitää olla omat piirrossymbolinsa. Edellä esitettyjen loogisten porttien piirrossymbolit ovat nähtävissä kuvassa 1.
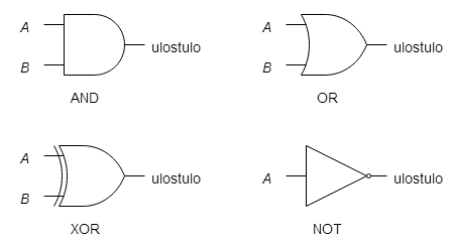
Piirikaavioeditorina TIM-järjestelmässä on käytössä JavaScriptillä toteutettu SimcirJS-ohjelma. Simcir-editori koostuu vasemman reunan komponenttivalikosta, piirikaavion muokkausalueesta ja alaosan painikkeista (katso esimerkki ennen kysymyksiä). Piirikaavio koostuu valituista komponenteista sekä niiden ulostulojen ja sisäänmenojen välisistä johtimista. Komponenteissa sisäänmenot ovat aina vasemmalla ja ulostulo oikealla. Sisäänmenot ja ulostulot esitetään renkaan muotoisilla kytkentäpisteillä. Kuhunkin sisäänmenoon voi liittää vain yhden johtimen, ja kuhunkin ulostuloon voi liittää yhden tai useamman johtimen.
Editorin alaosasta löytyvät seuraavat toiminnot:
Tallenna tallentaa sen hetkisen kytkennän. Voit tallentaa kytkentäsi niin usein kuin haluat ja kannattaakin tallentaa usein. Ensimmäisen tallennuksen jälkeen editorin yläreunaan ilmestyy alasvetolista, josta löytyvät kytkentöjen tallennusajat. Voit esimerkiksi palata mihin tahansa aiempaan tallennukseen ja jatkaa siitä. Arvosteltaessa tehtävää vain viimeisimmän aikaleiman omaava versio arvostellaan.
Muokkaa esittää kytkennän tekstimuodossa, jonka voit halutessasi kopioida esimerkiksi jonkin toisen kysymyksen Simcir-editoriin silloin, kun tehtävien lähtöasetelma on sama.
Alusta palauttaa editorin kytkennän alkutilaan, jos tulee tarve aloittaa tyhjältä pöydältä. Alusta tulee näkyviin, kun olet kerran tallentanut kytkentäsi. Kaikki tallentamasi kytkennän versiot säilyvät tallessa alustamisen jälkeenkin.
Piirikaavioeditorissa sisäänmenevät signaalit 0 ja 1 annetaan sulkeutuvilla painokytkimillä (myöhemmin kytkin). Kun kytkintä klikkaa hiirellä, muuttuu sisempi neliö tummemmaksi, mikä osoittaa kytkimen olevan alaspainettuna. Tällöin kytkimen sisäänmenoon tuleva signaali johdetaan kytkimen läpi ulostuloon. Ulostuloa ilmaisevan kytkentäpisteen reunan punainen väri kertoo, että sen hetkinen ulostulon arvo on 1. Vastaavasti kytkentäpisteen reunan musta väri kertoo, että ulostulo on 0. Renkaan muotoinen kytkentäpiste käyttäytyy samoin kaikissa komponenteissa sekä sisäänmenoille että ulostuloille.

Painikkeen sisemmän neliön värin ollessa sama kuin ulomman neliön, kytkin ei ole painettuna ja sen ulostuleva arvo on 0.

Totuustaulun ulostuloja kuvataan piirikaavioeditorissa ledeillä (LED). Ulostulon arvoa 1 vastaa se, että LED palaa (väri muuttuu kirkkaammaksi). Arvoa 0 vastaa se, että LED ei pala, mikä on alkutilana kaikissa kysymyksissä.
Kytkentää voi muokata raahaamalla hiiri pohjassa komponentin ulostulosta johtimen jonkin toisen komponentin sisäänmenoon. Komponenttien ulostulot on merkitty valkoisilla kytkentäpisteillä ja sisäänmenot keltaisilla kytkentäpisteillä. Komponentin saa poistettua kytkennästä raahaamalla komponentin komponenttivalikon päälle. Takaisin komponentin saa ottamalla uuden komponentin komponenttivalikosta. Johtimen saa irrotettua klikkaamalla komponentin sisäänmenoa, johon johdin on kytketty. Jos komponentit sijoittaa peräkkäin siten, että vasemman puoleisen komponentin ulostulosta on n. 1 cm oikeanpuoleisen komponentin sisäänmenoon, saa johtimen automaattisesti ilman raahaamista klikkaamalla vasemmanpuoleisen komponentin ulostuloa.
Transistori kytkimenä
Transistori on puolijohdekomponentti, jota voidaan käyttää sähköisten signaalien tai tehon vahvistamiseen tai kytkemiseen. Tietokoneissa transistoria käytetään sähköisten signaalien kytkemiseen, jotta saadaan aikaan loogisia portteja sekä piirejä. Transistorin kytkimenä toimimisen havainnollistamiseksi voit tutustua esimerkiksi JavaScriptillä toteutettuun visualisointiin. Valitse yläreunan menusta Circuits → Transistors → Switch. Kyseinen visualisointi vastaa ensimmäistä elektroniikkademojen tehtävää.
Tietokoneen loogisten piirien transistorit toteutetaan CMOS-tekniikalla, jolla saadaan transistorit pakattua hyvin pieneen tilaan. Eri tekniikoilla toteutetuilla transistoreilla on erilaisia ominaisuuksia, ja tekniikalla on vaikutusta myös siihen kuinka monta transistoria loogisten porttien toteutus vaatii. Kurssin elektroniikkalabroissa toteutetaan looginen AND-portti RTL (Resistor Transistor Logic) -logiikalla Kahdella NPN transistorilla. Lisäksi labroissa käytetään CMOS-tekniikalla tehtyjä mikropiirejä. Ennen CMOS-tekniikkaa tietokoneiden mikropiirit toteutettiin TTL (Transistor–transistor logic) -logiikalla. Ero TTL:n ja CMOS:n välillä on karkeasti se että CMOS käyttää paljon vähemmän virtaa pienillä taajuuksilla. Kun transistorien kytkentätaajuus kasvaa niin korkeilla taajuuksilla puolestaan TTL transistorit käyttävät vähemmän virtaa. TTL -logiikan mikropiirit toteutetaan NPN ja PNP tyyppisillä BJT (Bipolar junction transistor) transistoreilla. CMOS -logiikan mikropiirit toteutetaan MOSFET tai JFET tyyppisillä FET (Field effect transistor) -transistoreilla. Esimerkiksi AND-portin toteutukseen tarvittava transistorien määrä riippuu käytetystä transistorilogiikasta, ollen yleensä 2, 4 tai 6 transistoria. Kun AND-portti toteutetaan CMOS-tekniikalla, vaati se kuusi transistoria, mutta nämä saadaan mahtumaan pienempään tilaan kuin muissa transistorilogiikoissa. Erilaisten loogisten porttien toteuttaminen CMOS-tekniikalla vaatii eri määrän transistoreita.
Universaali looginen portti
Universaali looginen portti on looginen portti, jolla voidaan rakentaa kaikki muut loogiset portit. Näin ollen yhdellä universaalisella porttityypillä voidaan toteuttaa kaikki loogisista porteista muodostettavat loogiset piirit, kuten esimerkiksi tietokoneiden ja puhelinten prosessoripiirit ja muistipiirit. Aiemmin esitellyt AND, OR, XOR- ja NOT-portit eivät ole universaaleja portteja.
Mistä tiedetään, että jollain loogisella portilla voidaan toteuttaa kaikki muut loogiset portit? Kaikki loogiset funktiot voidaan esittää totuustaululla, joka ilmaisee funktion ulostulon arvon sisäänmenojen eri kombinaatioilla. Myöhemmin käydään läpi, kuinka binääristen muuttujien totuustaulun loogisen funktion voi toteuttaa käyttäen AND-, OR- ja NOT-portteja. George Boole osoitti kaikkien binääristen muuttujien loogisten operaatioiden olevan toteutettavissa soveltamalla pelkästään AND-, OR- ja NOT-funktioita. Täten universaali portti on portti, jolla voidaan muodostaa AND-, OR- ja NOT-portit. Täydellisellä porttijoukolla tarkoitetaan porttijoukkoja, joilla voi toteuttaa minkä tahansa loogisen funktion. Esimerkiksi porttijoukko, jossa on AND- ja NOT-porit, muodostaa täydellisen porttijoukon. Myöhemmin käydään läpi myös esimerkiksi se kuinka AND ja NOT porteilla saa rakennettua loogisen OR-funktion, sekä kuinka NAND portilla saadaan toteutettua kaikki loogiset funktiot.
NAND-, NOR- ja XNOR-portit
Universaaleista porteista eniten käytetyt ovat NAND-portti ja NOR-portti. Näiden ulostulot ovat vastakkaiset verrattuna AND- ja OR-portteihin. Kirjain N tuleekin loogisesta NOT-funktiosta ja loogisesti NAND on siis vastaava kuin NOT AND ja NOR on vastaava kuin NOT OR.
Loogisten NAND- ja NOR-porttien ulostuloarvon riippuminen sisäänmenojen arvoista esitetään seuraavaksi sekä sanallisesti että totuustauluina.
NAND-portin ulostulon arvo on 0, vain jos sen molemmissa sisäänmenoissa A ja B on arvo 1. Jos vähintään toinen sisäänmenoista on 0, niin ulostulo on 1.
| A | B | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR-portin ulostulon arvo on 1, vain jos sen molemmissa sisäänmenoissa A ja B on arvo 0. Jos vähintään toinen sisäänmenoista on 1, niin ulostulo on 0.
| A | B | NOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Myös XOR-portista on olemassa negatoitu versio, jonka nimi on XNOR-portti. XNOR portti siis kertoo, onko portin sisäänmenot samanarvoisia (XOR kertoo, onko sisäänmenot eriarvoisia). Alla XNOR ulostuloarvon riippuminen sisäänmenojen arvoista on esitelty sekä sanallisesti että totuustauluissa.
XNOR-portin ulostulon arvo on 1, jos sen sisäänmenot A ja B ovat samanarvoisia. Jos sisäänmenot eroavat toisistaan, niin ulostulo on 0.
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Loogisten NAND-, NOR-, ja XNOR-porttien piirrossymbolit eroavat AND-, OR- ja XOR-porttien piirrossymboleista siten että niiden ulostuloon on lisätty pieni ympyrä, joka ilmaisee sen, että ulostulo on negatoitu. Alla piirikaavioeditorissa on NAND-, NOR-, ja XNOR-portit, joissa piirrossymbolit näkyvät.
Harjoitustehtävissä selviää, kuinka NAND-portilla saa toteutettua kaikki muut loogiset portit. Alla voit kuitenkin itse jo kokeilla, saatko loogisen NOT toiminnon toteutettua NAND-port(e)illa.
Kokeilusivu TIM-järjestelmässä, jossa voi kokeilla erilaisia kytkentöjä.
Yllä oleva NOT-funktion toteuttaminen NAND:illa on vastaava tehtävä kuin Boolen logiikan ensimmäinen piirikaaviolla toteutettava harjoitustehtävä.
Loogiset portit laitteistokuvauskielellä
Piirikaavio on visuaalinen tapa esittää loogista funktiota vastaava kytkentä. Monimutkaisia mikropiirejä, esim. prosessori, suunniteltaessa käytetään laitteistokuvauskieliä (eng. Hardware Description Language - HDL), jotka muistuttavat ohjelmointikieliä. Laitteistokuvauskielellä toteutettu kytkentä voidaan muuntaa sellaiseen muotoon että sitä voidaan käyttää esimerkiksi prosessorien tai minkä tahansa mikropiirien toteutukseen sekä ohjelmoitavien logiikkapiirien 'ohjelmointiin'.
Kurssilla Nand2Tetris tehtävissä käytetty laitteistokuvauskieli on hyvin yksinkertainen. Tehdessäsi HDL -kielisiä toteutuksia komponenteista, muokkaa Nand2Tetriksen tarjoamia valmiita pohjatiedostoja. Toteutusten testaaminen hoidetaan Nand2Tetriksen tarjoamilla simulaattoreilla sekä testitiedostoilla.
Laitteistokuvauskielellä määritellään vastaavat komponentit ja niiden väliset kytkennät kuin piirikaavioeditorissakin. Piirikaavioeditorissa komponentit ja niiden väliset kytkennät, eli johtimet ovat visuaalisia. Laitteistokuvauskielellä kuvataan kytkennässä käytetyt komponentit ja kytkennät tekstimuodossa, laitteistokuvauskielen määritelmien mukaisesti.
Laitteistokuvauskielellä tehdyt kytkennät, eli piirit testataan samalla periaatteella, kuin piirikaavioeditorissakin. Tutkitaan ulostuloja sisäänmenojen eri arvoilla ja verrataan toimintaa siihen mitä haluttiin. Käytännössä siis verrataan suunnitellun ja toteutetun kytkennän totuustauluja.
Vaikka kurssilla käytetty laitteistokuvauskieli on yksinkertainen, voidaan sillä kuvata kytkennät, joita tarvitaan tietokoneen simuloimiseen. Käytännössä loogiset kytkennät suunnitellaan monimutkaisemmilla laitteistokuvauskielillä, joissa on paljon enemmän ominaisuuksia suunnittelun helpottamiseksi.
Yksi laitteistokuvauskielen etu piirikavioeditoreihin on se että useampi bittisten komponenttien käyttö on usein helpompaa kuin piirikaavioeditoreilla. Tosin tämä riippuu paljon ohjelmistosta ja siitä, minkälaisia valmiita komponentteja ohjelmistoon on tarjolla. Tässä materiaalissa rakennamme kaikki komponentit lähtien NAND-porteista, ja esimerkiksi 16-bittiset komponentit teemme vain laitteistokuvauskielellä.
Alla voit testata Not.hdl, And.hdl sekä Or.hdl toteutuksiasi kopioimalla muokkaamasi x.hdl tiedoston sisällön alle. Tarkistin hyväksyy käytettäväksi vain Nand-portteja toisin kuin Nand2Tetriksen simulaattori.
Boolen algebra
Loogisten porttien toteuttamat loogiset funktiot voidaan esittää myös lyhyemmässä muodossa kuin sanallisesti tai totuustauluna. Elektroniikassa esitystapana on tällöin matemaattinen lauseke. Tietokoneiden ja digitaalisten systeemien peruskomponentit suunnitellaan ja analysoidaan käyttäen matemaattista menetelmää, Boolen algebra. Boolen algebrassa käytetään muuttujia ja operaatioita. Muuttujat ovat loogisia muuttujia ja operaatiot loogisia operaatioita. Looginen muuttuja voi saada joko arvon 1, tosi, TRUE, T tai arvon 0, epätosi, FALSE, F. Tärkeimmät perusoperaatioit Boolen algebrassa ovat konjunktio eli AND, disjunktio eli OR ja negaatio eli NOT. Koulussa opetetussa algebrassa muuttujien arvot ovat numeroita ja perusoperaatiot ovat yhteenlasku ja kertolasku. Perusalgebran ja Boolen algebran säännöissä on joitain yhtäläisyyksiä ja joitain eroja. Seuraavaksi esitetään loogisten operaatioiden matemaattiset esitystavat, joiden avulla Boolen algebran lakien vertaaminen peusalgebran lakeihin on helpompaa. Olkoon A ja B loogisia muuttujia. Alla on esitetty loogisten muuttujien loogisten operaatioiden merkintätapoja.
| Sanallinen | Matemaattinen | Looginen | Vanha matemaattinen |
|---|---|---|---|
| NOT |
|||
Tällä kurssilla, sekä yleensä elektroniikassa, käytetään AND ja OR funktioille matemaattista merkintätapaa ja muille funktioille vanhaa matemaattista merkintätapaa, missä negaatiot ilmaistaan piirtämällä viiva muuttujan tai operaation yläpuolelle.
Nimi Funktio a 0 0 1 1
b 0 1 0 1
FALSE 0 0 0 0 0
AND a•b 0 0 0 1
a AND NOT b a•b 0 0 1 0
a a 0 0 1 1
NOT a AND b a•b 0 1 0 0
b b 0 1 0 1
XOR a•b + a•b 0 1 1 0
OR a + b 0 1 1 1
NOR a + b 1 0 0 0
XNOR a•b + a•b 1 0 0 1
NOT b b 1 0 1 0
a OR NOT b a + b 1 0 1 1
NOT a a 1 1 0 0
NOT a OR b a + b 1 1 0 1
NAND a•b 1 1 1 0
TRUE 1 1 1 1 1
Boolen algebran säännöt
Boolen algebran lait, säännöt sekä teoreemat ovat työkaluja Boolen lausekkeiden sieventämiseen, jotta toteutettava looginen kytkentä sisältäisi mahdollisimman vähän loogisia portteja. Lisäksi loogisia portteja voidaan vaihtaa toisiksi lakien avulla. Kytkentöjen sieventäminen esimerkiksi piirikaavioeditorissa olisi paljon hankalampaa.
Boolen algebrassa on voimassa seuraavat säännöt, lait ja teoreemat.
Liitännäisyys eli assosiatiivisuus a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki eli distributiivisuus a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus eli kommutatiivisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen algebran lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
Laskujärjestys
Boolen algebran operaatioilla on perusalgebraa vastaavat laskujärjestykset, eli AND operaatio tehdään ennen OR operaatiota ja sulkuja käyttämällä voidaan laskujärjestystä muuttaa. Negatointi toimii ikään kuin sulkuina, tarkoittaen sitä että negatointi-viivan alla olevat operaatiot tehdään ennen negatointia tai negatoinnin vieressä olevia operaatioita.
Liitännäisyys eli assosiatiivisuus
Liitänäisyyslain mukaan lausekkeen muuttujien laskujärjestystä voidaan vaihtaa vapaasti. Tämä pätee sekä AND että OR operaatioille. Kytkentänä laki tarkoittaa sitä että useamman sisäänmenon AND tai OR operaatiot voidaan kytkeä missä vaan järjestyksessä.
a + (b + c) = (a + b) + c
a • (b • c) = (a • b) • c
Osittelulaki eli distributiivisuus
Osittelulain mukaan voidaan ottaa yhteinen tekijä sekä kanden AND operaation OR operaatiosta että kahden OR operaation AND operaatiosta. Loogisiin piireihin sovellettuna laki mahdollistaa esimerkiksi yhden loogisen portin poistamisen kytkennästä.
a • (b + c) = (a • b) + (a • c)
a + (b • c) = (a + b) • (a + c)
Vaihdannaisuus eli kommutatiivisuus
Vaihdannaisuuslain mukaan AND ja OR operaatioiden muuttujat voidaan vaihtaa keskenään. Loogisten porttien osalta laki sanoo, että portin sisäänmenot ovat identtiset, eikä siis ole väliä sillä kumpaan sisäänmenoon tuleva signaali tai johdin kytketään.
a + b = b + a
a • b = b • a
De Morganin teoreemat
De Morganin teoreemat määrittelevät säännöt OR ja AND operaatioiden vaihtamiseksi toisikseen. Teoreemat ovat hyödyllisiä, kun muunnetaan loogisia kytkentöjä vain yhden tyyppisillä komponenteilla toteutettaviksi. Hyvin usein looginen piiri määritellään ensin käyttäen erityyppisiä komponentteja, koska se on ihmiselle helpompaa. Sen jälkeen kytkentä muutetaan joko NAND tai NOR porteilla toteutettavaksi. Implementointi käyttäen vain yhtä porttia mahdollistaa yleensä pienemmän ja halvemman toteutuksen. Valinta NAND ja NOR toteutusten välillä tehdään muun muassa sen mukaan tarvitaanko mahdollisimman pientä toteutusta tai virrankulutusta.
De Morganin NAND-teoreema
De Morganin NAND-teoreema määrittelee sen kuinka negatoitu AND operaatio voidaan vaihtaa OR operaatioksi, jonka sisäänmenot on negatoitu.
a • b = a + b
De Morganin NOR-teoreema
De Morganin NOR-teoreema määrittelee sen kuinka negatoitu OR operaatio voidaan vaihtaa AND operaatioksi, jonka sisäänmenot on negatoitu.
a + b = a • b
Boolen algebran lakeja ja sääntöjä
Seuraavia lakeja voidaan käyttää Boolen lausekkeiden sieventämiseen sekä operaatioiden vaihtamiseksi toisikseen.
Idempotent eli "itseään operoimisen" -laki
a • a = a
a + a = a
Identity eli identiteettilaki
a • 1 = a
a + 0 = a
Annulment eli kumoamislaki
a • 0 = 0
a + 1 = 1
Complement eli komplementtilaki
a • a = 0
a + a = 1
Double Negation eli kaksoisnegaatiolaki
a = a
Absorption eli absorptiolaki
a + (a • b) = a
a • (a + b) = a
Absorption with negation eli absorptiolaki negatoinnilla
a + a • b = a + b
a + a • b = a + b
Kokeile rakentaa Boolen lakeja vastaavia kytkentöjä ja totea että yhtäsuuruudet pitävät paikkansa. Eli toteuta esimerkiksi yhtäsuuruusmerkin vasemmanpuoleinen osa ylempään LED:iin ja oikeanpuoleinen osa alempaan LED:iin. Vakio 0 on tehty NOT-komponentilla ja vakio 1 on tehty Buffer-komponentilla.
Liitännäisyys
a + (b + c) = (a + b) + c
a • (b • c) = (a • b) • c
Osittelulaki
a • (b + c)
= (a • b) + (a • c)
a + (b • c)
= (a + b) • (a + c)
Vaihdannaisuus
a + b = b + a
a • b = b • a
De Morganin teoreema
a • b = a + b (NAND)
a + b = a • b (NOR)
Boolen algebran lakeja
1) a • a = a 2) a + a = a
3) a • 1 = a 4) a + 1 = 1
5) a • 0 = 0 6) a + 0 = a
7) a • a = 0 8) a + a = 1
9) a = a (kaksoisnegaatio)
10) a + a • b = a + b
11) a + a • b = a + b
— Boolen operaatioiden suoritusjärjestykselle on vastaavat säännöt kuin matematiikassa kerto- ja yhteenlaskulle. Lisäksi negatointi operaatio tehdään ennen AND ja OR operaatiota. Eli järjestys on 1) NOT 2) AND 3) OR. Toisaalta, jos negatointiviiva on AND tai OR operaation ja kahden tai useamman muuttujan yli, niin ensin suoritetaan 'pitkän' negatointiviivan alla oleva(t) operaatio(t).
Boolen lausekkeen muodostaminen totuustaulusta
Mikä tahansa Boolen funktio voidaan toteuttaa AND-, OR- ja NOT-funktioilla, eli elektronisessa muodossa vastaavilla porteilla, koska mainitut portit muodostavat universaalin porttien joukon.
Boolen funktion totuustaulusta puolestaan saadaan selvitettyä totuustaulua vastaava Boolen lauseke, joka voidaan toteuttaa AND-, OR- ja NOT-porteilla.
Boolen lausekkeen selvittämiseksi on kaksi menetelmää:
- Tulojen summamuoto
- Summien tulomuoto
Tulojen summamuoto (Sum of Products - SOP)
Tutustutaan seuraavaksi Boolen funktioiden tulojen summamuotoon ja sen muodostamiseen totuustaulusta. Otetaan esimerkiksi XOR-funktion totuustaulu.
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
XOR:in tulojen summamuoto
Tarkastellaan XOR:in totuustaulun rivejä, joissa XOR-funktion ulostulon arvo on 1, eli rivit, joissa XOR sarakkeen kohdalla on 1. Ylempi näistä riveistä ilmaisee, että A:n arvolla 0 ja B:n arvolla 1 on XOR-funktion ulostulo 1. Huomaa sana ja edellisessä ilmaisussa, eli kyseessä on kaksi ehtoa, joiden molempien tulee täyttyä, eli looginen AND-operaatio. AND operaation ulostulo on 1 vain silloin kuin molemmat sisäänmenot ovat 1, mutta nyt A:n pitäisi olla 0. Tämä voidaan sanoa käänteisenä, eli A on 0 on sama kuin A:n negaatio on 1, joten ehto voidaan lausua myös "A:n negaation arvolla 1 ja B:n arvolla 1 on XOR-funktion ulostulo 1".
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 1 | 1 | ⇒ | |||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 |
Eli saadaan lauseke
ja jos sen arvo on 1, niin XOR:in ulostulo on 1. Se on siis eräs totuustaulun mukainen ehto sille, että XOR:in ulostulo on 1. Vastaavasti alemmalle riville, että XOR-funktion ulostulo on 1, jos A on 1 ja B:n negaatio on 1.
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 1 | 1 | ||||
| 1 | 0 | 1 | ⇒ | |||
| 1 | 1 | 0 |
Eli saadaan toinen lauseke
jonka arvon ollessa 1 on XOR:in ulostulo 1. Saatuja lausekkeita kutsutaan minimitermeiksi.
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 1 | 1 | ⇒ | |
||
| 1 | 0 | 1 | ⇒ | |
||
| 1 | 1 | 0 |
Kun kootaan eo. tieto yhteen, havaitaan että XOR funktion ulostulo on 1 silloin kun on 1 (eli A=0
ja B=1) tai on 1 (eli A=1
ja B=0), mutta ei muulloin. Muuttamalla ehto loogiseksi lausekkeeksi (huomaa tai -sana), saadaan
Tällaista loogista lauseketta, joka on muodostettu tarkastelemalla totuustaulun rivejä, jotka antavat ulostuloksi 1, kutsutaan Tulojen summamuodoksi, englanniksi Sum of Products, mistä lyhenne SOP. Mistä tahansa Boolen funktion totuustaulusta voidaan vastaavasti muodostaa tulojen summamuoto, ja saatu lauseke voidaan siis toteuttaa käyttämällä AND-, OR-, ja NOT-portteja.
Kirjoita alle LaTeX:illa XOR:in SOP muotoinen lauseke, joka on johdettu yllä. Negaatio-viivan piirtämiseksi käytetään \overline{} komentoa, jossa siis {} -merkkien väliin laitetaan negatoitava muuttuja. AND-operaation merkitsemiseksi käytetään \cdot komentoa, joka piirtää kertomerkin. OR operaatiolle käytetään normaalia yhteenlaskun + -merkkiä
Alla on vertailukohdaksi XOR-portti. Toteuta XOR:in SOP muotoinen kytkentä, ja totea että kytkentäsi sytyttää SOP LED:in samoin kuin XOR sytyttää LED:in. Käytä SOP muotoisen XOR kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XOR-portin sisäänmenoina.
XNOR:in tulojen summamuoto
Kokeile seuraavaksi muodostaa XNOR:in Tulojen summamuotoinen lauseke tutkimalla XNOR:in totuustaulua. Menetelmä SOP muotoisen lausekkeen muodostamiseen on aina vastaava kuin mitä XOR:in tapauksessa esitettiin.
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Yleisesti SOP muoto saadaan totuustaulusta seuraavasti
- etsi rivit, joissa ulostulona on 1
- muodosta tulo rivin muuttujista, tai muuttujan negaatiosta, jos muuttuja on 0
- muodosta summa tulotermeistä
Muuttujien ja termien määrä voi olla mielivaltainen, eikä siis rajoitettu kahteen, kuten käsitellyissä esimerkeissä.
Alla on vertailukohdaksi XNOR-portti. Toteuta XNOR:in SOP muotoinen kytkentä, ja totea että kytkentäsi sytyttää SOP LED:in samoin kuin XNOR sytyttää LED:in. Käytä SOP muotoisen XNOR kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XNOR-portin sisäänmenoina.
Summien tulomuoto (Product of Sums - POS)
Summien tulomuodossa lähdetään tutkimaan totuustaulun rivejä, jotka antavat ulostuloksi nolla.
XOR:in summien tulomuoto
Totuustaulua voidaan tutkia myös siten että selvitetään, milloin ulostulon arvo on 0. Käyttäen taas XOR:in totuustaulua esimerkkinä, nähdään että XOR:in ulostulo on 0, jos A=0 ja B=0 tai A=1 ja B=1.
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Nyt siis jommankumman rivin tulee olla nolla. Jos mietitään ylintä riviä, niin huomataan, että OR-operaatiolla saadaan ulostuloksi nolla silloin kuin molemmat sisäänmenot ovat nolla.
Sanallisesti AND portteja käyttävä POS muoto saadaan ilmaisemalla, että ulostulo on yksi eli true, jos mikään sisäänmenojen kombinaatio ei aiheuta sitä, että taulukon oikean puoleisimman sarakkeen arvo 0 eli, XOR:in totuustaulusta
Käyttämällä De Morganin teoreemaa, saadaan edellisestä muodostettua POS muoto.
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ⇒ | |
||
| 0 | 1 | 1 | ||||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 | ⇒ | |
Eli ensimmäista riviä vastaavaksi termiksi saadaan
Vastaavasti alin rivi, eli ulostulo on nolla, kun sisäänmenot A=1 ja B=1, saadaan OR operaatiolla A:n ja B:n negaatioista
Kun ulostuloksi halutaan nolla silloin kuin jompikumpi termeistä tai
on nolla, voidaan se loogisesti toteuttaa AND-operaatiolla, eli
Tätä muotoa kutsutaan Summien tulomuodoksi, englanniksi Product of Sums, lyhennettynä POS.
Mistä tahansa Boolen funktion totuustaulusta voidaan vastaavasti muodostaa summien tulomuoto, ja saatu lauseke voidaan siis toteuttaa käyttämällä AND-, OR-, ja NOT-portteja.
Alla on vertailukohdaksi XOR-portti. Toteuta XOR:in POS-muotoinen kytkentä ja totea että kytkentäsi sytyttää POS LED:in samoin kuin XOR sytyttää LED:in. Käytä POS-muotoisen XOR-kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XOR-portin sisäänmenoina.
XNOR:in summien tulomuoto
Kokeile seuraavaksi muodostaa XNOR:in summien tulomuotoinen lauseke, eli POS-muototoinen lauseke XNOR:in totuustaulun perusteella.
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Yleisesti POS-muoto totuustaulusta saadaan seuraavasti
- etsi rivit, joissa ulostulona on 0
- summaa rivin muuttujat, tai muuttujan negaatio, jos muuttujan arvo on 1
- muodosta tulo summatermeistä
Muuttujien ja termien määrä voi olla mielivaltainen, eikä siis rajoitettu kahteen, kuten käsitellyissä esimerkeissä.
Alla on vertailukohdaksi XNOR-portti. Toteuta XNOR:in POS-muotoinen kytkentä, ja totea että kytkentäsi sytyttää POS LED:in samoin kuin XNOR sytyttää LED:in. Käytä POS-muotoisen XNOR-kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XNOR-portin sisäänmenoina.
Tulojen summamuoto (SOP) ja summien tulomuoto (POS), kumpaa kannattaa käyttää? Jos totuustaulun ulostulossa on vähemmän ykkösiä tai toteutukseen käytetään NAND-portteja, on SOP yleensä parempi vaihtoehto. Jos taas nolla-ulostuloja on vähemmän tai toteutus tehdään NOR-porteilla, on POS yleensä parempi vaihtoehto. Molemmilla kuitenkin saadaan totuustaulua vastaavat erilaiset Boolen funktiot, joiden toteutus on siis erilainen, mutta ulostulon logiikka toimii samoin.
Muunnos SOP-muodosta NAND-muotoon
Totuustaulusta suoraan saatava toteutus on usein turhan monimutkainen ja sitä voidaan sieventää Boolen algebran sääntöjen mukaan. XOR:in ja XNOR:in tapauksessa tosin saadaan minimaaliset AND-, OR-, ja NOT-porteilla toteutettavat kytkennät. Myöhemmin otamme käsittelyyn monimutkaisemman esimerkin, mutta sitä ennen tarkastellaan saisiko XOR toteutuksen porttimäärää pienennettyä käyttämällä täydellistä porttijoukkoa, joka koostuu yhdestä (universaalisesta) portista. Tarkastellaan ensin, kuinka XOR saadaan toteutettua käyttäen pelkästään NAND portteja, soveltamalla Boolen algebran sääntöjä. Lähtökohdaksi voi ottaa vapaasti SOP tai POS muodon, tosin useasti NAND-muoto on helpompi johtaa SOP-muodosta.
Lähdetään liikkeelle XOR:in SOP muodosta
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
Tarkoituksena on siis muodostaa lauseke, jossa on pelkkiä NAND operaatioita, eli tuloja joiden yli on vedetty viiva. Kaksoisnegaatiosäännön mukaan kaksi negaatiota kumoavat toisensa, eli ulostulo voidaan negatoida kaksi kertaa, eikä sillä ole vaikutusta
Kun OR- ja AND -operaatioita halutaan muuttaa toisikseen, voidaan käyttää De Morganin teoreemoja. Edellä kaksoisnegaatio tehtiin, jotta saadaan De Morganin teoreemaa vastaava lauseke. Tarkastelemalla edellisen yhtälön oikeaa puolta huomataan, että siinä on termien ja
NOR-operaatio (alempi pitkä negaatio-viiva) joka sitten vielä negatoidaan toisen kerran (ylempi pitkä negaatio-viiva). De Morganin NOR-teoreema sanoo, että "kahden termin NOR operaatio voidaan vaihtaa vastaavien negatoitujen termien AND operaatioksi", eli
Siis, alempi pitkä negaatioviiva plussan yli (NOR), poistuu ja tilalle tulee (lyhyemmät) negaatioviivat NOR:in termien päälle ja plus -operaatio vaihdetaan tulo -operaatioksi. Nyt lausekkeessa on jäljellä vain tuloja, joiden yläpuolella on negaatio-viiva. Nämä voidaan siis toteuttaa NAND-porteilla. Lisäksi NOT-operaatiot voidaan toteuttaa NAND-porteilla, kuten on todettu esimerkiksi Boolen logiikan piirikaaviotehtävissä.
Alla on vertailukohdaksi XOR-portti. Toteuta XOR-funktio käyttäen NAND-portteja, ja totea että kytkentäsi sytyttää NAND LED:in samoin kuin XOR sytyttää LED:in. Käytä kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XOR-portin sisäänmenoina. Voit vaikka ensin rakentaa XOR:in muilla komponenteilla ja vaihdella niitä sitten NAND:eiksi
Edellä saatiin XOR-funktiolle muoto, joka voidaan toteuttaa viidellä NAND-portilla. Jos lähtisi liikkeelle siitä, että XOR on XNOR:in negaatio, saisi johdettua XOR-funktiolle muodon, joka voidaan toteuttaa vain neljällä NAND-portilla. Neljän NAND:in versio johdetaan Boolen algebran tehtävissä.
Tarkastellaan vielä alkuperäistä SOP-muotoista lauseketta. Siinä NOT:in voi toteuttaa yhdellä NAND:illa, AND:n voi toteuttaa kahdella NAND:lla ja OR:n voi toteuttaa kolmella NAND:lla. Eli XOR suoraan totuustaulusta toteutettuna tarvitsisi yhdeksän NAND-porttia. NAND-muotoon muuttamisella saadaan joskus tarvittavien porttien määrää vähennettyä. Yleensä Boolen funktioita voidaan tosin sieventää jo ennen kuin niitä muutetaan toisiin muotoihin.
Muunnos POS-muodosta NOR-muotoon
Boolen algebran avulla voidaan selvittää myös NOR-porteilla toteutettava lauseke. Lausekkeen voi muodostaa joko SOP tai POS muodosta, mutta yleensä NOR-muoto on helpompi johtaa POS-muodosta. Otetaan XOR:in POS-muotoinen lauseke
ja kaksoisnegatoidaan se
Ja käytetään De Morganin teoreemaa, jonka mukaan "kahden termin NAND-operaatio voidaan muuttaa vastaavien negatoitujen termien OR-operaatioksi", eli
Jäljellä on enää NOR operaatioita, kun NOT-funktio voidaan tehdä myös NOR-porteilla. Kokeile tehdä lauseketta vastaava toteutus viidellä NOR portilla.
Alla on vertailukohdaksi XOR-portti. Toteuta XOR-funktio käyttäen NOR-portteja, ja totea että kytkentäsi sytyttää NOR LED:in samoin kuin XOR sytyttää LED:in. Käytä kytkentäsi sisäänmenoina samoja kytkimiä, joita käytetään XOR-portin sisäänmenoina.
Neljän NOR:in versio XNOR -funktiosta johdetaan Boolen algebran tehtävissä.
Boolen funktioiden sieventäminen
Mikä tahansa Boolen funktio voidaan toteuttaa elektronisessa muodossa porttien verkkona. Tarkastellaan esimerkkinä kolmesta loogisesta muuttujasta A, B ja C, riippuvaa Boolen funktiota, jonka totuustaulu on alla. Ulostuloa merkitään LED-muuttujalla. Totuustaulu ilmaisee ns. vähemmistö kolmesta -funktion. Tällöin siis LED saa arvon 1, kun nolla tai yksi sisäänmenoa on 1, ja arvon 0 muulloin.
| A | B | C | LED |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Toteuta vähemmistö kolmesta -kytkentä, totuustaulusta saatavan SOP-muotoisen lausekkeen perusteella. Sitten voit sieventää kytkentää samalla kun käyt läpi SOP-muotoisen lausekkeen sieventämistä.
Algebrallinen sieventäminen
Tulojen summamuoto totuustaulusta vähemmistö kolmesta -kytkennälle on
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
Lähdetään sieventämään lauseketta käyttäen avuksi Boolen algebran sääntöjä. Havaitaan että termeillä on yhteisiä tekijöitä. Osittelulakia soveltaen saadaan
Boolen algebran säännön, , mukaan muuttujan OR operaatio muuttujan negaation kanssa on aina 1, joten
ja, säännön, , mukaan muuttujan AND-operaatio arvon 1 kanssa ("ykkösellä kertominen") ei muuta muuttujan arvoa, eli ykkösen AND-operaatio voidaan sieventää pois
Seuraavaksi muokataan lauseketta, jotta myöhemmin päästään käyttämään Boolen algebran sääntöä, , jolle ei ole vastinetta kymmenlukujärjestelmän algebrassa. Otetaan yhteiseksi tekijäksi
Muuttujan () AND operaatiolla, jonkin toisen muuttujan (
) kanssa, ei ole vaikutusta, jos AND operaation tuloksesta (
) ja muuttujan negaatiosta (
) otetaan OR operaatio. Eli AND operaatio supistuu pois.
Poistetaan sulut osittelulain mukaan
jotta ottamalla yhteiseksi tekijäksi, löydetään toinen termi, johon voidaan myös soveltaa sääntöä
ja saadaan taas AND operaatio sievennettyä pois
Poistetaan vielä sulut osittelulain mukaan, vaikka edellisen lausekkeen toteutus vaatisi vähemmän komponentteja
koska seuraavaksi muutetaan lauseketta siten että se on toteutettavissa pelkillä NAND-porteilla, eli muunnetaan seuraavaksi lauseke ns. NAND-muotoon.
NAND muotoon sieventäminen
NAND-muotoon sievennettäessä, haetaan siis lauseketta, jossa on AND operaatioita, joiden päällä on negatointiviiva, tai useampia. Minkä tahansa operaation ulostulo voidaan negatoida kaksi kertaa, ilman vaikutusta koko lausekkeen ulostuloon. Jotta OR operaatiot saadaan muutettua NAND operaatioiksi, käytetään De Morganin NAND teoreemaa, joka sanoo: Jos OR operaation sisäänmenot on negatoitu, voidaan se vaihtaa negatoimattomien sisäänmenojen NAND operaatioksi. Eli tarvitsemme OR operaatioiden termeistä negaatiot. Lisätään kaksoisnegaatiot vaikka kahden ensimmäisen termin päälle (eli termin operaation ulostuloon)
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
ja De Morganin NAND teoreemaan mukaan saadaan OR operaatio muutettua NAND operaatioksi. Lisäksi jäljelle jääneet negaatiot alkuperäisen OR operaation termien (AND operaatioiden) päällä muuttivat ne NAND operaatioiksi
Muutetaan jäljellä oleva OR operaatio vastaavasti NAND operaatioksi, eli OR operaation termeistä kaksoisnegaatiot
ja De Morganin teoreeman mukaan saadaan
Huomaa 'ylimääräinen' negaatio termin päällä, mikä juontaa siitä että oletetaan että käytössämme on vain NAND-portteja, joissa on 2 sisäänmenoa. Jos käytettävissä on myös 3 sisäänmenoisia NAND:eja, niin lauseke olisi yksinkertaisemman näköinen
missä siis ylin koko lausekkeen (ja kahden tulo operaation) yli menevä NAND-operaatio toteutetaan 3-sisäänmenoisella NAND:illa. 3-sisäänmenoinen NAND voidaan korvata kytkennällä, jossa on 3 kpl 2-sisäänmenoisia NAND:eja. Kytkentä toteutetaan Boolen logiikan piirikaaviotehtävissä. Halutessasi voit kokeilla toteutusta alla myös käyttäen 3-sisäänmenoista NAND:ia.
Alla on vertailukohdaksi vähemmistö kolmesta kytkennän sievennetty SOP-muoto. Toteuta vähemmistö kolmesta käyttäen NAND-portteja.
Karnaughin kartta
Boolen lausekkeen yksinkertaistamista voidaan tehdä myös käyttäen Karnaughin karttaa. Tämä sopii kuitenkin vain, jos loogisia muuttujia on vähän, neljään - kuuteen muuttujan asti. Viiden ja kuuden muuttujan Karnaghin karttoja emme käsittele, ne poikkeavat hieman kahden - neljän muuttujan Karnaughin kartoista. Karnaughin kartta muodostuu taulukon alkiosta, jotka esittävät kaikkia mahdollisia
:n binäärisen muuttujan kombinaatioita.
Karnaughin kartasta SOP-muotoinen sievennetty lauseke
Karnaughin kartan voi muodostaa esimerkiksi totuustaulusta tai SOP- tai POS-muotoisesta lausekkeesta. Jos lausekkeen totuustaulu on annettu, niin Karnaughin kartta on helppo muodostaa. Jokaista totuustaulun riviä vastaa yksi ruutu kartassa. Muodostettaessa SOP-muotoista sievennettyä lauseketta Karnaughin karttaan merkitään tavallisesti vain arvot 1 näkyviin ja arvojen 0 paikat jätetään tyhjiksi. Tässä materiaalissa kuitenkin myös 0 arvot merkitään karttaan. Karttaan tulee reunoille sisäänmenot, ja ruutuihin tulee sisäänmenoja vastaavat ulostulon arvot. Käydään siis läpi jokainen totuustaulun rivi, jonka ulostulo on 1, eli ns. minimitermit (eng. minterms). Etsitään kartasta rivin sisäänmenojen arvot ja sitten etsitään sisäänmenoarvoja vastaavat arvot Karnaughin kartan reunoilta ja sijoitetaan ykkönen kyseiseen ruutuun.
Karnaughin kartat on muodostettu LaTeX:in tikz paketilla. Dokumentista löytyy koodit karttojen piirtoon, suurin osa kommenteissa.
—Huomattavaa Karnaughin kartan muodostamisessa on, että kartan reunalle tulevat sisäänmenot täytyy järjestää, siten että vierekkäisissä positioissa vain yksi bitti muuttuu. Tämä on vastaa Gray-koodia. Eli yläreunan bitit (B ja C) pitää tässä tapauksessa olla järjestyksessä 00, 01, 11, 10. Tästä siis juontuu vihreällä taustalla olevan (totuustaulun kolmannen rivin) ykkösen sijoittuminen kartassa.

Vastaavasti voitaisiin nollille katsoa paikat karttaan, tai vain jättää nolla-paikat tyhjiksi, tai kuten tässä materiaalissa, asetetaan nollat tyhjiin ruutuihin.
Seuraavaksi etsitään ykkösiä, joista voidaan muodostaa suorakaiteen muotoisia alueita, sillä rajoituksella, että suorakaiteessa saa olla vain jonkun kakkosen potenssin verran ruutuja. Mitä suurempi alue, sitä parempi (sitä enemmän voidaan lauseketta/kytkentää sieventää). Alue saa myös mennä reunojen yli, kartan voi ajatella kolmiulotteisena sylinterinä. Jokaisen ykkösen tulee kuulua ainakin yhteen alueeseen, mutta ne saavat kuulua useampaankin alueeseen.

Yllä on vähemmistö kolmesta totuustaulusta muodostettu Karnaughin kartta, johon on värjätty alueet, joissa on vierekkäiset ulostulon 1 antavat termit.
Muodosta seuraavaksi itse alle vastaava SOP-muotoinen Karnaughin kartta. Lisää ykköset ja nollat paikoilleen, älä poista taulukon piirtoon käytettäviä viivoja. Välilyöntien määrällä ei ole vaikutusta, eli pystyviivojen ei tarvitse olla samoilla kohdin.
Plugin has invalid values for these markup fields: autoupdate: expected number or undefined
—Korjattu
—av: Tarkistin päivitetty antamaan palautetta 18.10.2021
—Kun kartta on saatu luotua, niin voidaan kirjoittaa sievennetty algebrallinen lauseke huomioimalla ykkösten paikat kartalla. Jos kahdella vierekkäisellä ruudulla, pysty- tai vaakasuunnassa molemmissa on alkiona 1, niin ruutuja vastaavat SOP muotoiset tulotermit eroavat vain yhden muuttujan osalta. Eli lausekkeita sieventäessä tätä vastaa se, että samana säilyvät muuttujat voidaan ottaa yhteiseksi tekijäksi (ja muuttujan ja sen negaation OR operaatio sieventyy pois).
Esimerkiksi kuvassa oranssilla on värjätty ruudut, joita vastaa totuustaulusta saadut SOP -termit ja
. Eli vähemmistö kolmesta Boolen SOP-muotoisen lausekkeen osa näiden termien osalta olisi
. Koska
ei C muuttujalla ole vaikutusta lopputulokseen ja se voidaan siis sieventää pois, eli
.
Karnaughin kartasta tämä siis nähdään suoraan oranssilla taustalla olevista laatikoiden rivi- ja sarakemuuttujien arvoista. Oranssi alue on rivillä sekä sarakkeissa
ja
. Eli se muuttuja jonka arvo muuttuu (eli riveillä/sarakkeilla on sekä muuttuja että sen negaatio), voidaan sieventää pois. Mitä suurempi on ykkösten muodostama alue, sitä useampi tällainen muuttuja löytyy. Negaatiot muuttujien
ja
päälle tulee siitä, että ulostulo 1 saadaan silloin, kun sarakemuuttujien
ja
arvot ovat 0.
Kuvan eri värisistä alueista saadaan siis sievennetyt SOP-termit
| Väri | termi |
|---|---|
| oranssi | |
| sininen | |
| vihreä |
sievennetty SOP-muotoinen lauseke saadaan summaamalla termit
Karnaughin kartan käsittelyssä noudatetaan seuraavia sääntöjä, kun tavoitteena on SOP-muotoinen sievennetty lauseke
- Ykkösen sisältävien ruutujen joukosta etsitään sellaisia suorakaiteen muotoisia alueita, joiden koko on jokin kahden potenssi esim.
,
,
,
.
- Ykkösellä merkittyjen ruutujen joukosta valitaan suorakaidealueita, jotka ovat mahdollisimman suuria ja joiden lukumäärä on mahdollisimman pieni, siten että jokainen ykkönen kuuluu ainakin yhteen valittuun suorakaiteeseen.
Karnaughin kartasta POS-muotoinen sievennetty lauseke
POS-muotoinen sievennetty lauseke Karnaughin kartasta saadaan kartan nollien avulla. Ideana on muodostaa mahdollisimman suuria nollia sisältäviä suorakaiteenmuotoisia alueita. Näiden alueiden avulla saadaan sievennetyt termit POS-muotoiselle lausekkeelle.

Aiemmin opittiin, jotta POS-muotoisen termin ulostuloksi tulee nolla, täytyy POS-termin (OR operaation) ykkös-sisäänmenot negatoida. Jos tutkitaan oranssilla väritettyä aluetta, niin siihen sisältyy POS-termit ja
. Näiden tulo olisi siis
, ja osittelulain mukaan ottamalla yhteinen tekijä voidaan lauseke sieventää muotoon
. Koska
, niin se sieventyy pois.
Kuvasta nähdään, että oranssilla alueella reunojen A ja C sisäänmenot pysyvät vakiona ja B muuttuu, täten siis B sieventyy pois. Sievennettyä POS-termiä muodostettaessa täytyy sisäänmenot negatoida, koska oranssilla alueella A=1 ja C=1.
Kuvan eri värisistä alueista saadaan siis sievennetyt POS-termit
| Väri | termi |
|---|---|
| oranssi | |
| sininen | |
| vihreä |
ja sievennetty POS-muotoinen lauseke saadaan kertomalla termit
Quine-McCluskeyn menetelmä
Karnaughin kartta menettää hyötynsä suurella muuttujien määrällä, esimerkiksi viidellä muuttujalla tarvitaan kaksi 16 alkioista karttaa. Quine-McCluskeyn taulukointimenetelmä soveltuu paremmin, kun totuustaulussa on useita sisäänmenoja. Esitystapaa lukuun ottamatta menetelmä on identtinen Karnaughin kartan kanssa. Lisäksi se on tehokkaampi toteuttaa tietokoneen algoritmina ja mahdollistaa sen, että voidaan tarkistaa onko minimaalinen muoto löytynyt. Tosin ongelma, totuustaulua vastaavan minimaalisen lausekkeen muodostaminen, on luonteeltaan NP-kova, eli se on luonteeltaan vähintään yhtä vaikea kuin mikä tahansa NP-ongelma. Käytännössä tämä tarkoittaa sitä että algoritmin laskenta-aika kasvaa eksponentiaalisesti muuttujien määrän suhteen.
Kombinaatiologiikka
Kombinaatiologiikka on Boolen algebran soveltamista kytkentöjen (loogisten piirien) tekemiseen käyttäen loogisia portteja. Kombinaatiologiikkaa kutsutaan joskus myös ajasta riippumattomaksi logiikaksi, mikä tarkoittaa sitä että piirin ulostulo muuttuu heti kun piirin sisäänmeno muuttuu.
Todellisuudessa sisäänmenon muutoksessa, signaalin kulussa piirin kytkennän läpi sekä ulostulon muutoksessa on aina viivettä ja se tulee ottaa huomioon piirien transistoritason suunnittelussa. Lisäksi suunniteltaessa monimutkaisempaa sekvenssilogiikkaa täytyy komponenttien sekä piirien viiveet huomioida käytettävän kellotaajuuden suhteen. Kiinnostuksen herätessä asiaa voi opiskella lisää esimerkiksi edX:n tarjoamalla online kurssilla Computation Structures - Part 1: Digital Circuits Kurssin wiki sivuille on listattu muitakin kursseja sekä linkkejä kurssin jälkeiseen tiedon syventämiseen.
Tietokoneet käsittelevät useampi-bittisiä binäärilukuja, joten perus- sekä kombinaatio- että sekvenssilogiikan komponenteista tulee olla myös useampi-bittisiä versioita. Käytännössä tämä tarkoittaa sitä että bitit käsitellään rinnakkain.
Puolisummain
Tutkimalla binäärinumeroiden yhteenlaskun sääntöjä, havaitaan että enimmillään kahden binäärinumeron yhteenlaskun tuloksen ilmaisemiseen tarvitaan 2-bittinen binääriluku, eli tapauksessa 12 + 12 = 102. Muissa tapauksissa tulos on 1-bittinen, toki voidaan lisätä 1-bittisten tulosten eteen 0, muuttamatta tulosta, jolloin nekin ovat 2-bittisiä binäärilukuja.
Kahden binäärinumeron yhteenlaskun toteutukseen tarvitaan siis komponentti, jolla on kaksi kappaletta sisäänmenoja sekä kaksi kappaletta ulostuloja.
Olkoon sisäänmenot (yhteenlaskettavat binäärinumerot) ja
. Merkitään yhteenlaskun tuloksen oikeanpuoleista binäärinumeroa muuttujalla
(summabitti) ja vasemmanpuoleista binäärinumeroa muuttujalla
(muistibitti, eng. carry bit). Kirjoitetaan aiemmin esitetyt binäärisen yhteenlaskun säännöt hieman eri tavalla, käyttäen edellä esitettyjä muuttujia a, b, s ja c
1 c
0 0 1 1 a
+ 0 + 1 + 0 + 1 + b
00 01 01 10 cs
Muodostetaan seuraavaksi sääntöjä vastaava totuustaulu, eli kun ja
, niin
ja
ja vastaavasti muut totuustaulun rivit
| a | b | c | s | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Keskellä oleva tyhjä sarake on lisätty korostamaan sitä mitkä sarakkeet ovat sisäänmenoja ja mitkä ulostuloja. Totuustaulun rivien määrästä voi myös päätellä sisäänmenojen määrän, ottamalla 2-kantaisen logaritmin rivien määrästä, eli tässä tapauksessa . Totuustaulua vastaava komponentti on nimeltään puolisummain (eng. Half Adder). Puolisummain tulee siitä, että komponentilla ei pysty rakentamaan useampi bittistä binäärilukujen yhteenlasku-komponenttia. Seuraavassa luvussa esitellään komponentti, kokosummain (joka pitää sisällään kaksi puolisummainta), jolla voidaan rakentaa n-bitin summain- komponentteja.
Koska totuustaulussa on kaksi ulostuloa, muodostetaan molemmille ulostuloille omat lausekkeet. Tutkimalla muistibitin saraketta huomataan sen olevan vastaava kuin AND-portin totuustaulun ulostulosarake. Täten muistibitin lauseke on siis
Vastaavasti tutkimalla summabitin
saraketta, havaitaan että se on vastaava kuin erään toisen peruskomponentin totuustaulun ulostulon sarake. Harjoittele SOP-muodon toteutusta, kirjoittamalla alle summabitin SOP muoto totuustaulusta.
Toteuta seuraavaksi puolisummain alla olevaan piirikaavioeditoriin, haluamillasi tarjolla olevilla komponenteilla.
Puolisummaimella voi siis laskea yhteen kaksi binäärinumeroa eli bittiä. Kun binääriluvussa on kaksi tai useampia bittejä, niin kahden binäärinumeron yhteenlaskusta syntyvä muistibitti täytyy ottaa huomioon seuraavan position binäärinumeroita yhteen laskettaessa. Eli useampi bittisen yhteenlaskun toteuttamiseen tarvitaan komponentti, joka osaa laskea yhteen kolme bittiä, eli kaksi yhteenlaskettavaa binäärinumeroa sekä edellisen binääriposition yhteenlaskusta syntyvän muistibitin.
Kokosummain
Jotta voidaan rakentaa yhteenlaskin mielivaltaiselle bittimäärälle, rakennetaan seuraavaksi kokosummain, joka laskee yhteen kaksi bittiä ja lisäksi mahdollisen muistibitin eli muodostaan summan kolmesta 1-bittisestä binääriluvusta.
Tutkitaanpa kahden 2-bittisen binääriluvun yhteenlaskua ja käytetään indeksejä hakasulkeissa kuvaamaan binäärilukujen bittien positioita. Alla on esimerkkinä vierekkäin kahdeksan kappaletta yhteenlaskuja 2-bittisten binäärilukujen eri kombinaatioilla. Kombinaatioita on kahdeksan muutakin, mutta alla olevat kahdeksan visualisoivat tarpeeksi summa- ja muistibittien positioita.
0000001001111111c[2]c[1]c[0]0000101001011111a[1]a[0]+00+10+00+10+01+11+01+11+b[1]b[0]000010010100010100100110c[2]s[1]s[0]
Havaitaan että oikean puoleisimman bitin (vähiten merkitsevän bitin, eng. LSB = Least Signifigant Bit) yhteenlaskun voi toteuttaa puolisummaimella, koska nollanteen positioon, indeksi [0], ei voi tulla muistibittiä (ts. c[0] == 0). Ykkösposition (indeksi [1]) yhteenlaskuun tarvitaan uusi komponentti, jonka sisäänmenoina on c[1], a[1] ja b[1] ja ulostuloina on c[2] ja s[1]. Eli komponentti joka laskee yhteen kolme binäärinumeroa ja jonka ulostulo on 2-bittinen binääriluku. Komponentin sisäänmenot on esitetty punaisella ja ulostulot sinisellä värillä. Komponentin nimi on kokosummain (eng. Full Adder), koska kokosummaimen voi rakentaa kahdesta puolisummaimesta ja kokosummaajia käyttämällä voidaan toteuttaa -bittinen summaaja. Muodostetaan seuraavaksi kokosummaimen totuustaulu, käyttäen apuna binäärinumeroiden yhteenlaskun sääntöjä. Jätetään muuttujista indeksit pois ja merkitään edellisestä positiosta tulevaa muistibittiä termillä
ja laskutoimituksen tuloksen muistibittiä termillä
.
| cin | a | b | cout | s | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Kokosummaimen totuustaulusta voi ratkaista (SOP-muotoisen) loogisen lausekkeen molemmille ulostuloille ja
ja sitten sieventää sitä algebrallisesti tai vaikka Karnaughin kartalla. Jos tutkii totuustaulua tarkemmin, niin neljä ylintä riviä vastaa puolisummaimen totuustaulua. Jos taas vertaa neljän alimman rivin ulostuloja neljän ylimmän rivin ulostuloon, huomaa että sisäänmenoissa vain
arvo muuttuu nollasta ykköseksi. Vertailemalla ulostuloja, tulkiten
ja
2-bittiseksi binääriluvuksi, huomataan että alimpien rivien arvot ovat yhden suuremmat, kuin vastaavien ylempien rivien. Esimerkiksi rivin
ulostulot ovat
, eli
ja vastaavasti rivin
ulostulot ovat
, eli
. Eli neljä alinta riviä saadaan ottamalla vastaavan ylemmän rivin (puolisummaimen) ulostulo ja lisäämällä siihen
arvo toisella puolisummaimella. Jälkimmäisen puolisummaimen
ulostulo on siis kokosummaimen
ulostulo ja kokosummaimen
ulostulo tulee olla 1 silloin kun jommankumman tai molempien puolisummainten muistibitin arvo on 1.
Toteuta seuraavaksi kokosummain alla olevaan piirikaavioeditoriin, haluamillasi komponenteilla.
Kokosummaimilla saa siis toteutettua -bittisen yhteenlaskimen. Huomioitavaa on, kuten puolisummaimen tapauksessa, että yhteenlaskun tuloksen esittämiseen saattaa tarvita useamman bitin kuin mitä yhteenlaskettavien lukujen esittämiseen.
Jos järjestelmä voi tallentaa esimerkiksi vain 4 bittisiä lukuja (kuten yllä) ja laskutoimituksesta voi tuloksena olla 5-bittinen luku, tapahtuu ylivuoto, josta summaimen tulee ilmoittaa. Yleensä tämä tehdään johdottamalla viimeinen muistibitti ylivuoto (eng. overflow) ulostuloon. Toinen vaihtoehto, on rakentaa järjestelmä siten, ettei 'liian isoja' lukuja voi käyttää.
Tulo- ja lähtövalitsimet
Tulo- ja lähtövalitsimet ovat kombinaatiologiikan piirejä, joilla voidaan valita useamman vaihtoehdon väliltä se mikä piiriin tuleva sisäänmeno (tulo) valitaan kytkettäväksi ulostuloon tai valitaan mihinkä ulostuloon (lähtö) kytketään piiriin sisäänmenevä signaali. Tulovalitsin eli multiplekseri (eng. multiplexer) on kombinaatiologiikan piiri, jonka tehtävä on valita useista sisäänmenoista yksi signaali, joka johdetaan ulostuloksi niin kauan, kunnes valitaan jokin toinen sisäänmeno johdettavaksi ulostuloon. Lähtövalitsin eli demultiplekseri (eng. demultiplexer) on kombinaatiologiikan piiri, jonka tehtävä on puolestaan johdottaa sisään tuleva signaali yhteen useammasta ulostulovaihtoehdosta. Sisäänmeno- ja ulostulosignaalien määrä vaihtelee mutta on yleensä jokin kahden potenssi.
Tulovalitsin
Yksinkertaisin tulovalitsin on komponentti, jossa on kaksi sisäänmenoa, joista toinen johdetaan ulostuloon valintasignaalin perusteella. Olkoon sisään menevät signaalit A ja B, valintasignaali sel ja ulostulo out. Olkoon meillä tulovalitsin, joka valintasignaalin sel arvolla 0 valitsee sisäänmenon A ulostuloksi ja valintasignaalin sel arvolla 1 valitsee sisäänmenon B ulostuloksi. Toiminnan voi kuvata totuustaulun kaltaisella taulukolla, jossa ulostulo esitetään valintasignaalin eri arvoilla.
| sel | out |
|---|---|
| 0 | A |
| 1 | B |
Taulukkoa vastaavan tulovalitsimen totuustaulu on esitetty alla. Kombinaatiologiikan piirikaaviotehtävissä voit toteuttaa totuustaulun mukaisen tulovalitsimen.
| A | B | sel | LED |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Tulovalitsimen nimi kuvaa sisäänmenojen määrää, esimerkiksi edellisen tulovalitsimen nimi on 2-to-1 mux tai 2:1 mux. Komponentti 2:1 mux on universaali piiri, jolla voidaan esittää kaikki loogiset funktiot, samoin kuin esimerkiksi universaaleilla porteilla NAND ja NOR.
Enemmän kuin kaksi sisäänmenoa tulovalitsimeen
Kun tulovalitsimella on neljä sisäänmenoa, niin sen nimi on 4-to-1 mux (Nand2Tetris käyttää komponentin nimenä Mux4Way.hdl). Nyt valintaan tarvitaan kaksi bittiä, joilla voidaan ilmaista neljä eri arvoa. Merkintätavalla ei ole käytännössä merkitystä ja se vaihtelee lähteestä riippuen. Olkoon meillä valintasignaalit sel[0] ja sel[1] sekä sisään menevät signaalit A, B, C ja D. Tällöin voidaan 4:1 mux:in toiminta kuvata totuustaulun kaltaisella taulukolla esimerkiksi seuraavasti
| sel[1] | sel[0] | out |
|---|---|---|
| 0 | 0 | A |
| 0 | 1 | B |
| 1 | 0 | C |
| 1 | 1 | D |
Huomaa että valintasignaaliksi on valittu 2-bittinen valintasignaali sel[2], jossa 1-bittiset signaalit merkitään indekseillä sel[0] ja sel[1]. Neljän sisäänmenon tulovalitsimen 4:1 mux voi rakentaa käyttämällä 2:1 mux komponentteja. Komponentit ketjutetaan siten että ensin kahdella 2:1 mux:illa valitaan esimerkiksi A tai B ja C tai D valintasignaalilla sel[0]. Nämä valinnat johdotetaan kolmanteen 2:1 mux:iin, jota ohjaa valintasignaali sel[1].
Vastaavasti, lisäämällä yksi valintabitti, voidaan rakentaa 8:1 mux käyttäen 2:1 mux komponentteja tai käyttämällä myös 4:1 mux komponentteja.
| sel[2] | sel[1] | sel[0] | out |
|---|---|---|---|
| 0 | 0 | 0 | A |
| 0 | 0 | 1 | B |
| 0 | 1 | 0 | C |
| 0 | 1 | 1 | D |
| 1 | 0 | 0 | E |
| 1 | 0 | 1 | F |
| 1 | 1 | 0 | G |
| 1 | 1 | 1 | H |
Tulovalitsimesta voidaan tehdä myös useampi bittinen, eli se valitsee esimerkiksi kahdesta 16-bittisestä sisäänmenosta toisen, joka johdetaan 16-bittiseen ulostuloon. Valintalogiikka toimii samalla tavalla riippumatta valittavien signaaleiden bittimäärästä. Tulovalitsimia käytetään monissa tietokoneen käyttämissä piireissä silloin, kun sisään menevästä datasta tai kontrollisignaaleista täytyy valita vain yksi reititettäväksi eteenpäin piirin muihin osiin. Esimerkiksi aritmeettisloogisen yksikön (ALU) ohjauksen toteutuksessa käytetään tulovalitsimia ohjaamaan summaajalle valittavia summattavia lukuja sekä valitsemaan summaajan (aritmeettisen laskutoimituksen) ulostulo, eikä esimerkiksi loogisen operaation tulosta, johdettavaksi ALU:n ulostuloon.
Lähtövalitsin
Lähtövalitsimessa yksi sisäänmeno valitaan johdettavaksi yhteen useammasta ulostulosta. Olkoon sisäänmeno in, ulostulot A ja B sekä valintasignaali sel. Tällöin 2-ulostuloisen lähtövalitsimen toimintaa voidaan kuvata totuustaulua vastaavalla taulukolla
| sel | a | b |
|---|---|---|
| 0 | in | 0 |
| 1 | 0 | in |

Lähtövalitsin toteutetaan Kombinaatiologiikan piirikaaviotehtävien NAND tai NOR porteilla. Alla on esimerkki lähtövalitsimen totuustaulusta, jossa yksi sisäänmenosignaali a sytyttää tai sammuttaa keltaisen tai sinisen LEDin riippuen sel-signaalin arvosta. Piirikaavioon voit toteuttaa totuustaulun lähtövalitsimen haluamillasi porteilla.
| a | sel | Keltainen | Sininen |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Enemmän kuin kaksi ulostuloa lähtövalitsimesta
Lähtövalitsin voidaan laajentaa useamman ulostulon lähtövalitsimeksi. Neljän ulostulon lähtövalitsinta kuvaava taulukko on esitetty seuraavassa
| sel[1] | sel[0] | a | b | c | d |
|---|---|---|---|---|---|
| 0 | 0 | in | 0 | 0 | 0 |
| 0 | 1 | 0 | in | 0 | 0 |
| 1 | 0 | 0 | 0 | in | 0 |
| 1 | 1 | 0 | 0 | 0 | in |
Huomaa että valintasignaaliksi on valittu 2-bittinen valintasignaali sel[2], jossa 1-bittiset signaalit merkitään indekseillä sel[0] ja sel[1]. Vastaavaa merkintää käytetään Nand2Tetris tehtävien 4-ulostuloisen demultiplekserin (DMux4Way.hdl) toteutuksessa. Vastaavasti voitaisiin nimetä multiplekserin valintasignaalit, jolloin toiminta vastaisi Nand2Tetris tehtävien multiplekserin (Mux4Way.hdl) toteutusta. Lähtövalitsinta käytetään esimerkiksi muistiin tallennettaessa valitsemaan muistipaikka osoitteen perusteella.
Kahdeksan ulostulon lähtövalitsimen totuustaulu on esitetty alla.
| sel[2] | sel[1] | sel[0] | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | in | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | in | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | in | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | in | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | in | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | in | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | in | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | in |
Valintasignaalina on 3-bittinen valintasignaali sel[3], jossa 1-bittiset signaalit merkitään indekseillä sel[0], sel[1] ja sel[2]. Vastaavaa merkintää käytetään Nand2Tetris tehtävien 8-ulostuloisen demultiplekserin (DMux8Way.hdl) toteutuksessa.
Aritmeettislooginen yksikkö
Aritmeettislooginen yksikkö (Arithmetic Logic Unit, ALU) on yksi monimutkaisimmista kombinaatiologiikan komponenteista tietokoneessa. Kaikki aiemmin esitetyt komponentit ovat suurin piirtein samanlaisia eri tietokoneissa. ALU puolestaan on sidoksissa tietokoneen arkkitehtuuriin ja prosessorin toimintaan. ALU toteuttaa tietokoneen prosessorissa laskennalliset sekä loogiset perusoperaatiot. ALU käsittelee binäärisiä kokonaislukuja, liukuluvuille nykyisissä tietokoneen prosessoreissa on erillinen liukulukuyksikkö (FPU). ALU toimii myös esimerkiksi FPU:iden sekä grafiikkaprosessoreiden (GPU) rakennuspalikkana. Yhdessä prosessorissa voi olla useita ALU:ja. Käytännössä eri tyyppisissä (tietokoneen) prosessoreissa on erilaiset ALU:t, jotka on suunniteltu juuri kyseistä prosessoria varten, mutta ne on suunniteltu samoilla yleisillä periaatteilla.
ALU:n sisäänmenoina ovat laskentaan ja operaatioihin käytettävä data, operandit, sekä ohjausdata, opcode, joka ilmaisee ALU:lle suoritettavan operaation. ALU:n ulostulona on operaation suorittamisesta saatu tulos. Lisäksi optionaalisena ALU:n sisäänmenoina on rekistereistä sisään tuotavaa tilatietoa ja ulostuloina rekistereihin tallennettavaa tilatietoa, esim. oliko edellisen operaation ulostulo negatiivinen tai nolla.

ALU on yleensä ensimmäinen osa, joka suunnitellaan prosessoria suunniteltaessa. Sen jälkeen suunnitellaan prosessoriin logiikka, joka ohjaa ALU:n toimintaa syöttämällä ALU:n ohjausdatan sekä operandit.
Tyypillisesti ALU:n tarvitsee suorittaa AND, OR ja (operandien) NOT operaatiot sekä yhteenlasku- ja vähennysoperaatiot. Kaikki muut loogiset operaatiot ja laskutoimitukset voidaan toteuttaa em. perusoperaatioilla. Operandien invertointimahdollisuus sekä ulostulon invertointimahdollisuus mahdollistaa lisäksi OR operaation toteuttamisen AND komponentilla (De Morganin teoreema) sekä vähennyslaskun toteuttamisen yhteenlaskupiirillä.
Nykyajan tietokoneissa ALU:t kykenevät tekemään monimutkaisia laskutoimituksia ja mitä monimutkaisempia operaatioita ALU kykenee suorittamaan yhdellä kellojaksolla, sitä nopeampaa on prosessorin toiminta, tosin ALU on myös kalliimpi toteuttaa, eli vaatii enemmän transistoreita prosessorin toteutukseen. Mooren laki on Gordon Mooren 1965 ja 1975 havainnoima ja ennustama transistorien määrän kaksinkertaistuminen noin kahden vuoden välein integroiduissa piireissä, kuten prosessoreissa. Piirien suorituskyky kaksinkertaistuu noin puolentoista vuoden välein, tähän vaikuttaa lisäksi transistorien nopeutuminen transistorien fyysisen koon pienentyessä. Vuosina 2010-2016 transistorien määrä sekä CPU:issa että GPU:issa on noussut noin kahdesta miljardista noin seitsemään miljardiin. Tietokoneiden prosessoreissa kasvu on viime aikoina johtunut ydinten määrän lisäämisestä sekä välimuistin määrän lisäämisestä.
ALU:n hintaa voidaan laskea toteuttamalla monimutkaiset operaatiot liukuhihnoitettuna usean yksinkertaisen ALU:n läpi tai iteratiivisesti yhdellä yksinkertaisella ALU:lla, jolloin prosessorin kontrolliyksikkö ohjaa ALU:n toimintaa monimutkaisen operaation kaikkien vaiheiden suorittamiseksi. Kaikissa edellä mainituissa tapauksissa prosessorin konekielestä löytyy erillinen käsky, jolla monimutkainen operaatio suoritetaan. Tietokoneiden alkuaikoina monimutkaiset operaatiot suoritettiin ohjelmallisesti, eikä prosessorin konekielessä siis ollut tällöin käskyä operaatioon. Monimutkainen operaatio toteutettiin käytännössä käyttöjärjestelmään prosessorin konekielisistä käskyistä koostamalla, vastaavasti kuten tällä kurssilla toteutetaan Nand2Tetriksen HACK-tietokoneeseen kertolaskun toteutus sen Assembly-kielellä. Ohjelmallinen suorittaminen on vielä hitaampaa kuin iteratiivinen suorittaminen.
Seuraavaksi tutustumme tarkemmin erääseen yksinkertaiseen ALU:un, Nand2Tetriksen HACK-tietokoneen prosessoriin suunniteltuun ALU:un.
HACK-tietokoneen prosessorin ALU:n suunnittelu
Ennen kuin aloitetaan ALU:n suunnittelu, on hyvä tutkia HACK-tietokoneen prosessorin osia ja ALU:n suhdetta niihin. Prosessoria suunnitellessa tulee päättää ne funktiot, joita prosessori tulee toteuttamaan elektroniikalla. Lisäksi tulee suunnitella signaalit, joilla ohjataan prosessori suorittamaan haluttu funktio.
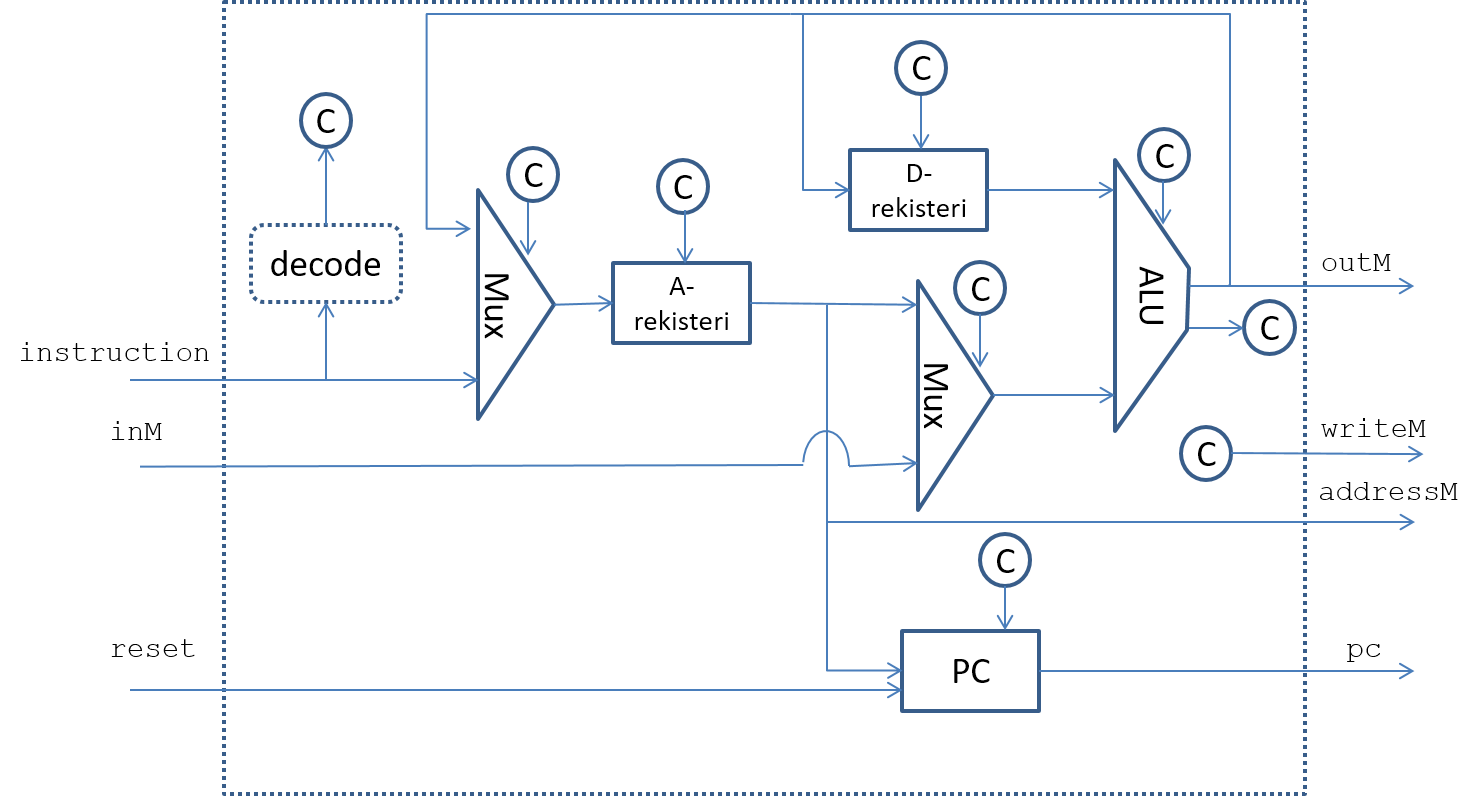
Nand2Tetriksen HACK-tietokoneen prosessorin ALU:n arkkitehtoninen suunnittelu on tehty valmiiksi, eli tietokoneen sanan leveys sekä ALU:n toteuttamat funktiot ja käskyt funktioiden toteuttamiseksi on valittu valmiiksi. Tällä kurssilla ALU:n suunnittelun tehtäväksi jää ALU:n organisatorinen suunnittelu, eli se kuinka ALU:n toiminta toteutetaan loogisilla komponenteilla. ALU:n toteuttamat funktiot ja ALU:a ohjaavat signaalit löydät kirjan The Elements of Computing Systems luvusta 2 sekä ALUn javascript versiosta, jolla voit myös tutkia ALUn toimintaa.
ALU:n funktiot voitaisiin jokainen toteuttaa omana kytkentänään ALU:n sisälle, mutta tarkastelemalla ALU:lle valittuja ohjaussignaaleita suhteessa ALU:n toteuttamiin funktioihin voidaan tarvittavien komponenttien määrää pienentää. ALU:a ohjataan kuudella ohjaussignaalilla, joista
- yksi negatoi ALU:n x-sisäänmenon (operandin),
- yksi nollaa ALU:n x-sisäänmenon (operandin),
- yksi negatoi ALU:n y-sisäänmenon (operandin),
- yksi nollaa ALU:n y-sisäänmenon (operandin),
- yksi negatoi ALU:n ulostulon,
- yksi valitsee suoritetaanko AND- vai ADD-operaatio, toisin sanoen ohjataanko ALU:n ulostuloksi yhteenlasku- vai AND-piirin ulostulo.
Nämä valinnat viittaavat siihen, että OR-funktiolle ei ole OR-piiriä eikä vähennyslaskulle ole vähennyslaskupiiriä vaan ne toteutetaan jollain muulla tavalla.
ALU:n OR-funktion toteutus
Tutkitaanpa ALU:n totuustaulun OR-funktiota vastaavaa riviä.
zx nx zy ny f no out 0 1 0 1 0 1 x|y
Rivin mukaan OR-funktio saadaan negatoimalla x-sisäänmeno (nx = 1), negatoimalla y-sisäänmeno (ny = 1), muodostamalla niiden AND-operaatio (f = 0) sekä negatoimalla ulostulo (no = 1). Kuvaus tuo varmaan mieleen De Morganin -teoreemat, De Morganin NOR -teoreeman oikeapuoli vastaa melkein kuvausta. Lisäämällä oikealle (ja vasemmalle) puolelle ulostulon negatoinnin, saadaan
ja kaksoisnegaatiosäännön mukaan
eli ALU:n OR-funktio toteutetaan soveltamalla De Morganin NOR -teoreemaa.
ALU:n vähennyslaskun toteutus
Voisiko ALU:n vähennyslaskun toteuttaa myös negatointien avulla ja yhteenlaskupiirillä? Negatiivisten lukujen binääriesityksessähän käytetään komplementteja, eli negaatioita. Tutkitaanpa ALU:n totuustaulun (erästä) vähennyslaskua vastaavaa riviä.
zx nx zy ny f no out 0 1 0 0 1 1 x-y
Rivin mukaan vähennyslasku saadaan negatoimalla x-sisäänmeno (
nx = 1), laskemalla yhteen negatoitu x ja y (f = 1) sekä negatoimalla ulostulo (no = 1). Tutkintaanpa ensin 10-lukujärjestelmän luvuilla negatointia, eli etumerkin vaihtamista vastakkaiseksi. Vähennyslasku voidaan vaihtaa yhteenlaskuksi ottamalla miinusmerkki yhteiseksi tekijäksi. Yhteiseksi tekijäksi otetaan siis -1, mutta ykkönen on jätetty merkitsemättä.
- Positiivisilla luvuilla
- 7 – 5 = 2
- -(-7 - -5) = -(-2)
- -(-7 + 5) = -(-2) = 2
- Vastaavasti negatiivisella luvulla
- −8 – 4 = −12
- −(+8 + 4)= −(12) = −12
Tässä siis sulkujen ulkopuolella oleva miinusmerkki vastaa ALU:n ulostulon negatoimista, ja ensimmäisen luvun edessä olevan etumerkin vaihtaminen ALU:n x-sisäänmenon negatointia. Toisin sanoen
- Muutetaan ensimmäinen termin merkkiä (negatoidaan)
- Muutetaan vähennyslasku yhteenlaskuksi
- Muutetaan lopputuloksen merkkiä (negatoidaan)
Eli ALU:n pitää vähennyslaskun toteuttamiseksi
- muuttaa
:n merkkiä
- käyttää yhteenlaskupiiriä
- muuttaa ulostulon merkkiä
Se miten merkin muunnos ALU:n sisällä tehdään ei vaikuta ALU:n ulkopuolella käytettävään negatiivisten lukujen binääriesitykseen. Yhden komplementti on yksinkertaisempi, niin se on valittu merkin muuntamiseksi ALU:n sisällä, eli pelkkä negatointi riittää. Alla on 8-bittisillä 2-komplementti binääriluvuilla esitetty ALU:n vähennyslaskun esimerkki. Huomaa että ALU:n sisällä (laatikoitu alue) olevat binääriluvut eivät ole kahden komplementtimuodossa, mutta sisäänmenot ja ulostulot ovat.
Esim.
negatoidaan ensimmäinen luku ja vaihdetaan vähennyslasku yhteenlaskuksi
input _______________ output
7 00000111 -----> | 11111000 |
- 5 - 00000101 -----> | + 00000101 |
---- ---------- | ---------- |
2 | 11111101 | -----> 00000010 (tämä on +2)
---------------
negatoidaan lopputulos
Esim.
negatoidaan ensimmäinen luku ja vaihdetaan vähennyslasku yhteenlaskuksi
input _______________ output
-8 11111000 -----> | 00000111 |
- 4 - 00000100 -----> | + 00000100 |
---- ---------- | ---------- |
-12 | 00001011 | -----> 11110100 (tämä on -12)
---------------
negatoidaan lopputulos
Kokonaislukujen ja
vähennyslaskun toteutus ALU:ssa
- Negatoidaan
- Lasketaan yhteen
- Negatoidaan lopputulos
Vastaavasti voidaan laske .
1-bittisen ALU:n toteuttaminen
ALU voidaan siis toteuttaa yhteenlaskupiirillä sekä AND -piirillä ja lisäksi pitää valita miten operandeja sekä ulostuloa käsitellään, eli
zxjanxohjaa multiplekseriä- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
- x, negatoitu x, 0 tai negatoitu 0
- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
zyjanyohjaa multiplekseriä- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
- y, negatoitu y, 0 tai negatoitu 0
- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
fohjaa multipekseriä,- jonka sisäänmenoina on yhteenlasku sekä AND -piirien ulostulot.
noohjaa multiplekseriä,- jonka sisäänmenoina on edellisen multiplekserin ulostulo ja sen negaatio
- edellisen multiplekserin ulostulo on ALU:n ulostulo
zrjangulostulot saadaan tutkimalla ALU:n ulostuloa
Toteuta 1-bittinen ALU, yhteenlaskupiiriksi soveltuu tällöin puolisummain, jonka muistibitti jätetään huomioimatta, koska ALU:un ei toteuteta ylivuodon tutkimista. Testaa 1-bittistä ALU:a ohjaussignaaleilla. Esimerkiksi, jos x = 1 ja y = 1 (napit on painettu) niin AND operaatio antaa ulostuloksi 1 ja ADD ulostuloksi 0 (summabitti, kun muistibitti jätetään huomioimatta), silloin kuin muut ohjaussignaalit ovat nollia.
Yllä oleva 1-bittinen ALU ei itsenään ole järkevä, mutta n-bittinen ALU rakentuu samalla periaatteella. Tällöin x ja y sekä komponentit ovat n-bittisiä, puolisummain on n-bittinen summaaja sekä ulostulo on n-bittinen. 1-bittisestä ALU:sta puuttuu zr ja ng ulostulot, zr on 1 silloin kun ulostulon kaikki bitit ovat 0 (mikään bitti ei ole 1), ng on 1 silloin kun ulostulon MSB bitti on 1.
HACK-tietokoneen 16-bittisen ALU:n toteutus vaatii 400 - 500 NAND-porttia, joista suurin osa menee 16-bittisyyden toteuttamiseen. 16-bittinen ALU voidaan esimerkiksi toteuttaa monistamalla 1-bittistä toteutusta, tai HDL-kielellä helpompi on käyttää aiemmin rakennettuja 16-bittisiä komponentteja.
Sekvenssilogiikka
Sekvenssilogiikka on ajasta riippuvaa logiikkaa, jossa loogisen piirin ulostulo riippuu sen hetkisten sisäänmenojen lisäksi aiemmista sisäänmenoista. Riippuvuus aiempaan sisäänmenoarvoon toteutetaan takaisinkytkennällä, eli kytkennän ulostulo tai useampi ohjataan takaisin yhdeksi tai useammaksi kytkennän sisäänmenoksi. Aikariippuvuus mahdollistaa elektronisten komponenttien käyttämisen muistina. Muistia tietokoneessa tarvitaan sekä ohjelmakoodin tallentamiseen, että ohjelmien käyttämien tietojen tallentamiseen. Ilman sähköistä muistia täytyisi tietokoneen ohjelmat ja niiden käsittelemä data syöttää koneelle käsky kerrallaan esimerkiksi reikäkortteja käyttämällä.
Yhden bitin tallentavan muistielementin voi toteuttaa esimerkiksi loogisilla porteilla. Yhden bitin muisti tallentaa jommankumman kahdesta eri vaihtoehtoisesta arvosta, mitä bitti voi saada. Tällaista kytkentää kutsutaan kiikuksi (eng. flip-flop). Kiikun voi toteuttaa joko NOR tai NAND porteilla. Kiikuilla voi toteuttaa tietokoneen tarvitseman muistin, kuten tulemme tekemään Nand2Tetris kirjan tietokoneen muistien toteutuksen. Tänä päivänä tietokoneiden muistipiirit toteutetaan muilla tekniikoilla, joilla saavutetaan nopeampaa muistia, joka mahtuu pienempään tilaan, käyttää vähemmän transistoreita ja on halvempaa.
Tutustutaan ensin kiikkuihin yhden bitin muisteina ja siihen, kuinka niistä rakennetaan suurempia muisteja. Sitten käydään läpi eri tyyppiset muistit, joita tietokoneissa on käytössä. Myöhemmin tietokoneen arkkitehtuuri osiossa tutustutaan SRAM ja DRAM muistien toteutukseen.
Kiikut
Kiikku (eng. Flip-Flop) tai Salpa (eng. latch) on piiri, jolla on kaksi pysyvää tilaa, joihin voidaan tallentaa informaatiota. Eli voidaan tallentaa esimerkiksi tila nolla tai tila yksi. Kiikkuja voidaan käyttää äärellisissä tila-automaateissa, jolloin seuraava tila riippuu sisäänmenoista sekä nykyisestä tilasta (eli aiemmista sisäänmenoista). Komponentin englannin kielinen nimi tulee kolikonheitto tai pelikortti -vertauksesta, jossa esine päätyy toiseen kahdesta tilasta, kun se 'flipataan', eli käännetään ympäri.
Kiikut voivat olla joko yksinkertaisia (ei-synkronoituja) tai kellotettuja (synkronoituja). Yleensä yksinkertaisia kiikkuja kutsutaan termillä salpa ja kellotettuja kiikkuja termillä kiikku. Monesti kuitenkin puhutaan yleisesti vain kiikuista, kuten tässäkin materiaalissa.
Kiikkuja on erityyppisiä, mutta niillä kaikilla on seuraavat ominaisuudet:
- Kiikku on kaksitilainen laite. Se on aina yhdessä kahdesta tilassa ja
sisäänmenon puuttuessa se säilyttää senhetkisen tilansa. Kiikku voi
täten toimia 1 bitin muistielementtinä. - Kiikulla on kaksi ulostuloa, jotka ovat toistensa komplementteja
ja niistä käytetään yleensä merkintöjäja
.
Kiikkujen toimintaa kuvataan yleensä kahdella erilaisella tilasiirtymiä kuvaavalla taululla. Toinen on
Characteristic table tai State transition table, suomeksi tilataulu tai karakteristinen taulu ja toinen on Excitation table, jolle ei ole vakiintunutta suomennosta.
Set-Reset -Kiikku
Yksinkertaisin sekvenssilogiikan kytkentä on nimeltään Set-Reset -kiikku, yleensä käytetään lyhennettyä nimeä SR-kiikku, jossa kahdesta sisäänmenosta toisella (Set) voidaan asettaa ulostulo arvoon 1 ja toisella (Reset) voidaan asettaa ulostulo arvoon 0. Kiikun toteuttavassa komponentissa, on yleensä myös toinenkin ulostulo, jota merkitään ~
tai
, joka on siis ulostulon
negaatio. Alla on SR-kiikun tilataulu.
| S | R | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | Q | pidä tila |
| 0 | 1 | 0 | resetoi |
| 1 | 0 | 1 | aseta |
| 1 | 1 | X | ei sallittu |
SR-kiikun toimintaa voit tutkia piirikaavioeditorissa, jossa on esitetty SR-kiikun toteutus NOR-porteilla. NOR-porttien toinen sisäänmeno on takaisinkytketty viereisen NOR-portin ulostulosta. Huomaa että käytössä olevassa piirikaavioeditorissa ei ole SR-kiikkua vaan sen negaatio RS-kiikku, joka toimii päinvastoin kuin SR-kiikku.
SR-kiikun kytkentä on kaksitilainen ja vakaa niin kauan, kun ja
. Täten kiikkua voidaan pitää yhden bitin muistielementtinä, kun ulostulo
kuvaa talletettavaa bittiä. Sisäänmenoja
ja
käytetään asettamaan bitille arvot
1 ja 0. Kun ,
,
ja
, ja sitten muutetaan
arvoon
1, niin viiveen jälkeen alempi NOR-portti asettaa
. Silloin sisäänmenoiksi ylemmälle NOR-portille tulee
ja
. Jälleen viiveen
jälkeen saadaan
ja saavutetaan vakaa tila. Alla olevasta kuviosta näkyy ajan kuluminen vasemmalta oikealla.
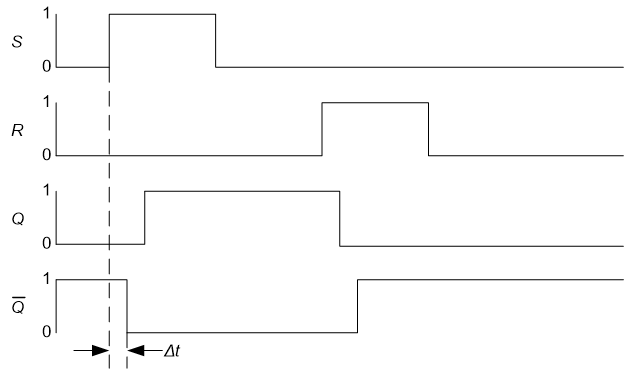
Sisäänmeno suorittaa päinvastaisen toimenpiteen. Kun
asetetaan arvoon
1, niin se asettaa arvot ja
riippumatta niiden aikaisemmista arvoista. Jälleen kuluu aikaviive
.
SR-kiikusta on myös olemassa negatoitujen sisäänmenojen versio NOT(S)NOT(R) kiikku, eli -kiikku, Esimerkiksi piirikaavioeditorissa oleva komponentti, jonka nimeksi on annettu
RS-FF, on siis -kiikku, mikä ilmenee sisäänmenojen nimeämisestä ~R ja ~S sisäänmenoiksi.
-kiikun tilataulu on esitetty alla. Kiikun nimeämisessä yleensä SR-kiikuksi nimetään negatoimaton versio ja koska aina ei ole mahdollista piirtää negatointiviivoja, on negatoitu versio nimetty RS-kiikuksi, mutta käytännöt vaihtelevat.
| Qnext | toiminta | ||
|---|---|---|---|
| 0 | 0 | X | ei sallittu |
| 0 | 1 | 1 | resetoi |
| 1 | 0 | 0 | aseta |
| 1 | 1 | Q | pidä tila |
SR-kiikku voidaan toteuttaa joko NOR-porteilla tai NAND-porteilla. Alla piirikaavioeditorissa on Set-Reset (SR) -kiikku toteutettu NOR-porteilla. SR-kiikun negatoitujen sisäänmenojen versio NOT(S)NOT(R) kiikku, kuten piirikaavioeditorin RS-FF -komponentti, toteutetaan kahdella NAND:illa samanlaisella takaisinkytkennällä kuin NOR:eilla toteutettava SR-kiikku.
Työkaluvalikon RS-FF -komponentti on siis NOT(R)NOT(S)-kiikku, eli sisäänmenoiksi pitää kytkeä R:n ja S:n negaatiot ~R ja ~S, jotta se toimisi kuten SR-kiikku. Jos sisään vie negatoimattomat S ja R, kuten yllä, niin kiikku ei toimi järkevästi, koska silloin oletuksena päällä on ei-sallittu tila. Kokeile lisätä negaatiot RS-kiikun sisäänmenojen ja kytkinten väliin.
Rakenna alle SR-kiikku NAND-porteilla. Voit lähteä liikkeelle joko NOR-porteilla toteutetusta versiosta, vaihtamalla NOR-portit, niiden NAND-muodoiksi ja sitten sieventää ylimääräiset portit pois tai sitten voit lähteä liikkeelle NOT(R)NOT(S)-kiikun NAND-versiosta ja muokata sitä.
D-Kiikku
SR-kiikun huono puoli on sen kielletty tila, kun sekä S=1 ja R=1, niin kiikun tila on epävakaa, riippuen siitä kumpi takaisinkytkentä ehtii ensin johtaa virtaa. Vastaavasti RS-kiikulla S=0 ja R=0 tila on kielletty, sen johtaessa kiikun epävakaaseen tilaan. Koska siis SR-kiikussa vain toinen, S tai R, saa olla yksi, ja toisen pitää silloin olla nolla, niin paranneltu versio kiikusta on sellainen, jossa on vain yksi data-sisäänmeno ja toinen tallennettava vaihtoehto tuotetaan negatoimalla ainoata data-sisäänmenoa. Tällaista kiikkua kutsutaan Data-kiikuksi tai yleensä D-kiikuksi. Sisäänmenon ollessa yksi, talletetaan D-kiikkuun 1 ja vastaavasti talletetaan 0, kun sisäänmeno on nolla. Nyt tosin jokainen sisäänmenon muutos aiheuttaa kiikun tilan muutoksen, joten jotta D-kiikku pitäisi datan muistissa, on kiikkuun lisätty erillinen kellosignaali, joka ohjaa sitä milloin data-sisäänmenossa oleva data voidaan tallentaa D-kiikun uudeksi arvoksi. Uuden data-arvon voi tallentaa vain kun kellosignaali on yksi. Englannin kielessä käytetään sekä clock että enable nimitystä signaalille, riippuen siitä ohjataanko signaalia kellolla vai satunnaisesti päälle kytkettävällä signaalilla.
Tällä kurssilla D-Kiikkuja käytetään tietokoneen muistielementtien perustana. Alla on D-kiikun tilataulu. Huomaa että taulusta on jätetty clock/enable -signaali pois. D-kiikku vaihtaa tilaansa vain silloin kuin clock/enable on 1.
| Q | D | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | 0 | resetoi |
| 0 | 1 | 1 | aseta |
| 1 | 0 | 0 | resetoi |
| 1 | 1 | 1 | aseta |
Alla on esitetty 4-bittinen muistielementti käyttäen D-kiikkua. Simulaattorin D-kiikun toteutustavasta johtuen D-kiikun ulostulo on päällä, eli 1, kun simulaattori ja sen kytkentä käynnistyy. Data-kytkinten tilan saa muistiin clocl/enable signaalilla.
T-kiikku
D-kiikkua voi käyttää taajuuden puolittajana takaisinkytkemällä ~Q ulostulon D-kiikun sisäänmenoksi. Tällöin Q ulostulo vaihtaa arvoaan puolet hitaammin, kuin kellosisäänmenoon tuotava kellosignaali vaihtaa arvoaan. Kun kytkentään vielä lisätään ominaisuus että D-kiikun datasisäänmenoon johdetaan joko takaisinkytketty ~Q ulostulo tai tai uusi sisäänmeno, niin saadaan kiikku, aina ulostuloaan muuttava Toggle-kiikku.
Toggle- eli T-kiikku vaihtaa tilaansa aina, kun sen sisäänmeno käy arvossa yksi. T-kiikun uusi tila on sen edellisen tilan komplementti. T-kiikkuja voidaan käyttää esimerkiksi binäärisissä laskureissa tai jakamaan sisään tulevan signaalin taajuus kahdella.
| T | Q | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | 0 | pidä tila |
| 0 | 1 | 1 | pidä tila |
| 1 | 0 | 1 | vaihda tila |
| 1 | 1 | 0 | vaihda tila |
J-K -kiikku
J-K -kiikku on yhdistelmä SR- ja T-kiikuista, missä SR-kiikun ei sallittu -tila, eli kun S = 1 ja R = 1, asettaa kiikun toimimaan T-kiikkuna, joka vaihtaa tilaansa kellosignaalin mukaan.
Laskurit
Seuraavassa piirikaavioeditorissa on toteutettu asynkroninen ylöspäin -laskuri T-kiikuilla. Laskurin arvoa on helppo lisätä yhdellä. Laskurilla, joka on toteutettu :llä kiikulla, voidaan laskea luvut nollasta arvoon
. Suurimman arvon saavutettuaan laskuri nollautuu, eli siinä ei tapahdu ylivuotoa. Laskenta suoritetaan siis modulo rekisterin koko (kiikkujen lukumäärä). Asynkronisessa laskurissa vain ensimmäisen kiikun kellosignaalia ohjataan, eli määritetään milloin laskuri muuttaa tilaansa. T-kiikkuja (ja JK-kiikkuja) käytettäessä kiikkujen sisäänmenot kytketään loogiseen ykköseen. D-kiikkuja käytettäessä D-kiikkujen sisäänmenoihin takaisin kytketään kiikkujen negatoidut ulostulot. Laskurissa siis kiikun ulostulo viedään aina sisäänmenoksi seuraavan kiikun kelloon. Tällaisen asynkronisen laskurin englannin kielinen nimi on ripple counter, eikä nimitykselle ole vakiintunutta suomennosta. Asynkroninen laskuri on hidas, koska laskurin ulostulo muuttuu vasta kun kaikkien kiikkujen tilat ovat muuttuneet. Eli seuraava kiikku ei pääse muuttamaan tilaansa ennen kuin edellinen kiikku on muuttanut tilaansa. Jos esimerkiksi viive yhden kiikun läpi on 5 ns, olisi kokonaisviive ao. laskurin tapauksessa 20 ns. Eli laskuria voisi käyttää korkeintaan
taajuudella. Useampi bittisen laskurin käyttötaajuus olisi vastaavasti pienempi.
Synkronisessa laskurissa kaikkien kiikkujen tila muuttuu samaan aikaan, eli jokaisen kiikun kello -sisäänmenoa ohjataan samalla kellosignaalilla. Jotta laskuri laskisi oikein silloin kuin kaikki kiikut vaihtavat tilaa yhtä aikaa, täytyy kytkentään lisätä AND portteja. Alla olevassa piirikaavioeditorissa on toteutettu synkroninen laskuri. Vähiten merkitsevä bitti saadaan vasemman puolimmaisesta kiikusta ja se vaihtaa tilaansa joka kellojaksolla. AND portit rajoittavat muiden kiikkujen toimintaa siten että ne vaihtavat tilaansa vain silloin kuin kaikki ko. kiikkua vähemmän merkitsevät bitit ovat ykkösiä.
Edellä olevien esimerkkien asynkronisen ja synkronisen laskurin eroa ei voi silmin havaita. Neljän bitin laskurin tapauksessa asynkronisen laskurin ulostulon muutos (numeron vaihtuminen) olisi noin neljä kertaa hitaampi. Kellotaajuuden kasvaessa asynkroninen laskuri alkaisi aikaisemmin laskea väärin. Käytössä oleva simulaattori ei ota ajoituksia huomioon ja toisaalta simulaattori on sen verran hidas, ettei se kykene kovin suuriin kellotaajuuksiin, joten tällä simulaattorilla ei voi visualisoida asynkronisen ja synkronisen laskurin eroja.
Alla on esimerkki laskurin avulla toteutetusta Ledi-näytöstä, jossa valo liikkuu vaakasuunnassa vähän niin kuin Ritari Ässän autossa.
Muistit
Muisti on elektroninen komponentti, joka kykenee säilyttämään aiemmin sisään saamaansa informaatiota. Muisteja on useita eri tyyppejä.
Tietokoneiden yleisimpänä muistina on luku-kirjoitusmuistia, RAM, random access memory. RAM muistiin voidaan kirjoittaa ja sitä voidaan myös lukea. Jokaisella sanalla on yksikäsitteinen osoite ja lukeminen ja kirjoittaminen tapahtuvat osoitteen avulla. RAM muistit ovat haihtuvia, volatile. Täten RAM muistit tarvitsevat koko ajan tasaisen virran, jos virta katkeaa, niin tietosisältö menetetään. RAM muistia voidaan käyttää siis vain tilapäiseen talletukseen. RAM muisteja on kahta tyyppiä: SRAM, static RAM ja DRAM, dynamic RAM.
ROM, Read Only Memory, muisti sisältää tietoa, joka voidaan vain lukea. ROM muistissa tieto säilyy, vaikka virta katkaistaan. Esimerkiksi tietokoneen käynnistysohjelma sijoitetaan ROM muistiin, samoin paljon erilaisia sulautettuja järjestelmiä toimii ROM muisteja käyttäen. ROM muisti on halvempaa kuin RAM, jos valmistusmäärät ovat suuria.
On olemassa myös kerran ohjelmoitava PROM, programmable ROM, muistia. Se säilyttää tiedon, mutta sinne voidaan kirjoittaa vain kerran. PROM muistin jokaisessa muistisolussa on sulake, joka voidaan polttaa erikoislaitteella.
Seuraava kehitysversio on EPROM, erasable PROM, joka myös säilyttää tiedon, mutta sen muistisoluihin voidaan kirjoittaa useammin kuin kerran. Ennen uudelleen kirjoittamista muistisolut tulee ensin pyyhkiä. Tämä tehdään pitämällä solut ultraviolettivalossa noin 15 – 20 minuuttia. EPROM on hiukan kalliimpi kuin PROM.
Nykyaikaisempi muoto uudelleen kirjoitettavista ROM muisteista on EEPROM, electrically erasable programmable ROM. Muistisolun pyyhkiminen ja kirjoittaminen voidaan tehdä muistipiirin ollessa paikallaan piirilevyssä. EEPROM muistisolut ovat suurempia kuin EPROM solut. Kirjoittaminen on noin 10 kertaa hitaampaa kuin DRAM muistisolulla ja noin 100 kertaa hitaampaa kuin SRAM muistisolulla.
Nykyään käytetään paljon EEPROM tyyppistä flash muistia. Se on elektronisesti pyyhittävää ja uudelleen kirjoitettavaa. Muistisolut ovat myös pieniä, talletus on tehokasta. Flash muistilla toteutettavat SSD levyt on syrjäyttämässä kiintolevyjä (HDD) varsinkin kannettavissa tietokoneissa.
Muistin toteutus kiikulla
Yksinkertainen RAM muisti voidaan toteuttaa D-kiikun avulla. Jotta kaikkia muistipaikkoja voidaan käsitellä samanaikaisesti, täytyy D-kiikkujen kellosignaalit kytkeä järjestelmän 'pääkelloon'. Eli koko tietokoneen komponentit toimivat samalla kellotaajuudella. Jotta D-kiikku säilyttää arvonsa jokaisella kellojaksolla täytyy sen ulostulo takaisin kytkeä sisäänmenoksi. Uuden arvon tallentamiseksi tarvitaan logiikkaa, jolla voidaan valita uuden ja vanhan arvon väliltä, eli tulovalitsin.
Yhden bitin muistin voi toteuttaa kytkennällä, jossa on erillinen aktivointisignaali sille, milloin muistiin tallennetaan uusi arvo. Signaalilla ohjataan multiplekseriä, joka valitsee D-kiikun sisäänmenon uuden arvon ja vanhan takaisinkytketyn arvon välillä.
Toteuta alle piirikaavioeditoriin yhden bitin muisti. D-kiikun kellosignaali on kytketty järjestelmän pääkelloon, jona toimii yhden Hertzin oskillaattori. Lisää kytkentään tulovalitsin, jota ohjataan Write -kytkimellä valitsemaan D-kiikun sisäänmenoksi Data in -signaali tai takaisinkytketty D-kiikun ulostulo. Testatessasi pidä Write -signaali pohjassa tarpeeksi pitkään, jotta kellosignaali ehtii vaihtaa D-kiikun arvoa.
Tietokoneet käsittelevät useampia bittejä kerrallaan kuin yhtä. Esimerkiksi 16-, 32- ja 64-bittiset prosessorit käsittelevät 16-, 32- ja 64-bittisiä kokonaisuuksia, joille yhteisenä nimityksenä käytetään termiä sana. Termille sana ei ole tarkkaa määritystä, mutta yleisesti se tietokoneissa määrittää sen kuinka moni bittisiä kokonaisuuksia prosessori kykenee kerrallaan käsittelemään. Tätä bittimäärää kutsutaan sanan kooksi, sanan leveydeksi tai sanan pituudeksi.
Nand2Tetris kirjan HDL-kielellä toteutettavan 16-bittisen prosessorin sanan leveys on siis 16 bittiä ja lukeminen sekä tallennukset muisteihin tehdään 16-bitin kokonaisuuksina. Tällöin muistin osoitteistus on ns. word addressable menetelmä, eli sana on pienin yksikkö, jolla on muistiosoite. Nykyään tietokoneet tosin käyttävät muistia tavun kokonaisuuksina, jolloin muistin osoitteistus on ns. byte addressable menetelmä, eli jokaisella tavulla on muistiosoite.
Muistirekisteri
Sanan tallennusta varten tarvitaan komponentti, joka kykenee tallentamaan rinnakkain sanan leveyden verran bittejä. Tällainen rekisteriksi kutsuttu komponentti voidaan toteuttaa rinnakkaisilla 1-bitin muistikomponenteilla.
Toteuta alle neljän bitin rekisteri, eli kytke neljä tulovalitsinta, kuten edellisessä yhden bitin muistin tapauksessa. D-kiikkujen kellosignaalit on kytketty järjestelmän pääkelloon. Rekisterin laajentaminen useammalle bitille toteutetaan samalla periaatteella.
Muistikomponentit
Rekistereitä käytetään prosessorin sisällä tallentamaan dataa väliaikaisesti, jottei aina tarvitse hakea dataa muistista tai tallentaa muistiin. Rekisteriä voidaan käyttää myös suurempien muistien rakennusosana. Esimerkiksi kahdeksalla n-bittisellä rekisterillä voidaan muodostaa muisti, jossa on kahdeksan n-bittistä muistipaikkaa. Tällöin kyseessä olisi siis n-bittinen 8-sanainen muisti (kuten Nand2Tetriksen RAM8.hdl, joka on 16-bittinen, 8-sanainen muisti). Se mihin muistipaikkaan data tallennetaan, valitaan lähtövalitsimella ja kahdeksan paikkaisen muistin tapauksessa komponenttina olisi 1:8 demux komponentti. Vastaavasti muistin ulostulo valitaan 16-bittisellä 8:1 mux komponentilla. Muistipaikkojen osoitteina toimisi lähtövalitsimen sekä tulovalitsimen 3-bittistä valintasignaalia vastaavat lukuarvot. Muistien laajentaminen useampi sanaiseksi tehdään vastaavasti, esim. 64-sanaisen muistin voi rakentaa kahdeksalla 8-sanaisella muistilla.
Alla on linkki 4-bitin rekistereitä käyttävään kahdeksan muistipaikkaiseen, eli 8-sanaiseen, muistiin. Muistipaikkoja on siis kahdeksan. Muistipaikan osoittamiseen käytetään kolmea sel-signaalia, joilla saadaan valittua yksi kahdeksasta muistipaikasta tallennusta tai lukua varten. Kun kolme valinta signaalia ajatellaan biteiksi ja niiden kombinaatiot 3-bittisiksi positiivisiksi kokonaisluvuiksi, saadaan jokaiselle muistipaikalle osoite, ensimmäinen osoite on 0, kun kaikki sel-bitit nollia. Viimeisen muistipaikan osoite on 7, eli 23-1, kun kaikki sel-bitit ovat ykkösiä.
Yllä oleva 8-sanainen muisti on pakattu omaksi komponentikseen ja sitten sitä on käytetty vastaavasti 64-sanaisen muistin toteutuksessa. Nyt kolme uutta MSB-bittiä, eli sel-signaalia, ohjaa sitä, mikä 8-sanaisista muistikomponenteista valitaan. Kolme aiempaa bittiä, LSB-bittiä, ohjaa 8-sanaisen muistikomponentin sisällä sitä, mikä rekisteri valitaan. Yhdessä 6-bittisellä sel-signaalilla voidaan osoittaa muistipaikkoihin alkaen nollasta ja päättyen arvoon 63, eli 26-1.
Suuremmat muistit saadaan samalla tekniikalla, rakentamalla seuraavan kokoinen muisti aina kahdeksasta kappaleesta pienempiä muistikomponentteja. Esimerkiksi seuraava, eli 256-sanainen muisti, saadaan kohdeksalla kappaleella 64-sanaisia muistikomponentteja. Valintabittejä tulee taas kolme kappaletta lisää valitsemaan 64-sanaisten muistikomponenttien välillä.
Ohjelmalaskuri
Ohjelmalaskuri, englanniksi Program Counter (PC), on yksi prosessorin tärkeimmistä komponenteista, joka mahdollistaa tietokoneohjelman ajamisen prosessorissa. Ohjelmalaskuria käytetään tietokoneohjelman osien hakemiseen muistista prosessorin käsiteltäväksi. Käytännössä ohjelmalaskuri antaa ulostulonaan osoitteen muistipaikkaan, josta seuraava konekielinen käsky tuodaan prosessorille. Ohjelmalaskuri kasvattaa normaalisti osoitetta yhdellä, eli haetaan peräkkäisiä rivejä, mutta sille voidaan ladata mikä tahansa osoite, jos pitää siirtyä esimerkiksi suorittamaan aliohjelmaa, joka sijaitsee muistissa jossain muualla.
Esimerkki 4-bittisestä ohjelmalaskurista:
Tietokoneen arkkitehtuuri
Tietokoneen arkkitehtuurilla viitataan yleensä sellaisiin tietokonejärjestelmän ominaisuuksiin, jotka ovat ohjelmoijalle nähtävissä eli piirteisiin, joilla on suora vaikutus ohjelman loogiseen suoritukseen. Tietokoneen organisaatiolla viitataan tietokoneen toiminnallisiin yksiköihin ja niiden välisiin yhteyksiin, jotka toteuttavat arkkitehtuurissa esitetyt määrittelyt. Arkkitehtuurin ominaisuuksista esimerkkejä ovat tietokoneen käskyjen joukko, erityyppisten tietojen esittämiseen tarvittava bittien lukumäärä, I/O-mekanismit sekä muistin osoitustekniikka. Organisaatooriset ominaisuudet sisältävät ne laitteiston yksityiskohdat, jotka ovat ohjelmoijalle pääosin näkymättömiä, kuten kontrollisignaalit, liitännät tietokoneen ja ulkoisten laitteiden välillä sekä käytetty muistiteknologia. Esimerkiksi arkkitehtuurinen kysymys on se, että tietokoneen käskykannassa on käskyt yhteenlaskulle ja vähennyslaskulle. Se että toteutetaanko vähennyslasku yhteenlaskupiirillä vai omalla piirillään on organisatoorinen kysymys.
Yleisen tietokoneen rakenteesta ja arkkitehtuurista
Tietokoneen rakenne
Tietokoneen voidaan katsoa muodostuvan keskusyksiköstä (suoritin, prosessori, CPU), keskusmuistista ja I/O-komponenteista. Nämä osat on liitetty toisiinsa siten että tietokoneen perustehtävä, tietokoneohjelman suorittaminen, on mahdollista. Liitynnöistä käytetään termiä väylä, englanniksi bus. Tietokonetta voidaan karkealla tasolla kuvata edellä mainituilla osilla ja niiden keskinäisellä käyttäytymisellä.
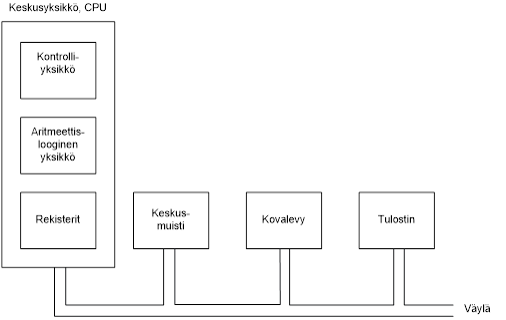
Kovalevy eli kiintolevy
Merkittävin ulkoinen muistilaite on kovalevy tai kiintolevy. Nykyään on kahden tyyppisiä kiintolevyjä HDD (Hard Disk Drive) ja SSD (Solid State Drive). Käsitellään ensin vanhempi tekniikka eli HDD-kiintolevy. Se on mekaaninen laite, johon tieto talletetaan magneettisesti. Kovalevyjä on useita erityyppisiä sekä toiminnaltaan että kooltaan. Periaatteeltaan kovalevyt eivät ole juurikaan muuttuneet niiden olemassaolon aikana. Niiden koko, kapasiteetti ja nopeus ovat kehittyneet ja myös se tapa miten tieto siirretään tietokoneelle käsittelyä varten. Kovalevy muodostuu yhdestä tai useammasta pyöreästä metallisesta kiekosta, joiden pinnalle on kiinnitetty ohut filmi magnetisoituvaa materiaalia. Useammat levyt sijoitetaan päällekkäin. Levy pyöri valmistajasta riippuen eri nopeudella. Tiedon luku ja kirjoitus tapahtuu levyn yläpuolella olevan liikkuvan luku/kirjoituspään kautta.
Kovalevyn molemmille pinnoille tieto talletetaan samankeskisiin uriin ja urat jaetaan sektoreihin vieressä olevan Wikipedista kopioidun kuvan mukaisesti. Kuvassa A esittää uraa, B geometrista sektoria ja C uran sektoria. D on useamman sektorin klusteri. Lisäksi päällekkäiset samalla kohdalla olevat urat muodostavat sylinterin. Yleensä kukin ura jakautuu samaan määrään sektoreita ja jokainen sektori sisältää saman määrän tavuja. Urat ja sektorit on numeroitu tunnistamista varten.
Yleensä luku/kirjoituspäitä on yksi kutakin levyn pintaa kohden ja luku/kirjoituspäät leijuvat pinnan yläpuolella.
Aikaa, joka kuluu luku/kirjoituspään siirtämisessä oikealle uralle, kutsutaan hakuajaksi. Pyörähdysviive on taasen se aika, joka kuluu siihen, että oikea sektori tulee luku/kirjoituspään kohdalle. Saantiaika on hakuajan ja pyörähdysviiveen summa. Jos saantiaikaan, vielä lisätään tiedon lukeminen levyltä, niin saadaan tiedon siirtoaika.
Nykyisissä pöytätietokoneissa yleisten 3,5 tuuman kokoluokan sekä kannettavissa tietokoneissa yleisten 2,5 tuuman levyjen kapasiteetit voivat olla jo muutamia teratavua. Tiedon siirtoajat ovat muutamia millisekunteja.
Magneettisella kovalevyllä on useita rajoituksia ja niiden ongelmien eräänä ratkaisuna on korvata kovalevy tiedon säilyttävällä RAM muistilla. SSD massamuisti muodostuu mikrokontrollerista ja esimerkiksi flashmuistista. Siinä ei ole lainkaan liikkuvia mekaanisia osia. Tiedon saantiajat ovat tavallisesti 100 kertaa nopeampia kuin kovalevyllä, mutta hinta on kalliimpi. Kapasiteetti lähenee pikku hiljaa kovalevyjen kokoa.
Tietokoneen arkkitehtuurista
Lähes kaikki nykyajan tietokoneet perustuvat ns. Von Neumannin arkkitehtuuriin, joka perustuu seuraaviin asioihin.
- Suoritettava ohjelma ja sen käyttämä data talletetaan samaan muistiin binäärisenä informaationa.
- Tämän muistin sisältö on osoitettavissa paikan mukaan huolimatta siitä, minkä tyyppistä tietoa sinne on talletettu.
- Ohjelman suoritus tapahtuu peräkkäin yhdestä käskystä seuraavaan paitsi, jos jostain syystä hypätään johonkin muuhun käskyyn.
Binäärisen tiedon tallettaminen ja erilaisten aritmeettisten ja loogisten operaatioiden suorittaminen binäärisellä tiedolla voidaan toteuttaa pienellä määrällä muutamia loogisia peruskomponentteja. Kun jokin toimenpide tulee suorittaa, niin sitä varten voidaan suunnitella ja valmistaa loogisten komponenttien rakennelma. Tällaisten loogisten komponenttien rakentamista voidaan pitää eräänlaisena ohjelmointina. Tuloksena on ohjelma laitteiston muodossa (hardwired program).
Tämän vaihtoehtona on rakentaa aritmeettisten ja loogisten funktioiden yleiskäyttöinen kokoonpano. Näin muodostettu laitteisto pystyy suorittamaan erilaisia toimenpiteitä kontrollisignaalien ohjaamana. Tällöin voidaan samalla laitteistolla saada erilaisten ohjelmien tuottamia tuloksia, rakentamatta aina uutta laitteistoa uudelle ohjelmalle. Tietokone perustuu tälle idealle, eli sen suorittimella voidaan toteuttaa mielivaltaisia ohjelmia antamalla sille kontrollisignaaleja, jotka ovat suorittimen käyttämän konekielen käskyjä.
Prosessori eli suoritin
Keskusyksikkö sisältää pienen määrän erittäin nopeaa muistia, rekisterit, joita käytetään muistiosoitteiden, väliaikaisten tulosten ja kontrollitiedon tallettamiseen. Eräs tärkeä rekisteri on ohjelmalaskuri, käskyosoitin (Program Counter, PC), joka ilmaisee mistä seuraavaksi suoritettava käsky noudetaan. Toinen tärkeä rekisteri on käskyrekisteri (Instruction Register, IR), joka sisältää kullakin hetkellä suoritettavana olevan käskyn. Keskusyksikkö sisältää myös aritmeettis-loogisen -yksikön, joka vastaa esimerkiksi laskutoimituksista.
Prosessorille annetaan suoritettava ohjelma kontrollisignaaleilla, jonona askeleita. Kussakin askeleessa suoritetaan jokin aritmeettinen tai looginen operaatio tiedolla. Kukin askel tarvitsee uuden kontrollisignaalien joukon. Kullekin mahdolliselle kontrollisignaalien joukolle annetaan oma koodi. Tätä varten lisätään laitteistokomponentti, joka hoitaa tämän koodien käsittelyn. Nyt ohjelmointi on helpompaa, kun voidaan antaa vain kontrollisignaalien koodien jono tarvitsematta tehdä muutoksia itse laitteistoon. Kukin koodi on itse asiassa prosessorin käsky ja osa laitteistoa tulkitsee käskyn ja muodostaa tarvittavat kontrollisignaalit. Tätä koodien jonoa kutsutaan siis tietokoneohjelmaksi (software).
Tietokonejärjestelmä tarvitsee käskyn tulkintayksikön ja yleisiä aritmeettis-loogisia toimenpiteitä varten oman yksikön. Tietokoneissa nämä toteutetaan suorittimessa. Prosessorin sisällä on lisäksi muistirekistereitä, joita käytetään esimerkiksi muistista haetun tiedon väliaikaiseen tallentamiseen ennen suorittamista sekä suorittamisen jälkeen.
Rekisterit
Prosessorin rekisterit ovat tietokoneen arkkitehtuurissa hyvin nopeaa muistia, jotka ovat prosessorin sisällä. Rekistereihin tallennetaan tietoa suuremmista muisteista, esimerkiksi keskusmuistista tai välimuistista. Rekisterin arvoilla tehdään aritmeettisia ja loogisia operaatioita, tallennetaan tuloksia sekä tutkitaan niiden sisältöä. Rekistereiden käyttöön on prosessorin konekielessä omat käskynsä. Rekisterit ovat yleensä yhden sanan kokoisia, mutta osaa niistä voidaan käyttää tavun tarkkuudella. Rekistereitä on eri tyyppisiä ja niitä käytetään eri tarkoituksiin:
- Konekielellä käsiteltävät rekisterit, esimerkiksi
- Datarekisterit
- Osoiterekisterit
- Yleiskäyttöiset rekisterit
- Tilarekisterit
- Liukulukurekisterit
- Prosessorin sisäiset rekisterit, vain prosessorin käytössä, esimerkiksi
- Käskyrekisteri (IR)
- Rekistereitä muistin käsittelyä varten (MBR, MDR, MAR)
I/O-moduulit
Toimivaa tietokonetta varten tarvitaan lisäksi muita komponentteja. Jonkinlainen syöttömoduuli tarvitaan tiedon ja käskyjen antamista varten. Lisäksi ratkaisun tulokset halutaan myös näkyville eli jonkinlainen tulostusmoduuli on tarpeen. Näitä kahta jälkimmäistä yhdessä kutsutaan syöttö- ja tulostuskomponenteiksi, I/O (S/T) -komponenteiksi, -yksiköiksi tai -moduuleiksi.
Syöttömoduuli ottaa tiedot ja käskyt peräkkäisessä järjestyksessä, mutta ohjelman käskyjä ei välttämättä suoriteta peräkkäisessä järjestyksessä. Myöskin käskyt voivat tarvita tietoalkioita muutoin kuin yksi kerrallaan syötetyssä järjestyksessä. Täten käskyjä ja tietoja tulee voida tallettaa jonnekin väliaikaisesti, tähän tarvitaan muistia, keskusmuistia. Sen on oltava erillään ulkoisista muistilaitteista. Von Neumannin mukaan tähän voidaan käyttää samaa muistia sekä käskyille että tiedoille.
Komponenttien väliset liitynnät
Seuraavassa kuviossa on esitettynä nämä mainitut komponentit ja niiden väliset liitäntäyhteydet. Keskusyksikkö ja muisti vaihtavat tietoa keskenään. Tähän käytetään usein kahta rekisteriä: muistiosoiterekisteri, MAR (memory address register), joka sisältää muistiosoitteen, johon seuraava operaatio, luku tai kirjoitus, kohdistuu ja lisäksi muistipuskurirekisteri, MBR (memory buffer register), joka sisältää muistiin kirjoitettavan datan tai muistista luetun datan. Vastaavasti toimii syöttö- ja tulostusosoiterekisteri, I/O AR, joka määrittelee syöttö- ja tulostuslaitteen. Syöttö- ja tulostuspuskurirekisteri, I/O BR, taasen sisältää tulostettavan tiedon tai siihen saadaan luettava tieto.
Muisti muodostuu joukosta muistipaikkoja, muistipaikka tunnistetaan osoitteen avulla. Muistiosoitteet ovat peräkkäisiä kokonaislukuja, kuvion mukaisessa muistissa on n muistipaikkaa ja osoitteet ovat kokonaislukuja väliltä 0, …, n-1. Muistipaikka siis sisältää binääristä tietoa, joka voi olla joko käsky tai data tai jokin osa niistä.
Tietoa siirretään moduulien välillä tietopolkua pitkin, jota kutsutaan yleensä väyläksi, bus.
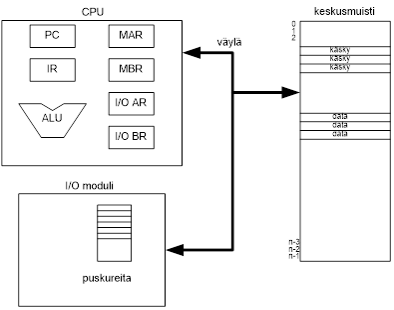
CISC- ja RISC-prosessorit
Käskykanta-arkkitehtuuri, englanniksi Instruction set architecture (ISA), on eräs tapa kuvata tietokoneen arkkitehtuuria. ISA toimii laitteiston ja ohjelmiston rajapintana. ISA määrittelee kaiken mitä konekielellä ohjelmoidan tarvitsee tietää ohjelmoidakseen tietokonetta. Ohjelmiston kehittämisen kannalta katsottuna ISA-malli antaa siis abstraktin kuvan laitteistosta. Tietokoneen organisaatiosta käytetään nimitystä mikroarkkitehtuuri, joka määrittelee tietokoneen toteutuksen siten, että siinä voidaan toteuttaa ISA. Mikroarkkitehtuuri on digitaalisen logiikkatason yläpuolella.
Käskyjoukkoja suunniteltaessa joskus pyritään muodostamaan hyvin monimutkaisia käskyjä, jotka tekisivät mahdollisimman helpoksi ohjelmointikielten kääntämisen prosessorin käskyiksi. Tällöin erilaisten käskyjen joukko kasvoi hyvin suureksi, tavallisesti 200 - 300 erilaista käskyä. Tällaisen käskykannan koneita kutsutaan joskus termillä CISC, Complex Instruction Set Computer. Intelin x86 prosessorien perhe on eräs esimerkki CISC arkkitehtuurista. Käskyt ovat pitkiä, eripituisia, mutkikkaita rakenteeltaan ja lähes kaikki mahdolliset osoitusmuodot ovat käytössä. On pyritty mahdollisimman lähelle korkean tason ohjelmointikieltä. Tämä on johtanut käskyjen suorittamisen hidastumiseen. Yhden monimutkaisen käskyn suorittaminen voi vaatia useita kellosyklejä. Varsinaisen käskyn suorittaminen tapahtuu mikrokoodin avulla. Mikrokoodi joutuu tulkitsemaan käskyn, joka hidastaa käskyn suoritusta ja asettaa omat vaatimukset laitteistolle.
Vastakohtana CISC-tyypin koneille kehiteltiin 1980-luvulla prosessoreita, joissa oli yksinkertainen käskykanta ja erilaisten käskyjen lukumääräkin saatiin säilytettyä pienenä, usein noin 50 käskyä. Silloin puhutaan RISC-tyypin koneesta, Reduced Instruction set Computer. Tällöin sellainen toimenpide, joka CISC-tyypin koneella voitiin suorittaa yhdellä käskyllä, joudutaan suorittamaan usealla käskyllä RISC-tyypin koneella. Mutta kaikki käskyt ovat samanpituisia, nykyään yleensä 64 bittiä, ja erilaisia käskymuotoja on vähän. Muistiviittaukset suoritetaan yleensä hakemalla tieto muistista ja viemällä tieto muistiin omilla käskyillä. Rekistereitä on yleensä RISC-koneissa enemmän, jopa useita satoja. Täten käskyt ovat tehokkaampia suorittaa ja vievät tietysti vähemmän muistitilaa. Intelin Pentium perhe ja MIPS arkkitehtuurit ovat esimerkkejä RISC tietokoneista.
Tietokoneen ja ohjelmiston yleinen rakenne
| Korkeantason kieli |
| Virtual machine |
| Assembly kieli |
| Konekieli |
| Tietokonealusta |
| Loogiset piirit |
- Loogisilla piireillä ja komponenteilla rakennetaan prosessori ja muistit
- Prosessorin rakenne määrää sen minkälaisia käskyjä sille voidaan antaa -> käskykanta (Instruction set)
- Konekieli on joukko binäärisiä ”sanoja” jotka vastaavat prosessorin käskyjä
- Assembly kieli antaa binäärisille bittijoukoille paremmin muistettavat vastineet, esimerkiksi HACK-assembly -kielessä:
- 1111110111001000
- M=M-1
- Jokaiselle prosessorityypille on oma konekieli ja siten myös assembly kieli
Tietokoneen toiminta
Tietokoneen toiminta voidaan esittää yksinkertaisella kahden rivin kuvauksella:
- Nouda käsky prosessorille
- Suorita käsky prosessorissa
Noudettavat ja suoritettavat käskyt ovat muistissa sijaitsevia konekielisiä käskyjä.

Tallennetun ohjelman konsepti
Tietokoneen oleellisin ero muihin koneisiin verrattuna on sen kyky toteuttaa käytännössä ääretön määrä erilaisia tehtäviä rajoitetulla laitteistolla. Eli sama tietokone toimii alustana lukemattomalle määrälle esim. pelejä, toimistosovelluksia tai simulointiohjelmistoja. Tämä joustavuus on seurausta 1930 luvulla kehitetystä tallennetun ohjelman ideasta. Sen sijaan että sovellusten logiikka tallennettaan laitteistoon kuten aiemmin, se tallennetaan tietokoneen muistiin samalla tavalla kuin sovelluksen käyttämä data. Laitteisto sen sijaan määritellään muuttumattomaksi ja sitä voi ohjata kiinteällä pienellä joukolla käskyjä, prosessorin konekieliset käskyt. Käskyjä yhdistämällä voidaan toteuttaa monimutkaisia ohjelmia, yksinkertaisena esimerkkinä kertolaskun toteutus yhteenlasku-käskyjen avulla tai muistin sekä rekistereiden hallinta käskyjen avulla. Tämä idea on nykyäänkin tietokoneiden perustana, eli tietokoneen toimintaa ja käyttötarkoitusta voidaan muuttaa eri tarkoituksiin erilaisia tallennettuja ohjelmia lataamalla.
Von Neumannin arkkitehtuuri
Von Neumannin arkkitehtuuri on yleisin käytännön toteutus tallennetun ohjelman konseptista ja se on melkein kaikkien nykyisten tietokoneiden perusta. Von Neumannin arkkitehtuuri perustuu prosessoriin, joka vuorovaikuttaa muistilaitteen sekä oheislaitteiden kanssa vastaanottaen ja lähettäen dataa. Prosessori pitää sisällään aritmeettis-loogisen yksikön, prosessorin rekistereitä sekä ohjausyksikön sisältäen ohjelmarekisterin ja ohjelmalaskurin. Tietokoneen toiminnan visualisoimiseksi voi tutustua esimerkiksi yksinkertaiseen Von Neumannin tietokoneen simulaattoriin, joka visualisoi tietokoneen toimintaa ladattuja ohjelmia ajaessa. Harvardin arkkitehtuuri poikkeaa Von Neumannin arkkitehtuurista siten että siinä ohjelma- ja datamuisti eivät sijaitse samassa muistissa, eli eivät ole saavutettavissa saman väylän ja saman osoitteistuksen kautta. Harvardin arkkitehtuuria käyttää nykyään jotkin digitaaliset signaaliprosessorit (DSP, Digital Signal Prosessor) sekä mikrokontrollerit. Hyötynä Von Neumann arkkitehtuurin verrattuna on mahdollisuus käyttää data- ja ohjelmamuistia samanaikaisesti. Välimuistin lisääntyvä käyttö on kuitenkin pienentänyt hyötyä.
Little Man Computer, on yksinkertainen Von Neumann arkkitehtuurin mukainen tietokone. LMC simulaattori.
Tunnetuin teoreettinen tietokoneen malli on universaali Turingin kone. Turingin kone on teoreettinen kone, joka käsittelee symboleita muistina toimivalla nauhalla. Koneen toimintaa ohjataan syöttämällä siihen nauha, jolla on suoritettavan ohjelman ohjeet. Nauhojen määrää ei ole rajattu, tosin yksinauhainen Turingin kone pystyy jäljittelemään useampinauhaista Turingin konetta. Universaali Turingin kone on kone, joka kykenee simuloimaan mitä tahansa Turingin konetta siihen ladattavien ohjeiden mukaan. Eli universaali Turingin koneen voi käsittää tallennetun ohjelman konseptilla toimivaksi tietokoneeksi ja Turingin koneen tallennettuna ohjelmana, joka toimii syötteiden mukaan. Universaalista Turingin koneesta löytyy useita simulaatiota, esimerkiksi Online Turing Machine.
Data- ja ohjelmamuisti
Von Neumannin arkkitehtuurissa suoritettava ohjelma ja ohjelman käyttämä data sijaitsevat samassa muistissa. Harvard arkkitehtuurissa ne sijaitsevat eri muistissa. Prosessorin konekieliset käskyt ovat siis suoritettava ohjelma. Käskyjen perusteella prosessori mm. tallentaa dataa muistiin ja hakee dataa muistista prosessorin käsiteltäväksi.
HACK-tietokoneen rakenne
Kurssilla rakennetaan simuloiden Nand2Tetris-kirjan mukainen tietokone, jolle tekijät ovat antaneet nimen HACK-tietokone.
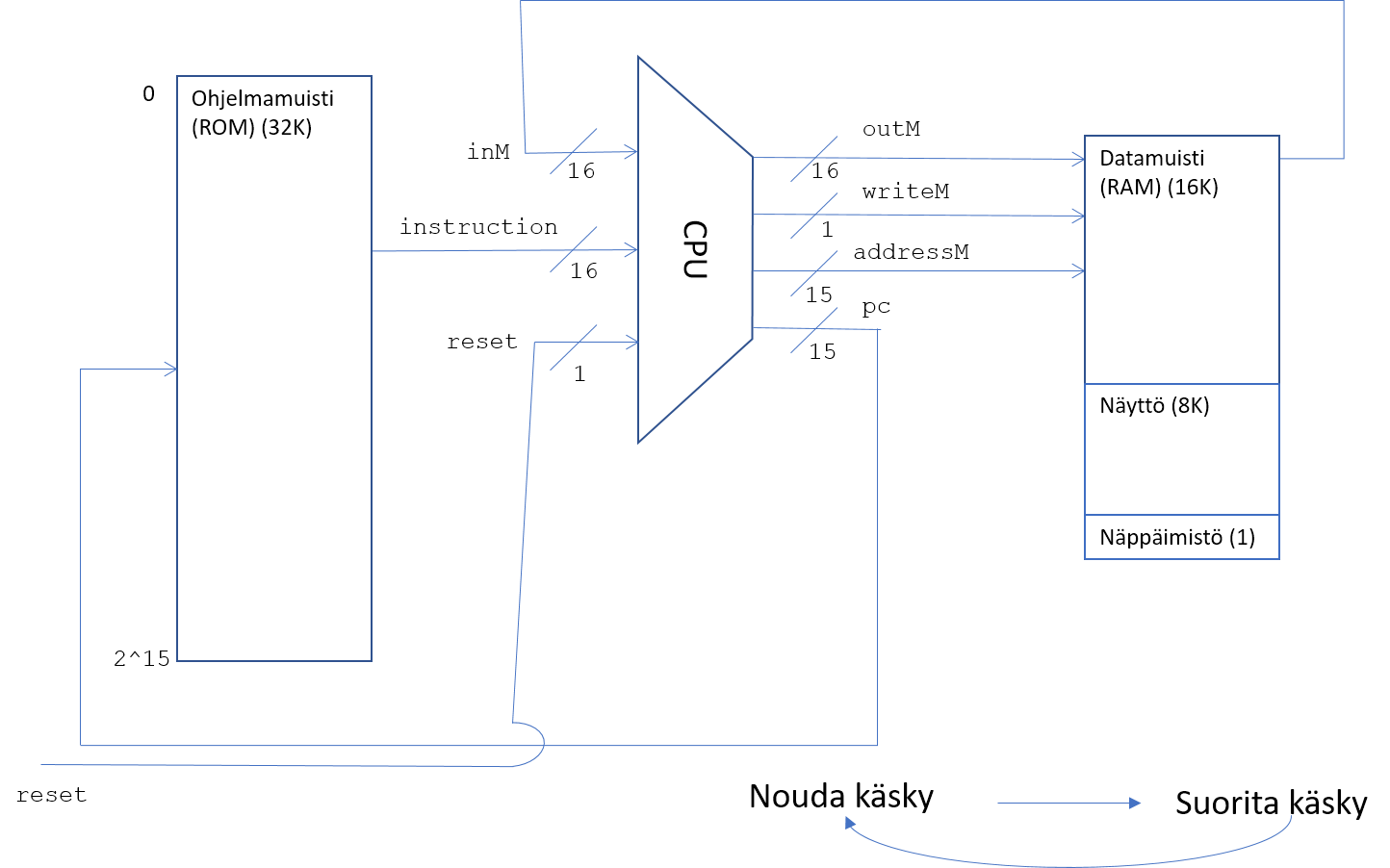
HACK tietokoneen muisti
- ROM muisti, ladataan konekielinen ohjelma
- RAM muisti, käytetään ohjelman parametrien tallentamiseen
- I/O laitteet, näyttö ja näppis
- Memory-mapped I/O
- I/O laitteet kytketty samaan väylään kuin muisti
- Laitteilla oma "muistiosoite"
- HACK-tietokoneessa RAM muistin jatkeena
HACK-prosessori
HACK-tietokoneen prosessori on vastaavasti nimetty HACK-prosessoriksi.

HACK-prosessorin assembly ja konekieli
Jokaisella prosessorilla on sisäänmenosignaalit, joilla prosessoria voidaan ohjata. Sisäänmenosignaalit ovat 2-järjestelmän mukaisia signaaleita, joten ohjaaminen tapahtuu binäärisillä luvuilla.
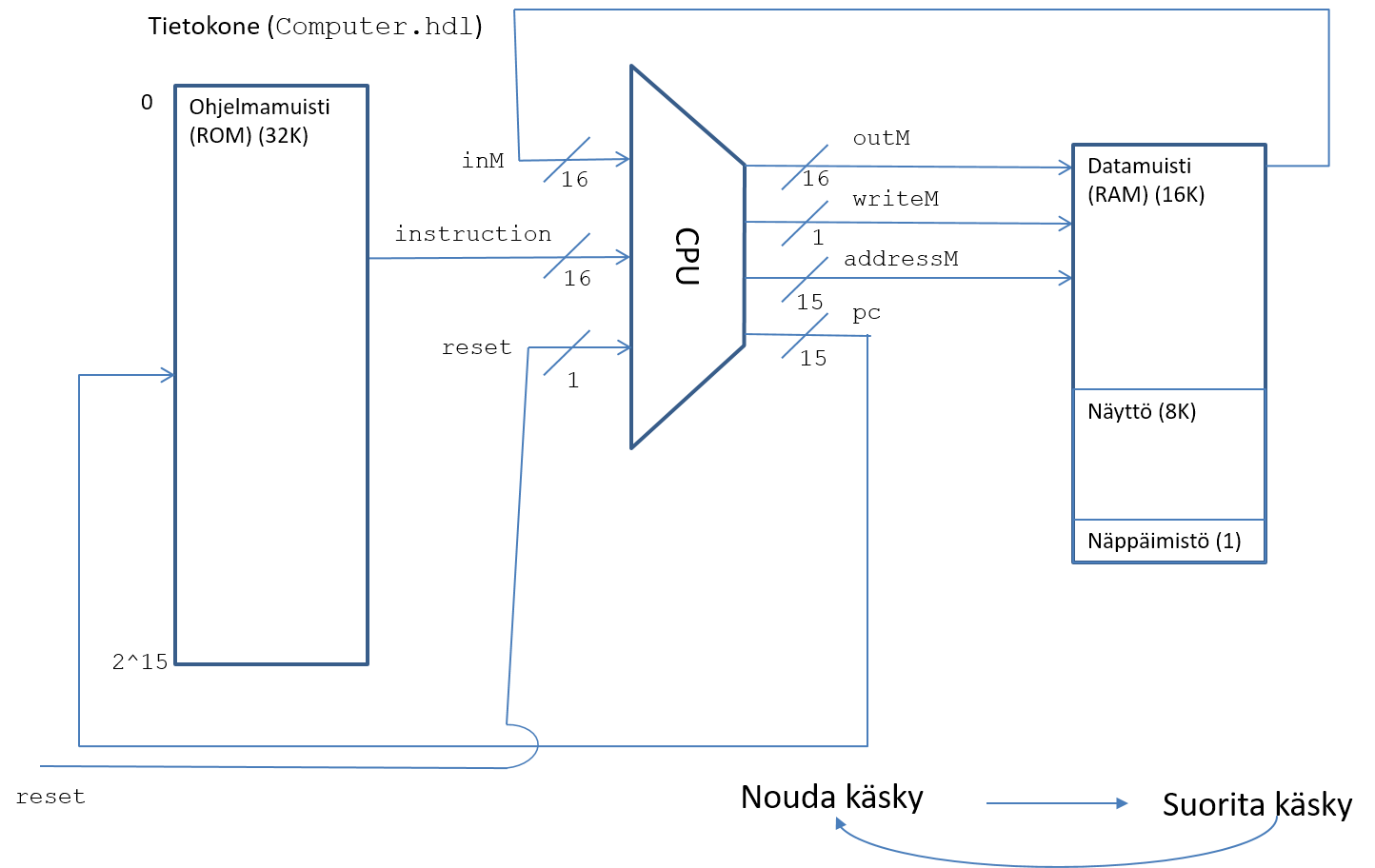
Assembly kielestä
HACK-tietokoneen toiminta
- HACK tietokone
- Hae A-käsky
- Suorita A-Käsky
- Hae C-käsky
- Suorita C-Käsky
- Toista alusta
- ’Normaali’ –tietokone
- Hae käsky
- Suorita käsky
- Toista alusta
Esimerkkiohjelma
Jokainen ohjelma muunnetaan lopulta konekielisiksi käskyiksi, prosessorin toiminnan ohjaamiseksi. Ennen konekielisiksi muuntamista tehdään muunnos assembly-kieliseksi koodiksi, joka on konekielisen koodin ihmisystävällinen esitystapa. Assembly-kieli on aina riippuvainen prosessorin toteutuksesta, esimerkiksi siitä mitä toimintoja ALU:uun on toteutettu ja mitä rekistereitä on käytössä.
// C# koodia
// Adds 1+...+5.
int i = 1;
int sum = 0;
while (i <= 5) {
sum += i;
Console.WriteLine(sum);
i++;
}Konsoliin tulostus on lisätty koodiin visualisointia varten, jos itse haluat ajaa ohjelman. Konsoliin tulostusta ei ole toteutettu alla oleviin Assembly-koodeihin.
C-kielinen koodi voitaisiin kirjoittaa kuvitteellisella pseudo Assembly-kiellä esimerkiksi seuraavasti.
// PSEUDO Assembly koodia
Alusta muuttujat i=1 ja sum=0 (varaa niille paikka muistista)
(LOOP)
Laske i-5
Jos ALU output > 0
niin indeksi liian suuri, hyppää LOPPU:un
muuten (ALU output <= 0)
kasvata summaa
kasvata indeksiä
hyppää LOOP:iin
(LOPPU)
Lopeta ohjelma
Alla on C-koodia vastaava koodi kirjoitettu Hack-prosessorin assembly-kielellä. Koodi löytyy myös tiedostona Add5.asm. Alla oleva assembly-versio on yksi tapa toteuttaa C#-koodin logiikka.
// Hack assembly koodi @i // assembler -kääntäjää valitsee muistipaikan, jonne i tallennetaan M=1 // i=1 (sijoitetaan indeksin aloitusarvo yo. muistipaikkaan) @sum // assembler -kääntäjää valitsee muistipaikan, jonne sum tallennetaan M=0 // sum=0 (alustetaan summa nollaksi tallentamalla 0 sum -muuttujan muistipaikkaan) (LOOP) // määrittää hyppyosoitteen @i // Asetetaan A-rekisterin arvoksi i-muuttujan muistipaikan osoite D=M // D=M[i] haetaan lukuarvo RAM muistin (M) osoitteesta i, tallennetaan D-rekisteriin @5 // asetetaan A-rekisteriin arvo 5 D=D-A // D=i-5, vähennetään A-rekisterin arvo D-rekisterin arvosta, tallennetaan D-rekisteriin @END // asetetaan A rekisteriin mahdollinen hyppy osoite eli (END):iä seuraavan rivin osoite D;JGT // Jos D:narvo positiivinen, hypätään (END):iin muuten jatketaan seuraavalle riville @i // Asetetaan A-rekisteriin i:n osoite D=M // D=M[i] haetaan i:n arvo muistista osoitteesta M[i] ja tallennetaan D-rekisteriin @sum // asetetaan A-rekisterin arvoksi sum parametrin osoite M=D+M // sum=i+sum, haetaan muistista M[sum] arvo, lisätään D-rekisterin arvoon, tallennetaan muistiin @i // Asetetaan A rekisteriin i:n osoite M=M+1 // i=i+1, haetaan i:n arvo yo. osoitteesta, lisätään 1 ja tallennetaan samaan osoitteeseen @LOOP // asetetaan A-rekisteriin (LOOP):ia seuraavan rivin osoite (muistipaikka ROM muistissa) 0;JMP // Goto LOOP, lasketaan "nolla", ja riippumatta laskutoimituksen tuloksesta hypätään (LOOP):iin (END) // määrittää hyppyosoitteen @END // Kirjan tekijöiden tapa lopettaa ohjelman suoritus (menemällä ikuiseen silmukkaan lopuksi) 0;JMP // Infinite loop
HACK Assembly kielen käskyt
A-Instruction
A-käskyä käytetään HACK-assembly -kielessä viemään positiivinen lukuarvo A-rekisteriin. A-käskyn assembly-kielinen muoto on
@value- Missä
valueon ei-negatiivinen kokonaisluku - Binäärisenä:
0vvv vvvv vvvv vvvv - Käytetään lukuarvon tallentamiseen A-rekisteriin
- A-rekisterin arvoa voidaan käyttää kolmella eri tavalla
- Tallennetaan vakio arvo (
A = value) - Valitaan RAM muistipaikka (
register = RAM[A]) - Valitaan ROM muistin seuraava suoritettava käsky (muistipaikka) (
PC = A)
- Tallennetaan vakio arvo (
- A-käskyä täytyy seurata C-käsky, joka määrää mitä A-rekisteriin tallennetulla lukuarvolla tehdään
C-Instruction
C-käskyä käytetään HACK-assembly -kielessä määrittämään ALU:lla suoritettava operaatio, ALU:lle vietävät operandit, ALU:n ulostulon talletuspaikka sekä se kuinka A-rekisterin arvoa käytetään. C-käskyn assembly-kielinen muoto on
dest=comp;jumpdest = M, D, MD, A, AM, AD, AMDtainull- Kertoo minne laskutoimituksen
comptulos tallennetaan
- Kertoo minne laskutoimituksen
jump = JGT, JEQ, JGE, JLT, JNE, JLE, JMPtainull- Kertoo millä ehdolla hypätään (ladataan ohjelmalaskurille (PC) uusi arvo)
comp = 0, 1, -1, D, A, !D, !A, -D, -A, D+1, A+1, D-1, A-1, D+A, D-A, A-D, D&A, D|A, M, !M, -M,M+1, M-1, D+M, D-M, M-D, D&M, D|M- Kertoo ALU:lle mikä operaatio suoritetaan
- Ja minkä rekisterin/muistipaikan arvoja käytetään operaatiossa

Comp(ute) -käsky
C-käskyn comp-osalla ohjataan multiplekseriä, jolla valitaan ALU:n sisäänmenoksi joko A-rekisterin arvo (a-bitti on 0) tai muistista tuleva arvo (a-bitti on 1). Loput bitit (c-bitit) ovat ALU:n ohjaussignaaleita, joilla ALU saadaan toteuttamaan siihen toteutettuja funktioita.
(a=0) c1 c2 c3 c4 c5 c6 (a=1)
------ -- -- -- -- -- -- -----
0 1 0 1 0 1 0
1 1 1 1 1 1 1
-1 1 1 1 0 1 0
D 0 0 1 1 0 0
A 1 1 0 0 0 0 M
!D 0 0 1 1 0 1
!A 1 1 0 0 0 1 !M
-D 0 0 1 1 1 1
-A 1 1 0 0 1 1 -M
D+1 0 1 1 1 1 1
A+1 1 1 0 1 1 1 M+1
D-1 0 0 1 1 1 0
A-1 1 1 0 0 1 0 M-1
D+A 0 0 0 0 1 0 D+M
D-A 0 1 0 0 1 1 D-M
A-D 0 0 0 1 1 1 M-D
D&A 0 0 0 0 0 0 D&M
D|A 0 1 0 1 0 1 D|MDest(ination)
C-käskyn dest-osalla ohjataan ALU:n ulostulon kirjoitusta A- tai D-rekisterin tai muistiin. Alla on Mnemonic -sarakkeessa taulukoitu assembly-kielinen C-käskyn komennon dest-osa. Lisäksi taulukoitu on dest-osan eri arvoja vastaava toiminto sekä niiden binäärinen muoto.
d1 d2 d3 Mnemonic Destination (minne tallennetaan)
0 0 0 null Operaation tulosta ei tallenneta
0 0 1 M Memory[A] (RAM muistipaikka A)
0 1 0 D D register
0 1 1 MD Memory[A] and D register
1 0 0 A A register
1 0 1 AM A register and Memory[A]
1 1 0 AD A register and D register
1 1 1 AMD A register, Memory[A], and D register
Hyppykäskyt
C-käskyn jump-osalla määritellään se millä ALU:n ulostulolla hypätään toiseen kohtaan ohjelmamuistia. Se mihin hypätään on pitänyt aiemmin tallentaa A-rekisteriin. Alla on Mnemonic -sarakkeessa taulukoitu assembly-kielinen C-käskyn komennon jump-osa. Lisäksi taulukoitu on jump-osan eri arvoja vastaava toiminto sekä niiden binäärinen muoto.
j1 j2 j3
(out < 0) (out = 0) (out > 0) Mnemonic Effect
0 0 0 null No jump
0 0 1 JGT If out > 0 jump
0 1 0 JEQ If out = 0 jump
0 1 1 JGE If out ≥ 0 jump
1 0 0 JLT If out < 0 jump
1 0 1 JNE If out ≠ 0 jump
1 1 0 JLE If out ≤ 0 jump
1 1 1 JMP Jump
Mnemonic ≈ muistisääntö (assembly kielinen toteutus)
Esimerkki A-käskyn jälkeisistä C-käskyistä
A-rekisterin arvoa voidaan käyttää HACK-tietokoneessa kolmeen eri toimintoon. Alla on esimerkkejä A-rekisterin eri käyttötavoista. Käyttötapa määräytyy A-käskyä seuraavan C-käskyn perusteella.
@47// A=47D=A// D=47@47// A=47D=M// D=RAM[47]@47// A=470;JMP// Ladataan PC:lle uusi arvo (ROM muistin muistipaikka, josta ohjelman suoritusta jatketaan)
Esimerkkejä A-käskyn jälkeisistä C-käskyistä ja niiden binääriesityksistä.
@47 // 0000000000101111
D=A // 111accccccdddjjj
@47 // 0000000000101111
D=M // 111accccccdddjjj
@47 // 0000000000101111
0;JMP // 111accccccdddjjj
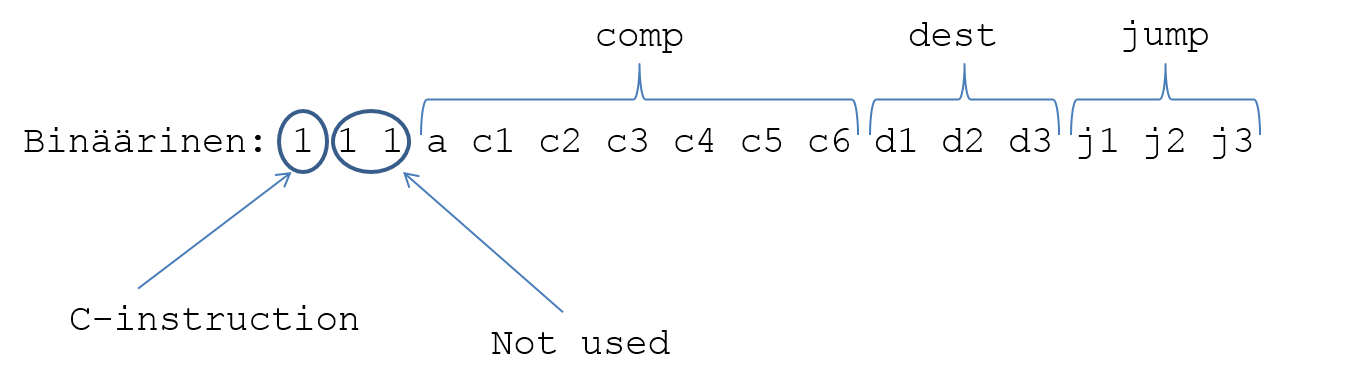
HACK tietokoneen näppäimistö ja näyttö
HACK-tietokoneen näyttö ja näppäimistö ovat ainoat I/O-laitteet, jotka on toteutettu simulaattoriin. Niitä ei tarvitse itse toteuttaa, vaan niille on omat sisäänrakennetut komponentit. Näppäimistö ja näyttö on toteutettu muistimapattuna (memory mapped), jolloin niillä on siis muistiosoitteet, kuten RAM muistillakin.
- Normaalia RAM muistia 16K, osoitteet väliltä 0 - 16383
- 14-bittinen osoite, 214 osoitetta
- yhteen osoitteeseen voidaan tallentaa 16-bittinen sana
- Näyttö, osoitteet väliltä 16384 - 24575
- Mustavalkoinen näyttö, väri tallennetaan yhteen bittiin
- yksi muistipaikka 16-bittinen = 16 pikseliä
- 256 riviä, 512 pikseliä per rivi
- 256 * 512 * 1 = 131072 bittiä
- 131072/16 = 8192 (8k) muistipaikkaa
- Ei voida lukea, muistipaikkaan kirjoittamalla valitaan väri
- Näppäimistön muistiosoite 24576
- Voidaan lukea mitä näppäintä on painettu, ei voi kirjoittaa
Esimerkki näppäimistön ja näytön käytöstä
Kurssin harjoitustehtävissä täytyy tehdä HACK-assembly -kielinen koodi, joka värjää näytön mustaksi näppäintä painettaessa ja vastaavasti valkoiseksi, kun näppäintä ei paineta.
Esimerkkiohjelmia näppäimistön ja näytön käytöstä
WHILE logiikka
// while condition // while (10 - y < 0) { while (y < 10) { code block 1 // esim. y++ } code block 2
(LOOP) // D = 10 - y tai D = y - 10 D // not condition // tallennetaan D:hen False // ehto, jolla hypätään @END D;JEQ // D ≠ 0 code block 1 //y++ etc. @LOOP 0;JMP (END) // D = 0 eli false code block 2
Assembly kielen käytäntö
True = -1 = 1111111111111111 False = 0 = 0000000000000000
IF logiikka
// if condition if (x != 0) { code block 1 } else { // x == 0 code block 2 } code block 3
D // negatoitu ehto (not x) // D = !x // jos x == 0 -> D == !x == -1 (bin) // jos x == -1 -> D == !x == 0 (bin) @IF_TRUE D;JEQ // if D == 0 then jmp // else x == 0 (D ≠ 0) code block 2 @END 0;JMP (IF_TRUE) // (x != 0) code block 1 (END) code block 3
Assembly kielen käytäntö
True = -1 = 1111111111111111 False = 0 = 0000000000000000
Aliohjelmakutsu
Code block 1Draw_letter(A);Code block 2Draw_letter(A);Code block 4... void Draw_letter(Char x) {Code block 3} // minne? miten palataan?
Code block 1 Assemblynä
// paluuosoite aliohjelmasta, joka tallennetaan takaisin –muuttujaan
@PALUUOSOITE
D=A
@takaisin
M=D
@DRAW_LETTER
0;JMP
(PALUUOSOITE) // tänne
Code block 2 Assemblynä
@PALUUOSOITE2
D=A
@takaisin
M=D
@DRAW_LETTER
0;JMP
(PALUUOSOITE2) // vai tänne
Code block 4 Assemblynä
// jossain ROM muistissa (DRAW_LETTER) Code block 3 Assemblynä @takaisin // paluuosoite A=M // RAM muistista 0;JMP
HACK-tietokoneen ja -prosessorin toteutus
Laitteistokuvauskiellellä toteutettava HACK-tietokone sisältää:
- ROM-muistin, jonne ladataan suoritettava konekielinen ohjelma,
- RAM-muistin, jota käytetään datamuistina,
- Näytön, joka on muistimapattu RAM-muistin jatkeeksi,
- Näppäimistön, joka on muistimapattu näytön perään,
- HACK-prosessorin, joka kommunikoi edellisten kanssa
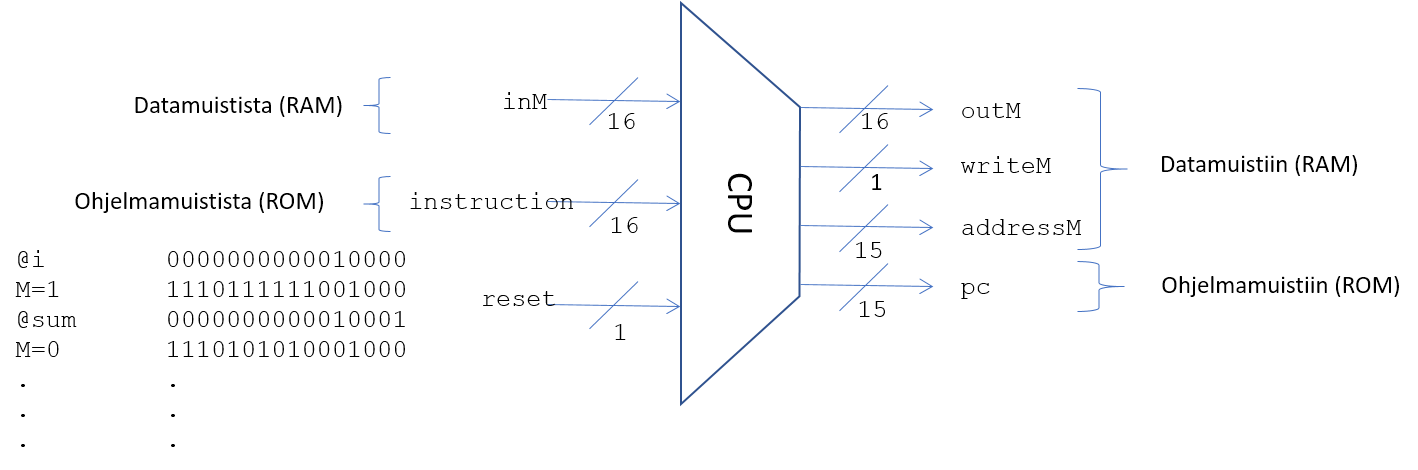
HACK-prosessorin sisäänmenot ja ulostulot on esitetty oheisessa kuvassa. Prosessorin ulostulona on RAM-muistin kontrolliväylä (writeM), osoiteväylä (addressM) ja väylä RAM-muistiin kirjoittamiseen (outM) sekä ROM-muistin osoiteväylä (pc), jonne syötetään ohjelmalaskurin arvo. Prosessorin sisäänmenoina on RAM-muistin väylä datan lukemiseen (inM), ROM-muistin dataväylä (instruction) käskyjen tuomiseksi prosessorille sekä kontrolliväylä (reset), jolla voidaan käynnistää prosessori uudestaan.
Von Neumanin arkkitehtuurin mukaisessa tietokoneessa on vain RAM-muisti, joka toimii ohjelma- ja datamuistina. Lisäksi dataväyliä ei ole omia molempiin suuntiin, vaan yksi dataväylä, mutta kontrolliväylä on monimutkaisempi, eli siellä signaloidaan se mikä laite kirjoittaa tai lukee tietoa dataväylän kautta.
HACK-prosessorin suunnittelu
HACK-prosessoria suunnitellessa voi ottaa lähtökohdaksi Nand2Tetris-kirjassa esitetyn prosessorin lohkokaavion, jossa on kuvattu prosessorin sisäiset komponentit ja niiden väliset kytkennät. Toteutettavaksi jää täten A- ja C-käskyjen mukaisten ohjaussignaaleiden muodostaminen, jotta prosessori toimii käskyjen mukaisella tavalla.

HACK-prosessorin toimintalogiikka
HACK-prosessori noudattaa logiikkaa, jossa noudetaan käsky ja sitten suoritetaan käsky. HACK-prosessorissa on kahden tyyppisiä käskyjä, joita normaalisti suoritetaan vuorotellen. Käskyt sijaitsevat ROM-muistissa ja ne tuodaan HACK-prosessorin instruction -sisäänmenoon. HACK-prosessorin tehtävänä on tulkita käskyt, eli toteuttaa käskyä vastaava logiikka HACK-prosessorin toimimiseksi käskyn mukaan. Alla HACK-prosessorin toiminta on esitetty jaettuna eri vaiheisiin.
- Tulkitaan käsky
instruction[16]- Jos A-käsky, niin
- Viedään
instruction[16]A-rekisteriin
- Viedään
- Jos C-käsky, niin selvitetään biteistä
- ALU:lle komento
- Rekisterien/muistin sisällön vienti ALU:lle
- ALU:n ulostulon tulkinta ja tallennus (rekisteriin/muistiin)
- Hyppyehdon täyttyminen?
- Asetetaan A-rekisterin arvo
PC:n uudeksi arvoksi - Jos ei hypätä niin
PC = PC + 1
- Asetetaan A-rekisterin arvo
- Jos A-käsky, niin
- Käskyn suorituksen jälkeen noudetaan
PC:n osoittama seuraava käsky
HACK-prosessorin logiikan toteutus
HACK-prosessoriin tulee toteuttaa logiikka, jolla sekä A- että C-käskyn bitit saadaan välitettyä oikeille komponenteille. Lisäksi on pidettävä huolta siitä että A- ja C-käskyjen bittejä ei viedä ristiin, eli esimerkiksi ei anneta A-käskyn bittien ohjata rekistereihin tallennusta.
HACK-prosessorin tulee ensimmäiseksi tulkita se, onko kyseessä A- vai C-käsky. Jos kyseessä on A-käsky, tulee käskyn mukana olevat bitit tallentaa A-rekisteriin, eli prosessoriin pitää toteuttaa tätä varten logiikka. Logiikalla esimerkiksi rakennetaan ehto-signaali uuden arvon lataamiseen A-rekisteriin. Huomaa, että A-rekisteriin voidaan tallentaa muutoinkin kuin A-käskyllä, jolloin ehdot käsitellään OR-funktiolla. Tällöin siis jonkin ehdon pitää olla tosi, jotta lataus-signaali saa tosi-arvon.
Tutkitaan seuraavaksi HACK-prosessorin C-käskyn sisältämiä loogisia osia ja niiden toteutuksen periaatteita.
C-käsky binäärisenä
Oheisessa kuvassa on esitetty HACK-prosessorin C-käsky binäärisenä, eli kuvassa on esitetty Assembly-kieliset C-käskyn comp, dest ja jump -osien sijoittuminen 16-bittisessä C-käskyssä. Lisäksi binääriesityksen alapuolella on esitetty HACK-prosessorin 16-bittisen instruction-sisäänmenon bittien suhde Assembly-esityksen bitteihin.

C-käskyn comp, dest ja jump -osien toimintalogiikka on koottu alle, eli toisin sanoen on esitetty Assembly-kielisiä C-käskyn osia vastaavat totuustaulut.


C-käskyn comp-bitit ohjaavat ALU:a, sekä määrittelevät ALU:lle vietävät operandit. Vertaamalla aiemmin esitettyä ALU:n totuustaulua comp-bittien c1 - c6 totuustauluun, huomataan niiden vastaavan toisiaan. C-käskyn bitit c1 - c6 tulee siis johdottaa ALU:n vastaaviin sisäänmenoihin. Periaatteessa pitäisi estää A-käskyn vastaavien bittipositioiden bittien johdottaminen ALU:un A-käskyn tapauksessa. Käytännössä niiden voidaan antaa ohjata ALU:a, kunhan pidetään huoli, ettei ALU:n ulostulon anneta vaikuttaa muun prosessorin toimintaan, eli A-käskyn ei anneta vaikuttaa muiden komponenttien ohjaussignaaleihin.
C-käskyn comp-biteistä on yksi bitti, a, varattu määrittelemään ALU:un toinen operandi y, eli tuodaanko operandi A-rekisteristä vai muistista. Jos operandi tuodaan muistista, niin muistipaikan osoite tulee A-rekisteristä. Toinen operandi x tuodaan ALU:lle aina D-rekisteristä.
Dest-bitit määrittävät sen, minne ALU:n ulostulo tallennetaan. Toteutuksessa täytyy siis tehdä logiikka joka ohjaa talletusehtoja A- ja D-rekistereihin sekä muistiin.
Jump-bitit määrittävät sen, milloin ohjelmalaskurille tallennetaan uusi arvo A-rekisteristä. Toteutuksessa täytyy siis tehdä logiikka joka ohjaa ohjelmalaskurin load-ehtoa. Latausehto on jump-bittien lisäksi riippuvainen ALU:n ulostulosta, eli siitä onko ulostulo positiivinen, negatiivinen, vai nolla.
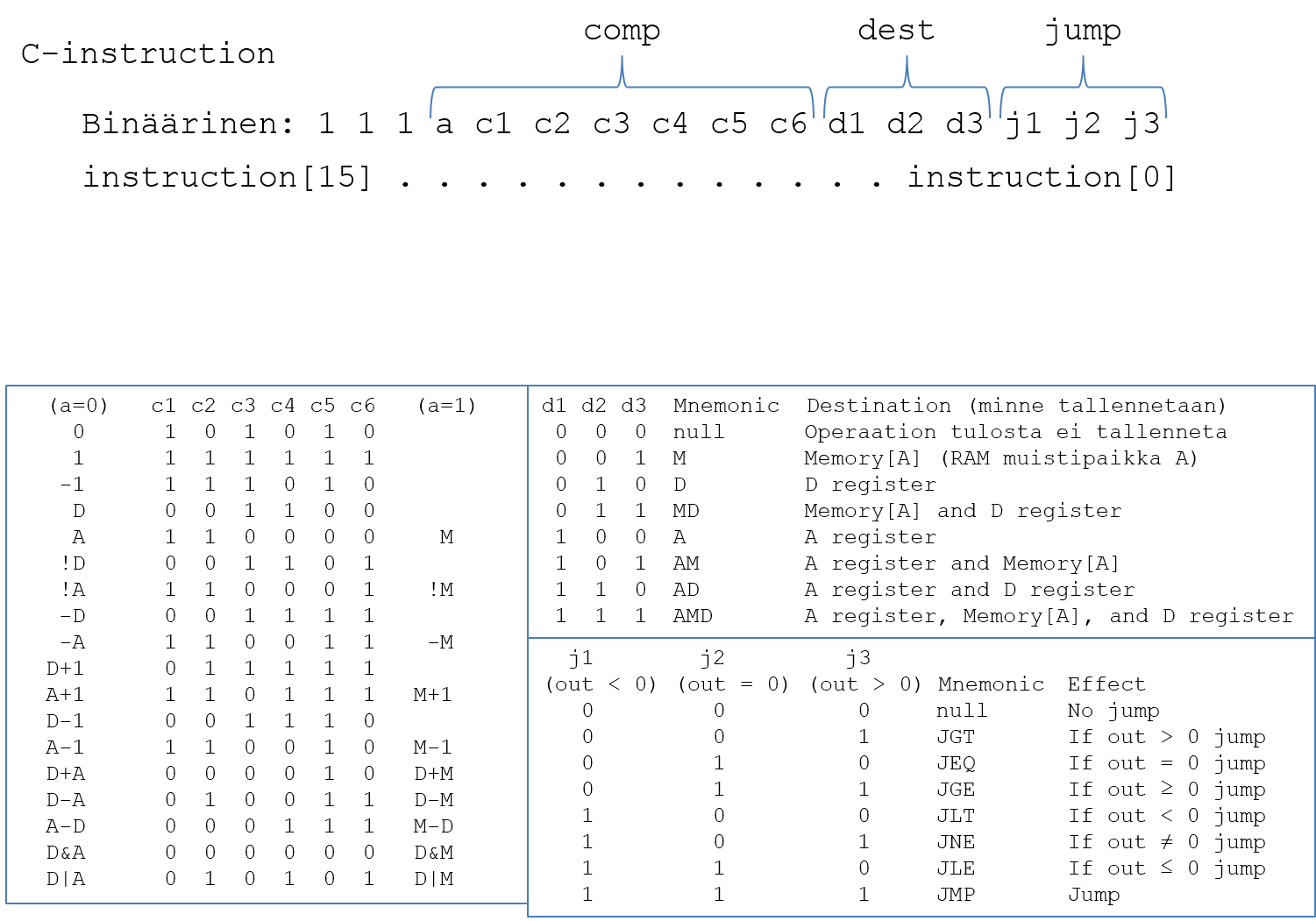
PC-Tietokone vs. HACK-tietokone
Suurin osa nykypäivän tietokoneista perustuu x86-perheen käskykanta-arkkitehtuureihin, englanniksi Instruction set architecture (ISA), jotka perustuvat Intelin 8086-prosessoriin ja ovat taaksepäin yhteensopivia. Mobiililaitteiden, kuten puhelinten ja tablettien prosessorit ovat pääasiassa toteutettu ARM-arkkitehtuurilla. HACK-tietokoneen suorituskykyä ei suoraan voi verrata nykyisiin tietokoneisiin, koska esimerkikiksi HACK-prosessorin kellotaajuutta ei ole määritelty ja prosessorin nopeus olisi riippuvainen toteutustekniikasta. Yleisesti voidaan todeta että HACK-tietokone olisi paljon hitaampi, koska suurin osa laskutoimituksista joudutaan toteuttaa ohjelmallisesti. Lisäksi HACK-koneessa ei ole välimuisteja, jotka oleellisesti nopeuttavat prosessorien toimintaa.
Tietokoneen suorituskyvystä
Suorituskyky on vain yksi parametri tietokonelaitteistoja vertailtaessa. Myös kustannus, koko, turvallisuus, luotettavuus ja virran kulutus on huomioitava laitteistoa valittaessa.
Suorituskykyvertailuja eri prosessoreiden kesken on vaikea tehdä. Mikä todella kiinnostaa on se miten prosessori suoriutuu tiettyä sovellusta ajettaessa. Valitettavasti sovelluksen suoriutuminen riippuu prosessorin nopeuden lisäksi esimerkiksi prosessorin käskyjoukosta, käytetystä ohjelmointikielestä, ohjelmointikielen kääntäjästä ja ohjelmoijan taidoista. Tarkastellaan seuraavaksi hiukan prosessorin nopeuden perinteistä mittausta.
Prosessorin suorittamia operaatioita hallitsee järjestelmän kello. Tavallisesti kaikki operaatiot alkavat kellosignaalin määrääminä. Täten periaatteessa prosessorin nopeuden määrää kellosignaalin taajuus, jota mitataan sykleinä sekunnissa tai Herzeinä, Hz. Kellosignaali saadaan värähtelevästä kiteestä, jonka analoginen signaali muutetaan kellosignaalin pulssiksi. Pulssin nopeus tunnetaan kellon nopeutena. Yhtä kellon pulssia kutsutaan kellon sykliksi, englanniksi clock cycle tai clock tick, ja kahden pulssin välinen aika on syklin aika. Esimerkiksi 1 GHz prosessori saa 1 000 000 000 pulssia sekunnissa. Kellon nopeuden tulee tietysti olla yhteensopiva prosessorin fyysiselle rakenteelle. Prosessorin toimenpiteet lähettävät signaaleja elementeiltä toisille elementeille ja kellosignaali ohjaa näitä.
Prosessorin käskyn suorittaminen käsittää useita diskreettejä askeleita, kuten käskyn hakeminen muistista, käskyn eri osien purkaminen eli dekoodaus, käsiteltävän tiedon lataaminen ja tallettaminen ja aritmeettisen tai loogisen operaation suorittaminen. Täten prosessorin käskyn suorittaminen vie monesti useita kellosyklejä. Joidenkin käskyjen suorittaminen vie muutamia syklejä, kun taas joidenkin muiden useita syklejä. Lisäksi liukuhihnaa käytettäessä useampia käskyjä suoritetaan samanaikaisesti. Täten eri prosessorien suora vertailu pelkkien kellonopeuksien kesken ei kerro koko kuvaa laitteiston suoritusnopeudesta.
Prosessorin suoritusta ohjaa siis kello, jolla on vakiotaajuus eli vakio sykliaika
, missä
. Määritellään käskyjen lukumäärä
, ohjelmalle sen suorittamien käskyjen lukumääränä siihen mennessä kunnes suoritus loppuu tai jollain määritellyllä aikavälillä. Eräs tärkeä tietokoneen nopeuteen liittyvä parametri on keskimääräinen syklien määrä käskyä kohden,
. Jos kaikki käskyt veisivät saman määrän kellosyklejä, niin
olisi prosessorille vakio. Useimmiten kuitenkin prosessorien käyttämien kellosyklien lukumäärä vaihtelee erityyppisillä käskyillä. Merkinnällä
tarkoitetaan tyypin
käskyjen viemää kellosyklien lukumäärää ja olkoon
se määrä tyypin
käskyjä, joka annetussa ohjelmassa suoritetaan. Silloin keskimääräinen syklien lukumäärä voidaan laskea seuraavan kaavan avulla
Tällöin prosessorin viemä suoritusaika ohjelmalle voidaan esittää kaavana
Tätä voidaan vielä tarkentaa huomioimalla, että käskyn suorituksessa osa ajasta kuluu prosessorin työskentelyyn ja osa ajasta kuluu sanojen siirtoon muistiin tai muistista. Muistioperaatioiden kesto riippuu muistin sykliajasta, joka voi olla suurempi kuin prosessorin sykliaika. Kirjoitetaan tällöin kaava muotoon
missä on käskyn tarvitsema prosessorin syklien lukumäärä käskyn koodin purkamiseen ja käskyn suoritukseen,
on tarvittavien muistiviittausten lukumäärä ja
on muistin sykliajan ja prosessorin sykliajan välinen suhde.
Näihin edellisessä kaavassa esiintyvään viiteen suorituskykyyn vaikuttavaan tekijään vaikuttavat neljä järjestelmän attribuuttia; prosessorin käskyjoukon suunnittelu eli käskyjoukon arkkitehtuuri, kääntäjätekniikka, prosessorin toteutus ja muistin hierarkkinen rakenne.
Yleinen mitta prosessorin suorituskyvylle on nopeus, jolla käskyjä suoritetaan ja se usein ilmoitetaan miljoonina käskyinä sekunnissa, MIPS. MIPS voidaan esittää kellonopeuden ja käskyn keskimääräisen suoritussyklien lukumäärän
avulla seuraavasti
Olkoon meillä ohjelma, joka suoritettaessa tekee 2 000 000 käskyä ja käytössä on 400 MHz:n prosessori. Ohjelman suorittamista käskyistä on aritmeettis-loogisia käskyjä 60 % ja niistä kunkin suorittaminen vaatii yhden kellosyklin. 18 % on muistiin viittauskäskyjä, jotka osuvat aina välimuistiin ja yhden sellaisen suorittaminen vie 2 kellosykliä. 12 % käskyistä on haarautumiskäskyjä ja yhden sellaisen suoritus vie 4 kellosykliä. Loput 10 % käskyistä on muistiin viittauskäskyjä, jotka eivät osu välimuistiin ja yhden sellaisen suoritus vaatii 8 kellosykliä.
Tällöin ohjelmaa suoritettaessa 400 MHz:n prosessorilla CPI on
Vastaava MIPS on
Toinen tavallinen suorituskyvyn mittari käsittelee vain liukulukuoperaatioita. Nämä ovat tavallisia tieteellisissä ja pelisovelluksissa. Tällöin kyseessä on miljoonien liukulukuoperaatioiden lukumäärä sekunnissa (MFLOPS), joka määritellään vastaavasti
Prosessorien suorituskykyä arvioitaessa mittarit MIPS ja MFLOPS ovat puutteellisia, koska käskyjen suoritusnopeudet eivät kelpaa eri arkkitehtuureja verrattaessa. Lisäksi jonkin ohjelman suorituskyky jollakin annetulla prosessorilla ei useinkaan ole käyttökelpoinen mittaamaan suorituskykyä erityyppiselle sovellukselle. Tämän takia suorituskykyä mitataan myös suorituskykytesteillä, benchmark. Siinä sama ohjelma suoritetaan eri prosessoreilla ja verrataan suoritusaikoja. Suorituskykytestiohjelma tulisi kirjoittaa siirrettävyyden takia korkean tason ohjelmointikielellä. Siinä tulisi olla mukana erityyppisiä ohjelmia, kaupallisia, tieteellisiä ja järjestelmäohjelmia. Edelleen sen tulisi olla helposti mitattavissa ja kaikille saatavilla.
Suorituskykytestejä määrittelee ja pitää yllä yhtiö System Performance Evaluation Corporation (SPEC). Tuorein SPEC suorituskykytesti tietokoneille on SPEC CPU2017, jota pidetään teollisuuden standardina sovelluksille, jotka suorittavat pääasiassa laskentaa eli muuta kuin runsaasti syöttö- ja tulostustoimintaa. Testisarja koostuu 43:sta erilaisesta testistä, sekä kokonais- että liukuluvuille. Tuoreimpia testituloksia löytyy osoitteesta https://www.spec.org/cpu2017/results/.
Kun järjestelmän suorituskykyä tarkastellaan, niin suunnittelijat pyrkivät parantamaan suorituskykyä erilaisilla teknologisilla tehostuskeinoilla tai muuttamalla tämänhetkisiä suunnitelmia. Tällaisia keinoja ovat esimerkiksi useamman rinnakkaisen prosessorin käyttö, erilaisten muistihierarkioiden käyttö tai muistin saantiaikojen nopeuttaminen tai syöttö- ja tulostustoimenpiteiden teknologiset parannuskeinot. Tällöin on tärkeä havaita, että yhden komponentin tehokkuuden parannus ei anna suoraan vastaavaa parannusta koko järjestelmälle. Tätä seikkaa huomioi Amhdalin laki.
Olkoon meillä ohjelma, joka ajettaessa yhden prosessorin järjestelmällä käyttää murto-osan suoritusajasta ohjelmakoodissa, joka on luontaisesti peräkkäistä. Ja murto-osa
suoritusajasta kuluu ohjelmassa, joka on täysin rinnakkaistettavissa usealle prosessorille ilman mitään ylimääräistä suoritusaikaa. Olkoon
ohjelman suorituksen kokonaissuoritusaika käytettäessä yhden prosessorin järjestelmää. Suoritetaan ohjelma käyttäen rinnakkaistuvassa ohjelman osassa
:ää prosessoria rinnakkaisesti. Silloin ohjelman suoritusajan nopeutuminen saadaan laskettua seuraavasti.
Tästä voidaan havaita, että kun on pieni, niin rinnakkaistamisella on hyvin pieni vaikutus. Kun taas
kasvaa rajatta, niin nopeutumista sitoo raja
. Amdahlin lakia voidaan yleistää käsittelemään mitä tahansa teknistä tai suunnittelullista parannusta tietokonejärjestelmiin. Määritellään nopeutus vastaavasti suhteen avulla seuraavasti.
Oletetaan, että järjestelmän tiettyä piirrettä käytetään murto-osa suoritusajasta ennen parannusta ja kyseisen piirteen nopeutus parannuksen jälkeen on
. Silloin järjestelmän kokonaisnopeutus on
Otetaan esimerkiksi ohjelma, joka käyttää 40 % suoritusajasta liukulukuoperaatioihin. Jos uudella laitteiston suunnittelulla liukulukuoperaatioita saadaan nopeutettua tekijällä , niin silloin kokonaisnopeutus on
Tällöin riippumatta siitä mikä :n arvo on, kun
kasvaa, niin paras mahdollinen nopeutus on
.
Välimuisti
Välimuistin, englanniksi cache, tarkoituksena on nopeuttaa muistin käyttöä tarjoamalla mahdollisuus suurempaan muistiin kuin rekisterit, mutta halvemmalla puolijohdetekniikalla. Tietokoneissa on suhteellisen suuri ja hidas keskusmuisti ja pienempi, mutta nopeampi välimuisti. Välimuisti sisältää kopioita osista keskusmuistia. Kun prosessori lukee sanaa muistista, niin ensin tutkitaan onko haettava sana välimuistissa. Jos se on, niin sana annetaan sieltä prosessorille. Jos sanaa ei löydy välimuistista, niin keskusmuistista luetaan lohko, kiinteä määrä sanoja, ensin välimuistiin, josta sana sitten annetaan prosessorille. Koska muistiviittaukset usein kohdistuvat lähelle edellisiä muistiviittauksia, niin juuri välimuistiin noudettu lohko sisältää todennäköisesti myös seuraavia muistiviittauksia.
Esitettyä välimuistin periaatetta on laajennettu myös useammalle välimuistin tasolle. Nykyään tietokoneissa prosessorin sisällä on nopea välimuisti L1 cache ja toinen hitaampi, mutta suurempi, välimuisti L2 cache. Lisäksi prosessorin ulkopuolella on vielä suurempi, mutta hitaampi, välimuisti L3 cache. Tyypillisesti L1 välimuistin tapauksessa datan lukeminen tai kirjoittaminen vie neljä sykliä, L2 välimuistin tapauksessa 10 sykliä ja L3 välimuistin tapauksessa 30-40 sykliä.
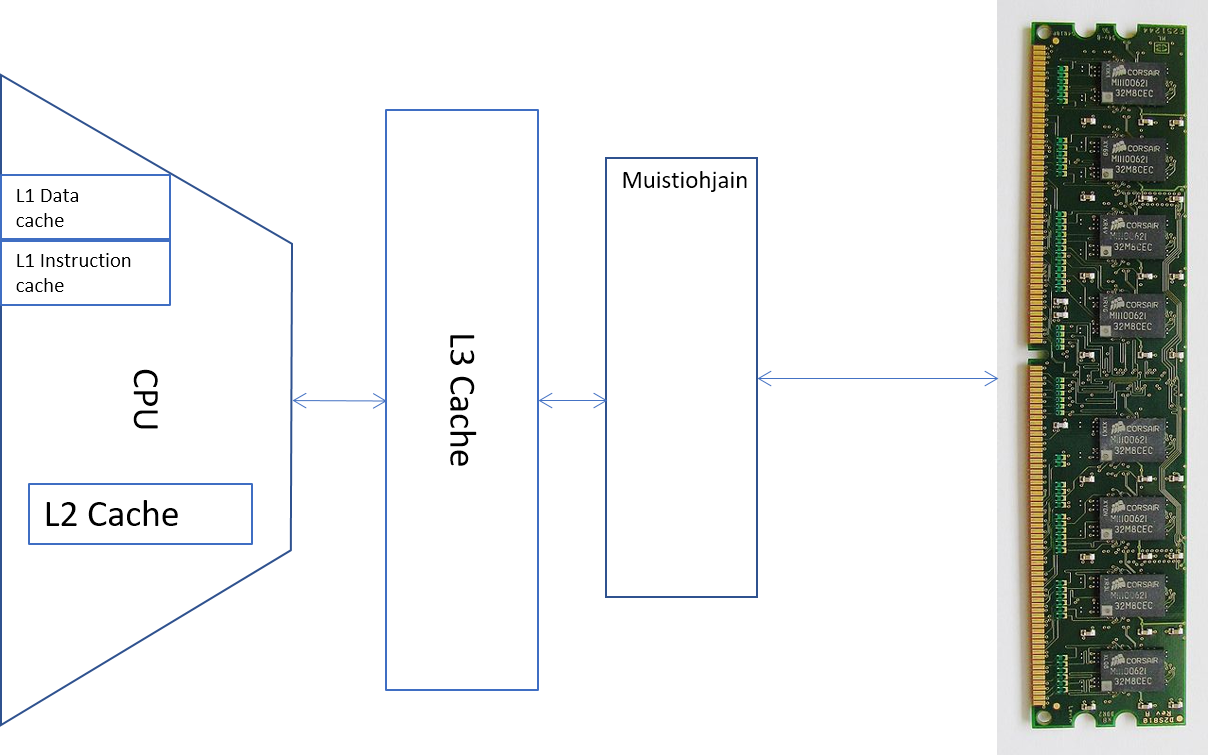
Eräs tehokkaimpia välimuistitekniikoita on käyttää jaettua välimuistia, jossa on eri välimuistit käskyille ja datalle. Usein rakenne on yllä olevan kaltainen. Samalle sirulle prosessorin kanssa sijoitetaan tason 1 välimuistit L1 Instruction cache ja L1 Data cache, eri välimuistit käskyille ja datalle. Nämä ovat kooltaan yleensä 16 KB – 64 KB. Sirun ulkopuolelle CPU:n välittömään yhteyteen asetetaan tason 2 välimuisti L2, joka on hiukan suurempi, mutta hitaampi. Tässä on sekä käskyjä että dataa ja tämän koko on luokkaa 256 KB – 1 MB. Prosessorin kanssa samalla alustalla on vielä tason 3 välimuisti L3, joka muodostuu muutaman MB:n SRAM muistista, joka on nopeampaa kuin keskusmuistina käytetty DRAM. Nykyään kun käytännössä kaikki prosessorit ovat moniytimisiä, niin L3 välimuisti on kaikille ytimille yhteinen. Yleensä kaikki tieto mikä on tason 1 välimuistissa on myös tason 2 välimuistissa ja samoin tason 2 välimuistin sisältö on myös tason 3 välimuistissa.
Välimuistin käyttö perustuu siis ensinnäkin sijainnin mukaiseen paikallisuuteen. Eli juuri viitatun muistiosoitteen läheisyydessä oleviin osoitteisiin on luultavasti tulossa myös viittauksia. Toisaalta on myös ajallista paikallisuutta eli jatkossa luultavasti viitataan samoihin muistipaikkoihin, joihin on juuri viime aikoinakin viitattu. Näitä seikkoja käytetään hyväksi välimuistin käytön suunnittelussa.
Moniprosessointi
Perinteisesti on tietokoneen ajateltu suorittavan käskyjä peräkkäisesti yksi kerrallaan. Täysin tämä ei ole pitänyt paikkaansa. Mikro-operaatiotasolla generoidaan useita kontrollisignaaleita samanaikaisesti ja liukuhihnoituksessa pyritään useita käskyjen osia suorittamaan rinnakkain. Superskalaari arkkitehtuurissa yhdessä prosessorissa on useita suoritusyksiköitä, jotka toimivat rinnakkain.
Monet vanhat tietokonejärjestelmät sisältävät yhden prosessorin. Näissä on yksi pääkeskusyksikkö, joka kykenee suorittamaan tavallisia käskyjä. Monissa tällaisissa järjestelmissä on lisäksi laitekohtaisia prosessoreita tai mikrokontrollereita esimerkiksi näppäimistöä, kovalevyä ja grafiikkaa varten. Nämä erikoisprosessorit toteuttavat rajoitettua käskyjoukkoa ja tavalliset käyttäjän prosessorit eivät käytä niitä suoraan. Joskus näitä hallitsee käyttöjärjestelmä lähettämällä tietoa seuravasta operaatiosta ja valvomalla niiden tilatietoja. Toisissa järjestelmissä nämä erikoisprosessorit ovat alemman tason komponentteja, jotka on rakennettu itse laitteistoon. Tällöin käyttöjärjestelmä ei kommunikoi näiden kanssa, vaan ne toimivat itsenäisesti. Nämä erikoistarkoitukselliset mikroprosessorit ovat hyvin tavallisia ja eivät muuta yhden prosessorin järjestelmää moniprosessorijärjestelmäksi
Moniydinprosessorit
Nykyään erilaiset moniprosessorijärjestelmät ovat nousseet yleisiksi. Moniprosessorijärjestelmässä kaksi tai useampi prosessori ovat läheisessä kommunikoinnissa keskenään jakaen esimerkiksi tietokoneen väylän tai muistin. Moniprosessorisysteemeillä on useita etuja.
- Parantunut töiden läpimeno; kasvattamalla prosessoreiden lukumäärää odotetaan saavan enemmän työtä tehtyä pienemmässä ajassa. Kuitenkin n:llä prosessorilla saatava tehokkuuden parannus on vähemmän kuin n-kertainen. Useiden prosessoreiden yhteistoiminta ja resurssien jakaminen vähentää moniprosessorisysteemeistä saatavaa hyötyä.
- Taloudellisuus; moniprosessorijärjestelmät maksavat vähemmän kuin vastaava määrä yksiprosessorisysteemejä, koska moniprosessorisysteemeillä on yhteisiä oheislaitteita, yhteistä muistia jne.
- Parantunut luotettavuus; jos toiminnot voidaan jakaa usean prosessorin kesken, niin yhden prosessorin vikaantuminen ei pysäytä järjestelmää, se vain hiukan hidastuu.
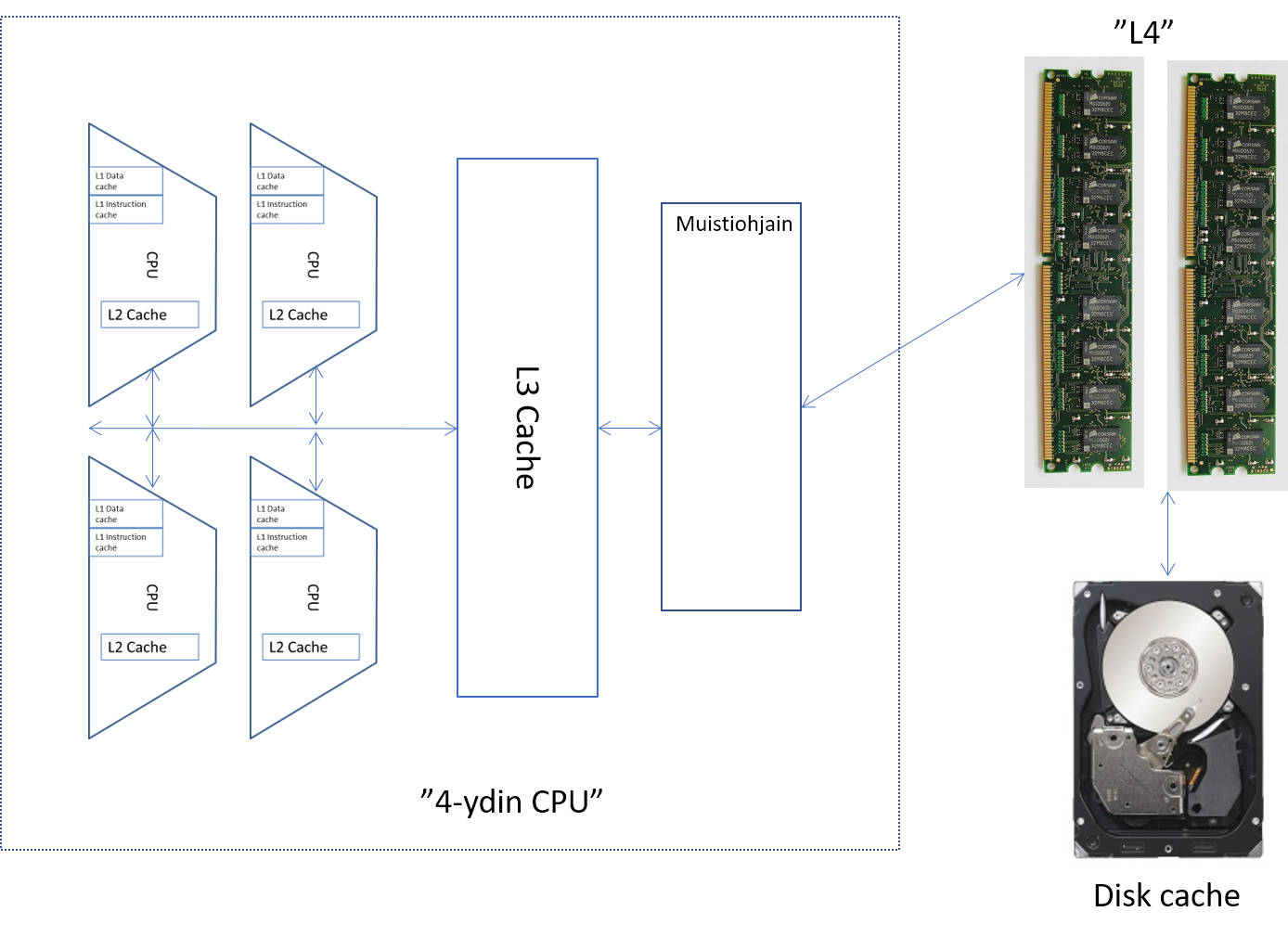
Monissa sovelluksissa tietokonejärjestelmän lisääntyvä luotettavuus on tärkeä tekijä. Joskus järjestelmältä vaaditaan jopa täydellistä vikasietoisuutta, jolloin järjestelmän mikä tahansa yksittäinen komponentti voi tulla vialliseksi, mutta järjestelmä silti jatkaa toimintaa. On olemassa järjestelmiä, joissa on sekä laitteiston että ohjelmiston kaksinkertaistus takaamassa järjestelmän toimintaa vikatilanteessa.
Moniprosessorijärjestelmiä on nykyään kahden tyyppisiä. Järjestelmä voi käyttää asymmetristä moniprosessointia, jolloin kullekin prosessorille on asetettu tietty tehtävä. Masterprosessori kontrolloi koko järjestelmää ja orjaprosessorit odottavat masterprosessorilta komentoja tai suorittavat jotain ennalta määrättyä tehtävää. Masterprosessori ajoittaa ja allokoi tehtäviä orjaprosessoreille.
Tavallisimmat moniprosessorijärjestelmät käyttävät symmetristä moniprosessoiontimenetelmää. Siinä kaikki prosessorit suorittavat kaikkia tehtäviä käyttöjärjestelmän alaisuudessa. Tällöin kullakin prosessorilla on yleensä oma rekisterijoukko ja oma paikallinen välimuisti. Sen sijaan kaikki prosessorit jakavat yhteisen keskusmuistin. kaikki yleisimmät käyttöjärjestelmät tukevat symmetristä moniprosessointia. Ero symmetrisen ja asymmetrisen moniprosessoinnin välillä voi johtua laitteiston tai ohjelmiston puolelta. Näitä varten on käyttöjärjestelmissä eri versioita.
Nykyinen trendi keskusyksikön suunnittelussa on sijoittaa useita ytimiä yhdelle sirulle. Nämä ovat itse asiassa moniprosessointisiruja. Ne voivat olla tehokkaampia kuin usean yhden sirun kokoelma, koska kommunikointi yhdellä sirulla on nopeampaa. Lisäksi usean ytimen siru kuluttaa vähemmän virtaa kuin monta erillistä sirua. Tällainen moniytiminen keskusyksikkö näkyy käyttöjärjestelmän kannalta useana erillisinä tavallisena prosessorina. Tämä vaatii paljon käyttöjärjestelmän suunnittelulta.
Korttipalvelimet ovat myös eräänlaisia moniprosessoreita. Siinä samaan asennuspohjaan on sijoitettu useita erilaisia prosessori ym. kortteja. Siinä kukin korttiprosessori toimii itsenäisesti omalla käyttöjärjestelmällään.
Toisen tyyppisiä usean keskusyksikön järjestelmiä ovat klusterijärjestelmät. Nämä eroavat moniprosessorijärjestelmistä siten, että ne muodostuvat kahdesta tai useammasta erillisestä järjestelmästä, solmusta, jotka on liitetty yhteen. Yleensä klusteroiduilla tietokoneilla on yhteinen keskusmuisti tai ne on linkitetty toisiinsa paikallisverkolla.
Klusteroinnilla pyritään usein hyvään saatavuuteen eli jos jokin järjestelmä menee epäkuntoon, niin palvelu siitä huolimatta toimii. Tämä saavutetaan lisäämällä kokonaisjärjestelmään ylimääräisiä alijärjestelmiä. Klusterisolmuissa suoritetaan klusteritason ohjelmaa. Solmut valvovat toisiaan ja jos valvottu kone epäonnistuu, niin jokin valvova kone ottaa viallisen koneen muistin hallintaan ja aloittaa epäonnistuneen koneen toiminnan. Asiakkaille ja sovelluksille tämä näkyy korkeintaan palvelun lyhyenä viivästyksenä.
Asymmetrisessä klusterissa yksi kone seisoo ja valvoo muita palvelimia. Jos jokin palvelin menee epäkuntoon, niin tästä valvojasta tulee aktiivinen palvelin. Symmetrisessä klusterissa useammat koneet toimivat ja valvovat toisiaan. Tämä muoto on tehokkaampi, koska siinä koko laitteisto on käytössä.
Jos klusteri sisältää useita tietokonejärjestelmiä, jotka ovat verkon välityksellä liitettynä, niin voidaan saavuttaa suuri suorituskyky. Nämä tietokonejärjestelmät voivat ajaa sovellusta rinnakkaisesti. Tällöin sovellus on erityisesti kirjoitettava sellaiseen muotoon, että rinnakkaiskäsittely osaa käyttää kaikkia resursseja tehokkaasti. Kukin verkon solmujärjestelmä ratkaisee oman osansa ongelmasta ja nämä ratkaisut yhdistämällä saadaan koko ongelmalle ratkaisu. Rinnakkaisessa klusterissa useammilla isäntäkoneilla on saanti samaan tietoon jaetussa muistissa. Jos käyttöjärjestelmä ei salli rinnakkaista muistin saantia, niin sovellusohjelman tulee sisältää tällainen muistin käyttö. Tällöin vaaditaan saannin valvonta ja lukitsemismahdollisuus ristiriitaisten operaatioiden välttämiseksi.
Liukuhihnoitus
Uusilla tietokonemalleilla pyritään aina tehokkaampiin koneisiin. Yksi mahdollisuus on samanaikaisten toimintojen lisääminen. Tällä tarkoitetaan useamman operaation suorittamista rinnakkain. Ja eräs sellainen keino liukuhihnoitus, pipelining, joka tarkoittaa käskytason rinnakkaistamista. Sen perustana on jakaa käskyn suoritus useaan vaiheeseen ja jokaisen vaiheen käsittelyä varten on oma osa laitteistoa. Nämä osat voidaan siten suorittaa rinnakkaisesti.
Tarkastellaan esimerkkinä käskyn suoritusta viidessä vaiheessa alla olevan kaavion mukaisesti. Vaiheessa S1 käsky haetaan keskusmuistista ja sijoitetaan puskuriin. Vaihe S2 dekoodaa käskyn, selvittäen käskyn tyypin ja mitä operandeja se tarvitsee. Vaiheessa S3 haetaan operandit. Vaiheessa S4 suoritetaan varsinainen käskyn työ. Lopulta vaiheessa S5 kirjoitetaan tulos takaisin muistiin.
Oletetaan siis kullekin vaiheelle oma suoritusyksikkö ja olkoon kunkin vaiheen viemä aika suunnilleen samanpituinen. Tällöin käskyjen suoritus voidaan ajatella etenevän seuraavan kuvion mukaisesti.
Kellosyklin 1 aikana käskystä 1 suoritetaan vaihe S1. Kellosyklin 2 aikana käskystä 1 suoritetaan vaihe S2 ja käskystä 2 vaihe S1.
Yllä oletetaan, että kaikki käskyt käyvät läpi kaikki viisi vaihetta. Näin ei tietenkään aina ole, esimerkiksi pelkkä latauskäsky ei suorita vaihetta S5. Yksinkertaisuuden vuoksi liukuhihnoituksessa oletetaan kaikkien käskyjen käyvän läpi kaikki 5 vaihetta. Lisäksi yllä oletetaan, että kaikki vaiheet voidaan aina suorittaa rinnakkaisesti. Esimerkiksi vaiheiden S1 ja S3 aikaisia muistista hakuja ei ehkä sallita samanaikaisesti. Jos kaikki vaiheet eivät ole kestoltaan yhtä pitkiä, niin joihinkin vaiheisiin voi kuulua odotusta.
Eräs ongelma tulee haarautumiskäskyjen ja keskeytysten kohdalla. Kun suorituksessa on ehdollinen haarautuminen, niin vasta vaiheen S4 aikana tiedetään, mikä käsky toteutetaan seuraavaksi. Tällöin voidaan joutua liukuhihna tyhjentämään käskyistä, joita ei suoriteta. Liukuhihna joudutaan siten aloittamaan alkuvaiheista uudestaan.
Näitä ongelmia kutsutaan nimellä liukuhihna este, pipeline hazard. Ensinnäkin kaksi tai useampia liukuhihnalla olevista käskyistä voi tarvita samaa resurssia, esimerkiksi muistista haku. Toisen tyypin este on dataeste. Kaksi käskyä toteutetaan peräkkäin ja molemmissa käskyissä on viittaus samaan muistipaikkaan tai rekisteriin. Silloin on mahdollista, että operandin päivitys aiheuttaa eri tuloksen liukuhihnalla suoritettuna kuin peräkkäisesti suoritettuna. Kolmas tyyppi on nämä haarautumisongelmat.
Keskeytykset
Lähes kaikissa tietokoneissa on mekanismi, jolla muut moduulit, I/O, muisti, voivat keskeyttää prosessorin normaalin toiminnan. Ohjelman suorituksen aikana voi jokin käsky generoida ehdon, joka aiheuttaa keskeytyksen. Tällaisia ehtoja voivat olla nollalla jakaminen, aritmeettinen ylivuoto, viittaus käyttäjän muistialueen ulkopuolelle jne. Kellolaite voi myös aiheuttaa keskeytyksen, kun jokin aikaväli on kulunut loppuun. I/O ohjain voi suorittaa keskeytyksen esimerkiksi ilmoituksena jonkin operaation loppumisesta. Laitteistovirhe, virran loppuminen tai pariteettivirhe, voivat myös suorittaa keskeytyksen.
Keskeytysten pääasiallinen tehtävä on parantaa tietokoneen tehokkuutta. Esimerkiksi ulkoiset laitteet ovat paljon hitaampia kuin prosessori. Oletetaan, että prosessori siirtää tietoa tulostimelle käskysyklin mukaisesti. Jokaisen tulostusoperaation jälkeen prosessori pysähtyy ja odottaa jouten, kunnes tulostin saa tiedon tulostettua. Tämä odotusaika voi kestää tuhansien käskysyklien ajan.
Kun ohjelmassa on tulostuskäsky, niin silloin suoritetaan seuraavaa. Todellisen I/O toiminnan hoitaa järjestelmän ohjelma. Tämä I/O ohjelma ensin suorittaa valmistavia käskyjä, siihen voi kuulua tiedon siirtoa puskuriin ja parametrien asetteluja. Tämän jälkeen suoritetaan varsinainen I/O-komento. Ilman keskeytyksiä ohjelman tulee odottaa, että I/O laite suorittaa tehtävänsä loppuun. I/O komennon jälkeen suoritetaan I/O ohjelmassa vielä muutamia käskyjä, esimerkiksi lippujen asetuksia kertomaan operaation onnistumisesta.
Keskeytysten avulla prosessori voidaan asettaa suorittamaan muita käskyjä sillä aikaa, kun I/O operaatio etenee I/O laitteella. Kun ohjelmassa tulee esimerkiksi tulostuskäsky, niin I/O ohjelmaa kutsutaan ja se suorittaa alustustoimenpiteet ja aloittaa varsinaisen I/O toiminnan. Kun nämä muutamat käskyt on suoritettu, niin kontrolli palautetaan käyttäjän ohjelmalle. Samalla aikaa ulkoinen I/O laite hakee tietoa muistista ja tulostaa sen. Nyt I/O toimenpidettä suoritetaan samanaikaisesti käyttäjän ohjelman käskyjen toteuttamisen kanssa.
Kun ulkoinen laite saa työnsä valmiiksi eli on valmis ottamaan vastaan uusia kirjoituskomentoja, niin se lähettää keskeytyksen pyyntö signaalin prosessorille. Prosessori vastaa signaaliin keskeyttämällä käyttäjän ohjelman suorituksen ja haarautumalla ohjelmaan, joka palvelee tätä kyseistä ulkoista laitetta. Tätä ohjelmaa kutsutaan keskeytysten käsittelijäksi. Kun keskeytys on tässä ohjelmassa käsitelty, niin prosessori jatkaa käyttäjän ohjelman suorittamista.
Käyttäjän ohjelmassa ei tarvitse olla mitään ohjelmakoodia keskeytyksiä varten, prosessori ja käyttöjärjestelmä vastaavat keskeytyksiin liittyvistä toimenpiteistä. Keskeytyksiä varten voidaan käskysykliä muuttaa lisäämällä siihen keskeytyssykli. Siinä prosessori tarkistaa onko keskeytyksiä tapahtunut. Jos keskeytyssignaaleja ei ole odottamassa, niin siirrytään käskyn hakuun. Jos keskeytyssignaali on päällä, niin prosessori keskeyttää käyttäjän ohjelman suorituksen. Tallettaa sen suoritusympäristöstä tarvittavat tiedot ja asettaa ohjelmalaskurin arvoksi keskeytyksen käsittelijärutiinin alkuosoitteen.
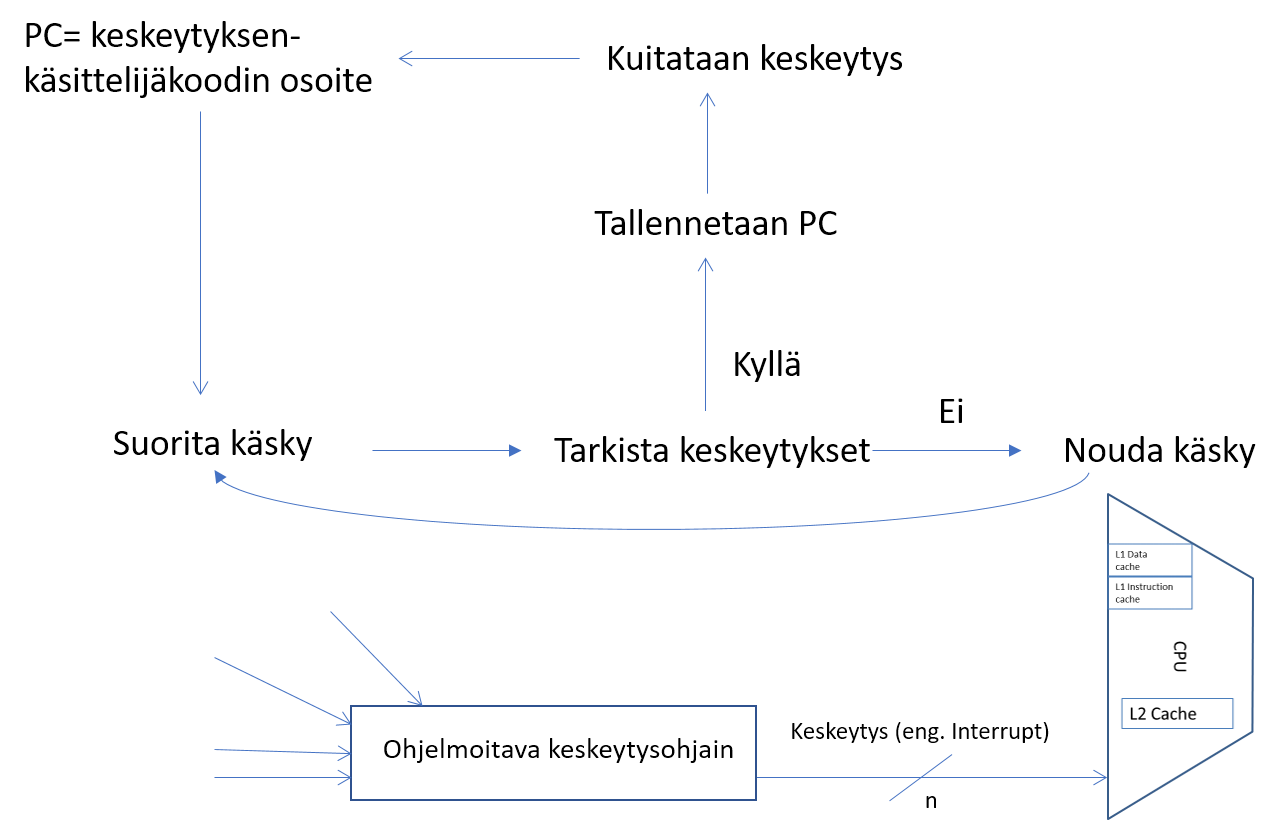
Prosessori jatkaa keskeytyksen käsittelijä ohjelman suoritusta. Tämä on siis tavallisesti käyttöjärjestelmän ohjelma. Siinä ensin tarkastetaan keskeytyksen tyyppi ja suoritetaan sen vaatimat toimenpiteet. Keskeytyksen käsittelijän saatua ohjelmansa valmiiksi jatketaan käyttäjän ohjelman suoritusta.
Vaikka keskeytysten käsittelyssä suoritetaan ylimääräisiä käskyjä, niin esimerkiksi I/O operaatioiden yhteydessä keskeytysten käyttö lisää huomattavasti prosessorin käytön tehokkuutta.
Käytännössä voi käydä niin, että on saatu signaaleja useammista keskeytyksistä. Tulostuksen yhteydessä voi esimerkiksi tulla tietoa kommunikaatiolinjalta ja se aiheuttaa toisen keskeytyksen. Useampien keskeytysten käsittelyyn käytetään kahta tapaa.
Ensinnäkin kun yhtä keskeytystä käsitellään, niin muut keskeytykset voidaan kieltää. Tällöin prosessori jatkaa toimintaansa ja ei huomioi mitenkään keskeytyksiä. Keskeytys jää odottamaan ja se tullaan tarkistamaan sitten, kun prosessori on jälleen sallinut keskeytykset. Tässä menetelmässä kun käyttäjän ohjelmaa suoritetaan ja havaitaan keskeytys, niin ensimmäiseksi kielletään keskeytykset. Kun keskeytys on käsitelty, niin ennen siirtymistä käyttäjän ohjelmaan sallitaan keskeytykset ja prosessori tarkistaa onko käsittelemättömiä keskeytyksiä odottamassa. Näin keskeytykset käsitellään peräkkäisesti. Tämän menetelmän huono puoli on, että se ei huomioi keskeytyksien tärkeyttä eli prioriteettia tai keskeytysten aikakriittisyyttä.
Toisessa keskeytysten käsittelytavassa asetetaan keskeytyksille prioriteetit ja korkeamman prioriteetin keskeytyksen sallitaan keskeyttää alemman prioriteetin keskeytyksen käsittelijän toiminta. Tällöin suoritetaan ensin loppuun korkeamman prioriteetin keskeytyksen käsittelijäohjelma ja sen päätyttyä jatketaan alemman prioriteetin keskeytyksen käsittelijäohjelman suoritusta.
x86 Assembly
- Assembly kieli, josta on kehittynyt nykyisten ’Intel-arkkitehtuuri’ –prosessorien assembly kielet
- Kehitetty alkujaan 16-bittisen Intel 8086 prosessorin kanssa
- Add5.c nykyisellä x86-64 assemblyllä
Esimerkki prosessorin toiminnasta
Harjoitustehtävissä tutustutaan prosessorin toimintaan tulkitsemalla konekielisiä käskyjä ja niiden vaikutusta prosessorin rekistereihin.
Muistien toteutus
SRAM ja DRAM
SRAM (Static random-access memory) ja DRAM (Dynamic random-access memory) ovat tällä hetkellä tietokoneissa käytettävät muistityypit. Staattinen muistityyppi on sellainen missä informaatio pysyy muistissa, kun muisti saa jatkuvasti virtaa. Dynaaminen muistityyppi on puolestaan sellainen, jossa informaatio katoaa muistista ajan kuluessa, vaikka muisti saisi virtaa, jos muistia ei virkistetä. DRAM muistien virkistystaajuus on kymmenien millisekuntien luokkaa riippuen DRAM muistityypistä sekä muistin koosta. Sekä SRAM että DRAM ovat haihtuvia, englanniksi volatile, muistityyppejä, joiden informaatio katoaa kun virta sammutetaan.
SRAM on eräänlainen kiikku, eli siinä on takaisinkytkentä, joka mahdollistaa bitin arvon pysymisen muistissa. SRAM poikkeaa kuitenkin aiemmin esitetyistä kiikuista siten että sitä ei toteuteta loogisilla porteilla, vaan transistorikytkentänä. Toki loogiset portit toteutetaan myös transistoreilla, NAND ja NOR molemmat toteutetaan neljällä CMOS transistorilla. Muistielementiksi soveltuva D salpa voidaan toteuttaa neljällä NAND portilla, mutta synkronoitu kellotettu D-kiikku vaatii viisi 2-input NAND porttia ja yhden 3-input NAND portin (voidaan toteuttaa kuudella transistorilla). Kiikuilla toteutettava 1-bitin muisti vaatii paljon enemmän transistoreita, vie enemmän tilaa ja on hitaampaa kuin SRAM.
SRAM on nopeampaa muistia, mutta se on kalliimpaa toteuttaa ja vie enemmän tilaa kuin DRAM. SRAM muistin käyttökohteita ovat tietokoneessa prosessorin sisäiset rekisterit sekä prosessorin sisäiset välimuistit (L1, L2 ja L3). Lisäksi SRAM muistia käytetään muistipuskureissa, kuten esimerkiksi kiintolevyn puskurissa.
DRAM on siis halvempaa toteuttaa, mahtuu pienempään tilaan mutta on hitaampaa kuin SRAM muisti. DRAM muistin käyttökohteena on tietokoneissa niiden keskusmuistit. Tänä päivänä yleisin tietokoneen keskusmuisti on DDR3 tai DDR4 SDRAM, missä S tulee siitä, että muisti on synkronoitu prosessorin toiminnan kanssa, mahdollistaen prosessorin käsittelevän dataa samaan aikaan kun uusi keskusmuistista tuleva data jo odottaa käsittelyyn pääsyä. DDR (Double Data Rate) tekniikalla on saatu teoriassa tuplattua DRAM:in nopeus. DDR SDRAM muisteista on eri versioita, jotka eivät ole yhteensopivia toistensa kanssa. Uudet versiot ovat kasvattaneet tiedonsiirtonopeutta muistin ja prosessorin välillä.
SRAM
SRAM muisti toteutetaan yleensä kuudella transistorilla, mutta siitä on olemassa myös 4-, 8- ja 10-transistoriset versiot. Esimerkiksi neljän transistorin (ja kahden vastuksen) SRAM muisti mahtuu pienempään tilaan, mutta sen valmistus on monimutkaisempaa ja se kuluttaa enemmän virtaa (koska jompikumpi vastus toimii koko ajan alasvetovastuksena).
Alla on kuva kuuden transistorin SRAM muistisolun kytkennästä. Transistorikytkennät ja
ovat molemmat CMOS NOT portteja. Molemman NOT portin ulostulo on siis takaisinkytketty toisen NOT portin sisäänmenoon säilyttäen muistisoluun tallennetun arvon, silloin kun
ja
eivät ole johtavassa tilassa.
Kuvassa on ns. Word Line, jolla ohjataan kokonaisen sanan muistista lukemista tai kirjoittamista muistiin. Esimerkiksi 32-bittisessä muistissa on rinnakkain 32 muistisolua, jotka kaikki on kytketty samaan
linjaan. Kun
linjalle tuodaan jännite, se kytkee
ja
transistorit johtavaan tilaan. Tällöin NOT portteihin tallennettu arvo voidaan lukea
linjalta ja sen negaatio
linjalta. Muistista lukua voidaan nopeuttaa nostamalla ennen lukua
ja
puoleeen loogisen nollan ja ykkösen välisestä jännitteestä ja
linjan jännitteen asettamisen jälkeen mitataan
ja
linjojen välistä jännite-eroa, koska toisen linjan jännite lähtee kohoamaan kohti maksimijännitettä ja toisen kohti nollaa volttia. Jos
on suurempi kuin
, niin tallennettu arvo on 1 ja päinvastoin tallennettu arvo on 0. Muistin nopeus on riippuvainen siitä, kuinka pieni jännite-ero kyetään luotettavasti lukemaan.
Kirjoittaminen tapahtuu asettamalla ensin linjalle tallennettava arvo ja
linjalle sen negaatio. Sitten
linjalla asetetaan transistorit
ja
johtavaan tilaan. Jos tallennettava arvo on esimerkiksi looginen 1, niin
linjan 1 johdetaan sisäänmenoksi
ja
transistoreille (NOT portille), joka negatoi arvon, joten transistorit
ja
saavat sisäänmenokseen loogisen nollan, jonka ne negatoivat arvoon 1, joka takaisin kytketään transistoreille
ja
. Kun
ja
lakkaavat johtamasta, jää arvo muistiin.
linjan tallennettavan arvon negaatio vahvistaa edellä kuvattua toimintaa.
DRAM
DRAM muistisolu rakennetaan transistorista ja kondensaattorista. Kondensaattori on passiivikomponentti, eli se kuluttaa energiaa. Kondensaattoriin voidaan tallentaa sähkövaraus, joka purkautuu ei-ideaalisesta kondensaattorista ajan kuluessa. Varaus näkyy kondensaattorin napojen välisenä jännite-erona. Kondensaattorin varattu tila vastaa binääristä arvoa 1 ja varaamaton binääristä arvoa 0. Käytännössä DRAM muisteissa käytetty kondensaattori menettää varauksensa aika nopeasti, joten varausta täytyy virkistää aika usein.
Kirjoittaminen ja lukeminen tehdään ohjaamalla World line linjalle jännite, jolloin kytkimenä toimiva nMOS transistori alkaa johtaa kondensaattorin ja Bit line linjan välillä. Luettaessa muistia kondensaattorissa oleva varaus purkautuu ja voidaan lukea bittilinjalta. Koska lukeminen purkaa varauksen, eli muistissa olleen arvon, täytyy luettu arvo tallentaa aina takaisin muistiin lukemisen jälkeen. Kirjoitettaessa muistiin laitetaan kirjoitettava arvo (jännite) Bit line linjalle ja transistorin johtaessa, kondensaattori joko varautuu tai ei, riippuen siitä onko bittilinjalla looginen 1 vai 0.
DRAM muistin nopeuteen vaikuttaa kondensaattorin varausnopeus kirjoittaessa sekä bittilinjan ei toivottu parasiittinen kapasitanssi. Kuvassa siis vaaleampi kondensaattori ei ole oikea komponentti, vaan kuvaa bittilinjan parasiittista kapasitanssia. Sähkömagneettiset häiriöt voivat satunnaisesti muuttaa DRAM muistin yhden bitin arvoa. DRAM muisteissa käytetään virheenkorjausmenetelmiä, joilla yhden bitin virheet voidaan korjata ja kahden bitin virheet havaita.
Flash muisti
Flash muisti on puolijohdetekniikalla toteutettu haihtumaton, englanniksi non-volatile, muistityyppi, jolle voidaan tallentaa tietoa ja jolta voidaan poistaa tietoa sähköisesti. Informaatio siis säilyy haihtumattomassa muistissa vaikka se ei saisi virtaa. Flash muisteja toteutetaan tänä päivänä joko NAND- tai NOR-tekniikalla. Tekniikat eivät kuitenkaan käytä CMOS transistoreista rakennettuja NAND- tai NOR-portteja. Vaan tekniikoiden muistisolujen floating-gate MOSFET (FGMOS) transistorit toimivat NAND- tai NOR-portin logiikalla ja ovat siten saaneet niistä johdetut nimet.
NAND-tekniikalla toteutetaan esimerkiksi muistitikut ja SSD-levyt, koska NAND-tekniikalla muistisolun tilantarve on pienempi, mahdollistaen suuremman tallennuskapasiteetin ja pienemmän virrankulutuksen bittiä kohden. NAND Flash -muistia ei kuitenkaan pysty lukemaan tavu kerrallaan, mikä yleensä on vaatimuksena nykyisissä mikroprosessoreissa ja mikrokontrollereissa. Esimerkiksi niiden käyttämät ohjelmoitavat ROM -muistit täytyy toteuttaa NOR Flash -tekniikalla. NOR logiikalla toteutettua FLASH muistia voidaan lukea random-access tekniikalla, kun taas NAND FLASH muistia ei. Yleisesti NAND FLASH:iin on nopeampaa kirjoittaa ja se käyttää vähemmän virtaa aktiivisena, kun taas NOR FLASH:ista on nopeampi lukea ja se käyttää vähemmän virtaa stand-by tilassa.
Käytettäessä CMOS-tekniikkaa molemmat NAND ja NOR voidaan toteuttaa neljällä transistorilla, mutta CMOS NAND portti vaatii vähemmän pinta-alaa piikiekolle toteutettaessa ja lisäksi se on myös nopeampi kuin CMOS NOR portti. Tänä päivänä suurin osa CMOS-tekniikkaa käyttävistä logiikkaa toteuttavista mikropiireistä on toteutettu NAND-logiikalla eli CMOS NAND porteilla.. CMOS NAND porteilla toteutetut muistielementit, kuten D-kiikkuihin pohjautuvat muistit, vaatisivat enenmmän transistoreita ja tilaa, ja olisivat hitaampia, kuin NAND- tai NOR-flash muistit.
Esimerkki kertolaskun toteutuksesta
Kertolaskun säännöt
0 0 1 1
x 0 x 1 x 0 x 1
0 0 0 1
Esim.
10 ab
x 11 x cd
10 ad bd (a AND d) (b AND d)
+ 10 + ac bc (a AND c) (b AND c)
110
Esim.
010 abc
x 111 x def
010 af bf cf (a AND f) (b AND f) (c AND f)
010 ae be ce (a AND e) (b AND e) (c AND e)
+ 010 + ad bd cd (a AND d) (b AND d) (c AND d)
01110
Assembler
- Assembler on ohjelma, joka kääntää Assembly kielisen ohjelman konekielelle
- Konekieli on joukko binäärisiä ”sanoja” jotka vastaavat prosessorin käskyjä
- Assembly kieli antaa binäärisille bittijoukoille paremmin muistettavat vastineet, esim.
- 1111110111001000
- M=M-1
- Jokaiselle prosessorityypille on oma konekieli ja siten myös assembly kieli
Toimintalogiikka
- Toista, kunnes
.asmtiedoston EOF- Lue seuraava Assembly kielinen komento
- Paloittele komento osiin
- Hae osia vastaava binäärikoodi
- Yhdistä koodit yhdeksi 16-bittiseksi konekieliseksi käskyksi
- Anna ulostulona konekielinen koodi
- kirjoita
.hacktiedostoon uusi rivi
- kirjoita
Toiminta ilman symboleita
- Jos tyhjä rivi tai kommentti → ei tehdä mitään
- Jos alkaa @ -merkillä, niin A-käsky
- Esim. String
@9→ pitää muuttaa String:iksi0000000000001001
- Esim. String
- Jos ei, niin tutkitaan löytyykö riviltä
=-merkkiä ja;-merkkiä,- jotta saadaan selville mitkä
dest=comp;jump-osat käskyssä on - Selvitetään
destosaa vastaava binääriluku - Selvitetään
composaa vastaava binääriluku - Selvitetään
jumposaa vastaava binääriluku - Kasataan 16-bittinen konekielinen C-käsky yhdistämällä osat
- jotta saadaan selville mitkä
- Voidaan olettaa että kommentit alkavat aina rivin alusta ja rivien lopussa ei ole kommentteja
HACK assembly -kielen symbolit
- Käydään koodi läpi etsimällä symbolit, esim.
@sumtai@LOOPtai(LOOP)- Lisäksi riveiltä poistetaan kaikki kommentit ja kommenttien jälkeiset merkit, jos niitä on, esim.
D=M // D = first number
- Kahdenlaisia symboleita
- Muuttujia, joille pitää varata muistiosoite, esimerkiksi
@sum - Osoitteita joihin pitää hypätä, eli jossain on sama symboli kaarisuluissa
- Esimerkiksi @LOOP ja
(LOOP) - rivinumero tulee selvittää, jotta saadaan hyppypaikka
- Esimerkiksi @LOOP ja
- Muuttujia, joille pitää varata muistiosoite, esimerkiksi
Toiminta symboleiden kanssa
- Ensin käydään läpi se, löytyykö symbolia vastaava hyppypaikka eli symboli suluissa, esim.
(LOOP)- Löytyykö sulkuja? Jos löytyy, lisää suluissa oleva symbolitaulukkoon ja tallenna sulku-rivin alapuolisen rivin numero vastaamaan symbolia
- Sen jälkeen käydään koodi uudestaan läpi, etsien symboleita, esim.
@sumtai@LOOP- Jos symbolitaulukossa, niin se on hyppy-symboli
- Jos symbolia ei taulukossa, kyseessä on muuttuja, jolle pitää varata paikka RAM muistista (aloitetaan muistipaikasta 16)
- Symbolitaulukon toteutus esim. Javan hashtable:lla
- Lisäksi taulussa pitää olla muutama etukäteen määritelty symboli, jotka pitää muuttaa RAM osoitteiksi, esim.
SCREEN - Kun taulu valmis korvataan Assembly koodin symbolit niitä vastaavilla osoitteilla
Assemblerin toteutus
- Millä tahansa ohjelmointikielellä
- Suositeltava arkkitehtuuri
- Parser moduuli: purkaa käskyt osiin
- Code moduuli: kääntää osat binääriseksi
- SymbolTable moduuli: hallinnoi symbolitaulua
- Main moduuli: tiedoston luku/kirjoitus, käyttää yo. moduuleja ulostulon rakentamiseen
- Testaa Assembleriasi testiohjelmilla (add.asm etc.)
- Versiot ilman symboleita tai symboleiden kanssa
- Lopuksi voit verrata Assembler-simulaattorilla simulaattorin kääntämää koodia sinun Assemblerin kääntämään koodiin
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.