TIEP114 Luentokalvot
Kurssin kotisivut lukuvuosittain
Kurssin opiskeluun liittyviä yleisiä asioita ja ohjeita löydät
Kurssin harjoitustehtävät lukuvuosittain
TIEP114 kurssin opiskelu tehdään käytännön harjoitustehtävillä.
Harjoitustehtäviä on erilaisia
- TIM-järjestelmässä tehtäviä
- Laboratoriossa tehtäviä
- HDL ja Assembly tehtäviä
- 5 op laajuuteen ohjelmointitehtävä
Kurssin esitiedoista
- Ei tarvitse ohjelmointitaitoa
- Asioiden havainnollistamiseen käytetään eri ohjelmointikieliä
- Matematiikasta riittää lukion matematiikasta
- potenssi- ja logaritmifunktio
- matemaattisen muuttujan käsite lausekkeessa
- yksinkertaisista lausekkeista muodostettujen yhtälöiden sieventäminen
Johdantoa Boolen logiikkaan
Tietokoneen rakenne
Tietokoneen rakenne
Von Neumannin arkkitehtuuri
Lähes kaikki nykyajan tietokoneet perustuvat ns. Von Neumannin arkkitehtuuriin, joka perustuu seuraaviin asioihin.
- Suoritettava ohjelma ja sen käyttämä data talletetaan samaan muistiin binäärisenä informaationa.
- Tämän muistin sisältö on osoitettavissa paikan mukaan huolimatta siitä, minkä tyyppistä tietoa sinne on talletettu.
- Ohjelman suoritus tapahtuu peräkkäin yhdestä käskystä seuraavaan paitsi, jos jostain syystä hypätään johonkin muuhun käskyyn.
Tiedon esitys tietokoneissa
Tiedon digitalisointi
Jatkuva-arvoinen
- Pyöristäminen, esimerkki
- \(4\frac{1}{3} \rightarrow 4\)
- \(4\frac{2}{3} \rightarrow 5\)
- Tarkempi pyöristäminen, esimerkki
- \(4\frac{1}{3} \rightarrow 4.3\)
- \(4\frac{2}{3} \rightarrow 4.7\)
Tiedon digitalisointi
Jatkuva-aikainen
Digitaalisen tiedon tallennus
2-järjestelmän tietomäärä
- Olkoon 2-järjestelmässä \(N\) muistipaikkaa (tai 2-järjestelmän luvussa \(N\) numeroa)
- Tällöin voidaan muodostaa \(2^N\) eri kombinaatiota
- Kombinaatioihin voidaan tallentaa jotain informaaatiota
- voivat vastata esimerkiksi lukuarvoja
- Vastaavasti on 10-järjestelmässä, eli \(N\) numerolla vaidaan esittää \(10^N\) kobinaatiota
- Esimerkiksi kolmella numerolla voidaan esittää \(10^3 = 1000\) eri kobinaatiota, kuten lukuarvot 000-999
Esimerkki
Esimerkki. Kuinka monta bittiä tarvitaan kaikkien välillä 0 - 999 olevien kokonaislukujen esittämiseen?
Esimerkki. Alle on kirjoitettu LaTeX:illa lauseke, joka antaa tulokseksi sen, kuinka monta eri numeroa voidaan esittää 9 bitillä. Muunna lauseke sellaiseksi että se antaa tulokseksi sen kuinka monta eri numeroa voidaan esittää 10 bitillä.
Esimerkki. Alle on kirjoitettu LaTeX:illa lauseke, joka antaa tulokseksi sen, kuinka monta bittiä tarvitaan sadan numeron esittämiseen. Muunna lauseke sellaiseksi, että se antaa tulokseksi sen kuinka monta bittiä tarvitaan tuhannen numeron esittämiseen.
Bittien ryhmittely
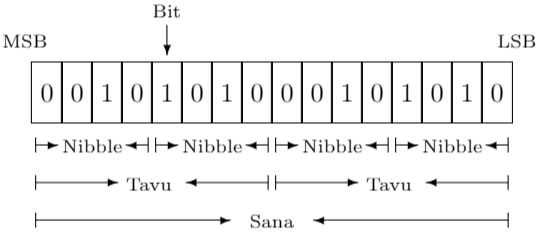
Toteutettu \(\LaTeX\) bytefield-paketilla, lähdekoodi
—MSB ja LSB
Esimerkki. Testaa MSB ja LSB bittien muuttamisen vaikutusta binääriluvun 000000002 arvoon.
Tavujärjestys
Olkoon meillä esimerkiksi seuraava 32 bittinen eli 4-tavuinen sana
10011111 00000000 10001010 11010101.
Big endian
Jos tämä sana talletetaan big endian -tavalla muistiin alkaen muistipaikkatavusta, jonka osoite 100, niin osoitepaikoissa olevien tavujen 100 – 103 sisällöt ovat seuraavat
100: 10011111 101: 00000000 102: 10001010 103: 11010101
Tavujärjestys
Olkoon meillä esimerkiksi seuraava 32 bittinen eli 4-tavuinen sana
10011111 00000000 10001010 11010101.
Little endian
Jos tämä sana sen sijaan talletetaan little endian -tavalla alkaen tavusta, jonka osoite 100, niin tavujen 100 – 103 sisällöt ovat seuraavat
100: 11010101 101: 10001010 102: 00000000 103: 10011111
Tietokoneisiin liittyvät mittayksiköt
| Value | SI | Value | IEC | ||
|---|---|---|---|---|---|
| 1000 | k | kilo | 1024 | Ki | kibi |
| 10002 | M | mega 1 | 0242 | Mi | mebi |
| 10003 | G | giga 1 | 0243 | Gi | gibi |
| 10004 | T | tera 1 | 0244 | Ti | tebi |
| 10005 | P | peta 1 | 0245 | Pi | pebi |
| 10006 | E | exa 1 | 0246 | Ei | exbi |
| 10007 | Z | zetta 1 | 0247 | Zi | zebi |
| 10008 | Y | yotta 1 | 0248 | Yi | yobi |
Lukujärjestelmät
Kymmenjärjestelmän luvut
Esimerkki.
Binääriluvut
Esimerkki.
Heksadesimaalijärjestelmä
Esimerkki.
Oktaalijärjestelmä
Esimerkki.
Lukujärjestelmät ohjelmointikielissä
Muuntaminen eri lukujärjestelmien välillä
Muuntaminen muista lukujärjestelmistä 10-järjestelmään
Muuntaminen eri lukujärjestelmien välillä
Muuntaminen 10-järjestelmästa muihin lukujärjestelmiin
Esim. 1 8610 muunnetaan binääriluvuksi
43 21 10 5 2 1 0
2 86 2 43 2 21 2 10 2 5 2 2 2 1
86 42 20 10 4 2 0
0 1 1 0 1 0 1
(binääriluku saadaan lukemalla jakojäännökset oikealta)
⇒ 8610 = 10101102
Muuntaminen eri lukujärjestelmien välillä
Muuntaminen 10-järjestelmästa muihin lukujärjestelmiin
Esim. 3 11010 muunnetaan heksaluvuksi
6 0
16 110 16 6
96 0
14(=E) 6
(heksadesimaaliluku saadaan lukemalla jakojäännökset oikealta)
⇒ 11010 = 6E16 = 0x6E
Jakojäännös pinoon
Lukujen esitys tietokoneissa
Binäärilukujen yhteenlasku
Negatiivisten lukujen esitys binäärilukujärjestelmässä
Negatiivisia lukuja Javalla
Negatiivisia lukuja C#:lla
Negatiivisia lukuja Pythonilla
Negatiivisten lukujen esitys binäärilukujärjestelmässä
Suora talletustapa
Jos positiivinen luku on
+6510 = 010000012
niin negatiivinen saadaan vaihtamalla MSB
110000012 = -6510
Vähennyslaskun muuttaminen yhteenlaskuksi
Binary Decimal
Vähennyslasku
00000111 +7 Dec Bin Yhteenlasku negatiivisella luvulla
00000110 +6 111
00000101 +5 7 00000111 00000111 (+7)
00000100 +4 -5 -00000101 +10000101 +(-5)
00000011 +3 2 == 00000010 10001100 != +2
00000010 +2
00000001 +1
00000000 +0
10000000 -0
10000001 -1 Binäärisen vähennyslaskun säännöt
10000010 -2
10000011 -3
10000100 -4
10000101 -5
10000110 -6
10000111 -7
Negatiivisten lukujen esitys binäärilukujärjestelmässä
Yhden komplementtimuoto
Jos positiivinen luku on
+6510 = 010000012
niin negatiivinen saadaan vaihtamalla kaikki bitit
101111102 = -6510
Vähennyslaskun muuttaminen yhteenlaskuksi
Binary Decimal 00000111 +7 Yhteenlasku negatiivisilla luvuilla 00000110 +6111111100000101 +500000111(+7)00000100 +4+ 11111010+(-5)00000011 +310000000100000010 +2 | Ylivuotobitti lisätään tulokseen 00000001 +1 | 1 00000000 +0 | 00000001 11111111 -0 -->+ 111111110 -100000010== +2 11111101 -2 11111100 -3 11111011 -4 Ylivuoto bitin lisäyksestä tulee 11111010 -5 nimeen Yhden komplementti 11111001 -6 11111000 -7
Negatiivisten lukujen esitys binäärilukujärjestelmässä
Kahden komplementtimuoto
Lähdetään yhden komplementtimuodosta
101111102(1-komplementti)
Lisätään ykkönen
101111102 + 000000012 = 101111112
Saatu tulos on esitys negatiiviselle luvulle
101111112(2-komplementti) = -6510
Vähennyslaskun muuttaminen yhteenlaskuksi
Binary Decimal 00000111 +7 Yhteenlasku negatiivisilla luvuilla 00000110 +61111111100000101 +5 00000111 (+7) 00000100 +4+11111011+(-5)00000011 +3 100000010 00000010 +2 00000001 +1 Ylivuotobitti yksinkertaisesti jätetään huomioimatta 00000000 +0 11111111 -1100000010 ⇒ 00000010 == +2 11111110 -2 11111101 -3 11111100 -4 11111011 -5 11111010 -6 11111001 -7 11111000 -8
2-komplementti bin ⇒ 10-järjestelmään
111110102(2-komplementti)
111110102 - 000000012 = 111110012
111110012(1-komplementti)
111110012 ⇒ 000001102
000001102 = 610
610 ⇒ -610
Muita binäärisiä esitystapoja
Kokonaislukujen esittämiselle binäärimuodossa on myös monia muita menetelmiä, esim.
- Offset binary - "Siirretty binäärimuoto", Excess-K
- Negative base - Negatiivinen kantaluku
- Binary-coded decimal - BCD-koodi
- Gray code - Gray koodi
Tietokoneet käyttävät siis sisäisessä toteutuksessa kahden komplementtimuotoa.
Reaaliluvun muuntaminen binääriseksi
- Binääriluvun desimaaliosa saadaan kertolaskulla 10-järjestelmän desimaaliosasta
- Kerrotaan kohdelukujärjestelmän kantaluvulla, eli luvulla 2
- Toistetaan: kerrotaan saadun tuloksen desimaaliosa kahdella
- Muunnetaan luvun desimaaliosa 0.37510 binääriseksi
- .375 × 2 = 0.75 (pienempi kuin yksi → ensimmäinen bitti on 0)
- .75 × 2 = 1.5 (suurempi kuin yksi → seuraava bitti on 1)
- vain desimaaliosa otetaan mukaan seuraavaan kertolaskuun
- .5 × 2 = 1.0 (yhtä suuri kuin yksi → seuraava bitti on 1)
- Jos saadaan tasan 1.0 ⇒ muunnos on valmis.
Desimaaliosan bitit saadaan laskemisjärjestyksessä ja ovat siis 011
Lopulta yhdistetään kokonaislukuosa ja desimaaliosa, eli saadaan
0.37510 = 0.0112
Reaaliluvun muuntaminen binääriseksi
Olkoon meillä luku 0.110, muunnetaan se binääriluvuksi
- .1 × 2 = 0.2 (pienempi kuin yksi → 0)
- .2 × 2 = 0.4 (pienempi kuin yksi → 0)
- .4 × 2 = 0.8 (pienempi kuin yksi → 0)
- .8 × 2 = 1.6 (suurempi kuin yksi → 1)
- .6 × 2 = 1.2 (suurempi kuin yksi → 1)
- .2 × 2 = 0.4 (pienempi kuin yksi → 0)
- .4 × 2 = 0.8 (pienempi kuin yksi → 0)
- .8 × 2 = 1.6 (suurempi kuin yksi → 1)
- …
- Nyt kertolaskut ei lopu koskaan, koska ei saada tulokseksi lukua 1
- 0.110 = 0.00011001100110011001100110011001100110011… 2
- Kertolasku lopetetaan ja binääriluvun desimaaliosa katkaistaan tallennusta varten
Reaaliluvun muuntaminen binääriseksi
Binääriluvun muuntaminen reaaliluvuksi
Paikan indeksi: 2 1 0 -1 -2 -3
Vastaava merkki: 1 1 0 . 0 1 1110.0112
= 1 × 22 + 1 × 21 + 0 × 20 + 0 × 2-1 + 1 × 2-2 + 1 × 2-3
= 4 + 2 + 0 + 0 + 1/4 + 1/8
= 63/8 = 6.37510
Reaalilukujen huomioiminen ohjelmoinnissa
C#:n double ja 0.1
Reaalilukujen esittäminen liukulukuina
IEEE Standard for Floating-Point Arithmetic (IEEE 754)

Reaaliluvun muunnos liukuluvuksi
Reaaliluvun muunnos binääriluvuksi
Olkoon meillä luku 0.1562510, muunnetaan se ensin binääriluvuksi
- .15625 × 2 = 0.3125 (pienempi kuin yksi → 0)
- .3125 × 2 = 0.625 (pienempi kuin yksi → 0)
- .625 × 2 = 1.25 (suurempi kuin yksi → 1)
- .25 × 2 = 0.5 (pienempi kuin yksi → 0)
- .0.5 × 2 = 1.0 (yhtäsuuri kuin yksi → 1)
- muunnos on valmis
- Desimaaliosan bitit saadaan siis laskemisjärjestyksessä ja ovat 00101
- Lopulta yhdistetään kokonaislukuosa ja desimaaliosa, eli saadaan
- 0.1562510 = 0.001012
- Sitten muunnetaan binääriluku liukuluvuksi
Binääriluvun muunnos liukuluvuksi
Normalisoidaan mantissa
0.001012 ⇒ 1.012 × 2-3
Eksponentti -3 biasoidaan lisäämällä siihen luku 127
-3 + 127 = 124
joka muutetaan etumerkittömäksi binääriluvuksi
124 ⇒ 01111100
32-bittinen Single precision -muoto:
00111110001000000000000000000000
Liukuluvun muunnos desimaaliluvuksi
001111100010000000000000000000002
Mantissan bitit desimaaliosaksi ja aina bitti 1 kokonaislukuosaksi
1.010000000000000000000002
Poistetaan eksponentin biasointi ja kerrotaan mantissa kannan eksponentilla
1.010000000000000000000002 × 2-3
Poistetaan normalisointi, liutetaan binääripistettä, jotta ekspontti menee nollaan
0.001010000000000000000002
Poistetaan ylimääräiset nollat
0.001012
Muunnetaan desimaaliluvuksi
0.001012 = 1 × 2-3 + 1 × 2-5 = 1/8 + 1/32 = 5/32 = 0.15625
Esimerkkejä
Merkistöt
ASCII
Unicode
- Standardi tekstin koodaamisesta binääriseksi
- Sisältää merkkien, kirjoitusjärjestelmien sekä symboleiden koodauksia
- Määrittelee niiden koodipisteden arvot
- Koodipisteiden arvojen muunnos binääriluvuiksi toteutetaan merkistökoodauksella
- Unicode määrittelee useita erilaisia merkistökoodausmenetelmiä, mm.
- UTF-8
- UTF-16
- UTF-32
UTF-8
Esimerkki
Tarkastellaan merkkiä ä.
ä (U+00E4) = 22810 = 111001002
kun binääriluku tallennetaan UTF-8 muotoon, niin se asetetaan tavuihin
11000011 10100100
UTF-8 vs UTF-16
Koodipistettä vastaava symboli tulostettuna
HTML ja Unicode
Byte order mark
- Unicode-merkki
U+FEFF, jota voidaan käyttää tekstitiedoston alussa - Voidaan käyttää sekä UTF-8, UTF-16 ja UTF-32 yhteydessä
- Ilmaisee esimerkiksi sen onko tavu little endian vai big endian muodossa
- UTF-8 merkistökoodauksen tavujen tunnistebiteistä voidaan päätellä endianness
- Usein UTF-8 merkistökoodausta käytettäessä ei tarvita BOM-merkkiä
- Kuitenkin, suurin osa Microsoftin kääntäjistä ja sovelluksista pitää BOM-merkkiä vaadittuna 'taikanumerona'.
- Lisäävät BOM-merkin aina kun tallentavat UTF-8 muodossa
- Ja eivät osaa tulkita UTF-8 ilman BOM-merkkiä
En ole varma menikö nämä oikein, mutta ainakin “Pisteet 0.1” näyttäisi olevan tekstiboxissa. Points: “0/0.1” näkyy kuitenkin pisteissä. Pitikö näistä kahdesta tehtävästä tulla pisteet normaalisti?
—No pitäisi, oli näköjään määritelty vääränlainen piste-funktio. Nyt antaa pisteet molemmat
—Merkistökoodausesimerkki HTML-tiedostolla
- Notepad++ ohjelmalla tallennettu ANSI merkistökoodauksella
- Notepad++ ohjelmalla tallennettu UTF-8 merkistökoodauksella
- Notepad++ ohjelmalla tallennettu ANSI merkistökoodauksella
- ja tiedostoon on lisätty HTML tagi
<meta charset="UTF-8">
- ja tiedostoon on lisätty HTML tagi
- Notepad++ ohjelmalla tallennettu UTF-8 merkistökoodauksella
- ja tiedostoon on lisätty HTML tagi
<meta charset="UTF-8">
- ja tiedostoon on lisätty HTML tagi
Loogiset portit ja funktiot
AND totuustaulu
| A | B | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
OR totuustaulu
| A | B | OR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
XOR totuustaulu
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOT totuustaulu
| A | NOT |
|---|---|
| 0 | 1 |
| 1 | 0 |
Loogisten porttien piirrossymbolit
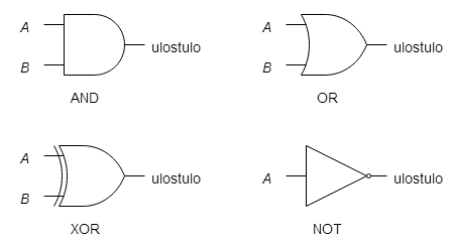
Loogiset portit piirikaaviosimulaattorissa
Transistori kytkimenä
- http://lushprojects.com/circuitjs/circuitjs.html
- Valitse yläreunan menusta Circuits → Transistors → Switch.
Universaali looginen portti
NAND totuustaulu
| A | B | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
NOR totuustaulu
| A | B | NOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
XNOR totuustaulu
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
NAND, NOR ja XNOR piirikaavioeditorissa
Toteuta NOT-funktio NAND-porteilla
Loogiset portit mikropiireinä

Loogiset portit laitteistokuvauskielellä
- Nand2Tetris
- Tehdään käyttäen Nand2Tetris ohjelmistopakettia
- Apuna kannattaa käyttää sivustolla tarjolla olevia kirjan lukuja ja muita materiaaleja
Boolen algebra
| Sanallinen | Matemaattinen | Looginen | Vanha matemaattinen |
|---|---|---|---|
| NOT |
|||
Boolen algebran säännöt
Laskujärjestys
- Ensin NOT, sitten AND, sitten OR
- Suluilla voi vaihtaa järjestystä
Liitännäisyys eli assosiatiivisuus
a + (b + c) = (a + b) + c
a • (b • c) = (a • b) • c
Osittelulaki eli distributiivisuus
a • (b + c) = (a • b) + (a • c)
a + (b • c) = (a + b) • (a + c)
Vaihdannaisuus eli kommutatiivisuus
a + b = b + a
a • b = b • a
De Morganin teoreemat
De Morganin NAND-teoreema
a • b = a + b
De Morganin NOR-teoreema
a + b = a • b
Boolen algebran lakeja ja sääntöjä
Idempotent eli "itseään operoimisen" -laki
a • a = a
a + a = a
Identity eli identiteettilaki
a • 1 = a
a + 0 = a
Annulment eli kumoamislaki
a • 0 = 0
a + 1 = 1
Complement eli komplementtilaki
a • a = 0
a + a = 1
Double Negation eli kaksoisnegaatiolaki
a = a
Absorption eli absorptiolaki
a + (a • b) = a
a • (a + b) = a
Absorption with negation eli absorptiolaki negatoinnilla
a + a • b = a + b
a + a • b = a + b
Liitännäisyys
a + (b + c) = (a + b) + c
a • (b • c) = (a • b) • c
Osittelulaki
a • (b + c)
= (a • b) + (a • c)
a + (b • c)
= (a + b) • (a + c)
Vaihdannaisuus
a + b = b + a
a • b = b • a
De Morganin teoreema
a • b = a + b (NAND)
a + b = a • b (NOR)
Boolen algebran lakeja
1) a • a = a 2) a + a = a
3) a • 1 = a 4) a + 1 = 1
5) a • 0 = 0 6) a + 0 = a
7) a • a = 0 8) a + a = 1
9) a = a (kaksoisnegaatio)
10) a + a • b = a + b
11) a + a • b = a + b
— Boolen lausekkeen muodostaminen totuustaulusta
| A | B | XOR |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Tulojen summamuoto (Sum of Products - SOP)
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ||||
| 0 | 1 | 1 | ⇒ | |
||
| 1 | 0 | 1 | ⇒ | |
||
| 1 | 1 | 0 |
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Yleisesti SOP muoto saadaan totuustaulusta seuraavasti
- etsi rivit, joissa ulostulona on 1
- muodosta tulo rivin muuttujista, tai muuttujan negaatiosta, jos muuttuja on 0
- muodosta summa tulotermeistä
Muuttujien ja termien määrä voi olla mielivaltainen, eikä siis rajoitettu kahteen, kuten käsitellyissä esimerkeissä.
Summien tulomuoto (Product of Sums - POS)
| A | B | XOR | ||||
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | ⇒ | |
||
| 0 | 1 | 1 | ||||
| 1 | 0 | 1 | ||||
| 1 | 1 | 0 | ⇒ | |
| A | B | XNOR |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Yleisesti POS-muoto totuustaulusta saadaan seuraavasti
- etsi rivit, joissa ulostulona on 0
- summaa rivin muuttujat, tai muuttujan negaatio, jos muuttujan arvo on 1
- muodosta tulo summatermeistä
Muuttujien ja termien määrä voi olla mielivaltainen, eikä siis rajoitettu kahteen, kuten käsitellyissä esimerkeissä.
Muunnos SOP-muodosta NAND-muotoon
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
Muunnos POS-muodosta NOR-muotoon
Boolen funktioiden sieventäminen
| A | B | C | LED |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 0 |
Algebrallinen sieventäminen
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
NAND muotoon sieventäminen
Liitännäisyys a + (b + c) = (a + b) + c a • (b • c) = (a • b) • c Osittelulaki a • (b + c) = (a • b) + (a • c) a + (b • c) = (a + b) • (a + c) Vaihdannaisuus a + b = b + a a • b = b • a De Morganin teoreemaa • b=a+b(NAND)a + b=a•b(NOR) Boolen lakeja ja sääntöjä 1) a • a = a 2) a + a = a 3) a • 1 = a 4) a + 1 = 1 5) a • 0 = 0 6) a + 0 = a 7) a •a= 0 8) a +a= 1 9)a= a (kaksoisnegaatio) 10) a +a• b = a + b 11)a+ a • b =a+ b
—
Karnaughin kartta
Karnaughin kartasta SOP-muotoinen sievennetty lauseke


Kuvan eri värisistä alueista saadaan siis sievennetyt SOP-termit
| Väri | termi |
|---|---|
| oranssi | |
| sininen | |
| vihreä |
sievennetty SOP-muotoinen lauseke saadaan summaamalla termit
Karnaughin kartasta POS-muotoinen sievennetty lauseke

Kuvan eri värisistä alueista saadaan siis sievennetyt POS-termit
| Väri | termi |
|---|---|
| oranssi | |
| sininen | |
| vihreä |
ja sievennetty POS-muotoinen lauseke saadaan kertomalla termit
Kombinaatiologiikka
Puolisummain
1 c
0 0 1 1 a
+ 0 + 1 + 0 + 1 + b
00 01 01 10 cs
| a | b | c | s | |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | |
| 0 | 1 | 0 | 1 | |
| 1 | 0 | 0 | 1 | |
| 1 | 1 | 1 | 0 |
Kokosummain
0000001001111111c[2]c[1]c[0]0000101001011111a[1]a[0]+00+10+00+10+01+11+01+11+b[1]b[0]000010010100010100100110c[2]s[1]s[0]
| cin | a | b | cout | s | |
|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | |
| 0 | 0 | 1 | 0 | 1 | |
| 0 | 1 | 0 | 0 | 1 | |
| 0 | 1 | 1 | 1 | 0 | |
| 1 | 0 | 0 | 0 | 1 | |
| 1 | 0 | 1 | 1 | 0 | |
| 1 | 1 | 0 | 1 | 0 | |
| 1 | 1 | 1 | 1 | 1 |
Tulovalitsin
| sel | out |
|---|---|
| 0 | A |
| 1 | B |
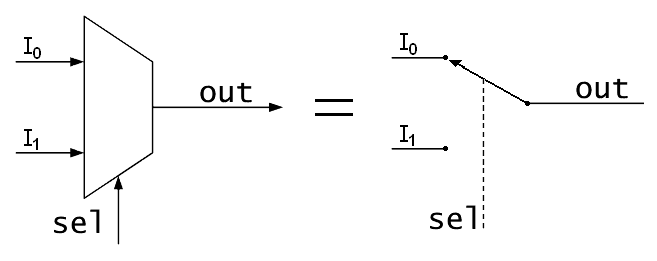
| A | B | sel | LED |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Enemmän kuin kaksi sisäänmenoa tulovalitsimeen
| sel[1] | sel[0] | out |
|---|---|---|
| 0 | 0 | A |
| 0 | 1 | B |
| 1 | 0 | C |
| 1 | 1 | D |
| sel[2] | sel[1] | sel[0] | out |
|---|---|---|---|
| 0 | 0 | 0 | A |
| 0 | 0 | 1 | B |
| 0 | 1 | 0 | C |
| 0 | 1 | 1 | D |
| 1 | 0 | 0 | E |
| 1 | 0 | 1 | F |
| 1 | 1 | 0 | G |
| 1 | 1 | 1 | H |
Lähtövalitsin
| sel | a | b |
|---|---|---|
| 0 | in | 0 |
| 1 | 0 | in |

Esimerkki lähtövalitsimesta
| a | sel | Keltainen | Sininen |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
Enemmän kuin kaksi ulostuloa lähtövalitsimesta
| sel[1] | sel[0] | a | b | c | d |
|---|---|---|---|---|---|
| 0 | 0 | in | 0 | 0 | 0 |
| 0 | 1 | 0 | in | 0 | 0 |
| 1 | 0 | 0 | 0 | in | 0 |
| 1 | 1 | 0 | 0 | 0 | in |
| sel[2] | sel[1] | sel[0] | a | b | c | d | e | f | g | h |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | in | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | in | 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | in | 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 | in | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | in | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | in | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | in | 0 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | in |
Aritmeettislooginen yksikkö

ALU:n suunnittelu
- Ihan ensin päätetään arkkitehtuurin bittimäärä
- eli sanan leveys
- meidän tapauksessa 16-bittinen arkkitehtuuri
- Mietitään funktiot jotka ALUn halutaan toteuttavan
- AND ja OR operaatio?
- Yhteen- ja vähennyslasku?
- Rautatoteutus kaikille halutuille funktioille?
- Mooren laki
- Komponenttien toteuttaminen raudalle maksaa (transistoreita)
- Voidaanko yksinkertaistaa?
- Mitä toteutetaan laitteistolla, mitä ohjelmistolla?
- Mietitään miten ALU:lle annetaan käskyt funktioiden toteuttamiseksi
- Määritellään sisääntulosignaalit
- ohjaus- ja datasignaalit
- Määritellään sisääntulosignaalit
HACK-tietokoneen prosessorin ALU:n suunnittelu
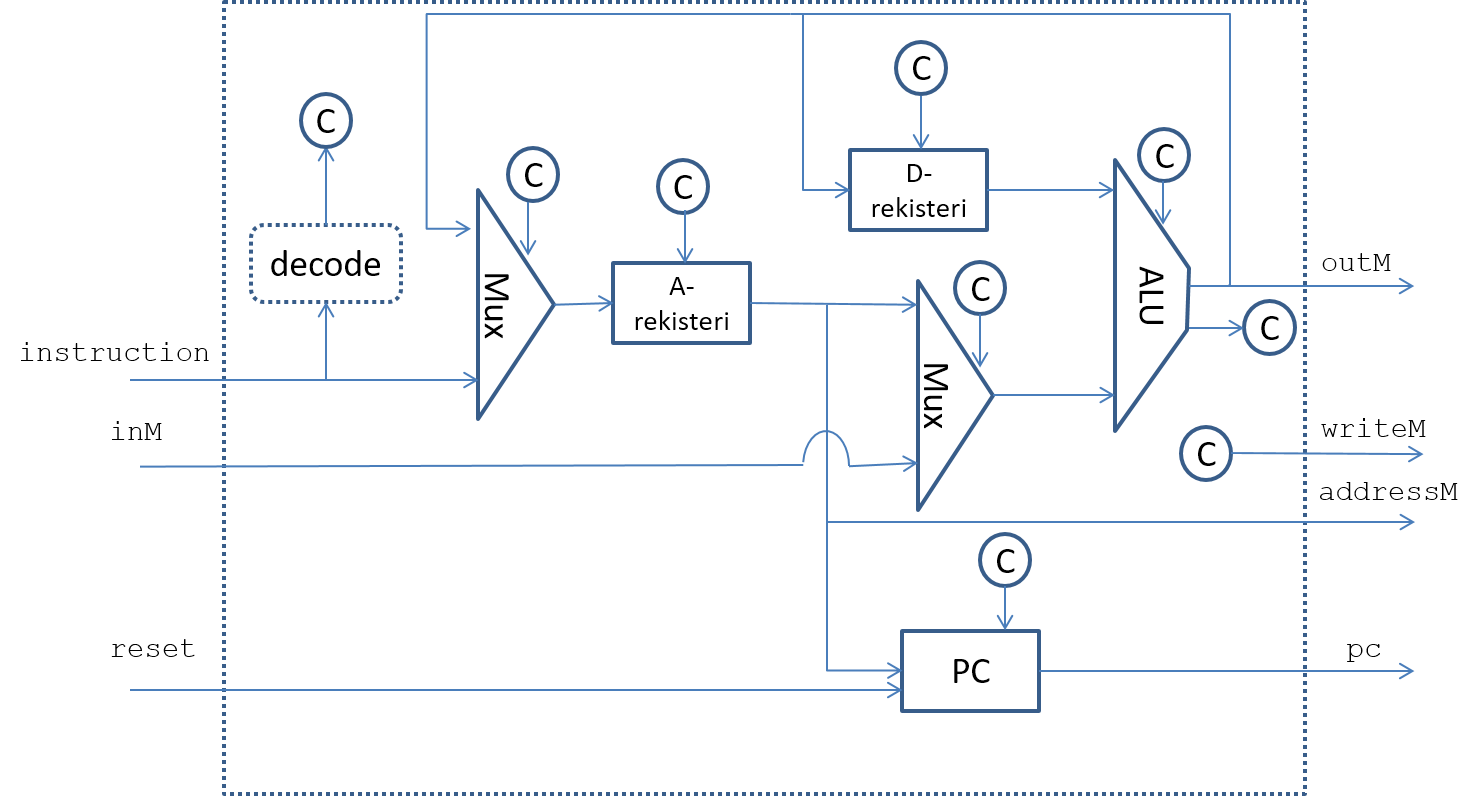
ALU:n ohjaussignaalit
- yksi negatoi ALU:n x-sisäänmenon (operandin),
- yksi nollaa ALU:n x-sisäänmenon (operandin),
- yksi negatoi ALU:n y-sisäänmenon (operandin),
- yksi nollaa ALU:n y-sisäänmenon (operandin),
- yksi negatoi ALU:n ulostulon,
- yksi valitsee suoritetaanko AND- vai ADD-operaatio, toisin sanoen ohjataanko ALU:n ulostuloksi yhteenlasku- vai AND-piirin ulostulo.
ALU:n OR-funktion toteutus
Tutkitaanpa ALU:n totuustaulun OR-funktiota vastaavaa riviä.
zx nx zy ny f no out 0 1 0 1 0 1 x|y
Rivin mukaan OR-funktio saadaan negatoimalla x-sisäänmeno (nx = 1), negatoimalla y-sisäänmeno (ny = 1), muodostamalla niiden AND-operaatio (f = 0) sekä negatoimalla ulostulo (no = 1). Kuvaus tuo varmaan mieleen De Morganin -teoreemat, De Morganin NOR -teoreeman oikeapuoli vastaa melkein kuvausta. Lisäämällä oikealle (ja vasemmalle) puolelle ulostulon negatoinnin, saadaan
ja kaksoisnegaatiosäännön mukaan
eli ALU:n OR-funktio toteutetaan soveltamalla De Morganin NOR -teoreemaa.
ALU:n vähennyslaskun toteutus
zx nx zy ny f no out 0 1 0 0 1 1 x-y
- Positiivisilla luvuilla
- 7 – 5 = 2
- -(-7 - -5) = -(-2)
- -(-7 + 5) = -(-2) = 2
- Vastaavasti negatiivisella luvulla
- −8 – 4 = −12
- −(+8 + 4)= −(12) = −12
Tässä siis sulkujen ulkopuolella oleva miinusmerkki vastaa ALU:n ulostulon negatoimista, ja ensimmäisen luvun edessä olevan etumerkin vaihtaminen ALU:n x-sisäänmenon negatointia. Toisin sanoen
- Muutetaan ensimmäinen termin merkkiä (negatoidaan)
- Muutetaan vähennyslasku yhteenlaskuksi
- Muutetaan lopputuloksen merkkiä (negatoidaan)
Eli ALU:n pitää vähennyslaskun toteuttamiseksi
- muuttaa
:n merkkiä
- käyttää yhteenlaskupiiriä
- muuttaa ulostulon merkkiä
Esim.
negatoidaan ensimmäinen luku ja vaihdetaan vähennyslasku yhteenlaskuksi
input _______________ output
7 00000111 -----> | 11111000 |
- 5 - 00000101 -----> | + 00000101 |
---- ---------- | ---------- |
2 | 11111101 | -----> 00000010 (tämä on +2)
---------------
negatoidaan lopputulos
Esim.
negatoidaan ensimmäinen luku ja vaihdetaan vähennyslasku yhteenlaskuksi
input _______________ output
-8 11111000 -----> | 00000111 |
- 4 - 00000100 -----> | + 00000100 |
---- ---------- | ---------- |
-12 | 00001011 | -----> 11110100 (tämä on -12)
---------------
negatoidaan lopputulos
ALU voidaan siis toteuttaa yhteenlaskupiirillä sekä AND -piirillä ja lisäksi pitää valita miten operandeja sekä ulostuloa käsitellään, eli
zxjanxohjaa multiplekseriä- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
- x, negatoitu x, 0 tai negatoitu 0
- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
zyjanyohjaa multiplekseriä- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
- y, negatoitu y, 0 tai negatoitu 0
- valitaan yhteenlasku ja AND-piirien toinen sisäänmeno
fohjaa multipekseriä,- jonka sisäänmenoina on yhteenlasku sekä AND -piirien ulostulot.
noohjaa multiplekseriä,- jonka sisäänmenoina on edellisen multiplekserin ulostulo ja sen negaatio
- edellisen multiplekserin ulostulo on ALU:n ulostulo
zrjangulostulot saadaan tutkimalla ALU:n ulostuloa
Sekvenssilogiikka
Set-Reset -Kiikku
| S | R | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | Q | pidä tila |
| 0 | 1 | 0 | resetoi |
| 1 | 0 | 1 | aseta |
| 1 | 1 | X | ei sallittu |
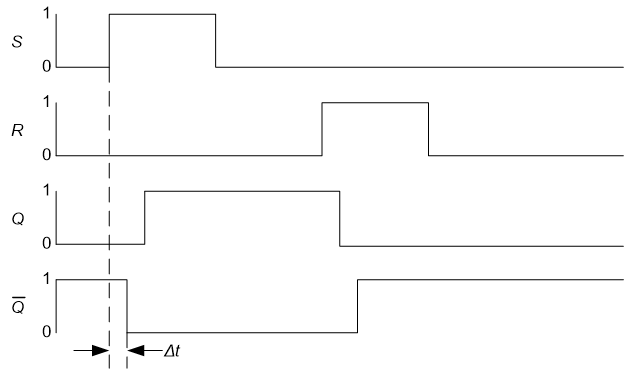
| Qnext | toiminta | ||
|---|---|---|---|
| 0 | 0 | X | ei sallittu |
| 0 | 1 | 1 | resetoi |
| 1 | 0 | 0 | aseta |
| 1 | 1 | Q | pidä tila |
D-Kiikku
| Q | D | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | 0 | resetoi |
| 0 | 1 | 1 | aseta |
| 1 | 0 | 0 | resetoi |
| 1 | 1 | 1 | aseta |
T-kiikku
| T | Q | Qnext | toiminta |
|---|---|---|---|
| 0 | 0 | 0 | pidä tila |
| 0 | 1 | 1 | pidä tila |
| 1 | 0 | 1 | vaihda tila |
| 1 | 1 | 0 | vaihda tila |
J-K -kiikku
Laskurit
Muistit
- Random Access Memory (RAM)
- tarvitsevat virtaa säilyttääksen muistinsa
- Static RAM
- Dynamic RAM
- pitää virkistää säännöllisesti virran saannin lisäksi
- Read Only Memery (ROM)
- Programmable PROM
- Erasable Programmable EPROM
- Electrically Erasable Programmable EEPROM
- Flash muistit
- Toteutus NAND- tai NOR-porteilla
- Flash muistit
Muistirekisteri
Muistikomponentit
Ohjelmalaskuri
Tietokoneen arkkitehtuuri
- Tietokoneen arkkitehtuuri
- ominaisuudet, jotka ovat ohjelmoijan nähtävissä
- Tietokoneen organisaatio
- komponentit, jotka toteuttavat arkkitehtuurin ominaisuudet
Tietokoneen rakenne
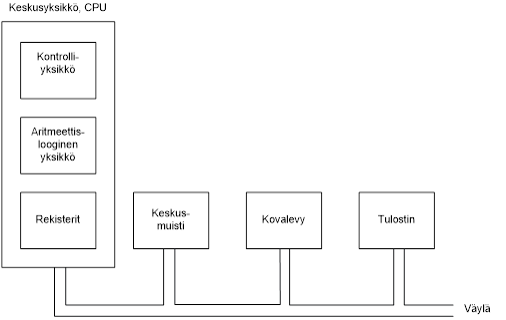
Prosessorin yhteydet
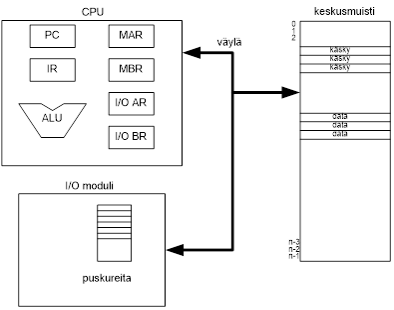
Tietokoneen ja ohjelmiston yleinen rakenne
| Korkeantason kieli |
| Virtual machine |
| Assembly kieli |
| Konekieli |
| Tietokonealusta |
| Loogiset piirit |
Tietokoneen ja ohjelmiston yleinen rakenne
- Loogisilla piireillä ja komponenteilla rakennetaan prosessori ja muistit
- Prosessorin rakenne määrää sen minkälaisia käskyjä sille voidaan antaa -> käskykanta (Instruction set)
- Konekieli on joukko binäärisiä ”sanoja” jotka vastaavat prosessorin käskyjä
- Assembly kieli antaa binäärisille bittijoukoille paremmin muistettavat vastineet, esimerkiksi HACK-assembly -kielessä:
- 1111110111001000
- M=M-1
- Jokaiselle prosessorityypille on oma konekieli ja siten myös assembly kieli
Tietokoneen toiminta

HACK-tietokoneen rakenne
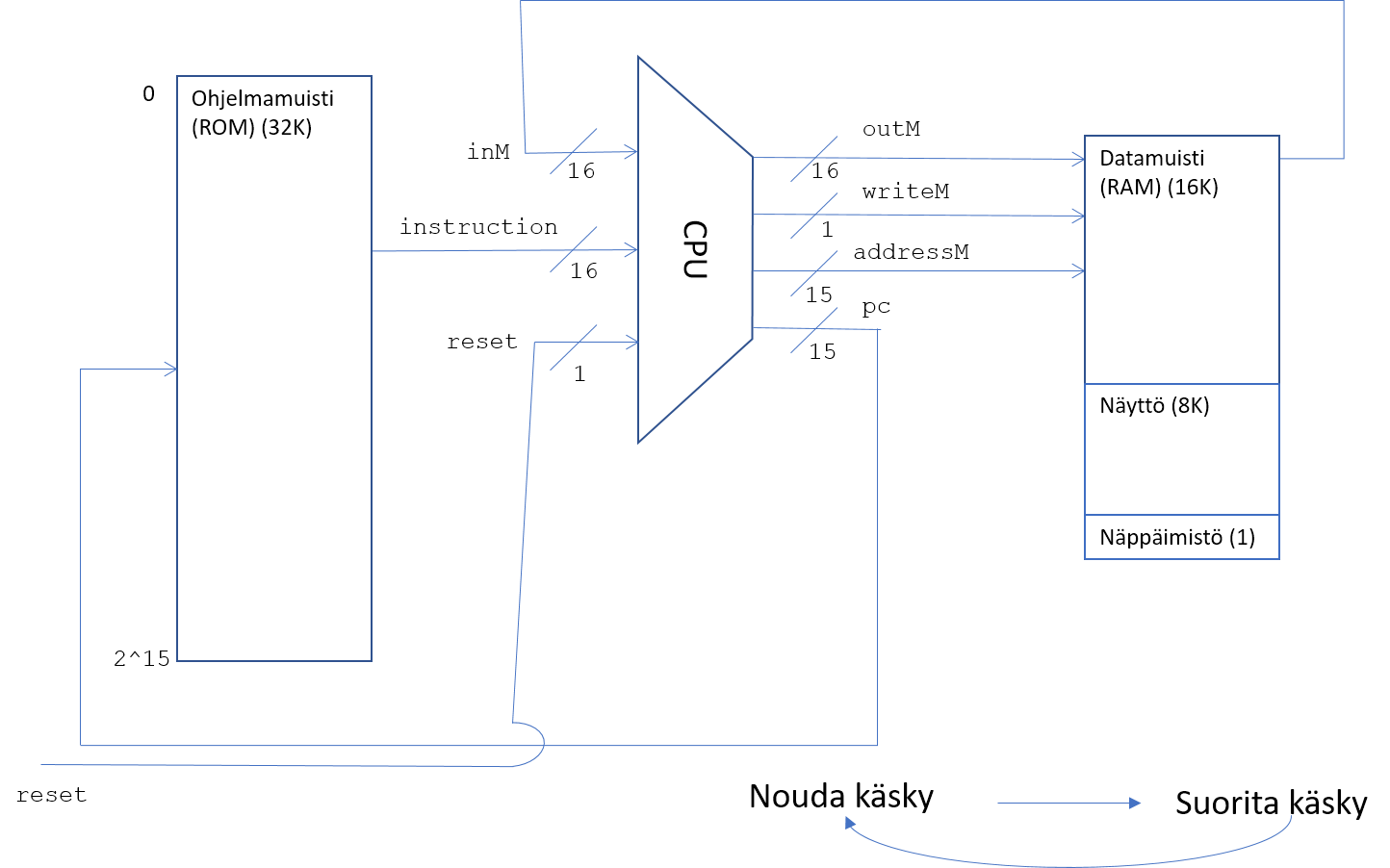
HACK tietokoneen muisti
- ROM muisti, ladataan konekielinen ohjelma
- RAM muisti, käytetään ohjelman parametrien tallentamiseen
- I/O laitteet, näyttö ja näppis
- Memory-mapped I/O
- I/O laitteet kytketty samaan väylään kuin muisti
- Laitteilla oma "muistiosoite"
- HACK-tietokoneessa RAM muistin jatkeena
HACK-prosessori

HACK-tietokoneen toiminta
- HACK tietokone
- Hae A-käsky
- Suorita A-Käsky
- Hae C-käsky
- Suorita C-Käsky
- Toista alusta
- ’Normaali’ –tietokone
- Hae käsky
- Suorita käsky
- Toista alusta
Esimerkkiohjelma
// C# koodia
// Adds 1+...+5.
int i = 1;
int sum = 0;
while (i <= 5) {
sum += i;
Console.WriteLine(sum);
i++;
}
// PSEUDO Assembly koodia
Alusta muuttujat i=1 ja sum=0 (varaa niille paikka muistista)
(LOOP)
Laske i-5
Jos ALU output > 0
niin indeksi liian suuri, hyppää LOPPU:un
muuten (ALU output <= 0)
kasvata summaa
kasvata indeksiä
hyppää LOOP:iin
(LOPPU)
Lopeta ohjelma
Esimerkin toteutus HACK-prosessorin assembly kielellä
// Hack assembly koodi @i // assembler -kääntäjää valitsee muistipaikan, jonne i tallennetaan M=1 // i=1 (sijoitetaan indeksin aloitusarvo yo. muistipaikkaan) @sum // assembler -kääntäjää valitsee muistipaikan, jonne sum tallennetaan M=0 // sum=0 (alustetaan summa nollaksi tallentamalla 0 sum -muuttujan muistipaikkaan) (LOOP) // määrittää hyppyosoitteen @i // Asetetaan A-rekisterin arvoksi i-muuttujan muistipaikan osoite D=M // D=M[i] haetaan lukuarvo RAM muistin (M) osoitteesta i, tallennetaan D-rekisteriin @5 // asetetaan A-rekisteriin arvo 5 D=D-A // D=i-5, vähennetään A-rekisterin arvo D-rekisterin arvosta, tallennetaan D-rekisteriin @END // asetetaan A rekisteriin mahdollinen hyppy osoite eli (END):iä seuraavan rivin osoite D;JGT // Jos D:narvo positiivinen, hypätään (END):iin muuten jatketaan seuraavalle riville @i // Asetetaan A-rekisteriin i:n osoite D=M // D=M[i] haetaan i:n arvo muistista osoitteesta M[i] ja tallennetaan D-rekisteriin @sum // asetetaan A-rekisterin arvoksi sum parametrin osoite M=D+M // sum=i+sum, haetaan muistista M[sum] arvo, lisätään D-rekisterin arvoon, tallennetaan muistiin @i // Asetetaan A rekisteriin i:n osoite M=M+1 // i=i+1, haetaan i:n arvo yo. osoitteesta, lisätään 1 ja tallennetaan samaan osoitteeseen @LOOP // asetetaan A-rekisteriin (LOOP):ia seuraavan rivin osoite (muistipaikka ROM muistissa) 0;JMP // Goto LOOP, lasketaan "nolla", ja riippumatta laskutoimituksen tuloksesta hypätään (LOOP):iin (END) // määrittää hyppyosoitteen @END // Kirjan tekijöiden tapa lopettaa ohjelman suoritus (menemällä ikuiseen silmukkaan lopuksi) 0;JMP // Infinite loop
HACK Assembly kielen käskyt
A-Instruction
@value- Missä
valueon ei-negatiivinen kokonaisluku - Binäärisenä:
0vvv vvvv vvvv vvvv - Käytetään lukuarvon tallentamiseen A-rekisteriin
- A-rekisterin arvoa voidaan käyttää kolmella eri tavalla
- Tallennetaan vakio arvo (
A = value) - Valitaan RAM muistipaikka (
register = RAM[A]) - Valitaan ROM muistin seuraava suoritettava käsky (muistipaikka) (
PC = A)
- Tallennetaan vakio arvo (
- A-käskyä täytyy seurata C-käsky, joka määrää mitä A-rekisteriin tallennetulla lukuarvolla tehdään
HACK Assembly kielen käskyt
C-Instruction
dest=comp;jumpcomp- Kertoo ALU:lle mikä operaatio suoritetaan
- Ja minkä rekisterin/muistipaikan arvoja käytetään operaatiossa
dest- Kertoo minne laskutoimituksen
comptulos tallennetaan
- Kertoo minne laskutoimituksen
jump- Kertoo millä ehdolla hypätään (ladataan ohjelmalaskurille uusi arvo)

Vertaa ALU:n toimintaan
Comp(ute) -käsky
(a=0) c1 c2 c3 c4 c5 c6 (a=1)
------ -- -- -- -- -- -- -----
0 1 0 1 0 1 0
1 1 1 1 1 1 1
-1 1 1 1 0 1 0
D 0 0 1 1 0 0
A 1 1 0 0 0 0 M
!D 0 0 1 1 0 1
!A 1 1 0 0 0 1 !M
-D 0 0 1 1 1 1
-A 1 1 0 0 1 1 -M
D+1 0 1 1 1 1 1
A+1 1 1 0 1 1 1 M+1
D-1 0 0 1 1 1 0
A-1 1 1 0 0 1 0 M-1
D+A 0 0 0 0 1 0 D+M
D-A 0 1 0 0 1 1 D-M
A-D 0 0 0 1 1 1 M-D
D&A 0 0 0 0 0 0 D&M
D|A 0 1 0 1 0 1 D|MDest(ination)
d1 d2 d3 Mnemonic Destination (minne tallennetaan)
0 0 0 null Operaation tulosta ei tallenneta
0 0 1 M Memory[A] (RAM muistipaikka A)
0 1 0 D D register
0 1 1 MD Memory[A] and D register
1 0 0 A A register
1 0 1 AM A register and Memory[A]
1 1 0 AD A register and D register
1 1 1 AMD A register, Memory[A], and D register
Hyppykäskyt
j1 j2 j3
(out < 0) (out = 0) (out > 0) Mnemonic Effect
0 0 0 null No jump
0 0 1 JGT If out > 0 jump
0 1 0 JEQ If out = 0 jump
0 1 1 JGE If out ≥ 0 jump
1 0 0 JLT If out < 0 jump
1 0 1 JNE If out ≠ 0 jump
1 1 0 JLE If out ≤ 0 jump
1 1 1 JMP Jump
Mnemonic ≈ muistisääntö (assembly kielinen toteutus)
HACK Assembly kielen käskyt
Esimerkki A-käskyn jälkeisistä C-käskyistä
@47// A=47D=A// D=47@47// A=47D=M// D=RAM[47]@47// A=470;JMP// Ladataan PC:lle uusi arvo (ROM muistin muistipaikka, josta ohjelman suoritusta jatketaan)
HACK Assembly kielen käskyt
Esimerkki A-käskyn jälkeisistä C-käskyistä
@47 // 0000000000101111
D=A // 111accccccdddjjj
@47 // 0000000000101111
D=M // 111accccccdddjjj
@47 // 0000000000101111
0;JMP // 111accccccdddjjj

HACK tietokoneen näppäimistö ja näyttö
- Normaalia RAM muistia 16K, osoitteet väliltä 0 - 16383
- 14-bittinen osoite, 214 osoitetta
- yhteen osoitteeseen voidaan tallentaa 16-bittinen sana
- Näyttö, osoitteet väliltä 16384 - 24575
- Mustavalkoinen näyttö, väri tallennetaan yhteen bittiin
- yksi muistipaikka 16-bittinen = 16 pikseliä
- 256 riviä, 512 pikseliä per rivi
- 256 * 512 * 1 = 131072 bittiä
- 131072/16 = 8192 (8k) muistipaikkaa
- Ei voida lukea, muistipaikkaan kirjoittamalla valitaan väri
- Näppäimistön muistiosoite 24576
- Voidaan lukea mitä näppäintä on painettu, ei voi kirjoittaa
Esimerkkiohjelmia näppäimistön ja näytön käytöstä
WHILE logiikka
// while condition // while (10 - y < 0) { while (y < 10) { code block 1 // esim. y++ } code block 2
(LOOP) // D = 10 - y tai D = y - 10 D // not condition // tallennetaan D:hen False // ehto, jolla hypätään @END D;JEQ // D ≠ 0 code block 1 //y++ etc. @LOOP 0;JMP (END) // D = 0 eli false code block 2
IF logiikka
// if condition if (x != 0) { code block 1 } else { // x == 0 code block 2 } code block 3
D // negatoitu ehto (not x) // D = !x // jos x == 0 -> D == !x == -1 (bin) // jos x == -1 -> D == !x == 0 (bin) @IF_TRUE D;JEQ // if D == 0 then jmp // else x == 0 (D ≠ 0) code block 2 @END 0;JMP (IF_TRUE) // (x != 0) code block 1 (END) code block 3
Aliohjelmakutsu
Code block 1Draw_letter(A);Code block 2Draw_letter(A);Code block 4... void Draw_letter(Char x) {Code block 3} // minne? miten palataan?
Code block 1 Assemblynä
// paluuosoite aliohjelmasta, joka tallennetaan takaisin –muuttujaan
@PALUUOSOITE
D=A
@takaisin
M=D
@DRAW_LETTER
0;JMP
(PALUUOSOITE) // tänne
Code block 2 Assemblynä
@PALUUOSOITE2
D=A
@takaisin
M=D
@DRAW_LETTER
0;JMP
(PALUUOSOITE2) // vai tänne
Code block 4 Assemblynä
// jossain ROM muistissa (DRAW_LETTER) Code block 3 Assemblynä @takaisin // paluuosoite A=M // RAM muistista 0;JMP
HACK-tietokoneen ja -prosessorin toteutus
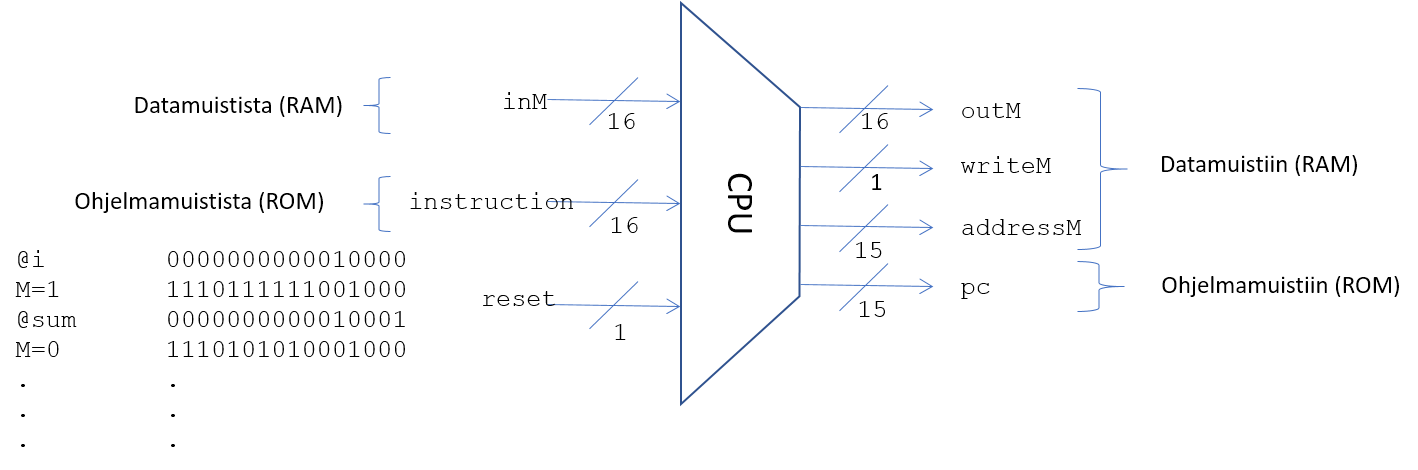

HACK-prosessorin toimintalogiikka
- Tulkitaan käsky
instruction[16]- Jos A-käsky, niin
- Viedään
instruction[16]A-rekisteriin
- Viedään
- Jos C-käsky, niin selvitetään biteistä
- ALU:lle komento
- Rekisterien/muistin sisällön vienti ALU:lle
- ALU:n ulostulon tulkinta ja tallennus (rekisteriin/muistiin)
- Hyppyehdon täyttyminen?
- Asetetaan A-rekisterin arvo
PC:n uudeksi arvoksi - Jos ei hypätä niin
PC = PC + 1
- Asetetaan A-rekisterin arvo
- Jos A-käsky, niin
- Käskyn suorituksen jälkeen noudetaan
PC:n osoittama seuraava käsky
C-käsky binäärisenä


PC-Tietokone vs. HACK-tietokone
Välimuisti
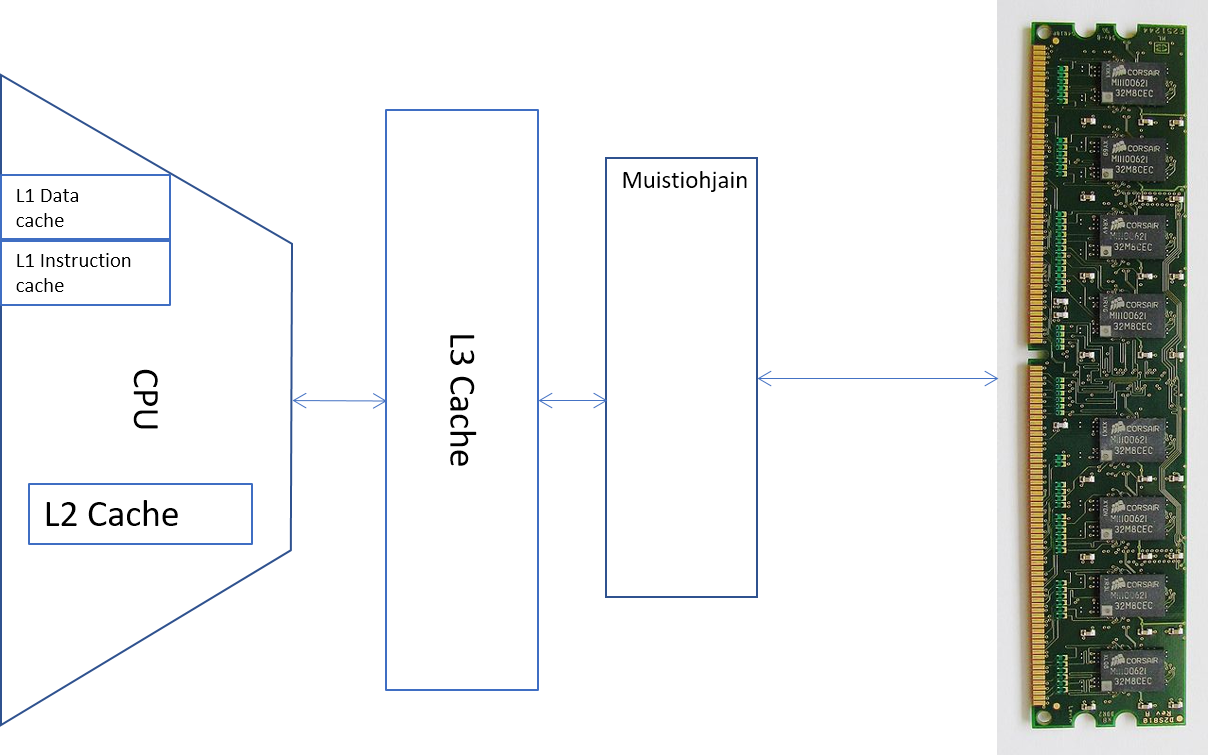
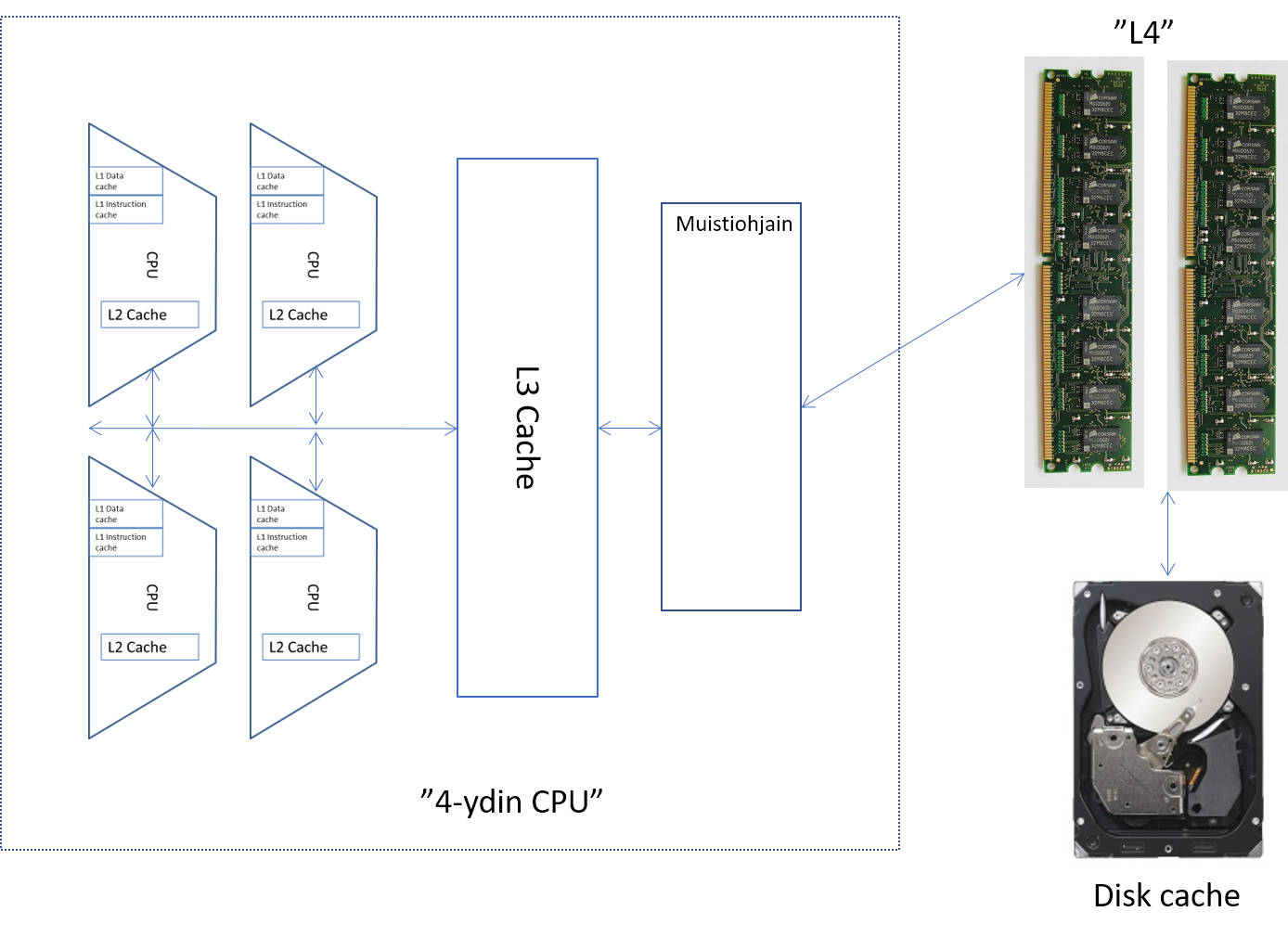
Moniydinprosessorit
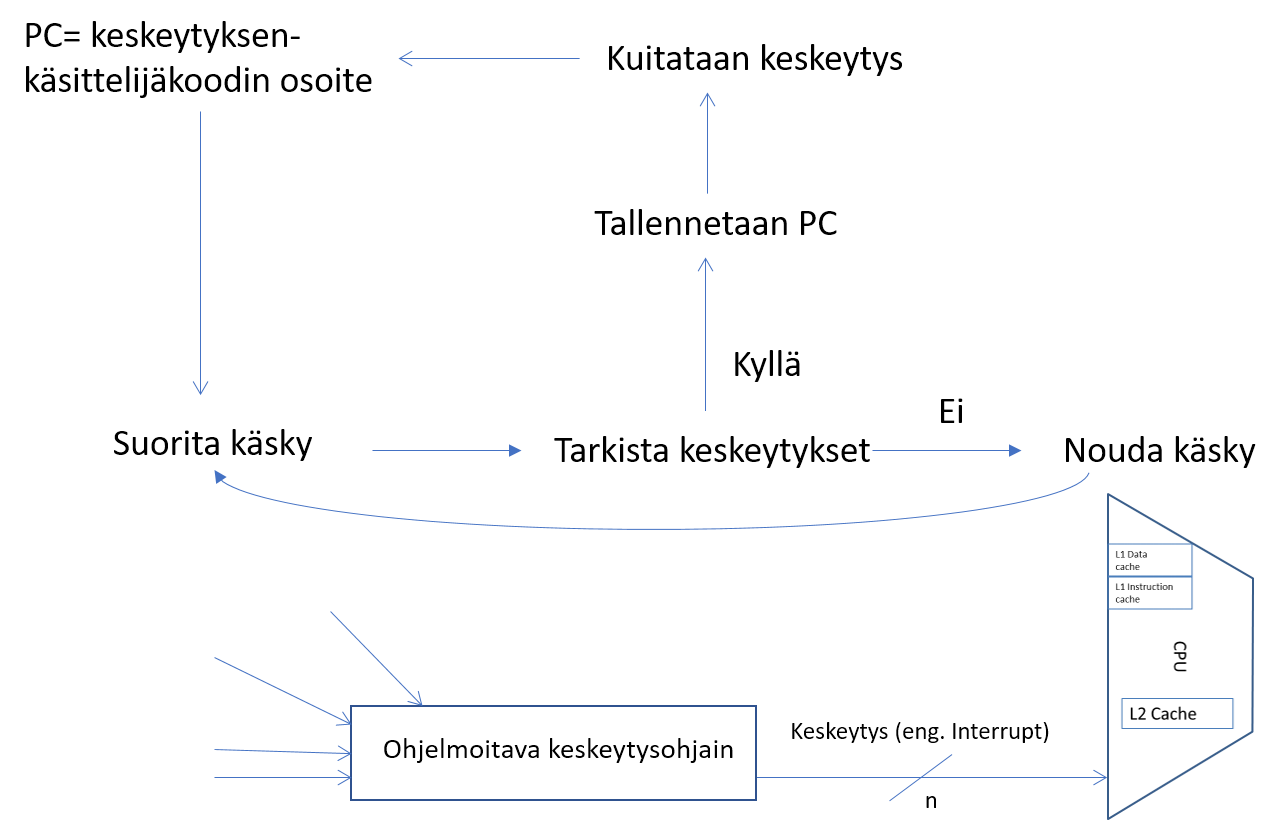
Keskeytykset
x86 Assembly
- Assembly kieli, josta on kehittynyt nykyisten ’Intel-arkkitehtuuri’ –prosessorien assembly kielet
- Kehitetty alkujaan 16-bittisen Intel 8086 prosessorin kanssa
- Add5.c nykyisellä x86-64 assemblyllä
Muistien toteutus
SRAM

DRAM
Flash muisti NAND tekniikalla
- SSD-levyt, muistitikut, ...
- muistisolu vie vähemmän tilaa
- suurempi tallennuskapasiteetti
- vähemmän virtaa per bitti
- ei voida lukea tavu kerrallaan
- Nopeampi kirjoittaa
- vähemmän virtaa aktiivisena
Flash muisti NOR tekniikalla
- Ohjelmoitavat ROM-muistit
- Prosessorien ja mikrokontrollereiden käyttöön
- Nopeampi lukea
- Vähemmän virtaa stand-by tilassa
Esimerkki kertolaskun toteutuksesta
Kertolaskun säännöt
0 0 1 1
x 0 x 1 x 0 x 1
0 0 0 1
Esim.
10 ab
x 11 x cd
10 ad bd (a AND d) (b AND d)
+ 10 + ac bc (a AND c) (b AND c)
110
Esim.
010 abc
x 111 x def
010 af bf cf (a AND f) (b AND f) (c AND f)
010 ae be ce (a AND e) (b AND e) (c AND e)
+ 010 + ad bd cd (a AND d) (b AND d) (c AND d)
01110
Assembler
- Assembler on ohjelma, joka kääntää Assembly kielisen ohjelman konekielelle
- Konekieli on joukko binäärisiä ”sanoja” jotka vastaavat prosessorin käskyjä
- Assembly kieli antaa binäärisille bittijoukoille paremmin muistettavat vastineet, esim.
- 1111110111001000
- M=M-1
- Jokaiselle prosessorityypille on oma konekieli ja siten myös assembly kieli
Toimintalogiikka
- Toista, kunnes
.asmtiedoston EOF- Lue seuraava Assembly kielinen komento
- Paloittele komento osiin
- Hae osia vastaava binäärikoodi
- Yhdistä koodit yhdeksi 16-bittiseksi konekieliseksi käskyksi
- Anna ulostulona konekielinen koodi
- kirjoita
.hacktiedostoon uusi rivi
- kirjoita
Toiminta ilman symboleita
- Jos tyhjä rivi tai kommentti → ei tehdä mitään
- Jos alkaa @ -merkillä, niin A-käsky
- Esim. String
@9→ pitää muuttaa String:iksi0000000000001001
- Esim. String
- Jos ei, niin tutkitaan löytyykö riviltä
=-merkkiä ja;-merkkiä,- jotta saadaan selville mitkä
dest=comp;jump-osat käskyssä on - Selvitetään
destosaa vastaava binääriluku - Selvitetään
composaa vastaava binääriluku - Selvitetään
jumposaa vastaava binääriluku - Kasataan 16-bittinen konekielinen C-käsky yhdistämällä osat
- jotta saadaan selville mitkä
- Voidaan olettaa että kommentit alkavat aina rivin alusta ja rivien lopussa ei ole kommentteja
HACK assembly -kielen symbolit
- Käydään koodi läpi etsimällä symbolit, esim.
@sumtai@LOOPtai(LOOP)- Lisäksi riveiltä poistetaan kaikki kommentit ja kommenttien jälkeiset merkit, jos niitä on, esim.
D=M // D = first number
- Kahdenlaisia symboleita
- Muuttujia, joille pitää varata muistiosoite, esimerkiksi
@sum - Osoitteita joihin pitää hypätä, eli jossain on sama symboli kaarisuluissa
- Esimerkiksi @LOOP ja
(LOOP) - rivinumero tulee selvittää, jotta saadaan hyppypaikka
- Esimerkiksi @LOOP ja
- Muuttujia, joille pitää varata muistiosoite, esimerkiksi
Toiminta symboleiden kanssa
- Ensin käydään läpi se, löytyykö symbolia vastaava hyppypaikka eli symboli suluissa, esim.
(LOOP)- Löytyykö sulkuja? Jos löytyy, lisää suluissa oleva symbolitaulukkoon ja tallenna sulku-rivin alapuolisen rivin numero vastaamaan symbolia
- Sen jälkeen käydään koodi uudestaan läpi, etsien symboleita, esim.
@sumtai@LOOP- Jos symbolitaulukossa, niin se on hyppy-symboli
- Jos symbolia ei taulukossa, kyseessä on muuttuja, jolle pitää varata paikka RAM muistista (aloitetaan muistipaikasta 16)
- Symbolitaulukon toteutus esim. Javan hashtable:lla
- Lisäksi taulussa pitää olla muutama etukäteen määritelty symboli, jotka pitää muuttaa RAM osoitteiksi, esim.
SCREEN - Kun taulu valmis korvataan Assembly koodin symbolit niitä vastaavilla osoitteilla
Assemblerin toteutus
- Millä tahansa ohjelmointikielellä
- Suositeltava arkkitehtuuri
- Parser moduuli: purkaa käskyt osiin
- Code moduuli: kääntää osat binääriseksi
- SymbolTable moduuli: hallinnoi symbolitaulua
- Main moduuli: tiedoston luku/kirjoitus, käyttää yo. moduuleja ulostulon rakentamiseen
- Testaa Assembleriasi testiohjelmilla (add.asm etc.)
- Versiot ilman symboleita tai symboleiden kanssa
- Lopuksi voit verrata Assembler-simulaattorilla simulaattorin kääntämää koodia sinun Assemblerin kääntämään koodiin
Kurssin luennot loppui
- Tehkää ahkerasti tehtäviä!
- Labraohjauksia tulee tarpeen mukaan myös ensi vuonna!
- Hyvää joulua kaikille!
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.