Jeder Sachverständige wird bestätigen, dass man selbst die Grundlagen der wissenschaftlichen Naturerklärung nur verstehen kann, wenn man wenigstens die Anfangsgründe der Differential- und Integralrechnung sowie der analytischen Geometrie, also den sogenannten niederen Teil der höheren Mathematik, kennt.

Jokainen asiantuntija vahvistaa, että tieteellisen luonnon selittämisen perusteet voi ymmärtää vain, jos tuntee ainakin differentiaali- ja integraalilaskennan sekä analyyttisen geometrian perusteet, eli niin sanotun korkeamman matematiikan alkeet.

- Klein, Felix (1902) Über den mathematischen Unterricht an den höheren Schulen, Jahresbericht der Deutschen Mathematiker-Vereinigung, 128-168 (käännös ChatGPT-3.5)

Tämä on Helsingin yliopiston Ympäristö- ja elintarviketalouden kandiohjelman Matematiikka 3:n (YET-034c) kurssimateriaali. Kurssi on jatkoa kursseille Matematiikka 1 ja Matematiikka 2.

Kysymykset ja kommentit: Jarmo Jääskeläinen jarmo.jaaskelainen@helsinki.fi (Taloustieteen osasto, Helsingin yliopisto)

Kurssin aiheet ovat

Integraali
Todennäköisyyslaskentaa
Matriisilaskentaa

Aihepiireihin liittyviä harjoitustehtäviä on koottu lukujen loppuun.

Materiaali perustuu kirjoihin

Sydsæter, Knut; Hammond, Peter J.; Strøm, Arne; Carvajal, Andrés, Essential mathematics for economic analysis (Fifth edition), Harlow, United Kingdom: Pearson Education, 2016.
- Kirja on saatavilla Helkassa.
- Alla kirjaan viitataan seuraavasti [EMEA, kohta].
Adams, Robert A.; Essex, Cristopher, Calculus: A Complete Course (Ninth edition), Pearson, 2018.
- Kirja on saatavilla Helkassa.

Apuna on käytetty myös Pauli Lapin Matematiikkaa taloustieteilijöille I -kurssin luentomonistetta ja virikkeitä on saatu Emma Leppälän ja Anni Laitisen peruskurssien luennoista Jyväskylän yliopistossa.

TIMin käytöstä 👈

Oranssit palkit: Tekstin oikeassa laidassa on oransseja palkkeja niissä kohdissa, joita et ole vielä lukenut. Ne auttavat sinua näkemään, missä olet menossa. Voit hävittää palkkeja klikkaamalla niitä sitä mukaan kun luet materiaalia.
Keltaiset palkit: Mikäli kappale muuttuu sen jälkeen kun olet sen lukenut (eli klikannut oranssin palkin pois), ilmestyy sen laitaan keltainen palkki. Sen vieressä on painike, josta voit tarkistaa mitä tekstissä on muuttunut.
- Jos koet palkit turhiksi, klikkaa vasemmalla ylhäällä hammasrattaan kuvaa. Sitten paina Merkitse kaikki luetuksi, jolloin palkit häviävät koko sivulta.
Kommentti: Jos jokin asia jää epäselväksi tai epäilet, että materiaalissa on virhe, voit klikata kappaleen oikeassa reunassa C-merkkiä, josta saa lisättyä kommentin. Kommentin voi asettaa näkymään vain itselle tai sitten kaikille, jolloin opettaja voi lukea kommentin ja vastata siihen.
"Sulkeutuvat kappaleet", kuten tämä, aukeavat painamalla -merkkiä tai kappaleen otsikkoa.

Alla olevan materiaalin joukkoon on laitettu lyhyitä videoita auttaaan itseopiskelussa. Nämä löytyvät -symbolilla.

Materiaalin seassa on myös pieniä tehtäviä, joiden oikeat vastaukset saa näkyviin saman tien. Tehtävillä voi harjoitella peruslaskutaitoa tai tarkastaa ymmärrystään opiskeltavasta aiheesta. Nämä tehtävät eivät vaikuta kurssisuorituksen pistemäärään. Osa tehtävistä on niin kutsuttuja STACK-tehtäviä. Suurin osa STACK-tehtävistä on Toni Hosiaisluoman käsialaa.

STACK-tehtävistä 👈

Osa näistä tehtävistä on niin kutsuttuja STACK-tehtäviä. STACK-tehtävät ovat taustaltaan sinisiä . Osa STACK-tehtävistä on satunnaistettuja eli saman tyylisiä harjoituksia voi tehdä useita - uuden tehtävän saa arvottua itselleen painikkeella Arvo uusi tehtävä, kunhan entiseen on vastattu jotakin. Vanhoja tehtäviä ja vastauksia voi selata ja kokeilla uudelleen. STACK-tehtävät on suunniteltu siten, että tehtävä lasketaan kynällä ja paperilla - ja vastaus tarkistetaan tietokoneella. STACK-tehtävien vastausten syöttäminen muistuttaa graafisen laskimen käyttämistä.

Peruslaskutoimitusten syöttäminen onnistuu seuraavasti:

Operaatio	Merkki
Yhteenlasku	+
Vähennyslasku	-
Kertolasku	*
Jakolasku	/
Potenssiin korotus	^
Sulut (ryhmittely)	()

Huomaa, että kertolaskua ei aina merkitä lausekkeissa, mutta STACK-vastauksissa jokainen kertolasku tulee merkitä. Esimerkiksi lauseke x + 2y annetaan muodossa x + 2*y.

Sulkujen avulla määritellään mihin lausekkeeseen laskutoimitukset kohdistuvat. Esimerkiksi $2^{1 + x}$ kirjoitetaan 2^(1 + x), jotta potenssiin korotus kohdistuu oikeaan lausekkeeseen.

# 1

1. Integraali

Tässä osassa käsitellään seuraavia asioita

integraalifunktio
määrätty integraali
- analyysin peruslause
integrointikaavat

Osiota vastaa [EMEA, 9.1-9.3].

1.1 Integrointikaavat ja analyysin peruslause

Integroinnilla voidaan laskea, kuinka suuri pinta-ala jää funktion kuvaajan ja -akselin väliin. Integraalin tarkka määrittely perustuu pinta-alaan; käytännössä funktioiden integrointi perustuu niin kutsuttuun analyysin peruslauseeseen 1.1.3, joka yhdistää derivaatan ja integraalin käsitteet, sekä integroinnin laskusääntöihin ja -kaavoihin (1.1.1, 1.1.2, 1.1.4).

Taloustieteessä funktion integraali esiintyy monissa yhteyksissä - esimerkiksi dynaamisissa malleissa.

Esimerkki

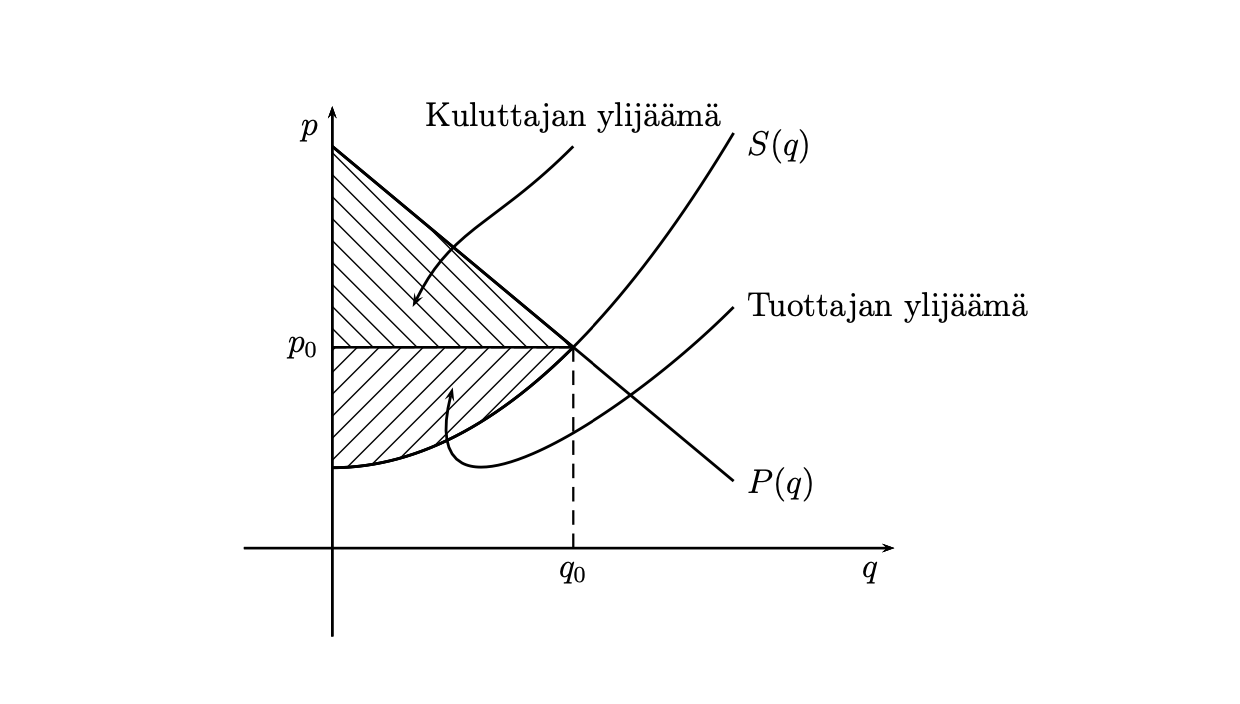
Mikrotaloustieteessä lasketaan kuluttajan ja tuottajan ylijäämää. Jos kysyntä- ja tarjontakäyrä ovat suoria, ylijäämä on helppo selvittää kolmion pinta-alan avulla. Entä jos tarjontakäyrän kuvaaja ei olekaan suora?

Kuva: Kuluttajan- ja tuottajan ylijäämät. Kuvan on tasapainomäärä ja vastaava tasapainohinta.

q_0 — Kuva: Kuluttajan- ja tuottajan ylijäämät. Kuvan on tasapainomäärä ja vastaava tasapainohinta.

Sanotaan, että funktio on funktion integraalifunktio, jos F'(x) = f(x) eli jos on funktion derivaatta.

Esimerkki

Esimerkiksi funktio , , on funktion , (eräs) integraalifunktio, sillä
Esimerkiksi funktio , $F(x) = \frac{1}{3}x^3 + 7$ , on funktion , , (eräs) integraalifunktio, koska $F'(x) = \frac13 \cdot 3x^2 + 0 = x^2 = f(x)$ .

Huomautus

Kaikilla funktioilla ei ole integraalifunktiota!

Joillakin on, ja se on helppo löytää (esimerkiksi polynomit).
Joillakin on, mutta se on vaikea löytää.
Joillakin on, mutta sen kirjoittaminen "lausekkeena" ei ole mahdollista.
- esimerkiksi $e^{-x^2}$ , $\frac{\sin x}{x}$ ,
Joillakin ei ole.

Integrointi on derivoinnin käänteisoperaatio.

Derivoimalla kustannusfunktio löydetään rajakustannusfunktio. Integroimalla rajakustannusfunktio saadaan kustannusfunktio.
Jos esimerkiksi tilastodatasta saadaan määritettyä jonkin kasvunopeus (eli derivaatta), voidaan tämä integroimalla löytää suuretta kuvaava funktio

Esimerkki

Funktiolla ei kuitenkaan ole pelkästään yhtä integraalifunktiota: $F_1(x) = x^2 + 1 \qquad \text{ja} \qquad F_2(x) = x^2 + 3$ määrittävät myös funktion , f(x) = 2x , integraalifunktion, sillä $F_1'(x) = 2x \qquad \text{ja} \qquad F_2'(x) = 2x$

Funktion kaikki integraalifunktiot saadaan (jostain) integraalifunktiosta lisäämällä siihen vakio .

Funktion yleistä integraalifunktiota eli niin kutsuttua määräämätöntä integraalia merkitään $\int_{}^{}f(x)\ \mathrm{d}x=F(x)+c, \quad \text{jossa} \quad F'(x)=f(x)$ ja on reaaliluku.

Merkintä tarkoittaa, että kaikilla vakion arvoilla F(x) + c on funktion integraalifunktio.

Vakiota kutsutaan integroimisvakioksi.

Huomautus

Määräämättömän integraalin merkinnässä $\mathrm{d}x$ tarkoittaa, että funktiota tarkastellaan muuttujan suhteen.
Jokaisen integroinnin voi tarkistaa derivoimalla vastaustaan ja katsomalla tuliko sama funktio kuin alkuperäinen integroitava.

# int

1.1.1 Sääntöjä integraalille

Seuraavat integrointisäännöt ovat voimassa ( on vakio): $\begin{align*} \int_{}^{}f(x)+g(x)\ \mathrm{d}x&=\int_{}^{}f(x)\ \mathrm{d}x+\int_{}^{}g(x)\ \mathrm{d}x, \\ \int_{}^{}af(x)\ \mathrm{d}x&=a\int_{}^{}f(x)\ \mathrm{d}x. \end{align*}$

# kaavat

1.1.2 Integrointikaavoja

Myös seuraavat integrointikaavat ovat voimassa ( on vakio): $\begin{align*} \int_{}^{}x^n\ \mathrm{d}x&=\frac{1}{n+1}x^{n+1}+c, \quad \text{jossa\ } n\neq-1, \\ \int_{}^{}\frac{1}{x}\ \mathrm{d}x&=\ln{\left|x\right|}+c, \quad \text{jossa\ } x\neq0, \\ \int_{}^{}e^x\ \mathrm{d}x&=e^x+c, \\ \int_{}^{}f'(x)f(x)^n\ \mathrm{d}x&=\frac{1}{n+1}f(x)^{n+1}+c, \quad \text{jossa\ } n\neq-1, \\ \int_{}^{}\frac{f'(x)}{f(x)}\ \mathrm{d}x&=\ln{\left|f(x)\right|}+c, \quad \text{jossa\ } f(x)\neq 0, \\ \int_{}^{}f'(x)e^{f(x)}\ \mathrm{d}x&=e^{f(x)}+c. \end{align*}$

Esimerkki

$\begin{align*} \int_{}^{}(2x+2x^3)\ \mathrm{d}x&=2\cdot\frac{1}{2}x^2+2\cdot\frac{1}{4}x^4+c=x^2+\frac{1}{2}x^4+c, \\ \int_{}^{}\sqrt{x^3}\ \mathrm{d}x&=\int_{}^{}x^{\frac{3}{2}}\ \mathrm{d}x=\frac{1}{\frac{3}{2}+1}x^{\frac{3}{2}+1}+c=\frac{2}{5}\sqrt{x^5}+c, \\ \int_{}^{}e^{2x}\ \mathrm{d}x&=\int_{}^{}\frac{2}{2}e^{2x}\ \mathrm{d}x=\frac{1}{2}\int_{}^{}2e^{2x}\ \mathrm{d}x=\frac{1}{2}e^{2x}+c. \end{align*}$

HUOMAA

Voit aina tarkastaa vastauksen derivoimalla. Esimerkiksi yllä ensimmäisessä kohdassa $D\left(x^2+\frac{1}{2}x^4+c\right) = 2x + 2 x^3 + 0 = 2x + 2x^3.$

Ongelma

Laske $\int \left(x^2 + \sqrt{x} - \frac{1}{x} + 1\right) \, \mathrm{d}x.$

# V2

Esimerkki

Seuraavassa esimerkissä kannattaa ensin suorittaa jakolasku: $\begin{align*} \int_{}^{}\frac{x^2-2x+1}{x^2}\ \mathrm{d}x&=\int_{}^{}\left(1-\frac{2}{x}+\frac{1}{x^2}\right)\ \mathrm{d}x\\ &=x-2\ln |x|+\frac{1}{-2+1}x^{-2+1}+c\\ &=x-2\ln |x|-\frac{1}{x}+c. \end{align*}$

Ongelma

Mitä integrointikaavaa on käytetty seuraavassa laskussa? $\int_{}^{}2x(x^2+10)^5\ \mathrm{d}x=\frac{1}{5+1}(x^2+10)^{5+1}+c=\frac{1}{6}(x^2+10)^6+c.$

Käytössä on integraalikaava $\int_{}^{}f'(x)f(x)^n\ \mathrm{d}x =\frac{1}{n+1}f(x)^{n+1}+c$ . Kaavassa f(x) = x^2 + 10 ja n = 5 .

Ongelma

Laske. $\int_{}^{}x(x^2+10)^5\ \mathrm{d}x.$

Tämä eroaa edellisestä ongelmasta vain vakiolla . Nyt vakion voi "pakottaa" sinne kertomalla lauseketta ykkösellä, $1 = \frac{2}{2}$ . Edellisen ongelman perusteella saamme $\int_{}^{}x(x^2+10)^5\ \mathrm{d}x = \int_{}^{}\frac{2}{2}\;x(x^2+10)^5\ \mathrm{d}x= \frac{1}{2}\int_{}^{}2x(x^2+10)^5\ \mathrm{d}x = \frac{1}{12}(x^2+10)^6+c.$

# Int1

# Int4

# Int7

# Int8

Lisää Stack-tehtäviä integroinnista löytyy +-merkin takaa.

# Int2

# Int3

# Int5

# Int9

Oletetaan, että on määritelty suljetulla välillä [a,b] . Niin kutsuttu määrätty integraali merkitään $\int_{a}^{b}f(x)\ \mathrm{d}x$

Määrätty integraali ja pinta-ala

Alueen, jota rajoittavat y = f(x) , y = 0 , x = a ja x = b , pinta-ala on $A = \int_a^b |f(x)| \, \mathrm{d}x.$

Määrätyn integraalin ja pinta-alan määritelmää ei tällä kurssilla käsitellä, mutta määrätyn integraalin ja pinta-alan yhteys perustuu seuraavan kuvan ideaan.

# geo1

# peruslause

1.1.3 Analyysin peruslause

Jos on jatkuva välillä ja on mikä tahansa funktion integraalifunktio, niin kaikilla $a, b \in I$ on $\int_a^b f(x) \, \mathrm{d}x = F(b) - F(a)$

Tässä niin kutsutussa "päätearvosijoituksessa" voidaan siis käyttää mitä tahansa n integraalifunktiota .
$\longrightarrow$ Voidaan valita se, jolla .

Huomautuksia ja nimityksiä

Merkinnässä $\displaystyle \int_a^b f(x) \, dx$

muuttuja on integroimismuuttuja
luvut ja ovat integroimisrajat (alaraja ja yläraja)
väli on integroimisväli
$\int$ on integraalimerkki
funktio on integroitava
differentiaali $\mathrm{d}x$ on merkintä; se kertoo, minkä muuttujan suhteen integroidaan

Sijoitusmerkintä

Muun muassa Suomessa käytetään sijoitusmerkintää $\int_a^b f(x) \, \mathrm{d}x = \bigg/^b_{\hspace{-8pt} a} F(x) = F(b) - F(a).$ Monissa lähteissä sijoitusmerkintä on hieman eri näköinen: $\displaystyle \; F(x)\bigg|_a^b = F(b) - F(a).$

# maar

1.1.4 Sääntöjä määrätylle integraalille

Seuraavat integrointisäännöt ovat voimassa määrätylle integraalille ( ja ovat vakioita): $\begin{align*} \int_{a}^{b}\left(f(x)+g(x)\right)\ \mathrm{d}x&=\int_{a}^{b}f(x)\ \mathrm{d}x+\int_{a}^{b}g(x)\ \mathrm{d}x, \\ \int_{a}^{b}cf(x)\ \mathrm{d}x&=c\int_{a}^{b}f(x)\ \mathrm{d}x, \\ \int_{a}^{b}f(x)\ \mathrm{d}x&=\int_{a}^{d}f(x)\ \mathrm{d}x+\int_{d}^{b}f(x)\ \mathrm{d}x,\quad \text{jossa\ } d\in[a,b], \\ \int_{a}^{b}f(x)\ \mathrm{d}x&\leq \int_{a}^{b}g(x)\ \mathrm{d}x,\quad \text{jossa\ } f(x)\leq g(x) \text{ \ välillä\ }[a,b]. \end{align*}$

Esimerkki

$\begin{align*} \int_{-1}^2 (3x - 2) \, dx &= \bigg/_{\hspace{-8pt}-1}^2 (\tfrac{3}{2}x^2 - 2x) \\ &= \left(\tfrac{3}{2} \cdot 2^2 - 2 \cdot 2\right) - \left(\tfrac{3}{2} \cdot (-1)^2 - 2 \cdot (-1)\right) \\ &= (6 - 4) - (\tfrac{3}{2} + 2)\\ &= 2 - \tfrac{7}{2} = - \tfrac{3}{2}. \end{align*}$

Alla olevalla sovelmalla havainnollistetaan määrätyn integraalin pinta-alatulkintaa. Liukusäätimistä voit muuttaa integroimisrajoja.

# geo2taso11

Esimerkki

$\int_{0}^{1}(x+e^x)\ \mathrm{d}x=\bigg/^1_{\hspace{-8pt} 0}\left(\frac{1}{2}x^2+e^x\right)=\frac{1}{2}\cdot1^2+e^1-\frac{1}{2}\cdot0^2-e^0=e-\frac{1}{2}.$

# V3

Esimerkki

Pohditaan määrätyn integraalin sovelluksena kuluttajan- ja tuottajan ylijäämiä. Olkoon tuotteen käänteiskysyntäkäyrä p=P(q) ja käänteistarjontakäyrä p=S(q) . Olkoon käänteiskysyntäkäyrä vähenevä ja käänteistarjontakäyrä kasvava tuotannon suhteen. Käänteiskysyntä edustaa kuluttajien maksuhalukkuutta tietystä tuotannon määrästä. Kokonaismaksuhalukkuus määrästä q_0 on siten $\int_{0}^{q_0}P(q)\ \mathrm{d}q.$ Kuluttajan ylijäämä on kokonaismaksuhalukkuuden ja ostamisesta koituvien kulujen erotus. Tuottajien kannalta käänteistarjontakäyrä edustaa tuotannon rajakustannusta, joten kokonaiskustannus määrästä q_0 on $\int_{0}^{q_0}S(q)\ \mathrm{d}q.$ Tuottajan ylijäämä on myyntitulojen ja kokonaiskustannuksen erotus. Kuluttajien ja tuottajien ylijäämien summa on siten $\int_{0}^{q_0}P(q)\ \mathrm{d}q-p_0q_0+\left(p_0q_0-\int_{0}^{q_0}S(q)\ \mathrm{d}q\right)=\int_{0}^{q_0}\left[P(q)-S(q)\right]\ \mathrm{d}q.$

q_0 — Kuva: Kuluttajan- ja tuottajan ylijäämät. Kuvan on tasapainomäärä ja vastaava tasapainohinta.

Esimerkki

Oletetaan, että saat tilillesi rahaa aikavälillä [t_0,t_1] ja että tämä tulovirta on jatkuvaa ja määräytyy funktion y=f(t) mukaisesti.

Mikä on tämän tulovirran nykyarvo (korkokannalla )?

Se lasketaan kaavalla $\int_{t_0}^{t_1}e^{-r(t-t_0)}f(t)\ \mathrm{d}t,$ ("käsiä heilutellen" integrointi vastaa infinidesimaalisten tulojen summaamista eli tässä tapauksessa sillä voidaan laskea jatkuvalla korolla diskonttaamista). Erityisesti, jos t_0=0 , niin tulovirran nykyarvo on $\int_{0}^{t_1}e^{-rt}f(t)\ \mathrm{d}t.$ Tässä voisi antaa funktiolle erilaisia muitakin tulkintoja. Se voisi olla esimerkiksi yrityksen voiton määrä.

Ongelma

Yrityksen rajakustannukset riippuvat tuotannon määrästä seuraavasti $C'(Q) = 2 e^{0,2 Q}.$

Tuotannosta riippumattomat vakiokustannukset ('fixed cost') ovat C_F = 90 (euroa) (eli kun Q = 0 , niin kustannukset ovat silti euroa, C(0) = 90 ).

Mikä on kokonaiskustannusfunktio ?

# V1

# Int6

Ongelma

Mikä on populaation koko ajan funktiona (populaation dynaaminen malli) eli niin kutsuttu aikaura?

Tiedämme populaatiosta, että sen koko muuttuu ajan funktiona $H'(t) = t^{-1/2}$ ja populaation koko on alussa 100 yksilöä.

Vastaus

$H(t) = 2t^{1/2} + 100$

# mint3

# mint4

# mint7

Lisää Stack-tehtäviä määrätystä integraalista löytyy +-merkin takaa.

# mint5

# mint6

Tehtäviä

Laske. $\text{(a) } \int 5 \, \mathrm{d}x \quad\quad\; \text{(b) } \int 3x^7 \, \mathrm{d}x \quad\quad\; \text{(c) } \int \sqrt{x} \, \mathrm{d}x \quad\quad\; \text{(d) } \int (x^4 - 6x + 7 + \frac{1}{x^5}) \, \mathrm{d}x$

Laske. $\text{(a) } \int_0^2 x^3 \, \mathrm{d}x \quad\quad\quad \text{(b) } \int_{\frac12}^1 \frac{1}{x^2} \, \mathrm{d}x \quad\quad\quad \text{(c) } \int_4^9 \left(\sqrt{x} - \frac{1}{\sqrt{x}} \right) \, \mathrm{d}x$

Olkoon rajakustannusfunktion lauseke Laske integroimalla kokonaiskustannusfunktio , kun kiinteät kustannukset ovat (eli ).

1. Laske $\int_{0}^{1} (e^x - e^{1-x})\, \mathrm{d}x.$
2. Laske $\int_{}^{} (4e^{8t} +t + 100)\, \mathrm{d}t.$
3. Olkoon parametrit (eli vakiot) , ja . Onko määrätty integraali $\int_{0}^{T} we^{-rt} \, \mathrm{d}t$ suurempi vai pienempi kuin $\frac{w}{r}$ ?

Alla on lisätehtäviä harjoittelua varten. Samantyylisiä tehtäviä eri lukuarvoilla saa "Uusi tehtävä"-napista. Geogebra-tehtävät ovat avustettuja: jos jäät jumiin ratkaisussa, voit klikata itsellesi tiedon, mitä seuraavaksi kannattaa tehdä, "Seuraava vaihe"-napista". Geogebra Copyright © International GeoGebra Institute, 2013

# geo2taso14

# geo2taso17

# geo2taso18

# geo2taso21

# 2

2. Todennäköisyyslaskentaa

Tässä osassa käsitellään seuraavia asioita

klassinen todennäköisyys
- tuloperiaate
- geometrinen todennäköisyys
- ehdollinen todennäköisyys
odotusarvo
varianssi ja keskihajonta
jatkuvat jakaumat
- tiheysfunktio

Osiota vastaa Kappale 7.8 kirjassa Adams, Robert A.; Essex, Cristopher, Calculus: A Complete Course (Ninth edition), Pearson, 2018.

2.1 Miksi/Mitä todennäköisyyslaskentaa?

Todennäköisyys on tapa mitata kuinka usein tiettyjä tapahtumia esiintyy esimerkiksi toistettavissa kokeissa. Todennäköisyys kuvastaa, kuinka "todennäköistä" on, että jokin tapahtuma toteutuu.

Jos todennäköisyys on , kyseinen tapahtuma ei toteudu. Toisin sanoen, se on mahdoton.
Jos todennäköisyys on , se tarkoittaa, että kyseinen tapahtuma tapahtuu varmasti.

Yleensä tapahtumien todennäköisyys on jossain näiden välillä. Todennäköisyyttä kuvataan yleensä käyttämällä todennäköisyysfunktiota $\mathbb{P}$ , joka saa arvoja välillä [0, 1] . Todennäköisyys on siis jotain 0% (ei toteudu) ja 100% (toteutuu varmasti) väliltä.

Todennäköisyyslaskenta on olennainen työkalu esimerkiksi taloustieteessä, tilastotieteessä ja uhkapeleissä. Se auttaa meitä ymmärtämään ja ennustamaan satunnaisiin tapahtumiin liittyviä ilmiöitä; ja tekemään parempia valintoja.

Todennäköisyyslaskennan yhteydessä satunnaiskokeeksi tai satunnaisilmiöksi kutsutaan prosessia, jonka lopputulosta ei alkutilanteen perusteella tiedetä varmasti, mutta kaikki mahdolliset lopputulokset tunnetaan. Satunnaiskoe on sellainen, että sitä voidaan toistaa samoin ehdoin useita kertoja.

Esimerkkejä satunnaisista ilmiöistä ja kokeista ovat nopanheitto, kolikonheitto korttien nostaminen, lapsen sukupuolen ennustaminen ja lottorivin arvonta.

Satunnaiskokeissa tai -ilmiöissä yksittäinen tulos on alkeistapaus, ja näistä muodostetaan erilaisia tapahtumia. Kaikkien mahdollisten tapahtumien joukkoa kutsutaan perusjoukoksi tai otosavaruudeksi. Tapahtumat ovat sitten perusjoukon osajoukkoja.

Esimerkki

Kolikonheiton alkeistapaukset ovat kruuna ja klaava (joskus lisätään myös kolikon pystyyn jääminen)
Nopanheiton alkeistapaukset ovat silmäluvut 1, 2, 3, 4, 5, ja 6.
Kahden peräkkäisen nopanheiton alkeistapauksia on 36 kappaletta. Ne ovat (merkinnässä (x, y) ensimmäisen heiton silmälukua merkitään x:llä ja toisen heiton y:llä)
- (1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6),
- (2, 1), (2, 2), (2, 3), (2, 4), (2, 5), (2, 6),
- (3, 1), (3, 2), (3, 3), (3, 4), (3, 5), (3, 6),
- (4, 1), (4, 2), (4, 3), (4, 4), (4, 5), (4, 6),
- (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6),
- (6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6),
  - Eräs kahden peräkkäisen nopanheiton tapahtuma on esimerkiksi, että saadaan ainakin kerran silmäluku 5. Tällöin mahdollisia tapahtumia on 10 kappaletta: (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (1, 5), (2, 5), (3, 5), (4, 5), (6, 5).

2.2 Klassinen todennäköisyys

Yksinkertaisimmillaan tapahtuman todennäköisyys voidaan laskea jakamalla suotuisten tapausten lukumäärä kaikkien vaihtoehtojen lukumäärällä $\text{todennäköisyys} = \frac{\text{suotuisat tapaukset}}{\text{kaikki vaihtoehdot}}.$

Klassinen todennäköisyys perustuu oletukseen, että kaikki alkeistapaukset ovat keskenään symmetrisiä eli yhtä todennäköisiä. Toisin sanoen jokainen alkeistapaus koetaan yhtä mahdolliseksi ja yhtä todennäköiseksi.

Todennäköisyys $\mathbb{P}$ lasketaan suotuisten alkeistapauksien lukumäärällä jaettuna kaikkien mahdollisten tapausten lukumäärällä.

Tapahtumalle suotuisien alkeistapausten määrä n_a jaetaan kaikkien tapausten määrällä $\mathbb{P}(A)=\frac{n_a}{n}.$

# todom

2.2.1 Ominaisuuksia todennäköisyysfunktiolle

Todennäköisyysfunktiolle pätee seuraavat ominaisuudet. Jos ja ovat tapahtumia ja perusjoukko (eli kaikki mahdolliset tapahtumat), niin

$0\leq \mathbb{P}(A) \leq 1$
$\mathbb{P}(S) = 1$
$\mathbb{P}(A \text{ ei tapahdu}) = 1 - \mathbb{P}(A)$
$\mathbb{P}(A \text{ tai } B \text{ tapahtuu}) = \mathbb{P}(A) + \mathbb{P}(B) - \mathbb{P}(A \text{ ja } B \text{ molemmat tapahtuvat})$

Esimerkki (Nopanheitto)

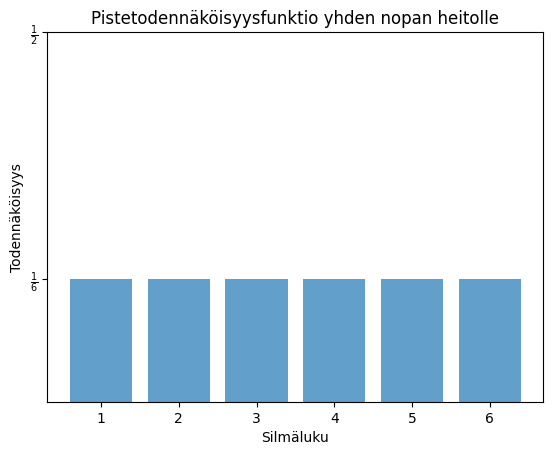
Yhden nopan heiton mahdolliset silmäluvut ovat ⚀ ⚁ ⚂ ⚃ ⚄ ⚅ eli 1, 2, 3, 4, 5, 6. Nämä ovat mahdolliset alkeistapaukset ja niitä on kuusi kappaletta. Todennäköisyys, että silmäluku on esimerkiksi 2 saadaan klassisesti todennäköisyydestä: suotuisia tapauksia on yksi kuudesta eli $\mathbb{P}(\text{silmäluku on 2}) = \frac{1}{6}.$ Sama pätee mille tahansa silmäluvulle, joten $\mathbb{P}(\text{silmäluku on } n) = \frac{1}{6}, \qquad \text{millä tahansa luvulla $n$ joukosta $\{1, 2, 3, 4, 5, 6 \}$}.$ Alkeistapausten todennäköisyyksistä muodostuu nopanheiton jakauma eli niin kutsuttu todennäköisyysjakauma.

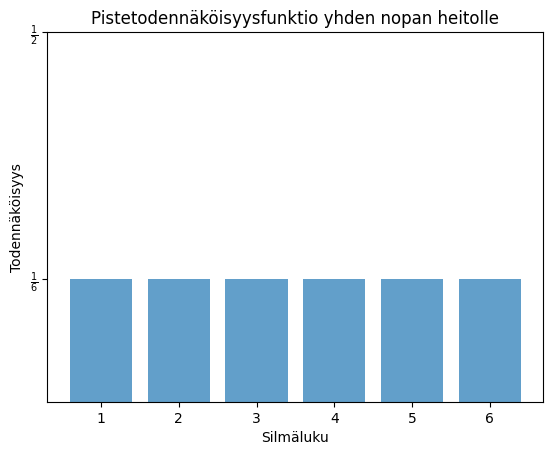
Koska heiton tulos on aina jokin luvuista 1, 2, 3, 4, 5, 6 $\begin{align*} &\mathbb{P}(\text{silmäluku on 1}) + \mathbb{P}(\text{silmäluku on 2}) \\ &\qquad+ \mathbb{P}(\text{silmäluku on 3}) + \mathbb{P}(\text{silmäluku on 4}) \\ &\qquad+ \mathbb{P}(\text{silmäluku on 5}) + \mathbb{P}(\text{silmäluku on 6}) \\ &\quad= \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{6}{6}\\ &\quad= 1 \\ &\quad= \mathbb{P}(\text{silmäluku on jokin luvuista 1, 2, 3, 4, 5, 6}), \end{align*}$ mikä heijastaa, että yhden nopan heiton tuloksena todellakin on yksi luvuista 1, ..., 6 eli tapahtuma on varma eli todennäköisyys on 1. Tässä on käytetty yllä olevaa 4. ominaisuutta (ja viimeinen yhtäsuuruus on ominaisuus 2).

Todennäköisyys, että yhden nopan heiton tuloksena saadaan jokin silmäluvuista 1, 2, 3 tai 4 on $\begin{align*} \frac{\text{suotuisat tapaukset}}{\text{kaikki vaihtoehdot}} &= \frac{4}{6} \\ &= \mathbb{P}(\text{silmäluku on 1}) + \mathbb{P}(\text{silmäluku on 2}) \\ &\quad+ \mathbb{P}(\text{silmäluku on 3}) + \mathbb{P}(\text{silmäluku on 4}). \end{align*}$

Voit heittää noppaa alla olevalla Python-koodinpätkällä. Nopanheitossa jokainen silmäluku on yhtä todennäköinen ( $1/6 \approx 16,7\%$ ). Alla saat tilastollisen jakauman nopanheitolle. Kun heittojen määrät alkavat kasvaa, jakauma "lähestyy" klassisen todennäköisyyslaskennan antamaa tasajakaumaa.

# noppapython

# kaksinoppaasumma

Esimerkki (Kahden nopanheiton summa)

Kuten edellä nähtiin kahden peräkkäisen nopanheiton mahdollisia tuloksia on 36 kappaletta: parit (x,y), missä x ja y ovat kokonaislukuja 1, 2, 3, 4, 5 tai 6. Yhden tälläisen lopputuloksen todennäköisyys on 1/36.

Mikä on todenneköisyys, että ensimmäisessä nopanheitossa saadaan silmäluku on 3 ja toisessa nopanheitossa 5?
Mikä on todennäköisyys, että silmäluvut 3 ja 5 esiintyvät kahden heiton aikana?
- Mahdollisia tapahtumia on kaksi: (3, 5) ja (5, 3), joten todennäköisyys on 2/36 = 1/18.

Seuraavaan taulukkoon on laskettu summa kahden peräkkäisen nopanheiton silmäluvuista.

summa	mahdollisuudet	todennäköisyys
2	(1,1)	1/36
3	(1,2), (2,1)	2/36 = 1/18
4	(1,3), (2,2), (3,1)	3/36 = 1/12
5	(1,4) (2,3), (3,2), (4,1)	4/36 = 1/9
6	(1,5), (2,4), (3,3), (4,2), (5,1)	5/36
7	(1,6), (2,5), (3,4), (4,3), (5,2), (6,1)	6/36 = 1/6
8	(2,6), (3,5), (4,4), (5,3), (6,2)	5/36
9	(3,6), (4,5), (5,4), (6,3)	4/36 = 1/9
10	(4,6), (5,5), (6,4)	3/36 = 1/12
11	(5,6), (6,5)	2/36 = 1/18
12	(6,6)	1/36

Todennäköisyysjakauma kahden nopan summalle.

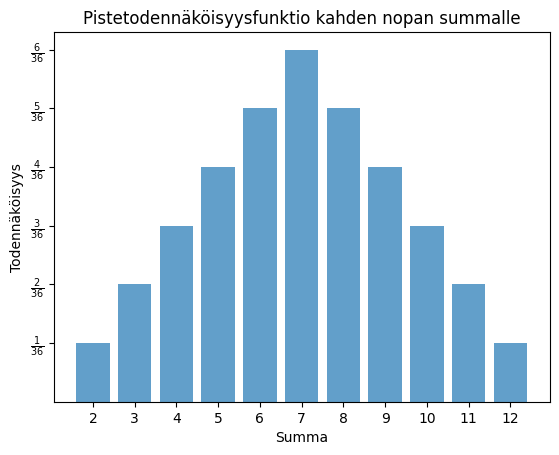
Mikä on todennäköisyys, että summa kahden peräkkäisen nopanheiton silmäluvuista on alle 10? $\begin{align*} \mathbb{P}(\text{summa on alle 10}) &= 1 - \mathbb{P}(\text{summa on 10 tai yli})\\ &= 1 - \left(\frac{3}{36} + \frac{2}{36} + \frac{1}{36}\right)\\ &= 1 - \frac{6}{36}\\ &= 1 - \frac{1}{6}\\ &= \frac{5}{6}. \end{align*}$

2.2.2 Tuloperiaate

Tuloperiaate soveltuu parhaiten tilanteisiin, joissa ilmiö tai koe on jaettu osiin, jotka tapahtuvat järjestyksessä. Jos ilmiö koostuu kahdessa sellaisesta peräkkäisessä vaiheessa, että ensimmäinen vaihe voi tapahtua eri tavalla ja toinen sen jälkeen aina (ensimmäisen vaiheen tuloksesta riippumatta) eri tavalla, voi ilmiö tapahtua $n\cdot m$ eri tavalla.

Tämän periaatteen voi yleistää useammalle peräkkäiselle vaiheelle, jolloin eri tapoja on $n_1 \cdot n_2 \cdot n_3 \cdots n_{l}$ , missä n_i on kuinka monella tavalla vaihe voi toteutua ja peräkkäisiä vaiheita on kappaletta.

Esimerkki

Tavallisessa vakioveikkauksessa veikataan kolmeatoista kohdetta, ja jokaisessa kohteessa on kolme vaihtoehtoa (1, X tai 2). Erilaisten veikkausrivien määrä on siten $3 \cdot 3 \cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3\cdot 3 = 3^{13}$ kappaletta tuloperiaatteen mukaan. Kuvassa puukaaviona kahden ensimmäisen kohteen eri vaihtoehdot.

$\begin{tikzpicture}[level distance=2cm, level 1/.style={sibling distance=3.5cm}, level 2/.style={sibling distance=1.5cm}] \node {Vakioveikkaus} child {node {1} child {node {1}} child {node {X}} child {node {2}} } child {node {X} child {node {1}} child {node {X}} child {node {2}} } child {node {2} child {node {1}} child {node {X}} child {node {2}} }; \end{tikzpicture}$

Tuloperiaate on tuttu esimerkiksi kertomasta. Joukko, jossa on alkiota/jäsentä, voidaan järjestää eri tavalla, missä kertoma on $n!=n\cdot (n-1) \cdot (n-2)\cdots 2\cdot1.$

Kertoma ja tuloperiaate yhdistettynä kertovat, kuinka moneen erilaiseen jonoon voimme järjestää -alkioisen joukon. Idea kertoman takana on seuraava.

Ensimmäinen vaihe: Valitsemme ensimmäisen alkion joukosta. Koska joukossa on alkiota, meillä on vaihtoehtoa ensimmäiselle paikalle.
Toinen vaihe: Valitsemme toisen alkion joukosta. Koska ensimmäinen alkio on jo valittu, meillä on vaihtoehtoa toiselle paikalle.
Kolmas vaihe: Jatkamme tätä prosessia valitsemalla seuraavat alkiot. Jokaisessa vaiheessa meillä on yksi vaihtoehto vähemmän, koska edelliset alkiot on jo valittu.
Viimeinen vaihe: Lopulta, kun olemme valinneet :n alkion, jäljellä on enää yksi alkio, joten meillä on vain yksi vaihtoehto viimeiselle paikalle.

Esimerkki

Heitetään kolmea noppaa, ja tarkastellaan erilaisia tapahtumia (nämä heitot voidaan ajatella tuloperiaatteen mukaisesti: yksi noppa on aina yksi vaihe, joten kolmen nopan heitto koostuu kolmesta vaiheesta).

Kolme kuutosta Suotuisia tapahtumia on 1 (kaikki kuutosia) ja eri tapoja on tuloperiaatteen mukaan $6 \cdot 6 \cdot 6 = 216$ . Todennäköisyys, että kaikki heitot ovat kutosia, on $\frac{1}{216}$ eli noin $0,\!46\%.$
Kolme samaa numeroa Ensimmäinen heitto voi olla mikä tahansa silmäluku (eli kuusi mahdollisuutta), ja seuraavat kaksi heittoa riippuvat ensimmäisestä (niiden on pakko olla sama, joten vaihtoehtoja on vain yksi). Suotuisia tapauksia on $6 \cdot 1 \cdot 1$ ja kaikkia vaihtoehtoja on edelleen $6 \cdot 6 \cdot 6 = 216$ . Todennäköisyys on siis $\frac{6}{6 \cdot 6 \cdot 6} = \frac{1}{36}$ eli noin $2,\!78\%.$
Vähintään yksi kuutonen Lasketaan todennäköisyys niin kutsutun vastatapahtuman kautta. Tapahtumia, että ei saada kutosta millään heitolla, on tuloperiaatteen mukaan $5 \cdot 5 \cdot 5 = 125$ kappaletta. Kaikkia vaihtoehtoja on edelleen $6 \cdot 6 \cdot 6 = 216$ kappaletta. Ei yhtään kuutosta toteutuu siis todennäköisyydellä $\frac{125}{216}$ . Vähintään yksi kuutonen on niin kutsuttu vastatapahtuma ja sen todennäköisyys on (katso 2.2.1 kohta 3) $1 - \frac{125}{216} = \frac{91}{216}$ eli noin $42\%.$

2.2.3 Summaperiaate

On myös niin kutsuttu summaperiaate eli jos meillä on ilmiö, joka koostuu kahdesta peräkkäisestä toisensa poissulkevasta vaiheista vaiheesta, ja meillä on tapaa tehdä ensimmäinen vaihe ja tapaa tehdä toinen vaihe, niin ilmiö voi tapahtua n + m eri tavalla.

Esimerkki

Kun heität noppaa, tapahtuma "silmäluvun kolme saaminen" ja tapahtuma "kakkosta suuremman silmäluvun saaminen" eivät sulje toisiaan pois.
Toisaalta tapahtuma "nelosta pienemmän silmäluvun saaminen" ja tapahtuma "nelosta suuremman silmäluvun saaminen" ovat toisensa poissulkevia, koska noppa ei voi näyttää samanaikaisesti sekä alle neljää että neljää tai enemmän.

Esimerkki

Tarkastellaan eri värisiä paitoja luentosalissa. Salissa on sata henkilöä, joilla on musta paita, ja viisikymmentä valkopaitaista henkilöä. Lisäksi luennolla neljäkymmentä henkilöä, joilla ei ole mustaa tai valkoista paitaa päällään. Tällöin (oletuksella, että kellään ei ole kahta eriväristä paitaa yhtä aikaa päällään) meillä on yhteensä 100+50+40=190 eri henkilöä luentosalissa.

Esimerkki

Maalataan noppa punakeltaiseksi. Tahkot, joissa on ykkönen (1) tai alkuluku (2, 3, 5) ovat maalattu punaiseksi ja muut (4, 6) keltaiseksi.

Noppaa heitetään kaksi kertaa. Tulosvaihtoehtoja on neljä: kahdesti punainen tahko, kahdesti keltainen tahko, ensin punainen tahko ja sitten keltainen tahko sekä ensin keltainen tahko ja sitten punainen tahko. Selvitetään näiden mahdollisuuksien kokonaismäärät.

Tuloperiaatteen mukaan eri tahkoparit voivat tulla tulokseksi $6 \cdot 6 = 36$ eri tavalla. Näistä molemmilla kerroilla voi punainen tahko tulla $4 \cdot 4 = 16$ eri tavalla ja molemmilla kerroilla keltainen tahko $2 \cdot 2 = 4$ eri tavalla. Ensin punainen tahko ja sitten keltainen tahko voi tulla $4 \cdot 2 = 8$ eri tavalla ja ensin keltainen tahko ja sitten punainen tahko voi taas tulla $2 \cdot 4 = 8$ eri tavalla.

Kuinka monella tavalla tulokseksi voi tulla toisella kerralla punainen ja toisella keltainen tahko (järjestyksestä riippumatta)? Summa- ja tuloperiaatteiden mukaan näin voi tapahtua $4 \cdot 2 + 2 \cdot 4 = 8 + 8 = 16$ tavalla. Siis todennäköisyys, että toisella heitolla punainen ja toisella keltainen tahko, on $\frac{16}{36} = \frac{4}{9}$ eli noin $44,\!4\%$ .

2.2.4 Geometrinen todennäköisyys

Geometrista mittaa (esimerkiksi pituus, pinta-ala, tilavuus, kulma) hyödyntävää todennäköisyyden laskemista kutsutaan geometriseksi todennäköisyydeksi. $\text{todennäköisyys} = \frac{\text{tapahtumalle suotuisa mitta}}{\text{koko kuvion mitta}}$

Esimerkki

Mikä on todennäköisyys osua Darts-taulun häränsilmään (punainen kiekko taulun keskellä), jos oletetaan tikan osuvan aina tauluun ja osumakohta on täysin satunnainen? Häränsilmän halkaisija on 12,7 mm ja taulun halkaisija on 451 mm.

Geometrisen todennäköisyyden kaavalla kyseessä on häränsilmän pinta-alan suhde koko taulun pinta-alaan. Ympyrän pinta-alahan on $\pi \cdot \text{säde}^2$ , joten kysytty todennäköisyys on $\frac{\pi (12,\!7 / 2)^2}{\pi (451 / 2)^2} = \frac{12,\!7^2}{451^2} \approx 0,\!079\%.$

Esimerkki

Meillä on ruudukoksi laatoitettu lattia, joka koostuu 10 cm x 10 cm -laatoista. Lattialle tipahtaa kolikko, jonka halkaisija on kaksi senttimetriä. Millä todennäköisyydellä kolikko peittää jonkin laatan kulman?

Kolikko peittää laatan kulman, jos sen keskipiste tipahtaa korkeintaan säteen päähän laatan kulmasta. Koska kolikon halkaisija on 2 cm, sen säde on 1 cm. Geometrisella todennäköisyydellä voimme selvittää kysytyn todennäköisyyden.

Alla olevassa kuvassa harmaalla ovat alueet, jotka ovat suotuisia alueita, joihin tipahtavan kolikon keskipisteen pitää jäädä (jotta laatan kulma peittyisi).

$\begin{tikzpicture}[scale=0.5] % Draw the square \draw (0,0) rectangle (10,10); % Draw shaded quarter circles at the corners \filldraw[fill=gray!50] (0,0) -- (0,1) arc (90:0:1) -- cycle; \filldraw[fill=gray!50] (0,10) -- (1,10) arc (0:-90:1) -- cycle; \filldraw[fill=gray!50] (10,0) -- (10,1) arc (90:180:1) -- cycle; \filldraw[fill=gray!50] (10,10) -- (9,10) arc (180:270:1) -- cycle; \end{tikzpicture}$

Suotuisan alueen mitta (pinta-ala) on koko kolikon pinta-ala ( kertaa neljäsosaympyrä) eli $\pi \cdot \text{säde}^2 = \pi \cdot 1^2 = \pi$ . Koko laatan pinta-ala on $10 \cdot 10 = 100$ . Kysytty todennäköisyys on siis $\pi$ prosenttia: $\frac{\pi}{100} \approx 3,\!14\%.$

Esimerkki

Bussit lähtevät päätepysäkiltä 20 minuutin välein ja avaavat ovensa 5 minuuttia ennen lähtöä. Reija, joka ei tunne aikatauluja, saapuu pysäkille. Selvitetään, millä todennäköisyydellä hän pääsee heti bussiin.

Tarkastellaan 20 minuutin mittaista ajanjaksoa, jota havainnollistaa 20 yksikön pituinen jana. Janan viiden yksikön mittainen osa vastaa aikaa, kun bussin ovet ovat auki. Koska Reija ei tiedä aikataulua, kaikki janan pisteet ovat yhtä mahdollisia. Suotuisan janan (kuvassa sinisellä) pituus on 5, kun taas koko janan pituus on 20. Etsitty todennäköisyys saadaan laskemalla suotuisan osan pituuden suhde koko pituuteen. $\mathbb{P}(\text{"heti bussiin"}) = \dfrac{5}{20} = \dfrac{1}{4}$

Esimerkki

Väliltä [0,5] arvotaan (satunnaisesti ja toisistaan riippumattomasti) luvut ja . Selvitetään, millä todennäköisyydellä lukujen ja summa on suurempi kuin .

Perusjoukko muodostuu oheiseen koordinaatistoon piirretyn neliön pisteistä. Se, että lukujen ja summa on suurempi kuin 6, voidaan kirjoittaa matemaattisesti muodossa x+y > 6 eli y > -x + 6 . Graafisesti tarkasteltuna kyseessä on punaisella piirretyn suoran y=-x+6 rajaama ylempi puolitaso, josta neliön sisälle jäävä osuus on väritettetty oheiseen kuvioon sinisellä. Suotuisan alueen (kuvassa sinisellä) pinta-ala on $\dfrac{1}{2} \cdot 4 \cdot 4 = 8$ . Koko neliön pinta-ala taas on $5 \cdot 5 = 25$ . Etsitty todennäköisyys saadaan laskemalla suotuisan alueen pinta-alan suhde koko pinta-alaan. $\mathbb{P}(\text{"summa suurempi kuin kuusi"}) = \dfrac{8}{25} = 0{,}32$

2.2.5 Ehdollinen todennäköisyys

Ehdollisen todennäköisyyden avulla tarkastellaan, miten toisen tapahtuman esiintyminen ilmiössä/kokeessa voi vaikuttaa tapahtuman todennäköisyyteen. Ajatellaan, että tapahtuma toteutuu ja tarkastellaan jonkin toisen tapahtuman todennäköisyyttä, kun tiedämme, että on jo tapahtunut. Tätä kutsutaan ehdolliseksi todennäköisyydeksi ja sitä merkitään $\mathbb{P}(A\,|\,B)$ .

Tapahtuman todennäköisyys ehdolla, että tapahtuu on $\mathbb{P}(A\,|\,B)=\frac{\mathbb{P}(\text{$A$ ja $B$ tapahtuvat})}{\mathbb{P}(\text{$B$ tapahtuu})}.$

Saadaan myös (yleistetty) kertolaskusääntö: $\mathbb{P}(\text{$A$ ja $B$ tapahtuvat}) = \mathbb{P}(A\,|\,B)\;\mathbb{P}(\text{$B$ tapahtuu}).$

Esimerkki

Nostetaan 52 kortin pakasta kortteja. Millä todennäköisyydellä toinen kortti on ässä, jos ensimmäinen kortti oli ässä?

Tapahtuma : ensimmäinen kortti on ässä
Tapahtuma : toinen kortti on ässä

Ehdollinen todennäköisyys $P(A\,|\,B)$ , eli todennäköisyys sille, että toinen kortti on ässä, kun ensimmäinen kortti on ässä, lasketaan kaavalla: $P(A\,|\,B) = \frac{P(\text{$A$ ja $B$ tapahtuvat})}{P(\text{$B$ tapahtuu})}.$

Ässiä on pakassa neljä kappalette, joten todennäköisyys, että ensimmäinen kortti on ässä on $P(B) = \frac{4}{52} = \frac{1}{13}$ . Tulosäännöllä tapahtumia, joissa ensimmäinen ja toinen kortti ovat ässiä on $4 \cdot 3 = 12$ kappaletta ja kaikkia mahdollisia kahden kortin pareja on $52 \cdot 51$ kappaletta. Siis $P(\text{$A$ ja $B$ tapahtuvat})) = \frac{4 \cdot 3}{52 \cdot 51}$ .

Nyt $P(A\,|\,B) = \frac{P(\text{$A$ ja $B$ tapahtuvat})}{P(\text{$B$ tapahtuu})} = \frac{\frac{4 \cdot 3}{52 \cdot 51}}{\frac{4}{52}} = \frac{3}{51} = \frac{1}{17}.$

Joten todennäköisyys, että toinen kortti on ässä, kun ensimmäinen kortti on ässä, on $\frac{1}{17}$ , mikä on noin $5,\!88\%$ .

Tämä todennäköisyys voidaan laskea myös suoraan, sillä yhden ässän poisottamisen jälkeen pakassa on 51 korttia, joista kolme on ässää eli $P(A\,|\,B) = \frac{3}{51} = \frac{1}{17}.$

Esimerkki

Mikä on todennäköisyys, että kahden nopan heiton summa on 10 tai yli ja ensimmäisellä nopan heitolla saadaan silmäluku 5?

Tapahtuma : ensimmäisellä nopalla saadaan viitonen
Tapahtuma : kahdella nopalla saadaan yhteensä vähintään 10

Kysytty todennäköisyys on $P(\text{$A$ ja $B$ tapahtuvat})$ . Käytetään yleistetty tulosääntöä. $\mathbb{P}(\text{$A$ ja $B$ tapahtuvat}) = \mathbb{P}(A\,|\,B)\;\mathbb{P}(\text{$B$ tapahtuu}).$

Ehdollinen todennäköisyys $P(A\,|\,B)$ , eli todennäköisyys sille, että summa on yli kymmenen, kun ensimmäinen silmäluku on 5 saadaan tarkastelemalla suotuisien tapahtumien ja kaikkien tapahtumien suhdetta. Kahden nopan heittoja, joissa ensimmäisen heiton silmäluku on 5 on yhteensä kuusi kappaletta (toinen silmäluku voi olla 1, 2, 3, 4, 5 tai 6). Näistä suotuisia eli summa on 10 tai yli on vain kaksi:

Siis $P(A\,|\,B) = \frac{2}{6} = \frac{1}{3}$ .

Ensimmäisellä nopalla saadaan viitonen -tapahtuman kannalta suotuisia tapauksia on 1 ja yhteensä nopanheitossa eri tapauksia on 6, joten $P(B) = \frac{1}{6}$ .

Kysytty todennäköisyys on $\mathbb{P}(\text{$A$ ja $B$ tapahtuvat}) = \mathbb{P}(A\,|\,B)\;\mathbb{P}(\text{$B$ tapahtuu}) = \frac{1}{3} \cdot \frac{1}{6} = \frac{1}{18} \approx 5,\!55\%.$

2.3 Odotusarvo

Satunnaismuuttujaksi sanotaan väljästi mitä tahansa satunnaisilmiöön tai -kokeeseen liittyvää reaaliarvoista funktiota, jonka arvo tiedetään täysin, kun tapahtuma tiedetään. Merkintänä on yleensä iso kirjain, esimerkiksi $X(\omega)$ . Todennäköisyyslaskennan merkinnöissä jätetään yleensä muuttuja $\omega$ kirjoittamatta funktioon eli $X = X(\omega)$ .

Esimerkki

Nopanheitossa satunnaismuuttuja voi olla esimerkiksi silmäluku, ⚀ ) = 1 , ⚁ ) = 2 , ⚂ ) = 3 , ⚃ ) = 4 , ⚄ ) = 5 ja ⚅ ) = 6 , missä muuttujana $\omega$ on nopan yläpuoli.

# odotusarvo

2.3.1 Odotusarvo

Satunnaismuuttujan odotusarvo $\mathbb{E}(X)$ (merkitään myös $\mu$ ) on sen todennäköisyyksillä painotettu keskiarvo eli jos satunnaismuuttuja saa arvot $x_1, x_2, x_3, \ldots, x_n$ , niin $\mathbb{E}(X) = x_1\cdot \mathbb{P}(X = x_1) + x_2\cdot \mathbb{P}(X = x_2) + x_3\cdot \mathbb{P}(X = x_3) + \ldots + x_n\cdot\mathbb{P}(X = x_n).$

Esimerkki

Pelaat nopanheittopeliä, jossa saat nopan silmäluvun verran euroja per heitto. Mahdolliset voitot ovat siis 1, 2, 3, 4, 5 ja 6 euroa. Jokaisen voiton todennäköisyys on $\frac{1}{6}$ .

Kuinka paljon peliin osallistumisesta kannattaa maksaa per heitto?

Voiton odotusarvo on $\begin{align*} & 1\cdot \mathbb{P}(\text{silmäluku on $1$}) + 2\cdot \mathbb{P}(\text{silmäluku on $2$}) + \ldots + 6\cdot\mathbb{P}(\text{silmäluku on $6$}) \\ &=1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6}\\ &= \frac{21}{6} = 3,\!5. \end{align*}$ Tässä tapauksessa odotusarvo ei mahdollinen nopanheitontulos. Odotusarvo ei siten välttämättä ole odotettavissa oleva arvo. Jos peliä pelaa pitkään ( peliä), niin odotettavissa on, että voitto on $3,\!5n$ euroa.

Jos peli maksaa yli 3,5 euroa per peli, keskimäärin pelaaja häviää rahaa. Pelaajan kannattaa maksaa alle 3,5 euroa per peli, jos aikoo jäädä voitolle pitkässä juoksussa.

Ongelma

Mikä on kahden nopan heiton summan odotusarvo?

2.3.2 Varianssi ja keskihajonta

Satunnaismuuttujan varianssi $\sigma^2 = \mathrm{Var}(X)$ on $\mathbb{E}((X- \mathbb{E}(X))^2).$ Jos satunnaismuuttuja saa arvot $x_1, x_2, x_3, \ldots, x_n$ ja odotusarvo $\mathbb{E}(X) = \mu$ , niin $\mathrm{Var}(X) = (x_1 - \mu)^2\cdot \mathbb{P}(X = x_1) + (x_2 - \mu)^2\cdot \mathbb{P}(X = x_2) + \ldots + (x_n - \mu)^2\cdot\mathbb{P}(X = x_n).$

Keskihajonta $\sigma$ on varianssin neliöjuuri $\sigma = \sqrt{\mathrm{Var}(X)}.$

Esimerkki

Nopanheiton varianssi on $(1 - 3,\!5)^2\cdot \frac{1}{6} + (2- 3,\!5)^2\cdot \frac{1}{6} + (3 - 3,\!5)^2\cdot\frac{1}{6} + (4 - 3,\!5)^2\cdot\frac{1}{6}+ (5 - 3,\!5)^2\cdot\frac{1}{6}+ (6 - 3,\!5)^2\cdot\frac{1}{6} = \frac{35}{12} \approx 2,\!92.$ ja keskihajonta $\sigma = \sqrt{\frac{35}{12}} \approx 1,\!71.$

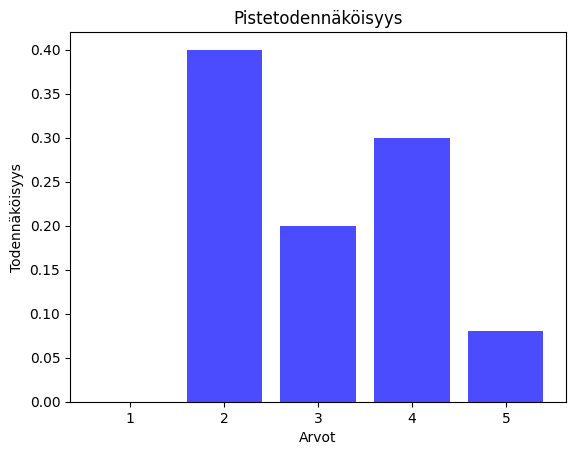
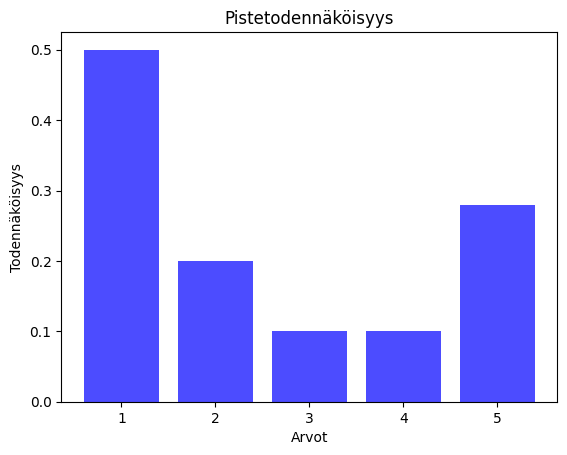
Alla on kahden satunnaismuuttujan pistetodennäköisyydet. Molemmat voivat saada arvoja 1, 2, 3, 4 ja 5. Odotusarvot ovat molemmissa 3.

Vasemmalla keskihajonta noin 1,01 ja oikealla noin 1,85. Keskihajonta kertoo suunnilleen kuinka "hajallaan" arvot ovat odotusarvosta.

2.3.3 Odotusarvon lineaarisuus

Jos satunnaismuuttujilla ja on odotusarvo, niin tällöin myös satunnaismuuttujalla aX + bY , missä ja ovat vakioita, on odotusarvo ja sillä pätee $\mathbb{E}(aX + bY) = a\mathbb{E}(X) + b\mathbb{E}(Y).$

Seuraus

Varianssin voi kirjoittaa myös seuraavasti. $\begin{align*} \sigma^2 = \mathrm{Var}(X) &= \mathbb{E}((X- \mathbb{E}(X))^2) \\ &= \mathbb{E}(X^2) - \mathbb{E}(X)^2 \end{align*}$

# jatkuvat_jakaumat

2.4 Jatkuvat todennäköisyysjakaumat

Yllä tarkastelemamme todennäköisyyslaskennan esimerkit ovat olleet arvoiltaan erillisiä: esimerkiksi nopanheiton silmäluvut, korttien nostot, eri värit ja niin edelleen. Jos satunnaismuutujan arvoja on vain "laskettava" (numeroituva) määrä, kuten esimerkiksi noppien silmäluvut 1, 2, 3, 4, 5 ja 6 tai yleisemmin $x_1, x_2, x_3, \ldots$ , niin satunnaismuuttujaa kutsutaan diskreetiksi satunnaismuuttujaksi.

Kaikkia satunnaisilmiöiden tai -kokeiden lopputulemia ei voida kuitenkaan kuvata vain laskettavilla arvoilla. Esimerkiksi puiden korkeus, puiden paksuus, elinikä ja rahasummat voivat saada kaikki arvot vaikkapa väliltä [0, 100] . Tälläisiä arvoja saavia satunnaismuuttujia kutsutaan jatkuviksi satunnaismuuttujiksi.

2.4.1 Tiheysfunktio

Diskreetin satunnaismuuttujan todennäköisyysfunktio (niin kutsuttu pistetodennäköisyysfunktio) $\mathbb{P}(X = x) \qquad \text{ eli todennäköisyys, että saavutetaan arvo $x$}$ voidaan laajentaa niin kutsutuksi tiheysfunktioksi jatkuville satunnaismuuttujille.

Tiheysfunktio

Funktio , joka on määritelty välillä [a, b] on tiheysfunktio (probability density function) jatkuvalle satunnaismuuttujalle, jos $\mathbb{P}(x_1 \leq X \leq x_2) = \int_{x_1}^{x_2} f(x)\; \mathrm{d}x$ (eli todennäköisyys, että arvo on välillä [x_1, x_2] saadaan integroimalla) ja

$f(x) \geq 0$ (todennäköisyys ei voi olla negatiivista)
$\int_{a}^{b} f(x)\; \mathrm{d}x = 1$ (eli $\mathbb{P}(a \leq X \leq b) = 1$ siis arvot ovat varmasti välillä )

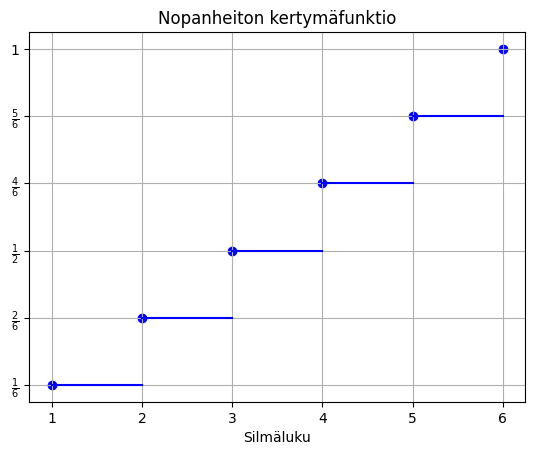
Kertymäfunktio

Satunnaismuuttuja :n kertymäfunktio (cumulative distribution function) on funktio $F \colon \R \to \R$ , jolle $F(x) = \mathbb{P}(X \leq x).$ Kertymäfunktiosta nähdään, miten eri tapahtumien todennäköisyydet ovat jakautuneet.

Diskreetissä tapauksessa se on summa kaikista pistetodennäköisyyksistä $\mathbb{P}(X = x_k),$ joilla $x_k \leq x$ eli matemaattisesti kirjoitettuna $F(x) = \sum_{x_k \leq x} \mathbb{P}(X = x_k).$
Jatkuvalle satunnaismuuttujalle $F(x)= \displaystyle \int_{a}^x f(t) \; \mathrm{d}t$ eli missä on tiheysfunktio (kertymäfunktio on siis tiheysfunktion integraalifunktio, jolla ).

Erityisesti $\mathbb{P}(x_1 \leq X \leq x_2) = \int_{x_1}^{x_2} f(x)\; \mathrm{d}x = F(x_2) - F(x_1).$

Huomaa, että välillä [a, b] määritelty funktio on jonkun todennäköisyysjakauman tiheysfunktio, jos

$f(x) \geq 0$
$\int_{a}^{b} f(x)\; \mathrm{d}x = 1$

Tällöin kyseisen todennäköisyysjakauman kertymäfunktio saadaan integroimalla ja valitsemalla integraalifunktioista se, joka saa arvon pisteessä x = a .

Esimerkki

Diskreetillä satunnaismuuttujalla pistetodennäköisyysfunktio on tiheysfunktion roolissa. Alla on nopanheiton todennäköisyysjakauma (eli pistetodennäköisyysfunktio $\mathbb{P}(\text{silmäluku on $x$})$ ja vasemmalla kertymäfunktio eli $\mathbb{P}(\text{silmäluku on $x$ tai alle})$ .

Ongelma

Olkoon satunnaismuuttujan tiheysfunktiona , $f(x) = \dfrac{2}{9} x$ , joka on määritelty välillä [0, 3] (siis satunnaismuuttuja saa arvoja välillä [0, 3] ).

Miksi on tiheysfunktio?
Todennäköisyys, että arvot ovat välillä on kuvaajan ja -akselin väliin jäävän alueen pinta-ala.

$\begin{tikzpicture} \begin{axis}[ width=8cm, height=6cm, axis lines=left, xlabel={$x$}, ylabel={$f(x)$}, ymin=0, ymax=1, xmin=0, xmax=3, xtick={1,2}, ytick={0,0.2,0.4,0.6,0.8,1}, legend pos=north east, legend style={draw=none}, ] % Function curve \addplot[blue, thick, domain=0:3, samples=100] {2/9*x}; \addlegendentry{$f(x) = \frac{2}{9}x$}; % Shaded area below the curve between x=1 and x=2 \addplot[fill=gray!30, domain=1:2, samples=100] {2/9*x} \closedcycle; % Vertical lines \draw[dashed] (axis cs:1,0) -- (axis cs:1,0.222); \draw[dashed] (axis cs:2,0) -- (axis cs:2,0.444); % Labels \node at (axis cs:1,-0.05) {$1$}; \node at (axis cs:2,-0.05) {$2$}; \end{axis} \end{tikzpicture}$

Harmaan alueen pinta-ala on $\mathbb{P}(1 \leq X \leq 2)$ . Mikä se on?

2.4.2 Tasajakauma

Jos tapahtumien todennäköisyys on jakautunut tasaisesti koko mahdolliseen arvojoukkon jakaumaa kutsutaan tasajakumaksi. Suljetulla välillä [a, b] arvoja saavan tasajakauman tiheysfunktio on $f(x) = \begin{cases} \frac{1}{b - a}, & a \leq x \leq b \\ 0, & \text{muuten} \end{cases}$

Esimerkiksi tasajakaumalla välillä :
- tiheysfunktio on $f(x) = \frac{1}{4-1} = \frac13$ .
$\begin{tikzpicture} % Axis \draw[->] (0,0) -- (6.1,0); \draw[->] (0,0) -- (0,1); % Function \draw[blue, thick] (-1,0) -- (1,0); \draw[blue, thick] (1,1/3) -- (4,1/3); \draw[blue, thick] (4,0) -- (6,0); % Labels \foreach \y in {1/3,2/3} \draw (0.1,\y) -- (-0.1,\y) node[left] {$\y$}; \foreach \x in {1,2,3,4,5} \draw (\x,0.1) -- (\x,-0.1) node[below] {$\x$}; \end{tikzpicture}$
- kertymäfunktio on , $F(x) = \int_{1}^{x} \frac{1}{4-1} \; \mathrm{d}t = \frac{1}{4-1} \bigg/^x_{\hspace{-8pt} 1} t = \frac13 (x - 1) = \frac{x-1}{3}.$ Kertymäfunktion arvo, kun , eli "todennäköisyys, että arvo on pienempää tai yhtä kuin 3" on alla olevassa kuvassa harmaan alueen pinta-ala.
$\begin{tikzpicture} % Axis \draw[->] (0,0) -- (6.1,0); \draw[->] (0,0) -- (0,1); % Curve y = 1/3 \draw[domain=1:4, smooth, variable=\x, blue] plot ({\x}, {1/3}); \draw[blue] (-1,0) -- (1,0); \draw[blue] (4,0) -- (6,0); % Shaded area \fill[fill=gray!30] (1,0) -- plot[domain=1:3, variable=\x] ({\x}, {1/3}) -- (3,0) -- cycle; \foreach \y in {1/3,2/3} \draw (0.1,\y) -- (-0.1,\y) node[left] {$\y$}; \foreach \x in {1,2,3,4,5} \draw (\x,0.1) -- (\x,-0.1) node[below] {$\x$}; \end{tikzpicture}$

Esimerkki

Tiputetaan neula lautalattialle. Oletetaan, että neulan pituus on suurempi kuin laudan leveys. Neulan muodostama terävä kulma laudan reunan kanssa (terävä kulma eli asteina ja väliltä) on tasaisesti jakautunut koko välille [0, 90] , sillä satunnaisesti tipahtavalle neulalle jokainen kulma on yhtä todennäköinen.

2.4.3 Odotusarvo ja varianssi

Jatkuvan satunnaismuuttujan , jolla on tiheysfunktiona $f \colon [a, b] \to \mathbb{R}$ , odotusarvo on $\mu = \mathbb{E}(X) = \int_a^b xf(x) \; \mathrm{d}x.$

Jos jatkuva satunnaismuuttuja on funktion muuttujana, tällöin n odotusarvo on $\mathbb{E}(g(X)) = \int_a^b g(x)f(x) \; \mathrm{d}x.$

Varianssi määritellään vastaavasti kuin diskreetissä tapauksessa eli $\sigma^2 = \mathrm{Var}(X) = \mathbb{E}((X- \mathbb{E}(X))^2) = \int_{a}^{b} (x - \mu)^2f(x)\;\mathrm{d}x.$ Keskihajonta $\sigma$ on varianssin neliöjuuri $\sigma = \sqrt{\mathrm{Var}(X)}.$

Myös jatkuvalla satunnaismuuttujalle ovat voimassa seuraavat tulokset.

2.3.3 Odotusarvon lineaarisuus

Seuraus

Varianssin voi kirjoittaa myös seuraavasti. $\begin{align*} \sigma^2 = \mathrm{Var}(X) &= \mathbb{E}((X- \mathbb{E}(X))^2) \\ &= \mathbb{E}(X^2) - \mathbb{E}(X)^2 \end{align*}$

Esimerkki

Tasajakaumalla välillä [1,4] , meillä oli jo tiheysfunktion lauseke $f(x) = \frac{1}{4-1} = \frac13$ . Nyt odotusarvo on määritelmän mukaan $\int_1^4 x\frac13 \, \mathrm{d}x = \frac13 \int_1^4 x \, \mathrm{d}x = \frac13 \bigg/^4_{\hspace{-8pt} 1} \frac12 x^2 = \frac13\left(\frac12 \cdot 4^2 - \frac12\cdot 1^2\right) = \frac13 \left(\frac{16}{2} - \frac12\right) = \frac{15}{6} = 2,\!5.$

# tarjous

2.4.4 Esimerkki

Olet valtiolla töissä ostamassa pieniä vesivoimapatoja yksityisiltä toimijoilta. Tavoitteena on ostaa patoja, jotta ne voidaan purkaa kalajoista.

Erään padon omistaja on valmis myymään patonsa, jos hänen ylimääräiset kulunsa on katettu. Teet hänelle "ota tai jätä"-tarjouksen.

Valtio on valmis maksamaan korkeintaan yksikköä. Valtio laskee hyötyvänsä 10-x yksikköä, missä on hyväksytty tarjous.

Padon omistajan hyöty on x - c yksikköä. Jos tarjousta ei hyväksytä sekä valtio ja padon omistaja hyötyvät yksikön edestä.

Padon omistajan kulut ovat vain hänen tiedossaan. Arvioit, että ne ovat tasaisesti jakautuneet välille [2, 7] .

Minkä tarjouksen teet valtion puolesta?
Mikä on todennäköisyys, että kauppa toteutuu?

Paras tarjous on sellainen, jolla valtion voiton odotusarvo on suurin. Tämän tilanteen satunnaisuus liittyy siihen hyväksytäänkö tarjous eli satunnaismuuttuja on "tarjous, jonka suuruus on , hyväksytään".

Valtion voiton odotusarvo on (voitto tarjouksella ) $\cdot$ (todennäköisyys, että tarjous hyväksytään).

Padon omistaja hyväksyy tarjouksesi , jos se on suurempaa tai yhtä kuin . Mahdolliset kustannukset ovat tasaisesti jakautuneet välille [2,7] eli kustannusten tiheysfunktio on , $f(x) = \frac{1}{7-2} = \frac15.$ Nyt todennäköisyys, että $c \leq x$ on $\mathbb{P}(\text{``$c$ on pienempää tai yhtä kuin $x$''}) = \int_{2}^{x} f(t) \, \mathrm{d}t = \int_{2}^{x} \frac15\, \mathrm{d}t =\frac15 \cdot(x - 2) = \frac{x - 2}{5},$ kun on välillä [2, 7] . Todennäköisyys on , jos x < 2 ja , jos x > 7 .

Valtion voiton odotusarvo (tarjouksella ) on $\aligned &0, &\text{kun $x$ on pienempää kuin $2$} \\ &(10 - x)\cdot\mathbb{P}(\text{``$c$ on pienempää tai yhtä kuin $x$''}) &\\ &\quad = (10 -x) \cdot \frac{x - 2}{5} = \frac{-x^2 + 12x -20}{5}, &\text{kun $x$ on välillä $[2,7]$}\\ &(10 - x), &\text{kun $x$ on suurempaa kuin $7$} \endaligned$ sillä, jos tarjous on alle , $\mathbb{P}(\text{``$c$ on pienempää tai yhtä kuin $x$''}) = 0$ , ja tarjous hyväksytään varmasti, jos x > 7 .

Odotusarvon voi toki laskea myös kaavalla $\mathbb{E}(g(X)) = \int_{a}^b g(x)f(x) \, \mathrm{d}x$ , missä g(x) = 10 -x on voittofunktio, esimerkiksi, kun on välillä [2,7] , $\mathbb{E}(\text{voitto tarjouksella $x$}) = \int_{2}^{x} (10 - x)\cdot f(t) \, \mathrm{d}t = \int_{2}^{x} (10 - x)\cdot \frac15\, \mathrm{d}t =\frac15 \cdot (10 -x)(x - 2).$

Meidän pitää etsiä voiton odotusarvon maksimia! Tähän auttavat tietomme derivaatasta ja sen käytöstä kurssilta Matematiikka 2. Kun $x \leq 2$ , voitto on nolla. Kun x = 7 , voitto on 10 - 7 = 3 ja sen jälkeen alle . Selvitetään löytyykö väliltä [2,7] voiton odotusarvon derivaatalle nollakohtaa. Koska voiton odotusarvon lauseke $\frac{-x^2 + 12x -20}{5}$ kyseisellä välillä on alaspäin aukeava paraabeli, derivaatan nollakohta on maksimi.

$D\left(\frac{-x^2 + 12x -20}{5} \right) = \frac{1}{5}(-2x + 12)$ ja $\frac{1}{5}(-2x + 12) = 0,$ kun x = 6 . Kyseinen piste on myös välillä [2, 7] .

Voiton odotusarvon maksimi löytyy siis tarjouksella x = 6 . Tämä on valtion optimaalinen tarjous, joka sinun kannattaa tehdä, ja voitto on 10 - 6 = 4 . Kaupan toteutumisen todennäköisyys $\mathbb{P}(\text{``$c$ on pienempää tai yhtä kuin $6$''}) = \frac{6 - 2}{5} = \frac{4}{5} = 0,\!80 =80\%.$

2.4.5 Muita jatkuvia jakaumia

Eksponenttijakauma (esimerkiksi aika, jonka radioaktiivinen atomi on koossa ennen hajoamistaan, noudattaa eksponenttijakaumaa): Sen tiheysfunktio on , $f(x) = \begin{cases} \lambda e^{-\lambda x}, & x \geq 0, \\ 0, & x < 0, \end{cases}$ missä $\lambda > 0$ .
Normaalijakaumalla on
- tiheysfunktio , $f(x) = \frac{1}{\sigma\sqrt{2\pi}} e^{-\frac12\frac{(x - \mu)^2}{\sigma^2}}$ ja
- kertymäfunktio , $F(x) = \displaystyle \int_{-\infty}^x f(t) \, dt$

Normaalijakauma kuvaa useita luonnon ilmiöiden ja ihmistieteiden tutkimuskohteiden jakaumia. Sen odotusarvo on $\mu$ ja keskihajonta on $\sigma$ . Kun $\mu = 0$ ja $\sigma = 1$ jakaumaa kutsutaan standardinormaalijakaumaksi. Jakaumaa käytetään myös monissa tilastollisissa analyyseissä ja testauksissa.

Yksi yleinen sovellus on Z-pistemäärän käyttö. Z-pistemäärä ilmaisee, kuinka monta keskihajontaa tarkasteltava arvo on keskiarvon ylä- tai alapuolella normaalijakaumassa. Tätä käytetään esimerkiksi normaalijakaumasta johdettujen tilastollisten testien yhteydessä, kuten Z-testeissä ja t-testeissä.

Normaalijakaumaa käytetään myös luottamusväleissä, p-arvojen laskennassa ja monissa tilastollisissa malleissa. Se tarjoaa yksinkertaisen ja kätevän tavan tehdä vertailuja eri aineistojen välillä ja tehdä päätelmiä tilastollisten testien tuloksista.

Lisäksi normaalijakaumaa käytetään laajasti eri tieteellisissä ja liiketaloudellisissa sovelluksissa, missä tilastollisia menetelmiä hyödynnetään tietojen analysoinnissa ja päätöksenteossa. Normaalijakauman hyödyllisyys perustuu osittain niin kutsuttuun keskeiseen raja-arvolauseeseen, joka sanoo että riittävän monen riippumattoman satunnaismuuttujan keskiarvo on likipitäen normaalijakautunut.

Tehtäviä

Uhkapelaaja antoi kaksi lausuntoa.
- Lausunto A: "Kannattaa lyödä vetoa sen puolesta, että heitettäessä noppaa neljä kertaa saadaan ainakin yksi kuutonen."
- Lausunto B: "Ei kannata lyödä vetoa sen puolesta, että heitettäessä kahta noppaa 24 kertaa saadaan ainakin yksi kuutospari."
  
  Onko hän todennäköisyysmielessä oikeassa? Voit käyttää laskinta apuna.
  1. Lausunnossa A
  2. Lausunnossa B

Vihje

Alkeistapausten, joissa tapahtuma ei toteudu, määrän laskeminen saattaa olla helpointa.

Lattia on laatoitettu ruudukoksi neliön mallisilla laatoilla, joiden sivun pituus on . Tiputetaan kolikko, jonka halkaisija on , lattialle. Kolikon halkaisija on pienempää kuin laatan sivun pituus eli . Kolikko voi tipahtaa lattialle siten, että se osittain peittää 1, 2, 3 tai 4 laattaa.

Millä todennäköisyydellä tiputettu kolikko peittää osittain 2 tai useampaa laattaa?

Heitetään kahta noppaa.
1. Laske noppien silmälukujen summan odotusarvo. Voit käyttää laskinta apuna.
2. Laske noppien silmälukujen summan varianssi. Voit käyttää laskinta apuna.

Meillä on kolme kolikkoa. Yksi on tavallinen eli siinä on kruuna ja klaava. Loput kaksi ovat väärennettyjä: toisessa on molemmilla puolilla kolikkoa kruuna ja toisessa molemmilla puolilla kolikkoa klaava.

Otamme sokkona yhden kolikon ja heitämme sen. Tuloksena on kruuna. Mikä on todennäköisyys, että meillä on väärennetty kolikko?

Vihje

Eräs tapa miettiä asiaa on "kuusi sivuisen" kolikon heitto...

1. Määritellään funktio välillä lausekkeeella . Välin ulkopuolella saa arvokseen . Millä vakiolla funktio on jonkun todennäköisyysjakauman tiheysfunktio?
2. Laske saatua tiheysfunktiota vastaavan jatkuvan satunnaismuuttujan odotusarvo.
3. Laske saatua tiheysfunktiota vastaavan jatkuvan satunnaismuuttujan varianssi.

1. Kuvassa on funktion kuvaaja. Näytä, että se on jonkun todennäköisyysjakauman tiheysfunktio.
$\begin{tikzpicture} % Axis \draw[->] (0,0) -- (2.03,0); \draw[->] (0,0) -- (0,2.5); % Function \draw[blue, thick] (-1,0)--(0,0) -- (0.5,2) -- (1,0) -- (2, 0); % Labels \foreach \y in {1,2} \draw (0.1,\y) -- (-0.1,\y) node[left] {$\y$}; \foreach \x in {0.5,1} \draw (\x,0.1) -- (\x,-0.1) node[below] {$\x$}; \end{tikzpicture}$
1. Mikä on :n kertymäfunktio?

Onko väite totta vai tarua? Perustele vastauksesi.
1. Toni osuu laukauksellaan vesisodassa aina 50% todennäköisyydellä. Hän ampuu ensin ohi, joten toisella kerralla hän osuu varmasti.
2. Arvonnassa on myynnissä yhteensä 1000 arpaa, joista yhdeksällä voittaa jotain. Yhdellä arvalla voittaa päävoiton 100 euroa ja kahdeksalla voitto on 50 euroa. Olet ostanut arvan 1 eurolla. Arvan tuoton odotusarvo on 50 senttiä.
3. Määritellään funktio välillä lausekkeeella $f(x) = 3 x - \frac12$ . Välin ulkopuolella saa arvokseen . Funktio on jonkun todennäköisyysjakauman tiheysfunktio.

1. Määritellään funktio välillä lausekkeella . Välin ulkopuolella saa arvokseen . Millä vakiolla funktio on jonkun todennäköisyysjakauman tiheysfunktio?
2. Osallistut tarjouskilpailuun tarjouksella miljoonaa euroa. Sinulla on yksi kilpailija. Arvioit, että kilpailijasi tekemä tarjous noudattaa a-kohdan tiheysfunktiota välillä (0:sta 1:een miljoonaan euroon)
- Millä todennäköisyydellä tarjouksesi on pienempi kuin kilpailijasi tarjous?
- Millä todennäköisyydellä tarjouksesti on suurempi kuin kilpailijasi tarjous?

Haluat voittaa tarjouskilpailun urakasta (tarjoat/kerrot millä summalla olet valmis suorittamaan urakan). Sinulla on vastassasi vain yksi kilpailija. Ostaja valitsee urakan suorittajaksi halvimman tarjouksen jättäjän. Arvioit, että kilpailijasi tekemä tarjous on tasaisesti jakautunut välille .

Mikä on todennäköisyys, että tarjouksesi on pienempi kuin kilpailijasi tarjous?

Jatkoa tehtävään 9. Jos voitat tarjouskilpailun (eli tarjoat tässä tapauksessa vähemmän), saat urakasta voittoa , missä on urakan kulut sinulle. Muuten voittosi on .

Laske voittosi odotusarvo, kun tarjouksesi on .
Mikä tarjous maksimoi voittosi odotusarvon (eli mikä on optimaalinen tarjous)?

Toni, Jarmo ja Ville ovat vesisodassa. Jokainen saa vuorollaan ampua yhden laukauksen. Pelistä putoaa pois heti, kun saa osuman. Voittaja on viimeinen tyyppi kuivana. Jokainen pyrkii maksimoimaan voittomahdollisuutensa ja jokainen pyrkii voittoon. Toni on huonoin ampuja ja hän osuu valitsemaansa vastustajaan todennäköisyydellä 0,5. Jarmo on aika haka ja osuu todennököisyydellä 0,8. Villellä on kultainen ampumamerkki ja hän osuu aina (siis todennäköisyydellä 1).

Koska Jarmo ja Ville ovat reiluja, he päättävät antaa Tonin aloittaa. Sen jälkeen on Jarmon vuoro ja sitten Villen. Jos vesisodan voittaja ei ole selvillä ampumiskierroksen jälkeen, jatketaan uudelle kierrokselle yhä uudestaan ja uudestaan.

Mihin Toni ampuu?

# geo2taso19

Seuraavassa tehtävässä c:llä liikutetaan tiheysfunktion huipun paikkaa. Mikä on kertymäfunktion arvo eri pisteissä? Voit tarkastaa tuloksesi liikuttamalla punaista pistettä.

# geo2taso20

# stack12

# Todari2

# Todari3

# Todari4

# Todari6

# 3

3. Matriisilaskentaa

Tässä osassa käsitellään seuraavia asioita

matriisit
- summa, tulo, transpoosi
- käänteismartiisi
determinantti
lineaarisen yhtälön esittäminen matriisimuodossa
Cramerin sääntö

Osiota vastaa [EMEA, 15.2-15.5 ja 16.1-16.3, 16.6].

3.1 Lineaarinen yhtälöryhmä

Matematiikka 1 -kurssilla käsitellyt lineaariset yhtälöparit ovat esimerkkejä lineaarisesta yhtälöryhmästä. Lineaarinen yhtälöryhmä, jossa on muuttujaa ja yhtälöä, näyttää seuraavalta $\left\{ \begin{array}{ccccccccc} a_{11}x_1&+&a_{12}x_2&+&\ldots & +&a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\ldots & +&a_{2n}x_n&=&b_2\\ &\vdots &&\vdots &&\vdots &&\vdots \\ a_{m1}x_1&+&a_{m2}x_2&+&\ldots & +&a_{mn}x_n&=&b_m\\ \end{array} \right.$ Yhtälöryhmässä tuntemattomat muuttujat ovat $x_1,\ldots,x_n$ (yhtälöpareissa meillä oli ja ), luvut $a_{ij}$ , $i=1,\ldots,m$ , $j=1,\ldots,n$ , ovat kertoimia ja luvut b_i ( $i=1,\ldots,m$ ) ovat vakioita.

Yhtälöryhmän ratkaisu on lukujoukko $x_1,\ldots,x_n$ , joka toteuttaa jokaisen yhtälöryhmän yhtälön.

Lineaarissa yhtälöryhmässä muuttujan korkein potenssi on (eli esimerkiksi x^2 -termejä ei voi olla).

Taloustieteen matemaattiset mallit koostuvat usein yhtälöistä, jotka muodostavat yhtälöryhmän. Yhtälöt kuvaavat kuinka yksi tai useampi muuttuja riippuu toisista muuttujista ja mallin parametreista. Lineaariset yhtälöryhmät ovat perusta myös ekonometrisille tekniikoille.

Lineaarisia malleja on helpompi ymmärtää (ja manipuloida), jos käytössä on tiettyjä matemaattisia käsitteitä, kuten matriisit ja determinantit. Näitä käsitellään seuraavaksi.

Matriisiksi kutsutaan on suorakaiteen muotoon riveiksi ja sarakkeiksi järjestettyä joukkoa lukuja. Matriisin koko ilmaistaan rivien ja sarakkeiden avulla. Kokoa $m \times n$ oleva matriisi sisältää -riviä ja -saraketta. Tällöin puhutaan $m\times n$ -matriisista. Matriiseja merkitään tavallisesti isoilla kirjaimilla ja niiden koot ilmoitetaan tarvittaessa alaindeksein.

$m\times n$ -matriisia $A_{m\times n}$ merkitään $A_{m\times n} = \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix}.$ Luku $a_{ij}$ on matriisin alkio, joka sijaitsee rivillä ja sarakkeella .

Esimerkiksi alkio $a_{21}$ sijaitsee rivillä ja sarakkeella .
Yllä olevassa matriisin merkinnässä on käytetty $[\ ]$ -sulkuja, mutta siinä voisi käyttää myös $(\ )$ -sulkuja. Matriisia, jonka koko on $m\times 1$ , voidaan kutsua sarakematriisiksi (tai sarakevektoriksi), ja matriisia, jonka koko on $1\times n$ , voidaan kutsua rivimatriisiksi (tai rivivektoriksi).

Matriisit ovat samat, jos ne ovat saman kokoisia ja niiden samassa paikassa olevat alkiot ovat yhtäsuuret.
Kaksi matriisia voidaan laskea yhteen, jos ne ovat saman kokoisia. Yhteenlaskussa samassa paikassa olevat alkiot lasketaan yhteen.

Esimerkki

$\begin{bmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \end{bmatrix}+ \begin{bmatrix} 1 & 1 & 1 & 1 \\ 1 & 1 & 1 & 1 \end{bmatrix}= \begin{bmatrix} 1+1 & 2+1 & 3+1 & 4+1 \\ 5+1 & 6+1 & 7+1 & 8+1 \end{bmatrix}= \begin{bmatrix} 2 & 3 & 4 & 5 \\ 6 & 7 & 8 & 9 \end{bmatrix}.$

Matriisi voidaan kertoa luvulla, jolloin sen jokainen alkio kerrotaan kyseisellä luvulla.

Esimerkki

$-10\cdot \begin{bmatrix} 1 & 2 \\ 5 & 6 \\ 9 & 10 \end{bmatrix}= \begin{bmatrix} -10\cdot 1 & -10 \cdot 2 \\ -10 \cdot 5 & -10 \cdot 6 \\ -10\cdot 9 & -10\cdot 10 \end{bmatrix}= \begin{bmatrix} -10 & -20 \\ -50 & -60 \\ -90 & -100 \end{bmatrix}.$

Matriisien tulo, siis matriisien kertominen toisillaan, on määritelty vain tietyn kokoisille matriiseille. Matriisien $A_{m\times n}$ ja $B_{p\times k}$ tulo $A_{m\times n}B_{p\times k}$ on määritelty, kun n=p , eli tulo on määritelty silloin, kun ensimmäisen matriisin sarakkeiden määrä on sama kuin jälkimmäisen matriisin rivien määrä.

Tulomatriisin koko on $m\times k$ . Tulo lasketaan seuraavasti: tulomatriisin kohdan alkio on $\sum_{h=1}^{n}{a_{ih}b_{hj}}$ eli summa alkioiden tuloista, joissa rivin . alkio kerrotaan :nnen sarakkeen :nnellä alkiolla.

Siis, jos tulomatriisia merkitään :llä, niin $A_{m\times n}B_{n\times k}=C_{m \times k}$ , jossa tulomatriisin alkiot ovat $c_{ij=}\sum_{h=1}^{n}{a_{ih}b_{hj}},$ kun $i=1,\ldots,m$ ja $j=1,\ldots,k$ .

Alla olevalla sovelmalla voit harjoitella matriisien kertolaskua.

# geo2taso10

Esimerkki

Jos $A_{2\times 2}=\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \quad \text{ja} \quad B_{2\times 2}=\begin{bmatrix} 2 & 4 \\ -1 & -2 \end{bmatrix},$ niin $A_{2\times 2}B_{2\times 2}= \begin{bmatrix} 1\cdot 2+2\cdot(-1) & 1\cdot 4 +2\cdot(-2) \\ 2\cdot 2+4\cdot(-1) & 2\cdot 4+4\cdot(-2) \end{bmatrix} =\begin{bmatrix} 0 & 0 \\ 0 & 0 \end{bmatrix}.$

Ongelma

Laske $B_{2\times 2}A_{2\times 2}$ äskeisen esimerkin matriiseilla $A_{2\times 2}=\begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix} \quad \text{ja} \quad B_{2\times 2}=\begin{bmatrix} 2 & 4 \\ -1 & -2 \end{bmatrix}.$

Vastaus

$\begin{bmatrix} 10 & 20 \\ -5 & -10 \end{bmatrix}$

Huomaa erityisesti, että $A_{2\times 2}B_{2\times 2} \neq B_{2\times 2}A_{2\times 2}$ !

Ongelma

Miten lasket seuraavien matriisien $A_{2\times 3}=\begin{bmatrix} 3 & 2 & 10\\ 2 & -4 & 7 \end{bmatrix} \quad \text{ja} \quad B_{3\times 2}=\begin{bmatrix} 12 & 1 \\ -1 & 0 \\ 0 & 4 \end{bmatrix}$ tulon $A_{2\times 3}B_{3\times 2}$ ?
Voiko tuloa $B_{3\times 2}A_{2\times 3}$ laskea? Jos voi, minkä kokoinen on tulomatriisi?

Tästä eteenpäin matriisien koot jätetään merkitsemättä - eli meillä ei enää ole alaindeksejä $m \times n$ .

Seuraavat säännöt ovat voimassa silloin, kun laskutoimitukset on määritelty. Seuraavassa , ja ovat matriiseja ja ja reaalilukuja. $\begin{align*} A+B&=B+A, & \quad (A+B)+C&=A+(B+C), \\ (c+d)A&=cA+dA, & \quad c(A+B)&=cA+cB, \\ (AB)C&=A(BC), & \quad A(B+C)&=AB+AC, \\ (A+B)C&=AC+BC. & \quad & \end{align*}$

Lisäksi A+0=A ja A+(-A)=0 , missä on matriisi, jonka jokainen alkio on luku .

Huomaa!

Yhtälöstä ei seuraa että tai .
Yhtälöstä ja ehdosta $A\neq 0$ ei seuraa että .

# Matriisit1

Lisää Stack-tehtäviä matriisien laskutoimituksista löytyy +-merkin takaa.

# Matriisit3

# Matriisit4

Matriisin transpoosia merkitään A^T ja se saadaan vaihtamalla matriisin rivit sarakkeiksi (ja sarakkeet riveiksi).

Esimerkki

Jos $A=\begin{bmatrix} {\color{red}3} & {\color{red}2} & {\color{red}10}\\ 2 & -4 & 7 \end{bmatrix},$ niin $A^T=\begin{bmatrix} {\color{red}3} & 2 \\ {\color{red}2} & -4 \\ {\color{red}10} & 7 \end{bmatrix}.$

Seuraavat kaavat ovat voimassa (kunhan laskutoimitukset on määritelty). Seuraavassa ja ovat matriiseja. $\left(A^T\right)^T=A, \quad (A+B)^T=A^T+B^T, \quad (AB)^T=B^TA^T, \quad (cA)^T=cA^T$

Edellisistä kannattaa erityisesti huomioida kolmannen kaavan matriisien järjestys tulossa.

Esimerkki

Laske $\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} + (-1)\left(\begin{bmatrix} 2 & 0 \\ 4 & 5 \end{bmatrix} + \begin{bmatrix} -3 & 1 \\ -8 & -7 \end{bmatrix}\right)\begin{bmatrix} 3 & 0 \\ 2 & 1 \end{bmatrix}^{T}$

# V4

Matriisi on neliömatriisi, jos sen rivien ja sarakkeiden lukumäärä on sama.
Neliömatriisin kohtien alkiot muodostavat neliömatriisin päädiagonaalin.
Neliömatriisi on symmetrinen, jos se on sama matriisi kuin sen transpoosi.
Neliömatriisi on identtinen matriisi, jos sen kaikki alkiot ovat nollia lukuun ottamatta kohtien alkioita, jotka ovat kaikki :iä. Identtistä matriisia merkitään :llä, ja sille on voimassa millä tahansa matriisilla (kunhan tulo on määritelty).

Esimerkki

$\begin{align*} \begin{bmatrix} 4 & 1 \\ 9 & 0 \end{bmatrix}& \text{ \ on neliömatriisi,} \\ \begin{bmatrix} 4 & {\color{red}9} \\ {\color{red}9} & 0 \end{bmatrix}& \text{ \ on symmetrinen neliömatriisi,} \\ \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}& \text{ \ on identtinen matriisi.} \end{align*}$

Matriisin käänteismatriisi on matriisi , jolle on voimassa yhtälöt AB=I=BA.

Esimerkki

Matriisin $A=\begin{bmatrix} 1 & 3 \\ 2 & 5 \end{bmatrix}$ käänteismatriisi on $B=\begin{bmatrix} -5 & 3 \\ 2 & -1 \end{bmatrix},$ koska $AB= \begin{bmatrix} {\color{red}1} & {\color{red}3} \\ {\color{red}2} & {\color{red}5} \end{bmatrix} \begin{bmatrix} -5 & 3 \\ 2 & -1 \end{bmatrix} = \begin{bmatrix} {\color{red}1} \cdot (-5) + {\color{red}3} \cdot 2 & {\color{red}1} \cdot 3 + {\color{red}3} \cdot (-1) \\ {\color{red}2} \cdot (-5) + {\color{red}5} \cdot 2 & {\color{red}2} \cdot 3 + {\color{red}5} \cdot (-1) \end{bmatrix} =\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}=I$ ja $BA=\begin{bmatrix} -5 & 3 \\ 2 & -1 \end{bmatrix}\begin{bmatrix} {\color{red}1} & {\color{red}3} \\ {\color{red}2} & {\color{red}5} \end{bmatrix} = \begin{bmatrix} (-5) \cdot {\color{red}1} + 3\cdot {\color{red}2} & (-5)\cdot {\color{red}3} + 3 \cdot {\color{red}5} \\ 2 \cdot {\color{red}1} + (-1) \cdot {\color{red}2} & 2 \cdot {\color{red}3} + (-1) \cdot {\color{red}5} \end{bmatrix}=\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}=I.$

Käänteismatriisille on voimassa seuraavat kaavat (kunhan laskutoimitukset on määritelty). $\begin{align*} \left(A^{-1}\right)^{-1}&=A, \quad &(AB)^{-1}&=B^{-1}A^{-1}, \\ \left(A^T\right)^{-1}&=\left(A^{-1}\right)^T, \quad &(cA)^{-1}&=c^{-1}A^{-1}. \end{align*}$

Käänteismatriisi on yksikäsitteinen.
Yksi tapa selvittää, onko jollain matriisilla käänteismatriisia, olisi etsiä matriisi, jolle yhtälöt ovat voimassa.
Käänteismatriisin käytännön laskeminen sivuutetaan tällä kurssilla.
Toinen tapa selvittää, onko käänteismatriisi olemassa, on käyttää apuna niin kutsuttua matriisin determinanttia.

Determinantti on määritelty vain neliömatriisille ja se on luku.

Matriisin determinanttia merkitään esimerkiksi |A| (tai $\det A$ ).

Matriisin , jonka koko on $1\times 1$ , determinantti on matriisin alkio.
Matriisin , jonka koko on $2\times 2$ , determinantti lasketaan kaavalla $|A|= \begin{vmatrix} {\color{red}a_{11}} & {\color{blue}a_{12}} \\ {\color{orange}a_{21}} & a_{22} \\ \end{vmatrix} ={\color{red}a_{11}}a_{22}-{\color{blue}a_{12}}{\color{orange}a_{21}}.$

Esimerkki

Matriisin $A=\begin{bmatrix} {\color{red}1} & {\color{blue}3} \\ {\color{orange}2} & 5 \end{bmatrix}$ determinantti on $|A|={\color{red}1}\cdot 5-{\color{blue}3}\cdot {\color{orange}2}=-1.$

Matriisin , jonka koko on $3\times 3$ , determinantti voidaan laskea kaavalla $\begin{align*} |A|&= \begin{vmatrix} a_{11} & {\color{red}a_{12}} & {\color{blue}a_{13}} \\ a_{21} & {\color{red}a_{22}} & {\color{blue}a_{23}} \\ a_{31} & {\color{red}a_{32}} & {\color{blue}a_{33}} \end{vmatrix}= a_{11}\begin{vmatrix} {\color{red}a_{22}} & {\color{blue}a_{23}} \\ {\color{red}a_{32}} & {\color{blue}a_{33}} \end{vmatrix} - {\color{red}a_{12}}\begin{vmatrix} a_{21} & {\color{blue}a_{23}} \\ a_{31} & {\color{blue}a_{33}} \end{vmatrix}+ {\color{blue}a_{13}}\begin{vmatrix} a_{21} & {\color{red}a_{22}} \\ a_{31} & {\color{red}a_{32}} \end{vmatrix} \\ &=a_{11}\left(a_{22}a_{33}-a_{23}a_{32}\right)-a_{12}\left(a_{21} a_{33}-a_{23}a_{31}\right)+a_{13}\left(a_{21}a_{32}-a_{22}a_{31}\right). \label{3x3} \end{align*}$

Esimerkki

Matriisin $\begin{bmatrix} 0 & 1 & 2 \\ 4 & 2 & 1 \\ 3 & 2 & 5 \end{bmatrix}$ determinantti on $\begin{vmatrix} 0 & 1 & 2 \\ 4 & 2 & 1 \\ 3 & 2 & 5 \end{vmatrix}=0\cdot (2\cdot 5-1\cdot 2)-1(4\cdot 5-1\cdot 3)+2(4\cdot 2-2\cdot3)=-13.$

# V5

$n\times n$ kokoisen matriisin determinantti voidaan laskea seuraavasti.

Merkitään symbolilla $A_{ij}$ sellaista matriisia, joka saadaan matriisista poistamalla siitä s rivi ja s sarake. Esimerkiksi $A_{23}$ on matriisi, joka on saatu matriisista poistamalla toinen rivi ja kolmas sarake.

Näitä matriiseja soveltamalla saadaan laskettua matriisin determinantti: $|A|=a_{11}\cdot C_{11}(A)+a_{12}\cdot C_{12}(A)+\ldots + a_{1n}\cdot C_{1n}(A),$ jossa on merkitty $C_{ij}(A)=\left(-1\right)^{i+j}|A_{ij}|$ . Tässä kaavassa determinantti on niin sanotusti kehitetty ensimmäisen rivin suhteen (eli kertoimina on $a_{11}, a_{12}, \ldots a_{1n}$ ).

# Det1

# Det2

Neliömatriisilla on käänteismatriisi jos ja vain jos $|A|\neq 0$ .

Ongelma

Onko matriisilla $A=\begin{bmatrix} 2 & -3 \\ -2 & 3 \end{bmatrix}$ käänteismatriisi?

Vihje

Laske matriisin determinantti ja katso onko se eri suuri kuin nolla.

Vastaus

Ei ole käänteismatriisia, sillä determinantti on .

# Kaanteismatriisi1

# Kaanteismatriisi2

3.2 Lineaarinen yhtälöryhmä ja matriisit

Lineaarinen yhtälöryhmä $\left\{ \begin{array}{ccccccccc} a_{11}x_1&+&a_{12}x_2&+&\ldots & +&a_{1n}x_n&=&b_1\\ a_{21}x_1&+&a_{22}x_2&+&\ldots & +&a_{2n}x_n&=&b_2\\ &\vdots &&\vdots &&\vdots &&\vdots \\ a_{m1}x_1&+&a_{m2}x_2&+&\ldots & +&a_{mn}x_n&=&b_m\\ \end{array} \right.$ voidaan aina kirjoittaa matriisimuotoon $A\mathbf{x}=b$ , jossa $\begin{align*} A&= \begin{bmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ a_{21} & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & \dots & a_{mn} \end{bmatrix}, \\ \mathbf{x}&= \begin{bmatrix} x_1 & x_2 & \dots & x_n \end{bmatrix}^T, \\ \mathbf{b}&=\begin{bmatrix} b_1 & b_2 & \dots & b_m \end{bmatrix}^T. \end{align*}$ Matriisia kutsutaan kerroinmatriisiksi ja matriisia $\mathbf{b}$ vakiomatriisiksi tai vakiovektoriksi.

Esimerkki

Yhtälöparilla $\left\{ \aligned -2x+y &=0 \\ x+y &=3 \endaligned \right.$ on täsmälleen yksi ratkaisu: x = 1 ja y = 2 .

Tämä yhtälöpari on matriisimuodossa $\begin{bmatrix} -2 & 1 \\ 1 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \end{bmatrix}= \begin{bmatrix} 0 \\ 3 \end{bmatrix}.$

Lineaarisella yhtälöryhmällä on yksikäsitteinen ratkaisu, jos kerroinmatriisin determinantti ei ole nolla.

Ratkaisu löytyy lineaarisen yhtälöryhmän matriisiesityksen avulla: Olkoon $A\mathbf{x}=\mathbf{b}$ lineaarisen yhtälöryhmän matriisiesitys. Koska determinantti ei ole nolla, matriisilla on käänteismatriisi $A^{-1}$ ja yhtälöryhmän ratkaisuksi saadaan $\mathbf{x}=A^{-1}\mathbf{b}$ .

Kyseessä on haluttu ratkaisu, sillä kertomalla yhtälö $A\mathbf{x}=\mathbf{b}$ puolittain käänteismatriisilla $A^{-1}$ , saadaan yhtälö $A^{-1}A\mathbf{x}=A^{-1}\mathbf{b}$ . Yhtälö $\mathbf{x}=A^{-1}\mathbf{b}$ seuraa tästä, koska käänteismatriisin määritelmän nojalla $A^{-1}A=I$ ja $I\mathbf{x}=\mathbf{x}$ .

# Matriisit

3.2.1 Cramerin sääntö

Cramerin sääntö

Olkoon neliömatriisi. Lineaarisen yhtälöryhmän $A\mathbf{x}=\mathbf{b}$ , jossa $|A|\neq 0$ , ratkaisut saadaan kaavalla $x_i=\frac{|B_i|}{|A|}\qquad i = 1,2,\ldots,n,$ jossa matriisi B_i on saatu matriisista korvaamalla sarake yhtälöryhmän vakiovektorilla $\mathbf{b}$ .

Cramerin sääntöä voidaan käyttää vain lineaariselle yhtälöryhmälle, jossa tuntemattomia muuttujia , $i = 1,2,\ldots,n$ , on yhtä monta kuin yhtälöitä.
Lineaarisen yhtälöryhmän ratkaisun hakemiseen on yleisempiä ja nopeampia keinoja kuin Cramerin sääntö, mutta Cramerin sääntö mainitaan usein taloustieteen sovelluksissa; esimerkiksi ympäristötaloustieteen komparatiivisessa statiikassa.

Ongelma

Ratkaise tuttu yhtälöparimme $\left\{ \aligned -2x+y &=0 \\ x+y &=3 \endaligned \right.$ Cramerin säännön avulla.

# V6

Esimerkki

Ratkaistaan matriisimuodossa kirjoitettu yhtälöryhmä $\begin{bmatrix} 2 & {\color{blue}1} \\ 1 & {\color{blue}3} \\ \end{bmatrix} \begin{bmatrix} x \\ y\\ \end{bmatrix} = \begin{bmatrix} {\color{red}1} \\ {\color{red}4}\\ \end{bmatrix}$ käyttäen Cramerin sääntöä. Saadaan $x=\frac{\begin{vmatrix} {\color{red}1} & {\color{blue}1} \\ {\color{red}4} & {\color{blue}3} \\ \end{vmatrix}}{\begin{vmatrix} 2 & {\color{blue}1} \\ 1 & {\color{blue}3} \\ \end{vmatrix}}=-\frac{1}{5} \quad \text{ja} \quad y=\frac{\begin{vmatrix} 2 & {\color{red}1} \\ 1 & {\color{red}4} \\ \end{vmatrix}}{ \begin{vmatrix} 2 & {\color{blue}1} \\ 1 & {\color{blue}3} \\ \end{vmatrix}}=\frac{7}{5}.$

Esimerkki

Yhtälöryhmiin törmätään esimerkiksi fysiikan virtapiirilaskuissa. Fysiikan lakeja soveltamalla ollaan muodostettu alla oleva yhtälöryhmä. Halutaan selvittää sähkövirrat I_1 , I_2 ja I_3 , kun , R_1 , R_2 ja R_3 ovat tunnettuja.

$\begin{cases} I_1 = I_2 + I_3 \\ E - R_1I_1 - R_2I_2 = 0 \\ E - R_1I_1 - R_3I_3 = 0 \end{cases}$

Yhtälöryhmä voidaan kirjoittaa seuraavassa muodossa.

$\begin{cases} I_1 - I_2 - I_3 = 0 \\ R_1I_1 + R_2I_2 = E \\ R_1I_1 + R_3I_3 = E \end{cases}$

Ratkaistaan yhtälöryhmä Cramerin säännöllä. Nyt

$D = \begin{vmatrix} 1 & -1 & -1 \\ R_1 & R_2 & 0 \\ R_1 & 0 & R_3 \end{vmatrix} = R_2 R_3 + R_1R_3 + R_1R_2,$

$D_{I_1}=\begin{vmatrix} 0 & -1 & -1 \\ E & R_2 & 0 \\ E & 0 & R_3 \end{vmatrix} = R_3E + R_2E,$

$D_{I_2}=\begin{vmatrix} 1 & 0 & -1 \\ R_1 & E & 0 \\ R_1 & E & R_3 \end{vmatrix} = R_3E + R_1E,$

$D_{I_3}=\begin{vmatrix} 1 & -1 & 0 \\ R_1 & R_2 & E \\ R_1 & 0 & E \end{vmatrix} = R_2E + R_1E.$

Näin ollen ratkaisuksi saadaan

$\begin{cases} I_1 = \dfrac{D_{I_1}}{D} = \dfrac{R_3E + R_2E}{R_2 R_3 + R_1R_3 + R_1R_2} \\ I_2 = \dfrac{D_{I_2}}{D} = \dfrac{R_3E + R_1E}{R_1 R_3 + R_1R_3 + R_1R_2} \\ I_3 = \dfrac{D_{I_3}}{D} = \dfrac{R_2E + R_1E}{R_2 R_3 + R_1R_3 + R_1R_2} \end{cases}$

Lineaarialgebraa ja matriisilaskentaa ei käytetä pelkästään lineaaristen yhtälöryhmien ratkaisemiseen. Opitut taidot ja menetelmät ovat hyödyksi differentiaali- ja differenssiyhtälöiden ratkaisemisessa (näitä käytetään mallinnuksessa), optimoinnissa, koneoppimisessa, tilastotieteessä ja ekonometriassa.

Lineaarialgebraa ja matriisilaskentaa voi opiskella esimerkiksi matematiikan ja tilastotieteen laitoksen kursseilla MAT11002 ja MAT21001. Kattava katsaus aiheisiin löytyy Pekka Pankan luentomonisteesta.

Tehtäviä

Olkoot $A = \begin{bmatrix} 5 & 1 \\ 2 & -2 \\ \end{bmatrix}\!, \; B = \begin{bmatrix} 3 & -2 & 4 \\ 2 & 4 & 0 \\ \end{bmatrix} \quad \text{ja} \quad C = \begin{bmatrix} 2 & 1 \\ 0 & 3 \\ \end{bmatrix}$
1. Laske .
2. Laske .
3. Voiko tuloa laskea? Jos voi, laske.
4. Voiko tuloa laskea? Jos voi, laske.

1. Laske matriisien $\begin{bmatrix} -6 & 7 \\ 4 & 2 \\ \end{bmatrix} \quad \text{ja} \quad \begin{bmatrix} 3 & 1 & 0 \\ 3 & 2 & 0 \\ -1 & -7 & 0 \end{bmatrix}$ determinantit.
2. Ratkaise yhtälö $\begin{vmatrix} x-1 & 4 \\ 1 & 2x \\ \end{vmatrix} = 0.$

1. Kirjoita yhtälöpari matriisimuodossa. $\left\{ \aligned 4x + 10y +1 &=0 \\ -5x+ 3y &=-3 \endaligned \right.$
2. Ratkaise yhtälöpari käyttäen niin kutsuttua Cramerin sääntöä.

# geo2taso15

# geo2taso16

Taloustieteen osasto, Helsingin yliopisto, elokuu 2025

Jarmo Jääskeläinen
jarmo.jaaskelainen@helsinki.fi

1. Integraali

1.1 Integrointikaavat ja analyysin peruslause

Esimerkki

Esimerkki

Esimerkki

1.1.1 Sääntöjä integraalille

1.1.2 Integrointikaavoja

Esimerkki

Ongelma

Esimerkki

Ongelma

Ongelma

Integrointi 4

Integrointi 5

Integrointi 6

Yhdistetyn funktion integrointi 2

Määrätty integraali ja pinta-ala

1.1.3 Analyysin peruslause

Sijoitusmerkintä

1.1.4 Sääntöjä määrätylle integraalille

Esimerkki

Esimerkki

Esimerkki

Esimerkki

Ongelma

Ongelma

Määrätty integraali 3

Määrätty integraali 4

Tehtäviä

2. Todennäköisyyslaskentaa

2.1 Miksi/Mitä todennäköisyyslaskentaa?

Esimerkki

2.2 Klassinen todennäköisyys

2.2.1 Ominaisuuksia todennäköisyysfunktiolle

Esimerkki (Nopanheitto)

Esimerkki (Kahden nopanheiton summa)

2.2.2 Tuloperiaate

Esimerkki

Esimerkki

2.2.3 Summaperiaate

Esimerkki

Esimerkki

Esimerkki

2.2.4 Geometrinen todennäköisyys

Esimerkki

Esimerkki

Esimerkki

Esimerkki

2.2.5 Ehdollinen todennäköisyys

Esimerkki

Esimerkki

2.3 Odotusarvo

Esimerkki

2.3.1 Odotusarvo

Esimerkki

Ongelma

2.3.2 Varianssi ja keskihajonta

Esimerkki

2.3.3 Odotusarvon lineaarisuus

Seuraus

2.4 Jatkuvat todennäköisyysjakaumat

2.4.1 Tiheysfunktio

Tiheysfunktio

Kertymäfunktio

Esimerkki

Ongelma

2.4.2 Tasajakauma

Esimerkki

2.4.3 Odotusarvo ja varianssi

2.3.3 Odotusarvon lineaarisuus

Seuraus

Esimerkki

2.4.4 Esimerkki

2.4.5 Muita jatkuvia jakaumia

Tehtäviä

Todari 1

Todari 2

Todari 3

Todari 4

Todari 5