In the fall of 1972 President Nixon announced that the rate of increase of inflation was decreasing. This was the first time a sitting president used the third derivative to advance his case for reelection.

- Rossi, Hugo (1996) Mathematics Is an Edifice, Not a Toolbox, Notices of AMS, volume 43, number 10

Tämä on Helsingin yliopiston Ympäristö- ja elintarviketalouden kandiohjelman Matematiikka 2:n (YET-034b) kurssimateriaali. Kurssi on jatkoa Matematiikka 1 -kurssille.

Kysymykset ja kommentit: Jarmo Jääskeläinen jarmo.jaaskelainen@helsinki.fi (Taloustieteen osasto, Helsingin yliopisto)

Kurssin aiheet ovat

Derivaatta
Eksponenttifunktio
Ääriarvot
Usean muuttujan funktiot

Aihepiireihin liittyviä harjoitustehtäviä on koottu lukujen loppuun.

Materiaali perustuu kirjaan

Sydsæter, Knut; Hammond, Peter J.; Strøm, Arne; Carvajal, Andrés, Essential mathematics for economic analysis (Fifth edition), Harlow, United Kingdom: Pearson Education, 2016.
Kirja on saatavilla Helkassa.
Alla kirjaan viitataan seuraavasti [EMEA, kohta].

Apuna on käytetty myös Pauli Lapin Matematiikkaa taloustieteilijöille I -kurssin luentomonistetta ja virikkeitä on saatu Emma Leppälän ja Anni Laitisen peruskurssien luennoista Jyväskylän yliopistossa.

TIMin käytöstä 👈

Oranssit palkit: Tekstin oikeassa laidassa on oransseja palkkeja niissä kohdissa, joita et ole vielä lukenut. Ne auttavat sinua näkemään, missä olet menossa. Voit hävittää palkkeja klikkaamalla niitä sitä mukaan kun luet materiaalia.
Keltaiset palkit: Mikäli kappale muuttuu sen jälkeen kun olet sen lukenut (eli klikannut oranssin palkin pois), ilmestyy sen laitaan keltainen palkki. Sen vieressä on painike, josta voit tarkistaa mitä tekstissä on muuttunut.
- Jos koet palkit turhiksi, klikkaa vasemmalla ylhäällä hammasrattaan kuvaa. Sitten paina Merkitse kaikki luetuksi, jolloin palkit häviävät koko sivulta.
Kommentti: Jos jokin asia jää epäselväksi tai epäilet, että materiaalissa on virhe, voit klikata kappaleen oikeassa reunassa C-merkkiä, josta saa lisättyä kommentin. Kommentin voi asettaa näkymään vain itselle tai sitten kaikille, jolloin opettaja voi lukea kommentin ja vastata siihen.
"Sulkeutuvat kappaleet", kuten tämä, aukeavat painamalla -merkkiä tai kappaleen otsikkoa.

Alla olevan materiaalin joukkoon on laitettu lyhyitä videoita auttaaan itseopiskelussa. Nämä löytyvät -symbolilla.

Materiaalin seassa on myös pieniä tehtäviä, joiden oikeat vastaukset saa näkyviin saman tien. Tehtävillä voi harjoitella peruslaskutaitoa tai tarkastaa ymmärrystään opiskeltavasta aiheesta. Nämä tehtävät eivät vaikuta kurssisuorituksen pistemäärään. Osa tehtävistä on niin kutsuttuja STACK-tehtäviä. Suurin osa STACK-tehtävistä on Toni Hosiaisluoman käsialaa.

STACK-tehtävistä 👈

Osa näistä tehtävistä on niin kutsuttuja STACK-tehtäviä. STACK-tehtävät ovat taustaltaan sinisiä . Osa STACK-tehtävistä on satunnaistettuja eli saman tyylisiä harjoituksia voi tehdä useita - uuden tehtävän saa arvottua itselleen painikkeella Arvo uusi tehtävä, kunhan entiseen on vastattu jotakin. Vanhoja tehtäviä ja vastauksia voi selata ja kokeilla uudelleen. STACK-tehtävät on suunniteltu siten, että tehtävä lasketaan kynällä ja paperilla - ja vastaus tarkistetaan tietokoneella. STACK-tehtävien vastausten syöttäminen muistuttaa graafisen laskimen käyttämistä.

Peruslaskutoimitusten syöttäminen onnistuu seuraavasti:

Operaatio	Merkki
Yhteenlasku	+
Vähennyslasku	-
Kertolasku	*
Jakolasku	/
Potenssiin korotus	^
Sulut (ryhmittely)	()

Huomaa, että kertolaskua ei aina merkitä lausekkeissa, mutta STACK-vastauksissa jokainen kertolasku tulee merkitä. Esimerkiksi lauseke x + 2y annetaan muodossa x + 2*y.

Sulkujen avulla määritellään mihin lausekkeeseen laskutoimitukset kohdistuvat. Esimerkiksi $2^{1 + x}$ kirjoitetaan 2^(1 + x), jotta potenssiin korotus kohdistuu oikeaan lausekkeeseen.

# 1

1. Derivaatta

Tässä osassa käsitellään seuraavia asioita

derivaatta
joitakin derivointisääntöjä ja -kaavoja
funktion kasvavuus ja vähenevyys derivaatan avulla
jousto

Osiota vastaa [EMEA, 6.1-6.3, 6.6-6.9 ja 7.7].

Lämmittelytehtävä

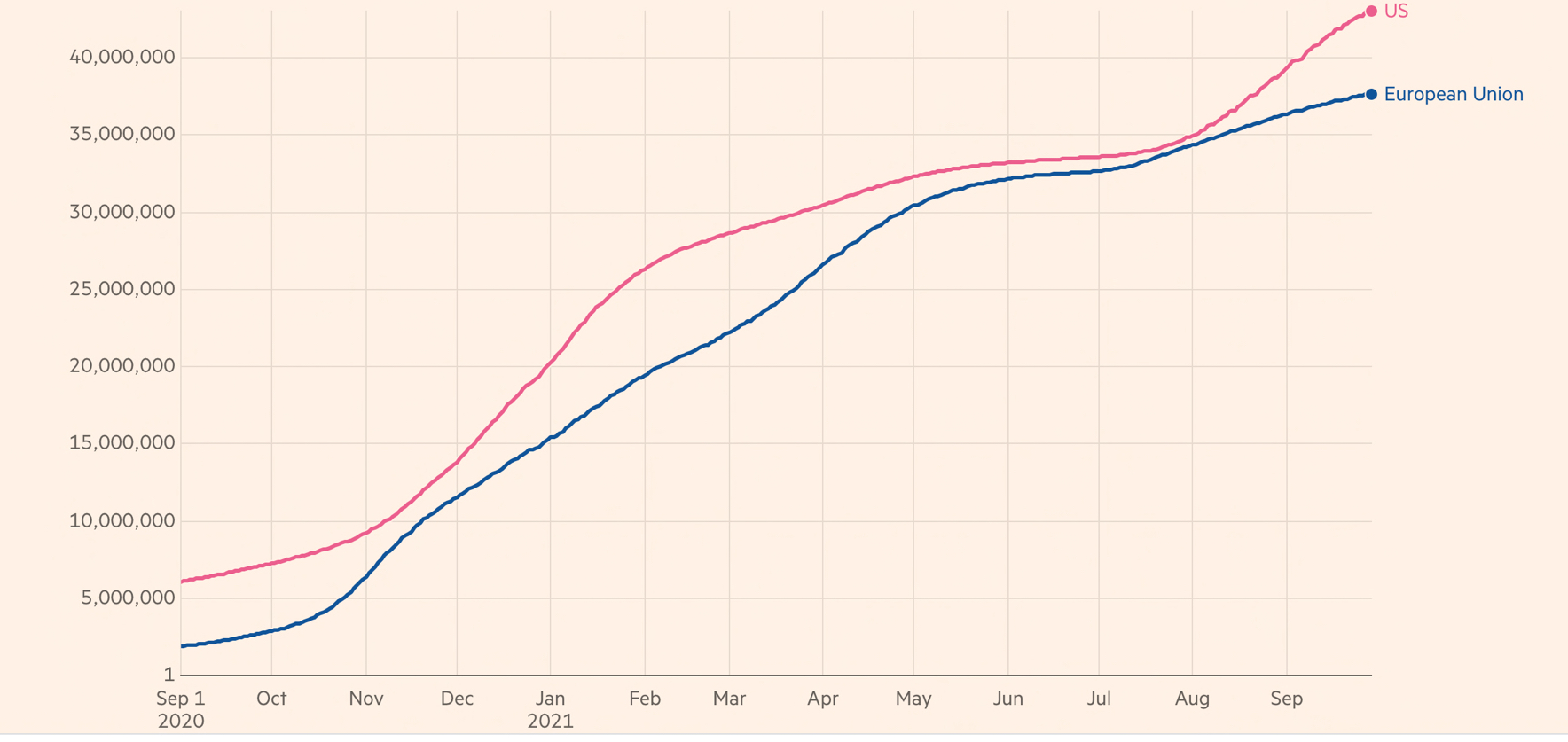
Varmistettujen Covid 19 -tartuntojen lukumäärä

Financial Times analysis of data from Johns Hopkins CSSE, World Health Organization, national public health agencies or ministries of heath. Interactive version: ft.com/covid19

Yllä olevassa kuvassa on koronatartuntojen lukumäärä ajanfunktiona Yhdysvalloissa ja EU:ssa.

Mikä on keskimääräinen lisääntymisnopeus ajanjaksolla 1. syyskuuta 2020 - 1. helmikuuta 2021?
Mikä on hetkellinen nopeus 15. joulukuuta 2020?

Hieman epämääräisesti sanoen funktion derivaatta pisteessä x_1 on funktion "hetkellinen muutosnopeus" kyseisessä kohdassa.

Tätä muutosnopeuden tarkastelua tarvitaan esimerkiksi, kun

halutaan tietää kuinka nopeasti lainapääoma pienenee
halutaan tietää kappaleen nopeus, kun tiedämme etäisyyden lähtöpisteestä ajan funktiona
etsitään suurinta tai pienintä arvoa
tutkitaan populaatiomalleja
halutaan selvittää miten joustavaa/herkkää kysyntä on muutoksille hintatasossa
halutaan tietää kuinka paljon tuotantokustannukset kasvavat, kun tuotannon kokoa kasvatetaan "yhdellä yksiköllä" (rajakustannus)

Derivaatta on pääroolissa, kun alamme optimoimaan eli etsimään parasta mahdollista tilannetta. Tästä näemme esimerkkejä luvussa 3 ääriarvojen etsinnässä.

Esimerkki

Jos yrityksen kustannukset riippuvat tuotantomäärästä funktion C(q) mukaisesti, niin funktion derivaatta (taloustieteen termein niin sanottu rajakustannus) pisteessä kertoo, kuinka paljon kustannus likimäärin kasvaa, jos tuotantomäärä kasvaa yhdellä yksiköllä.

Taloustieteessä rajakustannusten ja muiden rajasuureiden yhteydessä tulkintana sanotaan yleensä (kuten edellä): "Kuinka paljon tutkittava suure kasvaa, kun muuttuja kasvaa yhdellä yksiköllä." Sanonta ei ole kovin tarkka, vaan sillä yritetään havainnollistaa derivaatan käsitettä eli suureen "hetkellistä" muutosnopeutta.

Lähestytään derivaattaa ensin graafisesti/geometrisesti, jonka jälkeen otetaan käyttöön liuta derivoimiskaavoja, joita saa käyttää.

1.1 Sekantti

Käyrän sekantti on suora, joka kulkee kahden käyrällä olevan pisteen kautta.

1.1.1 Funktion kuvaajan sekantti

Jos pisteet (x_1,y_1) ja (x_2,y_2) ovat funktion kuvaajalla eli y_1 = f(x_1) ja y_2 = f(x_2) , niin näiden pisteiden kautta kulkevan sekantin kulmakerroin on $k = \frac{f(x_2) - f(x_1)}{x_2 - x_1} \quad \quad \text{ (``erotusosamäärä'')} \qquad \text{eli}\quad \frac{\text{funktion arvon muutos}}{\text{$x$n muutos}}$

# kayranTangentti

1.2 Tangentti

Käyrän tangentti on suora, joka "sivuaa" käyrää annetussa pisteessä.

kuvaa käyrän jyrkkyyttä
ei ole aina olemassa!

1.2.1 Funktion kuvaajan tangentti

Funktion kuvaajan y = f(x) tangentti pisteessä (x_1,y_1) on suora,

joka kulkee pisteen kautta ja
jonka kulmakerroin on pisteiden ja kautta kulkevan sekantin kulmakertoimen raja-arvo, kun $(x_2, y_2) \longrightarrow (x_1, y_1)$ ("piste menee kohti pistettä ) eli $k = \lim_{x_2 \to x_1} \frac{f(x_2) - f(x_1)}{x_2 - x_1}$ jos tämä raja-arvo on olemassa.

Kun merkitään , saadaan sama raja-arvo ilmaistuna myös toisessa muodossa: $k = \lim_{h \to 0} \frac{f(x_1 +h)-f(x_1)}{h}$

Tämä raja-arvo on funktion erotusosamäärän raja-arvo pisteessä x_1 . Tämä raja-arvo tulee olemaan derivaatan määritelmämme.

Tangenttisuoran yhtälö on siis y = k(x-x_1) + y_1.

# gv3_1

1.3 Derivaatta

Funktion derivaatta pisteessä $\, x_1$ , merkitään $\, f'(x_1)$ , on raja-arvo $\lim_{h \to 0} \frac{f(x_1+h) - f(x_1)}{h},$ jos tämä raja-arvo on olemassa.

Yllä $\lim_{h \to 0}$ tarkoittaa, että " menee kohti :aa".
Jos tämä raja-arvo on olemassa, sanotaan, että on derivoituva pisteessä .
Luku on funktion kuvaajan tangentin kulmakerroin pisteessä $\, (x_1, f(x_1))$ .

Huomautus

Aina derivaattaa ei siis ole olemassa. Esimerkiksi itseisarvofunktiolla , f(x) = |x| , ei ole derivaattaa nollassa eli pisteessä x = 0 . Itseisarvo-käsite on mainittu Matematiikka 1 -kurssilla.

# V8

# derivaatanMerkinta

1.3.1 Derivaatan merkintätapoja

Derivaatalle on useita erilaisia merkintätapoja, jotka tarkoittavat samaa: $f'(x), \quad D f(x), \quad D_x f(x), \quad \frac{d}{dx} f(x)$

Usein myös , jolloin voidaan merkitä tai $\cfrac{dy}{dx}$ .
Toisinaan merkitään lyhyesti tai kun on selvää, minkä muuttujan suhteen derivoidaan.

1.3.2 Derivaattafunktio

Derivaatan arvot eri kohdissa muodostavat uuden funktion , joka on määritelty kaikkialla, missä on derivoituva. Derivaattafunktion arvo pisteessä x_1 on siis funktion derivaatta pisteessä x_1 .

Derivaattafunktion laskemista kutsutaan derivoimiseksi. Myös derivaattafunktiota kutsutaan derivaataksi.

Lisää harjoitusta derivaatan peruskäsitteisiin voi etsiä Kisällioppinen-sivustolta.

# derivointisaannot

1.4 Derivointisääntöjä

Vakion derivaatta on nolla eli missä on jokin reaaliluku (ja derivoituva funktio määritellään ).
$D(x^r) = r x^{r-1} \quad\quad \text{kun} \;\; r \neq 0$

Jos ja ovat derivoituvia pisteessä , niin myös funktiot f+g ja ovat derivoituvia, samoin $\, \frac{f}{g}$ kunhan $g(x) \neq 0$ .

$\begin{array}{lll} \text{summa:} & (f+g)'(x) = f'(x) + g'(x) , & \quad \text{ } \\[4pt] \text{tulo:} & (fg)'(x) = f'(x)g(x) + f(x)g'(x) \\[8pt] \text{osamäärä:} & \displaystyle{\left(\frac{f}{g}\right)'\!\!(x) = \frac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}}, & \quad \text{jos } g(x) \not = 0 \\ \end{array}$

Erityisesti funktion, joka määritellään kaavalla af(x) , derivaatta on af'(x) (eli vakion voi siirtää derivointioperaation eteen).

Esimerkkejä

$\, f(x) = x^2 + 3: \quad f'(x) = 2x$
$\, g(x) = 10x^7-\frac{1}{2}x^5+3: \quad g'(x) = 70x^6-\frac{5}{2}x^4$

# V9

Esimerkki

Esimerkiksi funktion , $f(x)=x^{1/2}$ , derivaatta on $f'(x)=\frac{1}{2}x^{1/2-1}=\frac{1}{2}x^{-1/2}=\frac{1}{2}\cdot \frac{1}{x^{1/2}}=\frac{1}{2\sqrt{x}}.$

Esimerkki

Funktion , $f(x)=1/x=x^{-1}$ derivaatta on $f'(x)=-x^{-2}=-1/x^2$ .

# V10

Esimerkki

Jos funktion lausekkeessa on parametreja, parametrit ajatellaan vain tavallisiksi vakioiksi ja derivaatan laskemisessa sovelletaan yllä olevia sääntöjä.

Esimerkiksi funktion , f(x)=a-bx^c , derivaatta on $f'(x)=-cbx^{c-1}$ .

Esimerkki

Jos meillä on monopoliyritys, jonka tulofunktio on $R(q)=\left(12-\frac{1}{2} q\right)q$ ja kustannusfunktio on $C(q) = \frac{q^3}{27} + \frac{q^2}{4} + 3q + 12,$ missä on tuotettu määrä.

Tällöin yrityksen voittofunktio on $\pi(q)=R(q)-C(q) = \left(12-\frac{1}{2} q\right)q - \left(\frac{q^3}{27} + \frac{q^2}{4} + 3q + 12\right).$

Voiton muutosnopeus on voittofunktion derivaatta $\pi'(q) = 12 - q - \left(\frac{q^2}{9} + \frac{q}{2} + 3\right) = -\frac{q^2}{9} + \frac{q}{2} + 9$

Joskus derivointi on helpompaa, kun huomaa funktion muodostuvan sisä- ja ulkofunktiosta (katso Matematiikka 1:n yhdistetyt funktiot).

Jos on derivoituva pisteessä ja on derivoituva pisteessä g(x) , niin yhdistetty funktio f(g(x)) on derivoituva pisteessä ja D f(g(x)) = f'(g(x))g'(x)

Huomaa

Osamäärän derivointikaavaa $\displaystyle{\left(\frac{f}{g}\right)'\!\!(x) = \frac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}}, \quad \text{jos } g(x) \not = 0$ ei tarvitse muistaa enää ulkoa, sillä tulon derivointikaavasta ja yhdistetyn funktion derivoinnista saadaan: $\begin{align*} \left(\frac{f}{g}\right)'\!\!(x) &= (fg^{-1})'(x) = f'(x)g(x)^{-1} + f(x)(g^{-1})'(x) = f'(x)g(x)^{-1} - f(x)g'(x)g(x)^{-2} \\ &= \frac{f'(x)g(x) - f(x) g'(x)}{\left(g(x)\right)^2}. \end{align*}$

Esimerkki

Määritetään funktion derivaatta kahdella tavalla.

Tapa 1

Avataan sulut käyttämällä muistikaavaa (a+b)^2=a^2+2ab+b^2 ja derivoidaan sitten.

$f(x)=(4x+3)^2=(4x)^2+2\cdot 4x \cdot 3 + 3^2 = 16x^2 + 24x + 9$

f'(x) = 32x + 24

Tapa 2

Käytetään yhdistetyn funktion derivoimissääntöä $D(u(s(x)))=u'(s(x))\cdot s'(x)$ . Valitaan u(x)=x^2 ja s(x)=4x+3 . Tällöin u'(x)=2x ja s'(x)=4 .

$f'(x)=2(4x+3)\cdot4=8(4x+3)=32x+24$

Molemmilla tavoilla saatiin siis sama tulos, kuten pitääkin.

Määritetään funktion derivaatta kahdella tavalla.

Tapa 1

Avataan sulut ja derivoidaan sitten.

$\begin{align*} g(x) &= (4x+3)^3 = (4x+3)(4x+3)^2 \\ &= (4x+3)(16x^2+24x+9) \\ &= 64x^3 + 96x^2 + 36x + 48x^2 + 72x + 27\\ &= 64x^3 + 144x^2+108x+27 \end{align*}$

Näin ollen saadaan g'(x) = 192x^2 + 288x + 108 .

Tapa 2

Käytetään yhdistetyn funktion derivoimissääntöä $D(u(s(x)))=u'(s(x))\cdot s'(x)$ . Valitaan u(x)=x^3 ja s(x)=4x+3 . Tällöin u'(x)=3x^2 ja s'(x)=4 .

$g'(x) = 3(4x+3)^2 \cdot 4 = 12(4x+3)^2$

Saatu tulos on sama kuin aikaisemmalla tavalla, koska

12(4x+3)^2=12(16x^2+24x+9)=192x^2+288x+108 .

Huomioitavaa on, että ensimmäisellä tavalla tehtäessä joudutaan näkemään huomattavasti enemmän vaivaa, vaikka eksponentissa on vain luku kolme.

Määritetään funktion $h(x)=(4x+3)^{20}$ derivaatta.

Vaikka tässäkin tilanteessa olisi teoriassa mahdollista avata sulut ja derivoida sitten, tämä olisi erittäin työlästä. Binomin 4x+3 korottaminen kolmanteen potenssiin oli jo varsin työlästä. Korottaminen potenssiin 20 ei olisi missään määrin mielekästä (varsinkaan käsin). Tällaisessa tilanteessa yhdistetyn funktion derivoimissääntö näyttää hyödyllisyytensä.

Valitaan $u(x)=x^{20}$ ja s(x)=4x+3 . Tällöin $u'(x)=20x^{19}$ ja s'(x)=4 . Saadaan $h'(x)=20(4x+3)^{19} \cdot 4 = 80(4x+3)^{19}$ .

Esimerkki

$\,f(x) = (x^2+1)^{30} \,$ : $\quad f'(x) = 30(x^2+1)^{29} \cdot 2x = 60x(x^2+1)^{29}$

Esimerkki

$\,f(x) = \sqrt{x^2+1} \,$ : $\quad f'(x) = \cfrac{1}{2\sqrt{x^2+1}} \cdot 2x = \cfrac{x}{\sqrt{x^2+1}}$

# V11

Esimerkki

Esimerkiksi funktion , f(x)=(1+x)/(x^3-2) derivaatta on $f'(x)=\frac{1\cdot (x^3-2)-(1+x)\cdot 3x^2}{(x^3-2)^2}=\frac{-2x^3-3x^2-2}{(x^3-2)^2}.$

# V5

# funktionmonotonisuus

1.5 Funktion monotonisuus

Funktion monotonisuus tarkoittaa, että funktio on joko kasvava kaikkialla tai vähenevä kaikkialla.

Kasvavuutta voidaan tarkastella myös eri väleillä. Kasvavuuden (ja vähevyyden) näkee funktion kuvaajasta: funktio on kasvava, kun funktion arvot kasvavat liikuttaessa vasemmalta oikealle. Funktio on vähevevä, kun arvot vähenevät.

Funktio , , on välillä kasvava (nuoli yläviistoon) ja välillä vähenevä (nuoli alaviistoon). — Funktio , $f(x) = \frac{1}{3}x^{3}-\frac{1}{2}x^{2} -2x$ , on välillä kasvava (nuoli yläviistoon) ja välillä vähenevä (nuoli alaviistoon).

Funktio , $f(x) = \frac{1}{3}x^{3}-\frac{1}{2}x^{2} -2x$ , on välillä kasvava (nuoli yläviistoon) ja välillä vähenevä (nuoli alaviistoon).

# kasvava-vaheneva

1.5.1 Funktion kasvavuus ja vähenevyys

Välillä määritelty funktio on

kasvava välillä , jos $x_1 < x_2 \implies f(x_1) \leq f(x_2) \quad \text{kaikilla }\, x_1, x_2 \in I$
vähenevä välillä , jos $x_1 < x_2 \implies f(x_1) \geq f(x_2) \quad \text{kaikilla }\, x_1, x_2 \in I$
aidosti kasvava välillä , jos $x_1 < x_2 \implies f(x_1) < f(x_2) \quad \text{kaikilla }\, x_1, x_2 \in I$
aidosti vähenevä välillä , jos $x_1 < x_2 \implies f(x_1) > f(x_2) \quad \text{kaikilla }\, x_1, x_2 \in I$

# monotonisuus

1.5.2 Monotonisuus

Funktio on

monotoninen välillä , jos se on
- kasvava välillä tai
- vähenevä välillä
aidosti monotoninen välillä , jos se on
- aidosti kasvava välillä tai
- aidosti vähenevä välillä

Katso (aidosti) kasvavuuden ja vähenevyyden käsitteet yltä (1.5.1). Funktion pitää siis olla koko välillä joko kasvava tai vähenevä!

Huomaa

Kasvavuuden ja vähenevyyden voi tarkastaa funktion derivaatan avulla. Tämä on usein kätevämpi tapa. Tähän palataan seuraavien esimerkkien jälkeen.

Esimerkki

Funktio $f \colon \R \to \R$ , $\, f(x) = 2x - 3$ , on aidosti kasvava funktio kaikilla reaaliluvulla, koska $x_1 < x_2 \qquad \Longleftrightarrow \qquad 2x_1 < 2x_2 \qquad \Longleftrightarrow \qquad 2x_1 - 3 < 2x_2 -3 \qquad \Longleftrightarrow \qquad f(x_1) < f(x_2)$

Esimerkkejä

Funktio , , on aidosti kasvava, kun $x \geq 0$ ja aidosti vähenevä, kun $x \leq 0$ .
Funktio , $\, g(x) = \frac{1}{x}$ , on aidosti vähenevä, kun ja .

# V12

# kasvavuus_ja_derivaatta

1.6 Kasvavuus ja vähenevyys derivaatan avulla

Jos $\, f'(x) \geq 0 \,$ jollain välillä, niin on siellä kasvava.
Jos $\, f'(x) \leq 0 \,$ jollain välillä, niin on siellä vähenevä.
Jos $\, f'(x) > 0 \,$ jollain välillä, niin on siellä aidosti kasvava.
Jos $\, f'(x) < 0 \,$ jollain välillä, niin on siellä aidosti vähenevä.

Esimerkki

Tarkastellaan potenssifunktion , f(x)=x^r , monotonisuutta derivaatan avulla. Potenssifunktiomme on määritelty positiivisille luvuille (eli x > 0 ). Nyt $f'(x) = r x^{r - 1}.$ Koska x > 0 , niin $x^{r - 1} > 0$ .

Kahden positiivisen lukun tulo on positiivinen, joten kun , eli on aidosti kasvava, kun .
Positiivisen ja negatiivisen luvun tulo on negatiivinen, joten kun , eli on aidosti vähenevä, kun .

Ongelma

Tiedämme, että funktion , $f(x) = a\,x + b$ , kuvaaja on suora. Milloin funktio on kasvava ja milloin vähenevä?

# teht1

Lisää harjoitusta kasvavuudesta ja vähenevyydestä löytyy Kisällioppinen-sivustolta 5.1-5.7.

1.7 Korkeamman kertaluvun derivaatta

Koska funktion derivaatta on itsekin funktio, voi derivaattafunktiota mahdollisesti myös derivoida.

Funktion toisen derivaatan laskeminen suoritetaan soveltamalla yllä olevia kaavoja ja sääntöjä funktion ensimmäiseen derivaattaan. Vastaavasti funktion s derivaatta saadaan derivoimalla n-1 stä derivaattaa.

Funktion toista derivaattaa merkitään esimerkiksi . Funktion ttä derivaattaa voidaan merkitä $f^{(n)}$ , tai $\frac{d^n f}{d x^n}$ .
Funktion korkeampia derivaattoja käytetään esimerkiksi funktion ääriarvojen tutkimisessa. Ääriarvotehtävät (optimointitehtävät) ovat aivan keskeisintä matematiikan sovellusaluetta taloustieteessä. Ääriarvoihin tutustutaan ensi viikolla.

Esimerkki

Esimerkiksi funktion , f(x)=2x^3+x^2+x+3 ensimmäinen derivaatta on f'(x) = 6x^2 + 2x + 1, toinen derivaatta on f''(x) = D(6x^2 + 2x + 1) = 12x + 2 ja kolmas derivaatta on $f^{(3)}(x)= D(12x + 2) = 12,$ ja kaikki sitä korkeamman kertaluvun derivaatat ovat nollia (sillä vakion derivaatta on ).

1.8 Stack-tehtäviä derivoinnista

Harjoittele derivoimista STACK-tehtävien avulla.

# stack1

# stack2

# Derivointi8

# Derivointi1

Lisää perustehtäviä derivoinnista löytyy +-merkin takaa.

# Derivointi4

# Derivointi6

# Derivointi5

# Derivointi7

Stack-lisätehtäviä derivointiin liittyen löytyy +-merkin takaa.

# Derivointi9

# Derivointi10

# Derivointi11

# Derivointi12

# Derivointi13

Lisää harjoitusta derivoimiseen voi etsiä Kisällioppinen-sivustolta - esimerkiksi derivointisääntöjä I ja derivointisääntöjä II.

# jousto

1.9 Jousto

Esimerkkinä derivaatan käytöstä tarkastelemme joustoa.

Miten jonkin tuotteen kysyntä riippuu hinnasta? Esimerkiksi voidaan tutkia, miten kahvin kysyntään vaikuttaa kahvin hinnan nousu vaikkapa 3 eurolla per kilo; myyntidatasta voidaan nähdä kuinka monta kiloa kahvia myydään vähemman (tai enemmän), kun hinta kasvaa 3 eurolla per kilo.

Tässä mittarissa on se huono puoli, että kysynnän muutosta mitataan samoilla satunnaisilla suureilla kuin kysyntää ja hintaa. Esimerkiksi tietokoneen hinnan nousu kolmella eurolla ei luultavasti heiluta kysyntää ollenkaan, mutta kahvikilon tapauksessa hinnan muutos on jo merkittävä.

Tämä ongelma poistuu, kun puhutaan suhteellisista muutoksista: kuinka kysyntä muuttuu, kun hinta kasvaa yhdellä prosentilla. Tämä suure on niin kutsuttu hintajousto.

Hintajousto siis kertoo kuinka monta prosenttia kysyntä muuttuu, kun hinta nousee yhdellä prosentilla. Hintajousto siis mittaa kuinka kysyntä reagoi hinnan muutoksiin.

Esimerkki

Jos jäätelön hintajousto on , tämä tarkoittaa, että jos hinta kasvaa yhdellä prosentilla, jäätelön kysyntä pienenee kahdella prosentilla (kysyntä pienee, koska edessä on miinusmerkki).

Yleensä hyvän arvion hintajoustolle saa niin sanotulla keskipistemenetelmällä, johon törmätään esimerkiksi mikrotaloustieteen perusteissa: $\left(\frac{Q_2 - Q_1}{(Q_2 + Q_1)/2}\right)\bigg/\left(\frac{P_2 - P_1}{(P_2 + P_1)/2}\right).$ Tässä on kysytyn määrän muutos ja on hinnan muutos.

Taloustieteessä voidaan mitata muutakin muutosta kuin hinnan muutosta. Myös näiden muutosten herkkyyttä muuttujan arvon vaihteluun on hyödyllistä tutkia.

Joustoa voidaan yhtä hyvin mitata myös muidenkin muuttujien suhteen; esimerkiksi vaikka kysynnän muutosta tulojen suhteen. Näin ollen jousto määritellään yleisesti mille tahansa funktiolle ja muuttujalle (ei siis vain kysynnälle ja hinnalle).

Jouston on tarkoitus olla "suureeton" eli siellä ei näy euroja tai kiloja, vaan se kertoo suhteellisen muutoksen.

Joustolla yritetään havainnollistaa kuinka paljon tutkittava suure kasvaa, kun muuttuja kasvaa yhdellä yksiköllä. Sanonta ei ole kovin tarkka, koska siinäkin puhutaan yksiköistä - jousto mittaakin suureen "hetkellistä" suhteellista muutosnopeutta.

Funktion joustoa n suhteen merkitään $\mathrm{El}_x f(x)$ ja se määritellään kaavalla $\mathrm{El}_xf(x)=\frac{f'(x)}{f(x)/x}=\frac{xf'(x)}{f(x)}.$

Jousto kertoo kuinka monta prosenttia funktion arvo (likimäärin) muuttuu, kun muuttujan arvot kasvavat yhdellä prosentilla.

Esimerkki

Olkoon kysyntäfunktiona , $D(p)=100p^{-2}$ . Tällöin $D'(P) = -2\cdot 100p^{-2-1} = -2\cdot 100p^{-3}$ ja $\mathrm{El}_pD(p)=\frac{-2\cdot 100p^{-3}}{100p^{-2}/p}=-2.$

Joten, jos hyödykkeen hinta nousee yhdellä prosentilla, niin hyödykkeen kysyntä laskee likimäärin kaksi prosenttia.

Huomautus

Likimäärin tarkoittaa edellä, että jousto antaa arvion konkreettiselle muutokselle. Esimerkiksi jos hinta on eli P = 2 , niin kysyntä on $D(2) = 100\cdot 2^{-2} = 25.$

Jos hinta nousee yhdellä prosentilla, niin uusi hinta on $1,\!01\cdot 2 = 2,\!02$ ja mallimme mukainen kysyntä on $D(2,\!02) = 100\cdot (2,\!02)^{-2} = 24,\!507401\ldots$ ja kysynnän muutos $D(2,\!02) - D(2) = 24,\!507401\ldots - 25 = -0,\!492598\ldots$

Muutos prosentteina on siis $\frac{D(2,\!02) - D(2)}{D(2)} = -0,\!019703\ldots$ eli kysyntä laskee noin $1,\!97$ prosenttia, mikä on likimain prosenttia, minkä saimme edellisessä joustolaskussa.

Jos käytät jouston arviointiin tässä tapauksessa yllä mainittua mikrotaloustieteen keskipistemenetelmää saat joustolle arvioksi $-1,\!999950\ldots,$ mikä on aika lähellä joustoamme .

Ongelma

Liikennetaloustieteessä liikennemääriä voidaan mallintaa esimerkiksi seuraavasti: $T(K) = 0,\!4K^{1,06},$ missä on teiden rakentamismäärärahat ja T(K) on liikennemäärä, kun rakentamismäärärahat ovat .

Mikä on liikennemäärien jousto rakentamismäärärahojen suhteen?
Paljonka tämän mallin mukaan liikennemäärät muuttuvat (likimain), kun rakennusmäärärahat kasvavat yhden prosentin?

1.9.1 Joustava ja joustamaton

Matematiikka 1 -kurssin käsite itseisarvosta on käytössä taloustieteessä esimerkiksi, kun kerrotaan, onko kyseessä joustamaton vai joustava tilanne.

Jos $|\mathrm{El}_x f(x)| = 0$ , sanotaan, että on täysin joustamaton.
Jos $|\mathrm{El}_x f(x)| < 1$ , sanotaan, että on joustamaton.
Jos $|\mathrm{El}_x f(x)| = 1$ , sanotaan, että on yksikköjoustava.
Jos $|\mathrm{El}_x f(x)| > 1$ , sanotaan, että on joustava.
Jos $|\mathrm{El}_x f(x)| = \infty$ sanotaan, että on täysin joustava.

Joustavia tuotteita hinnan muutoksille ovat yleensä elektroniikka ja vaatetus. Joustamattomia taas tyypillisesti ruoka ja reseptilääkkeet.

Tehtäviä

Derivoi kohtien a-c funktiot. Hyödynnä derivaattaa d-kohdassa.
2. $\displaystyle{f(x) = 4\sqrt{x} - \frac{x}{3} + \frac{1}{x} - \frac{5}{x^3}}$
3. $g(t) = t^{1/3} + 2t^{1/4} + 3t^{6/5}$
4. Missä a-kohdan funktio on kasvava ja missä vähenevä?

Derivoi kohtien a-c funktiot. Hyödynnä derivaattaa d-kohdassa.

$\displaystyle{f(x) = \frac{x - 2}{x^2 + 1}}$
$f(x) = \sqrt{1-3x^2}$
Missä a-kohdan funktio on kasvava ja missä vähenevä?

Tarkastellaan monopolia, jonka tuotteista saatavan hinnan määrää funktio , . Monopolin kokonaistulot ovat
Niin kutsuttu rajatulo (merkitään ) on n derivaatta eli .
1. Mikä on tarkastelemamme monopolin rajatulo, kun ?
2. Monopoli saavuttaa suurimmat voitot, kun rajatulo on yhtäsuuri kuin niin kutsuttu rajakustannus . Jos rajakustannuksen määrittää lauseke $2 + 0,\!25Q$ , milloin monopolin voitot ovat suurimmat?
3. Minkä värinen kuvaaja on rajatulolla ()? Minkä värinen kuvaaja on rajakustannuksella ()? Musta, punainen, sininen, vihreä vai lila?

Laske funktion jousto kohdassa a. Tulkitse tulostasi kohdassa b.
1. , $D(p) = 2000p^{-0,\!1}$
2. Milloin tilanne on joustava ja milloin joustamaton?

Derivoi. $\text{(a) } f(x) = \frac{x^2+2x}{x-1} \quad\quad \text{(b) } g(x) = \frac{ax + b}{cx + d} \quad\quad \text{(c) } h(u) = \frac{u\sqrt{u} - 3}{u^2}$

Derivoi. $\begin{align*} &\text{(a) } f(x) = \frac{3}{5-4x} &&\text{(b) } F(t) = \left( 2+\tfrac3t \right)^{-10} \end{align*}$

Alla on lisätehtäviä harjoittelua varten. Tehtävät ovat avustettuja: jos jäät jumiin ratkaisussa, voit klikata itsellesi tiedon, mitä seuraavaksi kannattaa tehdä, "Seuraava vaihe"-napista". Samantyylisiä tehtäviä eri lukuarvoilla saa "Uusi tehtävä"-napista. Geogebra Copyright © International GeoGebra Institute, 2013

# geo2taso4

# geo2taso5

# 2

2. Eksponenttifunktio

Tässä osassa käsitellään seuraavia asioita

eksponenttifunktio
logaritmifunktio
korkolaskentaa
- korkoa korolle
- diskonttaus

Osiota vastaa [EMEA, 4.9, 4.10, 6.10, 6.11, 10.1-10.5 ja 10.7].

Eksponentiaalisen kasvun/vähenemisen malleja (missä $\, f(x) = C e^{kx}$ , ja ovat vakioita) käytetään paljon niin luonnontieteessä kuin taloustieteessä ja teknisillä aloilla. Esimerkiksi

jatkuva korko
radioaktiivinen hajoaminen
populaation kasvu (eksponentiaalinen kasvu, logistinen kasvu 2.4)

Funktio , f(x) = e^x , on eksponenttifunktioista tärkein. Tämä on niin kutsuttu luonnollinen eksponenttifunktio.

Englanniksi the exponential function
Monissa lähteissä käytetään myös merkintää $f(x) = \exp(x)$ .

Kantalukuna on , joka on Neperin luku (englanniksi Euler's number tai Napier's constant)

$e = 2{,}718281828459 \ldots$

Kantaluku voisi olla jokin muukin; esimerkiksi 2^x määrittää eksponenttifunktion, jonka kantaluku on .

Funktiota , f(x) = a^x, missä

kantaluku on vakio, $\, a > 0$
muuttuja on eksponenttina

kutsutaan (yleiseksi) eksponenttifunktioksi.

Alla on eksponenttifunktion kuvaaja. Voit muuttaa eksponenttifunktion kantalukua.

# g6

# eksponenttifunktion_ominaisuudet

2.0.1 Ominaisuuksia

Voimassa ovat tutut potenssien laskusäännöt:

$\, e^0 = 1$
$\, e^x e^y = e^{x+y}$
$\, \frac{e^x}{e^y} = e^{x-y}$
$\, (e^{x})^y = e^{xy}$

Lisäksi

$\, e^x > 0$
eksponenttifunktio on aidosti kasvava

Esimerkki

Radioktiivisesti hajoavan isotoopin määrä hetkellä saadaan yhtälöstä $N(t) = N_0 \left( \frac{1}{2} \right)^{t/t_0}$ missä N_0 on isotoopin määrä alkuhetkellä t = 0 ja t_0 on isotoopin niin kutsuttu puoliintumisaika.

Radium-226-isotoopin puoliintumisaika on 1 600 vuotta. Kuinka paljon isotooppia on jäljellä 100 vuoden kuluttua?

$N(100) = N_0 \left( \frac{1}{2} \right)^{100/1\,600} \approx 0,\!96N_0$ eli isotooppia on jäljellä noin 96% alkuperäisestä määrästä.

Seuraavan ongelman ratkaisussa auttaa logaritmin käsite. Logaritmifunktio on eksponenttifunktion niin kutsuttu käänteisfunktio.

Ongelma

Milloin Radium-226-isotooppia on jäljellä 1%?

2.1 Käänteisfunktio

Idea: "Jos tiedän funktion arvon , tiedänkö muuttujan arvon (eli millä , f(x) = y )?"

"Jos funktio saa kunkin arvon korkeintaan kerran, sillä on käänteisfunktio."

Kuvasta: funktion kuvaaja ei leikkaa mitään vaakasuoraa suoraa kuin korkeintaan kerran.

Katso seuraavia kuvaajia ja päättele onko funktioilla käänteisfunktiota.

# g8

# kaanteiskuvaus

Käänteisfunktio on määritelty kaikilla niillä arvoilla, joita saa (eli funktion arvojoukossa). Arvojoukko on maalijoukon osajoukko ja se sisältää lyhyesti sanottuna kaikki funktion arvot.

Olkoon $f\colon A\rightarrow B$ funktio, jossa on määrittelyjoukko ja arvojoukko

Funktion käänteisfunktio on funktio $g\colon B\rightarrow A$ , jos funktiolle pätee seuraavaa:

Funktion arvo kohdassa $y\in B$ on se yksikäsitteinen luku $x\in A$ , jolle on voimassa .

Usein funktion käänteisfunktiota merkitään $f^{-1}$ .

Esimerkki

Esimerkiksi kysyntäfunktion käänteisfunktiota kutsutaan käänteiskysyntäfunktioksi.

Tarkastellaan esimerkkinä jäätelön markkinakysyntää , joka määritellään vaikkapa yhtälöllä D(P) = 19 - 6P .

Tämän käänteisfunktion lauseke saadaan ratkaisemalla yhtälö Q = 19 - 6P muuttujan suhteen: $\begin{align*} \qquad &Q = 19 - 6P \\ \Longleftrightarrow \qquad &6P = - Q + 19 \\ \Longleftrightarrow \qquad &P = -\frac{1}{6}Q + \frac{19}{6} \end{align*}$ Käänteiskysyntäfunktio on siis $D^{-1}$ , missä $D^{-1}(Q) = -\frac{1}{6}Q + \frac{19}{6}$ . Taloustieteessä usein merkitään käänteiskysyntäfunktiota kirjaimella eli $P = D^{-1}$ .

Mikrotaloustieteen kysyntäkäyrä on käänteiskysyntäfunktion kuvaaja.

# V13

Esimerkki

Kurssilla Matematiikka 1 meillä oli ongelmana jäätelön markkinatasapaino, kun markkinakysyntä ( $D_{\text{Market}}$ ) oli $-\frac{1}{6}Q + \frac{19}{6}$ euroa ja markkinatarjonta ( $S_{\text{Market}}$ ) oli $\frac{1}{6}Q + \frac{5}{6}$ euroa. Tässä lausekkeet ovat käänteiskysyntä- ja käänteistarjontafunktioiden lausekkeet (erityisesti $D_{\text{Market}} = D^{-1} = P)$ .

Markkinatasapaino saavutetaan, kun kysyntä ja tarjonta ovat yhtä suuret. Kuvassa tämä nähdään funktioiden kuvaajien leikkauksena (voit tarkastella tätä alla Geogebralla).

# g9

Esimerkki

Yleisesti lineaarinen kysyntäfunktio on muotoa D(p)=a-bp , jossa a>0 ja b>0 . Sen käänteisfunktiota merkitään tavallisesti kirjaimella symbolin $D^{-1}$ sijasta.

Myös yleisen käänteiskysyntäfunktion lauseke löydetään ratkaisemalla yhtälö q=a-bp hinnan suhteen, jolloin $p=P(q)=\frac{a}{b}-\frac{1}{b}q.$

Kaikilla funktioilla ei ole käänteisfunktiota, mutta aidosti kasvavilta ja väheneviltä sellainen löytyy.

# kaanteinenon

Aidosti monotonisella funktiolla on käänteisfunktio. Aidosti monotonisen määritelmä oli edellä (1.5.2).

# Käänteisfunktio1

Lisää Stack-tehtäviä käänteisfunktion määrittämisestä on +-merkin takana.

# Käänteisfunktiox

# Käänteisfunktio2

2.1.1 Logaritmi

(Luonnollisen) eksponenttifunktion , f(x) = e^x , käänteisfunktio on luonnollinen logaritmifunktio, jota merkitään $f^{-1}(x) = \ln x.$

Tällöin $y = e^x \; \iff \; x = \ln y \quad \quad (y>0)$ sekä $\ln(e^x) = x \quad \text{ kaikilla } x \in \mathbb{R} \quad \quad \text{ ja } \quad \quad e^{\ln x} = x \quad \text{ kaikilla } x > 0.$

# g10

Huomaa

Luennollisen logaritmin määrittelyjoukko on positiiviset reaaliluvut eli reaaliluvut , joilla x > 0 .

Ongelma

Miksi logaritmifunktio $\ln$ on määritelty aidosti positiivisilla luvuilla?

Ratkaisu

Luonnollisen eksponenttifunktion arvojoukko on positiiviset kokonaisluvut (katso 2.0.1). Luonnollinen logaritmi on luonnollisen eksponenttifunktion käänteisfunktio, joten sen määrittelyjoukko on juurikin kyseinen arvojoukko.

# logaritminlaskut

2.1.2 Laskusäännöt

$\ln (xy)=\ln x+ \ln y$
$\ln \frac{x}{y}=\ln x-\ln y$
$\ln x^r=r \ln x$
$\ln 1=0$
$\ln e = 1$

Esimerkkejä

Yhtälön ratkaisu on $x=\ln 100$ , koska $e^{\ln 100}= 100$ .
Yhtälön ratkaisu on $x=\ln 2$ , koska $4e^{\ln 2}= 4 \cdot 2 = 8$ .

Ongelma

Miksi funktion, , $f(x)=e^x(x^3-a)\ln ((x+b)^2)$ , nollakohdat ovat $x=\sqrt[3]{a}$ , x=1-b ja x=-1-b ?

# V14

Yleisen eksponenttifunktion a^x käänteisfunktio on -kantainen logaritmifunktio, jonka arvoja merkitään $\log_a x$ . Näille funktioille on voimassa samantapaiset laskusäännöt kuin -kantaisille funktioille. Kurssilla (ja yleensä elämässäkin) selviää luonnollisella logaritmilla. Kaikki logaritmit voi toki vaihtaa luonnollisiksi kannanvaihdon avulla $\log_a(x) = \frac{\ln x}{\ln a}.$

# Logaritmi1

# Logaritmi3

Logaritmi on kätevä yhtälöiden ratkaisemisessa; erityisesti, kun ratkaistava muuttujamme on potenssina.

Esimerkki

Miten löydetään ratkaisu yhtälöön (1.04)^x=9 ?

Tavallinen tapa on 'ottaa puolittain luonnollinen logaritmi' ja soveltaa laskusääntöjä 2.1.2 seuraavasti: $\begin{align*} \qquad &(1.04)^x=9 \\ \Longleftrightarrow \qquad &\ln (1.04)^x=\ln 9 \\ \overset{3.}{\Longleftrightarrow} \qquad&x\ln (1.04)=\ln 9 \\ \Longleftrightarrow \qquad&x=\frac{\ln 9}{\ln (1.04)}. \end{align*}$

Ongelma

Ratkaise yhtälö $3^x = 9^{1-x}$

# V4

Ongelma

Nyt voimme myös ratkaista edellä esitetyn ongelma Radium-226-isotoopin hajoamisesta logaritmin avulla.

Siis milloin Radium-226-isotooppia on jäljellä 1%?

Isotooppin määrä hetkellä on $N(t) = N_0 \left( \frac{1}{2} \right)^{t/1\,600}.$ Nyt kysytty hetki ratkaisee yhtälön $N_0 \left( \frac{1}{2} \right)^{t/1\,600} = 0,\!01 N_0.$

Monet mitta-asteikot ovat logaritmisia. Logaritminen asteikko on hyödyllinen, kun mitattavat muutokset ovat todella isoja tai kun tarkastellaan suhteellista muutosta.

Esimerkkejä

Liuoksen pH on $\text{pH} = - \log_{10} a_{H^+}$ , missä $a_{H^+}$ on liuoksen aktiivisuus. 10-kertainen aktiivisuus pienentää pH-arvoa yhdellä.
Richterin asteikko (maanjäristyksen voimakkuus): maanjäristyksen magnitudi on $R = \log_{10}\left(\frac{I}{I_0} \right),$ missä on mitattu intensiteetti ja on normaali intensiteetti.
Äänen voimakkuus desibeliasteikolla (Wikipedia)

Esimerkki

Entä miten voidaan ratkaista yhtälö (1+r)^t=10 muuttujan suhteen?

TAPA 1: Esimerkiksi seuraavasti: $\begin{align*} \qquad &(1+r)^t=10 \\ \Longleftrightarrow \qquad & \ln (1+r)^t=\ln 10 \\ \overset{3.}{\Longleftrightarrow} \qquad& t\ln (1+r)=\ln 10 \\ \Longleftrightarrow \qquad &\ln (1+r)=\frac{1}{t}\ln 10 \\ \overset{3.}{\Longleftrightarrow}\qquad &\ln (1+r)=\ln 10^{1/t} \\ \Longleftrightarrow \qquad & 1+r=10^{1 / t} \\ \Longleftrightarrow \qquad & r=10^{1 / t}-1. \end{align*}$

Tässä täytyy olla hieman tarkkana, sillä logaritmi on määritelty vain positiivisilla luvuilla, joten jos otamme logaritmin puolittain, täytyy molempien puolien olla positiivisia. Miksi ne ovat tässä tapauksessa?

TAPA 2: Toinen tapa on yhtälön (1+r)^t=10 'korottaminen puolittain potenssiin 1/t ', jolloin saadaan suoraan $1+r=10^{1/t}$ . Miksi näin voidaan tehdä?

Miksit

Lausekkeen (1 + r)^t täytyy olla positiivinen, koska se on yhtä suurta kuin (mikä on aika selvästi positiivinen luku).

Toisessa tavassa voidaan korottaa puolittain potenssiin ilman, että mitään 'pahaa' tapahtuu, koska molemmat puolet ovat positiivisia! Negatiivisilla luvuillahan murtopotenssia ei ole edes määritelty.

HUOMAA puolittain potenssiin korottaminen on aina vaaratilanne!

Potenssiin korotuksessa vaarana on myös tilanteet, joissa potenssi on kokonaislukukin (esimerkiksi ), koska tällöin saatat vahingossa muuttaa negatiivisen luvun positiiviseksi; esimerkiksi (-1)^2 = 1 = 1^2 , vaikka $(-1) \neq 1$ .

Ongelma

Auto maksaa uutena $36\, 400$ euroa. Oletetaan, että auton arvo pienenee $10\%$ vuodessa. Milloin auton arvo on puolittunut?

Likiarvon laskemiseen kannattanee käyttää laskinta.

Vihje

Auton arvo vuoden kuluttua on $36\, 400 \cdot (1 - 0,\!10)^t$ .

Esimerkki

Logaritmi on hyödyllinen myös yritettäessä hahmottaa, miten tietyn parametrin käytös vaikuttaa kokonaisuuteen. Esimerkiksi taloustieteessä esiintyy usein Cobb-Douglas-hyötyfunktio, joka on muotoa $x_1^\alpha x_2^\beta$ . Tässä $\alpha$ ja $\beta$ ovat parametreja.

Nyt käytöstä esimerkiksi $\alpha$ n suhteen saattaa olla helpompi tutkia, jos lausekkeen sijasta tutkii sen logaritmia: $\ln (x_1^\alpha x_2^\beta) = \ln x_1^\alpha + \ln x_2^\beta = \alpha \ln x_1 + \beta \ln x_2.$ Edellä hyödynsimme logaritmin laskusääntöjä 2.1.2 1. ja 3.

Esimerkki (Eksponentiaalisen mallin sovittaminen havaintoihin)

Jos havaintoihin $(x_1, y_1), (x_2, y_2), \ldots$ pyritään sovittamaan eksponentiaalinen malli eli y = ca^x, missä ja ovat vakioita, tarkastelun voi palauttaa suoran sovittamiseen logaritmin avulla.

Idea on seuraavanlainen. Otetaan mallista logaritmi puolittain eli $\ln y = \ln(ca^x).$ Nyt jälleen logaritmin laskusääntöjen avulla (2.1.2 1. ja 3.), $\ln y = \ln(ca^x) = \ln c + \ln(a^x) = \ln c + x\cdot \ln a.$

Merkitään $Y = \ln y, k = \ln a, b = \ln c$ , jolloin edellisen perusteella $Y = \ln c + x\cdot \ln a = b + kx$ eli kyseessä on suora, jonka kulmakerroin on $k = \ln a$ ja se leikkaa -akselin pisteessä (0, b).

Eksponentiaalisen mallin parametrit saa siis sovittamalla suoran havaintoihin $(x_1, Y_1) = (x_1, \ln y_1), (x_2, Y_2) = (x_2, \ln y_2), \ldots$ , jolloin sovitetun suoran kulmkerroin on $k = \ln a$ ja pystyaskseli leikataan pisteessä (0, b) , missä $b = \ln c$ . Mallin parametrit saadaan tästä, sillä $a = e^{\ln a} = e^{k} \qquad \text{ja} \qquad c = e^{\ln c} = e^b.$

# Logaritmiyhtälö

2.2 Eksponenttifunktioiden derivointi

Eksponenttifunktiolle on D e^x = e^x

Esimerkki

Funktion , f(x) = x^3 e^x , derivaatta on tulon derivoimiskaavalla f'(x) = 3x^2e^x + x^3e^x.

# V6

Esimerkki

Yhdistetyn funktion , $f(x)=e^{g(x)}$ derivaatta on $f'(x)=g'(x)e^{g(x)}$ , joten esimerkiksi funktion , $h(x)=e^{2x}-2e^{-3x^4}$ , derivaatta on $h'(x)=2\cdot e^{2x}-(-12x^3)\cdot 2e^{-3x^4}=2e^{2x}+24x^3e^{-3x^4}.$

Koska e^x > 0 , luonnollinen eksponenttifunktio on aidosti kasvava, sillä myös sen derivaatta ( De^x = e^x ) on aina positiivista.

Ongelma

Mikä on funktion , $f(x) = e^{x^2 + 1},$ derivaatta?

# V7

# kaanteisfunktionderivaatta

2.3 Käänteisfunktion derivointi

Usein käänteisfunktion lausekkeen etsiminen on hankalaa tai mahdotonta.

Käänteisfunktion derivaatan arvon selvittäminen onnistuu ilman käänteisfunktion lausekettakin alkuperäisen funktion derivaatan avulla:

$(f^{-1})'(y) = \frac{1}{f'(x)}, \quad\; \text{kun } \, y = f(x)$

Esimerkki

Esimerkiksi funktion , f(x)=x^5+x+1 käänteisfunktion (miksi funktiolla on käänteisfunktio?) derivaatta pisteessä y=1 on $\left(f^{-1}\right)'(1)=\frac{1}{f'(0)}=\frac{1}{1}=1.$ Kaavassa on laskettu arvoa y=1 vastaava muuttujan arvo yhtälöstä 1=x^5+x+1. (Ratkaise tämä yhtälö!)

Tämä arvo on x=0 . Sijoittamalla tämä derivaattaan f'(x)=5x^4+1 saadaan f'(0)=1 .

Miksi funktiolla on käänteisfunktio?

Käänteisfunktion olemassa olo onkin vaikeampi selvittää. Mutta derivoimalla funktion huomaa, että derivaatta on aina positiivista! Näin ollen funktiomme on aidosti kasvava ja aidosti kasvavilla funktioilla on käänteisfunktio.

Yhtälön 1 = x^5 + x + 1 ratkaiseminen

1 = x^5 + x + 1 eli lisäämällä puolittain saadaan 0 = x^5 + x, josta ottamalla eteen: 0 = x(x^4 + 1)

Tulon nollasäännöllä x = 0 tai x^4 + 1 = 0 eli x= 0 tai x^4 = -1 .

Nyt x^4 on aina suurempaa tai yhtäsuurta kuin nolla, sillä (x^2)^2 = x^4 ja toiseen korottaminen "pakottaa" tuloksen ei-negatiiviseksi. Erityisesti x^4 ei voi koskaan olla .

Yhtälön ainoa ratkaisu on siis x = 0 .

Esimerkki

Voidaan osoittaa, että funktiolla f(x) = x^3 on käänteisfunktio. Määritetään $(f^{-1})'(8)$ .

Tapa 1

Tässä tilanteessa käänteisfunktion määrittäminen onnistuu varsin helposti. Ratkaisemalla yhtälö y = x^3 muuttujan suhteen saadaan $x = \sqrt[3]{y}$ . Näin ollen käänteisfunktio on $f^{-1}(x) =\sqrt[3]{x}$ . Muistamalla juurien ja murtopotenssien yhteys voidaan kirjoittaa $f^{-1}(x)=x^{\frac{1}{3}}$ .

Derivoidaan: $(f^{-1})'(x) = \dfrac{1}{3}x^{-\frac{2}{3}} = \dfrac{1}{3x^{\frac{2}{3}}} = \dfrac{1}{3\sqrt[3]{x^2}}$

Siten $(f^{-1})'(8) = \dfrac{1}{3 \cdot \sqrt[3]{8^2}} = \dfrac{1}{12}$ .

Tapa 2

Käytetään käänteisfunktion derivoimissääntöä $(f^{-1})'(y) = \dfrac{1}{f'(x)}$ . Tätä varten tulee ratkaista arvoa y=8 vastaava muuttujan arvo yhtälöstä y=x^3 . Tulee siis ratkaista yhtälö x^3 = 8 , josta saadaan x = 2 . Koska lisäksi f'(x)=3x^2 , saadaan $\begin{align*} (f^{-1})'(8) = \dfrac{1}{f'(2)} = \dfrac{1}{3 \cdot 2^2} = \dfrac{1}{12}. \end{align*}$

Molemmilla tavoilla päädyttiin siis tismalleen samaan ratkaisuun, kuten pitääkin.

Alla olevaan kuvaan on piirretty funktion kuvaaja sinisellä ja käänteisfunktion $f^{-1}$ kuvaaja punaisella. Huomaa näiden symmetrisyys mustalla katkoviivalla piirretyn suoran y=x suhteen. Mustalla piirretyn tangentin kulmakerroin puolestaan on etsitty käänteisfunktion derivaatan arvo.

Esimerkki

Voidaan osoittaa, että funktiolla f(x) = x^3 + x on käänteisfunktio. Määritetään $(f^{-1})'(2)$ .

Vaikka funktion lauseke on melkein sama kuin edellisessä esimerkissä, käänteisfunktion määrittäminen ei ole tässä tilanteessa kovin helppoa. Näin ollen tehtävän ratkaiseminen etsimällä käänteisfunktion lauseke ja derivoimalla sitten sitä ei tule kysymykseen. Sen sijaan tehtävä pystytään ratkaisemaan käyttämällä käänteisfunktion derivoimissääntöä $(f^{-1})'(y) = \dfrac{1}{f'(x)}$ . Huomataan, että 1^3 + 1 = 2 eli f(1) = 2 . Koska lisäksi f'(x)=3x^2+1 , saadaan $\begin{align*} (f^{-1})'(2) = \dfrac{1}{f'(1)} = \dfrac{1}{3 \cdot 1^2 + 1} = \dfrac{1}{4}. \end{align*}$

2.3.1 Logaritmifunktioiden derivointi

Luonnolliselle logaritmille on $D \ln x = \frac{1}{x}$

Esimerkki

Yhdistetyn funktion , $f(x)=\ln g(x)$ , derivaatta on f'(x)=g'(x) / g(x) , joten esimerkiksi funktion , $h(x)=x \ln x^3$ derivaatta on $h'(x)=1\cdot \ln (x^3)+x\cdot \frac{3x^2}{x^3}=\ln (x^3)+3=3+\ln x^3.$

# Derivointi15

# Derivointi14

Stack-lisätehtävä eksponenttifunktion derivoinnista on +-merkin takana.

# Derivointi16

Lisää harjoitusta löytyy Kisällioppinen-sivustolta: eksponentiaalinen malli ja eksponentti- sekä logaritmifunktiot, eksponenttifunktiot, logaritmifunktiot ja käänteisfunktio.

# logistisenkasvunmalli

2.4 Logistinen kasvu

Eksponenttifunktiota hyödynnetään esimerkiksi logistisen kasvun mallissa.

Jos tilaa ja ravintoa olisi tarjolla rajoittamattomasti ja olosuhteet muutenkin ihanteelliset, voitaisiin eliöpopulaation kokoa mallintaa eksponentiaalisen kasvun avulla.
käytännössä kasvua kuitenkin rajoittavat muun muassa rajallinen ravinto ja elintila sekä mahdolliset saalistajat.
Järjestelmän kantokyky on suurin mahdollinen populaatio, jonka ympäristö kestäisi "äärettömän kauan".

"Suureen eksponentiaalista kasvua rajoittaa järjestelmän kantokyky ." $y' = Ry\left( 1-\frac{y}{K} \right)$

Niin kutsutun alkuarvotehtävän $\begin{cases} y' = Ry\left( 1-\frac{y}{K} \right) \\ y(0) = y_0 \end{cases}$ ratkaisu on funktio $y(t) = \frac{K y_0}{y_0 + (K-y_0) e^{-Rt}}$

# geo3

Linkki sovelluksen Geogebra-sivulle: https://www.geogebra.org/m/dreagPrT.

2.5 Korkolaskentaa

Vielä yhtenä eksponenttifunktion sovelluskohteena tarkastelemme korkolaskentaa. Eksponenttifunktiota tarvitaan erityisesti jatkuvan koron tapauksessa, joka on tyypillinen vertailtaessa vaihtoehtoisia ratkaisuja mallissa.

2.5.1 Korkoa korolle

Korkolaskentaan olemme törmänneet jo Matematiikka 1 -kurssilla. Esimerkiksi

# osakesalkku

Ongelma

Osakesalkun arvo on alussa 1000 euroa ja salkun arvo kasvaa vuodessa $5\%$ . Mikä on salkun arvo 15 vuoden kuluttua?

Ratkaisu

Yksi prosentti ( $1 \%$ ) luvusta on $A\cdot 1/100$ . Näin ollen $5 \%$ luvusta 1000 on $1000\cdot 5/100 = 1000\cdot 0,\!05= 50$ .

Salkun alkupääoma on 1000 euroa ja pääomalle maksetaan prosentin korko kerran vuodessa, pääoma on siis vuoden vuoden kuluttua $1000 + 1000\cdot 0,\!05 = 1000(1 + 0,\!05) = 1050 \text{\,(euroa)}$ ja kahden vuoden kuluttua $1050 + 1050\cdot 0,\!05 = 1050\cdot(1 + 0,\!05) + 1000(1 + 0,\!05)\cdot (1 +0,\!05) = 1000(1 + 0,\!05)^2 = 1102,\!50 \text{\,(euroa)}.$ Viidentoista vuoden kuluttua pääomaa on kertynyt $K=1000\left(1+\frac{5}{100}\right)^{15}\approx 2078,\!90 \text{\, (euroa)}.$

Edellisen ongelman päättelyn voi yleistää mille tahansa periodille tai vuosimäärälle .

Talletuksen pääoma (tai jokin muu suure), jonka suuruus ensimmäisen periodin alussa on ja joka kasvaa prosenttia per periodi, on kasvanut periodin kuluttua arvoon , $K=A\left(1+\frac{p}{100} \right)^n.$

Lukua voidaan kutsua korkoprosentiksi, lukua p/100 korkokannaksi ja lauseketta 1+p/100 korkotekijäksi. Korkokantaa merkitään usein kirjaimella . Luku on korkokausien (tai periodien) lukumäärä.

Näin on, koska ensimmäisen periodin lopussa talletuksen suuruus on lisättynä korolla $A\cdot p/100$ eli $A+A\cdot p/100=A(1+p/100).$

Toisen periodin lopussa talletuksen suuruus on A(1+p/100) lisättynä korolla $A(1+p/100)\cdot p/100$ eli $A(1+p/100)+A(1+p/100)\cdot p/100=A(1+p/100)^2$ ja niin edelleen.

Esimerkki

Esimerkiksi tilin, jonka alkupääoma on 1000 euroa ja jolle maksetaan prosentin korko kerran vuodessa, pääoma on vuoden kuluttua $K=1000\left(1+\frac{5}{100}\right)^{15}\approx 2078.9 \text{\ euroa.}$

# Korkolasku

2.5.2 Korko maksetaan useasti vuodessa

Usein korko ilmoitetaan nimellisenä vuosikorkona , mutta korkoa lisätään pääomaan esimerkiksi kuukausittain.

Jos korko maksetaan yhden kerran sijasta useamman kerran vuodessa ja vuosikorko on edelleen niin "korkoa korolle" -yhtälömme muokkautuu seuraavaan muotoon.

Jos talletus tehdään tilille, jolle korko maksetaan kertaa periodissa käyttäen korkoprosenttia p/m , niin periodin päästä tilillä on rahaa $\begin{equation} K = A\left(1+\frac{p/m}{100} \right)^{nm} \tag{$*$}. \end{equation}$

Tämän voi kirjoittaa myös korkokannan (missä r = p/100 ) avulla muotoon $K = A(1+r/m)^{nm}.$

Lauseke (*) antaa talletuksen määrän periodin kuluttua, kun pääomaan lisätään korkoa kertaa per periodi.

Kasvatetaan arvoa eli montako kertaa vuodessa korko maksetaan. Alkupääomamme on euro ja korkomme on 100 prosenttia.

Kerran vuodessa: $1\cdot (1 + \frac{100/1}{100})^{1 \cdot 1} = 2$ euroa
Viisi kertaa vuodessa: $1\cdot (1 + \frac{100/5}{100})^{1 \cdot 5} \approx 2,\!49$ euroa
Kerran kuussa eli kertaa vuodessa: $1\cdot (1 + \frac{100/12}{100})^{1 \cdot 12} \approx 2,\!61$ euroa
Kun kasvaa isommaksi ja isommaksi arvosta tulee noin $2,\!72$ euroa eli Neperin luku .

2.5.3 Jatkuva korkolaskenta

Vastaavasti kuin edellä euron tapauksessa antamalla n lähestyä ääretöntä, lauseke (*) lähestyy lauseketta $K = Ae^{(p/100)n} = Ae^{rn}.$ Tällöin puhutaan jatkuvasta korkolaskennasta.

# geo2

Linkki sovelluksen Geogebra-sivulle: https://www.geogebra.org/m/JGBJgMDF.

2.5.4 Prosentuaalinen väheneminen

Alkuarvo voi myös vähetä vuosittain tietyn prosentin verran, tällöin aiempi "korkoa korolle" -yhtälömme tulee seuraavanlaiseen muotoon.

Jos talletus (tai jokin muu suure) vähenee prosenttia per periodi, niin periodin päästä talletuksen suuruus on $K=A\left(1-\frac{p}{100} \right)^n.$

Ongelma

Jos eläinpopulaation kannan koko on 1200 yksikköä ja se vähenee prosenttia vuodessa, kuinka kauan kestää, että kannasta on jäljellä alle 400 yksikköä?

Ratkaisuidea

Ratkaistaan yhtälöstä $400=1200\left(1-\frac{3}{100} \right)^n.$

Ottamalla $\ln$ puolittain, saadaan $n\approx 36,\!1$ .

Kestää siis hieman yli 36 vuotta.

Esimerkki

Alkupääomamme on 100 euroa, korkoprosentti on ja korkolaskenta on jatkuvaa.

Tällöin sijoituksen arvo on viiden vuoden päästä $K=100e^{0,\!02\cdot 5}\approx 110,\!5$ .

Jos korko olisi maksettu kerran vuodessa jatkuvan korkolaskennan sijaan, sijoituksen arvo viiden vuoden päästä olisi $K=100\cdot (1+0,\!02)^5\approx 110,\!4$ .

# diskonttaus

2.5.5 Diskonttaus

Esimerkki

Kuinka paljon olisi pitänyt tallettaa vuotta sitten, jotta nyt tilillä olisi 700 euroa, kun tilille maksetaan prosentin korko kerran vuodessa?

Vastaavasti kuin 1000 euron osakesalkkuongelmassamme, saamme $700 =A\left(1+\frac{4}{100}\right)^{6}.$ 700 vastaa ongelman ta ja osakesalkun alkupääomaa 1000 .

Ratkaistaan yhtälöstä . $\begin{align*} \qquad &A\left(1+\frac{4}{100} \right)^6=700 \\ \Longleftrightarrow \qquad &A\left(1+\frac{4}{100} \right)^6{\color{red}\left(1+\frac{4}{100} \right)^{-6}}=700{\color{red}\left(1+\frac{4}{100} \right)^{-6}} \\ \Longleftrightarrow \qquad &A{\color{blue}\left(1+\frac{4}{100} \right)^{6-6}}=700\left(1+\frac{4}{100} \right)^{-6} \\ \Longleftrightarrow \qquad &A\cdot {\color{blue}1}=700\left(1+\frac{4}{100} \right)^{-6} \\ \Longleftrightarrow \qquad &A=700\left(1+\frac{4}{100} \right)^{-6} \end{align*}$

Laskimella voi selvittää likiarvon talletukselle : $A \approx 553,\!2$ euroa.

Oletetaan, että korko maksetaan kerran periodissa. Kuten olemme nähneet, yhtälö $K = A\left(1+\frac{p}{100} \right)^{n}.$ antaa talletuksen suuruuden periodin kuluttua;

Kuten edellisessä esimerkissä, tästä voidaan ratkaista $A=K\left(1+\frac{p}{100} \right)^{-n}.$

Lauseketta $\left(1+p/100 \right)^{-n}$ kutsutaan (n periodin) diskonttaustekijäksi.
$K\left(1+ p/100 \right)^{-n}$ on tulevan pääomamäärän diskontattu arvo .

Jos (syystä tai toisesta) satutaan tietämään talletuksen tuleva arvo , niin alkuperäisen talletuksen suuruuden selvittämistä yllä olevan yhtälön avulla kutsutaan diskonttaamiseksi, ja n suuruutta talletuksen nykyarvoksi (korkokannalla p/100 ).

Esimerkki

Jos on sovittu, että 10 000,00 euron korvaus maksetaan vuoden kuluttua, kuinka suuri on kohtuullinen maksun arvon alennus (diskontto), kun korvaus maksetaankin

heti,

4 kuukautta sovittua aikaisemmin,

kun korkokanta on 3% vuodessa?

Tulevan 10 000 euron nykyhetkeen diskontattu arvo on $K\left(1+ p/100 \right)^{-n} = 10\, 000\left(1+ 3/100 \right)^{-1} = \frac{10\,000}{1,\!03} = 9\,708,\!737\ldots,$ joten diskontto on noin 291,26 euroa.
Nyt tulevan pääomamäärän diskontattu arvo on $K\left(1+ p/100 \right)^{-n} = 10\, 000\left(1+ 3/100 \right)^{-4/12} = \frac{10\,000}{1,\!03^{4/12}} = 9901,\!954\ldots,$ joten diskontto on noin 98,05 euroa.

Jatkuvalla korkolaskennallakin voidaan diskonttata. Tässä tilanteessa diskonttaustekijä on $e^{-rn}$ ja tulevan talletuksen, jonka suuruus on , nykyarvo on $Ke^{-rn}$ .

Esimerkki

Ostat joukkovelkakirjan, joka takaa 20 000,00 euroa, kun laina-aika on päättynyt.

Mikä on joukkovelkakirjan hinta eli nykyarvo, kun laina-aika on

vuosi
4 kk

ja velkakirjan nimellinen vuosikorko on 5% ja korkoa lisätään lainapääomaan jatkuvasti.

Talletuksen nykyarvo on $Ke^{-rn} = 20\,000,\!00\,e^{-5/100 \cdot 1} = 20\,000,\!00\cdot 0\,95122\ldots \approx 19\,024,\!59 \text{ euroa}.$
Talletuksen nykyarvo on $Ke^{-rn} = 20\,000,\!00\,e^{-5/100 \cdot 4/12} = 20\,000,\!00\cdot 0,\!98347\ldots \approx 19\,669,\!43 \text{ euroa}.$

Ongelma

Kannattaako ottaa 1000 euroa tänään vai 1000 euroa kolmen vuoden kuluttua?

# rahatheti

Perusperiaate on, että raha saatuna nyt on arvokkaampaa kuin, jos sen saisi myöhemmin.

Diskonttaamisen avulla voidaan vertailla kahta eri vaihtoehtoa, esimerkiksi

kannattaako metsää kaataa nyt ja laittaa rahat tilille kasvamaan korkoa vai
kannattaako odottaa ja kaataa metsää vasta vuoden päästä

Diskonttaamalla voidaan "yhteismitallistaa" eri vuosina saatavat tulot ja kustannukset nykyarvoksi.

Esimerkiksi innvestoinnissa on suuri alkukustannus, mutta se tuottaa tulevina vuosina.

Mikä on investoinnin nettonykyarvo?

Jos jokin investointi maksaa alussa ${\color{blue} x_0}$ yksikköä (alkuinvestointi) eli x_0 < 0 ja tuottaa tuloa tulevien periodien $1,\ldots,n$ aikana ${\color{red} x_k}$ , $k=1,\ldots, n$ , per periodi, niin investoinnin nykyarvo $P_{n+1}$ on $P_{n+1}=x_0+x_1(1+r)^{-1}+x_2(1+r)^{-2}+\dots+x_n(1+r)^{-n},$ missä on korkokantamme.

Tätä voidaan verrata toisiin investointeihin, joissa tulot tai kustannukset tulevat eri suuruisina ja vaikkapa eri vuosina.

Diskonttausta käytetään esimerkiksi ympäristö- ja luonnonvaraekonomiassa, kun lasketaan paljaan maan arvo (the bare land value). Metsän paljaan maan arvo kertoo tulojen ja menojen nykyarvon.

Voidaan arvioida eri metsähoitotoimenpiteitä yhteismitallisesti. Kannattaako kaataa puita ja milloin?
Malliin voidaan ottaa mukaan myös hiilensidonta, jolloin voidaan laskea kuinka arvokasta hiilensidonnan kannalta on jättää puu kaatamatta verrattuna esimerkiksi siitä saatuun myyntihintaan.

Esimerkki

Yritys harkitsee 300 000 euron investointia, joka tuottaisi vuosittain 36 000 euron tuloja ja aiheuttaisi 2 000 euron kustannukset. Vuotuinen korkokanta on 6%, ja investoinnin poistoarvo 10 vuoden kuluttua on 40 000 euroa. Onko investointi kannattava?

Idea

Nettotulot ovat $36\, 000 - 2 000 = 34 000$ euroa per vuosi. Nämä kaikki diskontataan korkokannalla $r = 0,\!06$ kymmenen vuoden ajalta. Ensimmäiseltä vuodelta diskontattu arvo on $34\,000\cdot(1 + 0,\!06)^{-1} =32\,075,\!47\ldots.$ Toiselta vuodelta $34\,000\cdot(1 + 0,\!06)^{-2}=30\,259,\!87\ldots$ ja kymmenenneltä $34\,000\cdot(1 + 0,\!06)^{-10} =18\,985,\!42\ldots.$ Lisäksi diskontataan poistoarvo $40\, 000$ euroa nykyhetkeen eli $40\,000\cdot(1 + 0,\!06)^{-10} =22\,335,\!79\ldots$ .

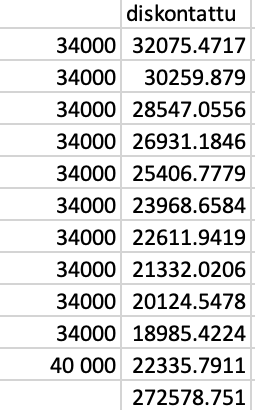
Näiden kaikkien diskontattujen tulojen ja poistoarvojen summa on noin 272 600 euroa. Koska tämä on pienempi kuin investointi 300 000 euroa, investointi ei ole kannattava.

2.5.6 Geometrinen sarja

Geometrista sarjaa tarvitaan useissa sovelluksissa - esimerkiksi diskonttauksesssa.

Esimerkiksi summa $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\dots$ on eräs geometrinen sarja.

Ongelma

Miten edellisen summan peräkkäiset luvut liittyvät toisiinsa?

Määritelmä

Summa $x_1+x_2+x_3+\ldots=\sum_{k=1}^{\infty}{x_k}$ on geometrinen sarja, jos millä tahansa luvulla $k = 1, 2, \ldots$ ja jollain luvulla pätee $\frac{x_{k+1}}{x_k} =q$ (eli peräkkäisten termien suhde on aina sama).

Geometrinen sarja voidaan esittää muodossa
$a+aq+aq^2+\ldots=\sum_{k=1}^{\infty}{aq^{k-1}}.$

Lukua kutsutaan geometrisen sarjan suhdeluvuksi ja lukua ensimmäiseksi termiksi.

Geometrisen sarjan summa

Geometrisen sarjan summa on $\frac{a}{1-q}, \quad \text{kunhan \ } -1<q<1.$

Soveltamalla yllä olevaa kaavaa ongelmamme geometriseen sarjaan, saadaan sarjan $\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\dots$ summan arvoksi . Alla oleva sovelma havainnollistaa visuaalisesti, miksi tämä käy järkeen.

# geo2taso8

# osasumma

2.5.7 Geometrisen sarjan osasumma

Jos $q \neq 1$ , niin geometrisen sarjan niin kutsutun nen osasumman $a+aq+aq^2+\ldots+aq^{n-1} =\sum_{k=1}^{n}{aq^{k-1}}$ arvo on $\frac{a(1-q^n)}{1-q}.$

Tätäkään kaavaa ei tarvitse muistaa ulkoa, vaan sen voi palautella helpohkosti mieleensä.

\[\begin{array}{c r *{11}{c@{\hspace{6pt} + \hspace{6pt}}} c} \, & \sum\limits_{k=1}^{n} q^{k-1} = & 1 &+ & q &+ & q^2 &+ & \ldots & + & q^{n-2} & + & q^{n-1} &\, \\ - & q\sum\limits_{k=1}^{n} q^{k -1} = & \, & - & q & - & q^2 & - & \ldots & - & q^{n-2} & - & q^{n-1} & - & q^{n} \\ \hline \, & (1 - q)\sum\limits_{k=1}^{n} q^{k-1} = & 1 & \, & \, & \, & \, & \, & \, & \, & \, & \, & \, & - & q^{n} \end{array}\]

Mökkiesimerkki

Oletetaan, että suvun kesämökki vaatii joka vuosi (eli periodi) huoltoa ja että jokaisen vuoden kulut maksetaan vuoden lopussa. Olkoot vuosittaiset kulut seuraaville lle vuodelle x_k , $k=1,\ldots,n$ .

Suku päättää kerätä tarvittavat varat ensimmäisen vuoden alussa, ja tallettaa ne tilille tulevia maksuja varten. Tilin korkokanta on p/100=r ja korko maksetaan vuoden lopussa (ennen huoltokulun maksamista).

Kuinka paljon rahaa suvun pitää tallettaa tilille?

Meidän pitää selvittää tulevien maksujen yhteenlaskettu nykyarvo, joka on tilille talletettava summa. Tähän käytämme diskonttausta.

Nykyarvo (ja tilille talletettava summa) P_n saadaan kaavalla $P_n=x_1(1+r)^{-1}+x_2(1+r)^{-2}+\ldots+x_n(1+r)^{-n},$ koska minkä tahansa periodin maksun nykyarvo on $x_k(1+r)^{-k}$ (eli jokainen kulu x_k on diskontattu tilin korkokannan avulla) ja P_n on vain näiden maksujen nykyarvojen summa.

Jos kaikki tulevat huoltokulut ovat aina yhtäsuuret - vaikkapa 5000 euroa joka vuosi -, korkoprosentti on ja suku kerää rahat seuraavaa vuotta varten, niin kuinka paljon rahaa pitää kerätä?

Nyt kustannusten nykyarvo on $P_{20}=5000\frac{1}{1+2/100}+5000\frac{1}{(1+2/100)^2}+\ldots+5000\frac{1}{(1+2/100)^{20}}.$ Kyseessä on geometrisen sarjan osasumma, jossa ensimmäinen termi on $5000/(1+2/100) = 5000/1,\!02$ ja suhdeluku on $1/(1+2/100) = 1/1,\!02$ . Näin ollen, käyttämällä geometrisen sarjan osasumman kaavaa (katso 2.5.7) $\begin{align*} P_{20}&=\frac{(5000/1,\!02)\left(1-\left(\frac{1}{1,\!02}\right)^{20} \right)}{1-1/1,\!02}=\frac{5000\left(1-\left(\frac{1}{1,\!02}\right)^{20}\right)}{1,\!02 -1}=\frac{5000}{0,\!02}\left(1-\left(\frac{1}{1,\!02}\right)^{20}\right)\\ &\approx 81 757 \qquad \text{(euroa)}. \end{align*}$

Mökin huollot toteuttaa ulkopuolinen yritys. Oletetaan, että yritys tallettaa saadut tulot tilille, jolle maksetaan korkoa korkokannan $r = 0,\!03$ mukaisesti kunkin periodin lopussa.

Kuinka paljon rahaa yritykselle on kertynyt mökkiprojektista korkoineen on välittömästi viimeisen maksun jälkeen?

Yritys saa nyt 5000 euroa vuosittain ja se talletetaan tilille, jolle maksetaan prosentin korko.

Nyt tulovirran yhteenlaskettu tuleva arvo on $F_{20}=x_1(1+0,\!03)^{20-1}+\ldots+x_{20-1}(1+0,\!03)+x_{20} = 5000(1,\!03)^{20-1}+\ldots+5000(1,\!03)+5000$ koska kyseissä tilanteessa viimeinen tulo $x_{20}$ ei ehdi kasvaa lainkaan korkoa

Voimme laskea tämän geometrisen sarjan osasumman kaavalla (katso 2.5.7) $F_{20} = \frac{5000(1 - 1,\!03^{20})}{1 - 1,\!03} = \frac{5000}{0,\!03}\left(1,\!03^{20} -1 \right) \approx 134 352 \qquad \text{(euroa)}.$

Tehtäviä

1. Derivoi funktio , $f(x) = e^x + x\ln x$ .
2. Derivoi funktio , $g(x) = \ln(6x^6 - 5x^5 - 4)$ .
3. Laske a-kohdan funktion toinen derivaatta ja kolmas derivaatta .

1. Ratkaise yhtälö $e^{x^2 -1} = 1.$
2. Ratkaise yhtälö $2^{x+1} = 3^{x}.$
3. Ratkaise muuttujan suhteen yhtälö $A = K\left(1 + \frac{p}{100}\right)^{-n}.$
4. Ratkaise Henderson–Hasselbalch-yhtälö ${\mathrm{pH}}={\mathrm{p}} K_{a}+\log_{10}\left({\frac {[{\mathrm{A^-}}]}{[{\mathrm{HA}}]}}\right)$ $[{\mathrm{HA}}]$ :n suhteen.

Selvitä/kerro annetun funktion () määrittelyjoukko ja funktion nollakohta/nollakohdat. $\text{(a) } f(x) = e^{\sqrt{x}} \quad\quad\quad \text{(b) } g(x) = e^x(x^2 - 1) \quad\quad\quad \text{(c) } h(x) = \dfrac{x^2 + 1}{\ln (x+5)}$

Laske funktion jousto kohdassa. Tulkitse tulostasi kohdassa b.
1. $f(x) = -e^{8x}$
2. Milloin tilanne on joustava ja milloin joustamaton?

Tässä tehtävässä voit käyttää laskinta tai taulukko-ohjelmaa.
1. Yritys harkitsee investointia, joka maksaisi 80 000 euroa. Investoinnin myötä yritys saisi neljän vuoden kuluttua yhden maksusuorituksen, jonka arvo on 92 000 euroa. Jos vuotuinen korko on 5% ja käytetään diskonttauksessa jatkuvaa korkoa, niin kannattaako yrityksen sijoittaa investointihankkeeseen?
2. Koneen ostohinta on 130 000 euroa. Käyttöikä on viisi vuotta, jonka jälkeen koneella on vielä 20 000 euroa poistoarvoa.
  
  Koneen vuosittainen tuotto on 25 000 euroa. Laske koneen poistoarvon ja koneen tuottojen ostohetkeen muunnetut nykyarvot, kun vuotuinen korkokanta on 0,05 eli 5%. Päättele tuloksesta kannattaako koneen osto.

Ratkaise yhtälöt. $\text{(a) } e^{x^3 +1} = 1 \quad\quad \text{(b) } 2^{x^2-3} = 4^x$

Onko väite totta vai tarua? Perustele vastauksesi.
- Omistat joukkovelkakirjan, jolla saat kymmenen vuoden kuluttua 10 000 euroa. Jos diskonttaat joukkovelkakirjan tulevan arvon 10 000 euroa jatkuvalla korkolaskennalla, kun $r = 0,\!03$ , niin sen nykyarvo tänään on pienempi kuin 10 000 euroa.

# geo2taso18

# 3

3. Ääriarvot

Tässä osassa käsitellään seuraavia asioita

funktion paikalliset (lokaalit) ääriarvot
funktion globaalit (absoluuttiset) ääriarvot
ääriarvojen etsiminen
- paikalliset ääriarvot
- globaalit ääriarvot

Osiota vastaa [EMEA, 8.1-8.6].

Monet mallit sisältävät ääriarvotehtäviä (eli maksimointi- tai minimointitehtäviä). Yhden muuttujan funktion maksimointitehtävä voidaan esittää seuraavasti: $\max_{x} f(x).$ Tässä etsitään sitä funktion määrittelyjoukon pistettä, jolla funktion arvo on suurin. Taloustieteessä funktiota kutsutaan tavoitefunktioksi ja muuttujaa valintamuuttujaksi.

Minimointitehtävä määritellään samoin, mutta $\min$ -operaattorin avulla, eli etsitään pistettä, jossa funktion arvo on pienin.

Funktion ääriarvoista

"globaalit ääriarvot" (absoluuttiset ääriarvot) eli funktion suurin ja pienin arvo:
- koko määrittelyjoukossa saavutetuista arvoista suurin ja pienin - esimerkiksi Mount Everestin huippu on korkein kohta Maassa.
ääriarvot annetussa joukossa:
- rajoitetaan tarkastelu annettuun joukkoon - esimerkiksi Suomen korkein kohta löytyy Haltin rinteestä
"paikalliset ääriarvot" (lokaalit ääriarvot):
- jollakin etäisyydellä ei löydy suurempia arvoja - "kukkulan huippu"
- jollakin etäisyydellä ei löydy pienempiä arvoja - "laakson pohja"

Tavallisia ääriarvotehtävään (eli missä on suurin tai pienin arvo) liittyviä kysymyksiä ovat

Onko tehtävällä ratkaisua?
Jos tehtävällä on ratkaisu, mikä se on ja mitä ehtoja se toteuttaa?
Minkälaisia ominaisuuksia ratkaisulla on?

Tällä kurssilla ja esimerkiksi kurssilla Talousmatematiikka harjoitellaan menetelmiä, joilla pystytään mahdollisesti vastaamaan kysymykseen 2. Kurssilla Mathematics for economists III (AGERE-009) ja myöhemmillä kursseilla tutkitaan myös kysymyksiä 1. ja 3.

3.1 Funktion paikalliset ääriarvot

Määritelmä

Määrittelyjoukon piste on funktion paikallinen (tai lokaali) maksimipiste, jos on funktion suurin arvo pisteen "pienessä" ympäristössä. Tällöin on funktion paikallinen maksimiarvo.
Määrittelyjoukon piste on funktion paikallinen (tai lokaali) minimipiste, jos on funktion pienin arvo pisteen "pienessä" ympäristössä. Tällöin on funktion paikallinen minimiarvo.

Huomautuksia

Funktion ääriarvopiste on joko maksimi- tai minimipiste.
paikallisia maksimeja/minimejä voi olla monta (ja erisuuria), globaaleja vain yhdet - jotka tosin voidaan saavuttaa useassa kohdassa
lokaaleja/globaaleja ääriarvoja ei välttämättä ole yhtään!

3.1.1 Paikallisten ääriarvojen etsiminen

Funktion paikallisia ääriarvoja voi löytyä

derivaatan nollakohdista
pisteistä, joissa ei ole derivoituva
määrittelyjoukon reunapisteistä (yleensä määrittelyjoukko on väli tai välien yhdiste)

Määrittelyjoukon pistettä, jossa funktion derivaatta on nolla, kutsutaan funktion kriittiseksi pisteeksi. Kriittinen piste on siis yhtälön f'(x)=0 ratkaisu eli derivaatan nollakohta.

Tarkemmin lokaalien ääriarvojen löytymisestä:

Jos on väli (välit mainittiin kurssilla Matematiikka 1) ja funktiolla $f \colon \, I \to \, \mathbb R$ on paikallinen ääriarvo kohdassa x = x_0 , niin x_0 on joko funktion kriittinen piste tai välin päätepiste tai funktio ei ole pisteessä x_0 derivoituva.

Erityisesti

Ensimmäisen kertaluvun välttämätön ehto ääriarvolle

Olkoon on väli ja oletetaan, että funktiolla $f \colon \, I \to \, \mathbb R$ on derivaatta jokaisessa välin pisteessä.

Jos funktiolla on paikallinen ääriarvo kohdassa x = x_0 , joka ei ole välin päätepiste, niin x_0 on funktion kriittinen piste eli f'(x_0) = 0 .

Huomautuksia

Näin saatiin keino etsiä paikallisia ääriarvoja - mutta nämä ovat vain ehdokkaita.

Pitää tutkia, löytyykö kohdasta ääriarvoa vai ei!

3.1.2 Paikalliset ääriarvot kulkukaavion avulla

Oletetaan, että on jatkuva ja derivoituva kaikkialla paitsi ehkä yksittäisissä pisteissä.

Etsi mahdolliset paikalliset ääriarvokohdat:
- kriittiset pisteet (missä $\, f'(x) = 0 \,$ )
- pisteet, missä ei ole derivoituva (tai et ole varma onko se derivoituva)
- välien päätepisteet
Tutki derivaatan merkkiä näiden pisteiden välillä.
- Merkitse kasvavuus/vähenevyys, niin näet onko kyseessä lokaali maksimi, lokaali minimi vai ei kumpikaan.
  - derivaatta kasvava, derivaatta vähenevä.
    $\quad\; \longrightarrow$ niin kutsuttu kulkukaavio
Laske funktion arvot näissä pisteissä.

Kriittinen piste ei välttämättä ole ääriarvopiste. Esimerkiksi funktion , f(x)=x^3 kriittinen piste on x=0 , mutta se ei ole ääriarvopiste.

Kohdan 2. voi kirjoittaa myös "testiksi"

# ensimmainen_derivaatta

Ensimmäisen derivaatan testi paikalliselle ääriarvopisteelle

Olkoon f'(x_0)=0 . Jos derivaatta vaihtaa merkkiä pisteen x_0 kohdalla, niin piste x_0 on paikallinen ääriarvopiste. Lisäksi

Jos derivaatta muuttuu positiivisesta negatiiviseksi, niin piste on paikallinen maksimipiste.
Jos derivaatta muuttuu negatiivisesta positiiviseksi, niin piste on paikallinen minimipiste.

Esimerkki

Esimerkiksi funktion , f(x)=x^2+2x , kriittinen piste on x=-1 , koska f'(x)=2x+2 ja 2x + 2 = 0 , kun x=-1 .

Tämä kriittinen piste on paikallinen minimipiste, koska derivaatta on negatiivinen kriittisen pisteen vasemmalla puolella ja positiivinen oikealla puolella. Alla on kulkukaavio, jossa derivaatan nollakohta on "laakson pohjalla" eli se on (paikallinen) minimi

$\begin{array}{l} \hspace{28pt} \quad \hspace{15pt} -1 \hspace{14pt} \; \\ \begin{array}{c|c|c|c} f'(x) : & - & + & \!\!\! \\ \hline f(x) : & \searrow & \nearrow \end{array} \end{array}$

Yllä derivaatan merkin voi selvittää usealla tavalla:

Testaamalla, mitä arvoja derivaatta saa, kun ja ; esimerkiksi sijoittamalla $f'(-2) = 2 \cdot (-2) + 2 = -4 + 2 = - 2 < 0$ ja $f'(0) = 2\cdot 0 + 2 = 2 > 0$
Muistamalla, miltä derivaatan kuvaaja näyttää; se on suora, jonka kulmakerroin on , joten se on kasvava, eli derivaatta on negatiivista nollakohdan vasemmalla puolella ja positiivista oikealla.
Ratkaisemalla epäyhtälön eli epäyhtälön .

Esimerkki

Tutkitaan paloittain määritellyn funktion , $f(x) = \begin{cases} x^2 + 1, & \text{kun } x \in [-1,2] \\ -x + 7, & \text{kun } x \in \; ]2,4] \\ -2x + 11, & \text{kun } x \in \; ]4,6] \end{cases}$ kulkua.

Ratkaisuidea - alla on myös video ratkaisusta

Funktiolla on kriittinen piste kohdassa x = 0 (Miksi tämä on (ainoa) kriittiinen piste?) sekä kaksi pistettä, missä se ei ole derivoituva; x = 2 ja x = 4 (voit myös todeta, että nämä ovat ongelmallisia pisteitä, koska määritelmä vaihtuu, joten ne pitää tutkia).

Meillä on nyt neljä tarkasteluväliä: [-1, 0] , [0,2] , [2, 4] , [4,6] .

Selvitetään derivaatan merkki kullakin tarkasteluvälillä:

$\, f'(-\frac{1}{2}) = -1 < 0$ ( $\; - \;$ ), joten välillä on vähenevä ( $\; \searrow \;$ )
$\, f'(1) = 2 > 0$ ( $\; + \;$ ), joten välillä on kasvava ( $\; \nearrow \;$ )
$\, f'(3) = -1 < 0$ ( $\; - \;$ ), joten välillä on vähenevä ( $\; \searrow \;$ )
$\, f'(5) = -2 < 0$ ( $\; - \;$ ), joten välillä on vähenevä ( $\; \searrow \;$ )

Nämä tiedot kootaan niin kutsuttuun kulkukaavioon, jossa ylimmällä rivillä näkyy derivaatan merkki ja alemmalla funktion kasvavuus/vähenevyys.

$\begin{array}{l} \hspace{28pt} -1 \hspace{15pt} 0 \hspace{14pt} 2 \hspace{15pt} 4 \hspace{15pt} 6 \\ \begin{array}{c|c|c|c|c|c} f'(x) : & - & + & - & - & \!\!\! \\ \hline f(x) : & \searrow & \nearrow & \searrow & \searrow \end{array} \end{array}$

Kulkukaaviosta nähdään, että funktiolla on paikalliset maksimit kohdissa x = -1 ja x = 2 (huippu) ja paikalliset minimit kohdissa x = 0 ja x = 6 (laakso). Pisteessä x = 4 ei ole kumpaakaan (suunta ei vaihdu).

Paikalliset maksimit ovat siis f(-1) = 2 ja f(2) = 5 ja paikalliset minimit f(0) = 1 ja f(6) = -1 .

# geo1

# V1

3.2 Globaalien ääriarvojen etsiminen

Globaali (tai absoluuttinen) maksimiarvo on funktion suurin arvo funktion koko määrittelyjoukossa.

Vastaavaan tyyliin määritellään myös globaali (tai absoluuttinen) minimiarvo eli se on pienin arvo funktion koko määrittelyjoukossa.

Onko funktiolla suurinta tai pienintä arvoa?

Tähän alun 1. kysymykseen eli "Onko ääriarvotehtävällä ratkaisua?" voimme vastata esimerkiksi jatkuvan funktion tapauksessa. Funktio on jatkuva, jos sen kuvaaja on katkeamaton käyrä eli funktion kuvaajan voi piirtää nostamatta kynää paperista. Tämä on havainnollistava, mutta ei kovin täsmällinen määritelmä jatkuvuudelle.

Suljetulla välillä [a,b] jatkuva funktio saa siellä pienimmän ja suurimman arvonsa.

Siis, jos tarkasteltava väli on suljettu ja jatkuva, niin funktiolla on suurin ja pienin arvo. Tällöin

globaali maksimi on suurin paikallisista maksimeista
globaali minimi on pienin paikallisista minimeistä

Esimerkki

Funktiolla , g(x) = x^2 , kun $x \in [-2, 3]$ , tutkittavia pisteitä ovat välin päätepisteet ja sekä mahdollinen kriittinen piste eli derivaatan nollakohta.

Derivaatta on g'(x) = 2x, joten derivaatalla on nollakohta pisteessä x = 0 . Tämä on siis kriittinen (ja tutkittava) piste.

Tutkimalla funktion kulkua nähdään (Tutki!), että funktiolla on paikallinen maksimi g(-2) = 4 ja g(3) = 9 sekä paikallinen minimi g(0) = 0 .

Paikallinen minimi on myös globaali minimi (pienin kaikista paikallisista minimeistä) ja paikallinen maksimi g(3) = 9 on myös globaali maksimi, koska se on suurin kaikista paikallisista maksimeistä (sillä 9> 4 ).

# V2

# Derivointi2

# SJPASV

Yleensä kätevintä on tutkia kulkukaaviota, mutta joskus tutkimuksissa näkee mainintoja testeistä. Tässä on yksi niistä, joka perustuu juurikin kulkukaavioihin.

Ensimmäisen derivaatan testi globaalille ääriarvopisteelle

Olkoon f'(x_0)=0 .

Jos $f'(x)\geq 0$ kaikilla $x\leq x_0$ ja $f'(x)\leq 0$ kaikilla $x\geq x_0$ , niin on globaali maksimipiste.
Jos $f'(x)\leq 0$ kaikilla $x\leq x_0$ ja $f'(x)\geq 0$ kaikilla $x\geq x_0$ , niin on globaali minimipiste.

Oleellista tässä on, että esimerkiksi kohdassa (i) epäyhtälö $f'(x)\geq 0$ on voimassa kaikilla funktion määrittelyjoukon pisteillä, jotka toteuttavat ehdon $x\leq x_0$ . Se, että kyseinen ehto ja muut ehdot ovat voimassa kaikilla määrittelyjoukon pisteillä, takaa ääriarvopisteen globaaliuden.

Paikallisen ääriarvon tapauksessa riitti tutkia vain derivaatan merkkiä kriittisen pisteen läheisyydessä.

Ongelma

Onko funktiolla , f(x)=-e^x+x , globaalia maksimia?

Vastaus

Kriittinen piste ratkaisee yhtälön -e^x+1=0 . Se on x=0 . Tämä piste on paikallinen ja myös globaali maksimipiste (näytä joko kulkukaaviolla tai yllä olevalla testillä).

# V15

Ongelma

Ilmaan viskatun kappaleen korkeus metreinä on s(t) = 1 + 4t - 4t^2, missä on kulunut aika sekuntteina.

Miten korkealla kappale käy?
Mikä on kappaleen nopeus sen iskeytyessä maahan?

# Nopeustehtävä1

# Nopeustehtävä2

Edelleen, jos kulkukaavio tylsistyttää, kahdesti derivoituville funktioille on vielä testi, joka kertoo kriittisen pisteen laadun.

# toinen_derivaatta

3.2.1 Toisen derivaatan testi

Olkoon funktio kahdesti derivoituva pisteessä x_0 ja f'(x_0)=0 . Tällöin

Jos , niin piste on paikallinen maksimipiste.
Jos , niin piste on paikallinen minimipiste.

Matematiikka 1 -kurssilla meillä oli ongelmana miettiä milloin yrityksen voitto on nolla:

Ongelma

Mallinnetaan yrityksen voittoa lausekkeella $pq - \frac{1}{2}cq^2.$

Muuttujana on tuotantomäärä . Parametreinä meille on annettu lopputuotteen hinta ja , joka antaa yritykselle lankeavan kustannuksen $\frac{1}{2}cq^2$ , kun tuotantomäärä on .

Millä tuotantomäärällä voitto on nolla?

Käytetään edeltäviä tuloksia kyseisen voiton maksimointiin.

Esimerkki

$\max_{ q } \left (pq-\frac{1}{2}cq^2\right )$ Derivoidaan: $D_q(pq-\frac{1}{2}cq^2) = p - \frac{1}{2}\cdot 2 q^{2-1} = p -cq.$ Nyt tavoitefunktion $\pi$ , $\pi(q) = pq-\frac{1}{2}cq^2$ , kriittinen piste (eli derivaatan nollakohta) voidaan selvittää ratkaisemalla yhtälö p-cq=0 . Kriitinen piste on q=p/c .

Se on paikallinen maksimipiste esimerkiksi toisen derivaatan testin (katso 3.2.1) perusteella: sillä $\pi''(q)= D_q(p - cq) = -c<0$ , sillä on positiivinen luku (kustannusten $\frac{1}{2}cq^2$ täytyy olla positiiviset, jotta tilanne on taloustieteellisesti järkevä).

Toisaalta voiton $\pi$ kuvaaja on alaspäin aukeava paraabeli (toisen asteen termin kerroin $-\frac12 c$ on negatiivinen), joten pisteessä p/c saavutetaan myös globaali maksimi.

Siis voitto on suurimmillaan, kun tuotantomäärä on p/c .

Ongelma

Oletetaan, että seuraavalla voiton maksimointitehtävällä on ratkaisu ja ja ovat derivoituvia ( on tulo ja on kustannukset). $\max_{ q } (R(q)-C(q))$ Maksimipiste on tällöin kriittinen piste ja toteuttaa siten yhtälön R'(q)=C'(q).

Mitä tämä ehto tarkoittaa sanallisesti?

# rajatulkinta

Ongelma

Oletetaan, että yllä olevassa voiton maksimointitehtävässä vaadittaisiin lisäksi, että $0 \leq q \leq q_{\text{max}},$ jossa $q_{\text{max}}$ tulkitaan yrityksen tuotantokapasiteetiksi.

Mistä pisteistä voittoa maksimoiva tuotantomäärä voi nyt löytyä?

# missa_maksimi

# Optimointi1

# Optimointi2

Lisää harjoitusta ääriarvoista löytyy Kisällioppinen-sivustolta.

Tehtäviä

1. Derivoi funktio , .
2. Etsi derivaatan nollakohdat.
3. Mitkä ovat funktion paikalliset ääriarvopisteet?

Määritä funktion , missä on vakio/parametri, paikalliset ääriarvopisteet käyttäen toisen derivaatan testiä (katso 3.2.1).

Onko funktiolla $f \colon [-3, 100] \to \R$ , $f(x) = \cfrac{x}{x^2+1},$ paikallisia tai globaaleja ääriarvoja? Jos on, selvitä missä ja mitkä ne ovat.

Huomaa, että yllä olevassa merkinnässä funktion määrittelyjoukko on suljettu väli .

Tutki maksimointitehtävää $\max_{x}\left( 100x^{1/2} - 2x \right).$
1. Mikä on tehtävän ratkaisu?
2. Miksi kyseessä on globaali maksimipiste?

Derivoi.
1. $f(x) = -\frac 32 x^3 + 2x^2$
2. $\pi(q) = 100q - \frac 12 q^2 - \left(10 + \frac 14 q^2 \right)$

Selvitä tehtävässä 5 laskettujen derivaattojen nollakohdat.

Mitkä ovat tehtävän 5 funktioiden (, $\pi$ ) paikalliset ääriarvopisteet?

Etsi lokaalit ja globaalit ääriarvot ja ääriarvopisteet funktiolle , , suljetulla välillä .

Onko väite totta vai tarua? Perustele vastauksesi.
- Jos funktiolla on derivaatta, :llä on aina lokaali ääriarvokohta.

Olkoon puun myyntihinta hetkellä Diskonttaamalla voimme selvittää sen niin kutsutun nykyarvon. Nykyarvo jatkuvalla korkolaskennalla on $P(t)e^{-rt}.$ Milloin (eli millä n arvolla) puun myyntihinnan nykyarvo on suurimmillaan, jos korkokantana on $r = 0,\!05$ ?

Jos laskut alkavat hirvittää, käytä laskinta.

# geo2taso14

# geo2taso12

# 4

4. Usean muuttujan funktiot

Tässä osassa käsitellään seuraavia asioita

usean muuttujan funktiot
osittaisderivaatat
- gradientti

Osiota vastaa [EMEA, 11.1-11.3].

Funktio on sääntö, joka liittää jokaiseen määrittelyjoukon alkioon täsmälleen yhden maalijoukon alkion.

Merkitään $f \; \colon A \longrightarrow B$ missä

$f \quad$ on funktion nimi
$A \quad$ on määrittelyjoukko
$B \quad$ on maalijoukko

Määrittelyjoukko on se joukko, jonka alkioita funktio kuvaa. Maalijoukko on sellainen joukko, joka sisältää kaikki nämä kuvat.

Olemme käsitelleet yhden muuttujan funktioita. Usean muuttujan reaaliarvoinen funktio määritellään samaan tyylin kuin yhden muuttujan funktio: funktio liittää jokaiseen määrittelyjoukon pisteeseen yksikäsitteisen reaaliluvun.

Tällä kurssilla tarkastellaan pääasiassa vain kahden muuttujan funktiota.

Esimerkki

Jos määrittelyjoukko on -taso, niin kahden muuttujan funktio liittää jokaiseen tason pisteeseen yksikäsitteisen reaaliluvun pisteen; esimerkiksi funktio , $f(\hspace{-0.7cm}\underbrace{x, y}_{\text{kaksi muuttujaa}}\hspace{-0.7cm}) = x^2 + y^2,$ liittää jokaiseen tason pisteeseen yksikäisitteisen luvun. Esimerksiksi pisteeseen liitetään luku .

# Umf1

# Umf2

# Umf3

Funktion kuvaaja

Funktion kuvaaja on graafinen esitys, joka havainnollistaa funktion käytöstä.

Yhdenmuuttujan kuvaaja on pisteiden (x,f(x)) joukko -tasossa, missä kuuluu funktion määrittelyjoukkoon.

Yhden muuttujan funktioita

Esimerkkejä

Funktion , missä , kuvaaja on suora ja määrittelyjoukko koko $\mathbb R$ .
Funktion $g : [0, 1] \to \mathbb R$ , $\;g(x) = x^2$ , kuvaaja on paraabelin se osa, jossa $x \in [0,1] \;$ (eli paraabelin pisteiden ja välinen osa).
Kuten jo aikaisemmin näimme, funktion , missä , määrittelyjoukko on kaikki reaaliluvut paitsi , koska nollalla ei saa jakaa.

Alta löydät näiden esimerkkien kuvaajat.

# g4

Kahden muuttujan funktion kuvaaja on kolmiulotteisessa koordinaatistossa oleva joukko (tai pinta): funktion , missä muuttujina ovat ja , kuvaaja on z=f(x,y) eli kaikki pisteet (x, y, z), joilla pätee, että z = f(x, y) .

Yllä meidän esimerkissämme oli f(x,y) = x^2 + y^2 . Tämän funktion kuvaaja on seuraavanlainen (kuvassa -akseli on sininen).

# g2

Miksi useampia muuttujia?

Maailman tutkiminen ja mallintaminen vain yhden tutkittavan suureen avulla on vaikeaa, jos ei suorastaan mahdotonta. Asioiden tutkimiseen tarvitaan useita muuttujia

Esimerkkiksi viljellyltä pellolta tuleva ravinnehuuhtouma riippuu lannoituksen määrästä ja suojakaistan leveydestä.
Sijainnista keskilämpötilaan: Esimerkiksi seuraavassa on keskilämpötila maapallolla (keskiarvoistettu per vuosi vuosina 1961-1990). 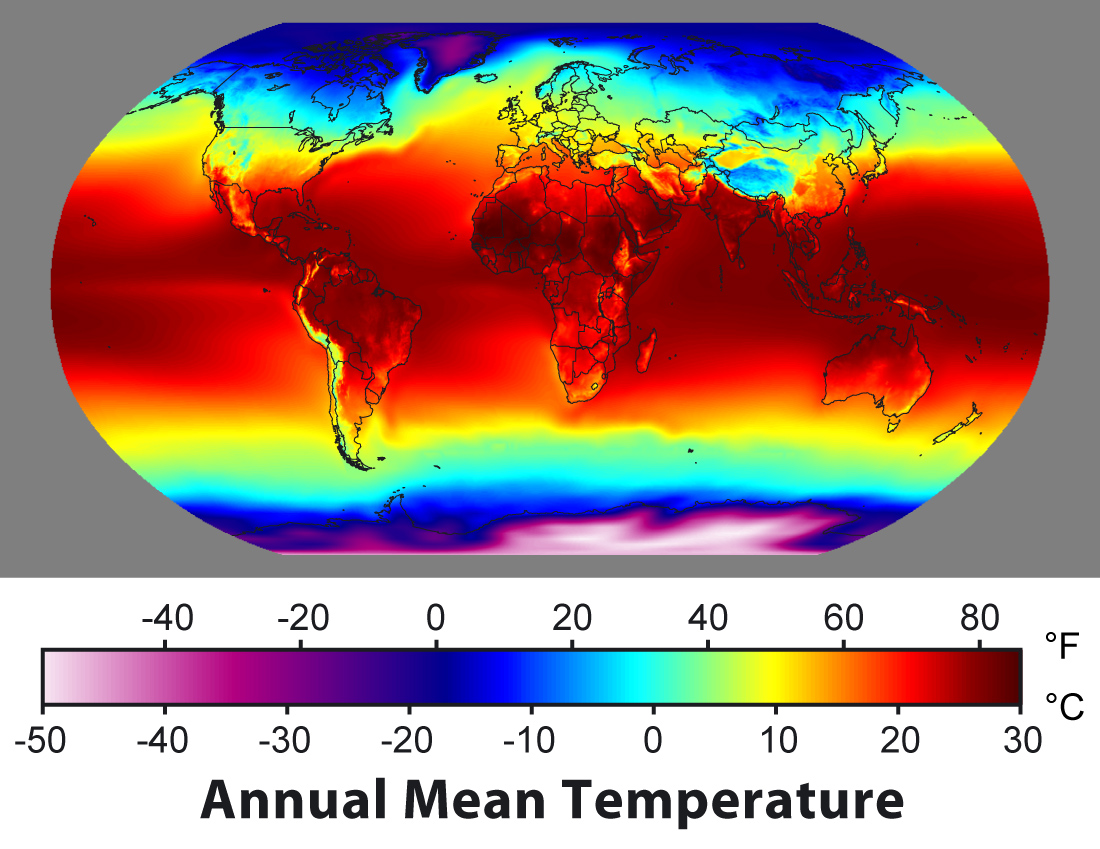Robert A. Rohde for Global Warming Art: Annual Avarage Temperature Map Wikipedia Commons CC BY-SA 3.0 Tällöin lämpötilaa voisi kuvata (monimutkainen) funktio , jossa muuttujina on sijainnin maapallolla antavat leveyspiiri ja pituuspiiri , jolloin lämpötila sijainnin funktiona olisi
Kuluttajan "hyöty" riippuu yleensä usean hyödykkeen määristä. Esimerkiksi kahden hyödykkeen hyötyfunktio antaa kokonaishyodyn , kun hyödykkeiden määrät ovat ja , eli .
Jos tuotanto riippuu kahden panoksen määristä, niin tätä riippuvuutta voidaan esittää tuotantofunktion avulla. Tuotantomäärä olisi tällöin , missä muuttuja on panoksen määrä (esimerkiksi saatavissa oleva työvoima) ja muuttuja panoksen määrä (esimerkiksi raaka-aineen määrä).
Yrityksen voitto riippuu esimerkiksi panosmäärän lisäksi henkilötyöpanoksesta , voittofunktio on tällöin kahden muuttujan funktio $\pi$ , $\pi(x, h)$ .

Cobb-Douglas

Hyötyfunktio (ja myös tuotantofunktio) voisi olla esimerkiksi niin sanottua Cobb-Douglas-tyyppiä: u(x,y)=Ax^ay^b, missä , ja ovat (yleensä aidosti positiivisia) vakioita.

Klassisesti tuotannon mallinnuksessa n tilalla on ollut muuttuja (pääoma, capital) ja n tilalla muuttuja (työvoima, labour).

Ongelma

Millä parametreilla ja tuotantomäärä vähintään kaksinkertaistuu, jos pääoma ja työmäärä kaksinkertaistetaan Cobb-Douglas-tuotantofunktiossa $u(K,L)=AK^a L^b\; ?$

Vihje

Selvitä, mikä on u(2K, 2L) . Milloin $u(2K, 2L) \geq 2 u(K, L)$ ?

Useamman muuttujan funktioiden analysointi

Matematiikassa on kaksi perustavanlaatuista analyysin työkalua:

derivointi ja
integrointi

Derivointi kertoo funktion muutosnopeudesta, kun muuttujien arvoja vaihdellaan, esimerkiksi

kuinka paljon lämpötila muuttuu, kun liikutaan maapallon pinnalla johonkin suuntaan
kuinka paljon voitto muuttuu, kun panosmäärää muutetaan, tai kuinka henkilötyöpanoksen muutos vaikuttaa voittoon

Integrointi taas on derivoinnin käänteisoperaatio (kuten vähennyslasku on yhteenlaskun käänteisoperaatio ja jakolasku on kertolaskun käänteisoperaatio); intgroinnissa lasketaan yhteen pienen pieniä lisäyksiä funktion arvossa. Integrointiin tutustumme kursseilla Matematiikka 3 ja Talousmatematiikka.

Derivointia teimme jo yhden muuttujan funktioilla luvussa 1. Mikä on nyt erilaista? Useamman muuttujan tapauksessa meidän pitää kuvailla muutosta jokaisen muuttujan kohdalla erikseen ja mahdollisesti myös muutosta johonkin annettuun suuntaan.

4.1 Osittaisderivaatat

Usean muuttujan funktiolle voidaan muodostaa derivaattakäsite. Tämä käsite jätetään muille kursseille.

Tutustumme tällä kurssilla osittaisderivointiin eli kuinka funktion arvot muuttuvat, kun voimme 'liikuttaa'/muuttaa vain yhtä muuttujista.

Tämä on käytännössä tavallista yhden muuttujan funktion derivointia: Laskettaessa osittaisderivaattaa jonkin muuttujan suhteen, lasketaan tavallinen derivaatta kyseisen muuttujan suhteen pitämällä muut muuttujan kiinteinä (eli laskettaessa muut muuttujat ajatellaan vakioiksi).

Kahden muuttujan funktion f = f(x,y) , osittaisderivaatta muuttujan suhteen pisteessä (x_0,y_0) on $\frac{\partial f(x_0,y_0)}{\partial x}=\lim_{h \to 0}\frac{f(x_0+h,y_0)-f(x_0, y_0)}{h}.$ ja muuttujan suhteen $\frac{\partial f(x_0,y_0)}{\partial y}=\lim_{h \to 0}\frac{f(x_0,y_0+h)-f(x_0, y_0)}{h}.$

Näitä määritelmiä ei käytännön laskuissa tarvita:

osittaisderivaatta $\partial f / \partial x$ lasketaan derivoimalla funktiota muuttujan suhteen pitäen muuttuja vakiona ja
osittaisderivaatta $\partial f / \partial y$ lasketaan derivoimalla funktiota muuttujan suhteen pitäen muuttuja vakiona.

Esimerkki

Funktion , f(x,y)=4x^2-xy+y^2-15x , osittaisderivaatat ovat $\frac{\partial f(x,y)}{\partial x}=8x-y-15 \quad \text{ja} \quad \frac{\partial f(x,y)}{\partial y}=-x+2y.$

Muita merkintöjä osittaisderivaatalle $\partial f / \partial x$ ovat esimerkiksi $f_x, \quad \partial_x f, \quad f_x', \quad f_1, \quad f_1'.$ Neljännessä ja viidennessä merkinnässä luku 1 johtuu siitä, että on ensimmäinen muuttuja.

Osittaisderivaatan arvo riippuu tavallisesti siitä, missä funktion määrittelyjoukon pisteessä se lasketaan. Eli merkinnän $\partial f / \partial x$ sijaan on joskus tarkoituksenmukaista merkitä osittaisderivaattaa pisteessä (x,y) merkinnöin $\partial f(x,y) / \partial x$ . Näin tehtiin yllä.

# Osittaisderivaatta1

# Osittaisderivaatta3

Jos muuttujia on enemmän kuin kaksi, niin osittaisderivaatat lasketaan vastaavasti.

Esimerkki

Funktion , $f(x,y,z)=1/x-x^3y+z\ln y^2$ , osittaisderivaatat ovat $\begin{align*} f_x(x,y,z)&=-x^{-2}-3x^2y, \\ f_y(x,y,z)&=-x^3+z\frac{2y}{y^2}=-x^3+\frac{2z}{y}, \\ f_z(x,y,z)&=\ln y^2. \end{align*}$

# V3

Gradientti

Funktion osittaisderivaatoista muodostettu vektori eli sarakematriisi on gradienttivektori $\nabla f$ $\nabla f = \begin{bmatrix} f_x \\ f_y \end{bmatrix}.$

Gradienttivektori osoittaa suuntaan, johon funktion arvo kasvaa voimakkaimmin.

Tärkein muistettava asia gradientista tällä hetkellä

Gradientti $\nabla f$ pisteessä osoittaa voimakkaimman kasvun suuntaan.
Intuitio: jos olet mäen rinteessä, gradientti osoittaa jyrkimmän nousun.

Esimerkki

Funktion f(x,y)=4x^2-xy+y^2 gradienttivektori on $\begin{bmatrix} f_x \\ f_y \end{bmatrix} = \begin{bmatrix} 8x-y \\ -x+2y \end{bmatrix}.$

Vektoria merkitään joskus myös pisteparina $\begin{bmatrix} 8x-y \\ -x+2y \end{bmatrix} =(8x-y,-x+2y).$

# g7

Korkeamman kertaluvun osittaisderivaatat

Osittaisderivaattoja $\partial f / \partial x$ ja $\partial f / \partial y$ voi mahdollisesti osittaisderivoida. Jos se onnistuu, puhutaan toisen kertaluvun osittaisderivaatoista. Niitä voidaan merkitä seuraavasti $\frac{\partial^2 f}{\partial x\partial x}, \quad \frac{\partial^2 f}{\partial y\partial y}, \quad \frac{\partial^2 f}{\partial x\partial y}, \quad \frac{\partial^2 f}{\partial y\partial x}.$

Eräs toinen merkintä esimerkiksi ensimmäiselle näistä on $f_{xx}$ .

Youngin lause

Jos n derivaatta on derivoituva, niin $f_{xy}=f_{yx}$ eli osittaisderivointijärjestyksen voi vaihtaa ilman, että niin sanotun ristiderivaatan arvo muuttuu.

Tämä pätee usein sovelluksissa.

Esimerkki

Funktion f(x,y)=4x^2-xy+y^2 toiset osittaisderivaatat ovat $\frac{\partial^2 f(x,y)}{\partial x\partial x}=8, \quad \frac{\partial^2 f(x,y)}{\partial y\partial y}=2, \quad \frac{\partial^2 f(x,y)}{\partial x\partial y}=-1, \quad \frac{\partial^2 f(x,y)}{\partial y\partial x}=-1.$

Tehtäviä

Osittaisderivoi seuraavat funktiot () kaikkien muuttujien suhteen ja käytä osittaisderivaattoja c-kohdassa.
3. Laske ja .

Osittaisderivoi seuraavat funktiot () kaikkien muuttujien suhteen.
2. $k(x,y)=\ln(-x^3 -y^3) + x^2y$

Jatkoa seuraa kurssilla Matematiikka 3.

Taloustieteen osasto, Helsingin yliopisto, elokuu 2025

Jarmo Jääskeläinen
jarmo.jaaskelainen@helsinki.fi