1. Geometrian peruskäsitteitä
Tässä kappaleessa kerrataan tasokuvioiden ja avaruuskappaleiden ominaisuuksia. Kerrataan laskemaan erilaisten kappaleiden pinta-aloja sekä tilavuuksia. Lisäksi kappaleessa käsitellään mittasuhteita ja kuvioiden yhdenmuotoisuutta.
Yksikkömuunnokset liittyät kiinteästi geometriaan. Jos yksikkömuunnokset eivät vielä ole tuttuja, tai kaipaat kertailua, ohessa on Matikkamatskujen video yksikkömuunnoksista.
Harjoitustehtävät tähän kappaleeseen löydät täältä!
1.1 Kulmat
Kulmaan kuuluu kaksi kylkeä sekä kärki. Kulmat voidaan nimetä kolmella eri tavalla:
- Kärkipisteen mukaan
- Kolmen pisteen mukaan siten, että kirjoitetaan ensin oikean kyljen piste, sitten kärkipiste ja lopuksi vasemman kyljen piste
- Aukeaman avulla
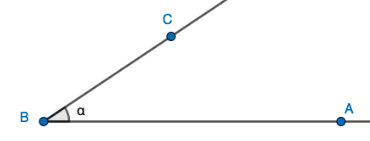Esimerkiksi ylläolevan kulman voi nimetä kolmella eri tavalla: \(\measuredangle B\), \(\measuredangle ABC\) ja \(\alpha\)
Kulmat voidaan luokitella niiden suuruuksien avulla seuraavasti:
| Kulman suuruus | Nimi | Piirros |
|---|---|---|
| \(0°\) | Nollakulma |  |
| \(0°<\alpha<90°\) | Teräväkulma |  |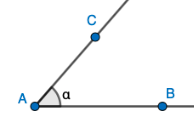
| \(90°\) | Suorakulma |  |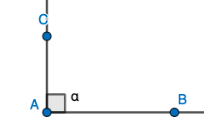
| \(90°<\alpha<180°\) | Tylppäkulma |  |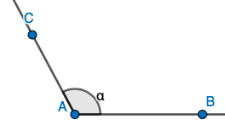
| \(180°\) | Oikokulma |  |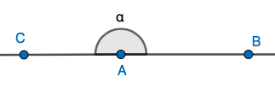
| \(360°\) | Täysikulma |  |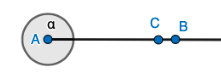
| \(0°<\alpha<180°\) | Kovera kulma |  |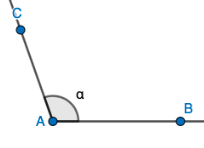
| \(180°<\alpha<360°\) | Kupera kulma |  |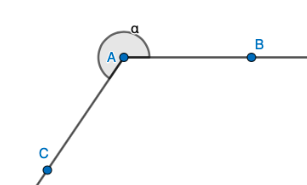
Kahden suoran leikkauksessa muodostuu neljä kulmaa. Näistä kulmista aina kaksi ovat yhtä suurta. Suorien välinen kulma tarkoittaa aina sitä pienempää kulmaa, joka suorien leikkauksessa muodostuu.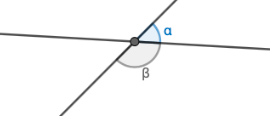 
Yllä olevassa kuvassa, kahden suoran leikkauksessa "suorien välinen kulma" on kulma \(\alpha\). Kulma \(\alpha\) on näistä kahdesta kulmasta terävämpi ja suuruudeltaan pienempi.
Vieruskulmat
Kun suora \(k\) ja \(l\) leikkaavat toisensa, vieruskulmat syntyvät leikkauspisteeseen vierekkäin. Vieruskulmien yhteenlaskettu kulma on \(180°\), eli ne muodostavat oikokulman.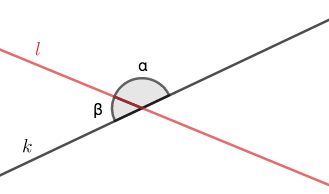 
Ristikulmat
Kun suorat \(k\) ja \(l\) leikkaavat toisensa, ristikulmat syntyvät leikkauspisteen vastakkaisille puolille. Nämä syntyneet ristikulmat ovat toistensa kanssa yhtä suuret.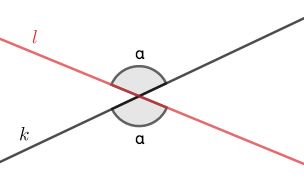 
Samankohtaiset kulmat
Kun yksi suora \(s\) leikkaa kaksi samansuuntaista suoraa \(k\) ja \(l\), leikkauspisteeseen muodostuvat kulmat ovat yhtä suuret.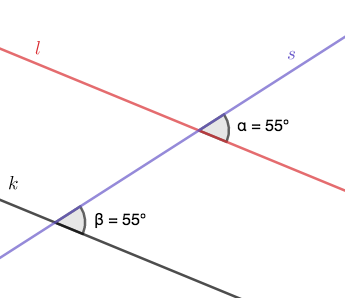 
Laske kulmien \(\alpha\) ja \(\beta\) suuruudet.
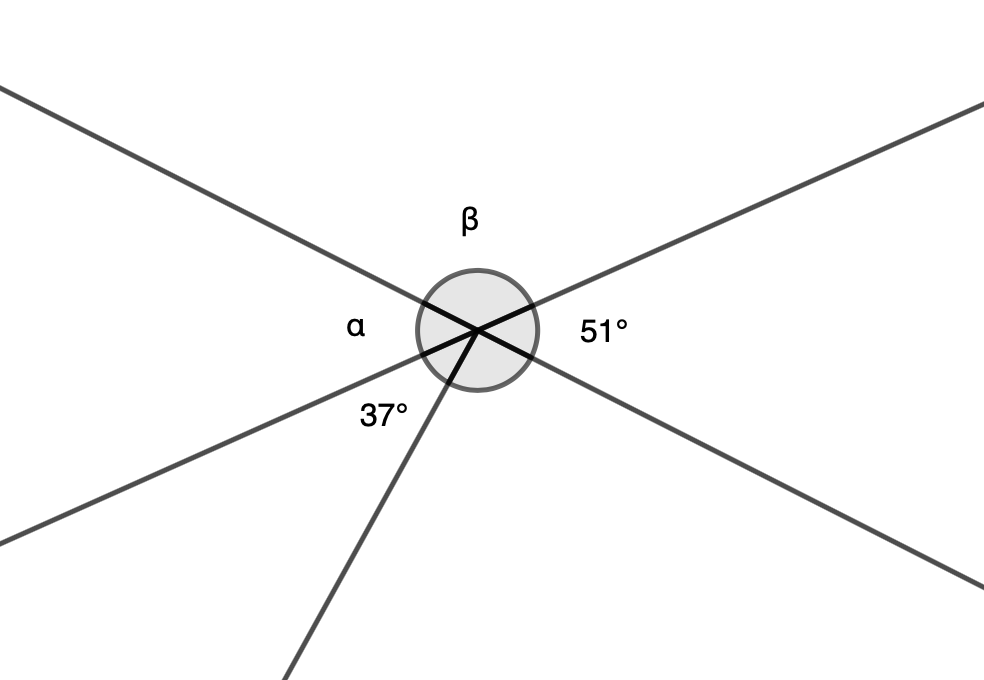
Ratkaisu
Huomataan, että kulma \(\alpha\) on \(51\) asteen kulman ristikulma, eli kulmat ovat yhtäsuuret.
\(\alpha = 51°\)
Kulma \(\beta\) saadaan kulman \(\alpha\) avulla, sillä ne ovat vieruskulmat. Vieruskulmien summa on \(180°\), joten
\[\begin{align} 51°+ \beta &= 180°& \quad &| -51° \\ \beta &= 180° - 51°& \quad &| \text{ suoritetaan vähennyslasku} \\ \beta &= 129 ° \end{align}\]
Suorat \(s\) ja \(t\) ovat yhdensuuntaiset. Laske kulmien \(\alpha\) ja \(\beta\) suuruudet.
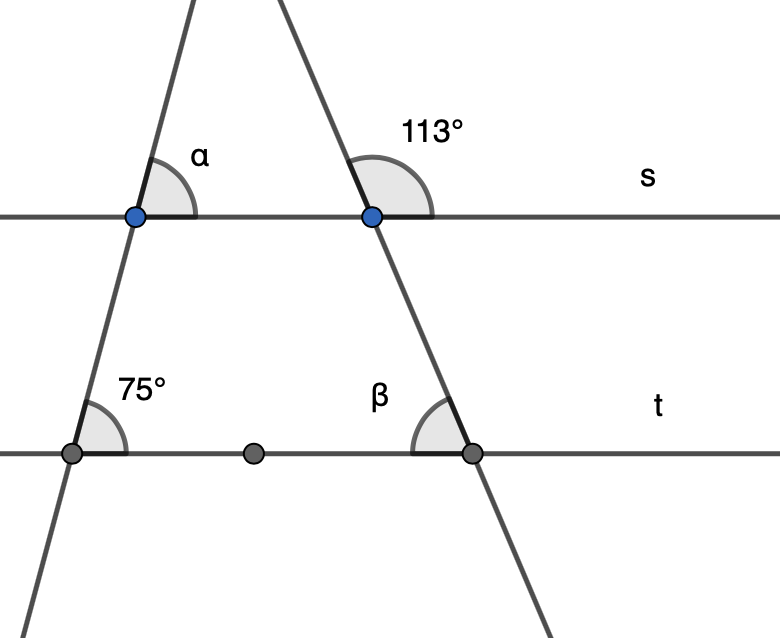
Ratkaisu
Koska suorat \(s\) ja \(t\) ovat yhdensuuntaiset, niin kulma \(\alpha\) ja 75 asteen kulma ovat samankohtaiset, jolloin ne ovat samat. Tällöin
\(\alpha = 75°.\)
Kulman 113° samankohtainen kulma muodostaa kulman \(\beta\) kanssa oikokulman, eli
\[\begin{align} 113° + \beta &= 180°& \quad &| -113° \\ \beta &= 180° - 113°& \quad &| \text{ suoritetaan vähennyslasku} \\ \beta &= 67°. \\ \end{align}\]
1.2 Yhdenmuotoisuus
Kaksi kuviota on yhdenmuotoisia, kun toinen kuvio saadaan siirtämällä, kiertämällä, peilaamalla, suurentamalla tai pienentämällä kuvio. Suurennoksessa kappale näyttää muuten samalta, mutta se on vain suurentunut.
Yhdenmuotoisuus
Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat samat riippumatta siitä, mitä sivuja tarkastellaan. Yhdenmuotoisissa kuvioissa vastinkulmat ovat aina yhtä suuret.
Yhdenmuotoisuutta voidaan merkitä lyhyesti symbolilla \(\sim\). Esimerkiksi \(K_1\sim K_{2}\) tarkoittaa, että kuvio \(K_1\) on yhdenmuotoinen kuvion \(K_2\) kanssa.
Jos kokoa ei muuteta ollenkaan, ja toinen kuvio saadaan toisesta kuviosta esimerkiksi kiertämällä tai peilaamalla, sanotaan, että kuviot ovat yhtenevät. Tälläiset kuviot ovat keskenään samankokoisia ja -muotoisia.
Yllä olevassa GeoGebra-appletissa oranssi nelikulmio on ns. vertailukuvio, joka pysyy koko ajan samana. Sen sijaan vihreää nelikulmiota pystyy muokkaamaan.
Kierrä vihreää nelikulmiota vetämällä “kierto”-liukusäädintä ja huomaa, että vihreä nelikulmio on silti yhdenmuotoinen oranssin nelikulmion kanssa.
Muuta seuraavaksi vihreän nelikulmion kokoa raahaamalla “koko”-liukusäädintä. Huomaa, että vihreän nelikulmion kulmien suuruudet pysyvät samoina kuin oranssissa nelikulmiossa, vaikka viheän nelikulmion koko muuttuisi.
Siirrä vihreää nelikulmiota eri suuntiin raahaamalla “siirto”-liukusäädintä. Vihreän nelikulmion muoto pysyy samana, vaikka se olisi eri paikassa. Se on siis edelleen yhdenmuotoinen oranssin nelikulmion kanssa.
Lopuksi lisää valinta kohtaan “peilaus”, jolloin vihreä nelikulmio peilataan pystysuoran akselin suhteen. Huomaa jälleen, että nelikulmioiden vastinkulmat pysyvät yhtä suurina, vaikka vihreä nelikulmio peilataan.
Näiden kohtien perusteella voidaan todeta, että jos kuviota kiertää, siirtää, peilaa tai sen kokoa muuttaa joka suunnassa, kuvio säilyy yhdenmuotoisena alkuperäisen kuvion kanssa.
Kokeile lopuksi muuttaa oranssin nelikulmion kärkipisteiden paikkoja raahamalla sinisiä kärkipisteitä eri paikkoihin. Huomaa, että vihreä ja oranssi nelikulmio pysyvät koko ajan yhdenmuotoisina.
Laske sivun x pituus, kun kolmiot \(ABC\) ja \(EDC\) ovat yhdenmuotoiset.
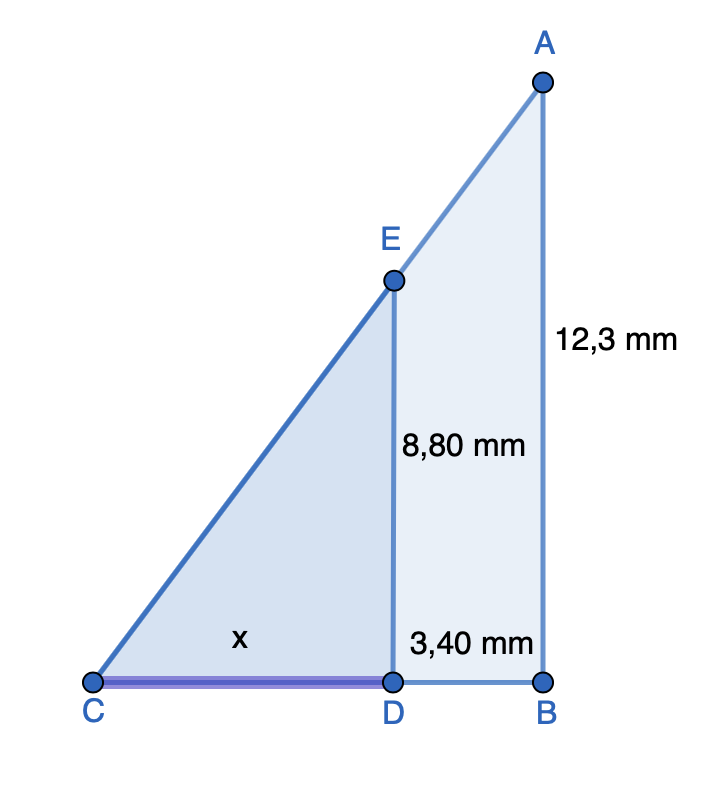
Ratkaisu
Sivun \(AB\) vastinjana pienemmässä kolmiossa on \(ED\) ja sivun \(CB\) vastinjana \(CD\).
Yhdenmuotoisilla kolmioilla vastinjanojen suhde on sama.
\[\begin{align} \frac{|AB|}{|ED|} &= \frac{|CB|}{|CD|} \\ \frac{12,3}{8,80} &= \frac{x+3,40}{x}& \quad &| \text{ kerrotaan ristiin}\\ 12,3x &= 8,80(x + 3,40)& \quad &| \text{ sievennetään} \\ 12,3x &= 8,80x + 29,92& \quad &| -8,80x \\ 3,5x &= 29,92& \quad &| :3,5 \\ x &= 8,5485... \text{ (mm)}& \quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x &≈ 8,55 \text{ (mm)} \end{align}\]
Sivun x pituus on 8,55 mm.
1.3 Kolmioiden yhdenmuotoisuus
Kolmioiden yhdenmuotoisuudesta voit lukea myös M niinkuin matematiikka -teoksesta, joka on lukiotason matematiikan tietosanakirja.
Kolmiot ovat yhdenmuotoisia, jos niillä on kaksi yhtä suurta kulmaa. Kahdesta yhtä suuresta kulmastahan seuraa myös, että kolmioiden kolmas kulma on yhtä suuri.
Kun siirrät yllä olevassa GeoGebra-appletissa kolmion ABC kärkipisteitä, huomaat, että kolmio DEF muuttuu samalla. Voit muuttaa kolmion DEF kokoa raahamalla pistettä E ja siirtää sitä raahaamalla pistettä D.
Koska kolmioiden vastinkulmat ovat koko ajan yhtä suuret, ovat kolmiot yhdenmuotoisia. Riittää, että kolmioissa on kaksi yhtä suurta vastinkulmaa, koska tällöin kolmioiden kolmannetkin vastinkulmat ovat välttämättä yhtä suuria.
Yhdenmuotoisuus
Kaksi tasokuviota \(K_1\) ja \(K_2\) ovat yhdenmuotoiset, kun
- kuvioiden vastinjanojen suhde on vakio
- kuvioiden vastinkulmat ovat yhtä suuret
Tällöin voidaan merkitä \(K_{1}\sim K_{2}\).
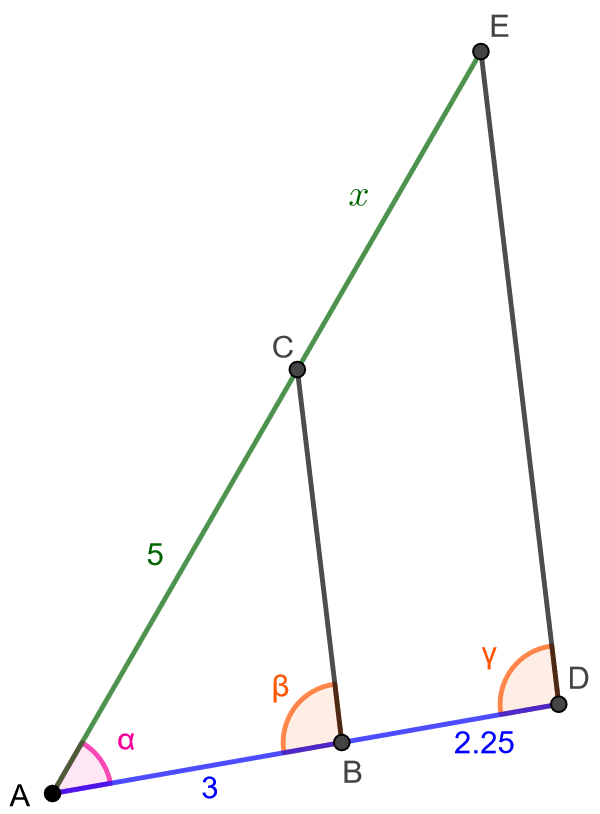
Määritä alla olevan kuvion janan \(CE\) pituus, joka on merkitty kuvioon kirjaimella \(x\). Janat \(BC\) ja \(DE\) ovat yhdensuuntaisia.
Ratkaisu
Huomataan, että kuviossa on oikeastaan kaksi päällekkäistä kolmiota: \(ABC\) ja \(ADE\). Kolmioilla on yksi yhteinen kulma \(\alpha\) joka on siis molemmissa kolmioissa yhtä suuri. Tarkastellaan seuraavaksi kulmia \(\beta\) ja \(\gamma\). Koska janat \(BC\) ja \(DE\) ovat yhdensuuntaisia, ja jana \(AD\) on molempien kulmien vasempana kylkenä, kulmat \(\beta\) ja \(\gamma\) ovat samankohtaisia. Tämä tarkoittaa, että kulmat \(\beta\) ja \(\gamma\) ovat yhtä suuria. Koska kolmioissa \(ABC\) ja \(ADE\) on kaksi yhtä suurta vastinkulmaparia, voidaan yhdenmuotoisuuslauseen KK perusteella sanoa, että kolmiot \(ABC\) ja \(ADE\) ovat yhdenmuotoiset.
Koska kolmiot ovat yhdenmuotoisia, sivun \(x\) pituuden määittämiseen voidaan käyttää yhdenmuotoisuussuhdetta. Vastinsivuparit ovat nyt \(AB\) ja \(AD\) sekä \(AC\) ja \(AE\). Näiden parien suhteet ovat yhtä suuret, joten saadaan yhtälö \[\frac{AD}{AB}=\frac{AE}{AC},\] johon sijoitetaan kunkin sivun pituus: \[\frac{3+2,25}{3}=\frac{5+x}{5}.\] Sievennetään yhtälöä, kerrotaan se ristiin ja ratkaistaan siitä \(x\): \[ \begin{aligned} \frac{5,25}{3} &= \frac{5+x}{5}& \quad &| \text{ kerrotaan ristiin} \\ 5,25 \cdot 5 &= 3 \cdot (5+x)& \quad &| \text{ sievennetään} \\ 26,25 &= 15 + 3x& \quad &| -15 \\ 11,25 &= 3x &\quad &| :3 \\ 3,75 &= x & \quad &| \text{ vaihdetaan yhtälön puolia} \\ x & = 3,75 \end{aligned} \]
Vastaukseksi saadaan, että janan \(CE\) pituus on \(3,75\).
Kk-lause
Kaksi kolmiota ovat yhdenmuotoiset, jos kolmioissa on kaksi yhtä suurta vastinkulmaparia.
Jos kolmion kulmien suuruuksia ei tiedetä, voidaan kolmioiden yhdenmuotoisuus päätellä myös niiden sivujen pituuksien avulla. Kuten aiemmin olet opiskellut, yhdenmuotoisissa kuvioissa niiden vastinsivujen suhteet ovat vakioita. Tätä ominaisuutta käytetään hyväksi yhdenmuotoisuuslauseessa SSS.
Kolmioiden yhdenmuotoisuuslause SSS
Jos kolmion kaikki sivut ovat verrannolliset vastinsivuihin toisessa kolmiossa, kolmiot ovat yhdenmuotoiset.
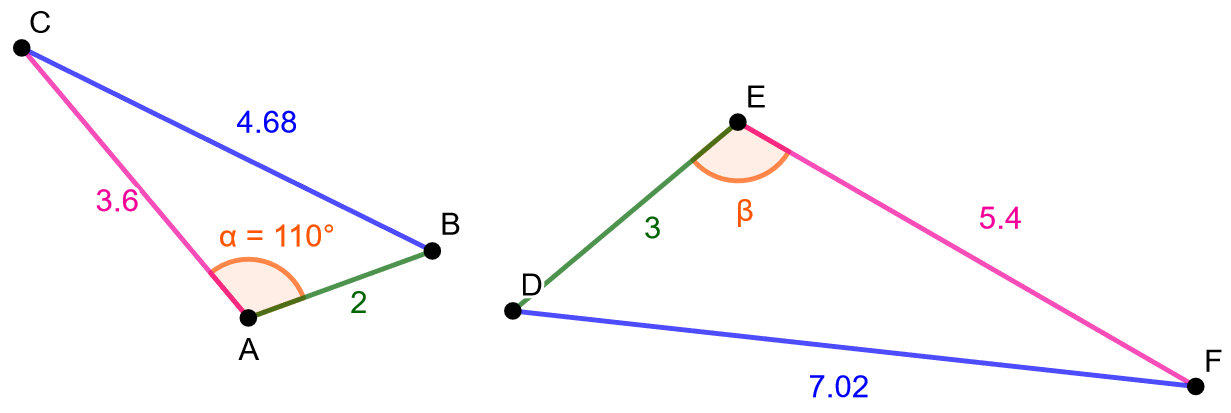
Määritä kuvaan merkityn kulman \(\beta\) suuruus.
Ratkaisu
Tutkitaan ensin, ovatko kolmiot yhdenmuotoisia. Koska molemmista kolmioista on tiedossa vain sivujen pituuksia, lasketaan kunkin vastinsivuparin suhde. Jos suhteet ovat samoja, voidaan käyttää kolmioiden yhdenmuotoisuuslausetta SSS. Sinisellä merkittyjen vastinsivujen suhde on \[\frac{7,02}{4,68}=1,5.\] Pinkillä merkittyjen vastinsivujen suhde on \[\frac{5,4}{3,6}=1,5.\] Vihreällä merkittyjen vastinsivujen suhde on \[\frac{3}{2}=1,5.\] Koska kaikkien vastisivuparien suhteet ovat samoja, yhdenmuotoisuuslauseen SSS mukaan kolmiot ovat yhdenmuotoisia. Koska kulmat \(\alpha\) ja \(\beta\) ovat vastinkulmia, ne ovat yhtä suuret. Kulma \(\beta\) on siis \(110^{\circ}\).
Jos kahdesta kolmiosta tiedetään, että vain kaksi vastinsivua on verrannollisia keskenään, ei vielä voida päätellä, ovatko kolmiot yhdenmuotoisia. Jos lisäksi tiedetään vielä, että kahden verrannollisen vastinsivun välissä olevat kulmat ovat molemmissa kolmioissa yhtä suuret, voidaan sanoa, että kolmiot ovat yhdenmuotoisia.
Kolmioiden yhdenmuotoisuuslause SKS
Jos kolmion kaksi sivua ovat verrannolliset vastinsivuihin toisessa kolmiossa ja niiden välinen kulma on yhtä suuri kuin vastinkulma toisessa kolmiossa, niin kolmiot ovat yhdenmuotoiset.
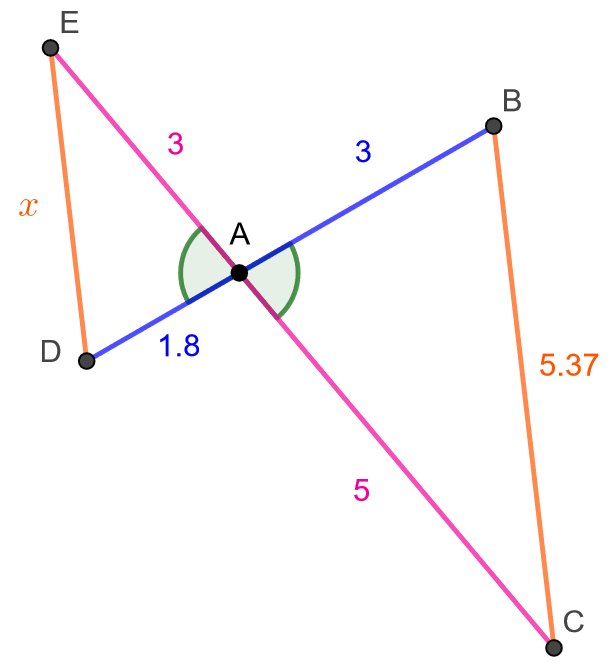
Määritä alla olevan kuvion sivun \(DE\) pituus, joka on merkitty kuvaan kirjaimella \(x\).
Ratkaisu
Sivun \(DE\) pituus saadaan helpoiten määritettyä, jos tiedetään, että kuviossa olevat kolmiot \(ABC\) ja \(ADE\) ovat yhdenmuotoiset. Kuvioon merkityt kulmat \(\angle EAD\) ja \(\angle CAB\) ovat toistensa ristikulmia ja siten yhtä suuria. Sinisellä mekittyjen vastinsivujen suhde on \[\frac{1,8}{3}=0,6\] ja pinkillä merkittyjen vastinsivujen suhde on \[\frac{3}{5}=0,6.\] Koska kahden vastinsivun suhteet ovat samat ja lisäksi näiden sivujen välinen kulma on kummassakin kolmiossa yhtä suuri, kolmiot ovat yhdenmuotoiset kolmioiden yhdenmuotoisuuslauseen SSS mukaan.
Oranssilla merkittyjen vastinsivujen suhteen tulee olla sama kuin muidenkin sivujen suhteet, joten saadaan seuraava yhtälö, joka ratkaistaan \[ \begin{aligned} \frac{x}{5,37}&=0,6 &\quad &|\cdot 5,37 \\ x &= 5,37 \cdot 0,6 &\quad &| \text{ sievennetään} \\ x &= 3,222 & \quad &| \text{ pyöristetään kahden desimaalin tarkkuudelle} \\ x &\approx 3,22 \end{aligned} \]
Kuvion sivun \(DE\) pituus on noin \(3,22\).
1.4 Mittakaava eli yhdenmuotoisuussuhde
Yhdenmuotoisissa kuvioissa vastinsivujen suhteet ovat siis vakioita. Vastinsivut määritellään vastinpisteiden avulla. Alla olevassa kuvassa vastinpisteitä ovat \(A\) ja \(D\), \(E\) ja \(B\) sekä \(C\) ja \(F\). Näiden avulla voidaan määrittää vastisivut: \(a\) ja \(d\), \(b\) ja \(e\) sekä \(c\) ja \(f\). Lasketaan jokaisen vastisivuparin suhde, ja huomataan, että se on jokaisen vastinsivuparin tapauksessa \(1,5\).
Tätä suhdetta kutsutaan yhdenmuotoisuussuhteeksi ja se määritellään alla.
Yhdenmuotoisuussuhde eli mittakaava
Jos kuviot ovat yhdenmuotoiset, yhdenmuotoisuussuhde tarkoittaa suhdetta \[\frac{s_1}{s_2},\] missä \(s_1\) on sivun pituus ensimmäisessä kuviossa ja \(s_2\) sitä vastaavan sivun pituus toisessa kuviossa.
Yllä olevassa GeoGebra-appletissa on korostettu vastinpisteet ja vastinsivut samoilla väreillä. Lisäksi vasemmalla olevassa CAS-ikkunassa on laskettu kunkin vastinsivuparin suhde.
Kokeile siitää kolmioiden \(ABC\) ja \(DEF\) kärkipisteitä ja huomaa, että vastinsivujen suhteet pysyvät koko ajan samoina. Tuota suhdetta kutsutaan siis mittakaavaksi tai yhdenmuotoisuussuhteeksi.
Maratoonari harjoittelee kilpailuihin reitillä, jonka pituus on 50 km.
- Kuinka pitkä on lenkin reitti kartalla, jonka mittakaava on 1:400 000?
- Mikä on sellaisen kartan mittakaava, jossa maratoonarin reitti on 5,1 cm kartalla?
Ratkaisu
Pituus kastalla ilmoitetaan senttimetreinä, joten muunnetaan maratoonarin todellinen reitti myös senttimetreiksi.
\(50 \text{ km} = 50 000 \text{ m} = 5 000 000 \text{ cm}\)
Merkitään reitin pituutta kartalla kirjaimella x ja ratkaistaan pituus verrannolla kokoamalla tiedot taulukkoon. Pituus kartalla on suoraan verrannollinen pituuteen luonnossa.
Pituus kartalla (cm) Todellinen pituus (cm) x 5000000 1 400000 Suoraan verrannollisuuden avulla taulukosta saadaan
\[\begin{align} \frac{x}{1 \text{ cm}} &= \frac{5000000 \text{ cm}}{400000 \text{ cm}} \\ x &= 12,5 \text{ cm} \\ \end{align}\]
Koska tiedetään reitin pituus sekä kartalla (5,1 cm) että luonnossa (5 000 000 cm), niin mittakaava saadaan suoraan näiden kahden suhteena.
\(k = \frac{2,5\text{ cm}}{5 000 000 \text{ cm}}^{(2,5} = \frac{1}{2 000 000} =\) 1:2 000 000
1.5 Pinta-alan suhde
Aiemmin tarkastelit vain kuvioiden vastinkulmien suuruuksia (jotka olivat samoja) sekä vastisivujen pituuksien suhteita (jotka pysyivät vakioina riippumatta siitä mitä sivupareja tarkasteltiin). Yhdenmuotoisuuden avulla voidaan päätellä lisäksi myös kuvioiden pinta-aloihin liittyviä suhteita.
Yhdenmuotoisten kuvioiden pinta-alalause
Jos kuviot ovat yhdenmuotoiset yhdenmuotoisuussuhteessa \(s_1 : s_2\), niiden pinta-alojen suhde on \[\frac{A_1}{A_2} =\left(\frac{s_1}{s_2}\right)^2.\]
Tutki yllä olevaa GeoGebra-applettia siirtämällä suorakulmion \(ABCD\) kärkipisteitä sekä raahaamalla yhdenmuotoisuussuhde-liukusäädintä. Vasemmalla olevaan CAS-ikkunaan lasketaan vastinsivujen \(a\) ja \(e\) sekä \(b\) ja \(f\) väliset suhteet sekä suorakulmioiden pinta-alojen \(m1\) ja \(m2\) välinen suhde. Lisäksi lasketaan yhdenmuotoisuussuhteen neliön lukuarvo. Huomaa, että pinta-alojen suhde ja yhdenmuotoisuussuhteen neliö ovat koko ajan yhtä suuria.
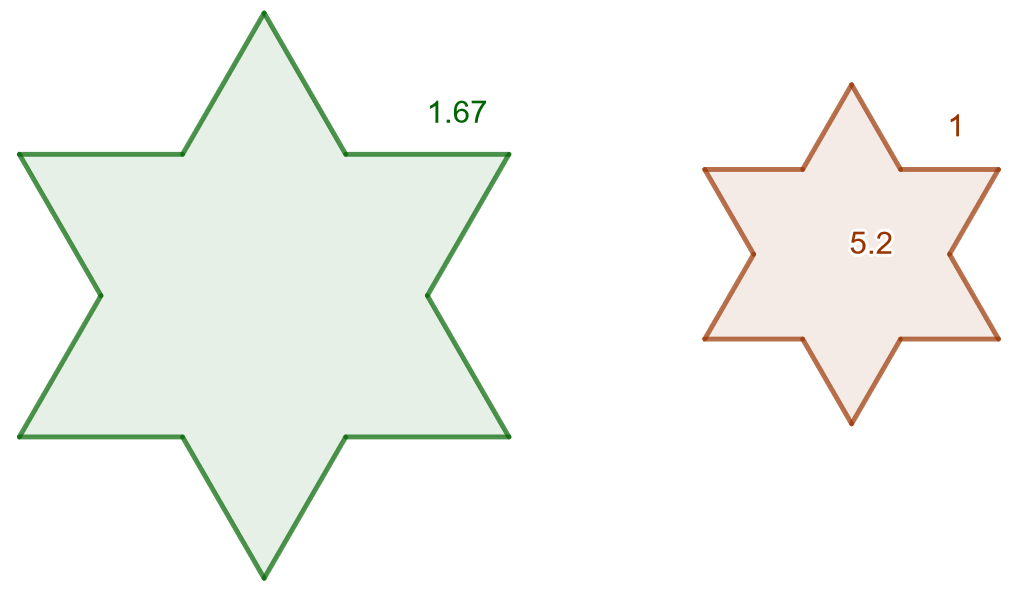
Laske alla olevan kuvan isomman tähden pinta-ala, kun tiedetään, että tähdet ovat yhdenmuotoiset.
Ratkaisu
Koska kuviot ovat yhdenmuotoisia, voidaan käyttää yhdenmuotoisten kuvioiden pinta-alalausetta. Kuvioiden yhdenmuotoisuussuhde on \[\frac{1,67}{1}=1,67.\] Merkitään kysyttyä isomman tähden pinta-alaa kirjaimella \(x\). Tehdään verranto yhdenmuotoisten kuvioiden pinta-alalauseen avulla ja ratkaistaan siitä \(x\): \[ \begin{aligned} \frac{x}{5,2}&=1,67^2 &\quad &| \cdot 5,2 \\ x &= 5,2 \cdot 1,67^2 &\quad &| \text{ sievennetään lauseke} \\ x &= 14,50228 &\quad &| \text{ pyöristetään kahden desimaalin tarkkuuteen} \\ x & \approx 14,5 \end{aligned} \] Isomman tähden pinta-ala on noin \(14,5\).
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.