MAB3-tehtäviä
1. Peruskäsitteitä
1.1 Kulmat
Tehtävä
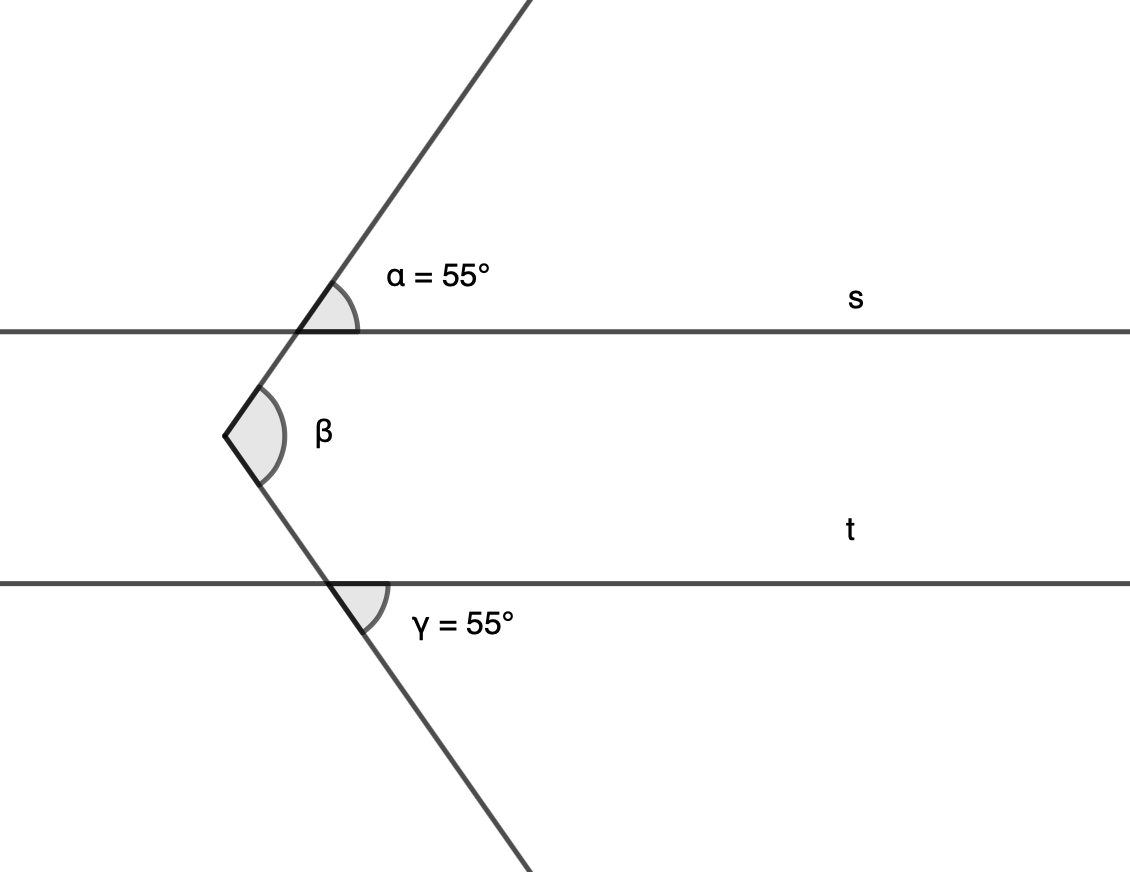
Määritä kulman \(\beta\) suuruus, kun suorat \(s\) ja \(t\) ovat yhdensuuntaiset.
Tehtävä
Laske kulmien \(\alpha\), \(\beta\) ja \(\gamma\) suuruudet.
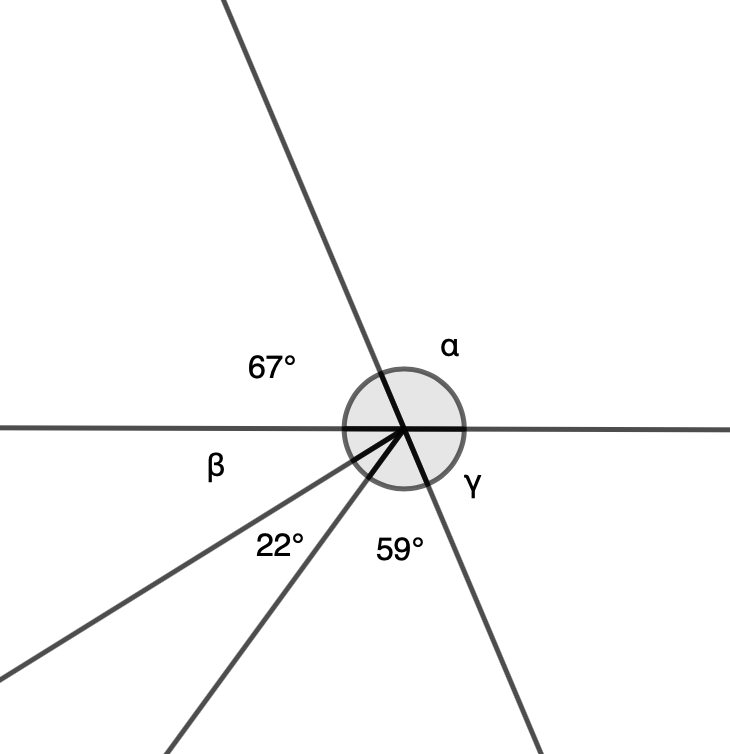
Tehtävä
Tutki, ovatko suorat \(s\) ja \(t\) yhdensuuntaiset.
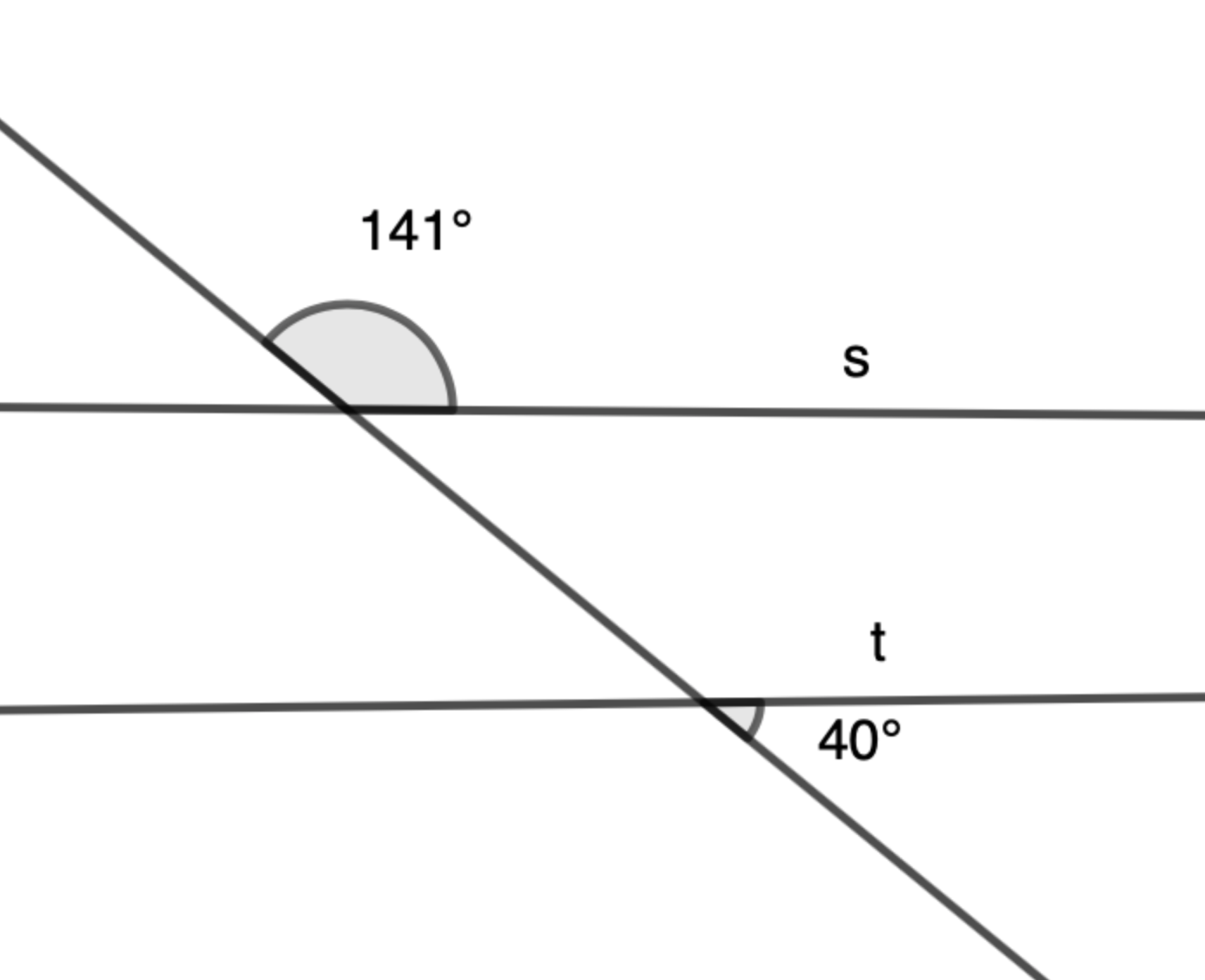
Yhdensuuntaisilla suorilla samankohtaiset kulmat ovat yhtä suuret.
1.2- 1.3 Yhdenmuotoisuus
Tehtävä
Tehtävä
Ovatko alla olevat kolmiot keskenään yhdenmuotoisia? Valitse **Tosi**, jos kolmiot ovat yhdenmuotoisia, ja **Epätosi** jos kuviot eivät ole yhdenmuotoisia.
Tehtävä
Alla olevassa kuvassa on kaksi yhdenmuotoista kolmiota. Päättele sivun \(x\) pituus ja kulman \(\alpha\) suuruus.
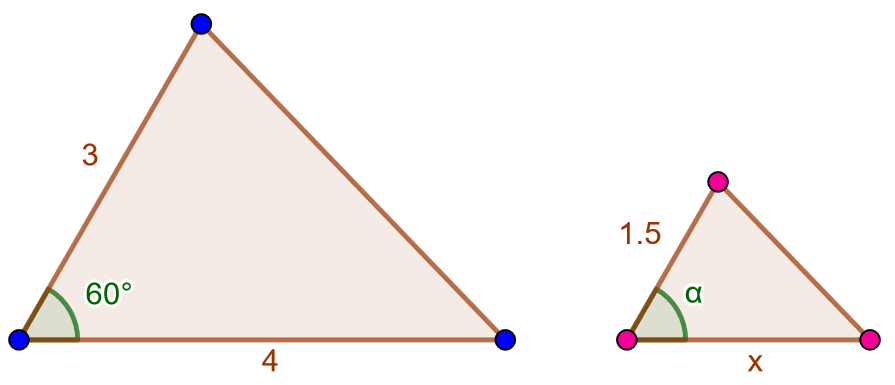
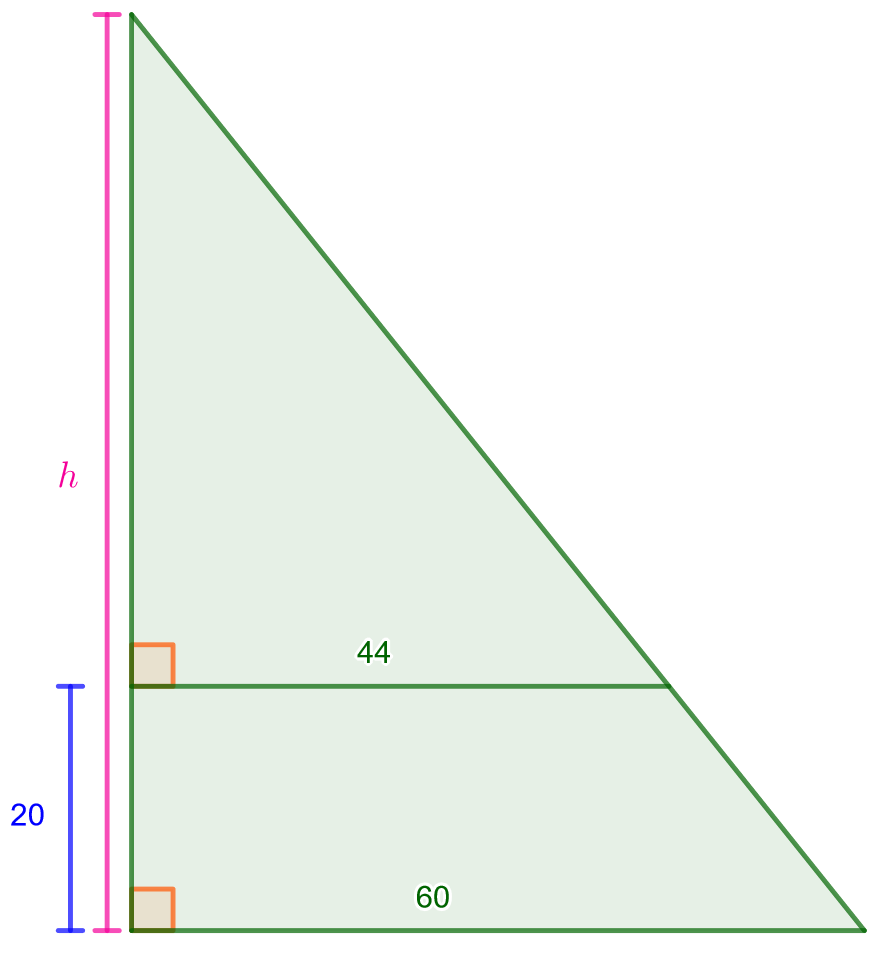
Tehtävä
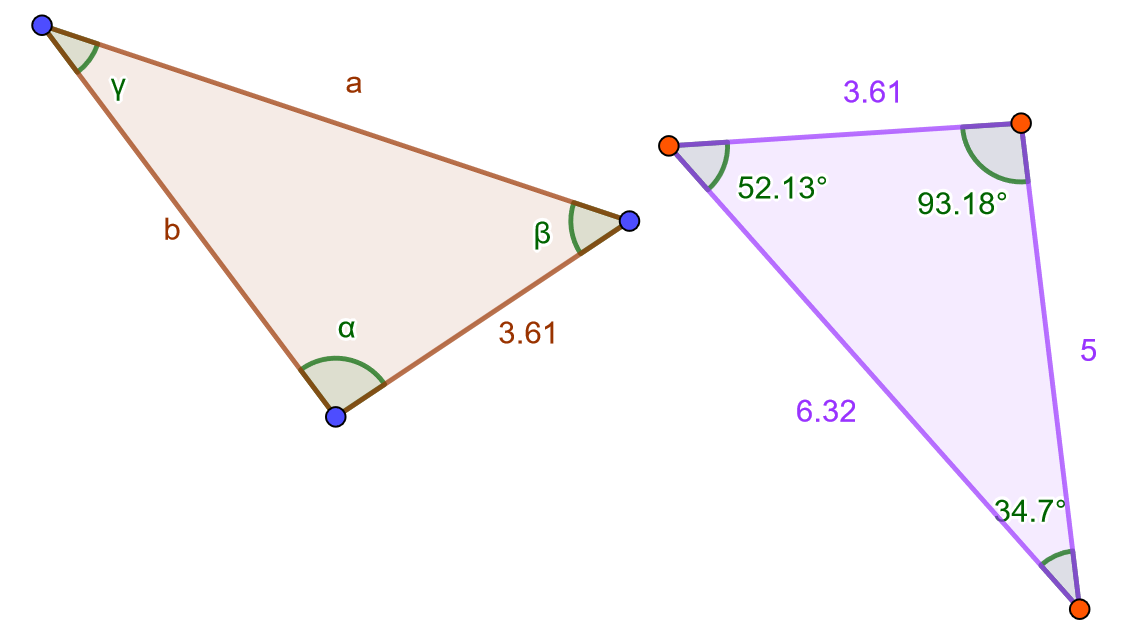
Yllä olevat kolmiot ovat yhdenmuotoisia. Päättele puuttuvat sivujen pituudet ja kulmien suuruudet. Huom! Käytä desimaalipistettä! Älä laita kulmien suuruuksiin astemerkkiä.
Tehtävä
Talon pihalla on lipputanko ja \(0,9 \text{ m}\) mittainen pystysuora keppi. Eräänä päivänä kepin varjon pituudeksi mitattiin \(1,3 \text{ m}\) ja lipputangon varjon pituudeksi \(11,6 \text{ m}\). Kuinka korkea lipputanko on?
Tehtävä
Täydennä alla olevaa GeoGebra-appletti niin, että siinä on kaksi yhdenmuotoista kolmiota. Käytä hyväksesi valmiina appletissa olevaa kolmion sivua.
Tarkista lopuksi, että piirtämäsi kolmion kulmien nimet ovat D, E ja F.
Vinkkejä GeoGebran käyttöön.
- Jana ED voi vastata mitä tahansa sivua kolmiossa ABC.
- Syöttökentän avulla voit lisätä uuden pisteen esimerkiksi kohtaan (0,0) yksinkertaisesti kirjoittamalla syöttökenttään
(0,0). - Kokeile kirjoittaa syöttökenttään
D+(2;90°)(astemerkin saat painamalla ALT + o). Huomaa, että sulkeissa on pilkun sijaan puolipiste. Pohdi, miten voisit tätä tietoa käyttää yllä olevassa tehtävässä.
1.4 Mittakaava
Tehtävä
Määritä alla olevan kuvan kolmioiden mittakaava, kun oikeanpuoleinen kolmio on saatu pienentämällä vasemmanpuoleinen kolmio.
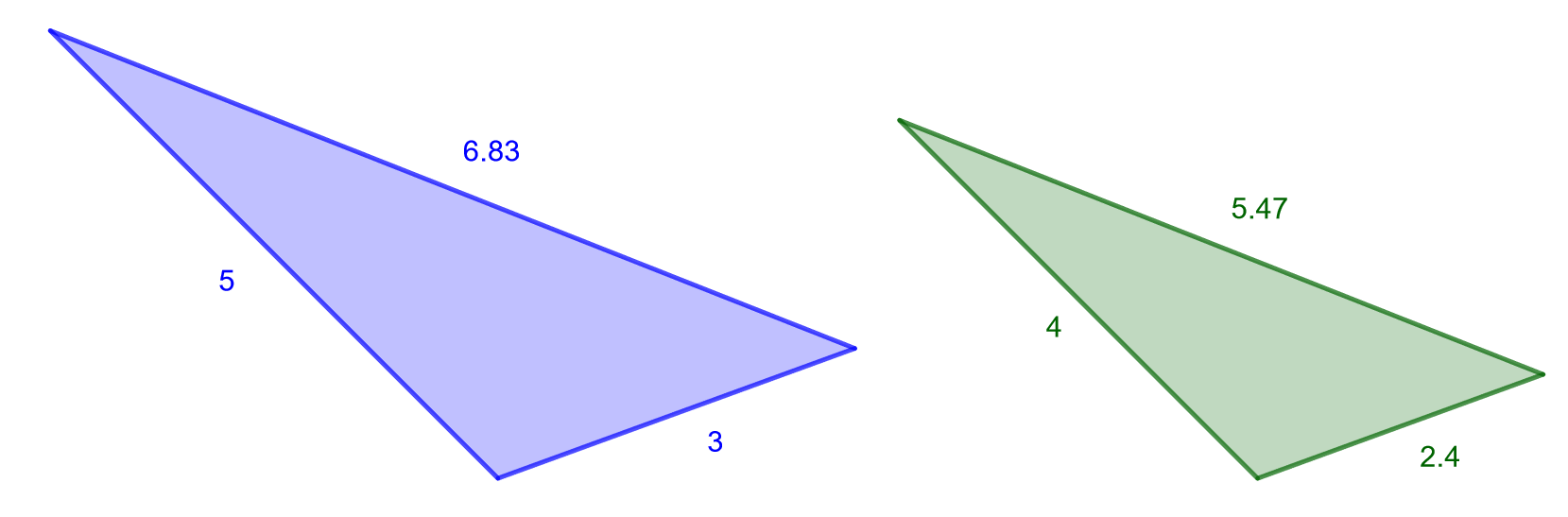
Tehtävä (S2015/3a)
Kuntopolun pituus kartalla on \(17,5 \text{ cm}\). Mikä on polun pituus maastossa, kun kartan mittakaava on \(1:20 \, 000\)? Anna vastaus \(100\) metrin tarkkuudella.
Tehtävä
Kartan mittakaava on \(1:80 \, 000\). Kallen työpaikan ja keskustan välimatka kartalla on \(24,5 \text{ cm}\). Kuinka paljon välimatka on luonnossa?
Tehtävä
Mikä on kartan mittakaava, kun \(1 \, 200 \text{ km}\) pitkä Suomineito on kartalla \(25 \text{ cm}\) mittainen?
Tehtävä
Biologian kirjassa on suurennos kukasta mittakaavassa \(3:1\). Jos kirjassa olevan kukan leveys on \(45 \text{ mm}\), kuinka leveä on alkuperäinen kukka?
Tehtävä
Seuraavalla sivulla biologian kirjassa on suurennos muurahaisesta. Suurennoksen pituus on \(12 \text{ mm}\). Tekstissä kerrotaan muurahaisen pituuden luonnossa olevan \(3 \text{ mm}\). Mikä on suurennoksen mittakaava?
1.5 Pinta-alojen suhde
Tehtävä
Tehtävä
Taikinasta leivotaan pallonmuotoisia munkkeja, joiden pinta sokeroidaan. Tarvittavan sokerin määrä on suoraan verrannollinen pallon pinta-alaan. Vaihtoehtona on leipoa 24 pientä tai 3 isoa munkkia. Laske sokerin kokonaismäärien suhde näille kahdelle vaihto- ehdolle. [11/S14]
Tehtävä
Laske pienemmän kolmion pinta-alan suhde suuremman kolmion pinta-alaan.
Kuvan kolmiot \(ABC\) ja \(EFD\) ovat yhdenmuotoisia. Laske kolmioiden yhdenmuotoisuussuhde eli mittakaava ja a.-kohdan pinta-alojen suhde käyttäen mittakaavaa.
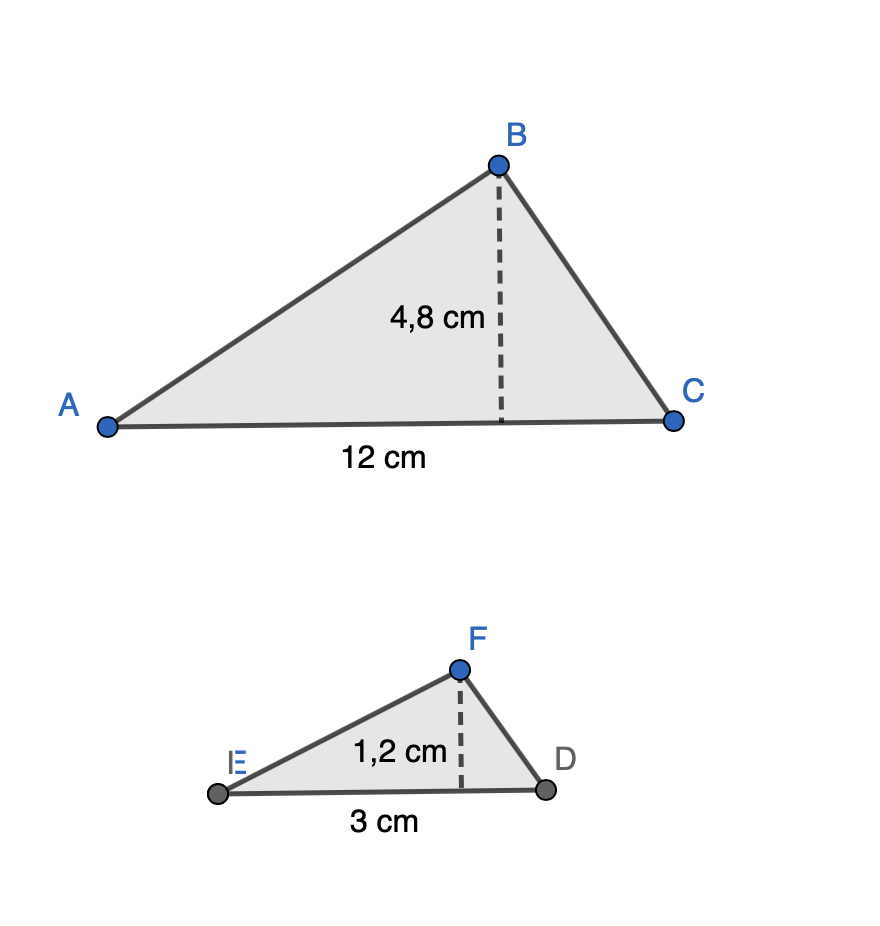
Yhdenmuotoisten kuvioiden pinta-alojen suhde on mittakaavan neliö.
Tehtävä
Millan kartan mittakaava on \(1:30 000\). Vesialueen koko kyseisellä kartalla on \(3,8\) \(cm^2\). Laske vesistön todellinen pinta-ala ja anna vastaus hehtaareina.
Millan toisessa kartassa olevan suorakulmion muotoisen istutetun metsän mitat ovat \(2,0\) \(cm\) ja \(1,4\) \(cm\). Metsän todellinen pinta-ala on 70 a.
2. Monikulmioiden geometriaa
Kolmioiden geometriaa
2.1 Kolmion rakenne
Tehtävä
2.2 Kolmion pinta-ala
Tehtävä
Tehtävä
Tehtävä
Tehtävä
MathCheck laskee kulmia aina radiaaneina. Jos haluat kirjoittaa sin(60°), sinun on kirjoitettava sen sijaan sin(60 * pi/180).
Tehtävä
Kolmion kantasivun pituus on \(2 \sqrt{2}\) ja kolmion korkeus on \(\sqrt{2}\). Laske kolmion pinta-ala.
Tehtävä
Maastossa olevan lammen pinta-ala on \(2,8 \text{ ha}\). Maastosta piirretään kartta, jonka mittakaava on \(1 : 20 \, 000\). Mikä on lammen pinta-ala kartalla?
Tehtävä
Kartan mittakaava on \(1 : 15 \, 000\). Kartalla olevan pellon pinta-ala on \(25 \text{ cm}^2\). Mikä on pellon pinta-ala hehtaareissa?
Tehtävä
Kahden suorakulmaisen kolmion mittakaava on \(2 : 5\). Suuremman kolmion kannat ovat pituudeltaan \(8\) ja \(13\). Määritä pienemmän kolmion pinta-ala.
Tehtävä
Kolmio \(ABC\) leikataan kahteen osaan kannan \(AB\) suuntaisella suoralla \(PQ\) siten, että \(AP:PC=2:3\). Missä suhteessa suora jakaa kolmion alan?
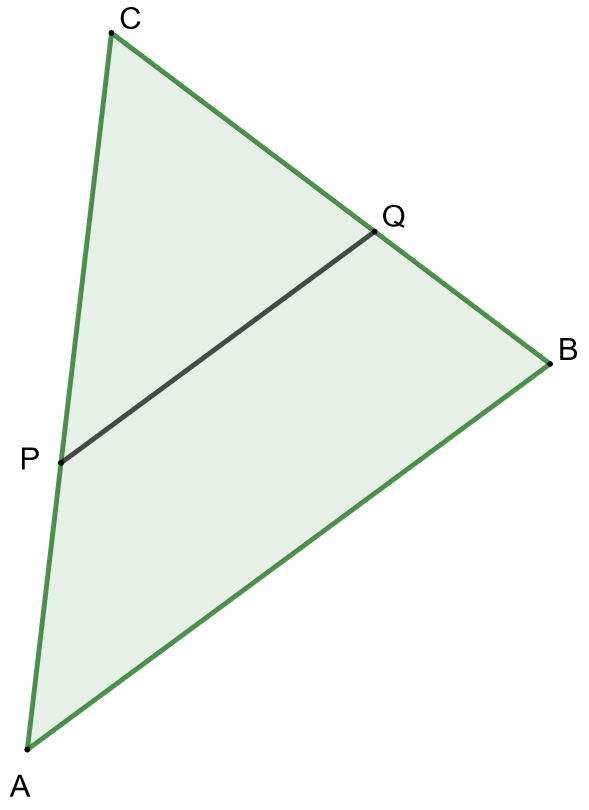
Osoita ensin, että kolmiot \(ABC\) ja \(CPQ\) ovat yhdenmuotoisia, minkä jälkeen voit ratkaista yhdenmuotoisuussuhteen.
2.3 Suorakulmainen kolmio ja Pythagoraan lause
Tehtävä
Tehtävä (S2011/1b)
Suorakulmaisen kolmion hypotenuusan pituus on \(5\) ja toisen kateetin pituus \(2\). Laske toisen kateetin pituus.
Tehtävä
Seitsemän metriä korkea puu kasvaa kohtisuoraan maan pintaa vastaan. Puu taittuu kahden metrin korkeudelta niin, että puun latvaosa osuu maahan. Latva ja tyviosa eivät irtoa toisistaan. Piirrä tilanteesta mallikuva oikeanpuoleiselle piirtoalueelle (ei vaikuta tehtävän pisteytykseen) ja laske vasemmanpuoleiselle CAS-alueelle, kuinka suuri kulma on maanpinnan ja taittuneen latvan välillä.
Anna vastaus vasemmanpuoleisella CAS-alueella tallentamalla se muuttujaan nimeltä v. Pyöristä vastaus kokonaislukujen tarkkuudelle käyttämällä komentoa round.
Vinkki GeoGebran käyttöön
- Tekstin lisääminen
Monesti on hyödyllistä lisätä tehtävän ratkaisuun tekstiä, jossa selität, miten teit tehtävän. Valitse CAS-alueen oikeassa yläkulmassa oleva valikko  ja valitse sieltä teksti
ja valitse sieltä teksti  . Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.
. Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.
- Muuttujan tallentaminen
Joskus on hyödyllistä tallentaa lukuarvo tai vastaus muuttujaan. Tällöin lukuarvon käyttäminen myöhemmin on kätevää. Jos haluat sijoittaa muuttujaan a arvon 4, kirjoita komento a := 4. Jos myöhemmin haluat laskea laskun \(5a\), kirjoita komento 5*a, jolloin saat vastaukseksi 20.
- Yhtälön ratkaiseminen
Jos haluat ratkaista muuttujan \(a\) yhtälöstä \(a^2+3a-4=0\), syötä CAS-laskimeen komento Ratkaisut(a^2+3a-4,a). Vastaukseksi saat listan {-4,1}. Helpoiten ratkaisuihin pääsee käsiksi, kun tallentaa ne muuttujaan: vastaukset := Ratkaisut(a^2+3a-4,a). Tällöin komento vastaukset(1) tuottaa luvun -4, ja komento vastaukset(2) tuottaa luvun 1.
- Lukuarvon näyttäminen
Joskus GeoGebra näyttää vastauksen hyvinkin monimutkaisessa muodossa. Käytä tällöin komentoa Lukuarvona(). Jos kirjoitat esimerkiksi komennon a:=sin^(-1)(1/2), GeoGebra tulostaa vastaukseksi saman eli a:=sin^(-1)(1/2). Jos haluat vastauksen lukuarvona, kirjoita komento Lukuarvona(a), jolloin GeoGebra tulostaa 60°.
Tehtävä
Suorakulmaisessa kolmiossa \(ABC\) kateetin \(AB\) pituus on \(4,4\) cm ja hypotenuusan \(AC\) pituus \(8,14\) cm.
- Laske kateetin \(BC\) pituus
- Laske kolmion pinta‐ala \(0,1\) neliösenttimetrin tarkkuudella. [4/K15]
Tehtävä
Suorakulmaisen kolmion kummankin kateetin pituus on 5. Sen sisään on piirretty neliö kahdella eri tavalla kuvioiden mukaisesti. Kumman neliön pinta-ala on suurempi? [10/S14] 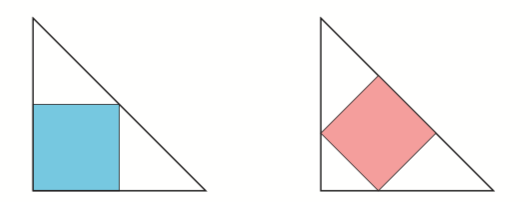
2.4 Käänteinen Pythagoraan lause
Tehtävä
Kolmion sivujen pituudet ovat \(3\), \(5\) ja \(6\). Onko kolmio suorakulmainen?
Tehtävä
Kolmion sivujen pituudet ovat \(3 \sqrt{2}\), \(4 \sqrt{2}\) ja \(5 \sqrt{2}\). Onko kolmio suorakulmainen?
2.5 Trigonometriset funktiot
Tehtävä
Määritä lausekkeen \(\sin(18^{\circ})\) tarkka arvo käyttämällä alla olevaa tasakylkistä kolmiota.
!
—Ratkaise alkuperäisen kolmion kolmannen sivun pituus.
Lisää valinta kohtaan "vihje 1". Millainen kolmio muodostuu mustan janan oikealle puolelle? Voiko sitä verrata alkuperäiseen kolmioon? Saatko ratkaistua mustan janan pituuden?
Pidä edelleen valinta kohdassa "Vihje 1". Mustan janan oikealle puolelle muodostuu kolmio, joka on yhdenmuotoinen alkuperäisen kolmion kanssa (perustele tämä kulmien suuruuksien avulla). Käytä verrantoa ratkaistaksesi kolmion kolmannen sivun (ja samalla mustan janan) pituus.
Lisää valinta kohtaan "Vihje 2" ja huomaa, että \(\frac{36^{\circ}}{2}=18^{\circ}\).
Nelikulmioiden geometriaa
2.6 Nelikulmioiden rakenne
Tehtävä
Tehtävä
Tehtävä
Pöytäliinan alkuperäinen koko on 2 m kertaa 4 m. Se kutistuu pesussa 5 % sekä pituus- että leveyssuunnassa. Kuinka monella prosentilla pöytäliinan pinta-ala pienenee? [5/S16]
Tehtävä
Peppi rakentaa oheisen kuvan mukaisista laudankappaleista linnunpöntön. Yksikkönä on senttimetri. [6/K16]
- Paljonko linnunpönttö painaa? Sisääntuloaukkoa ei tarvitse huomioida eikä käytettäviä nauloja. Laudan tiheys on \(550 \frac{kg}{m^3}\)ja paksuus \(2,0 cm\).
- Mikä on linnunpöntön sisätilavuus?
Tehtävä
Kuvan kaari-ikkunassa on lasin tukena rimoja. Kuinka paljon rimaa tarvitaan kuvan mukaiseen kaari-ikkunaan, kun \(x=20\)cm ja \(y=40\) cm? Rimaa käytetään kaikkiin kuvion janoihin ja puoliympyröiden kaariin. [4/S13]
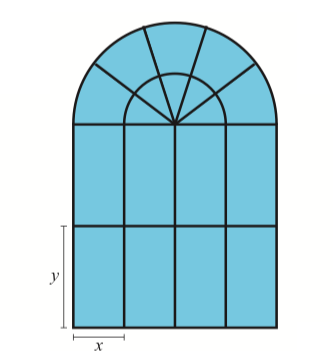
Suorakulmio
Tehtävä
Määritä alla olevan kuvan suunnikkaan pinta-alan osuus suorakulmion pinta-alasta.
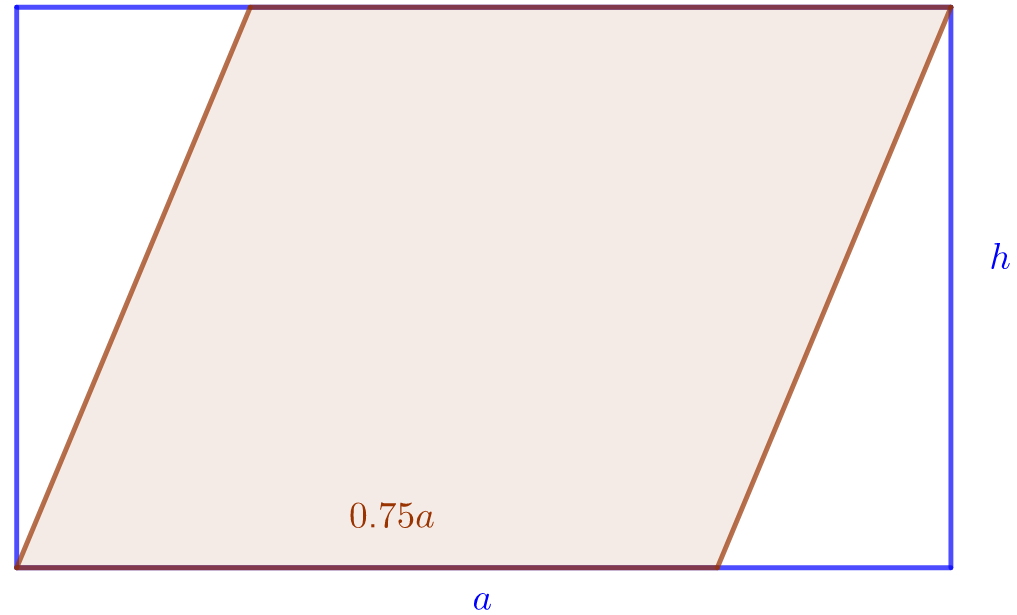
Tehtävä
Olkoot \(d_1\) ja \(d_2\) suorakulmion \(ABCD\) piirillä olevan pisteen \(P\) etäisyydet lävistäjistä \(AC\) ja \(BD\).
Piirrä annettuja tietoja vastaava dynaaminen kuvio, jossa voit liikuttaa pistettä \(P\) suorakulmion ympäri pitkin suorakulmion piiriä.
Mitä voit todeta summan \(d_1+d_2\) arvosta?
Miten arvo riippuu suorakulmion koosta?
Perustele havaintosi matemaattisesti.
Tutkitaan yllä olevaa GeoGebra-applettia siirtämällä punaista pistettä \(P\) suorakulmion reunalla. Huomataan, että summa \(d_1+d_2\) pysyy koko ajan samana.
Muutetaan suorakulmion kokoa raahaamalla pisteitä \(B\) ja \(C\). Huomataan, että summan \(d_1+d_2\) arvo muuttuu, mutta jos pistettä \(P\) liikuttaa, se pysyy edelleen samana. Summa on siis sitä suurempi, mitä suurempi suorakulmio on.
Lisätään valinta GeoGebra-appletin kohtaan "Matemaattinen perustelu", jolloin kuvioon ilmestyy kulmia. (Huom! kulmat toimivat GeoGebrassa oikein vain, jos piste \(P\) on pisteiden \(A\) ja \(D\) välissä.) Merkitään kulmaa \(\angle BAC\) kirjaimella \(\alpha\) ja kulmaa \(\angle CAD\) kirjaimella \(\beta\). Koska suorakulmion kaikki kulmat ovat suoria, saadaan \(\alpha + \beta = 90^{\circ}\). Merkitään vihreää lävistäjää kirjaimella \(\ell\). Sen pituus voidaan ratkaista Pythagoraan lauseella: \[ \begin{aligned} \ell^2 &= a^2+b^2 \\ \ell &= \sqrt{a^2+b^2}. \end{aligned} \] Nyt voidaan merkitä \[ \cos \alpha = \frac{a}{\ell} = \frac{a}{\sqrt{a^2+b^2}}. \] Merkitään etäisyyttä \(DP\) kirjaimella \(x\), jolloin etäisyys \(AP\) on \(b-x\). Pienistä suorakulmaisista kolmioista saadaan \[ \cos \alpha = \frac{d_1}{b-x} \quad \Leftrightarrow \quad d_1 = (b-x) \cdot \cos \alpha \] ja \[ \cos \alpha = \frac{d_2}{x} \quad \Leftrightarrow \quad d_2 = x \cdot \cos \alpha \] jolloin summa saa arvon \[ \begin{aligned} d_1 + d_2 &= (b-x) \cdot \cos \alpha + x \cdot \cos \alpha \\ &= (b-x+x) \cdot \cos \alpha \\ &= b \cdot \frac{a}{\sqrt{a^2+b^2}} \\ &= \frac{ab}{\sqrt{a^2+b^2}}. \end{aligned} \] Tästä voidaan päätellä, että jos suorakulmion koko pysyy samana, summa \(d_1+d_2\) pysyy myös vakiona. Toisaalta jos suorakulmion koko kasvaa, myös summa kasvaa.
Tehtävä
Luomuviljelijä on hankkinut materiaalin 400 metrin pituiseen aitaan. Hän aikoo rajata sillä niitystä suorakulmion muotoisen alan, joka lisäksi jaetaan kuvion mukaisesti kolmeen yhtäsuureen osaan kahdella ulkoreunan suuntaisella sisäaidalla. Määritä aitauksen suurin mahdollinen kokonaispinta-ala [13/S18]. 
Neliö
Tehtävä
Neliöllä ja suorakulmaisella kolmiolla on sama pinta-ala. Kumman piiri on pidempi?
Tehtävä
Alla olevassa kuvassa on neliö, jonka pinta-ala on \(12\). Sen jokaiselle sivulle on piirretty tasasivuinen kolmio. Mikä on punaisella merkityn alueen pinta-ala?
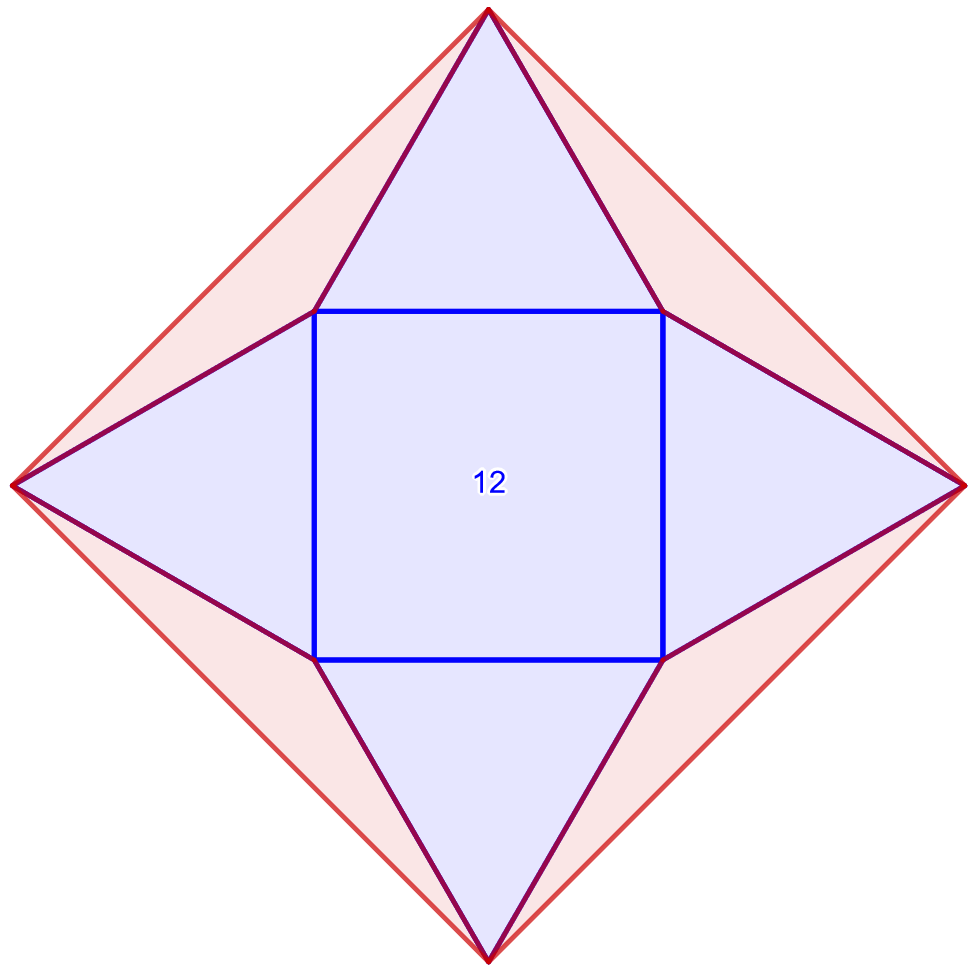
Suunnikas
Tehtävä
Tehtävä
Tehtävä
Suunnikkaan sivujen pituudet ovat \(3\) ja \(5\), ja sen pinta-ala on \(13\). Kuinka suuri kulma sivujen välissä on?
Tehtävä
Suunnikkaan sivujen välinen kulma on \(45^{\circ}\). Lyhyempi sivuista on pituudeltaan \(a\) ja pidempi \(4a\). Määritä suunnikkaan ala.
Tehtävä
Aakkoskarkkien sivujen pituudet ovat \(2 \text{ cm}\) ja sen lyhyempi halkaisija on \(2,3 \text{ cm}\). Laske yhden karkin pinta-ala.

Tehtävä
Suunnikkaan sisälle piirretään pienempi suunnikas, jonka kärjet ovat alkuperäisen suunnikkaan sivujen keskipisteissä. Laske pienen suunnikkaan pinta‐ala käyttämällä kuvioon merkittyjä pituuksia.[2/S15] 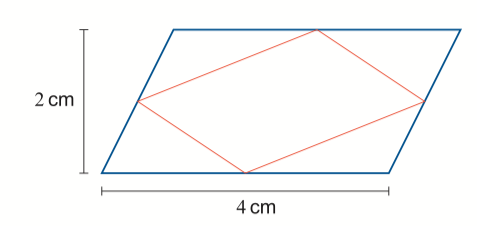
Puolisuunnikas
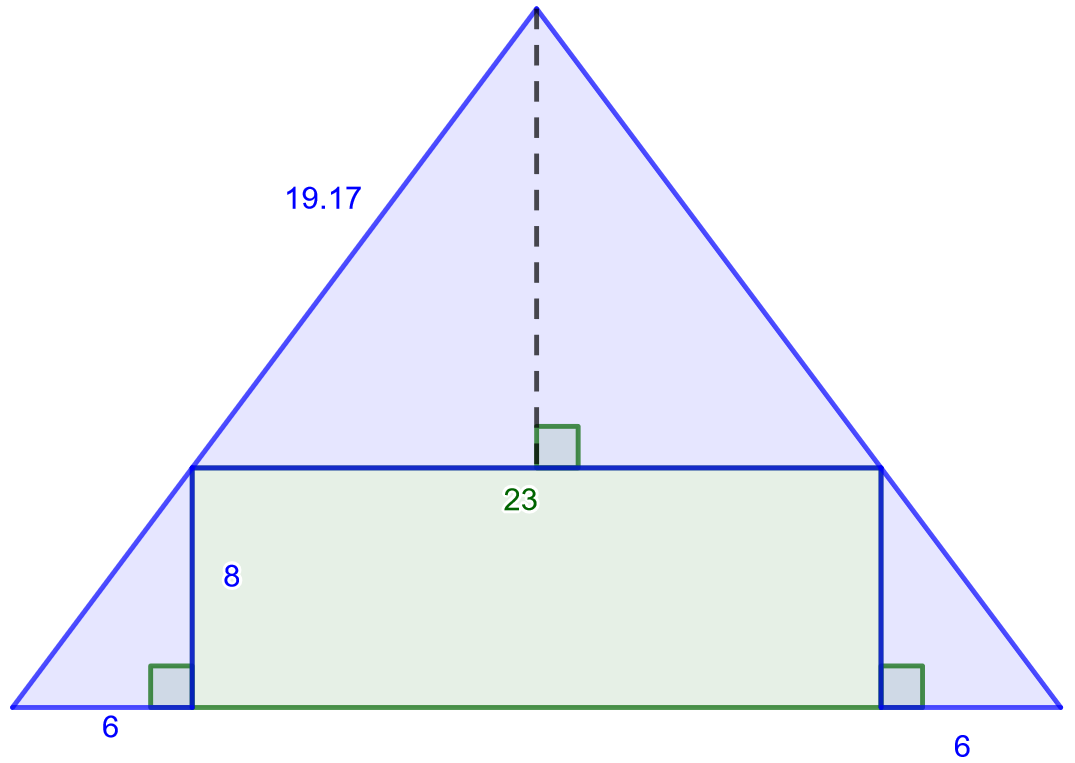
Tehtävä
Tehtävä
Tehtävä
2.7 Muut monikulmiot
Tehtävä
Säännöllisen viisikulmion sivun pituus on \(3\). Laske viisikulmion pinta-ala.
2.8 Monikulmiot koordinaatistossa
Tehtävä
Kolmion kärjet ovat pisteissä \((-6,1)\), \((0,0)\) ja \((4,9)\).
- Laske kolmion kulmat asteen kymmenesosan tarkkuudella.
- Laske kolmion pinta-ala yhden desimaalin tarkkuudella. [9/K09]
Tehtävä
- Suorakulmion kolme kärkeä ovat origossa, pisteessä \((2,1)\) ja pisteessä \((2,-4)\). Määritä neljännen kärjen koordinaatit.
- Määritä a-kohdan suorakulmion pinta-ala.
- Yhdysjanat origosta pisteisiin \((1,2,1)\), \((1,-1,1)\) ja \((2,0,-2)\) muodostavat suorakulmaisen särmiön kolme särmää. Mihin pisteeseen päättyy origosta alkava särmiön avaruuslävistäjä? [15/K15]
Tehtävä
Havaintopisteessä \(A\) nähtiin trombi merellä suunnassa \(133,8°\) ja havaintopisteessä \(B\) sama trombi suunnassa \(205,0°\). Suunnat on ilmoitettu pohjoissuunnasta lähtien myötäpäivään. Pisteiden \(A\) ja \(B\) koordinaatit ovat \((6670801,2549572)\) ja \((6670015,2554955)\) koordinaatistossa, jonka x-akseli suuntautuu pohjoiseen ja y-akseli itään ja jonka yksikkönä on metri. Laske trombin sijainti. [12/K11]
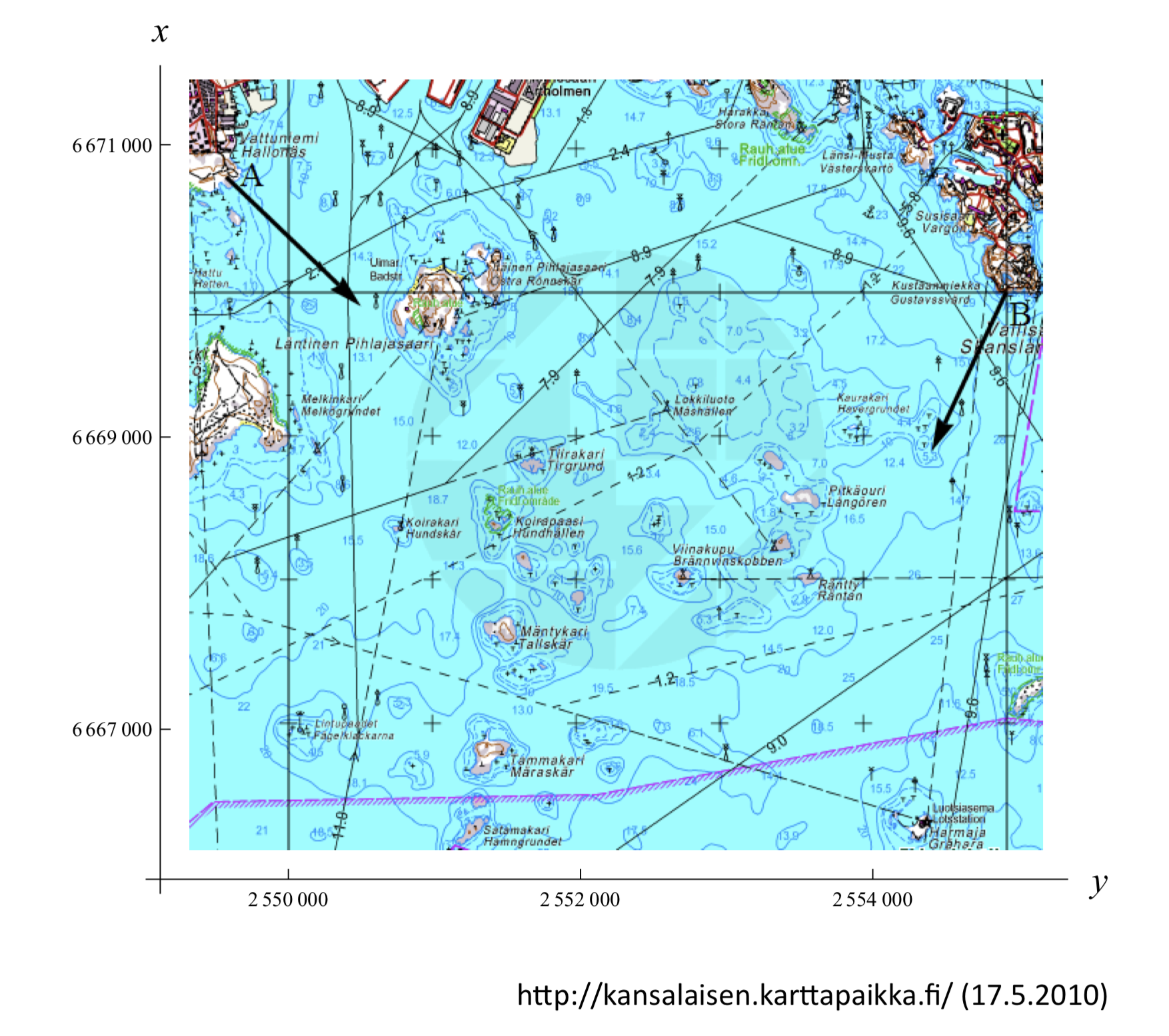
Vaihda laskua varten x- ja y-akselit keskenään ja vaihda lopuksi koordinaatit takaisin trombin alkuperäiseen koordinaatistoon vaihtamalla x- ja y-akselien koordinaatit päikseen.
3. Ympyrä
Tehtävä
3.1 Säde, halkaisija ja piiri
Tehtävä
Oleletaan, että maapallo on täysin pyöreä. Eräs puhelinyhtiö on vetänyt puhelinlinjan päiväntasaajaa pitkin maapallon ympäri. Kuinka paljon linjaa tarvitaan lisää, jos se halutaan nostaa \(10 \text{ m}\) korkeille tolpille. Anna vastaus metreinä ja yhden desimaalin tarkkuudella.
Tehtävä
Polkupyörän renkaan koko on \(28"\) eli sen halkaisija on \(28\) tuumaa. Pyörään halutaan laittaa matkamittari, jota varten tarvitaan yhdellä renkaan pyörähdyksellä kuljettu matka. Laske pyörän yhden renkaan täydellä pyörähdyksellä kulkema matka ja ilmoita vastaus yhden desimaalin tarkkuudella senttimetreinä.
Tehtävä
Halkaisijaltaan \(60 \text{ cm}\) pyörä pyörähtää \(10\) kertaa. Kuinka pitkän matkan pyörä etenee?
Kuinka monta pyörähdystä pyörä etenee \(200 \text{ m}\) matkalla?
Tehtävä
Mari haluaa laittaa kukkia kasvamaan täsmälleen ympyrän muotoon. Hänellä on \(24\) kukkaa ja hän haluaa, että kukkien välinen etäisyys ympyrän kaarta pitkin mitattuna on tasan \(20 \text{ cm}\). Mikä on tällaisen ympyrän halkaisija?
Tehtävä
Osoita, että kahden leikkaavan ympyrän keskipisteiden välinen jana on ympyröiden leikkauspisteiden välisen janan keskinormaali.
Alla olevan kuvan merkinnöillä, sinun tulee osoittaa, että kuvaan punaisella merkittyjen janojen \(AB\) ja \(OO'\) välinen kulma on \(90^{\circ}\) ja että janat \(BC\) ja \(AC\) ovat keskenään yhtä pitkiä.
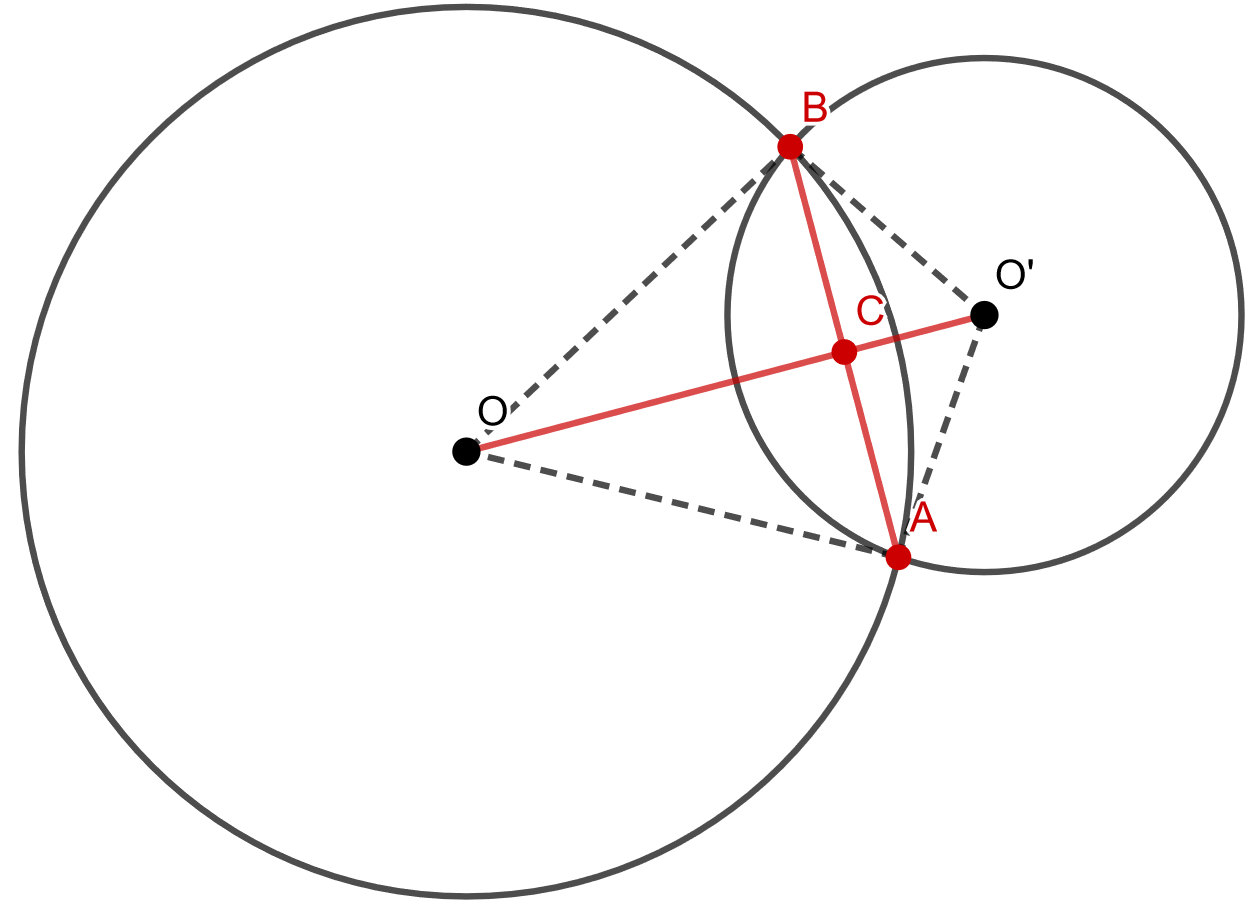
Tarkastellaan ensin kolmioita \(OO'B\) ja \(OO'A\). Kolmioiden sivut \(OB\) ja \(OA\) ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Samoin sivut \(O'B\) ja \(O'A\) ovat yhteneviä, sillä ne ovat saman ympyrän säteitä. Sivu \(OO'\) on molemmissa kolmioissa sama, joten kolmiot ovat yhteneviä (eli niiden kaikki mitat ovat yhtä suuria). Tällöin myös janat \(BC\) ja \(AC\) ovat keskenään yhtä pitkiä.
Kuvassa piste \(C\) on janojen \(AB\) ja \(OO'\) leikkauspiste, jolloin kulmat \(BCO\) ja \(OCA\) muodostavat oikokulman. Tarkastellaan seuraavaksi kolmioita \(BCO\) ja \(ACO\). Sivut \(OB\) ja \(OA\) ovat yhteneviä (kuten aiemmin todettiin). Lisäksi sivu \(OC\) on yhteinen kummallekin kolmiolle. Lisäksi kulmat \(COB\) ja \(AOC\) ovat yhteneviä, sillä kolmiot \(OO'B\) ja \(OO'A\) ovat yhteneviä (kuten aiemmin todettiin). Näin ollen kolmioiden \(BCO\) ja \(ACO\) on oltava yhtenevät ja kulmien \(BCO\) ja \(OCA\) on myös oltava yhtenevät. Tällöin \(BCO=OCA = \frac{180^{\circ}}{2}=90^{\circ}\).
3.2 Pinta-ala
Tehtävä
\(150\) metrin köydellä rajataan alue. Laske alueen pinta-ala, kun se on muodoltaan
- neliön muotoinen.
- ympyrän muotoinen.
Tehtävä
Piirretään A4-arkille (\(210 \text{ mm} \times 297 \text{ mm}\)) mahdollisimman suuri ympyrä. Mikä on tämän ympyrän pinta-ala?
Tehtävä
Seitsemän mäntytukkia sidotaan vaijerilla alla olevan poikkileikkauskuvion mukaisesti. Kuinka paljon vaijeria tarvitaan yhteen kierrokseen? Jokaisen tukin halkaisija on 20 cm. Anna vastaus senttimetrin tarkkuudella. [7/K14] 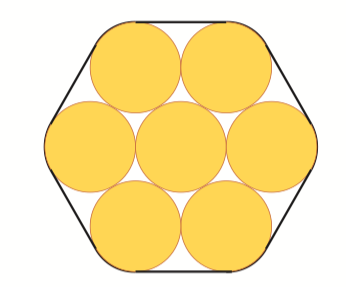
3.3 Keskuskulma, kaaren pituus, sektorin pinta-ala
Tehtävä
Tehtävä
Ympyräsektorin pinta-ala on \(52,9\) ja sen säde on \(5,4\). Kuinka suuri on sektorin keskuskulma?
Tehtävä
Kumpi alla olevista pizzapaloista kannattaa ottaa, jos haluaa rahalleen eniten vastinetta?
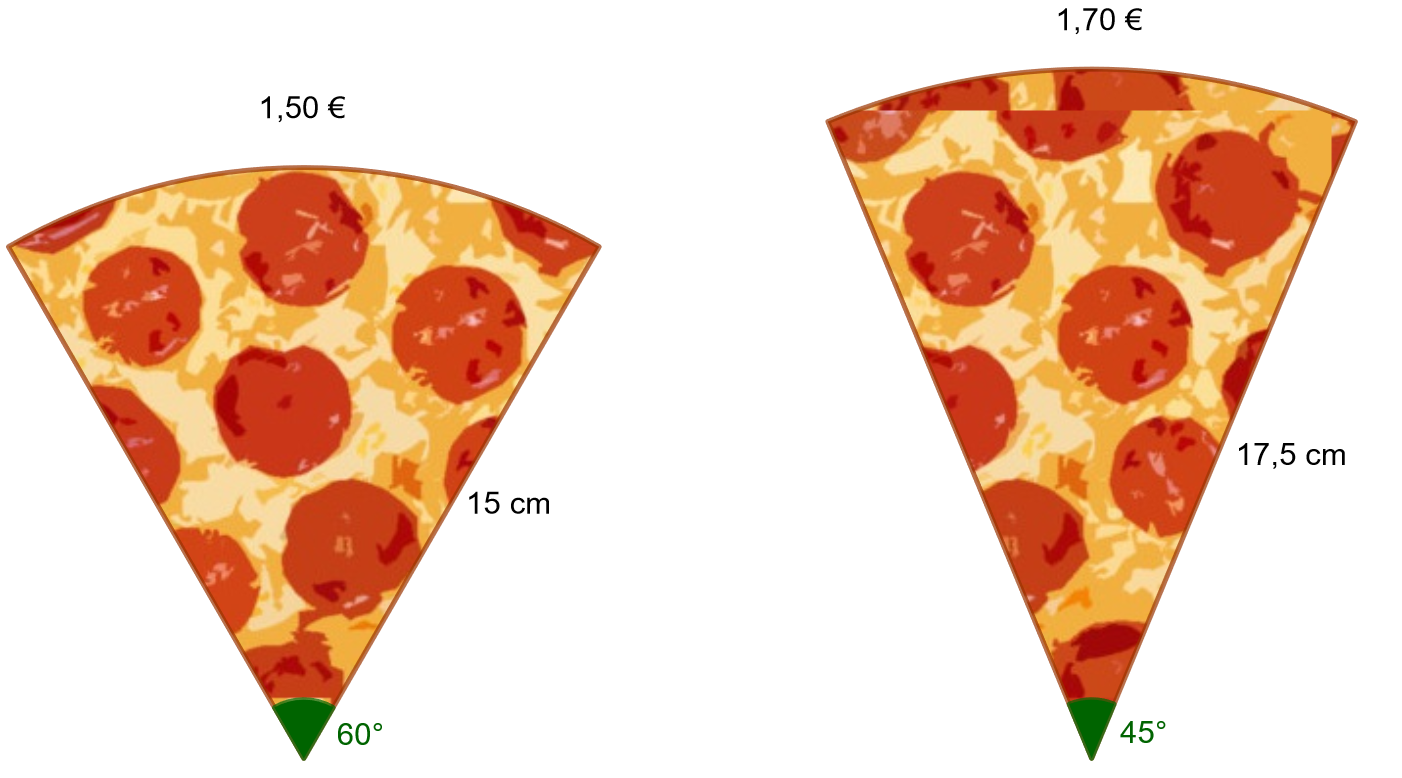
Tehtävä
Alla on kuva kuulantyöntöringistä ja -sektorista. Ringin halkaisija on \(7\) jalkaa eli \(2,135 \text{ m}\).
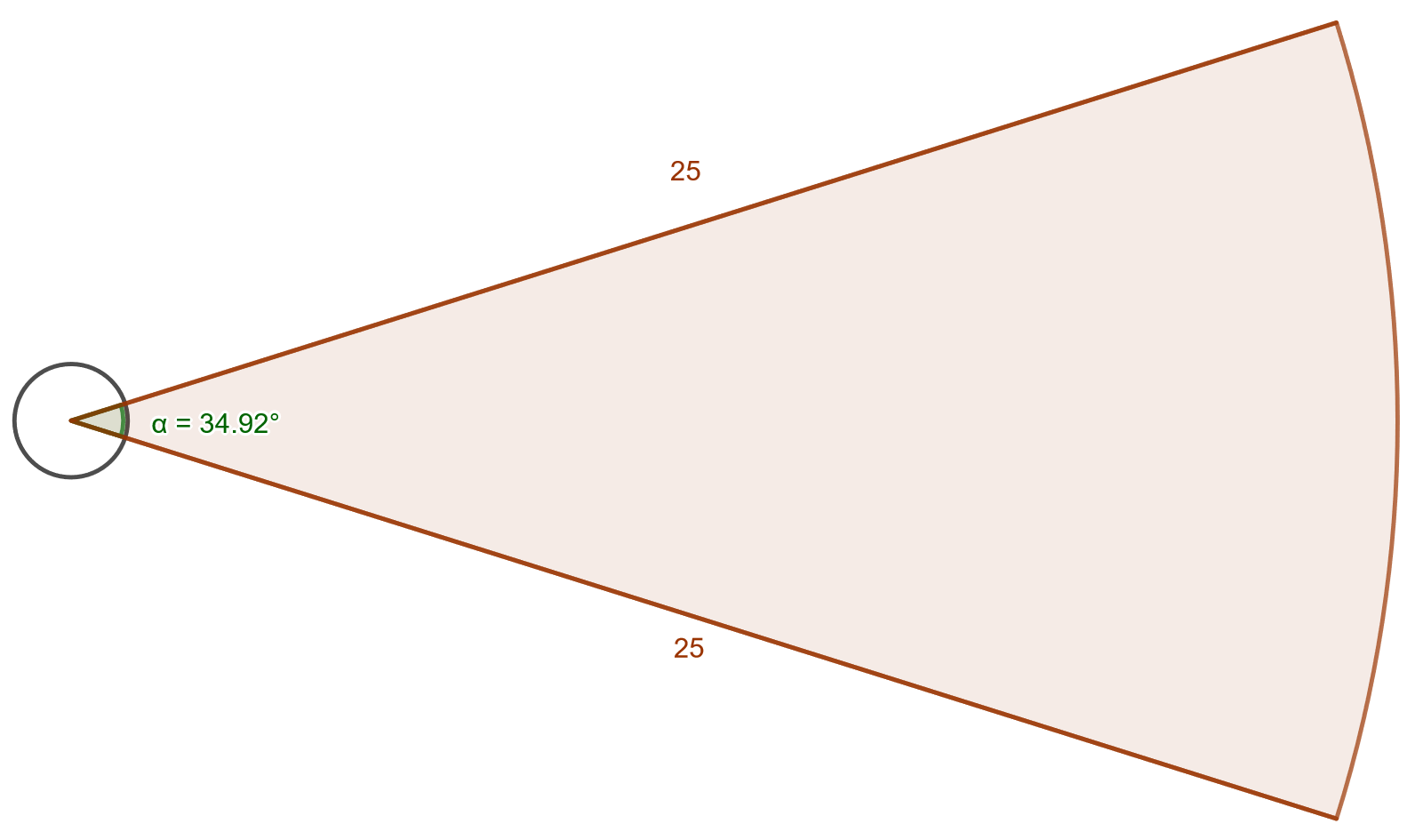
- Kuulantyöntösektori peitetään hiekalla. Kuinka suuri pinta-ala peitetään? Rinkiin ei laiteta hiekkaa.
- Sektori ja rinki ympäröidään ulkoreunoja pitkin merkintänauhalla. Kuinka paljon nauhaa tarvitaan?
Tehtävä
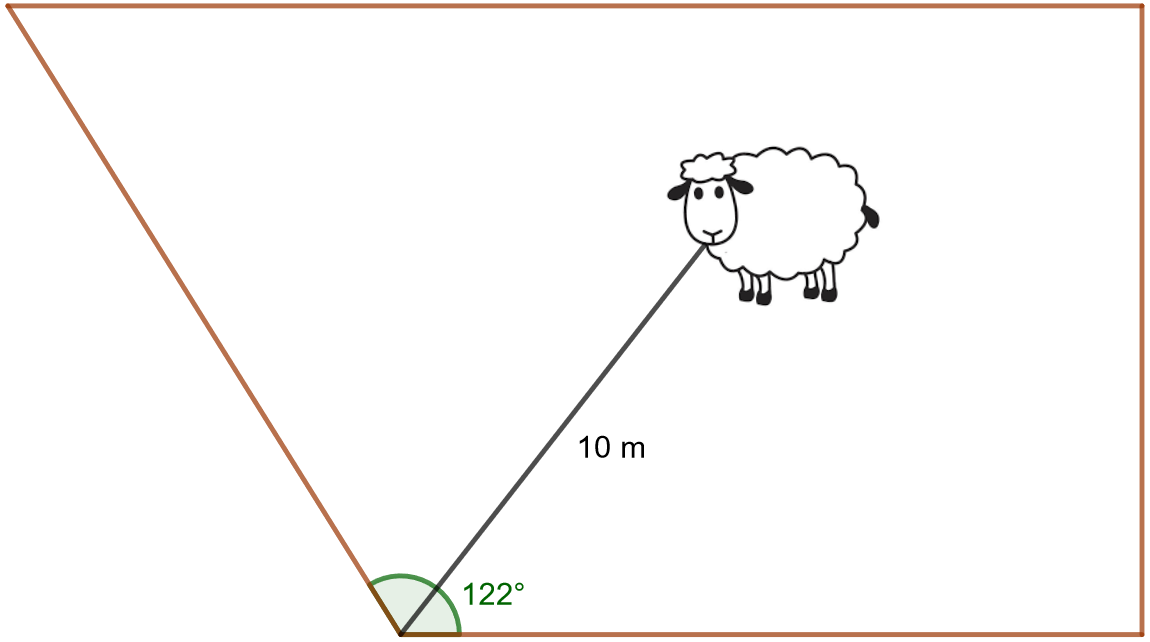
Lammas on kiinnitetty \(10 \text{ m}\) pitkällä hihnalla aidoitetun alueen kulmaan. Laske, kuinka suurelta alueelta lammas voi syödä ruohoa.
3.4 Jänne, segmentti
Tehtävä
Ympyrän säde on \(2\) ja segmentin keskuskulman suuruus on \(138^{\circ}\). Mikä on pienemmän muodostuvan segmentin pinta-ala?
Tehtävä
Ympyrän säde on \(3\) ja segmentin keskuskulman suuruus on \(300^{\circ}\). Mikä on suuremman muodostuvan segmentin pinta-ala?
Tehtävä
Ympyrän halkaisija on \(14\). Ympyrään on piirretty segmentti, jota vastaavan kaaren pituus on \(17\). Kuinka suuri on pienemmän segmentin pinta-ala?
Tehtävä
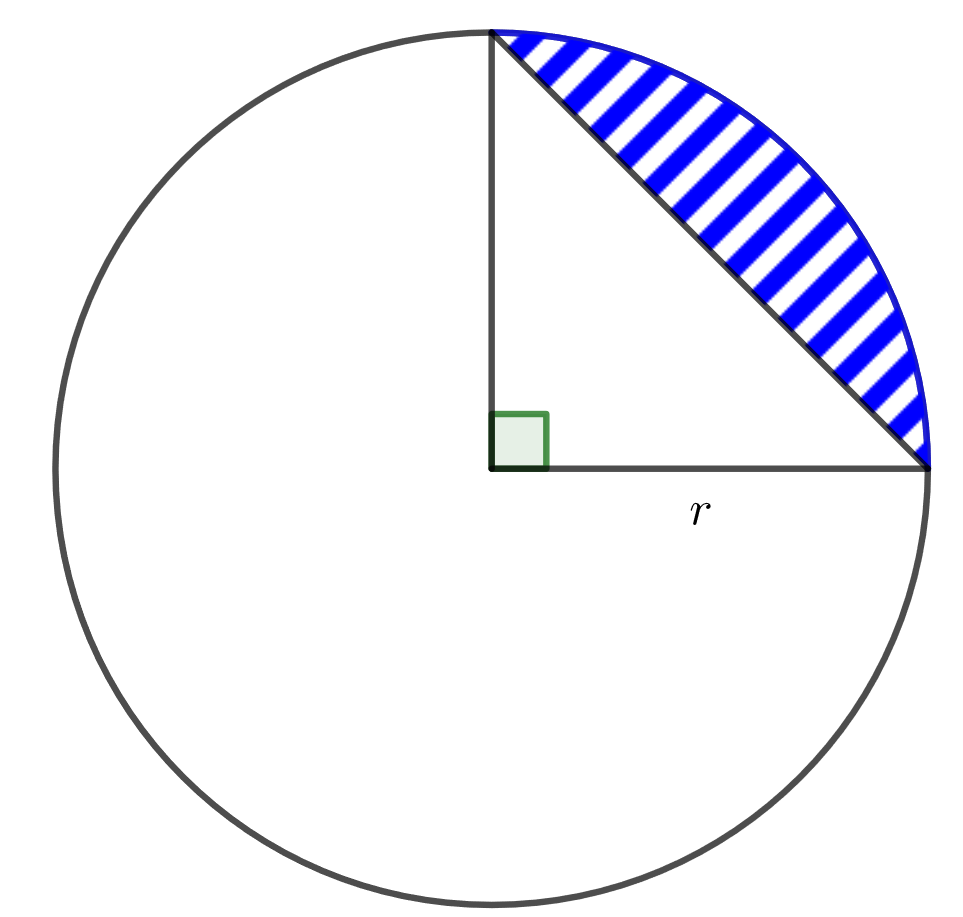
Kuinka monta prosenttia ympyräneljännekseen piirretyn segmentin pinta-ala on koko ympyrän pinta-alasta? Ympyrän säde on \(r\).
3.5 Tangentti, tangenttikulma
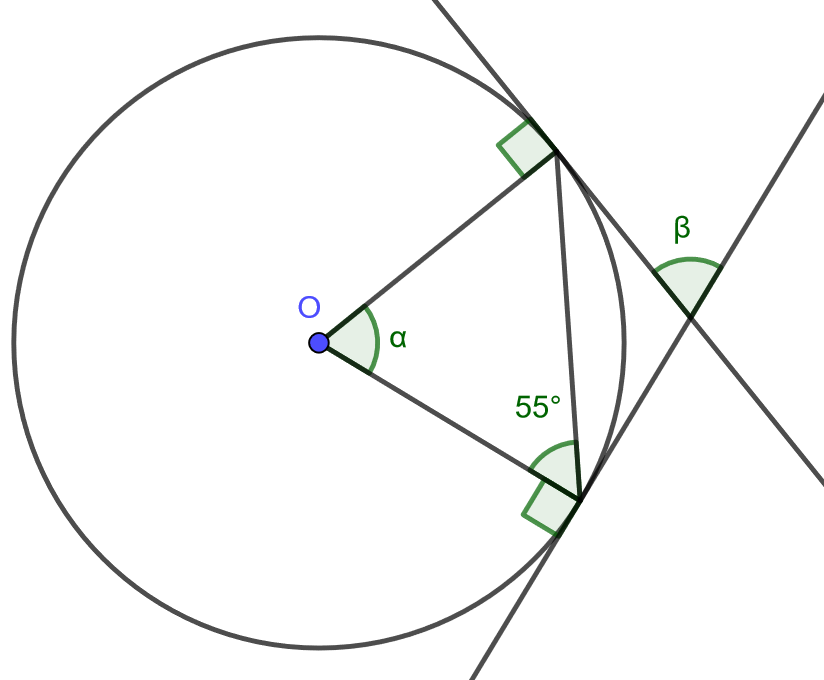
Tehtävä
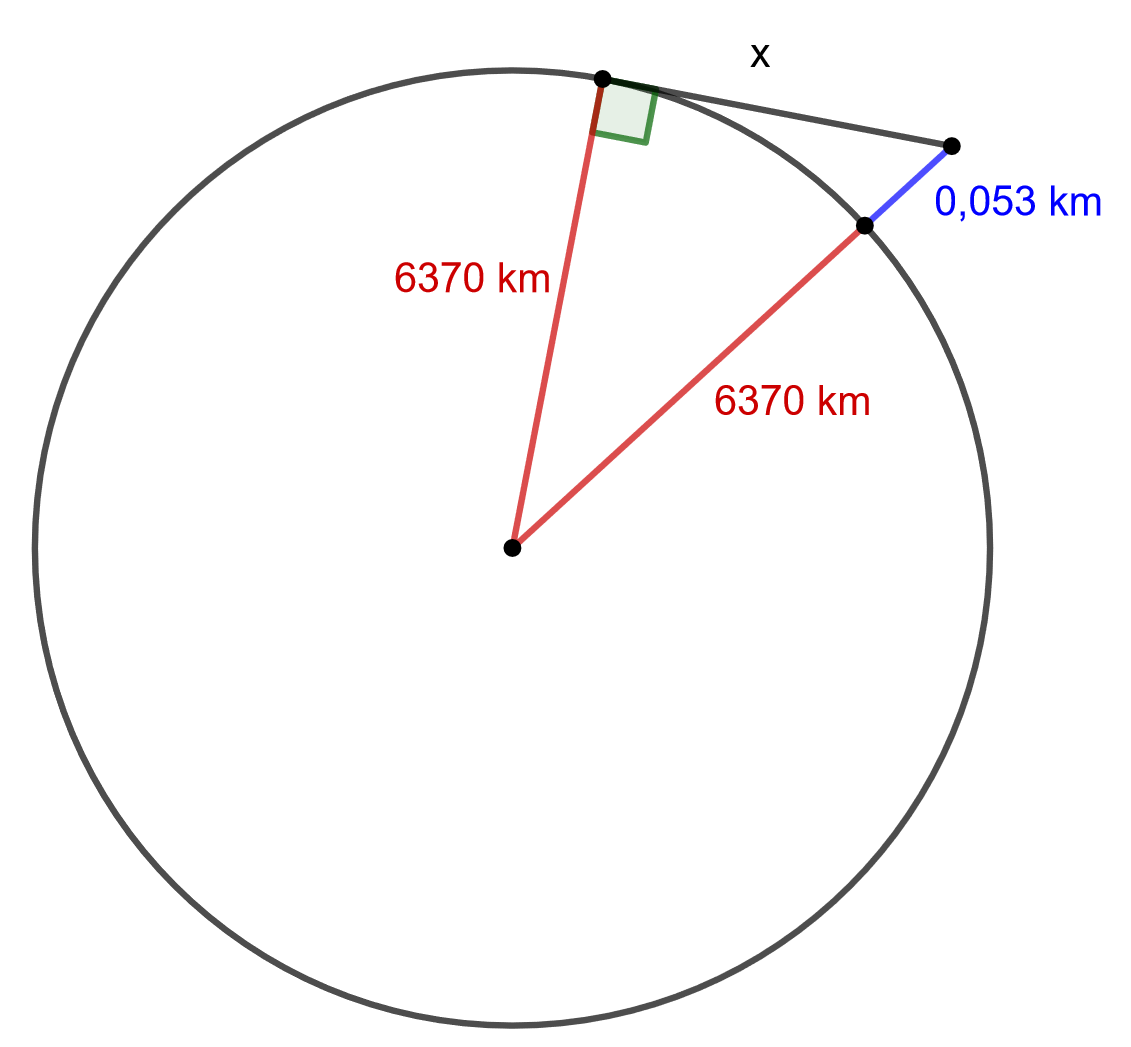
Kuinka pitkälle \(53 \text{ m}\) korkeasta vesitornista voi nähdä? Maapallon säde on \(6370 \text{ km}\). Oletetaan, että katsojan silmät ovat myös \(53 \text{ m}\) korkeudella maan pinnasta. Piirrä ensin mallikuva tilanteesta.
Huom! Mallikuva ei ole mittakaavassa!
Tehtävässä tulee ratkaista kuvaan merkitty pituus \(x\).
Tehtävä
Ympyrälle piirretään tangentit kehän ulkopuolisesta pisteestä \(C\). Tangenttien sivuamispisteet \(E\) ja \(D\) ovat etäisyydellä \(10\) pisteestä \(C\). Piirretään ympyrälle vielä yksi tangentti pisteen \(F\) kautta. Olkoon tämän tangentin ja aiempien tangenttien leikkauspisteet \(A\) ja \(B\). Laske kolmion \(ABC\) piiri. [H]
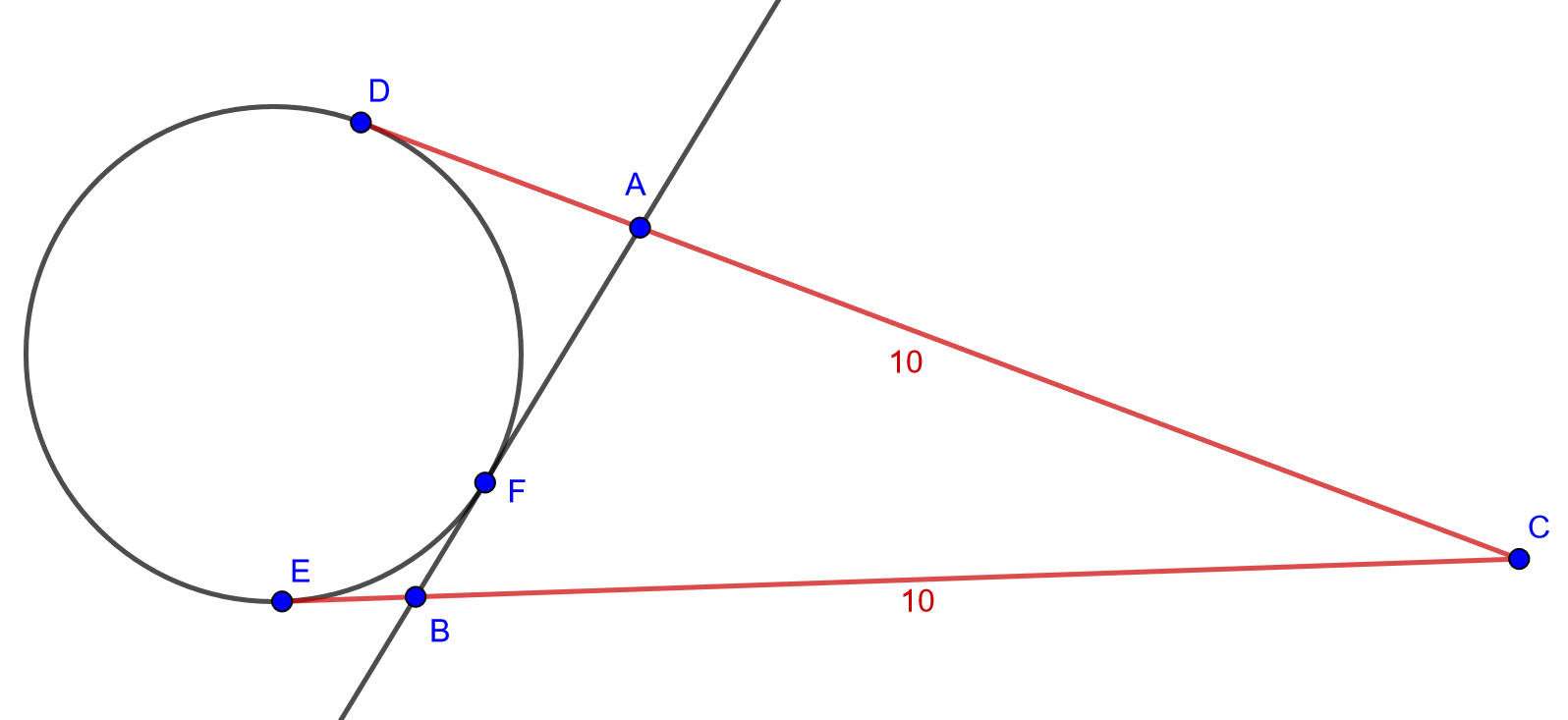
Pisteet A, B ja C ovat tangenttikulmien kärkiä, eli ne ovat yhtä etäällä molemmista tangenttipisteistään.
3.6 Keskuskulma, kehäkulma
Tehtävä
Jos nelikulmion kaikki kulmat ovat saman ympyrän kaarella, nelikulmiota kutsutaan jännenelikulmioksi. Osoita, että jännenelikulmiossa vastakkaisten kulmien summa on aina \(180 ^{\circ}\).
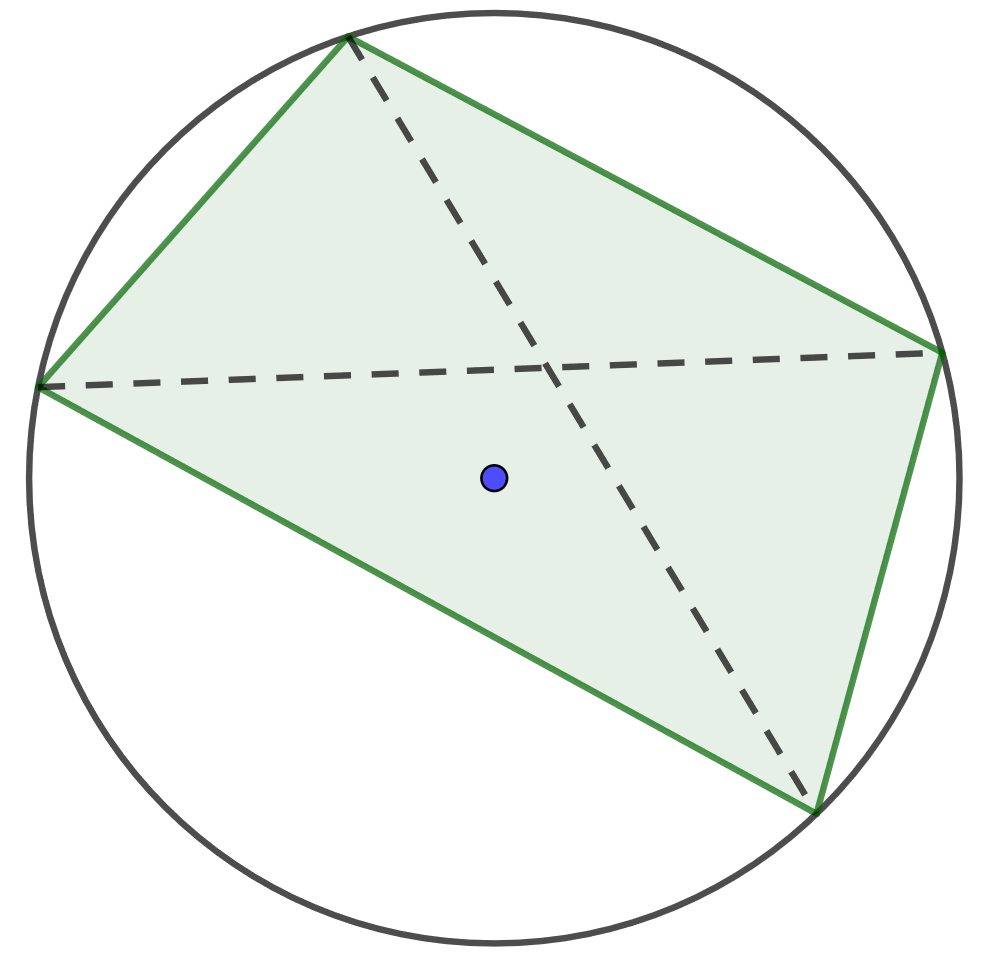
Kokeile käyttää kehäkulmalausetta.
Käytetään alla olevan kuvan merkintöjä.
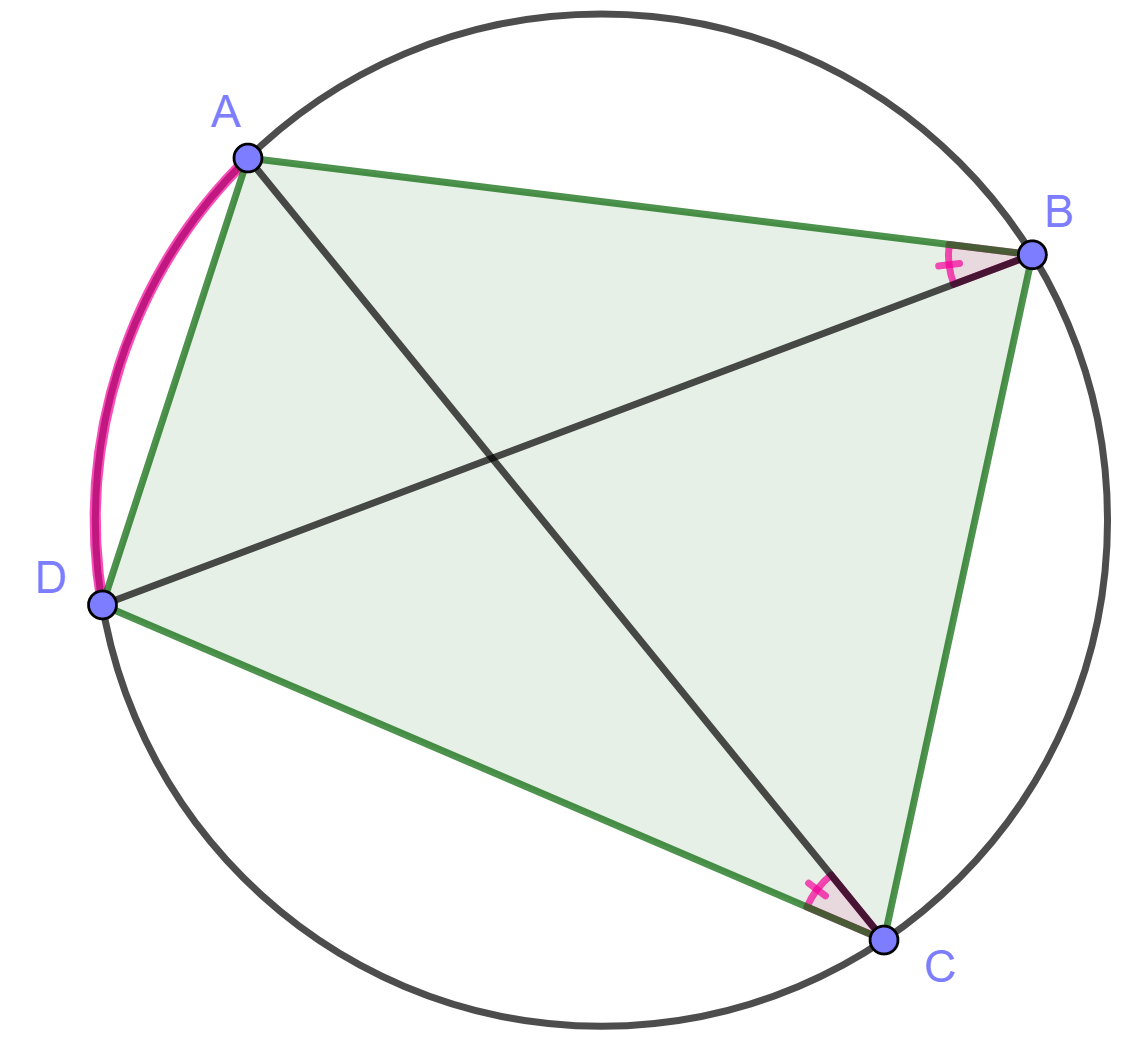
Kulmat \(ABD\) ja \(ACD\) ovat yhtä suuria, sillä ne ovat samaa kaarta \(AD\) vastaavia kehäkulmia.
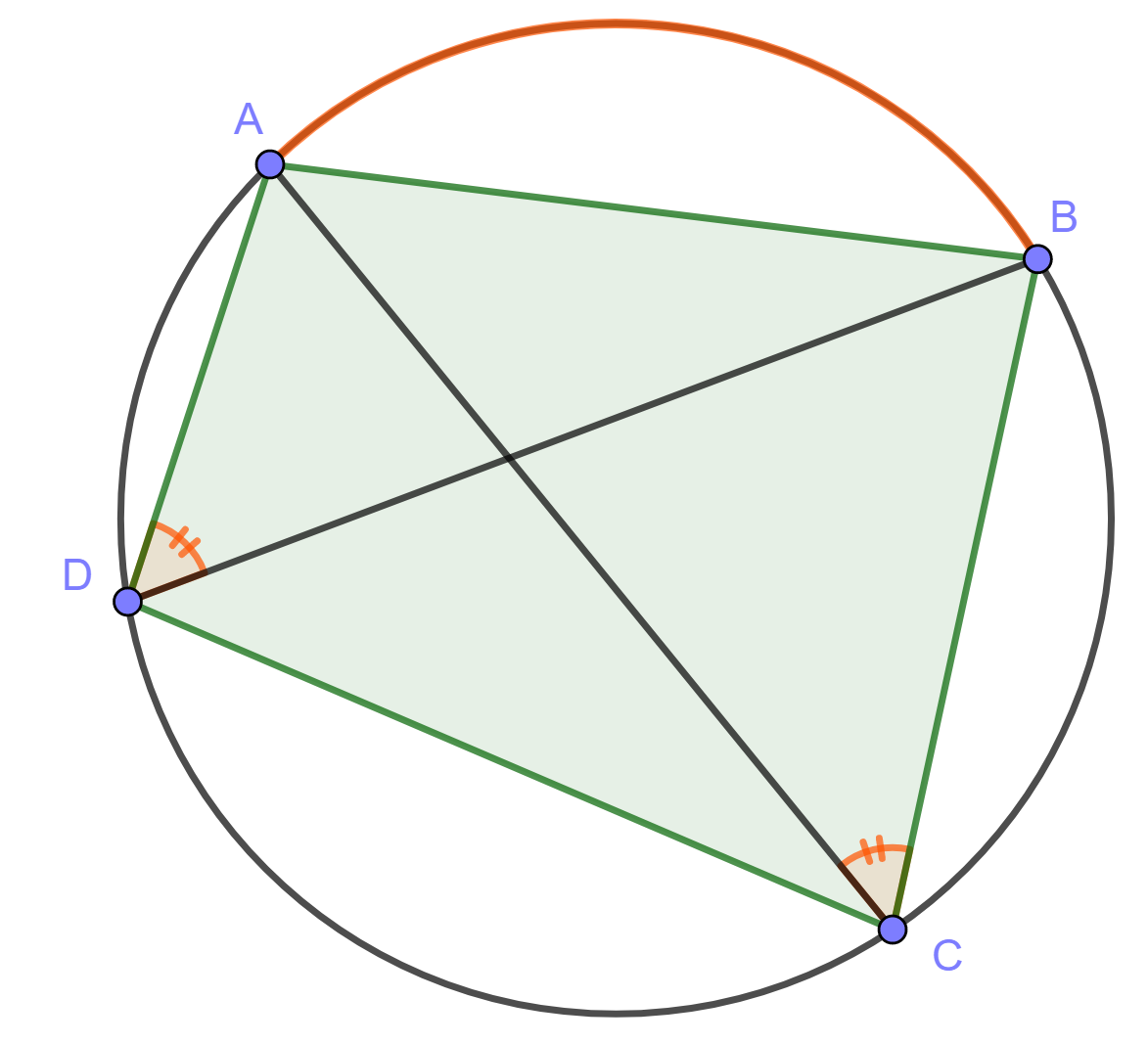
Vastaavasti kulmat \(BDA\) ja \(BCA\) ovat yhtä suuria, sillä ne ovat samaa kaarta \(AB\) vastaavia kehäkulmia.
Sekalaisia tehtäviä
Tehtävä
Laske tukkikasan korkeus, kun tukin säde on \(40,0 \text{ cm}\). Oletetaan tukkien poikkileikkaukset ympyröiksi. Ympyrät sivuavat toisiaan.
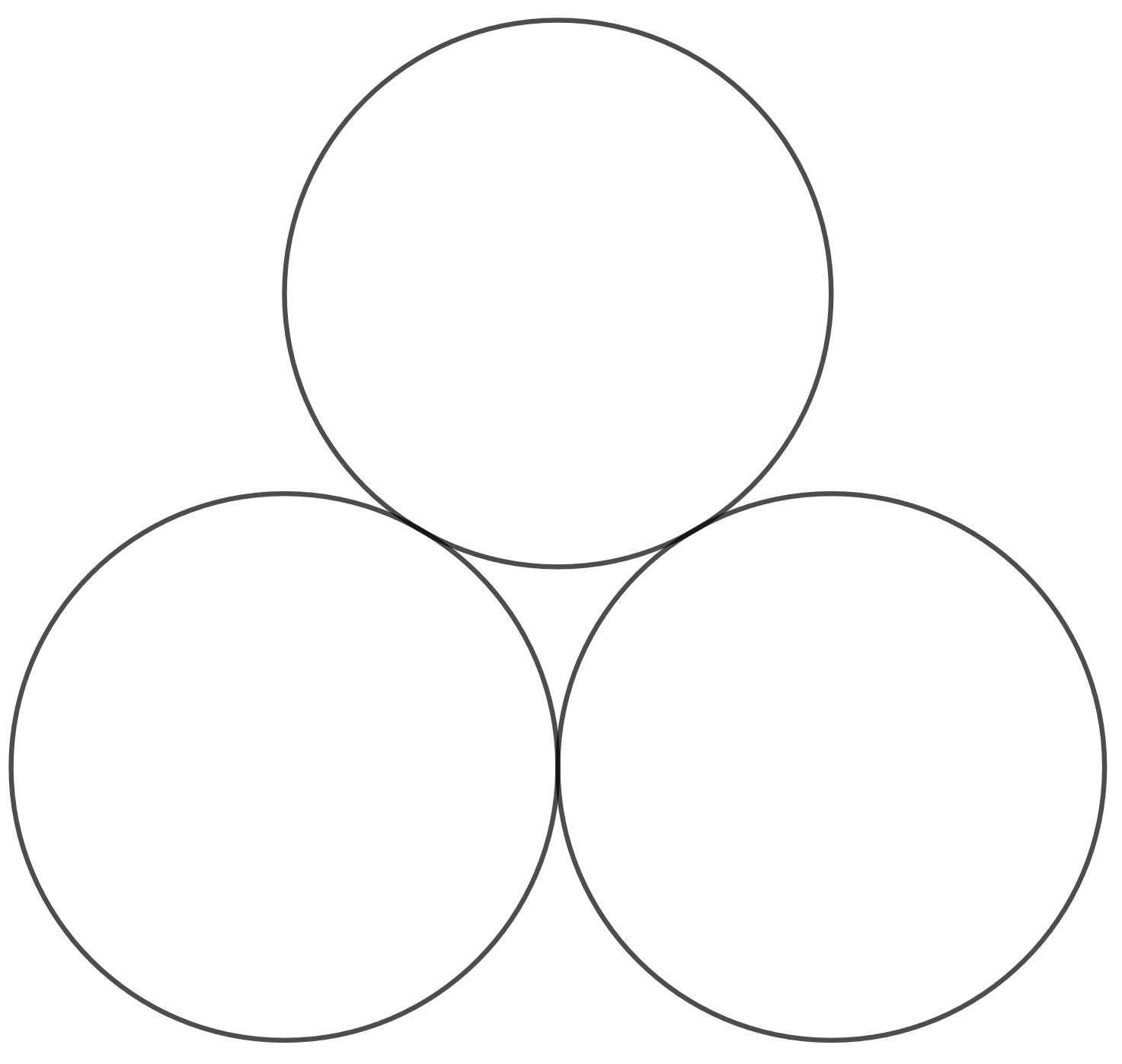
Tehtävä
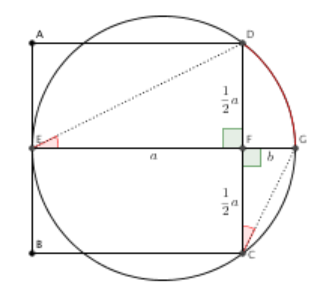
Ratkaise alla olevan kuvan pienemmän ympyrän halkaisija isomman ympyrän säteen \(a\) avulla.
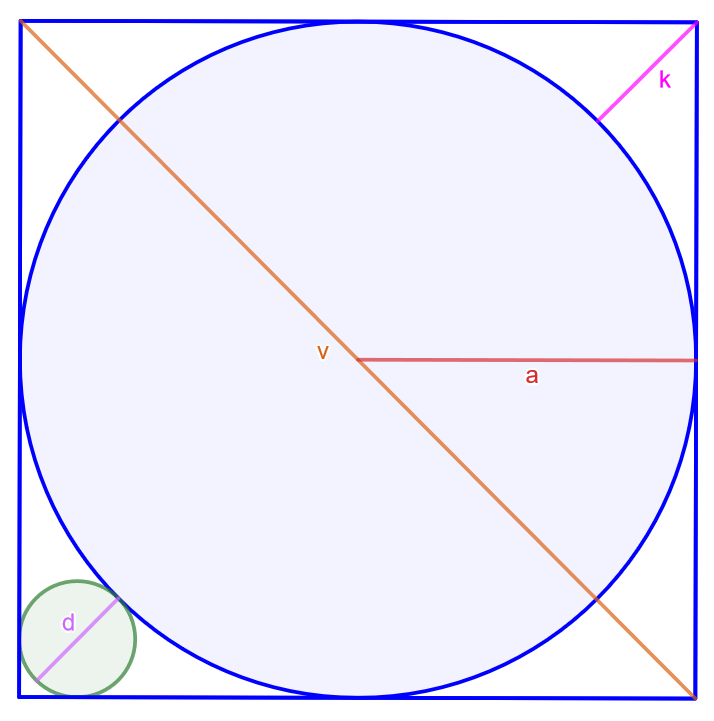
Verranto: \(\dfrac{d}{k}=\dfrac{2a}{2a+k}\)
Tehtävä
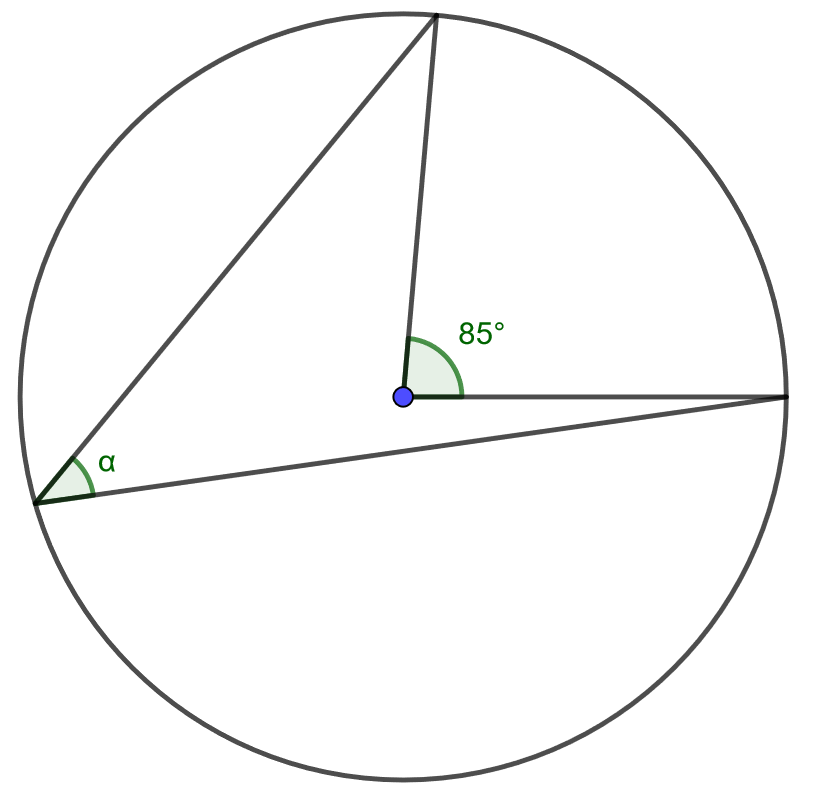
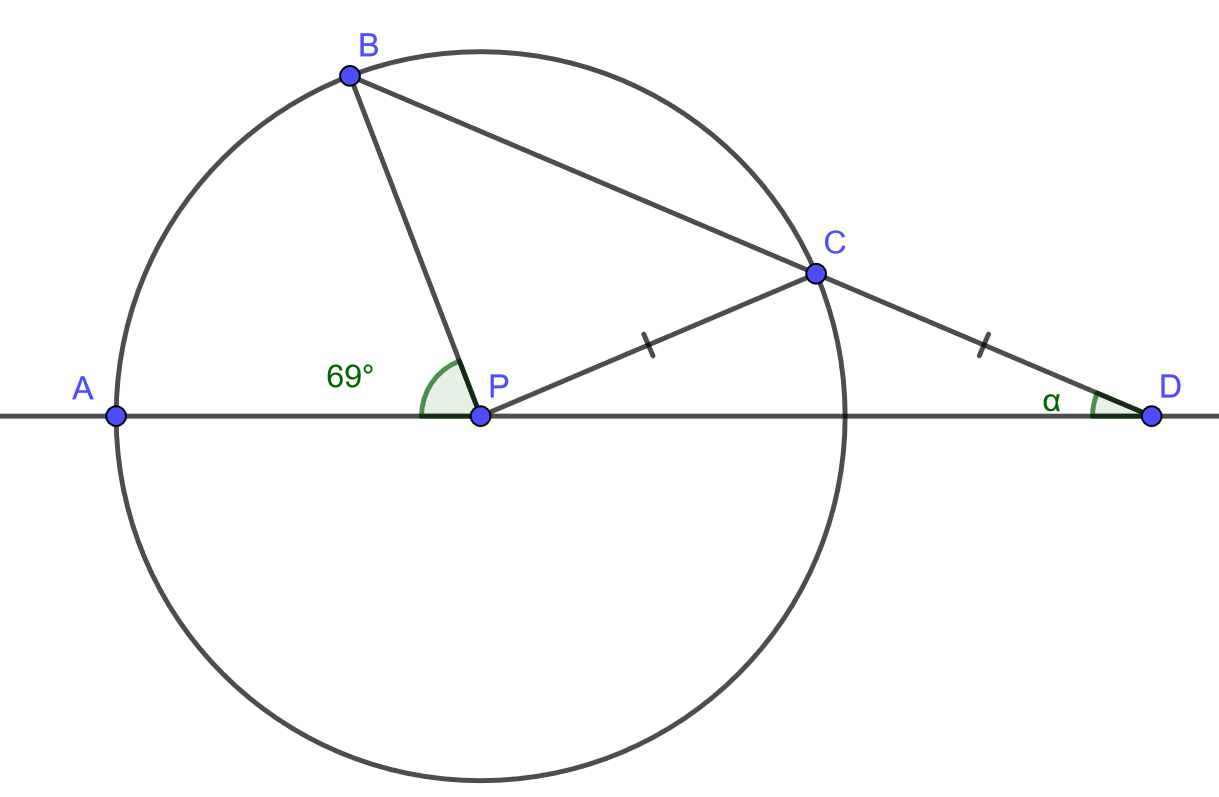
Alla olevassa kuvassa piste \(P\) on ympyrän keskipiste ja pisteet \(A\), \(B\) ja \(C\) ovat ympyrän kehän pisteitä. Piste \(D\) on suorien \(AP\) ja \(BC\) leikkauspiste ja janat \(PC\) ja \(CD\) ovat yhtä pitkät. Kulman \(\angle BPA\) suuruus on \(69^{\circ}\). Kuinka suuri on kulma \(\alpha\)? [H]
Tehtävä
Neliön sisään piirretään neljännesympyrä siten, että neliön ylänurkasta voidaan erottaa neljännesympyrää koskettava suorakulmio, jonka sivujen pituudet ovat \(1\) ja \(8\). Kuinka pitkä on neliön sivu?
Tehtävä
Ympyränkaaret, joiden säteet ovat \(2a\) ja \(a\), leikkaavat alla olevan GeoGebra-appletin mukaisesti. Mikä on kaarien rajaaman alueen pinta-ala? [T]
Alue voidaan laskea kahden segmentin pinta-alojen summana.
Tehtävä
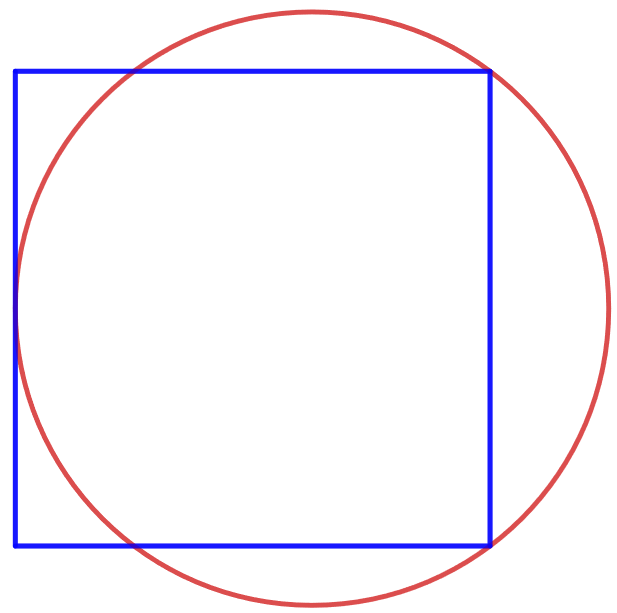
Neliön kaksi kärkeä ja näiden vastaisen sivun keskipiste ovat ympyrän kehällä.
Kummalla on suurempi piiri, neliöllä vai ympyrällä? [H]
Tehtävä
Mikä on suurimman mahdollisen \(r\)-säteisen ympyrän sisään mahtuvan säännöllisen \(n\)-kulmion pinta-ala?
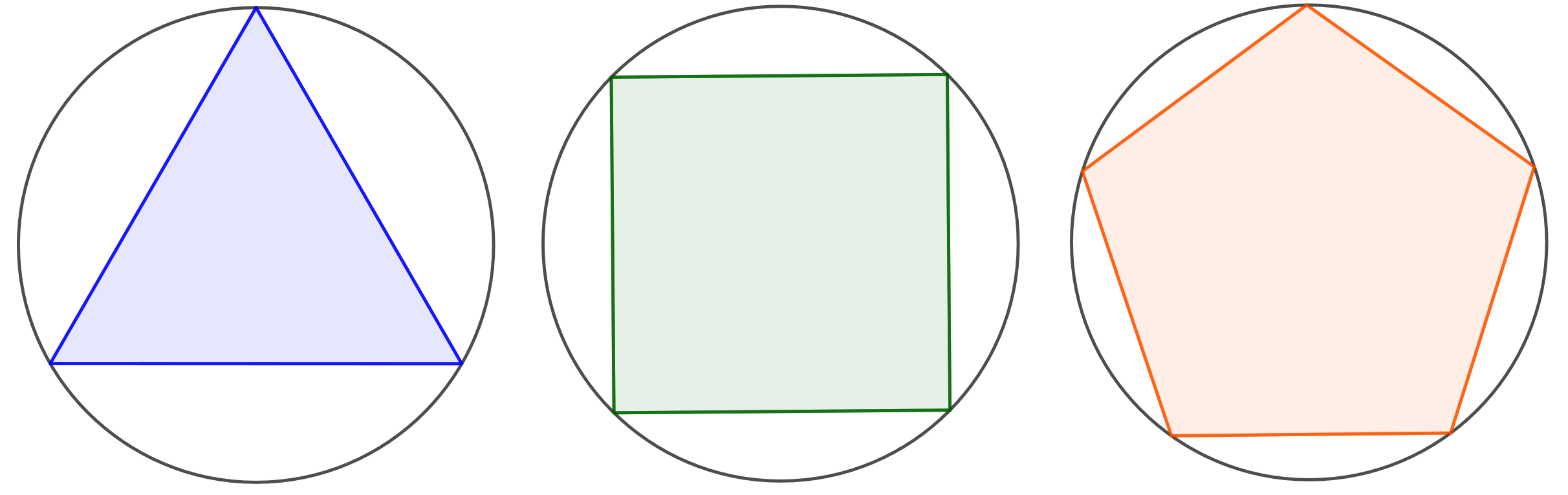
Tehtävän voi ratkaista monilla eri tavoilla, joista tässä esitetään vain yksi. Käytetään hyväksi alla olevaa kuvaa.
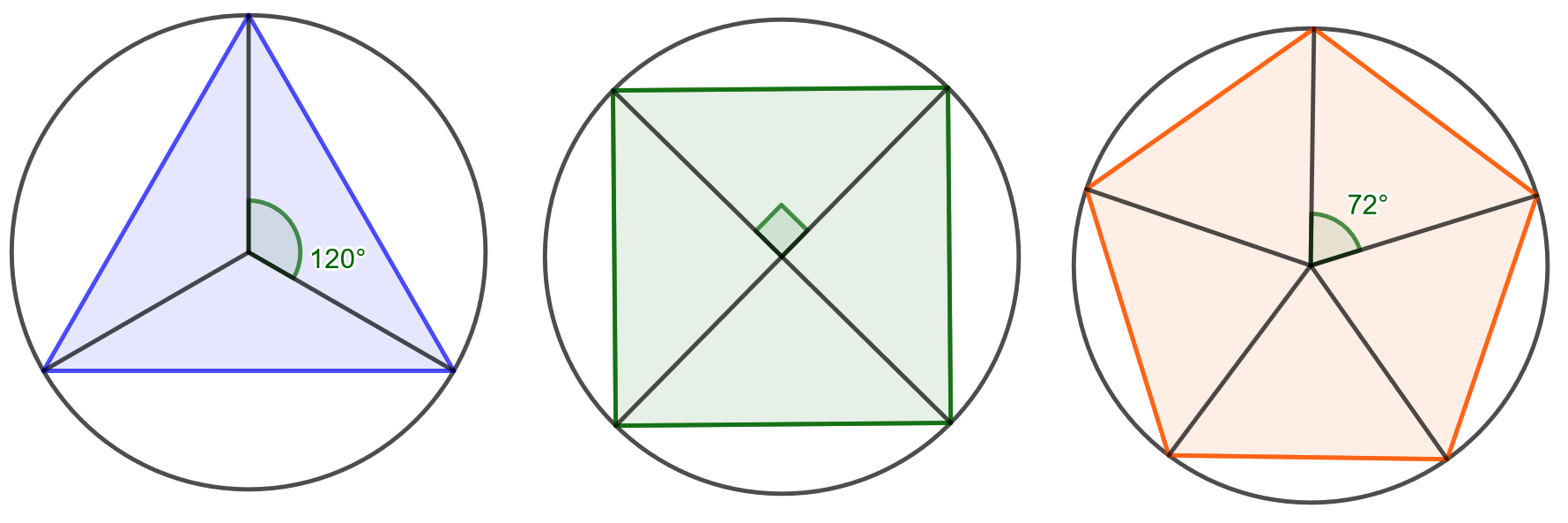
Jos monikulmiossa on \(n\) kulmaa, jaetaan monikulmio \(n\) kolmioon. Kolmiot muodostetaan piirtämällä janat ympyrän keskipisteestä monikulmion jokaiseen kulmaan. Kolmion kulma, jonka kärki on ympyrän keskipisteessä, on \(\frac{360^{\circ}}{n}\). Tämän kulman viereiset sivut ovat ympyrän säteen \(r\) mittaisia. Kolmion pinta-alan trigonometrisella kaavalla saadaan yhden kolmion alaksi \[A_k = \frac{r^2}{2} \cos \left( \frac{360^{\circ}}{n} \right).\] Koska kolmioita muodostuu monikulmion sisään \(n\) kappaletta, on koko monikulmion pinta-ala \[A=n \cdot A_k = \frac{r^2n}{2} \cos \left( \frac{360^{\circ}}{n} \right).\]
Tehtävä
Alla olevassa GeoGebra-appletissa on isompi \(R\)-säteinen ympyrä, jonka sisällä on kolme pienempää \(r\)-säteistä ympyrää. Määritä pienempi säde \(r\) isomman säteen \(R\) avulla.
Tehtävä
Ympyrän, jonka halkaisija on \(5,0 \text{ cm}\) sisälle piirretään mahdollisimman suuri viisikulmio. Määritä viisikulmion pinta-ala yhden desimaalin tarkkuudella.
Tehtävä
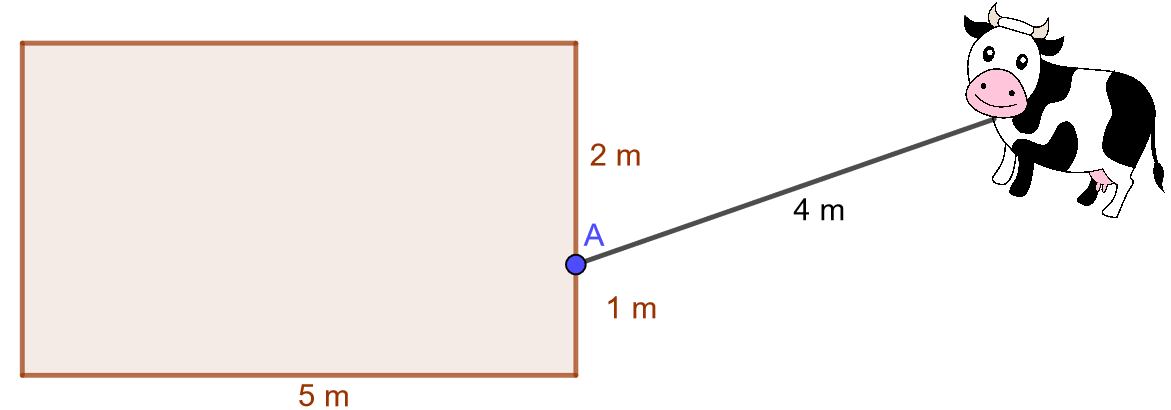
Kuinka suurella alueella lehmä voi laiduntaa, kun sen kaulassa oleva köysi on kytketty kuvan mukaisesti ladon seinustalle pisteeseen \(A\) ja köyden pituus on \(4 \text{ m}\)?
4. Avaruusgeometria
4.1 Avaruuskappaleita ja kulmia
Tehtävä
Tehtävä
Suorakulmaisen särmiön muotoisen laatikon sivujen pituudet ovat \(x=10\), \(y=3\) ja \(z=8\). Laatikon sisään asetetaan lauta kuvan mukaisesti. Kuinka suuri on laatikon pohjan ja laudan välinen kulma? 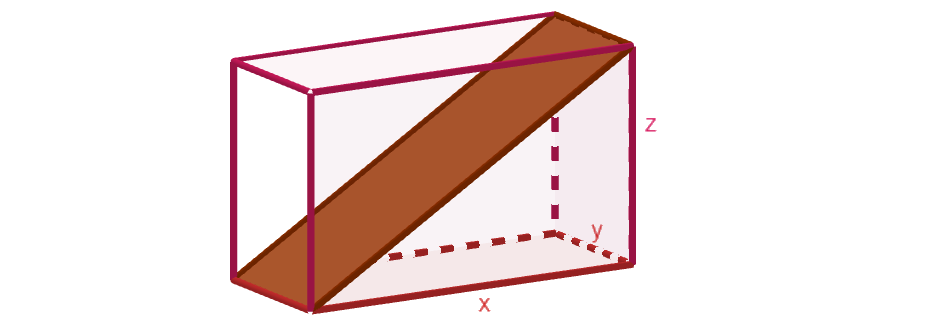
Tehtävä
Matti valmistaa pahvista kuution, jonka sivun pituus on \(20 \text{ cm}\).
- Kuinka paljon pahvia tarvitaan kuution tekoon?
- Matti haluaa asettaa kuution sisään mahdollisimman pitkän ohuen riman. Kuinka pitkä rima kuutioon mahtuu?
4.2 Pallo
Tehtävä
Täydellisessä auringonpimennyksessä kuu peittää maasta katsottuna auringon kokonaan. Jos auringon etäisyys maasta on \(387\)-kertainen kuun etäisyyteen maasta, kuinka moninkertainen auringon tilavuus on kuun tilavuuteen verrattuna?
Tehtävä (K2016/6)
Maapallon säde on \(6371 \text{ km}\), ja sen pohjoisen napapiirin leveysaste on \(66,5\). Pohjoiselta napapiiriltä valitaan pisteet \(A\) ja \(B\), joiden pituusasteiden erotus on \(90\) astetta.
- Määritä pisteiden \(A\) ja \(B\) välisen viivasuoran tunnelin pituus.
- Määritä pisteiden \(A\) ja \(B\) välisen lyhimmän napapiirin kaaren pituus.
Tehtävä
Pallon pinta-ala on \(2,5 \text{ m}^2\). Pallo jaetaan kahteen yhtä suureen osaan. Laske muodostuvan puolipallon tilavuus.
Tehtävä
Vesi peittää noin \(70 \%\) maapallon pinnasta. Jos maapallon säde on noin \(6 370 \text{ km}\), kuinka suuren pinta-alan vesi peittää?
Tehtävä
Maapallon vesien yhteenlaskettu määrä on noin \(1,386 \cdot 10^9 \text{ km}^3\). Oletetaan, että maapallon säde on noin \(6370 \text{ km}\) ja että maapallo on täydellinen pallo. Jos kaikki vesi levittäytyisi maapallon pinnalle tasaisesti, kuinka syvä vesikerros olisi?
4.3 Lieriö
Tehtävä
Palaa tehtävään, jossa laskettiin aakkoskarkin pinta-alaa. Jos aakkoskarkin paksuus on \(0,7 \text{ cm}\), mikä on yhden karkin tilavuus?
Jos karkin tiheys on \(1,5 \text{ g/cm}^3\) ja yksi pussi painaa \(315 \text{ g}\), kuinka monta karkkia yhdessä pussissa on?
Tehtävä
Vesitornin sylinterin muotoiseen säiliöön mahtuu vettä \(4000 \text{ m}^3\) ja säiliön korkeus on \(23\) metriä. Mikä on säiliön halkaisija?
Tehtävä
Alla olevassa kuvassa on havainnekuva maitotölkistä sekä tölkin mitat (senttimetreinä). Laske koko tölkin tilavuus.
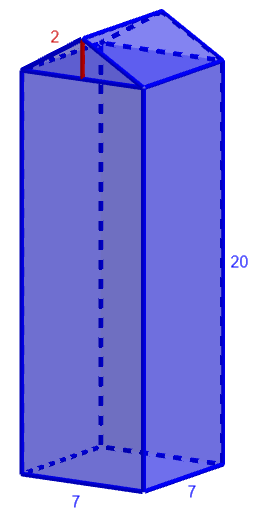
Tehtävä
Muurahainen aloittaa kulkunsa kuution kulmasta. Kuution särmän pituus on \(1\). Mikä on lyhin matka, jonka kulkemalla muurahainen pääsee kuution vastakkaiseen kulmaan?
Tehtävä
Jos pallon tilavuus on \(1\), mikä suurimman sen sisään mahtuvan kuution tilavuus?
Tehtävä
Mahdollisimman pienen ympyräpohjaisen lieriön sisälle laitetaan mahdollisimman suuri pallo. Määritä pallon tilavuuden suhde lieriön tilavuuteen.
4.4 Kartio
Tehtävä
Suoran ympyräkartion pohjan säde on \(4\) ja sen korkeus on \(12\). Kartion huipusta katkaistaan pienempi suora ympyräkartio. Tämän pienemmän kartion pohjan säde on \(1\). Kuinka korkea pienempi kartio on?
Tehtävä
Olkoon edelleen kartion pohjan säde \(4\) ja korkeus \(12\). Sen huipusta leikataan pois pienempi kartio, jonka pohjan säde on \(1\). Mikä on jäljelle jäävän osan tilavuus?
Tehtävä
Suoran ympyräkartion korkeus on \(h\) ja pohjan säde \(r\). Kartion huipulta katkaistaan pienempi kartio, jonka korkeus on \(\frac{1}{4}h\). Kuinka moninkertainen ison kartion tilavuus on verrattuna pienempään kartioon?
Tehtävä
 Kheopsin pyramidin muoto on lähellä neliöpohjaista kartiota. Matti mittaa pyramidin pohjan sivun pituudeksi \(230 \text{ m}\) ja kuulee oppaalta pyramidin korkeuden olevan \(137 \text{ m}\). Laske annettujen tietojen avulla arvio pyramidin tilavuudelle.
Kheopsin pyramidin muoto on lähellä neliöpohjaista kartiota. Matti mittaa pyramidin pohjan sivun pituudeksi \(230 \text{ m}\) ja kuulee oppaalta pyramidin korkeuden olevan \(137 \text{ m}\). Laske annettujen tietojen avulla arvio pyramidin tilavuudelle.
Tehtävä
\(3,0 \text{ m}\) korkean kartion pohja muodostuu tasasivuisesta kolmiosta. Kartion tilavuus on \(150 \, \ell\). Määritä pohjakolmion sivun pituus.
Tehtävä
Kartion muotoisen jäätelötötterön sivun pituus on \(15 \text{ cm}\) ja sen suuaukon halkaisija on \(8 \text{ cm}\). Jäätelötötteröön asestetaan täsmälleen pallon muotoinen jäätelöpallo, jonka halkaisija on \(8 \text{ cm}\). Jos pallon annetaan sulaa kokonaan, mahtuuko se jäätelötötterön sisään?
4.5 Maapallo
Tehtävä
Merkitään Suomen kuntien koordinaatteja niin, että x-koordinaattina on pohjoinen leveys N ja y-koordinaattina itäinen pituus E. Merkitään esimerkiksi Helsingin koordinaatteja seuraavasti: \(60.2°\)N, \(24.9°\)E \(= (60.2, 24.9)\).
Tehtävä
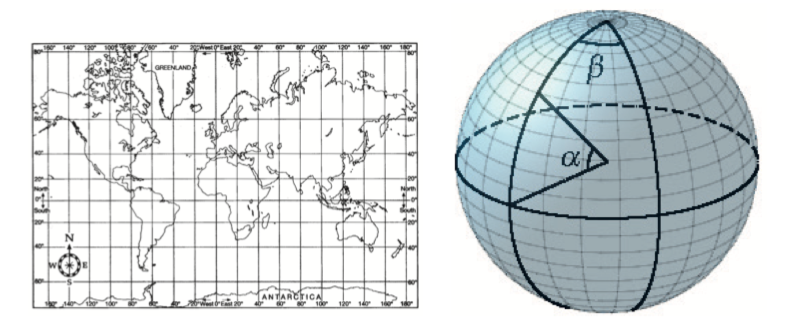
Monet hallinnolliset rajat seuraavat luonnollisia maaston piirteitä, kuten jokia ja vuo- ristoja. Sen sijaan Yhdysvalloissa Coloradon osavaltion rajat määräytyvät Maapallon leveys- ja pituusasteiden avulla seuraavista ehdoista:
\[\begin{align*} 37° N ≤ \text{leveysaste} ≤ 41° N\\ 102° W ≤ \text{pituusaste} ≤ 109° W. \end{align*}\]
- Laske Coloradon osavaltion länsirajan pituus.
- Kumpi on pitempi, Coloradon osavaltion eteläraja vai pohjoisraja? Perustele.
Tässä tehtäväassä Maa oletetaan palloksi, jonka säde on \(R=6 371\text{km}\). Tilanteen hahmottamisen helpottamiseksi on oikean puolen kuvaan merkitty päiväntasaajan suhteen mitattava leveysaste \(\alpha\) ja Greenwichin meridiaanin suhteen mitattava pituusaste \(\beta\). [8/S17]
4.6 Avaruuskappaleita koordinaatistossa
Tehtävä
Suorakulmaisen kolmion kärkipisteet ovat \(A(-4,2)\), \(B(2,2)\) ja \(C(2,5)\). Kolmio pyörähtää sivun \(BC\) ympäri. Laske syntyvän pyörähdyskappaleen tilavuus desilitroina yhden desimaalin tarkkuudella, kun koordinaatiston yksikkönä on senttimetri.
Muodostuva pyörähdyskappale on ympyräpohjainen kartio.
Tehtävä
Pallon kuoren yksi piste on \(A(1,2,-2)\) ja sen keskipiste on \(O(0,1,0)\). Laske pallon pinta-ala yhden desimaalin tarkuudella.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.