Kolmioiden geometriaa

suorakulmaisen kolmion geometria
pythagoraat yms
sini kosini ja tangentti
pinta-ala

Tässä kappaleessa käsitellään kolmioiden geometriaa, mikä tarkoittaa esimerkiksi kolmion pinta-alan laskemista sekä sen sivujen pituuksien ja kulmien suuruuksien ratkaisua erilaisten lauseiden avulla.

Kappaleeseen liittyvät harjoitustehtävät löydät täältä!

Kolmion rakenne

Kolmio on yksinkertaisin monikulmio, ja nimensä mukaisesti se koostuu kolmesta kulmasta ja kolmesta sivusta. Kolmion kulmat nimetään kreikkalaisin kirjaimin, $\alpha$, $\beta$ ja $\gamma$.

Kolmion kaikkien kulmien yhteenlaskettu suuruun on aina $180°$, eli $\alpha+ \beta+\gamma=180°$ .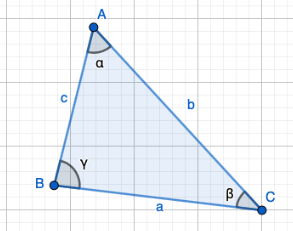

Kaiken muotoisille kolmioille voidaan piirtää korkeusjana $h$, joka kulkee kolmion huipusta kohtisuorasti kohti kolmion kantaa: 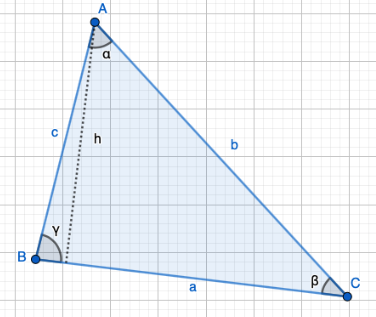Tämä korkeusjana $h$ ilmoittaa kolmion korkeuden. Korkeusjanaa käytetään, kun tarkoituksena on määrittää kolmion pinta-ala.

Kolmion pinta-ala

\[\begin{align*} A=\frac{a\cdot h}{2}=\frac{1}{2}a\cdot h \end{align*}\]

Kolmiot voidaan jakaa ominaisuuksien avulla suorakulmaisiin kolmioihin, tasakylkisiin kolmioihin ja tasasivuisiin kolmioihin.

Suorakulmaisessa kolmiossa vähintään yksi kolmion kulmista on $90°$. Tasakylkisessä kolmiossa kolmion kaksi sivua ovat yhtä pitkiä, ja tasasivuisessa kolmiossa kaikki kolmion sivut ovat yhtä pitkiä.

Tasasivuisen kolmion tilanteessa kolmion kaikki kulmat ovat suuruudeltaan $60°$.

# kolmion-ala

Kolmion pinta-ala

Kolmion pinta-ala voidaan laskea tutulla tavalla, eli kerrotaan kolmion kanta ja korkeus keskenään ja jaetaan tulos kahdella. Joskus kolmion korkeus on kuitenkin vaikea määrittää. Yleisemmässä tapauksessa kolmion pinta-ala voidaan määrittää vain, kun tiedetään kahden kolmion sivun pituudet ja niiden sivujen välisen kulman suuruus.

Kolmion pinta-ala

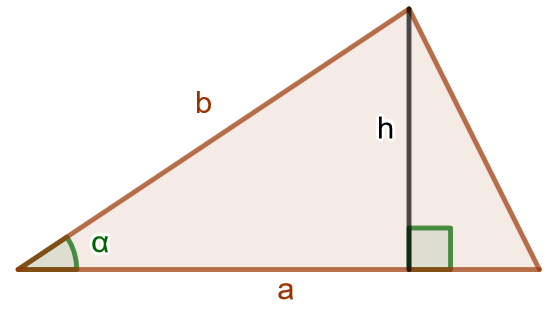
Jos kolmion kannan pituus on $a$ ja korkeus $h$, kolmion pinta-ala on \[A=\frac{1}{2} ah.\] Jos kolmion kahden sivun pituudet ovat $a$ ja $b$ ja näiden välisen kulman suuruus $\alpha$, voidaan kolmion pinta-ala ilmaista lausekkeella \[A=\frac{1}{2} ab \sin \alpha.\]

# pythagoras

Suorakulmainen kolmio, Pythagoraan lause

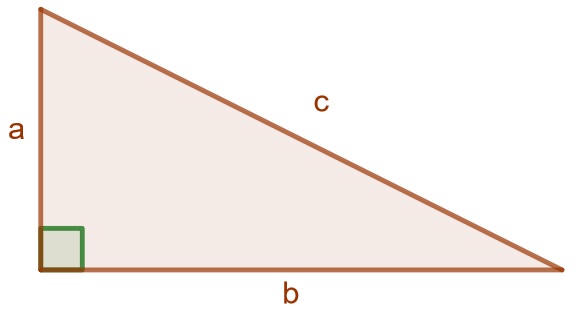
Suorakulmainen kolmio on sellainen kolmio, jonka yksi kulma on suorakulma eli $90^{\circ}$. Suoran kulman kylkinä olevia sivuja kutsutaan kateeteiksi ja suoran kulman vastaista sivua hypotenuusaksi.

Suorakulmaiseen kolmioon liittyy oleellisesti Pythagoraan lause, jonka mukaan suorakulmaisen kolmion kateettien neliöiden summa on yhtä suuri kuin kolmion hypotenuusan neliö. Jos siis tiedetään kolmion kahden sivun pituudet, voidaan kolmannen sivun pituus ratkaista. Voit lukea lisää Pythagoaan lauseen historiasta.

Pythagoraan lause

Suorakulmaisen kolmion kateettien $a$ ja $b$ neliöiden summa on yhtä suuri kuin sen hypotenuusan $c$ neliö, eli \[a^2+b^2=c^2.\]

Esimerkki 2.1.1

# suorakulmainen-kolmio-geo

# kaant-pythagoras

Käänteinen Pythagoraan lause

Pythagoraan lauseen kohdalla todettiin, että se pätee vain suorakulmaisille kolmioille. Eli jos kolmio on suorakulmainen, sen kateettien neliöiden summa on yhtä suuri kuin hypotenuusan neliö. Sama päättely voidaan kääntää toisinpäin. Jos kolmion kahden lyhyemmän sivun neliön summa on yhtä suuri kuin pisimmän sivun neliö, kyseessä on suorakulmainen kolmio. Jos suoraa kulmaa ei ole merkitty kuvaan tai sitä ei ole kerrottu erikseen, tulee aina tarkistaa, onko kolmio suorakulmainen, vaikka se saattaisi näyttää siltä.

# trig

Trigonometriset funktiot

Suorakulmaisen kolmion terävien kulmien suuruudet voidaan ratkaista, jos tiedetään kolmion kateettien tai kateetin ja hypotenuusan pituudet. Tämä on mahdollista, sillä kolmion sivujen suhteet ovat tietyillä kulmilla aina vakioita. Näitä suhteita kutsutaan trigonometrisiksi funktioiksi.

Suorakulmaisen kolmion sini, kosini ja tangentti

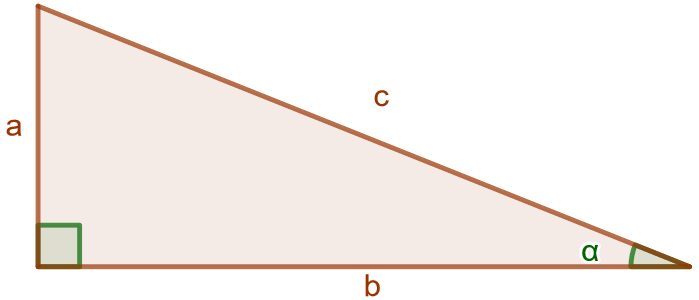
Suorakulmaisessa kolmiossa kulman $\alpha$ sini, kosini ja tangentti tarkoittavat seuraavia suhteita: \[\sin(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{hypotenuusa}}=\frac{a}{c}\] \[\cos(\alpha)=\frac{\text{kulman viereinen kateetti}}{\text{hypotenuusa}}=\frac{b}{c}\] \[\tan(\alpha)=\frac{\text{kulman vastainen kateetti}}{\text{kulman viereinen kateetti}}=\frac{a}{b}\]

Esimerkki 2.2.1

# trig-geo

Kokeile laskea eri kulmien sini, kosini ja tangentti sekä sivujen suhteet vasemmalla olevassa cas-ikkunassa. Voit syöttää uuden komennon napauttamalla hiirellä rivinumeron 3 vieressä. Voit käyttää kuvassa näkyviä muuttujien nimiä. Kokeile myös raahata kolmion kärkipisteitä ja tutki, miten lukuarvot muuttuvat.

Muutama ohje cas-laskimen käyttöön:

Jos haluat laskea kuvan $\gamma$-kulman sinin, kirjoita riville suoraan $\sin(\gamma)$.
Kreikkalaiset kirjaimet saat näppäimistöltä:
- Alt + a = $\alpha$
- Alt + b = $\beta$
- Alt + g = $\gamma$
Jos laskin antaa vastauksen, kirjoita komento Lukuarvona($n)]{.red}, missä korvaat n-kirjaimen sen rivin numerolla, jonka likiarvon haluat näkyviin. Voit myös kirjoittaa suoraan [Lukuarvona($()$).
Kokeile ensin laskea jonkin kulman sini ja sen jälkeen muuttaa pisteiden paikkaa kuvaajassa. Mitä sinin arvolle tapahtuu?