Kolmioiden geometriaa: tehtävät

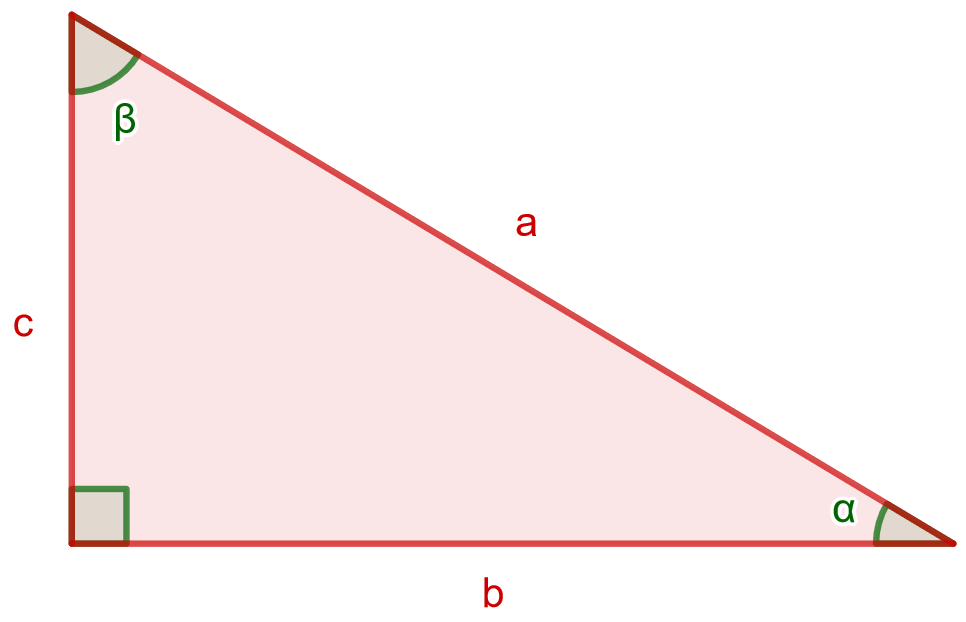
Kolmion rakenne

Kolmion pinta-ala

# kolmion_ala1

Kolmion kannan pituus on \(a=4\) ja korkeus on \(h=6\). Mikä on kolmion pinta-ala \(A\)?

<=> A=

 
# kolmion_ala2

Kolmion kannan pituus on \(a=6\) ja pinta-ala on \(A=19\). Mikä on kolmion korkeus \(h\)?

<=> h=

 
# kolmion_ala3

Kolmion korkeus on \(h=8\) ja pinta-ala on \(A=11\). Mikä on kolmion kannan pituus \(a\)?

<=> a=

 
# teht_kolmion_ala2

Tehtävä

MathCheck laskee kulmia aina radiaaneina. Jos haluat kirjoittaa sin(60°), sinun on kirjoitettava sen sijaan sin(60 * pi/180).

# kolmion_ala4

Kolmion kahden sivun pituudet ovat \(a=8\) ja \(b=3\), ja niiden välinen kulma on \(\alpha=^{\circ}\). Mikä on kolmion pinta-ala \(A\)?

<=> A=

 
# teht_kolmion_ala3

Tehtävä

Kolmion kantasivun pituus on \(2 \sqrt{2}\) ja kolmion korkeus on \(\sqrt{2}\). Laske kolmion pinta-ala.

# kolmion_ala

Pinta-alan tarkka avo

=

 
# teht_tasasivuinen_ala

Tehtävä

Tasasivuisen kolmion sivun pituus on 3. Mikä on kolmion pinta-ala?

# tasasivuisen_kolmion_ala

Pinta-alan tarkka avo

=

 
# teht_lampi

Tehtävä

Maastossa olevan lammen pinta-ala on \(2,8 \text{ ha}\). Maastosta piirretään kartta, jonka mittakaava on \(1 : 20 \, 000\). Mikä on lammen pinta-ala kartalla?

# pintaala1

Lammen pinta-ala neliösentteinä yhden desimaalin tarkkuudella (ilman yksikköä)

=

 
# teht_pelto

Tehtävä

Kartan mittakaava on \(1 : 15 \, 000\). Kartalla olevan pellon pinta-ala on \(25 \text{ cm}^2\). Mikä on pellon pinta-ala hehtaareissa?

# pintaala2

Pellon pinta-ala hehtaareina yhden hehtaarin tarkkuudella (ilman yksikköä)

=

 
# teht_suorakulmainen_kolmio

Tehtävä

Kahden suorakulmaisen kolmion mittakaava on \(2 : 5\). Suuremman kolmion kannat ovat pituudeltaan \(8\) ja \(13\). Määritä pienemmän kolmion pinta-ala.

# pintaala3

Pienemmän kolmion pinta-ala kahden desimaalin tarkkuudella

=

 
# teht_kolmion_jako

Tehtävä

Kolmio \(ABC\) leikataan kahteen osaan kannan \(AB\) suuntaisella suoralla \(PQ\) siten, että \(AP:PC=2:3\). Missä suhteessa suora jakaa kolmion alan?

 
 
# pintaala4

Suhde jakolaskuna (esimerkiksi suhde \(3:4\) kirjoitetaan 3/4)

=

 

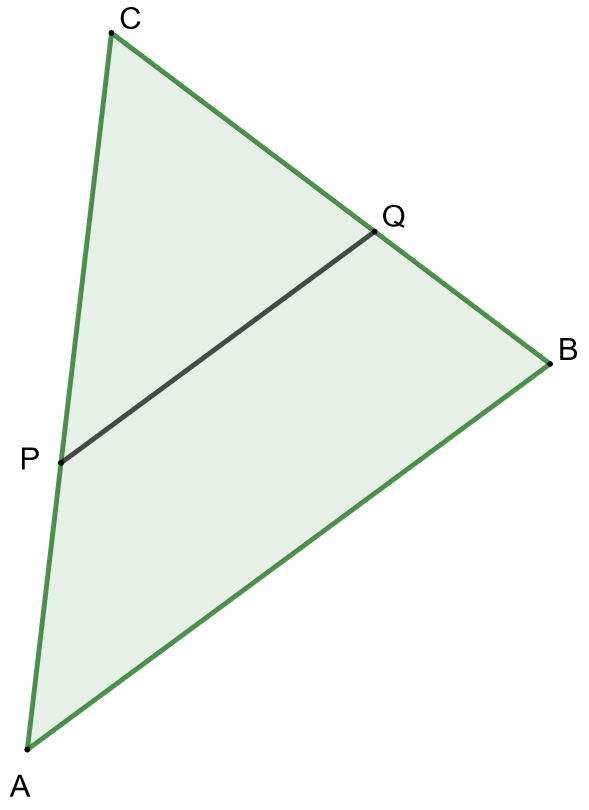
Vinkki

Osoita ensin, että kolmiot \(ABC\) ja \(CPQ\) ovat yhdenmuotoisia, minkä jälkeen voit ratkaista yhdenmuotoisuussuhteen.

Suorakulmainen kolmio ja Pythagoraan lause

# pythagoras1

Jos suorakulmaisen kolmion kateettien pituudet ovat \(6\) ja \(9\), kuinka pitkä on kolmion hypotenuusa?

=

 
# teht_S11T1b

Tehtävä (S2011/1b)

Suorakulmaisen kolmion hypotenuusan pituus on \(5\) ja toisen kateetin pituus \(2\). Laske toisen kateetin pituus.

# pythagoras2 
=

 
# teht_geogebra_puu

Tehtävä

Seitsemän metriä korkea puu kasvaa kohtisuoraan maan pintaa vastaan. Puu taittuu kahden metrin korkeudelta niin, että puun latvaosa osuu maahan. Latva ja tyviosa eivät irtoa toisistaan. Piirrä tilanteesta mallikuva oikeanpuoleiselle piirtoalueelle (ei vaikuta tehtävän pisteytykseen) ja laske vasemmanpuoleiselle CAS-alueelle, kuinka suuri kulma on maanpinnan ja taittuneen latvan välillä.

Anna vastaus vasemmanpuoleisella CAS-alueella tallentamalla se muuttujaan nimeltä v. Pyöristä vastaus kokonaislukujen tarkkuudelle käyttämällä komentoa round.

# puu-kaatuu
Avaa GeoGebra tuomalla osoitin tähän

 

Vinkki GeoGebran käyttöön

  • Tekstin lisääminen

Monesti on hyödyllistä lisätä tehtävän ratkaisuun tekstiä, jossa selität, miten teit tehtävän. Valitse CAS-alueen oikeassa yläkulmassa oleva valikko ja valitse sieltä teksti . Nyt voit kirjoittaa tavallista tekstiä niin pitkään, kunnes painat enteriä ja teksti tallentuu.

  • Muuttujan tallentaminen

Joskus on hyödyllistä tallentaa lukuarvo tai vastaus muuttujaan. Tällöin lukuarvon käyttäminen myöhemmin on kätevää. Jos haluat sijoittaa muuttujaan a arvon 4, kirjoita komento a := 4. Jos myöhemmin haluat laskea laskun \(5a\), kirjoita komento 5*a, jolloin saat vastaukseksi 20.

  • Yhtälön ratkaiseminen

Jos haluat ratkaista muuttujan \(a\) yhtälöstä \(a^2+3a-4=0\), syötä CAS-laskimeen komento Ratkaisut(a^2+3a-4,a). Vastaukseksi saat listan {-4,1}. Helpoiten ratkaisuihin pääsee käsiksi, kun tallentaa ne muuttujaan: vastaukset := Ratkaisut(a^2+3a-4,a). Tällöin komento vastaukset(1) tuottaa luvun -4, ja komento vastaukset(2) tuottaa luvun 1.

  • Lukuarvon näyttäminen

Joskus GeoGebra näyttää vastauksen hyvinkin monimutkaisessa muodossa. Käytä tällöin komentoa Lukuarvona(). Jos kirjoitat esimerkiksi komennon a:=sin^(-1)(1/2), GeoGebra tulostaa vastaukseksi saman eli a:=sin^(-1)(1/2). Jos haluat vastauksen lukuarvona, kirjoita komento Lukuarvona(a), jolloin GeoGebra tulostaa 60°.

Tehtävä

Suorakulmaisessa kolmiossa \(ABC\) kateetin \(AB\) pituus on \(4,4\) cm ja hypotenuusan \(AC\) pituus \(8,14\) cm.

  1. Laske kateetin \(BC\) pituus
# suorakulmaisenkateetinpituus

Anna vastauksesi senttimetrin kymmenesosan tarkkuudella ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 
  1. Laske kolmion pinta‐ala \(0,1\) neliösenttimetrin tarkkuudella. [4/K15]
# suorakulmaisenpinta-ala

Anna vastauksesi ilman yksikköä.

Avaa tehtävä viemällä kursori tähän

 

Tehtävä

Suorakulmaisen kolmion kummankin kateetin pituus on 5. Sen sisään on piirretty neliö kahdella eri tavalla kuvioiden mukaisesti. Kumman neliön pinta-ala on suurempi? [10/S14]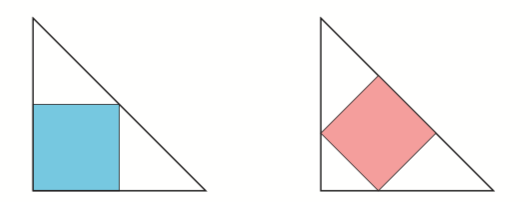

# punainensininennelio

+ question

Käänteinen Pythagoraan lause

# teht_onko_suorakulmainen1

Tehtävä

Kolmion sivujen pituudet ovat \(3\), \(5\) ja \(6\). Onko kolmio suorakulmainen?

# kaantpyhtagoras2

Open plugin
# teht_onko_suorakulmainen2

Tehtävä

Kolmion sivujen pituudet ovat \(3 \sqrt{2}\), \(4 \sqrt{2}\) ja \(5 \sqrt{2}\). Onko kolmio suorakulmainen?

# kaantpythagoras3

Open plugin

Trigonometriset funktiot

# teht_trig1

Tehtävä

Tehtävien 3.2.1-3.2.6 merkinnät vastaavat alla olevan kolmion merkintöjä.

 
 
# trig1

Jos \(a=1\), \(b=5\) ja \(c=9\), mitä on \(\sin\alpha\)?

=

 
# teht_trig2

Tehtävä

# trig2

Jos \(a=10\), \(b=10\) ja \(c=10\), mitä on \(\cos\alpha\)?

=

 
# teht_trig3

Tehtävä

# trig3

Jos \(a=1\), \(b=5\) ja \(c=8\), mitä on \(\cos\alpha\)?

=

 
# teht_trig3

Tehtävä

# trig6

Jos \(a=9\), \(b=3\) ja \(c=4\), mitä on \(\tan\alpha\)?

=

 
# teht_trig4

Tehtävä

# trig5

Jos \(a=2\), \(b=7\) ja \(c=3\), mitä on \(\sin\beta\)?

=

 
# teht_trig3

Tehtävä

# trig4

Jos \(a=5\), \(b=2\) ja \(c=4\), mitä on \(\tan\alpha\)?

=

 
# teht_sin18

Tehtävä

Määritä lausekkeen \(\sin(18^{\circ})\) tarkka arvo käyttämällä alla olevaa tasakylkistä kolmiota.

# geo_sin18
Avaa GeoGebra tuomalla osoitin tähän

 

Vinkki 1

Ratkaise alkuperäisen kolmion kolmannen sivun pituus.

Vinkki 2

Lisää valinta kohtaan "vihje 1". Millainen kolmio muodostuu mustan janan oikealle puolelle? Voiko sitä verrata alkuperäiseen kolmioon? Saatko ratkaistua mustan janan pituuden?

Vinkki 3

Pidä edelleen valinta kohdassa "Vihje 1". Mustan janan oikealle puolelle muodostuu kolmio, joka on yhdenmuotoinen alkuperäisen kolmion kanssa (perustele tämä kulmien suuruuksien avulla). Käytä verrantoa ratkaistaksesi kolmion kolmannen sivun (ja samalla mustan janan) pituus.

Vinkki 4

Lisää valinta kohtaan "Vihje 2" ja huomaa, että \(\frac{36^{\circ}}{2}=18^{\circ}\).

# sin18

\(\sin (18^{\circ})\)

=

 

These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.