3. Toisen asteen polynomifunktio- ja yhtälö: tehtäviä

3.1 Toisen asteen polynomifunktio

3.1.1 Tehtävä

3.1.2 Tehtävä

3.1.3 Tehtävä

Funktion lauseke	Nollakohdat


	$x=-4\;\text{ja}\;x=-1$
	$x=-4\;\text{ja}\;x=-1$
	$\text{ei ole}$
	$\text{ei ole}$

Yhdistä funktiot oikeisiin kuvaajiin ilman teknisiä apuvälineitä. Tehtävästä saa pisteet, kun funktion nimen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

# MAA5_1a

3.1.4 Tehtävä

# t31444

3.1.5 Tehtävä

Pesäpallopelissä lukkari syöttää pallon suoraan ylöspäin. Kuvaajassa on esitetty pallon etäisyys maasta metreinä ajan funktiona.

# Plugin2

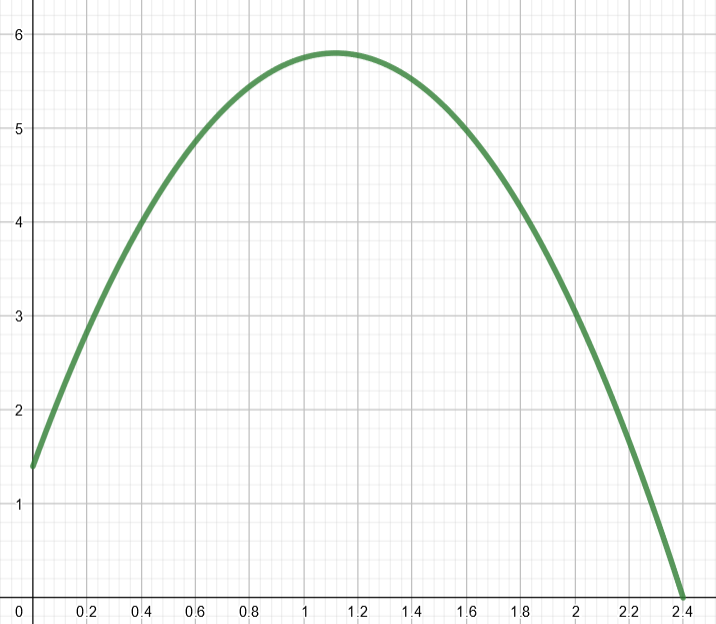
3.1.6 Tehtävä

Piirrä paraabeli f(x)=-x^2+2x+3 oheisella GeoGebralla tai muulla sopivalla ohjelmalla. Määritä funktion kuvaajan perusteella

GeoGebra

Geogebra

# p315a

# p315b

c) paraabelin huipun koordinaatit

# huippux

# huippuy

3.1.7 Tehtävä

Sovita GeoGebralla toisen asteen polynomifunktio, joka kulkee pisteiden A=(0,10), B=(15,28) ja C=(30,10) kautta. Käytä komentoa SovitaPolynomi.

# funktio

3.1.8 Tehtävä

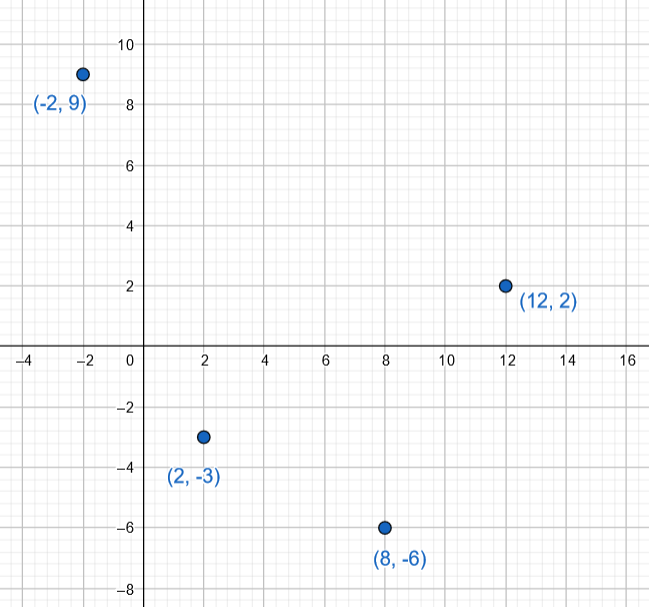
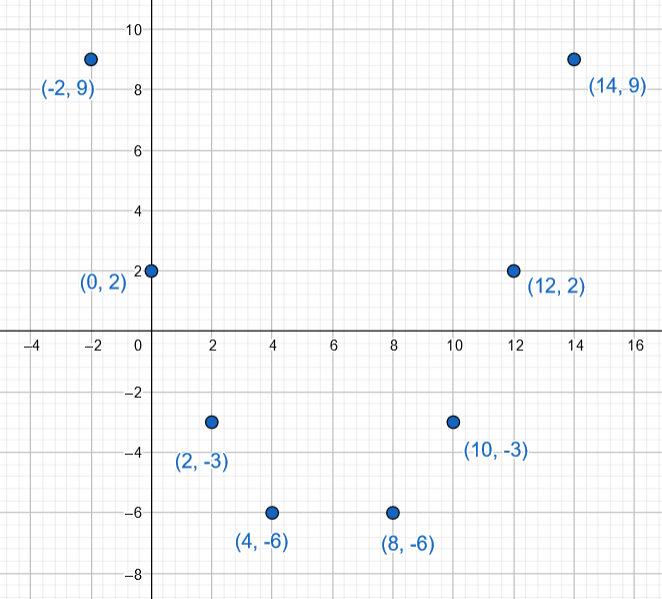
Toisen asteen polynomifunktiosta tiedetään, että se saa alla olevan taulukon mukaisia arvoja. Täydennä taulukkoon puuttuvat funktion arvot kuvaajan symmetrisyyttä hyödyntäen. Taulukossa ei ole automaattitarkistusta.

# taulukko4

Open plugin

Vihje

Pisteiden piirtäminen koordinaatistoon voi auttaa hahmottamisessa.

Ratkaisu

# p318

3.2 Toisen asteen yhtälö

3.2.1 Tehtävä

Poimi taulukkoon toisen asteen yhtälön ax^2+bx+c=0 kertoimet ja . Tehtävässä ei ole automaattitarkistusta.

# taulukko1

Open plugin

Ratkaise tehtävät 3.2.2-3.2.7 ilman laskinta. Hahmottele ratkaisusi paperille tai käytä tehtävien alta löytyvää Abitti-editoria. Jos yhtälöllä on kaksi ratkaisua, kirjoita ratkaisu muodossa x= or x=. Jos yhtälöllä ei ole ratkaisua, vastaa FF.

3.2.2 Tehtävä

Ratkaise täydelliset toisen asteen yhtälöt.

# p322a

# p322b

3.2.3 Tehtävä

Ratkaise vaillinaiset toisen asteen yhtälöt.

# p323a

# p323b

3.2.4 Tehtävä

Ratkaise vaillinaiset toisen asteen yhtälöt.

# p324a

# p324b

3.2.5 Tehtävä

Ratkaise toisen asteen yhtälöt.

# p325a

# p325b

3.2.6 Tehtävä

Ratkaise toisen asteen yhtälöt. Kerro tai jaa yhtälön molemmat puolet ensin sopivalla luvulla.

# p326a

# p326b

3.2.7 Tehtävä

# Plugin1

# p329a

3.2.8 Tehtävä

# p328

3.2.9 Tehtävä (s2014/3a)

# p326

3.2.10 Tehtävä

Paraabelin hahmottelemiseksi ilman laskinta riittää piirtää kuvaaja, jossa näkyy

paraabelin aukeamissuunta
nollakohdat.

Laske nollakohdat ja hahmottele funktion

kuvaaja ilman laskinta alla olevaan koordinaatistoon. Alareunan Undo-napista saat peruttua viimeisimmän piirron ja Reset-napista saat aloitettua kuvaajan piirron alusta.

# p314

3.2.11 Tehtävä

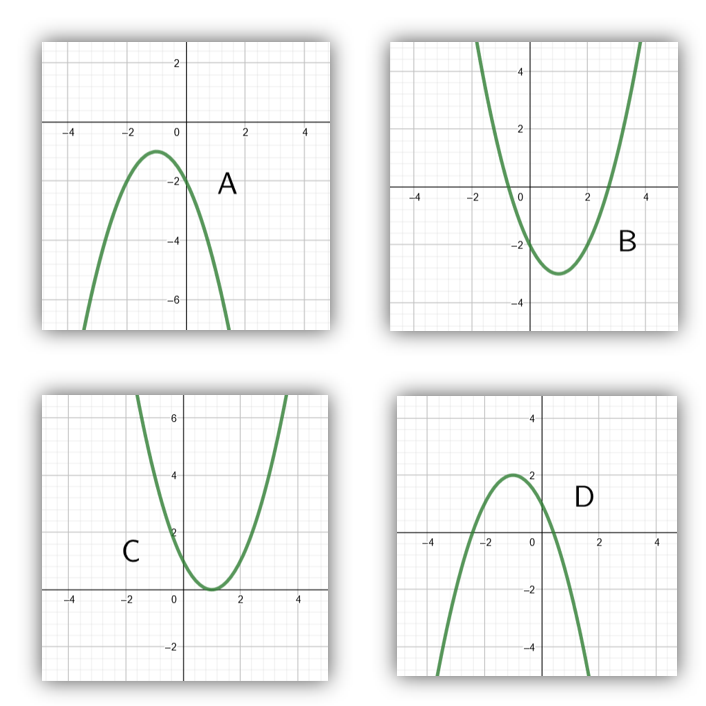
Yllä on näkyvissä toisen asteen polynomifunktioiden kuvaajia. Päättele kuvaajan avulla funktion nollakohtien lukumäärä. Päättele myös, onko yhtälön diskriminantti positiivinen, negatiivinen vai nolla, ja täydennä nämä tiedot taulukkoon. Tehtävässä ei ole automaattitarkistusta.

# taulukko2

Open plugin

3.2.12 Tehtävä

# p327

3.2.13 Tehtävä

Kahden peräkkäisen kokonaisluvun tulo on 1260 . Mitkä ovat nämä luvut?

# p3213a

# p3213b

3.3 Toisen asteen polynomifunktio matemaattisena mallina

3.3.1 Tehtävä

Auton pysähtymismatka koostuu reaktiomatkasta ja jarrutusmatkasta. Reaktiomatkaksi sanotaan aikaa, jonka auto kulkee ennen kuin kuljettaja aloittaa jarrutuksen. Erään auton pysähtymismatka metreinä märällä tiellä noudattaa yhtälöä s=0,0046v^2+0,42v .

Auton kuljettaja näkee tiellä metrin päässä hirven.

# p331

3.3.2 Tehtävä

Vapaassa pudotuksessa pudottu matka metreinä on ajan funktio s(t)=4,91t^2, jossa on putoamisesta kulunut aika sekuntteina.

Linnanmäen huvipuiston korkein laite on vapaapudotustorni Kingi, joka on metriä korkea. Oletetaan, että Kingi putoaa koko matkan noudattaen yllä olevaa ajan funktiota.

# lintsia

# lintsib

3.3.3 Tehtävä

Uudelle asuinalueelle kaavoitetaan suorakulmion muotoisia tontteja. Halutaan, että tontin pituus on $25\;\text{m}$ suurempi kuin sen leveys. Merkitään tontin leveyttä kirjaimella .

# p333a

# p333b

# 333c

3.3.4 Tehtävä: muokkaaaa

Pariisissa sijaitsevan Eiffel-tornin kaari on likimain paraabelin muotoinen. Säädä GeoGebra-appletissa toisen asteen polynomifunktion kertoimia niin, että saat selville, mitä paraabelia Eiffel-tornin kaari noudattaa.

Tehtävässä ei ole automaattitarkistusta, joten siitä ei myöskään tule pisteitä.

# eiffel

3.3.5 Tehtävä

San Fransiscossa sijaitsevan Golden Gate -sillan riippuköysi on paraabelin muotoinen. Köyden korkeutta metreinä merenpinnasta kahden pylonin välissä kuvaa likimain yhtälö y=0,00038x^2-0,48x+230 , missä on etäisyys vaakasuunnassa ensimmäiseen pyloniin. Pyloni tarkoittaa kannatinpylvästä, johon siltaa kannattavat köydet tukeutuvat.

Vastaa jokaiseen kohtaan kymmenen metrin tarkkuudella.

# gatea

# gateb

# gatec

3.3.6 Tehtävä

Iglun leikkaus sivusta päin noudattaa likimain funktion f(x)=-0,54x^2+1,86 kuvaajan ja akselin rajaamaa aluetta.

# 335a

md:a\) Laske mahtuisiko $160\;\text{cm}$ pitkä eskimo seisomaan suorana $0,8$ metrin päässä iglun keskikohdasta.

Open plugin

# iglub

3.3.7 Tehtävä

Markus myy Berliinissä pretzeleitä turisteille. Jos pretzeleiden myyntihinta on $3\;\text{€/kpl}$ , Markus myy niitä päivässä $70\;\text{kpl}$ . Hinnan nostaminen sentillä vähentää myytyjen pretzeleiden lukumäärää neljällätoista.

# 336a

a\) Kannattaako Markuksen nostaa vai laskea myyntihintaa?

Open plugin

# 336b

Vihje

Esimerkki 3.3.2

3.3.8 Tehtävä

Kultaisessa leikkauksessa jana jaetaan kahteen osaan niin, että lyhyemmän osan suhde pidempään osaan on sama kuin pidemmän osan suhde koko janaan. Kultaista leikkausta noudattavat pituudet ja muodot koetaan usein esteettisesti miellyttävänä. Tämän takia kultaista leikkausta on Antiikin ajoista lähtien paljon taiteessa ja arkkitehtuurissa.

Jotta ihmiskeho hipoisi täydellisyyttä, pitäisi navan jakaa vartalo pituussuunnassa kultaisen leikkauksen suhteessa. Antiikin kreikkalainen veistos Milon Venus edustaa tällaista ihmiskehoa. Mitkä ovat veistoksen "kultaiset mitat", kun patsaan korkeus on 2,03 metriä? Vastaa sentin tarkkuudella.

# 337a

# 337b

Vihje

Merkitään pitempää osaa muuttujalla , jolloin lyhyempi osa on 203-x .

Lyhyemmän osan suhde pitempään: $\dfrac{203-x}{x}$

Pidemmän osan suhde koko janaan: $\dfrac{x}{203}$

Nyt siis pätee yhtälö $\dfrac{203-x}{x}=\dfrac{x}{203}$ .

Sieventämällä ja ratkaisemalla toisen asteen yhtälö saadaan vastaus $\dots$

3.3.9 Tehtävä (yo s2017/6)

Suomalaisen liigajoukkueen johto pohtii vuotuisen päätapahtumansa lippujen hinnoittelua. Aikaisempien vuosien perusteella he arvioivat, että katsojia tulee 3000, jos lipun hinta on euroa. Jokaista yhden euron hinnankorotusta kohti katsojien määrä vähenee sadalla, ja vastaavasti yhden euron hinnanalennuksesta katsojamäärä kasvaa sadalla.

# 339a

# 339b