3. Toisen asteen polynomifunktio ja -yhtälö

3.1 Toisen asteen polynomifunktio

Toisen asteen polynomifunktio

Toisen asteen polynomifunktio on muotoa

f(x)=ax^2+bx+c,

missä ja ovat reaalilukuja ja $a\neq0$ .

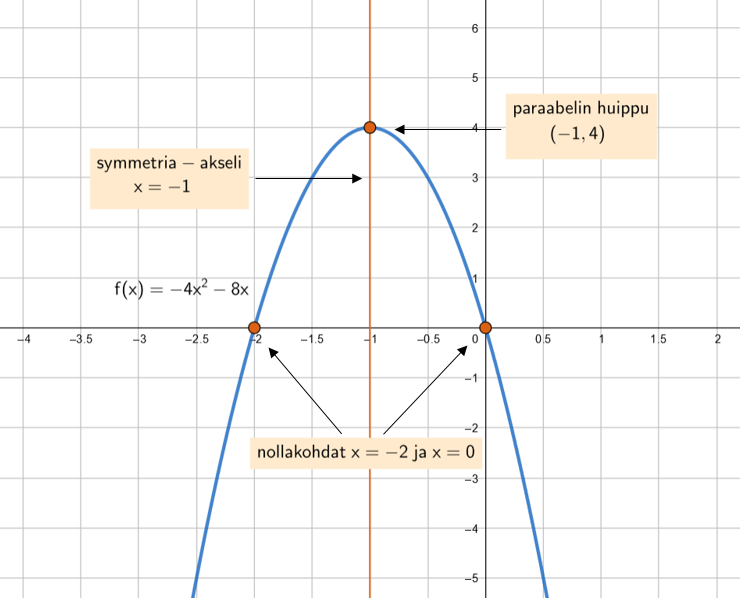
Toisen asteen polynomifunktion kuvaaja on nimeltään paraabeli. Paraabelin kaikken kaarevinta kohtaa sanotaan huipuksi. Huipun kautta kulkeva akselin suuntainen suora on nimeltään paraabelin akseli. Paraabeli on symmetrinen akselinsa suhteen, joten samalla korkeudella olevat paraabelin pisteet ovat yhtä kaukana paraabelin akselista. Tästä seuraa, että huipun koordinaatti on funktion nollakohtien välissä.

3.1.1 Esimerkki: paraabelin tulkintaa

Määritetään toisen asteen funktion f(x)=-4x^2-8x kuvaajasta funktion nollakohdat, paraabelin huipun koordinaatit ja symmetria-akselin yhtälö.

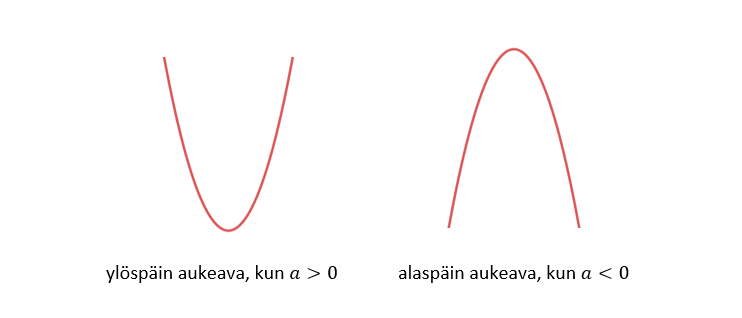
Kerroin määrää paraabelin aukeamissuunnan. Toisen asteen polynomifunktion kuvaaja on

ylöspäin aukeava paraabeli, kun
alaspäin aukeava paraabeli, kun .

3.1.2 Esimerkki: kertoimien vaikutus paraabelin kuvaajaan GeoGebralla

Vaihtele liukusäätimillä kertoimien ja arvoja ja tarkkaile niiden vaikutusta paraabelin f(x)=ax^2+bx+c kuvaajaan. Oikealta saat näkyviin paraabelin huipun ja akselin.

Voidaan tehdä muun muassa seuraavat havainnot:

Paraabeli on sitä kapeampi, mitä suurempi on itseisarvoltaan.
Kun kerroin muuttuu, paraabeli siirtyy pystysuunnassa.
Kerroin vaikuttaa paraabelin sijaintiin sekä vaaka- että pystysuunnassa.
Polynomifunktiolla on tai nollakohtaa.

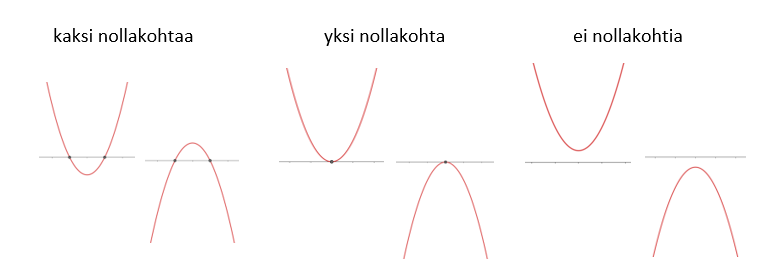
Kuten edellisestä esimerkissä huomattiin, paraabeli voi sijaita koordinaatistossa niin, että paraabelin ja akselin leikkauspisteitä on tai . Toisen asteen polynomifunktiolla on siis joko yksi, kaksi tai ei yhtään nollakohtaa.

3.2 Toisen asteen yhtälö

Kun toisen asteen polynomi ax^2+bx+c merkitään nollaksi, syntyy toisen asteen yhtälö.

Toisen asteen yhtälö

Toisen asteen yhtälö voidaan esittää muodossa

ax^2+bx+c=0,

missä $a\neq0$ .

Toisen asteen yhtälö on vaillinainen, jos b=0 tai c=0 . Muulloin sen sanotaan olevan täydellinen.

	Yleinen muoto	Esimerkki
Täydellinen toisen asteen yhtälö
Vaillinainen toisen asteen yhtälö ()
Vaillinainen toisen asteen yhtälö ()

Vaillinainen toisen asteen yhtälö, jossa

Kun b=0, toisen asteen yhtälö saa muodon ax^2+c=0. Tämän tyyppisen yhtälön eli potenssiyhtälön ratkaiseminen käytiin läpi MAY1-kurssilla. Potenssiyhtälön ratkaisun vaiheet:

Siirretään vakiotermi yhtälön oikealle puolelle.
Jaetaan yhtälö puolittain toisen asteen termin kertoimella.
Ratkaistaan yhtälö neliöjuuren avulla.

3.2.1 Esimerkki: vaillinainen toisen asteen yhtälö

Ratkaise yhtälö.

Ratkaisu:

Potenssiyhtälön ratkaisussa täytyy ensin muokata yhtälö muotoon, jossa toisella puolella on muuttuja ja toisella vakio, ja sen jälkeen ottaa puolittain neliöjuuri. Ratkaisussa pitää huomioida myös negatiivinen juuri.

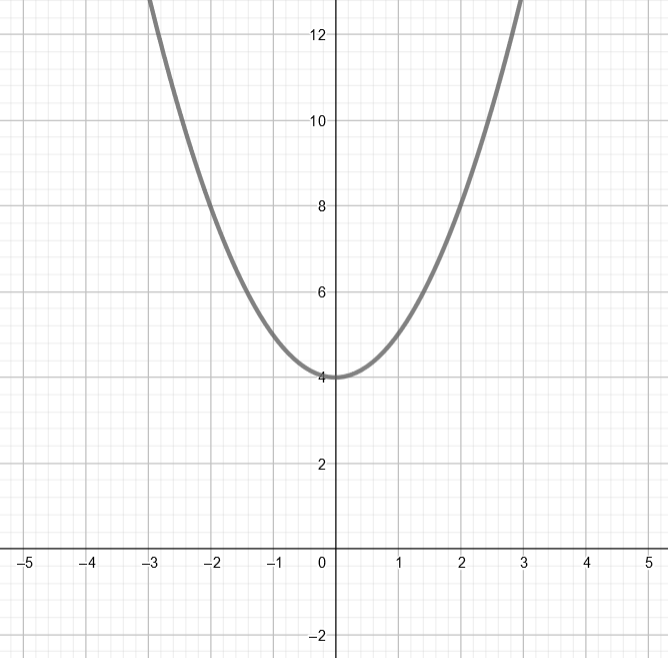
$\begin{align*} 3x^2-27&=0 \\ 3x^2&=27 \\ x^2&=9\;\;\;\;\;\;\;\;\;\;\;\;\;\;|\sqrt{}\\ x&=\pm \sqrt{9} \\ x&=\pm 3 \end{align*}$

$\begin{align*} x^2+4=0 \\ \underbrace{x^2}_{\ge0}=\underbrace{-4}_{<0} \end{align*}$

Koska x^2 ei voi saada negatiivista arvoa, yhtälöllä ei ole ratkaisua. Yhtälön y=x^2+4 kuvaaja ei leikkaa akselia.

Vastaus:

tai
Yhtälöllä ei ole reaalijuuria.

Vaillinainen toisen asteen yhtälö, jossa

Kun c=0, toisen asteen yhtälö saa muodon ax^2+bx=0. Nyt yhtälön vasen puoli voidaan jakaa tekijöihin eli muuttaa tulomuotoon, kun erotetaan tuntematon yhteiseksi tekijäksi.

$ax^2+bx=a\cdot x\cdot \textcolor{red}{x}+b\cdot \textcolor{red}{x}=\textcolor{red}{x}(ax+b)$

Tätä muotoa oleva yhtälö voidaan ratkaista tulon nollasäännön avulla.

Tulon nollasääntö

Tulo on nolla vain silloin, kun jokin sen tekijä on nolla.

Tutkitaan siis, milloin jompikumpi tulon tekijöistä on nolla.

3.2.2 Esimerkki: vaillinainen toisen asteen yhtälö

Ratkaise yhtälö.

Ratkaisu:

Yhtälön vasen puoli on valmiiksi tulomuodossa, joten voidaan suoraan soveltaa tulon nollasääntöä. Tulon tekijöitä ovat (x+3) ja (x-1) . Merkitään ne erikseen yhtä suuriksi kuin nolla.

$\begin{align*} (x+3)(x-1)&=0 \\ x+3=0\;\;&\text{tai}\;\; x-1=0 \\ x=-3 \;\;&\text{tai}\;\; x=1 \end{align*}$

Erotetaan ensin lausekkeesta 2x^2-6x=0 yhteinen tekijä .

$\begin{align*} 2x^2-6x&=0 \\ 2\cdot x\cdot \textcolor{red}x -6\cdot \textcolor{red}x &=0\\ \textcolor{red}x(2x-6)&=0 \\ \end{align*}$

Tulon nollasäännön mukaan

$\begin{align*} x=0\;\;\text{tai}\;\;2x-6&=0 \\ 2x&=-6 \\ x&=-3 \end{align*}$

Vastaus:

Täydellinen toisen asteen yhtälö

Kaikki toisen asteen yhtälöt voidaan ratkaista ratkaisukaavalla.

Toisen asteen yhtälön ratkaisukaava

Toisen asteen yhtälön $ax^2+bx+c=0,\,a\neq0$ ratkaisut ovat

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

on toisen asteen termin kerroin
on ensimmäisen asteen termin kerroin
on vakio

Toisen asteen yhtälön ratkaisun vaiheet:

Sievennetään yhtälö muotoon .
Poimitaan toisen asteen polynomista termien kertoimet ja .
Sijoitetaan kertoimien lukuarvot ratkaisukaavaan ja lasketaan merkityt laskutoimitukset.

3.2.3 Esimerkki: toisen asteen yhtälön ratkaisukaava

Ratkaise yhtälö x^2+2x-8=0 .

Ratkaisu:

Yhtälö on valmiiksi muodossa ax^2+bx+c=0 . Yhtälön kertoimet ovat

$a=\textcolor{red}1,\;b=\textcolor{blue}2\;\text{ja}\;c=\textcolor{green}{-8}$

Sijoitetaan kertoimet ratkaisukaavaan.

$\begin{align*} x&=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ x&=\frac{-\textcolor{blue}2\pm\sqrt{\textcolor{blue}2^2-4\cdot\textcolor{red}1\cdot (\textcolor{green}{-8})}}{\textcolor{blue}2\cdot \textcolor{red}1} \\ x&=\frac{-2\pm\sqrt{4+32}}{4} \\ x&=\frac{-2\pm\sqrt{36}}{4} \\ x&=\frac{-2\pm6}{4} \end{align*}$

Kirjoitetaan vastaus kahtena eri lausekkeena.

$x=\frac{-2-6}{4}=\frac{-8}{4}=-4\;\;\;\;\text{tai}\;\;\;\;\frac{-2+6}{4}=\frac{4}{4}=1$

Vastaus: $x=-4\;\;\text{tai}\;\;x=1$

3.2.4 Esimerkki: toisen asteen yhtälöllä yksi ratkaisu tai ei ratkaisua

Ratkaise funktion nollakohdat ja tarkista graafisesti.

Ratkaisu:

Ratkaistaan funktion nollakohdat toisen asteen yhtälöstä . Yhtälön kertoimet ovat

$a=\textcolor{red}1,\;b=\textcolor{blue}{-2}\;\text{ja}\;c=\textcolor{green}1$

Sijoitetaan kertoimet ratkaisukaavaan.

$\begin{align*} x&=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ x&=\frac{-(\textcolor{blue}{-2})\pm\sqrt{(\textcolor{blue}{-2})^2-4\cdot\textcolor{red}1\cdot\textcolor{green}1}}{2\cdot\textcolor{red}1} \\ x&=\frac{2\pm\sqrt{4-4}}{2} \\ x&=\frac{2\pm\sqrt{0}}{2} \end{align*}$

Koska osoittajan toinen yhteenlaskettava on nolla, yhtälöllä on vain yksi ratkaisu $x=\frac{2}{2}=1$

Piirretään funktion f(x)=x^2-2x+1 kuvaaja.

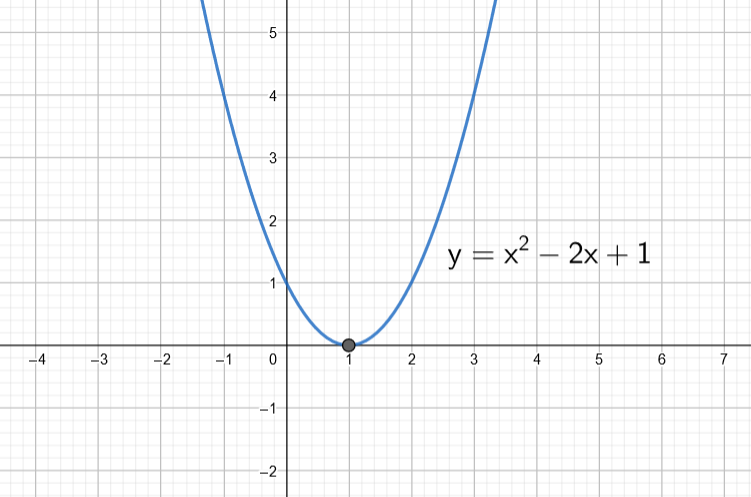
Funktion kuvaaja sivuaa akselia pisteessä x=1.

Ratkaistaan funktion nollakohdat toisen asteen yhtälöstä . Yhtälön kertoimet ovat

$a=\textcolor{red}{-10},\;b=\textcolor{blue}{15}\;\text{ja}\;c=\textcolor{green}{-25}$

Sijoitetaan kertoimet ratkaisukaavaan.

$\begin{align*} x&=\frac{-b\pm\sqrt{b^2-4ac}}{2a} \\ x&=\frac{-(\textcolor{blue}{15})\pm\sqrt{(\textcolor{blue}{15})^2-4\cdot\textcolor{red}{-10}\cdot\textcolor{green}{-25}}}{2\cdot\textcolor{red}{-10}} \\ x&=\frac{-15\pm\sqrt{225-1000}}{-20} \\ x&=\frac{-15\pm\sqrt{-775}}{-20} \end{align*}$

Koska juurrettava on negatiivinen luku, neliöjuurelle $\sqrt{-775}$ ei voida laskea arvoa ja yhtälöllä ei ole ratkaisua.

Piirretään funktion f(x)=-10x^2+15x-25=0 kuvaaja.

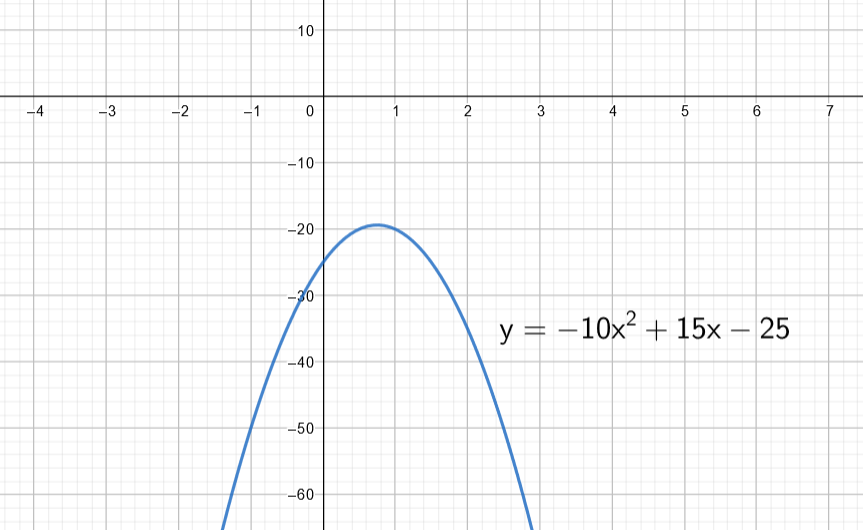
Funktion kuvaaja ei leikkaa akselia.

Vastaus:

Ei ratkaisua

3.2.5 Esimerkki: erilaisia toisen asteen yhtälöitä

Ratkaise yhtälö.

$-\dfrac{1}{3}x^2+\dfrac{1}{3}x=\dfrac{1}{3}x^2-1$

Ratkaisu:

Kerrotaan yhtälön molemmat puolet luvulla jotta saadaan poistettua yhtälöstä nimittäjät, ja muokataan yhtälö normaalimuotoon

$\begin{align*} -\dfrac{1}{3}x^2+\dfrac{1}{3}x&=\dfrac{1}{3}x^2-1 \;\;\;\;\;\;\;|\cdot3 \\ -x^2+x&=x^2-3 \\ -x^2-x^2+x+3&=0 \\ -2x^2+x+3&=0 \end{align*}$

Yhtälön kertoimet ovat

$a=-2,\;b=1\;\text{ja}\;c=3$

Sijoitetaan kertoimet ratkaisukaavaan.

$\begin{align*} x&=\frac{-1\pm\sqrt{1^2-4\cdot(-2)\cdot3}}{2\cdot(-2)} \\ x&=\frac{-1\pm\sqrt{1+25}}{-4} \\ x&=\frac{-1\sqrt{25}}{-4} \\ x&=\frac{-1\pm5}{-4} \\ x&=\frac{-1+5}{-4}=\frac{4}{-4}=-1\;\;\text{tai}\;\;x=\frac{-1-5}{-4}=\frac{-6}{-4}=\frac{3}{2} \end{align*}$

Avataan yhtälöstä sulkeet ja muokataan yhtälö normaalimuotoon.

$\begin{align*} x(x-5)=2 \\ x^2-5x=2 \\ x^2-5x-2=0 \end{align*}$

Yhtälön kertoimet ovat

$a=1,\;b=-5\;\text{ja}\;c=-2$

Sijoitetaan kertoimet ratkaisukaavaan.

$\begin{align*} x&=\frac{5\pm\sqrt{(-5)^2-4\cdot1\cdot(-2)}}{2\cdot1} \\ x&=\frac{5\pm\sqrt{25+8}}{2} \\ x&=\frac{5\pm\sqrt{33}}{2} \end{align*}$

Luku ei ole minkään kokonaisluvun neliö, joten yhtälön ratkaisujen tarkat arvot ovat.

$x=\frac{5-\sqrt{33}}{2}\;\;\text{tai}\;\;x=\frac{5+\sqrt{33}}{2}$

Vastaus:

$x=-1\;\text{tai}\;x=\frac{3}{2}$
$x=\dfrac{5\pm\sqrt{33}}{2}$

Diskriminantti

Täydellisen toisen asteen yhtälön ratkaisukaavassa

$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$

juurimerkin alla olevaa lauseketta sanotaan diskriminantiksi.

Diskriminantti

Diskriminantiksi sanotaan lauseketta

D=b^2-4ac.

Toisen asteen yhtälön reaalijuurten lukumäärän tutkiminen ei edellytä yhtälön ratkaisemista, vaan diskriminantin arvo määrää, kuinka monta juurta toisen asteen yhtälöllä on.

Reaalijuurien määrä

Jos yhtälöllä on kaksi eri juurta.
Jos yhtälöllä on yksi juuri (kaksoisjuuri).
Jos yhtälöllä ei ole juuria.

Alla oleva GeoGebra havainnollistaa diskriminantin vaikutusta juurten määrään ylöspäin aukeavan paraabelin kuvaajalla.

3.2.6 Esimerkki: toisen asteen yhtälön ratkaisujen määrä

Kuinka monta reaalijuurta yhtälöllä on?

Ratkaisu:

Yhtälön kertoimet ovat

$a=6,\;b=-1\;\text{ja}\;c=-5$

Lasketaan diskriminantti.

$\begin{align*} D&=b^2-4ac \\ &=(-1)^2-4\cdot6\cdot(-5) \\ &=1+120=121 \end{align*}$

Koska D>0, niin yhtälöllä on kaksi reaalijuurta.

Muokataan yhtälö normaalimuotoon.

$\begin{align*} x^2&=2x-5 \\ x^2-2x+5&=0 \end{align*}$

Yhtälön kertoimet ovat

$a=1,\;b=-2\;\text{ja}\;c=5$

Lasketaan diskriminantti.

$\begin{align*} D&=b^2-4ac \\ &=(-2)^2-4\cdot1\cdot5 \\ &=4-20=-16 \end{align*}$

Koska D<0, niin yhtälöllä ei ole reaalijuuria.

Vastaus:

kaksi
ei yhtään

3.3 Toisen asteen polynomifunktio matemaattisena mallina

Käytännön tehtävien matemaattinen mallintaminen johtaa joskus toisen asteen yhtälöön. Ratkaisemalla yhtälö saadaan vastaukseksi kaksi, yksi tai ei yhtään arvoa. Jos yhtälöllä ei ole ratkaisua, tarkoittaa se sitä, ettei ongelmallakaan ole ratkaisua. Kahden juuren tapauksessa usein vain positiivnen juuri kelpaa ratkaisuksi.

3.3.1 Esimerkki: lentopallon rata toisen asteen funktiona

Arttu ja Samuli pelaavat rantalentopalloa. Arttu syöttää pallon, jonka korkeutta maan pinnasta metreinä kuvaa funktio h(x)=-0,4x^2+2,2x+1,5 , missä on etäisyys metreinä, jonka pallo on edennyt vaakasuunnassa.

Kuinka korkealla pallo on, kun se on edennyt vaakasuunnassa metriä?
Samulin keskittyminen herpaantuu, eikä hän osu palloon. Kuinka kaukana syöttöpaikasta pallo osuu maahan?

Ratkaisu:

Pallon korkeus saadaan laskemalla funktion arvo, kun .

$h(2)=-0,4\cdot2^2+2,2\cdot2+1,5=4,3\;\;\;\text{(m)}$

Pallo osuu maahan, kun pallon korkeus on .

$\begin{align*} h(x)&=0 \\ -0,4x^2+2,2x+1,5&=0 \\ x&=-0,613...\;\;\text{tai}\;\;x=6,113... && \text{(laskimesta)} \end{align*}$

Etäisyys ei voi olla negatiivinen, joten $x=6,113...\;\text{m}\approx6,1\;\text{m}.$

Vastaus:

$4,3\;\text{m}$
$6,1\;\text{m}$

3.3.2 Esimerkki: makkaran myyntihinnan optimointi

Urheilutapahtumassa myydään kisamakkaroita. Makkaranmyyjä arvioi menekiksi 320 makkaraa, jos makkaran hinta on $1,50\;\text{€}$ . Jokainen sentin korotus hinnassa alentaa menekkiä makkaralla.

Muodosta funktio , joka ilmaisee myynnin kokonaisarvon tilanteessa, jossa makkaran hintaa on nostettu euroa kertaa.
Kuinka suuret ovat myyntitulot, jos makkaran hinta on $1,8\;\text{€}$ ?
Mikä makkaran hinnan pitää olla, jotta myynnin kokonaisarvo on mahdollisimman suuri? Paljon myyntitulot tällöin ovat?

Ratkaisu:

Tutkitaan ensin tilannetta taulukon avulla.

Hinnan korotusten määrä	Makkaran hinta ( $\text{€}$ )	Myydyt makkarat (kpl)	Myyntitulot ( $\text{€}$ )
			$1,50\cdot320$

	$1,50+2\cdot0,05$	$320-2\cdot8$	$(1,50+2\cdot0,05)(320-2\cdot8)$
	$1,50+3\cdot0,05$	$320-3\cdot8$	$(1,50+3\cdot0,05)(320-3\cdot8)$
$\textcolor{red}x$	$1,50+\textcolor{red}x\cdot0,05$	$320-\textcolor{red}x\cdot8$	$(1,50+\textcolor{red}x\cdot0,05)(320-\textcolor{red}x\cdot8)$

Myyntituloa kuvaava funktio on siis

$\begin{align*} T(x)&=(1,50+0,05x)(320-8x) \;\;\;\;\;\;\;\;\text{(sievennetään laskimella)}\\ T(x)&=-0,4x^2+4x+480 \end{align*}$

Jos makkaran hinta on $1,80\;\text{€}$ , niin alkuperäiseen hintaan on lisätty senttiä $\textcolor{red}6$ kertaa. Myyntitulot ovat tällöin

$T(\textcolor{red}6)=-0,4\cdot6^2+4\cdot6+480=489,6\;\text{(€)}$

Piirretään laskimella funktion kuvaaja. Myyntitulot saavat suurimman arvonsa paraabelin huipussa. Selvitetään laskimen avulla huipun koordinaatit. Esimerkiksi GeoGebralla huipun koordinaatit saa Ääriarvot-painikkeesta. Pienennä kuvaajanäkymää niin, että saat paraabelin huipun näkyviin.

Huipun koordinaatti x=5 ja koordinaatti y=490 .

Muuttuja kuvaa viiden sentin hinnankorotusten lukumäärää, joten kisamakkaroita tulisi myydä hintaan

$1,5\;\text{€}+5\cdot0,05\;\text{€}=1,75\;\text{€}.$

Tällöin myyntitulot olisi $490\;\text{€}.$

Vastaus:

$489,60\;\text{€}$
Makkaran hinta: $1,75\;\text{€}$
Myyntitulot: $490\;\text{€}$