4. Lukujonot ja summat: tehtäviä

4.1 Lukujono: tehtäviä

Tämän kappaleen teoria.

4.1.1 Tehtävä

Lukujonon yleinen jäsen on muotoa a_n=6n+5 . Määritä lukujonon neljä ensimmäistä jäsentä.

# p411a

# p411b

# p411c

# p411d

4.1.2 Tehtävä

# Plugin1

4.1.3 Tehtävä

# p412

4.1.4 Tehtävä

Määritä lukujonon seitsemäs jäsen, kun yleinen jäsen on

$a_n=\dfrac{n^2-6n}{3}$

# p414a

$a_n=\dfrac{1}{3}\cdot3^{n-1}$

# p414b

4.1.5 Tehtävä

Appletissa on piirrettynä lukujonon, jonka yleinen jäsen on muotoa $a_n=4\cdot2^{n-1},$ kuvaaja.

# p418a

# p418b

4.1.6 Tehtävä

Päättele lukujonon yleinen jäsen.

$3,\;9,\;27,\;81,\dots$

# p415a

$4,\;-4,\;4,\;-4,\dots$

# p415b

$1,\;3,\;1,\;3,\dots$

# p415c

Rekursiivinen lukujono

Joskus lukujonoon liittyvä sääntö voidaan esittää niin, että sen mukaan seuraava jäsen a_n saadaan laskettua edellisen jäsenen $a_{n-1}$ avulla. Tällaisessa tilanteessa sanotaan, että lukujono on määritelty rekursiivisesti.

Esimerkiksi jos tiedetään, että lukujonon ensimmäinen jäsen on a_1=1 ja että seuraava jäsen saadaan lisäämällä aina edelliseen jäseneen kolme, sääntö voidaan kirjoittaa muodossa:

$\begin{align*} \begin{cases} a_1=1 \\ a_{n}=a_{n-1}+3,\;\text{kun}\;n=2,3,4,\dots \end{cases} \end{align*}$

Rekursioyhtälön avulla voidaan laskea, että

$\begin{align*} a_2&=a_1+3=1+3=\textcolor{red}4 \\ a_3&=a_2+3=\textcolor{red}4+3=\textcolor{blue}7 \\ a_4&=a_3+3=\textcolor{blue}7+3=10 \\ &\dots \end{align*}$

4.1.7 Tehtävä

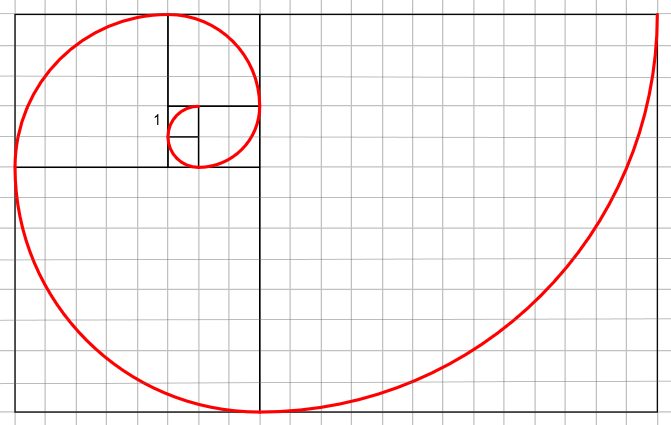
Fibonacci oli italialainen matemaatikko, joka toi arabialaisen lukujärjestelmän keskiajalla Eurooppaan. Fibonacci esitteli 1200- luvulla kuuluisan lukujononsa, joka on muotoa

$\begin{align*} \begin{cases} a_1=1 \\ a_2=1 \\ a_{n}=a_{n-1}+a_{n-2},\;\text{kun}\;n=3,4,5,\dots \end{cases} \end{align*}$

a) Määritä Fibonaccin lukujonon kuusi ensimmäistä jäsentä.

# p417a

# p417b

# p417c

# p417d

# p417

4.2 Aritmeettinen lukujono: tehtäviä

Tämän kappaleen teoria.

4.2.1 Tehtävä

Tarkastele aritmeettista lukujonoa $1,\;5,\;9,\;13,\;17,\dots$

# p421a

# p421b

# p421c

# p421d

4.2.2 Tehtävä

# p421

4.2.3 Tehtävä

Muodosta ja sievennä aritmeettisen jonon yleinen jäsen a_n, kun

jonon ensimmäinen jäsen ja differenssi

# p424a

# p424b

4.2.4 Tehtävä

# p424

Vihje

Muodostetaan yleisen jäsenen lauseke niiden tietojen perusteella, että a_1=-1000 ja d=3 . Sen jälkeen ratkaistaan yhtälö a_n=-520 .

4.2.5 Tehtävä

Valitse aritmeettisen lukujonon kuvaajaa vastaava lukujonon yleinen jäsen a_n .

# p425a

a) \ ![](/images/193152/Screenshot_375.png){width=350}

Open plugin

# p425b

b) \ ![](/images/193160/Screenshot_377.png){width=400}

Open plugin

4.2.6 Tehtävä

Sannalla on Instagramissa 354 seuraajaa. Seuraavan kuukauden ajan Sanna saa joka päivä uutta seuraajaa.

a) Muodosta ja sievennä seuraajien määrää kuvaavan lukujonon yleinen jäsen a_n, jossa on päivämäärän numero.

# p422a

# p422b

4.2.7 Tehtävä

Inkeri avaa ASP-tilin (lyh. sanoista asuntosäästöpalkkio) ja laittaa sinne vuoden alussa 450 euroa. Inkeri tallettaa tilille joka kuukausi 150 euroa. ASP-tilille on säästettävä vähintään $10\;\%$ asunnon hankintahinnasta, minkä jälkeen pankki voi myöntää lainan.

# p423

4.3 Aritmeettinen summa: tehtäviä

Tämän kappaleen teoria.

4.3.1 Tehtävä

Laske aritmeettisen lukujonon viidentoista ensimmäisen jäsenen summa, kun

# p431a

# p431b

4.3.2 Tehtävä

Laske aritmeettisen summan arvo ilman laskinta summakaavan avulla.

# p432a

# p432b

4.3.3 Tehtävä

# p433

4.3.4 Tehtävä

Perinteinen korttitalo rakentuu niin, että ylimmällä kerroksella on korttia ja korttien määrä lisääntyy aina kolmella per rivi alaspäin mentäessä.

# p434

4.3.5 Tehtävä

Oheinen kuviojono muodostuu niin, että kuvioon tulevat osuudet muodostavat aritmeettisen jonon. Ensin kuvion pituus kasvaa kahdella, sen jälkeen neljällä, sen jälkeen kuudella...

# p435

# p435b

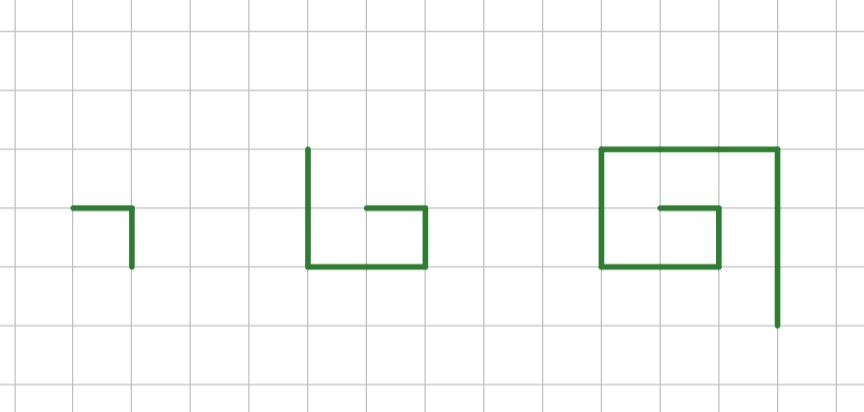
4.3.6 Tehtävä

Valitse summamerkintää vastaava summa.

# p436a

md:a) $$\sum_{i=1}^{4}(5i)$$

Open plugin

# p436b

md:b) $$\sum_{i=1}^{7}(i+3)$$

Open plugin

# p436c

md:c) $$\sum_{i=1}^{5}(-3i+4)$$

Open plugin

4.4 Geometrinen lukujono: tehtäviä

Tämän kappaleen teoria.

4.4.1 Tehtävä

Tarkastele geometristä lukujonoa $\dfrac{1}{4},\;\dfrac{1}{2},\;1,\;2,\;4,\dots$

# p441a

# p441b

# p441c

# p441d

4.4.2 Tehtävä

# p441

4.4.3 Tehtävä

Muodosta geometrisen lukujonon yleinen jäsen a_n, kun

jonon ensimmäinen jäsen ja suhdeluku

# p443a

# p443b

4.4.4 Tehtävä

Geometrisen jonon kolmas jäsen a_3=450 ja jonon suhdeluku q=3.

Mikä on lukujonon toinen jäsen?

# p445a

Mikä on lukujonon ensimmäinen jäsen?

# p445b

Mikä on lukujonon yleinen jäsen?

# p445c

4.4.5 Tehtävä (yo lyhyt s2018/3)

Määritä positiivinen kokonaisluku jolla lukujono $27,\;x,\;3$ on

# t445a

# t445b

Vihje

Aritmeettisessa lukujonossa peräkkäisten jäsenten erotuksen tulee olla vakio, josta saadaan

x-27=3-x

Geometrisessa lukujonossa peräkkäisten jäsenten suhteen tulee olla vakio, josta saadaan

$\dfrac{3}{x}=\frac{x}{27}$

4.4.6 Tehtävä

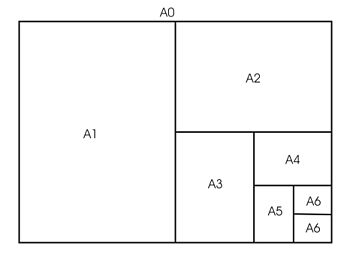
Paperiarkkien $A0,\;A1,\;A2,\;A3$ jne. pinta-alat muodostavat geometrisen jonon. Peruskoko A0- arkin pinta-alaksi on valittu yksi neliömetri ja seuraavan paperiarkin pinta-ala on aina puolet edellisen arkin pinta-alasta.

# p446

4.4.7 Tehtävä

Peetu aloittaa säästämisen laittamalla tilille $1\;\text{€}$ . Kuvitellaan, että Peetun rahasumma kasvaisi joka päivä korkoa $0,1\;\%$ .

# p444

Vihje

Määritetään tilille kertyvistä rahasummista muodostuvan lukujonon yleinen jäsen.

Lukujonon ensimmäinen jäsen on $a_1=1,00\;(\text{€})$ . Koska rahasumma kasvaa joka päivä $0,1\;\%,$ kasvua kuvaava prosenttikerroin on $100\;\%+0,1\;\%=100,1\;\%=1,001$

Seuraavan päivän rahasumma saadaan, kun edellinen kerrotaan kertoimella 1,001 . Tilille kertyvistä rahasummista muodostuu siis geometrinen jono, jonka suhdeluku q=1,001 .

Kun lukujonon yleinen jäsen on saatu muodostettua, täytyy selvittää, kuinka monen päivän jälkeen $a_n>1\;000\;000\dots$

4.5 Geometrinen summa: tehtäviä

Tämän kappaleen teoria.

4.5.1 Tehtävä

Laske geometrisen lukujonon kymmenen ensimmäisen jäsenen summa, kun

# p451a

# p451b

4.5.2 Tehtävä

Tarkastele geometrista summaa $5+15+45+\dots+3645+10935$ .

# p456a

# p456b

4.5.3 Tehtävä

Laske geometrisen summan arvo summakaavan avulla.

# p452b

# p452a

4.5.4 Tehtävä

# p454

4.5.5 Tehtävä

Pyramidi koostuu kerroksesta. Pyramidin pohjimmainen kerros muodostuu 6400 kivilohkareesta. Jokainen kerros sisältää $22\;\%$ vähemmän kivilohkareita kuin edellinen. Kuinka monta kappaletta kivilohkareita koko pyramidi sisältää?

# p453

4.5.6 Tehtävä (yo lyhyt k2014/8)

Pyramidihuijari avaa pankkitilin ja siirtää ensimmäisessä vaiheessa tilille $100\;\text{€}$ . Tämän jälkeen hän houkuttelee mukaan kolme sijoittajaa, joista jokainen siirtää toisessa vaiheessa huijarin tilille $100\;\text{€}$ . Kolmannessa vaiheessa kukin näistä kolmesta houkuttelee edelleen mukaan kolme uutta sijoittajaa, joista jokainen siirtää $100\;\text{€}$ huijarin tilille. Huijaus jatkuu saman kaavan mukaisesti.

# p455

Vihje

Ensimmäisen vaiheen jälkeen rahaa tilillä: $100\;\text{(€)}$

Toisen vaiheen jälkeen rahaa tilillä : $100+3\cdot100$

Kolmannen vaiheen jälkeen rahaa tilillä: $100+3\cdot100+3\cdot3\cdot100$

Neljännen vaiheen jälkeen rahaa tilillä: $100+3\cdot100+3^2\cdot100+3^3\cdot100$

Tilille kertyvä rahasumma muodostaa geometrisen summan. Vastaavan lukujonon ensimmäinen jäsen a_1=100 ja suhdeluku q=3 . Rahaa on tilillä vaiheen jälkeen

$S_n=100\cdot\frac{1-3^n}{1-3}=50(3^n-1)$

Halutaan selvittää milloin S_n ylittää talousarvion $\dots$