4. Lukujonot ja summat

4.1 Lukujono

Tietyssä järjestyksessä olevien lukujen luetteloa kutsutaan lukujonoksi. Lukujono voi olla päättyvä eli äärellinen, jolloin sen pituus on rajattu. Lukujono voi myös olla päättymätön eli ääretön, jolloin siinä ei ole viimeistä lukua ja jono jatkaa loputtomasti. Kolme pistettä lukujonon perässä kuvaa sitä, että lukujono ei pääty.

$\begin{align*} &1,\;3,\;5,\;7,\;9&&\text{päättyvä lukujono, jossa on viisi lukua} \\ &1,\;0,\;1,\;0,\;1,\;0\dots&&\text{päättymätön lukujono} \end{align*}$

Lukujonon lukuja kutsutaan jonon jäseniksi tai termeiksi. Esimerkiksi ensimmäisen lukujonon toinen jäsen on ja viides termi .

Lukujonosta on helpompi puhua, jos sille annetaan nimi. Lukujonon nimi voi esimerkiksi (a_n), (b_n) tai (x_n) . Tässä sulut ilmoittavat, että kyseessä on koko lukujono eikä vain sen yksittäinen jäsen. Jos lukujono on nimetty esimerkiksi (a_n), tarkoittaa a_1 sen ensimmäistä jäsentä, a_2 sen toista jäsentä ja niin edelleen. Alaindeksi siis kertoo, kuinka mones jonon jäsen on kyseessä.

4.1.1 Esimerkki: lukujono

Tarkastele lukujonoa, joka alkaa $3,\;6,\;9,\;12,\;15\dots$ ja määritä

Ratkaisu:

on jonon neljäs jäsen eli .
Jonossa seuraava jäsen saadaan aina lisäämällä edelliseen jäseneen luku , joten .
.

Lukujonon jäsenet muodostuvat usein jonkun tietyn säännön mukaan, joka voidaan kirjoittaa lausekkeena, jossa muuttujana on jäsenen järjestysnumero. Edellisen esimerkin lukujonon s jäsen eli yleinen jäsen on $a_n=3n,\;n=1,\,2,\,3\dots$

4.1.2 Esimerkki: lukujonon jäsenen määrittäminen

Määritä lukujonon neljä ensimmäistä jäsentä, kun jonon yleinen jäsen on muotoa

Ratkaisu:

Jonon neljä ensimmäistä jäsentä saadaan sijoittamalla ja lausekkeeseen .

a_{\textcolor{red}1}=5\cdot\textcolor{red}1-1=4

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file 900db679c83beba25e68388491d3e03f08218d85.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}1}=5\cdot\textcolor{r...
No pages of output.
Transcript written on 900db679c83beba25e68388491d3e03f08218d85.log.

a_{\textcolor{red}2}=5\cdot\textcolor{red}2-1=9

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file baa65ecc4a67eabf5ce299efdad31fe1f1765d63.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}2}=5\cdot\textcolor{r...
No pages of output.
Transcript written on baa65ecc4a67eabf5ce299efdad31fe1f1765d63.log.

a_{\textcolor{red}3}=5\cdot\textcolor{red}3-1=14

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file da88adfe93d1f52ce36ba0789ce47a0b5f3eadcf.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}3}=5\cdot\textcolor{r...
No pages of output.
Transcript written on da88adfe93d1f52ce36ba0789ce47a0b5f3eadcf.log.

a_{\textcolor{red}4}=5\cdot\textcolor{red}4-1=19

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file afcf36bc5fc28d92d1caecd9fd60762d76598a70.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}4}=5\cdot\textcolor{r...
No pages of output.
Transcript written on afcf36bc5fc28d92d1caecd9fd60762d76598a70.log.

Sijoitetaan ja lausekkeeseen .

a_{\textcolor{red}1}=(-1)^{\textcolor{red}1}=-1

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file b57d331f90276880f4a0d5de162d83c49c6124e6.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}1}=(-1)^{\textcolor{r...
No pages of output.
Transcript written on b57d331f90276880f4a0d5de162d83c49c6124e6.log.

a_{\textcolor{red}2}=(-1)^{\textcolor{red}2}=1

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file 51b05a8ce9fd2c08914ff2cf6818f11cf87b9c6b.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}2}=(-1)^{\textcolor{r...
No pages of output.
Transcript written on 51b05a8ce9fd2c08914ff2cf6818f11cf87b9c6b.log.

a_{\textcolor{red}3}=(-1)^{\textcolor{red}3}=-1

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file a915cabfa3aadd99187d9c857e562e06f95c2f53.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}3}=(-1)^{\textcolor{r...
No pages of output.
Transcript written on a915cabfa3aadd99187d9c857e562e06f95c2f53.log.

a_{\textcolor{red}4}=(-1)^{\textcolor{red}4}=1

Latex failed
This is XeTeX, Version 3.141592653-2.6-0.999993 (TeX Live 2022/dev/Debian) (preloaded format=xelatex)
 restricted \write18 enabled.
**entering extended mode
LaTeX2e <2021-11-15> patch level 1
L3 programming layer <2022-01-21>
*(/usr/share/texlive/texmf-dist/tex/latex/base/article.cls
Document Class: article 2021/10/04 v1.4n Standard LaTeX document class
(/usr/share/texlive/texmf-dist/tex/latex/base/size10.clo))
*(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsmath.sty
For additional information on amsmath, use the `?' option.
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amstext.sty
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsgen.sty))
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsbsy.sty)
(/usr/share/texlive/texmf-dist/tex/latex/amsmath/amsopn.sty))
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amsfonts.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/amssymb.sty)
*(/usr/share/texlive/texmf-dist/tex/latex/geometry/geometry.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/keyval.sty)
(/usr/share/texlive/texmf-dist/tex/generic/iftex/ifvtex.sty
(/usr/share/texlive/texmf-dist/tex/generic/iftex/iftex.sty)))
*
*(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mathtools.sty
(/usr/share/texlive/texmf-dist/tex/latex/tools/calc.sty)
(/usr/share/texlive/texmf-dist/tex/latex/mathtools/mhsetup.sty))
*(/usr/share/texmf/tex/latex/preview/preview.sty
(/usr/share/texlive/texmf-dist/tex/generic/luatex85/luatex85.sty)
(/usr/share/texmf/tex/latex/preview/prtightpage.def))
(/usr/share/texlive/texmf-dist/tex/latex/l3backend/l3backend-xetex.def
(|extractbb --version))
No file 38b56dd1a457a73dfaee246896bc98bec16feb3a.aux.
(/usr/share/texlive/texmf-dist/tex/latex/base/ts1cmr.fd)
*geometry* driver: auto-detecting
*geometry* detected driver: xetex
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphicx.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/graphics.sty
(/usr/share/texlive/texmf-dist/tex/latex/graphics/trig.sty)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-cfg/graphics.cfg)
(/usr/share/texlive/texmf-dist/tex/latex/graphics-def/xetex.def)))
Preview: Fontsize 10pt
Preview: PDFoutput 1

*(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsa.fd)
(/usr/share/texlive/texmf-dist/tex/latex/amsfonts/umsb.fd)
! Undefined control sequence.
<*> ...ke-width: 0.05pt;}]]></style>}a_{\textcolor
                                                  {red}4}=(-1)^{\textcolor{r...
No pages of output.
Transcript written on 38b56dd1a457a73dfaee246896bc98bec16feb3a.log.

Vastaus:

$4,\;9,\;14,\;19$
$-1,\;1,\;-1,\;1$

4.1.3 Esimerkki: Onko luku lukujonon jäsen?

Tarkastellaan lukujonoa, joka yleinen jäsen on muotoa a_n=4n+5 .

Onko luku lukujonon jäsen?
Onko luku lukujonon jäsen?

Ratkaisu:

Luku on lukujonon jäsen, jos löytyy sellainen positiivinen kokonaisluku jolla . Jos tällainen luku on olemassa, se kertoo, kuinka mones jonon jäsen luku on.

Koska tiedetään, että lukujonon yleinen jäsen on a_n=4n+5, voidaan yhtälö

a_n=21

kirjoittaa muodossa

4n+5=21.

Ratkaistaan tästä tuntematon .

$\begin{align*} 4n+5&=21 \\ 4n&=16 \\ n&=\frac{16}{4}=4 \end{align*}$

Koska yhtälön ratkaisuna oleva luku on on positiivinen kokonaisluku luku on lukujonon jäsen, tarkemmin sanottuna jäsen.

Luku on lukujonon jäsen, jos löytyy sellainen positiivinen kokonaisluku jolla . Muodostetaan ja ratkaistaan yhtälö.

$\begin{align*} a_n&=35 \\ 4n+5&=35 \\ 4n&=31 \\ n&=\frac{31}{4}=7,75 \end{align*}$

Koska yhtälön ratkaisuna oleva luku 7,75 ei ole positiivnen kokonaisluku, luku ei ole lukujonon jäsen.

Vastaus:

Luku on lukujonon jäsen.
Luku ei ole lukujonon jäsen.

4.1.4 Esimerkki: lukujono laskimella

Tämän sivun ensimmäisen videon lopussa esitellään, kuinka lukujonoja piirretään GeoGebralla. Katso tarvittaessa video, ennen tämän esimerkin lukemista.

Tarkastellaan lukujonoa, jonka yleinen jäsen on muotoa $a_n=3\cdot2^{n-2}$ .

Piirrä lukujonon kuvaaja.
Määritä kuvaajasta lukujonon kuudes jäsen .

Ratkaisu:

Piirretään lukujonon kuvaaja yleisen jäsenen lausekkeen avulla GeoGebralla. GeoGebraan syötetään käsky Jono((n,3*2^(n-2)),n,1,10). Kaksi viimeistä parametriä kertovat ensimmäisen ja viimeisen termin järjestysnumeron. Nyt siis GeoGebra piirtää kymmenen ensimmäistä lukujonon jäsentä.

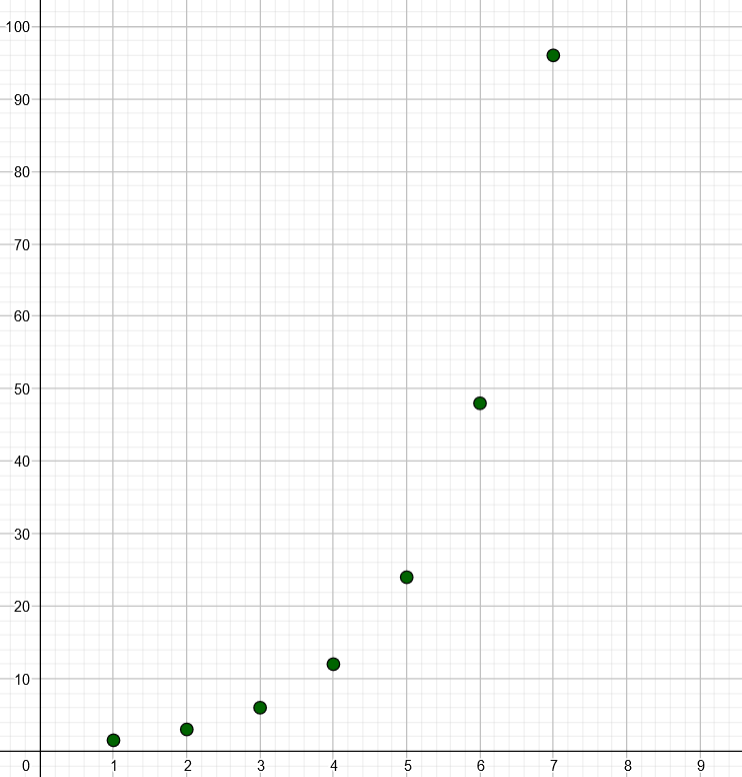
Koordinaatiston akselien asteikkoja on muutettu nyt niin, että kuvaajasta nähdään lukujonon seitsemän ensimmäistä jäsentä.

Kuvaajan pisteen ensimmäinen koordinaatti kertoo jäsenen järjestysluvun ja toinen koordinaatti kertoo jäsenen arvon. Halutaan siis selvittää kuvaajalta piste, jonka ensimmäinen koordinaatti on .

Lukujono voidaan ajatella funktiona. Samaan tapaan kuin funktion arvo kohdassa x=6 saadaan selvittämällä f(6), voidaan nyt syöttää GeoGebraan l1(6) ja saadaan pisteen koordinaatit. (GeoGebra nimeää jonon automaattisesti nimellä l1, jos sille ei anna itse nimeä.)

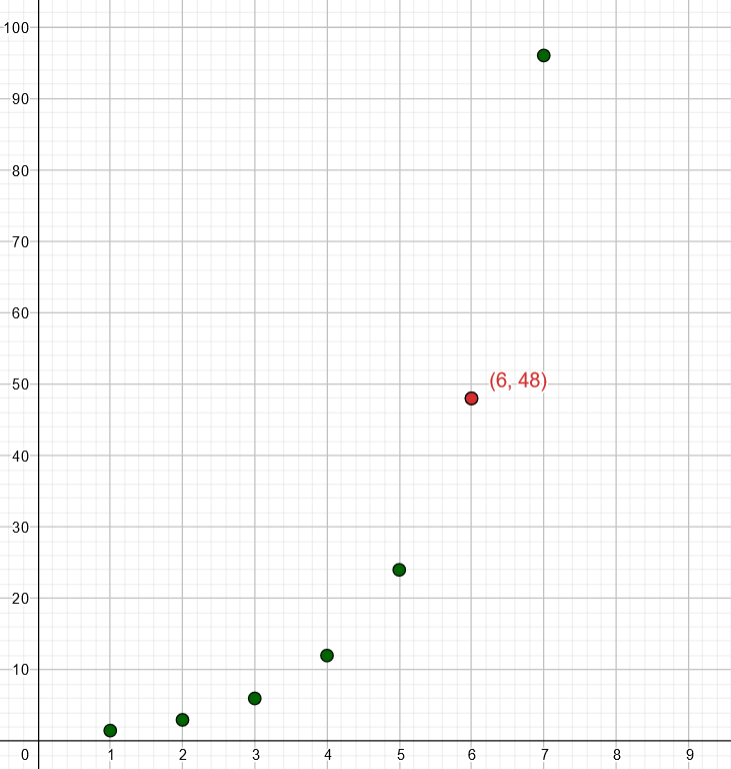
Kuudennen pisteen toinen koordinaatti on 48, joten a_6=48 .

4.2 Aritmeettinen lukujono

Tarkastellaan lukujonoa $3,\;7,\;11,\;15,\dots$ . Huomataan, että jonon seuraava jäsen voidaan laskea lisäämällä edelliseen jäseneen luku neljä. Tällaista lukujonoa sanotaan aritmeettiseksi lukujonoksi. Aritmeettisessa lukujonossa seuraava jäsen saadaan aina lisäämällä edelliseen jäseneen sama vakiona pysyvä luku.

$3\xrightarrow{\text{+4}}7\xrightarrow{\text{+4}}11\xrightarrow{\text{+4}}15\dots$

Aritmeettinen lukujono

Lukujono on aritmeettinen, jos sen kahden peräkkäisen jäsenen erotus on vakio.

Peräkkäisten jäsenten erotusta $d=a_n-a_{n-1}$ sanotaan jonon erotusluvuksi eli differenssiksi.

Lukujonon aritmeettisuus voidaan siis osoittaa tutkimalla peräkkäistän jäsenten erotusta.

4.2.1 Esimerkki: aritmeettinen lukujono

Voiko lukujono olla aritmeettinen?

$2,\;4,\;8,\;16,\dots$
$0,\;-\dfrac{1}{2},\;-1,\;-\dfrac{3}{2},\dots$

Ratkaisu:

Lasketaan lukujonon peräkkäisten jäsenten erotuksia.

a_2-a_1=4-2=2

a_3-a_2=8-4=4

a_4-a_3=16-8=8

Lukujonon peräkkäisten jäsenten erotus ei ole vakio, joten lukujono ei ole aritmeettinen.

Lasketaan lukujonon peräkkäisten jäsenten erotuksia.

$a_2-a_1=-\dfrac{1}{2}-0=-\dfrac{1}{2}$

$a_3-a_2=-1-\left(-\dfrac{1}{2}\right)=-1+\dfrac{1}{2}=-\dfrac{1}{2}$

$a_4-a_3=-\dfrac{3}{2}-(-1)=-\dfrac{3}{2}+1=-\dfrac{1}{2}$

Lukujonon peräkkäisten jäsenten erotus on aina $-\dfrac{1}{2},$ joten lukujono saattaa olla aritmeettinen. Tätä ei voi kuitenkaan varmasti sanoa, koska ei tiedetä, miten lukujono jatkuu.

Minkä tahansa aritmeettisen jonon jäsenet voidaan määrittää, kun tiedetään jonon ensimmäinen jäsen a_1 ja differenssi .

$a_1\xrightarrow{+d}a_2\xrightarrow{+d}a_3\dots a_{n-1}\xrightarrow{+d}a_n$

a_2=a_1+d

a_3=a_1+d+d=a_1+2d

a_4=a_1+d+d+d=a_1+3d

$\vdots$

a_n=a_1+(n-1)d

Aritmeettisen lukujonon yleinen jäsen

Aritmeettisen lukujonon jäsen on

a_n=a_1+(n-1)d,

jossa

on lukujonon ensimmäinen jäsen
on erotusluku eli differenssi.

4.2.2 Esimerkki: aritmeettisen lukujonon yleisen jäsenen määrittäminen

Määritä aritmeettisen jonon yleinen jäsen a_n, jos jonon kaksi ensimmäistä jäsentä ovat

ja
ja $\dfrac{5}{2}$

Ratkaisu:

Lasketaan erotusluku jäsenten erotuksesta

Muodostetaan jonon yleinen jäsen tietojen a_1=-3 ja d=5 perusteella.

$\begin{align*} a_n&=a_1+(n-1)d \\ &=-3+(n-1)\cdot5 \\ &=-3+5n-5 \\ &=5n-8 \end{align*}$

Lasketaan erotusluku jäsenten erotuksesta $d=\dfrac{5}{2}-4=-\dfrac{3}{2}$

Muodostetaan jonon yleinen jäsen tietojen a_1=4 ja $d=-\dfrac{3}{2}$ perusteella.

$\begin{align*} a_n&=a_1+(n-1)d \\ &=4+(n-1)\cdot\left(-\dfrac{3}{2}\right) \\ &=4-\dfrac{3}{2}n+\dfrac{3}{2} \\ &=-\dfrac{3}{2}n+\dfrac{11}{2} \end{align*}$

Vastaus:

$a_n=-\dfrac{3}{2}n+\dfrac{11}{2}$

Tämän sivun toisen videon lopussa esitellään, miten aritmeettinen lukujono piirretään GeoGebralla. Kun aritmeettisesta lukujonosta piirretään kuvaaja, jonon jäseniä kuvaavat pisteet asettuvat suoralle. Piirretään esimerkiksi edellisen esimerkin a-kohdan kuvaaja.


	$5\cdot1-8=-3$
	$5\cdot2-8=2$
	$5\cdot3-8=7$
	$5\cdot4-8=12$
$\dots$	$\dots$

4.2.3 Esimerkki: isopandojen määrän kasvu

Uhanalaisia isopandoja oli vuonna 2000 1600 yksilöä. Kymmenen vuotta myöhemmin isopandoja oli 1850 yksilöä.

Muodosta pandojen vuosittaista lukumäärää (vuodesta alkaen) kuvaavan aritmeettisen lukujonon yleinen jäsen.
Jos pandojen kannan kasvu on jatkunut samanlaisena, paljon pandoja on vuonna ?

Ratkaisu:

Isopandojen määrä lisääntyy aina vuosittain yhtä paljon. Merkitään tätä lisäystä kirjaimella . Tiedetään, että pandojen määrä nousee kymmenessä vuodessa eli yhdessä vuodessa pandojen määrä nousee $d=\dfrac{250}{10}=25$ .

Nyt aritmeettisesta lukujonosta tiedetään

ensimmäinen jäsen
differenssi .

Näiden tietojen perusteella voidaan muodostaa lukujonon yleinen jäsen

$\begin{align*} a_n&=a_1+(n-1)d \\ &=1600+(n-1)\cdot250 \\ &=1600+250n-250 \\ &=250n+1575 \end{align*}$

Jonon ensimmäinen jäsen kuvaa pandojen määrää vuonna jonon toinen jäsen kuvaa pandojen määrää vuonna jonon kolmas jäsen kuvaa pandojen määrää $2002\dots$

Pandojen määrää vuonna 2019 kuvaa siis lukujonon jäsen $a_{20}$ .

$\begin{align*} a_{20}=250\cdot20+1575=2075 \end{align*}$

Vastaus:

pandaa

4.3 Aritmeettinen summa

Kun äärellinen määrä aritmeettisen lukujonon peräkkäisiä jäseniä lasketaan yhteen, muodostuu aritmeettinen summa. Tarkastellaan esimerkiksi lukujonoa, jonka yleinen termi on a_n=3n-2 . Sen neljän ensimmäisen termin summa on

$\begin{align*} S_n&=a_1+a_2+a_3+a_4 \\ &=1+4+7+10 \\ &=22 \end{align*}$

Artimeettiset summat voidaan laskea myös helpommin ilman, että luvut lasketaan yksitellen yhteen.

Aritmeettinen summa

Aritmeettisen summan $S_n=a_1+a_2+\dots +a_n$ arvo voidaan laskea kaavalla

$S_n=n\cdot\dfrac{a_1+a_n}{2},$

jossa

on yhteenlaskettavien määrä
on ensimmäinen yhteenlaskettava
on viimeinen yhteenlaskettava.

4.3.1 Esimerkki: aritmeettinen summa

Laske aritmeettisen summan $7+10+13+\dots+61$ arvo.

Ratkaisu:

Aritmeettisen summan laskemiseksi tarvitaan

yhteenlaskettavien lukumäärä
ensimmäinen jäsen
viimeinen jäsen

Selvitetään yhteenlaskettavien lukunmäärä. Määritetään differenssi

d=10-7=3

ja yleinen jäsen

$\begin{align*} a_n&=7+(n-1)\cdot3 \\ &=7+3n-3 \\ &=3n+4 \end{align*}$

Yhteenlaskettavien määrä saadaan selvittämällä mones jäsen luku on.

$\begin{align*} 3n+4=61 \\ 3n=57 \\ n=19 \end{align*}$

Lasketaan summa sijoittamalla arvot n=19, a_1=7 ja $a_{19}=61$ aritmeettisen summan kaavaan.

$\begin{align*} S_{19}&=19\cdot\dfrac{a_1}{a_{19}} \\ &=19\cdot\dfrac{7+61}{2} \\ &=19\cdot\dfrac{68}{2} \\ &=19\cdot34 \\ &=646 \end{align*}$

Vastaus: 646

4.3.2 Esimerkki: kirjakaupan myynnin seuraaminen aritmeettisen summan avulla

Kirjakauppa tilasi 8025 kappaletta uutuuskirjaa. Ensimmäisellä viikolla kirjaa myytiin 325 kappaletta. Tuotteen myynti kasvoi joka viikko kappaletta. Kuinka monen viikon päästä tuote myytiin loppuun?

Ratkaisu:

Muodostetaan myydyistä kirjoista aritmeettinen summa S_n, jossa kuluneita viikkoja merkitään kirjaimella . Koska myynti kasvaa joka viikko kirjalla, differenssi d=30 . Aritmeettisen jonon ensimmäinen jäsen on ensimmäisen viikon kirjamyynti a_1=325 .

Viimeinen yhteenlaskettava jäsen saadaan aritmeettisen jonon yleisen jäsenen lausekkeella.

$\begin{align*} a_n&=325+(n-1)\cdot30 \\ &=325+30n-30 \\ &=30n+295 \end{align*}$

Aritmeettisen summan

yhteenlaskettavien lukumäärä
ensimmäinen yhteenlaskettava
viimeinen yhteenlaskettava

Muodostetaan kirjamyyntiä kuvaavalle aritmeettiselle summalle lauseke.

$\begin{align*} S_n&=n\cdot\dfrac{325+(30n+295)}{2} \;\;\,\;\;\text{(sievennetään laskimella)}\\ &=15n^2+310n \end{align*}$

Nyt selvitetään millä viikolla arvolla kirjamyynti saavuttaa 8025 kappaleen rajan.

$\begin{align*} S_n=8025 \\ 15n^2+310n=8025 \\ \end{align*}$

Toisen asteen yhtälön ratkaisuiksi laskimella saadaan n=-35,67 ja n=15, joista vastaukseksi kelpaa vain positiivinen luku. Kirja myytiin loppuun siis viikolla .

Vastaus: Kirja myytiin loppuun viikon päästä.

Lukujen summa voidaan merkitä lyhyesti käyttämällä summamerkintää.

Summamerkintä

Summa $a_1+a_2+a_3+\dots+a_n$ voidaan merkitä lyhyemmin muodossa

$\sum_{i=1}^{n} a_i.$

Summamerkinnässä symbolin $\sum$ alapuolelle merkitään ensimmäisen yhteenlaskettavan järjestysluku (symbolin sijalla voisi olla mikä tahanka muukin kirjain), yläpuolelle viimeisen yhteenlaskettavan järjestysluku ja perään lukujonon yleinen jäsen.

4.3.3 Esimerkki: aritmeettinen summa summamerkinnän avulla

Laske aritmeettinen summa $\sum_{i=1}^{5} (3i+4)$

Ratkaisu:

TAPA 1:

Summassa lasketaan yhteen lukujonon, jonka yleinen jäsen on muotoa a_i=3_i+4 , jäseniä.

Yhteenlaskettavien numerointi alkaa alkaa järjestysluvun arvosta ja päättyy arvoon . Lasketaan summa summaamalla termit yksitellen yhteen.

$\begin{align*} \sum_{i=1}^{5} (a_i)&=a_1+a_2+a_3+a_4+a_5 \\ \sum_{i=1}^{5} (3i+4)&=(3\cdot1+4)+(3\cdot2+4)+(3\cdot3+4)+(3\cdot4+4)+(3\cdot5+4) \\ &=7+10+13+16+19 \\ &=65 \end{align*}$

TAPA2:

Lasketaan summa käyttäen aritmeettisen summan kaavaa.

ensimmäinen yhteenlaskettava
viimeinen yhteenlaskettava
yhteenlaskettavien lukumäärä

$S_5=5\cdot\dfrac{7+19}{2}=65$

TAPA3:

Monista laskimista löytyy summatoiminto, jonka avulla summa voidaan laskea. GeoGebrassa summa saadaan laskettua syöttämällä jonon yleinen jäsen, muuttuja sekä ensimmäisen ja viimeisen yhteenlaskettavan järjestysluvut. Kyseinen summa menisi käskyllä

Summa(3n+4,n,1,5)

Vastaus:

4.4 Geometrinen lukujono

Tarkastellaan seuraavaksi lukujonoa $4,\;8,\;16,\;32,\dots$ . Huomataan, että jonon seuraava jäsen voidaan laskea kertomalla edellinen jäsen kahdella. Tällaista lukujonoa sanotaan geometriseksi lukujonoksi. Geometrisessa lukujonossa seuraava jäsen saadaan aina kertomalla edellinen jäsen samalla vakiona pysyvällä luvulla.

$4\xrightarrow{\cdot2}8\xrightarrow{\cdot2}16\xrightarrow{\cdot2}32\dots$

Geometrinen lukujono

Lukujono on geometrinen, jos sen kahden peräkkäisen jäsenen suhde eli osamäärä on aina sama.

Peräkkäisten jäsenten suhdetta $q=\dfrac{a_{n+1}}{a_n}$ sanotaan jonon suhdeluvuksi.

Lukujonon geometrisuus voidaan siis osoittaa tutkimalla peräkkäistän jäsenten osamäärää.

4.4.1 Esimerkki: geometrinen lukujono

Voiko lukujono olla geometrinen, jos jonon ensimmäiset jäsenet ovat

ja
$\dfrac{4}{5}$ ja $\dfrac{8}{25}$

Ratkaisu:

Lasketaan lukujonon peräkkäisten jäsenten osamääriä.

$\dfrac{a_2}{a_1}=\dfrac{6}{3}=2$

$\dfrac{a_3}{a_2}=\dfrac{9}{6}=\dfrac{3}{2}$

Lukujonon peräkkäisten jäsenten suhde ei ole vakio, joten lukujono ei ole geometrinen.

Lasketaan lukujonon peräkkäisten jäsenten osamääriä.

$a_2:a_1=\dfrac{4}{5}:2=\dfrac{4}{5}\cdot\dfrac{1}{2}=\dfrac{4\cdot1}{5\cdot2}=\dfrac{4}{10}=\dfrac{2}{5}$

$a_3:a_2=\dfrac{8}{25}:\dfrac{4}{5}=\dfrac{8}{25}\cdot\dfrac{5}{4}=\dfrac{8\cdot5}{25\dot4}=\dfrac{40}{100}=\dfrac{2}{5}$

Lukujonon peräkkäisten jäsenten suhde on aina $\dfrac{2}{5},$ joten lukujono voi olla geometrinen. Tätä ei voi kuitenkaan varmasti sanoa, koska ei tiedetä, miten lukujono jatkuu.

Minkä tahansa geometrisen jonon jäsenet voidaan määrittää, kun tiedetään jonon ensimmäinen jäsen a_1 ja suhdeluku .

$a_1\xrightarrow{\cdot q}a_2\xrightarrow{\cdot q}a_3\dots a_{n-1}\xrightarrow{\cdot q}a_n$

$a_2=a_1\cdot q$

$a_3=a_1\cdot q\cdot q=a_1q^2$

$a_4=a_1\cdot q\cdot q\cdot q=a_1q^3$

$\vdots$

$a_n=a_1q^{n-1}$

Geometrisen lukujonon yleinen jäsen

Geometrisen lukujonon jäsen on

$a_n=a_1\cdot q^{n-1},$

jossa

on lukujonon ensimmäinen jäsen
on suhdeluku.

4.4.2 Esimerkki: geometrinen lukujono

Tarkastele geometristä lukujonoa, jonka ensimmäinen jäsen on a_1=2 ja suhdeluku q=-3 . Määritä lukujonon

yleinen jäsen
jäsen $a_{16}$ .

Ratkaisu:

Muodostetaan yleisen jäsenen lauseke ensimmäisen jäsenen ja suhdeluvun avulla.

$\begin{align*} a_n&=a_1\cdot q^{n-1} \\ &=2\cdot(-3)^{n-1} \end{align*}$

Lukujonon jäsen saadaan sijoittamalla yleisen jäsenen lausekkeeseen .

$\begin{align*} a_{16}&=2\cdot(-3)^{16-1} \\ &=2\cdot(-3)^{15} \\ &=2\cdot(-14\;348\;907) \\ &=-28\;697\;814 \end{align*}$

Vastaus:

$a_n=2\cdot(-3)^{n-1}$
$a_{16}=-28\;697\;814$

4.4.3 Esimerkki: kunnan asukasmäärän lasku

Kunnan asukasluku laskee vuosittain $2,3\;\%$ . Vuonna 2015 kunnassa oli 8756 asukasta.

Muodosta eri vuosien asukasmääristä muodostuvan lukujonon yleinen jäsen, kun jonon ensimmäinen jäsen on vuoden asukasluku.
Tutki laskimen avulla, minä vuonna kunnan asukasluku laskee alle asukkaan.

Ratkaisu:

Lukujonon ensimmääinen jäsen . Koska asukasluku laskee joka vuosi $2,3\;\%,$ kasvua kuvaava kerroin on $100\;\%-2,3\;\%=97,7\;\%=0,977$ .

Seuraavan vuoden asukasluku saadaan kertomalla prosenttikertoimella 0,977 eli asukasluvuista muodostuu geometrinen jono, jonka suhdeluku q=0,977 .

Lukujonon yleinen jäsen $a_n=8756\cdot(0,977)^{n-1}$ .

Piirretään lukujonon kuvaaja. Etsitään se lukujonon jäsen, joka on ensimmäisen kerran pienempi kuin .

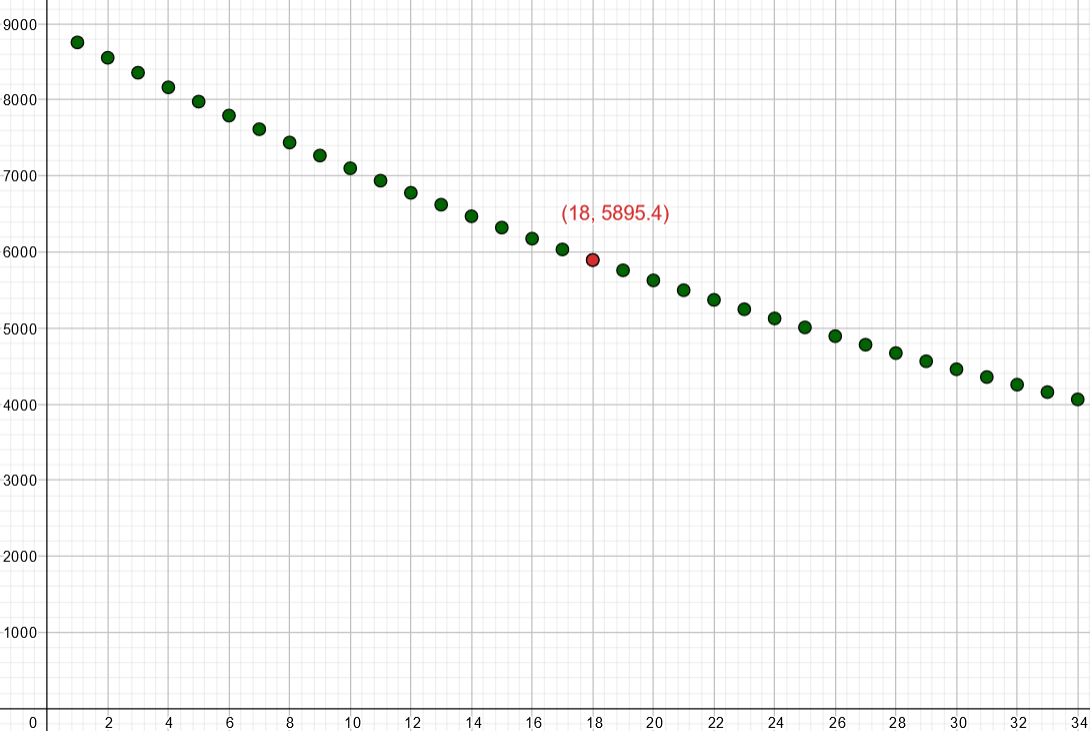
Lukujonon 18. jäsen on ensimmäinen, jonka arvo on pienempi kuin 6000 . Lukujonon 18. jäsen kuvaa vuoden 2015+17=2032 asukaslukua.

Vastaus:

$a_n=8756\cdot(0,977)^{n-1}$
vuonna

4.5 Geometrinen summa

Myös geometrisen summan arvo saadaan laskettua helposti kaavalla, kun tiedetään ensimmäinen termi a_1, suhdeluku ja yhteenlaskettavien lukumäärä .

Geometrinen summa

Geometrisen summan $S_n=a_1+a_2+\dots +a_n$ arvo voidaan laskea kaavalla

$S_n=a_1\cdot\dfrac{1-q^n}{1-q},$

jossa

on yhteenlaskettavien määrä
on ensimmäinen yhteenlaskettava
on suhdeluku.

Jos suhdeluku q=1, niin summa $S_n=n\cdot a_1$ .

4.5.1 Esimerkki: geometrinen summa

Laske geometrisen lukujonon $-4,\;-16,\;-64,\dots$ yhdeksän ensimmäisen jäsenen summa.

Ratkaisu:

Geometrisen summan laskemiseksi tarvitaan

yhteenlaskettavien lukumäärä
ensimmäinen jäsen
suhdeluku $q=\dfrac{a_2}{a_1}=\dfrac{-16}{-4}=4$

Yhdeksän ensimmäisen jäsenen summa on

$\begin{align*} S_9&=a_1\cdot\dfrac{1-q^n}{1-q} \\ &=-4\cdot\dfrac{1-4^9}{1-4} \\ &=-349\;524 \end{align*}$

Vastaus: $-349\;524$

4.5.2 Esimerkki: kesätyöpalkka toive

Anna esitti työnantajalleen toiveen heinäkuun palkasta: "Haluan ensimmäiseltä päivältä senttiä ja joka päivä kaksinkertaisen summan edelliseen päivään verrattuna". Kuinka suuri olisi Annan heinäkuun palkka työpäivältä, jos työnantaja suostuisi ehdotukseen?

Ratkaisu:

Koska seuraavan päivän palkka on aina kaksinkertainen edellisen päivän palkkaan verrattuna, muodostavat heinäkuun palkat geometrisen jonon, jonka ensimmäinen jäsen on $a_1=0,5\;\text{(€)}$ ja suhdeluku q=2 . Lasketaan tämän jonon ensimmäisen termin summa geometrisen summan kaavan avulla.

$\begin{align*} S_{16}&=a_1\cdot\dfrac{1-q^{16}}{1-q} \\ &=0,5\cdot\dfrac{1-2^{16}}{1-2} \\ &=32\;767,5 \end{align*}$

Vastaus: Heinäkuun palkka olisi $32\;767,50\;\text{€}$