1. Lausekkeilla laskeminen: tehtäviä
Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Lausekkeilla laskeminen. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.
1.1 Lauseke ja polynomi: tehtäviä
Tämän kappaleen teoria.
1.1.1 Tehtävä
Täydennä taulukko. Tehtävässä ei ole automaattitarkistusta.
Open plugin
1.1.2 Tehtävä
Vastaa polynomia koskeviin kysymyksiin?
1.1.3 Tehtävä

1.1.4 Tehtävä
1.1.5 Tehtävä
Laske lausekkeen arvo, kun
1.1.6 Tehtävä

1.1.7 Tehtävä
Olkoon polynomi Laske polynomin arvot, kun
1.1.8 Tehtävä
Täydennä taulukkoon polynomien arvot käyttäen laskinta hyväksi. Tehtävässä ei ole automaattitarkistusta.
Open plugin
1.2 Lausekkeiden ja polynomien laskutoimituksia: tehtäviä
Tämän kappaleen teoria.
Laske kappaleen tehtävät ilman ohjelmistoja, jos tehtävässä ei erikseen mainita ohjelmiston käytöstä.
1.2.1 Tehtävä
Yhdistä lausekkeisiin oikea sievennetty muoto.
1.2.2 Tehtävä
Muodosta ja sievennä binomien ja
1.2.3 Tehtävä
a) Merkitse kuvan lausekkeesta keskenään samanmuotoiset termit samalla tavalla, esimerkiksi samalla värillä. Tehtävässä ei ole automaattitarkistusta.

1.2.4 Tehtävä
Sievennä.
1.2.5 Tehtävä
Sievennä.
1.2.6 Tehtävä
Sievennä.

1.2.7 Tehtävä
Sievennä.
1.2.8 Tehtävä
Seuraavien muistikaavojen avulla lausekkeiden sieventäminen on tietyissä tilanteissa helpompaa.
- Summan ja erotuksen tulo
- Summan neliö
- Erotuksen neliö
Käytä muistikaavoja hyväksesi ja sievennä seuraavat lausekkeet.
1.2.9 Tehtävä
Muodosta ja sievennä monomien ja
1.2.10 Tehtävä
Murtolausekkeet, joiden osoittajana on polynomi ja nimittäjänä jokin luku, ovat polynomeja. Murtolausekkeesta voidaan muokata polynomi tekemällä jakolasku termeittäin seuraavasti:
Viimeisestä muodosta nähdään, että kyseessä on ensimmäisen asteen polynomi.

1.2.11 Tehtävä (yo lyhyt k2015/2)
Sijoitetaan yhtälöön
ja ratkaistaan
muodostuvasta yhtälöstä.
1.2.12 Tehtävä
Sievennetään funktion lauseke osissa.
Nyt siis funktio sievennettynä on
1.3 Lausekkeet ongelmien ratkaisussa: tehtäviä
Tämän kappaleen teoria.
1.3.1 Tehtävä
Sievennä suorakulmion pinta-alan lauseke, kun sen sivujen pituudet ovat
1.3.2 Tehtävä
Miesten pesäpallokentällä kotipesältä ykköspesälle kulkeva lähtöpolku on metriä pitkä. Ykkös- ja kakkospesän välinen polku on
metriä pitempi kuin lähtöpolku. Kakkos- ja kolmospesän välinen poikkipolku taas on
metriä pitempi kuin edellinen väli. Jos pelaaja lyö kunnarin, hän juoksee yhteensä
metriä.

Kotipesästä ykköspesällä: (m)
Ykköspesältä kakkospesälle: (m)
Kakkospesältä kolmospesälle: (m)
Kunnarin lyödessään pelaaja juoksee kaikki kolme polkua, joten saadaan yhtälö
1.3.3 Tehtävä
Aloittelijoiden kyykkyhaasteessa ideana on tehdä päivän ajan kyykkyjä niin, että vaikeustasoa nostetaan pikkuhiljaa. Ensimmäisenä päivänä kyykkyjä tehdään
toistoa ja sen jälkeen toistojen määrää nostetaan viisi päivässä. Haasteeseen kuuluu myös lepopäivät, mutta tässä tehtävässä oletetaan, ettei niitä pidetä.

a) Muodosta polynomi , joka kuvaa kyykkyjen määrää
päivän jälkeen haasteen aloittamisesta.
1.3.4 Tehtävä
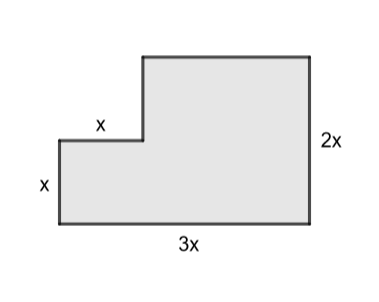
1.3.5 Tehtävä
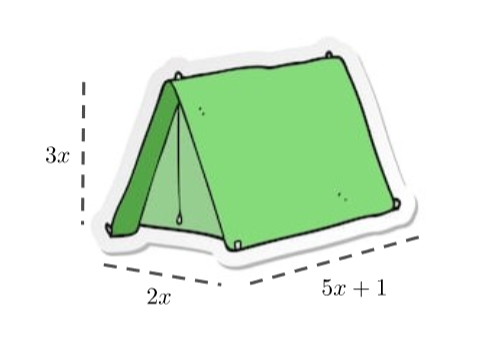
Teltta muodostaa lieriön, jonka pohjana on kolmio. Lieriön pinta-ala lasketaan kertomalla pohjan ala korkeudella .
Nyt pohjan pinta-ala ja korkeus
1.3.6 Tehtävä
Mikko tekee ystävälleen matemaatikon taikatempun ja pyytää häntä suorittamaan seuraavat vaiheet:
- Ajattele jotain numeroa.
- Lisää siihen luku
.
- Kerro saamasi summa luvulla
.
- Vähennä tuloksesta luku
.
- Lisää tähän alussa alussa ajattelemasi luku.
- Jaa saamasi summa luvulla
.
- Kerro minulle saamasi luku.
Olkoon ystävän ajattelema numero. Kysytty lauseke muodostuu seuraavasti.
1.3.7 Tehtävä
Jääkiekkokaukalon pinta-alasta saa melko hyvän arvion, kun arvioi sen olevan suorakulmio. Vielä paremman arvion saa, kun arvioi kaukalon ulkopuolelle jäävien alueiden muodostuvan kolmioista ja vähentää ne suorakulmion pinta-alasta.
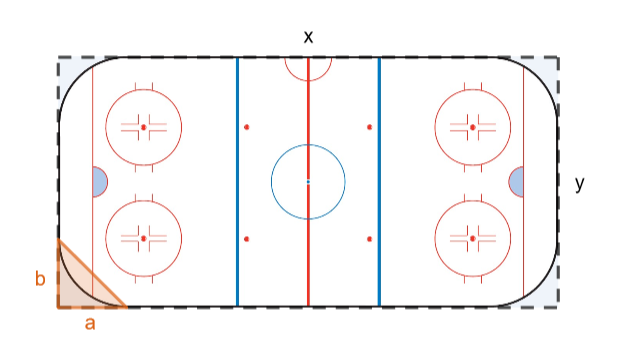
1.3.8 Tehtävä
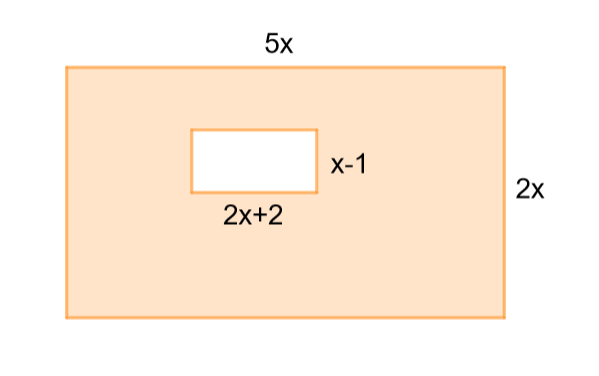
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.
