1. Lausekkeilla laskeminen

Ensimmäisessä kappaleessa käsitellään lausekkeita ja polynomeja. Käymme läpi polynomien peruskäsitteitä sekä lausekkeilla ja polynomeilla tehtäviä laskutoimituksia. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

1.1 Lauseke ja polynomi

MAY1-kurssilla opittiin, että merkittyä laskutoimitusta tai pelkkää lukua kutsutaan lausekkeeksi. Lausekkeita ovat esimerkiksi

$x^2,\;x+1\;\text{ja}\;8.$

Lausekkeista osa luokitellaan polynomeiksi.

Polynomi

Polynomi on muuttujista ja vakioista yhteen-, vähennys- ja kertolaskulla aikaansaatu lauseke.

Polynomin yhteenlaskettavia kutsutaan termeiksi. Jokainen termi koostuu kertoimesta ja muuttujaosasta.

Termin muuttujaosan eksponentti on termin asteluku. Jos eksponentti on nolla, niin termi on pelkkä luku eli vakiotermi. Polynomin asteluku määräytyy sen muuttujan mukaan, jolla on suurin eksponentti.

1.1.1 Esimerkki: polynomien peruskäsitteet

Tarkastellaan polynomia -4x^5+x^2-7 . Polynomin termejä ovat -4x^5, x^2 ja . Näistä termi on vakiotermi. Taulukoidaan termien kertoimet, muuttujaosat sekä asteluvut.

Termi	Kerroin	Muuttujaosa	Asteluku

Polynomin asteluku on sillä se on korkeimman asteen termin -4x^5 asteluku.

Polynomeja luokitellaan myös termien lukumäärän mukaan:

Jos termejä on yksi, polynomia sanotaan monomiksi.
Jos termejä on kaksi, polynomia sanotaan binomiksi.
Jos termejä on kolme, polynomia sanotaan trinomiksi.

Edellisen esimerkin polynomi oli siis trinomi. Jos termejä on enemmän kuin kolme, polynomilla ei ole erityistä nimeä.

Polynomeja nimetään yleensä isoilla kirjiamilla, usein kirjaimilla tai . Kun polynomin muuttujan paikalle asetetaan jokin lukuarvo, saadaan laskettua polynomin arvo.

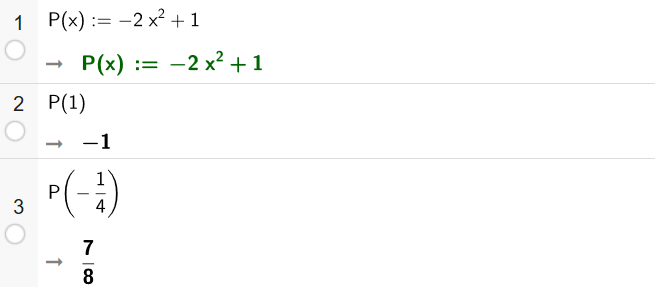
1.1.2 Esimerkki: polynomin arvon laskeminen

Laske polynomin P(x)=-2x^2+1 arvo, kun

$x=-\dfrac{1}{4}$

Ratkaisu:

Polynomin arvo, kun saa jonkin arvon, saadaan sijoittamalla kyseinen arvo muuttujan paikalle ja laskemalla merkityt laskutoimitukset.

$P(1)=-2\cdot 1^2 +1 = -2+1=-1$
$P\left(-\dfrac{1}{4}\right)=-2\cdot\left(-\dfrac{1}{4}\right)^2+1=-2\cdot\dfrac{1}{16}+1=-\dfrac{1}{8}+1=\dfrac{7}{8}$

Vastaus:

b. $\dfrac{7}{8}$

1.1.3 Esimerkki: polynomin arvon laskeminen ohjelmistolla

Polynomin arvon laskemista varten kannattaa polynomi tallentaa laskimen muistiin käyttämällä := merkkiä. Tällöin polynomin arvo saadaan suoraan laskimella eikä sijotusta tarvitse tehdä erikseen.

Tarkistetaan edellinen esimerkki GeoGebran CAS-laskimella.

Lauseke ja polynomi: tehtäviä

1.2 Lausekkeiden ja polynomien laskutoimituksia

Suureet, joilla on sama yksikkö, voidaan laskea yhteen tai vähentää toisistaan. Esimerkiksi voidaan laskea $4\;\text{kg}-3\;\text{kg},$ mutta ei $4\;\text{kg}-3\;\text{€}$ .

Jos polynomin termien muuttujaosat ovat samat, ne voidaan yhdistää. Tällaisia termejä kutsutaan samanmuotoisiksi.

Polynomien yhteen- ja vähennyslasku

Yhteenlaskussa samanmuotoiset termit yhdistetään laskemalla termien kertoimet yhteen.

Vähennyslaskussa samanmuotoiset termit yhdistetään vähentämällä termien kertoimet toisistaan.

Muuttujaosa säilyy ennallaan.

1.2.1 Esimerkki: polynomien yhteen- ja vähennyslasku

Laske polynomien P(x)=x^2+4x+2 ja Q(x)=-2x^2+3

summa
erotus

Ratkaisu:

$\begin{align*} P(x)+Q(x)&=(x^2+4x+2)+(-2x^2+3) &&|\;\text{poistetaan sulut}\\ &=\textcolor{red}{x^2}+4x+\textcolor{blue}2\textcolor{red}{-2x^2}+\textcolor{blue}3 &&|\;\text{yhdistetään samanmuotoiset termit}\\ &=\textcolor{red}{-x^2}+4x+\textcolor{blue}5 &&|\;\text{järjestetään termit asteluvun mukaan} \end{align*}$

$\begin{align*} P(x)-Q(x)&=(x^2+4x+2)-(-2x^2+3) &&|\;\text{poistetaan sulut}\\ &=\textcolor{red}{x^2}+4x+\textcolor{blue}{2}+\textcolor{red}{2x^2}\textcolor{blue}{-3} &&|\;\text{yhdistetään samanmuotoiset termit}\\ &=\textcolor{red}{3x^2}+4x\textcolor{blue}{-1} &&|\;\text{järjestetään termit asteluvun mukaan} \end{align*}$

Vastaus:

Lausekkeiden ja polynomien kertolaskuissa sovelletaan MAY1-kurssilta tuttuja vaihdanta-, liitäntä- ja osittelulakeja.

Vaihdantalaki	Liitäntälaki	Osittelulaki

Lausekkeen kertominen luvulla

Kun lauseketta kerrotaan luvulla, jokainen termi kerrotaan luvulla erikseen ja saadut tulot lasketaan yhteen.

$\textcolor{red}a(b+c)=\textcolor{red}ab+\textcolor{red}ac$

1.2.2 Esimerkki: geometrinen perustelu lausekkeen kertomiselle luvulla

Jaetaan suorakulmio kahdeksi pienemmäksi suorakulmioksi ja muodostetaan pinta-alan lauseke kahdella eri tavalla.

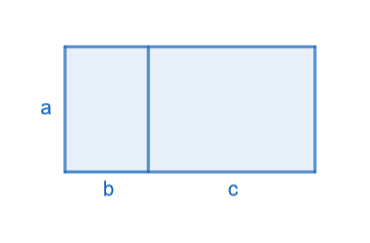
Merkitään pinta-alan lauseketta kirjaimella .

Tapa 1:

Suorakulmion kannan pituus on b+c ja korkeus .

Suorakulmion pinta-ala on kannan korkeuden ja korkeuden tulo, joten saadaan suorakulmiolle lauseke

A=a(b+c)

Tapa 2:

Suorakulmio muodostuu kahdesta pienemmästä suorakulmiosta, joiden kantojen pituudet ja . Kun lasketaan pienempien suorakulmioiden pinta-alat yhteen saadaan suorakulmiolle lauseke

A=ab+ac

Nyt siis 5(a+b)=5a+5b . Tähän perustuu lausekkeen kertominen luvulla.

1.2.3 Esimerkki: lausekkeen kertominen luvulla

Sievennä.

$(7x-3)\cdot2$

Ratkaisu:

$\begin{align*} &\textcolor{red}4(3x+1) \\ &=\textcolor{red}4\cdot3x +\textcolor{red}4\cdot1 &&|\;\text{kerrotaan jokainen termi erikseen}\\ &=12x+4 \end{align*}$

$\begin{align*} &(7x-3)\cdot2 &&|\;\text{vaihdetaan tulon tekijöiden paikkaa} \\ &=\textcolor{red}2(7x-3) \\ &=\textcolor{red}2\cdot7x+\textcolor{red}2\cdot(-3) &&|\;\text{kerrotaan jokainen termi erikseen}\\ &=14x-6 \end{align*}$

$\begin{align*} &\textcolor{red}{-3}(a^2-2a+5) \\ &=\textcolor{red}{-3}\cdot a^2\textcolor{red}{-3}\cdot(-2a)\textcolor{red}{-3}\cdot5 &&|\;\text{kerrotaan jokainen termi erikseen}\\ &=-3a^2+6a-15 \end{align*}$

Vastaus:

Monomilla kertominen

Kahden monomin tulossa kertoimet kerrotaan keskenään ja muuttujaosat keskenään.

Monomin ja polynomin tulossa monomilla kerrotaan jokainen polynomin termi.

Muuttujaosien kertomisessa keskenään sovelletaan samankantaisten potenssien laskusääntöjä. Samankantaisten potenssien tulossa eksponentit lasketaan yhteen.

$a^ma^n=a^{m+n}$

1.2.4 Esimerkki: monomilla kertominen

Sievennä.

$7x^3\cdot5x^6$

Ratkaisu:

Kerrotaan kertoimet keskenään ja muuttujaosat keskenään.

$\begin{align*} \textcolor{red}7\textcolor{blue}{x^3}\cdot\textcolor{red}5\textcolor{blue}{x^6}=\textcolor{red}7\cdot\textcolor{red} 5\cdot \textcolor{blue}{x^3} \cdot \textcolor{blue}{x^6}=35x^{3+6}=35x^9 \end{align*}$

Kerrotaan jokainen polynomin termi monomilla -4y^2 .

$\begin{align*} &\textcolor{red}{-4y^2}(y^2-2y+6) \\ &=\textcolor{red}{-4y^2}\cdot y^2 \textcolor{red}{-4y^2} \cdot (-2y)\textcolor{red}{-4y^2} \cdot 6 \\ &=-4y^{2+2}-4 \cdot(-2)\cdot y^{2+1} -4\cdot6 y^2 \\ &=-4y^4 +8y^3 -24y^2 \end{align*}$

Vastaus:

Kahden polynomin tulo

Kahden polynomin tulossa kerrotaan kertojapolynomin jokaisella termillä kerrottavan kaikki termit ja lasketaan saadut tulot yhteen.

$(\textcolor{red}a+\textcolor{blue}b)(c+b)=\textcolor{red}ac+\textcolor{red}ad+\textcolor{blue}bc+\textcolor{blue}bd$

1.2.5 Esimerkki: geometrinen perustelu kahden polynomin tulolle

Jaetaan suorakulmio neljäksi pienemmäksi suorakulmioksi ja muodostetaan pinta-alan lauseke kahdella eri tavalla.

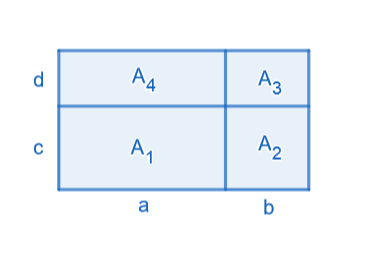
Merkitään pinta-alan lauseketta kirjaimella .

Tapa 1:

Suorakulmion kannan pituus on a+b ja korkeus c+d .

Suorakulmion pinta-ala on kannan korkeuden ja korkeuden tulo, joten saadaan suorakulmiolle lauseke

A=(a+b)(c+d)

Tapa 2:

Pienempien suorakulmioiden pinta-alojen lausekkeet ovat A_1=ac, A_2=bc, A_3=bd ja A_4=ad . Kun lasketaan pienempien suorakulmioiden pinta-alat yhteen saadaan suorakulmioille lauseke

A=ac+bc+bd+ad=ac+ad+bc+bd

Kun asetetaan pinta-alat yhtä suuriksi, saadaan polynomien tulon laskusääntö: (a+b)(c+d)=ac+ad+bc+bd

1.2.6 Esimerkki: kahden polynomin tulo

Laske.

Ratkaisu:

Kerrotaan termeillä $\textcolor{red}{3x}$ ja $\textcolor{blue}{-1}$ molemmat jälkimmäisen polynomin termit.

$\begin{align*} &(\textcolor{red}{3x}\textcolor{blue}{-1})(x+2) \\ &=\textcolor{red}{3x}\cdot x+\textcolor{red}{3x}\cdot 2\textcolor{blue}{-1}\cdot x\textcolor{blue}{-1}\cdot2 \\ &=3x^2+6x-x-2 \\ &=3x^2+5x-2 \end{align*}$

Kerrotaan termeillä $\textcolor{red}{x^2}$ ja $\textcolor{blue}{-2}$ kaikki jälkimmäisen polynomin termit.

$\begin{align*} &=(\textcolor{red}{x^2}\textcolor{blue}{-2})(2x^2-3x+5) \\ &=\textcolor{red}{x^2}\cdot2x^2+\textcolor{red}{x^2}\cdot (-3x)+\textcolor{red}{x^2}\cdot5 \textcolor{blue}{-2}\cdot2x^2\textcolor{blue}{-2}\cdot (-3x)\textcolor{blue}{-2}\cdot5 \\ &=2x^4-3x^3+5x^2-4x^2+6x-10 \\ &=2x^4-3x^3+x^2+6x-10 \end{align*}$

Vastaus:

Jos lasku sisältää useita eri laskutoimituksia, sievennettäessä täytyy noudattaa tuttua laskujärjestystä.

Laskujärjestys

Lasketaan sulut.
Lasketaan kerto- ja jakolaskut sekä potenssiin korotukset.
Lasketaan yhteen- ja vähennyslaskut.

1.2.7 Esimerkki: useampia laskutoimituksia

Laske.

Ratkaisu:

Vaihdantalain perusteella ei ole väliä, missä järjestyksessä kertolaskut lasketaan. Valitaan, että lasketaan ensin polynomien ja 2x+4 tulo.

$\begin{align*} &\textcolor{red}{-x}(\textcolor{red}{2x+4})(x^2-x) \\ &=(\textcolor{red}{-x\cdot2x-x\cdot4})(x^2-x) \\ &=(-2x^2-4x)(x^2-x) &&|\;\text{sievennetään kertolaskun tulos}\\ &=-2x^2 \cdot x^2-2x^2 \cdot (-x)-4x \cdot x^2-4x\cdot(-x) &&|\;\text{lasketaan kahden polynomin tulo}\\ &=-2x^4 +2x^3 -4x^3+4x^2 &&|\;\text{yhdistetään samanmuotoiset termit}\\ &=-2x^4 -2x^3 +4x^2 \end{align*}$

Kirjoitetaan potenssi kahden polynomin tulona ja lasketaan se ensin.

$\begin{align*} &4x-(\textcolor{red}{2x-3})^ {\textcolor{red}2} \\ &=4x-(\textcolor{red}{2x-3})(\textcolor{red}{2x-3}) \\ &=4x-(\textcolor{red}{2x\cdot 2x-2x\cdot(-3)-3\cdot 3x-3\cdot(-3)}) \\ &=4x-(4x^2-6x-6x+9) &&|\;\text{sievennetään kertolaskun tulos}\\ &=4x-(4x^2-12x+9) \\ &=4x-4x^2+12x-9 \\ &=-4x^2+16x-9 &&|\;\text{järjestetään termit asteluvun mukaan} \end{align*}$

Vastaus:

Lausekkeiden ja polynomien laskutoimituksia: tehtäviä

1.3 Lausekkeet ongelmien ratkaisussa

1.3.1 Esimerkki: suorakulmion piiri

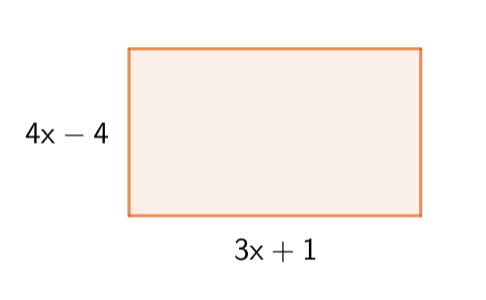
Muodosta polynomi joka kuvaa kuvan suorakulmion piiriä.
Laske polynomin arvo, kun .

Ratkaisu:

Kuvan suorakulmion kannan pituus on ja korkeus joten sen piiriä kuvaa polynomi $P(x)=2\cdot(3x+1)+2\cdot(4x-4)$ . Sievennetään käyttäen opittuja laskusääntöjä.

$\begin{align*} P(x)&=2\cdot(3x+1)+2\cdot(4x-4) \\ &=2\cdot4x+2\cdot(-4)+2\cdot3x+2\cdot1 \\ &=8x-8+6x+2 \\ &=12x-6 \end{align*}$

Suorakulmion piiriä kuvaa siis polynomi P(x)=12x-6.

Polynomin arvo saadaan sijoittamalla lausekkeeseen .

$P(2)=12\cdot 2-6=24-6=18$

Kun x=2, suorakulmion piirin pituus on 18.

Vastaus:

1.3.2 Esimerkki: päiväkodin ongelma

Päiväkodin hoitaja huomasi, että neliönmuotoiset askartelupaperit ovat liian suuria tarhalaisten askarteluun. Hoitaja päätti ottaa käyttöön suorakuolmion muotoiset askarteluarkit, joiden yksi sivu on $5\;\text{cm}$ pidempi ja toinen sivu $5\;\text{cm}$ lyhyempi kuin neliöiden sivun pituudet. Kuinka paljon pienempi on pinta-alaltaan suorakaiteen muotoinen askartelupaperi kuin neliön muotoinen askartelupaperi?

Ratkaisu:

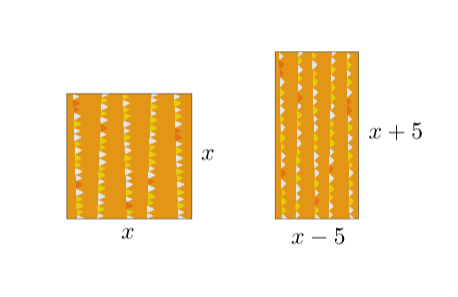
Olkoon neliön sivu. Tällöin neliön pinta-ala on $A_{1}=x^2\;(\text{cm}^2)$

Suorakulmion pinta-ala saadaan kannan ja korkeuden tulona, joten suorakulmion pinta-ala on

$\begin{align*} A_2&=(x+5)(x-5) \\ &=x^2-5x+5x-5^2 \\ &=x^2-25\;(\text{cm}^2) \end{align*}$

Lasketaan pinta-alojen erotus $A_1-A_2=x^2-(x^2-25)=x^2-x^2+25=25\;(\text{cm}^2)$

Vastaus: Suorakaiteen muotoinen askartelupaperi on pinta-alaltaan $25\;\text{cm}^2$ pienempi kuin neliön muotoinen askartelupaperi.

Lausekkeet ongelmien ratkaisussa: tehtäviä