3. Toisen asteen polynomifunktio- ja yhtälö: tehtäviä

Tällä sivulla on tehtäviä, jotka liittyvät kappaleeseen Toisen asteen polynomifunktio ja -yhtälö. Tehtävät on ryhmitelty samojen otsikoiden alle kuin aiemmin mainitussa kappaleessakin.

3.1 Toisen asteen polynomifunktio: tehtäviä

Tämän kappaleen teoria.

3.1.1 Tehtävä

# p312

3.1.2 Tehtävä

# p313

3.1.3 Tehtävä

Funktion lauseke	Nollakohdat


	$x=-4\;\text{ja}\;x=-1$
	$x=-4\;\text{ja}\;x=-1$
	$\text{ei ole}$
	$\text{ei ole}$

Yhdistä funktiot oikeisiin kuvaajiin ilman teknisiä apuvälineitä. Tehtävästä saa pisteet, kun funktion nimen sininen pallo osuu oikean kuvaajan alapuolella olevaan ruutuun.

# MAA5_1a

3.1.4 Tehtävä

Toisen asteen polynomifunktiosta tiedetään, että se saa alla olevan taulukon mukaisia arvoja. Täydennä taulukkoon puuttuvat funktion arvot kuvaajan symmetrisyyttä hyödyntäen. Taulukossa ei ole automaattitarkistusta.

# taulukko4

Open plugin

Vihje

Pisteiden piirtäminen koordinaatistoon voi auttaa hahmottamisessa.

Ratkaisu

# p314

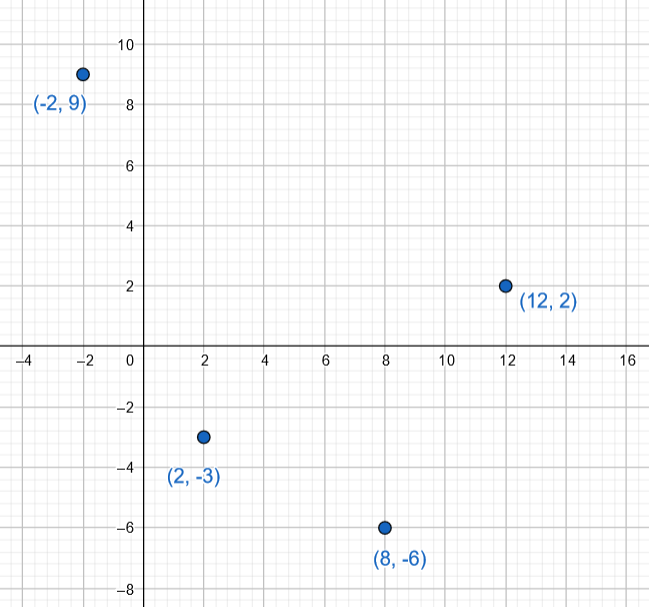
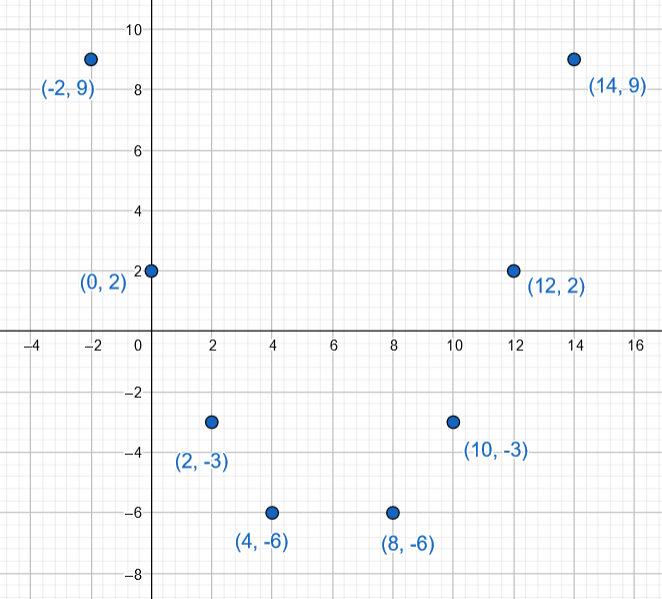
3.1.5 Tehtävä

Käy pelaamassa Super Mario Quadratics -peliä oheisesta linkistä. Pelissä tarkoituksena on muodostaa erilaisia toisen asteen yhtälöitä kerätäkseen kolikoita ja tähtiä Super Mario -tasoilta.

Peliin pääset tästä:
https://teacher.desmos.com/activitybuilder/custom/5c7614041509d870d4838bfd

3.2 Toisen asteen yhtälö: tehtäviä

Tämän kappaleen teoria.

Ratkaise tehtävät 3.2.1-3.2.6 ilman laskinta. Hahmottele ratkaisusi paperille tai käytä tehtävien alta löytyvää Abitti-editoria. Jos yhtälöllä on kaksi ratkaisua, kirjoita ratkaisu muodossa x= or x=. Jos yhtälöllä ei ole ratkaisua, vastaa FF.

3.2.1 Tehtävä

Ratkaise täydelliset toisen asteen yhtälöt.

# p322a

# p322b

3.2.2 Tehtävä

Ratkaise vaillinaiset toisen asteen yhtälöt.

# p323a

# p323b

3.2.3 Tehtävä

Ratkaise vaillinaiset toisen asteen yhtälöt.

# p324a

# p324b

3.2.4 Tehtävä

# Plugin1

# p329a

3.2.5 Tehtävä

Ratkaise toisen asteen yhtälöt.

# p326b

# p326a

3.2.6 Tehtävä

# p326

3.2.7 Tehtävä

San Fransiscossa sijaitsevan Golden Gate -sillan riippuköysi on paraabelin muotoinen. Köyden korkeutta metreinä merenpinnasta kahden pylonin välissä kuvaa likimain yhtälö y=0,00038x^2-0,48x+230 , missä on etäisyys vaakasuunnassa ensimmäiseen pyloniin. Pyloni tarkoittaa kannatinpylvästä, johon siltaa kannattavat köydet tukeutuvat.

Vastaa jokaiseen kohtaan kymmenen metrin tarkkuudella.

# gatea

# gateb

Vihje

Ensin täytyy selvittää pylonien korkeus, joka saadaan yhtälöstä, silloin kun x=0.

Kun korkeus on selvillä, halutaan selvittää, millä toisella muuttujan arvolla, yhtälö saa muuttujan arvoksi selvitetyn korkeuden $\dots$

# gatec

Vihje

Köyden matalin kohta on pylonien puolessa välissä $\dots$

3.2.8 Tehtävä

Kultaisessa leikkauksessa jana jaetaan kahteen osaan niin, että lyhyemmän osan suhde pidempään osaan on sama kuin pidemmän osan suhde koko janaan. Kultaista leikkausta noudattavat pituudet ja muodot koetaan usein esteettisesti miellyttävänä. Tämän takia kultaista leikkausta on Antiikin ajoista lähtien paljon taiteessa ja arkkitehtuurissa.

Jotta ihmiskeho hipoisi täydellisyyttä, pitäisi navan jakaa vartalo pituussuunnassa kultaisen leikkauksen suhteessa. Antiikin kreikkalainen veistos Milon Venus edustaa tällaista ihmiskehoa. Mitkä ovat veistoksen "kultaiset mitat", kun patsaan korkeus on 2,03 metriä? Vastaa sentin tarkkuudella.

# 337a

# 337b

Vihje

Merkitään pitempää osaa muuttujalla , jolloin lyhyempi osa on 203-x .

Lyhyemmän osan suhde pitempään: $\dfrac{203-x}{x}$

Pidemmän osan suhde koko janaan: $\dfrac{x}{203}$

Nyt siis pätee yhtälö $\dfrac{203-x}{x}=\dfrac{x}{203}$ .

Sieventämällä ja ratkaisemalla toisen asteen yhtälö saadaan vastaus $\dots$

3.3 Diskriminantti: tehtäviä

Tämän kappaleen teoria.

3.3.1 Tehtävä

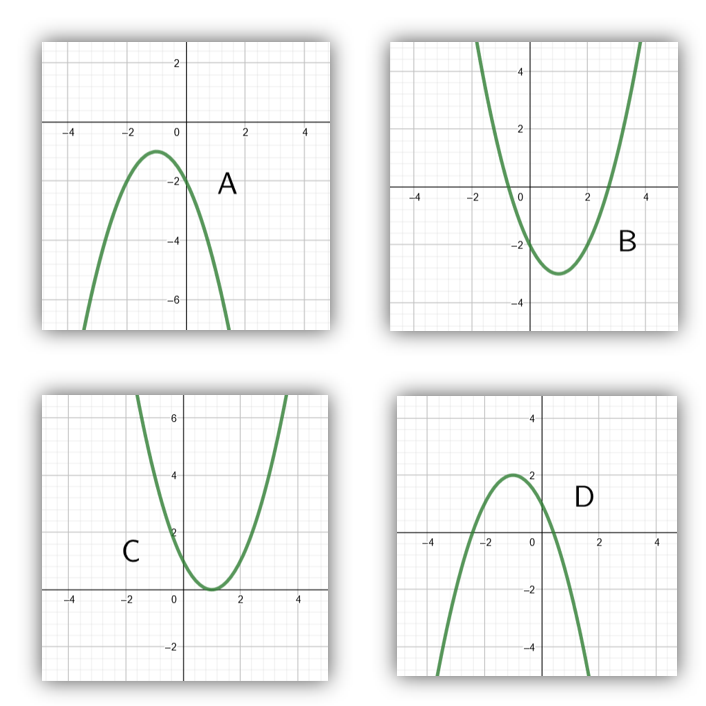
Yllä on näkyvissä toisen asteen polynomifunktioiden kuvaajia. Päättele kuvaajan avulla funktion nollakohtien lukumäärä. Päättele myös, onko yhtälön diskriminantti positiivinen, negatiivinen vai nolla, ja täydennä nämä tiedot taulukkoon. Tehtävässä ei ole automaattitarkistusta.

# taulukko2

Open plugin

3.3.2 Tehtävä

Tarkastellaan yhtälöä $214x^{2}-102x=-12$ .

# p332

# MAA2_6

3.3.3 Tehtävä

Tarkastellaan funktiota $f(x)= 0,9x^{2}+14,4-7,2x$ .

# MAA2_7a

# MAA2_7b

3.3.4 Tehtävä

# p327

Vihje

Yhtälöllä on tasan yksi ratkaisu, kun sen diskriminantti on nolla. Saadaan siis yhtälö

$D=(-3a)^2-4\cdot1 \cdot 9=0,$

jonka ratkaisuna saadaan kysytyt vakion arvot.

3.3.5 Tehtävä

# MAA2_8

3.3.6 Tehtävä

Tarkastellaan funktiota $f(x)=x^{2}+2mx+4$ .

# p330

Vihje

Funktion kuvaaja on ylöspäin aukeva paraabeli, joten se on kokonaan -akselin yläpuolella, kun sillä ei ole yhtään nollakohtaa. Tällöin funktion determinantti D<0 .

Funktion determinantti $D=(2m)^2-4\cdot 1\cdot 4=4m^2-16$ .

Funktiolla ei ole nollakohtia, kun

$\begin{align*} 4m^2-16&<0 \\ \dots \end{align*}$

Vastaus

-2<m<2

3.3.7 Tehtävä

Funktion $f(x)=\dfrac{1}{3}x^{2}+nx+12$ kuvaaja on muodoltaan ylöspäin aukeava paraabeli.

# p331

3.4 Toisen asteen polynomin jakaminen tekijöihin: tehtäviä

Tämän kappaleen teoria.

3.4.1 Tehtävä

Polynomin 3x^2+3x-6 nollakohdat ovat x_1=1 ja x_2=-2 .

# pl341

Tällöin polynomi jaettuna tekijöihinsä on muotoa

3.4.2 Tehtävä

Lausekkeen $6x^{2}-x-1$ nollakohdat ovat $x_1=-\dfrac{1}{3}$ ja $x_2=\dfrac{1}{2}$ .

# p122a6

3.4.3 Tehtävä

Toisen asteen yhtälöllä 4x^2-20x+25=0 on vain yksi ratkaisu $x_1=\dfrac{5}{2}$ .

# p122a2

3.4.4 Tehtävä

Jaa lauseke tekijöihin muistikaavojen avulla.

# p122a

# p122a4

3.4.5 Tehtävä

Tarkastellaan polynomia $36x^{2}+60x+25$ .

# p345a

# p122a3

3.4.6 Tehtävä

Supista murtolauseke.

# p122a7

Vihje

Osoittaja täytyy jakaa ensin tekijöihin.

x^3-x=x(x^2-1)=x(x+1)(x-1)

# p122a8

Vihje

Osoittajan saa jaettua tekijöihin erotuksen neliön muistikaavalla. Nimittäjän taas saa jaettua tekijöihin erottamalla yhteisen tekijän.

3.4.7 Tehtävä

Jaa lauseke tekijöihin.

# p122a10

# p122a9

Vihje

Lausekkeet voi ratkaista erottamalla yhteisen tekijän. a)-kohdassa yhteinen tekijä on (2+x) ja b)-kohdassa (y^2-1) .

Tällaista tapaa kutsutaan ryhmittelyksi ja siihen palataan seuraavassa luvussa.

Ratkaisu

$\begin{align*} &x(2+x)-(2+x) \\ &=(2+x)(x-1) \end{align*}$

$\begin{align*} &y(y^2-1)+(y^2-1) \\ &=(y^2-1)(y+1) \\ &=(y+1)(y-1)(y+1) \end{align*}$

3.5 Toisen asteen epäyhtälö: tehtäviä

Tämän kappaleen teoria.

3.5.1 Tehtävä

# p351a

b) Hahmottele funktion f(x)=x^2-3x-4 kuvaaja. Riittää, että kuvaajasta näkyy paraabelin aukeamissuunta ja nollakohdat.

# p351b

# p351c

3.5.2 Tehtävä

Valitse kuvaajaan sopiva epäyhtälö.

# p352a

# p352b

3.5.3 Tehtävä

Ratkaise edellisen tehtävän epäyhtälöt kuvaajien perusteella.

# p353a

# p353b

3.5.4 Tehtävä

Ratkaise epäyhtälö ilman teknisiä apuvälineitä. Tarkista tulos symbolisen laskennan ohjelmalla.

# p354a

# p354b

3.5.5 Tehtävä

Ohessa on funktion kuvaaja. Valitse epäyhtälöihin oikea ratkaisu.

# p355a

# p355b

# p355c

# p355d

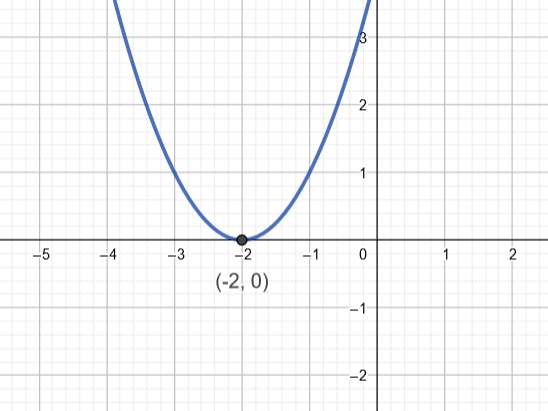
3.5.6 Tehtävä

Markus myy Berliinissä pretzeleitä turisteille. Jos pretzeleiden myyntihinta on $3\;\text{€/kpl}$ , Markus myy niitä päivässä $70\;\text{kpl}$ . Hinnan nostaminen sentillä vähentää myytyjen pretzeleiden lukumäärää neljällätoista.

# p356a

# p356b