Normalisoinnin perusteet

Osissa 2 ja 3 opimme tapoja suunnitella relaatiotietokanta ns. "hyvien oppien" mukaisesti. Relaatiomallin oikeanlainen käyttö tarjoaa suojan ja jotain varmistuksia tietokannassa olevalle datalle. Esimerkiksi jos suunniteltaisiin relaatio OPISKELIJA(optun, syntymäaika), jossa perusavain olisi {optun}, on mahdotonta edes vahingossa saattaa taulu tilanteeseen, jossa samalla opiskelijalla olisi kaksi eri syntymäaikaa:

optun syntymäaika
o1 1.2.1990
o1 2.3.2000

Tämä tilanne on relaatiomallin kannalta mahdoton, sillä taulun jokainen rivi pitää pystyä erottamaan toisistaan perusavaimen perusteella, eikä siis tauluun voisi lisätä kahta riviä, joilla on sama opiskelijatunnus.

Osassa 4 opimme myös, että relaatiotietokannanhallintajärjestelmät (RDBMS) automaattisesti varmistavat tietokannan oikeellisuuden aina, kun dataa lisätään, muokataan poistetaan. Esimerkiksi RDBMS:t tarkistavat datan tyypin, varmistavat perusavaimen mukaisen rivien yksikäsitteisyyden ja vieläpä katsovat, että viiteavainten viite-eheys säilyy.

Aina kuitenkaan relaatiomallin peruspalikat eivät riitä takaamaan datan loogisuutta. Yleisesti, jos taulu voidaan saattaa kohdealueen kannalta "järjettömään" tilaan, vika on usein tietokannan rakenteessa. Tässä osassa tutustumme normalisointiin, eli miten tietokannan rakenteen suunnittelulla suojataan datan loogisuutta ja vähennetään toisteisuutta.

Normalisoinnin tarkoitus

Normalisoinnilla on kaksi päätarkoitusta:

  1. korjata tietokannan datan oikeellisuusvirheille alttiita rakenteita ja
  2. vähentää datan toisteisuutta (redundancy) muuten loogisesti oikeellisesti suunnitellussa rakenteessa.

Tämän lisäksi normalisointi helpottaa tietokannan käyttöä seuraavasti:

  • Normalisoituja tauluja ovat yksinkertaisempia ymmärtää, ei ole ns. "turhia" sarakkeita.
  • Normalisoituja tauluja on helppoa laajentaa kattamaan uusia kohdealueen tarpeita. Parhaimmillaan laajentaminen ei vaadi muutoksia tietokannan rakenteeseen.
  • Normalisoidut taulut ovat paremmin suojattu lisäys-, poisto- ja muokkausoperaatioista johtuvista poikkeamista (eli datan ristiriidoilta).

Datan oikeellisuusvirheille alttiilla rakenteella tarkoitetaan huonosti kohdealuetta kuvaavien attribuuttien nimiä, rakenteita, jotka suosivat runsaasti tyhjäarvoja sekä relaatiorakenteita, joihin on tarpeettomasti valittu attribuutteja useasta reaalimaailman kohteesta.

Datan toisteisuudella tarkoitetaan puolestaan samojen arvojen tarpeetonta toistamista. Datan toisto luonnollisesti kasvattaa tallennustilatarpeita. Datan toisto johtaa myös helpommin myös datan oikeellisuuden poikkeamiin.

Esimerkki

Tarkastellaan seuraavaa opiskelijatietokantaa, joka sisältää yhden taulun. Taulu pitää kirjaa opiskelijoista, kurssisuorituksista, kursseista ja suorituksen arvosanoista:

optun opnimi kurssitun kurssinimi arvosana
o7111 Aatami Laippa itka204 Tietokannat 5
o7111 Aatami Laippa itkp113 Oliosuunnittelu 4
o7111 Aatami Laippa tjta114 Tietohallinto HYV
o6800 Bertta Hukari itka204 Tietokannat 5
o6604 Cecilia Rastas tjta114 Tietohallinto HYV

Nykyisellä rakenteella tietojen lisäys, muokkaus tai poisto voi helposti aiheuttaa poikkeamia tietokantaan. Poikkeama tarkoittaa sitä, että tietokannan tieto jää ristiriitaiseksi itsensä tai kohdealueen kanssa tietokantaan kohdistuvan operaation jälkeen.

Millaisia lisäys-, muokkaus- ja poistopoikkeamia keksitään tälle tietokannalle?

  • Oletetaan, että tauluun lisätään seuraava rivi:

    optun opnimi kurssitun kurssinimi arvosana
    o6800 Bertta Hukari tjta114 Tietohallinnon perusteet 5

    Kurssin tjta114 nimestä tulee ristiriitainen, sillä lisäyksen jälkeen kurssin nimi voi olla "Tietohallinto" tai "Tietohallinnon perusteet".

    Kyseessä on siis lisäyspoikkeama.

  • Oletetaan, että taulusta poistetaan seuraava rivi:

    optun opnimi kurssitun kurssinimi arvosana
    o7111 Aatami Laippa itkp113 Oliosuunnittelu 4

    Nyt Aatami Laipalta poistui Oliosuunnittelu-kurssin suoritus, mutta nyt myös koko tietokannasta poistui tieto Oliosuunnittelu-kurssin olemassaolosta. Nyt jos tietokannan avulla haluttaisiin selvittää, mitä kaikkia kursseja opetetaan, tietokannasta ei löytyisi Oliosuunnittelu-kurssia. Tämä olisi ristiriidassa kohdealueen kanssa.

    Kyseessä on poistopoikkeamia.

  • Oletetaan, että kurssin itka204 kurssikoodi muuttuu koodiksi itka2004 ja nimi muuttuu "Tietokantojen perusteet". Muutoksen takia muutetaan rivi

    optun opnimi kurssitun kurssinimi arvosana
    o7111 Aatami Laippa itka204 Tietokannat 5

    muotoon

    optun opnimi kurssitun kurssinimi arvosana
    o7111 Aatami Laippa itka2004 Tietokantojen perusteet 5

    Nyt kuitenkin unohdimme, että taulussa on opiskelija o6800, jonka rivi pitäisi myös päivittää! Tietokannan dataan tulee ristiriita: yhdellä opiskelijalla on uuden kurssikoodin ja kurssin nimen suoritus, mutta toisella opiskelijalla on vanhan, olemattoman kurssikoodin mukainen suoritus.

    Päädyimme siis muokkauspoikkeamaan.

Nykyinen tietokanta kaipaa siis kipeasti normalisointia!

PS: Yleisestikin, jos kohdealueen kaikkia eri kohteita mallinnetaan samaan tauluun, poikkeamat ovat erittäin mahdollisia.

Funktionaalinen riippuvuus

Kuten huomattiin, datan liiallinen toisteisuus aiheuttaa ongelmia, ja normalisoinnin ytimessä on sen vähentäminen. Toisaalta jonkinlainen toisteisuus on välttämätöntä: yllä olevassa esimerkissä perusavaimeen kuuluvat opiskelijan tunnus ja kurssikoodi on pakko toistaa taulussa, jotta perusavaimen takaama rivien yksilöllisyys voidaan taata. Toisin sanoin toisteisuus on virhealtista, mutta kaikkea datan toistoa ei voida välttää. Miten voidaan siis erottaa "sallittua" toisteisuutta sellaisesta, joka voisi olla altista poikkeamille?

Esimerkki

Palataan hetkeksi Luvussa 3.1 perusavaimen yhteydessä olevaan esimerkkiin taulusta OPISKELIJA(opnro, hetu, etunimi, sukunimi, postinro, paikkakunta).

Keksitäänpä malliksi jotain dataa, jotta ongelmia on helpompaa tarkastella:

opnro hetu etunimi sukunimi postinro paikkakunta
o101 120196-111X Matti Meikäläinen 33720 Tampere
o102 130280-112X Lumi Sinkki 40520 Jyväskylä
o103 130280-321Z Lumi Sinkki 40520 Jyväskylä
o104 121240-111A Aku Ankka 60200 Seinäjoki
o105 241252-321X Taavi Ankka 33720 Tampere

Muistellaan, että avainehdokas on jakamaton joukko sarakkeita, jotka yksilöivät koko rivin. Toisin sanoin avainehdokkaan sarakkeiden arvojen perusteella voidaan yksilöllisesti tietää tasan tarkkaan jonkun rivin kaikkien muiden sarakkeiden arvot.

Luvun 3.1 esimerkissä totesimme, että:

  • {opnro} on avainehdokas, sillä opnro-sarakkeen arvon perusteella tiedetään yksilöllisesti sarakkeiden {hetu, etunimi, sukunimi, postinro, paikkakunta} arvot.
    • Esimerkiksi jos tiedetään, että jonkun opiskelijan opnro on o101, tiedetään, että sen opiskelijan hetu on "120196-111X", etunimi Matti, sukunimi Meikäläinen, postinro 33720 ja paikkakunta Tampere.
  • {hetu} on myös avainehdokas samalla perustelulla: jos tiedetään jonkun opiskelijan hetu, tiedetään yksilöllisesti sitä vastaavat arvot {opnro, etunimi, sukunimi, postinro, paikkakunta}.

Taulun ja kohdealueen perusteella voidaan tehdä seuraava mielenkiintoinen huomio: vaikka {postinro} ei yksilöi kaikkia taulun sarakkeita, se yksilöi sarakkeen paikkakunta. Jos tiedetään, että jonkun oppilaan osoitteen postinumero on 33720 tiedämme yksikäsitteisesti, että paikkakunta on Tampere.

Toisin sanoin {postinro} ei ole OPISKELIJA-taulun avainehdokas, mutta se silti käyttäytyy sen tapaisesti paikkakunta-sarakkeen suhteen: postinumero ei yksilöi kaikkia taulun sarakkeita, mutta se silti yksilöi jotain sarakkeita. Näemme taulussa myös, että paikkakunta-sarakkeessa on toisteisuutta.

Kokeillaan tehdä taulu PAIKKAKUNTA(postinro, paikkakunta) ja kopioidaan tietoa OPISKELIJA-taulusta:

postinro paikkakunta
33720 Tampere
40520 Jyväskylä
60200 Seinäjoki

Tässä relaatiossa nyt {postinro} on avainehdokas, sillä se yksilöi sarakkeen paikkakunta, joka on ainoa avainehdokkaan ulkopuolella oleva sarake. Se on myös ainoa avainehdokas, eli myös perusavain. Erityisesti toisteisuutta on vähennetty: samaa postinumeron ja paikkakunnan yhdistelmää ei toistu turhaan.

Esimerkistä voimme päätellä, että normalisointiin liittyy läheisesti se, miten hyvin sarakkeiden arvot ovat yksilöitävissä toisten sarakkeiden arvojen perusteella. Asia liittyy myös osin avainehdokkaiden ja perusavainten määritelmään, mutta vähän yleisemmällä tasolla. Tästä päästäänkin funktionaalisiin riippuvuuksiin.

Funktionaalisen riippuvuuden määritelmä

Normalisoinnin tärkein käsite on funktionaalinen riippuvuus (functional dependency). Annetaan alkuun tarkka määritelmä relaatiomallin sanoin:

Määritelmä

Jos joukko relaation R attribuutteja X yksilöi jonkun toisen joukon saman relaation attribuutteja Y, sanotaan, että relaatiossa pätee funktionaalinen riippuvuus

{X} -> {Y}

Funktionaalisessa riippuvuudessa X on määräävä attribuuttijoukko. Sanotaan, että "Attribuutit Y riippuvat funktionaalisesti attribuuteista X" tai "Y on funktionaalisesti riippuvainen X:stä". Yleisemmin voi sanoa, että "X yksilöi Y:n".

Toisin sanoen jokaisella monikolla, jossa attribuuteilla X on tietty arvo a, on attribuuteilla Y korkeintaan yksi arvo b.

Käytännössä funktionaalinen riippuvuus on tosi lähellä avainehdokkaan määritelmää. Avainehdokas on mikä tahansa (jakamaton) relaation attribuuttijoukko, joka yksilöi monikon kaikki muut attribuutit. Funktionaalinen riippuvuus taas on mikä tahansa relaation attribuuttijoukko, joka yksilöi minkä tahansa muun joukon relaation attribuutteja.

Otetaan vielä pari esimerkkiä käsitteen selkeyttämiseksi:

Esimerkki

Palataan taas Luvussa 3.1 perusavaimen yhteydessä olevaan esimerkkiin taulusta OPISKELIJA(opnro, hetu, etunimi, sukunimi, postinro, paikkakunta) sekä aiemmassa esimerkissä keksittyyn mallidataan:

opnro hetu etunimi sukunimi postinro paikkakunta
o101 120196-111X Matti Meikäläinen 33720 Tampere
o102 130280-112X Lumi Sinkki 40520 Jyväskylä
o103 130280-321Z Lumi Sinkki 40520 Jyväskylä
o104 121240-111A Aku Ankka 60200 Seinäjoki
o105 241252-321X Taavi Ankka 33720 Tampere

Aiemmassa esimerkissä totesimme, että {opnro} on avainehdokas. Avainehdokas yksilöi taulun kaikki muut sarakkeet: jos tiedetään opiskelijan opiskelijanumero, tiedetään yksikäsitteisesti opiskelijan muiden sarakkeiden arvot. Toisin sanoin on voimassa seuraava funktionaalinen riippuvuus:

{opnro} -> {hetu, etunimi, sukunimi, postinro, paikkakunta}

Tämä ei kerro mitään uutta mitä ei avainehdokkaasta tiedettä; se on vaan eri tapa merkitä asiaa.

Vastaavasti koska {hetu} on avainehdokas, pätee myös seuraava funktionaalinen riippuvuus:

{hetu} -> {opnro, etunimi, sukunimi, postinro, paikkakunta}

Aiemmassa esimerkissä huomattiin, että sarake postinro yksilöi sarakkeen paikkakunta. Jos tiedetään, että jonkun opiskelijan postinro on 33720, tiedetään yksikäsitteisesti, että opiskelijan paikkakunta on aina Tampere. Funktionaalisen riippuvuuden merkinnöillä siis:

{postinro} -> {paikkakunta}

Esimerkki

Tarkastellaan seuraavaa taulua HENKILÖ(htun, nimi):

htun nimi
010160-ABCD Aatami Laippa
020270-EFGH Bertta Hukari
030380-IJKL Aatami Laippa
040490-MNOP Cecilia Rastas

Vaikka emme tietäisi mitään kohdealueesta, voidaan taulun tietojen perusteella päätellä, että seuraava funktionaalinen riippuvuus pätee:

{htun} -> {nimi}

Se pätee, koska jokaista htun-sarakkeen arvoa vastaa yksikäsitteinen nimi. Esimerkiksi, jos tiedetään, että rivin htun-sarakkeen arvo on 010160-ABCD, tiedetään, että sitä vastaa yksikäsitteisesti nimi Aatami Laippa.

Seuraava funktionaalinen riippuvuus ei päde:

{nimi} -> {htun}

Se ei päde, sillä esimerkiksi nimi-sarakkeen arvolla Aatami Laippa löytyy kaksi eri mahdollista htun sarakkeen arvoa: 010160-ABCD ja 030380-IJKL. Funktionaalinen riippuvuus tarkoittaa, että vastaavuus on yksikäsitteinen: jokaiselle nimelle pitäisi löytyä korkeintaan yksi henkilötunnus, mutta näin ei tässä ole.

On syytä huomata, että yllä olevissa esimerkeissä funktionaaliset riippuvuudet on johdettu esimerkkidatasta. Tavallisesti normalisointi saatetaan tehdä jo tietokannan suunnittelun vaiheessa, kun dataa ei vielä ole. Silloin funktionaaliset riippuvuudet on pääteltävä kohdealuetta ymmärtämällä. Vaikka funktionaalisten riippuvuuksien esittämiseen käytetään matemaattista notaatiota, ei kysymyksessä ole matemaattinen ilmiö vaan nimenomaan relaation merkityksen ymmärtäminen.

kurssikoodi kurssinimi vuosi opettajatun laajuus
itka201 Algoritmit 2015 op447 4
itka201 Algoritmit 2014 op051 3
itka204 Tietokannat 2014 op300 5
itka204 Tietokannat 2015 op300 5
itka204 Tietokannat 2013 op300 4
tjta118 IT-infra 2014 op411 3
tjta118 IT-infra 2015 op411 3
# monifd

Päättelysäännöt

Yllä olevasta määritelmästä ja esimerkeistä voi päätellä, että jotkut funktionaaliset riippuvuudet voidaan päätellä muista riippuvuuksista. Esimerkiksi jos tiedetään, että opiskelijan opiskelijatunnus yksilöi opiskelijan etunimen, sukunimen ja hetun yhdessä:

{optun} -> {hetu, etunimi, sukunimi}

niin selvästi opiskelijan tunnus yksilöi myös erikseen hetun, etunimen ja sukunimen:

{optun} -> {hetu}
{optun} -> {etunimi}
{optun} -> {sukunimi}

Eli: jos tiedetään, että optun:lla voi löytää tietyn opiskelijan hetun, etunimen sekä sukunimen, niin totta kai optun:lla voi löytää jokaisen tiedon yksittäin.

Armstrong [1] on esittänyt joukon sääntöjä, joilla funktionaalisia riippuvuuksia voi päätellä muiden riippuvuuksien kautta. Sellaisia funktionaalisia riippuvuuksia, joita voidaan päätellä näiden sääntöjen avulla, kutsutaan triviaaleiksi.

  1. Refleksiivisyyssääntö (axiom of reflectivity): jos attribuuttijoukko Y on toisen attribuuttijoukon X osajoukko, pätee triviaali funktionaalinen riippuvuus "X yksilöi Y:n". Eli:

    Jos Y ⊂ X, niin {X} -> {Y}.

    Säännön seurauksena attribuuttien joukko X riippuu aina itsestään, eli:

    {X} -> {X}

    Esimerkki: Opiskelijan etunimi riippuu opiskelijan etunimestä, eli {etunimi} -> {etunimi}. Opiskelijan etunimi riippuu myös etunimen ja sukunimen yhdistelmästä: {etunimi, sukunimi} -> {etunimi}.

  2. Transitiivisuussääntö (axiom of transitivity): jos pätevät funktionaaliset riippuvuudet "X yksilöi Y:n" ja "Y yksilöi Z:n" pätee myös funktionaalinen riippuvuus "X yksilöi Z:n". Eli:

    Jos {X} -> {Y} ja {Y} -> {Z}, niin {X} -> {Z}.

    Esimerkki: Opiskelijan hetusta tiedetään hänen etunimensä ja sukunimensä, eli {hetu} -> {etunimi, sukunimi}. Toisaalta jos tiedetään etunimi ja sukunimi, tiedetään hänen nimikirjaimet, eli {etunimi, sukunimi} -> {nimikirjaimet}. Siispä opiskelijan hetusta tiedetään hänen nimikirjaimensa, eli {hetu} -> {nimikirjaimet}.

  3. Yhdistesääntö (axiom of union): jos pätevät funktionaaliset riippuvuudet "X yksilöi Y:n" ja "X yksilöi Z:n", pätee myös funktionaalinen riippuvuus "X yksilöi Y:n ja Z:n yhdisteen". Eli:

    Jos {X} -> {Y} ja {X} -> {Z}, niin {X} -> {Y, Z}.

    Esimerkki: Opiskelijan opiskelijatunnus yksilöi opiskelijan etunimen, eli {optun} -> {etunimi}. Toisaalta myös opiskelijan opiskelijatunnus yksilöi myös opiskelijan sukunimen, eli {optun} -> {sukunimi}. Siispä opiskelijan tunnus yksilöi opiskelijan etunimen sekä sukunimen, eli {optun} -> {etunimi, sukunimi}.

  4. Jakosääntö (axiom of decomposition): jos pätee funktionaalinen riippuvuus "X yksilöi Y:n ja Z:n yhdisteen", pätevät myös funktionaaliset riippuvuudet "X yksilöi Y:n" ja "X yksilöi Z:n". Eli:

    Jos {X} -> {Y, Z}, niin {X} -> {Y} sekä {X} -> {Z}.

    Esimerkki: Opiskelijan hetu yksilöi etunimen ja sukunimen, eli {hetu} -> {etunimi, sukunimi}. Siispä opiskelijan hetu yksilöi etunimen ({hetu} -> {etunimi}) sekä se yksilöi sukunimen ({hetu} -> {sukunimi}).

  5. Täydentämissääntö (axiom of augmentation): jos pätee funktionaalinen riippuvuus "X yksilöi Y:n", pätee myös funktionaalinen riippuvuus "X:n ja Z:n yhdistelmä yksilöi Y:n", ts. jos "X yksilöi Y:n", niin "X:n ylijoukot myös yksilöivät Y:n". Eli:

    Jos {X} -> {Y}, niin {X, Z} -> {Y}.

    Esimerkiksi: Opiskelijan hetu yksilöi opiskelijan sukunimen, eli {hetu} -> {sukunimi}. Riippuvuus pätee, vaikka määräävään joukkoon lisättäisiin vaikkapa etunimi, eli {hetu, etunimi} -> {sukunimi}.

Huomautus

Jakosäännön ja yhdistesäännön yksi olennainen seuraus on, että funktionaalinen riippuvuus

{X} -> {Y1, Y2, ..., Yn}

on yhtäpitävä sen kanssa, että kaikki seuraavat riippuvuudet pätevät samaan aikaan

{X} -> {Y1}
{X} -> {Y2}
...
{X} -> {Yn}

ja myös toisinpäin. Toisin sanoin ei ole väliä, merkitseekö funktionaaliset riippuvuudet erillään tai sitten yhdistettynä samaan riippuvuuteen.

Huomautus

Huomaa, että yllä olevat säännöt ovat muotoa "jos (1) niin (2)". Sääntö ei välttämättä päde toisin päin, eli "jos (2) niin (1)" ei ole aina totta!

Esimerkiksi yleisin virhepäätelmä on, että määräävää attribuuttijoukkoa voi aina jakaa säilyttäen funktionaalinen riippuvuus!

Tämän luvun alussa olevassa opintosuoritusten tietokannassa on seuraava perusavaimen mukainen riippuvuus:

{optun, kurssitun} -> {opnimi, kurssinimi, arvosana}

(opiskelijatunnus ja kurssitunnus yhdessä yksilöivät opiskelijan nimen, kurssin nimen ja suorituksen arvosanan).

Tässä voi tulla esimerkiksi halu jättää kurssitun pois määräävästä attribuuttijoukosta, sillä esimerkiksi opiskelijan nimi ei riipu kurssin tunnuksesta. Kuitenkaan tämä riippuvuus

{optun} -> {opnimi, kurssinimi, arvosana}

ei enää välttämättä päde, sillä kahdella eri opiskelijalla voi olla sama nimi, suoritettu kurssi ja jopa sama saatu arvosana. Samasta syystä opiskelijan tunnusta ei voi jättää pois määräävästä joukosta.

Sen sijaan tässä tapauksessa huomataan, että ottamalla attribuutteja pois sekä määräävästä että riippuvasta joukosta saadaan useampi validi funktionaalinen riippuvuus:

{optun} -> {opnimi}
{kurssitun} -> {kurssinimi}
{optun, kurssitun} -> {arvosana}

Ole siis tarkkana, että sovellat säännöt ns. oikein päin!

Alla olevassa kuviossa on esitetty toinen tapa kuvata funktionaalisia riippuvuuksia. Nuoli osoittaa tässäkin määräävästä attribuuttijoukosta riippuvaan attribuuttiin. Funktionaaliset riippuvuudet on numeroitu monivalintatehtävän vuoksi.

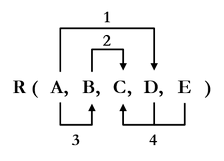
Kuvio: relaation R attribuutit funktionaalisine riippuvuuksineen.
Kuvio: relaation R attribuutit funktionaalisine riippuvuuksineen.
# moniarmax

These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.