Johdanto

Verkon avoimet oppimateriaalit ja lukion uusi opetussuunnitelma muodostavat yhdistelmän, jossa opettaja väistämättä pohtii pedagogisia käytänteitään. Teknologia muuttaa sekä opiskelijan suhdetta matematiikkaan ja luonnontieteisiin että opettajan ja opiskelijan välistä suhdetta. Näistä lyhyistä blogityyppisistä teksteistä saat näkökulmia oman työsi kehittämiseen. Voit pohtia verkko-oppimisen antamia mahdollisuuksia käänteisen opetuksen järjestämiseen ja sulautuvaan, sekä verkossa että kasvokkain tapahtuvaan, oppimiseen. Voit mietiskellä kokeellisuuden ja projektityöskentelyn antamia mahdollisuuksia ja haasteita, sekä arvioinnin suuntaamista opiskelijoiden itseohjautuvuuden tukemiseen itsearvioinnin ja vertaisarvioinnin keinoin. Tekstit myös herättelevät pohtimaan matematiikan tehtävien kielellisiä piirteitä. Tuleva koulu on kielitietoinen ja yhteisöllinen ja yhteisopettajuus eräs sen voimavaroista.

Käänteisen oppimisen pedagogiikkaa

Näkökulmia laadukkaan käänteisen opetuksen järjestämiseen ja opiskelijoiden itseohjautuvuuden tukemiseen.

Opettajan ohje Vuonna 1982 J. Wesley Baker sai idean siirtää luentomateriaalinsa sähköisin keinoin oppituntien ulkopuolelle opiskelijoittensa saataville. Teknologioiden kehittyessä tämä kävi juohevammaksi ja huomattuaan, että opiskelijoiden oli helppo tutustua sisältöihin itsenäisesti etukäteen, Baker huomasi joutuvansa miettimään, miten käyttää luennoilta jäävän ylimääräisen ajan. Hän kehitti mallin, joka keskittyi neljään verbiin: selvennä, laajenna, sovella ja harjoittele. Toinen uranuurtaja käänteisen opetuksen kehittämisessä 1990-luvun alussa oli Harvardin yliopiston fysiikan professori Erik Mazur, joka kehitti menetelmiä yksilöllistääkseen ja räätälöidäkseen opetustaan.

Opettajan ohje Vuonna 1998 Baker alkoi kutsua kehittämäänsä menetelmää nimellä "The Classroom Flip". Samoihin aikoihin Lage, Platt ja Treglia (2000) kehittivät ja toteuttivat vastaavaa menetelmää, jota he kutsuivat nimellä "The Inverted Classroom". Käänteisen menetelmän popularisointi tapahtui kuitenkin vasta, kun kemian yliopistonopettajat Aaron Sims ja Jonathan Bergmann ottivat sen käyttöönsä ja saivat näin merkittävästi lisää aikaa laboratoriotyöskentelylle ja keskusteluille.

Koko idean lähtökohta oli siis laadukkaampi oppimiskokonaisuus. Vaikka luento onkin opetusmenetelmänä tehokas, sen ongelmana on etenemisnopeus. Osa kuulijoista tietää jo asiat tai muuten vain etenisi nopeammin. Joidenkin mielestä edetään liian nopeasti tai heiltä puuttuu tarvittavia esitietoja. Oppitunnin aika kuluu ja jotkut oppilaat olisivat voineet käyttää ajan tehokkaammin. Toisaalta oppilailla ei ole tukea kotona, kun heidän tulisi jatkaa oppimista ja soveltaa luennolla opittuja asioita käytännön tehtäviin. Käänteisen oppimisen etuna oli, että perinteisen ja usein behavioristisen opetuksen osuus voitiin siirtää etukäteisvalmistautumiseen kotona ja konstruktivistinen tai sosio-konstruktivistinen opetus luokkaan.

Käänteinen oppiminen ei ole vain yksilöllistä tehtävien tekemistä

Koko käänteisen oppimisen menetelmä perustuu huolelliseen suunnitteluun (Butzler, 2016).

ENNEN OPPITUNTIA:

Käytä suunnitteluun aikaa, jotta saat mietittyä, miten sisältö puretaan ennen oppituntia ja oppitunnin aikana tehtäviin osiin ja rakenna selkeä yhteys näiden aktiviteettien välille. Linkitä ennen tuntia ja tunnilla tehtävät osat niin, että menestyäkseen opiskelijan tulee tehdä ne molemmat. Anna opiskelijalle mahdollisuus tutustua uuteen aiheeseen ennen oppituntia ja ohjeista ennen oppituntia tehtävä työskentely niin, että oppilas tietää, mitä hänen tulee osata tunnille tultaessa. Tarkoitus on, että kaikki opiskelijat valmistautuvat oppituntiin ja esimerkiksi laativat materiaalista kysymyksiä. Kannusta siis heitä valmistautumaan tunneille. Kotona tehtävän valmistautumisen perustana voivat olla videot, interaktiiviset elementit, valokuvat, tekstit ja helpot, mekaaniset harjoitteet.

OPPITUNNILLA:

Tunti alkaa kyselytuokiolla, tarkastellaan muistiinpanoja ja kysymyksiä materiaalista ja keskustellaan yhdessä aiheesta. Anna opiskelijoille mahdollisuus kysyä ennakkotehtävistä epäselviksi jääneitä asioita, mutta vältä asioiden uudelleen opettamista. Anna sen sijaan opiskelijoiden huomata, että heidän tulee valmistautua tunnille itse ja ottaa vastuuta oppimisestaan.

Opiskelijoiden sosiaalisten ja emotionaalisten tarpeiden täyttäminen on yhtä tärkeää kuin tiedollisten tarpeiden täyttäminen. Siispä oppitunneista tulee tilanteita, joilla ratkotaan ongelmia, syvennetään käsitteitä ja työskennellään yhdessä. Luo oppitunneilla edellytykset oppimisyhteisön syntymiselle ja asioiden pureskelulle, äläkä kuormita opiskelijoita liiallisella määrällä sisältöjä ja tehtäviä. Valikoi huolella käyttämäsi materiaalit ja suuntaa tunnilla tehtävät aktiviteetit niin, että kehität opiskelijoiden ajattelutaitoja ja asiantuntijuutta. Tarjoa työskentelyn tueksi tuttuja tai helposti käytettäviä teknologioita ja anna riittävästi aikaa tehdä tehtäviä. Mieti hyvin, miten ohjaat, jotta opiskelijoiden taidot perustella ja kyseenalaistaa kehittyvät. (Tucker, 2012.)

ARVIOINTI:

Kun oppimisprosessi muuttuu, myös arviointi muuttuu -- opiskelijat voivat osoittaa osaamisensa monin eri tavoin. He voivat tehdä esimerkiksi projekteja, videopelejä, esityksiä, postereita, blogeja. Anna nopeaa ja kohdennettua palautetta yksilö- ja ryhmätyöskentelystä ja mikäli mahdollista anna tilaisuus korjata työtä tai työskentelyä palautteen pohjalta. Anna myös opiskelijalle itselleen mahdollisuus arvioida tietojaan, taitojaan, toimintatapojaan ja asenteitaan. Tarvitaan myös vertaisarviointia ja itsearviointia, jotta opiskelijat huomaavat, mitä he jo osaavat ja mitä eivät vielä osaa, ja milloin he voivat edetä eteenpäin (Abeysekera & Dawson, 2015).

Käänteinen oppiminen edellyttää ja kehittää monia taitoja

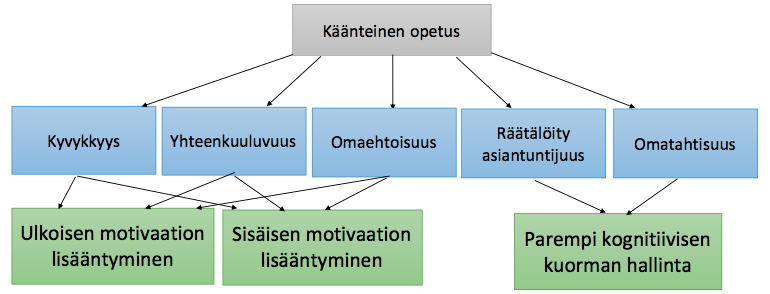
Yleisesti ajatellaan, että käänteinen oppiminen lisää opiskelumotivaatiota. Tämä perustuu ajatukseen siitä, että opiskelijalla on mahdollisuus edetä omaan tahtiin, tehdä omaehtoisia valintoja ja kokea onnistumisia. Usein ajatellaan myös, että näin opiskelijalla on mahdollisuus hallita oppimisensa kognitiivista kuormaa. Opettajan tulee kuitenkin varautua siihen, että osa opiskelijoista kokee epävarmuutta siitä, miten menestyä uudella opetustavalla. Heitä arveluttaa, ovatko heidän tekemänsä valinnat riittäviä ja heitä kuormittaa menetelmän itseohjautuvuuden vaatimukset. Lisäksi omatahtisuus ja omaehtoisuus helposti rajoittavat yhdessä työskentelyä ja ryhmä vähitellen eteneekin aivan eri tahtiin. Siksi opettajan on hyvä pitää kirkkaana mielessään, että oppitunnin tehtävät tukevat juuri niitä taitoja, joita yksin tehty valmistelu ei tue. (Abeysekera & Dawson, 2015).

Opettajalta käänteinen oppiminen edellyttää myös uudenlaisia pedagogisia valmiuksia. Menetelmään soveltuvat aktiviteetit saattavat kaivata lisäkäsiä. Niinpä on syytä tukeutua yhteisopettajuuteen. Samalla opettajat voivat varmistaa, että opiskeltavat aiheet syvenevät myös monitieteisemmiksi ja saavat ulottuvuuksia tiedon soveltamiseen. Lisäksi opettajan on hyvä varautua siihen, että hän joutuu muokkaamaan opetusmateriaalejaan ja kehittelemään niihin enemmän yhdessä tehtäviä osia, jos ne eivät näytä toimivan toivotulla tavalla. Eräs tärkeä käänteisen oppimisen onnistumisen välineistä on vahvistaa opiskelijoiden itseohjautuvuutta.

Miten opettaja voi tukea itseohjautuvuutta?

Itseohjautuvuutta on vaikea määritellä lyhyesti, sillä se koostuu useasta eri ulottuvuudesta. Ensimmäinen näistä ulottuvuuksista on vastuullisuus. Sillä tarkoitetaan vastuunottoa opiskelusta, säännöllistä kotitehtävien tekemistä ja opiskeluvälineistä huolehtimista. Toinen ulottuvuus on halu oppia. Siinä korostuvat puolestaan sisäinen motivaatio, kiinnostus opiskeltavasta asiasta ja halu oppia ilman toivetta ulkoisesta palkkiosta tai pelkoa rangaistuksesta. Kolmas ulottuvuus on kyky luovaan ja itsenäiseen ongelmanratkaisuun. Tähän ulottuvuuteen sisältyy toisaalta opiskelijan avoimuus ja uteliaisuus uusille haasteille, toisaalta epävarmuuden sietokyky. Itseohjautuva opiskelija osa suhtautua opiskeluun terveen kriittisesti. Hän on valmis kyseenalaistamaan ja kokeilemaan, ja näkee eteen tulevat ongelmat pikemminkin haasteina kuin esteinä. Neljäs itseohjautuvuuden ulottuvuus on itsenäisyys ja varmuus. Opiskelija kykenee vastaanottamaan palautetta ja itse arvioimaan omaa oppimistaan. Viides ulottuvuus on itseluottamus. Opiskelija osaa hakea joustavia ratkaisumalleja ja luottaa omaan toimintaansa.

Opiskelijan rooli	Kuvaus	Opettajan keinot
Epäitsenäinen	Opiskelija on riippuvainen ja epäitsenäinen, ja tarvitsee opettajan ohjausta.	Opettaja tukee itseluottamuksen kehittymistä varmistamalla, että opiskelija saa paljon myönteisiä oppimiskokemuksia.
Kiinnostunut	Opiskelija on halukas oppimaan ja odottaa opettajalta kannustusta ja selkeää ohjausta.	Opettaja tukee opiskelijan sisäistä motivaatiota antamalla hänelle mahdollisuuksia vaikuttaa omaan opiskeluunsa.
Sitoutunut	Opiskelija tietää oppimisstrategioista ja osaa soveltaa niitä. Hän kykenee toimimaan ryhmässä ja odottaa pohtivaa työskentelyä.	Opettaja suunnittelee vaihtoehtoisia opiskelutapoja ja ohjaa valintojen tekemiseen.
Itseohjautuva	Opiskelija ottaa itsenäisesti vastuun opinnoistaan ja hän odottaa opettajalta asiantuntijatukea.	Opettaja huolehtii laadukkaasta ohjauksesta ja riittävistä haasteista.

Kirjallisuutta:

Abeysekera, L., & Dawson, P. (2015). Motivation and cognitive load in the flipped classroom: definition, rationale and a call for research. Higher Education Research & Development, 34(1), 1-14.

Butzler, K. B. (2016). The Synergistic Effects of Self-Regulation Tools and the Flipped Classroom, Computers in the Schools, 33:1, 11-23.

Lage, M. J., Platt, G. J., & Treglia, M. (2000). Inverting the classroom: A gateway to creating an inclusive learning environment. The Journal of Economic Education, 31(1), 30-43.

Niemi, H. (2001). Vahvaksi verkossa--kohti itseohjautuvuutta ja oppimisen taitoja. Helsingin yliopisto, kasvatustieteen laitos. V OSA, 167, 102-107.

Salo, O. P. (2015). Oppilaan itseohjautuvuuden tukeminen. Julkaisussa Hildén, R. & Härmälä, M. Hyvästä paremmaksi--kehittämisideoita kielten oppimistulosten arviointien osoittamiin haasteisiin. Kansallinen koulutuksen arviointikeskus ja Opetushallitus. Koulutuksen seurantaraportit, 6, 21-39.

Tucker, B. (2012). The flipped classroom. Education next, 12(1), 82-83.

Kielen merkitys matematiikan opiskelussa

Näkökulmia matematiikan tehtävien kielellisiin piirteisiin, oppitunnilla tapahtuvaan monikieliseen matemaattiseen vuoropuheluun ja matemaattiseen perustelemiseen.

Matematiikan kielen traditio on pitkä ja se on myös kulttuurisesti määräytynyt. Elegantti matematiikan kieli on tiivistä, tarkkaa ja yksiselitteistä, jossa väärinymmärryksen mahdollisuudet on minimoitu äärimmilleen. Matematiikan kieleen kuuluvat sanasto, symbolit, kuvat ja kuviot. Näiden lisäksi voidaan tarkastella erikseen käsitteitä ja prosesseja. Matematiikan kielellä on myös tietty rakenne, joka joskus määräytyy matemaattisen päättelyn perusteella kuten todistuksissa ja joskus vain tavoista ilmaista jokin matemaattinen ajatus.

Matematiikan sanasto on moniulotteista esimerkiksi sana tulo tarkoittaa sekä itse prosessia \(a \bullet b\), että tulosta ja arkikielessä se liittyy mielessämme moniinkin eri yhteyksiin. Voimme puhua lumen tulosta, perille tulosta ja ansiotulosta. Lisäksi matematiikassa jotkin sanat saavat uuden merkityksen, kuten itseisarvo, joka esimerkiksi etiikassa tarkoittaa arvoa, jota ei tarvitse eikä voida perustella muilla arvoilla. Matematiikan kielessä käytämme myös teknisiä termejä kuten sieventäminen, todistaminen, osoittaminen, hahmotteleminen. Niillä kaikilla tarkoitetaan jotain tietynlaista matemaattista toimintaa. Lisäksi matematiikkaan kuuluu muitakin prosesseja kuten luokittelu ja järjestäminen, jotka tosin ovat samalaisia useillakin tieteenaloilla. Matematiikassa on myös omat vakiintuneet tapansa perustella ja selittää.

Kielentäminen on työkalu oman ajattelun kuvaamiseen, kehittämiseen ja arviointiin. Perusopetuksen matematiikan oppimistulosten pitkittäisarvioinnissa (vuosina 2005-2012), jossa samoja oppilaita seurattiin kolmannelta luokalta yhdeksännelle luokalle, huomattiin, että yksittäisten luokan aktiviteettien joukossa eräs tehokas tapa oppia näytti olevan se, että oppilaat neuvoivat toisiaan ja selittivät omia ratkaisujaan toisille oppilaille. On siis tärkeää käyttää tunnilla tehtäviä, joissa tällainen työskentely on mahdollista.

Sanalliset tehtävät haastavat opiskelijoita kielellisesti

Sanallisia tehtäviä käytetään matematiikan tunneilla opeteltaessa ongelmanratkaisua ja kytkettäessä matematiikkaa arjen ilmiöihin. Sanalliset tehtävät ovat tehtäviä, joissa tulee vastata yhteen tai useampaan kysymykseen käyttäen apuna tehtävässä annettua matemaattista informaatiota. Sanalliset tehtävät voidaan jakaa kahteen joukkoon: arjen sanallisilla sovellustehtävillä tutustutaan reaalimaailman ongelmiin, keinotekoisilla sanallisilla tehtävillä harjoitetaan matematiikan menetelmiä. Monet menetelmiä harjoittavat tehtävät ovat tehtäviä, joita arkielämässä tuskin koskaan tarkasteltaisiin matematiikan avulla. Hyvä esimerkki on tuttu lampaiden ja kanojen jalkojen ongelma, tuskin kukaan selvittäisi niiden lukumääriä yhtälöparilla.

Koulun arjessa, ja myös monissa tutkimuksissa on havaittu, että sanallisia tehtäviä ratkoessaan opiskelijat usein vain poimivat lukuja tekstistä ja suorittavat niillä joitain laskutoimituksia, joita kyseisessä kappaleessa harjoitellaan. Miksi näin? Ensimmäisen haasteen heittää sanojen määrä. Opiskelijat eivät tunnu jaksavan lukea pitkiä tehtävänantoja. Toinen haaste syntyy tehtävän kompleksisuudesta. Ei välttämättä kielellisestä kompleksisuudesta, vaan esimerkiksi visuaalisten elementtien lukumäärästä. Usein sanallisiin tehtäviin liittyy muutakin informaatiota, diagrammeja ja kuvioita, tutkittavaksi samanaikaisesti. Nämä yhdessä lisäävät kognitiivista kuormaa ja asioiden mielessä pitämistä. On myös huomattu, että kontekstin tuttuudella on merkitystä. Jos aihealue on itselle vieras, niin silloin tekstin joukkoon mahtuu ihan outoja käsitteitä ja muutenkin on vaikea hahmottaa tehtävässä esiteltyä tilannetta. Tämä käy ilmi esimerkiksi talousmatematiikassa. Muutenkin matematiikan osa-alueella on merkitystä.

Mittaamiseen ja geometriaan liittyvien tehtävien on huomattu olevan vaikeimpia hahmottaa pelkän sanallisen tekstin perusteella. Kaiken tuon lisäksi vaikuttaa se, millaista matemaattista osaamista tehtävässä edellytetään. Pitäisikö tehtävänannon perusteella tietää jotain, soveltaa jotakin, vai jopa osata perustella jotakin? Myös tilasto- ja todennäköisyystehtävät ovat kielellisesti vaikeita. Niissä on yleensä paljon pitkiä sanoja ja tiiviisti kirjoitettuna. Realistisuuden nimissä tehtäviin on myös lisätty seurojen, yritysten ja henkilöiden nimiä. Tilastotehtäviin liittyy myös tarkkuutta lisääviä sanoja kuten enemmän, yhteensä, varmuudella, verrattuna, lainkaan ja niin edelleen, joilla on tässä yhteydessä aivan erityinen merkitys. Joukossa on myös sanontoja, joilla on erityinen, tekninen merkitys kuten "alle 14 vuotta" tai "yhtä suuri kuin".

Matikkapuhetta ja perustelemista

Opettajan kannattaa siis suosia tehtäviä, jotka herättävät keskustelua. Monikielisessä luokassa tämä tarkoittaa myös kunkin oman äidinkielen käyttämistä. Sillä äidinkielemme on myös usein ajattelumme kieli. Monikielisessä luokassa annat myös mahdollisuuden sille, että opiskelijoilla on tilaisuus testata ymmärrystään aiheesta. Tällaisia keskusteluja herättäviä tehtäviä ovat yleensä käsitteellistä ymmärrystä edellyttävät tehtävät. Vertaile seuraavia esimerkkejä, niin huomaat, mitä tarkoitan.

Matemaattisia menetelmiä harjoittavia tehtäviä	Käsitteellistä ymmärrystä kehittäviä tehtäviä
Laske huoneen pinta-ala.	Arvioi huoneen pinta-ala ja perustele arviosi.
Jos nukut 9 tuntia yössä, kuinka monta prosenttia se on vuorokaudesta?	Voidaanko väittää, että ihmiset nukkuvat keskimäärin 30 % vuorokaudesta? Miksi näin on?
Laske \(\frac{\mathbf{1}}{\mathbf{2}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{4}}\) .	Laskematta päättele, kuinka paljon on \(\frac{\mathbf{1}}{\mathbf{2}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{3}}\mathbf{+}\frac{\mathbf{1}}{\mathbf{4}}\). Perustele.
Yhdistä avaruuskappale ja sen tilavuutta ilmaiseva kaava.	Kerro, miten päättelit, mikä kaava liittyy mihinkin avaruuskappaleeseen.
Laske 24 · 12.	Kerro, miten laskisit päässäsi tulon 24 · 12. Voitko laskea sen jollain toisella tavalla, miten?
Kirjoita yhtälöksi ja ratkaise.	Keksi yhtälöön sopiva käytännön esimerkki. Mistä tiedät olevasi oikeassa?

Lähde: http://teachingmathliteracy.weebly.com/conceptual-vs-procedural-knowledge.html

Lukiolaisilta odotetaan, että he oppisivat rakentamaan päteviä perusteluja ja arvioimaan toistensa päättelyä. Eräs keino saavuttaa näitä taitoja on opetella väittelemään. Väiteltäessä jokainen saa tilaisuuden kehittää ja yhdistellä ideoitaan, tunnistaa yhtäläisyyksiä ja eroavaisuuksia, syventää käsitteellistä tai menetelmällistä osaamistaan, sekä keksiä esimerkkejä perusteluidensa tueksi. Väiteltäessä oikeaa tietoa muodostetaan lisäksi yhteistoimin ja joskus jopa rikkaammin kuin mitä opetusmateriaalit esittävät. Väittelytehtäviä voi kehitellä esimerkiksi seuraavilla keinoilla:

Keksi esimerkkejä, joista opiskelijoiden tulee tunnistaa se, joka ei > kuulu joukkoon. Joskus olisi hyvä, jos vastaukseksi kävisi > vaihtoehdoista mikä tahansa. Valinnan perustelut vain olisivat > erilaisia.
Ideoi aiheesta perinteisiä puolesta ja vastaan väittämiä.
Esitä jokin virheellinen tai puutteellinen ratkaisu. Opiskelijoiden > tulee sitten korjata tai täydentää ratkaisua.
Näytä useampi erilainen ratkaisu samaan tehtävään. Opiskelijat > voivat vertailla ratkaisuja eri näkökulmista.
Esitä jokin väite, laki tai määritelmä ja opiskelijoiden tulee > perustella, miksi se pitää paikkansa.
Kerro jostain ilmiöstä ja opiskelijoiden tulee tunnistaa, mihin > teoreettiseen näkökulmaan ilmiö liittyy.
Esittele jokin käsite tai menetelmä ja opiskelijoiden tulee keksiä > esimerkki tai vastaesimerkki siihen liittyen.

Kun opettajana ohjaat väittelyä, anna riittävästi aikaa, jotta opiskelijat ennättävät muodostaa oman mielipiteensä. Jatka työskentelyä niin, että pienryhmät tai parit saavat hetken porista keskenään, näin varmistat, että jokaisella on mahdollisuus sanoa ajatuksensa ääneen. Kootkaa lopuksi yhdessä erilaisista perusteluista listaa ja vetäkää yhteen, mihin lopputulokseen keskustelussa päädytään. Uskon, että huomaat näissä keskusteluissa myös sen, millaisia virhekäsityksiä opiskelijoiden ajatteluun saattaa sisältyä ja pääset helpommin niitä korjaamaan.

Kirjallisuutta:

Abedi, J. & Lord, C. (2001). The language factor in mathematics tests. Applied Measurement in Education, 14(3), 219--234.

Ahlholm, M. & Portaankorva-Koivisto, P. (2018). The language factor -- what exactly is it? Bilingual speakers of Russian and Finnish solving mathematical tasks. Nordic Studies in Mathematics Education, 23(3--4), 101--123.

Bergvall, I., Wiksten Folkeryd, J. & Liberg, C. (2016). Linguistic features and their function in different mathematical content areas in TIMSS 2011. Nordic Studies in Mathematics Education, 21(2), 45--68.

Hoogland, K., Pepin, B., de Koning, J., Bakker, A. & Gravemeijer, K. (2018). Word problems versus image-rich problems: an analysis of effects of task characteristics on students' performance on contextual mathematics problems. Research in Mathematics Education, 20(1), 37--52.

Joutsenlahti, J. & Rättyä, K. (2015). Kielentämisen käsite ainedidaktisessa tutkimuksessa. -- Kauppinen, M. & Tarnanen, M. (toim.) Rajaton tulevaisuus: kohti kokonaisvaltaista oppimista, s. 45--61.

Legrand, M. (2001). Scientific debate in mathematics courses. Teoksessa The teaching and learning of mathematics at university level (ss. 127-135). Springer, Dordrecht.

Osborne, J., Erduran, S., & Simon, S. (2004). Enhancing the Quality of Argumentation in School Science. Journal of Research in Science Teaching, 41(10), 994-1020.

Piippo, I., & Portaankorva-Koivisto, P. (2019). Monikielinen käsitteenoppiminen valmistavassa opetuksessa, esimerkkinä matematiikka. Kieli, koulutus ja yhteiskunta, 10(3).

Verschaffel, L., Greer, B. & De Corte, E. (2000). Making sense of word problems. Lisse, The Netherlands: Swets & Zeitlinger.

Sulautetun opetuksen pedagogiikkaa

Näkökulmia siihen, miten teknologia muuttaa sekä opiskelijan suhdetta matematiikkaan että opettajan ja opiskelijan välistä suhdetta.

Suhtautumisemme teknologiavälitteiseen oppimiseen määrittyy sen mukaan, mitä ajattelemme oppimisen olevan. Onko oppiminen yksin tapahtuvaa tiedonhankintaa, osallistuvaa tiedon rakentelua vai tiedonluomista? Sulautuva oppiminen (blended learning) voi sisältää näitä kaikkia. Siihen voi kuulua yksilöllistä, reflektoivaa oppimista, tiimioppimista, projektipohjaista toiminnallista oppimista sekä luokkatyöskentelyn tukemista etäopetuksen välityksellä. Usein pohditaan, miten teknologiavälitteinen oppiminen eroaa perinteisestä oppimisesta, mutta mikä oikeastaan on perinteistä?

Liitutaulu tuli luokkahuoneisiin 1800-luvulla. Esimerkiksi Ranskassa vuodesta 1882 liitutaulu oli käytännössä jokaisessa luokkahuoneessa ja hyvän opettajan tunnisti käytetyn liidun määrästä. Liitutaulu mahdollisti sen, että koko luokka saattoi lukea ja kirjoittaa yhtä aikaa. Samalla voitiin välttää virheitä ja väärinymmärryksiä. Vihkot ja ruutupaperit ilmestyivät luokkiin 1900-luvun taitteessa ja mahdollistivat visuaalisuuden lisäämisen matematiikan opetukseen. Silloin esimerkiksi funktioiden opiskelusta matematiikassa alkoi olla iloa myös luonnontieteiden opiskelussa. Vähitellen myös oppikirjat ilmestyivät luokkiin ja ne lisäsivät opetuksen yhdenmukaisuutta.

Matematiikan toimintavälineiden käytöstä opetuksessa on puhuttu sen sijaan matematiikan opetuksen historiassa monissa eri vaiheissa. Pikkukivet, sormet, helmitaulut, mekaaniset laskurit ja laskimet ovat kautta aikain tuottaneet matematiikan oppimiseen erilaista ymmärrystä. Ne ovat herättäneet kiinnostusta ja auttaneet oppijoita keksimään matemaattisia faktoja ja käsitteitä tai tekemään yleistyksiä. Kautta aikain on myös käyty kiivasta keskustelua esimerkiksi laskimien käytöstä. Esimerkiksi vuonna 1974 Yhdysvalloissa tehdyssä tutkimuksessa 66,6 % vastaajista oli sitä mieltä, että perusasteen matematiikan oppimisen tärkein tehtävä oli aritmetiikassa ja laskemisessa ja 87 % piti nopeutta ja tarkkuutta tärkeinä arjen taitoina (Kidwell, Ackerberg-Hastings & Roberts, 2008). Samaan aikaan kannettiin myös huolta laskimien kalleudesta ja epäiltiin laskimien lisäävän opiskelijoiden laiskuutta. Samanlaisia keskusteluja on kuultu myöhemminkin.

Tietokoneiden tulo matematiikan luokkaan alkoi 1980-luvulla ja silloin tutkijat viittasivat niiden tuomiin uusiin mahdollisuuksiin. Nyt saatettiin tehdä nopeita laskelmia, tuottaa grafiikkaa ja käyttää tutkivia oppimismenetelmiä. Samaan aikaan kuitenkin pohdittiin, voisivatko tietokoneet myös muuttaa matematiikkaa. Tämän kysymyksen ääressä olemme edelleenkin. Olisiko matematiikkakin tutkiva luonnontiede? Voisiko visuaalisuus parantaa matematiikan ymmärtämistä? Tietokoneet kun saavat jotkin tutut matematiikan käytänteet näyttämään vanhanaikaisilta ja tylsiltä, ja muuttavat matematiikan tehtäviä. Mekaanisista tehtävistä onkin mielekkäämpää esimerkiksi siirtyä tutkimaan parametreja ja niiden vaikutuksia.

Matematiikan verkko-oppimisesta

Matematiikan verkko-oppimisen historia lähtee liikkeelle Logo-kielestä ja ohjelmista kuten Cabri (1994) ja Geometer's Sketchpad (1995). Tuskin oli päästy selville niiden mahdollisuuksista, kun jo seuraavat mahdollisuudet kurkkivat ovella. Objektien raahaaminen näytöllä oli seuraava askel. Sen myötä oli mahdollista tutkia ja mallintaa matematiikkaa. Sitä seurasi Internetin tulo ja online-työskentely, joka antoi tilaisuuden vuorovaikutukseen ja yhdessä työskentelylle. Tätä seurasivat avoimet verkkokurssit, MOOCit, ja yksilöllistetty oppiminen. Lisäksi nyt oli mahdollista tallentaa huimia määriä digitaalista informaatiota ja hyödyntää tietokoneiden laskentatehoa. Seuraava vaihe olivatkin sitten mobiililaitteet, ja niiden tuomat mahdollisuudet matematiikan oppimiseen. Matematiikan verkko-oppimisen tutkimuksessa onkin tänä päivänä rinnakkain nähtävissä viisi trendiä: mobiiliteknologian käyttö opetuksessa, avoimet verkkokurssit, digitaaliset kirjastot ja tarkoitukseen suunnitellut välineet, yhteisöllinen oppiminen verkossa ja sulautuvan opetuksen käyttö opettajankoulutuksessa. Yhtä kaikki teknologistuvan matematiikan oppimisen tavoitteena on kaiken aikaa ollut käsitteellisen matemaattisen ymmärryksen helpottaminen ja tukeminen.

Verkko-oppiminen edellyttää opiskelijalta aivan uusia taitoja

Verkkoympäristöt ovat monipuolisia ja rikkaita ja tarjoavat useita vaihtoehtoja oppimisessa etenemiseen. Verkkomateriaaleissa voidaan käyttää luokkavideoita, matemaatikoiden haastatteluja, opetusvideoita, animaatioita, simulaatioita, pelejä ja ohjelmointitehtäviä. Tämä muuttaa opetusta, sillä nyt opiskelijoilla on mahdollista selvittää asioita itse kysymättä ensin opettajalta tai tutkimatta oppikirjaa. Verkossa on mahdollista rakentaa erilaisia tekstin, kuvan ja äänen yhdistelmiä. Opiskelijan tiatoja Opiskelija voi valita oman polkunsa hypertekstiviidakossa ja linkittää oppimiseensa oppimistyylilleen sopivia elementtejä ja omia kiinnostusalueitaan. Tämä kaikki edellyttää kuitenkin sekä itsetuntemusta että itsensä hallintaa. Eikä siinä kaikki, se edellyttää myös verkkoyhteisöltä paljon, sillä verkko mahdollistaa uudenlaista yhteisöllisyyttä. Opiskelijoiden tulisi oppia tukemaan toistensa työskentelyä ja osallistua yhteiseen tiedonrakenteluun.

Itsetuntemuksen ja itsensä hallinnan lisäksi verkossa tarvitaan muitakin taitoja, ensinnäkin epämääräisyyden sietokykyä. Se vaihtelee tutkimusten mukaan eri ihmisillä ja on havaittu, että henkilöt, jotka kykenevät epämääräisyyden sietoon, ovat kykenevämpiä myös ongelmanratkaisuun ja erilaisten vaihtoehtojen löytämiseen. Opettajan kannalta haastavia ovat opiskelijat, joilla tätä kykyä on vähän, sillä he tarvitsevat paljon enemmän palautetta verkkotyöskentelystään.

Verkkotyöskentely saattaa myös aiheuttaa ahdistuneisuutta, sillä se koetaan liian avoimeksi ja strukturoimattomaksi. Kun mahdollisuuksia on paljon ja itseohjautuvuus heikkoa, opettajalta odotetaan paljon tukea. Verkossa työskenneltäessä itsenäiset opiskelijat osaavat paremmin ohjata toimintaansa ja luottavat omiin päätelmiinsä. Heille verkon antamat runsaat mahdollisuudetkaan eivät tule hidasteeksi. Tutkimuksissa puhutaan myös ulkoa ohjautuvista ja sisäisesti ohjautuvista opiskelijoista. Ulkoa ohjautuvat tarvitsevat enemmän opettajan kontrollia, kun taas sisäisesti ohjautuvat näkevät mahdollisuuksia vaikuttaa asioihin omilla toimillaan ja hyötyvät verkkoympäristöstä. Tärkein oppimisen menestykseen vaikuttavista tekijöistä on kuitenkin itsevarmuus ja luottamus omiin kykyihin.

Verkko-opetuksen suunnittelua

Verkkotyöskentelyä suunniteltaessa tulee pohtia, miten tukea opiskelijoiden itseohjautuvuutta. Zimmermann (2000) jakaa itseohjautuvuuden kolmeen osaan: miten opiskelija ennakoi tehtävää ja omaa työskentelyään siinä, miten hän ohjaa itseään työskentelyn aikana ja miten hän arvioi oppimisensa tuloksia. Kun opiskelija aloittaa työskentelyn, hän analysoi saamiaan tehtäviä ja omaa osaamistaan. Hän asettaa tavoitteita ja luo odotuksia lopputuloksesta. Lisäksi hän pohtii tehtävän merkitystä itselleen. Onkin tärkeää, että verkossa on tarjolla riittävästi tukea ja motivoivia elementtejä, jotka vahvistavat työskentelyn käyntiin lähtemistä. Työskentelyn aikana opiskelija opettaa itselleen opittavan asian ja jotta se onnistuisi parhaalla mahdollisella Verkkomateriaalissa tavalla, verkkomateriaalin tulisi sisältää elementtejä, joilla opiskelijan huomio kiinnitetään oleellisiin asioihin, ohjataan häntä tehtävän vaatimien menetelmien hallintaan ja synnytetään mielikuvia, jotka sitten linkittävät asioita ja parantavat mieleenpainamista ja muistamista. Kun opiskelija on sitten saanut verkkotehtävät valmiiksi, materiaalin tulisi auttaa tehtävän onnistumisen tai epäonnistumisen syiden tulkintaa, kannustaa ja muokata jatkotyöskentelyä esimerkiksi sopeuttaen sitä saatuihin tuloksiin.

Usein opettajia huolettaa opiskelijoiden itseohjautuvuus. Itseohjautuvuus on tilannesidonnaista ja taito, jota opitaan vähitellen. Tämän taidon oppimisessa on Norrenan (2016) mukaan neljä vaihetta ja ne edellyttävät opettajalta erilaisia käytänteitä. Ensimmäinen vaihe kuvaa riippuvaa oppijaa. Hänelle hyvin organisoitu ja selkeä opetus toimii tukena kohti seuraavaa itseohjautuvampaa vaihetta. Kiinnostuneelle oppijalle sopivat motivointi, korkeat tavoitteet, rohkaisu ja ohjaus. Sitoutunut oppija kaipaa kuuntelevaa, yhdessä työskentelevää ja yhteistyöhön ohjaavaa opettajaa. Itseohjautuneelle oppijalle opettaja sen sijaan voi jo asettaa haasteita, hioa oppimiskykyä ja kannustaa pitkän tähtäimen tavoitteisiin.

Yhteisöllisyyden merkitys oppimiselle

Monet tutkijat ovat pohtineet, miksi opiskelijoiden keskinäiseen vuorovaikutukseen kiinnitetään matematiikan opetuksessa niin vähän huomiota. Materiaaleja ja opetusta suunnitellaan opettajien ja opiskelijoiden vuorovaikutuksen tai oppimateriaalin ja opiskelijoiden vuorovaikutuksen helpottamiseksi, ja unohdetaan opiskelijoiden keskinäinen vuorovaikutus. Verkkotyöskentelyssä tulisikin kiinnittää erityisesti huomiota tähän opiskelijoiden väliseen vuorovaikutukseen. Sen avulla opiskelijoille syntyy tilaisuuksia kehitellä ideoita ja pohtia käsitteitä. Verkkotyöskentely voi myös tukea luokassa tapahtuvaa oppimista, sillä opiskelijat voivat etukäteen tutustua, tutkia ja pohdiskella ideoita ja käsitteitä. Sulautuvan oppimisen onkin tutkimusten mukaan katsottu lisäävän opiskelijoiden oppimisen omistajuutta, omatahtisuutta ja itselle sopivaa työskentelyjärjestystä, vähentävän muuhun kuin tehtävään käytettyä aikaa, lisäävän tehtävään käytettävää aikaa ja parantavan oppimistuloksia. Ehkä yksi tärkeä näkökulma on myös se, että sulautetussa oppimisessa oppitunnilla on voitu paneutua enemmän miksi-kysymyksiin ja pureutua asioihin syvemmin.

Verkkomateriaalin suunnittelussa tulisikin miettiä, miten materiaali järjestetään niin, että se tukee tällaista itsenäistä tiedon etsintää. On myös tärkeä miettiä, miten sosiaalinen vuorovaikutus verkossa järjestetään. Usein opiskelijat esimerkiksi haluaisivat neuvotella keskenään tehtävistä ennen niiden palauttamista varmistaakseen, että ovat ymmärtäneet tehtävänannon oikein. Opettajan tulee myös pohtia omia työmenetelmiään. Luokkatyöskentelyyn käytettävä aika kannattaisi käyttää aiheen syventämiseen ja lisätyöstämiseen pikemminkin kuin perinteiseen opetukseen.

Kirjallisuutta:

Borba, M. C., Askar, P., Engelbrecht, J., Gadanidis, G., Llinares, S., & Aguilar, M. S. (2016). Blended learning, e-learning and mobile learning in mathematics education. ZDM, 48(5), 589-610.

Ford, P. (2015). Flipping a math content course for pre-service elementary school teachers. Primus, 25(4), 369-380.

Kidwell, P., Ackerberg-Hastings, A., & Roberts, D. (2008). Tools of American Mathematics Teaching, 1800--2000. Baltimore: The Johns Hopkins University Press.

Kotilainen, M-L. (2015). Itseohjautuvuuden tukeminen vieraan kielen etäopetuksessa. Design-perustainen oppimisympäristön kehittämistutkimus perusasteen 5.-6. luokilla. Acta Universitatis Lapponiensis 298.

Niemi, H. (2001). Vahvaksi verkossa: kohti itseohjautuvuutta ja oppimisen taitoja. Helsingin yliopisto, kasvatustieteen laitos. https://www.edu.helsinki.fi/svy/kvanti/mittavaline/mat/vahvaksi_verkossa.pdf

Norrena, J. (2016). Laaja-alainen osaaminen käytäntöön. Arviointi, opetuksen suunnittelu ja oppilaiden ohjaaminen. Keuruu: Otavan Kirjapano Numminen, 1997.

Villarreal, M. E., & Borba, M. C. (2010). Collectives of humans-with-media in mathematics education: notebooks, blackboards, calculators, computers and... notebooks throughout 100 years of ICMI. ZDM, 42(1), 49-62.

Zimmerman, B.J. (2000). Attaining self-regulation. A social cognitive perspective. Teoksessa Boekaerts, M., Pintrich, P. & Zeidner, M. (Toim.) Handbook of self-regulation (ss. 13-39). Academic Press.

Itse- ja vertaisarvioinnista

Näkökulmia itse- ja vertaisarvioinnin hyödyistä.

Arviointi ohjaa opiskelijoiden opiskelua ja oppimista. Jos haluat muuttaa opiskelijoiden oppimista, muuta arviointia. Arvioinnin tulisi olla linjassa ei vain tavoitteiden kanssa, vaan myös opetusmenetelmien ja opiskelustrategioiden kanssa. Uudet opetussuunnitelmat ovat nostaneet tieteenalakohtaisten tietojen ja taitojen rinnalle myös geneeriset taidot, joilla tarkoitetaan vuorovaikutustaitoja, kriittisen ajattelun taitoja, ongelmanratkaisutaitoja, tietoteknisiä taitoja ja ilmaisutaitoja. Näiden oppimiseen voidaan vaikuttaa huomattavasti opetusmenetelmällisillä valinnoilla. Lisäksi opetussuunnitelmissa tavoitellaan akateemisen asiantuntijuuden kehittymistä, joka lukio-opinnoissa tarkoittaa kykyä tunnistaa ja kehittää omaa osaamistaan eli niin sanottuja reflektiotaitoja. Jotta näitä geneerisiä taitoja ja oppimaan oppimisen taitoja voitaisiin kehittää, tulisi myös niitä arvioida. Tähän tarkoitukseen sopivat itse- ja vertaisarviointi.

Mitä tarkoitetaan itsearvioinnilla ja mitä hyötyjä siitä on?

Itsearvioinnissa opiskelija vertaa työskentelyään ja sen tuloksia kriteereihin ja pohtii, miten hyvin on onnistunut täyttämään ne. Nämä kriteerit voivat olla opettajan antamia tai yhdessä opiskelijoiden kanssa konstruoituja. Itsearvioinnin tarkoituksena ei ole antaa itselleen arvosanaa, vaan kehittää omia oppimaan oppimisen taitojaan. Itsearviointitaidot ovat tulevan työelämän kannalta arvokkaita ja välttämättömiä.

Itsearvionnilla on paljon etuja verrattuna opettajan toteuttamaan arviointiin. Ensinnäkin opiskelija saa palautteen työskentelystään heti, kun sitä tarvitsee. Kun kriteerit ovat käytössä jo työskentelyä aloitettaessa, opiskelija sitoutuu työskentelyprosessiin ja arviointiin vakavammin. Koska itsearviointi on koko ajan avointa opiskelijalle, se lisää myös luottamusta arviointiin. Opettajan näkökulmasta itsearviointi säästää opettajan työtä. Kun opiskelijat ottavat myös arvioijan roolin, he saavat samalla sen hyödyt.

Tieteenalakohtaisten tietojen ja taitojen arvioinnissakin voidaan käyttää itsearviointia. Tieteenalakohtaisia tietoja ovat faktatiedot, kuten lukujoukot, atomin osat, fysiikan suureet tai kemialliset merkit. Tieteenalakohtaisiin tietoihin luetaan myös käsitetiedot, kuten matematiikan laskulait, fysiikan peruslait, metallien sähkökemiallinen jännitesarja tai alkuaineiden jaksollinen järjestelmä. Tieteenalakohtaisiin taitoihin sisällytetään tieteenalan menetelmätieto, kuten laskukaavat ja ratkaisutavat, ongelmanratkaisumenetelmät, kokeelliset työmenetelmät, tilastomenetelmät tai turvalliset työtavat laboratoriossa. Itsearvioinnin voi tällöin toteuttaa esimerkiksi niin, että opettajalla on tehtävään mallivastaus, johon opiskelijat voivat verrata omaa ratkaisuaan. Tämän arviointimenetelmän heikkous on siinä, että opiskelijat tulkitsevat vain mallin ratkaisun oikeaksi. Tällöin muut oikeat ratkaisut jäävät huomioimatta. Jos opiskelijat saavat useampia mahdollisia ratkaisuja tehtävään, niin samalla heidän tulee pohdittua niiden eroja ja yhtäläisyyksiä ja aiheen prosessointikin syvenee. Toinen toteutustapa on antaa joko yksi tai useampi esimerkki riittävästä suorituksesta ja korostaa esimerkkisuorituksen sekä hyviä, että heikkoja puolia. Opiskelijat voivat nyt arvioida työnsä hyvät ja heikot puolet ennen työn palautusta ja opettajan tehtäväksi jää lähinnä kommentoida itsearvioinnin osuvuutta. Työn lopullinen palautus voidaan sopia siihen, kun havaitut puutteet on korjattu. Kolmas toteutustapa on antaa opiskelijoille lyhyt palaute työstä, jonka jälkeen he tutustuvat siihen ensin itsekseen, keskustelevat siitä ainakin kahden muun opiskelijan kanssa ja lopuksi täydentävät ratkaisuaan ennen työn palauttamista.

Itsearvioinnissa opiskelijat joutuvat miettimään, miten paljon käyttävät resurssejaan opiskeluun ja mitä tavoitteita itselleen asettavat. He oppivat reflektointia, itsesäätelytaitoja ja metakognitiivisia taitoja. Tutkimuksissa onkin havaittu, että itsearviointi parantaa oppimistuloksien lisäksi vastuunottamista opiskelusta ja oman osaamisen tunnistamista.

Mitä tarkoitetaan vertaisarvioinnilla ja mitä hyötyjä siitä on?

Vertaisarviointia voidaan toteuttaa joko niin, että opiskelijaparit arvioivat toistensa työskentelyä tai työskentelyn tuotoksia. Käytettäessä projektioppimista tai muita ryhmätyöskentelyn muotoja vertaisarviointia voidaan tehdä joko ryhmän sisällä niin, että jokainen ryhmän jäsen arvioi yhden tai kaikkien muiden työskentelyä tai sitten ryhmien välillä, jolloin ryhmät tekevät vertaisarvioinnin.

Vertaisarvioinnin kohteenakin voivat olla joko geneeriset tai metakognitiiviset oppimaan oppimisen taidot tai sitten se voidaan kohdentaa tieteenalakohtaisten tietojen ja taitojen arviointiin. Geneeristen taitojen vertaisarvioinnissa voitaisiin huomioida esimerkiksi seuraavia asioita: miten opiskelija arvostaa ryhmän muiden jäsenten ideoita, miten hän sitoutuu ryhmän tavoitteisiin, osaako tarvittaessa ottaa johtajan tehtävät tai muuten kantaa vastuuta työskentelystä tai kuinka onnistuneesti hän osaa organisoida yhteistä työskentelyä. Lisäksi voidaan tarkastella osallistumista, oppitunnille valmistautumista, laadukasta työskentelyä, aloitteiden tekemistä, aikatauluissa pysymistä, sisällön hallintaa, kommunikointia toisten kanssa, yhteistyötä ja kykyä ratkaista konflikteja tai kannustaa. Helppo ja nopea tapa on joko antaa jokaiselle ryhmän jäsenelle arvosana kustakin arvioitavasta kohdasta tai sitten antaa ryhmän jakaa esimerkiksi sata pistettä ryhmän jäsenten kesken oikeassa suhteessa.

Tieteenalakohtaisten tietojen ja taitojen vertaisarvioinnin suurimmat edut ovat siinä, että aiheen parissa työskentely jatkuu oppitunnin tai aiheen käsittelyn jälkeenkin. Lisäksi tarkistettaessa toisten ratkaisuja oikeat ratkaisut vahvistuvat ja opiskelijat oppivat ymmärtämään arvioinnin kriteerejä. Samalla he huomaavat, miten tärkeää on ilmaista ajatuksensa selkeästi ja ymmärrettävästi. Sekavaa ratkaisua kun on todella vaikea seurata ja pisteyttää. Opettajan rooli muuttuu myös, sillä se vaihtuu nyt arvioijasta neuvonantajaksi.

Usein ajatellaan, että opiskelijat eivät voi tehdä vertaisarviointia, sillä heillä ei ole riittävää asian hallintaa. Tähän voidaan kuitenkin vaikuttaa sillä, että käytettävissä on laadukasta materiaalia, josta opiskelijat voivat selvittää asioita itselleen. Samalla heidän tulee paneuduttua aiheeseen uudelleen tai joskus ehkä ensimmäistä kertaa. Toinen epäilyksen aihe on, että opiskelijat eivät ehkä osaa antaa hyödyllistä palautetta. Ajatellaan, että opiskelijat antavat kavereilleen liian hyviä arvioita tai eivät halua antaa heille lainkaan negatiivista palautetta. Ensimmäisillä vertaisarvioinnin kerroilla näin saattaa ollakin, mutta havaitessaan, miten paljon vertaisarviointi tukee omaa oppimista, laadukkaiden palautteidenkin antaminen lisääntyy. Toki opiskelijat tarvitsevat tuekseen arviointiohjeita. Kolmas huolenaihe liittyy siihen, että opiskelijat eivät käytä riittävästi aikaa palautteen antamiseen ja paneudu tehtävään kunnolla. Tämäkin huoli hälvenee, kun arviointityöstä tulee tutumpaa. Neljäs opettajien usein esittämä epäilys on, että opiskelijat saavat näin tilaisuuksia "varastaa" ideoita omaan työhönsä. Varmasti näin onkin, mutta samalla he oppivat aiheesta lisää ja monissa tehtävissä se saattaa olla eduksikin. Toki keskustelut tekijänoikeuskysymyksistä ja siitä, miten toisen työhön viitataan ovat paikallaan.

Kirjallisuutta:

Aksela, M. K., Tikkanen, G. M., & Kärnä, P. (2012). Mielekäs luonnontieteiden opetus: Miten tukea oppilaiden ajattelua ja ymmärtämistä?. Teoksessa Kärnä P., Houtsonen L. & Tähkä, T. (toim.) Luonnontieteiden opetuksen kehittämishaasteita 2012. Opetushallitus. 9-28.

Alaoutinen, Satu. (2012). Evaluating the effect of learning style and student background on self-assessment accuracy. Computer Science Education, 22:2, 175-198.

Taras, M. (2010). Student self-assessment: processes and consequences, Teaching in Higher Education, 15: 2, 199-209.

Zhang, Aimao (2012). Peer Assessment of Soft Skills and Hard Skills. Journal of Information Technology Education (11).

Kokeellisuutta ja projektityöskentelyä

Näkökulmia kokeellisuuden ja projektityöskentelyn hyötyihin ja haasteisiin.

Kokeellisuus ja projektityöskentely kuuluvat luontevasti fysiikan ja kemian opetukseen. Luonnontieteissä (science) yhdistyvät perinteisesti sekä tulos (product), prosessi (process) että yritteliäisyys (enterprise). Tällä hetkellä kirjoitetaan paljon STEM ja STEAM-aineista (science, technology, engineering, art design & mathematical knowledge), Maker-kulttuurista, laaja-alaisesta osaamisesta ja luonnontieteellisestä lukutaidosta sekä niiden yhteydessä tekemällä oppimisesta. Lisäksi fysiikassa ja kemiassa pidetään tärkeänä myös sitä, että opiskelijat oppivat tieteellisen tiedon lisäksi menetelmiä, joilla tämä tieto on saavutettu, ja perusteita, miksi saavutettua tietoa pidetään oikeana.

Kansainvälisissä tutkimuksissa on havaittu, että kokeellinen työskentely on mieluista ja opiskelijat kokevat sen hyödylliseksi ja tehokkaaksi tavaksi oppia. Sen avulla voidaan myös kehittää opiskelijoiden minäpystyvyysuskomuksia. Minäpystyvyysuskomukset näyttävät vaikuttavan siihen, innostuvatko opiskelijat luonnontieteistä ja hakeutuvatko myöhemmin lukio-opintojensa jälkeen luonnontieteelliselle alalle. Erityisesti opiskelijat, jotka uskovat omiin kykyihinsä oppia ja kehittää itseään, vaikka välillä epäonnistuisivatkin, näyttävät sitoutuvan oppimiseen.

Sitoutuminen opiskeluun edellyttää kiinnostuksen heräämistä, riittäviä taitoja ja sopivasti haasteita. Sitoutuneet opiskelijat taas menestyvät opinnoissaan, saavat enemmän myönteistä palautetta opettajiltaan, löytävät helpommin tehokkaita oppimisstrategioita, ovat itseohjautuvampia ja sitkeämpiä ja käyttävät enemmän aikaa hyödylliseen työskentelyyn. Näin syntyy myönteinen oppimisen kehä. Tutkimusten mukaan Suomessa luonnontieteiden oppitunnista suurin osa on kuuntelemista. Lukiolaisille tehdyssä tutkimuksessa havaittiin, että vain 3,6 % oppitunnista käytettiin kokeelliseen työskentelyyn, 6,3 % laskemiseen ja 10,9 % keskusteluun. Opiskelijat kuitenkin ilmoittivat kokeellisen työskentelyn lisäävän heidän mielestään eniten kiinnostusta ja luonnontieteellisiä taitoja ja laskemisen eniten haasteita. Sitoutumista voitaisiinkin lisätä aktivoimalla opiskelijoita keskusteluihin ja yhdistämällä kokeelliseen työskentelyyn matemaattisia haasteita. Yläkoulussa tilanne on vielä hiukan toinen, mutta PISA-tutkimusten valossa kuitenkin noin kolmasosa vastasi, ettei kokeellisuutta ollut lainkaan tai tuskin koskaan ja yli 78 % mielestä omia tutkimuksia ei oppitunneilla tehty koskaan.

Mitä kokeellisella työskentelyllä tarkoitetaan?

Tutkijat liittävät kokeelliseen työskentelyyn kaksi tavoitetta. Työskennellessä tehdään havaintoja ja niitä kytketään ideoihin. Tämä edellyttää keskusteluja ja yhteistä pohdiskelua työskentelyn lomassa. Tutkijat myös korostavat, että tieteellinen tutkimus eroaa luokkatilassa tehtävästä tutkimuksesta. Luokassa yleensä pyritään jo olemassa olevan, ei niinkään uuden tiedon, löytämiseen.

Kokeellista työskentelyä voidaan jaotella useilla tavoilla. Perusteina voivat olla toimintatavat, lähestymistavat, lopputulos tai roolit. Eri tavat myös tuottavat erilaista oppimista. Todentavassa kokeellisuudessa sekä opiskelija että opettaja tietävät työn tavoiteltavan tuloksen. Puhutaan myös deduktiivisesta ja induktiivisesta kokeellisuudesta. Todentava kokeellisuus on deduktiivista kokeellisuutta. Siinä lähdetään liikkeelle teoriasta ja sitä sovelletaan käytäntöön. Induktiivista lähestymistapaa käytetään keksintöperustaisessa kokeellisuudessa. Siinä tehdään havaintoja jostain ilmiöstä ja johdetaan havaintojen perusteella jokin yleisempi periaate. Keksintöperustaisessa kokeellisuudessa opettaja yleensä tietää työn tuloksen, mutta opiskelijat eivät tiedä. Ongelmaperustaisessa kokeellisuudessa samoin opettaja tietää, mitä koe tuottaa. Tutkimuksellinen kokeellisuus taas voi olla niin avointa, ettei edes opettaja tiedä, mitä työn tuloksena syntyy. Hämäläinen (2017) pitää tärkeänä, että osa kokeellisesta työskentelystä on niin sanottua merkityksellistä kokeellisuutta. Merkityksiä luova koe luo hänen mukaansa uusia käsitteitä ja yhteyksiä. Tarvitaan myös sekä kvalitatiivisia kokeita että kvantitatiivisia kokeita. Hämäläisen (2017) mukaan käsitteitä opitaan kvalitatiivisesti ominaisuuksia tutkimalla ja suureita kvantitatiivisesti.

Kuka kokeellisen työn tekee, se riippuu paljon käytettävästä ajasta ja muista resursseista. Joskus kerrottu kokeellisuuskin riittää. Arvostettuja luonnontieteiden opettajia havainnoidessa on huomattu, että he osaavat taitavasti käyttää metaforia, analogioita, roolileikkejä, ajankohtaisia uutisia ja tarinoita opetuksessaan. He osaavat yhdistää opiskeltavat asiat oppilaan arkeen, aikaisemmin opittuun tai muuhun tietoon yli ainerajojen. He myös kykenevät huomioimaan historialliset, yhteiskunnalliset ja ekologiset näkökulmat, ja kertovat tarinoita omista kokemuksistaan.

Opettajan mallintaessa tai demonstroidessa opiskelijat tekevät havaintoja ja keskeistä on ylläpitää mielenkiintoa ja auttaa opiskelijoita tekemään oleelliset havainnot. Jos opettaja kuvailee kaiken aikaa, mitä tapahtuu, perustelee, miksi käyttää tiettyjä välineitä ja miksi toimii tietyllä tavalla ja pohtii myös vaihtoehtoisia tapoja, hän saattaa onnistua hyvin vastaamaan edellä mainittuihin haasteisiin.

Itse tehty kokeellinen työ opettaa kuitenkin eniten. Opettajan rooli on silloin tukea neuvoin tai ohjein, antaa palautetta ja kannustaa. Valmentava opettaja sen sijaan seurailee sivusta ja pyrkii kehittämään uusia tehtäviä sen mukaisesti, kun opiskelijat kehittyvät kokeellisessa työskentelyssä. Opettajan tulisi kuitenkin antaa tilaa dialogisuudelle, opiskelijoiden ehdotuksille ja olettamuksille. Tähän kannattaa erityisesti panostaa, sillä joissakin tutkimuksissa on havaittu, että Suomessa dialoginen luonnontieteiden opetus on melko harvinaista.

Kokeellisuuden haasteita

Kokeellisuuden haasteena on, että usein opiskelijat tekevät havaintoja tai mittauksia, jotka ovat keskeneräisiä, vääriä tai riittämättömiä joko lukumäärän tai tarkkuuden suhteen. Monasti syynä ovat aika- ja laiteresurssit, mutta myös kokemattomuus tehdä luonnontieteellistä tutkimusta. Puutteellisten mittausten tai havaintojen avulla on kuitenkin lähes mahdotonta saavuttaa työssä tavoiteltuja tuloksia. Lisäksi joskus, vaikka tehdyt havainnot tai mittaustulokset olisivatkin riittäviä, itse päätelmien teko osoittautuu liian vaativaksi. Tieteelliset selitykset eivät noin vain pomppaa esiin havainnoista. Tarvitaankin opettajaa auttamaan yhteyksien näkemisessä. Tämä taas usein johtaa siihen, että opiskelijat eivät malta pohtia asiaa syvemmin, vaan odottavat valmista selitystä opettajalta.

Eräs usein mainittu haaste kokeellisessa työskentelyssä on reseptin mukainen työskentely. Opiskelijat noudattavat pikkutarkkoja ohjeita, eivätkä pysähdy miettimään, mitä ja miksi tekevät niin kuin tekevät. Ongelmallista on myös, jos kokeellinen työskentely edellyttää taitoja, joita ei vielä olla ennätetty harjoitella. Näin saattaa olla, jos kokeessa tulee käyttää mittalaitteita tai ohjelmistoja. Opettajan tulisikin huolehtia, että niiden käyttö opetellaan rauhassa etukäteen tai sitten hän voi tietoisesti integroida harjoittelun osaksi laajempaa kokeellista työskentelyä.

Mitä otan huomioon suunnitellessani kokeellista työskentelyä?

Kokeellisella työskentelyllä ja projekteilla tavoitellaan, että opiskelijat oppivat: (1) tekemään havaintoja ilmiöistä ja objekteista, (2) omaksuvat faktoja, (3) oppivat käsitteitä, (4) havaitsevat yhteyksiä ja (5) oppivat teorioita ja malleja.

Kokeellista työskentelyä voidaan havainnollistaa erilaisilla malleilla. POE (predict -- observe -- explain) sopii hyvin sellaisiin töihin, joista opiskelijoilla on jo teoreettista tietoa ja he voivat tehdä hyödyllisiä ennusteita, tutkia niiden paikkansapitävyyttä havainnoilla ja lopulta selittää saatuja tuloksia teorian pohjalta. Näissä töissä tehdään siis ensin kirjallinen ennuste siitä, mitä tulee tapahtumaan, sitten tehdään itse koe ja lopulta selitetään, tukivatko havainnot ennustetta ja miksi näin kävi tai ei käynyt. Toinen työskentelymalli lähtee liikkeelle opettajan antamasta yleisestä periaatteesta. Opiskelijat tutkivat periaatteen toimivuutta erilaisin kokein ja raportoivat, voidaanko saadut tulokset esittää opettajan idean mukaisesti. Kolmas malli perustuu opettajan esittämään analogiaan, johon opiskelijat suhteuttavat omia havaintojaan tehdystä työstä ja tarkastelevat, miltä osin ne sopivat analogian kanssa yhteen ja miltä osin eivät.

Hyviä kokeellisia töitä ovat sellaiset, joissa opiskelijat eivät vain tee käsillään, vaan johon he myös uppoutuvat. Valitse työt niin, että niissä ei ole liikaa havainnoitavaa ja opiskelijoiden on helppo kiinnittää huomio oleellisiin näkökulmiin. Suunnittele työ niin, että se haastaa pohtimaan asiaa ennen työn aloittamista. Hyvä työ on myös sellainen, jota opettajan on helppo seurata ja joka houkuttelee keskustelemaan työskentelyn lomassa. Parhaat kokeelliset työt johtavat siihen, että opiskelijat oppivat käsitteitä ja havaitsevat yhteyksiä tai riippuvuuksia, ja joutuvat työskentelyn päätteeksi perustelemaan tuloksiaan. Ne siis luovat siltoja havaitun tiedon ja tieteellisen tiedon välillä. Yleensä onnistunut työskentely myös auttaa opiskelijoita myöhemmin palauttamaan mieleensä, mitä olivat tehneet ja havainneet työtä tehdessään.

Jos mahdollista valitse töitä, joissa opiskelijat voivat tehdä johtopäätöksiä siitä, mitä työn tulos tarkoittaa, eikä vain todentaa jotain aiemmin opittua. Kannusta myös ongelmanratkaisuun ja neuvottelemiseen ja erityisesti työskentelyn aikana, ei vain sen päätteeksi. Anna opiskelijoille tilaisuuksia valita itse työmenetelmiä ja keskustele niistä heidän kanssaan. Kun tutkijat ovat havainnoineet opiskelijoiden kokeellista työskentelyä oppitunneilla, he ovat huomanneet, että opettajat olettavat, että työskennellessään kokeellisesti opiskelijat omaksuvat tieteellisen tutkimuksen suunnittelemista ja toteuttamista. Näin ei kuitenkaan ole, sillä useimmiten työvaiheet on kuvattu niin tarkoin, ettei opiskelijoiden mieleen tule kiinnittää huomiota välineiden valintaan tai työvaiheiden järjestykseen. Työskentelytaidotkaan eivät kehity vain työohjeita seuraamalla, eikä näennäinen työohjeen seuraaminen takaa, että opiskelija rakentaa aktiivisesti tietoa, vaikka puuhaileekin touhukkaasti.

Entä voivatko videotallenteet korvata kokeellisen työskentelyn?

Videot ovat parhaimmillaan silloin, kun kyseessä on työ, jota ei voi tehdä luokkatilassa. Ne ovat myös paikallaan silloin, kun havaittavaa ilmiötä tulee tarkastella eri näkökulmista ja useaan kertaan, jotta saataisiin kaikki sen antama informaatio kerätyksi. Silloin videota voidaan katsoa useita kertoja peräkkäin. Videot eivät voi kuitenkaan korvata kokeellista työskentelyä. Sama pätee simulaatioihin. Niitä on hyvä käyttää, kun valmistaudutaan kokeelliseen työskentelyyn, sillä yksinkertaistetussa simulaatiossa on helpompi ohjata opiskelijoiden tarkkaavaisuus tapahtuman oleellisiin piirteisiin. Lisäksi simulaatioissa ilmiöihin voidaan yhdistää niitä kuvaavia malleja.

Pyri löytämään oppimista parhaiten tukevat videot. Ne rinnastavat todellisia tapahtumia ja teoreettisia konstruktioita ja linkittävät havainnot ja ideat toisiinsa. Tällaiset videot voivat esimerkiksi näyttää kemiallisen reaktion ja sen rinnalla saman prosessin atomitasolla tai linssin toiminnan ja vieressä kuvion säteiden kulusta.

Entä miten projektioppiminen eroaa muusta kokeellista työskentelystä?

Projektioppimisessa (PBL -- problem based learning) projektit muodostavat pääosan opetussuunnitelmasta. Niissä työskentely lähtee liikkeelle reaalimaailman kysymyksestä tai ongelmasta, johon opiskelijalähtöisesti työskentelemällä pyritään löytämään ratkaisu. Projektioppiminen sopii hyvin luonnontieteisiin, sillä siinä itse prosessi on yhtä tärkeässä osassa kuin tavoiteltu lopputulos. Projektioppimisessa opitaan myös laaja-alaisia taitoja ja kokeellisia menetelmiä, sillä valmiita työohjeita ei ole. Projektit voivat liittyä muotoiluun tai teknisiin hankkeisiin, työvälineiden, rakenteiden tai materiaalien suunnitteluun ja testaukseen tai oppiaineen sisältöihin, tieteen historiaan tai luonteeseen. Tutkimuksissa on havaittu, että projektioppiminen parantaa opettajan ja opiskelijoiden välistä suhdetta merkittävästi ja lisää iloa oppimiseen. Nämä yhdessä parantavat oppimisilmapiiriä. Lisäksi projektioppiminen näyttää parantavan oppimistuloksia ja tukee erityisesti heikompia opiskelijoita. Projektioppimiseen löydät helposti hyviä ideoita Internetistä. Kokeile esimerkiksi hakua, jossa yhdistyvät STEM ja PBL.

Kirjallisuutta:

Abrahams, I., & Millar, R. (2008). Does practical work work? A study of the effectiveness of practical work as a teaching and learning method in school science. International Journal of Science Education, 30(14), 1945-1969.

Han, S., Capraro, R., & Capraro, M. M. (2015). How science, technology, engineering, and mathematics (STEM) project-based learning (PBL) affects high, middle, and low achievers differently: The impact of student factors on achievement. International Journal of Science and Mathematics Education, 13(5), 1089-1113.

Hugerat, M. (2016). How teaching science using project-based learning strategies affects the classroom learning environment. Learning Environments Research, 19(3), 383-395.

Hämäläinen, A. (2017). Lukiofysiikan kokeellisuus. LUMAT-B: International Journal on Math, Science and Technology Education, 2(1), 8-25.

Inkinen J., Klager, C., Schneider, B., Juuti, K., Krajcik, J., Lavonen, J., & Salmela-Aro, K. (2019). Science classroom activities and student situational engagement. International Journal of Science Education, 41(3), 316 - 329

Kärnä, P., Harmoinen, S., Vesterinen, V. M. J., & Aksela, M. (2018). Opettajan puhe esimerkillisten fysiikan ja kemian opettajien tunneilla. FMSERA Journal.

Lederman, J., Lederman, N., Bartels, S., Jimenez, J., Akubo, M., Aly, S., ... & Buntting, C. (2019). An international collaborative investigation of beginning seventh grade students' understandings of scientific inquiry: Establishing a baseline. Journal of Research in Science Teaching, 56(4), 486-515.

Lehtinen, A., & Nissinen, K. (2018). 7. Tutkimuksellisuus luonnontieteissä ja sen yhteys luonnontieteelliseen osaamiseen Suomessa. Kasvatusalan tutkimuksia, (77).

Millar, R. (2004). The role of practical work in the teaching and learning of science. High school science laboratories: Role and vision, 1-24.

Tomperi, P., & Aksela, M. (2011). Opettajien kokeellisten laboratoriotöiden valinnat. Kansainvälinen kemian vuosi: Kemia osaksi hyvää elämää, 84-95.

van Aalderen‐Smeets, S. I., Walma van der Molen, J. H., & Xenidou‐Dervou, I. (2019). Implicit STEM ability beliefs predict secondary school students' STEM self‐efficacy beliefs and their intention to opt for a STEM field career. Journal of research in science teaching, 56(4), 465-485.

Wang, T. H., Lim, K. Y., Lavonen, J., & Clark-Wilson, A. (2019). Maker-Centred Science and Mathematics Education: Lenses, Scales and Contexts. International Journal of Science and Mathematics Education, 1-11.

Voimaa yhteisopettajuudesta

Näkökulmia opettajien yhteistyöhön ja opetuksen kehittämiseen.

Uudet opetussuunnitelmat odottavat meidän työskentelevän yhteistyössä toistemme kanssa. Olemmehan siihen jossain määrin tottuneetkin, vaikka yksin tekemisen ja henkilökohtaisen vastuun vahva korostuminen ovatkin tutkimusten perusteella suomalaiselle koululle tyypillisiä piirteitä. Yhteisopettajuus on kuitenkin tulollaan myös lukioihin. Yhtäältä se muodostuu lukiolain edellyttämästä yhteistyöstä korkeakoulujen kanssa, toisaalta yhteistyöstä toisten aineenopettajien kanssa järjestettäessä laajempia oppiainerajat ylittäviä opintojaksoja ja kolmanneksi myös yhteistyöstä erityisopettajien kanssa.

Yhteisopettajuus haastaa uudenlaiseen kulttuuriin, mutta sillä on myös paljon hyviä vaikutuksia opetukseen. Anna Rytivaara on tutkinut jo useita vuosia yhteisopettajuutta ja hän listaa näitä positiivisia asioita seuraavasti: yhdessä opettaessaan opettajat saavat enemmän aikaa yksittäisen opiskelijan kohtaamiseen, käytetyt opetusmenetelmät monipuolistuvat, opiskelijat saavat mallin yhteistyöstä ja yhteisopetus lisää yhteisöllisyyttä ja opettajien ammatillista kasvua.

Yhteisopettajuudesta on useita malleja

Villa, Thousand ja Nevin (2008) kuvailevat neljä yhteisopettajuuden mallia: (1) toinen opettaja tukena, (2) opetetaan rinnakkain, (3) täydennetään toisen opetusta ja (4) tiimiopettajuus.

Ensimmäisellä näistä malleista opettajat jakavat roolit siten, että vuorotellen toinen on päävastuussa opetuksesta ja toinen avustaa. Näin yksilölliselle ohjaukselle jää enemmän aikaa. Kun päävastuuta vaihdellaan, opettajien omat vahvuusalueetkin voidaan ottaa huomioon.

Rinnakkain opettamista voidaan toteuttaa monin eri tavoin. Opetusryhmä voidaan jakaa osiin ja molemmat opettavat omaa ryhmäänsä. Tällöin eri ryhmissä voi olla esimerkiksi erilainen pedagoginen lähestymistapa. Voidaan myös käyttää pistetyöskentelyä tai pysäkkiopetusta, jolloin kummallakin opettajalla on omat pysäkkinsä. Näin voidaan käyttää pienempiä ryhmäkokoja, mutta opittavat sisällöt ovat kaikille identtiset. Pysäkit voidaan toteuttaa joko niin, että opiskelijat kiertävät tilasta toiseen tai sitten niin, että opettajat kiertävät. Rinnakkain opettamista on myös se, että opiskelijaryhmät etenevät saamiensa ohjeiden mukaisesti ja opettajat kiertelevät ryhmien tukena. Näihin malleihin on helppo lisätä eriyttäviä sisältöjä, jos opettajat päättävät jo ennalta ryhmien kokoonpanoista ja kunkin ryhmän tavoitteina olevista pysäkeistä.

Kolmannessa mallissa opettajilla on yhtäläiset roolit ja he täydentävät toistensa opetusta. Se voi tapahtua esimerkiksi niin, että toisen opettaessa toinen havainnollistaa opetusta tai valmistelee seuraavaa tehtävää tai vaikkapa huolehtii työskentelyn sujuvuudesta ja yksilöllisestä ohjauksesta. Täydentävää opetusta voidaan myös toteuttaa keskustelevana opetuksena, jolloin molemmat opettajat voivat toimia oman alansa asiantuntijoina keskustelussa.

Tiimiopetus on malleista vaativin, sillä siinä opettajat ovat jatkuvassa vuorovaikutuksessa toistensa kanssa ja vaihtavat saumattomasti opetustehtäviä.

Onnistunut yhteisopettajuus

Yhteisopettajuuden perustana ovat vuorovaikutus, tasa-arvo, luottamus ja ammatillisuus. Tähän tarvitset kollegan, joka on kanssasi yhtä lailla innostunut kokeilemaan yhteisopettajuutta. Vuorovaikutus onnistuu parhaiten, jos käsitykset opettajan roolista, opettamisesta ja oppimisesta eivät ole liian kaukana toisistaan. Yhteisopettajuus edellyttää myös kykyä joustaa ja tehdä kompromisseja. Molempien tulee voida luottaa siihen, että toinen huolehtii lupaamansa asiat ja kantaa vastuuta ammatillisesti. On myös luotettava toisen ammattitaitoon ja annettava tilaa toimia sen mukaisesti.

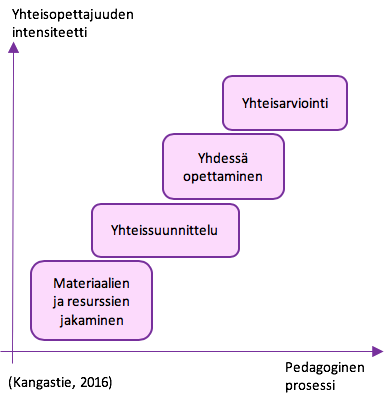Laajimmillaan yhteisopettajuus kattaa koko pedagogisen prosessin suunnittelusta ja opetuksesta aina arviointiin saakka. Kangastie (2016) on muotoillut pedagogisesta prosessista ja yhteisopettajuudesta kuvion, josta havaitaan, että pedagogisen prosessin eri vaiheet edellyttävät yhteisopettajuudeltakin eri tavoin. Jos koko oppimisprosessi toteutetaan yhteisesti, niin joudutaan suunnitteluun ja toteutukseen käyttämään varsinkin ensimmäisellä kerralla huomattavasti aikaa. Tarvitaan sopimuksia yhteisistä säännöistä ja rutiineista, opetuksen tavoitteista ja sisällöistä, käytettävistä opetusmenetelmistä, opiskelijoiden ryhmittelystä ja opettajien rooleista ja toiminnasta

Yhteisopettajuus kuitenkin onnistuu, jos ajanhallinta toimii ja onnistutaan suunnittelemaan tehokkaasti, tehdään yhteisiä päätöksiä ja jaetaan vastuuta, sekä puhutaan avoimesti opetuksen toteuttamisesta.

Kirjallisuutta:

Baeten, M., and Simons, M. (2014). Student Teachers' Team Teaching: Models, Effects, and Conditions for Implementation. Teaching and Teacher Education, 41, 92--110.

Erkkilä, R. & Perunka, S. (2016). Näkökulma tiimiopettajuuteen. ePooki. Oulun ammattikorkeakoulun tutkimus- ja kehitystyön julkaisut 28. Hakupäivä 7.10.2016. http://urn.fi/urn:nbn:fi-fe2016092824453.

Kangastie, H. (2016). Yhteisopettajuus Lapin ammattikorkeakoulussa - näkökulmia ja käytänteitä oppimisen organisointiin. Sarja B. Raportit ja selvitykset 8/2016. Lapin ammattikorkeakoulu, Rovaniemi.

Palmu, I., Kontinen, J. & Malinen, O.-P. (2017). Pedagogiset menetelmät yhteisopetusluokassa. Teoksessa Malinen, O.-P. & Palmu, I. (Toim.) Tavoitteena yhteisopettajuus -- näkökulmia ja toimintamalleja onnistuneeseen yhdessä opettamiseen. Niilo Mäki Instituutti, Kummi 16,
Arviointi-, opetus- ja kuntoutusmateriaaleja. Fram, Vaasa.

Pulkkinen, J. & Rytivaara, A. 2015. Yhteisopetuksen käsikirja. Jyväskylän yliopisto. Verkkojulkaisu. https://jyx.jyu.fi/bitstream/handle/123456789/48450/Yhteisopetuksen%20k%C3%83%C2%A4sikirja.pdf?sequence=1

Rytivaara, A., Palmu, I., Ahtiainen, R., Kontinen, J., & Pulkkinen, J. (2018). Yhteisopettajuudesta monipuolisuutta opettamiseen. LukSitko : moniammatillinen aikakausilehti oppimisvaikeuksista ja erilaisesta oppijuudesta, 2018(1), 16-19.

Rytivaara, A. & Kershner, R. 2012. Co-teaching as a context for teachers' professional learning and joint knowledge construction. Teaching and Teacher Education, 28 (7), 999--1008