Tehtävien ratkaisut

Tältä sivulta löydät tehtävien oikeat vastaukset ja ratkaisut monimutkaisimpiin tehtäviin.

1.

a. \(16b+16\)

b. \(\dfrac{2x}{1-x^{2}}\)

c. \(33\)

2.

Matka \(s\) kuljetaan nopeudella \(v\) ajassa \(t_{1}=s/v\).

Jos matkan alkuosa \(0,6s\) kuljetaan nopeudella \(v\) ja loppuosa \(0,4s\) nopeudella \(1,2v\), kuluu matkaan aika \(t_{2}=0,6s/v+\frac{0,4s}{1,2v}=\frac{1,12s}{1,2v}\). Aikojen suhte on \(\frac{t_{2}}{t_{1}}=\frac{1,12}{1,2}≈0,9333=1-0,0667.\)

V. Aika lyhenee \(6,7\%\).

3.

a. kun \(x=0\) tai \(x=8\)

b. \(a\)

4.

Oikea järjestys: A B D E C F

5.

a. \(L=\displaystyle\frac{1}{4\pi^{2} C t^{2}}\)

b. 1

6.

V: \(4\) osaa päärynämehua ja \(3\) osaa omenamehua

Ratkaisu: Tehdään oletus, että päärynämehua(\(14\%\)) on yksi litra tässä liuoksessa. Merkitään omenamehun(\(7\%\)) määrää muuttujalla \(x\).

Sekoitetun mehun määrä on siis \(x+1\).

Tästä saadaan ensimmäisen asteen yhtälö. \[\begin{align*} 1\cdot14\%+x\cdot7\%=(x+1)\cdot11\%\\ 14\%+x\cdot7\%=x\cdot11\%+11\%\\ x\cdot7\%-x\cdot11\%=11\%-14\%\\ x(7\%-11\%)=3\%\\ x=\frac{3\%}{4\%}\\ x=\frac{3}{4} \end{align*}\]

Eli päärynämehua ollessa \(1\) litra, omenamehua tarvitaan \(\frac{3}{4}\) litraa. Sekoitussuhde on siis

\[\begin{align*} \frac{\text{päärynä}}{\text{omena}}=\frac{1}{\frac{3}{4}}=\frac{4}{3} \end{align*}\]

Eli sekoitussuhde on 4 osaa päärynämehua ja 3 osaa omenamehua.

7.

Totta ovat:

• Lausekkeen \(1,1^{3}\) arvo on \(1,331\)
• Luvun \(-a+b\) vastaluku on \(a-b\).
• Tuotteen hinta nousee ensin \(10\%\) ja laskee sitten \(10\%\), joten lopullinen hinta on \(99\%\) alkuperäisestä hinnasta

8.

a.

Prosenttiyksikön muutos on \(22-8=14\) prosenttiyksikköä.

V: 14

b. Olkoon tuotteella veroton hinta \(a\). Tästä hinnasta maksettava arvonlisävero on vanhalla ALV:lla \(0,22\cdot a\) ja uudella ALV:lla \(0,08\cdot a\).

Uusi arvonlisävero on \(\frac{0,08\cdot a}{0,22\cdot a}=\frac{0,08}{0,22}=0,3636..≈36,3\%\) vanhasta arvonlisäverosta.

Tuotteesta maksettiin siis \(63,6\%\) enemmän vanhalla arvonlisäveroprosentilla.

MAA2

1.

Oikeat vastaukset:

• Funktion kuvaajan ja y-akselin leikkauspiste on pisteessä \((0,5)\)
• Muodostuneen suoran kulmakerroin on 2

2.

\(x\geq5\)

3.

\(x>9\) ja \(x<-1\)

4.

• \(f(2)=4\)

• \(f(4)=-3\)

3. funktio on \(f(x)\)
4. funktio on \(g(x)\)
5. funktio on \(h(x)\)

5.

\(b≥-6\)

6.

Merkitään ruusujen lukumäärää leveyssuunnassa muuttujalla \(x\). Tällöin pituussuunnassa ruusuja on \(x+9\).

Koska pelto on suorakulmion muotoinen, saadaan ruusujen lukumäärä merkittyä \[\begin{align*} 190=x\cdot(x+9) \end{align*}\] Ratkaistaan tästä yhtälöstä \(x\). \[\begin{align*} 190&=x\cdot(x+9)\\ 190&=x^{2}+9x\\ x^{2}+9x-190&=0\\ x&=\frac{9\pm\sqrt{9^{2}+4\cdot 1\cdot (-190)}}{2\cdot1}\\ x&=-19\;\;\text{ tai }\;\;x=10 \end{align*}\]

Tuloksen negatiivinen arvo ei kelpaa koska kyseessä on lukumäärä.

V. Ruusuja on leveyssuunnassa 10 kappaletta.

7.

b. Ratkaisut ovat 0 ja -1.

8.

Kirjoitetaan tehtävänanto matemaattisesti. Merkitään kylkeä kirjaimella \(b\) ja kantaa kirjaimella \(a\). Tasasivuisessa kolmiossa kyljet ovat yhdenmittaiset ja kanta voi olla eri mittainen.

"Kolmion kannan suhde kyljen pituuteen" tarkoittaa siis \(\frac{a}{b}\).

"Kyljen pituuden suhde kyljen ja kannan pituuden summaan" tarkoittaa siis \(\frac{b}{b+a}\).

Ja tehtävänannon mukaan nämä kaksi suhdetta ovat yhtäsuuria, eli merkitään \[\begin{align*} \frac{a}{b}&=\frac{b}{b+a}\;\;\;\;|a=5\\ \frac{5}{b}&=\frac{b}{b+5}\;\;\;\;\;|\cdot b\\ 5&=\frac{b^{2}}{b+5}\\ 5&=b^{2}\cdot\frac{1}{b+5}\;\;\;\;\;\;|\cdot (b+5)\\ 5(b+5)&=b^{2}\\ 5b+25&=b^{2}\;\;\;\;\;|-5b,-25\\ b^{2}-5b-25&=0\\ b&=-\frac{-5(\sqrt{5}-1)}{2}\;\;\text{ tai }b=\frac{5\cdot(\sqrt{5}+1)}{2}\\ b&≈-3,09\;\text{ tai }\;\;\;\;\;\;\;\;\;\;\;\;\;\; b≈8,09 \end{align*}\]

Kyseessä on pituus, joten negatiivinen ratkaisu ei käy.

Kolmion kyljen pituus on siis \(8,1\).

MAA3

1.

Piirretään tilanteesta kuva.
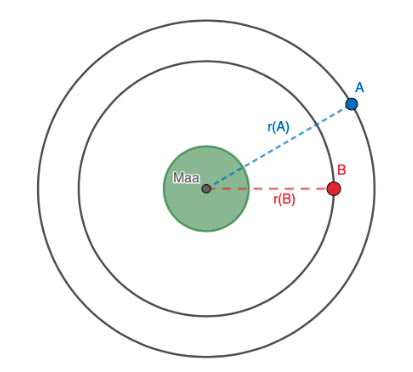Merkitään kiertoratojen etäisyyttä \(x\):llä. 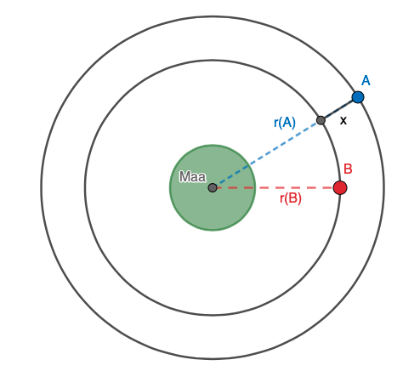Tehtävänannon mukaisesti tekokuun A kiertorata on 50km pitempi kuin tekokuu B kiertorata. Eli

\(p_{A}=p_{B}+50\), jossa \(p\) on ympyrän kehä. \[\begin{align*} p_{A}&=p_{B}+50\\ p_{A}-p_{B}&=50\;\;\;\;\;\;\;\;\;\;|p=2\pi\cdot r\\ 2\pi\cdot r_{A}-2\pi\cdot r_{B}&=50\\ 2\pi(r_{A}-r_{B})&=50\\ r_{A}-r_{B}&=\frac{50}{2\pi}\\ r_{A}&=\frac{50}{2\pi}+r_{B} \end{align*}\]

Tekokuulle A pätee myös \(r_{A}=r_{B}+x\)

Muokataan nyt tekokuun A kehän lauseketta: \[\begin{align*} \frac{50}{2\pi}+r_{B}&=r_{B}+x\;\;\;\;|-r_{B}\\ \frac{50}{2\pi}&=x\\ x&=7,96 \end{align*}\]

Vastaus: Tekokuu A on 8,0 km kauempana Maasta kuin tekokuu B.

2.

Piirretään tilanteesta kuva.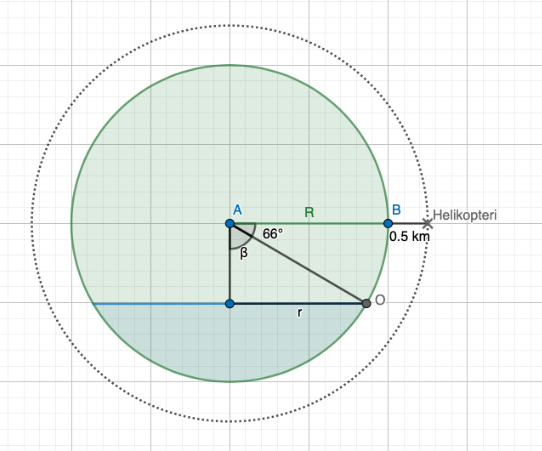

Helikopterin etäisyys maapallon keskipisteestä on \(6370\text{ km}+0,5\text{ km}=6370,5\text{ km}\).

Ratkaistaan nyt kulma \(\beta\).

Ratkaistaan seuraavaksi säde \(r\): \[\begin{align*} \sin\alpha&=\frac{r}{637,05\text{ km}}\\ r&=\sin(24°)\cdot6370,5\text{ km}\\ r&=2591,12\text{ km}. \end{align*}\]

Mantereen ympärysmitta (kehä) saadaan nyt laskemalla

\(p=2\pi\cdot r=2\pi\cdot2591,12\text{ km}=16280,5\text{ km}\).

Helikopterin lentomatka on siis \(16280\text{ km}\).

3.

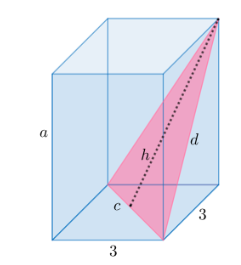
Ratkaistaan laatikon kannan ja tilavuuden avulla laatikon korkeus: \[\begin{align*} V&=\text{kanta}\cdot\text{kanta}\cdot\text{korkeus}\\ 45&=3\cdot3\cdot a\\ a&=5 \end{align*}\] Laatikon korkeus on \(5\).

Lasketaan sitten kolmion kannan pituus hyödyntäen tietoa laatikon pohjan kannan pituudesta. Kolmion kanta saadaan ratkaisemalla Pythagoraan lauseesta hypotenuusa: \[\begin{align*} 3^{2}+3^{2}=c^{2}\\ c=\pm3\sqrt{2}\\ \end{align*}\] Ja ratkaisuista vain positiivinen ratkaisu käy, eli kolmion kanta on \(3\sqrt{2}\).

Ratkaistaan seuraavaksi kolmion sivun pituus hyödyntämällä laatikon kantaa, korkeutta sekä Pythagoraan lausetta: \[\begin{align*} 3^{2}+5^{2}=d^{2}\\ d=\pm\sqrt{34} \end{align*}\] Ja ratkaisuista vain positiivinen ratkaoisu käy, eli kolmion sivun pituus on \(\sqrt{34}\).

Kolmion pinta-alan ratkaisuun tarvitaan kolmion kanta sekä sen korkeus. Ratkaistaan vielä kolmion korkeus \(h\): \[\begin{align*} h^{2}+\left(\frac{3\sqrt{2}}{2}\right)^{2}=d^{2}\\ h=\pm\frac{\sqrt{118}}{2} \end{align*}\] Ja ratkaisuista vain positiivinen ratkaoisu käy, eli kolmion korkeus \(h\) on \(\frac{\sqrt{118}}{2}\).

Nyt saadaan laskettua kolmion pinta-ala \(A\): \[\begin{align*} A=c\cdot h\\ A=3\sqrt{2}\cdot\frac{\sqrt{118}}{2}\\ A≈23,04 \end{align*}\]

Kolmion pinta-ala on noin 23.

4.

a. Lasketaan kuplan pinta-ala \(A\): \[\begin{align*} A&=4\pi r^{2}\\ A&=4\pi\cdot 3^{2}\\ A&=36\pi≈113,097 \end{align*}\]

Tästä pinta-alasta \(\frac{2}{3}\) on jäässä. Eli \(\frac{2}{3}\cdot36\pi=75,4\).

V: \(75,4\text{ cm}^{2}\) on jäässä.

b. Pinta-alasta ei ole jäässä \(\frac{1}{3}\cdot36\pi=37,6991\text{ cm}^{2}.\)

Tämä jäätymätön alue on kalotti, jonka pinta-ala on \(A_{kalotti}=2\pi\cdot rh\).

Ratkaistaan tästä yhtälöstä korkeus \(h\). \[\begin{align*} A_{kalotti}&=2\pi\cdot rh\\ h&=\frac{A_{kalotti}}{2\pi\cdot r}\\ h&=\frac{37,6991\text{ cm}^{2}}{2\pi\cdot 3\text{ cm}}\\ h&=2. \end{align*}\]

V. Pienemmän kalotin korkeus on \(2,0\).

c. Jäätymättömän segmentin tilavuus on \(V_{segmentti}=\pi\cdot h^{2}\left(r-\frac{h}{3}\right)\).

\[\begin{align*} V_{segmentti}&=\pi\cdot 2,0^{2}\left(3-\frac{2,0}{3}\right)\\ V_{segmentti}&=\frac{28\pi}{3}\\ V_{segmentti}&≈29,32 \end{align*}\]

V: Segmentin pinta-ala on \(29,3\).

5.

a. Tehtävänä on määrittää pisteen \(N\) etäisyys pisteestä \(O\).

Kuviosta voidaan huomata, että jana on kohtisuorassa pisteiden \(O\) ja Laavun välistä janaa.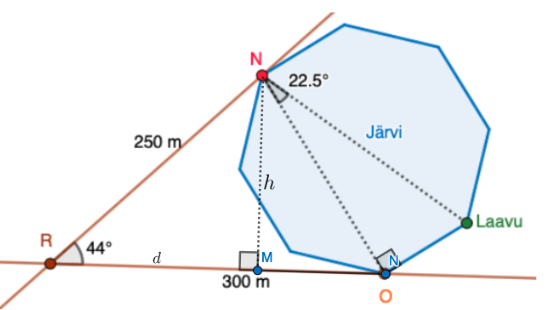

Ratkaistaan ensin janan \(h\) pituus: \[\begin{align*} h=\sin(44°)\cdot250\text{ m}=173,665\text{ m} \end{align*}\]

Etäisyys pisteestä \(M\) pisteeseen \(O\) saadaan, kun vähennetään \(300\) metristä pisteiden \(R\) ja \(M\) etäisyys.

Ratkaistaan pisteiden \(R\) ja \(M\) välinen etäisyys \(d\): \[\begin{align*} \tan(44°)&=\frac{h}{d}\\ d&=\frac{173,665}{\tan(44°)}=179,835\text{ m} \end{align*}\]

Pisteiden \(M\) ja \(O\) välinen etäisyys on tällöin \(300-179,835=120,165\text{ m}\).

Nyt voidaan määrittää Pythagoraan lauseen avulla pisteiden \(N\) ja \(O\) välinen etäisyys \[\begin{align*} h^{2}+(MO)^{2}=(NO)^{2}\\ 173,665^{2}+120,165^{2}=(NO)^{2}\\ (NO)=211,185 \end{align*}\]

Matka mökiltä \(N\) mökille \(O\) on \(211\text{ m}\)

b. Etäisyys mökiltä \(N\) laavulle saadaan hyödyntämällä \(22,5\) asteen kulmaa sekä a-kohdassa laskettua etäisyyttä.

\[\begin{align*} \cos(22,5°)=\frac{(NO)}{(NL)}\\ (NL)=\frac{(NO)}{\cos(22,5°)}\\ (NL)=\frac{211,185}{\cos(22,5°)}\\ (OL)=228,585 \end{align*}\]

Etäisyys mökiltä \(O\) Laavulle on \(229\) metriä.

6.

Huom. Tehtävässä kannattaa käyttää tarkkoja arvoja. Likiarvot ovat malliratkaisussa siksi, jotta voi vertailla välituloksia.

Ratkaistaan ensin suuremman pallon säde hyödyntämällä tietoa sen materiaalin määrästä (eli pinta-alasta).

\[\begin{align*} A=4\pi r^{2}\\ r^{2}=\frac{A}{4\pi}\\ r=\pm\frac{15\sqrt{2}}{2\sqrt{\pi}} \end{align*}\] Ja ratkaisuista vain positiivinen käy. Isomman pallon säde \(r=\frac{15\sqrt{2}}{2\sqrt{\pi}}≈5,98\text{ cm}\).

Ratkaistaan seuraavaksi isomman pallon tilavuus \(V_{iso}\): \[\begin{align*} V_{iso}&=\frac{4}{3}\pi r^{3}\\ V_{iso}&=\frac{4}{3}\pi \left(\frac{15\sqrt{2}}{2\sqrt{\pi}}\right)^{3}\\ V_{iso}&=\frac{1125\sqrt{2}}{\sqrt{\pi}} \end{align*}\]

Isomman pallon tilavuus \(V_{iso}=\frac{1125\sqrt{2}}{\sqrt{\pi}}≈897,62\text{ cm}^{3}\).

Pienemmän pallon tilavuus on neljännes suuremman pallon tilavuudesta, eli

\(\frac{1}{4}\cdot\frac{1125\sqrt{2}}{\sqrt{\pi}}=\frac{1125\sqrt{2}}{4\sqrt{\pi}}\).

Pienemmän pallon säde on siis: \[\begin{align*} V_{pieni}=\frac{4}{3}\pi r^{3}\\ r=\sqrt[3]{\frac{V_{pieni}}{\frac{4}{3}\pi}}\\ r≈3,76977 \end{align*}\]

Ja edelleen pienemmän pallon pinta-ala (eli materiaalin määrä): \[\begin{align*} A_{pieni}=4\pi r^{2}\\ A_{pieni}=178,583 \end{align*}\]

Pienemmässä pallossa on materiaalia

7.

Piirretään tilanteesta kuva.

a.

Lasketaan ensin pyramidin tilavuus \(V_{pyramidi}\). Tilavuuden laskemiseksi ratkaistaan pyramidin korkeus \(h\): 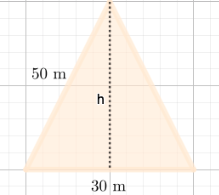\[\begin{align*} h^{2}+15^{2}&=50^{2}\\ h&=\pm5\sqrt{91}\text{ m} \end{align*}\] Ja näistä ratkaisuista käy ainoastaan positiivinen. Ratkaistaan nyt pyramidin tilavuus \(V_{pyramidi}\):

\[\begin{align*} V_{pyramidi}&=\frac{A_{pohja}\cdot h}{3}\\ V_{pyramidi}&=\frac{30\text{ m}\cdot 30\text{ m}\cdot5\sqrt{91}\text{ m}}{3}\\ V_{pyramidi}&=1500\cdot\sqrt{91}\text{ m}^{3} \end{align*}\]

Hautakammion tilavuus on \(2\%\) koko pyramidin tilavuudesta, eli \(V_{kammio}=0,02\cdot1500\cdot\sqrt{91}\text{ m}^{3}≈286,2\text{ m}^{3}\)

b.

Kammio on kuution muotoinen, joten sen tilavuus on \(V=a^{3}\), jossa \(a\) on huoneen seinän pituus. Kammion tilavuus on \(286,2\text{m}^{3}\), joten sen seinän pituus on \[\begin{align*} V&=a^{3}\\ a&=\sqrt[3]{V}=\sqrt[3]{0,02\cdot1500\cdot\sqrt{91}\text{ m}^{3}}\\ a&=6,58993\text{m} \end{align*}\]

Yhden seinän pinta-ala \(A_{\text{seinä}}=a^{2}=6,58993^{2}\text{m}^{2}=43,4271\text{m}^{2}\).

Yhdelle seinälle menevän kullan tilavuus on \[\begin{align*} V_{\text{kulta}}=1\text{cm}\cdot A_{\text{seinä}}=0,01\text{m}\cdot A_{\text{seinä}}=0,01\text{m}\cdot43,4271\text{m}^{2}=0,434271\text{m}^{3} \end{align*}\]

Kuution mallisessa kammiossa on yhteensä kuusi seinää, jotka kullalla päällystetään, joten kokonaisuudessaa kultaa kuluu \[\begin{align*} V=6\cdot0,434271\text{m}^{3}=2,606\text{m}^{3}. \end{align*}\]

Kullan tiheys on \(19,32\frac{\text{g}}{\text{cm}^{3}}=19329\frac{\text{g}}{\text{m}^{3}}\).

Kullan paino \(m_{\text{kulta}}=19329\frac{\text{g}}{\text{m}^{3}}\cdot2,606\text{m}^{3}=50364,2\text{g}≈50,4\text{kg}\).

8.

Tehtävänannon kuva on symmetrinen, näin ollen kaarien leikkauspisteet muodostavat maljakon keskelle neliön: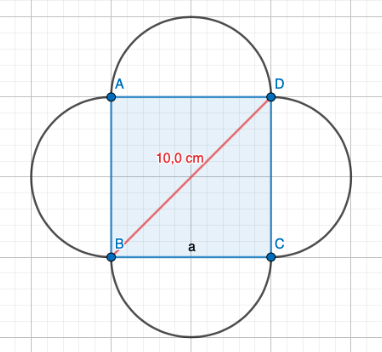

Kuvan puoliympyrät voidaan yhdistää, jolloin saadaan kaksi ympyrää ja yksi neliö.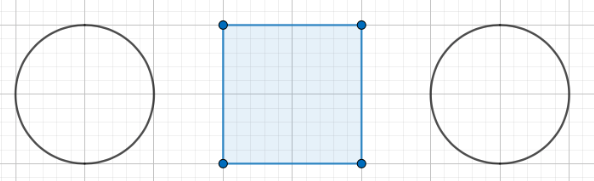

Maljakon tilavuus saadaan laskettua nyt yhdistämällä suorakulmaisen särmiön tilavuuden kahteen ympyrälieriön tilavuuteen. Kaikkien näiden korkeus on \(12\text{cm}\).

Lasketaan ensin suorakulmaisen särmiön tilavuus \(V_{\text{särmiö}}\). Tilavuuden laskemiseksi täytyy ratkaista neliön kanta \(a\). Hyödynnetään tässä Pythagoraan lausetta: \[\begin{align*} 2a^{2}&=(10\text{cm})^{2}\\ a&=\sqrt{\frac{(10\text{cm})^{2}}{2}}\\ a&=\pm5\cdot\sqrt{2}\text{cm} \end{align*}\] Ratkaisuista vain positiivinen käy.Nyt voidaan laskea särmiön tilavuus: \[\begin{align*} V_{\text{särmiö}}&=a^{2}\cdot12\text{cm}\\ V_{\text{särmiö}}&=(5\cdot\sqrt{2}\text{cm})^{2}\cdot12\text{cm}\\ V_{\text{särmiö}}&=600\text{cm}^{3} \end{align*}\] Lasketaan seuraavaksi ympyrälieriöiden tilavuus \(V_{\text{lieriö}}\). Lieriön pohjan säde saadaan jakamalla kanta \(a\) kahdelle. \[\begin{align*} V_{\text{lieriö}}&=A_p\cdot12\text{cm}\\ V_{\text{lieriö}}&=\pi\cdot r^{2}\cdot12\text{cm}\\ V_{\text{lieriö}}&=\pi\cdot (\frac{a}{2})^{2}\cdot12\text{cm}\\ V_{\text{lieriö}}&=150\pi\;\text{cm}^{3} \end{align*}\]

Lieriöitä on yhteensä kaksi ja särmiöitä yksi, joten kokonaistilavuus on \(V_{\text{kok}}=2\cdot V_{\text{lieriö}}+V_{\text{särmiö}}\) \[\begin{align*} V_{\text{kok}}&=2\cdot V_{\text{lieriö}}+V_{\text{särmiö}}\\ V_{\text{kok}}&=2\cdot150\pi\;\text{cm}^{3}+600\text{cm}^{3}≈1542,48\text{cm}^{3} \end{align*}\]

Tulos on nyt kuutiosenttimetreinä ja ne pitäisi muuntaa desilitroiksi. Muistetaan, että \(1\text{dm}^{3}=1\;l\). \[\begin{align*} 1\text{cm}^{3}=\frac{1}{1000}\text{dm}^{3}=\frac{1}{1000}\;l=\frac{1\cdot10}{1000}\text{dl}=0,01\text{dl}. \end{align*}\]

Maljakon kokonaistilavuus \(V_{\text{kok}}=0,01\cdot1542,48\text{dl}=15,4248\text{dl}≈15,4\text{dl}\)

MAA4

1.

a.

Kolmannella rivillä on virhe \(x+2=1\). Edellä pitäisi olla \(\pm\).

b.

Vastauksessa on virhe. Ympyrän keskipiste on \((-2,-2)\).

2.

a.

Limen siivun keskipiste pitäisi olla pisteessä \((\frac{4}{3},-\frac{4}{3})\).

b.

Banaanit sijoittuvat koordinaattiakseleille siten, että oikealle avautuvan "paraabelin" huippu on pisteessä \((0,0)\) ja vasemmalle aukeavan "paraabelin" huippu on pisteessä \((-1,0)\).

3.

a.

Hyödynnetään teoriaa pisteen etäisyys suorasta. Tässä suora on \(y=0,14x+4,6\) ja piste on \((-4,7;-5)\).

Muokataan suoran yhtälö normaalimuotoon \[\begin{align*} &y=0,14x+4,6\;\;\;\;\;\;\;|-y\\ &0,14x-y+4,6=0 \end{align*}\] Pisteen etäisyys suorasta on \[\begin{align*} \dfrac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}=\dfrac{|0,14\cdot(-4,7)+(-1)\cdot(-5)+4,6|}{\sqrt{0,14^{2}+(-1)^{2}}}=8,8556 \end{align*}\]

Mittakaava on \(1:56\), eli luonnossa infopisteen etäisyys asemakadusta on \(56\cdot8,8556\text{m}≈496\text{m}\).

b.

Liljan kulkureitti on ympyrän \((x+10,4)^{2}+(y+1,6)^{2}=4\). Ympyrän normaalimuodosta voidaan päätellä, että ympyrän säde on \(2\), koska \(4=2^{2}\). Lisäksi ympyrän keskipiste on pisteessä \((-10,4;1,6)\).

Ratkaistaan nyt ympyrän kehän lyhin etäisyys suoraan \(y=0,14x+4,6\). Tämä saadaan laskemalla ensin, kuinka kaukana ympyrän keskipiste on suorasta ja sen jälkeen vähennetään tuloksesta ympyrän säde.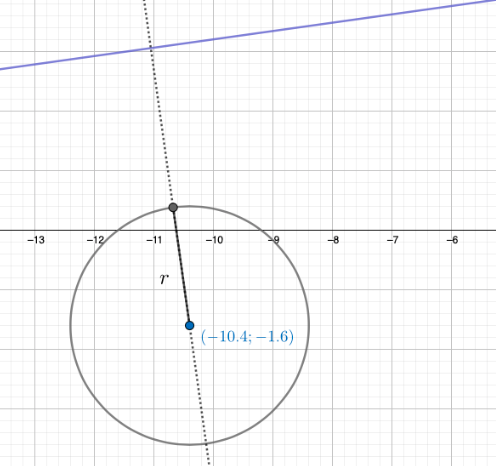

\[\begin{align*} \dfrac{|ax_{0}+by_{0}+c|}{\sqrt{a^{2}+b^{2}}}=\dfrac{|0,14\cdot(-10,4)+(-1)\cdot(-1,6)+4,6|}{\sqrt{0,14^{2}+(-1)^{2}}}=4,698 \end{align*}\]

Ympyrän keskipisteen etäisyys suorasta on \(4,698\). Tehtävänannossa kysytään ympyrän kehän etäisyyttä suorasta, joten vähennetään tästä etäisyydestä ympyrän säde \(2\). \[\begin{align*} 4,698-2=2,698 \end{align*}\]

Mittasuhde on \(1:56\), joten etäisyys on \(56\cdot2,698≈151\text{m}\).

4.

a.

Piirretään tilanteesta kuva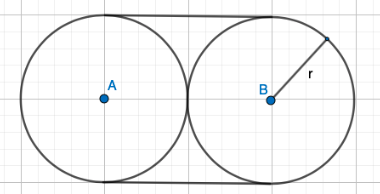

Ympyröiden yhdysjana alkaa aina ympyrän puolesta välistä ja päättyy ympyrän puoleen väliin. Hevonen ravaa kaarteessa siis yhteensä kahden puoli ympyrän verran, eli yhden kokonaisen ympyrän, jonka säde on \(r\).

Ympyrän säde \(r=85\text{m}\). Ympyrän kehän pituus \(p=2\pi r=2\pi\cdot85\text{m}=170\pi\text{m}≈534,1\text{m}\)

b.

Olkoon Brunon vektoriesitys \(\overline{B}=-\frac{2}{3}\overline{i}+\frac{2}{3}\overline{j}\) ja Hillevin vektoriesitys \(\overline{H}=-\frac{2}{3}\overline{i}-\overline{j}\).

Lasketaan näiden kahden vektorin välinen kulma. \[\begin{align*} \cos(\overline{H},\overline{B})=\dfrac{\overline{H}\cdot\overline{B}}{|\overline{H}||\overline{B}|}, \end{align*}\] jossa \(\overline{H}\cdot\overline{B}\) tarkoittaa vektorien välistä pistetuloa.

Pistetulo on: \[\begin{align*} \overline{H}\cdot\overline{B}=-\frac{2}{3}\cdot(-\frac{2}{3})+-1\cdot\frac{2}{3}=-\frac{2}{9}. \end{align*}\]

Lasketaan myös vektoreiden pituudet: \[\begin{align*} |\overline{H}|=\sqrt{\left(-\frac{2}{3}\right)^{2}+(-1)^{2}}=\\ |\overline{B}|=\sqrt{\left(-\frac{2}{3}\right)^{2}+\left(\frac{2}{3}\right)^{2}}= \end{align*}\] Sijoitetaan tämä kulman yhtälöön \[\begin{align*} \cos(\overline{H},\overline{B})=\dfrac{-\frac{2}{9}}{|\overline{H}||\overline{B}|}, \end{align*}\]

5.

Asetetaan paraabeli koordinaatistoon siten, että sen lähtöpiste on \((-200,0)\) ja laskeutusmispiste \((200,0)\). Paraabeli huippu on tehtävänannon mukaisesti \(5\) m radiomaston yläpuolella, eli pisteessä \((0,25)\).

Paraabelin yhtälö on muotoa \(y-y_{0}=a(x-x_{0})^{2}\), jossa \((x_{0},y_{0})\) on paraabelin huipun koordinaatit.

\[\begin{align*} y-y_{0}=a(x-x_{0})^{2}\\ y-25=a(x-0)^{2}\\ y=ax^{2}+25 \end{align*}\]

Ratkaistaan vielä kerroin \(a\). Paraabeli kulkee pisteen \((-200,0)\) kautta (kuumailmapallon lähtöpiste). Sijoitetaan tämä piste nyt paraabelin yhtälöön: \[\begin{align*} 0=a\cdot(-200)^{2}+25\\ a=-\frac{1}{1600} \end{align*}\] Joten lentoradan paraabelin lauseke on \(y=-\frac{1}{1600}x^{2}+25\).

6.

7.

Kuvasta voidaan huomata, että siihen muodostuu kolme samanmuotoista kolmiota: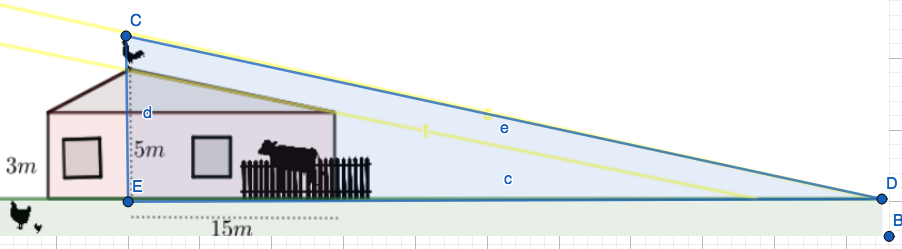

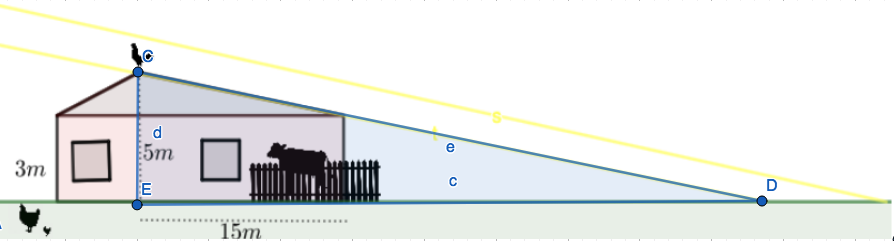
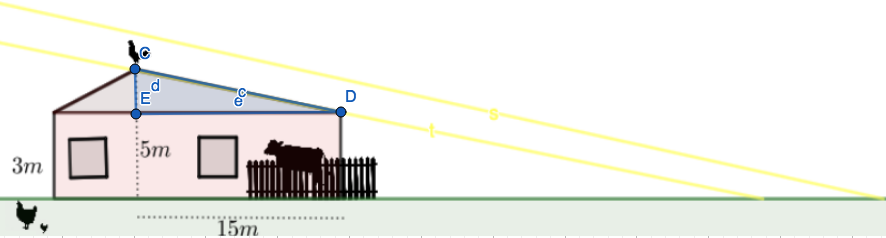
Tehtävän ratkaisun kannalta oleellisimmat samanmuotoiset kolmiot ovat suurin ja pienin kolmio.

Koska kolmiot ovat samanmuotoiset, myös niiden kulmat \(ECD\) ovat samansuuruiset. Ratkaistaan tämän kulman suuruus pienimmän kolmion avulla, sillä sen kateettien pituudet tunnetaan.

Pienimmälle kolmiolle kateettien pituudet ovat \(2\) m ja \(15\) m. 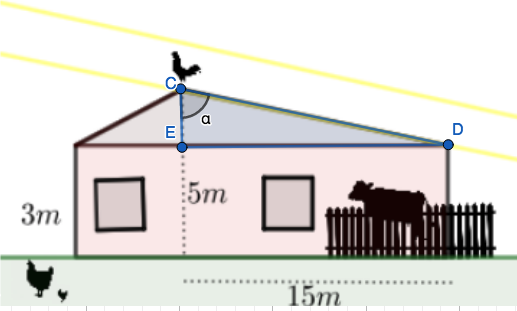\[\begin{align*} \tan\alpha&=\frac{\text{vastainen kateetti}}{\text{viereinen kateetti}}=\frac{15\text{ m}}{2\text{ m}}\\ \alpha&=82,4054° \end{align*}\]

Sama kulma on myös suuremman kolmion kulmana. Lasketaan seuraavaksi suuremman kolmion pisimmän kannan pituus. Merkitään pisintä kateettia \(x\):llä.

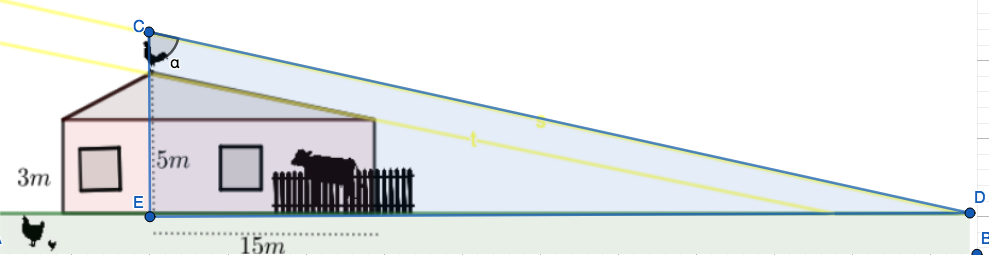
\[\begin{align*} \tan\alpha&=\frac{\text{vastainen kateetti}}{\text{viereinen kateetti}}=\frac{x}{5,5\text{ m}}\\ x&=\tan\alpha\cdot5,5\text{ m}\\ x&=41,25\text{ m} \end{align*}\]

Nyt kukon pään varjon etäisyys talon seinästä saadaan erotuksella \[\begin{align*} 41,25\text{ m}-15\text{ m}=26,25\text{ m}. \end{align*}\]

8.

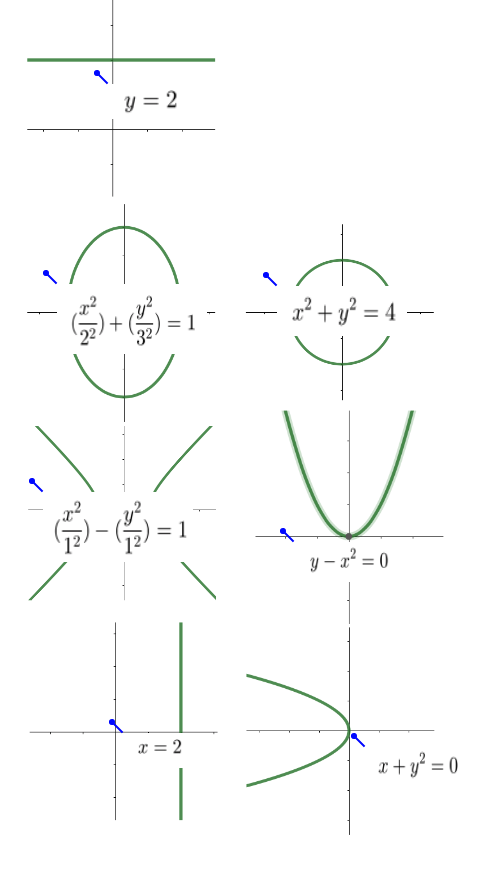
MAA5

1.

a.

b.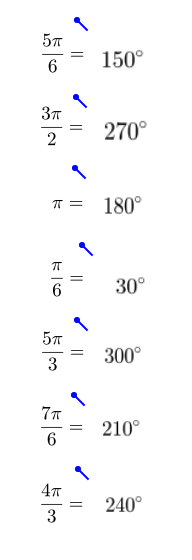

2.

Eksponenttifunktio on \(f(x)=a^{x}+1\), jossa \(a>0,a≠0\). Funktion kuvaaja kulkee pisteen \((4,3)\).

Ratkaistaan ensin kantaluku \(a\).

Koska funktion kuvaaja kulkee pisteen \((4,3)\) kautta, niin tällöin \(f(4)=3\). Sijoitetaan piste funktioon \(f(x)\): \[\begin{align*} f(x)&=a^{x}+1\\ f(4)&=a^{4}+1=3\\ a^{4}+1&=3\\ a^{4}&=2\\ a&=\sqrt[4]{2} \end{align*}\]

Eli eksponenttifunktio on muotoa \(f(x)=\sqrt[4]{2}^{x}\).

Ratkaistaan vielä \(f(8)\). \[\begin{align*} f(8)=\sqrt[4]{2}^{8}=4 \end{align*}\]

Vastaus: Kantaluku \(a=\sqrt[4]{2}\) ja \(f(8)=4\).

3.

a.

Jodi-131:n puoliintumisaika on tehtävänannon mukaan \(8\) päivää. Joka päivä jodin määrä \(I\) elimistössä \(k\)-kertaistuu:

Ensimmäisenä päivänä: \(k\cdot I\)

Toisena päivänä: \(k\cdot(kI)\)

Kolmantena päivänä \(k\cdot(k^{2}I)\)

Edelleen kahdeksantena päivänä jodia on elimistössä \(k^{8}I\) ja tämä on puolet alkuperäisestä määrästä \(I\) eli \(\frac{1}{2}I\): \[\begin{align*} k^{8}I=\frac{1}{2}I\\ k=\sqrt[8]{\frac{1}{2}}=0,917 \end{align*}\] Eli yhden päivän jälkeen elimistössä on jodia jäljellä \(91,7\%\).

b.

Yhdessä tabletissa on vaikuttavaa ainetta \(130\) mg. Jos tabletteja otetaan kaksi, vaikuttavaa ainetta elimistössä on \(260\) mg.

Puolikkaassa tabletissa vaikuttavaa ainetta on \(130/2=65\) mg.

\[\begin{align*} 260\text{ mg}\cdot\left(\sqrt[8]{\frac{1}{2}}\right)^{x}=65\text{ mg}\\ x=16 \end{align*}\]

Eli siis \(16\) päivän kuluttua jodia on elimistössä puolikkaan tabletin verran.

4.

a.

Sinifunktiossa, joka on muotoa \(f(x)=a\cdot \sin(bx+c),\) parametri \(a\) kuvaa aallon amplitudia eli suurinta etäisyyttä \(x-\)akselista.

Eli tässä tilanteessa amplitudi löydetään suoraan sähkövirran yhtälöstä \(i=\color{green}{0,48}\color{black}\cdot\sin(100\pi t)\).

Sinifunktion amplitudi on \(0,48\).

b.

Sinifunktiossa, joka on muotoa \(f(x)=a\cdot \sin(bx+c),\) parametri \(b\) kuvaa aallon tiheyttä. Nyt sekä sähkövirran, että jännitteen yhtälöissä \(b=100\pi\) eli siniaallot ovat samantaajuisia.

Parametri \(c\) puolestaan siirtää kuvaajaa vaakasuunnassa, joten parametrien \(c\) erotus kertoo sinifunktioiden vaihe-eron.

Tässä tilanteessa vaihe-ero saadaan laskettua