LOGARITMIT


Tämän materiaalin tavoitteena on auttaa sen käyttäjää logaritmin käsitteen ymmärtämisessä ja logaritmeihin liittyvien pitkän matematiikan sisältöjen oppimisessa. Käsiteltäviä sisältöjä ovat mm.
- Eksponenttiyhtälöt ja logaritmin määritelmä
- Logaritmifunktiot
- Logaritmien laskusäännöt
- Logaritmiyhtälöt
Huomaa, että tässä materiaalissa ei käsitellä logaritmiepäyhtälöitä ja logaritmin derivointia.
Ohjeita käyttäjälle
Materiaali koostuu neljästä alaluvusta, jotka sisältävät tehtäviä, teoriaa sekä pieniä tutkimuksia. Löydät sisällysluettelon linkkeineen sivun vasemmasta reunasta.
Materiaali on pyritty suunnittelemaan niin, että sitä voidaan hyödyntää sekä oppitunneilla että itsenäisessä opiskelussa. Tehtäviä ja tutkimuksia suositellaan tekemään annetussa järjestyksessä, sillä jokainen osio sisältää oman oppisisältönsä sekä mahdollisesti tärkeää taustatietoa seuraaviin tehtäviin.
Tehtävät, joissa on merkki *, on luokiteltu hieman muita tehtäviä haastavammiksi.
Suurin osa tehtävistä on rakennettu siten, että vastaukset voi tallentaa tai
tarkistaa tehtävän yhteydessä. Siitä huolimatta kaikki tehtävät saa halutessaan tehdä käyttäen mitä tahansa (ylioppilaskokeessa sallittua) ohjelmistoa.
Hyviä työkaluja ovat esimerkiksi
- Geogebra (onlineversio)
- Texas Instruments TI-Nspire CAS
- Abitin Matikkaeditori
- Casio ClassPad Manager
- LibreOffice
- WxMaxima
Jos tehtävässä käsketään hyödyntämään vapaavalintaista ohjelmistoa, sen yhteyteen on lisätty kohta, johon voit ladata kuvakaappauksen tai vastaustiedoston, kun olet saanut tehtävän valmiiksi. Näin voit tallentaa kaikki vastaukset tälle sivulle. Jos teet tehtävän paperille, voit ottaa siitä kuvan ja ladata palautuskohtaan.
Ohjeita vastaamiseen:
- Osa tehtävistä avautuu kokonaiseksi vasta kun viet kursorin tehtävän päälle.
 -merkki tarkoittaa sulkeutuvaa aluetta, jota klikkaamalla saat näkyviin piilotetun sisällön, esim. vastausikkunan, kysymykset tai mallivastauksen.
-merkki tarkoittaa sulkeutuvaa aluetta, jota klikkaamalla saat näkyviin piilotetun sisällön, esim. vastausikkunan, kysymykset tai mallivastauksen.- MathCheck-tehtävissä pyydetään kirjoittamaan vastaus yhtälönä tai lukuna.
- Tästä linkistä löydät ohjeita matematiikan kirjoittamiseen MathCheck-editorilla.
- Tehtävän vastausruudussa saattaa olla valmiina merkkejä, kuten
<=> x=. Tällöin vastaus halutaan kyseisessä muodossa. Älä siis poista merkkejä vaan kirjoita vastaus merkkien jatkoksi. - MathCheck-tehtävät ilmoittavat automaattisesti onko vastaus oikein vai väärin ja saat oikeasta vastauksesta pisteitä. Alta löydät esimerkkejä:
Väärin:


Oikein:

- Kaikista tehtävissä ei tule erillistä ilmoitusta, menikö vastaus oikein vai väärin. Etsi tällöin
Pointstehtävän yläreunasta:- Jos
Points: 0niin vastaus ei ole oikein. Alusta tehtävä ja kokeile uudelleen. Huom. joissain tehtävissä vastauskertojen määrä on rajoitettu. - Jos
Points: 1tai enemmän, vastaus meni oikein.
- Jos
- Tekstivastauksista ei tule automaattisesti pisteitä eikä oikein/väärin -ilmoitusta, mutta opettaja voi halutessaan pisteyttää nämä tehtävät.
Muita vinkkejä:
- Voit merkitä alueen luetuksi klikkaamalla sivun oikeassa reunassa näkyvää oranssia palkkia.
- Oikean reunan
 merkistä voit lisätä kyseiseen kohtaan julkisen kommentin tai tehdä muistiinpanoja, jotka näkyvät vain itsellesi (
merkistä voit lisätä kyseiseen kohtaan julkisen kommentin tai tehdä muistiinpanoja, jotka näkyvät vain itsellesi (Just me). - Jos reuna on keltainen, materiaaliin on tehty muutoksia sen jälkeen, kun olet lukenut sen.
- Materiaalin lopusta löytyy ylimääräisiä paikkoja vastaustiedostojen palauttamiselle.
1. Johdatus logaritmin käsitteeseen

Tässä luvussa on tavoitteena löytää vastaukset mm. seuraaviin kysymyksiin:
- Mikä on logaritmi?
- Miten eksponenttiyhtälöitä ratkaistaan?
- Millainen yhteys on eksponenttifunktiolla ja logaritmifunktiolla?
1.1 Tehtävä: Johdantotehtävä
Ratkaise seuraavista yhtälöistä luku \(x\) ilman laskinta.
1.2 Tutkimus: Eksponentti- ja logaritmifunktio
Avaa avuksesi jokin ohjelmisto, jolla voit piirtää funktioiden kuvaajia, esimerkiksi GeoGebra.
Noudata alla näkyviä ohjeita vaiheittain ja vastaa järjestyksessä kaikkiin niiden alta löytyviin kysymyksiin.
1. Piirrä funktion \(f(x)=2^x\) kuvaaja koordinaatistoon.
- Arvioi kuvaajasta katsomalla, mikä on \(x\) kun
2. Lue kuvaajasta ja taulukoi funktion \(f(x)=2^x\) pisteiden koordinaatteja (väh. 4). Voit muokata alla olevaa valmista taulukkoa tuplaklikkaamalla haluamaasi taulukon solua. Edit table-ikkunan, saa raahattua pois tieltä tarttumalla turkoosiin yläreunaan.
Please
Open plugin
3. Käännä sitten koordinaatit uuteen taulukkoon niin, että \(x\)- ja \(y\)-koordinaatit vaihtavat paikkaa eli \(y=x’\) ja \(x=y’\).
Open plugin
Uudet koordinaatit \((x’, y’)\) ovat funktion \(f(x)\) käänteisfunktion koordinaatteja.
4. Piirrä taulukoidut pisteet \((x’,y’)\) samaan koordinaatistoon funktion \(f(x)=2^x\) kanssa.
- Mitä havaintojasi voit tehdä pisteiden kulusta?
5. Lisää samaan kuvaan vielä logaritmifunktion \(g(x)=\log_2x\) kuvaaja. (Geogebrassa voit kirjoittaa log(2,x))
- Mitä huomaat? (Vinkki: piirrä avuksi suora \(y=x\).)
- Minkä johtopäätöksen voit tehdä eksponenttifunktion ja logaritmifunktion välisestä suhteesta?
1.3 Teoriaa: Logaritmi
Johdantotehtävässä yhtälöt voitiin ratkaista päättelemällä ja äskeisessä tutkimuksessa vastaukset arvioitiin funktion kuvaajalta. Näillä keinoilla ei kuitenkaan ole mahdollista saada kaikille eksponenttiyhtälöille täsmällistä vastausta. Vastaus tähän ongelmaan on logaritmi.
Esim. Yhtälö \(2^x=5\) on mahdoton ratkaista päättelemällä. Ratkaisu saadaan esimerkiksi käyttämällä logaritmia, jolla on sama kantaluku: \[ \begin{align*} \color{blue}2\color{red}^x&=\color{green}5 \\ \color{red}x&=\log\color{blue}_2\color{green}5 \end{align*} \]
Eli yhtälön ratkaisun tarkka vastaus on \(x=\log_25\) ja likiarvo voidaan nyt laskea syöttämällä laskimeen \(\log_25\), jolloin saadaan \(x=2,321928…≈2,3\).
1.4 Tehtävä: Logaritmin määritelmä
- Tutki alla olevaa taulukkoa ja päättele viimeisen rivin eksponenttiyhtälöä vastaava logaritmiyhtälö.
Open plugin
Muodosta yhtälö siirtämällä osat oikeaan järjestykseen (vie hiiri kooditekstin päälle, jotta palikat näkyvät oikein):
Please
Merkintä \(\log_kr\) voitaisiin lausua luonnollisella kielellä esimerkiksi ”\(k\)-kantainen logaritmi luvusta \(r\)” tai ”\(r\):n \(k\)-kantainen logaritmi” ja se tarkoittaisi eksponenttiyhtälön \(k^x=r\) ratkaisua \(x\). Toisin sanoen \(k\)-kantainen logaritmi \(r\):stä antaa vastauksen kysymykseen "Mihin potenssiin \(k\) on korotettava, jotta vastaukseksi saadaan \(r\)?".
- Kirjoita a-kohdan taulukon logaritmiyhtälöt luonnollisella kielellä.
- Muodosta lauseke "\(x\) on 2-kantainen logaritmi luvusta kahdeksan" ja ratkaise siitä \(x\) a-kohdassa päättelemälläsi säännöllä eli logaritmin määritelmällä.
- Selitä omin sanoin, mikä on logaritmi ja miten se liittyy eksponenttiyhtälöön ja/tai eksponenttifunktioon.
1.5 Tehtävä: Logaritmin arvoja eksponenttifunktion kuvaajasta
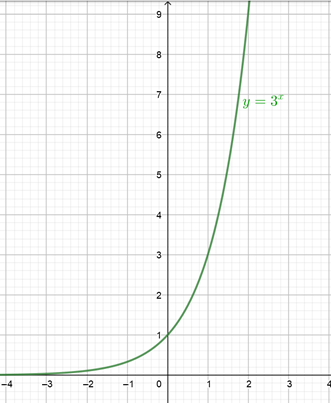
Logaritmi vastaa kysymykseen, mihin potenssiin kantaluku täytyy korottaa, jotta saadaan arvo y.
Katso kuvasta seuraavat logaritmien arvot:
Logaritmi \(\log_39\) tarkoittaa siis \(x\)-arvoa kohdassa \(y=9\).
Logaritmin määritelmä
Olkoon \(a > 0, a ≠ 1\) ja \(b > 0\).
Logaritmi \(\log_a b\) tarkoittaa lukua \(x\), joka toteuttaa eksponenttiyhtälön \(a^x = b\). Toisin sanoen \[ a^x=b \quad\Leftrightarrow\quad x=\log_ab \]
1.6 Tehtävä: Tunnetuimmat logaritmit
Ota selvää tai päättele
- Mitä logaritmia tarkoittaa merkintä \(\ln(x)\)? Mikä on tämän logaritmin kantaluku symbolina ja likiarvona?
- Mikä on oltava sellaisen logaritmin kantaluku, jota merkitään \(\lg(x)\), kun tiedetään, että \(\lg(10)=1\) ja \(\lg(100)=2\)?
Kirjoita seuraavat lausekkeet luonnollisella kielellä, eli siten kuin lausuisit ne. Apua saat tehtävästä 1.4, jossa myös harjoiteltiin logaritmilausekkeiden ilmaisemista luonnollisella kielellä.
- \(\ln(x-2)\)
- \(\lg3\)
Näille logaritmeille on annettu omat merkinnät niiden yleisyyden takia. Useimmissa laskimissa on siksi niille omat pikanäppäimet ja . Huomaa, että myös pelkkä laskimessa tarkoittaa usein kymmenkantaista logaritmia.
\(e\)-kantaista logaritmia kutsutaan luonnolliseksi logaritmiksi ja sitä merkitään yleensä \(\log_e(x)=\ln(x)\).
\(10\)-kantaista logaritmia kutsutaan Briggsin logaritmiksi tai kymmenkantaiseksi logaritmiksi ja sitä merkitään usein \(\log_{10}(x)=\lg(x).\)
Huom! Vaikka näille logaritmeille on annettu omat nimet ja merkinnät, niille pätevät samat säännöt kuin muillekin logaritmeille.
Esimerkki
Logaritmin \(\ln\) avulla voidaan ratkaista \(e\)-kantaisia eksponenttiyhtälöitä ja toisinpäin.
- \(e^x-3=0\).
Ratkaisu: \[ \begin{align*} e^x-3&=0\\ e^x&=3\\ x&=\log_e3\\ x&=\ln3 \\ \end{align*} \]
- \(\ln(x-1)-1=0\).
Ratkaisu: \[ \begin{align*} \ln(x-1)-1&=0\\ \ln(x-1)&=1\\ (x-1)&=e^1 \\ x&=e+1 \\ \end{align*} \]
1.7 Lisätehtävä: Logaritmin määritelmän käyttöä
Ratkaise yhtälöistä \(x\).
Muunnetaan yhtälöt eksponenttimuotoon logaritmin määritelmää käyttäen ja päätellään \(x\), eli \(5^2=x\).
2. Logaritmifunktio

Tässä luvussa tutkitaan logaritmifunktion ehtoja ja ominaisuuksia.
Logaritmifunktio \[ f(x)=\log_a(x) \] on määritelty ja jatkuva kun \(a>0,a≠1\) ja \(x>0\).
2.1 Tehtävä: Logaritmifunktion ehdot *
Pohditaan seuraavaksi, miksi logaritmifunktiolle on annettu ehdot \(a>0,a≠1\) ja \(x>0\).
Jos \(f(x)=\log_a(x)\) niin logaritmin määritelmän mukaan \(a^{f(x)}=x\). Tutkitaan asiaa vastaoletuksella, eli etsitään perusteluja sille, miksi EI voi pitää paikkansa, että \(a≤0,a=1\) tai \(x≤0\). Valitse se vaihtoehto, joka pitää paikkansa:
joten \(a\ne0\).
joten \(a>0\).
joten \(a\ne1\).
mutta edellä todettiin, että niin ei voi olla, joten \(x\ne0\).
mutta edellä todettiin, että niin ei voi olla, joten \(x>0\).
2.2 Tutkimus: Logaritmifunktion kulku
Tutki logaritmifunktioiden kuvaajia GeoGebra-appletin avulla vaihtamalla kantalukua \(a\) liukusäätimellä ja vastaa alla oleviin kysymyksiin.
- Mitä yhteistä kaikilla logaritmifunktioiden kuvaajilla on kantaluvusta riippumatta?
- Millainen funktion kuvaaja on kun logaritmin kantaluku \(a>1\)?
- Millainen funktion kuvaaja on kun \(0<a<1\)?
- Mitä voidaan päätellä logaritmifunktion määrittelyjoukosta ja arvojoukosta?
2.3 Tehtävä: Logaritmifunktion määrittelyjoukko
Logaritmi on määritelty vain positiivisilla luvuilla. Siksi logaritmifunktiosta ja logaritmiyhtälöstä täytyy aina ensin tutkia, millä muuttujan arvoilla logaritmin "sisus" on suurempaa kuin nolla.
Esim. Millä muuttujan \(x\) arvoilla funktio \(f(x)=\log_2(\color{blue}{2x-1})\) on määritelty?
Ratkaisu: Logaritmifunktio on määritelty kun \[ \begin{align*} \color{blue}2x-1\color{black}&>0\\ 2x&>1\quad|∶2\\ x&>\frac{1}{2} \end{align*} \] Eli määrittelyehtona on \(x>\frac{1}{2}\).
Funktion kuvaajasta voidaan tarkistaa, näyttääkö määrittelyehto oikealta:
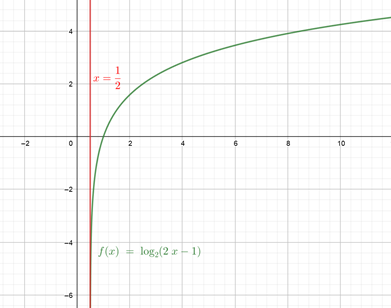
- Voidaanko seuraavat funktion \(f(x)=\log_2(2x-1)\) arvot laskea?
- Milloin funktio \(g(x)=\log_5(x+2)\) on määritelty?
- Näytä laskemalla, että funktion \(g(x)=\log_5(x+2)\) nollakohta on \(x=-1\). Kuvaaja tai solve-toiminto ei riitä.
Palauta vastaustiedosto tähän:
Huom. Muista kääntää epäyhtälön merkki, jos jaat tai kerrot puolittain negatiivisella luvulla!
3. Logaritmin laskusääntöjä

Tässä luvussa tutustutaan logaritmeja koskeviin laskusääntöihin ja harjoitellaan logaritmilausekkeiden sieventämistä.
3.1 Tehtävä: Erityistapauksia *
Kerrataan logaritmin määritelmä:
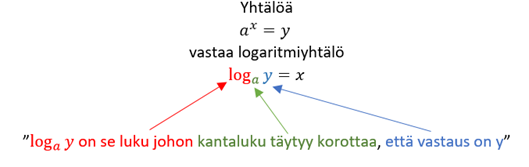
Ratkaise seuraavat logaritmit ja kirjoita niille perustelut.
Olkoot \(a>0,a≠1,x>0\) ja \(y>0\).
- \(\log_aa\)
- \(\log_a1\)
- \(\log_aa^x\)
3.2 Teoriaa: Laskusäännöt
Edellisten sääntöjen lisäksi logaritmeille on voimassa seuraavat tärkeät laskusäännöt, joita käytetään mm. logaritmilausekkeiden sieventämiseen:
Laskusääntöjä: (\(a>0, \; a≠1, \; x>0, \; y>0\))
- \(\log_ax^r=r\log_ax\)
- \(\log_a(xy)=\log_ax+\log_ay\)
- \(\log_a(\frac{x}{y})=\log_ax-\log_ay\)
Huom. Sääntöjä voidaan käyttää molempiin suuntiin!
Nämä laskusäännöt on johdettu logaritmin määritelmää ja potenssin laskusääntöjä hyödyntäen. Tutustu alta löytyviin laskusääntöjen todistuksiin.
Olkoon \(m=\log_ax\). Se voidaan kirjoittaa eksponenttimuotoon \(a^m=x\). Korotetaan tämä puolittain potenssiin \(n\), eli \[\begin{align*} (a^m)^n&=x^n\\ a^{mn}&=x^n. \end{align*}\] Muutetaan sitten yhtälö takaisin logaritmimuotoon, eli \[\begin{align*} \log_a(x^n)=mn. \end{align*}\] Lopuksi sijoitetaan \(m=\log_ax\): \[\begin{align*} \log_ax^n=n\log_ax. \end{align*}\]
Olkoon \(r=\log_a(xy)\), \(m=\log_ax\) ja \(n=\log_ay\). Nämä kirjoitettuna eksponenttimuodossa ovat \(a^r=xy\), \(a^m=x\) ja \(a^n=y\). Jos sijoitetaan kaksi jälkimmäistä yhtälöä ensimmäiseen, saadaan \[\begin{align*} a^r&=a^ma^n\\ a^r&=a^{m+n}\\ r&=m+n. \end{align*}\] Sijoitetaan lopuksi kirjainten paikalle alkuperäiset logaritmit, eli \[\begin{align*} \log_a(xy)=\log_ax+\log_ay. \end{align*}\]
Olkoon \(r=\log_a(\frac{x}{y})\), \(m=\log_ax\) ja \(n=\log_ay\). Nämä kirjoitettuna eksponenttimuodossa ovat \(a^r=\frac{x}{y}\), \(a^m=x\) ja \(a^n=y\). Jos sijoitetaan kaksi jälkimmäistä yhtälöä ensimmäiseen, saadaan \[\begin{align*} a^r&=\frac{a^m}{a^n}\\ a^r&=a^{m-n}\\ r&=m-n. \end{align*}\] Sijoitetaan lopuksi kirjainten paikalle alkuperäiset logaritmit, eli \[\begin{align*} \log_a(xy)=\log_ax-\log_ay. \end{align*}\]
Esimerkki
- Sievennä lauseke \(2 \ln{2}+\ln{3}\).
Ratkaisu: Laskusäännön 1 perusteella \[ \begin{align*} 2 \ln{2}=\ln{2^{2}}=\ln{4} \end{align*} \] Tämän jälkeen voidaan vielä käyttää laskusääntöä 2 toisin päin: \[ \begin{align*} \ln{4}+\ln{3}=\ln{(4\cdot 3)}=\ln{12} \end{align*} \]
- Sievennä lauseke \(\log_36-\log_32\).
Ratkaisu: Käytetään 3. laskusääntöä toisin päin: \[ \begin{align*} \log_36-\log_32 &=\log_3\Bigl(\frac{6}{2}\Bigr)\\ &=\log_33 \qquad |\text{ aiemmin osoitettiin }\log_aa=1\\ &=1 \end{align*} \]
3.3 Tehtävä: Logaritmilausekkeen sieventäminen
Maija on muokannut lausekkeen \(\lne^2+2\lg4-\lg8\) sievennettyyn muotoon \(2+\lg2\).
Millaisin välivaihein sievennys on voinut tapahtua? Päättele puuttuvat välivaiheet ja kirjoita jokaiselle vaiheelle mahdollisimman kattavat perustelut kokonaisin lausein.
Tee tehtävä valitsemallasi ohjelmistolla tai paperille. Voit esimerkiksi luoda taulukon, johon vasemmalle puolelle kirjoitat laskun välivaiheet ja oikealle puolelle kunkin välivaiheen perustelut, eli mitä tehdään tai mitä sääntöä sovelletaan.
Palauta vastaustiedosto tähän:
3.4 Teoriaa: Logaritmifunktio on aidosti monotoninen
Koska logaritmifunktiot ovat aidosti kasvavia tai aidosti väheneviä, niille pätee seuraava sääntö:
Positiivisilla luvuilla \(r\) ja \(s\) pätee, että
\(\log_ar=\log_as\) täsmälleen silloin kun \(r=s\).
Alla oleva kuvaaja \(f(x)=\ln(x)\) perustelee tätä sääntöä, sillä se havainnollistaa sitä, että aidosti monotoninen funktio voi saada jokaisella \(x\)-arvolla vain yhden funktion arvon \(y\). Esimerkiksi jos tiedetään että \(\ln(a)=\ln(2)\) niin voidaan tehdä johtopäätös, että luvun \(a\) on oltava \(2\).
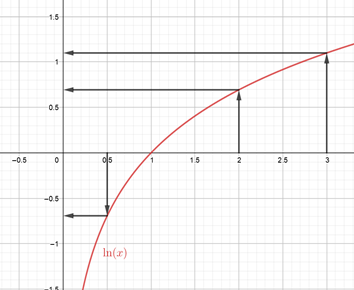
Tämän perusteella, jos tiedetään, että yhtälön molemmat puolet ovat positiivisia, voidaan ottaa logaritmi puolittain, mistä saattaa olla hyötyä eksponenttiyhtälön ratkaisemisessa. Tästä esimerkki seuraavassa tehtävässä.
3.5 Tutkimus: kantaluvun vaihto
Kurssikokeessa oli tehtävänä ratkaista yhtälöstä \(4^x=10\) muuttujan \(x\) tarkka arvo. Alla näet Matin ja Miian ratkaisut tehtävään. Molemmat ratkaisut ovat oikein. Tutki ratkaisuja ja seuraa sitten alta löytyviä ohjeita.

Seuraa ohjeita ja hyödynnä valitsemaasi ohjelmistoa:
1. Merkitse Matin ja Miian vastaukset yhtä suuriksi. Miksi näin voidaan tehdä?
2. Vaihda sitten luvut kirjaimiksi: \(4=a, 10=b\) ja \(e=c\). Näin olet johtanut kaavan, jolla logaritmi voidaan kirjoittaa halutun kantaluvun logaritmien avulla.
3. Sovella johtamaasi kaavaa ja ilmoita \(\log_23\) kymmenkantaisten logaritmien avulla. Tarkista laskimella, eli kokeile tuleeko yhtälön molemmista puolista sama desimaaliluku.
Palauta vastaustiedosto tähän:
Kantaluvun vaihto: \[ \log_ab=\dfrac{\log_cb}{\log_ca} \]
Joskus kantaluvun vaihto voi auttaa logaritmin sieventämisessä.
Esim. \(\log_816\).
Ratkaisu: Vaihdetaan logaritmi 2-kantaiseksi. \[ \log_816=\dfrac{\log_216}{\log_28}=\dfrac{\log_22^4}{\log_22^3}=\dfrac{4}{3} \]
4. Logaritmiyhtälö

Tässä luvussa sovelletaan logaritmin laskusääntöjä, sekä opetellaan ratkaisemaan logaritmiyhtälöitä ja määrittämään kahden funktion leikkauspisteet.
Logaritmiyhtälön ratkaiseminen aloitetaan aina tutkimalla määrittelyehdot kaikille niille logaritmilausekkeille, jotka sisältävät muuttujan \(x\). Jos määrittelyehtoja on useampia, ne yhdistetään yhdeksi ehdoksi, joka kattaa ne kaikki.
Esimerkki
\[\begin{align*} &\log_3(x+2)+\log_3(x)=\log_3(2) \\ &M: \color{red}x>-2 \color{black}\text{ ja } \color{blue}x>0\\ &\color{black}\text{eli ehdoksi valitaan ehtojen yhteinen alue } x>0. \end{align*}\]
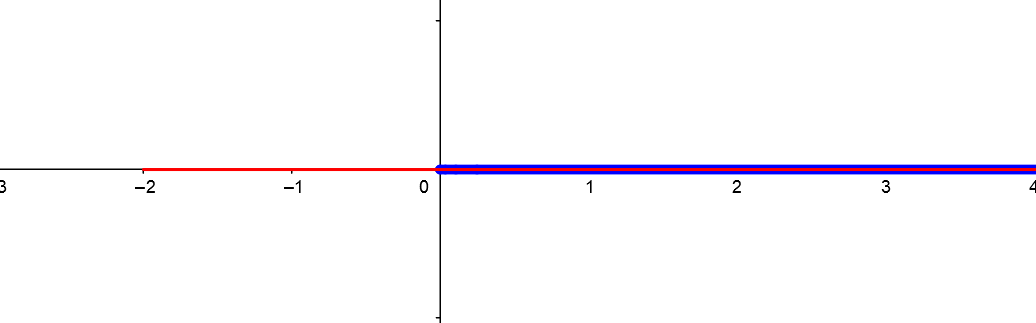
Jos valittaisiin \(x>-2\) niin sallittaisiin esimerkiksi \(x=-1\), joka ei kuitenkaan täytä toista ehtoa, \(x>0\), eli ehto olisi virheellinen.
4.1 Tehtävä: Virheen etsintä
Alla on Kallen kirjoittama ratkaisu yhtälölle \(\log_5(x-2)=1-\log_5x\). Vastaus ei kuitenkaan ole mennyt oikein.
Huom. Jos kuva ei näy, vie hiiren nuoli sen päälle.
- Tutki ratkaisun välivaiheita ja etsi kohta, jossa Kalle on tehnyt virheen. Kirjoita sitten koko lasku korjattuna ja ratkaise \(x\). Käytä välivaiheiden kirjoittamiseen haluamaasi ohjelmistoa.
Laskettuasi tehtävän uudelleen, muista verrata vastauksia määrittelyehtoihin!
- Kirjoita lyhyt arvostelu Kallen vastaustyylille, eli perustele, mikä vastauksessa on hyvää ja mitä voisi vielä lisätä tai tehdä paremmin, jotta lukijan olisi helpompi ymmärtää, mitä Kalle on ajatellut tehtävää ratkaistessaan.
4.2 Teoriaa: Keino logaritmiyhtälön ratkaisuun
Palautetaan mieleen edellisessä luvussa tutuksi tullut sääntö:
Positiivisilla luvuilla \(r\) ja \(s\) \[ \begin{align*} \log_ar=\log_as \quad\Leftrightarrow\quad r=s. \end{align*} \]
Tämä sääntö on hyödyllinen logaritmiyhtälöiden ratkaisemisessa.
Esimerkki
\(\ln(x-2)-\ln(5)=0\)
Ratkaisu: Ensin tarkistetaan määrittelyehdot: \(x>2\). Jos yhtälö on mahdollista muokata muotoon \(\log_ar=\log_as\), voidaan soveltaa äskeistä sääntöä, eli \[ \begin{align*} \ln(x-2)&=\ln(5)\\ x-2&=5\\ x&=7 \end{align*} \]
4.3 Tehtävä: Logaritmiyhtälön ratkaiseminen
Järjestä yhtälön \(\log_3(2-x)+\log_3(-x)=\log_315\) ratkaisun vaiheet oikeaan järjestykseen ja ratkaise yhtälö välivaiheineen.
Kaavoja:
\(\log_ar=\log_as \quad\Leftrightarrow\quad r=s\)
\(\log_a(z \cdot y)=\log_a(z)+\log_a(y)\)
Palauta vastaustiedosto tähän:
Määrittelyehdot:
\[
\begin{align}
2-x>0 \quad \text{ ja}\quad -x>0\\
\color{darkturquoise}x<2 \qquad \qquad \color{purple}x<0
\end{align}
\] 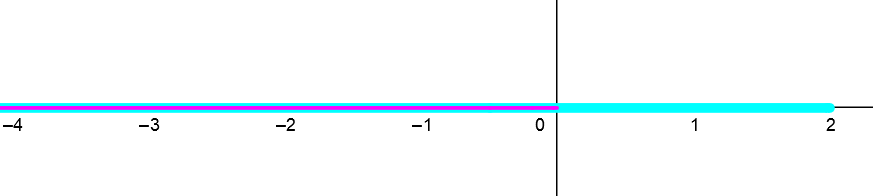 Yhdistetään ehdot, eli valitaan ehdoksi yhteinen alue \(x<0\).
Yhdistetään ehdot, eli valitaan ehdoksi yhteinen alue \(x<0\).
\[ \begin{align} \log_3(2−x)+\log_3(−x)&=\log_315 \\ \log_3((2−x)(−x))&=\log_315\\ (2−x)(−x)&=15\\ -2x+x^2&=15\\ x^2-2x-15&=0 \end{align} \] Ratkaistaan toisen asteen yhtälön ratkaisukaavalla: \[ \begin{align} x&=\dfrac{2\pm \sqrt{2^2-4\cdot 1 \cdot (-15)}}{2\cdot 1}\\ x&=-3 \text{ tai } x=5 \end{align} \] Näistä vastauksista vain \(x=-3\) täyttää ehdon \(x<0\), joten yhtälön vastaus on \(x=-3\).
Muista, että yhtälön ratkaisu aloitetaan aina tutkimalla määrittelyehdot jokaisesta logaritmista erikseen, ennen kuin yhtälöä sievennetään!
4.4 Tehtävä: Kolmen kielen yhteys
- Ilmaise alla olevassa taulukossa luonnollisella kielellä annettu selitys matematiikan symbolikielellä (esim. yhtälöt, laskut, muut symbolimerkinnät) ja kuviokielellä (esim. funktioiden kuvaajat). Käytä haluamiasi ohjelmistoja.
Voit esimerkiksi tehdä tekstinkäsittelyohjelmalla alla näkyvän taulukon ja täydentää sen kuvakaappauksilla. Tai jos käytössäsi on TI-Nspire, voit luoda sillä tiedoston, jossa käytät muistikirjaa ja kuvaajat-sovellusta. Myös luonnollisen kielen saraketta saa täydentää.
- Ratkaise pisteen A koordinaatit.
Funktioiden leikkauspiste selvitetään merkitsemällä ne yhtäsuuriksi ja ratkaisemalla \(x\). Sen jälkeen voidaan selvittää \(y\) sijoittamalla \(x\) jompaan kumpaan funktioon.
\(1=\lg(10)\)
Muokkaa yhtälö muotoon, jossa molemmin puolin on pelkästään logaritmilauseke, niin voit hyödyntää aiemmin käsiteltyä sääntöä (kohta 4.2).
Palauta vastaustiedosto tähän:
Ylimääräisiä palautuspaikkoja vastaustiedostoille
Tähän voit tarvittaessa palauttaa tiedostoja, jos esimerkiksi tehtävän vastaus koostuu useammasta kuin yhdestä tiedostosta. Pyri kuitenkin palauttamaan vastaustiedosto vain yhtenä tiedostona itse tehtävän yhteyteen, jotta opettajan on helpompi löytää se.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.