Nelikulmioiden geometriaa

Nelikulmioiden rakenne

Tehtävä

Pöytäliinan alkuperäinen koko on 2 m kertaa 4 m. Se kutistuu pesussa 5 % sekä pituus- että leveyssuunnassa. Kuinka monella prosentilla pöytäliinan pinta-ala pienenee? [5/S16]

Tehtävä

Peppi rakentaa oheisen kuvan mukaisista laudankappaleista linnunpöntön. Yksikkönä on senttimetri. [6/K16]

1. Paljonko linnunpönttö painaa? Sisääntuloaukkoa ei tarvitse huomioida eikä käytettäviä nauloja. Laudan tiheys on \(550 \frac{kg}{m^3}\)ja paksuus \(2,0 cm\).

2. Mikä on linnunpöntön sisätilavuus?

Tehtävä

Kuvan kaari-ikkunassa on lasin tukena rimoja. Kuinka paljon rimaa tarvitaan kuvan mukaiseen kaari-ikkunaan, kun \(x=20\)cm ja \(y=40\) cm? Rimaa käytetään kaikkiin kuvion janoihin ja puoliympyröiden kaariin. [4/S13]

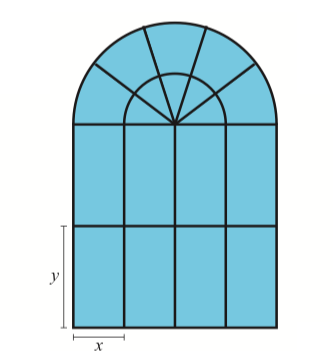
Suorakulmio

Tehtävä

Määritä alla olevan kuvan suunnikkaan pinta-alan osuus suorakulmion pinta-alasta.

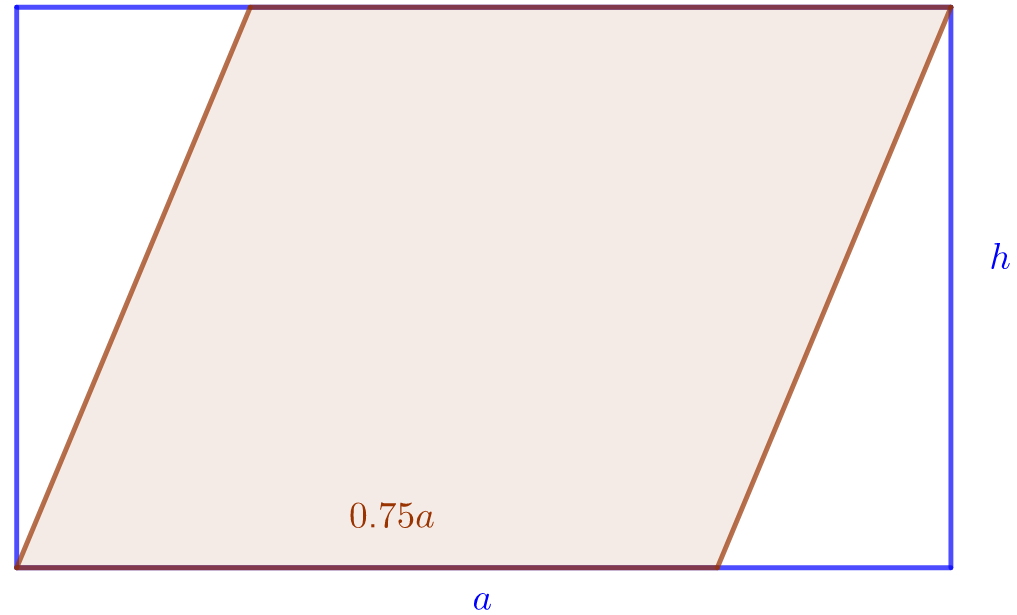
Tehtävä

Laske alla olevaan kuvaan sinisellä merkityn alueen pinta-ala.

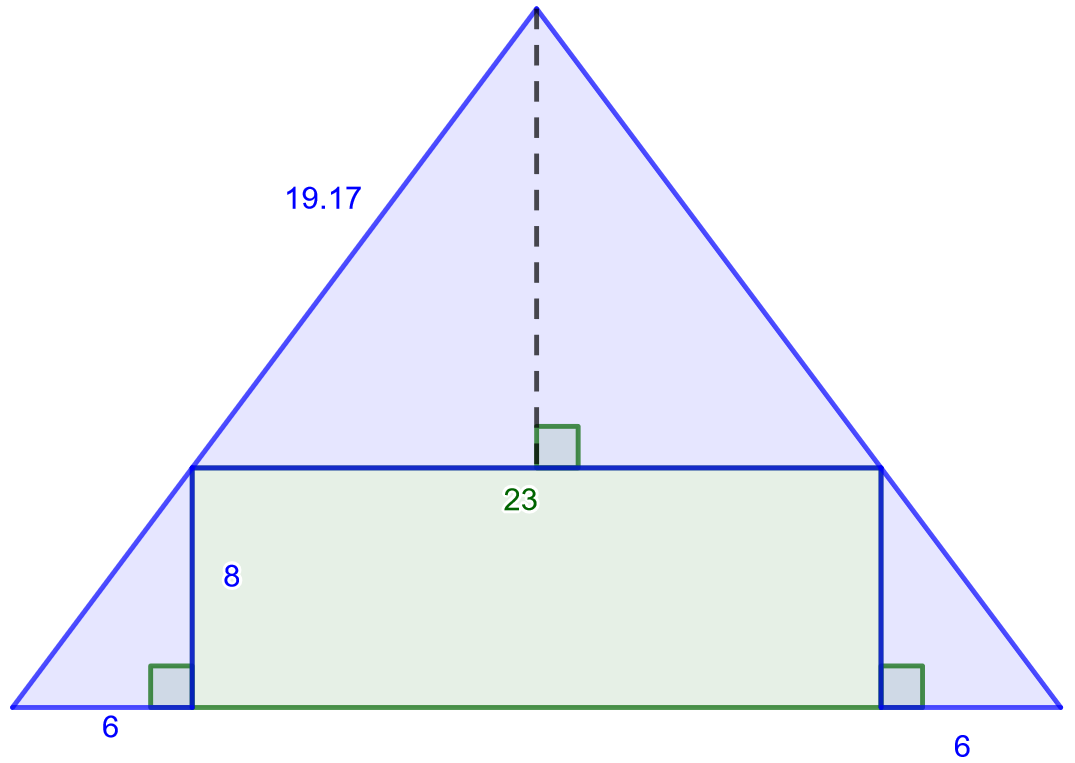
Tehtävä

Olkoot \(d_1\) ja \(d_2\) suorakulmion \(ABCD\) piirillä olevan pisteen \(P\) etäisyydet lävistäjistä \(AC\) ja \(BD\).

1. Piirrä annettuja tietoja vastaava dynaaminen kuvio, jossa voit liikuttaa pistettä \(P\) suorakulmion ympäri pitkin suorakulmion piiriä.

2. Mitä voit todeta summan \(d_1+d_2\) arvosta?

3. Miten arvo riippuu suorakulmion koosta?

4. Perustele havaintosi matemaattisesti.

Ratkaisu

2. Tutkitaan yllä olevaa GeoGebra-applettia siirtämällä punaista pistettä \(P\) suorakulmion reunalla. Huomataan, että summa \(d_1+d_2\) pysyy koko ajan samana.

3. Muutetaan suorakulmion kokoa raahaamalla pisteitä \(B\) ja \(C\). Huomataan, että summan \(d_1+d_2\) arvo muuttuu, mutta jos pistettä \(P\) liikuttaa, se pysyy edelleen samana. Summa on siis sitä suurempi, mitä suurempi suorakulmio on.

4. Lisätään valinta GeoGebra-appletin kohtaan "Matemaattinen perustelu", jolloin kuvioon ilmestyy kulmia. (Huom! kulmat toimivat GeoGebrassa oikein vain, jos piste \(P\) on pisteiden \(A\) ja \(D\) välissä.) Merkitään kulmaa \(\angle BAC\) kirjaimella \(\alpha\) ja kulmaa \(\angle CAD\) kirjaimella \(\beta\). Koska suorakulmion kaikki kulmat ovat suoria, saadaan \(\alpha + \beta = 90^{\circ}\). Merkitään vihreää lävistäjää kirjaimella \(\ell\). Sen pituus voidaan ratkaista Pythagoraan lauseella: \[ \begin{aligned} \ell^2 &= a^2+b^2 \\ \ell &= \sqrt{a^2+b^2}. \end{aligned} \] Nyt voidaan merkitä \[ \cos \alpha = \frac{a}{\ell} = \frac{a}{\sqrt{a^2+b^2}}. \] Merkitään etäisyyttä \(DP\) kirjaimella \(x\), jolloin etäisyys \(AP\) on \(b-x\). Pienistä suorakulmaisista kolmioista saadaan \[ \cos \alpha = \frac{d_1}{b-x} \quad \Leftrightarrow \quad d_1 = (b-x) \cdot \cos \alpha \] ja \[ \cos \alpha = \frac{d_2}{x} \quad \Leftrightarrow \quad d_2 = x \cdot \cos \alpha \] jolloin summa saa arvon \[ \begin{aligned} d_1 + d_2 &= (b-x) \cdot \cos \alpha + x \cdot \cos \alpha \\ &= (b-x+x) \cdot \cos \alpha \\ &= b \cdot \frac{a}{\sqrt{a^2+b^2}} \\ &= \frac{ab}{\sqrt{a^2+b^2}}. \end{aligned} \] Tästä voidaan päätellä, että jos suorakulmion koko pysyy samana, summa \(d_1+d_2\) pysyy myös vakiona. Toisaalta jos suorakulmion koko kasvaa, myös summa kasvaa.

Tehtävä

Luomuviljelijä on hankkinut materiaalin 400 metrin pituiseen aitaan. Hän aikoo rajata sillä niitystä suorakulmion muotoisen alan, joka lisäksi jaetaan kuvion mukaisesti kolmeen yhtäsuureen osaan kahdella ulkoreunan suuntaisella sisäaidalla. Määritä aitauksen suurin mahdollinen kokonaispinta-ala [13/S18].

Neliö

Tehtävä

Neliöllä ja suorakulmaisella kolmiolla on sama pinta-ala. Kumman piiri on pidempi?

Tehtävä

Alla olevassa kuvassa on neliö, jonka pinta-ala on \(12\). Sen jokaiselle sivulle on piirretty tasasivuinen kolmio. Mikä on punaisella merkityn alueen pinta-ala?

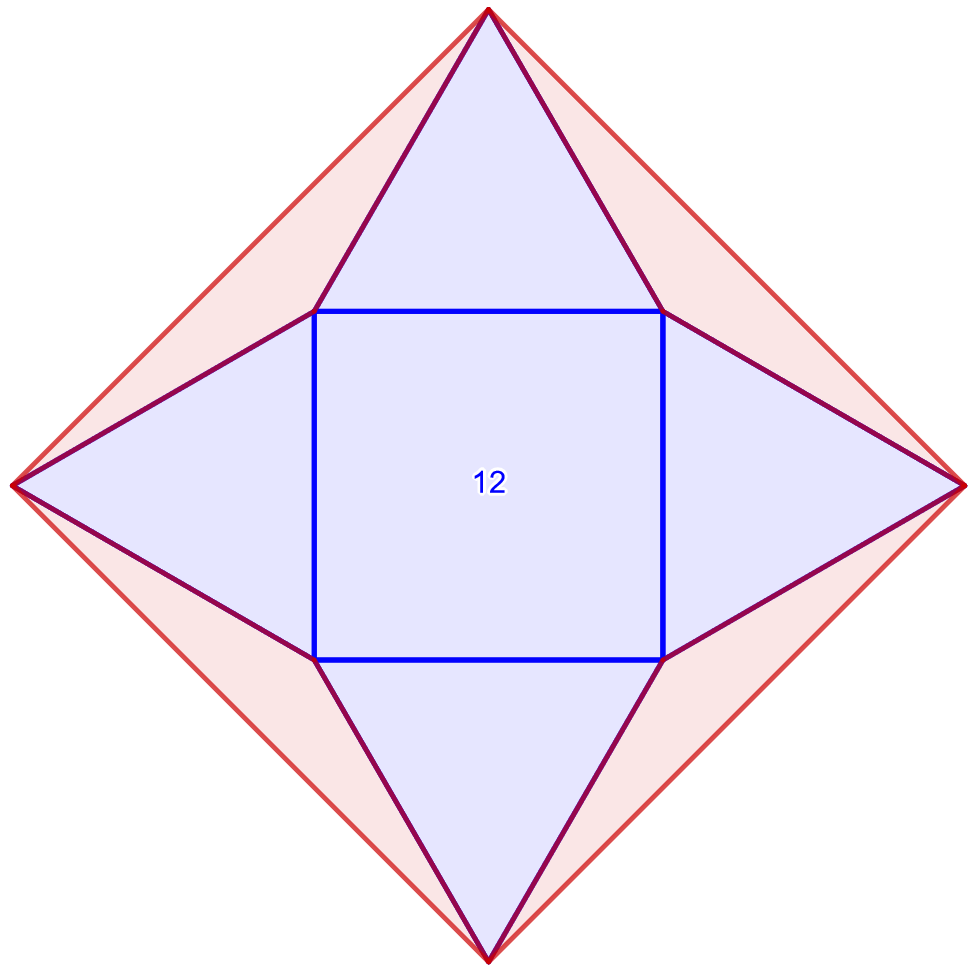
Suunnikas

Tehtävä

Suunnikkaan sivujen pituudet ovat \(3\) ja \(5\), ja sen pinta-ala on \(13\). Kuinka suuri kulma sivujen välissä on?

Tehtävä

Suunnikkaan sivujen välinen kulma on \(45^{\circ}\). Lyhyempi sivuista on pituudeltaan \(a\) ja pidempi \(4a\). Määritä suunnikkaan ala.

Tehtävä

Aakkoskarkkien sivujen pituudet ovat \(2 \text{ cm}\) ja sen lyhyempi halkaisija on \(2,3 \text{ cm}\). Laske yhden karkin pinta-ala.

Tehtävä

Suunnikkaan sisälle piirretään pienempi suunnikas, jonka kärjet ovat alkuperäisen suunnikkaan sivujen keskipisteissä. Laske pienen suunnikkaan pinta‐ala käyttämällä kuvioon merkittyjä pituuksia.[2/S15]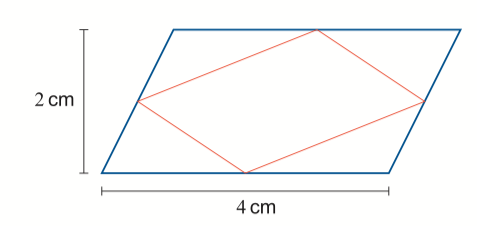

Puolisuunnikas

Muut monikulmiot

Tehtävä

Säännöllisen viisikulmion sivun pituus on \(3\). Laske viisikulmion pinta-ala.