5. Rationaaliyhtälö ja -funktio

Tässä kappaleessa tutustutaan rationaalifunktioihin. Liikkeelle lähdetään rationaalilausekkeen käsitteestä sekä rationaalilausekkeilla tehtävistä laskutoimituksista. Lopuksi opitaan ratkaisemaan rationaaliyhtälöitä. Kappaleeseen liittyvät tehtävät ovat omalla sivullaan.

5.1 Rationaalilauseke

Rationaalilauseke tarkoittaa kahden polynomin osamäärää. Esimerkiksi lausekkeet

$\dfrac{x+3}{x-1}\;\;\;\text{ja}\;\;\;\dfrac{2}{x^2-4x}$

ovat rationaalilausekkeita.

Rationaalilauseke

Rationaalilauseke on muotoa $\dfrac{P(x)}{Q(x)}$ oleva lauseke, missä P(x) ja Q(x) ovat polynomeja ja $Q(x)\neq0$ .

Rationaalilauseke voidaan sieventää supistamalla. Supistaminen onnistuu, jos sekä osoittaja että nimittäjä voidaan muuttaa tulomuotoon ja niistä löytyy $\textcolor{blue}{\text{yhteinen tekijä}}$ .

$\dfrac{2x+6}{3x^2+9x}=\dfrac{2\textcolor{red}{(x+3)}}{3x\textcolor{red}{(x+3)}}=\dfrac{2}{3x}$

Rationaalilauseke on $\textcolor{yellow}{polynomi}$ , mikäli se sievenee polynomiksi ja vastaavasti $\textcolor{cyan}{murtolauseke}$ , mikäli se ei sievene polynomiksi.

5.1.1 Esimerkki: rationaalilausekkeen sieventäminen

Sievennä rationaalilauseke ja tutki, onko kyseessä oleva rationaalilauseke murtolauseke vai polynomi.

$\dfrac{x+1}{x+1}\;\;\;\;$ b. $\dfrac{x+1}{x-1}\;\;\;\;$ c. $\dfrac{2x+2}{x+1}\;\;\;\;$ e. $\dfrac{x^2-1}{x+1}$

Ratkaisu:

Koska rationaalilausekkeen osoittaja ja nimittäjä ovat samat, lauseke sievenee muotoon

$\dfrac{x+1}{x+1}=1.$

Kyseessä on siis polynomi, joka muodostuu vakiotermistä.

Rationaalilausekkeen $\dfrac{x+1}{x-1}$ osoittajalla ja nimittäjällä ei ole yhteisiä nollakohtia, joten lauseketta ei voi sieventää. Kyseessä on tällöin murtolauseke.

Erotetaan osoittajasta yhteinen tekijä, jolloin lauseke sievenee muotoon

$\dfrac{2x+2}{x+1}=\frac{2\textcolor{red}{(x+1)}}{\textcolor{red}{x+1}}=2.$

Kyseessä on siis polynomi, joka muodostuu vakiotermistä.

Sovelletaan osoittajaan summan ja erotuksen tulon muistikaavaa, jolloin lauseke sievenee muotoon

$\dfrac{x^2-1}{x+1}=\frac{\textcolor{red}{(x+1)}(x-1)}{\textcolor{red}{x+1}}=x-1.$

Kyseessä on siis polynomi.

5.2 Rationaalilausekkeiden laskutoimituksia

Rationaalilausekkeiden summa, erotus, tulo ja osamäärä lasketaan murtolukujen laskusääntöjä noudattaen.

Rationaalilausekkeiden tulo

Rationaalilausekkeiden kertolaskussa osoittajat ja nimittäjät kerrotaan keskenään.

5.2.1 Esimerkki: rationaalilausekkeiden kertolasku

Laske kertolasku $\dfrac{x^2+x}{x-1}\cdot \dfrac{x}{x+1}$ .

Ratkaisu:

Kerrotaan osoittajat ja nimittäjät keskenään. Ennen sulkujen avaamista kannattaa tarkistaa, onko osoittajassa ja nimittäjässä yhteisiä tekijöitä, jotka voisi supistaa pois.

$\begin{align*} \dfrac{x^2+x}{x-1}\cdot \dfrac{x}{x+1}&=\dfrac{(x^2+x)\cdot x}{(x-1)(x+1)} \\ &=\dfrac{x\textcolor{red}{(x+1)}\cdot x}{(x-1)\textcolor{red}{(x+1)}} \\ &=\dfrac{x\cdot x}{x-1} \\ &=\dfrac{x^2}{x-1} \end{align*}$

Vastaus: $\dfrac{x^2}{x-1}$

Rationaalilausekkeiden yhteen- ja vähennyslasku

Rationaalilausekkeiden yhteen- ja vähennyslaskussa lausekkeet lavennetaan ensin samannimisiksi. Tämän jälkeen lasketaan osoittajat yhteen tai vähennetään ne toisistaan.

5.2.2 Esimerkki: rationaalilausekkeiden yhteen- ja vähennyslasku

Laske yhteen- ja vähennyslasku $1-\dfrac{x}{1+x}+\dfrac{1}{x^2+x}$ .

Ratkaisu:

Lausekkeet saadaan samannimisiksi, kun lavennetaan ensimmäinen termillä x^2+x ja toinen termillä .

$\begin{align*} ^{x^2+x)}1-\,^{x)}\dfrac{x}{1+x}+\dfrac{1}{x^2+x}&=\dfrac{x^2+x}{x^2+x}-\dfrac{x^2}{x^2+x}+\dfrac{1}{x^2+x} \\ &=\frac{x^2+x-x^2+1}{x^2+x} \\ &=\frac{x+1}{x^2+x} \\ &=\frac{\textcolor{red}{x+1}}{x\textcolor{red}{(x+1)}}=\frac{1}{x} \end{align*}$

Vastaus: $\dfrac{1}{x}$

Rationaalilausekkeiden osamäärä

Rationaalilausekkeiden jakolasku muutetaan kertolaskuksi kertomalla jaettava jakajan käänteisluvulla.

5.2.3 Esimerkki: rationaalilausekkeiden jakolasku

Laske jakolasku $\dfrac{3x^2-3x}{2x+4}:\dfrac{6x-6}{x}$ .

Ratkaisu:

Kerrotaan jaettava jakajan käänteisluvulla. Jälleen supistukset kannattaa tehdä ennen sulkujen avaamista.

$\begin{align*} \dfrac{3x^2-3x}{2x+4}:\dfrac{6x-6}{x}&=\dfrac{3x^2-3x}{2x+4}\cdot\dfrac{x}{6x-6} \\ &=\frac{(3x^2-3x)\cdot x}{(2x+4)(6x-6)} \\ &=\frac{3x\textcolor{red}{(x-1)}\cdot x}{(2x+4)\cdot 6\textcolor{red}{(x-1)}} \\ &=\frac{\textcolor{blue}3x^2}{\textcolor{blue}3\cdot2(2x+4)} \\ &=\frac{x^2}{2(2x+4)}=\frac{x^2}{4x+8} \end{align*}$

Vastaus: $\dfrac{x^2}{4x+8}$

5.3 Rationaalifunktio ja -yhtälö

Rationaalifunktiot ovat funktiota, jotka on määritelty jonkin rationaalilausekkeen avulla. Esimerkiksi

$f(x)=x^2-\dfrac{6}{x-1}$

on rationaalifunktio.

Rationaalifunktio

Rationaalifunktio on muotoa $f(x)=\dfrac{P(x)}{Q(x)}$ oleva funktio, missä P(x) ja Q(x) ovat polynomeja ja $Q(x)\neq0$ .

Rationaalifunktion kuvaajassa on katkos, kun nimittäjän Q(x)=0, koska nollalla jakamista ei ole määritelty.

5.3.1 Esimerkki: rationaalifunktion kuvaaja

Tutkitaan funktiota $f(x)=\frac{1}{x^2-4}$

Missä kohdissa funktio ei ole määritelty?
Miten nämä kohdat näkyvät funktion kuvaajassa?

Ratkaisu:

Rationaalifunktio ei ole määritelty nimittäjän nollakohdissa, joten ratkaistaan ne ensin.

$\begin{align*} x^2-4&=0 \\ x^2&=4 \\ x&=-2\; \text{tai}\; x=2 \end{align*}$

Funktio ei ole siis määritelty, kun $x=\pm2$ .

Piirretään funktion kuvaaja laskinohjelmalla.

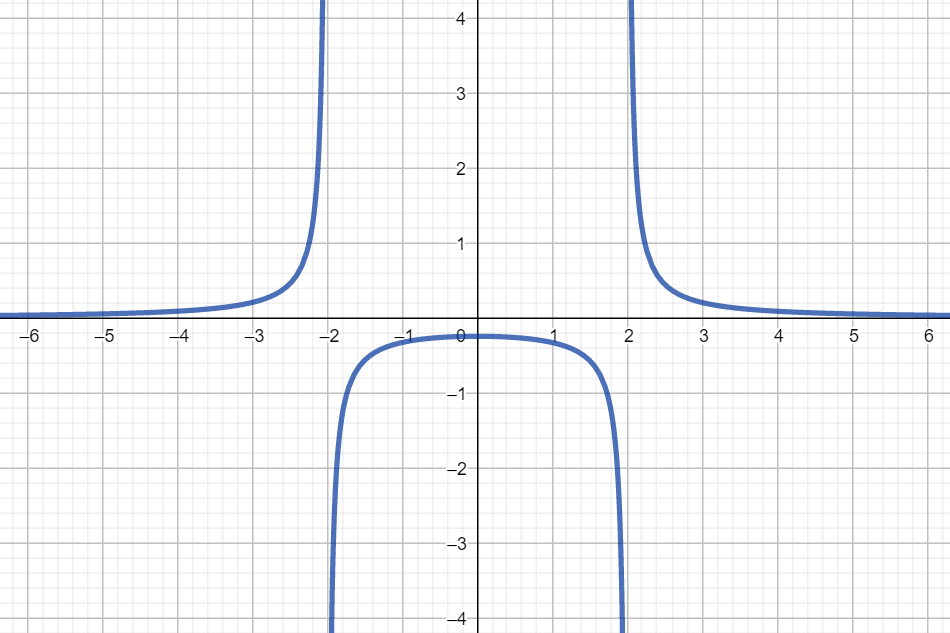
Huomataan, että kohdissa, jossa funktiota ei ole määritelty, funktion kuvaaja katkeaa. Nimittäjän nollakohdat siis antavat kuvaajalle niin kutsutut pystysuorat asymptootit. Näissä kohdissa funktion kuvaaja lähestyy äärettömyyttä.

Kun tutkitaan, missä kohdassa jokin rationaalifunktio saa tietyn arvon, päädytään ratkaisemaan rationaaliyhtälö.

Rationaaliyhtälö

Rationaaliyhtälö on muotoa $\dfrac{P(x)}{Q(x)}=0$ oleva yhtälö, missä P(x) ja Q(x) ovat polynomeja ja $Q(x)\neq0$ .

Jos rationaaliyhtälölle saadaan ratkaisu, joka on nimittäjän nollakohta, kyseinen ratkaisu hylätään. Rationaaliyhtälöä ratkaistaessa pyritään tilanteeseen, jossa ei esiinny rationaalilausekkeita. Tässä muodossa yhtälö ratkaistaan, kuten olet aiemmissa kursseissa oppinut.

5.3.2 Esimerkki: rationaaliyhtälö

Ratkaise rationaaliyhtälö $\dfrac{3x+5}{x^2-1}=0$ .

Ratkaisu:

Rationaalilauseketta ei ole määritelty, jos nimitäjä on nolla. Ratkaistaan siis ensiksi nimittäjän nollakohdat.

$\begin{align*} x^2-1 &= 0 \\ x^2 &= 1 \\ x &= -1 \text{ tai } x=1 \end{align*}$

Eli lauseketta $\dfrac{3x+5}{x^2-1}=0$ ei ole määritelty, kun $x=\pm1$ .

Rationaalilauseke saa arvokseen nolla, jos ja vain jos rationaalilausekkeen osoittaja on nolla ja nimittäjä nollasta poikkeava. Näin ollen ratkaistaan osoittajan nollakohdat.

$\begin{align*} 3x+5 &= 0 \\ 3x &= -5 \\ x &= -\dfrac{5}{3} \end{align*}$

Koska $-\dfrac{5}{3}\neq \pm 1$ , niin ratkaisu on käypä.

Vastaus: $x=-\dfrac{5}{3}$

5.3.3 Esimerkki: rationaaliyhtälö

Ratkaise rationaaliyhtälö $\dfrac{x}{x+1}+\dfrac{x-1}{x}=2$ .

Ratkaisu:

Ennen yhtälön ratkaisua huomataan, että yhtälö ei ole määritelty nimittäjien nollakohdissa. Eli luvut x=-1 ja x=0 eivät kelpaa yhtälön ratkaisuksi.

Rationaaliyhtälöiden ratkaisemisessa ensimmäisenä tavoitteena on päästä eroon nimittäjistä. Tämä voidaan tehdä muokkaamalla yhtälön kumpikin puoli samannimisiksi murtolausekkeiksi sopivasti laventamalla.

$\begin{align*} \dfrac{x}{x+1}+\dfrac{x-1}{x}&=2 \\ \dfrac{\textcolor{green}x\cdot x}{\textcolor{green}x(x+1)}+\frac{\textcolor{blue}{(x+1)}(x-1)}{x\textcolor{blue}{(x+1)}}&=\frac{2\cdot \textcolor{red}{x(x+1)}}{\textcolor{red}{x(x+1)}} \\ \dfrac{x^2+(x+1)(x-1)}{x(x+1)}&=\frac{2x(x+1)}{x(x+1)} \end{align*}$

Tämä yhtälö toteutuu ainoastaan silloin, kun osoittajat ovat yhtä suuria.

$\begin{align*} x^2+(x+1)(x-1)&=2x(x+1) \\ x^2+(x^2-1)&=2x^2+2x \\ 2x^2-1&=2x^2+2x \\ -1&=2x \\ x&=-\dfrac{1}{2} \end{align*}$

Koska $x=-\dfrac{1}{2}$ ei ole minkään yhtälössä esiintyvän nimittäjän nollakohta, se todella on yhtälön ratkaisu.

Vastaus: $x=-\dfrac{1}{2}$