6. Harjoituskoe MAY1

Tällä sivulla on harjoituskoe MAY1-kurssille. Huomaa, että pisteytys ei vastaa oikean kurssikokeen pisteytystä. Vastaa tehtäviin ilman laskinta. Tehtävissä apuvälineet on sallittu. Tehtävässä ei ole automaattitarkistusta.


6.1 Tehtävä

# tehtava1

Onko väittämä tosi vai epätosi?

6.2 Tehtävä

Sievennä.

# tehtava2

a)

Avaa tehtävä viemällä kursori tähän

 
# tehtava2b

b)

Avaa tehtävä viemällä kursori tähän

 
# tehtava3c

c)

Avaa tehtävä viemällä kursori tähän

 

6.3 Tehtävä

Kuvassa on funktion kuvaaja. Vastaa kuvan perusteella kysymyksiin.


# tehtava3

a) Millä muuttujan arvoilla funktion arvo on ?

Avaa tehtävä tuomalla osoitin tähän

 
# tehtava3b

b) Millä muuttujan arvolla funktio saa pienimmän arvonsa?

Avaa tehtävä tuomalla osoitin tähän

 
# Plugin1

c) Millä muuttujan arvoilla funktion arvo on pienempi kuin ?

Avaa tehtävä tuomalla osoitin tähän

 

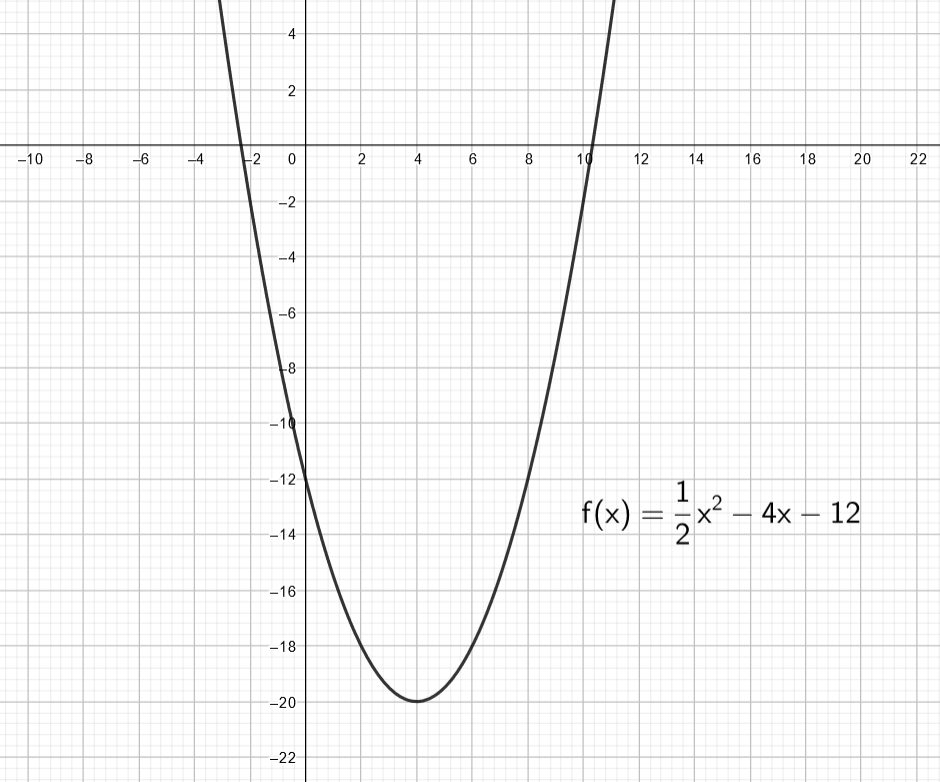
6.4 Tehtävä

Ratkaise yhtälöparit. Hahmottele halutessasi Abitti-editorilla.

  1. \[\begin{cases} 3x+5y=4\\ 4x=-2y+3 \end{cases}\]
# tehtava4a
Avaa tehtävä tuomalla osoitin tähän

 
# tehtava4b
Avaa tehtävä tuomalla osoitin tähän

 
  1. \[\begin{cases} \frac{x}{3}-\frac{y}{7}=2\\ x-\frac{y-1}{3}=-5 \end{cases}\]
# tehtava4ab
Avaa tehtävä tuomalla osoitin tähän

 
# tehtava4bb
Avaa tehtävä tuomalla osoitin tähän

 

Abitti-editori


6.5 Tehtävä

# tehtava5a

a) Puhelimen hinta :n alennuksen jälkeen oli . Mikä oli puhelimen alkuperäinen hinta?

Avaa tehtävä tuomalla osoitin tähän

 
# tehtava5b

b) Osakkeiden arvo nousi ensin ja laski sen jälkeen . Kuinka monta prosenttia osakkeiden arvo nousi alkuperäisestä?

Avaa tehtävä tuomalla osoitin tähän

 
# tehtava6

c) Oletetaan, että jarrutusmatka on suoraan verrannollinen nopeuden neliöön. Kuinka monta prosenttia jarrutusmatka kasvaa, jos nopeus kasvaa ?

Avaa tehtävä tuomalla osoitin tähän

 

6.6 Tehtävä

Kuntosalin jäsenyys maksaa euroa. Kertalipun hinta jäsenelle on ja ei-jäsenelle

# tehatva8

Kuinka monta kertaa salilla pitää vähintään käydä, jotta jäsenyys kannattaa (eli kustannukset jäsenelle ja ei-jäsenelle ovat yhtä suuret)?

Avaa tehtävä tuomalla osoitin tähän

 

6.7 Tehtävä

Tästä tehtävässä ei ole automaattitarkistusta.

Etsi Geogebralla piirtämällä funktioille ja sellaiset lausekkeet, että

  1. funktioiden kuvaajat ovat suoria, eivätkä leikkaa toisiaan.
# tehtava7
Avaa tehtävä tuomalla osoitin tähän

 
  1. funktioiden kuvaajat ovat suoria, jotka leikkaavat pisteessä .
# tehtava7b
Avaa tehtävä tuomalla osoitin tähän

 

6.8 Tehtävä

Kurssin aikana määriteltiin juurifunktiot ja , missä ja . Neliöjuuri antaa vastauksen siihen, mikä luku korotettuna toiseen on neliöjuuren sisällä oleva luku ja vastaavasti kuutiojuuri siihen, mikä luku korotettuna kolmanteen potenssiin on kuutiojuuren sisällä oleva luku.

Voidaan määrittää yleisempi juurifunktio, juuri, joka vastaa kysymykseen, mikä luku korotettuna potenssiin on juuren sisällä oleva luku.

Olkoon positiivinen kokonaisluku. Jos on parillinen ja , niin

Jos on pariton ja , niin

juurta voidaan hyödyntää korkeamman asteen potenssiyhtälön ratkaisemisessa.

Jos on parillinen ja , niin potenssiyhtälö voidaan ratkaista seuraavasti:

Jos on pariton, niin potenssiyhtälö voidaan ratkaista seuraavasti:

Parillisen tapauksen ratkaiseminen vastaa siis neliöyhtälön ratkaisemista ja parittoman kuutioyhtälön.


Täältä juuri löytyy Geogebran CAS-laskimella.


# tehtava9

a) Ratkaise yhtälö .

Avaa tehtävä tuomalla osoitin tähän

 
# tehtava9b

b) Ratkaise yhtälö .

Avaa tehtävä tuomalla osoitin tähän

 
# tehtava9c

c) Annin vanhemmat tallettavat säästötilille euroa. :n vuoden kuluttua talletus on kasvanut miljoonan euron suuruiseksi. Kuinka suuri on säästötilin talletuskorko prosentin kymmenysosan tarkkuudella?

Avaa tehtävä tuomalla osoitin tähän

 

These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.