4. Tilavuuden ja massan riippuvuus

Tutkitaan suureiden tilavuus \(V\) ja massa \(m\) riippuvuutta toisistaan. Asetetaan ensin hypoteesi eli alkuoletus riippuvuudesta. Massa ja tilavuus voivat olla suoraan tai kääntäen verrannollisia. Suoraan verrannollisuus tarkoittaisi sitä, että tilavuuden kasvaessa massakin kasvaa. Kääntäen verrannollisuus taas tarkoittaisi sitä, että kun tilavuus kasvaa, niin massa pienenee. Arkielämän kokemusten perusteella asetetaan hypoteesi, että tilavuus ja massa ovat suoraan verrannolliset. Asian varmistamiseksi suoritetaan mittaus, josta saatavia mittaustuloksia voidaan analysoida.

Dekantterilasi asetettiin vaa’alle, jonka jälkeen vaaka nollattiin. Tämän jälkeen dekantterilasiin mitattiin 5 ml suolaa ja punnittiin se. Suolan lisäämistä jatkettiin 5 ml kerrallaan ja joka lisäyksen jälkeen punnittiin. Kaikki tulokset koottiin taulukkoon.

Tilavuus V (ml)	Massa m (g)
0	0
5	10,5
10	21,5
15	32,8
20	44,8
25	53,2
30	61,8
35	72,8
40	83,8
45	95,9
50	108,1

Taulukosta voidaan nähdä, että suolan lisääminen eli tilavuuden kasvattaminen todella kasvattaa myös massaa. Tehty hypoteesi siis piti paikkansa ja voimmekin mittauksen perusteella todeta tilavuuden ja massan suoraan verrannollisiksi suureiksi. Taulukoidut mittaustulokset eivät kuitenkaan vielä kerro verrannollisuuskerrointa. Sen selvittämiseksi tarkempi mittaustulosten analysointi on tarpeen. Tätä varten piirretään kuvaaja.

Mittauksessa tilavuutta muutettiin ja tutkittiin muutoksen vaikutusta massaan. Täten siis tutkittiin massan riippuvuutta tilavuudesta eli massa oli tilavuuden funktio m(V). Tämä pohdinta on tarpeen, sillä sen perusteella valitaan pystyakseliksi riippuva suure eli massa m sekä vaaka-akseliksi muuttuja eli tilavuus \(V\). Piirretään siis mittapisteet \(V, m\) -koordinaatistoon.

Graafinen malli

Varsinainen graafinen malli tehdään sovittamalla mittapisteisiin kuvaaja eli graafisesti tasoittamalla. Tietokoneella sovituksen teko on helppoa, sillä kone laskee sovitteen kohdan automaattisesti käyttäjän valittua, millaisen sovituksen haluaa tehdä. Hyvän sovituksen tunnistaa siitä, että mittapisteet asettuvat piirtyvälle kuvaajalle tai sen ympäristöön tasaisesti. Tietokoneella voi kokeilla erilaisia sovituksia ja valita niistä parhaan. Mikäli käytössä ei ole sähköisiä apuvälineitä, on sovitus tehtävä käsin arvioimalla. Tärkeää on, ettei mittapisteitä milloinkaan saa yhdistää murtoviivalla. Lisäksi sovitus on aina tehtävä, jotta saadusta kuvaajasta voidaan lukea tai tulkita mitään.

Esimerkin mittauksessa pisteet näyttäisivät asettuvan suoralle, joten sovitukseksi valitaan lineaarinen. Lineaarinen sovitus tuottaa aina kuvaajaksi suoran.

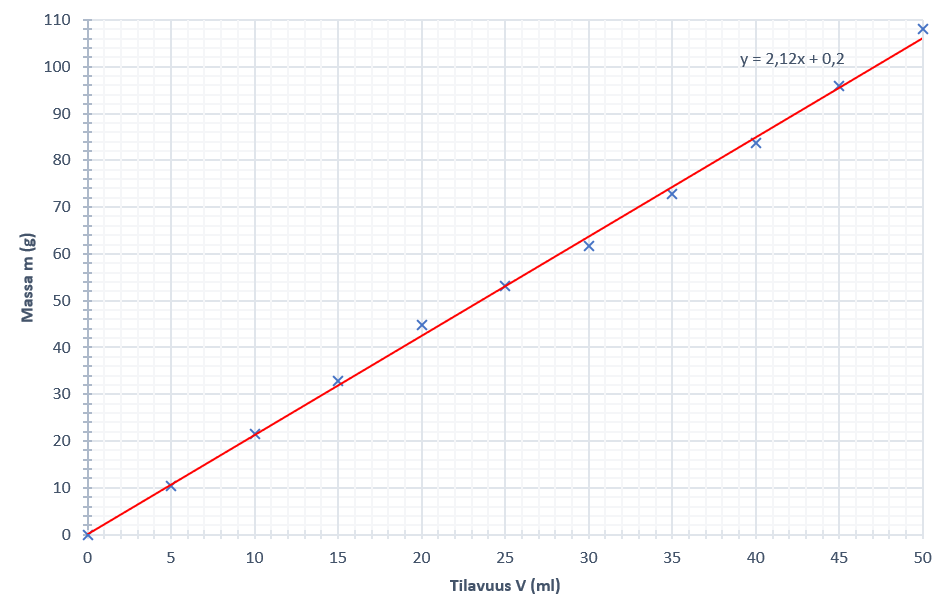
Saadussa kuvaajassa on siis massa tilavuuden funktiona eli \(m(V)\) ja saatu kuvaaja on suora. Edellisessä luvussa suoran yhtälön kerrottiin olevan muotoa \(y = f(x) = kx + b\). Tietokone näyttää sovittamansa kuvaajan lisäksi sitä kuvaavan yhtälön. Tässä yhtälö on \(m = kV + b\). Kun tätä verrataan suoran yhtälön yleiseen muotoon, voidaan päätellä seuraavaa

\(k= 2,12\)
\(b= 0,2\)

Vakiotermi \(b\) kertoo pisteen, jossa kuvaaja leikkaa pystyakselin. Tällöin vaaka-akselin suureen arvo on aina nolla. Tässä mittauksessa tutkittiin massan muuttumista, kun tilavuus muuttuu. Kun vaaka-akselin eli tässä mittauksessa tilavuusakselin arvo on nolla, vaa'alla ei ole ollenkaan suolaa. Täten myös massan pitäisi tietenkin olla nolla. Tässä mittauksessa tuloksena saatu vakiotermin \(b\) arvo on kuitenkin 0,2 eli massa tilavuuden ollessa olisi 0,2 grammaa. Tätä voidaan pitää mittausvirheestä johtuvasta epätarkkuudesta.

Kulmakerroin k kertoo kuvaajan muutosnopeuden eli suoran jyrkkyyden. Tässä mitattiin kahta suuretta, massaa ja tilavuutta, jolloin kulmakerroin ilmaisee näiden kahden suureen riippuvuuden. Tällöin voidaan puhua fysikaalisesta kulmakertoimesta. Fysikaalinen kulmakerroin ilmoittaa siis suureiden muutoksen suhteen eli

\(k=\frac{\Delta m}{\Delta V}\).

Yhtälössä \(\Delta\) on kreikkalainen aakkonen delta, jota käytetään fysiikassa kuvaamaan muutosta. Muutoksen määrittämiseksi on valittava suoralta kaksi pistettä ja määritettävä niiden koordinaatit. Muutosta laskettaessa miinustetaan aina vasemmanpuoleisen pisteen koordinaatti oikeanpuoleisesta, vaikka se tuottaisikin negatiivisen tuloksen. Tässä tapauksessa muutokset lasketaan siis

\(\Delta m = m_2 - m_1\)
\(\Delta V = V_2 - V_1\).

Huomaa, että koordinaattien \(m_1\) ja \(V_1\) on oltava saman pisteen koordinaatit ja koordinaattien \(m_2\) ja \(V_2\) saman. Valittujen pisteiden on sijaittavalla sovitetulla suoralla, eikä niitä saa lukea suoraan taulukoiduista mittaustuloksista.

Saatu kulmakerroin siis kertoo, massan ja tilavuuden suhteen. Tässä tapauksessa kulmakerrointa kutsutaan aineen tiheydeksi. Tiheys on fysikaalinen suure, jonka tunnus on \(\rho\) (kreikkalainen aakkonen ”rhoo”).

\(\rho=\frac{\Delta m}{\Delta V}\)

Tiheyden yksikkö saadaan massan ja tilavuuden yksiköistä. SI-järjestelmässä massan yksikkö on kilogramma. Tilavuutta ilmaistaan litroina tai kuutiometreinä. Tässä mittauksessa massan yksikkö oli gramma ja tilavuuden millilitra. Täten tiheydelle saadaan johdannaisyksikkö

\([\rho]=\frac{[\Delta m]}{[\Delta V]} = 1 \frac{g}{ml}\).

Tilavuuden yksikkönä voidaan käyttää myös kuutiometrejä litrojen sijaan. Näiden kahden vetomitan välillä pätee yhteys

\(1dm^3=1l\)

\(1cm^3=1ml\)

Aiemmassa esimerkissä mitattiin pieniä massoja ja pieniä tilavuuksia. Jos puhutaan suurista massoista, on ne tapana ilmoittaa SI-järjestelmän mukaisessa yksikössä kilogramma ja tilavuus taas litroina tai kuutiodesimetreinä. Tällöin tilavuudelle voidaan käyttää yksikköä \(\frac{kg}{dm^3}\). Huomaa, että

\(\frac{1 kg}{1 dm^3}=\frac{1000 g}{1000 cm^3}=\frac{1 g}{1 cm^3}\)

\(1 \frac{kg}{dm^3}=1 \frac{g}{cm^3}\)

Näin fysikaalisen kokeen kautta päästiin käsiksi uuteen käsitteeseen ja saatiin määritelty uusi suure, tiheys. Graafisen mallin avulla saatiin tiheydelle matemaattinen malli eli suureyhtälö

\(\rho =\frac{m}{V}\)

Suureyhtälöllä voidaan laskea myös muita siinä esiintyviä suureita. Kolmen suureen yhtälöstä kaksi on tiedettävä, jotta kolmannen voi ratkaista. Ratkaisu on puhdasta matemaattista yhtälönratkaisua.

Ratkaistaan suureyhtälöstä massa \(m\)

\(\rho = \frac{m}{V}\space |\cdot V\)
\(V\rho = m\)
\(m = \rho V\)

Ratkaistaan suureyhtälöstä tilavuus \(V\)

\(\rho = \frac{m}{V} \space|\cdot V\)
\(V\rho = m \space|:\rho\)
\(V = \frac{m}{\rho}\)

Tehtävä

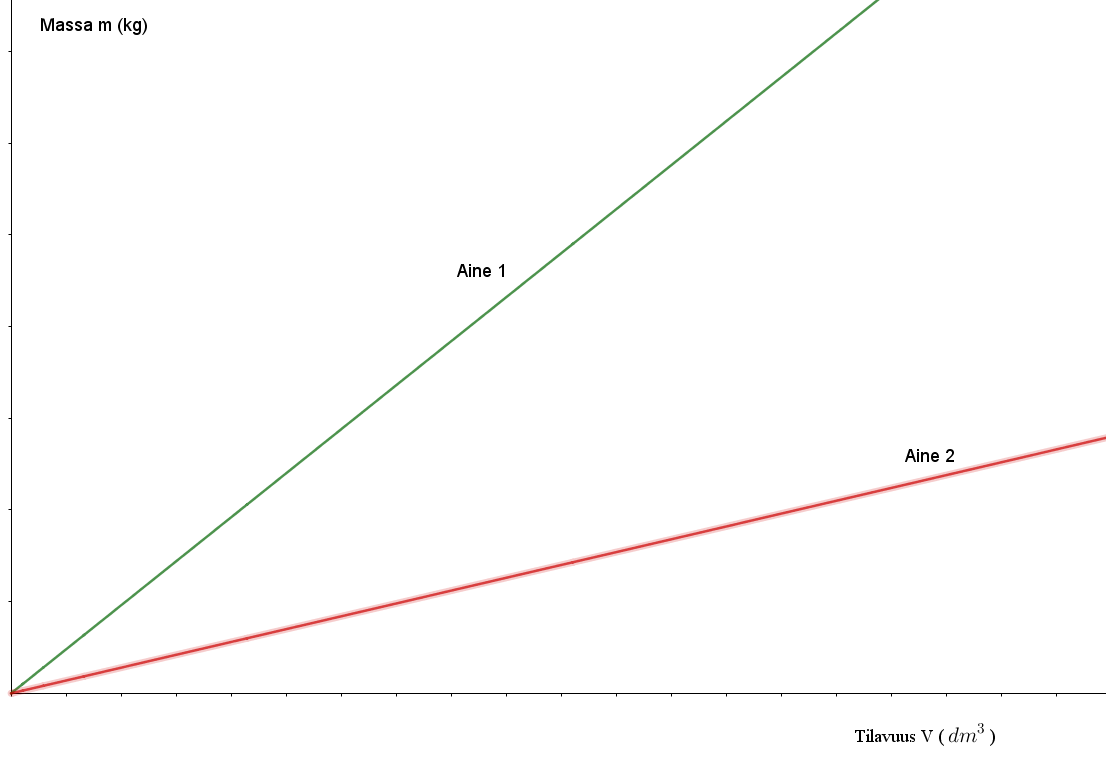
Oheiseen kuvaajaan on piirretty kahden eri aineen massan riippuvuus tilavuudesta. Kummalla aineella on suurempi tiheys? Miksi?

# eritiheydet

Tehtävä

Vettä mitattiin astiaan noin 0,1 l kerrallaan. Joka lisäyksen jälkeen astiassa oleva vesi punnittiin. Saatu mittausdata on liitteenä .txt-tiedostona. Määritä mittaustuloksista veden tiheys. Palauta kuvakaappaus, josta selviää määritystapa sekä määritetty arvo. Lopuksi vertaa saamaasi tulosta kirjallisuusarvoon.

Ohje mittausdatan käyttöön: Avaa .txt-tiedosto ja kopioi sisältö leikepöydälle. Avaa sitten haluamasi ohjelma kuvajaan piirtämiseen ja liitä kopioimasi mittausdata taulukkoon.

Veden tiheys mittausdata

# Vedentiheys

# vedentiheys1

# vedentiheys2

Tehtävä

Rautakappaleen massa on 76,0 kg ja tilavuus 9,66 \(dm^3\). Laske raudan tiheys.

# raudantiheys

Tehtävä

Kokeessa määritettiin eri tilavuuksisten alumiinikappaleiden massoja. Mittaustulokset on liittenä .txt-tiedostona. Avaa tiedosto ja kopioi tiedot haluamaasi taulukko-ohjelmaan. Piirrä mittaustulosten perusteella sopiva kuvaaja alumiinin tiheyden määrittämiseksi. Palauta kuvankaappaus tuottamastasi kuvaajasta alle.

Alumiinin tiheyden määritys, mittausdata

# alumiinintiheys

# alumiinintiheys_a

# alumiinintiheys_b

# alumiinintiheys_c

# alumiinintiheys_d

Tehtävä

Ikkunan leveys on 1,19 m ja korkeus 1,20 m. Lasin tiheydeksi tiedetään 2,50 \(\frac{kg}{dm^3}\). Laske ikkunan lasien massa, kun ikkunassa on kaksi 4,00 mm paksuista lasia.

# ikkunanmassa

Tehtävä

Kuulantyönnössä kilpakuulina voidaan käyttää teräskuulia.

# kuulantiheys

# kuulanhalkaisija

# Plugin1

Tehtävä

Arkhimedes oli ennen ajanlaskun alkua elänyt fyysikko, matemaatikko ja filosofi. Arkhimedes on tunnettu tarinasta, jossa hänen asuinpaikkansa Syrakusan kuningas Hiero II antoi hänelle tehtäväksi määrittää kruununsa valmistusmateriaali. Kuningas oli tilannut täysin kultaisen kruunun, mutta epäili sepän huijanneen ja sekoittaneen joukkoon myös halvempaa ainetta, hopeaa. Arkhimedes tiesi, että jos hän saisi määritettyä kruunun tiheyden, hän saisi selville myös materiaalin. Kruunu oli kuitenkin epäsäännöllisen muotoinen, joten tilavuuden määrittäminen osoittautui ongelmaksi. Tarinan mukaan Arkhimedes meni aivan täyteen täytettyyn kylpyammeeseen ja huomasi, että vesi alkoi tulvimaan yli. Silloin hän oivalsi, että veteen upotettu kappale syrjäyttää vettä oman tilavuutensa verran. Hän saisi siis määritettyä kruunun tilavuuden upottamalla sen täyteen vesiastiaan.

Arkhimedes sai kruunun tilavuudeksi ? ja massaksi ?. Mikä on kruunun tiheys? Etsi kullan kirjallisuusarvo ja vertaa kokeellisesti määritettyä arvoa siihen. Onko kruunu kultaa?

# FY1_Arkhimedes

# FY1_arkhimedes2

Tehtävä

Etanolin tiheyden määrittämiseksi astiaan lisättiin etanolia puoli desilitraa kerraallaan ja astian sisältö punnittiin joka lisäyksen jälkeen. Saadut mittaustulokset ovat liitteenä. Tulosten perusteella hahmottele graafinen malli, josta tiheys saadaan määritettyä. Palauta kuvakaappaus kuvaajasta alle.

# Etanolintiheyskuvaaja

# Etanolintiheys_a

# Etanolintiheys_b