2. Mittaaminen

Mittaaminen on edellytys fysikaalisen tiedon saamiselle. Myös arjessa mitataan monia asioita. Koulumatkan kesto on tarpeen mitata, jotta ehtii perille ajoissa. Leipoessa raaka-aineita on lisättävä oikea määrä, tai leipomus menee pilalle.

Mittaaminen on mitattavan asian vertaamista mittayksikköön. Esimerkiksi aikaa mitattaessa saatua tulosta verrataan sekunteihin tai minuutteihin,jotka molemmat ovat ajan yksiköitä. Mittaus tulos esitetään muodossa

lukuarvo \(\cdot\) yksikkö

8 \(\cdot\) s = 8 s = "kahdeksan sekuntia"

Mittausvirheet

Mittaaminen on lopulta aina arvioimista. Vaikka sen suorittaisi kuinka tarkasti, on tulos parhaimmillaankin vaan likiarvo. Mittaustulokseen siis liittyy aina epätarkkuuksia ja virheitä. Virheitä on erilaisia ja niiden vaikutus mittaustulokseen on erilainen.

Karkea virhe

Karkeat virheet syntyvät esimerkiksi mittauslaitteiston vääränlaisesta käytöstä tai tulkinnasta. Kaikki saadut mittaustulokset voidaan havaita virheellisiksi tai vain yksittäinen mittapiste. Karkeat virheet voi tuloksia analysoitaessa jättää tarkastelun ulkopuolelle. Niitä ei saa kuitenkaan poistaa tuloksista kokonaan, sillä se olisi tulosten manipulointia. Mittapistettä tai mittaustulosta ei saa tulkita karkeaksi virheeksi, mikäli ei ole käsitystä siitä, mistä virhe johtuu. Karkeita virheitä voidaan välttää työskentelemällä tarkasti ja keskittyen koko mittauksen ajan, sekä varmistamalla mittauslaitteiston toiminta ja toimivuus mittaustilanteessa.

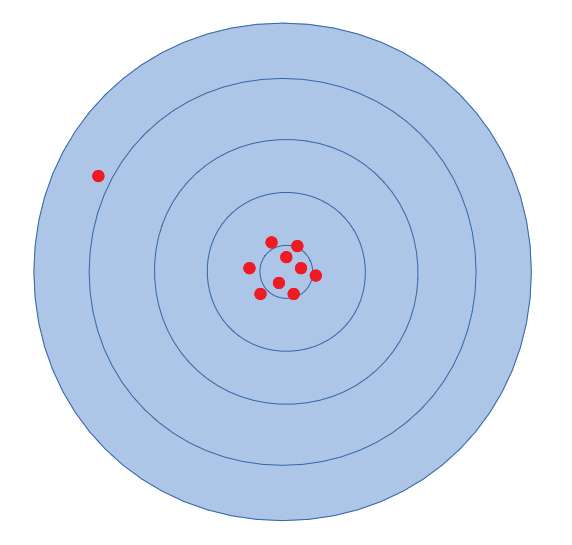
Systemaattinen virhe

Systemaattinen virhe aiheuttaa mittaukseen epätarkkuutta aina samaan suuntaan. Jos esimerkiksi mitataan pituuksia ja mittaaja lukee mittaa vinosti, aiheutuu jokaiseen mittaukseen katselukulmasta johtuva virhe. Toinen esimerkki systemaattisesta virheestä voisi olla mittaus, jossa vaakaa ei ole kalibroitu eli nollakohtaa ei ole asetettu oikein. Tällöin vaaka näyttää aina kalibrointivirheen verran väärin. Systemaattinen virhe voi olla vaikea huomata, mutta esimerkiksi saman asian mittaaminen eri menetelmällä voi paljastaa systemaattisen virheen.

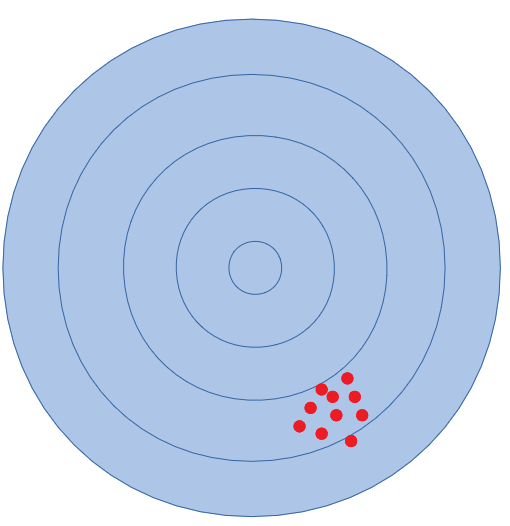
Systemaattisessa virheessä mittauspisteet asettuvat kyllä lähelle toisiaan, mutta eivät keskelle taulua eli tuloksena ei saada oikean suuruisia arvoja.

Tätä vaakaa ei ole kalibroitu. Mittauksessa se aiheuttaisi jokaiseen tulokseen 0,3 gramman systemaattisen virheen.

Satunnainen virhe

Satunnaista virhettä esiintyy kaikissa mittauksissa. Se havaitaan mittaamalla samaa asiaa moneen kertaan. Mittaustulosten pitäisi olla samat, jos mitattava asiakin on sama. Näin ei kuitenkaan ole, vaan saadut mittausarvot heittelevät suuntaan ja toiseen. Vaikka satunnaisvirhettä ei voikaa poistaa täysin, sitä voi silti pienentää. Toistamalla samaa koetta useaan kertaan suuntaan ja toiseen heittelevät arvot kumoavat toistensa vaikutusta ja näin päästään lähemmäs oikeaa arvoa. Myös mittauslaitteen tai -menetelmän kehittäminen ja parantaminen vähentää satunnaista virhettä.

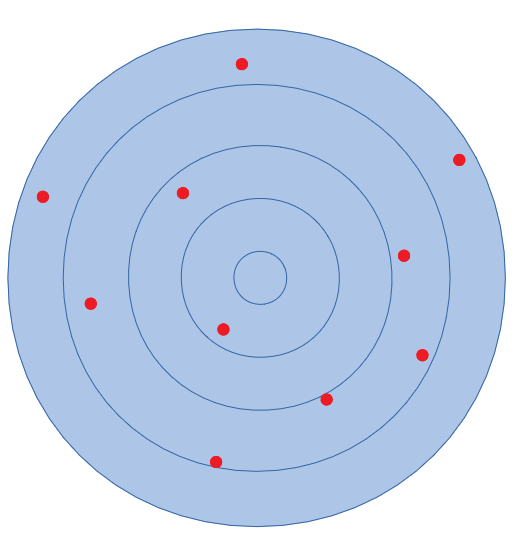
Mittapisteet sijoittuvat ympäri maalitaulua, vaikka on mitattu samaa asiaa. Niiden keskiarvo voi silti olla lähellä oikeaa tulosta, joten useiden toistojen tekeminen mittauksessa parantaa lopputuolosta.

Merkitsevät numerot

Mittaustulokset ja niistä lasketut arvot ovat likiarvoja. Ei ole sattumanvaraista, kuinka monta numeroa vastaukseen kirjoitetaan näkyviin. Näkyviin kirjoitettuja numeroita kutsutaan merkitseviksi numeroiksi. Merkitseviä numeroita ovat luvussa kaikki paitsi

Nollat desimaaliluvun alussa
Joskus nollat kokonaisluvun lopussa

Huomaathan, että desimaliluvun lopussa nollat ovat aina merkitseviä numeroita. Täten esimerkiksi luku 0,10 on ilmoitettu tarkemmin kuin luku 0,1. Merkitsevien numeroiden määrä voi määräytyä esimerkiksi tehtävänannosta. Vastaus on tapana ilmoittaa yhtä tarkasti kuin tehtävässä annettu epätarkin arvo. Omassa mittauksessa mittaustulosten ja lopulta tuloksen tarkkuutta on arvioitava.

Esimerkki

100: 1 merkitsevä numero (1)
101: 3 merkitsevää numeroa (1,0 ja 1)
0,21: 2 merkitsevää numeroa (2 ja 1)
0,930: 3 merkitsevää numeroa (9, 3 ja 0)
8,0: 2 merkitsevää numeroa (8 ja 0)

Pyöristäminen

Jos tulos on jotain muuta tarkkuutta, kuin pitäisi, on lopputulosta pyöristettävä. Joskus tehtävänannossa on annettu pyöristystarkkuus, mutta toisinaan se pitää itse päätellä lähtöarvojen tarkkuudesta. Pyöristämisessä katsotaan ensimmäinen poisjäävä numero ja mikäli se on alle viisi, pyöristetään luku alaspäin. Jos viimeinen poisjäävä luku on viisi tai enemmän, luku pyöristetään ylöspäin.

Esimerkki

Pyöristä kahden desimaalin tarkkuuteen
a) 0,561 \(\approx\) 0,56
b) 1,247 \(\approx\) 1,25
c) 29,997 \(\approx\) 30,00

Laskettaessa pitkää laskua vasta lopputulos pyöristetään. Mahdollisia välituloksia ei siis pyöristetä, sillä se aiheuttaisi epätarkkuutta lopulliseen tulokseen. Fysiikassa onkin usein tapana välituloksen numeerisen arvon laskemisen sijaan sijoittaa tarvittavat suureet suureyhtälöinä, mikäli niille ei ole tehtävänannossa annettu suoraan arvoa. Tällöin lopullisen tuloksen laskemisessa käytetään varmasti tarkkaa arvoa ja lopputuloksessa on mahdollisimman vähän välituloksista johtuvaa virhettä.

Tehtävä

Montako merkitsevää numeroa on seuraavissa luvuissa

Työ: Työntömitta

Tarvikkeet: Työntömitta, viivotin
Selvitä, mikä on työntömitta ja miten se toimii.
Mittaa sekä viivottimella että työntömitalla jonkin kirjan paksuus. Kirjaa tulokset ylös ja vertaile niitä. Mittaa seuraavaksi jonkin kartionmallisen putken tai johdon paksuus jälleen sekä viivottimella että työmtömitalla. Kirjaa tulokset ylös ja vertaile niitä.
Arvioi lopuksi, millä tarkkuudella voit mitata asioita viivottimella ja millä taas työntömitalla.

Tehtävä

Arvioi mahdollisia virhelähteitä seuraavissa mittauksissa. Muista erilaiset virhetyypit! Kuinka tarkkuutta voitaisiin parantaa?

# virheet_teht1a

# virhe_teht1b

# virhe_teht1c

Työ: Putoamisaika toistokokeella

Mitä tarkoitetaan toistokokoeella?

Välineet: Pyyhekumi, sekuntikello
Suorita toistokoe, jossa mittaat aikaa, joka kuluu pyyhekumin pudotessa pöydän korkeudelta lattialle. Suorita vähintään viisi toistoa ja kirjaa tuloksesi ylös. Laske tulosten pohjalta keskimääräinen putoamisaika. Miksi toistokokeella määritetty mittaus antaa yksittäistä mittausta tarkemman tuloksen?

Työ: Reaktioaika

JustParkin reaktioaikatesti

Alla olevasta linkistä pääset JustParkin reaktioaikatestiin. Suunnittele ja toteuta leikkimielinen koe, jossa mittaat omaa reaktioaikaasi kyseisellä testillä. Käytä ainakin viiden mittauksen toistokoetta ja laske lopulliseksi tulokseksi näiden mittausten keskiarvo. Voit myös miettiä tekijöitä, jotka voisivat vaikuttaa reaktioaikaan, ja testata näitä teoriota suorittamalla mittaukset uudelleen eri tilanteessa. Lopuksi pohdi tulosten luotettavuutta.