Kuvaajien piirtäminen
Tässä luvussa löytyy ohjeita kuvaajien piirtämiseen. Ylioppilaskokeessa sallituista ohjelmista kuvaajia voidaan piirtää ainakin LibreOfficcen Calcilla, GeoGebralla, LoggerProlla sekä Texas Instruments TI-Nspire CAS*:lla.
LibreOffice Calc
LibreOfficen Calc soveltuu hyvin käytettäksi useissa fysiikan graafisissa mallintamista vaativissa tehtävissä. Ohjelma antaa mallipisteisiin sovitetun kuvaajan matemaattisen yhtälön, joten ainakin kulmakertoimen ja pystyakselin leikkauspisteen määrittäminen on helppoa. Vaativampiin graafisiin menetelmiin ohjelma on vähän kömpelö, sillä taulukko-ohjelmana esimerkiksi hetkellisten arvojen määrittämiseen tarivttavien toimintojen määrä on rajallinen. Näihin perhdytään kuitenkin vasta myöhemmillä fysiikan kursseilla, joten tällä kurssilla Calc on oikeinkin riittävä ohjelma kuvaajien piirtämiseen.
Geogebra
GeoGebra tulee varmasti tutuksi matematiikan opinnoissa, mutta oiva se on fysiikassakin. Kuvaajien tuottaminen mittapisteistä onnistuu kuten LibreOfficellakin. GeoGebra tosin sovittaa mittapisteisiin kuvaajan miinus äärettömästä äärettömään eli mittausalueen ulkopuolelle. Kuten ekstapoloinnissa puhuttaessa opimme, tämä ei läheskään aina kuvaa todellista tilannetta eikä ole fysikaalisesti oikein. Tämä voidaan kuitenkin estää ainakin piirtämällä sovitetun kuvaajan päälle toinen suora, jolle on annettu mittausaluetta vastaava väli. GeoGebralla myös onnistuu myös esimerkiksi hetkellisten arvojen määrittäminen.
Kuvaajien piirtämisessa huomioitavaa
Graafista mallintamista tarvitaan mittaustulosten analysointiin, ja niiden pohjalta laaditaan edelleen matemaattisia malleja. Graafisilla malleilla on siis suuri merkitys fysikaalisen tiedon jäsentelyssä ja rakentamisessa. Siksi onkin tärkeää, että graafiset mallit ovat selkeitä ja noudattavat tiettyjä sovittuja sääntöjä. Mallin pitää aina olla muidenkin, kuin tekijän ymmärrettävissä. Tarpeellinen informaatio on pystyttävä lukemaan graafisestä mallista vaivatta ja riittävällä tarkkuudella.
Graafisen mallin on oltava riittävän suuri, jotta kuvaajaa pystyy lukemaan. Myös akseleiden skaalaus on tehtävä niin, että lukeminen on mahdollista. Jos kuvaaja saa arvoja esimerkiksi välillä \([0, 20]\), eli ole tarpeen skaalata akseleita esimerkiksi välille \([-50, 50]\). Kuvaajan on täytettävä koordinaatisto mahdollisimman tasaisesti. Skaalauksen lisäksi akseleiden jakoväleihin on kiinnitettävä huomiota. Hyvä nyrkkisääntö on katsoa, saisiko koordinaatistoon piirretyn mittapisteen koordinaatit määritettyä edes lähes samalla tarkkuudella, kuin millä mittaus on tehty. Jakovälit on myös aina merkittävä selkeästi näkyviin.
Graafisesta mallista on selvittävä, mitä se kuvaa. Koordinaatistoon on merkittävä akseleiden nimet näkyviin. Usein tapana on merkitä suuren nimi ja tunnus sekä yksikkö. Yksikön merkitsemiseen on monta tapaa, mutta hyvä tapa on merkitä se sulkuihin suureen ja suureen tunnuksen perään. Muutoin graafiselle mallille ei yleensä anneta otsikkoa, jos se on osana kirjoitettua tekstiä. Jos otsikko annetaan, on sen oltava informatiivinen ja kerrottava, mitä kuvaaja esittää. Myös kuvateksti voidaan lisätä kertomaan muutamalla lauseella, mitä malli kuvaa. Myös joidenkin ohjelmien automaattisesti luomat selitteet on tapana jättää pois.
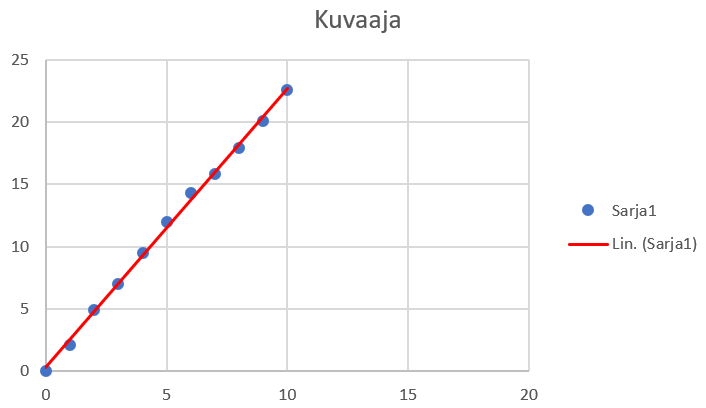
Mittapisteiden ja kuvaajan merkitseminen koordinaatistoon on oltava sellaista, että se ei vaikuta tarkkuuteen mallia luettaessa. Koordinaatistossa, jossa on pienet jakovälit, suuren pisteen tai neliön käyttö mittapisteen symbolina tuo epätarkkuutta mallin lukemiseen. Rasti on tällaisessa tilanteessa sopivampi symboli. Kuvaajaa merkitään jatkuvalla ja riittävän paksulla viivalla, jotta se erottuu taustasta. Kuvaaja arvoja on voitava lukea kuvaajan kaikista kohdista vaivatta. Myös väreihin on syytä kiinnittää huomiota. Mittapisteillä ja kuvaajalle on hyvä valita eri värit. Värien on kuitenkin oltava riittävän vahvoja, jotta ne erottuvat.
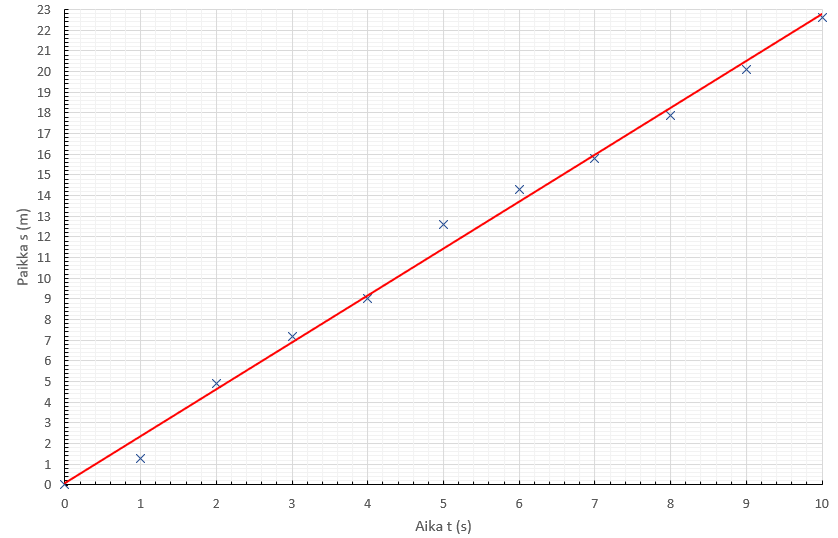
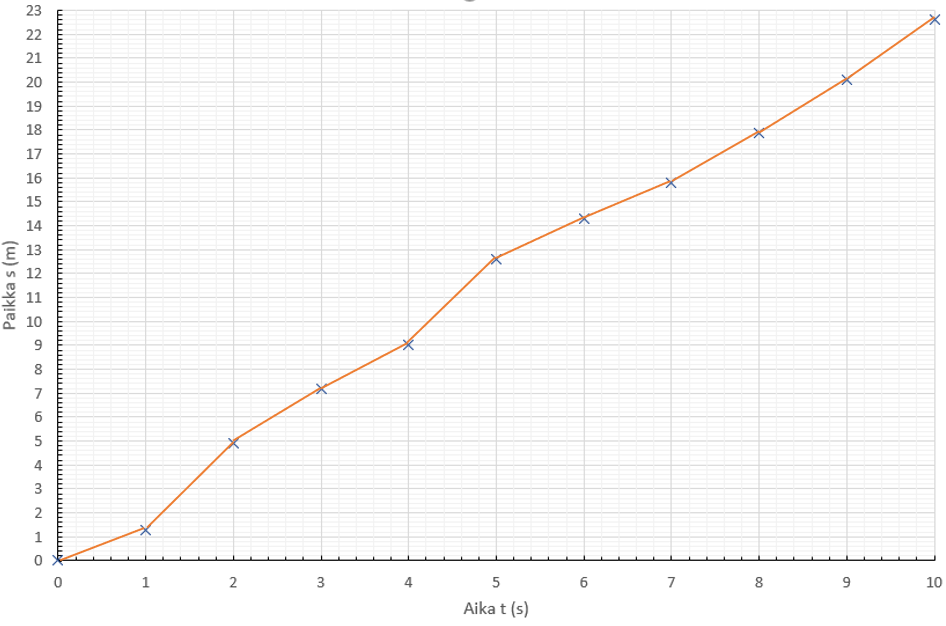
Kun mittapisteet on piirretty koordinaatistoon, kuvaajaan sovittaminen on tehtävä niiden perusteella. Tietokone ohjelma sovittaa kuvaajan suoraan laskemalla sille oikein paikan ja suunnan mittapisteiden perusteella. Käyttäjän on ainoastaan valittava sopiva matemaattinen malli kuvaajalle. Hyvä sovitus on sellainen, jossa pisteet asettuvat sovitteelle tai sen lähistöön hyvin. Erityisen tarkka on oltava mittausalueen ääripäissä. Missään nimessä mittapisteitä ei saa yhdistää toisiinsa murtoviivalla, vaan aina on tehtävä graafinen tasoitus ja etsittävä oikea sovitus. Kun sovitus on tehty, kuvaajalta voidaan lukea yksittäisiä arvoja. Sen sijaan mittapisteistä ei ikinä saa lukea yksittäisiäkään arvoja. Sovitteen tarkoituksena on minimoida yksittäisten mittapisteiden virheitä ja optimoida saatua tulosta.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.