5. Ajan ja paikan riippuvuus

Juoksukilpailuissa mitataan aikaa, joka kuluu tiettyä matkaa juostessa. Pikamatkoja pidemmillä matkoilla on tapana mitata myös väliaikoja. On selvää, että nopeinten on juossut se, jolta samaan matkaan on kulunut lyhin aika. Autoa tai mopoa ajaessa voimme tarkistaa nopeusmittarista ajonopeuden. Kun kaasua painaa enemmän, nopeusmittarin viisari kohoaa suurempiin nopeuksiin. Auton tai mopon tapauksessa mittari näyttää kilometrejä tunnissa (\(\frac{km}{h}\)). Meteorologi taas varoittaa rivakasta tuulesta ja käyttää tuulennopeudelle yksikköä metriä sekunnissa (\(\frac{m}{s}\)).

Seuraavaksi perehdytään tarkemmin matkan ja ajan riippuvuuteen. Kokeessa mitattiin matkaa \(s\), jonka juoksija liikkuu aina 10 sekunnissa, yhteensä minuutin ajan. Tulokset on koottu taulukkoon.

Aika t (s)	Matka s (m)
0	0
10	51
20	124
30	187
40	251
50	305
60	371

Tarkempaa tarkastelua varten on tarpeen tuottaa graafinen malli, joka kuvaa juostun matkan riippuvuutta ajasta. Tämä tarkoittaa siis akselivalintaa, jossa matka on pystyakselina ja aika vaaka-akselina. Kuten massan ja tilavuuden riippuvuutta määrittäessä opittiin, pelkistä mittapisteistä koordinaatistossa ei voida vielä tarkastella kahden suureen riippuvuuksia kovinkaan syvällisesti. Mittapisteille tuleekin jälleen tehdä graafinen tasoitus eli sovittaa niihin jokin matemaattinen sovite. Jälleen huomataan, että lineaarinen malli sopii mittapisteisiin kaikkein parhaiten.

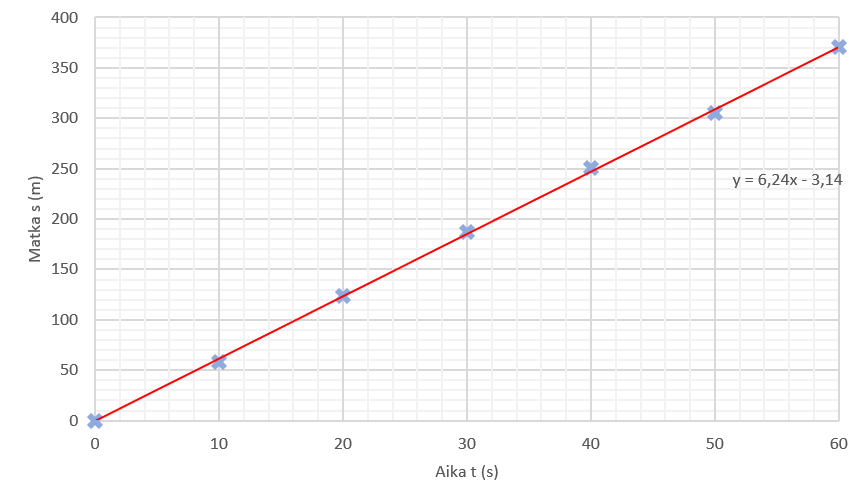
Saatu graafinen malli on siis jälleen lineaarinen. Tutkittaessa kuvaajan kulkua tarkemmin, voidaan huomata, että jokaisen kymmenen sekunnin aikana juoksija juoksee lähes yhtä pitkän matkan, noin 60 metriä. Tällaista liikettä sanotaan tasaiseksi liikkeeksi.

Sovitetun suoran yhtälöstä nähdään suoraa suoran kulmakerroin sekä vakiotermi.

k= 6,24

b=3,14

Vakiotermi on nyt likimain nolla. Kuvajassa tämä tarkoittaa sitä, että suora kulkee origon kautta. Tässä mittauksessa se tarkoittaisi sitä, että ajan hetkellä 0 sekuntia oltiin kuljettu matka 0 metriä. Tässä kokeessa tämä pitää paikkansa.

Kulmakertoimeksi saatiin \(k=6,24\). Kuten aiemmin opittu, kulmakerroin saadaan laskemalla akselien suureiden muutos tietyllä välillä ja jakamalla pystyakselin muutos vaaka-akselin muutoksella. Nyt kulmakerroin on siis

\(k= \frac{\Delta s}{\Delta t} =\frac{s_2-s_1}{t_2-t_1}\)

Kulmakerroin kuvaa muutosten suhdetta. Kun edellisen matemaattisen lausekkeen merkitystä miettii tarkemmin, huomaa sen kuvaaman matkan muuttumista tietyssä ajassa. Tässä tapauksessa kulmakerroin on siis nopeus. Nopeuden tunnus on \(\overline{v}\), joten saadaan

\(\overline{v}=\frac{\Delta s}{\Delta t}\)

Huomaa, että nopeus on vektorisuure, eli sillä on suuruuden lisäksi suunta. Yksikkötarkastelulla nopeuden yksiköksi saadaan

\([\overline{v}]=\frac{[s]}{[t]}=1\frac{m}{s}\)

Tässä mittauksessa juoksija juoksi siis nopeudella noin \(6,2 \frac{m}{s}\). Tulos on pyöristetty vastaamaan taulukon arvojen tarkkuutta.

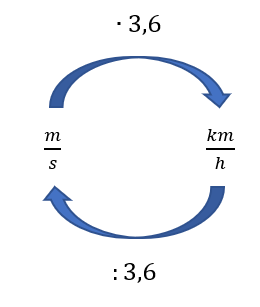
Nopeudelle on myös toinen usein käytetty yksikkö, \(\frac{km}{h}\). Tämä ei ole SI-järjestelmän mukainen yksikkö, mutta sen käyttö etenkin pitkillä matkoilla ja suurilla nopeuksilla on järkevää. Tämän yksikön ja nopeuden SI-järjestelmän mukaisen yksikön välillä pätee yhteys

\(\frac{1km}{1h}=\frac{1000 m}{60 min}=\frac{1000m}{3600s}=\frac{1m}{3,6s}\)

Keskinopeus

Yllä kuvatussa tilanteessa liike oli tasaista, sillä samassa ajassa kuljettin likimain sama matka. Tällöin nopeus pysyy vakiona. Liike on myös aina suoraviivaista, sillä vakionopeuksisen kappaleen suunta ei muutu. Edellä opimme, että nopeus on vektorisuure eli sillä on suunta. Suunta voi olla myös negatiivinen, mutta arkikielessä emme puhu negatiivisista nopeuksista. Usein puhuttaessa nopeudesta tarkoitetaankin itseasiassa vauhtia, joka on nopeuden itseisarvo.

Tässä kappaleessa tutustutaan tilanteeseen, jossa nopeus ei olekaan vakio, vaan se muuttuu ajan funktiona. Ajatellaan tilannetta, jossa autolla ajetaan kaupungista toiseen. Matkan varrella on välillä taajama, välillä 80 \(\frac{km}{h}\) nopeusrajoitus, välillä peräti 100 \(\frac{km}{h}\). Nopeus siis vaihtelee matkan varrella. Jotta matkaan kuluvaa aikaa voitaisiin arvioida, on tiedettävä auton keskinopeus.

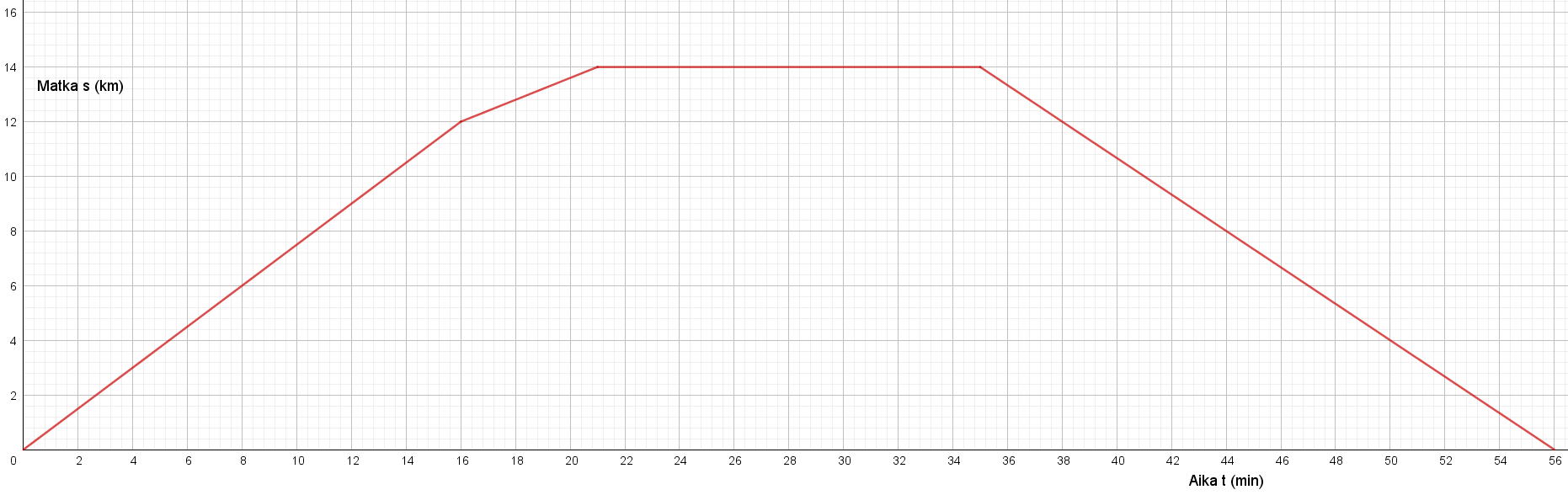
Tarkastellaan 500 metrin kävelymatkaa kaupungissa. Kävelyä on kuvattu alla olevassa aika-paikka-koordinaatistossa. Kuvaaja on yksinkertaistettu, jotta sen tarkastelu olisi helpompaa.

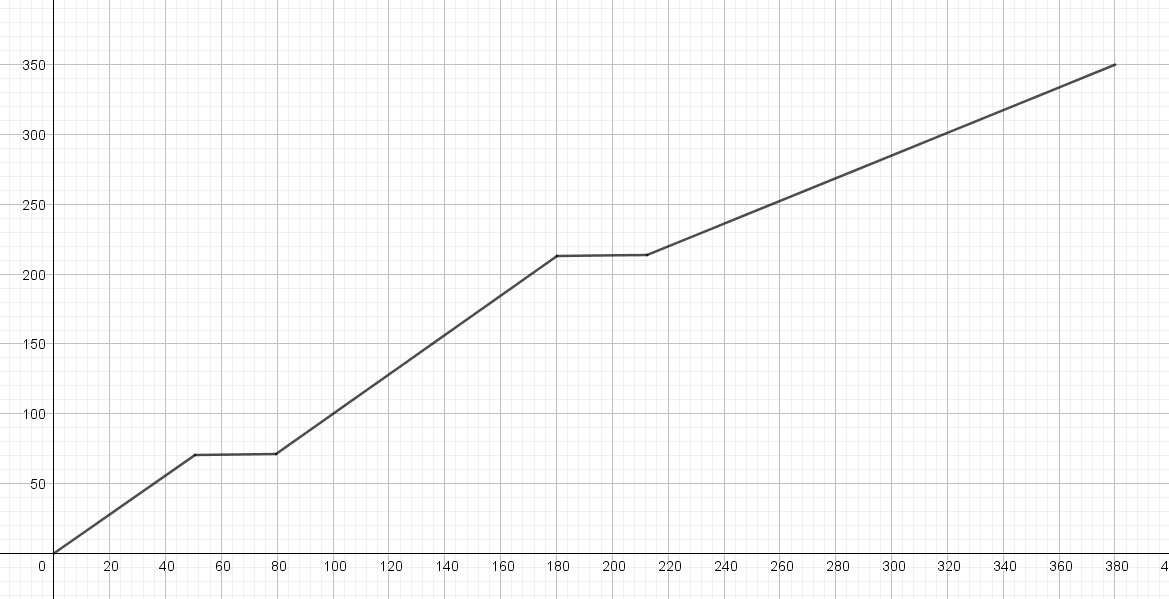
Tälläisessä tapauksessa liikettä ei kuvaakaan yksinkertainen lineaarinen malli, sillä liike ei ole tasaista. Itse asiassa liike on pysähtynyt kohdissa X, Y ja Z. Kaupungissa kävellessä nämä pysähdykset voisivat johtua esimerkiksi liikennevaloista. Kävelijälle voidaan kuvaajan avulla laskea keskinopeus. Keskinopeus ei kerro tietyn ajanhetken nopeutta, vaan koko tarkasteluajan nopeuden keskiarvon. Keskinopeus määritetään lukemalla kuvaajasta ensin kokonaismatka ja kokonaisaika. Näitä arvoja ja nopeuden suureyhtälöä käyttämällä saadaan määritetty keskinopeus.

Tässä keskinopeus olisi....

Työ: Keskinopeus

Tarvikkeet: Rullamitta, teippiä ja sekuntikello, jolla saa mitattua väliaikoja Mittaa esimerkiksi koulun käytävälle tai pihalle 25 metrin matka siten, että merkitset välietapit viiden metrin välein. Käytä esimerkiksi teippiä välietappien merkitsemiseen. Toinen parista kävelee mahdollisimman tasaisesti 25 metrin matkan ja toinen ottaa aikaa. Aika otetaan väliaikoina jokaisella viiden metrin matkalla. Taulukoi mittaustulokset. Tee mittaustulosten perusteella graafinen malli, joka kuvaa matkaa ajan funktiona, ja määritä sen avulla keskinopeus.

Tehtävä

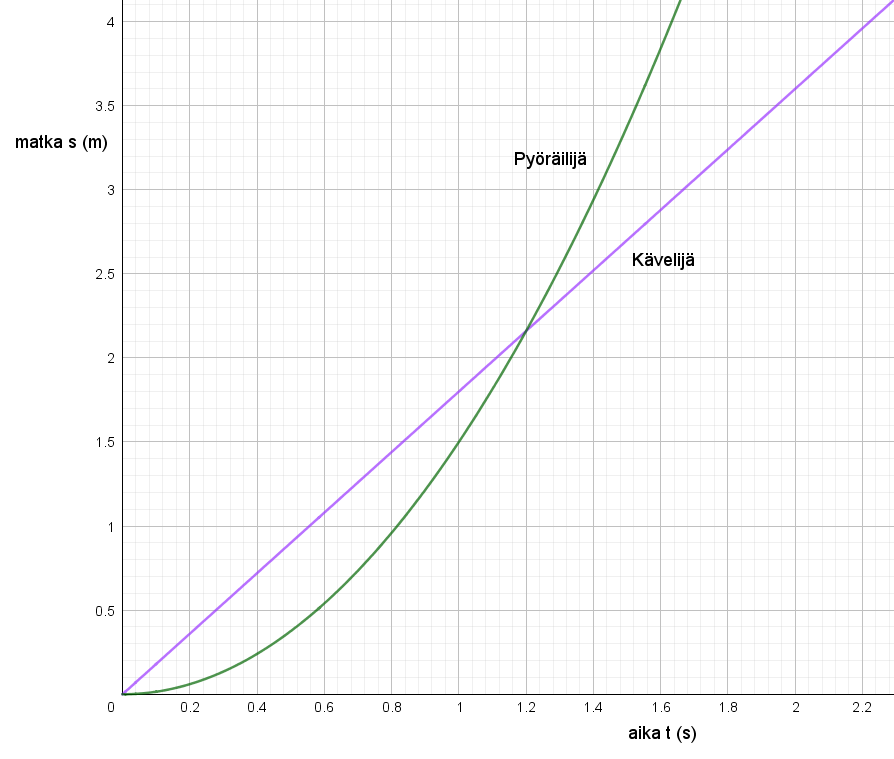
Oheisessa kuvassa on graafisesti mallinnettu kävelijän (violetti) ja pyöräilijän (vihreä) liikettä. Tutki kuvaajia ja vastaa kysymyksiin.

Tehtävä

Liikunnantunnilla mitattiin aikaa, joka kuluu 4 kilometin juoksemiseen. Opettaja mittasi väliaikoja 500 metrin välein. Erään opiskelijan ajat ovat liittenä. Määritä niiden perusteella oppilaan keskinopeus juoksun aikana.

Tehtävä

Oheinen kuvaaja esittää liikettä eräällä kulkuneuvolla. Vastaa kuvaajan perusteella kysymyksiin.

# mopokuvaaja_a

# moponliike_b

# moponliike_c

# moponliike_d

# moponliike_e

# moponliike_kuva

Tehtävä

Kahden juna-aseman (asema 1 ja asema 2) etäisyys on 165 km. Tutkitaan kahden junan, Pendolinon ja Intercityn, liikettä asemalta toiselle. Oletetaan junien liike asemien välillä lähes tasaiseksi. Junien liikettä asemien välillä on kuvattu alla.

Pendolino

Lähtee asemalta 1 klo 10.
Saapuu asemalle 2 klo 10.45.
Klo 10.30 juna on 110 kilometrin päässä asemasta 1.

Intercity

Lähtee asemalta 2 klo 10.
Saapuu asemalle 1 klo 10.50.
Klo 10.30 juna on 100 kilometrin päässä asemasta 2.

Yllä mainittujen tietojen perusteella tee graafinen malli junien liikkeestä. Piirrä junien liikettä kuvaavat kuvaajat samaan aika, paikka -koordinaatistoon ja määritä kuvaajista junien keskinopeudet. Palauta kuvakaappaus tuottamastasi graafisesta mallista alle.

# junakuvaaja

# juna_a

# juna_b