Tekoälyn perusteita ja sovelluksia
Esipuhe
Tämä kirja pohjautuu Jyväskylän yliopiston IT-tiedekunnassa lukuvuonna 2018-2019 pidettyyn kurssiin Tekoälyn perusteita ja sovelluksia. Kirjassa kerrotaan tekoälyn perusteista ja kymmeniä käytännön esimerkkejä, joissa käytetään tekoälyä. Tekoälysovelluksista kerrotaan sekä yleisesti, IT-tiedekunnan tutkimuksen näkökulmasta sekä tarkastelemalla kurssin opiskelijoiden vastauksia tekoälysovelluksia koskeviin kysymyksiin. Lisäksi tutustutaan neuroverkkojen matemaattiseen taustaan.
Kirjoittajina eri luvuissa ovat olleet Martti Lehto, Pekka Neittaanmäki, Esko Niinimäki, Riku Nyrhinen, Anniina Ojalainen, Ilkka Pölönen, Ilkka Rautiainen, Toni Ruohonen, Heli Tuominen, Petri Vähäkainu, Sami Äyrämö ja Sanna-Mari Äyrämö.
Kiitos avusta Anthony Ogbechie ja Matti Savonen.
Jyväskylässä 29.5.2019,
Heli Tuominen ja Pekka Neittaanmäki
1. Johdanto
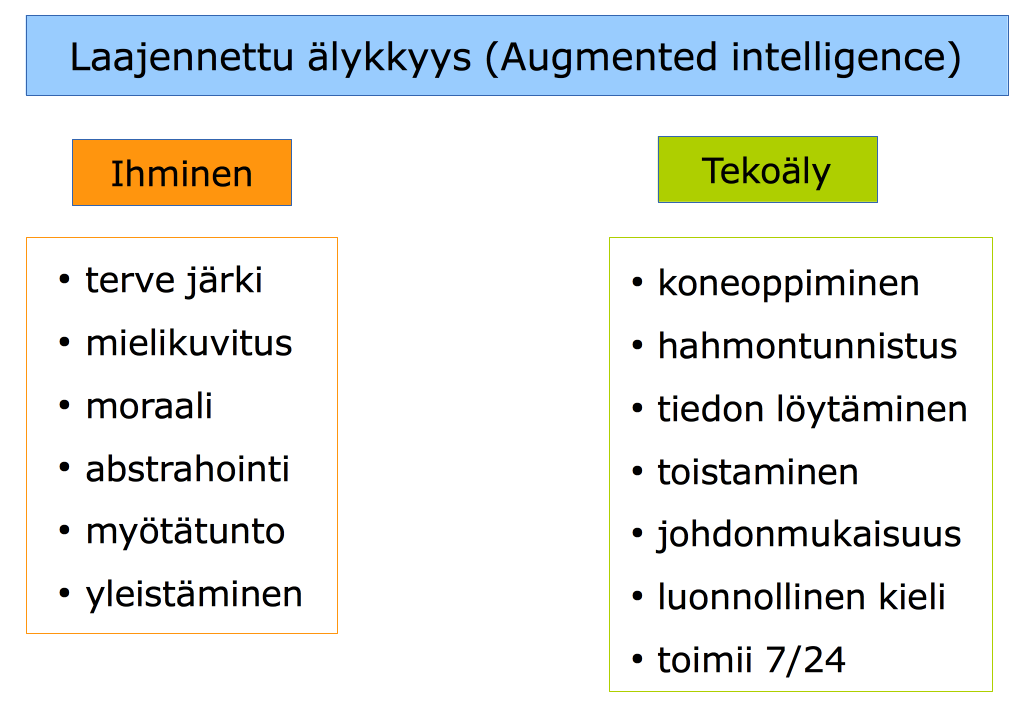
Tekoäly esiintyy lähes päivittäin uutisotsikoissa ja mielipidekirjoituksissa. Sitä ihastellaan, tutkitaan, mystifioidaan ja pelätäänkin. Tekoälyllä ei ole tarkkaa yleistä määritelmää, vaan määritelmä riippuu asiayhteydestä. Tekoälyn käsite viittaa ohjelmiin ja laitteisiin, jotka kykenevät oppimaan ja jotka auttavat ihmistä niissä toiminnoissa, joita varten ne on suunniteltu. Avustavaa puolta korostettaessa käytetään monesti myös termiä laajennettu älykkyys (augmented intelligence).
Tekoäly on taustalla esimerkiksi hakukoneissa, pysäköintihallien rekisterintunnistimissa, kameroiden kasvojentunnistuksessa, älypuhelinten ääniohjauksessa ja kohdennetussa mainonnassa. Näiden toimintojen rakentamiseen käytetään erilaisia oppimismenetelmiä ja algoritmeja, joiden kaikkien takana on matematiikka. Tekoälyn taustalla olevan matematiikan ymmärtäminen on tärkeää, sillä sopivien funktioiden, algoritmien ja minimointimenetelmien valinta vaikuttaa tulosten tarkkuuteen, tekoälymenetelmän koulutusajan pituuteen, mallin monimutkaisuuteen ja yleistettävyyteen sekä tarvittavien parametrien ja muiden komponenttien lukumäärään.
Ihmisen aivojen toimintaa jäljittelevät keinotekoiset neuroverkot keksittiin jo 1940-luvulla. Kiinnostus niitä kohtaa heräsi uudelleen 1990-luvulla, mutta käyttöinto hiipui nopeasti. Neuroverkot eivät olleet muita menetelmiä parempia ja silloisilla tietokoneilla ei ollut mahdollisuutta käsitellä neuroverkkojen koulutuksessa tarvittavia suuria datamääriä. 2010-luvulla koneiden nopeutuminen ja datan määrän valtava kasvaminen ovat lisänneet innostusta tuhansia neuroneja sisältäviin syviin neuroverkkoihin. Neuroverkkoja käytetään esimerkiksi kuvantunnistuksessa, konenäössä, puheentunnistuksessa, kieltenkääntäjissä, peleissä ja lääketieteellisissä diagnooseissa.
Modernit tekoälysovellukset perustuvat pääosin datasta oppimiseen. Tietokoneet kykenevät ratkaisemaan monimutkaisia logiikan päättelyitä ja laskutehtäviä mutta tosielämän tapausten mallintamiseen tarvittavan informaation kerääminen on monesti vaikeaa. Ihmiselle helppojen mutta vaikeasti formaalissa muodossa esitettävien tehtävien ratkominen on tekoälylle haastavaa. Jotta tekoäly kykenisi ihmismäiseen toimintaan, sen pitäisi pystyä oppimaan asioita esimerkiksi kuvista, puheesta, muista äänistä, teksteistä ja tapahtumaketjuista. Nykyiset tekoälyalgoritmit eivät pysty lisäämään tai luomaan oppimaansa malliin sellaista tietoa, jota niiden opettamiseen käytettävässä datassa ei ole. Tekoälyn laatu ja kattavuus on siis varsin pitkälle datasta riippuvaista.
Tekoälyn opettamisessa käytettävän datan käsittelyyn tarvitaan ja käytetään monenlaisia tekniikoita, joita esitellään tässä kirjassa. Datan käsittelyn lisäksi tutustutaan neuroverkkojen taustalla olevaan matematiikkaan, kyberturvallisuuteen ja tekoälyn käyttöön eri yhteyksissä. Tekoälyllä on satoja sovellutuksia. Sovellutukset kattavat perinteisten koneoppimisen, kuva-analyysin, päätöksenteon tukijärjestelmien lisäksi puheen- ja tekstintunnistuksen. Nämä ovat nopeasti kehittyviä tekoälyn sovellutusaloja. Tekoäly voi toimia ongelmanratkaisijan asemassa kyberuhkien havaitsemisessa, ratkaisemisessa ja torjunnassa. Uusimmat ratkaisut automatisoivat kyberturvallisuustoimenpiteitä ja siten helpottavat ihmisen toimintaa.
Luvussa 2 tutustutaan tekoälyn keskeisiin käsitteisiin ja termeihin.
Luvun 3 teemana ovat ohjatun oppimisen luokittelualgoritmit ja ennustemenetelmät. Tekoälyn avulla suoritettavat tehtävät ovat lähes aina tulkittavissa ennustustehtäviksi. Perinteisessä selittävässä mallintamisessa pyritään selvittämään selittävien ja selitettävien muuttujien väliset riippuvuudet ja syy-seuraussuhteet kun taas ennustavassa mallintamisessa pyritään mahdollisimman tarkkaan ennustustulokseen yhteyksien jäädessä useimmiten mustalaatikko -tyyppisen mallin taakse.
Luvun alussa käydään läpi koneoppimisen oppimistyylejä: ohjattu oppiminen, ohjaamaton oppiminen ja vahvistettu oppiminen. Luvussa käsitellään muuttujatyyppejä, aineiston esikäsittelyä ja validointia. Validointi kertoo, kuinka hyvin opetusdatalla opetettu malli toimii riippumattomilla aineistoilla. Luvun lopussa tutustutaan lyhyesti erilaisiin luokittelumenetelmiin.
Luvussa 4 tutustutaan neuroverkkojen rakenteeseen, toimintaan ja niiden taustalla olevaan matematiikkaan. Luvussa käsitellään eteenpäin syöttäviä neuroverkkoja ja niiden opettamista gradienttimenetelmällä.
Luvun 5 aiheena on prosessinlouhinta, simulointimallit ja tekoälytuettu päätöksenteko. Aihetta käsitellään sosiaali- ja terveydenhuollon kehittämisen näkökulmasta.
Luku 6 käsittelee tietokoneistettua kielenkäsittelyä. Siinä kerrotaan, mitä kaikkea tekstille tehdään ja mitä siitä voidaan saada selville tekstianalytiikan keinoin.
Luvussa 7 käsitellään tekoälyä ja kyberturvallisuutta. Aiheesta kerrotaan sekä yleisesti että esitellään useita tekoälyä hyödyntäviä kyberturvallisuusratkaisuja.
Luvussa 8 kerrotaan ensin Jyväskylän yliopistossa tehtävästä, tekoälyyn liittyvästä tutkimuksesta ja sitten lyhyesti Suomen muiden yliopistojen ja tutkimuslaitosten tekoälytutkimuksesta.
Luvussa 9 esitellään tekoälyn sovelluskohteita. Luvun alussa kerrotaan sovelluksista lyhyemmin terveydenhuollon, lääkehuollon, palvelurobotiikan ja rakennus- ja kiinteistöalan näkökulmasta, luvun loppuosa antaa laajan katsauksen sovelluksiin eri alueilla.
Luvussa 10 tarkastellaan Jyväskylän yliopiston IT-tiedekunnan kurssin Tekoälyn perusteita ja sovelluksia 2019 suorittaneiden vastauksia kurssin tehtäviin.
Luku 11 esittelee tekoälyn toimijoita Suomessa tutkimus- ja yritysmaailmassa.
Appendix A keskittyy luvussa 4 tarvittavaan matematiikkaan: analyysiin, ääriarvotehtäviin ja lineaarialgebran perusteisiin.
2. Peruskäsitteet ja termit
Tässä luvussa selitetään lyhyesti joitakin keskeisiä tekoälyyn liittyviä käsitteitä. Osaan niistä palataan muissa luvuissa syvällisemmin.
2.1 Tieteellinen laskenta
Tieteellinen laskenta/laskennallinen tiede (computational science/scientific computing) edustaa kolmatta tieteen paradigmaa. Siinä simuloidaan tietokoneen avulla reaalimaailman ilmiöitä tai tilanteita, joita reaalimaailmassa ei välttämättä vielä ole. Tieteellinen laskenta on leikkaus matematiikasta, tilastotieteestä, tietojenkäsittelytieteestä ja perustieteiden (fysiikka, kemia, biologia, taloustiede, yhteiskuntatiede, insinööritiede jne.) ydinalueista. Tämä yhdistelmä muodostaa uuden omanlaisen tutkimusalueensa joka poikkeaa osasistaan. Tieteellisen laskennan kattava tavoite saavuttaa täysin ennustettavia tieteellisiä malleja on sen ominaispiirre. Tähän tavoitteeseen pyritään kehityksellä, joka yhdistää mallintamisen, numeerisen analyysin, algoritmit, simulaatiomenetelmät, data-analytiikan, suurteholaskennan ja tieteellisten ohjelmistojen kehittämisen.
2.2 Big data - massadata
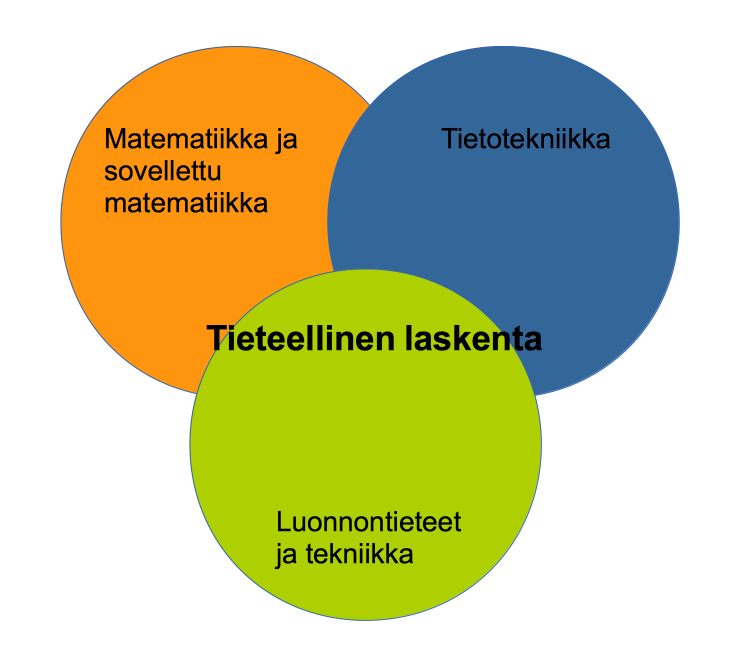
Big datalla (Big Data) tarkoitetaan massiivisten, jatkuvasti kasvavien, strukturoitua ja ei-strukturoitua tietoa, kuvia, äänitteitä ja videoita sisältävien tietojoukkojen keräämistä, säilyttämistä ja tiedon käyttämistä. Tällaisten datamäärien hallitseminen ja tiedon analysoiminen ovat perinteisillä tietokantatyökaluilla joko mahdotonta tai erittäin vaikeaa. Big datalle tyypillisiä tunnusmerkkejä ovat 5 V:tä:
- Määrä (volume) - luodun ja varastoidun datan määrä on niin suurta, että sitä on mahdotonta käsitellä perinteisin menetelmin.
- Valikoima (variety) – datan tyyppi, laatu ja alkuperä vaihtelee suuresti. Dataa tulee monista lähteistä, se koostuu erilaisista osista eikä ole jäsenneltyä.
- Nopeus (velocity) – datan tuottonopeus, analysointi ja käsittely on nopeaa.
- Arvo (value) – data ja siitä saatava tieto on yrityksille hyödyllistä.
- Todenmukaisuus (veracity) – datan laatu ja luotettavuus ovat tärkeitä asioita.
Massadataa syntyy nykyisin monesta lähteestä kuten internetsivujen ja sosiaalisen median käyttötiedoista, sää- ja navigointidatasta, terveydenhuollon tiedoista ja erilaisten laitteiden toimintatiedoista.
2.3 Tiedonlouhinta
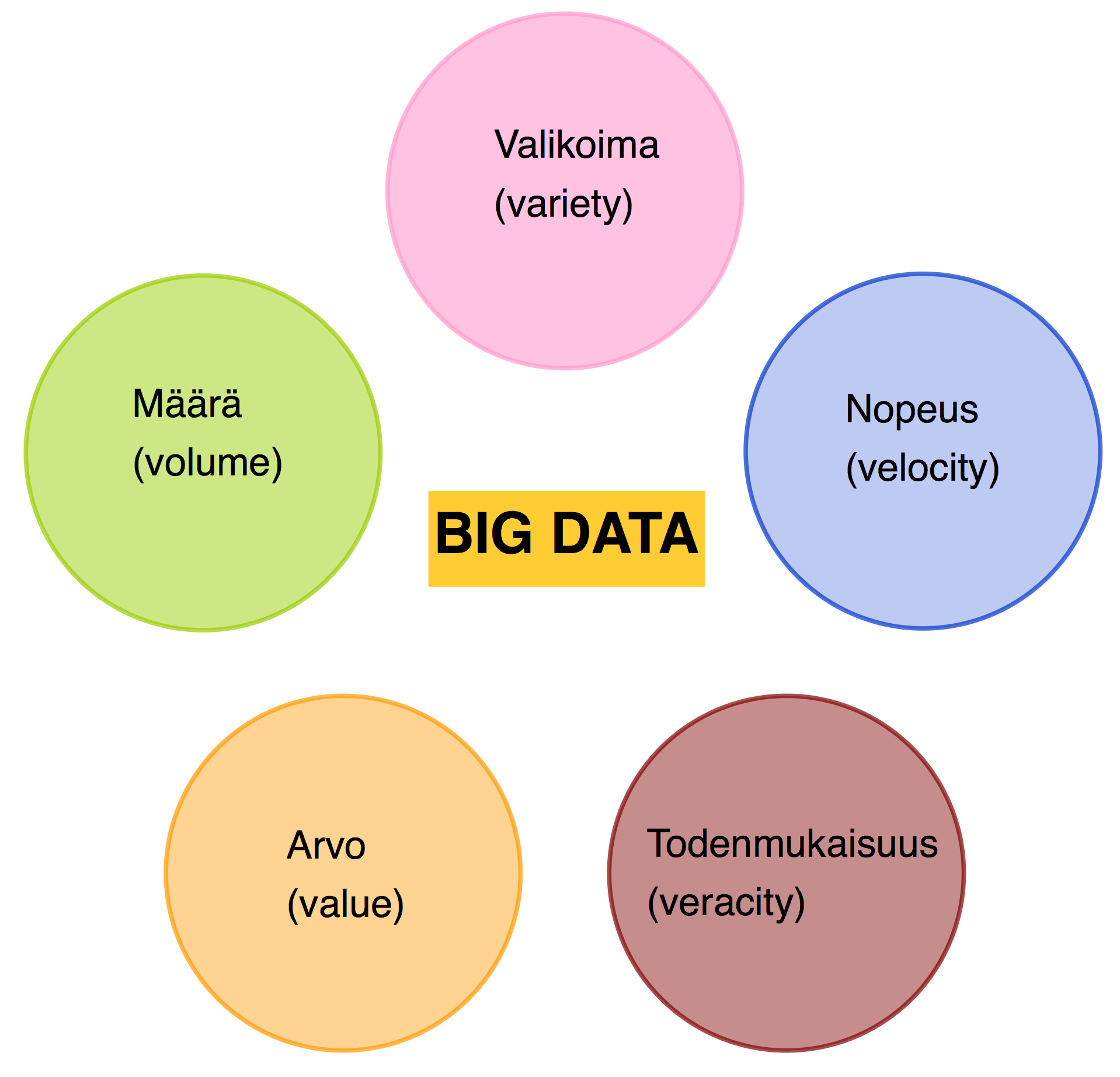
Tiedonlouhinta (data mining) tarkoittaa joukkoa menetelmiä, joilla pyritään oleellisen tiedon löytämiseen suurista tietomassoista. Toimintaan liittyy tietomassojen keräämistä, säilyttämistä, jakamista, etsimistä, analysointia sekä esittämistä tilastotiedettä, tietotekniikkaa ja koneoppimisen menetelmiä hyödyntäen.
2.4 Koneoppiminen
Koneoppiminen (machine learning) on tekoälyn osa-alue, jonka tarkoituksena on saada ohjelmisto toimimaan entistä paremmin pohjatiedon ja mahdollisen käyttäjän toiminnan perusteella. Koneoppimisessa kone oppii toistuvista tapahtumista ilman, että ihminen erikseen opettaa sitä. Koneoppimisella pyritään automatisoimaan tiedon tulkintaa ja laajentamaan koneen havainnointikykyä monimutkaisten algoritmien avulla perinteisen raja-arvoihin tukeutuvan mallin sijasta. Koneoppiminen voidaan jakaa kolmeen eri kategoriaan, ohjattuun oppimiseen, ohjaamattomaan oppimiseen ja vahvistettuun oppimiseen, joita käsitellään tarkemmin luvussa.
2.5 Neuroverkko
Neuroverkot (artificial neural network) ovat informaation käsittelyn, matematiikan tai laskennan malleja, jotka perustuvat yhdistävään laskentaan. Ihmisen aivojen toimintaa jäljittelevät keinotekoiset neuroverkot keksittiin jo 1940-luvulla. Neuroverkkojen uusi aalto alkoi 1990-luvulla mutta niiden käyttöinto hiipui nopeasti siihen, että ne eivät olleet muita menetelmiä parempia ja silloisilla tietokoneilla ei ollut mahdollisuutta käsitellä neuroverkkojen koulutuksessa tarvittavia suuria datamääriä. 2010-luvulla koneiden nopeutuminen ja datan määrän valtava kasvaminen ovat kasvattaneet innostusta syväoppimiseen.
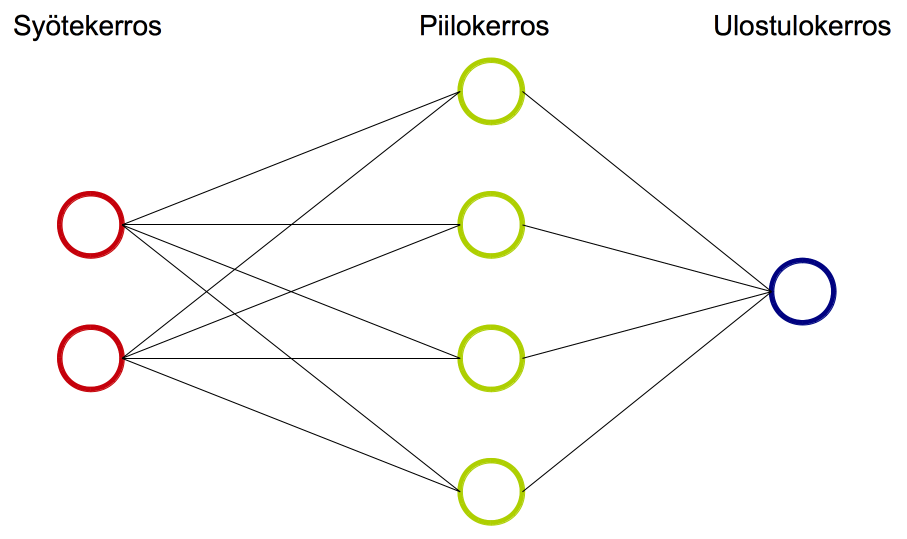
Neuroverkkoja käytetään esimerkiksi kuvantunnistuksessa, konenäössä, puheentunnistuksessa, kieltenkääntäjissä, peleissä ja lääketieteellisissä diagnooseissa. Neuroverkko koostuu syöte- ja ulostulokerroksesta ja niiden välissä olevista piilokerroksista, jotka koostuvat neuroneista. Neuroverkkoja käsitellään tarkemmin luvussa.
2.6 Tekoälyn matematiikka
Tekoälyn varhaiset versiot, joita voidaan käyttää esimerkiksi automaattiseen todistamiseen ja erilaisten loogisten ongelmien ratkaisemiseen, pohjautuvat logiikkaan. Monissa koneoppimisen menetelmissä tarvitaan todennäköisyyslaskennan ja graafien teoriaa.
Neuroverkkojen käsittelyssä tärkeitä matematiikan aloja ovat moniulotteinen analyysi, lineaarialgebra ja todennäköisyyslaskenta. Verkkoa opetettaessa yritetään minimoida virhefunktioita ja piilokerroksen painoja ja vakiotermejä muutetaan valitun algoritmin avulla. Virhefunktio riippuu suuresta määrästä parametreja, joten sen minimointi on haastava ongelma. Monesti minimoinnissa käytetään gradientteihin perustuvia menetelmiä, joissa tarvitaan virhefunktion derivaattoja verkon parametrien suhteen. Syöte ja verkon parametrit muutetaan verkon laskutoimituksissa yleensä vektori- ja matriisimuotoihin ja laskuissa käytetään lineaarialgebraa. Taustalla olevan matematiikan ymmärtäminen on tärkeää, sillä neuroverkoissa sopivien funktioiden, algoritmien ja minimointimenetelmien valinta vaikuttaa tulosten tarkkuuteen, verkon koulutusajan pituuteen, mallin monimutkaisuuteen sekä tarvittavien parametrien ja muiden komponenttien lukumäärään. Neuroverkkojen taustalla olevaa matematiikkaa käsitellään luvussa.
2.7 Syväoppiminen
Syväoppis-termi (deep learning) on saanut nimensä siitä, että neuroverkoissa käytetään monia piilokerroksia, joilla on kullakin oma tehtävänsä. Syvät neuroverkot ovat piirteenmuodostukseen kykeneviä monikerroksisia neuroverkkoja. Syväoppimisen haasteena on opettamiseen tarvittavan datan määrä. Koska syvissä neuroverkoissa voi olla miljoonia neuroneita ja siten miljoonia muutettavia parametreja, niin opetusdataa tarvitaan valtavasti. Jos dataa on liian vähän, niin verkot ylioppivat helposti eivätkä tulokset yleisty uusiin ennalta tuntemattomiin havaintoihin.
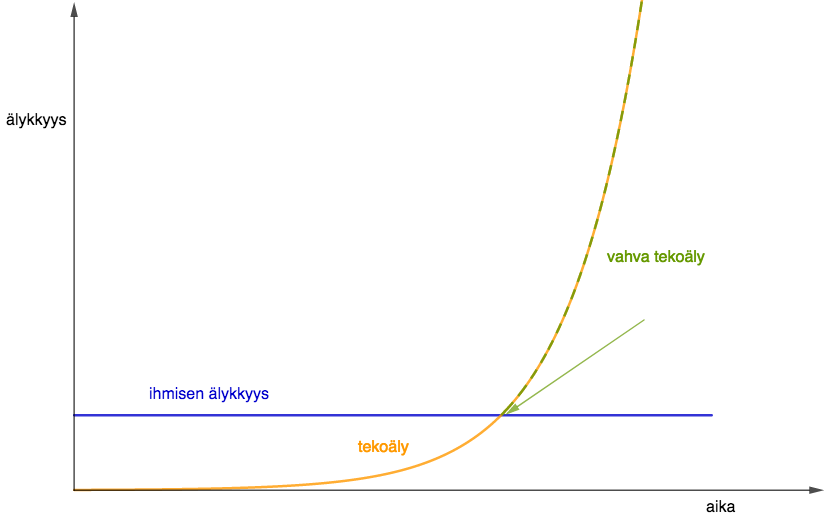
2.8 Vahva ja heikko tekoäly
Tekoäly voidaan jakaa heikkoon ja vahvaan tekoälyyn (artificial superintelligence). Heikolla tekoälyllä tarkoitetaan yksittäisissä tehtävissä taitaviin suorituksiin kykeneviä algoritmeja, kuten hakukoneita, roskapostisuodattimia tai vaikkapa robotti-imureita. Tässä kategoriassa pystytään tekemään jo paljon edistyneempiäkin toimintoja, kuten kasvojen- ja puheentunnistusta, hahmontunnistusta tai avustavaa tutkimustyötä. Vahvalla tekoälyllä puolestaan tarkoitetaan tulevaisuuteen ennustettavaa tekoälyä, joka tulee toimimaan täysin irrallaan ihmisälystä. Vahvaa tekoäly on tutkimuksen kohteena ja siihen liittyy voimakasta eettistä kritiikkiä.
2.9 Konenäkö
Konenäöllä (machine vision) pyritään yleensä matkimaan ihmisnäköä tai laajentamaan sen mahdollisuuksia. Konenäköjärjestelmä koostuu valonlähteestä, kohteesta, kamerasta, tietokoneesta ja siinä toimivassa kuvankäsittelyohjelmasta, joka tulkitsee kuvan automaattisesti.
Konenäön ja hahmontunnistuksen tavoitteena on hyödyllisten ja merkittävää lisäarvoa tuottavien sovellusten tuottaminen erityisesti digitaalista kuvankäsittelyä ja kuva-analyysiä hyödyntäen. Konenäkö on tarkka, nopea ja väsymätön rutiinitehtävien suorittaja, jolla voidaan parantaa prosessiteollisuuden tehokkuutta. Sitä käytetään esimerkiksi liukuhihnalla tapahtuvissa tuotetarkastuksissa ja pullonpalautusautomaateissa.
Termejä konenäkö ja tietokonenäkö (computer vision) käytetään monesti hieman ristiin. Jälkimmäisellä tarkoitetaan tietokoneiden korkeatasoista digitaalisten kuvien ja videoiden ymmärrystä. Se luokitellaan usein tekoälyn osaksi ja sitä käytetään esimerkiksi lääketieteellisissä kuva-analyyseissä.
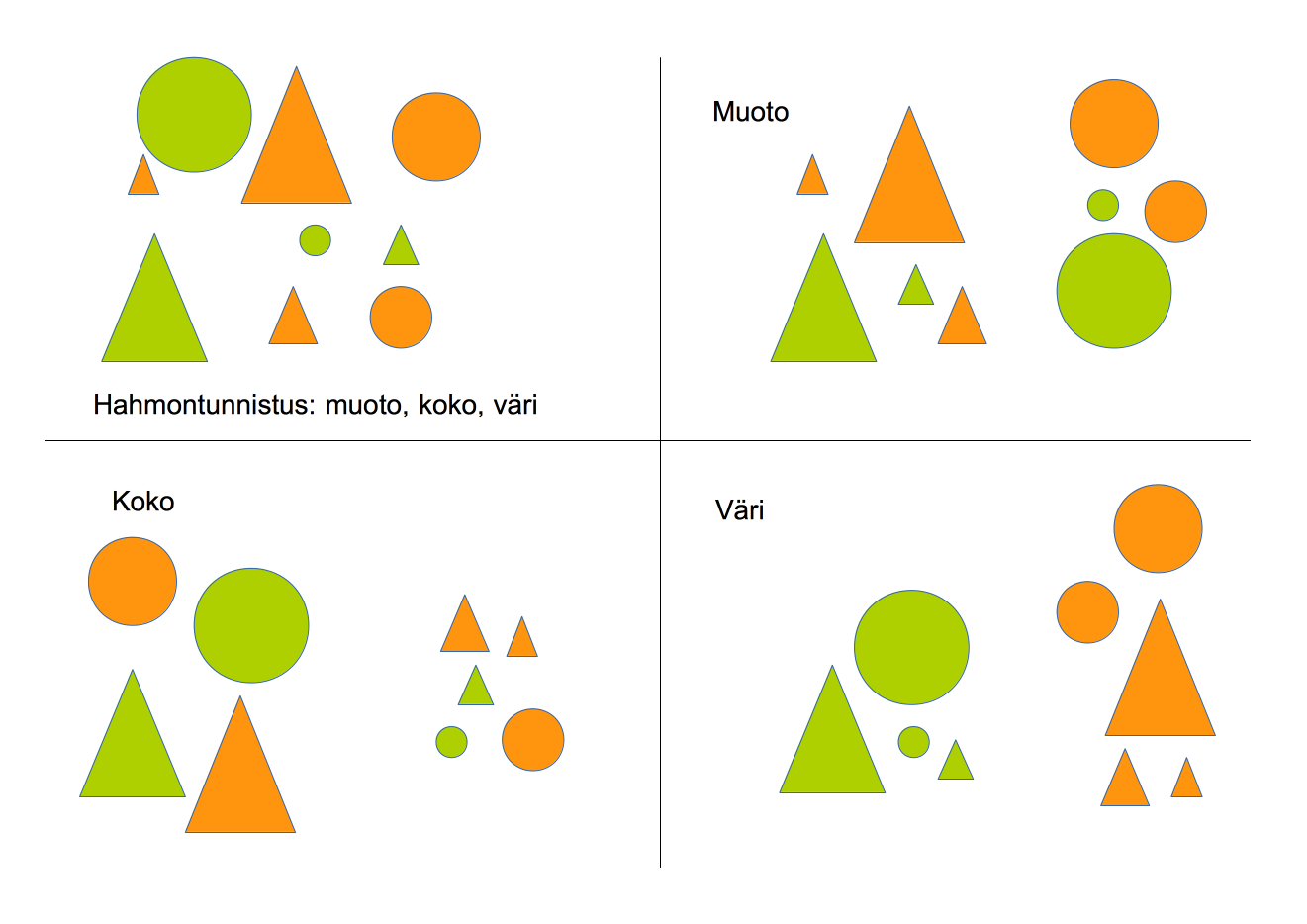
2.10 Hahmontunnistus
Hahmontunnistus (pattern recognition) on koneoppimisen osa-alue, jonka tavoitteena on kehittää datasta malleja tai kaavoja tunnistavia järjestelmiä. Käytännön esimerkkejä hahmontunnistuksen sovelluksista ovat esimerkiksi puheen automaattinen tallentaminen tekstiksi, kirjasta skannatun tekstin siirtäminen tekstinkäsittelyohjelmaan, ihmisten kasvojen tunnistaminen tai roskapostien tunnistaminen saapuneiden sähköpostien joukosta.
Hahmontunnistusmenetelmät voidaan jakaa kolmeen luokkaan: tilastollinen hahmontunnistus, syntaktinen hahmontunnistus ja neuraalinen hahmontunnistus. Näistä tilastollisessa hahmontunnistuksessa oletetaan, että etsittävällä hahmolla on tilastollinen jakauma kussakin luokassa, joihin kyseisen piirteen avulla halutaan luokitella. Syntaktinen hahmontunnistus olettaa vastaavasti, että on olemassa jokin rakenne, jonka perusteella luokittelu voidaan tehdä. Neuraalinen hahmontunnistus on epälineaarinen regressiomalli, joka osaa itsenäisesti kaivaa datasta olennaiset piirteet ja muodostaa näiden välille monimutkaisia riippuvuussuhteita.
2.11 Kuvantunnistus
Kuvantunnistuksella (image recognition) konenäön yhteydessä on kyky tunnistaa esineitä, paikkoja, ihmisiä, kirjoitusta ja toimintaa kuvissa. Kuvantunnistuksessa käytetään kameroita, konenäkötekniikoita ja koneoppimisen menetelmiä. Konvoluutioneuroverkkojen avulla onnistutaan nykyisin tekemään haastaviakin tunnistustehtäviä.

2.12 Puheentunnistus
Puheentunnistus (speech recognition) on joukko kieli- ja puheteknologian alaan kuuluvia hahmontunnistusmenetelmiä, joiden avulla tietokone voi tunnistaa ihmisten puhetta. Puheentunnistusmenetelmien avulla voidaan esimerkiksi valmistaa puheohjattavia laitteita tai taltioida puhetta tekstimuotoiseksi.
3. Luokittelu- ja ennustemenetelmät
(Esko Niinimäki, Ilkka Pölönen, Ilkka Rautiainen, Heli Tuominen, Sami Äyrämö)
Modernit tekoälysovellukset perustuvat pääosin datasta oppimiseen. Tosielämän tapausten mallintamiseen vaadittavan kokonaisvaltaisen informaation kerääminen voi olla äärimmäisen vaikeaa. Vaikka monimutkaisten matemaattisten tehtävien ratkaiseminen tietokoneen avulla on nopeuttanut maailman kehittymistä monin tavoin, ihmiselle intuitiivisen oloisten mutta vaikeasti formaalissa muodossa esitettävien tehtävien ratkominen on tekoälylle suuri haaste. Ollakseen älykäs ja vuorovaikutuskykyinen tietokoneen täytyy pystyä oppimaan asioita esimerkiksi kuvista, äänistä, teksteistä, sähkösignaaleista ja tapahtumasekvensseistä eli suurista matalan abstraktiotason tietomassoista. Menetelmien älykkyydestä ja oppimiskyvystä huolimatta varsinainen sovellusalakohtainen tieto on kuitenkin datassa. Tekoälylgoritmit eivät pysty lisäämään tai luomaan oppimaansa malliin sellaista tietoa, jota niiden opettamiseen käytettävä data ei sisällä. Tekoälyn laatu ja kattavuus on siis varsin pitkälle datasta riippuvaista. Toisaalta ilman data- ja koneoppimisalan ammattitaitoa suurten datamassojen valtava potentiaali on mahdotonta hyödyntää.
3.1 Koneoppiminen
Koneoppiminen (Machine learning) on tekoälyn osa-alue, jossa kone/ohjelma oppii pohjatiedon ja käyttäjän toiminnan perusteella tunnistamaan, luokittelemaan ja ennustamaan asioita. Kaikkia eri tilanteita varten ei ole erillistä ohjetta vaan oppiminen tapahtuu kokemuksen avulla.
Mitchell 1997: (A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E.)
Miten datasta oppiminen eroaa perinteisestä dataa selittävästä analytiikasta?
Tekoälytehtävät ovat pääasiassa tavalla tai toisella ennustustehtäviä. Selittävän mallintamisen (explanatory modeling) avulla pyritään ymmärtämään selittävien ja selitettävien muuttujien väliset riippuvuudet ja kausaliteetit. Ennustavassa mallintamisessa (predictive modeling) taas pyritään mahdollisimman tarkkaan ennustustulokseen syötteiden ja vasteiden välisten yhteyksien luonteen jäädessä useimmiten mustalaatikko -tyyppisen mallin taakse. Tämän vuoksi ennustavassa mallintamisessa, ja siten koneoppimiseen perustuvassa tekoälyssäkin, datasta opetettujen mallien validointi riippumattomilla aineistoilla on äärimmäisen tärkeää ennen niiden käytäntöön viemistä.
Koneoppiminen voidaan jakaa kolmeen luokkaan oppimisen tyylin perusteella.
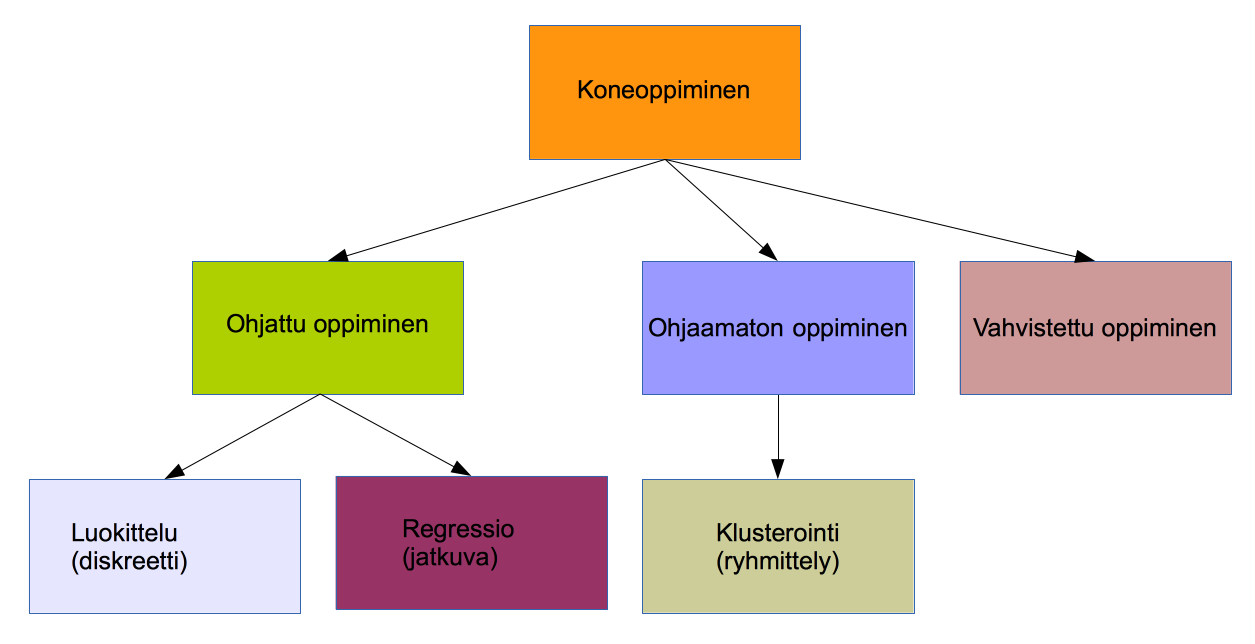
Ohjattu oppiminen
Ohjatussa oppimisessa (supervised learning) konetta opetetaan syöte-tavoite-pareista koostuvan aineiston avulla. Tavoitteena on, että kone osaa tehdä jaottelun samankaltaiselle aineistolle. Ohjattu oppiminen voidaan jakaa tavoitedatan luonteen perusteella kahteen luokkaan, luokitteluun ja regressioon. Jos data on diskreettiä eli se voidaan jakaa erillisiin ryhmiin, niin kyse on luokittelusta. Jos datan on jatkuvaa, niin jaottelu on regressiota. Esimerkkejä luokittelusta ovat käsinkirjoitettujen numeroiden tunnistus ja sähköpostin jaottelu roskapostiin ja tärkeään postiin. Regressiota ovat esimerkiksi lämpötilan tai jonkin tuotteen hinnan määrittäminen.
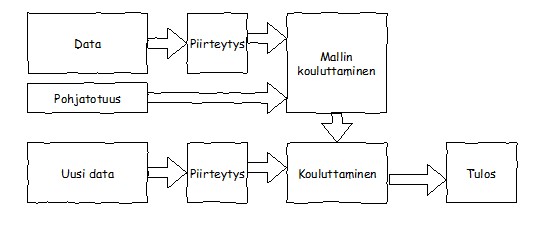
Ohjaamaton oppiminen
Ohjaamaton oppiminen (unsupervised learning) jäljittelee ihmisen oppimista. Opettamiseen käytettävästä datasta yritetään tunnistaa eri syötteiden välillä olevia riippuvuuksia, suhteita ja samankaltaisuuksia. Syötteet pyritään ryhmittelemään niin, että yksittäisellä syötteellä on enemmän samanlaisia ominaisuuksia samaan ryhmään kuuluvien syötteiden kuin muihin ryhmiin kuuluvien syötteiden kanssa. Esimerkki ohjaamattomasta oppimisesta on akateemikko Teuvo Kohosen (1934) 1980-luvulla kehittämä itseorganisoituva kartta.
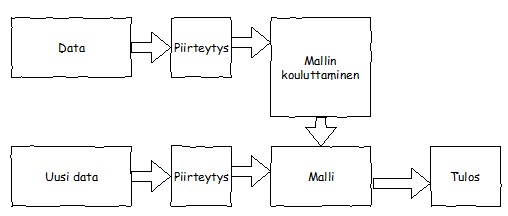
Vahvistettu oppiminen
Vahvistetussa oppimisessa (reinforcement learning) kone, "älykäs agentti", oppii ympäristön antaman palautteen perusteella. Kone saa toiminnastaan dynaamisessa ympäristössä positiivista ja negatiivista palautetta.
Se tekee valintoja aiemmin koettujen palkittujen vaihtoehtojen ja tuntemattomien vaihtoehtojen välillä ja oppii toimimaan niin, positiivisen palautteen määrä kasvaa ja negatiivisen vähenee. Vahvistetusta oppimisista käytetään esimerkiksi itseohjautuvissa autoissa ja robotiikassa.
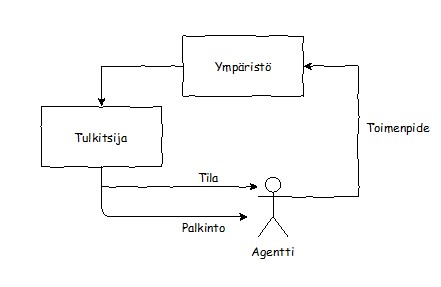
Kuhunkin oppimistyyliin sopivia algoritmeja on useita. Ratkaistavana olevaan ongelmaan sopivan algoritmin valinta riippuu oppimistyylin lisäksi esimerkiksi datan määrästä, koosta ja tyypistä, algoritmin oppimisnopeudesta, opetuksessa tarvittavasta tallennustilasta ja siitä, kuinka tehokasta tai yleistettävää ratkaisua ollaan etsimässä. Jos dataa on vähän, niin yksinkertaiset algoritmit vähentävät ylioppimisen riskiä. Paras algoritmi ei välttämättä löydy ensimmäisellä kokeilulla.
3.2 Muuttujatyypit
Aineiston käsittely edellyttää yleensä muuttujien tyyppien tunnistamista, sillä käsittelyssä sallitut toimenpiteet riippuvat muuttujan luonteesta. Muuttujat voidaan jakaa diskreetteihin ja jatkuviin.
Diskreetti muuttuja
Diskreetin muuttujan (discrete variable) arvot voidaan ilmaista joko tekstinä tai numeerisesti. Diskreetti muuttuja saa arvonsa jollain tavalla rajatusta joukosta. Muuttuja voi olla joko nominaalinen tai ordinaalinen. Nominaalisten arvojen välille ei voi muodostaa mielekästä järjestystä. Esimerkiksi paitatehtaalla voidaan määritellä paidalle mahdollinen väri joukosta {sininen, valkoinen, punainen, musta}. Ordinaalisen muuttujan arvot voidaan sen sijaan järjestää. Esimerkiksi joukko {välttävä, tyydyttävä, hyvä, kiitettävä, erinomainen} on järjestetty merkityksellisellä tavalla.
Jatkuva muuttuja
Jatkuva-arvoiset muuttujat (continuous variable) ilmaistaan tyypillisesti reaalilukuja käyttäen. Esimerkki jatkuva-arvoisesta muuttujasta on jokin automaattisen mittausvälineen tuottama lukema, vaikkapa lämpötila.
3.3 Aineiston esikäsittely
Aineiston esikäsittely (data preprocessing) sisältää kaikki ne toimet, joilla aineisto saatetaan valmiiksi analyysiä varten. Vaadittavat toimenpiteet riippuvat analysoitavasta aineistosta. Ensimmäisiä aineiston esikäsittelyn vaiheita ovat siivous ja yhdistäminen.
Siivous
Paljon käsinsyötettyä tietoa sisältävässä perinteisessä tietokannassa on hyvin todennäköisesti virheellisesti tai moneen kertaan syötettyä tietoa ja osa tiedosta on väistämättä puutteellista. Näitä puutteita ja virheitä korjaavia toimenpiteitä kutsutaan datan siivoukseksi (data cleaning) .
Yhdistäminen
Käsiteltävä aineisto voi myös olla jakautuneena useammassa eri lähteessä. Tällöin eri lähteissä olevat aineistot on yhdistettävä samassa muodossa olevaksi kokonaisuudeksi. Tätä toimenpidettä kutsutaan aineiston yhdistämiseksi (data integration).
Aineiston vähentäminen
Aineiston vähentämisellä tarkoitetaan niitä toimia, joilla analysoitavan aineiston määrää pyritään vähentämään analysoinnin nopeuttamiseksi ja selkeyttämiseksi. Vähentäminen pyritään tekemään niin, että mahdollisimman suuri osa alkuperäisen aineiston olennaisesta informaatiosta säilyy. Aineiston vähentämisen menetelmiä ovat ominaisuuksien valinta, piirreirrotus sekä näytteenotto.
Ominaisuuksien valinta
Ominaisuuksien valinnan (feature selection) aikana karsitaan datajoukosta varsinaisen analyysin kannalta epäolennaiset ja toisteiset ominaisuudet. Samalla aineiston ymmärrettävyys ja esitettävyys yleensä paranee tiedon karsimisen ansiosta. Ominaisuuksien valinta voi olla joko kiinteänä osana ennustamistehtävän suorittavaa algoritmia tai se voidaan suorittaa erillisenä tehtävänä.
Piirreirrotus
Piirreirrotuksessa (feature extraction) pyritään kuvaamaan alkuperäinen muuttujajoukko pienemmällä määrällä ulottuvuuksia. Eräs käytetyimmistä piirreirrotuksen menetelmistä on pääkomponenttianalyysi (principal component analysis). Pääkomponenttianalyysi luo kokonaan uuden joukon muuttujia, joihin se pyrkii projisoimaan alkuperäisen aineiston olennaiset ominaisuudet. Uusi muuttujajoukko on yleensä alkuperäistä aineistoa pienempi.
Näytteenotto
Näytteenotto (sampling) on datan vähentämisen menetelmä, jolla aineistosta valitaan osajoukko analyysiä varten.
Aineiston muunnokset
Aineiston muunnoksilla muuttujat valmistellaan sopivaan muotoon analyysiä varten. Muunnosten menetelmiä ovat normalisointi, diskretisointi sekä ominaisuuksien luonti.
Normalisointi
Normalisoinnilla (normalisation) skaalataan eri muuttujien arvot keskenään vertailukelpoiselle vaihteluvälille.
Diskretisointi
Diskretisoinnilla (discretisation) muunnetaan jatkuvat muuttujien arvot diskreeteiksi. Muunnosta voidaan tarvita eri syistä, esimerkiksi siksi, että monet luokitteluun perustuvat ennustusmenetelmät osaavat hyödyntää ainoastaan diskreettejä muuttujia. Muunnoksessa aineisto saadaan myös usein helpommin esitettävään ja ymmärrettävään muotoon.
Ominaisuuksien luonti
Ominaisuuksien luonnissa (feature construction/feature generation) aineistoon luodaan kokonaan uusia ominaisuuksia käyttämällä hyväksi aineistossa jo olemassa olevia muuttujia.
3.4 Validointi
Validoinnin eli vahvistamisen (validation) perusajatuksena on selvittää, kuinka hyvin opetusaineiston pohjalta muodostettu malli toimii aineistolla, jota malli ei ole ennen nähnyt. Validointi- eli vahvistusaineistolla tarkoitetaan opetusaineistosta irrotettua osajoukkoa, jota ei käytetä mallin opetusvaiheessa. Aineistosta voidaan myös alussa jättää kokonaan sivuun osajoukko, johon ei kosketa ennen mallin lopullista arviointia. Tällaista aineistoa kutsutaan testiaineistoksi (test examples).
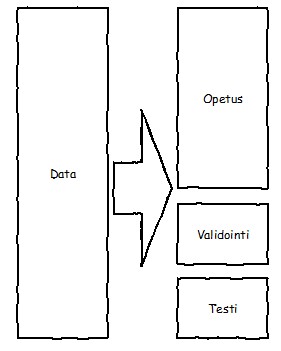
Yleisiä validointimenetelmiä ovat
Holdout
Holdout-validoinnissa datajoukko jaetaan kahteen osaan. Tyypillisesti opetusaineistona voidaan käyttää esimerkiksi kahta kolmasosaa aineistosta ja validointiaineistona loppuaineistoa.
k-kertainen ristiinvalidointi
-kertaisesssa ristiinvalidoinnissa (
-fold cross-validation) aineisto jaetaan
:hon likimain yhtä suureen osaan. Yhtä näistä osista käytetään validointiaineistona ja loppuja opetusaineistona. Validointi suoritetaan
kertaa ja jokaista osaa käytetään vuorollaan kerran validointiaineistona. Lopuksi mallin toimivuutta voidaan arvioida laskemalla kaikkien validointikertojen keskiarvo.
Leave-one-out-ristiinvalidointi
Leave-one-out-ristiinvalidointi (Leave-one-out) on -fold-ristiinvalidoinnin erikoistapaus, jossa
:n arvoksi määritellään opetusaineiston havaintojen lukumäärä. Tällöin jokainen havainto muodostaa oman joukkonsa ja jokaista havaintoa käytetään vuorollaan validointiaineistona.
3.5 Luokittelumenetelmiä
Ohjatun oppimisen luokittelu voi olla binääristä luokittelua tai luokittelua useampaan luokkaan. Binäärisessä luokittelussa (binary classification) mahdollisia luokkia, joihin yksittäinen datan alkio voi kuulua, on kaksi. Esimerkiksi sähköposti on roskapostia tai oikeaa postia ja vain kissojen ja koirien kuvia sisältävässä joukossa jokainen kuva on joko kissan tai koiran kuva, ei molempia. Jotkut algoritmit, kuten logistinen regressio, on suunniteltu erityisesti binääriseen luokitteluun ja ne ovat tehtävässään tehokkaita. Useampaan luokkaan luokittelu vaatii monimutkaisemman algoritmin. Seuraavassa on esitelty lyhyesti yleisiä selittävään ja ennustavaan mallintamiseen kuuluvia algoritmeja.
Logistinen regressio
Logistinen regressio (Logistic regression) sopii binääriseen luokitteluun. Malli kertoo, millä todennäköisyydellä datapiste kuuluu ongelmassa oleviin luokkiin. Se sopiii parhaiten tilanteisiin, jossa data voidaan erottaa lineaarisesti (suoralla, hypertasolla).
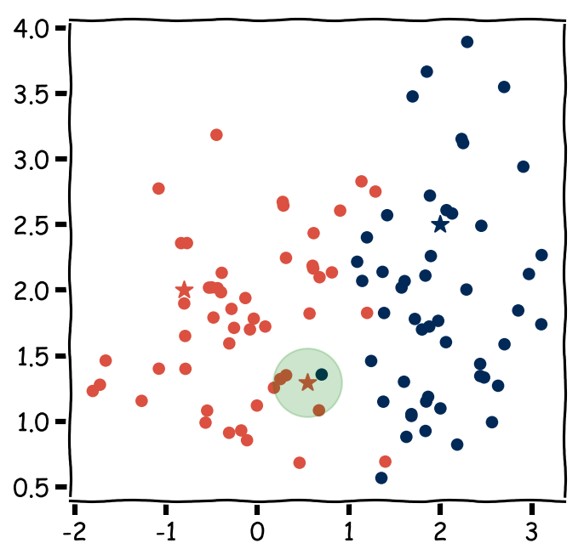
k:n lähimmän naapurin menetelmä
:n lähimmän naapurin menetelmässä (
-Nearest Neighbor,
NN) datapisteet (opetusesimerkit) ovat pisteitä
-ulotteisessa avaruudessa. Jokaiselle datapisteelle etsitään euklidisen (tai muun) etäisyyden mielessä
lähintä pistettä ja datapiste luokitellaan naapureiden luokkien avulla käyttäen esimerkiksi keskiarvoa regression ja moodia luokittelun tapauksessa. Koko data on kerralla muistissa.
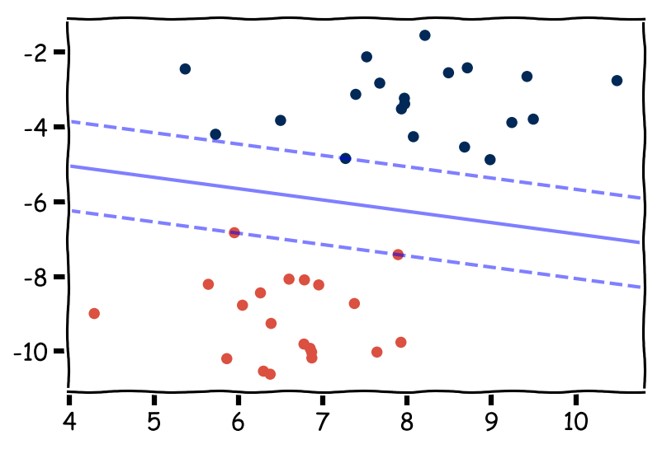
Tukivektorikone
Tukivektorikoneen (Support vector machine) perusversiota käytetään binääriseen luokitteluun. Se luokittelee dataa etsimällä lineaarista päätöspintaa (hypertasoa), joka erottaa kahteen eri luokkaan kuuluvat datapisteet toisistaan. Jos data on lineaarisesti erotettava, niin paras erotteleva hypertaso on se, joka erottelee luokat toisistaan suurimmalla marginaalilla. Jos data ei ole lineaarisesti erotettava, niin väärällä puolella hypertasoa oleville pisteille käytetään virhefunktiota.
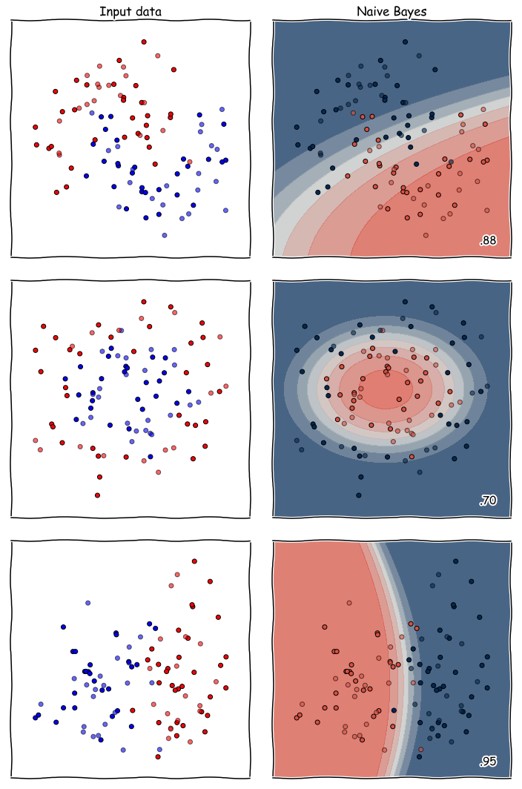
Naiivi Bayes-luokittelija
Naiivi Bayes-luokittelija (naive Bayes classifier) on yksinkertainen luokittelija, joka käsittelee alkioiden ominaisuuksia toisistaan riippumattomina. Luokittelu tehdään todennäköisyyksien avulla ja siinä käytetään ehdolliseen todennäköisyyteen liittyvää Bayesin kaavaa. Se on helppo toteuttaa ja hyvä menetelmä pienehkölle datalle, jossa on useita parametreja.
Klassinen esimerkki naiivista Bayes-luokittelijasta on roskapostisuodatin, joka tutkii sähköposteissa esiintyviä sanoja. Suodattaminen opettamisen jälkeen luokittelija kertoo, millä todennäköisyydellä tietyt sanat sisältävä viesti on roskaa.
Diskriminanttianalyysi
Diskriminattianalyysi (discriminant analysis) luokittelee dataa etsimällä sellaisia ominaisuuksien lineaarikombinaatioita, jotka joko karakterisoivat tai erottavat eri luokkiin kuuluvia datapisteitä. Diskriminantianalyysissä oletetaan, että eri luokat noudattavat normaalijakaumaa. Opetettaessa etsitään normaalijakauman parametreja eri luokille ja niiden avulla etsitään luokkia erottavat lineaariset tai kvadraattiset funktiot.
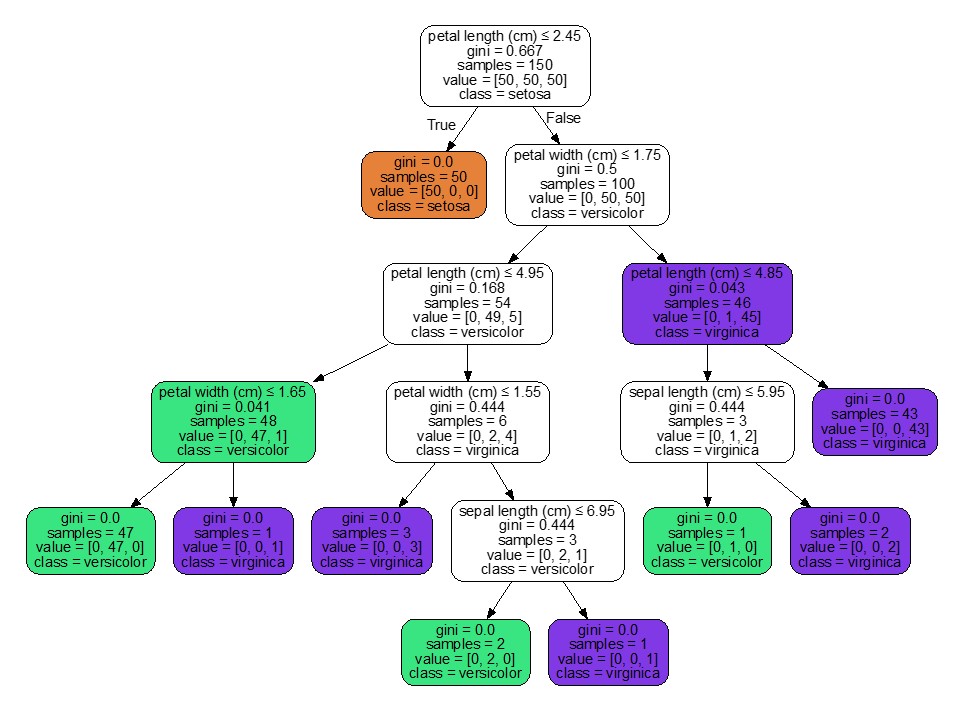
Päätöspuu
Päätöspuu (decision tree) on helposti toteutettava ja vähän muistia käyttävä luokittelualgoritmi. Luokittelu tehdään valitsemalla luokiteltavan data-alkion ominaisuuksien perusteella binääripuun solmuissa vasen tai oikea haara. Datapiste viedään ensin juurisolmuun, josta se lopulta päätyy lehteen, joka kertoo luokan.
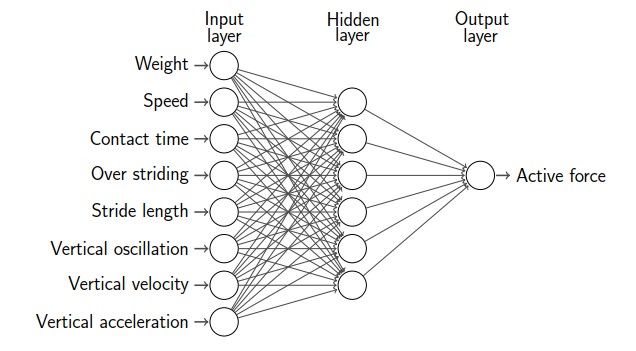
Neuroverkko
Neuroverkkoja (neural network) eli ihmisen aivojen toimintaa jäljitteleviä oppivia verkkoja käsitellään seuraavissa luvuissa tarkemmin.
Lisätietoa koneoppimisesta
- T.Kohonen: MATLAB Implementations and Applications of the Self-Organizing Map
- R.S. Sutton ja A.G. Barto: Reinforcement Learning, An Introduction
- Y. Zhang: New Advances in Machine Learning
- H. Daumé: A Course in Machine Learning (University on Maryland)
- Machine Learning Mastery: Your First Machine Learning Project in Python Step-By-Step
- Machine Learning Mastery: Machine Learning Algorithms
- Machine Learning Mastery: How To Implement The Decision Tree Algorithm From Scratch In Python
- A Complete Tutorial on Tree Based Modeling from Scratch in R and Python
- Decision Trees (Scikit learn)
- Python and Machine Learning
4. Neuroverkkojen matemaattiset perusteet
(Heli Tuominen)
Tässä luvussa tutustutaan neuroverkkojen rakenteeseen, toimintaan ja matemaattisiin perusteisiin. Modernien tekoälysovellusten taustalla on monenlaisia neuroverkkoja, esimerkiksi kuvantunnistukseen hyvin soveltuvia konvoluutioneuroverkkoja. Yksinkertaisuuden vuoksi tässä luvussa käsitellään vain eteenpäinsyöttäviä "tavallisia" neuroverkkoja.
4.1 Keinotekoiset neuroverkot
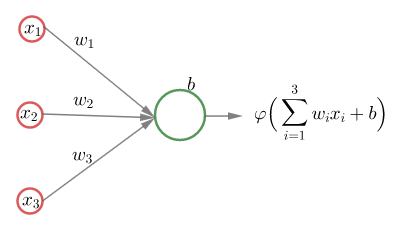
Keinotekoinen neuroverkko (Artificial neural network) jäljittelee ihmisen aivoja. Neuroverkko koostuu syöte- ja ulostulokerroksesta (input layer, output layer) ja niiden välissä olevista piilokerroksista (hidden layer). Kerrokset puolestaan rakentuvat neuroneista (neuron), joihin liittyy verkon opetuksessa muutettavia parametreja.
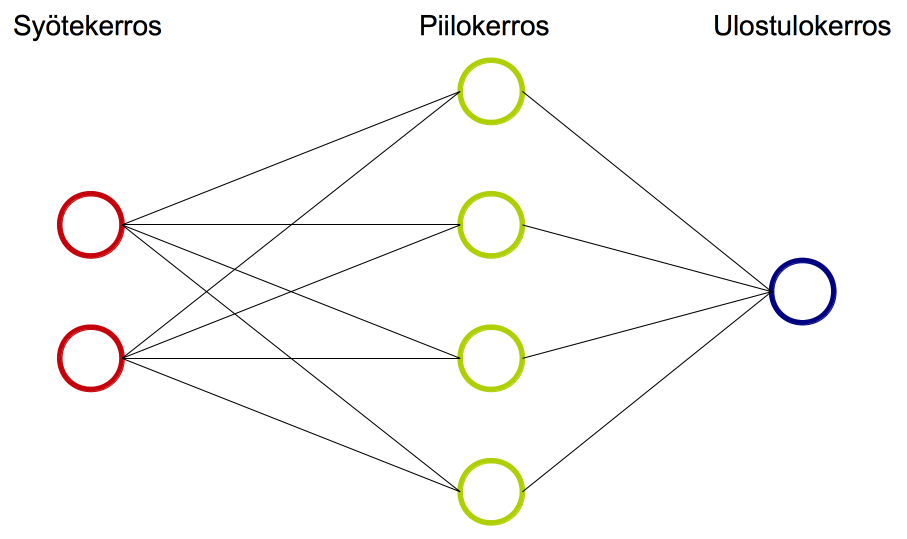
Data annetaan neuroverkon käsiteltäväksi syötekerroksessa. Syötekerroksen neuroneiden määrä riippuu esimerkiksi siitä, montaako ominaisuutta syötteestä tutkitaan. Piilokerroksien ja ulostulokerroksen kaikissa neuronissa lasketaan syötekerroksesta tai piilokerroksesta tulleiden syötteiden painotettu summa ja siihen lisätään neuronin vakiotermi. Ennen neuronin tuloksen lähettämistä seuraavalle neuronille summa viedään aktivointifunktioon, joka muuttaa lineaarisen (affiinin eli ensimmäisen asteen polynomin) syötteen epälineaariseksi.
Usean piilokerroksen neuroverkkoja sanotaan syviksi neuroverkoiksi (deep neural network).
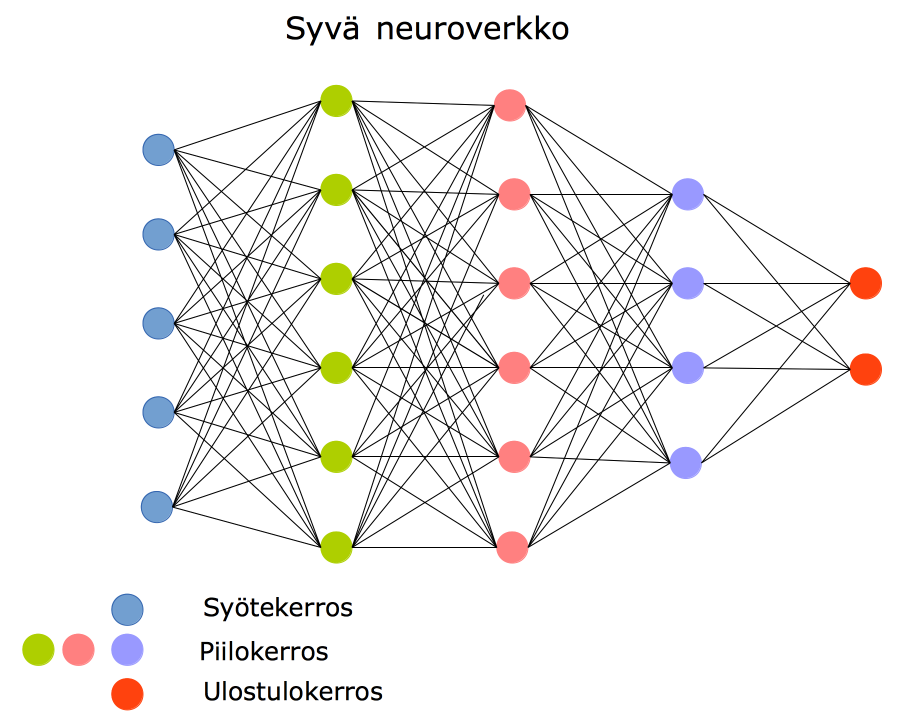
Neuroverkon toimintaan liittyviä kaavoja tarkastellaan ensin esimerkin avulla ja sitten yleisemmin luvussa.
Esimerkki
Verkossa on yksi piilokerros, jossa on neljä neuronia. Syöte on vektori . Ulostulokerroksessa on yksi neuroni, jolta saadaan syötettä
vastaava tulos
.
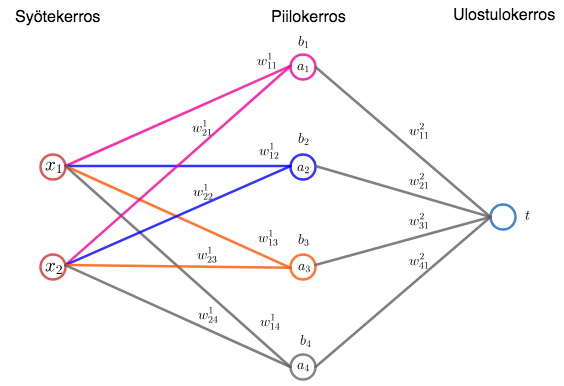
Syötevektorin komponentit kerrotaan piilokerroksen neuroneiden painoilla , tulot lasketaan yhteen ja summaan lisätään piilokerroksen neuronin
vakiotermi
:
Nämä summat viedään piilokerroksen aktivointifunktiolle, jolloin piilokerroksen neuronien antamat syötteet ulostulokerrokselle ovat
Verkon antama tulos saadaan käyttämällä piilokerroksen ja ulostulokerroksen välisiä painoja ja aktivointifunktiota:
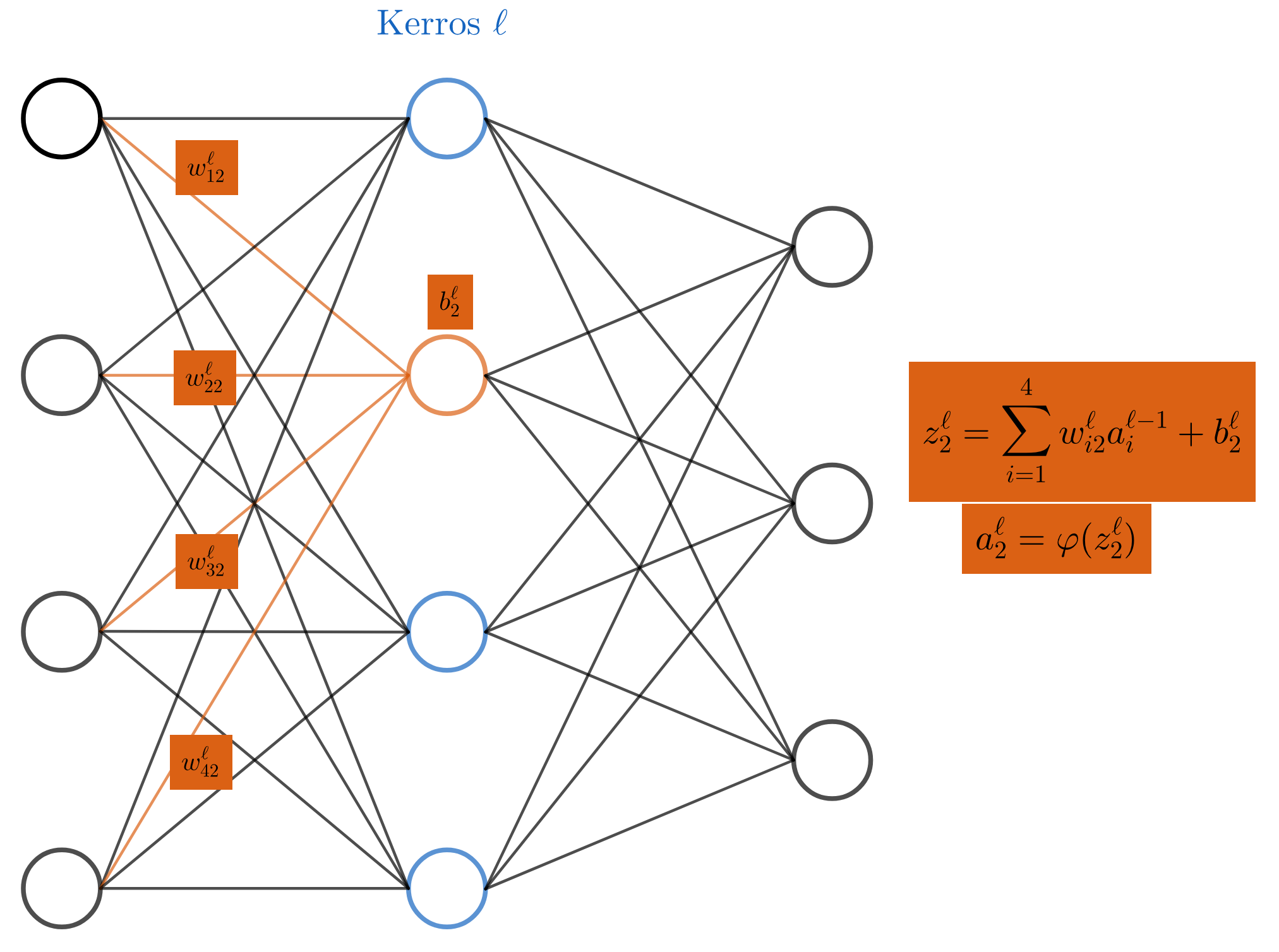
4.1.1 Neuroverkkoihin liittyviä käsitteitä ja merkintöjä
Neuroni
Neuroverkon kerrokset koostuvat neuroneista (neuron). Jokaiseen piilokerrosten ja ulostulokerroksen neuroniin liittyy kahdenlaisia parametreja, neuroneiden välillä olevat painot (weight) ja neuronikohtainen kynnysarvon/vakiotermi (bias).
Parametreistä käytetään seuraavia merkintöjä. Kerrosindeksiä merkitään kirjaimella . Indeksi
viittaa syötekerrokseen ja indeksi
ulostulokerrokseen.
kerroksen
neuronien lukumäärä,
syötteen
komponentit (
kappaletta),
kerroksen
neuronin
ja kerroksen
neuronin
välillä oleva paino,
kerroksen
neuronin
vakiotermi,
kerroksen
neuronia
vastaava painotettu summa
kerroksen
neuronin
tulos eli syöte seuraavaan kerrokseen
missä
on aktivointifunktio (joka voi vaihdella kerroksesta toiseen).
Huomaa, että kaikilla
.
Kaavat vektorimuodossa
Merkintöjen yksinkertaistamiseksi neuroverkon kaavat kirjoitetaan monesti vektori- ja matriisimuodossa.
Kerroksen kynnysarvoja/vakiotermejä vastaa vektori
kerroksen
neuronien painotettuja summia vektori
ja kerroksen
neuronien tuloksia vektori
Kerroksen
painoja vastaa
-matriisi
Painotettujen summien ja neuronien tuloksien vektorit saadaan esitettyä lyhyesti muodossa
Huomaa, että jos edellä vektorit ,
ja
määriteltäisiin pystyvektoreina, niin olisi
Joissain lähteissä painojen
neuroni-indeksit
ja
ovat päinvastaisessa järjestyksessä. Tällöin vastaava matriisi
on
-matriisi ja
missä
on vektorin
transpoosi.
Matriisien ja vektoreiden ominaisuuksia kerrataan liitteessä Appendix A.
Neuroni ja neuroverkko funktioina
Neuroverkkoa voi ajatella funktiona ; syöte on
-ulotteinen vektori
, piilokerrokset hoitavat laskutehtävän ja funktion arvo
saadaan ulostulokerroksesta. Verkon käyttötarkoitus määrää, miten funktion arvo
tulkitaan.
Piilokerroksen neuronit voidaan tulkita funktioiksi ,
, missä
on yleensä edellisen kerroksen painotettu summa lisättynä vakiotermillä eli
ja
on kerroksen
aktivointifunktio. Ulostulokerroksen funktioille
arvojoukko on
.
4.1.2 Harjoitus
Tarkastellaan neuroverkkoa, jonka syöte on , jossa on yksi neljän neuronin piilokerros, jonka ulostulokerroksessa on kaksi neuronia ja jonka aktivointifunktio sekä piilo- että ulostulokerroksessa on
. (Kuvassa vain osa painoista merkitty.)
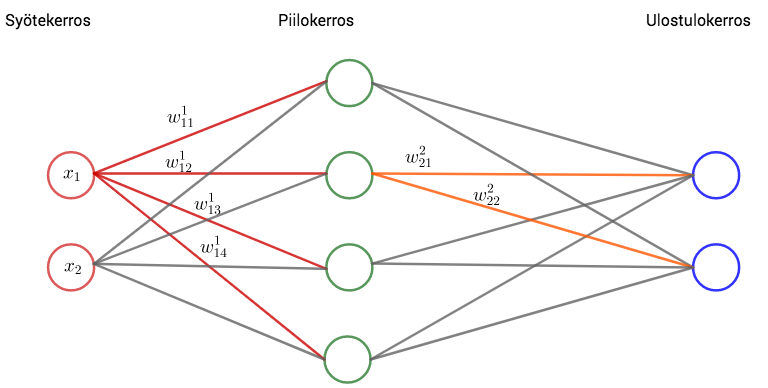
Kirjoita verkkoon liittyvät neuronien painotetut summat ja neuronien tulokset
vektoreiden ja painomatriisien avulla.
4.1.3 Perseptroni
Perseptroni (perceptron) on syötekerroksen ja yhden neuronin muodostama minimaalinen neuroverkko, jonka syöte on ja tulos on
.
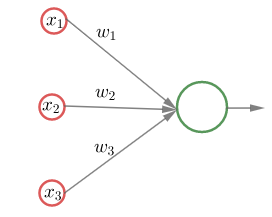
Perseptonia, jonka painojen muodostama vektori on , vakiotermi on
ja aktivointifunktio on yksikköporrasfunktio (Heavisiden funktio)
,
vastaa funktio
,
missä
on vektoreiden
ja
sisätulo.
Kysymykseen, millaiset funktiot voidaan esittää perseptronilla, on yksinkertainen vastaus nollan ja ykkösen alkukuvien lineaarisen erotettavuuden avulla.
Joukot ja
ovat lineaarisesti erotettavat (linearly separable), jos on vakiot
ja
, joille
ja
Tasossa tämä tarkoittaa sitä, että joukkoja
ja
vastaavat pisteet voidaan erottaa suoralla ja
:ssa sitä, että pistejoukot voidaan erottaa tasolla.
Lause
Funktio voidaan esittää perseptronilla jos ja vain jos alkukuvat
ja
ovat lineaarisesti erotettavat.
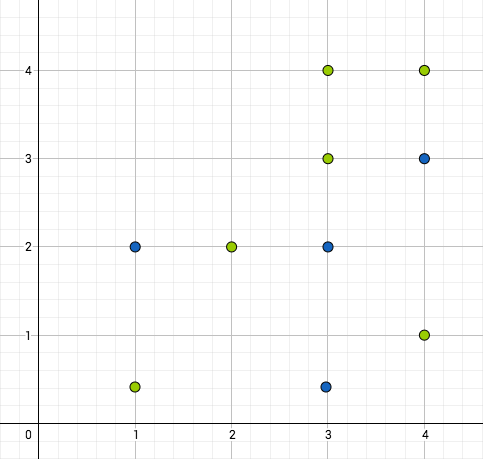
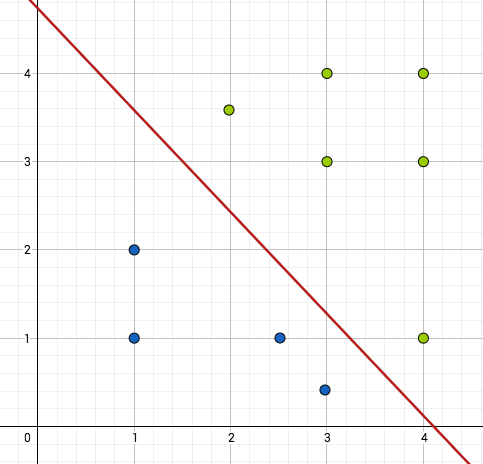
Esimerkki
Ensimmäisen kuvan pistejoukko ei ole lineaarisesti erotettava, toisen kuvan on.
Funktio, jonka arvot vihreitä palloja vastaavissa tason pisteissä on ja sinisiä palloja vastaavissa pisteissä on
, voidaan siis toisessa tapauksessa esittää perseptronilla, ensimmäisessä ei.
Esimerkki
Looginen konnektiivi AND (JA) voidaan esittää yhdellä perseptronilla mutta konnektiivia XOR (poissulkeva TAI) ei voi. Konnektiiveja vastaavat funktiot ovat ja
ja
Nollan ja ykkösen alkukuvat ovat siis
ja
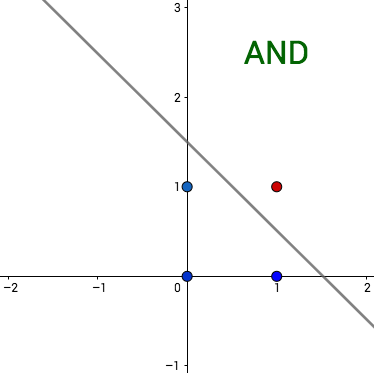
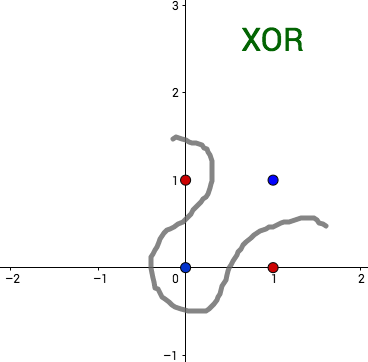
Edellisen esimerkin looginen konnektiivi AND seuraavan kuvan perseptronilla.
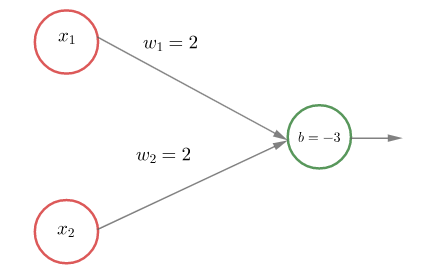
Muuttamalla painoiksi ja vakiotermiksi
, saadaan AND-konnektiivin negaatio, NAND, jonka arvo parille
on
ja muille lukupareille
. NAND konnektiivin esityksen olemassaolosta seuraa, että perseptronien avulla voidaan rakentaa verkko, joka tekee minkä tahansa halutun loogisen päättelyn.
Perseptronin ongelma on se, että pienet muutokset painoissa tai syötteissä aiheuttavat ison muutoksen tuloksessa . Tämä on huono asia verkon opettamisen kannalta. Perseptronin yksikköporrasfunktion sijaan käytetäänkin yleensä verkon opettamiseen paremmin soveltuvia aktivointifunktioita.
4.1.4 Harjoitus
Loogista konnektiivia OR (TAI) vastaava funktio on
,
- Määritä alkukuvat
ja
.
- Voidaanko OR esittää perseptronilla? Jos voidaan, niin etsi kertoimet
ja
ja perseptronin vakiotermi
.
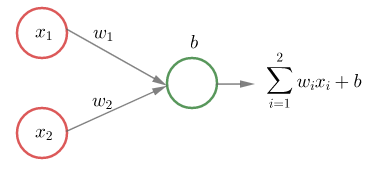
4.1.5 Aktivointifunktiot
Neuroverkon piilo- ja ulostulokerroksissa käytetään aktivointifunktioita (activation function).
Ennen neuronin tuloksen lähettämistä seuraavalle neuronille tai ulostulokerroksesta ulos, edellisen kerroksen syötteistä laskettu painotettu summa viedään aktivointifunktioon . Aktivointifunktiot muuttavat lineaarisen (affiinin eli ensimmäisen asteen polynomin) syötteen epälineaariseksi ja niillä olisi toivottavaa olla seuraavia ominaisuuksia:
- epälineaarisuus: Koska summa ja yhdistetty funktio lineaarisista funktioista on lineaarinen ja affiineista affiini ja neuroneiden summalausekkeet
ovat affiineja, niin lineaarisilla (tai affiineilla) aktivointifunktioilla saadaan affiini kuvaus.
- (jatkuvasti) derivoituvuus: Vastavirta-algoritmissa ja muissa virhefunktion minimointitavoissa tarvitaan aktivointivointifunktion derivaattaa. Jos aktivointifunktio ei ole derivoituva, niin virhefunktion minimoinnissa pitää käyttää muita kuin gradienttiin perustuvia keinoja.
- identtisen funktion approksimointi: Jos aktivointifunktio on nollan lähellä lähellä identtistä funktiota
,
kaikilla
, niin neuroverkko oppii tehokkaasti kun painot alustetaan satunnaisluvuilla. Muussa tapauksessa painot pitää alustaa huolellisesti.
Se, onko aktivointifunktio rajoitettu vai ei, vaikuttaa verkon oppimisnopeuteen ja oppimisen vakauteen. Rajoitetuilla aktivointifunktioilla oppiminen on yleensä vakaata ja rajoittamattomilla monesti tehokasta. Rajoittamattomia aktivointifunktioita käytettäessä kannattaa käyttää pieniä oppimisnopeuksia.
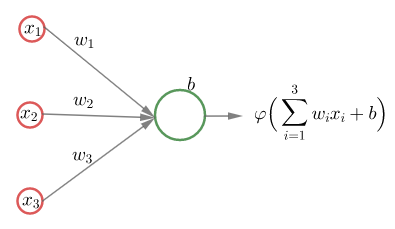
Esimerkkejä aktivointifunktioista ovat sigmoid-funktio, hyperbolinen tangentti ja ReLu-funktio. Tutustutaan näihin lyhyesti.
Sigmoid-funktio (logistinen funktio)
Sigmoid-funktiolla ,
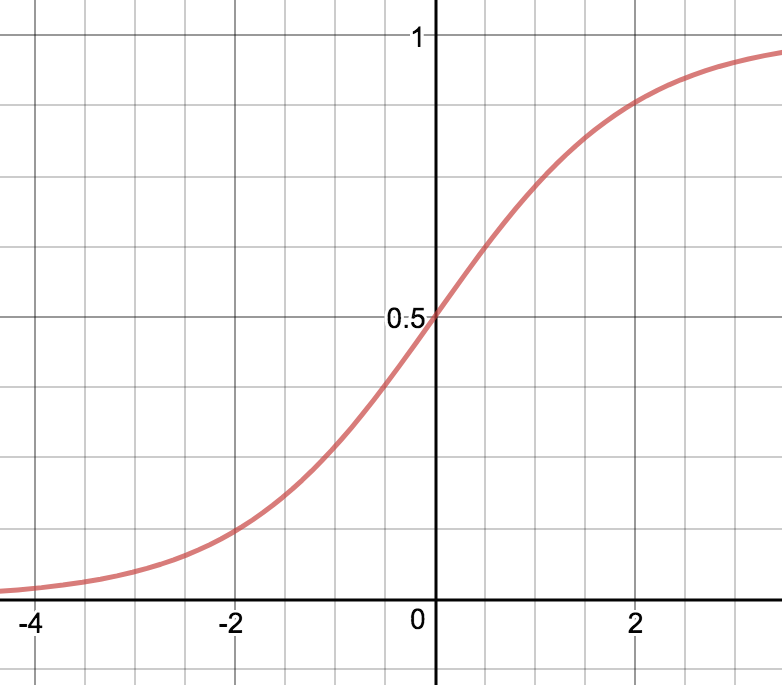
on seuraavat ominaisuudet:
- rajoitettu, aidosti kasvava ja jatkuva
,
eli funktiolla
on kaikkien kertalukujen jatkuvat derivaatat ja
Sigmoid-funktio on yksikköporrasfunktion
,
silotettu versio. Sigmoid-funktion huonoin ominaisuus johtuu siitä, että se kasvaa hyvin hitaasti kun
kasvaa ja vähenee hyvin hitaasti kun
vähenee. Sen derivaatta on hyvin lähellä nollaa kun
on suuri tai pieni. Tästä seuraa ongelmia silloin kun verkkoa opetetaan derivaattoihin perustuvilla menetelmillä.
Vastavirta-algoritmin kaavoista nähdään, että virhefunktion osittaisderivaatat neuronin painojen ja vakiotermien suhteen riippuvat aktivointifunktion derivaatasta ja että painojen ja vakioiden muutoksen koulutettaessa ovat pieniä jos osittaisderivaatat ovat pieniä. Tällöin verkko oppii hitaasti.
Toinen sigmoid-funktion huono puoli on se, että se ei ole symmetrinen nollan suhteen. Nykyisin sitä käytetään lähinnä ulostulokerroksessa varsinkin jos verkon tulokset ovat välillä .
Hyperbolinen tangentti (tanh)
Hyperbolisella tangenttilla ,
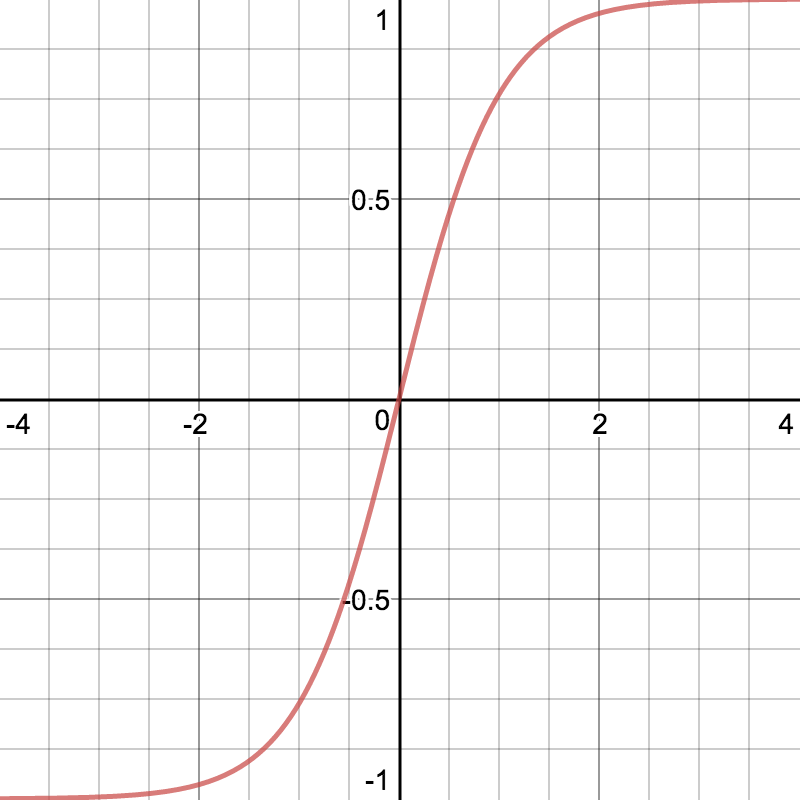
on monia samoja ominaisuuksia kuin sigmoid-funktiolla mutta se on symmetrinen nollan suhteen ja se kasvaa nopeammin nollan lähellä, jolloin sen derivaatta on suurempi.
Hyperbolinen tangentti on
- rajoitettu, aidosti kasvava ja jatkuva
,
ja
.
Gradientin pienuus isoilla ja pienillä arvoilla on myös hyperbolisen tangentin ominaisuus, joten sen käyttö aktivointifunktiona saattaa aiheuttaa verkon oppimisen hitautta.
ReLu
Neuroverkkojen piilokerroksissa paljon käytetty aktivointifunktifunktio on ReLu-funktio (Rectified Linear Unit) ,
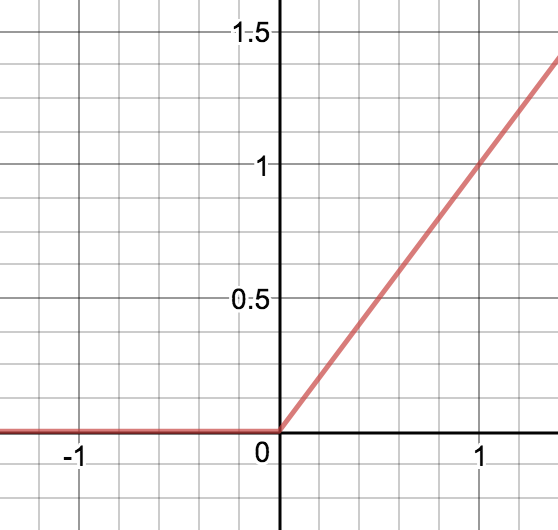
Jotta verkon toimintaan saadaan epälineaarisuutta, niin ulostulokerroksessa käytetään epälineaarista aktivointifunktiota. ReLu-funktio ei ole derivoituva nollassa. Sen toinen huono ominaisuus on se, että se on nolla ja sen derivaatta on nolla negatiivisilla arvoilla. Tästä syystä joidenkin neuronien painot saattavat päivittyä oppimisen aikana nollaksi jolloin neuronit "kuolevat". Neuronien kuoleentumisongelmaa pyritään välttämään muuttamalla aktivointifunktiota hieman.
Yksi ReLun variantti on "Leaky ReLu", ,
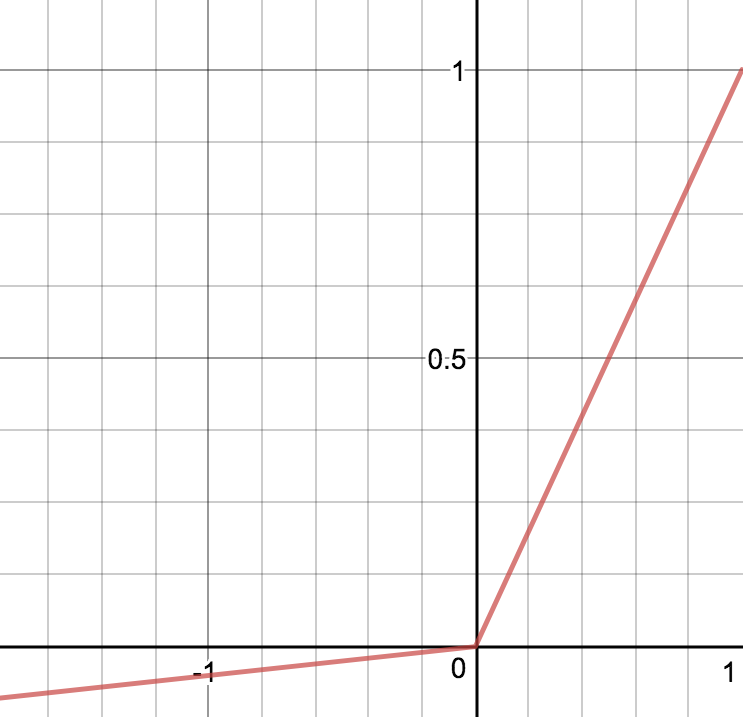
Toimivimpien aktivointifunktioiden valinta riippuu siitä, mitä verkolla ollaan tekemässä eli mitä funktiota sillä approksimoidaan. Jos verkkoa vastaavalla funktiolla on samoja ominaisuuksia kuin aktivointifunktiolla, niin oppiminen on nopeampaa. Esimerkiksi sigmoid-funktiota kannattaa käyttää ulostulokerroksessa jos verkkoa käytetään luokitteluun .
4.1.6 Universaali approksimointilause
Funktionaalianalyysin keinoin voidaan todistaa neuroverkkojen universaali approksimointilause, joka sanoo, että jos aktivointifunktio on rajoitettu, kasvava ja jatkuva, niin mille tahansa :n kompaktin joukon jatkuvalle funktiolle on tätä aktivointifunktiota käyttävä neuroverkko, joka approksimoi haluttua funktiota hyvin. (Joukko on kompakti, jos se on suljettu ja rajoitettu.)
Universaali approksimointilause
Olkoon rajoitettu, kasvava ja jatkuva funktio. Olkoon
kompakti joukko. Olkoon
ja olkoon
jatkuva funktio. Tällöin on
,
, ja
,
, siten, että
kaikilla
funktiolle
4.1.7 Harjoitus
- Näytä, että jos aktivointifunktiona käytetään affiinia funktiota
,
niin neuroverkkoa vastaava kuvaus on affiini. Huomaa, että riittää todeta, että affiinien kuvausten summa ja yhdistetty kuvaus ovat affiineja.
- Laske sigmoid-funktion ja hyperbolisen tangentin derivaatat osamäärän derivointisäännön ja ketjusäännön avulla. Muista, että eksponenttifunktiolle
,
on
kaikilla
.
4.1.8 Neuroverkon opettaminen
Ohjattua oppimista käytettäessä neuroverkkoa opetetaan syöte-tavoite-pareilla eli opetusesimerkeillä (training examples). Verkon syötteelle
antamaa tulosta
verrataan valitulla virhefunktiolla tavoitteeseen
. Opettamisen aikana yritetään minimoida virhefunktioita ja piilokerroksen parametreja muutetaan esimerkiksi vastavirta-algoritmin avulla.
Verkon toiminta varmistetaan ja oppimisnopeus- ja muita hyperparametreja säädetään vahvistus- eli validointiesimerkkijoukon (validation examples) avulla.
Kun verkko toimii halutulla tavalla opetusesimerkeille, sen toimintaa tarkastetaan testiesimerkeillä (test examples).
4.1.9 Vastavirta-algoritmi
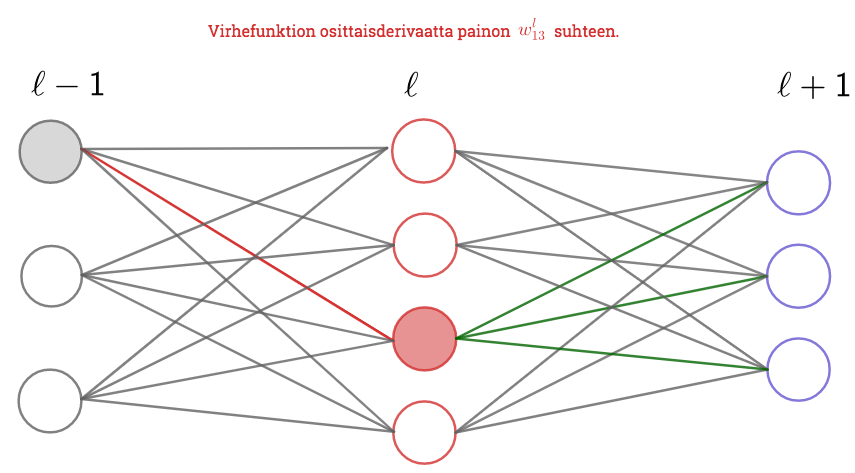
Eteenpäin kytketyssä neuroverkossa syötekerroksen syötteen komponentit viedään ensimmäisen piilokerroksen neuroneille. Jokaista syötekerroksen neuronia vastaa täsmälleen yksi syötteen komponetti. Jokaisessa ensimmäisen piilokerroksen neuronissa komponentit kerrotaan piilokerroksen neuroneita vastaavilla painoilla, tulot lasketaan yhteen ja summaan lisätään neuronin vakiotermi. Tämä summa syötetään aktivointifunktioon, joka antaa kyseisen neuronin syötteen seuraavalle kerrokselle. Seuraava kerros käyttää omia painojaan, vakiotermejään ja aktivointifunktioitaan. Näin jatketaan kaikkien kerrosten läpi.
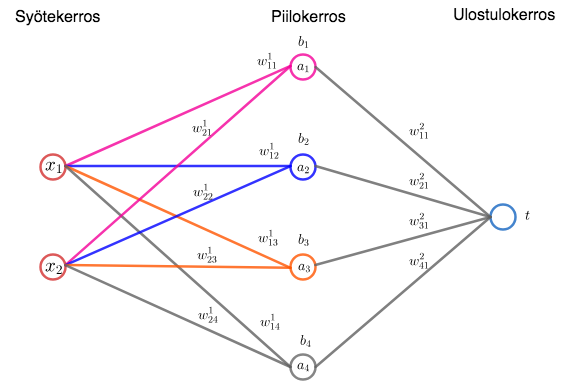
Esimerkiksi kuvan ainoan piilokerroksen toiseen (siniseen) neuroniin tulee syötteen kaksi komponenttia, ja
. Komponentit kerrotaan vastaanottavan neuronin painoilla
ja
, missä alaindeksit kertovat syötekerroksen ja piilokerroksen neuronin järjestysluvun ja yläindeksi
kertoo piilokerroksen järjestysluvun (
. piilokerros). Painotettuun summaan lisätään piilokerroksen toisen neuronin vakiotermi
ja saatu summa
viedään ensin aktivointifunktiolle
ja sitten luku
lähetetään ulostulokerrokseen.
Kun neuroverkon laskutoimitukset on tehty, niin syötteen (tai syötejoukon) antamaa tulosta verrataan tavoitteeseen ja lasketaan virhefunktion arvo. Tavoitteena on minimoida opetusesimerkkijoukkoa vastaava virhefunktio ja löytää minimointia vastaavat painot neuroneille.
Useissa virhefunktion minimointikeinoissa kuten gradienttimenetelmässä (gradient descent) tarvitaan virhefunktion osittaisderivaatat
ja
verkon kaikkien painojen
ja vakiotermien
suhteen. Osittaisderivaatat ja jokaisen neuronin vaikutus virheeseen lasketaan usein vastavirta-algoritmilla (backpropagation). Gradienttimenetelmässä neuroneille saadaan uudet painot ja vakiotermit muuttamalla edellisiä arvoja neuronien parametrien osittaisderivaatoista koostuvan gradientin vastavektorin suuntaan (eli virhefunktion nopeimman pienenemisen suuntaan).
Monesti yksittäistä syötettä vastaavan tavoitteen
ja verkon antaman tuloksen
virhefunktiona käytetään erotuksen euklidisen normin neliötä
ja opetusesimerkkijoukon A virhefunktiona keskineliösummaa (mean squared error)
missä
on joukon
opetusesimerkkien lukumäärä.
Seuraavaksi lasketaan virhefunktion E osittaisderivaatat ja
verkon kaikkien painojen
ja vakiotermien
suhteen vastavirta-algoritmilla. Derivaatan ja osittaisderivaattojen määritelmät esimerkkeineen löytyvät luvusta.
Ulostulokerroksen osittaisderivaatat
Ulostulokerroksen parametreihin liittyvät osittaisderivaatat on helppo laskea. Aloitetaan esimerkillä.
Esimerkki
Ulostulokerroksessa (. kerros) on kaksi ja viimeisessä piilokerroksessa (
kerros) kolme neuronia. Virhefunktio on
ja ulostulokerroksen neuronien tulokset ovat
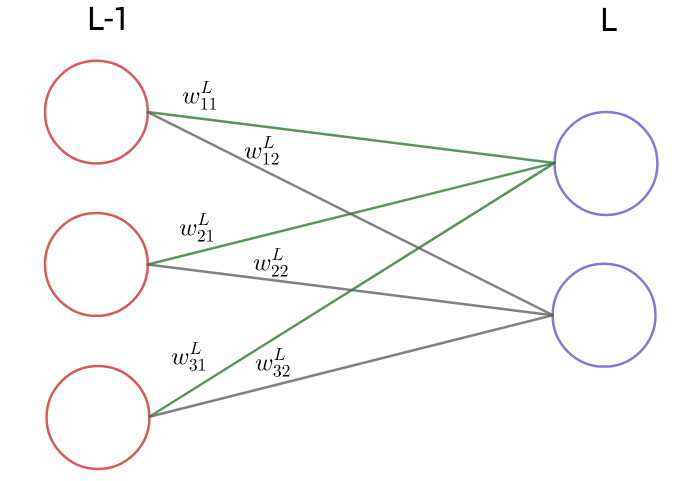
Oletetaan, että aktivointifunktio on identtinen funktio ja että ulostulokerroksen vakiotermit ovat nollia. Tällöin
ja
.
Lasketaan virhefunktion osittaisderivaatat painojen
suhteen. Koska kaavan perusteella painot
,
ja
eivät vaikuta ulostuloon
, niin virhefunktion termi
on vakio osittaisderivoinnessa painojen
,
ja
suhteen. Siten derivoinnin ketjusäännön avulla nähdään, että kaikilla
on
Koska summan termit, joissa on kertoimena
,
, ovat muuttujan
suhteen vakiota, niin kaikilla
on
Vastaavasti saadaan, että
ja
Palataan nyt yleiseen tilanteeseen. Olkoon ulostulokerros verkon . kerros ja olkoon siinä
neuronia.
Osittaisderivaatat painojen  suhteen
suhteen
Koska virhefunktiossa termit ovat vakioita painon
suhteen kun
, niin derivoinnin ketjusääntöä käyttämällä saadaan
Huomaa, että syötteiden tulokset ovat vakioita kaikkien painojen
suhteen ja siten niiden osittaisderivaatat ovat nollia. Siten kaikilla
saadaan ketjusäännön avulla
Koska
ja muut termit summassa paitsi
ovat vakioita painon
suhteen, niin
Yhdistämällä nämä laskut saadaan Tämän kaavan indeksistä
riippuvaa osaa merkitään usein
Laskemalla huomataan, että
Siten on
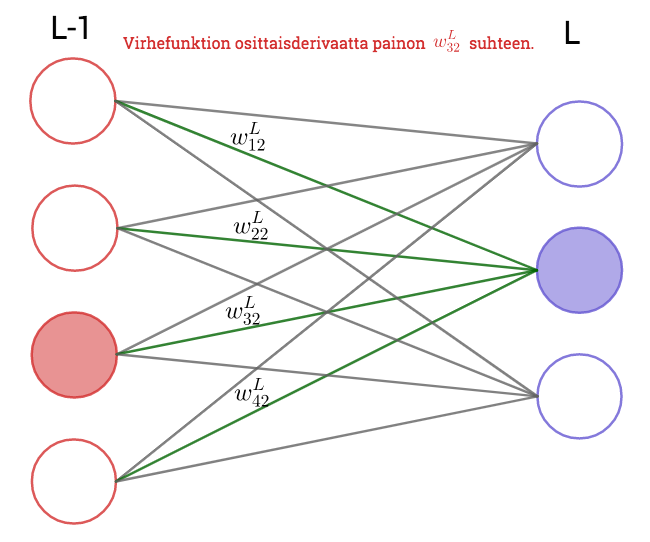
Osittaisderivaatat vakiotermien  suhteen
suhteen
Ulostulokerroksen osittaisderivaatat vakiotermien suhteen saadaan laskettua samaan tapaan kuin painojen suhteen. Virhefunktiossa termit ovat vakioita termin
suhteen kun
, joten ketjusääntöä käyttämällä saadaan
sillä viimeisessä osittaisderivoinnissa ainoastaan summan termi
vaikuttaa derivointiin ja sen osittaisderivaatta
:n suhteen on
. Siten saadaan
Huomautus
Ulostulokerroksen . neuroniin liittyvää virhettä
, ketjusääntöä ja
:n laskukaavaa käyttäen saadaan vastaavat kaavat myös muille virhefunktioille, joita merkitään tässä myös
:llä,
Seuraavaksi lasketaan virhefunktion osittaisderivaatat piilokerroksien painojen ja vakiotermien suhteen. Laskun avulla nähdään, että osittaisderivaatat kerroksen suhteen saadaan laskettua rekursiivisesti kun tiedetään yhtä ylemmän kerroksen osittaisderivaatat. Osittaisderivaattoja laskettaessa lähdetään siis liikkeelle ulostulokerroksen osittaisderivaatoista ja niitä käytetään ensimmäisen piilokerroksen derivaattojen laskemiseen. Osittaisderivaatat viimeisen piilokerroksen painojen ja vakioiden suhteen antavat vastaavat osittaisderivaatat viimeistä edelliselle piilokerrokselle. Näin jatketaan kunnes virhefunktion kaikki osittaisderivaatat saadaan laskettua. Nimi vastavirta-algoritmi tulee siitä, että osittaisderivaattoja lasketaan takaperoisesti ulostuloskerroksesta syötekerrosta kohti vastavirtaan.
Osittaisderivaatat piilokerroksen painojen  suhteen
suhteen
Lasketaan virhefuntion osittaisderivaatat piilokerroksen painojen suhteen Huomatuksen tyylillä. Lasku on teknisesti hieman haastavampi sillä paino, jonka suhteen osittaisderivoidaan, vaikuttaa virheeseen yhden tai useamman piilokerroksen kautta. Siksi laskussa tarvitaan tavallisen ketjusäännön lisäksi osittaisderivaattojen ketjusääntöä.
Käytetään tässäkin merkintää kerroksen
neuroniin
liittyvälle virheelle.
Osittaisderivaatat piilokerroksen vakiokertoimien  suhteen
suhteen
Samaan tapaan kuin painojen tapauksessa saadaan ja
Huomioita osittaisderivaattojen kaavoista
Kaavasta nähdään, että jos edellisen kerroksen syöte
on pieni, niin kerroksen
painoa vastaava virheen osittaisderivaatta
on pieni. Tällaiset painot muuttuvat vastavirta-algoritmin aikana vähän, monesti sanotaan, että ne oppivat hitaasti.
Kaavoista nähdään myös, että aktivointifunktion derivaatat vaikuttavat virheen osittaisderivaattoihin ja siten neuroneiden parametrien muutokseen. Jos derivaatta on hyvin pieni, niin parametrit muuttuvat vähän ja neuronit oppivat hitaasti. Tästä syystä verkon käyttötarkoituk-seen sopivan virhefunktion valinta on tärkeää.
Verkon eri kerroksissa voidaan käyttää eri aktivointifunktioita. Jos näin on, niin äskeisissä laskuissa ja kaavoissa aktivointifunktioon lisätään verkon kerrosta vastaavat alaindeksit
.
4.1.10 Harjoitus
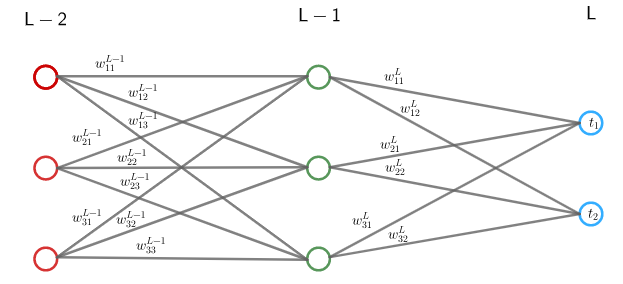
- Laske virhefunktion osittaisderivaatat piilokerroksen
painojen
suhteen virhefunktiolle
samaan tapaan kuin ulostulokerroksen osittaisderivaatat. Mieti, mitkä painoista
vaikuttavat ulostuloon
.
Koodissa on kätevää ja nopeaa käyttää vastavirta-algoritmin kaavojen vektori- ja matriisiversioita. Lue näistä esimerkiksi linkkilistan lähteestä. Lähteessä pohditaan myös sitä, miksi vastavirta-algoritmi on paljon nopeampi tapa laskea tarvittavat osittaisderivaatat kuin osittaisderivaattojen erotusosamäärien raja-arvomääritelmään pohjautuva tapa.
Tarkastellaan neuroverkkoa, jonka syöte on
, jossa ei ole piilokerroksia, jonka ulostulokerroksessa on yksi neuroni ja jonka ulostulokerroksen aktivointifunktio on derivoituva funktio
. Käytetään syöte-tavoiteparin
ja verkon antaman tuloksen
vertailuun virhefunktiota
Laske virhefunktion osittaisderivaatat painojen
,
ja
suhteen.
Lisätietoa vastavirta-algoritmista
Vastavirta-algoritmista löytyy paljon monentasoista luettavaa, esimerkkejä ja koodia. Osassa selitetään matemaattinen tausta ja painojen muutoksen vaikutus verkon toimintaan hyvin, osan selitys on turhan monimutkaista. Kaavoissa indeksien käyttö on monesti epämatemaattista (osittaisderivaatan indeksit ja summausindeksit samoja).
4.1.11 Gradienttimenetelmä
Tavoitteena on minimoida verkon parametreista riippuvaa virhefunktiota eli syötteiden ja verkon antamien tulosten välistä virhettä. Virhefunktio on monen muuttujan (kaikkien neuronien painojen ja vakiotermien) funktio, jolle etsitään pienintä arvoa.
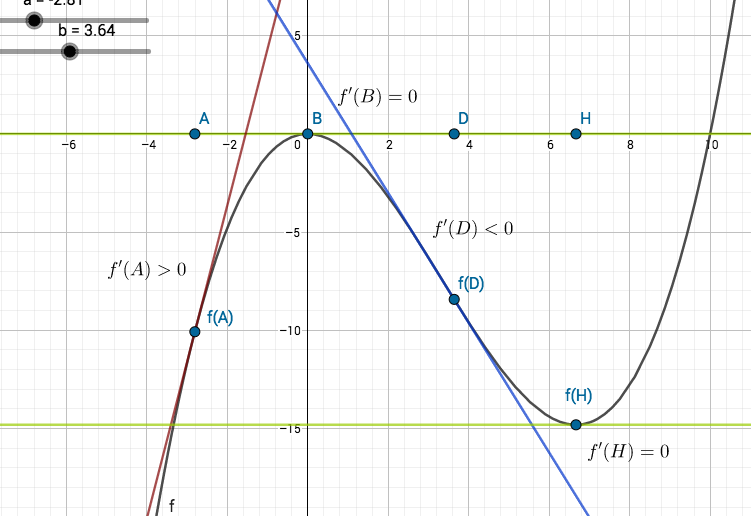
Matemaattisen analyysin keinoin monen muuttujan funktion ääriarvoja etsitään riittävän siistille funktiolle gradientin nollakohdista ja niistä pisteistä, joissa funktiolla ei ole osittaisderivaattaa. Gradientin nollakohtien etsimisen sijaan virhefunktion minimoinnissa käytetään erilaisia algoritmeja kuten gradienttimenetelmää (gradient descent). Siinä minimin etsiminen aloitetaan laskemalla tarkasteltavan funktion arvo aloitusparametreilla. Funktion gradientti kertoo nopeimman kasvun ja siten gradientin vastavektori nopeimman vähenemisen suunnan. Sopivilla askelilla nopeimman vähenemisen suuntaan siirtymällä löydetään (menetelmään sopiville funktioille) lokaali minimi.
Minimin etsimistä gradienttimenetelmällä havainnollistetaan usein yhden tai kahden muuttujan funktiolla. Kahden muuttujan tilanteessa funktion kuvaajan voi ajatella kumpuilevaksi maastoksi, missä rinteellä seisova ihminen haluaa mennä laakson pohjalle jyrkkyydestä välittämättä. Gradienttimenetelmän keinolla alas mennään vähän matkaa jyrkintä rinnettä (gradientin vastavektorin suuntaan), pysähdytään ja valitaan taas jyrkin suunta. Näin jatketaan, kunnes päästään laakson pohjalle. Huomaa, että jos maastossa on useita laaksoja, niin liian pitkä siirtymä yhteen suuntaan voi johtaa väärän laakson pohjalle.
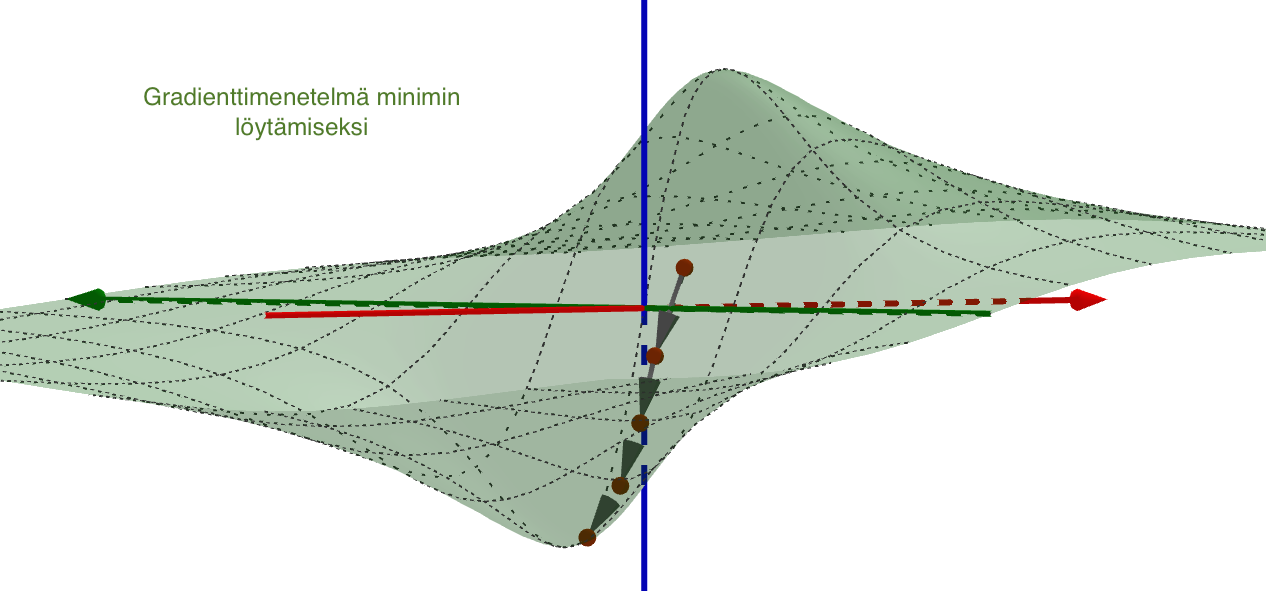
Neuroverkon opettaminen vastavirta-algoritmilla ja gradienttimenetelmällä
Vastavirta-algoritmia ja gradienttimenetelmää käytettäessä suoritetaan seuraavat tehtävät:
- Syötetään opetusesimerkkijoukon
kaikki opetusesimerkit
neuroverkolle.
- Kaikille opetusesimerkeille
:
- Lasketaan vastavirta-algoria varten neuronikohtaiset summat
ja ulostulot
.
- Lasketaan syötettä vastaavan virhefunktion osittaisderivaatat vastavirta-algoritmin avullla (ensin ulostulokerroksen painojen ja vakiotermien suhteen, sitten kerros kerrallaan alaspäin).
- Lasketaan vastavirta-algoria varten neuronikohtaiset summat
- Korjataan neuronien parametrit gradienttimenetelmän avulla. Matriisi- ja vektorimuodossa ilmoitettuna parametrien muutokset ovat
missä
on verkon oppimisnopeus ja
opetusesimerkkijoukon
alkioiden lukumäärä.
Huomaa, että jos opetusesimerkkijoukko koostuu yhdestä syötteestä, niin yksittäiten neuronien uudet painot vastavirta-algoritmin jälkeen ovat
Gradienttimenetelmän eri versioita
(Satsi)gradienttimenetelmä ((Batch/Vanilla) Gradient descent)
Perinteisessä gradienttimenetelmässä yksittäistä opetusesimerkkiä vastaava virhe
lasketaan jokaisen opetusesimerkin jälkeen ja minimoitavana virhefunktiona käytetään opetusesimerkkien virheiden summaa
missä
on opetusesimerkkijoukon alkioiden lukumäärä. Verkon parametrit päivitetään vasta, kun koko opetusesimerkkijoukko on käyty läpi.
Jos parametrit laitetaan jonoon ja niistä muodostetaan vektori , niin parametrien päivityskaava on
missä
on verkon oppimisnopeus ja virhefunktion osittaisderivaatat parametrien suhteen ovat gradientissa samassa järjestyksessä kuin parametrit vektorissa
.
Gradienttimenetelmässä koko opetusesimerkkijoukon tiedot ovat kerralla muistissa ja verkko saattaa oppia hitaasti isoilla opetusesimerkkijoukoilla. Päivityksiä on vähän, joten menetelmä on virheen pienenemisen suhteen vakaa mutta se saattaa supeta liian aikaisin ja huonommilla parametreilla kuin stokastinen versio. Gradienttimenetelmällä löydetään globaali minimi konvekseille virhefunktioille (harvinainen tilanne) ja lokaali minimi ei-konvekseille virhefunktioille.
Stokastinen gradienttimenetelmä (Stochastic gradient descent)
Stokastisessa gradienttimenetelmässä virhe lasketaan ja neuronien parametrit päivitetään opetusesimerkkijoukon jokaisen syötteen jälkeen. Tällä menetelmällä saadaan nopea tieto verkon oppimisesta, sillä verkko oppii koko ajan. Menetelmä on helppo ymmärtää ja toteuttaa. Tiheä päivittäminen on kuitenkin hidasta, parametrien arvot saattavat heilua paljon päivittämisen aikana ja häiriöherkkyys voi hidastaa virhefunktion lokaalin minimin löytymistä. Joissain tilanteissa heiluminen on etu tavalliseen gradienttimenetelmään verrattuna - stokastinen versio saattaa päätyä pienempään lokaaliin minimiin.
Minisatsi gradienttimenetelmä (Mini batch gradient descent)
Minisatsigradienttimenetelmä on perinteisen ja stokastisen gradienttimenetelmän välimuoto. Siinä opetusesimerkkijoukko jaetaan osajoukkoihin, jotka syötetään verkolle, lasketaan virhefunktio ja päivitetään parametrit. Tämä vähentää parametrien heiluntaa päivityksissä ja mahdollistaa paremman ja vakaamman suppenemisen lokaaliin minimiin kuin toisilla versioilla. Menetelmässä voidaan käyttää ohjelmakirjastojen tehokkaita lineaarialgebran laskurutiineja.
Lisätietoa gradienttimenetelmästä
Types of Optimization Algorithms used in Neural Networks and Ways to Optimize Gradient Descent
Ruder: An overview of gradient descent optimization algorithms
A Gentle Introduction to Mini-Batch Gradient Descent and How to Configure Batch Size
3Blue1Brown: Gradient descent, how neural networks learn | Deep learning, chapter 2
4.1.12 Virhefunktiot
Verkon oppimisen kannalta on tärkeää, että pieni muutos neuronin painossa aiheuttaa vain pienen muutoksen ulostulossa. Vastavirta-algoritmin vaiheita tutkiessa huomataan, että jos opetusesimerkkijoukon virhe saadaan keskiarvona yksittäisten opetusesimerkkien virheistä, niin opetusesimerkkijoukon virheen osittaisderivaatat saadaan laskettua opetusesimerkkien virheiden avulla.
Vastavirta-algoritmin yhteydessä käytettiin yksittäisen syötteen tavoitteen
ja verkon antaman tuloksen
välisenä virheenä erotuksen euklidisen normin neliötä
ja
:n alkion opetusesimerkkijoukon
virhefunktiona keskineliösummaa
Logistisen regression virhefunktio
Jos ulostulokerroksen arvot kuuluvat välille , niin voidaan käyttää myös logistisen regression virhefunktiota (ristientropian virhefunktio), (cross-entropy cost function),
missä vektorit
ovat syötteiden
tavoitteita, vektorit
neuroverkon syötteille
antamia tuloksia ja
on opetusesimerkkijoukon koko.
Laskemalla nähdään, että sigmoid-aktivointifunktiota käytettäessä tämän virhefunktion osittaisderivaatat neuroneiden painojen ja vakiotermien suhteen eivät riipu aktivointifunktion derivaatoista vaan pelkästään tavoitteiden ja tulosten erotuksista, ja
(Muista, että ulostulokerroksen tulos
on syötettä
vastaava tulos
.) Siksi sigmoid-funktion derivaatan pienuus suurilla ja pienillä arvoilla ei hidasta verkon oppimista niissä tapauksissa, joissa tavoitteet erovat paljon syötteistä.
Joissain lähteissä syöte-tavoite-parin välisistä virhefunktioista käytetään nimeä tappiofunktio (loss function) ja opetusesimerkkijoukon virhefunktiosta virhe-/maksufunktio (cost function).
Lisätietoa virhefunktioista
4.1.13 Yli- ja alisovittaminen
Neuroverkon ja yleisemmin koneoppimisen opettaminen suoritetaan opetusesimerkkien avulla, oppiminen varmistetaan ja oppimisnopeus- ja muita hyperparametreja säädetään vahvistusesimerkkijoukon avulla ja lopuksi toiminta testataan testiesimerkkijoukolla. Tarkoitus on, että verkko osaa yleistää oppimansa ja toimii lopulta riittävän tarkasti tuntemattomalle datalle. Joskus käy niin, että verkko tuntuu oppivan hyvin mutta sitten tulee ongelmia:
- Opettamisen edetessä virhefunktion pieneneminen hidastuu tai tarkkuus huononee.
- Verkko toimii hyvin opetusesimerkeille mutta ei (opetusesimerkkien kaltaisille) vahvistus- tai testiesimerkeille.
Tätä ilmiötä sanotaan ylisovittamiseksi (overfitting). Siinä verkko on oppinut opetusesimerkkijoukon liian hyvin ja säätänyt parametrinsa sen erityisominaisuuksien ja häiriöiden mukaan. Ylisovittaminen on yleinen ongelma suurissa tuhansien parametrien neuroverkoissa joissa opetusesimerkkijoukko ei ole ole riittävän suuri suhteessa verkon kokoon.
Ylisovittamista voidaan estää seuraavilla tavoilla:
- opetusesimerkkijoukon kasvattaminen
- (verkon koon pienentäminen)
- opettamisen lopettaminen riittävän aikaisin (early stopping)
- neuroneiden osittainen poistaminen verkosta (dropout layer)
- painojen pienentämien
- ja
- säännöstelyllä (regularization)
Opetusesimerkkijoukon kasvattaminen
Opetusesimerkkijoukon koon kasvattaminen saattaa olla vaikeaa mutta joissain tilanteissa sitä voi kasvattaa olemassaolevan datan avulla. Esimerkiksi uusia tunnistettavia kuvia saadaan helposti kiertojen, siirtojen ja skaalauksen avulla.
Aikainen lopettaminen
Verkon toimintaa testattaessa vahvistusesimerkkijoukolla opetusesimerkkijoukon jälkeen tarkastetaan tulosten tarkkuus jokaisen osajoukon jälkeen. Kun tarkkuus pienenee, lopetetaan.
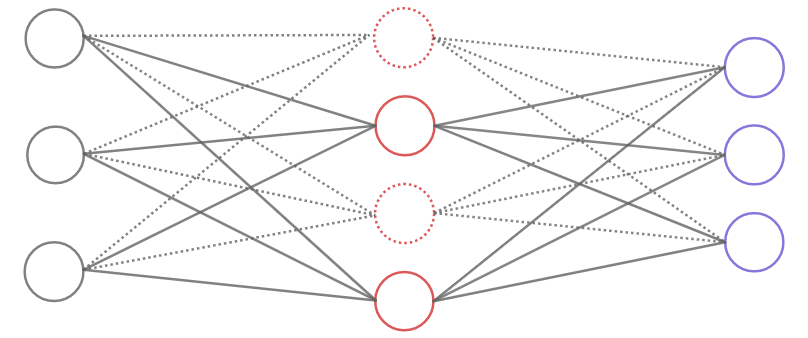
Osittainen poistaminen
Yksi tapa pienentää ylisovittamista on neuroneiden hetkellinen poistaminen verkosta. Tässä tekniikassa osa piilokerrosten neuroneista poistetaan väliaikaisesti. Vajaaseen verkkoon syötetään opetusesimerkkejä, käytetään vastavirta-algoritmia ja päivitetään verkon parametrit. Tämän jälkeen poistetut neuronit palautetaan, poistetaan uusi neuronijoukko ja jatketaan opettamista. Menetelmässä jälkeen verkko on tavallaan keskiarvo monesta samaa tehtävää tekevästä verkosta. Koska neuroneiden lähellä olevat neuronit eivät välttämättä ole mukana jokaisella opetuskierroksella niin neuroneista tulee itsenäisempiä ja verkosta robustimpi.
Säännöstely
Virhefunktion muuttaminen niin, että minimi löytyy pienillä painoilla perustuu siihen, että monesti verkot toimivat itseisarvoiltaan pienillä painoilla paremmin kuin suurilla. Säännöstelyssä virhefunktiota muutetaan niin, että minimi löytyy pienemmillä painoilla.
Jos verkossa on käytössä virhefunktio , niin
-säännöstelyn virhefunktio on
missä
on opetusesimerkkijoukon koko,
ovat neuroneiden painot ja
on säännöstelyparametri. Neuroneiden vakiotermejä ei oteta mukaan säännöstelyosaan.
Virhefunktion jälkimmäinen osa on pieni kun painot ovat itseisarvoltaan pieniä. Minimoinnissa suuret painot ovat hyviä vain jos niillä saadaan alkuperäinen virhefunktio
hyvin pieneksi.
Virhefunktion osittaisderivaatat painojen
suhteen ovat
ja vakiotermien suhteen samat kuin alkuperäisellä virhefunktiolla
. Siten gradienttimenetelmän antamat uudet painot saadaan kaavalla
missä
on verkon oppimisnopeus.
Säännöstelyssä yritetään siis samanaikaisesti käyttää mahdollisimman pieniä painoja ja saada virhefunktio pieneksi.
-säännöstelyssä käytetään painojen neliöiden sijaan itseisarvoja. Virhefunktio on
missä
on alkuperäinen virhefunktion,
on opetusesimerkkijoukon koko,
ovat neuroneiden painot ja
on säännöstelyparametri.
Virhefunktion osittaisderivaatat painojen
suhteen ovat
missä
, kun
,
, kun
ja nolla kun paino on nolla. Vakiotermien suhteen osittaisderivaatat ovat samat kuin alkuperäisellä virhefunktiolla
.
Gradienttimenetelmän antamat uudet painot saadaan kaavalla missä
on verkon oppimisnopeus.
-säännöstelyssä painot pienenevät askelilla, joiden pituus ei riipu painon koosta.
-säännöstelyssä askeleen koko on paino kerrottuna vakiolla.
Alisovittamisessa (underfitting) verkon parametrit päivittyvät hyvin hitaasti ja verkko oppii huonosti.
Lisätietoa yli- ja alisovittamisesta
- A. Ng: Machine Learning, The Problem of Overfitting (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Regularization (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Why regularization reduces overfitting? (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Dropout Regularization (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Understanding Dropout (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Other regularization methods(Coursera)
- Chatbot's Life: Regularization in deep learning
- J. D. McCaffrey: Implementing Neural Network L2 Regularization
- J. D. McCaffrey: Neural Network L2 Regularization using Python, Visual Studio Magazine 09/2017
- M. Nielsen: Neural Networks and Deep learning, Chapter 3
4.1.14 Muita virhefunktion minimointikeinoja
Vastavirta-algoritmi ja muut osittaisderivaattoihin (gradientteihin) perustuvat menetelmät ovat monesti hitaita. Vastavirta-algoritmin tapauksessa hitaus johtuu paljosta laskemisesta: neuronien parametrien muutoksessa tarvittavia osittaisderivaattoja lasketaan koko ajan iteratiivisesti. Vastavirta-algoritmin erilaisilla muunnoksilla ja muilla verkon opetusmenetelmillä haetaan lisää nopeutta. Osassa menetelmiä käytettään ensimmäisen kertaluvun osittaisderivaattojen lisäksi toisen kertaluvun derivaattoja, joiden avulla saadaan tietoa ensimmäisen kertaluvun osittaisderivaattojen kasvusta.
5. Prosessienlouhinta
(Toni Ruohonen)
Tässä luvussa tutustutaan prosessinlouhintaan ja simulointimalleihin sosiaali- ja terveydenhuollon kehittämisen menetelminä.
Prosessienlouhinta on menetelmä, joka mahdollistaa prosessien automaattisen kuvaamisen visuaalisessa ja tilastollisessa muodossa. Päätavoitteena prosessienlouhinnalla on identifioida, monitoroida sekä kehittää kirjattuun tietoon perustuvia faktapohjaisia prosesseja (ei oletettuja prosesseja) louhimalla tapahtumalokeja tai tietorekisterejä. Prosessienlouhintaa on kolmea eri tyyppiä. Nämä eri louhintatyypit ovat:
- Automaattisen prosessien tunnistaminen (Automated Process Discovery)
- Mallien vertailu (Conformance Checking)
- Mallien laajentaminen (Enhancement).
Automaattisella prosessien tunnistamisella tarkoitetaan mallien louhimista lokeista tai rekistereistä ilman tarkempia ennakkomääritteitä. Mallien vertailussa olemassa olevaa prosessia verrataan lokeista louhittuun prosessiin ja katsotaan noudattaako lokeista louhittu prosessi olemassa olevaa prosessia ja päinvastoin. Mallien kehittämisellä tarkoitetaan olemassa olevan mallin kehittämistä tai laajentamista perustuen lokeihin tallennettuun dataan. Tässä prosessienlouhinnan luvussa keskitytään erityisesti automaattiseen prosessien tunnistamiseen.
Prosessienlouhinta koostuu seuraavista elementeistä:
- Tapaus/Case: yksi prosessi-instanssi
- Aktiviteetti: prosessin yksittäinen, hyvin määritelty vaihe
- Tapahtuma: prosessin yksittäisen vaiheen suorittaminen, yhdistää tapauksen + aktiviteetin (+ tapahtumisajankohdan)
- Variantti: prosessin sisällä tietty vaiheiden suorittamisjärjestys
- Attribuutti: tapahtumaan tai tapaukseen liittyvä lisätieto, kuten ikä, resurssi, diagnoosi, kustannus
Prosessienlouhinnan lähtökohtana on käytössä oleva tietolähde, joka on normaalisti joko tapahtumaloki tai tietorekisteri. Louhinnan mahdollistamiseksi tietolähteestä pitää olla identifioitavissa seuraavat kolme perustietoelementtiä:
- Tunniste (yksilöivä tunniste, jolla voidaan identifioida esimerkiksi henkilö tai tuote)
- Tunnisteeseen liittyvä(t) tapahtuma(t) (esimerkiksi henkilön asiointiin tai tuotteen valmistukseen/kulkuun liittyvät tapahtumat)
- Ajallinen tieto tapahtuman ajankohdasta (vähintään päivätasolla, mitä tarkemmalla tasolla ajallinen informaatio on saatavilla, sitä tarkemmin asiakasvirrat/prosessit pystytään kuvaamaan)
Edellä mainittujen kolme perustietoelementin perusteella eri asiointitapahtumille voidaan määrittää ajallinen järjestys, kuvaten jokaista tapahtumaa edeltäneet sekä niitä seuranneet tapahtumat. Muut tunnisteeseen ja asiointitapahtumaan liittyvät tiedot toimivat luokittelevina muuttujina, joiden avulla käytössä olevaa dataa voidaan luokitella ja ryhmitellä tarkemmin (esimerkiksi tietyn asiakas/tuoteryhmän tarkempi tarkastelu).
Prosessienlouhintaa on mahdollisuus hyödyntää hyvin monilla eri sovellusalueilla. Käytännössä kaikki toimintakokonaisuudet, joissa tarkasteltavaan kohteeseen on mahdollista liittää tunniste, eri tunnisteisiin tapahtuma(t) sekä ajallinen tieto, ovat analysoitavissa prosessienlouhinnalla. Eniten prosessienlouhintaa on sovellettu palvelu-, tuotanto- ja toimitusprosessien analysoinnissa ja kehittämisessä. Tässä luvussa prosessienlouhinnan soveltamista tarkastellaan erityisesti palveluprosessien näkökulmasta, käyttäen soveltamisalana sosiaali- ja terveydenhuoltoa.
5.1 Prosessienlouhinta sosiaali- ja terveydenhuollon palveluprosessien kehittämisessä
Sosiaali- ja terveydenhuollon sektorilla tarkastelua voidaan tehdä monista eri näkökulmista. Tarkasteltavaksi näkökulmaksi voidaan ottaa esimerkiksi asiakasryhmä, hoitokokonaisuus tai hoitoketju eri vaiheineen, eri ammattiryhmillä asiointi ja ohjautuvuus eri ammattilaisten välillä tai vaikka asiakkaiden asiointi ja kulku eri toimi- ja palvelupisteissä. Näkökulma on vapaasti valittavissa käytettävissä olevan datan puitteissa. Asiakkaiden asiointia, palvelujen käyttöä ja tarvetta sekä kulkua voidaan tarkastella lisäksi monilla eri tasoilla. Tarkasteltavaksi voidaan ottaa yksittäisen asiakkaan prosessi, eri asiakasryhmien palvelu- ja hoitoketjut tai vaihtoehtoisesti voidaan tarkastella toimintaa koko palveluverkoston tasolla (maakunta ja kansallinen taso).
Perinteisessä prosessienlouhinnassa jokaisen asiointitapahtuman/prosessivaiheen osalta kuvataan, kuinka monta asiakasta kyseisessä vaiheessa on asioinut, kuinka monta kertaa asiointitapahtuma on tapahtunut ja riippuen lähtötiedosta (onko saatavilla vai ei) myös vaihe-/asiointitapahtumakohtaisesti syntyneet kustannukset. Tapahtumakohtaisen tiedon lisäksi visuaalisessa graafissa esitetään myös yhteydet välittömästi edeltäviin ja seuraaviin tapahtumiin asiakasmäärineen ja siirtymäkertoineen.
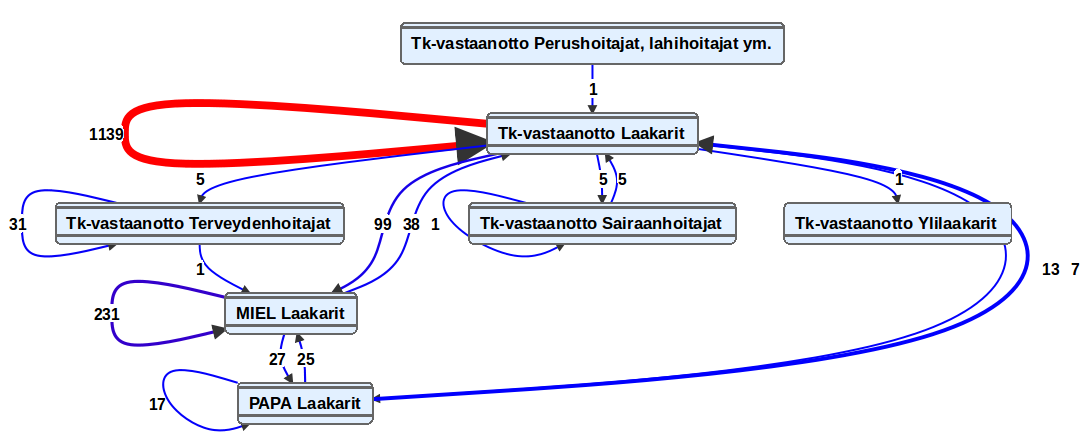
Useissa prosessienlouhinnan sovelluksissa graafi on interaktiivinen ja jokaiseen asiointivaiheeseen sekä siirtymään pääsee pureutumaan tarkemmin. Tämä mahdollistaa asiakkaiden taustamuuttujien analysoinnin ja profiloinnin sekä myös ajallisen tarkastelun eri asiointitapahtumien välillä vain muutamalla klikkauksella.
Prosessienlouhinnassa käytetään erilaisia algoritmeja hyödyntämään edellä kuvattua tapahtumatason dataa. Yleisimmin käytetyt algoritmit ovat:
- Aplha miner
- Heuristic miner
- Fuzzy miner
Ongelmana tässä lähestymistavassa on, erityisesti sosiaali- ja terveydenhuollon stokastisessa kentässä, että juuri tiettyyn hoitokokonaisuuteen liittyvien asiointitapahtumien määrittely on hankalaa ja taustamuuttujiin perustuvat luokittelut (esimerkiksi tietty asiakasryhmä) ottavat mukaan ko. asiakasryhmän kaikki tapahtumat. Valitessa tarkasteluun esimerkiksi diabetespotilaat, tulevat mukaan diabeteksen hoitotapahtumien lisäksi myös kaikki ko. hoitokokonaisuuteen liittymättömät asiointitapahtumat.
Kehittyneimmissä prosessienlouhinnan sovelluksissa tätä varten on kehitetty erillisiä ns. episodimääritealgoritmeja, jotka mahdollistavat hyvin tarkan määrityksen tarkasteltavalle asiakokonaisuudelle ehtoineen ja rajoitteineen. Näihin algoritmeihin perustuviin sovellusten toiminnallisuuksien avulla lopputulokseen syntyvään visuaaliseen prosessikuvaukseen voidaan sisällyttää suuresta aineistosta vain haettavaan prosessiin liittyvät tapahtumat. Kiinnostamattomat muut tapahtumat voidaan suodattaa pois. Tarkasteltavalle prosessille/hoitokokonaisuudelle voidaan hyvin tarkkaan määrittää mitä asiointitapahtumia otetaan mukaan, missä järjestyksessä ja aikaikkunassa niiden on pitänyt tapahtua. Tämän lisäksi voidaan vielä hyvin tarkkaan määrittää millä taustamuuttujin asiakkaat ovat voineet ja saaneet eri asiointitapahtumiin ohjautua.
Seuraavassa kuvassa on esimerkki määrityksestä kotihoidon prosessin osalta. Esimerkissä on haettu kolme vaihetta sisältävää prosessia, jossa prosessi alkaa Yhteydenotto-tapahtumalla. Seuraavassa vaiheessa tapahtuma on kotihoidon tarpeen Arviointikäynti niin, että tapahtumien välillä on kulunut yli 7 vuorokautta. Kolmas vaihe on määritelty Päätös-tapahtumaksi, jonka lisätietokentän Tulos arvon on oltava Kyllä. Näiden tapahtumien välissä olevat mahdolliset muut määriteltyyn prosessiin liittymättömät tapahtumat suodatetaan pois tähtivaiheoperaattorilla. Näin esimerkkihaussa on löydetty lähempään tarkasteluun suuresta aineistosta juuri ne asiakkaat, joiden tapauksessa kotihoidon tarpeen arviointikäynnin toteutumisen ja siihen liittyvien yhteydenottojen välillä on kulunut pidempi aika kuin 7 vuorokautta ja jotka on arviointikäynnin käynnin jälkeen otettu kotihoidon asiakkaaksi. Tarkemmat analyysit voidaan näin kohdistaa prosessihakuehdot täyttävien asiakkaiden tarkempiin oheistietoihin (esimerkiksi terveydentilaan ja hoidon tarpeeseen liittyvät tiedot, mikäli aineisto sisältää niitä).
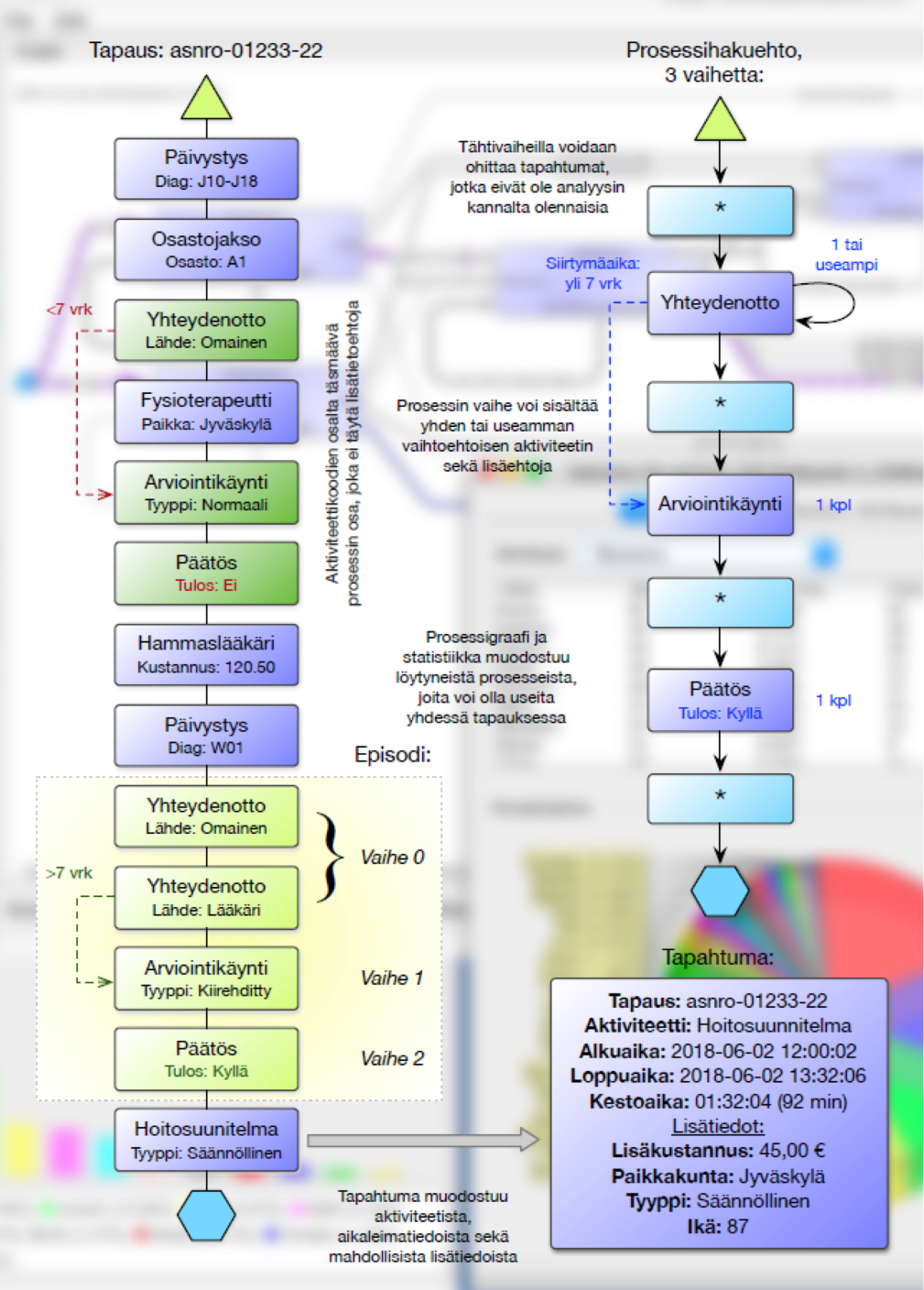
5.2 Prosessienlouhinnan vaiheet
Prosessienlouhinnan suorittaminen alkaa käytettävien datalähteiden määrityksestä. Eri prosessienlouhinnan työkalut käsittelevät sisään syötettävää dataa hieman eri tavoin ja eri formaateissa mutta pääsääntöisesti datalle tehdään aluksi tietosisällön määritykset (ts. määritetään mistä löytyy tunniste, visualisoitavat aktiviteetit, ajallinen informaatio sekä optiona luokittelevat numeeriset ja ei-numeeriset taustamuuttujat). Alkumääritysten ja datan sisään tuonnin jälkeen voidaan edetä suoraan louhintaan tai tehdä lisäluokitteluja, rajaten aineistoa esimerkiksi koskemaan tiettyä asiakasjoukkoa tai ajankohtaa. Episodiperusteisissa prosessienlouhinnan työkaluissa seuraava vaihe on tarkempi tarkasteltavan prosessin määritys, joka pitää sisällään eri prosessivaiheiden, niiden järjestyksen, vaiheiden välisten aikaikkunoiden sekä vaihekohtaisten erityisehtojen määrittämistä (miten ja millä ehdoilla prosessi etenee). Tämän jälkeen tarkasteltava kokonaisuus on valmis visualisoitavaksi ja tilastollisesti kuvattavaksi (ts. suoritetaan louhinta).
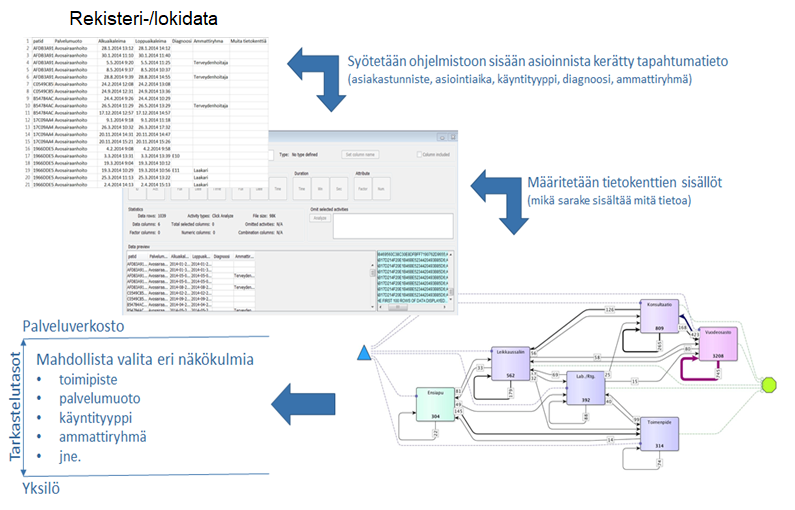
5.3 Prosessienlouhinta ja tekoäly
Puhuttaessa tekoälystä prosessienlouhinnan yhteydessä tarkoitetaan sillä
- prosessien/(hoito)episodien automaattista tunnistamista loki- ja rekisteritiedoista tarkan manuaalisen määrityksen sijaan,
- ongelmien ja niiden juurisyiden automaattista tunnistamista,
- kehittämis- ja ratkaisuehtojen automaattista määritystä sekä
- erilaisten ennustemallien tekemistä (polku-/prosessiennusteet).
Tällä hetkellä eri aktiviteettien välistä yhteyttä ja sen vahvuutta pystytään analysoimaan monin eri algoritmein mutta varsinaisten tiettyyn hoitoepisodiin liittyvien tapahtumien linkittäminen toisiinsa on vielä osin erillisin algoritmein ja manuaalisesti tehtävää määritystyötä. Tulevaisuudessa tämän voi automatisoida analysoimalla esimerkiksi eri asiointitapahtumien sisältöä, jonka jälkeen samansisältöiset tai tiettyyn hoitokokonaisuuteen määritetyt käyntisisällöt voidaan automaattisesti tunnistaa ja yhdistää toisiinsa.
Prosessissa ilmenevät viiveet ja poikkeamat sekä ilmiöt pystytään jo tällä hetkellä tuomaan näkyviksi visuaalisiksi ja tilastollisiksi kuvauksiksi. Tämä mahdollistaa kehittämiskohteiden ja ns. pullonkaulojen monipuolisen tunnistamisen. Tämän lisäksi käytössä on erilaisia influence ja root cause analysis algoritmeja, joilla voidaan vielä tarkemmin analysoida ja ymmärtää poikkeavien tapahtumien ja ilmiöiden taustalla olevat syyt.
Seuraavan viiden vuoden aikana ongelmien juurisyyt pystytään tunnistamaan vielä monipuolisemmin ja automatisoidummin (esimerkiksi klikattaessa mitä tahansa prosessihavaintoa, tekoäly tarjoaa tärkeysjärjestyksessä olevan listan taustalla olevista syistä sekä edelleen niiden taustalla olevista syistä, jne.). Seuraavan 10 vuoden aikana päästään mahdollisesti jo tilanteeseen, jolloin tekoäly pystyy löytämään ratkaisun jo valmiiksi määritettyjen tietolähteiden lisäksi ulkoisista tarjolla olevista tietolähteistä (automatisoitu internethaku).
Kun ongelmat on tunnistettu ja juurisyyt on saatu selvitettyä, on seuraavassa vaiheessa tavoitteena löytää parhaat ratkaisut ongelmien ratkaisemiseksi. Tällä hetkellä prosessienlouhinnan mallit on mahdollista viedä automatisoidusti diskreeteiksi simulointimalleiksi, jotka mahdollistavat erilaisten toimintaehdotusten arvioinnin. Kehittämisehdotukset tosin tuotetaan vielä asiantuntijoiden toimesta mutta seuraavan 10 vuoden aikana päästään jo tilanteeseen, jolloin tekoäly ja oppivat algoritmit osaavat automatisoidusti suositella erilaisia kehittämistoimenpiteitä ja tuottaa niistä priorisoidun listan kehittäjille hyödynnettäviksi. Tämä nostaa prosessianalytiikan ja kehittämisen aivan uudelle tasolle, jossa tekoäly toimii kehittäjän älykkäänä apulaisena.
5.4 Tutkimukset
Prosessienlouhintaa ja tapahtumapohjaista simulointia on hyödynnetty useissa isoissa hankekokonaisuuksissa yhdessä Sitran, Kelan, STM:n, kuntien, sairaanhoitopiirien ja yritysten kanssa. Tällaisia hankkeita ovat olleet muun muassa
- Monikanavarahoitushanke
- Paljon palveluja tarvitsevien asiakkaiden -hanke
- Asiakas online -hanke
5.4.1 Monikanavarahoitus -hanke
Hankkeessa selvitettiin monikanavaisen rahoituksen näkymistä alueiden diabetes-, silmä- ja lonkkaproteesiasiakkaiden palveluprosesseissa. Tutkimushankkeen rahoitus koostui Suomen itsenäisyyden juhlarahaston (Sitra), Kainuun sosiaali- ja terveydenhuollon kuntayhtymän, Jyväskylän kaupungin peruspalvelujen, Keski-Suomen sairaanhoitopiirin sekä Jyväskylän yliopiston rahoitusosuuksista.
Tutkimus toteutettiin hyödyntämällä prosessienlouhintaa sekä tapahtumapohjaista simulointia. Tutkimuksen aineistossa yhdistettiin aikaleimallisia rekisteritietoja molempien tarkastelualueiden perusterveydenhuollon, erikoissairaanhoidon sekä Kelan tiedoista. Eri tietolähteitä yhdistämällä saatiin laaja aineisto, josta pystyttiin selvittämään eri hoitotoimenpiteiden ajallinen sijoittuminen ja ennen kaikkea eri maksajien osuudet kunkin tapahtuman kohdalla.
Valittujen asiakasryhmien osalta rahoituksen monikanavaisuuden problematiikka tuli hyvin ilmi. Tuki- ja liikuntaelinten sairaudet, diabetes ja kaihi ovat kaikki merkittäviä kansansairauksia, joista kärsivillä hoidon tarve on useimmiten jatkuvaa ja palvelutarpeet voivat muutoinkin olla moninaisia. Tästä syystä myös maksajataho ehti vaihtua tarkastelujakson aikana tiheään tutkittavien ryhmien hoitoprosessien aikana.
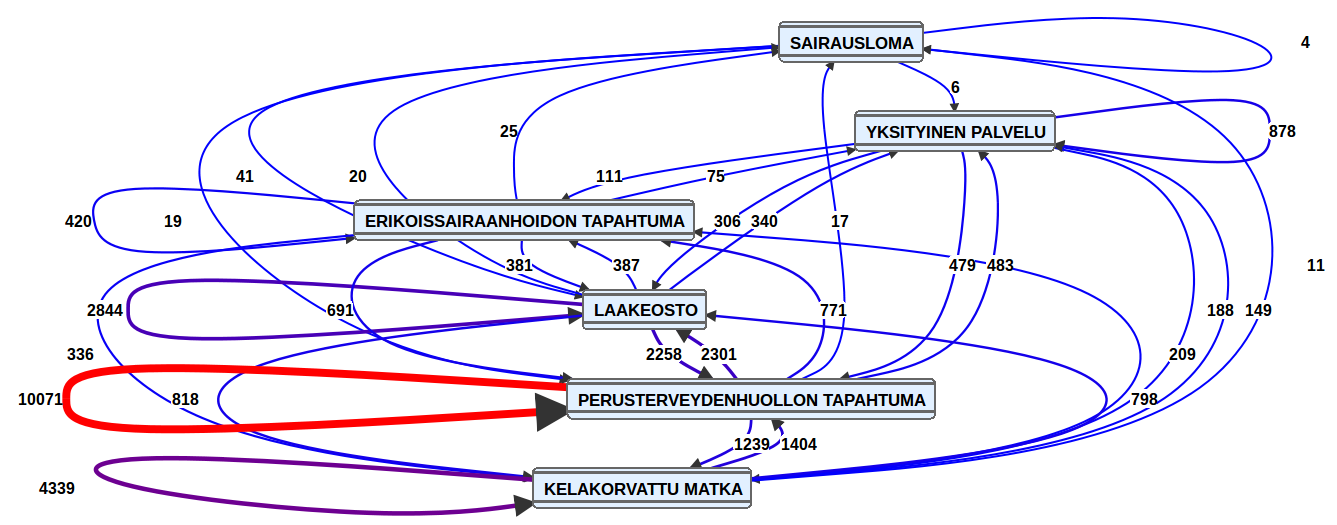
Tarkasteltaessa rahoittajien vaihtumista eri hoitopoluissa havaittiin, että rahoittaja vaihtui kahden vuoden tarkastelujakson aikana Keski-Suomessa enimmillään 711 kertaa (kaihiasiakas) ja Kainuussa 559 (aikuistyypin diabeetikko). Keskimäärin eniten rahoittajan vaihtumista oli sekä Keski-Suomessa että Kainuussa aikuisiän diabeetikoiden hoitoprosessissa, jossa kahden vuoden aikana rahoittaja vaihtui Keski-Suomessa keskimäärin 38 ja Kainuussa keskimäärin 43 kertaa. Monikanavainen rahoitus ei välttämättä kannustakaan hoitoprosessien tehostamiseen ja esimerkiksi työkyvyttömyysajan lyhentämiseen, koska odotusajan ja sairausloma-ajan kustannuksista vastaa asiakas, työnantaja ja Kela ja näin ollen kunnat ja sairaanhoitopiirit eivät hahmota pitkien odotusaikojen todellisia kustannuksia.
Sairauslomien ja odottamisen yhteiskunnallisia kustannuksia arvioitiin hankkeessa lonkkaprotetisoitujen asiakkaiden hoitoprosessissa, jossa leikkausta edeltävät hoitotapahtumat, itse leikkaus ja leikkauksen jälkeiset kontrollikäynnit ovat kunnan ja asiakkaan kustantamia palveluita. Sen sijaan leikkaukseen tai kontrollikäynteihin jonottamisajan kuin myös kuntoutuksen kustantaa pääasiassa Kela ja asiakas. Tämä tarkastelu toteutettiin tapahtumapohjaisen simuloinnin avulla.
Karkeasti arvioituna Kainuussa yhteiskunnalliset kustannukset leikkaukseen odottamisesta olivat vajaat 2 miljoonaa euroa kahdelta vuodelta ja Keski-Suomessa vastaavasti vajaat 4 miljoonaa euroa samalta tarkastelujaksolta. Leikkauksen jälkeisen kuntoutuksen yhteiskunnalliset kustannukset olivat sen lisäksi kahdelta vuodelta sekä Kainuussa että Keski-Suomessa n. 4,5 miljoonaa euroa. Näiden kustannusten ohella on syytä huomioida, että työnantajille koituvat kustannukset sekä polven että lonkan tekonivelleikkauksista nousivat Kainuussa yli 40000 euroon asiakasta kohden ja Keski-Suomessa yli 50000 euroon asiakasta kohden.
Yhteensä voidaan siis ajatella, että pelkästään jonottamista ja odottamista lyhentämällä on saatavilla miljoonien eurojen säästöt Keski-Suomen ja Kainuun alueella.
Hankkeessa saatujen tulosten avulla voidaan helposti osoittaa kuinka haastavaa eri palveluntarjoajien ja maksajatahojen näkökulmasta on eri hoitopolkujen kokonaiskustannusten hahmottaminen. Rahoituksen selkiyttäminen etenkin paljon ja pitkäkestoisia hoitoa tarvitsevien ryhmien kohdalla olisi ensiarvoisen tärkeää ja rahoituksen selkiyttämisellä olisikin todennäköisesti suora vaikutus kokonaiskustannusten läpinäkyvyyden lisääntymiseen ja sitä kautta palveluketjujen kustannustehokkuuden parantumiseen.
https://hoivajaterveys.fi/sotkuinen-hoitopolku-luo-sotkuiset-kustannukset/
5.4.2 Paljon palveluja tarvitsevat asiakkaat
Tutkimukset ovat osoittaneet, että pieni joukko asiakkaista aiheuttaa suurimman osan sosiaali- ja terveydenhuollon kustannuksista. Tämän tutkimuksen tehtävänä oli selvittää Kainuun sosiaali- ja terveydenhuollon kuntayhtymän (Kainuun sote) ja Jyväskylän yhteistoiminta-alueen terveyskeskus (JYTE) -kuntien alueella paljon palveluja käyttävät asiakasryhmät, sekä identifioida ja validoida parhaat mahdolliset, kokonaisedullisimmat kehitysmallit palveluiden tuottamiseksi tulevaisuudessa. Hankkeessa selvitettiin, minkälaisia palvelutarpeita paljon palveluja käyttävillä asiakkailla on ja miten heidän hoitotoimintaansa voitaisiin organisoida tehokkaammin ja paremmin. Lisäksi kuvattiin, minkälaisia vaikutuksia muutoksilla olisi mahdollista saada aikaan. Tutkimuksen aineisto koottiin Kainuun sosiaali- ja terveydenhuollon kuntayhtymän (Kainuun sote) ja Keski-Suomen Jyväskylän yhteistoiminta-alueen terveyskeskuksen (JYTE) kuntien alueilta vuosilta 2013–2014. Aineistoon koottiin erikoissairaanhoidon, perusterveydenhuollon, työterveyshuollon ja sosiaalihuollon asiakasdataa. Aineistoa täydennettiin Kelan sairausvakuutuslain mukaisten korvausten ja tulonsiirtojen asiakasdatalla.
Data-analytiikan, prosessienlouhinnan sekä asiantuntijatyöpajojen avulla visioitujen uudistusten arvo saatiin mitattua simulointimallinnuksen menetelmillä myös rahassa. Tarkasteluun otettiin perusterveydenhuollon ja erikoissairaanhoidon saumaton yhteistyö, erikoisalat ylittävä yhteistyö, päivystyskäynnit ja niiden tarpeellisuus sekä matkajärjestelyt kodin ja palvelujen välillä. Tulos on merkittävä: kahden vuoden aikana on mahdollista saavuttaa miljoonien eurojen säästöt. Keski-Suomessa JYTE-alueen säästöpotentiaali on 10–13 miljoonaa euroa (6–8 prosenttia) ja Kainuun soten alueella vastaava säästöpotentiaali on 5–6,5 miljoonaa euroa (7–9 prosenttia).
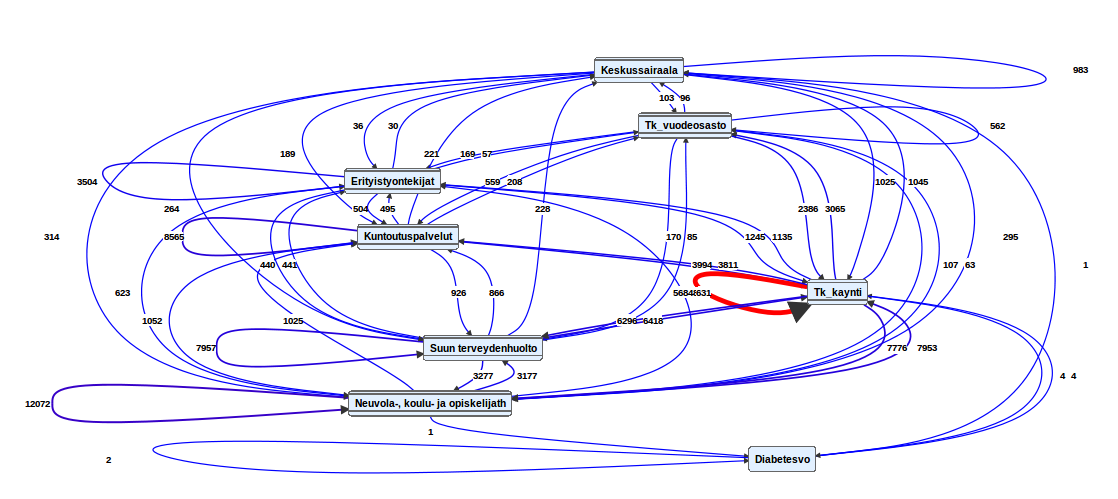
Skaalattaessa tämä koko maan väestöpohjalle se tarkoittaa noin 500 miljoonan euron säästöjä. Laskennassa käytetyn simulointimallin vieminen käytäntöön vaatisi kokonaisvaltaisen hoitosuunnitelman tekemistä ja eri ammattiryhmien välistä saumatonta yhteistyötä. Tarkastelussa saadut kustannushyödyt koskevat pidemmän aikaa paljon palveluja tarvitsevien ryhmää eli alle kymmentä prosenttia alueiden väestöstä. Laajentamalla vastaavia tarkasteluja myös muihin asiakasryhmiin tulokset ovat aivan eri suuruusluokkaa. Tehokkaamman toiminnan lisäksi myös asiakastyytyväisyys voi kasvaa: parempia hoitotuloksia, vähemmän matkustamista ja siten vähemmän asiakkaille koituvia kustannuksia.
5.4.3 Asiakas online- hanke
Asiakas on-line -hanke toteutettiin Jyväskylän yliopistossa 1.1.2016-31.12.2017. Keskeisenä tavoitteena oli muodostaa kokonaiskuva tarkasteluun valittujen asiakasryhmien kotoa-kotiin -palveluketjujen nykytilasta sekä digitaalisten ratkaisuiden hyödyntämisestä osana nykyistä tai tulevaisuuden palveluketjua. Hankkeessa hyödynnettiin dosentti, FT Toni Ruohosen tutkimusryhmän kokoamaa sosiaali- ja terveyspalveluiden sekä Kelan rekisteriaineistoa vuosilta 2012-2014. Analyyseissa keskityttiin Keski-Suomen Jyväskylän yhteistoiminta-alueen terveyskeskus (JYTE) –kuntiin. Rekisteriaineistoanalyysit toteutettiin prosessienlouhinnan ja data-analytiikan avulla. Tämän lisäksi tehtiin haastattelututkimusta selittämään analyysien tuloksia. Kirjallisuudesta haettiin sekä kotimaisia että kansainvälisiä lähteitä, jotta saatiin mahdollisimman hyvä kuva digitaalisten ratkaisuiden olemassaolosta, käytöstä ja kokemuksista. Hankkeen viimeisessä vaiheessa muotoiltiin digitaalisia palvelumalleja sekä koottiin eri asiakasryhmien käyttöön soveltuvia digitaalisia ratkaisuideoita. Digitaalisen palvelumallin toteutettavuuden arvioimisen tueksi tehtiin asiakaskysely. Lisäksi hyötyjä arvioitiin laskennallisen simuloinnin avulla.
6. Tekstianalytiikka
(Riku Nyrhinen)
Tietokoneistettu kielenkäsittely on alati kasvava ja nopeasti kehittyvä tieteenala. Kieli on ihmiselle tärkeä kommunikaatiotyökalu. Jotta ihminen voisi joskus luontevasti kommunikoida tietokoneiden kanssa, on tietokoneet saatava ymmärtämään ihmiskielten monimuotoisuutta. Myös digitaaliset datamassat kasvavat sellaisella tahdilla, ettei ole järkevää käyttää ihmisresursseja informaation uuttamiseen ja käsittelemiseen, mikä lisää luonnollisten kielten käsittelyn tärkeyttä myös suoran viestinnän ulkopuolella. Tietokonepainotteisuudestaan huolimatta luonnollisten kielten käsittely koskee informaatioteknologian lisäksi myös monitieteellisiä aloja - tai oikeastaan kaikkea, missä voidaan käyttää kieltä viestimiseen sekä tiedon kuvaamiseen ja tallettamiseen (Kibble 2013).
Luonnollisten kielten käsittelyn termistö on monitulkintainen, ei kovin vakiintunut ja vaihtelee teoksesta toiseen. Tässä tekstissä luonnollisten kielten käsittely on sateenvarjotermi kaikelle kieltä koskevalle tietokoneistetulle analyysille: puheen muuntaminen tekstiksi, puhutun kielen analysointi, tekstin muuttaminen puheeksi, jne. Tekstianalyysillä tai tekstin louhimisella viitataan luonnollisten kielten käsittelyn alakategoriaan, johon kuuluu vain kirjoitetun - useimmiten digitaalisen - tekstin käsitteleminen.
Tekstianalyysille suotuisaa aineistoa löytyy lukuisista lähteistä, mutta tässä tekstissä ei tutustuta tekstin louhimisen tekniseen puoleen. Kun teksti on kuitenkin saatu poimittua lähteestä, sitä voidaan esikäsitellä halutulla tavalla tai jättää se sellaiseksi. Esikäsittely on yksinkertaisimmillaan tavoitteen kannalta turhien merkkien tai sanojen poistamista. Käsiteltävä teksti esiintyy tyypillisesti kahdessa muodossa: raakana (annotoimattomana) tai selityksin varustettuna (annotoituna). Raakateksti koostuu merkeistä, jotka muodostavat sanoja, jotka muodostavat lauseita, jotka muodostavat virkkeitä, jotka lopulta muodostavat tekstikokonaisuuksia. Raakatekstissä näitä tasoja ei ole kuitenkaan selvästi eroteltu vaan se jää käsittelijän tehtäväksi. Raakatekstissä ei myöskään ole eroteltuna kielikohtaisia, semanttisia tai rakenteellisia tasoja, kuten lauseenjäseniä tai taivutusmuotoja. Annotoidussa tekstissä sen sijaan voi raakatekstin ohella olla myös merkittynä esimerkiksi sanojen välinen semanttinen yhteys tai erisnimet tai mitä tahansa mielekkääksi koettua informaatiota, joka on poimittavissa tekstistä työkaluilla, algoritmeilla tai käsivoimin.
Suomen kielen käsittelyyn on kehitetty lukuisia valmiita työkaluja ja tietokantoja, joista seuraavaksi esitellään kolme: Turun yliopiston NLP-ryhmän Finnish-dependency-parser - sekä Turku Neural Parser -annotointityökalut; ja Helsingin yliopiston ylläpitämä synonymia- ja hyperonymiatietokanta FinnWordNet.
Finnish-dependency-parser - sekä Turku Neural Parser
Finnish-dep-parser, FDP, on Turun yliopiston BioNLP Group'in ensimmäinen työkalu suomen kielen hienostuneempien rakenteiden löytämiseen tekstistä. Turku Neural Parser ajaa samaa asiaa, mutta kehittyneemmin. Molemmat työkalut perustuvat kattavaan pohjatietoon, joka on listattuna TurkuNLP:n sivuilla. Työkalut tuottavat raakatekstistä käsitellyn tulosteen, joka noudattaa yleisesti hyväksyttyä ConLL-U-standardia, jossa näkyvät sanojen lemmojen lisäksi mm. niiden taivutukset sekä semanttiset yhteydet toisiin sanoihin. Työkalut ovat juuri niin täydellisiä kuin niiden koulutusaineisto eli eivät aivan: etenkin erisnimiä kuvastavien sanojen kielellisten ominaisuuksien selvittäminen tuottaa virheellisiä tuloksia. Työkalut ovat kuitenkin tarpeeksi tarkkoja ollakseen päteviä ja sovellettavissa olevia - tekstianalytiikkaprojekti tuskin kärsii työkalujen harvoin tuottamista virheistä. Turku Neural Parser on työkaluista uudempi ja siten myös tarkempi ja monipuolisempi. Syväluotaavaa työkaluja vertailevaa raporttia ei ole vielä julkaistu (TurkuNLP, 2018).
FinnWordNet
FinnWordNet on kokoelma suomen kielen sanoja, jotka on ryhmitelty merkityksen mukaan niiden käsitteitä edustaviksi synonyymijoukoiksi. Joukot on yhdistetty toisiinsa erilaisilla suhteilla, esimerkiksi antonymian, synonymian tai hypernymian mukaan, jolloin sanat muodostavat semanttisen eli merkitysopillisen verkon. FinnWordNet'iä käyttämällä tekstistä poimituille sanoille voi luoda lisämerkityksiä ja täten saada hienostuneempaa informaatiota esille (FIN-CLARIN, 2018). Esimerkkejä muista tietokannoista ovat muun muassa poistosanalistat (stop words), jotka sisältävät sanoja, joiden mielletään kantavan hyvin vähän informaatiota tavoitteen kannalta ja jotka voidaan käsittelyn nopeuttamiseksi tai tilan säästämiseksi leikata tekstistä pois menettämättä mitään tärkeää.
Tilastollinen ja lingvinstinen tekstianalyysi
Informaatiota voi loihtia esiin tekstistä lukuisilla menetelmillä, jotka jaetaan perinteisesti kahteen kategoriaan: tilastolliseen ja lingvistiseen. Tilastollinen tekstianalyysi ei edellytä esitietoja käsiteltävästä kielestä tai edes kielen rakenteesta. Lingvistinen lähestymistapa, jota usein kutsutaan "semanttiseksi tekstianalyysiksi", pohjautuu lähes puhtaasti esitietoon käsiteltävästä kielestä. Suomen kielen kohdalla se voi tarkoittaa esimerkiksi agglutinaatiossa sanan vartaloon liitettävien päätteiden ja affiksien tunnistamista ja sitä, miten nämä taivutusmuodot liittävät sanoja virkkeen tai lauseen sisällä toisiinsa.
Tilastollinen tekstianalyysi keskittyy tyypillisesti tekstin mitattaviin suureisiin, kuten sanojen määrään, sanojen keskipituuteen, esiintyvyyteen tai sanastolliseen monipuolisuuteen. Tilastollisin menetelmin voidaan tunnistaa esimerkiksi tiettyjä aihepiirejä koskevat tekstit selvittämällä, millaisia sanoja eri aihepiirit sisältävät ja miten sanat ovat jakautuneet tekstiin. Kun aihepiirin dokumenteille on muodostettu kuvaava profiili, joka kertoo, millaisia tekstit ovat, voidaan uusia tekstejä verrata tähän profiiliin ja päätellä, koskeeko teksti jo entuudestaan tunnettua ja profiloitua aihetta. Esimerkiksi sanomalehden ulkomaat-osiossa tekstissä esiintynee useammin vieraiden maiden nimiä kuin kotimaa-osiossa.
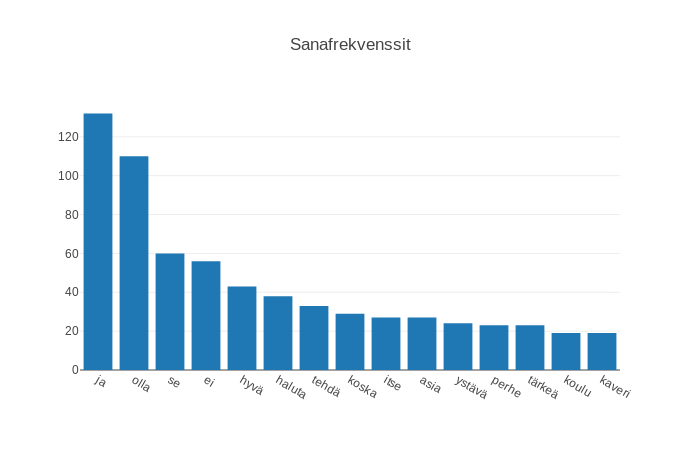
Tilastollinen menetelmä sisältää kuitenkin omat haasteensa. Frekvenssijakauma on oiva tapa dokumenttien tunnistamiseen niiden leksikon eli sanaston kautta, mutta suomen kielen ja monien muiden kielten tapauksessa suurin osa sanoista toistuu läpi aihepiirien. Sanat, kuten "olla", "kuin", "ja", "että", ovat äärimmäisen yleisiä ja ilmaantuvat lähes poikkeuksetta frekvenssilistojen kärkeen. Tähän voi vaikuttaa siivilöimällä sanoja niiden numeeristen ominaisuuksien mukaan. Voidaan esimerkiksi jättää pois sanat, joiden pituus on alle kuusi merkkiä. Voidaan jättää pois sanat, jotka eivät sisällä isoa kirjainta. Voidaan jättää pois sanat, jotka löytyvät edellä mainitusta poistosanatietokannasta, Lähestymistapa ei ole kieleen vaan mielikuvitukseen sidottu (Bird, Klein ja Edward Loper, 2018).
Kielikohtainen tai semanttinen lähestymistapa vaatii hienostuneempien rakenteiden kokoamista lähdetekstin pohjalta. Se keskittyy kielen rakennuspalasten keskinäisiin suhteisiin sekä merkitykseen. Tällä tavalla voidaan esimerkiksi yrittää selvittää, mitä yksittäinen sana tarkoittaa tai mitä kokonainen virke tarkoittaa; mitä ne viestivät. Koska raakateksti ei kerro, mitä sen osaset tarkoittavat varsinkaan korkeammalla, ihmisten ymmärtämällä tasolla, on semanttisia menetelmiä pohjustettava esitiedoilla tai kielen konventioilla, joita voi hyödyntää laskennallisesti.
Esimerkki ensimmäisestä tapauksesta on jo edellä mainittu FinnWordNet, joka sisältää listoja eri sanoista ja niiden semanttisista verkoista. FDP:n ja TNP:n kaltaiset työkalut osaavat esitietojensa pohjalta yhdistää lähdetekstin sanat toisiinsa lauseensisäisten riippuvuuksien kautta: mikä on predikaatti, mikä on tekijä, mihin tekeminen kohdistuu? Esimerkki jälkimmäisestä on John Rupert Firth'in kuuluisa toteamus, jonka mukaan sanan tunnistaa sen seuralaisista. Toisin sanottuna Firth'in idea yhdistää samalla tavalla käyttäytyvät ja samoissa konteksteissa esiintyvät sanat merkitysopillisesti toisiinsa (Potts, 2013). Esimerkiksi sanat "auto" ja "juna" esiintyvät samankaltaisten verbien ("ajaa", "matkustaa", "kulkea", "nousta [kyytiin]") ja aihepiirien läheisyydessä, joten niiden voidaan olettaa olevan merkitykseltään lähellä toisiaan. Merkityksen esittäminen tällä tavalla numeerisesti on voimakas työkalu, jonka toteuttamiseen on kehitetty runsaasti erilaisia menetelmiä; kuuluisimpana Word2Vec (Mandelbaum, Shalev, 2016).
Painottaminen frekvenssin suhteen
Tekstiä voi hahmotella sen ominaisuuksien pohjalta käyttämällä tilastollisia menetelmiä, jotka keräävät tekstistä dataa, joka voidaan esittää numeerisesti. Tällaisia menetelmiä ovat muun muassa painottamiset frekvenssien suhteen. Painotustavan valitseminen riippuu sen sopivuudesta tehtävään. Tekstin voi painottaa yksinkertaisesti laskemalla sen uniikkien eli vain kerran esiintyvien sanojen esiintymismäärät. Tätä kutsutaan raakafrekvenssiksi. Hienostuneempi ja hyvin yleinen tekniikka on TF-IDF (Term Frequency - Inverse Document Frequency), jossa sanojen frekvenssit painotetaan suhteessa muihin dokumentteihin esimerkiksi vertaamalla sanan esiintyvyyttä yksittäisessä dokumentissa sen esiintyvyyteen kaikissa kokoelman dokumenteissa. Tällöin saadaan kokoelmakeskeisempi numeerinen arvo kullekin sanalle ja tämän avulla voidaan luoda aihepiirin dokumenteille numeerinen frekvenssiprofiili (Manning, Raghavan ja Hinrich Schütze, 2018).
Frekvenssit ovat hyvin rakennekeskeinen lähestymistapa, joka ei huomioi kielen rakenneosien välisiä suhteita. Jos frekvenssien vertaileminen ei tuota haluttua tulosta, voidaan sitä parantaa muuntamalla suhteet tarkasteltaviksi suureiksi käyttämällä esimerkiksi kielimalleja, jotka kertovat, kuinka todennäköistä on, että tietyt rakenneosaset (kuten sanat tai lauseet) esiintyvät peräkkäin, tai millaiset lauseenosaset rakentavat yleisiä isompia kokonaisuuksia kielen sisällä. Kielimalli määrittää dokumentille todennäköisyyteen perustuvan harvinaisuuden tai yleisyyden. Dokumentti on harvinainen, jos se menee kielimallia vastaan; yleinen, jos se noudattaa kieleltä odotettua rakennetta.
Semanttinen menetelmä
Semanttinen eli merkitysopillinen lähestymistapa vaatii kielen tuntemista. Semanttisessa menetelmässä kielen rakenneosasten väliset suhteet pyritään selittämään lingvistisestä näkökulmasta. Millaisia predikaattiverbejä tekstissä esiintyy? Millaisia merkitysketjuja (tekijä-tekeminen-objekti; adjektiivi-nomini; nominirypäs) tekstissä esiintyy? Miten kokonaiset virkkeet liittyvät toisiinsa? Turku Neural Parser'n kaltaiset työkalut kertovat käyttäjälleen semanttiset riippuvuudet, lauseenjäsenet ja taivutukset valmiiksi, minkä jälkeen niitä voi käyttää helposti. Vastaavaa tietoa ei voi kerryttää tekstistä ilman esitietoja kielestä (Potts, 2013).
Vertailu
Kun dokumenteille on saatu luotua kieliprofiili, voidaan niitä alkaa vertailla toisiin dokumentteihin. Vertailuunkin on runsaasti erilaisia menetelmiä, jotka vaihtelevat tavoitteen ja hienostuneisuutensa mukaan. Avainsanojen esiintyvyys ja frekvenssilistojen vertailu on triviaalia. Sen sijaan dokumenteista kootuille ominaisuusvektoreille on kehitetty matemaattisia vertailumenetelmiä, jotka yleensä perustuvat lineaarialgebraan. Tällaisia ovat muun muassa kosinisimilaarisuus eli kahden ominaisuusvektorin välisen kulman laskeminen käyttäen kosinisimilaarisuuden yhtälöä, jossa kahden vektorin pistetulo jaetaan niiden pituuksien summalla, tai vektorien etäisyyden laskeminen euklidisessa avaruudessa mukailemalla tuttua Pythagoraan lausetta. Jaccard'in etäisyys on joukko-opin menetelmä, jossa kahden dokumenteista muodostetun ominaisuusjoukon leikkaus jaetaan niiden unionilla. Tulos sijaitsee välillä . Mitä lähempänä ykköstä tulos on, sitä lähempänä dokumentit ovat toisiaan (Tan, Steinbach, Kumar Vipin, 2005).
Kategorisointi
Tekstianalyysin menetelmien soveltaminen riippuu tavoitteista. Dokumenttien kategorisointi niiden ominaisuuksien suhteen ja merkityksen "opettaminen" tietokoneelle ovat yleisiä pyrkimyksiä tekstianalyysin kentällä. Dokumenttien kategorisointi on luokitteluongelma, jonka tavoitteena on jakaa dokumentit kahteen tai useampaan kategoriaan niiden yksilöllisten ominaisuuksien mukaan, kuten aikaisemmin mainitussa uutistekstiesimerkissä. Tietokoneistetussa kielenkäsittelyssä oletetaan, että eri kategorioihin kuuluvat tekstimassat omaavat erilaisia, mutta kuitenkin kategorialle uskollisia, piirteitä, jotka opettamalla saadaan algoritmi tai ohjelma jaottelemaan sille syötetyt uudet tekstimassat oikeisiin kategorioihin.
Kategorisointi jaetaan tyypillisesti kahteen kategoriaan: itseoppivaan ja käsin opetettuun. Käsin opetettu luokittelija kerryttää valmiiksi annotoitua esitietoa, jossa voidaan esimerkiksi listata negatiiviseksi ja positiiviseksi miellettyjä sanoja, jolloin algoritmi oppii erottelemaan tekstimassojen sanat niiden sävyn mukaan. Esitieto voi myös koostua tekstiprofiileista ja profiilit muodostavista ominaisuuksista, jolloin algoritmi oppii yhdistämään sen löytämät ominaisuudet tiettyihin kategorioihin. Itseoppivat menetelmät tekevät tämän ilman esitietoa tutkimalla annotoimatonta harjoitusdataa yleensä neuroverkkojen avustuksella. Lopulta kategorisointi tapahtuu käyttäen esimerkiksi "Naive Bayes" -luokittelijaa (Manning, Raghavan ja Hinrich Schütze, 2018), joka perustuu bayesilaiseen teoreemaan, "Support Vector" -kojeisiin (DTREG Inc., 2018), jotka ovat eräänlainen neuroverkkoratkaisu, tai ominaisuusvektoreita vertailemalla edellä mainituilla tavoilla.
Semanttinen analyysi
Aikaisemman kappaleen semanttinen lähestymistapa valottaa tekstin väittämää merkitystä. Tekstistä voidaan esimerkiksi poimia subjekti-predikaatti-objekti-ketjuja, jotka ihmisen on helppo tulkita. Hakualgoritmit mahdollistavat informaation "kyselemisen" tekstiltä. Suurelta aineistolta voidaan esimerkiksi kysyä, mikä on Suomen pääkaupunki? Jos tekstissä lukee "Suomen pääkaupunki on Helsinki", "Suomi"- ja "pääkaupunki"-avainsanat ohjaavat algoritmin oikeille poluille, jonka jälkeen semanttinen tarkastelu osaa yhdistää "on"-verbin kautta "Helsinki"-sanan "Suomen" "pääkaupunkiin".
Semanttisten ketjujen muodostaminen sanoille käyttäen sanaupotteita on suhteellisen uusi ja kiinnostava tapa lähestyä semanttista analyysiä. Tekniikat, kuten Word2Vec, LSA, BLSA, LDA ja PCA tutkivat tekstissä esiintyviä ominaisuuksia ja yrittävät löytää sanoille semanttisia yhteyksiä, joita ovat muun muassa synonyymit, hyperonyymit sekä aihepiirisanat, kuten aikaisemminkin esitellyt "juna" ja "auto". Stanford'n yliopiston suosittelema työnkulku semanttiseen analyysiin lukee ensin tekstin ja jakaa sen rakenneyksiköiksi (esimerkiksi sanoiksi). Sanat annotoidaan lingvistisin perustein ja halutut ominaisuudet poimitaan talteen. Tekstit ryhmitellään perusteen mukaan, minkä jälkeen dokumentit muunnetaan matriiseiksi, joiden rivit ja sarakkeet voivat kuvata esimerkiksi sanoja ja dokumentteja, sanoja ja sanoja, verbejä ja argumentteja tai sanoja ja niiden välisiä lauseensisäisiä riippuvuussuhteita. Matriisit painotetaan esimerkiksi TF-IDF:llä tai kielimallilla, minkä jälkeen niihin sovelletaan aikaisemmin mainittuja sanaupotetekniikoita (Potts, 2013).

7. Tekoäly ja kyberturvallisuus
(Martti Lehto ja Petri Vähäkainu)
Tekoälyn kehitys ottaa huimia harppauksia. Se tulee mahdollistamaan aikaisemmin ihmisen osaamista vaatineiden tehtävien automatisoinnin. Kehitys avaa paljon uusia mahdollisuuksia ja uudistaa monia toimialoja samalla vaikuttaen työn tekemiseen ja kansalaisten arkeen. Tekoäly vie yhteiskunnan digitalisaatiokehityksen aivan uudelle tasolle. Tekoälyn avulla koneet, laitteet, ohjelmat, järjestelmät ja palvelut voivat toimia tehtävän ja tilanteen mukaisesti järkevällä tavalla.
Tekoäly kykenee tekemään päätelmiä olemassa olevan tiedon perusteella ja avustamaan ihmistä arjessa ja työssä.
Tekoälyllä on vahva suhde kyberturvallisuuteen. Suomen kyberturvallisuusstrategia (2013) määrittelee kyberturvallisuuden turvalliseksi ja luotettavaksi toimintaympäristöksi sekä kriittisen infrastruktuurin resilienssiksi. Kyberturvallisuus rakentuu ihmisten toiminnasta, organisaatioiden toimintaprosesseista ja informaatioteknologiasta. Tekoälyn laajentuessa ihmisten arkeen ja yhteiskunnan eri toimintojen alueelle tekoälyn turvallisuudesta tulee keskeinen kansalliseen kokonaisturvallisuuteen vaikuttava tekijä.
Tekoäly mahdollistaa suurten datamäärien varastoinnin sekä prosessoinnin älykkäällä tavalla ja muuntaa relevanttia informaatiota funktionaalisiksi työkaluiksi. Tekoälyä on käytetty hyvin monella sovellusalueella, joista tunnetuimpia ovat kyberturvallisuuden ja avaruustutkimuksen alueet, joissa menestys ongelmien ratkaisemisessa tietyillä osa-alueilla on ollut menestyksekästä. Tekoälyn sovellusalue on sittemmin laajentunut terveydenhuoltoon, jossa sitä hyödynnetään muun muassa diagnosoinnissa, hoitosuosituksien tekemisessä ja leikkaushoidossa.
Tekoäly ei kuitenkaan ole mitenkään uusi käsite, vaan se on kulkenut pitkän tien aina Alan Turingin koneesta nykypäivän kognitiivisiin tekoälyä hyödyntäviin innovaatioihin saakka. Toisen maailmansodan aikoihin Alan Turing alkoi kehittää teknologioita, kuten neuroverkot, jotka mahdollistavat tekoälyn sellaisena kuin me sen nykypäivänä tunnemme. Tekoäly voidaan käsittää eräänlaisena sateenkaariterminä, jonka tarkoituksena on saada tietokoneet ajattelemaan ihmisten kaltaisesti ja simuloimaan ihmisten tekemiä asioita sekä ratkaisemaan ongelmia nopeammin ja paremmin kuin ihmiset niitä kykenevät ratkaisemaan. Tekoälyä hyödyntäen voidaan suorittaa erilaisia tehtävätyyppejä, kuten luovia tehtäviä, suunnittelua, liikkumista, puhumista, objektien ja äänien tunnistamista, sosiaalisten ja liiketoiminnallisten transaktioiden suorittamista. Tehtävätyyppien suorittamiseksi on mahdollista hyödyntää erilaisia menetelmiä, kuten evidenssipohjaisia menetelmiä, luonnollisen kielen prosessointia, tekstin louhintaa, prediktiivista ja preskriptiivista analytiikkaa, suosittelujärjestelmiä sekä kone- ja syväoppimista. Edellä mainittuja tekoälyä hyödyntäviä menetelmiä voidaan soveltaen käyttää myös kyberturvallisuuden ongelmien ratkaisemiseen.
7.1 Kyber ja kyberturvallisuus
Organisaatiot ovat aloittamassa tekoälyn hyödyntämistä kyberturvallisuuden saralla tarjoten aiempaa parempaa tietoturvaa yhä taitavampia hyökkääjiä vastaan. Tekoäly auttaa automatisoimaan monimutkaisia prosesseja hyökkäysten tunnistamiseksi ja reagoimalla tietomurtoihin. Tämänkaltaiset sovellukset ovat kehittymässä entistä paremmiksi tekoälyn hyödyntämisen myötä. Tekoälyn yksi osa-alue, koneoppiminen, viittaa teknologioihin, joiden avulla tietokoneet voidaan saada oppimaan ja mukautumaan kokemuksien kautta. Se simuloi ihmiskognitiota, kuten kokemuksista ja malleista oppimista päättelyn sijasta (syy ja seuraus). Nykyään syväoppimisen kehitysaskeleet koneoppimisen osa-alueella tarjoavat koneille mahdollisuuden oppia rakentamaan hahmontunnistuksen malleja ilman ihmisen puuttumista asiaan. Potentiaalista haitallisuustasoa hahmotettaessa uuden mallin tunnistusta voidaan verrata jo tunnettuihin malleihin. Tunnistusprosessin nopeus ja tarkkuus eivät ole mahdollisia ihmisasiantuntijoille mielekkäässä ajassa.
Kyberturvallisuus yleisesti viittaa kykyyn kontrolloida pääsyä verkossa sijaitseviin järjestelmiin ja niiden sisältämään informaatioon. Kyberturvallisuuden kontrollien ollessa tehokkaita, myös kyberavaruutta voidaan pitää varmana, joustavana ja luotettavana digitaalisena infrastruktuurina. Mikäli kyberturvallisuuden kontrollit ovat puutteelliset, epätäydelliset tai heikosti suunnitellut, kyberavaruutta voidaan pitää digitaalisen ajan niin sanottuna villinä läntenä. Kyberturvallisuus jättää tulkinnan varaa, sillä jopa heillä, jotka työskentelevät kyberturvallisuuden parissa, on toisiinsa verrattuna näkemyseroja kyberavaruudesta, jonka kanssa he henkilökohtaisesti ovat tekemisissä. Olkoon systeemi fyysinen palvelu tai kokoelma kyberavaruuden komponentteja, turvallisuusammattilaisen rooli kyseisen järjestelmän suhteen on tehdä suunnitelmia potentiaalisten hyökkäysten ja niistä aiheutuvien seurauksien estämiseksi.
7.2 Tekoälyä hyödyntäviä kyberturvallisuusratkaisuja
Tekoäly voi toimia ongelmanratkaisijana. Tekoälyratkaisuja ja kognitiivista tietojenkäsittelyä sovelletaan kyberhyökkäysten havaitsemiseen, torjuntaan ja selvittämiseen.
Analytiikkapohjaiset ratkaisut pohjautuvat sääntöihin, joita kyberturvallisuusasiantuntijat ovat luoneet. Ne jättävät huomioimatta kyberhyökkäykset, jotka eivät täsmää laadittujen sääntöjen kanssa. Perinteiset haittaohjelmien tunnistusohjelmat ovat yltäneet 80% tunnistusasteeseen, joka jää lähes 20 prosenttia syväoppimisen algoritmeja hyödyntävistä sovelluksista. Haittaohjelmien tunnistamista varten toteutetut sovellukset ovat kehittyneet jälkiin (signature), heurestiikkoihin ja käyttäytymiseen perustuvien tunnistusmenetelmien ajasta sandbox-menetelmien (hiekkalaatikko, joka luo väliaikaisen rajoitetun alueen järjestelmän sisään ja jota voidaan käyttää mm. haittaohjelmilta suojautumiseen) kautta kone- ja syväoppimiseen perustuvia menetelmiä hyödyntäviin ohjelmiin.

7.2.1 PatternEx AI2
Massachusetts Institute of Technologyn (MIT) Computer Science and Artificial Intelligence Laboratory (CSAIL) ja koneoppimiseen erikoistunut startup PatternEx kehittivät tekoälyalustan AI2, joka ennustaa tietoverkkohyökkäyksiä tehokkaammin kuin nykyiset järjestelmät. Tutkimuksissa AI2-alustan avulla päästiin 85% hyökkäysten tunnistamistarkkuuteen. Testit toteutettiin 3,6 miljardilla lokitietorivillä (log lines), joita generoivat miljoonat käyttäjät kolmen kuukauden tarkasteluajanjakson aikana. Estääkseen hyökkäyksiä AI2 käy dataa lävitse ja tunnistaa epäilyttävän toiminnan klusteroimalla datan merkityksellisiksi malleiksi ohjaamatonta koneoppimista hyödyntäen. Tämän jälkeen lopputulokset esitetään analyytikoille, jotka varmistavat, mitkä tapahtumat ovat todellisia hyökkäyksiä. Analyytikot myös sisällyttävät lopputuloksen alustan malleihin (ohjattu oppiminen) seuraavaa analysoitavaa tietojoukkoa varten, jolloin järjestelmä oppii lisää. Järjestelmä kykenee myös jatkuvasti generoimaan uusia malleja jopa tunneissa, jolloin sen hyökkäysten tunnistamisten nopeus voi merkittävästi ja nopeasti parantua.
Alla olevassa kuvassa verrataan ohjaamattoman koneoppimisen ja AI2-alustan kustannuksia. AI2:n algoritmin avulla 86% hyökkäysten tunnistusasteeseen voidaan päästä jo :n ollessa 200, jolloin se on vielä alle 9% koneoppimista hyödynnettäessä.
:n tulee olla hyvin suuri (yli 1000), jolloin käyrät voivat leikata eli budjetit ovat yhtä suuret. A2 toimii siis huomattavasti pienemmillä investoinneilla kuin ohjaamaton koneoppiminen yksinään. Kuvasta voidaan myös havaita, että ohjaamatonta koneoppimista hyödyntäen voidaan saavuttaa 73,5% hyökkäyksien tunnistusaste väärien hälytysten ollessa yli 22% epäilyttävistä tapahtumista. AI2-järjestelmää hyödyntäen voitiin päästä 86% tunnistustarkkuuteen väärien positiivisten ollessa 4.4% luokkaa.
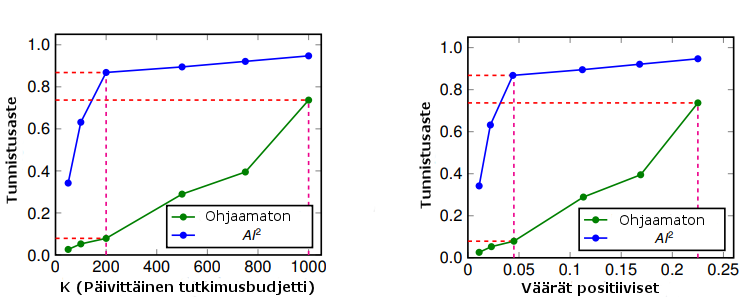
7.2.2 Amazon Macie
Amazon Macie on koneoppimista hyödyntävä tietoturvapalvelu. Tekoälyn avulla Macie kykenee löytämään, luokittelemaan ja suojelemaan sensitiivistä dataa Amazonin Web-palveluissa (Amazon Web Services, AWS). Macie tunnistaa sensitiivisen datan, kuten henkilötiedot tai tekijänoikeudet. Lisäksi se kykenee monitoroimaan, miten tekijänoikeussuojattua materiaalia, kuten dokumentteja, kopioidaan, siirretään tai tarkastellaan. Palvelu monitoroi jatkuvasti datan käyttöä ja epäsäännöllisyyksiä sekä tuottaa yksityiskohtaisia hälytyksiä, mikäli dataan kohdistuu luvatonta käyttöä tai kyseessä on muutoin tahaton datavuoto. Macie kykenee myös automaattisesti tunnistamaan esimerkiksi liiketoiminnalliseen dataan kohdistuvan riskin, mikäli sitä on luvatta jaettu organisaation ulkopuolelle tai siihen on muulla tavoin tahattomasti päästy käsiksi.
7.2.3 Cyberlytic
Cyberlytic profiler on WWW-uhkien tunnistamiseen kehitetty työkalu, joka tunnistaa ja priorisoi hyökkäyksiä dataan kohdistuvien riskien suuruuden mukaan. Profiler analysoi kaikkea HTTP-protokollaan pohjautuvaa Web-liikennettä analysoimalla Web-palvelinpyyntöjä ja vastauksia sekä tuottamalla reaaliajassa kattavan riskiarvion, jota voidaan tarkastella käyttöliittymän (dashboard) kautta. Profiler käyttää tekoälyä tunnistamaan kehittyneitä hyökkäyksiä, joita useimmat tavanomaiset Web-sovelluspohjaiset sähköistä allekirjoitusteknologiaa hyödyntävät palomuuriratkaisut eivät kykene tunnistamaan. Profiler käyttää Web-sovellusta ja ohjaamatonta koneoppimista analysoimaan datavirtoja. Itsenäisesti oppivat algoritmit profiloivat normaalia Web-liikennekäyttäytymistä tekemällä itse päätöksiä. Profiler käyttää patentoitua luokittelijalähestymistapaa määrittämään hyökkäyksen ominaisuuksia seuraaville hyökkäystyypeille: SQL Injection, Cross-site Scripting (XSS) ja Bash.
7.2.4 CylanceProtect
CylanceProtect on integroitu tietoturvauhkien estämiseen kehitetty työkalu, joka yhdistää tekoälyn tarjoamat hyödyt tietoturvakontrollien kanssa haittaohjelmainfektioiden estämiseksi. Tietoturvakontrolleja hyödynnetään suojautumisessa skriptipohjaisia, muistiin kohdistuvia ja ulkoisia laitteita hyödyntäviä hyökkäyksiä vastaan. CylanceProject
- Hyödyntää tekoälyä (ei allekirjoituksia) identifioidakseen ja estääkseen tunnettujen ja tuntemattomien haittaohjelmien suorituksen päätelaitteissa.
- Ennaltaehkäisee tunnettuja ja tuntemattomia nollapäivä-hyökkäyksiä.
- Suojelee päätelaitteita häiritsemättä loppukäyttäjää.
7.2.5 Darktrace
Darktrace soveltaa ihmisten immuunijärjestelmään liittyviä biologisia periaatteita suojellakseen yrityksiä kehittyneiltä kyberuhilta. Darktracen teknologia auttaa yrityksiä reaaliajassa tunnistamaan tietoverkoissa tapahtuvia epänormaaleja tapahtumia jo ennen kuin ne kehittyvät haittaa aiheutuviksi kyberhyökkäyksiksi.
Darktracen avulla voidaan havaita ja tunnistaa kehittyviä kyberuhkia, jotka kykenevät kiertämään perinteiset tietoturvallisuusratkaisut. Darktrace käyttää alla olevassa kuvassa esitettävää Enterpise Immune System-teknologiaa (EIS) . Se hyödyntää koneoppimista ja Bayesin teoreemaa (myös Bayesin sääntö tai Bayesin laki, joka on ehdolliseen todennäköisyyteen liittyvä matemaattinen teoreema), seuratakseen käyttäytymistä ja havaitakseen poikkeavuuksia organisaation tietoverkossa. Koska EIS hyödyntää matemaattisia lähestymistapoja, se ei tarvitse allekirjoituksia tai sääntöjä, vaan se kykenee tunnistamaan tuntemattomiakin hyökkäyksiä, jollaisia ei olla aiemmin nähty. EIS kykenee tunnistamaan suurimman osan verkossa piilevistä kyberuhista, mukaan lukien sisäpiiristä ilmenevät uhat, ja reagoimaan niihin. Koneoppimista ja matematiikkaa hyödyntäen EIS pystyy automaattisesti ja mukautuen oppimaan jokaisen käyttäjän, laitteen ja verkon tavan toimia tunnistaakseen käyttäytymismalleja, jotka ilmentävät todellisia kyberuhkia. Darktracen itseoppiva teknologia tarjoaa yrityksille kattavan näkyvyyden verkon toimintaan ja sallii niiden vastata ennakoivasti uhkiin ja vähentää riskiä.
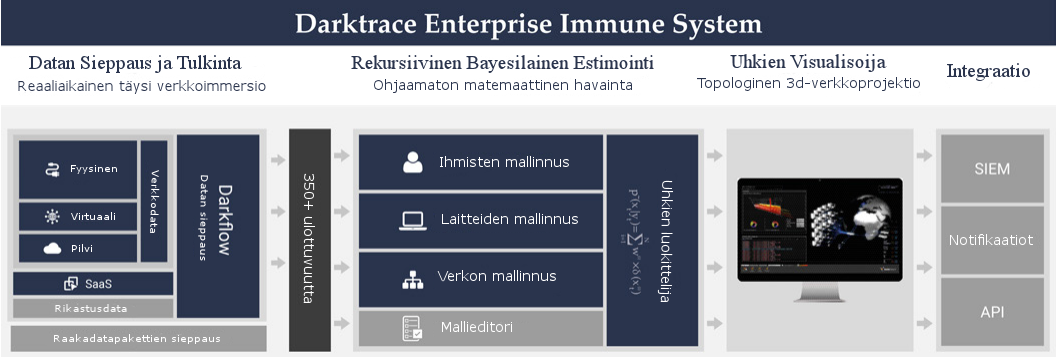
Darktracen ytimessä on neljä matemaattista toimintalogiikkaa, jotka hyödyntävät useita matemaattisia lähestymistapoja, kuten rekursiivinen bayesilainen estimointi. Ensimmäiset kolme toiminnallisuutta tuottavat käyttäytymismalleja yksittäisille ihmisille ja laitteille, sekä yrityksille kokonaisuudessaan. Havaittaessa epätavallista käyttäytymistä yksi tai useampi näistä toiminnoista lähettää viestin uhkien luokittelijalle (threat classifier), jonka tehtävänä on luokitella väärät positiiviset tapaukset ja raportoida aidoista poikkeamista, joiden tarkempi tarkastelu on relevanttia. Bayesilaisen lähestymistapojen kombinaatio, jota uhkien luokittelija korreloi ja mittaa, mahdollistaa tarkan poikkeamien tunnistamisen yrityksen mittakaavassa. Darktrace hyödyntää myös integroitua moduulia (model editor), jolla voidaan seurata ja valvoa toimintaperiaatteita. Tämä tukee muiden säännönmukaisuuskäytäntöjen- ja mallien määrittelyä, jotka voidaan yhdistää haluttuihin tunnistamisvaatimuksiin.
7.2.6 Deep Instinct
Deep Instinctin ohjelmisto on suunniteltu suojelemaan organisaatiota, mobiililaitteita ja palvelimia tunnettuja ja tuntemattomia haittaohjelmahyökkäyksiä vastaan reaaliajassa. Ohjelmisto perustuu neuroverkkojen hyödyntämiseen. Tekoälyn avulla Deep Instinct kykenee tunnistamaan haitallisia ohjelmia mobiililaitteissa, palvelimissa ja työasemissa. Käyttämällä soveltuvia syväoppimisen algoritmeja ohjelmisto kykenee ennakoimaan ennalta tuntemattomia kyberhyökkäyksiä.
Deep Instinct on onnistunut hyödyntämänsä neuroverkkoteknologian avulla torjumaan hyökkäyksiä, kuten Spora, WannaCry, NotPetya ja Badrabbit ilman SOC:n (Security Operations Center) apua ja ennen kuin haittaohjelmilla on ollut minkäänlaista vaikutusta organisaation IT-ratkaisuihin. Deep Instinctin kehittäjät hyödyntävät syväoppimisen algoritmeja, joiden avulla on mahdollista tunnistaa haittaohjelmiin viittaavia rakenteita.
7.2.7 SparkCognition DeepArmor
Uudenlaiset uhkat vaativat kehittyneitä nykyaikaisia ratkaisuja yhä kehittyvällä kyberturvallisuuden sektorilla. Tähän saakka hyökkääjät ovat helposti voineet välttää allekirjoituksiin perustuvia virustorjuntaratkaisuja, mistä johtuen 95% kybermurroista tapahtuu loppukäyttäjien päässä. SparkCognition DeepArmor kykenee tunnistamaan ja estämään haittaohjelmien, virusten, matojen, troijalaisten ja kiristysohjelmien uhkan hyödyntäen matemaattisia menetelmiä, kuten koneoppimisen metodeja ja luonnollisen kielen prosessointia.
DeepArmor-arkkitehtuuri koostuu pienestä päätelaitegentista (endpoint agent), joka on integroitu pilvipohjaisen kognitiiviseen moottoriin ja uhkia tarkastelevan alustan kanssa. Päätelaiteagentti tunnistaa ja estää haittaohjelmia ja muita kehittyneempiä uhkia allekirjoituksista riippumatta. Agentti on suunniteltu suojelemaan asiakasta, palvelinta, mobiili- ja IoT-laitteita sekä tarjoamaan yhdistetyn kyberturvallisuuden koko yritykseen. Agentti voidaan myös konfiguroida toimimaan autonomisesti ilman käyttöliittymää ja tarjoamaan tietoturvaratkaisun IoT-laitteille.
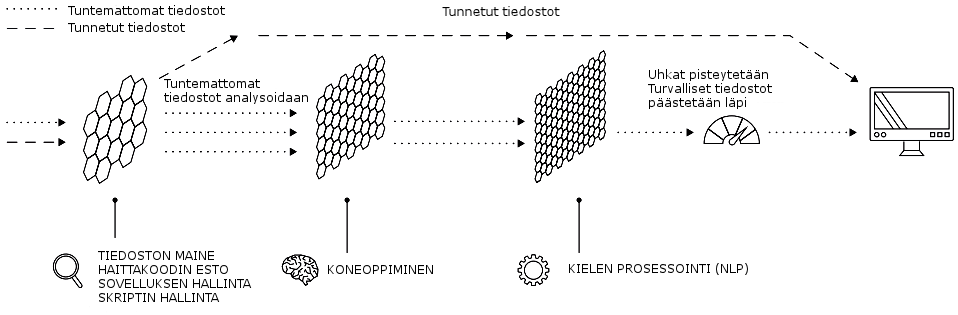
DeepArmor-ratkaisun pilvipohjainen kognitiivinen moottori käyttää useampikerroksista suodatusprosessia uhkien tunnistamisessa. Ensimmäisessä suojauskerroksessa toteutetaan tiedostoanalyysi sekä sovelluksen- ja riskien kontrollointi, jolloin voidaan nopeasti tunnistaa tunnetut haitalliset ja poikkeavat tiedostot. Tunnistettujen tiedostojen suodattamisen jälkeen DeepArmor käyttää kognitiivisia algoritmeja, jotka tutkivat tuntemattomien tiedostojen DNA:n ja muodostavat uhkapisteytyksen jokaiselle tiedostolle. Uhkan tunnistamisen jälkeen pilvipohjainen hallintakonsoli tarjoaa luonnollisen kielen prosessointityökalun (Natural Language Processing, NLP). DeepNLP ei vain etsi Internetistä evidenssiä uhkista, vaan myös ymmärtää uhkien ympärillä olevan kontekstin. Näin menettelemällä DeepArmor kykenee erottamaan todella haitalliset tapaukset pelkästään poikkeavista tapauksista.
7.2.8 Vectra Networks Cognito
Cognito hyödyntää tekoälyä reaaliaikaisen kuvan muodostamiseen meneillään olevista kyberhyökkäyksistä yksityiskohtineen, mikä mahdollistaa välittömän reagoinnin. Cognito yhdistää kehittyneitä koneoppimisen teknologioita jatkuvasti oppivien käsitemallien kanssa löytääkseen nopeasti ja tehokkaasti piilossa olevat ja tuntemattomat hyökkääjät ennen kuin ne aiheuttavat vahinkoa. Cognito eliminoi myös niin sanotut "sokeat pisteet" analysoimalla kaikkea tietoturva- ja autentikointijärjestelmien sekä SaaS-sovellusten verkkoliikennettä ja lokitiedostoja.
Vectra Cognito hyödyntää kyberhyökkäysten torjunnassa ja tunnistamisessa kehittyneitä ohjatun ja ohjaamattoman koneoppimisen tekniikoita, kuten syväoppimista ja neuroverkkoja. Perinteiset tietoturvajärjestelmät koettavat löytää hyökkäyksiä etsimällä järjestelmään kohdistuvista hyökkäyksistä tunnettuja allekirjoituksia (signature) ja hyväksikäytön mahdollistavia aukkoja (exploit). Cognito oppii koko verkossa tapahtuvasta toiminnasta pitkällä aikavälillä päivien, viikkojen tai kuukausien aikana. Cognito tunnistaa hyökkääjän verkkokäyttäytymisen kyberhyökkäysketjun jokaisessa vaiheessa. Tunnistettu hyökkääjän käyttäytyminen kategorisoidaan ja verrataan normaaliin palvelimien kanssa tapahtuvaan verkkokäyttäytymiseen, jotka on pisteytetty riskitasojen ja niiden määrittämisen suhteen. Hyökkäyskäyttäytymisestä tunnistetaan erityisesti sellaiset, jotka ovat osa yksittäistä koordinoitua hyökkäyskampanjaa. Tällöin ylläpitäjät voivat keskittyä suuntaamaan voimavaransa hyökkäyksiin, jotka aiheuttavat kaikkein suurimman liiketoiminnallisen riskin.
7.2.9 IBM Security-tietoturvaratkaisu
IBM:n kyberturvallisuusratkaisu (IBM Security) on integroitu ratkaisu, joka auttaa organisaatioita tunnistamaan, kohdistamaan ja estämään tietoturvauhkia. IBM Security on konsepti integroidusta kyberturvallisuusratkaisusta, jossa analytiikkakyvykkyys on asetettu ratkaisun keskiöön.
IBM Security koostuu kahdeksasta osasta: ulkoinen tiedustelutieto (threat intelligence), tietoverkko (network), edistyneet huijaukset (advanced fraud), identiteetti ja pääsynhallinta (identity & access), data, sovellukset (apps), mobiili (mobile) ja loppukäyttäjä (endpoint). Tietoturvaratkaisun tarkoituksena on olla kokonaisvaltainen ratkaisu, jonka avulla koko organisaation kyberturvallisuus voidaan järjestää aina tietoverkon turvaamisesta mobiililaitteisiin, sovelluksiin ja loppukäyttäjiin saakka.
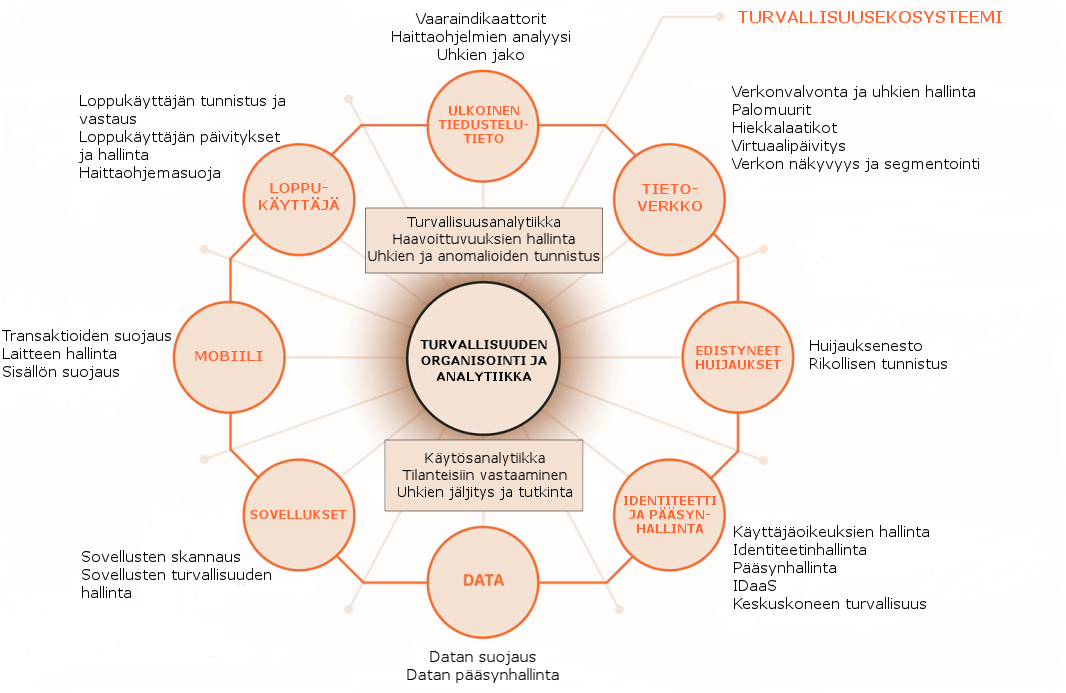
Alla olevassa kuvassa esitellään IBM Security -ratkaisuun liittyvät sovellukset. Alustan keskeisenä sovelluksena on IBM QRadar Watson Advisor, joka hyödyntää Watsonin opettamiseksi kerättyä tietoa kyberturvallisuuskorpusta. IBM QRadar Watson Advisor ja sen sisältämät kognitiiviset kyvykkyydet ovat hyödynnettävissä IBM QRadar Security Intelligence Platformin kautta. Potentiaalisten uhkien tunnistamiseksi voidaan hyödyntää Watsonin luonnollisen kielen ymmärtämisen kyvykkyyksiä, jolloin muun muassa blogien, verkkosivujen, tutkimusraporttien ja QRadarin tarjoaman datan läpikäynti helpottuu ja nopeutuu. Prosessi voi nopeuttaa tietoturvauhan selvitykseen kuluvaa aikaa viikoista ja päivistä minuutteihin. IBM SOC -alusta kykenee lisäksi hyödyntämään IBM:n i2-analytiikkatyökalua ja IBM X-Force Exchange-tietokantaa. Tulevaisuudessa asiantuntijoiden avuksi on SOC:hin tarkoitus kehittää puhuva assistentti, joka kykenee vuorovaikutteiseen toimintaan ja avustamaan tietoturva-analyytikoita muun muassa reaaliaikaisissa tietoturvauhkapäivityksissä ja suosituksien antamisessa uhkatilanteiden korjaamiseksi.
Ulkoisen tiedustelutiedon hallintaan on tarjolla X-Force Exchange-alusta. Se on yhteistyöalusta, joka tuo uhkien analytiikkapalveluita ja teknologioita pilvipalveluun SaaS (Software as a Service) palveluna, joka nopeuttaa yritysten valmiuksia priorisoida uhkia sekä lisää joustavuutta ja ammattiosaamista. IBM Exchangen käyttäjät voivat hyödyntää IBM:n kyberturvallisuusaineistoa ja koko verkoston asiantuntijoiden tietotaitoa. Kyberturvallisuusuhkien tutkimiseksi ja estämiseksi IBM on lisäksi perustanut tietoturva-alan ammattilaisista koostuvan X-Force IRIS (Incident Response and Intelligence Services) -ryhmän, jonka tarkoituksena on vahvistaa asiakasorganisaatiota yhä kehittyviä globaaleja tietoturvauhkia vastaan.
IBM Security-ratkaisun tietoverkko-osa-alueeseen kuuluvat QRadar Incident Forensics ja QRadar Network Insights sekä Management Network Security Secure ja Secure SD-Wan-palvelut. QRadar Incident Forensics tarjoaa kyberturvallisuusasiantuntijoille mahdollisuuden jäljittää askel askeleelta potentiaalisen hyökkääjän toimia ja toteuttaa nopeasti tutkimuksia epäilyttävistä ja mahdollisesti haitallisista tietoverkkoihin kohdistuvista tapahtumista. QRadar Incident Forensics myös nopeuttaa QRadarin keräämän informaation tutkimista ja prosessi voi nopeutua päivistä tunteihin tai jopa minuutteihin. QRadar Network Insights analysoi tietoverkossa liikkuvaa dataa reaaliajassa ja pyrkii paljastamaan hyökkääjän "jalanjäljet" ja piilossa olevat tietoturvauhat, esimerkiksi haittaohjelmat, ennen kuin ne vahingoittavat organisaatiota. Managed Network Security Services tarjoaa monitorointi-, hälytys- ja verkon tietoturvateknologiapalveluita osana IBM Security-ratkaisua.
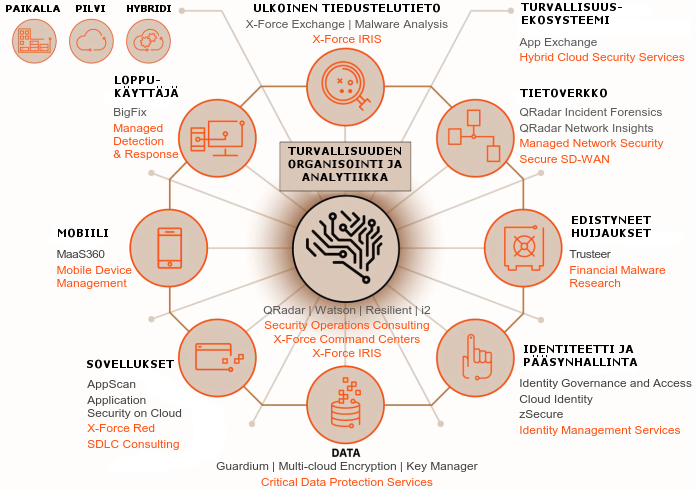
IBM I2 Enterprise Insight Analysis (EIA)
Infrastruktuurin, asiakasyhteyden ja datan turvaaminen ovat kriittisiä asioita liiketoiminnassa ja niin yritysten kuin työntekijöidenkin maineen säilyttämisessä. Kyberhyökkäykset voivat pysyä salassa jopa kahdeksan kuukautta. Nykyajan kyberhyökkäyksistä on tulossa yhä kehittyneempiä, ketterämpiä ja kykenevämpiä läpäisemään lähes minkä tahansa tietoverkon turvallisuusratkaisun, joten yritysten tulee korvata perinteisiä kyberturvallisuusstrategioita proaktiivisella tietopohjaisella ratkaisulla.
IBM i2 Enterprise Insight Analysis-tietoturvaratkaisun avulla organisaatiot voivat proaktiivisesti saavuttaa kattavan ymmärryksen organisaation haavoittuvuuksista ja kehittää kyberhyökkäysskenaarioita, jotka nopeuttavat hyökkäyksiä koskevien selvityksien ja korjauksien tekemistä. Tulevaisuudessa tapahtuvien hyökkäyksien ehkäisemiseksi organisaatiot voivat koettaa tunnistaa ja tutkia kyberhyökkääjien toimia hyökkäystapahtumien jälkeen sekä päivittää saadun informaation perusteella kyberturvallisuusstrategiaansa ja taktiikkaansa. Perinteisten tietoturvallisuuteen liittyvien operaatioiden ollessa rajoittuneita IT-pohjaiseen dataan ja metriikoihin, proaktiivinen kybertiedustelu tarjoaa mahdollisuuden yhdistää dataa muuhun sisäiseen dataan, kuten HR-tietokantoihin sekä kybertoimijoiden ja ryhmien analysointiin.
IBM i2 Enterprise Insight Analysis käyttää jo olemassa olevaa tietoturvainfrastruktuuria, muuta infrastruktuuridataa ja avointa lähdekoodia hyödyntävien järjestelmien tarjoamaa dataa. Tietomurron, sen metodien ja tietomurron tekijän tietomurtoon liittyvien henkilökohtaisten tapahtumien tunnistaminen ja tutkiminen perustuvat näiden useiden tietolähteiden hyödyntämiseen. Ratkaisu käyttää myös sosiaalisesta mediasta saatua kerroksittaista dataa, jotta on mahdollista selvittää organisaatioon hyökkäävä taho, hänen/heidän sijaintinsa, kohteensa ja kumppaninsa. Näihin tietoihin perustuen organisaatio voi omaksua uusia toimintatapoja ja puolustusta koskevia strategiamuutoksia.
IBM i2 EIA kykenee laajentamaan jo olemassa olevaa kyberturvallisuusratkaisua lisäominaisuuksilla, kuten moniulotteisella visuaalisella analytiikalla. Sen avulla tutkijat voivat saada paremman kuvan hyökkäyksestä visualisoimalla kattavan tilannekuvan kaikista tilanteeseen liittyvistä elementeistä. EIA:n avoin ja modulaarinen arkkitehtuuri on skaalautuva ja lisäksi täysin räätälöitävissä kolmannen osapuolen sovelluksien ja niiden tarjoamien ominaisuuksien kanssa. Näitä ominaisuuksia ovat esimerkiksi luonnollisen kielen prosessointi sekä analytiikka taktisella, operationaalisella ja strategisella tasolla. EIA tarjoaa myös yhteensopivuuden organisaation sisällä ja ulkopuolella. Avoin malli ei pelkästään integroi jo olemassa olevaan arkkitehtuuriin ja muihin sovelluksiin, vaan antaa käyttäjille mahdollisuuden jakaa helposti informaatiota tietoturvauhkista organisaation laajuisesti sekä kumppaneiden, asiakkaiden ja muiden organisaatioiden kanssa.
Perinteinen palomuuri kykenee kuvassa esitetyn käyrän mukaisesti ehkäisemään maksimissaan 80% kyberhyökkäyksistä. IBM:n QRadarin tuoma lisäarvo traditionaalisen palomuurin käyttöön on 0-10% yksikköä, jolloin on mahdollista saavuttaa 90% taso. Kyberanalyysia hyödyntävä ja eniten käytännön työtä vaativan IBM:n EIA:n avulla turvallisuutta voidaan edelleen lisätä ja saavuttaa jopa 99.9% taso.
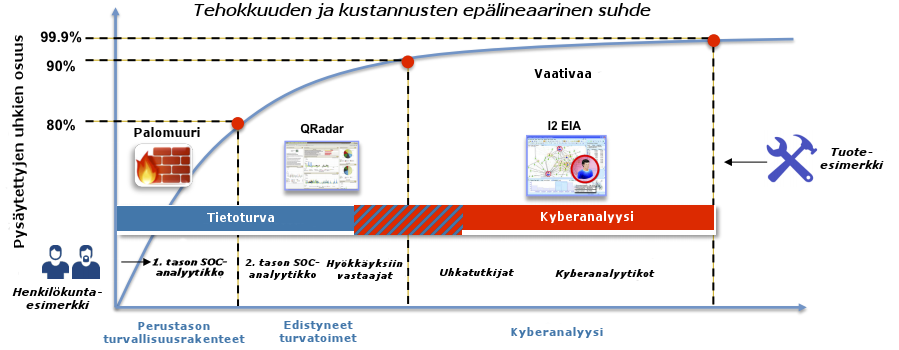
IBM MaaS360 with Watson
IBM MaaS360 on IBM:n kehittämä mobiililaitteiden hallintasovellus, joka mahdollistaa kaikkien organisaation mobiilien henkilökohtaisten laitteiden, sovelluksien ja sisällön hallinnan ja tietoturvan ilman, että se rasittaa IT-tuen resursseja. MaaS360 tarjoaa tietoturvallisen ympäristön, joka pitää yrityksen mahdollisia liikesalaisuuksia sisältävät tiedostot erossa mobiililaitteeseen asennetuistaa sovelluksista. Tämä mahdollistaa sen, että organisaatioiden työntekijät voivat työskennellä vaarantamatta dataan ja laitteeseen liittyvää tietoturvaa. Ratkaisu yksinkertaistaa IT:n hallintaa, sillä riittää monitoroida koko laitteen sijaan ainoastaan ympäristöä kontrolloivaa sovellusta.
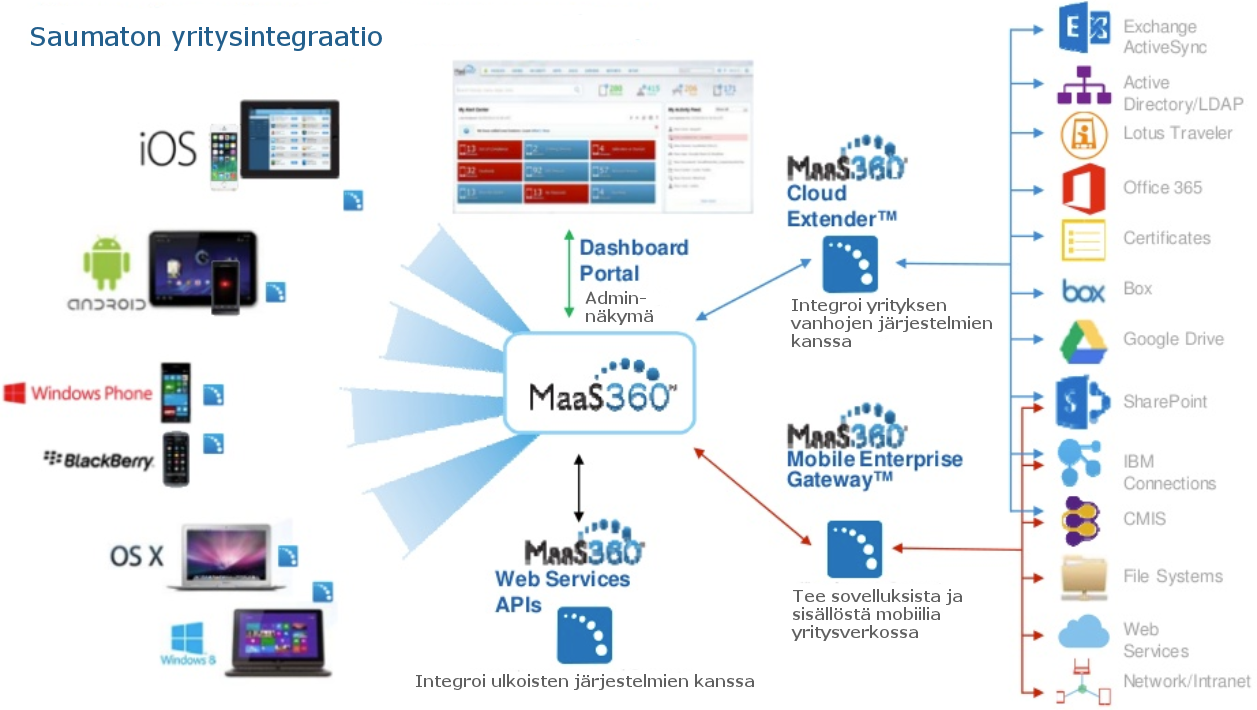
Sovelluksen avulla kaikkia laitteita voidaan monitoroida yhdestä paikasta ja valvoa langattomasti. MaaS360:n tarjoaman mobiililaitteiden hallintakyvyn avulla yritykset voivat antaa työntekijöille mahdollisuuden käyttää työtehtäviensä toteutuksessa omia mobiililaitteitaan.
MaaS360:n avulla organisaatiot voivat hallita sovelluksia interaktiivisen luettelon välityksellä. Luettelon kautta ne voivat ohjata käyttämään valittuja sovelluksia, jakaa niitä käyttäjille ja päivittää niitä tarpeen vaatiessa. Lisäksi MaaS360 varmistaa, että yrityksen data on salattuna ja että se pidetään erillään muista mobiililaitteisiin asennetuista sovelluksista, jotta ne eivät pääse dataan käsiksi. MaaS:n avulla organisaatiot voivat myös rajoittaa työntekijöiden oikeuksia dataan ja sallia heille kontrolloidusti oikeuksia, joita he tarvitsevat työtehtäviensä hoitamiseksi.
Yksi tärkeimmistä MaaS360:n ominaisuuksista on IBM Watsonin tarjoama kognitiivinen analytiikka, jolloin historiatietoja, nykyisyyttä ja tulevaisuuden ennusteita hyödyntäen voidaan parantaa päätöksentekoprosessia ja auttaa IT- sekä tietoturvallisuusjohtajia EU:n tietoturva-asetuksen GDPR:n (General Data Protection Regulation) huomioinnissa.
IBM QRadar Advisor with Watson
Watson for Cyber Security laajentaa kyberturvallisuusanalyytikon kyvykkyyksiä kehittyneiden uhkien tunnistamisessa ja ymmärtämisessä pureutuen rakenteettomaan dataan (blogit, WWW-sivut, tutkimuspaperit) ja korreloiden sitä paikallisten kyberturvallisuushyökkäyksien kanssa. QRadar tulkitsee rakenteetonta dataa, joka on luotu välittämään informaatiota ihmiseltä ihmiselle ja korreloi sitä rakenteellisen datan kanssa paljastaen uutta relevanttia informaatiota kyberturvallisuushyökkäyksistä. QRadar Advisor etsii pimennossa olevia datapisteitä, joita muut sovellukset tai palvelut eivät löydä ja siten kykenee tarkemmin tunnistamaan uhkia. Tavoitteena on muodostaa strategia tietoturvauhkien torjumiseksi.
IBM QRadar Advisor with Watson hyödyntää IBM Watsonin kognitiivisia kyvykkyyksiä (tekoälyä) ja QRadar Security Platformin kyberturvallisuusanalyysiin kehitettyä alustaa paljastaessaan piilossa olevia uhkia ja automatisoidessaan niiden tunnistusprosessia. Järjestelmä tutkii automaattisesti vaarallisia indikaattoreita, hyödyntää kognitiivisia kyvykkyyksiä tarjoten kriittisiä näkemyksiä ja lopuksi nopeuttaa kyberturvallisuusuhkien reaktiosykliä.
QRadar Advisor with Watson toimii seuraavien kuvassa näkyvien vaiheiden kautta:
- QRadar Security Intelligence-alustan tunnistaessa kyberturvallisuusuhan, analyytikko voi siirtää sen -QRadar Advisor with Watsonille tarkempaa tutkimusta varten. Advisor tekee ensin uhkaa koskevan laajemman kartoituksen louhimalla lokaalista QRadar-ohjelmistosta saatavaa dataa. Tämän jälkeen ohjelmisto hyödyntää Watson for Cyber Security-ohjelmistoa tarkemman analyysin suorittamiseksi uhasta.
- Watson for Cyber Security tutkii tietokantaa, joka koostuu sadoista tuhansista lähteistä, jotka on kerätty esimerkiksi WWW-sivuilta, kyberturvallisuusfoorumeilta ja uutiskoosteista, ja koostaa näistä ymmärrettävän kokonaisuuden. Tämän jälkeen ohjelmisto etsii kyberturvallisuusuhkaan liittyvää lisäinformaatiota koskien haitallisia tiedostoja ja epäilyttäviä IP-osoitteita.
- Lopuksi QRadar Advisor with Watson prosessoi informaatiota, jota se saa Watson for Cyber Security-ohjelmistolta etsien kyberturvallisuusuhkaan liittyviä avaintekijöitä.
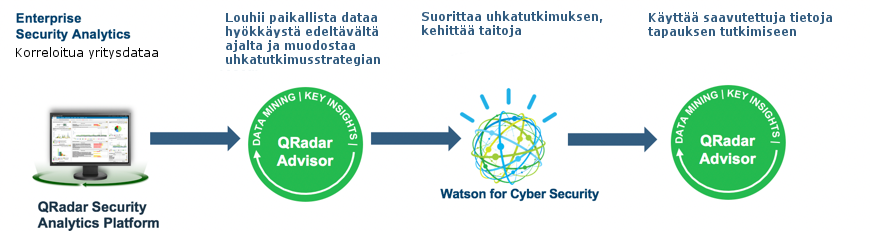
IBM QRadar with Watsonin avainominaisuuksia ovat automaattinen uhkatapausten tutkiminen, tekoälyn hyödyntäminen ja korkean tason riskien havaitseminen. QRadar toteuttaa paikallista tiedon louhintaa kyberturvallisuushyökkäyksistä keräten aineistoa. Tämän jälkeen sovellus tarkastaa, onko jokin tai jotkin uhista läpäisseet kerroksittaiset suojaukset vai ovatko ne estetty. Luetteloiden ja tiettyjen sopivien indikaattoreiden avulla tarkastusta voidaan automatisoida. Kognitiivisen päättelyn avulla voidaan tunnistaa todennäköisimmät uhat ja yhdistää ne alkuperäisiin tapahtumiin, esimerkiksi haitalliset tiedostot ja epäilyttävät IP-osoitteet, yhteyksien piirtämiseksi uhkien ja tapahtumien välille. Lisäksi QRadar käyttää automaattisesti Watson for Cyber Securitya ulkoisen rakenteettoman datan, kuten WWW-sivujen, foorumien ja uhka-analyysin hyödyntämiseksi. IBM QRadar myös paljastaa tapahtumien kriittisyyden, eli onko haittaohjelma aktivoitunut vai ei.
IBM QRadar Information Security and Event Mgmt (SIEM)
SIEM-ohjelmistot yhdistävät useita erilaisia kyberturvallisuusohjelmistokomponentteja yhdeksi alustaksi. Yritykset hyödyntävät SIEM-ohjelmistoja keskittääkseen kyberturvallisuusoperaatiot yhteen sijaintiin. Asiantuntijaryhmät, jotka hoitavat IT- ja kyberturvallisuusoperaatioita, voivat päästä käsiksi samaan informaatioon ja hälytyksiin tehokkaamman kommunikaation ja suunnittelun mahdollistamiseksi. Tämänkaltaiset tuotteet tarjoavat kyvykkyyksiä, joiden avulla kyberturvallisuusasiantuntijat voivat tunnistaa ja saada hälytyksiä IT-järjestelmissä havaituista anomalioista. Anomaliat voivat olla uusia haittaohjelmia, hyväksymättömiä järjestelmään kirjautumisia tai uusia havaittuja haavoittuvuuksia.
IBM QRadar SIEM:n avulla voidaan kerätä, normalisoida ja korreloida tietoverkoissa liikkuvaa dataa hyödyntämällä vuosien aikana kertynyttä kokemusta. QRadar SIEM integroituu satoihin IBM:n ja muiden valmistajien tuotteisiin. Lisäksi QRadar tarjoaa kattavan näkymän kyberturvallisuustapahtumiin, jotka voivat liittyä organisaation tiloissa, hybridi- tai pilviympäristöissä tapahtuviin tapahtumiin. SIEM-ratkaisun keskiössä on kehittynyt analytiikkamoottori, joka on suunniteltu keräämään reaaliaikaista lokitietoa ja tietoverkon virtausinformaatiota sekä hyödyntämään kehittynyttä analytiikkaa mahdollisten hyökkääjien tunnistamiseksi.
QRadar SIEM on skaalautuva ratkaisu, joka kerää ja hyödyntää tuhansien hajautettujen tietoverkon laitteiden lähettämää dataa tallentaen kaiken toiminnan ja tietoturvatapahtumat tietokantaan sekä käyttää analytiikkakyvykkyyksiä erottamaan oikeat uhat vääristä positiivisista. Lisäksi ratkaisu kaappaa TCP-IP-kerroksen 4 verkon virtausdataa ja kerroksen 7 sovelluksien hyötykuormia hyödyntämällä IP-pakettien tarkastusteknologiaa. QRadarin intuitiivinen käyttöliittymä auttaa IT-asiantuntijoita nopeasti tunnistamaan ja puuttumaan kyberhyökkäyksiin oikealla prioriteetilla. Ratkaisu karsii satojen hälytyksien ja poikkeavien tapahtumien joukosta huomattavasti pienemmän ydinjoukon, jota voidaan tarkastella lähemmin. Nämä poikkeavat tapahtumat voivat sisältää sovelluksien sopimatonta käyttöä tai hyödyntämistä laittomiin tarkoituksiin, organisaation sisäisiä huijausyrityksiä ja varkauksia sekä uhkia, jotka useimmiten hukkuvat miljoonien tietoturvatapahtumien joukkoon.
QRadar kykenee tunnistamaan eri tavoilla anomalioita, jotka voivat olla indikaatioita organisaation sisäisistä uhista. Se havaitsee tilanteet, jossa sovelluksia tai pilvipalveluita käytetään huomattavasti tai ne eivät ole käytössä ollenkaan. Lisäksi QRadar osaa tunnistaa, mikäli tietoverkon aktiivisuustila eroaa huomattavasti historiallisesta tai keskimääräisestä aktiivisuudesta ja oppii tunnistamaan nämä päivittäiset tai viikoittaiset käyttöprofiilit. Tämä auttaa kyberturvallisuusasiantuntijoita nopeasti tunnistamaan merkittäviä anomalioita.
QRadar SIEM kykenee monitoroimaan sovelluksia sekä järjestelmiä, kuten ERP, tietokannat, Skype, VoIP ja sosiaalinen media. Monitorointi sisältää informaation, kuka käyttää ja mitä, analyysit sekä hälytykset koskien sisällön siirtoa ja korreloinnin muun tietoverkossa tapahtuvan aktiviteetin kanssa, jotta luvattomat tiedonsiirrot ja poikkeavat käyttäytymismallit voivat paljastua. QRadar SIEM sisältää useita erilaisia anomalioiden ja käyttäytymisen tunnistuksen säännöstöjä ja lisäksi kyberturvallisuusasiantuntijat voivat luoda omia sääntöjään.
IBM QRadar User Behavior Analytics
Loppukäyttäjien käyttäytymisanalyysi (User Behavior Analytics UBA) on ollut jo viime aikoina paljon huomiota saanut keskustelunaihe. Organisaation ulkoisia uhkia vastaan rakennettua suojausta kehitettäessä on myös huolehdittava sisältäpäin tulevista uhkista. Uhkia voivat aiheuttaa muun muassa tahallista haittaa aiheuttava työntekijä, huolimaton liiketuttavuus tai ulkoinen toimija. Tämänkaltaiset uhat ovat vaikeita tunnistaa ja ne voivat aiheuttaa huomattavaa tuhoa yrityksen omaisuudelle heikentäen yrityksen aineetonta omaisuutta ja kuluttajien luottamusta sekä vahingoittaa organisaation brändiä ja mainetta.
Esimerkiksi vuonna 2016 tapahtunut hyökkäys sähköverkkoa kohtaan Ukrainassa aiheutti sähkökatkoksen 200 000 asiakkaalle. Hyökkäys sai alkunsa työntekijän avatessa infektoituneen Word-dokumentin, jonka kautta hyökkääjät onnistuivat lähettämään haittaohjelman sähkölaitoksen työntekijöille ja kykenivät sen avulla varastamaan kriittistä informaatiota ja sulkemaan sähkölaitoksen järjestelmiä.
Edellä mainitun kaltaisia hyökkäyksiä vastaan on kehitetty käyttäytymisanalyysiin perustuvia ratkaisuja kuten IBM QRadar UBA-sovellus. Se on tunnistanut muun muassa seuraavanlaisia käyttäytymismalleja:
- Järjestelmien ylläpitäjät ovat muuttaneet loppukäyttäjien attribuutteja ilman lupaa.
- Käyttäjät ovat jakaneet VPN-verkon pääsytietoja.
- Laitteita on viety pois maasta käyttäjien ollessa lomalla.
- Käyttäjät esimerkiksi Pohjois-Amerikassa ovat lukeneet sähköpostiviestejä pilvipalvelussa ja muutamien minuuttien päästä tileille on koetettu kirjautua ulkomailta.
- SOC:n asiantuntijoiden tilit ovat infektoituneet haittaohjelmien vuoksi.
- Tietoturvatyökalujen havaitut väärinkäytökset.
- Käyttäjät ovat avanneet henkilökohtaisia tilejä palvelimilla.
- Enemmän kuin oletettu määrä sisäänkirjautumisia.
Koneoppimisen algoritmeja voidaan hyödyntää loppukäyttäjän tavanomaisen käyttäytymisen ymmärtämisessä ja merkityksellisten poikkeamien havaitsemisessa. Koneoppimisen algoritmeja on sisällytetty IBM:n QRadar UBA-sovellukseen, jotta loppukäyttäjien epäilyttävä käytös ja poikkeava toiminta voidaan havaita. Nämä koneoppimisen algoritmit kykenevät tunnistamaan ajallisia ja aikasarjan poikkeavuuksia. Poikkeavuuksien tunnistamiseksi käyttäjien toimintaa monitoroidaan ja monitoroinnin perusteella luodaan normaalin käyttäytymisen, resurssien ja verkkoviestinnän hyödyntämisen toimintamallit. Näitä malleja voidaan hyödyntää haluttaessa määrittää, milloin loppukäyttäjä alkaa tehdä jotain uutta. Algoritmit kykenevät tunnistamaan ja ilmoittamaan poikkeavasta käyttäytymisestä sekä käynnistävät UBA-sovelluksen, jonka käyttäjien riskipisteitä nostetaan aina tarpeen vaatiessa.
Monitoroimalla jokaisen organisaation tietojärjestelmän loppukäyttäjän aktiviteettia, työkalu kykenee tunnistamaan käyttäjällä organisaatiossa olevia rooleja. Tällöin käyttäjät voidaan jakaa roolipohjaisiin vertaisryhmiin. Näistä rooleista poikkeava uudenlainen käyttäytyminen voidaan tunnistaa ja se voi olla alkuvaiheen indikaattori haitallisista tarkoitusperistä. Algoritmit toimivat itsenäisesti ja tarkkailevat käyttäjän aktiviteetteja useista eri näkökulmista, jotta väärien positiivisten tulosten määrä voi vähentyä. Kyseiset algoritmit monitoroivat laajaa käyttötapausten aluetta, kuten:
- Loppukäyttäjien aktiviteettien muutokset ilman muutosta niiden toistuvuudessa.
- Muutokset aktiviteetin toistuvuudessa ilman aktiviteettiin kohdistuvia muutoksia.
- Muutokset loppukäyttäjien aktiviteetin aikaikkunaan.
- Datan suodattaminen laitteesta tai verkon kautta.
UBA-sovellus toimii QRadar-järjestelmän kanssa keräten dataa organisaation verkossa olevista käyttäjistä. UBA-sovelluksen graafiseen käyttöliittymään kerätään tietoja Docker-säiliöstä (SQLite-tietokanta). Kerättäviä tietoja ovat muun muassa käyttäjänimet, viimeiset riskipisteet, järjestelmän pisteet, hälytykset ja trendit. Käyttöliittymään päivittyy informaatiota myös QRadar-järjestelmän puolelta. QRadar-järjestelmän toimittamaa tietoa ovat hyökkäykseen liittyvä informaatio, tila ja lähteet. Lisäksi QRadar-järjestelmän ARIEL-tietokannasta saadaan muun muassa yleislaatuista dataa ja käyttäjien aktiviteetin kirjaustietoja, jotka vastaavat käyttäjänimillä toteutettuja aktiviteetteja. UBA-sovellus lähettää QRadar-järjestelmälle informaatiota meneillään olevista hyökkäyksistä tarkempia tutkimuksia varten.
IBM Resilient Incident Response Platform (IRP)
IBM Resilient Incident Response Platform (IRP) on alusta tapahtumaprosessien automatisoimiseksi. IRP integroituu organisaation jo olemassa oleviin kyberturva- ja IT-ratkaisuihin ja tarjoaa keskitetyn alustan kyberhyökkäysten tutkintaan ja niiden estämiseen. IRP antaa kyberturvallisuusasiantuntijoille mahdollisuuden analysoida ja reagoida kyberhyökkäyksiin nopeammin, älykkäämmin ja tehokkaammin.
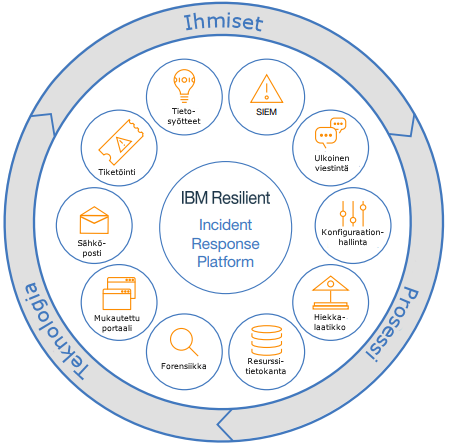
IBM Resilient Incident Response-alusta jakaantuu kuvassa esitettäviin kolmeen osa-alueeseen: ihmiset, teknologia ja prosessit. Osa-aluseeseen ihmiset kuuluu organisaatioiden välinen koordinaatio HR-, IT-osastojen, johdon ja SOC:n välillä. Teknologia-osa-alue käsittää IBM Resilient Incident Response-alustan tarjoaman avoimen alustan, joka integroituu organisaation kyberturvainfrastruktuuriin muodostaen ytimen kyberturvallisuustapahtumien käsittelemiseksi. Osa-alue prosessit tarjoaa dynaamisen ohjeistuksen organisaation jäsenille, jotta he ymmärtävät roolinsa ja vastuunsa kyberturvallisuustapahtuman (kuten hyökkäys) suhteen, sitä ennen, sen aikana ja jälkeen.
Seuraavassa kuvassa on havainnollistettu QRaradar- ja Resilient Incident Response alustan integraatiota, jonka malli on hyödynnettävissä minkä tahansa SIEM-ratkaisun kanssa. SIEM-ratkaisu tarkkaile organisaation tietojärjestelmiä ja -verkkoja sekä hälyttää havaitessaan normaalista poikkeavaa toimintaa. Mikäli kyberturvauhat havaitaan aikaisessa vaiheessa, nopea reagointi niihin mahdollistuu vahingot minimoiden. SIEM-ratkaisun taustalla on ajatus, että tekniset ratkaisut, kuten palomuurit ja IDS/IPS-tuotteet eivät aukottomasti kykene torjumaan kaikkia uhkia. Ulkoisten uhkien lisäksi myös organisaatioiden sisäiset kyberturvallisuusuhat ja tietovarkaudet saattavat olla ulkoisia hyökkäyksiä vaikeammin torjuttavia. SIEM:n tarkoitus on auttaa havaitsemaan suojausratkaisut läpäisevät hyökkäykset ja reagoimaan niihin mahdollisimman nopeasti. Organisaation jo olemassa olevaan SIEM-ratkaisuun yhdistetty QRadar- ja Relisient Incident Response Platform-ratkaisut tehostavat organisaation jo hyödyntävää SIEM-ratkaisun toimivuutta tarjoten työkaluja haittaohjelmien tunnistamiseen ja kyberturvallisuusuhkiin reagoimiseen.
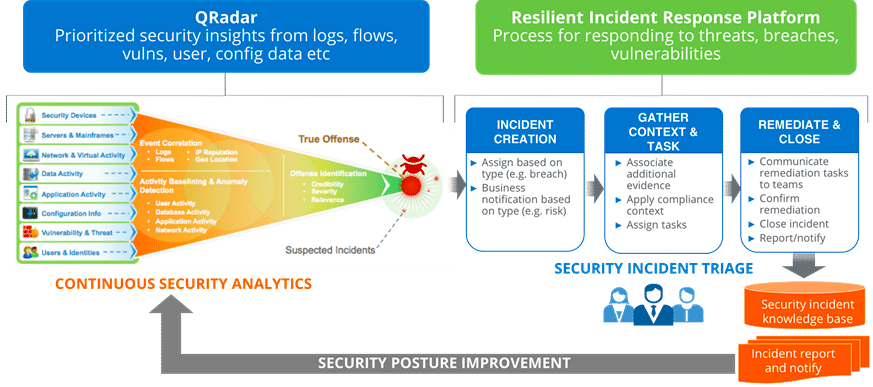
IBM X-Force Exchange
Useat yritykset hyödyntävät kyberturvallisuusuhkiin keskittyviä analyysimenetelmiä ja tietämystä eri uhkista (Threat Intelligence), joiden analyysi perustuu relevantin datan ja informaation tunnistamiseen, keräämiseen ja rikastamiseen. Organisaatiot hyödyntävät usein useita menetelmiä sekä tietolähteitä kyberturvallisuusuhkien tunnistamiseen. Se voi olla aikaa vievää, eivätkä tietolähteet ole aina luotettavia. Lisäksi organisaatio voi kohdata tilanteita, joissa informaatiota ei voida prosessoida riittävän nopeasti, jolloin sen hyödyntäminen käytännön tilanteissa tuottaa vain vähän hyötyä ja suojaa.
IBM X-Force Exchange on pilvipohjainen kyberturvallisuusuhkia koskevan informaation jakamiseen keskittynyt alusta, joka mahdollistaa nopean globaaleihin kyberturvallisuusuhkiin keskittyvien tutkimuksien tarkastelemisen, kyberturvallisuusuhkia koskevan tietämyksen kokoamisen yhteen paikkaan, asiantuntijakonsultaatiot ja yhteistyön muiden kyberturvallisuuteen keskittyvien tahojen kanssa. Alusta sisältää tällä hetkellä yli 700 teratavua raakadataa sekä reaaliaikaista tietoa kyberhyökkäyksistä koottuna yhteen paikkaan. Alustan avulla organisaatiot voivat tehdä yhteistyötä ja jakaa tietoa keskenään. Lisäksi Exchangen käyttäjät voivat hyödyntää IBM:n kyberturvallisuusaineistoa sekä yhteisön jäsenten ja IBM:n asiantuntijoiden tietämystä.
X-Force Exchange tarjoaa ajan tasalla olevan tietoturvauhkien analyysimenetelmiin keskittyvän alustan käyttäen pohjana mm. hunajapurkeista (honeypot), Darknet:sta ja Spamtrapista, saatua dataa. Alusta on yksi laajimmista ja kattavimmista haavoittuvuuspankeista ja se kykenee analysoimaan päivittäin tuhansia haitallisia indikaattoreita tunnissa, alustalla olevaa Threat Intelligence-tietämystä päivittäen. Alustassa on uhkatietopankki, joka kerää tietoa yli 15 miljardista tietoturvatapahtumasta päivittäin. Lisäksi se tarjoaa pääsyn yli 270 miljoonasta päätelaitteesta kerättyihin haittaohjelmatietoihin. Uhkatietoja alustaan on kerätty yli 25 miljardilta sivustolta ja se kattaa informaatiota yli kahdeksasta miljoonasta haitta- ja kalasteluhyökkäyksestä sekä yli miljoonasta haitallisesta IP-osoitteesta, jotka ovat kategorisoituja maantieteellisen sijainnin ja vaarallisuuden mukaan.
Exchange-alusta on informaation jakamista varten toteutettu sivusto, jossa käyttäjät voivat etsiä, kommentoida, kerätä ja jakaa informaatiota ja muut käyttäjät voivat tarkastella ja etsiä raportteja. Alustan "Aktiviteetti"-alueella käyttäjät voivat tarkastella viimeisimpiä haavoittuvuuksia, etsiä linkkejä kyberturvallisuusaiheisiin blogeihin tai tarkastella trendikirjoituksia sekä koko yhteisön viimeaikaisia historiatietoja. Henkilökohtaisella välilehdellä käyttäjät voivat lisätä raportteja tai ladata evidenssiä ulkoisista tietolähteistä ja asettaa ne julkiseksi tai yksityiseksi.
IBM X-Force IRIS
Nykyään kyberhyökkäykset ja -turvallisuusuhkat kohdistuvat voimakkaasti useisiin organisaatioihin, eikä yksikään organisaatio ole täysin immuuni tämänkaltaisille hyökkäyksille organisaation kyberturvallisuuspanostuksista huolimatta. Haasteena on, että organisaatiot joutuvat usein suuntaamaan paljon resursseja kyberturvallisuushyökkäyksistä selviytymiseen ja toipumiseen, vaikka organisaatioiden tulisi varautua hyökkäyksiin jo ennalta. Vuoden 2017 WannaCry ja NonPetya kyberhyökkäysten jälkeisiin korjauskustannuksiin on käytetty jo yli 6 miljardia dollaria.
IBM X-Force Incident Response and Intelligence Services (IRIS) toteuttaa ennakoivaa kyberturvallisuusuhkien torjuntaa IBM X-Forcen asiantuntemusta hyödyntäen. IRIS tarjoaa tilannekuvaa kyberturvallisuustapahtumista ja strategisista korjaustoimenpiteistä, joiden avulla organisaatio voi paremmin kontrolloida kyberturvallisuustapahtumia ja -murtoja. IBM:n X-Force IRIS:n kyberturvallisuusasiantuntijoista koostuva ryhmä tarjoaa kokonaisvaltaisen lähestymistavan haitallisten kyberturvallisuustapahtumien tunnistamiseen, niihin vastaamiseen ja niiden estämiseen aiempaa tehokkaammin.
7.3 Älykkäitä kyberturvallisuusratkaisuja tarvitaan
Kyberturvallisuushyökkäyksiin ja -tapahtumiin vastaaminen on oleellista, mutta niihin varautuminen on huomattavasti tehokkaampaa ja myös kustannustehokkaampi tapa hallita kyberturvallisuusriskejä. Oikeanlaisten palveluiden ja ratkaisujen hyödyntäminen auttaa organisaatiota tunnistamaan potentiaalisia riskejä jo ennen kuin ne tapahtuvat ja aiheuttavat tuhoa sekä muodostamaan ennakoivan tilannekuvan pahimmasta mahdollisesta skenaariosta ennen kuin haitalliset kyberturvallisuustapahtumat realisoituvat. Kyberturvallisuussuunnitelmaan tulee sisällyttää varautuminen, tilannekuvan ja -ymmärryksen muodostaminen, toimenpiteet kyberhyökkäystilanteessa ja palautumissuunnitelma. Näin voidaan muodostaa kokonaisvaltainen kyberturvallisuussuunnitelma, joka säästää kustannuksia ja vähentää korjaavien toimenpiteiden tarvetta. Heikko varautuminen kyberturvallisuusuhkiin voi johtaa merkittäviin kustannuksiin ja vaatia huomattavia korjaustoimenpiteitä kyberhyökkäyksen jälkeen.
Luomalla tehokkaan kyberturvallisuussuunnitelman sekä seuraamalla parhaita käytänteitä ja reagoimalla haitallisiin tietoturvatapahtumiin, kuten hyökkäyksiin organisaatioiden tietojärjestelmiin, jo ennen niiden tapahtumista, hyökkäyksen aikana tai hyökkäyksen jälkeen, organisaatio voi huomattavasti vähentää organisaatiolle aiheutuvia menetyksiä, jotka kohdistuvat immateriaalioikeuksiin (Intellectual Property Rights, IPR), liikevaihtoon, asiakasdataan (GDPR sankiot) tai organisaation maineeseen liiketoiminnassa. Osaamisen hallinta ja ennakoivat investoinnit kyberturvallisuuteen, voivat auttaa organisaatiota suojaamaan toimintojaan ja liiketoimintaansa kyberhyökkäyksiä vastaan.
Tällä hetkellä on tarjolla useita kyberturvallisuusratkaisuja ja -työkaluja organisaatioiden tarpeisiin. Haasteena ovat ratkaisujen ja työkalujen fragmentaarisuus sekä uusien systeemien implementaation ja ylläpidon ongelmat, mitkä aiheuttavat koko järjestelmän kompleksisuuden kasvun ja hallinnan vaikeudet. Systeemien kompleksisuuden takia pitää kehittää integroituja järjestelmiä, joissa on tunnistettu sekä ulkoiset että sisäiset uhat ja rakennettu kokonaisvaltainen kyberturvallisuusjärjestelmä.
Kyberturvallisuusjärjestelmän tulee sisältää älykkäitä analyysiratkaisuja organisaation koko IT-infrastruktuurin alueella. Järjestelmällä tulee olla kyvykkyys nähdä sekä organisaation sisälle, että ulkopuoliseen maailmaan, joista uhat tulevat. IT-infrastruktuurin tulee sisältää itsessään tarvittavat turvallisuuskyvykkyydet. Järjestelmän tulee havaita oireet verkkohyökkäyksestä, joita voivat olla esimerkiksi epänormaali kirjautuminen tärkeää tietoa sisältävälle palvelimelle tai epämääräisten pilvipalvelusovellusten käyttö ja reagoida siihen nopeasti. Uusia keinoja uhkien paljastamiseen tarvitaan, sillä organisaatio saattaa kohdata 200000 tietoturvatapahtumaa päivässä. Tapahtumien tarkistaminen ihmistyönä on aivan liian hidasta ja kallista.
Integroiduilla ratkaisuilla saadaan tarvittava näkyvyys ICT-järjestelmän kaikille tasoille, jolloin suojautuminen ja torjunta voidaan toteuttaa kokonaisuutena eikä yksittäisinä toimenpiteinä. Tekoälyn kyvykkyys tulee esille erityisesti alkuvaiheen analyyseissä ja havaintojen läpikäynnissä. Tekoäly kykenee käsittelemään hetkessä satoja tuhansia asiakirjoja ja tietolähteitä. Tällä hetkellä julkaistaan päivittäin suuri määrä tietoturvaa käsittelevää artikkelia, joiden käsittelyyn ja hyödyntämiseen tarvitaan älykästä konetta.
Hyökkääjä käyttää hyväkseen organisaatioiden siiloutuneita ratkaisuja, joilla kuitenkin on vaikuttavuutta organisaation koko ICT-järjestelmään. Erityisesti perinteiset suojauskehiin perustuvat turvallisuusratkaisut eivät vastaa tämän päivän sofistikoituneisiin uhkiin organisaation ulko- ja sisäpuolella. Integroidussa turvallisuusjärjestelmässä luodaan vahva tietoverkon suojaus, päätelaitteiden hallinta ja turvallisuus, datavirtojen aktiivinen monitorointi, havaintokyvykkyyden luominen ja erilaisten hyökkäysvektoreiden torjunta. Järjestelmä edellyttää kyvykkyyttä ymmärtää alati muuttuvaa hyökkäysalaa ja uusia hyökkäysvektoreita. Älykkäästä kyberturvallisuudesta muodostuu alusta, joka tarjoaa laajan ekosysteemin integroituja turvallisuusratkaisuja. Alustaratkaisu mahdollistaa tehokkaan kyberturvallisuusasiantuntijan ja tekoälysovelluksen yhteistyön, jossa tekoäly toimii avustavan asiantuntijan roolissa toteuttamalla tarvittavia toimenpiteitä ja samalla tuottamalla jalostettua informaatiota päätöksenteon pohjaksi.
Lähteet
- Bayuk, J., L., Healey, J., Rohmeyer, P., Sachs, M., H., Schmidt, J. ja Weiss, J. 2012. Cyber Security Policy Guidebook. USA: A John Wiley & Sons, Inc.
- Bell, J. 2014. Machine Learning: Hands-On for Developers and Technical Professionals. Wiley
- Borana, J. 2016. Applications of Artificial Intelligence & Associated Technologies. Department of Electrical Engineering, Jodhpur National University. Proceeding of International Conference on Emerging Technologies in Engineering, Biomedical, Management and Science.
- Brenner, W. 2010. Cybercrime - Criminal Threats from Cyberspace. Santa Barbara, California, USA: ABC-CLIO LLC.
- Goodfellow, I., Bengio, Y. ja Courville, A. 2016. Deep Learning. USA: MIT Press, 755.
- Lehto, M. 2014. Kybertaistelun toimintaympäristön teoreettinen tarkastelu kirjassa Kybertaistelu 2020. (Tuija Kuusisto Edit.) Maanpuolustuskorkeakoulu, Taktiikan laitos, Julkaisusarja 2, n:o 1. 67-89
- Lehto, M. 2017. Tekoäly ja turvallisuus. Futura 2/2017. 6-14
- Lehto, M. 2019. Onko tekoäly turvallinen? Kirjassa Siukonen T. ja Neittaanmäki P. Mitä tulisi tietää tekoälystä, Docendo Oy, 2019
- Lehto, M. ja Limnéll, J. 2017. Kybersodankäynnin kehityksestä ja tulevaisuudesta., kirjassa M. Silvasti (Edit.) Tiede- ja Ase 2017, 179-212
- Lehto Miikael ja Lehto Martti. 2017. Kyberturvallisuus sairaalajärjestelmissä., osa 1, Jyväskylän yliopisto, IT-tiedekunta, tutkimusraportti, 8/2017
- Lehto, M. ja Neittaanmäki, P. 2015. (Edit.) Cyber Security: Analytics, Technology and Automation. Berlin, Springer International Publishing
- Lehto M. ja Neittaanmäki P. 2018 (Edit.) Cyber Security: Cyber power and technology. Berlin, Springer International Publishing
- Limnéll, J., Majewski, K. ja Salminen, M. 2014. Kyberturvallisuus. Saarijärvi: Docendo
- Neittaanmäki P. ja Lehto M. 2018. Tekoäly muuttaa suomalaista yhteiskuntaa. Tiedepolitiikka 1/2018, 45-54
- Ottis R. 2008. Analysis of the 2007 Cyber Attacks Against Estonia from the Information Warfare Perspective. Proceedings of the 7th European Conference on Information Warfare and Security University of Plymouth, UK, 30 June - 1 July 2008. 163-167
- Pöyhönen J., Lehto M. ja Lehto M. 2019 Kyberturvallisuus sairaalajärjestelmissä, toiminnan kehittäminen. University of Jyväskylä, Faculty of Information Technology, research paper, 75/2019
- Veeramachaneni, K., Arnaldo, I., Cuesta-Infante, A., Korrapati, V., Bassias, C. ja Li, K. 2016. Ai2: Training a Big Data Machine to Defend. Big Data Security on Cloud. IEEE International Conference on High Performance and Smart Computing (HPSC), IEEE International Conference on Intelligent Data and Security (IDS), IEEE 2nd International Conference on Intelligent Data and Security (IDS). New York: USA.
- Vähäkainu P., Lehto M. ja Neittaanmäki P. 2019. Tekoäly ja kyberturvallisuus. Jyväskylän yliopisto, IT-tiedekunta, tutkimusraportti, xx/2019 (valmisteilla)
- Vähäkainu P. ja Lehto M. 2019. Artificial intelligence in the cyber security environment. Conference proseedings, the 14th International Conference on Cyber Warfare and Security, 28 February - 1 March 2019, Stellenbosch University, South Africa
- Zhao, R., Song, W., Zhang, W., Xing, T., Lin, J., Srivastava, M., Gupta, R. ja Zhang, Z. 2017. Accelerating Binarized Convolutional Neural Networks with Software-Programmable FPGAs. Proceedings of the 2017 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays, 15 - 24, Monterey, California, USA.
8. Tekoäly Suomen yliopistoissa
(Pekka Neittaanmäki, Heli Tuominen)
8.1 Tekoälyn tutkimus Jyväskylän yliopistossa
Jyväskylän yliopiston IT-tiedekunnan monipuolisessa toimintaympäristössä tehdään tekoälyyn liittyvää teoreettista menetelmätutkimusta yhteistyössä useiden tekoälyteknikoiden käyttäjien kanssa. Tiedekunnan tekoälytutkimuksen tärkeitä teemoja ovat
- uusien metodien ja sovellusten kehittäminen
- datan esikäsittely (kohinanpoisto, puuttuvien piirteiden käsittely)
- numeeristen ja matemaattisten menetelmien tuntemus
- riskianalyysi.
IT-tiedekunnan tutkimusryhmät tekevät aktiivista yhteistyötä sekä kotimaisten että ulkomaisten yhteistyökumppaneiden kanssa. Seuraavassa kuvataan lyhyesti ryhmien tutkimusta.
Optimointiryhmä
Professori Kaisa Miettisen johtama ryhmä tutkii optimointia ja päätöksenteon tukemista. Ryhmä kehittää menetelmiä, teoriaa ja ohjelmistoja päätöksenteon tukemiseen tilanteissa, joissa usean ristiriitaisen tavoitteen kesken tulee löytää paras tasapaino.
Ryhmä soveltaa päätöksentekijää osallistavia interaktiivisia menetelmiä ja luonnon inspiroimia evoluutiopohjaisia menetelmiä eri alojen ongelmiin prosessien ohjaamisesta metsänhoidon suunnitteluun ja syövän sädehoidosta inventaariohallintaan. Lisäksi ryhmässä tehdään interaktiivisten menetelmien ohjelmistokehitystä. Kehityksen lähtökohtana ovat joko simulointimallit tai data. Tutkimuksessa hyödynnetään tekoälyn ja koneoppimisen keinoja esimerkiksi menetelmien sisällä ja mallien luomisessa ja muokkaamisessa.
Laskennallisten tieteiden ja koulutusteknologian tutkimusryhmä
Professori Tommi Kärkkäisen johtama ryhmä tutkii, kehittää ja soveltaa tiedonlouhinnan, neurolaskennan sekä koneoppimisen menetelmiä. Ryhmälle tärkeitä sovellusalueita ovat oppimista ja koulutusta kuvaavien aineistojen analysointi, nanorakenteet sekä muut laajat, epätäydelliset ja haastavat aineistot. Koulutusteknologian alalla ryhmä tutkii ja kehittää etä- ja projektioppimista sekä tehokkaita tutkimusmenetelmiä.
Tietoliikenteen tutkimusryhmä
Professori Timo Hämäläisen johtama ryhmä toimii tietoverkkojen (langattomat, kiinteät, IoT) parissa ja kehittää älykkäitä menetelmiä resurssien ja palveluiden hallintaan. Jotta verkkojen toiminta voidaan taata myös verkkoon kohdistuvien hyökkäysten aikana, verkkoliikenteen massadatan analyysiin tarvitaan tehokkaita ja nopeita työkaluja. Tätä varten ryhmä kehittää tekoälyyn tukeutuvia verkkoliikenteen poikkeavuuksien havainnointiohjelmistoja (anomaly detection).
Kyberturvallisuusteknologian tutkimusryhmä
Professori Pekka Neittaanmäen ja professori Martti Lehdon johtama ryhmä käyttää ja analysoi tekoälyä kybertoimintaympäristössä. Ryhmä soveltaa tekoälyratkaisuja ja kognitiivista tietojenkäsittelyä kyberhyökkäysten havaitsemiseen, torjuntaan ja selvittämiseen.
Ryhmä tutkii kriittisen infrastruktuurin suojaamista ja kyberpuolustusta. Kriittisen infrastruktuurin suojaamisessa keskeisiä tutkimusalueita ovat energiajärjestelmät, uuden sukupolven tietoliikenneverkot, kyberturvallisuuden tilannekuvajärjestelmät, terveydenhuollon ICT-järjestelmä ja lääkinnälliset laitteet, ajoneuvojen CAN-väylä sekä siviili-ilmailu. Kyberpuolustuksen alalla ryhmä tutkii kyber- ja informaatiosodankäynnin eri muotoja.
Kognitiotieteen tutkimusryhmä
Professori Pertti Saariluoman johtaman ryhmän keskeisiä tutkimuskysymyksiä ovat luonnollisen älykkyyden (kognitio) ja tekoälyn suhde sekä älykkään teknologian suunnittelu kognitiivisen mimetiikan (cognitive mimetics) keinoin.
Ryhmässä tutkitaan ihmisen ja ICT-järjestelmien vuorovaikutusta ja siihen vahvasti liittyvää tekoälyn etiikkaa. Erityinen tutkimusala on kognitiivinen mimetiikka, jossa informaatioprosessien pohjalta ideoidaan teknologisia ratkaisuja.
Aivosignaalinkäsittelyn ryhmä
Professori Tapani Ristaniemen johtaman ryhmän tavoitteena on löytää vastaavuuksia mitatun aivovasteen (MEG, EEG, FMRI) ja mittaustilanteessa käytetyn kuulo- tai näköärsykkeen välillä.
Ryhmä on tutkinut esimerkiksi luonnollisen musiikin vaikutuksia aivoissa, epileptikon kohtausten varhaista ennustamista, ihmisen valvetilan monitorointia ja lasten lukihäiriöiden tunnistamista. Tutkimusaineiston multimodaalisuudesta johtuen työssä tarvitaan mm. koneoppimismenetelmiä ja tensorilaskentaa usean eri muuttujan välisen vuorovaikutuksen selvittämiseen.
Yksilötason terveyden ja hyvinvoinnin koneoppimispohjaiset teknologiat -ryhmä
Dosentti Sami Äyrämön johtama ryhmä kehittää ja soveltaa koneoppimismenetelmiä yksilöllisen harjoittelun, ennaltaehkäisevän terveydenhuollon, yksilöllisen lääketieteen ja kliinisen diagnostiikan tutkimusongelmiin. Etsimällä datamassoista ennustavia muuttujia ja opettamalla malleja mahdollistetaan sairauksien varhaisempi diagnosointi, tarkemmat ennusteet ja yksilöllisesti optimoidut liikuntareseptit. Ryhmä tekee yhteistyötä dataa tuottavien kumppanien kanssa, käyttää mallien opettamisessa mahdollisuuksien mukaan myös avoimia aineistoja ja koneoppimismallien kehittämisessä avoimia kirjastoja. Ryhmä tekee koneoppimismenetelmäkehityksessä soveltavaa yhteistyötä Jyväskylän yliopistossa liikuntabiologian ja terveystieteen tutkijoiden kanssa.
Spektrinkuvantamislaboratorio
Dosentti Ilkka Pölösen johtama ryhmä työskentelee monikanavakuvissa esiintyvien ilmiöiden mallintamisen, simuloimisen ja tunnistamisen parissa. Ryhmä käyttää ja kehittää sovelletun matematiikan keinoja: esimerkiksi wavelet-pohjaisilla menetelmillä toteutetaan signaalin karakterisointia ja kohinan poistoa ja syvillä neuroverkoilla hahmontunnistusta. Ryhmä tekee tiivistä yhteistyötä sekä koti- että ulkomaisten tutkimuslaitosten että teollisuuden kanssa.
Kollektiivisen älykkyyden ryhmä
Ryhmää johtaa professori Vagan Terziyan. Ryhmän suunnittelee massadatan käsittelyyn ja analysointiin soveltuvia tekoälyyn pohjautuvia metodeja ja algoritmeja kognitiivisen tietojenkäsittelyn (cognitive computing), syväoppimisen, yhdistetyn tiedon (linked data), kollektiivisen älykkyyden (collective intelligence) ja kyberturvallisuuden keinoin. Ryhmässä on kehitetty itseään hallitsevia ohjelmia älykkäille ja turvallisille kyberfyysisille systeemeille.
Sosiaalisen median analyysin ryhmä
Ryhmää johtaa professori Jari Veijalainen. Ryhmä tutkii ja analysoi sosiaalisesta mediasta kuten Twitteristä, Youtubesta, Facbookista ja Livejournalista kerättyä dataa ja siellä tapahtuvaa viestintää. Kerättyä dataa analysoidaan monitieteellisin keinoin käyttäen matemaattista mallinnusta, tietotekniikkaa sekä psykologian, sosiologian ja kielitieteen keinoja. Ryhmä on kehittänyt algoritmeja valetilien ja identiteettivarkauksien paljastamiseksi ja rakentanut käyttäjien profiilitietojen perusteella erilaisia verkostomalleja.
Startup-laboratorio
Professori Pekka Abrahamssonin johtamassa laboratoriossa tutkitaan tekoälyn etiikkaa ja sitä, miten tekoälyjärjestelmät voidaan insinöörilähtöisesti toteuttaa eettisesti kestävin periaattein. Laboratoriossa keskitytään autonomisten ja älykkäiden järjestelmien suunnitteluun liittyviin eettisiin ulottuvuuksiin, tekoälyjärjestelmien eettisten vaikutusten arvioimiseen sekä sääntelyn ja metodien kehittelyyn järjestelmien sulautuessa osaksi yhteiskunnan rakenteita. Lisäksi laboratoriossa kartoitetaan Euroopan laajuisesti tietoa state-of-practice kyselyssä eettisten periaatteiden noudattamisessa osana tekoälysuunnittelua sekä sovelletaan osaamista eurooppalaisissa tutkimushankkeisssa.
Tekoälytuetut digitaaliset palvelualustat -hanke
Professori Chihiro Watanaben ja professori Pekka Neittaanmäen johtamassa tutkimusryhmässä tutkitaan digitalisaation ja digitaalisten palvelujen vaikutusta globaaleihin liiketoimintoihin. Tutkimusaiheita ovat esimerkiksi digitalisaation kehitytys eri maissa ja uusien digitaalisten palvelualustojen vaikutus BTK:n kehitykseen. Lisäksi ryhmässä tutkitaan johtavien tekoälyä soveltavien (mobiililaitteiden, kaupan, liikenteen, pankkialan, musiikin, hotellitoiminnan) yritysten kehitystä.
Tekoälytuettu tekstianalytiikka sosiaali- ja terveydenhuollossa
Ryhmän vastuuhenkilöt ovat professori Pekka Neittaanmäki ja tutkimusavustajat Riku Nyrhinen ja Joonas Keppo. Ryhmä hyödyntää tekstianalytiikkaa syrjäytymisen varhaisen vaiheen havaitsemisessa ja ennaltaehkäisevien palveluiden tehostamisessa. Erityisenä kiinnostuksen kohteena on tunneilmaisun näkyminen tekstistä. Aihetta ei suomen kielen kohdalla ole muualla laajemmin tutkittu sen suuresta hyödystä huolimatta. Ryhmä tekee yhteistyötä psykologian laitoksen kanssa.
Musiikin kognition dynamiikka
Musiikkitieteen professorin Petri Toiviaisen johtama ryhmä käyttää koneoppimista aivokuvantamis- ja liikekaappausdatan analyysissä. Aivokuvantamisdatasta ennustetaan esimerkiksi, mitä musiikkia koehenkilö kuunteli kuvantamisen aikana tai mikä on koehenkilön musiikillinen koulutus. Tanssimisesta kerätystä liikekaappausdatasta tunnistetaan koneoppimisen avulla tanssin kinemaattisista piirteitä, esimerkiksi tanssittavan musiikin tyylilajia ja tanssijan henkilöllisyyttä.
Sosiaali- ja terveydenhuollon palveluprosessit
Dosentti Toni Ruohosen johtama ryhmä kehittää ja soveltaa prosessienlouhinnan, tapahtumapohjaisen simuloinnin sekä prediktiivisen analytiikan menetelmiä sosiaali- ja terveydenhuollon tutkimiseen. Lokitiedostoista, rekisteriaineistosta ja tietokannoista saatujen asiakasvirta-, palvelupolku- sekä hoitoprosessikuvauksien avulla saadaan tietoa asiakkaiden palvelujen käytöstä ja tarpeista, ohjautuvuudesta eri palvelukokonaisuuksissa, syy- ja seuraussuhteista eri palvelukokonaisuuksien ja asiointitapahtumien välillä sekä ongelmista. Prosessienlouhinnan avulla muodostetut asiakasvirta- ja palveluprosessikuvaukset voidaan konversioalgoritmeilla kääntää diskreeteiksi simulointimalleiksi. Ryhmä tekee yhteistyötä eri sairaanhoitopiirien, kuntien, Kelan, STM:n, VM:n, Sitran, muiden tutkimuslaitosten sekä yliopistojen ja yritysten kanssa.
Interventiot ja niiden vaikuttavuus
Ryhmän vastuuhenkilöt ovat dosentti Toni Ruohonen ja terveystieteiden tohtori Karoliina Kaasalainen. Ryhmä tutkii, kehittää ja soveltaa data-analytiikan menetelmiä riskiryhmissä olevien asiakkaiden tunnistamiseen ja interventioiden arviointiin. Väestön hyvinvointia voidaan edistää ja kustannuksia alentaa tunnistamalla riskiasiakkaat ajoissa, tarjoamalla heille toimiva interventio oikeaan aikaan sekä luomalla tarvittavat kannustimet. Tähän tarvitaan uudenlaisia toimintamalleja, johon osallistuvat hoitajien ja lääkärien lisäksi myös kolmas sektori sekä hyvinvointitoimijat. Ryhmä tekee yhteistyötä kuntien, sairaanhoitopiirien, kolmannen sektorin, hyvinvointitoimijoiden, ministeriöiden, yritysten ja tutkimuslaitosten kanssa.
Tekoälytuettu numeerinen simulointi
Tekoälyn matematiikkaan keskittyvään ryhmään kuuluvat professorit Sergey Repin ja Pekka Neittaanmäki ja dosentti Heli Tuominen. Ryhmä tutkii neuroverkkojen hyödyntämistä osittaisdifferentiaaliyhtälöiden numeerisessa ratkaisemisessa. Tavoitteena on matemaattisten mallien numeerisen simuloinnin nopeuttaminen ja tarkkuuden parantaminen erilaisia tekoälymenetelmiä hyödyntäen. Opiskelijoille on tarjolla kurssi neuroverkkojen taustalla olevasta matematiikasta. Ryhmän tutkimusalaan liittyvä Eccomas konferenssi Computational Sciences and AI in Industry (CSAI): ”The new digital technologies for solving future societal and economical challenges” järjestetään kesäkuussa 2019 Jyväskylässä.
Matematiikan ja tilastotieteen laitos
Tilastotieteen professori Juha Karvasen johtama ryhmä tekee laaja-alaista tutkimusta laskennallisten tieteiden alueella, erityisesti Bayes-analyysin parissa. Professori Karvanen on DEMO-profilointialan (päätösanalytiikka hyödyntäen kausaalimalleja ja monitavoiteoptimointia) yksi kolmesta vastuuhenkilöstä, muut ovat IT-tiedekunnan professorit Kaisa Miettinen ja Tommi Kärkkäinen.
8.2 Tekoäly ja sote-järjestelmät
Huhtikuussa 2019 ilmestyneessä Jyväskylän yliopiston IT-tiedekunnan neljän kirjan sarjassa raportoidaan Tekoäly ja terveydenhuolto Suomessa -hankekokonaisuudesta ja esitellään IT-tiedekunnan tutkijoiden 10 toimenpide-ehdotusta uuden sukupolven tietojärjestelmien käyttöön ja tekoälyn hyödyntämiseen sote-järjestelmissä.
Hanke koostui kahdesta osahankkeesta vuosina 2016-2019: Value from Public Health Data with Cognitive Computing ja Watson Health Cloud Finland. Hankekokonaisuus on toteutettu samaan aikaan, kun Suomen sosiaali- ja terveysalan tietojärjestelmiä ja lainsäädäntöä on uudistettu.
Kirjoissa esitellään toimenpideohjelma, joka käsittelee tietojärjestelmien lisäksi esimerkiksi tekoälyn käyttöä johtamisessa, diagnostiikassa, hoitoprosesseissa ja interventioissa sekä kyberturvallisuudessa. Kirjasarjan ensimmäisessä osassa esitellään tekoälyn perusteita ja suomalaista tekoälytutkimusta.
Kirjat ovat ladattavissa JYX-arkistosta.
8.3 Tekoälyn tutkimus muualla Suomessa
Suomen useissa yliopistoissa, korkeakouluissa, tutkimuslaitoksissa ja yrityksissä tehtävää tekoälytutkimusta käsitelläään edellisessä luvussa mainitun kirjasarjan 1. kirjan Tekoäly ja terveydenhoito Suomessa osan 1. luvussa 2. Tekoälytutkimus Suomen yliopistoissa. Tiedot on koottu tammi–maaliskuussa 2019 yliopistojen ja tutkimuslaitosten viestintäyksiköiden ja internetsivujen kautta.
Tässä luvussa kerrotaan lyhyesti muualla kuin Jyväskylän yliopistossa tehtävästä tutkimuksesta. Tarkempia tietoja löytyy yllä mainitun kirjan lisäksi tutkimusta tekevien laitosten internetsivuilta.
Suomen tekoälykeskus (Finnish Center for Artificial Intelligence FCAI)
Suomen tekoälykeskus on Aalto-yliopiston, Helsingin yliopiston ja VTT:n perustama osaamiskeskus. Aalto-yliopiston tietojenkäsittelytieteen professorin Samuel Kasken johtamassa FCAI:ssa tehdään tekoälyn perustutkimusta yhteistyössä yritysten ja julkisen alan toimijoiden kanssa ja kehitetään käytännön tekoälysovelluksia.
FCAI sai tammikuussa 2019 Suomen Akatemian lippulaivaohjelmasta yli 8 miljoonan euron rahoituksen. Hankkeen tutkimustoiminta kattaa laajan joukon tutkimusaloja ja monipuolista koulutusta sekä yhteistyötä teollisuuden kanssa.
Suomen tekoälykeskuksen visio on kehittää aidosti älykkäitä, ihmisten kanssa yhteistyössä toimivia tekoälysovelluksia. Tutkimuksen vahvuuksia ovat asiantuntemus koneoppimisessa, erityisesti probabilistisessa mallintamisessa ja syväoppimisessa sekä monitieteellinen yhteistyö muiden alojen asiantuntijoiden kanssa. Tärkeitä asioita ovat datatehokkuus, ymmärrys, luottamus, tekoälyn etiikka ja yhteiskunnalliset vaikutukset. FCAI osallistuu Suomen tekoälyohjelmaan tavoitteiden toteuttamiseen teollisuuden, terveydenhuollon ja työelämän uudistamisessa sekä tutkimukseen perustuvien innovaatioiden käyttöönotossa.
FCAI:ssa on tällä hetkellä viisi tutkimusohjelmaa, joiden toimintaan osallistuu useita tutkimusryhmiä eri tieteenaloilta.
Tietotekniikan tutkimuslaitos (Helsinki Institute for Information Technology HIIT)
HIIT on vuonna 1999 perustettu Aalto-yliopiston ja Helsingin yliopiston yhteinen Tietotekniikan tutkimuslaitos, johon kuuluu noin 150 tutkijaa. Tutkimuslaitoksessa tehdään sekä perustutkimusta että soveltavaa tutkimusta. Soveltavalla puolella kehitetään tietojenkäsittelytieteen uusia sovelluksia ja tutkitaan tietotekniikan vaikutusta ihmisiin ja yhteiskuntaan. Tällä hetkellä tutkimuksen keskeiset alueet tutkimusohjelmineen ovat laskennallinen mallinnus ja suurten tietomassojen analysointi sekä hajautettu ja läsnäoleva tietojenkäsittely nykypäivän verkottuneessa maailmassa. FCAI kuuluu HIIT:n organisaatioon.
Aalto-yliopisto
Aalto-yliopisto on mukana Suomen tekoälykeskuksessa. Tekoälyyn liittyvää tutkimusta tehdään useilla laitoksilla. Tietotekniikan laitoksella on pitkät perinteet koneoppimisen ja neuroverkkojen tutkimisessa ja kehittämisessä. Tutkimuksen pioneereja ovat Teuvo Kohonen and Erkki Oja. Signaalinkäsittelyn- ja akustiikan laitoksella tehdään monipuolista signaalinkäsittelyn tutkimusta yhteistyössä yritysmaailman kanssa. Sähkötekniikan ja automaation laitoksella tutkitaan tekoälyä automaatiossa.
Helsingin yliopisto
Helsingin yliopisto on mukana Suomen tekoälykeskuksessa. Yliopiston tekoälytutkimuksessa kehitetään uusia tekoälyn, koneoppimisen ja tiedonlouhinnan menetelmiä. Tutkimuksen tavoitteena on luoda laskennallisesti tehokkaita, teoreettisesti perusteltuja ja luotettavia menetelmiä.
Tutkimusryhmissä tehdään sekä perustutkimusta että soveltavaa tutkimusta. Niissä tutkitaan esimerkiksi tietokoneellista mallintamista kompleksisissa systeemeissä, luonnollisen kielen prosessointia, laskennallista kielitiedettä, massadatan interaktiivista käsittelyä, yksityisyyden säilyttävää koneoppimista ja laskennallista systeemibiologiaa geenitutkimuksen tarpeisiin, tilastollista koneoppimista, neuroinformatiikkaa koneoppimiseen avulla, laskennallisia algoritmeja ja teorioita evoluution ymmärtämiseksi ja massadatan käsittelyyn biolääketieteellisissä sovelluksissa sekä päätöksenteko-, haku- ja optimointimenetelmiä.
Itä-Suomen yliopisto
Itä-Suomen yliopistossa tutkitaan tekoälyn käyttöä lääketieteessä, terveydenhoidossa ja biologiassa sekä puheentunnistusta ja tekoälytekniikoita.
Ryhmissä tutkitaan esimerkiksi tekoälyn käyttöä hoidon tehon ennustamisessa ja lääkekehityksessä ja laskennallista puheenkäsittelyä. Tekoälyn menetelmistä tutkitaan esimerkiksi algoritmista data-analyysia, koneoppimista, ja itseorganisoituvia neuroverkkoja.
Lapin yliopisto
Lapin yliopistossa tutkitaan johtamisen tekoälyä, informaatioteknologian filosofiaa ja tulevaisuudentutkimusta, tekoälyn juridisia oikeuksia ja älykkäiden ympäristöjen käyttökokemuksia.
Lappeenrannan–Lahden teknillinen yliopisto LUT
Lappeenrannan–Lahden teknillisessä yliopistossa tutkitaan esimerkiksi konenäköä ja hahmontunnistusta, robotiikan ja tekoälyn käyttöä hyvinvontipalveluissa, tekoälyohjattua päätöksentekoa, investointianalytiikkaa sekä tekoälyn käyttöä erilaisten skenaarioiden tutkimuksessa ja teollisuustoimintojen monitoroinnissa ja kehittämisessä.
Oulun yliopisto
Oulun yliopistossa tekoälytutkimusta tehdään useassa tutkimusryhmässä ja -keskuksessa. Yliopisto sai vuonna 2018 Suomen Akatemian lippulaivahankkeen 6Genesis, jonka osana kehitetään reunalaskennan hajautettua tekoälyä.
Konenäön ja signaalianalyysin tutkimuskeskuksessa on useita tutkimusryhmiä. Siellä tutkitaan esimerkiksi kasvojen-, ilmeiden- ja tunteidentunnistusta, lisättyä todellisuutta, tunnetekoälyä, lääketieteellisten signaalien ja kuvien analysointia ja konenäköä.
Tampereen yliopisto
Tampereen yliopistossa tutkitaan erityisesti tekoälyn teollisia sovelluksia ja älykkäitä koneita.
Ryhmien tutkimusaiheita ja sovelluskohteita ovat koneoppimisen, tekoälyn ja data-analyysin sovellukset teollisuudessa ja robotiikassa, tehdasautomaatio, teollisuuden informatiikka, terveydenhuollon automaatio, älykäs liikkuminen, tekoäly puheen, musiikin ja audiosignaalien tulkinnassa, tekoäly ja multimedia, kuvantaminen ja moderni konenäkö.
Turun yliopisto
Turun yliopistossa tehdään tekoälytutkimusta useissa tiedekunnissa. Yliopiston tekoälykoulutusta ja -tutkimusta koordinoi ja kehittää Tekoälyakatemia.
Tutkimuksen pääsuunnat ovat monialainen yleissivistävä tekoäly; syventävä teknologinen tekoälyosaaminen sekä tekoäly terveydenhuollossa. Tutkimuksessa korostetaan tieteidenvälisiä aiheita: tekoälyn etiikka ja vastuullisuus, alustatalous, tietoturva, ihmisen ja koneen yhteistyö, oppimisanalytiikka, pelillisyys ja lisätty todellisuus. Tulevaisuuden teknologioiden laitoksella tehdään myös perustutkimusta koneoppimisen ja kieliteknologian alueilla.
Vaasan yliopisto
Vaasan yliopiston Digital Economy -ryhmässä tutkitaan uusia teknologioita ja niiden vaikutuksia eri tieteenalojen näkökulmista. Tekoäly ja koneoppiminen kuuluvat ryhmän tutkimusaiheisiin.
Muita tekoälyn tutkimuslaitoksia
Yliopistojen lisäksi tekoälytutkimusta tehdään yrityksissä ja ammattikorkeakouluissa. Näistä tärkeitä esimerkkejä ovat Teknologian tutkimuskeskus VTT, Tieteen tietotekniikan keskus CSC sekä Jyväskylän ja Kajaanin ammattikorkeakoulut.
9. Esimerkkejä tekoälyn soveltamisesta
(Pekka Neittaanmäki, Anniina Ojalainen, Heli Tuominen, Petri Vähäkainu, Sanna-Mari Äyrämö)
Tässä luvussa esitellään tekoälyn eri sovelluskohteita ja konkreettisia esimerkkejä. Luvun alussa tehdään tiivistetty katsaus soveltamisaloina terveydenhuolto Suomessa ja ulkomailla, lääkehuolto, palvelurobotiikka sekä rakennus- ja kiinteistöala. Luvun loppuosassa on laajempi katsaus tekoälyn sovelluksiin koulutuksen, teollisuuden, bisnesmaailman, terveydenhoidon ja lakipalveluiden näkökulmasta.
Tekoäly terveydenhuollossa
Digitaalisen terveyden ja älykkään terveydenhuollon tarkoituksena on helpottaa diagnosointia ja hoitoprosesseja, säästää kustannuksissa, sekä parantaa työ- ja asiakastyytyväisyyttä hoitolaitoksissa. Tekoäly on kyennyt jo auttamaan lääkäreitä diagnosoinnissa ja lääkekehityksen edistämisessä. Tekoälyn avulla diagnooseista tulee tarkempia ja nopeampia. Se myös tulee laajentamaan hoitohenkilökunnan käsittelykykyä ja tarjoamaan mahdollisuuksia laajamittaiselle yhteistyölle eri instituuttien välillä. Tekoälyä on hyödynnetty esimerkiksi unihäiriöiden hoidossa, onkologiassa, kardiologiassa sekä keuhkosairauksien tutkimuksessa ja hoidossa.
Tekoälyn lisäksi terveydenhoitoa mullistavat puettavat laitteet ja sensorit, joiden avulla etähoito ja telelääketiede mahdollistuvat. Mahdollisuudet elintärkeiden elintoimintojen monitorointiin ovat valtaisat ja tulevaisuudessa on mahdollista, että potilas lähettää dataa reaaliaikaisesti sairaalaan, missä datan avulla tehdään uusia hoitosuosituksia. Tekoäly tukee hoitohenkilökuntaa datan käsittelyssä tässäkin skenaariossa. Tekoälyn hyödyntäminen terveydenhuollossa on jatkuvasti kasvava ala, sillä ennusteiden mukaan terveydenhuollon tekoälymarkkinat ylittävät kuuden miljardin dollarin rajan vuoteen 2021 mennessä.
Tekoäly terveydenhuollossa ulkomailla
Tekoälyä on kehitetty terveydenhuollon tarpeisiin ympäri maailmaa. Kehityskilpailua johtavat monien arvioiden mukaan Kiina ja Yhdysvallat. Muita terveydenhuollon tekoälyyn satsanneita maita ovat esimerkiksi Saksa, Iso-Britannia, Japani, Singapore ja Etelä-Korea.
Aasia voidaan nähdä yhtenä tiennäyttäjänä terveydenhuollon tekoälykehityksessä. Esimerkiksi maailman johtava tekoälyvaltio Kiina kehittää jatkuvasti uusia tekoälyn sovelluksia terveydenhoitoalle ja maassa on otettu käyttöön ensimmäinen älysairaala. Japanissa, Singaporessa ja Etelä-Koreassa on kehitetty esimerkiksi sairauksien tunnistukseen käytettäviä tekoälysovelluksia, tekoälyllisiä hoitoalan robotteja ja silmäsairauksia lääkäreitä paremmin havaitseva tekoälyjärjestelmä. Japanissa tekoälylliset robotit ovat käytössä jo vanhainkodeissa ympäri maan.
Terveydenhuollon tekoälyä on kehitetty lisäksi stressin seurantaan, lääkärin dokumentaatiotyön helpottamiseen, aivojen kuvantamisen ja kuvien rekonstruoinnin kehittämiseen, terveystiedon louhintaan ja yksilön itsenäiseen terveyden seurantaan sekä hallintaan.
Tekoälyn hyödyntäminen lääkehuollossa
Suomen sosiaali- ja terveysalalla on käytössä useita erilaisia rekistereitä ja tietokantoja. Tällä hetkellä tieto on hyvin hajanaista ja sen takia tietoa on haasteellista hyödyntää esimerkiksi lääkkeitä tutkittaessa, uusia lääkeaineita etsittäessä ja lääkereseptejä määrätessä. Farmasiassa laskennalliset mallit ja koneoppiminen helpottavat lääkeaineiden etsintäprosessia eri lääkeaineyhdisteiden löytämiseksi. Mallien avulla lääkeaineiden aiheuttamista sivuvaikutuksista voidaan saada oleellista informaatiota jo silloin kun lääkeaineyhdistettä ollaan vasta etsimässä. Lääkehuoltoa halutaan jatkuvasti kehittää, jotta lääkkeiden turha päällekkäinen käyttö ja haittavaikutukset vähenisivät. Samalla sekä yksilön että yhteiskunnan kulut laskisivat.
Suomessa on jo käytössä useampi hoitohenkilökuntaa opastava lääketietokanta ja lääketyökalu. Niiden avulla voidaan tähdätä parempaan lääkityksen kokonaisarviointiin. Tekoäly voi myös tukea lääkkeen määräämisprosessia esimerkiksi käymällä läpi mahdollisia lääkkeiden haittavaikutuksia valtavista tietomassoista, selvittämällä potilaan lääkkeiden päällekkäisyyksiä sekä potilaalle sopivaa lääkeannoksen määrää. Tekoälyn avulla on jo esimerkiksi selvitetty uuden lääkkeen haittavaikutuksia sosiaalisen median datamassoja tutkimalla. Tekoälyn ja lääkehuollon yhdistelmällä voidaan myös luoda konkreettisia ratkaisuja sairaaloihin. Tästä hyvänä esimerkkinä ovat älykkäät lääkekaapit, jotka voidaan integroida potilastietojärjestelmiin, josta selviää lääkityksen kohteena olevan potilaan henkilötiedot, paikkatiedot ja lääkityksen tarkat tiedot.
Palvelurobotiikka
Vuonna 2012 päivitetty ISO-8373 -standardi (ISO, 2012) määrittää robotin seuraavasti:
actuated mechanism programmable in two or more axes with a degree of autonomy, moving within its environment, to perform intended tasks
Robotit ovat siis ISO-standardin mukaan ohjelmoitavia, ainakin osittain autonomisia sekä tehtävien suorittamiseen kykeneviä. Robotiikkaa hyödynnetään sosiaali- ja terveysalalla vielä vähäisesti sen mahdollisiin hyötyihin nähden. Yleisimpiä robotiikan sovellutuksia nykyhetkellä ovat vähäisen autonomian robotit, kuten leikkausrobotit, ja ohjelmistorobotiikka. Haasteita laajemmalle palvelurobottien käytölle ovat kehitystä vaativa teknologia, eettiset kysymykset, lainsäädäntö ja muutosvastarinta. Toisaalta esimerkiksi Japanissa robotit ovat yleisesti hyväksyttyjä ja laajalti käytettyjä, jopa terveydenhoitoalalla.
Robotiikan mahdollisuuksien hyödyntäminen tulee olemaan edellytys sosiaali- ja terveysalan toimintojen tehokkuuden takaamiseksi tulevaisuudessa. Palvelurobotiikka tulee takaamaan palvelun laadun ja kaiken lisäksi parantamaan sitä, sillä robotiikan avulla voidaan siirtää hoitohenkilökunnan työpanosta välillisestä hoitotyöstä välittömään hoitotyöhön. Robotiikan nopean kehityksen ja tunnistetun tarpeen myötä voidaan odottaa, että palvelurobotit tulevat olemaan osana sosiaali- ja terveysalan toimintoja myös Suomessa.
Kiinteistö- ja rakennusala
Kiinteistö- ja rakennusala on kompeksinen kokonaisuus, jossa digitalisation myötä tekoälyä voidaan soveltaa monipuolisesti koko rakennuksen elinkaaren ajan. Tekoälyä voidaan käyttää apuna rakennuksen suunnittelussa ja rakentamisprosessissa esimerkiksi eri vaihtoehtojen valinnassa. Valmiissa kiinteistöissä tekoälyä voidaan käyttää kulun- ja kunnonvalvonnassa sekä osana rakennuksen toimintoja ohjaavia automaatiojärjestelmiä.
Tekoälyä voidaan käyttää älykkäiden rakennuksien kunnossapidossa. Älykäs rakennus on järjestelmäkokonaisuus, jossa rakennuksen sensorit mittaavat rakennuksen käyttöä, toimintaa ja tilaa kuvaavia lukuja. Mittauksien perusteella voidaan seurata ja säädellä esimerkiksi energiankulutusta, sisälämpötilaa, vedenkäyttöä ja muita rakennuksen fyysisiä ominaisuuksia pintojen kosteudesta betonissa havaittaviin poikkeuksiin. Yhdistämällä neuroverkot ja koneoppiminen tähän prosessiin, saadaan rakennuksien ennakoiva kunnossapito automatisoitua.
Muita sovellusalueita
Esimerkkejä muista sovelluskohteista ovat finanssiala, energiateollisuus ja turvallisuusala. Tekoälyä on kehitetty paljon turvallisuusalalla kyberturvallisuuden parantamiseksi. Tekoälyratkaisuja ja kognitiivista tietojenkäsittelyä sovelletaan kyberhyökkäysten havaitsemiseen, torjuntaan ja selvittämiseen. Tekoälyä hyödyntäviä kyberturvallisuuden ratkaisuja ovat kehittäneet monet erikokoiset yritykset. Tunnettuja ratkaisujen kehittäjiä ovat muun muassa teknologiajätit Amazon (Amazon Macie), Google (Deep Instinct) ja IBM (QRadat ja X-Force).
Laajempi katsaus tekoälyn sovelluksiin
Tämän luvun loppuosan tavoitteena on hahmotella yleiskuvaa tekoälyn tämänhetkisistä käyttötavoista erilaisia toimialoja tarkastellen. Aihetta kartoitettiin erilaisten verkkoaineistojen ja tekoälyä yleistajuisesti käsittelevän, viime vuosina julkaistun kirjallisuuden avulla. Käytetyt verkkolähteet sisältävät tekoälyn käyttöä tietyillä toimialoilla tarkastelevia yleiskuvauksia, eri aloihin liittyviä tekoälyuutisia, tieteellisiä artikkeleita ja myös tekoälykehityksessä toimivien yritysten omia artikkeleita, jotka kuvailevat tuotteita ja niiden avulla tavoitettuja vaikutuksia. Selvityksen painopiste on jo käytössä olevissa tekoälysovelluksissa. Tekoälyratkaisujen kehittämistyö on voimakasta ja tämä trendi vaikuttaa luonnollisesti myös siihen, millaisista sovelluksista tietoa on erityisesti saatavilla. Usein onkin suorastaan mahdotonta välttyä tarkastelemasta myös sitä, millaiseen tekoälyn hyödyntämiseen ollaan parhaillaan siirtymässä, toisin sanoen millaisten sovellusten käyttöä vasta testataan. Niinpä tässäkin selvityksessä painottuvat erityisesti viime vuosien uudistukset, eivät niinkään tekoälysovellukset, joiden käyttö on jo vahvasti arkipäiväistynyt.
Tekoälyn tämänhetkistä hyödyntämistä erilaisilla toimialoilla kuvataan erittelemällä niitä aloihin liittyviä tehtäviä ja työvaiheita, joita tekoäly voi ottaa hoitaakseen. Lisäksi kuhunkin toimialaan liittyen kuvaillaan esimerkkejä tarjolla olevista tekoälysovelluksista ja niiden käytöstä. Esimerkkisovellusten tarkastelu toteutettiin saatavilla olevan tiedon ehdoilla vähintään seuraaviin kysymyksiin tiiviisti vastaten:
- Minkä niminen sovellus on kyseessä?
- Millaisen ongelman ratkaisemiseksi tai minkä tehtävän suorittamiseksi sovellus on kehitetty?
- Mitä sovellus tekee?
- Millaisia hyötyjä sovelluksen avulla on saavutettu? / Miten sovelluksen käyttö muuttaa alan työntekijän toimenkuvaa?
Tarkastellaan seuraavaksi, millä tavoin tekoälyä tällä hetkellä hyödynnetään koulutuksen, uraohjauksen ja rekrytoinnin alueella, teollisuudessa, varastoinnissa ja kuljetuksessa, rahoitus- ja bisnesaloilla, terveys- ja sosiaalipalveluiden sekä lääketeollisuuden aloilla ja lakipalveluissa.
9.1 Koulutus, uraohjaus ja rekrytointi
9.1.1 Koulutus
Ensimmäiset digitaaliset yliopistot ovat jo aloittaneet toimintansa. Suuryrityksistä esimerkiksi Google ja Microsoft tarjoavat palveluita opettajien ja koululaisten tarpeisiin. Onpa jo huomautettu myös mahdollisuudesta rakentaa digitalinen globaali koulu tai yliopistokin, mikä ainakin teknisesti olisi jo mahdollista (Neittaanmäki 2017).
Opettamista on kehitetty eri aikoina erilaisten oppimiskäsitysten näkökulmista, mutta tämän päivän koulutusmaailma kohtaa myös työelämän muutoksista johtuvia haasteita: jotkut perinteiset ammatit katoavat ja uusia aloja syntyy kaiken aikaa. Tämä kehitys on nopeaa ja hyvin vaikeasti ennustettavaa. Uraohjauksen alalla on päädytty havaintoon, jonka mukaisesti lähtökohta, jossa asiakas valitsee omien ominaisuuksiensa perusteella tiettyyn ammattiin johtavan kiinteä urapolun (ja tähän liittyvät opinnot), ei enää vastaa nykyisen tai tulevaisuuden työelämän todellisuutta (Savickas 2012). Niinpä uran ja elämän suunnittelun täytyy nojautua käsitykseen, jossa jokaista varten on enemmän kuin yksi oikea ammatti (Savickas 2012). Tämän vuoksi myös elämänmittaisen oppimisen idean hyväksyminen osaksi arkipäivää on välttämätöntä - jokaisen on oltava ajoittain valmis päivittämään osaamistaan.
Digitaalisen koulutuksen avulla eri aloihin liittyviä oppisisältöjä voidaan tuoda opiskelijoiden kannalta selvästi aikaisempaa helpommin saataville. Lisäksi digitaalisia kanavia pitkin voidaan myös tarjota opetusta niin kutsuttujen tulevaisuustaitojen alalla. Digitaalisen opetuksen yleistyessä yhä voimakkaammin voitaneen tämän kehityksen olettaa vaikuttavan myös perinteisiin koulu- ja yliopistorakennuksiin, jotka saavat uuden muodon ja osittain ehkä myös katoavat.
Kouluopetuksesta, digitaalisista apuvälineistä ja tekoälystä puhuttaessa voi törmätä toteamukseen, jonka mukaan tekoäly ei korvaa opettajaa, mutta voi muuttaa tapaa, jolla opettajat opettavat ja oppilaat oppivat. Mutta mitä tällä käytännössä tarkoitetaan? Millaisista muutoksista on kyse? Opettajan näkökulmasta tekoälyllä voidaan esimerkiksi automatisoida opetuksen arviointia. Toistaiseksi tämä on mahdollista lähinnä monivalintatehtäviin perustuvien testien yhteydessä. Luokkatilanteissa opettajat voivat myös saada sovelluksilta palautetta tehtävänantojen ja opetusmateriaalien toimivuudesta. Tällainen palaute voi edistää parhaiden opetuskäytänteiden leviämistä ja vahvistaa opettajien vastuuta omasta opetuksestaan. (Lynch 2018.)
Lisäksi tekoälysovellukset voivat hoitaa joitakin opettajien rutiinitehtäviä ja avustaa oppilaiden kanssa kommunikoinnissa. Georgia Institute of Technologyssa toteutettu kokeilu antoi viitteitä siitä, miten tekoälyavustaja saattoi vastailla sellaisiin oppilaiden sähköpostitse esittämiin rutiinikysymyksiin, joiden vastauksiin se arvioi vastaavansa oikein 97% todennäköisyydellä, ilman että oppilaista juuri kukaan havaitsi viestivänsä tietokoneen kanssa (Furness 2016).
Tekoälyn avulla oppimista tukevilla sovelluksilla pyritään myös tuottamaan pitkäaikaista hyötyä. Ihannetilanteessa oppilaiden rinnalle onnistuttaisiin kehittämään koko elämän mittainen tekoälykumppani, joka tuntee oppilaan oppimishistorian ja pystyy siten tunnistamaan heidän vahvuutensa ja heikkoutensa. Tällainen AI-kumppani kykenee huomioimaan oppilaan erityistarpeet esimerkiksi opetusaineistoja mukauttamalla. Lisäksi tekoälykumppani voi tarjota personoitua tukea myös luokkahuoneen ulkopuolella kehittäen henkilön osaamista kulloisiakin tavoiteita vastaavalle tasolle harjoittamalla oppilaan puutteellisesti hallitsemia taitoja tai auttamalla häntä ymmärtämään uusia ideoita. (Holz 2017; Lynch 2018.)
9.1.2 Esimerkki tekoälyjärjestelmän kehittämisen haasteista: mukautuvat koulutusjärjestelmät
Koulutuksen alalla tekoälyyn on kohdistettu suuria odotuksia erityisesti mukautuvien koulutusjärjestelmien (adaptive educational systems) kehityksessä. Tällaiset järjestelmät perustuvat adaptiivisen oppimisen idealle. Mukautuvien koulutusjärjestelmien yhteydessä korostetaan yksilöiden erilaisuutta ja oppimisympäristön kykyä reagoida tähän erilaisuuteen. Niinpä menestyksekkään kehitystyön kannalta ensiarvoisen tärkeää on onnistua keräämään oppijoista juuri oikeanlaista dataa, jota sitten voidaan hyödyntää asiantuntijoiden ja suunnittelijoiden työssä sekä tietoteknisen systeemin dynaamisen itseoppimiskapasiteetin kehittämisessä. Niinpä mukautuvien opetussysteemien kehitystyön kannalta merkittävään rooliin nousevat työn taustalla käytetyt tiedonkeruu- ja analysointimetodit. (Colchester, Hagras, Alghazzawi, Aldabbagh 2017)
Yksi merkittävä oppimisdatan lähde - ja samalla keskeinen tekoälyn käyttöalue - ovat massiiviset avoimet verkkokurssit eli MOOC:it (Massive open online course). MOOC:it ovat internetin kautta järjestettyjä maksuttomia ja kaikille avoimia kursseja, joita järjestävät verkkokurssiympäristöt ovat niin kutsuttuja avoimia oppimissysteemejä. MOOC:eja tarjoavat esimerkiksi kaupalliset Coursera ja Udacity sekä ei-kaupalliset edX ja HarvardX (Harvardin yliopisto). Suomalaiskehitteisiä esimerkkejä ovat mooc.helsinki.fi (Helsingin yliopisto) sekä Eliademy (Aalto-yliopisto). Näiden ympäristöjen avulla kuka tahansa voi kouluttaa itseään valtavaa kurssitarjonnan kirjoa hyödyntäen.
Jotta MOOC:ien osuus koulutuksen kentällä kasvaisi, niitä täytyy kuitenkin vielä kehittää. On havaittu, että vaikka MOOC-ympäristöihin ilmoittautuu suuri määrä osallistujia, kurssin läpisuorittavien opiskelijoiden prosentuaalinen määrä jää alle 13%:n. Ongelman ratkaisemiseksi on ehdotettu esimerkiksi oppijan käytösanalyysin perusteella toteutettavaa mukautuvaa oppimista (Colchester et al. 2017). Oikeanlaisen analytiikan keinoin järjestelmä voisi kartoittaa esimerkiksi oppijan lähtötasoa, motivaatiotasoa ja oppimistyyleihin liittyviä piirteitä, ohjata opiskelua näitä seikkoja huomioiden ja tarjota opiskelun etenemisen mittaan juuri oikeanlaista materiaalia opiskelijan saataville. Vaikka tekoälyyn ja oppimiseen liittyvät odotukset ovat korkealla, ovat aidosti adaptoituvat koulutusjärjestelmät, jotka todella itsenäisesti oppisivat ja reagoisivat opiskelijan käytöksen perusteella, vielä harvassa (Kay, Reimann, Diebold, Kummerfeld 2013; Yu, Miao, Leung, White 2017; Colchester et al. 2017).
MOOC:ien yhteydessä tekoälyyn liittyvä toiveikkuus viriää erityisesti siitä tosiasiasta, että MOOC:eja tarjoavien oppimissysteemien kautta on mahdollista koota huomattavan runsaat määrät erilaisten oppijoiden interaktioihin liittyvää dataa. MOOC-ympäristöjen toimivuuden ja mukautuvuuden kehittämisen kannalta keskeisin haaste kytkeytyy oikeanlaisten päättelyketjujen rakentamiseen: miten hyvin opiskelijoiden ja oppimisympäristön välisistä interaktioista kerättyä dataa onnistutaan lopulta yhdistämään tekoälytekniikoihin. Lisäksi oikein hyödynnettynä opiskelijainteraktioista koottu data saattaa myös tarjota kokonaan uutta tietoa inhimillisestä adaptoituvasta oppimisesta.
Suurikokoiset oppijadatat ovat hyödyllisiä, mikäli niiden pohjalta pystytään muodostamaan luotettavia oppijaprofiileja. Opiskelijaprofiileita pystytään muodostamaan monentyyppistä dataa analysoimalla. Profiilinmuodostuksessa hyödynnetty tieto voi esimerkiksi koskea opiskelijoiden tarpeita, kykyjä tai persoonallisuuden piirteitä. Myös opiskelijoiden ennakkotietojen ja -taitojen tyyppiä ja laajuutta erittelevä data tai oppimisprosessin mittaan koettuja tunnetasoja kartoittava aineisto voivat toimia oppijaprofiilien muodostamisen lähtökohtina. MOOCit mahdollistavat tämänkaltaisten datojen keräämisen ja niinpä näiden ympärtistöjen kehitys- ja tutkimustyössä onkin pyritty hyödyntämään esimerkiksi erilaisia tiedonlouhinta (data mining) -tekniikoita. Massiivisiin avoimiin verkkokursseihin liittyvää tiedonlouhinta- ja tekoälyaiheista tutkimusta ovat eritelleet Fauvel ja Yu (2016).
9.1.3 Oppimista tukevat ohjelmistot ja robotit
Oppimisen tueksi on kehitetty monenlaisia tekoälyä hyödyntäviä robotteja, joista muutamia on parhaillaan testikäytössä myös suomalaisissa kouluissa. Robotit voivat tukea opettamista esimerkiksi valittuun aihepiiriin liittyviä harjoituksia teettämällä. Esimerkiksi muutamissa Tampereen alueen kouluissa kokeiltavana oleva Al Robotsin kehittämä Pöllö-robotti harjoituttaa oppilaita yhteenlaskussa. Tammelan koulussa oppilastestauksessa on puolestaan kieliä opettava SoftBankin ja Utelias Oy:n kehittämä Elias-robotti. Tekoälyominaisuuksia ajatellen Pöllön ja Eliaksen tekoäly perustuu erityisesti puheentunnistusteknologiaan. Lisäksi niihin on pyritty kehittämään myös mukautuvuusominaisuuksia, sillä robottien kerrotaan valitsevan tarjoamansa tehtävät opiskelijan taitotasoon nähden sopivaksi. (Pesonen 2018; Mansikka, Tikkamäki 2018.)
Liikkuvat, elehtivät ja juttelevat robotit vetoavat tyypillisesti lapsiin, mutta ne voivat saada muutamilla ulkoisilla vihjeillä aikuisenkin kuvittelemaan robotille älykkäämmän tai inhimillisemmän olemuksen kuin mihin niissä oleva tekoälyteknologia muutoin antaisi aihetta. Tällainen vaikutelma voi luonnollisesti vaikuttaa robotin kanssa työskentelevien oppilaiden mielentilaan. Opetusrobottien etuina onkin, paitsi niiden väsymättömyys samojen asioiden toistamisessa, myös mahdollisuus edistää käyttäjää pääsemään oppimiselle suotuisaan rentoon ja avoimeen mielentilaan. Robotin kanssa epäonnistumisia ei tarvitse jännittää.
Kiinalaisyritys Lingin luoma Luka-pöllö on robotti, jonka tarkoitus on tarjota lukemisesta kiinnostuneille lapsille seuraa kirjojen ääressä ja auttaa heitä saamaan lukutaidosta kiinni samaan tapaan kuin tarinoita lapsille ääneen lukeva aikuinenkin voi tehdä. Luka pystyy lukemaan kuva- ja tekstikirjoja, jotka löytyvät yrityksen noin 50 000 kirjaa kattavasta tietokannasta. Robotti on siten tarkoitettu tukea antavaksi ja yrittelijäisyyttä ylläpitäväksi seuraksi lapsille, jotka haluavat oppia lukemaan. Ajatuksena ei ole korvata lasten ja aikuisten yhteisiä lukutuokioita vaan tarjota lapsille mahdollisuus jatkaa kirjan kanssa vietettyä aikaa. (BBC News 2018)
Sosiaaliseksi robotiksi luonnehdittu Nao pystyy hyödyntämään kulloisenkin käyttötarkoituksen mukaan useita erilaisia sisäänrakennettuja ominaisuuksia ja sovelluksia. Näihin ominaisuuksiin lukeutuvat kamerat ja kasvojentunnistusohjelma, joiden avulla robotti näkee, verbaalisesta kommunikaatiosta huolehtivat mikrofonit ja kaiuttimet, esteiden havaitsemiseksi asennetut kaikuluotaimet, bluetooth-, wifi- ja ethernetyhteysmahdollisuudet sekä voimaa aistivat resistorit mukautuvien liikkeiden tuottamiseksi. Nao-robottia on kehitetty erilaisia oppimisen erityistilanteita ajatellen, esimerkiksi kokemusperustaisen tieto-taidon välittämiseen ihmiseltä toiselle (Hoopes 2015). Tällaista oppimista ihminen tarvitsee erityisesti tilanteissa, joissa uuden työntekijän tulisi ottaa haltuunsa häntä edeltäneen työntekijän paikka työskentelyryhmässä. Usein tilanne on kuitenkin sellainen, ettei vanha työntekijä ole enää paikalla perehdyttämässä uutta tulokasta. Naoa on kehitetty myös erityisopetuksen tueksi, esimerkiksi autismin kirjon piirteitä omaavien oppilaiden tarpeita ajatellen. Toisin kuin edellä esitellyt Pöllö ja Elias, Naoa ei ole ohjelmoitu oppiainesidonnaisten tehtävien mukaisesti. Sen sijaan se soveltuu avustajaksi monenlaisille oppitunneille, peleihin ja muihin tilanteisiin, joissa harjoitellaan vuoron ottamista, tunteiden arvaamista, kommunikaatiota ja ohjeiden seuraamista. (Holz 2017)
Oppimisessa hyödynnettyihin tekoälyrobotteihin kuuluu myös emergenttejä käyttötapauksia. Esimerkiksi IPA:t (intelligent personal assistant) ovat mobiililaitteilla toimivia puheentunnistuspohjaisia sovelluksia, jotka voivat hoitaa käyttäjänsä puolesta erilaisia tehtäviä ja suorittaa annetusta aiheesta tiedonhakuja. On havaittu että näitä sovelluksia voidaan myös hyödyntää esimerkiksi vieraan kielen oppimisen apuvälineinä. IPA-sovelluksia ovat esimerkiksi Amazon Echo -älykaiutin, BlackBerry- puhelimien BlackBerry Assistant, Brainasoftin Microsoft Windowsille kehittämä Braina, Googlen Google Now -sovellus, Microsoftin Cortana, Samsungin 'S Voice', Cognitive Coden kehittämä SILVIA, Applen 'Siri', Nuancen Vlingo, LGn Voice Mate, IBM: 'Watson' sekä Facebookin M eli Moneypenny. (Colchester et al. 2017, Canbek, Mutlu 2016) Tähän aiheeseen liittyen omasta hyvinvoinnista huolehtimista tukevista - ja samalla tätä taitoa opettavista - roboteista kerrotaan AI-robotit mielenterveyspalveluiden tukena -luvussa.
Suomalainen LukiMat on tietoverkkovälitteinen lukemisen ja matematiikan oppimis- ja arviointiympäristö esikouluikäisille ja peruskoulun luokilla 1-4 oleville lapsille. Hankkeessa (LukiMat) arvioitiin, että 5–10% ikäluokasta on suuria vaikeuksia luku- ja kirjoitustaidon oppimisessa ja noin 5–7% matematiikassa. Tuki- tai erityisopetusta tarvitsevien osuus on paljon suurempi, jopa 15-20%.
LukiMat-ympäristöllä pyritään ennaltaehkäisemään lukemisen ja matematiikan oppimiseen liittyviä ongelmia ja tarjoamaan eritasoisia verkkopohjaisia harjoituksia lapsille, joilla on oppimisongelmia. Verkkopalvelu jakautuu lukemisen, matematiikan ja oppimisen arvioinnin osa-alueisiin. Mukautuvan oppimateriaalin lisäksi se sisältää tutkimustietoa oppimisvaikeuksista ja taitojen kehityksestä.
9.1.4 Uraohjaus ja rekrytointi
Tekoälyn tuominen teollisuuteen tai muille toimialoille ei merkitse ihmistyöntekijöiden muuttumista kokonaan tarpeettomiksi tai muutenkaan passiivisiksi. Tätä teknologisen kehityksen murrosvaihetta ei tulisikaan olettaa perusluonteeltaan samanlaiseksi kuin vaikkapa höyrykoneen tai sähköistymisen vaiheita, joiden myötä uusilla keksinnöillä saatettiin nimenomaan korvata ihmistyöntekijöitä. Ammattien muuttuvien toimenkuvien ja uudenlaisten osaamistarpeiden taustalla on ennen kaikkea koneen ja ihmisen uudenlainen suhde. (Järvensivu, Ilmakunnas ja Kyrki 2018.)
Meneillään olevan muutoksen myötä ihmisille jää enemmän aikaa työn niiden osuuksien tekemiseen, joissa ihminen on edelleenkin korvaamaton. Tällainen luova ja luonteeltaan vaihteleva työ on myös yleensä ihmiselle mielekkäämpää. Robotit sopivat erityisen hyvin tehtäviin, joissa oleellista on toistaa samoja toimenpiteitä yhä uudestaan, aina yhtä täsmällisesti. Sen sijaan ihminen kokee runsaasti toistoa sisältävän työn usein puuduttavaksi ja väsyttäväksi. Tällainen mielentila puolestaan lisää esimerkiksi työtapaturmien riskiä. Niinpä robottien käyttö tehtaissa (tai muissa ihmiselle vaarallisissa ympäristöissä) voi myös parantaa työntekijöiden työssä viihtymistä ja työturvallisuutta.
Jo nyt uusi teknologia on merkittävästi muuttanut työelämää. Moni perinteinen ammatti on hävinnyt tai häviämässä ja tulevaisuudessa tämän maailmanlaajuisen kehityksen odotetaan edelleen jatkuvan. Palveluyhteiskunta on muuttumassa itsepalvelu- ja robottipalveluyhteiskunnaksi, jossa asiakkaat omaksuvat "tee se itse"-asenteen ja tekoälyrobotit jaksavat palvella asiakkaita viikon jokaisena päivänä, vuorokauden jokaisena tuntina. Näiden apulaisten taholta ei ole odotettavissa myöskään lakonuhkaa.
Automaation ja tekoälyn mahdollisuudet ovatkin jo tällä hetkellä vaikuttaneet opiskelijamääriin ja työllisyystilanteeseen erityisesti sellaisia aloja, joiden bisnesmalli on perinteisesti perustunut rajallisesti saatavilla olevaan tietoon ja suhteellisen pitkälti toistoon perustuviin taitoihin. Tekoälyn ja automaation mahdollistamat palvelut sallivat asiakkaan tehdä pitkälti itse niitä asioita, joihin käyttämäänsä aikaa ammatinharjoittajat aikaisemmin laskuttivat. Erityisesti lakialalla, missä lakimies tai -neuvoja tyypillisesti laskuttaa työstään tuntiperustaisesti, automaation ja tekoälyn mahdollisuuksiin on suhtauduttu ristiriitaisin tuntein ja automaation tuoma tehokkuus on ymmärrettävästi herättänyt myös vastustusta. Tuntiperusteisesti työstään palkan saava asiantuntija ei ensisijaisesti halua säästää aikaa. Lakialalla tekoälyn- ja automaatiokehityksen kerrotaan jo nyt näkyvän opiskelijamäärien laskuna ja madaltuneina palkkoina. Sama pätee myös esimerkiksi matkailualaan, missä matkatoimistovirkailijoiden työttömyysluvut ovat kasvaneet ja niiden myös odotetaan yhä edelleen kasvavan. (Kaplan 2016)
Autonomisten koneiden merkitys on kasvanut suuresti työkoneteollisuudessa ja esimerkiksi Uudenkaupungin autotehdas tarjoaakin esimerkin tästä meneillään olevasta työelämän muutoksesta. Suomalainen työvoima on liian kallista autojen kokoonpanotyöhön. Tilanne muuttuu, kun raskas tekninen vaihe toteutetaan robottien avulla ja roboteille soveltumattomat työvaiheet hoitaa ihmistyövoima. Tässä ratkaisussa yhden tekoälyrobotin arvioidaan luoneen noin 15 uutta työpaikkaa, kun taas ilman robottien käyttöönottoa alan työpaikat olisivat hävinneet Suomesta. Aalto-yliopiston automaatiotekniikan professorin Ville Kyrki esitti jo vuonna 2013 Talouselämän haastattelussa arvion, jonka mukaan robotteihin liittyvät työt, sekä niiden valmistuksessa että palvelusektorilla, tulevat kaiken kaikkiaan luomaan 200 000 - 250 000 uutta työpaikkaa vuoteen 2020 mennessä (Tekniikka ja talous 2013).
Koska työelämän työnkuvat muuttuvat, myös uutta osaamista tarvittaisiin nopeasti. Suomessa uudelleenkoulutuksen arvioidaan kohdistuvan miljoonaan kansalaiseen - siis miltei joka toiseen työntekijään seuraavan kymmenen vuoden aikana. Euroopan tasolla vastaava uudelleenkouluttautumistarve koskee noin 100 miljoonaa työntekijää. Tämä ei kuitenkaan ole ainoa muuttuvan työelämän haaste. Työntekijät eivät aina tunnista kaikkea olemassaolevaa osaamistaan tai sitten tarjolla oleva työvoima ja 'avoimet työpaikat eivät kohtaa muista syistä. Niinpä Suomessa (kuten myös Suomen ulkopuolella) odotetaan, että tähän niin kutsuttuun kohtaanto-ongelmaankin voitaisiin löytää apua juuri tekoälyteknologiasta (TE-palvelut 2018).
Työmaailma ja ura-ajattelu muuttuvat kovaa vauhtia, eivätkä menneiden aikojen ajatusmallit kiinteistä ammateista ja niihin johtavista vakiintuneista opintopoluista vastaa enää nykypäivän tai huomisen todellisuutta. Jo nyt on kuitenkin olemassa useita tekoälysovelluksia, jotka on kehitetty auttamaan oman osaamisen ja työelämää koskevien toiveiden yhteensovittamisessa ja seuraavan työtilaisuuden löytämisessä. Esimerkiksi Mosaic auttaa kirjoittamaan ansioluettelon, jossa käsitellään hakijan kiinnostuksen ja tavoitteiden kannalta oikeita asioita ja avainsanoja. Toiset sovellukset, kuten Leap, Newton, Stella, Woo, Wade ja Wendy, voivat auttaa työnhaussa etsimällä ja suosittelemalla hakijalle hänen kykyihinsä ja kiinnostuksen kohteisiinsa nähden sopivia yrityksiä ja työpaikkoja tai ehdottamalla uusia ammatillisia vaihtoehtoja.
9.2 Teollisuus
Teollisuus sisältää runsaasti sen kaltaisia osatehtäviä, joihin tekoälytuetut robotit soveltuvat erityisen hyvin. Tehtaissa itsenäisesti tai ihmistyöntekijöiden kanssa yhteistyössä toimivat robotit ovatkin yksi keskeinen tekoälyn soveltamiskohde teollisuuden alalla, mutta käytössä on myös esimerkiksi pilvipalvelimien ja esineiden internetin (IoT) perustalla toimivia seuranta-, tiedonhaku- ja analysointijärjestelmiä. Tekoäly voi osallistua teollisuuden prosesseihin nopeuttamalla, helpottamalla ja tehostamalla ihmisen tekemää työtä tai suorittamalla toimenpiteitä itsenäisesti. (Mueller, Massaron 2018) Näin saadaan alennettua työvoimakustannuksia, vähennettyä tuotantoprosessin virheitä ja suunnittelemattomia seisokkeja sekä lisättyä tuotantonopeutta.
Erilaisia tekoälyä hyödyntäviä robotteja käytetäänkin jo laajasti puolijohdeteollisuudessa, työkoneteollisuudessa ja esimerkiksi elintarviketeollisuudessa ja suuri osa tuotantolinjojen töistä hoituu teollisuusrobottien toimesta. Esimerkkejä tehtaissa suoritettavista automatisoiduista tehtävistä, joissa hyödynnetään vaihtelevissa määrin tekoälyä, ovat materiaalien ja tuotteiden valmistus ja kokoaminen (esimerkiksi hitsaamis ja maalaustehtävät), elintarvikkeiden valmistus (sisältäen esimerkiksi lihanleikkuuta, vihannesten poimintaa ja leivonnaisten koristelua), tuotteiden lajittelu, pinoaminen ja pakkaaminen. Esimerkkivideoita tehtaissa toimivista roboteista löytyy runsaasti verkosta, muun muassa Alex Owen-Hillin (2017) elintarvikkeiden valmistuksessa käytettyihin tehdasrobotteihin keskittyvästä verkkoartikkelista "Top 6 Robotic Applications in Food Manufacturing" ja Jon Walkerin (2018) Techemergencen sivustolle kirjoittamasta artikkelista, joka tarkastelee tehdasympäristöön suunniteltuja koneoppimisperustaisia sovelluksia.
Geissbauer, Schrauf, Berttram ja Cheraghi (2017) ovat tarkastelleet raportissaan, miten pitkällä suuret teollisuusyritykset tällä hetkellä ovat tehtaiden digitalisoimisessa. Yli puolet selvitykseen haastatelluista ilmoitti jo hyödyntävänsä koneoppimisperustaisia sovelluksia voidakseen tehdä parempia operationaalisia ratkaisuja, joiden odotetaan ajanmittaan tuottavan monessa muodossa myös mittavia säästöjä. Toimiakseen ja tuottaakseen merkittävää hyötyä tekoäly tarvitsee tietoa eli dataa. Teollisiin prosesseihin taas liittyy usein hyvin monenlaisia muuttujia ja suureita, jotka ovat mitattavissa ja siten jo valmiiksi tietokoneen kannalta hyvin ymmärrettävässä muodossa. Yleisesti ottaen pätee sääntö: mitä enemmän asianmukaisesti muotoiltua dataa tekoälyjärjestelmä voi saada käyttöönsä, sitä paremmin se voi palvella tehtävässään. Niinpä yksi tärkeä osa tekoälyjärjestelmää ovat erilaiset sensorit, joiden kautta järjestelmä voi kerätä dataa ja siten tarkkailla prosessien kulkua. (Mueller, Massaron 2018)
Sensoreiden avulla voidaan saada tietoa miltei mistä tahansa tuotanoprosesseissa tapahtuvista mitattavista muutoksista (määristä, mitoista, pitoisuuksista, lämpötiloista, liikkeistä, jne). Erilaisia internetiin kytkettyjä sensoreita on olemassa satoja miljardeja, mikä on kymmenkertainen määrä puhelimiin nähden. Huippunopeat tekoälyteknologioita hyödyntävät tietokoneet kykenevät analysoimaan sensoreiden keräämää tietoa reaaliaikaisesti ja saattavat myös automaattisesti ohjata koneiden suorittamia prosesseja keräämänsä sensoritiedon perusteella. Niinpä esimerkiksi laaduntarkkailussa konenäkö on jo ajat sitten korvannut ihmissilmän. Kun robotit lisäksi joutuvat toisinaan työskentelemään muuttuvassa toimintaympäristössä tai ominaisuuksiltaan vaihtelevan materiaalin (esimerkiksi hedelmien ja vihannesten) parissa, nousee reaaliaikaisen sensoritiedon käsittelyvaatimuksen rinnalle myös tarve oppia aikaisemmista kokemuksista. (Mueller, Massaron 2018)
Robottien käyttö voi parantaa työturvallisuutta jo pelkästään siksi, ettei ihmistyöntekijöiden tarvitse enää työskennellä ihmiskeholle lähtökohtaisesti vaarallisissa olosuhteissa (kuten korkeissa lämpötiloissa) tai tehdä paljon toistoa sisältävää työtä vaarallisia työkaluja käyttäen. Teollisuusrobotit ovat kuitenkin itsessään sisältäneet ihmistyöntekijöille turvallisuusriskejä niiden ihmistä havaitsemattoman "tyhmyyden" vuoksi. Niinpä ihmisten ja robottien on täytynyt työskennellä turvallisuusaitojen rajaamilla omilla alueillaan.
Kiinalais-saksalainen KUKA on yksi maailman suurimmista teollisuusrobottien valmistajista, ja yrityksen yhtenä tavoitteena on ollut tarttua tähän turvallisuusongelmaan. Yritys on valmistanut LBR iiwa -nimisen robotin, joka soveltuu erityisen hyvin ihmisen ja robotin väliseen yhteistyöhön. Robotin tekoäly sisältää erityisherkkyyden, joka muodostuu tehokkaiden sensoreiden ja älykkään ohjaustekniikan yhteistoiminnasta. LBR iiwan ominaisuuksien ansiosta ihminen ja robotti voivat turvallisesti työskennellä rinnakkain ilman että robotti saattaisi liikkeillään vahingoittaa ihmistä. Tämä robotti voidaan sijoittaa yhä uudelleen erilaisiin, tarpeenmukaisiin tehtäviin. Tähän mennessä sitä hyödyntävät KUKAn omien tehtaiden lisäksi muun muassa BMW Group Plant Munich.
Tekoäly voi osallistua myös automaation itsensä luomiseen miltei kaikissa luomisprosessin vaiheissa. Itseasiassa ihmisen on välttämätöntä ainoastaan luoda työ ja ilmaista se koneelle ymmärrettävässä muodossa. Tämän jälkeen tekoälyjärjestelmä voi auttaa prosessin seuraavissa vaiheissa määrittelemällä työn toteuttamisen vaihtoehdot, esittämällä suosituksen parhaista vaihtoehdoista ja määrittämällä prosessin edellyttämät toimenpiteet. Onkin havaittu, että valtaosa suuryrityksistä, jotka valmistavat koneoppimisperustaisia työkaluja, käyttää samoja työkaluja myös omaan tuotantoonsa (Walker 2018). Näin ollen yritys itse toimii sekä kehittäjän, testaajan että ensimmäisen asiakkaan ominaisuudessa. Esimerkiksi Siemens ja GE ovat pyrkineet luomaan tekoälyn avulla kokonaisvaltaisesti tehostettua teollisuuden kehitys- ja valmistusprosessia ja näitä järjestelmiä on otettu käyttöön ensisijaisesti yritysten omissa tehtaissa.
Siemensin kehittämä "IoT käyttöjärjestelmä" MindSphere tallentaa erilaisia operatiivisia tietoja ja saattaa ne sovellustensa kautta helpommin luoksepäästävään muotoon. Järjestelmä pyrkii monitoroimaan, tallentamaan ja analysoimaan kaikkia teollisen prosessin vaiheita aina valmistuksesta jakeluun saakka ja tunnistamaan ja ratkaisemaan ennaltaehkäisevästi mahdollisia ongelmia. MindSphere-järjestelmän avulla teollisuusasiakkaat voivat siis hankkia hyödyllisiä tietoja päätöksentekonsa tueksi. MindSpheren kerrotaan esimerkiksi tehostaneen Siemensin kaasuturbiinien päästöjen hillitsemistä 10-15% menestyksekkäämmin kuin mihin alan ihmisasiantuntijat parhaimmillaan pystyivät (Siemens päiväämätön).
GE:n vuonna 2015 lanseerama Brilliant Manufacturing Suite on toinen esimerkki laaja-alaisemmasta teollisuusjärjestelmästä, joka pyrkii jäljittämään ja käsittelemään kohdetehtaan prosesseja kokonaisvaltaisesti havaitakseen mahdolliset ongelmat ja tehottomuuskohdat jo ennen kuin niistä on ehtinyt syntyä varsinaista haittaa. Järjestelmän avulla yritykset voivat hankkia sekä tuotesuunnittelussa että tuotantoprosesseissa hyödynnettävää tietoa. GE:n näissä tehtävissä hyödyntämät teknologiaratkaisut perustuvat konenäköön, robotteihin ja IoT:iin. Järjestelmän ytimenä toimii Predix, teollinen IoT-alusta, joka kykenee seuraamaan tarkkaavaisesti eri työvaiheiden sensoritietoja ja laiteohjausta. GE:llä on yli viisi sataa omaa tehdasta ympäri maailman, joista seitsemää se on vuodesta 2015 alkaen ryhtynyt muuttamaan Brilliant Manufacturing Suiten piiriin. GE:n hankeen lopullisena päämääränä on muodostaa maailmanlaajuisesti skaalautuva älykäs järjestelmä, jossa yhdistyvät suunnittelu, valmistus, toimitusketju, jakelu sekä palvelut. GE:n itse kuvaamissa esimerkkitapauksissa Brilliant Manufacturing Suiten avulla esimerkiksi GE:n Vietnamin tuuligeneraattoritehtaan kerrotaan kasvattaneen tuottavuuttaan 5% ja Muskegonin suihkumoottoritehtaan aikataulutuksen katsotaan parantuneen 25%:lla (GE päiväämätön).
Japanilainen FANUC, joka myöskin on yksi johtavista teollisuusrobotiikkaan keskittyneistä yrityksistä, on tehnyt yhteistyötä Ciscon, Rockwell Automationin ja NVIDIAn kanssa ja kehittänyt FIELD-nimistä teollisen IoT:n alustaa tehtaille (FANUC 2018). Alustaan liitetyn tekoälyn avulla robotit opettavat itseään suorittamaan tietyn tehtävän vaaditulla tarkkuudella. Robottien yhdistettävyyttä on pyritty kehittämään edelleen siten, että useampi robotti voisi edistää oppimistaan yhdessä. Robottien yhteisoppimisen taustaidean mukaisesti sen, minkä yksi robotti kykenee oppimaan kahdeksassa tunnissa, kykenee kahdeksan robottia oppimaan yhdessä tunnissa. (Walker 2018.)
Tekoälyohjelma
Työ- ja elinkeinoministeriön tekoälyohjelman tarkoitus oli pohtia tekoälyn soveltamisen tulevaisuutta ja viedä Suomi tekoälyaikaan (TEM). Selvityshankkeen tammikuussa 2019 valmistuneessa loppuraportissa Tekoälyn kokonaiskuva ja kansallinen osaamiskartoitus (TEM 2019) käsitellään tekoälyn kymmentä osaamisaluetta:
- Data-analyysi.
- Havainnointi ja tilannetietoisuus.
- Luonnollinen kieli ja kognitio.
- Vuorovaikutus ihmisen kanssa.
- Digitaidot työelämässä, ongelmanratkaisu ja laskennallinen luovuus.
- Koneoppiminen.
- Järjestelmätaso ja systeemivaikutukset.
- Tekoälyn laskentaympäristöt, alustat ja palvelut, ekosysteemit.
- Robotiikka ja koneautomaatio – tekoälyn fyysinen ulottuvuus.Etiikka, moraali, regulaatio ja lainsäädäntö.
Ohjausryhmän lisäksi ohjelmassa oli neljä alatyöryhmää: Osaaminen ja innovaatiot, Yhteiskunnan ja työn muutos, Data ja alustatalous ja Etiikka. Hankkeeseen ja yleisesti tekoälyyn liittyviä uutisia ja raportteja julkaistiin tekoalyaika.fi -sivustolla.
9.3 Varastointi ja kuljetus
Tulevaisuutta ennakoivan laskennan avulla voidaan pyrkiä tunnistamaan tulevien myyntisesonkien trendejä, jotta näihin osattaisiin varautua jo ennakolta. Tekoälyn avulla verkkokaupan tai monikanavaisen kaupan liiketoimintaa voidaan myös pyrkiä optimoimaan. Voidaan esimerkiksi analysoida, millainen tuotevalikoima tietyssä sijainnissa palvelevan kivijalkaliikkeen hyllyille kannattaa sijoittaa ja kuinka paljon hyllytilaa kunkin tuoteryhmän varastointiin kannattaa varata. Näiden arvioiden onnistuminen riippuu pitkälti siitä, saako tekoäly käyttöönsä riittävän määrän edustavaa historiadataa. (Syväniemi, Raunama 2018.)
Verkkokauppatoiminnassa tuotteet toimitetaan suoraan kotiin tai suunnitellun aikataulun mukaisesti tiettyyn jakelupisteeseen - ellei kyse ole digitaalisessa muodossa olevasta tuotteesta. Nämä järjestelmät hyödyntävät kansainvälisiä, alhaiset postitusmaksut mahdollistavia sopimuksia. Seuraavaksi ostotapahtumasta ollaan automatisoimassa tilaus- ja toimitusvaiheita. (Rokka 2017.)
Tällä hetkellä useissa erilaisissa varastoissa hyödynnetään mobiilirobotteja. Verkkokauppa Amazonin kerrotaan jo tällä hetkellä käyttävän varastoissaan robotteja, joiden avulla se on kyennyt tehostamaan logistiikkakeskuksissa tehtyä työtä siinä määrin, että tilausten käsittelyajat ovat supistuneet tunnista viiteentoista minuuttiin. Robotit pystyvät palvelemaan myös hotelleissa ja sairaaloissa osallistumalla erilaisiin kuljetuksiin. (Högström 2017; Wingfield 2017.) Suomessa esimerkiksi Oulun yliopistollinen sairaala ja Seinäjoen keskussairaala ovat ottaneet koekäyttöön logistiikkarobotteja (esimerkiksi Aethonin valmistamia TUG-robotteja), jotka kuljettavat lääkkeitä, tarvikkeita tai esimerkiksi pyykkiä. Koska logistiikkajärjestelmän avulla kuljetukset voivat toimia joka päivä kellon ympäri, voivat robotit parantaa tarvikkeiden saatavuutta, helpottaa sairaalakäytävien ruuhkaisuutta sekä madaltaa kuljetuskustannuksia (Juopperi 2017; Uusiteknologia.fi 2017). Koska nämä robotit ainakin osassa tapauksista kulkevat samoilla käytävillä, missä ihmisetkin, on yksi näidenkin laitteiden tekoälyyn liittyvä vaatimus se, etteivät ne saa törmäillä ihmisiin.
Erityisesti suurten keskusvarastojen tarpeisiin pyritään kehittämään yhä pidemmälle automatisoidumpia trukkeja. Tavoitteena on, että jo muutaman vuoden kuluttua tällaiset mobiilirobotit pystyisivät liikkumaan varastoissa ympärivuorokautisesti ilman erillistä kuljettajaa. (Rokka 2017.)
9.4 Rahoitus ja bisnes
9.4.1 Rahoitus
Tekoälyn aikaansaaman kehityksen myötä pankkimaailman toiminnan voidaan odottaa mullistuvan suuresti. Finanssialalle odotetaan syntyvän uudenlaisia palveluita ja liiketoimintamalleja. Rutiininomainen manuaalinen työ ja paperinkäyttö vähenevät, fyysiset pankit ovat jopa häviämässä, eikä fyysistä rahaa enää juurikaan käytetä. Koska pankit ovat luonnostaan niin sanotusti dataintensiivisiä organisaatioita, tekoälyn ja lohkoketjujen odotetaan lähitulevaisuudessa muodostavan pankkitoiminnan perustan.
Palvelunäkökulmasta tällä hetkellä ollaan siirtymässä tilanteeseen, jossa tekoälytuettu robotti hoitaa asiakaspalvelun rutiinitehtäviä vastaten asiakkaiden usein esittämiin peruskysymyksiin ja ohjaten heitä tarvittaessa edelleen oikeisiin asiointikanaviin. Näin päästään lyhentämään palvelujen jonotusaikoja. Lisäksi robotit kykenevät muodostamaan arvion asiakkaan riskitasosta ja myöntämään tämän pohjalta lainan tai vakuutukset. Ihmistyöntekijät toimivat kasvokkaispalvelua tarjoavina taloudellisina neuvonanatajina ja rahoitusalan teknologian kehittäjinä. Robottien ottaessa haltuun luonteeltaan ennakoitavissa olevan rutiinityön odotetaan ihmistyöntekijöiltä entistä laaja-alaisempaa finanssialan tuntemusta, luovuutta ja kykyä kohdata toinen ihminen (Rauhala 2018).
Tällä hetkellä rahoitusalalla tekoälysovelluksia käytetään muun muassa luottoarvioita tehtäessä, osakesalkkujen käsittelyssä sekä rahoitusennakoinnissa ja -suunnittelussa. Useat tutkimukset ovatkin vahvistaneet, että tekoälymetodit (keinotekoiset neuroverkot, asiantuntijajärjestelmät ja älykkäät hybridijärjestelmät) ovat tarkkuudessaan erinomaisia edellä mainittuihin tehtäviin perinteisesti käytettyihin laskennallisiin metodeihin verraten (Bahrammirzaee 2010).
Perinteisen rahan rinnalle on ilmestynyt yhä enemmän muunlaisia, sopimukseen pohjautuvia vaihdannan välineitä, joista esimerkin tarjoaa jo nyt olemassaoleva bitcoin-valuutta. Termi finanssitekniikka, myös FinTech tai fintech, viittaa teknologiaan ja ratkaisuihin, jotka kilpailevat perinteisten rahoitusmenetelmien kanssa käyttämällä tekniikkaa, kuten älypuhelimia ja sitä kautta mobiilipankkia, rahoituksen kehittämiseen ja rahoituspalvelujen tarjoamiseen laajemman yleisön saataville. Fintech liittyy niin uusiin start up -yrityksien tarjoamiin innovaatioihin kuin jo finanssialalla vakiintuneen aseman saavuttaneiden yritysten uusiin ratkaisuihin. Tällä hetkellä fintechin ydinalueita ovat vakuutukset, kauppa ja riskienhallinta. Esimerkiksi vakuutusalalla robotiikkaa käytetään korvauskäsittelyjen automatisointiin. (Finanssialalle opintomateriaali.)
Riskinarvioinnissa ja luottopäätöksien hoitamisessa tekoälyllä voidaan luoda skenaario, jonka avulla pystytään arvioimaan ostoksen takaisinmaksuun liittyvää riskitason nousua esimerkiksi sellaisen asiakkaan kohdalla, jolla on maksuhäiriömerkintä muutaman vuoden takaa. Analyysin tuloksesta riippuen asiakkaan kanssa saatetaan tehdä luottokauppa vanhasta merkinnästä huolimatta, mikäli riskin ei katsota nousevan liikaa. Toistaiseksi fintech-yritykset joutuvat kuitenkin usein kamppailemaan rahoitusalan sääntelyviranomaisten epäluuloja vastaan. Myös tietoturvakysymykset herättävät usein viranomaisten huolen arkaluontoisten kuluttaja- ja yritystietojen suojaamisen osalta.
9.4.2 Asiakkuuksista huolehtiminen
Useat yritykset käyttävät sivustoillaan chatboteja sujuvan asiakaspalvelun varmistamiseksi. Nämä robotit hoitavat esimerkiksi asiakkaiden tyypillisimpiin kysymyksiin vastaamisen ja tilausten viimeistelyn tehtäviä. Esimerkiksi Facebook tarjoaa ohjeita Messenger-chatbotin luomiseen sekä näytekeskusteluja hyödyntävän alustan (wit.ai bot engine), jolla chatbotteja voi kouluttaa ja pitää yllä niiden jatkuvaa asiakasvuorovaikutukseen liittyvää oppimista. Muita esimerkkejä toistuvien palvelutehtävien automatisointiin tarkoitetuista järjestelmistä ovat Sundown ja Electra by Lore. Nykyaikaisessa bisnestoiminnassa tekoäly pystyy kuitenkin paljon enempään kuin pelkkien rutiinitehtävien hoitamiseen. Ennen kaikkea tekooäly tehostaa asiakassuhteiden rakentamis- ja lujittamisprosessia.
Erityisesti digitaalisen markkinoinnin yhteydessä asiakkuuden elinkaarta voidaan jäsentää RACE-viitekehyksen avulla neljään vaiheeseen: tavoittaminen, toiminta, konversio ja sitouttaminen. Kaaren jokaiseen neljään vaiheeseen sisältyy osatehtäviä, joihin automaatio tai digitaalinen analytiikka voivat tuoda merkittävää lisätehoa. (Allen 2017.) Lisäksi perinteinen tehtäväjako on muuttumassa siten, että markkinoinnin ja asiakaspalvelun välinen raja katoaa: personoitu henkilökohtainen markkinointi on jo asiakaspalvelua. Markkinointityön painopiste siirtyy yksittäisten markkinointitaktiikoiden laatimisesta kokonaisvaltaisten markkinointistrategioiden suunnitteluun. (Syväniemi, Raunama 2018)
Tekoälyn avulla yrityksen sivuille voidaan houkutella lisää kävijöitä ja sivujen ääreen tiensä löytäneille voidaan tarjota entistä mielenkiintoisempia kokemuksia. Tekoälytuotettu sisältö auttaa takaamaan, että sivuilta löytyy uutta, asiakaskuntaa kiinnostavaa luettavaa säännöllisesti. Minkä tahansa aiheisen artikkelin tai pakinan itsenäiseksi kirjoittajaksi tekoäly ei kuitenkaan sovellu. Sen sijaan automaatiota kannattaa hyödyntää sen luontaisten vahvuuksien mukaisesti säännönmukaisten, aineistokeskeisten tapahtumien raportoijana. Tällaisia aiheita ovat esimerkiksi yrityksen osavuosikatsaukset, markkinatiedot tai vaikkapa urheilutulokset. Vuonna 2016 AI-perustaisen kirjoitusohjelma WordSmithin arvioidaan tuottaneen verkkoon 1,5 miljardia sisältökokonaisuutta. Sivustoilla esitettyjä sisältöjä voidaan myös personoida vierailijasta kerättyjen tietojen perusteella. Tämän päivän kuluttajat ovatkin jo varsin tottuneita näkemään verkkokauppojen sivuilla "asiakas joka osti tämän tuotteen, oli kiinnostunut myös näistä" -tyyppisiä suosituksia.
Googlen, Amazonin ja Applen kaltaisten suurten toimijoiden kehittämien äänihakutoimintojen kehittyessä myös hakukoneoptimointi muuttuu. Äänihaun myötä puhutaan semanttisesta hakukoneoptimoinnista (semantic SEO), mikä on ehkä aikaisempaa hakukoneoptimointia hieman työläämpää, mutta tehokkaasti toteutettuna se voi tuoda yritykselle huomattavia näkyvyysetuja. Verkkomainonnan ohjelmallista kilpailutusta ja ostamista taas kehitetään koneoppimisalgoritmien tuottamien vastaustaipumusmallien avulla (propensity models). Tässä yhteydessä sovelluksen tehtävänä on varmistaa, ettei mainoksia päädytä sijoittamaan vahingossa sisällöltään epäilyttäville sivuille (mikä voisi vahingoittaa yrityksen mainetta).
Asiakassuhteen elinkaaren toisessa vaiheessa (RACE-viitekehyksessä tämä vaihe on nimetty toiminnaksi) asiakkaat ovat kaupan tai palvelun "sisällä" ja heidät tulee saada tehokkaasti tietoisiksi tarjolla olevista tuotteista. Mainosten valmistamisessa ihmisen tehtäväksi jää edelleen mainoksien luovan sisällön kehittäminen. Usein mainoksista tehdäänkin useita hieman erilaisia versioita. Tekoäly auttaa profiloimaan asiakkaita ja tunnistamaan, mitkä käytössä olevista mainoksista toimivat parhaiten asiakkuuden missäkin vaiheessa. Näin tekoäly auttaa optimoimaan mainosten valintaa ja sijoittelua paljon aikaisempaa tehokkaammin.
Asiakashistoriaa kartoittavan datan ja koneoppimisen avulla tuotettuja vastaustaipumusmalleja voidaan hyödyntää yrityksen myyntitiimin ajankäytön suuntaamiseksi mahdollisimman tehokkaasti. Kun vastaustaipumusmalleja sovelletaan ennakoivan analytiikan alueella, voidaan muodostaa ennusteita asiakkaiden käyttäytymisestä. Mikäli käytössä on riittävä määrä hyvälaatuista dataa, voidaan arvioida esimerkiksi ketkä potentiaalisista asiakkaista tulevat tekemään ostoksia ja ketkä näistä asiakkaista todennäköisesti tekevät ostoksia toistuvasti. Vastaustaipumusmalleja voidaan edelleen opettaa pisteyttämään mahdollisten asiakkaiden (liidien) kiinnostavuus, jolloin voidaan päätellä, mitkä mahdollisista asiakkaista ovat niitä, joihin myyntitiimin resursseja erityisesti kannattaa käyttää. Tällainen ennakointi on erityisen tärkeää sellaisilla aloilla, joilla yksittäinen myyntitapahtuma edellyttää henkilökunnalta huomattavaa ajankäyttöä. Lähtökohtaisesti myyntitiimin ajankäyttö kannattaa kohdistaa niihin mahdollisiin asiakkaisiin, joilla tunnistetaan olevan kohtalainen taipumus muuttua asiakkaiksi, sillä juuri he tarvitsevat usein erityistarjouksen tai alennuksen ostopäätöksensä syntymisen tueksi (muihin ryhmiin jäävät ne sivustolla vierailevat henkilöt, jotka eivät toimenpiteistä huolimatta muutu asiakkaiksi, sekä ne, joista tulee asiakkaita ilman erityistä houkutteluakin).
Konversiovaiheessa kiinnostuneesta kuluttajasta pyritään saamaan yrityksen vakioasiakas. Verkkokaupalla yksittäisiä asiakkaita voi kuitenkin olla niin paljon, etteivät ihmistyöntekijät voi oppia tuntemaan edes kaupassa usein asioivien asiakkaidensa mieltymyksiä. Niinpä yksittäisen asiakkaan vaihetta niin sanotulla "ostajan matkalla" kartoitetaan vastaustaipumus- ja ennustemallien avulla ja näiden perusteella muodostetun arvion pohjalta verkkosivuston ja sovellusten sisältöjen syvyyttä pyritään personoimaan asiakkaan tarpeita vastaavaksi. Vastaustaipumusmalleja voidaan hyödyntää myös dynaamisen hinnoittelun tarpeisiin, jolloin yleisen alennusmyynnin sijaan alennuksia tarjotaan vain juuri niille asiakkaille, joiden asiakassuhde todennäköisimmin vahvistuu juuri tarjouksien avulla. Ennustavalla analytiikalla voidaan myös kartoittaa, millaiset ominaisuudet yhdistävät niitä asiakkaita, jotka katkaisevat tilauksensa tai asiakkuutensa, jolloin tätä tilannetta voidaan pyrkiä ennalta välttämään. Lisäksi ennusteet auttavat valitsemaan tietyn asiakkaan takaisinhoukutteluun tarkoitettuun mainontaan juuri oikeanlaisia sisältöjä.
Asiakkuuden elinkaaren sitouttamisvaiheeseen asiakaskunnasta etenee vain pieni osa. Tästä asiakasjoukosta huolehtiminen on kuitenkin yrityksille erityisen tärkeää, sillä sitoutuneet asiakkaat levittävät positiivista tietoa yrityksestä ja tuovat näin mukanaan myös uusia asiakkaita. Koneoppimisen keinoin voidaan tarkemmin määritellä, milloin ja millaisin sanavalinnoin sitoutuneisiin asiakkaisiin kannattaa ottaa yhteyttä. Myös uutiskirjeiden esittelemä tuotevalikoima ja hinnoittelu voidaan kustomoida erityisesti näiden asiakkaiden tarpeiden ja mieltymysten mukaisiksi.
9.4.3 Kuluttajanäkökulma
Myös kuluttajat osaavat hyödyntää verkosta löytyviä apuvälineitä: tuotteiden ja palveluiden hinta- ja laatuvertailun sekä saatavuustietojen etsiminen verkosta on jo arkipäiväistä. Yleinen toimintatapa on, että ensin tuotteita ja hintoja vertaillaan verkossa, mutta varsinainen ostos tehdään kivijalkakaupassa. Vaikka monet kivijalkamyymälät ovatkin joutuneet sulkemaan ovensa, verkkokauppatoiminta ei välttämättä tarkoita kivijalkakauppojen täydellistä katoamista. Sen sijaan kauppojen varastoimat tuotemäärät pienenevät ja liiketilojen käyttötavassa siirrytään yhä elämyksellisempään suuntaan.
Tekoäly mahdollistaa myös asiointitapojen uudelleenajattelun. Esimerkiksi Amazon on kehittänyt kassatonta Amazon Go -kauppaa, johon asiakas voi vain kävellä, noutaa ostokset ja poistua ilman kassajonossa seisoskelua. Kauppaan tultaessa asiakas skannaa kännykkänsä näytöltä Amazon Go -sovelluksen antaman QR-koodin. Kaupan katossa toimivat infrapunakamerat puolestaan tunnistavat mukaan poimitut tuotteet ja erottavat asiakkaat toisistaan. Joissain tuotteissa on myös visuaalinen pistekoodi tuotteen tunnistamisen helpottamiseksi. Kun tuote nostetaan hyllystä käteen tarkasteltavaksi, havaitsevat hyllyihin asennetut vaakasensorit, mikäli tuote kuitenkin palautetaan myöhemmin takaisin hyllyyn. Kehittäjät vertaavat Amazon Go:n hyödyntämää tekniikkaa itsestään ajavien autojen hyödyntämään tekoälyyn. Asiakkaan poistuessa kaupasta on hänen ostoksistaan koostettu lopullinen lista ja tämän perusteella ostokset veloitetaan automaattisesti hänen luottokortiltaan ja kuitti lähetettään Amazon Go-sovellukseen. (Johnston 2018.)
9.4.4 Yrittäjän ajankäyttö ja kertyvän datan hyödyntäminen
Yrittäjälle on tarjolla lukuisia yleisesti työskentelyä tukevia ja tehostavia sovelluksia, yrityksen palveluita alasta riippumatta tehostavia sovelluksia sekä erityisesti tiettyjen alojen tarpeita silmällä pitäen kehitettyjä järjestelmiä. Yrityksen pyörittämiseen liittyvissä tehtävissä tekoälysovellukset voivat avustaa esimerkiksi ajankäytön, työtehtävien ja yhteystietojen hallinnassa. Digitaalisten kansioiden ja pilvipalvelimien uumeniin hukkuneita tietoja voidaan etsiä pelkän yleisluontoisen kuvailun perusteella esimerkiksi Findo-järjestelmällä. Erilaisten digitaalisten aineistojen hyödyntämistä ja ajankäytön ja työskentelyn suunnittelua on myös pyritty lähestymään uusista näkökulmista murtamalla perinteisten muistin ja suunnittelun apuvälineiden, kuten kalentereiden ja yhteystietomuistioiden, muodostamia jäsennyksiä. Esimerkiksi Aloe-sovellus lupaa parantaa työskentelyn sujuvuutta ja tuottavuutta organisoimalla kokous- ja muut muistiinpanot sekä tehtävät niihin liittyvien ihmisten ja yritysten mukaisesti ja tarjoamalla käyttäjän tueksi luonnollisella kielellä toimivan päivyriassistentin.
Yrittäjillä on tyypillisesti käytössään useita digitaalisia järjestelmiä, kuten sähköposti- ja kalenterisovellukset, erilaisilla toimistotyökaluilla rakennetut raportit, esitysmateriaalit ja kokousmuistiot, sekä pilvipalveluiden arkistot ja työskentely-ympäristöt. Niinpä aineistot, jotka kertyvät vuosien mittaan yrityksen pyörittämisestä, kokouksista, tapahtumissa pidetyistä esityksistä ja muista tilanteista, paisuvat helposti laajoiksi. Yrittäjien avuksi onkin kehitetty sovelluksia, jotka auttavat paitsi hallinnoimaan laajoja aineistomääriä myös ottamaan dokumenteista ja yhteystiedoista kaiken mahdollisen hyödyn irti. Tekoälyjärjestelmät voivat esimerkiksi luodata näitä tiedonlähteitä läpi tulevan yritystoiminnan kannalta hyödyllisiä tietoja ja kontaktihenkilöitä etsien. Etsinnän tuloksena tekoälyjärjestelmä voi esimerkiksi antaa vinkkejä mahdollisista uusista työntekijöistä, asiakkaista ja partnereista. Esimerkkejä tällaisista työkaluista ovat Trove sekä Prospex, joista erityisesti jälkimmäinen on suunniteltu edistämään yritysten myyntitiimien työtä. Myös Nudge on sovellus, joka tarkastelee käyttäjän sähköpostiyhteystietoja sekä selattuja verkkosivuja ja esimerkiksi joitakin myyntityötä tukevia tietokantoja (esimerkiksi asiakassuhteiden hoitamiseen liittyvää salesforce.com:ia) voidakseen ehdottaa mahdollisia asiakkaita ja muodostaa hyödyllisiä havaintoja samalla kun käyttäjä selaa verkkosivuja.
Yritysten käyttöön on olemassa myös puheentunnistusta hyödyntäviä sovelluksia, joilla voi transkriptioida eli kääntää audiodataa kirjoitettuun muotoon (esimerkiksi Capio ja Deepgram) tai järjestää audiodatan haettavaan muotoon (esimerkiksi nykyisin Applen omistama Pop Up Archive). Tarjolla on myös esimerkiksi Gridspace-järjestelmä, joka lupaa mahdollistaa asiakas-työntekijä-keskustelujen reaaliaikaiseen tarkastelun liiketoimintaviestinnän parantamista varten.
Jotkut sovellukset, kuten Ecosystem.AI, erikoistuvat BigData-pohjaiseen vastausten etsimiseen bisnesnäkökulmasta (muilla osa-alueilla kuin jo edellämainitussa asiakkuuden rakentamisessa) ja näillä työkaluilla voidaan etsiä vastauksia monitahoisiin ilmiöihin liittyviin kysymyksiin, kuten mihin markkinaekosysteemin osa-alueeseen kannattaisi keskittyä tai mitkä monista tuoteideoista kannattaisi valita jatkokehittelyyn. Lisää yleisluontoisia sekä tiettyyn alaan erikoistuneita tekoälyperustaisia bisnestyökaluja on listattu esimerkiksi Liam Hänelin blogikirjoituksissa.
9.4.5 Esimerkkejä palvelualoilta
Robottiteknologiaa hyödynnetään jo myös erilaisilla palvelualoilla. Erityisesti Kiinassa, mutta myös Japanissa, robotteja on jo usean vuoden ajan näkynyt esimerkiksi ravintola-alalla, missä robotit kykenevät hoitamaan sekä tarjoilu- että ruuanlaittotehtäviä. Kesällä 2012 Kiinan Harbinissa avatiin nimenomaan "robottikokemukseen" erikoistunut ravintola, jossa kerrotaan toimivan 18 erilaista robottia. Robotit on toteuttanut Harbin Haohai Robot Company. Nämä ravintolarobotit poikkeavat toisistaan värin, korkeuden sekä erilaisten tehtäviensä suhteen. Robotit hoitavat tarjoilua, erityyppisten ruokien valmistamista sekä asiakkaiden viihdyttämistä. Ravintolarobottien kerrotaan omaavan jopa kymmenen erilaista ilmettä ja puhuvan yksinkertaistettua kiinaa. Tarjoilurobotit on varustettu myös havaintosensorein, jotta ne kykenevät liikkumaan ravintolassa törmäilemättä asiakkaisiin. Tätä nykyä jo useammat kiinalaiset ravintolat ovat ottaneet käyttöönsä robotteja aterioiden ja astioiden kuljetteluun sekä keittiön puolelle ruuan esivalmistelutehtäviin. (Chinadaily 2012.)
Erilaisissa asiakaspalveluun liittyvissä opastustehtävissä sekä asiakkaiden viihdyttämisessä hyödynnetyistä roboteista esimerkin tarjoaa "humanoidirobotti" Pepper, jonka on suunnitellut SoftBank Robotics. Suomesta Pepper löytyy tällä hetkellä esimerkiksi Jyväskylän avoimesta yliopistosta, Helsingin Kalasataman terveyskeskuksesta, Helsingin Elisa Kulmasta ja Lempäälän Ideaparkista. Tämän robotin ominaisuuksissa on tähdätty erityisesti robotin kykyyn tunnistaa ihmisten tunnetiloja ja käyttäytyä ja kommunikoida kohtaamiensa ihmisten kanssa tulkintojaan hyödyntäen. Tunnetilojen tulkinnassa Pepper hyödyntää mm. kasvonilmeiden, äänensävyn, liikkeiden ja sanojen havainnointia. Pepperiä käsitellään lisää myös tämän raportin vanhustenhoitoa käsittelevässä luvussa. Pepper-robotilla pyritään sujuvoittamaan palveluita ja lyhentämään asiakkaisen jonotusaikoja, mutta myös keräämään tietoja asiakkaista.
Yhä kasvavan turismin myötä eri palvelualat hyötyvät myös tekoälyratkaisuista, jotka on suunniteltu erityisesti kielimuurin ylittämiseksi. Sakura-sovellus on esimerkki tällaisesta eri palvelualoille suunnitellusta sovelluksesta, joka osaa japania, englantia, kiinaa ja koreaa ja pystyy tulkkaamaan palvelutilanteen valittujen kielien välillä. Yksi Sakuran suunnittelussa erityisesti huomioitu sovellusala on japanilaisen lääkärin ja ulkomaalaisen potilaan välinen kommunikaatiotilanne, jossa osapuolilla ei ole yhteistä kieltä. Sakura kääntää potilaalle lääkärin puheen ja auttaa näin lääkäriä haastattelemaan potilasta potilaan omalla äidinkielellä luonnolliseen keskusteluun pyrkivää tyyliä tavoitellen (Tifana AI Business 2018; Ojalainen-Neittaanmäki 2018).
9.5 Terveys- ja sosiaalipalvelut sekä lääketeollisuus
Lääketieteen alalla tekoälyteknologioilta odotetaan paljon. Palvelurakenteita muutetaan, digitaalisten aineistojen ja järjestelmien hyödyntämistä pyritään lisäämään ja samanaikaisesti terveysalan painopiste pyritään siirtämään terveyden omaehtoiseen ja ennaltaehkäisevään toimintaan. Tekoälyn soveltamisen näkökulmasta tämä tarkoittaa muun muassa ihmisten itse keräämän terveysdatan hyödyntämistä oikeanlaisen aktiivisuuden varmistamiseksi, työhyvinvoinnin parantamiseksi ja jo kehittymässä olevien vammojen tai sairauksien varhaisempaa diagnosointia ja hoitoa varten. Diagnosoinnin ja hoitosuunnitelmien tekeminen tekoälyavusteisesti edellyttävät myös saatavilla olevan tutkimus- ja potilastiedon tehokasta hyödyntämistä tekoälyn opettamisessa.
Tekoäly tehostaa lääkärin työtä, sillä käyttöön on kehitteillä useita erilaisia työkaluja, joiden avulla esimerkiksi sairauksien diagnosointi ja hoidon suunnittelu käyvät helpommin, nopeammin ja luotettavammin. Kuva-analytiikkaperustaiset sovellukset tarjoavat nopeita ja täsmällisyydessään asiantuntijatyöskentelyyn rinnastettavia vastauksia radiologian, patologian ja dermatologian alueilla. Nimenomaan koneen ja ihmisasiantuntijan yhteistyö voi tehostaa merkittävästi diagnosointiprosessia. (Miller, Brown 2017)
Sovelluksilla pyritään keventämään myös hoitajien työtaakkaa, sillä esimerkiksi valvontaan erikoistuneet laitteet, kuten älykkäät sängyt, voivat auttaa potilaan voinnin ja elintoimintojen seurannassa. Lisäksi erilaiset kommunikoivat ja liikkuvat ihmishahmoa jäljittelevät robotit voivat auttaa hoitajia potilaiden tarkkailussa, kuntouttamisessa ja virkistämisessä. Useissa sairaaloissa käyttöön on myös otettu logistiikkarobotteja, jotka hoitavat osan tarvikkeiden kuljettamisessa. Kaikki nämä ratkaisut tehostavat hoitohenkilökunnan työtä tavalla, jolla saadaan säästöjä alan kustannuksiin ja jolla henkilökunnan työaikaa voidaan kohdistaa enemmän esimerkiksi lääkärin ja potilaan väliseen kohtaamiseen ja hoitotoimiin.
Kun terveysdataa voidaan kerätä missä ja milloin tahansa ja kun tieto voi vaihtaa omistajaa ilman erillistä asiointia terveysasemalle, voivat lääkärit saada potilaiden seurantaan tarvitsemansa tiedot ilman odottelua juuri silloin kun he sitä tarvitsevat. Samoin potilaat voivat saada ohjeita ja esimerkiksi kuntoutusliikkeiden tekemiseen liittyvää palautetta ilman useiden viikkojen odotusaikaa. Tekoälyteknologialla voidaan myös varmistaa, ettei monialaisina tiimitöinä toteuttettavissa hoitoprosesseissa pääse syntymään henkilökunnan kommunikaatiopuutteiden tai -katkosten vuoksi riskitilanteita.
Tekoälyrobotiikka voi avustaa lääkäreitä myös suorittamaan väsymätöntä tarkkuutta ja täsmällisyyttä vaativia toimenpiteitä, kuten leikkauksia. Kirurgian sovellusalalla tekoälytuettu automaatio liittyy leikkauksen valmisteluun, leikkauksen aikaisiin tapahtumiin sekä esimerkiksi toimenpiteiden harjoittelemiseen. Tekoälyteknologia parantaa tuloksia vähentämällä leikkauksiin liittyviä virheitä ja jälkikomplikaatioita sekä lyhentämällä toimenpiteen jälkeistä toipumisaikaa. Joitakin nykyaikaisista toimenpiteistä ei edes pystyttäisi toteuttamaan ilman tekoälyteknologiaa. (Mueller, Massaron 2018.)
Uusien lääkeaineiden tutkimus- ja kehitystyössä koneoppimisperustaisilla tekoälysovelluksilla pyritään ennen kaikkea nopeuttamaan prosessin aikaa vieviä vaiheita sekä madaltamaan alan kustannuksia. Tekoälysovelluksien avulla voidaan myös etsiä tietylle yksilölle parhaiten soveltuvaa lääkinnällistä ratkaisua. Seuraavissa alaluvuissa käydään läpi esimerkkejä tekoälysovelluksista, jotka liittyvät tässä yleissilmäyksessä mainittuihin terveydenhoidon erityistehtäviin.
Tekoälytutkimuksen yhteydessä esitellyn Jyväskylän yliopiston IT-tiedekunnan hankekokonaisuuden Tekoäly ja terveydenhuolto Suomessa neljän kirjan sarjan ensimmäisestä osasta Tekoäly ja terveydenhuolto Suomessa löytyy lisää esimerkkejä ja tuloksia esimerkiksi lääkehuollosta ja syrjäytymisen ehkäisystä.
9.5.1 Diagnosointi
Diagnosoinnin tarpeisiin kehitetyt tekoälyjärjestelmät tarjoavat lääkäreille tukea tyypillisesti tutkimalla laajoja potilas- ja tutkimustietovarantoja tavalla, johon ihmistyöntekijän aika ei millään riittäisi. Useat olemassaolevat järjestelmät hyödyntävät myös diagnosointia tukevaa kuvantunnistamiseen perustuvaa tekniikkaa. Lääkärin työskentelyn helpottamiseksi nämä järjestelmät on usein suunniteltu siten, että käyttäjät voivat kommunikoida niiden kanssa luonnollista kieltä käyttäen ja tulostaa laajojen tietohakujen tuloksia suhteellisen helposti ymmärrettävässä visuaalisessa muodossa. Tällaisilla ominaisuuksilla pyritään myös tukemaan käyttäjän ongelmanratkaisutyötä.
IBM Watson on suuri tuoteperhe ja brändi, johon ei tekoälysovelluksia tarkastellessa juurikaan voi välttyä törmäämästä. Vaikka tämä brändi nykyisin kytkeytyy useisiin eri sovellusaloihin, ovat Watsoniin kohdistuneet odotukset nimenomaan lääketieteen alalla olleet jo pitkään korkealla. Tekoälysovelluksena Watson on kielellistä dataa käsittelevä todistemoottori, jonka toiminta lähtee liikkeelle kysymyksestä, listasta oireita tai taloudellisia tavoitteita. Watson käy läpi mittavan määrän tietoaineistoa ja tuottaa lopulta etsintäprosessin tuloksena vastauksen, diagnoosin tai ohjeita. Tulos perustuu Watsonin rakentamalle argumentille, jonka se perustaa löytämilleen kilpaileville vastausvaihtoehdoille.
Prosessin alussa sovellus määrittelee päättelytoimillensa tavoitteen, minkä se tekee kartoittamalla sille syötettyä kielellistä dataa tiettyä sääntöjoukkoa soveltaen. Tässä prosessissa Watson koettaa perustasolla tunnistaa, millaisesta informaatiotarpeesta on kyse. Watsonin itselleen konstruoima tavoite on eräänlainen vastausmalli, jota Watson myöhemmin etsii lukemistaan teksteistä. Käytännössä Watsonin käyttämät erilaiset säännöt tuottavat oman vastauksensa toteutettavan tehtävän tavoitteesta ja seuraavaksi kukin näistä säännöistä suunnataan saatavilla olevan tekstikorpuksen tarkasteluun, minkä ääreltä ne sitten palaavat tuoden mukanaan kukin omat vastauksensa. Saadut vastaukset Watson pisteyttää sen mukaan, kuinka moni sääntö tuotti saman vastauksen. Saman vastauksen antaneet säännöt vahvistavat siis toinen toistensa asemaa, kun taas eri vastauksen antavat säännöt päätyvät keskinäiseen kilpailuasemaan. Tuloksena tarjottu vastaus, diagnoosi tai ohjeet ovat niitä, jotka saivat pistekilpailussa parhaimmat kokonaispisteet.
Watsonin käyttämät säännöt liittyvät esimerkiksi lauseoppiin eli syntaksiin ja merkitykseen eli semantiikkaan. Lisäksi se soveltaa tarvittaessa joitakin kontekstisidonnaisia erityissääntöjä. Esimerkiksi diagnosointitehtävän yhteydessä Watson osaa odottaa, että kysymys sisältää listan oireista. Watsonissa on myös oppimiskomponentti, jonka avulla se pistää merkille eri sääntöjen saaman painoarvon eri kysymysten ja niihin sopivien, tunnettujen vastausten suhteen. Siten Watsonin kuvaillaan ottavan opikseen omasta päättelyprosessistaan siten että se hyödyntää yhä enemmän parhaimmiksi osoittautuneita menettelytapoja. (Hammond 2015, s.26-27)
Syövän hoito
Onkologian alaan liittyvissä tekoälytutkimuksissa on erityisesti painotettu syväoppimiseen ja kuvantunnistukseen perustuvien sovellusten kehittämistä. Usein nämä sovellukset voivat auttaa paitsi sairauden diagnosoinnissa, myös hoidon suunnittelussa.
Onkologian alaan liittyen on Japanissa kehitetty tekoälysovellus, jonka tarkoituksena on pystyä tunnistamaan syövän etäpesäkkeiden tila kuvien perusteella. Sovelluksen kehittäjät ovat Tokion yliopisto ja Tokyo Medical and Dental University. Perinteisesti syöpäpesäkkeitä on tutkittu patologisista näytteistä mikroskooppia käyttäen. Erityisesti pienet poikkeamat jäävät tällaisissa tutkimuksissa usein huomaamatta. Tutkimusryhmä hyödynsi tekoälyn syväoppimista ja opetti sitä käyttämällä 300 000 kuvaa rintasyöpäpotilaiden imusolmukekudoksista. Kehitetty tekoäly onnistui luomaan analyysin, jonka perusteella tutkimusryhmä loi syöpäsolujen "olemassaolon todennäköisyyden kartan". Tämän avulla on mahdollista arvioida paremmin etäpesäkkeiden tilaa ja suunnitella potilaan syöpähoitoa. (AI Biblio 2017)
Tsukuban yliopisto sekä japanilainen yritys Kyocera ovat kehittäneet sovelluksen, jolla pyritään parantamaan ihon solunmuutosten arviointia ja mahdollisen syöpätyypin tunnistamista. Tässä tapauksessa tekoälyä opetettiin syväoppimisen keinoin 4000 syöpäkuvan avulla. Näin kehitettiin järjestelmä, joka pystyy päättelemään ihon muutoksesta otetun valokuvan perusteella, onko potilaalla ihosyöpää vai ei. Lisäksi järjestelmä esittää ehdotuksen siitä, minkä tyyppinen ihosyöpä kuvassa mahdollisesti esiintyy. Yhdysvaltalaisen Stanfordin yliopiston tutkijat ovat kehittäneet algoritmin ihosyövän diagnosoinnin tueksi. Syöpädiagnosointiin erikoistunut algoritmi opetettiin 130 000 ihosairauskuvaa käyttäen, jolloin se oppi diagnosoimaan visuaalisesti potentiaalisia syöpätapauksia. Ihosyöpien tunnistamiseksi tietokantaan ladattiin iholeesiokuvat, jotka ennustivat 2000 eri sairautta. Tekoäly oppi tunnistamaan pahanlaatuiset melanoomat ja karsinoomat. Opetetun algoritmin syöpientunnistuskyky kehittyi lopulta vastaamaan ihotautilääkärien suorituksen tasoa. (Sina 2017.)
Myös Watson -kokonaisuuden alle kuuluu erityinen sovellus, Watson for Oncology, joka on tarkoitettu syöpäsairauksien diagnosointityön tueksi. Syöpätapauksiin liittyvien näytekuvien tutkiminen perinteisellä tavalla on hidasta ja vaikeaa, mutta Watson for Oncology tarkastelee pilvipohjaisen supertietokoneen avulla valtavia määriä dataa, johon kuuluu lääkäreiden muistiinpanoja ja tutkimusaineistoja, ja pystyy tarjoamaan lääkärin diagnosointityön ja potilaan hoitoon ja lääkitykseen liittyvän päätöksenteon tueksi arvionsa jopa muutamassa minuutissa. (KTI 2016) Tokion yliopistollisessa sairaalassa sovelluksen avulla havaittiin, että potilaalla oli samanaikaisesti kaksi eri leukemiatyypiä. (Bort 2016.)
9.5.2 Kehon osien kuvantaminen ja simuloiminen
Toimiiko sydän tai jokin muu elin kuten sen pitäisi ja jos toiminnassa on jokin poikkeama, miten se ilmenee? Esimerkiksi Arterys on radiologien työn tehostamiseksi kehitetty web-pohjainen lääketieteellisen kuvantamisen analytiikka-alusta. Järjestelmä käyttää pilvipalvelua, mutta pyrkii parantamaan potilaiden tietosuojaa poistamalla potilastiedot kuvien yhteydestä siten, että toisiinsa liittyvät tiedot ja kuvat voidaan uudelleen yhdistää vain oikeiden tunnistetietojen avulla. Arteryksessa on erilliset työkalut sydänlihaksen, keuhkojen ja maksan toimintaa käsittelevän visuaalisen datan analysointiin. Analytiikkasovellus nopeuttaa esimerkiksi sydämen pumppausvolyymin laskennan perinteisen menetelmän 30-60 minuutista muutamaan sekuntiin.
Lontoon Imperial Collegessa on kehitetty sovellus, jolla voidaan mallintaa potilaan sydänlihaksen toimintatapaa 3D-kuvana. Sovelluksen tekoäly kykenee oppimaan, mitkä ominaisuudet sydämen toiminnassa ennustavat todennäköisimmin sydämen vajaatoimintaa ja lisäävät kuolemanriskiä. Mallia muodostaessaan järjestelmä käyttää MRI-kuvausta yhdessä veri- ja muiden koetulosten tarjoaman informaation kanssa. Mallin kehityksessä käytettiin 250 potilaan MRI-kuvista koostuvaa dataa. Tältä pohjalta ohjelmisto loi virtuaalisen 3D-sydämen, jonka avulla se oppi, mitkä seikat ennustivat sydänsairauksia ja kohonnutta kuolleisuusriskiä. (Borgan 2017.)
9.5.3 Hengitysnäytteestä usean eri sairauden diagnosoiva menetelmä
Uudenlainen tekoälyä hyödyntävä nanoteknologiaan perustuva puhalluslaite ja tekoälyalgoritmi auttavat diagnosoimaan potilaan puhalluksesta erilaisia sairauksia jopa 86%:n tarkkuudella. Laitteen kehitystyöhön liittyvässä tutkimuksessa puhallusnäytteitä kerättiin 1404 koehenkilöltä, joiden joukosta voitiin löytää 17 erilaista sairautta puhalluslaitetta käyttäen. Ihmisen henkäys sisältää happea, hiilidioksidia ja typpeä sekä sen lisäksi 100 muuta haihtuvaa kemiallista komponenttia, joista muodostuu Volatile Chemical Components, eli VOC. VOC-komponenttien haihtuminen riippuu henkilön suhteellisesta terveydentilasta. Nanoteknisen laitteen kehitystyön ohessa havaittiin, että jokaisella sairaudella on oma uniikki "hengitysjälki", minkä vuoksi yhden sairauden "hengitysjäljen" esiintymisen ei pitäisi aiheetta nostaa esiin muihin sairauksiin viittaavaa tulosta, eikä yhden sairauden diagnosoimisen pitäisi myöskään estää toisten sairauden (jonka hengitysjälki tunnetaan) diagnosointia. (Nakhleh ym. 2016)
Puhalluslaite kerää hengitysnäytteestä VOC-komponenttinäytteitä ja pyrkii siis määrittämään tältä pohjalta mahdollisen sairauden. Tekoälyalgoritmeihin perustuvan sovelluksen avulla tunnistettavat sairaudet voidaan luokitella ja diagnosoida näytteestä. Tutkimusryhmän suorittamassa kokeellisessa tutkimuksessa oli mukana viisi maata, jotka olivat Israel, Ranska, USA, Latvia ja Kiina. Tämä teknologia esitteleekin käytännönläheisen tavan seuloa ja diagnosoida erilaisia sairauksia helposti, halvalla ja myös kannettavalla tavalla. (Nakhleh ym. 2016) Tutkimuksen diagnosoidut sairaudet olivat:
- Chronin tauti (Crohn's Disease)
- Epätyypilinen Parkinsonismi (Atypical Parkinsonism)
- Eturauhassyöpä (Prostrate Cancer)
- Haavainen koliitti (Ulcerative Colitis)
- Idiopaattinen Parkinsonin tauti (Idiopathic Parkinson?s Disease)
- Keuhkosyöpä (Lung Cancer)
- Keuhkoverenpainetauti (Pulmonary Arterial Hypertension)
- Krooninen munuaissairaus (Chronic Kidney Disease)
- Mahasyöpä (Gastric Cancer)
- Multippeli Skleroosi (Multiple Sclerosis)
- Munasarjasyöpä (Ovarian Cancer)
- Munuaissyöpä (Kidney Cancer)
- Paksusuolen syöpä (Colorectal Cancer)
- Pää- ja niskasyöpä (Head and Neck Cancer)
- Raskausmyrkytys (Pre-eclampsia)
- Virtsarakon syöpä (Bladder Cancer)
- Ärtyvän suolen oireyhtymä (Irritable Bowel Syndrome)
9.5.4 Kliininen päätöksenteko ja riskien arviointi
Lääketieteelliset hoitoprosessit toteutetaan usein tiimityönä, johon osallistuu useita eri erityisalojen ammattilaisia. Aina tiimin jäsenet eivät tule kommunikoineeksi tarpeeksi keskenään, jolloin jokin tärkeä seikka voi jäädä huomiotta, mistä voi seurata erilaisia riskitilanteita. Toisaalta jo yksittäisestä potilaasta saattaa kertyä niin valtava määrä monentyyppistä aineistoa, ettei hoitohenkilökunnalla mitenkään riitä aika potilaan kokonaistilanteen hahmottamiseen tämän aineiston perusteella. Tällaisten monimuotoisten aineistojen tarkastelemiseksi ja riskien ennakoimiseksi on kehitetty useita tekoälyä hyödyntäviä alustoja. Seuraavassa niistä kaksi esimerkkiä.
CloudMedX Clinical Analyzer -ohjelmiston tarkoitus on havaita riskitilanteiden mahdollisuus hyvissä ajoin. Tämän lääketieteen tarpeisiin kehitetyn alustan avulla pyritään tarkastelemaan sekä rakenteistettua että ei-rakenteistettua dataa, joka voi sisältää sekä kliinistä että ei-kliinistä sisältöä. Tavoitteena on arvioida potilaan tapaukseen liittyvää dataa yhdessä statistiseen tietoon perustuvien aineistojen kanssa. Nämä aineistot voivat liittyä esimerkiksi olosuhteisiin, lääkkeisiin, suoritettuihin testeihin ja muihin muuttujiin. Sovelluksen tekoälyratkaisu perustuu koneoppimiseen, luonnollisen kielen prosessointiin ja kliinisen kontekstuaalisen käsitteistön soveltamiseen. CloudMedX:n kotisivuilla nimettyjen esimerkkitapausten perusteella ohjelmistoa on tähän mennessä sovellettu esimerkiksi tekolonkka- ja tekopolvileikkausten, sydämen vajaatoiminnan, kroonisen munuaisen vajaatoiminnan ja diabeteksen hoitoprosesseissa.
Käytännössä sovellus kokoaa tiimin toimijoiden syötteet (potilaskertomukset, toimenpiteistä saatavat tiedot yms.), hyödyntää erilaisia demografisia aineistoja ja suorittaa syöteaineistolle riskianalyysin. Tuloksena sovellus pyrkii tarjoamaan holistisen katsauksen käsilläolevan hoitoprosessin mahdollisiin lopputuloksiin.
Yhteistyössä Fujitsun Euroopan laboratorion, Fujitsun Espanjan yksikön, HCSC:n Madridin innovaatioyksikön kanssa kehittämä HIKARI-rajapinta hyödyntää tekoälyä helpottaakseen kliinistä päätöksentekoa ja riskien arviointia. Tässä tehtävässä lääkärien haasteena on löytää relevantti informaatio potilaista päivittäin kerättävän valtavan datamäärän seasta. Tutkimustietojärjestelmä HIKARI tuo yhteen joukon tiedonhakua helpottavia mikropalveluita, joiden avulla lääkärit voivat erotella ja analysoida tietoja useita datalähteitä käyttäen. Hyödynnetty data voi olla peräisin sekä kliinisistä että ei-kliinisistä lähteistä (Aguilar 2017). Järjestelmän avulla terveydenhuollon henkilöstö voi lopulta tehokkaammin hyödyntää dataa, joka HIKARIN avulla tarjoutuu käytettäväksi integroituna, ryhmiteltynä ja anonymisoituna. Vastaava aineisto on kyllä aikaisemminkin ollut terveydenhoitohenkilöstön saatavilla paperisessa muodossa, mutta Fujitsun alustavien kokeilujen mukaan HIKARI voi jopa puolittaa potilasrekistereihin käytetyn ajan. Niinpä lääkäreillä jää enemmän aikaa potilastyöskentelyyn (Fujitsu 2016).
HIKARI järjestelmä kokoaa potilasta koskevaa dataa kansallisesta terveydenhuollon järjestelmästä, digitaalisista potilastietueista tai muista terveydenhuollon palveluita tarjoavista keskuksista. Data anonymisoidaan ja siirretään prosessointimoottorille, johon kerätään myös avointa terveydenhuollon dataa (esimerkiksi tutkimustuloksia). Dataa prosessoidaan data-analytiikan keinoin ja prosessoitu data lähetetään rajapinnan kautta Fujitsun pilvipalveluun, jonka kautta lääkärit voivat tarkastella sitä erilaisten visualisointien ja raporttien muodossa.
Sopivan hoidon tai toimenpiteiden määrittämiseksi lääketieteen ammattilaisen tulee ensin pystyä hahmottamaan kaikki potilaan tapaukseen mahdollisesti vaikuttavat riskitekijät. HIKARI:in ennakointiominaisuuksien avulla potilaat voidaan kategorisoida diagnoosityypin tai yleisimpien psykiatristen riskien perusteella. Fujitsun testien perusteella järjestelmä kykenee tällä hetkellä tunnistamaa päihteidenkäyttöön tai itsemurhakäyttäytymiseen liittyvät riskit 85% tarkkuudella.
HIKARI:n tarjoaman tiedon ja ennakoivien mallien avulla potilaita voidaan kannustaa ottamaan omasta terveydestään ja elämästään huolehtimisessa aikaisempaa aktiivisempi rooli. Näin ollen odotetaan, että tekoäly auttaa kehittäämään ennustavaa, osallistavaa ja yksittäiselle henkilölle räätälöidympää terveydenhuoltoa. Tässä mallissa potilas ottaa itse vastuun terveytensä hoitamisesta, kun taas lääkäri toimii konsultin roolissa. (Aguilar, 2017). Lisäksi terveydenhuolto-organisaation odotetaan myös saavuttavan hallinnollisia hyötyjä HIKARI:n avulla, sillä sen käytön myötä saatetaan myös tehdä havaintoja siitä, miten eri resurssit ja käytänteet vaikuttavat potilaiden hoitoon. (Fujitsu 2016.)
9.5.5 AI-robotit ja kirurgia
Robotit ja muut tekoälyä hyödyntävät laitteet voivat auttaa sekä leikkauksiin valmistautumisessa että leikkauksien aikana. Leikkauksiin valmistautumisessa robotit auttavat sekä salin valmisteluun (mukaan lukien logistiikkarobottien palvelut), leikkauksen suunnitteluun (mukaan lukien kuvantamisjärjestelmät) että toimenpiteen simulaatio-pohjaiseen harjoittelun. Leikkauksen aikana robotit avustavat esimerkiksi tarjoamalla lääkärille hänen pyytämiään tietoja ilman että kirurgin täytyy keskeyttää työskentelyään. Robotit voivat myös nopeuttaa toimenpiteiden kulkua tarjoamalla tarvittavat työkalut oikea-aikaisesti ja -suuntaisesti tarkasti oikeaan paikkaan. Näin oli esimerkiksi vuoden 2018 alussa uutisoidussa Töölön sairaalassa tehdyssä koekäytössä, jossa robotti avusti kirurgia erityistä tarkkuutta vaatineessa parkinsonpotilaan aivoleikkauksessa, jossa miespotilaan aivoihin asennettiin neljä katetria, joiden avulla hänelle annostellaan Parkinsonin tautiin kehitettyä lääkettä (Pajunen, Koivuranta 2018).
Erilaiset leikkausrobotit avustavat esimerkiksi urologisissa leikkauksissa, eturauhassyöpäleikkauksissa, munuaisleikkauksissa, sydän- ja thoraxkirurgiassa, gynekologisissa leikkauksissa, tietyissä vatsan alueen leikkauksissa sekä korva-, nenä- ja kurkkutautien leikkauksissa. Leikkausrobotit voivat tarjota kirurgin käyttöön tarkan kameran ja muita apuvälineitä. Robotit voivat mahdollistaa myös esimerkiksi merkkiainekuvantamisen, mitä voidaan hyödyntää esimerkiksi munuaisleikkauksissa.
Robottien avulla erityistä tarkkuutta vaativaa työtä voidaan tehdä entistäkin tarkemmin. Kun tähystysleikkaus toteutetaan robottiavusteisesti, leikkauskonsolia käyttävä kirurgi tarkastelee leikattavaa aluetta moninkertaisesti suurennetun, kolmiulotteisen kamerakuvan kautta. Robottikäsien avulla hän pystyy operoimaan kohdealueella millin tarkkaa työtä tehden. Kirurgin käden on tunnetusti oltava vakaa, mutta robotit voivat entisestään parantaa näitä lääkärin ominaisuuksia esim. poistamalla sen vähäisenkin vapinan, joka ihmiskäden työskentelyssä väistämättä on. Näin päästään lopputulokseen, johon ihminen ei ilman robottia pystyisi. (Mueller, Massaron 2018)
Robottien parantamalla työskentelytarkkuudella on havaittu olevan suotuisia vaikutuksia potilaiden toipumiseen ja toimenpiteistä koituvien komplikaatioiden vähenemiseen. Kun leikkauksenaikaista verenvuotoa esiintyy vähemmän, potilaan toipuminen ja esimerkiksi inkontinenssin ja potenssiongelmien kaltaiset jälkivaivat vähenevät. Leikkausrobotit myös nopeuttavat toimenpiteiden kulkua kauttaaltaan aina alkuvalmisteluista lähtien, minkä lasketaan myös tuottavan säästöjä.
Da Vinci Surgery -järjestelmä on esimerkki leikkausrobottijärjestelmästä, jota käyttäviä lääkäreitä löytyy myös Suomesta. Järjestelmää on tähän mennessä käytetty tietyntyyppisissä sydänleikkauksissa, paksusuoli-peräsuolileikkauksissa, yleiskirurgiassa, gynekologisissa leikkauksissa, pään ja kaulan alueen leikkauksissa, rintakehän alueen leikkauksissa ja urologisissa leikkauksissa. Systeemi mahdollistaa kirurgin työskentelyn muutaman pienen viillon kautta. Järjestelmään kuuluu ergonominen konsolipiste, jossa kirurgi istuu leikkauksen aikana, potilastuoli, suurentava 3D-näkymä ja ranneinstrumentit, jotka taipuvat ja pyörivät huomattavasti enemmän kuin ihmiskäsi. Yksi järjestelmään kuuluvista, kehon sisään menevistä pienistä instrumenteistä on labaroskooppi, joka lähettää operaatiosta videokuvaa leikkaussalin monitoriin.
9.5.6 Seuranta ja kuntoutus
Tekoälyllä ratkaistaan tällä hetkellä sekä yleisiä hoitoalaan liittyviä haasteita että spesifimpiä alakohtaisia ongelmia. Yleiset hoitoalaan liittyvät ongelmat nousevat esimerkiksi jatkuvasti kasvavaan hoitajapulaan ja toisaalta esimerkiksi vanhuspotilaiden määrän kasvuun. Seurantaan, kuntoutukseen ja muuhun hoitoon liittyvien erityisalojen kirjo on luonnollisesti suuri. Tässä esimerkkejä on poimittu kuulo-ongelmiin liittyvistä ratkaisuista.
Esimerkki erityisalalta: kuulon apuvälineet
Huhtikuussa 2018 uutisoitiin (Kiger 2018) Googlen tekoälytutkijoista, jotka ovat kehittäneet teknologiaa yksittäisen henkilön äänen erottamiseksi taustahälystä, joka voi sisältää myös toisten henkilöiden puhetta. Tätä sovellusta saatetaan jatkossa pystyä hyödyntämään, paitsi tarkempien automaattisten tv- ja videotekstitysten tekemisessä, myös kuulon apuvälineiden puheenerottelun haasteisiin liittyvässä kehitystyössä. Väentungoksessa, esimerkiksi juhlissa, toisen henkilön puheen seuraaminen edellyttää äänten erottelutyötä, jonka tervekuuloinen tekee keskittymällä kuuntelemaansa puheeseen ja sulkemalla mentaalisesti epäoleellisen hälyn huomionsa ulkopuolelle. Huonokuuloiselle, ja myös kuulokojeita käyttävälle henkilölle, tämä on yleensä vaikea ja voimia vaativa tehtävä. Edes digitaaliset kuulokojeet eivät välttämättä osaa vaimentaa hälyääniä tarkoituksenmukaisesti taustalle ja saattavat myös päätyä vahvistamaan kuuntelua vaikeuttavia hälyääniä. Googlen sovelluksen tapauksessa tekoälyä opetettiin tarkkailemaan visuaalisesti puhujan kasvoja, kuten esimerkiksi suun liikkeitä. Sovellus havaitsi, milloin valittu henkilö puhui, ja pystyi yhdistämään havaintonsa sanoihin, jolloin ohjelma pystyi eristämään yksittäistä puhujaa koskevan puhtaan audiosignaalin.
Olemassaolevissa kuulokojeissa on jo vuosia hyödynnetty tekoälyä, jolla pyritään ratkaisemaan nimenomaan meluisten tilanteiden ongelmaa. Jo ennen kuin digitaalisten kuulokojeiden yhteydessä alettiin puhua tekoälyratkaisuista, useita erilaisia teknisiä ratkaisuja kehitettiin ja otettiin käyttöön kuuntelun helpottamiseksi erilaisissa ääniympäristöissä. Esimerkiksi Oticonin Syncro -kojeissa sovellus arvioi ääniympäristöä ja sitten valitsee näistä olemassa olevista helpotuskeinoista ongelmanratkaisualgoritmeja soveltaen tilanteeseen nähden parhaimman yhdistelmän. Ääniympäristöä tarkkaillessaan Oticon Syncro tarkkailee kuuluuko puhetta, kuuluuko melua, esiintyykö tilanteessa ilmavirran aiheuttamaa ääntä, mistä suunnasta mahdollinen puhe tulee ja mikä on yleinen äänten taso. Arvion perusteella sovellus ottaa käyttöön vahvistusstrategian, joka on optimaalinen puheen vastaanottamiseksi tunnistetuissa olosuhteissa. Valinta sisältää tarkoituksenmukaisen mikrofonien suuntauksen, melunhallintaratkaisun ja pakkausjärjestelmien yhdistelmän, joka tarjoaa mahdollisimman selkeän puhesignaalin käsillä olevalle akustiselle ympäristölle. Ääniympäristön muuttuessa sovellus arvioi tilanteen uudestaan. (Donald 2004.)
9.5.7 Robotit vanhustenhoidossa
Hoitoalalla roboteista ja tekoälyratkaisuista haetaan apua keventämään hoitajien työtaakkaa sekä tarjoamaan esimerkiksi vanhuksille virikkeitä ja fyysistä ja kognitiivistä kuntoutusta leikkisässä ja paineettomassa ilmapiirissä. Tekoälyä, robotiikkaa ja koneoppimista yhdistäviä järjestelmiä pyritään kehittämään siten, että robotit voisivat huomata potilaan tarpeet (esim. tarve päästä vessaan) tai sen jos potilaan olemuksessa on jotain poikkeuksellista ja hälyttävää. Tämän kaltaisia robotteja on kehitetty erityisesti Japanissa.
Japanilaisissa vanhainkodeissa erilaisia robotteja käytetään jo verrattain paljon ja vanhukset vaikuttavat myös pitävän roboteista (Foster 2018). Esimerkkejä käytössä olevista roboteista ovat pörröinen, hoivaa pyytävä Paro-hylje, sekä Pepper ja Parlo. SoftBankin kehittämää Pepperiä on käytetty vanhuspotilaiden hoidon ja valvomisen tukena, joskin tätä robottia voidaan käyttää myös muilla asiakaspalvelun aloilla (Pepper mm. osaa 20 eri kieltä). Yksi vanhustenhoidon haaste on, että hoitajien tulisi havaita muutokset potilaan tilassa riittävän pian, joskus vain vähäisesti ulospäin näkyvistä hälytysmerkeistä. Pepper-robotti muistaa ihmiset, joiden kanssa se on kommunikoinut. Robotti seuraa ihmisäänen sävyjä, pyrkii tulkitsemaan tunteita ja mukautumaan tilanteeseen. Pepperin on kerrottu tuovan lisäarvoa potilaiden arkeen ja helpottavan hoitajien työtä valvomalla potilaita ja raportoimalla hoitajille, mikäli se havaitsee esimerkiksi jonkun potilaan vaikuttavan alakuloiselta. (Guardian 2017)
Myös Fujisoftin kehittämän Parlon tehtävänä on auttaa vanhustenhoitajia työssään ja osaltaan myös tuoda helpotusta yhä kasvavaan hoitajapulaan. Japanissa hoitajapulasta ja kulttuurisista tavoista seuraa, että vanhainkodissa asuvat japanilaiset eivät haluaisi lainkaan häiritä kiireisiä hoitajia. Tämän vuoksi hoitajien ja vanhusten välinen kommunikointi voi jäädä lopulta hyvin vähäiseksi. Yhtenä ratkaisuna tähän tilanteeseen on kokoeiltu Parlo-robottia, joka osallistuu keskusteluihin ja väittelyihin, tunnistaa tunnetiloja ja voi tanssia ja kuntoilla, ja saada myös vanhukset liikkumaan kanssaan. Myös Parlo pystyy muistamaan yli 100 henkilön nimen ja kasvot, mikä on avuksi potilaiden seurantaa ajatellen. Tämä robotti oppii yksittäisen ihmisen käytöskaavoja ja voi myös muistuttaa potilaita usein unohtuvista asioista. Parlon on koettu madaltavan potilaiden kynnystä kommunikoida ja keskustella, ja tämä taas helpottaa myös asiakkaiden terveydentilan seuraamista. (Terashima 2016.)
9.5.8 AI-robotit mielenterveyspalveluiden tukena
Newyorkilainen yritys Koko on luonut KokoBot-keskustelurobotin, jossa tekoälyn mahdollisuudet yhdistetään joukkoistamiseen ja kognitiiviseen terapiaan. Tämä vertaisverkkoteknologia tarjoaa apua stressiin, levottomuuteen ja depressioon liittyvien tilanteiden käsittelyyn. Käyttäjät kertovat KokoBotille ongelmistaan ja robotti ohjaa viestin sopivalle KokoBot-jäsenelle, eli todelliselle ihmiselle, joka on lupautunut olemaan tarvittaessa avuksi. KokoBotin kerrotaan myös avaavan käyttäjälleen kognitiivisen terapian lähestymistapaa (Mack 2016). KokoBotin käyttäjä saa kysymyksiinsä keskimäärin neljä vastausta, joista ensimmäinen saapuu jo viidessä minuutissa. Selvitysten mukaan 99% kysymyksistä saadaan vastaus ja 90% vastauksista on koettu hyödyllisiksi.
Woebot-keskustelurobotti on kehitetty depressiosta ja levottomuudesta kärsivien henkilöiden tueksi. Järjestelmä on täysin robotiikkaan perustuva, eikä sillä pyritä useiden muiden terveydenhuoltoalan tekoälysovellusten tavoin suorittamaan diagnooseja tai laajentamaan reaalimaailman terapeutin tai ei-kliinisten henkilöiden kykyjä. Sitä vastoin järjestelmä tarjoa käyttäjälleen mahdollisuuden keskustella itselle raskaista aiheista ilman tuomitsemisen pelkoa. Näin ollen sen käyttö voi auttaa sellaisiakin ihmisiä, jotka eivät muulla tavoin hakisi hoitoa mielenterveyteen liittyvään oireiluunsa. (Mack 2017.)
Woebot-robottia käytetään Facebook Messengerin kautta. Robotti herätetään toimintaan lähettämällä sille viesti. Jatkossa Woebot kartoittaa henkilön mielentilaa ja ajatuksia ja hyödyntää kognitiivisen käyttäytymisterapian tekniikoita muotoillakseen uudelleen depressioon ja levottomuuteen liittyviä ajatusmalleja ja negatiivisia tunteita. Käyttäjä voi kuitenkin myös itse ohjailla keskustelun kulkua.
Woebotilla pyritään ennen kaikkea tarjoamaan vaihtoehtoinen kokemus niille, jotka jättävät hakematta mielenterveyteen liittyviin ongelmiin apua muun muassa häpeän pelkoon liittyvien syiden vuoksi. Reaalimaailman terapiapalveluihin nähden yksi ratkaisun merkittävä etu on, että robotti voi väsymättä tarjota keskusteluseuraa 24 tuntia seitsemänä päivänä viikossa ja lisäksi se muistaa, mistä sen kanssa on aikaisemmin puhuttu. Anonyymin ja henkilökohtaisen kokemuksen tarjoamiseksi Woebotin kerrotaan kehitetyn siten, etteivät Woebotin kehittäjät näe keskusteluja tai saa tietoa, ketkä robotin kanssa keskustelevat. Woebot-järjestelmä on maksullinen ja toimii Facebook Messengerin kautta.
Massachusetts Institute of Technologyn (MIT) tietojenkäsittelytieteen ja tekoälyn laboratorion (Computer Science and Artificial Intelligence Laboratory, CSAIL) sekä lääketieteen tekniikan ja tieteen instituutin (Institute of Medical Engineering and Science, IMES) tutkijat ovat työstäneet eräänlaista "sosiaalista valmentajaa", päälle puettavaa teknologiaa, joka kykenee tunnistamaan, mikäli käyttäjän käymän keskustelun taso on onnellinen, surullinen tai neutraali. Sovellusta voidaan siis hyödyntää henkilön mielialojen analysoinnissa. Tällaisen apuvälineen käytöstä voi olla hyötyä henkilöille, jotka kärsivät esimerkiksi Aspergerin oireyhtymästä tai ahdistuneisuushäiriöstä. Järjestelmän muodostama arvio perustuu henkilön puheen (äänensävy, korkeus ja energia ja sanasto) ja fyysisten tekijöiden (liike, sydämen syke, verenpaine, veren virtaus ja ihon lämpötila) seurantaan ja analyysiin. (Smith 2017.) Emotionaalista sävyä voidaan luokitella jopa reaaliajassa, tai järjestelmää voidaan käyttää myös menneiden kokemusten tarkasteluun, jolloin paikannetaan jälkikäteen tilanteita, joissa henkilö on kokenut ahdistusta (Conner-Smith 2017).
9.5.9 Ennakoiva hyvinvoinnin seuranta
Useat olemassaolevat sovellukset pyrkivät tukemaan käyttäjäänsä aktiivisessa omasta elämästä ja terveydentilasta huolehtimisessa, masentuneisuuden merkkien varhaisessa havaitsemisessa ja päivittäisen stressitason seuraamisessa.
Columbian ja Cambridgen yliopistojen yhteistyönä kehittämän Wysa-keskustelurobotin tai digitaalisen elämänhallintavalmentajan avulla käyttäjät voivat ylläpitää päivittäistä hyvinvointiaan ja palautua esimerkiksi henkisesti uuvuttavan päivän jäljiltä. Robotin kanssa käydäänkin yli 4 miljoonaa keskustelua vuodessa ja sillä on yli 90 000 käyttäjää maailmanlaajuisesti yli 30 maassa. Wysa ohjaa käyttäjää mindfulness-meditaation ja erilaisten aktiviteettien, kuten hengitysharjoitteiden ja niskan venyttelyn, läpi. Toteuttaessaan harjoitteita käyttäjä välittää robotille kuvan olotilastaan. Jos järjestelmän kanssa vuorovaikutuksessa oleva henkilö yhdistää järjestelmän myös muihin älylaitteissa oleviin terveyssovelluksiin, Wysa kykenee seuraamaan henkilön fyysistä aktiviteettia ja tunteiden vaihteluita myös näiden tarjoamia tietoja hyödyntäen. Viikon loputtua robotti tuottaa henkilön tunteista ja tavoista yhteenvedon ja tunnistaa, mikäli henkilö vaikuttaa alakuloiselta. Tällöin järjestelmä tekee käyttäjälle depressiotestin (PHQ9). Mikäli teksti indikoi henkilön olevan masentunut, robotti suosittelee lääkärikäyntiä. Wysan toimintamalleissa on hyödynnetty esimerkiksi kognitiivista käyttäytymisterapiaa, jonka avulla robotti pyrkii auttamaan käyttäjää muokkaamaan negatiivisia ajatuksiaan positiivisempaan suuntaan. (McIntyre 2016.)
Erityisesti oman stressaantuneisuuden arvioiminen ilman ulkoista apua voi olla hankalaa, minkä vuoksi omaa stressitasoa onkin suhteellisen helppo päätyä vähättelemään. Esimerkiksi NTT Docomo ja Keion Yliopisto ovat kehittäneet stressitason omaseurannan työkalua, älypuhelimessa toimivaa sovellusta, joka pystyy arvioimaan stressitasoa n.70% tarkkuudella. Sovellus hyödyntää tietoa käyttäjän sydämen lyöntien intervallimuutoksista sekä hänen älypuhelimestaan kerättyä dataa (sisältäen noin 130 käyttäytymiseen liittyvää muuttujaa). Testien perusteella sovelluksen käyttö paransi henkilön tietoisuutta omasta stressitasosta, mikä puolestaan auttaa stressin ehkäisyssä ja hallinnassa. (AI Biblio 2018.)
9.5.10 Lääkekehitys
Lääkekehityksessä tekoälyjärjestelmät toimivat paitsi olemassaolevien käytänteiden tehostajina myös uusien käytänteiden mahdollistajina. Esimerkiksi lääkeaineyhdistelmien seulontatehtäviin kehitetyllä "robottitutkija" Evellä pyritään muun muassa madaltamaan lääketutkimuksesta koituvia kuluja. Tämä laboratorioautomaatiojärjestelmä käyttää tekoälyä oppiakseen aiemmista onnistuneista lääkelöydöksistä. Mahdollisten erilaisten yhdistelmien määrä on valtava, joten Eve valitsee tarkasteltavaksi sellaisia yhdisteitä, joilla on korkea todennäköisyys aktivoitua selvityksen kohteena olevaan sairauteen. Even hyödyntämä älykäs menetelmää auttaa sitä seulomaan vaihtoehdoista soluille myrkylliset yhdisteet ja valitsemaan jatkotarkasteluun ne, jotka estävät parasiittiproteiinien toiminnan. Menetelmä vähentää merkittävästi lääkkeiden seulontaan kuluvaa aikaa, työn kustannuksia ja epävarmuutta. (Williams ym. 2015.)
Myös Atomwise pyrii tehostamaan uusien lääkeaineiden etsimisprosessia. Sovellus käyttää valtavaa molekyylirakennetietokantaa, jonka avulla se pyrkii selvittämään, mitkä molekyylit vastaavat tiettyyn tarpeeseen. Vuonna 2015 sovelluksen avulla löydettiin lääkeainekandidaatti, jolla saatettaisiin pystyä estämään ebolan tarttuminen sairastajasta toisiin ihmisiin. Erityisen huomionarvoista oli se, että sovelluksen ehdottamalle yhdisteelle ei ollut aikaisemmin kuvattu viruksen vastaista vaikutusta, joten kokeilun perusteella sovellus todella pystyy tunnistamaan uusia ja yllättäviäkin mahdollisia lääkeyhdisteitä tai olemassaolevien lääkkeiden käyttökohteita. Toinen tärkeä seikka oli prosessin nopeus: Atomwise tuotti ehdotuksensa yhdessä päivässä, kun vastaava prosessi vie ihmistutkijoilta kuukausia ellei jopa vuosia (Atomwise 2015).
Erilaisia lääkkeitä täytyy kehittää paitsi erilaisiin sairauksiin, myös yhteen ja samaan sairauteen erilaisia potilaita varten. Lääke joka sopii yhdelle ihmiselle ei välttämättä sovellu toisen henkilön käyttöön. Turbine-sovelluksen avulla voidaan suorittaa simulaatioita, joilla on paikannettavissa tietyn henkilön kehossa todennäköisesti parhaiten toimivat lääkkeet. Sovellus perustuu solun toiminnan mallintamiselle, eikä siis olemassaolevalle lääkkeisiin ja hoitovasteeseen liittyvälle tiedolle. Tuloksena voidaan saada esimerkiksi ennuste herkkyys- tai resistanssibiomarkkereiden ilmenemisestä, ehdotuksia uusista lääkeainekokonaisuuksista, annoksesta riippuvan synergian ennuste kolmelle tai useammalle lääkkeelle sekä mallinnus lisäaineisiin liittyvästä myrkyllisyydestä. Toistaiseksi Turbinen kehityksessä pääpaino on ollut syöpähoidoissa.
Lääkintä ei aina tarkoita pillereiden syömistä tai ruiskeen antamista. Mikrobiomit tarkoittavat ihmisen ihoa ja ruumiinonteloiden limakalvoja asuttavia monimuotoisia mikrobistoja. Emme tulisi toimeen ilman näitä mikrobeja ja näihin liittyvien poikkeamien on havaittu liittyvän useisiin erilaisiin sairauksiin. Whole Biome on yritys, jonka käyttämän tutkimusalustan avulla pyritään kehittämään mikrobiomi-interventioita ja tarjoamaan näihin perustuvia julkisia terveystoimenpiteitä. Tämä systeemi käyttääkin useita eri keinoja parantaakseen mikrobien toimintaa elimistössä. Laboratorioanalyysit yhdistettynä laskennalliseen analyysiin muodostavat kuvan yksilön mikrobiologiasta. Sovellus käyttää koneoppimisalgoritmeja väestön biokemiallisten ja aineenvaihduntateiden laajempien trendien tunnistamiseksi. Näiden tietojen ja työkalujen avulla Whole Biome pyrkii tunnistamaan relevantteja mikrobiomarkkereita ja muotoilemaan uudenlaisia hoitotoimenpiteitä, esimerkiksi ns. lääketieteellisiä ruokia.
Lääkekehityksen uusiin näkökulmiin liittyy myös geneettisen lääketieteen ala, johon liittyvää tekoälysovellusta edustaa Deep Genomicsin tekoälyperustainen alusta. Deep Genomics keskittyy kehittämään prekliinisen tason geneettisiä lääkkeitä, rajautuen oligonukleotidi-lääkevalmisteisiin. Alustansa avulla etsitään lääkeainekandidaattia, joka vastaa asetettuja ominaisuuksia. Haettujen lääkkeiden teho perustuu taudin geneettisiin tekijöihin vaikuttamiseen DNA:n tai RNA:n tasolla. Oligonukleotidihoitojen suunnittelu tapahtuu kymmenien miljardien yhdistelmämahdollisuuksien muodostamassa tilassa, joten tekoälyalustaa tarvitaan tämän tilan tehokkaan tutkimisen mahdollistajaksi.
9.6 Lakipalvelut
Tekoäly liittyy ja vaikuttaa lakialaan monin tavoin. Yksityishenkilöinä olemme esimerkiksi yllättävän tottuneita tekemään sitovia sopimuksia tilanteissa, joissa toisena sopimusosapuolena on käytännössä tietokone. Näin on esimerkiksi verkkokauppa- ja verkkomaksutilanteissa. Tekoälysovelluksia kehitetään niin suuren yleisön kuin alan ammattilaistenkin käyttöön. Lisäksi tekoälykehityksen tarpeet kohdistuvat toisinaan myös lain itsensä ilmaisemiseen.
Lakipalveluihin liittyy perinteisesti runsaasti lomakkeiden täyttämiseen perustuvaa työtä, jota voitaisiin tehostaa lomakkeita muokkaavalla automaatiolla (jolloin lomakkeista voitaisiin esimerkiksi jättää kokonaan pois tarpeettomat, kulloiseenkin tapaukseen soveltumattomat kysymykset). Amerikkalainen teknologiayritys LegalZoom auttaa perheitä ja pieniä yrityksiä lakiasioissa, esimerkiksi testamentin laatimisessa tai tekijänoikeusasioissa. Yritys hyödyntää tietotekniikkaa, jonka avulla se pystyy tarjoamaan edullisia, asiakkaan tarpeiden mukaisesti muotoiltuja dokumentteja. Palvelut tarjotaan suoraan internetin välityksellä. Tällaisten mahdollisuuksien käyttöönotto ei kuitenkaan ole mutkatonta. Esimerkiksi edellä mainittu LegalZoom on saanut useita syytteitä laittomasta lain harjoittamisesta (unauthorized practice of law). (Kaplan 2016)
Kuten työelämän muutoksista puhuttaessa tuli esiin, tuntiperustaisesti työstään laskuttavien lakialan ammattilaiset eivät aina ensisijaisesti innostu siitä uutisesta, jonka mukaan uudet tekoälytyökalut tehostavat merkittävästi näiden asiantuntija-ammattilaisten ajankäyttöä. Juristien työhön liittyvien pitkien ja yksityiskohtaisten sopimusten lukemisen, tarkistamisen ja analysoinnin odotetaan hoituvat tekoälyn avulla huomattavasti aikaisempaa nopeammin, tarkemmin ja tehokkaammin. Tekoälypohjaiset työkalut pystyvät kuitenkin helpottamaan lakimiesten urakkaa merkittävästi erityisesti sellaisissa tapauksissa, jotka nykyaikaisen aineistomäärien edessä voisivat muutoin muuttua jopa täysin mahdottomiksi suorittaa. Luonnollisesti myös kaikki alat, joiden keskiössä ovat erilaiset laskelmat ja numeroiden analysointi, esimerkiksi tilintarkastus ja kirjanpito, hyötyvät ohjelmistorobottien tekemästä työstä. Esimerkiksi ROSS on lakialaan liittyviä tiedonhakuja varten kehitetty tekoälyperustainen tutkimusväline, joka on tarkoitettu lakialan ammattilaisten käytettäväksi.
Electronic discovery (myös e-discovery tai ediscovery) on alue, jolla tekoäly voi auttaa lakimiesten ja -avustajien työtä merkittävästi. Oikeudenkäynnin aikana tapauksen molemmilla osapuolilla on pääsy toistensa relevanttien dokumenttien tarkasteluun asiaankuuluvien todisteiden löytämiseksi. Tutkittavan aineiston laajuus voi kuitenkin olla valtava, joissain tapauksissa jopa miljoonia sivuja. Lisäksi elektroninen aineisto sisältää myös metadataa, mikä voi sisältää tarkastelun kannalta merkittävää tietoa. Tällaisissa tapauksissa koko aineiston huolellinen läpikäyminen käytössä olevan ajan ja työvoiman puitteissa voi olla täysin mahdotonta. Tähän haasteeseen on pyritty vastaamaan predictive coding-tekniikalla, jossa ohjelmisto pyritään opettamaan, jotta se kykenisi itsenäisesti poimimaan laajasta aineistosta lähemmän tarkastelun kannalta relevantit dokumentit. (Kaplan 2016)
Tekoälyä sovelletaan myös, jotta voitaisiin muodostaa ennusteita käsilläolevan lakijutun lopputuloksesta. Tällaista ohjelmiston tarjoamaa ennustetta asianajaja voi hyödyntää tapauksensa valmistelemisessa ja asiakkaansa neuvomisessa.
Lakiin itseensä keskittyvää tekoälyn sovellusaluetta kutsutaan nimellä computational law. Tällä hetkellä lakia ja uusia lakiehdotuksia ilmaistaan luonnollisen kielen avulla, mutta juuri tekoälykehitys on synnyttänyt tilanteita, joissa lakia pitäisi pystyä ilmaisemaan matemaattisen muodon kautta. Formaalimman kielen käyttö voisi myös vähentää monitulkintaisuusongelmia, auttaa tarkistamaan lain kattavuutta ja johdonmukaisuutta sekä avata mahdollisuuksia automaattisten systeemien käyttöönottamiseksi lakiasioiden tulkinnassa ja lain soveltamisessa. Tällä hetkellä tarjolla on esimerkiksi sovelluksia, joihin on pyritty muotoilemaan verotukseen liittyviä lakeja ja joilla käyttäjä voi tarkastella vaikkapa omaisuutensa arvoa. Itsenäisesti ajavia autoja kehitettäessä taas liikennesäännöt tulee pystyä esittämään laskennallisten mallien puitteissa. (Kaplan 2016)
9.7 Tekoäly kiinteistö- ja rakennusalalla
Rakennus- ja kiinteistöala on perinteisesti ollut hidas muuttumaan ja ottamaan uusinta teknologiaa käyttöönsä. Uusien teknologioiden omaksumista näillä aloilla on yritetty helpottaa esimerkiksi tekemällä palvelualustoja sekä tarjoamalla alan yrityksille dataa ja kertomalla sen käyttömahdollisuuksista.
Rakennusten monitorointi ja kunnonvalvonta on tullut yhä tärkeämmäksi korjausrakentamisen kustannusten noustessa. Kustannusten nousupaineet vaativat aiempaa tehokkaampien menetelmien kehittämistä ja soveltamista rakennusten kunnossapitoon. Rakenneterveystarkastelussa keskitytään rakennusten rakenteisiin ilmaantuneiden vikojen tunnistamiseen ja luokittelemiseen. Apuna voidaan käyttää tilanteeseen soveltuvia sensoreita. Erilaisia rakenteita, kuten siltoja, patoja ja tuuliturbiineita on tarpeellista suojella tekijöiltä, kuten rakenteiden heikkenemiseltä, liialliselta kuormitukselta ja lämpötilan muutoksilta. Sensoreista kerätyn datan analysointi ja tekoälypohjaiset ratkaisut, kuten neuroverkot, voivat parantaa muun muassa edellä mainittujen asioiden ennakoitavuutta, jolloin mahdollisiin ongelmiin voidaan puuttua ajoissa. Ennakonnin avulla voidaan säästää korjauskustannuksissa ja parantaa turvallisuutta.
Maailmalla rakennusten ja rakenteiden kunnossapidossa sensorit keräävät monimuotoista dataa tutkittavasta kohteesta. Data voi vaihdella perinteisistä olosuhdemittauksista, kuten lämpötilasta ja kosteudesta, portaiden värähtelyyn tai talon katon lumikuorman aiheuttamaan paineeseen ja paineesta johtuvan katon pinnan muodonmuutokseen. Talvisin lumen kasaantuminen kiinteistöjen piha-alueille voi aiheuttaa haasteita ja vaaratilanteita. Datan kerääminen lumikertymistä mahdollistaa uudenlaisten älykkäiden aurauspalveluiden toteuttamisen. Rakennekunnossapidosta vuosien mittaan kirjoitetuista artikkeleista on nähtävissä trendi, jonka perusteella langattomat sensorit ovat yleistymässä. Mikäli mitattavan datan määrä on huomattava, voi olla järkevintä käyttää datan keräämiseen niin kutsuttuja älysensoreita. Suurehkon muistitilan ja laskentatehon avulla näitä sensoreita voidaan käyttää tekoälyalgoritmien kouluttamiseen. Tekoälysovelluksilla voidaan esimerkiksi prosessoida datasignaali jo sensoritasolla ja ilmoittaa käyttäjälle mahdollisista poikkeamista.
Rakennus- ja kiinteistöalalla on käytetty konvoluutio- ja rekursioneuroverkkoja kuvantunnistuksessa. Esimerkiksi Cha ja ym. (2017) käyttivät syviä konvoluutioneuroverkkoja betonihalkeamien tunnistamiseen kuvista. Schnackenburg ja Leife (2017) puolestaan käyttivät niin kutsuttuja päätösviidakkoja hotellihuoneiden sisäilman parametrien ja virhetilanteiden ennustamiseen hyödyntäen lisäksi käyttäjäpalautteita. Kang ja ym. (2017) vertailivat ELM:n (extreme learning machine) ennusteita sillan muodonmuutoksille ja kyseisen algoritmin kouluttamisen helppoutta muihin tehtävään soveltuviin algoritmeihin verrattuna. Muita tekoälyn sovelluskohteita kiinteistöalalla ovat olleet esimerkiksi asunnon myyntihinnan arvioiminen, energiankulutuksen ennustaminen ja ohjaus sekä sisäilman homeitiöiden lukumäärän kasvun laskeminen. Lisäksi kiinteistö- ja rakennusalalla on pohdittu, kuinka tekoälyä ja geneettisiä algoritmeja voisi käyttää rakennusten suunnittelussa aina sisäilmankierrosta reitittimien sijoitteluun ja käyttäjäkokemukseen asti.
Kustannustehokkuuden ja ilmastonmuutoksen takia on oletettavissa, että älykkäiden talojen lukumäärät tulevat vuosi vuodelta kasvamaan. Älykkäiden talojen yleistyessä datamäärät kasvavat ja tekoälyn hyödyntämisestä tulee näin ollen entistä tärkeämpää, kun massadatasta on louhittava oleellista informaatiota. Tulevaisuudessa älykkäät talot kehittyvät entisestään ja saattavat muuttua täysin automaattisiksi. Älytalojen automaattisuus voi tarkoittaa, että älytalo osaa lämpötilan ennustamisen lisäksi muuttaa lämpötilasäätöjä vastaamaan asukkaan toiveita ja energiayhteisön resursseja itsenäisesti reaaliajassa. Lisäksi on mahdollista, että älytalot tulevat oppimaan, kuinka tilataan esimerkiksi huolto ilmastointilaitteelle tai nuohous hormille ennen kuin laitteistot menevät rikki. Älykkäiden talojen kehittyminen vaatii tietotaidon ja tahtotilan lisäksi suuria tietoaltaita ja tekoälyä.
Älykkäiden rakennusten ennakoivaa kunnossapitoa, niiden hyötyjä ja haittoja, kunnossapidon kustannuksia ja säästöjä, kunnossapidon prosessia ja esimerkkejä ennakoivan kunnossapidon ratkaisuista on tutkittu KIRA-Digi-hankkeessa (viite).
9.8 Tekoälyn muita sovelluksia
Siukosen ja Neittaanmäen kirjassa (2019) on esitelty tekoälyn toimijoita ja kehitystrendejä edellämainittujen alojen lisäksi myös julkishallinnossa, liiketoiminnassa sekä kulttuurissa. Lisäksi kirjassa on luotu katsaus tekoälyn tulevaisuuteen.
9.9 Lopuksi
Digitaalisten sovellusten älykkyys juontuu siis koneen aistimus-, päättely- tai toimimiskyvystä. Tällaisilla ominaisuuksilla varustetut laitteet voivat toimia monentyyppisissä ympäristöissä ja tehtävissä ja niinpä ne voivat muuttaa ihmistyöntekijöiden ajankäyttöä, työnkuvaa ja osaamistarpeita hyvinkin radikaalisti. Lisäksi kone on väsymätön, se kykenee työskentelemään tunteiden ja ennakkoasenteiden vaikuttamatta ja se voidaan rakentaa tarpeen mukaan monin tavoin ihmiskehoa haavoittumattomammaksi. Niinpä tekoälyteknologia voi tarjota tukensa esimerkiksi kasvojen, käsialan ja puheen tunnistamistehtäviin, lääketieteelliseen tai pedagogiseen diagnosointiin ja profilointiin, strategiseen suunnitteluun, kuvankäsittelyyn ja erilaisten fyysisten tai virtuaalisten robottien epälineaarisen ohjauksen tehtäviin. Tekoälyrobotteja voidaan niinikään sijoittaa toimimaan ihmiselle riskialttiissa ympäristöissä, kuten vedenalaisissa tehtävissä, ydinvoimaloiden purkutöissä tai avaruudesta käsin suoritettavissa kaukokartoitusmittauksissa. Koneet ja sovellukset voivat ottaa tehdäkseen monet rutiinien sanelemat työtehtävät ja jättää ihmistyöntekijälle enemmän aikaa luovuutta tai ihmiskontaktia edellyttävien tilanteiden hoitamiseen. Kaikki nämä ominaisuudet voivat vaikuttaa niin työntekijöiden hyvinvointiin, työn miellekkyyteen kuin työn tai palveluiden laatuunkin.
Tekoälykehityksen taloudellisia voittajia ovat tällä hetkellä USA ja Kiina, sillä maailman johtavista IT-yrityksistä 80% löytyy USA:sta ja 20% Kauko-Idästä. Tämän suhdeluvun odotetaan kuitenkin olevan muuttumassa. Toistaiseksi USA:n valtti on sen vahva ohjelmistotekniikan osaaminen, kun taas Kauko-Itä hallitsee tuotantoa. Johtavat amerikkalaisyritykset ovat sijoittaneet tulojaan uuteen kehitystyöhön ja panostaneen paljon myös kehitysmaita tukeviin hankkeisiin. Kauko-Idässä on sensijaan panostettu uusiin teknologioihin ja tuotantohintojen minimoimiseen laitteiden hinnan madaltamiseksi.
Tähän asti USA on hyötynyt tilanteesta, jossa juuri amerikkalaiset yliopistot ovat onnistuneet houkuttelemaan maailman lahjakkaimmat opiskelijat ja tutkijat itselleen. Yksi syy tähän etulyöntiasemaan on ollut englannin kielen ylivertainen merkitys tiedemaailmassa. Niinpä USA:n valteiksi voidaan nimetä korkea teknologiaosaaminen, liiketoimintaosaaminen ja englannin kieli. Kiinan menestyksessä keskeinen avaintekijä muodostuu maan suurista sisäisistä markkinoista. Monet uudet teknologiat saavat vankan alkusysäyksen jo omilta markkinoilta. USA:ssa sen sijaan tähdätän suoraan globaaleille markkinoille.
Tekoälypohjaiset tuotteet ja palvelut ovat globaaleja ja niiden kehityksestä voi hyötyä koko maailma. Järjestelmien opettamisen ja toimivuuden kannalta nimenomaan suurten datojen saatavuus on avainasia, joten Alibaban, Amazonin, Fujitsun, Googlen, IBM:n ja Microsoftin kaltaisilla isoilla toimijoilla on tekoälykentällä selvä kilpailuetu.
Käytännössä tekoälypohjaiset palvelurobotit toimivat globaalisti ympärivuorokautisesti viikon jokaisena päivänä ja yksittäiseen palvelutapahtumaan voi osallistua toimijoita useasta eri maasta. Palveluiden käyttö voi olla ilmaista, mutta palvelutapahtuma saattaa sisältää mainoksia sekä palvelun käyttäjästä tehtävän tiedonkeruun. Internetin ja halpojen päätelaitteiden myötä tekoälykoneistot voivat palvella ilmaiseksi, tai ainakin melkein ilmaiseksi, kaikkia kansalaisia ympäri maailman. Tällainen kehitys edellyttää kuitenkin kansainvälistä yhteistyötä ja valmiutta sopeutua muutoksiin.
Kiinan, Japanin ja USA:n johtoasema tekoälykehityksessä piirtyy esiin nimenomaan taloudellisesta perspektiivistä. Toisilla mittareilla tarkastellessa esiin voi nousta muitakin menestyjämaita. Esimerkiksi - kuten Suomen valtioneuvoston aihetta käsittelevän väliraportin julkaisusivulta käy ilmi - tekoälyyn liittyvän tutkimuksen tasoa huippututkimuksen tasolla vertailtaessa sijoittuu Suomi asukasmääräänsä suhteuttaen Amerikan, Kiinan ja Saksan edelle (Valtioneuvoston viestintäosasto 2018).
Etlatieto Oy:n toteuttamassa vuosittaisessa Digibarometri-tutkimuksessa, jossa tarkastellaan digitaalisuuden etenemistä 22 maassa, Suomen on vuonna 2018 arvioitu sijoittuvan digitalisaatiokehtyksessä kolmannelle sijalle, Norjan ja Yhdysvaltojen jälkeen. Suomalainen yhteiskunta onkin ottanut monipuolisesti käyttöön digitalisaation ja tekoälyn mukanaan tuomat mahdollisuudet. Kahden viimeisimmän barometritutkimuksen valossa Suomen keskeisimmät kehitysalueet liittyvät ennen kaikkea osaajapulaan ja siten koulutustarpeeseen sekä digitalisuuden vaikuttavuuden, siis lopulta käteen jäävien käytännön hyötyjen, maksimoimiseen.
Lähteet
- Aguilar, G. S. 2017. Taking advantage of the possibilities offered by Artificial Intelligence is essential for public health to stop managing the disease and move towards generating health Customer Case Study. Viitattu 10.4.2018.
- AI Biblio. 2017. Julkaistu 09.05.2017. Viitattu 3.9.2018.
- AI Biblio. 2018. Viitattu 19.06.2018.
- Allen, R. 2017. 15 Applications of Artificial Intelligence in Marketing. Smart Insights. Julkaistu 2.5.2017. Viitattu 31.8.2018.
- Atomwise. 2015. New Ebola Treatment Using Artificial Intelligence. Julkaistu 24.3. 2015. Viitattu 30.8.2018.
- Bahrammirzaee, A. 2010. A comparative survey of artificial intelligence applications in finance: artificial neural networks, expert system and hybrid intelligent systems. Neural Computing and Applications 19 (8), 1165-1195.
- BBC News. 2018. CES 2018: Luka owl robot reads bedtime stories to kids. Julkaistu 12.1.2018. Viitattu 30.8.2018.
- Brogan, C. 2017. Artificial Intelligence Creates 3D Hearts to Predict Patient Survival. Imperial College London, verkkouutinen. Julkaistu 16.1.2017. Viitattu 4.9.2018.
- Bort, J. 2016. How IBM Watson saved the life of a woman dying from cancer, exec says. Business Insider. Julkaistu 7.12.2016. Viitattu 3.9.2018.
- Canbek, N. G. ja Mutlu, M. E. 2016. On the track of Artificial Intelligence: Learning with intelligent personal assistants. Journal of Human Sciences 13 (1), 592-601.
- Cha, Y.-J., Choi, W. ja Büyüköztürk, O. 2017. Deep Learning-Based Crack Damage Detection Using Convolutional Neural Networks. Computer-Aided Civil and Infrastructure Engineering, 32(5), 361-378.
- Chinadaily. 2012. Robot-themed restaurant attracts business. Chinadaily.com verkkouutinen. Julkaistu 25.6.2012. Viitattu 31.8.2018.
- Colchester, K., Hagras, H., Alghazzawi, D. ja Aldabbagh, G. 2017. A survey of artificial intelligence techniques employed for adaptive educational systems within E-learning platforms. Journal of Artificial Intelligence and Soft Computing Research 7 (1), 47-64.
- Conner-Smith. 2017. Wearable AI System Can Detect a Conversation's Tone. MIT News. Viitattu 19.9.2017
- Donald, J.S. 2004. Artificial Intelligence: The New Advanced Technology in Hearing Aids. Audionolyonline verkkoartikkeli. Julkaistu 7.6.2004. Viitattu 31.8.2018.
- FANUC. 2018. FIELD System. Intelligent Edge Link & Drive System Esite. Oshino-mura, Yamanashi: Fanuc Corporation. Viitattu 31.8.2018. 16.Fauvel, S. ja Yu, H. 2016. A Survey on Artificial Intelligence and Data Mining for MOOCs. arXiv:1601.06862
- Finanssialalle -opintomateriaali. Tekoäly. Päiväämätön. Finanssialalle.fi-sivusto. Finanssiala ry. Viitattu 3.9.2018.
- Foster, M. 2018. Aging Japan: Robots may have role in future of elder care. Julkaistu 28.3.2018. Viitattu 4.9.2018.
- Fujitsu. 2016. Fujitsu's Human-Centric AI Helps Enable Faster, Improved Clinical Decision-Making. Viitattu 07.05.2018.
- Furness, D. 2016. A college professor used an AI teaching assistant for months, but his students didn't notice. Digital Trends. Julkaistu 12.5.2016. Viitattu 30.8.2018.
- GE. Winning in the Environment. Ge-verkkosivuston Letter to Shareowners -osio. Päiväämätön. Viitattu 31.8.2018.
- Geissbauer, R., Schrauf, S., Berttram, P. ja Cheraghi, F. 2017. Digital Factories 2020: Shaping the future of manufacturing. PwC. Viitattu 28.6.2018.
- Guardian. 2017. Meet Pepper the Robot - Southend's newest social care recruit. The Guardian. Viimeisin muokkaus 16.11.2017. Viitattu 4.9.2018.
- Holz, S. 2017. How AI is changing special education. Neo Blog. Julkaistu 22.6.2017. Viitattu 30.8.2018.
- Hoopes, H. 2015. "Autobiographical memory" lets robots act as knowledge go-betweens for ISS crews. New Atlas. Julkaistu 9.9.2018. Viitattu 30.8.2018.
- Hänel, L. 2017. A list of artificial intelligence tools you can use today? - for personal use (1/3). Julkaistu 1.5.2017. Viitattu 30.08.2018.
- Hänel, L. 2017 A list of artificial intelligence tools you can use today? - for businesses (2/3). Julkaistu 11.7.2017. Viitattu 30.08.2018.
- Hänel, L. 2017 A list of artificial intelligence tools you can use today? - for businesses (2/3) continued. Julkaistu 7.9.2017. Viitattu 30.08.2018.
- Hänel, L. 2017 A list of artificial intelligence tools you can use today? - for industry specific (3/3). Julkaistu 12.9.2017. Viitattu 19.06.2018.
- Högström, H. 2017. Yhteistyössä robottien kanssa. Helins.fi-sivuston artikkeli. Helsingin insinöörit hi ry. Julkaistu 24.11.2017. Viitattu 31.8.2018.
- Johnston, C. 2018. Amazon opens a supermarket with no checkouts. BBC News verkkouutinen. Julkaistu 22.1.2018. Viitattu 31.8.2018.
- Juopperi, H. 2018. Toivo puurtaa yksin sairaalan kellarikäytävässä - vuorotta töitä paiskiva robotti ja muut keksinnöt vapauttavat aikaa hoitotyöhön. YleUutiset-sivusto. Viimeisin päivitys 9.3.2018. Viitattu 31.8.2018.
- Järvensivu, A., Ilmakunnas, S. ja Kyrki, V. 2018. Tekoälyn kasvu ja työllisyysvaikutukset. Tekoälyajan työ. Tekoälyaika. Julkaistu 20.6.2018. Viitattu 10.8.2018.
- Kang, F., Liu, J., Li, J. ja Li, S. 2017. Concrete dam deformation prediction model for health monitoring based on extreme learning machine. Structural Control Health Monitoring. John Wiley & Sons, Ltd.
- Kaplan, J. 2016. Artificial Intelligence: What Everyone Needs to Know. New York: Oxford University Press.
- Kay, J., Reimann, P., Diebold, E. ja Kummerfeld, B. 2013. MOOCs: So Many Learners, So Much Potential... IEEE Intelligent systems 28 (3), 70-77.
- Kiger, P. 2018. Artificial Intelligence Can Help Pick Voices Out of a Crowd. AARP. Julkaistu 30.4.2018. Viitattu 30.8.2018.
- KUKA. 2017. Joining side members by human-robot-collaboration. Kuka.com-verkkosivuston uutinen. Julkaistu 28.6.2017. Viitattu 31.8.2018.
- LukiMat-hanke. LukiMat, Niilo Mäki Instituutti
- Lynch, M. 2018. 7 Roles for Artificial Intelligence in Education. The Tech Edvocate. Julkaistu 5.5.2018. Viitattu 30.8.2018.
- Mack, H. 2016. Cognitive Therapy Startup Koko Raises $2.5M, Launches Chatbot with Kik Messaging Service. MobiHealthNews. Julkaistu 9.8.2016. Viitattu 29.8.2018.
- Mack, H. 2017. Woebot Labs Debuts Fully AI Mental Health Chatbot via Facebook Messenger. MobiHealthNews. Julkaistu 6.6.2017. Viitattu 29.8.2018.
- Mansikka, H., Tikkamäki, M. 2018. Robotti opettaa lapsille englantia kärsivällisesti ja väsymättä: "Ei se aina tottele, mutta eihän opettajakaan tottele aina." Viimeisin päivitys 8.5.2018. Viitattu 30.8.2018.
- McIntyre, K. 2016. Upset About Trump's Win? This Penguin Chatbot Helps Combat Depression. Tech in Asia. Julkaistu 12.11.2016. Viitattu 25.9.2017.
- Miller, D. D. ja Brown, E. W. 2017. Artificial Intelligence in Medical Practice: the Question to the Answer? The American Journal of Medicine 131 (2), 129-133.
- Mueller, J. ja Massaron, L. 2018. Artificial Intelligence For Dummies. For Dummies (Computer/Tech) -sarja. New Jersey: John Willey & Sons Inc.
- Nakhleh, M. K., Amal, H., Jeries, R., Broza, Y. Y., Aboud, M., Gharra, A., ... ja Glass-Marmor, L. 2016. Diagnosis and classification of 17 diseases from 1404 subjects via pattern analysis of exhaled molecules. ACS nano, 11(1), 112-125. Julkaistu 21.12.2016. Viitattu 4.9.2018
- Neittaanmäki, P. 2017. Globaali digitaalinen koulu. Julkaistu 21.2.2017. Viitattu 29.8.2018.
- Owen-Hill, A. 2017. Top 6 Robotic Applications in Food Manufacturing Robotiq. Julkaistu 8.8.2017. Viitattu 30.8.2018.
- Pajunen, I., Koivuranta, E. 2018. Yle seurasi, kun Töölön sairaalassa tehtiin poikkeuksellinen aivoleikkaus - Robotti avusti kirurgia Parkinson-potilaan hoidossa. Yle Uutiset. Julkaistu 27.3.2018. Viitattu 31.8.2018.
- Pesonen, H. 2018. Puhuvat robotit alkavat auttaa tamperelaislapsia koulussa - "On jännittävää, kuinka lapset suhtautuvat". Aamulehti. Julkaistu 13.3. 2018. Viitattu 30.8.2018.
- Purvis, K. 2017. Meet Pepper the Robot - Southend's newest social care recruit. The Guardian. Julkaistu 6.10.2017. Viitattu 29.8.2018.
- Rauhala, T. 2018. Finanssialan tulevaisuus on tuolileikkiä tekoälyn kanssa. Ammattiliitto Pron verkkosivusto proliitto.fi, Työ ja talous -osasto. Julkaistu 11.1.2018. Viitattu 3.9.2018.
- Rokka, H. 2017. Robotti nakertaa valkokaulustyöläisen tulevaisuutta. DNA yrityksille -sivuston blogikirjoitus. Julkaistu 10.5.2017. Viitattu 31.8.2018.
- Russell, S. J. ja Norvig, P. 2016. Artificial intelligence: a modern approach. Malaysia: Pearson Education Limited.
- Savickas, M. L. 2012. Life design: A paradigm for career intervention in the 21st century. Journal of Counseling & Development, 90 (1), 13-19.
- Schnackenburg, E. C., ja Leife, K. 2017. Maskininlärning i fastighetsbranschen: Prediktion av felanmälningar gällande inomhusklimat baserat på sensordata. Digitala Vetenskapliga Arkivet. Sweden: Uppsala University.
- Siemens. The Future of Manufacturing: Tomorrow's Information Factories. Päiväämätön. Siemens.com-verkkosivuston yleiskatsaus-osion artikkeli. Viitattu 31.8.2018.
- Sina. 2017. Sina Julkaistu 16.09.2017. Viitattu 3.9.2018.
- Siukonen, T. ja Neittaanmäki, P. 2019. Mitä tulisi tietää tekoälystä. Docendo
- Smith, C. 2017. MIT's New AI Understands the Hardest Part of Human Language. BGR. Julkaistu 2.2.2017. Viitattu 4.9.2018
- Syväniemi, A. ja Raunama, J. 2018. Tekoäly tekee verkkokaupan markkinoinnista palvelua. Profit- sivuston blogikirjoitus. Julkaistu 22.11.2017. Otavamedia Oy. Viitattu 31.8.2018.
- Tekniikka ja talous. 2013. Tekniikka ja talous Tekniikka ja talous. Julkaistu 26.11.2013. Viitattu 30.8.2018.
- TE-palvelut. 2018. Työministeri Jari Lindström: Tekoäly voi tulevaisuudessa nopeuttaa uuden työn löytämistä. TE-palvelujen verkkosivut. Julkaistu 11.6.2018. Viitattu 30.8.2018.
- TEM. Työ- ja elinkeinoministeriön tekoälyohjelma
- TEM. 2019. TEM:n tekoälyohjelman loppuraportti
- Terashima, T. 2016. Japan use robotics to help ease burden in health care. CGTN America. Julkaistu 29.07.2016. Viitattu 4.9.2018.
- Uusiteknologia.fi. 2017. Robotit tulevat sairaalaan - tässä kehitysnäkymät. Uusiteknologia.fi -sivuston artikkelit ja raportit -osio. Julkaistu 30.8.2017. Viitattu 31.8.2017.
- Valtioneuvoston viestintäosasto. 2018. Selvitys avaa tekoälyn käsitteistöä ja kartoittaa alan suomalaisosaamista. Suomen Valtioneuvoston viestintäosaston tiedote 312/2018, 19.6.2018. Viitattu 9.8.2018.
- Vinobha K.T. 2016. Manipal Hospitals Deploys Cognitive Computing Platform Watson for Oncology. The Times of India. Julkaistu 29.9.2016. Viitattu 4.9.2018.
- Walker, J. 2018. Machine Learning in Manufacturing - Present and Future Use-Cases. Techemergence. Julkaistu 29.5.2018. Viitattu 15.8.2018.
- Wikipedia contributors. 2018. Artificial intelligence. Wikipedia, The Free Encyclopedia. Viimeisin muokkaus 30.8.2018. Viitattu 30.8. 2018.
- Wikipedia contributors. 2018. Weak AI. Wikipedia, The Free Encyclopedia. Viimeisin muokkaus 27.8.2018. Viitattu 30.8. 2018.
- Williams,K., Bilsland, E., Sparkes, A., Aubrey, W., Young, M., Soldatova, L.N., Grave, K. De, Ramon, J., Clare, M. de, Sirawaraporn, W., Oliver, S.G. ja King, R.D. 2015. Cheaper faster drug development validated by the repositioning of drugs against neglected tropical diseases. Journal of the Royal society Interface 12 (104), 20141289.
- Wingfield, N. 2017. As Amazon Pushes Forward With Robots, Workers Find New Roles. The New York Times -verkkolehti. Julkaistu 10.9.2017. Viitattu 31.8.2018.
- Yu, H., Miao, C., Leung, C. ja White, T. J. 2017. Towards AI-powered personalization in MOOC learning. Science of Learning 2 (1), 15.
10. Tekoälyn perusteet ja sovellukset 2018-2019 -kurssin satoa
(Heli Tuominen)
Tässä luvussa tarkastellaan kurssin Tekoälyn perusteita ja sovelluksia (TIEP1000) 2018-2019 lukuun 8 liittyvän, professori Pekka Neittaanmäen pitämän luennon vastauksia. Luennon kaksi ensimmäistä kysymystä olivat:
- Kerro, kuinka voisit hyödyntää tekoälyä opiskelussa/työtehtävissä ja myöhemmin elämässä.
- Kerro viisi mielestäsi hyödyllisintä/mielenkiintoisinta tekoälysovellysta.
10.1 Tekoäly opiskelussa, työelämässä ja arjessa.
Ensimmäisen kysymyksen vastauksissa mainittiin useita tapoja käyttää tekoälyä niin nykyhetkessä kuin tulevaisuudessakin. Taulukossa on listattu 313 vastauksessa 30 eniten mainintoja saanutta tapaa/sovellusta.
| Tekoälyn käyttöalue/sovellus | kpl |
|---|---|
| tiedonhaku hakukoneilla (esim. Google) | 122 |
| kääntäjät, kommunikointi, puhe tekstiksi, teksti puheeksi | 69 |
| tutkimus (esim. artikkeleiden/luentojen tiivistäminen) | 42 |
| uraohjaus, rekrytointi (esim. Mosaic) | 38 |
| suurten aineistojen käsittely | 30 |
| itseajavat autot (lentokoneiden autopilotit ja muut itseajavat ajoneuvot) | 30 |
| roskapostin suodatus | 28 |
| sairauksien diagnoosit | 27 |
| kohdennettu mainonta | 27 |
| älykkäät oppimateriaalit | 26 |
| opetuksen arviointi, tehtävien tarkastaminen, palaute | 25 |
| älykäs opintoneuvoja (kurssien valinta, aikataulutus) | 22 |
| terveydentilan mittaus ja ennustus | 21 |
| MOOC-verkkokurssit, tekoälyopettajat, oppimisympäristöt | 21 |
| älytalot | 20 |
| hintavertailut (esim. Momondo) | 20 |
| chatbotit | 20 |
| päivittäinen/projektien aikataulutus | 17 |
| virtuaaliavustajat (esim. Siri, Alexa, Hound) | 15 |
| kuvantunnistus | 15 |
| karttasovellukset, reittisovellukset, ruuhkatiedot (esim. Google Maps) | 15 |
| tietoturvallisuuden sovellukset, kyberturvallisuus | 14 |
| tiedonhaku tietokannoista tai tilastoista | 13 |
| hoitorobotit ja sosiaaliset robotit | 12 |
| tekoäly tehtaissa (robotiikka, varastointi, logistiikka, laaduntarkkailu) | 12 |
| sijoitusneuvonta, talousavustajat, lainananto, luottoarviot | 11 |
| oppimisavustaja, oppimista tukevat sovellukset | 11 |
| ohjelmistokehitys | 11 |
| virtuaalinen kunto/ravintovalmennus | 10 |
| fyysisen rasituksen arviointi | 10 |
Opiskelussa ja arkielämässä eniten käytetyt tekoälysovellukset ovat hakukoneet ja kääntäjät. Useissa vastauksissa mainittuja, toivottuja toimivia sovelluksia olivat aikataulutusavustaja sekä opintojen kurssien suunnitteluun että muiden menojen järjestelyyn, tieteellisten tekstien ja lähdemateriaalien tiivistämiseen ja etsintään käytettävät työkalut sekä uraohjauksen avustajat työnhaun helpottamiseen. Roskapostin suodattimet, kohdennettu mainonta, chatbotit ja hintavertailusovellukset ovat osa useimpien arkea. Terveydenhuollon alalla tulevaisuudessa odotetaan sairauksien diagnosointia tekoälyn avulla ja tekoälyavusteisia kunto- ja ravintovalmentajia. Opiskelun apureiksi toivotaan älykkäitä oppimisympäristöjä. Useita mainintoja saivat myös tuotantoon ja bisnesmaailmaan sekä eri ammatteihin liittyvät sovellukset.
Seuraavissa taulukoissa kerrotaan käyttöalueittain eniten mainintoja saaneet sovellukset/käyttökohteet.
| Tiedon haku ja käsittely, kommunikointi (Yht. 282 kpl) | kpl |
|---|---|
| tiedonhaku hakukoneilla (esim. Google) | 122 |
| kääntäjät, kommunikointi, puhe tekstiksi, teksti puheeksi | 69 |
| suurten aineistojen käsittely | 30 |
| roskapostin suodatus | 28 |
| chatbotit | 20 |
| Avustajat (Yht. 217 kpl) | kpl |
|---|---|
| uraohjaus, rekrytointi (esim. Mosaic) | 38 |
| kohdennettu mainonta | 27 |
| hintavertailut (esim. Momondo) | 20 |
| älytalot | 20 |
| päivittäinen/projektien aikataulutus | 17 |
| Opiskelu (Yht. 159 kpl) | kpl |
|---|---|
| tutkimus (esim. artikkeleiden/luentojen tiivistäminen) | 42 |
| älykkäät oppimateriaalit | 26 |
| opetuksen arviointi, tehtävien tarkastaminen, palaute | 25 |
| älykäs opintoneuvoja(kurssien valinta, aikataulutus) | 22 |
| MOOC-verkkokurssit, tekoälyopettajat, oppimisympäristöt | 21 |
| Terveydenhoito (Yht. 99 kpl) | kpl |
|---|---|
| sairauksien diagnoosit | 27 |
| terveydentilan mittaus ja ennustus | 21 |
| hoitorobotit ja sosiaaliset robotit | 12 |
| fyysisen rasituksen arviointi | 10 |
| virtuaalinen kunto/ravintovalmennus | 10 |
| Yritysmaailma (Yht. 80 kpl) | kpl |
|---|---|
| tietoturvallisuuden sovellukset, kyberturvallisuus | 14 |
| tekoäly tehtaissa(robotiikka, varastointi, logistiikka, laaduntarkkailu) | 12 |
| ohjelmistokehitys | 11 |
| turvallisuusala, (liikenne)valvonta, poliisin tehtävät, hätäkeskukset | 9 |
| asiakaspalvelurobotiikka | 8 |
| Liikenne (Yht. 52 kpl) | kpl |
|---|---|
| itseajavat autot (lentokoneiden autopilotit ja muut itseajavat ajoneuvot) | 30 |
| karttasovellukset, reittisovellukset, ruuhkatiedot (esim. Google maps) | 15 |
| rekisterintunnistus esim. parkkihalleissa | 7 |
Alla on kerättynä osia muutamista vastauksista ensimmäiseen kysymykseen aihealueittain.
Tekoäly, opiskelu ja opettaminen
Opintoja suunnitellessa tekoäly voisi ehdottaa kursseja kiinnostavista aihepiireistä ja auttaa rakentamaan järkevää opintokokonaisuutta. Kun kurssit on valittu, niin tekoäly voisi ehdottaa hyvin aikataulutettuja suunnitelmia kurssien toteuttamiseksi. Aikataulussa ne kurssit, jotka pitää suorittaa tietyissä jaksoissa, menisi tietysti omille paikoilleen, ja aikatauluttomat kurssit tekoäly voisi sijoittaa opintojen sekaan tasaisesti. Tämän tapainen suunnittelutyö auttaisi varmasti opiskelijoita luomaan parempia opintosuunnitelmia, sillä opiskelun alussa on hankala hahmottaa näin isoa kokonaisuutta, tai edes löytää kaikkia tarjolla olevia kursseja.
Tekoäly voisi seurata varsinaista oppimista. Teoreettisemmissa aiheissa voisi olla pieniä välitenttejä, joiden perusteella tekoäly tietäisi mitä aukkoja opiskelijan tietämyksessä on. Näin tekoäly pystyisi tarjoamaan opiskelijalle henkilökohtaisesti oppimateriaalia tietämyksen paikkaamiseen.
Tekoäly voisi analysoida opiskelijan tehtäviä ja harjoitustöitä kesken kurssin ja antaa niistä palautetta. Näin opiskelija tietäisi missä mennään oikeaan suuntaan ja mitkä kohdat kaipaavat vielä petrausta.
Uskon ja toivon, että arvioinnissa tekoäly auttaisi opettajan työtä tulevaisuudessa. Luennoissa ja materiaalissa mainittiin muun muassa älykkäät opetusmateriaalit, jotka muuttavat taitotasoa oppilaan kykyjen mukaan. Tällaiset helpottaisivat opettajan työtä ja kohdentaisivat avun tarvitsijoita. Varsinkin luokat alkavat olla hyvin suuria ja oppilaiden taitotaso hyvin vaihteleva. Välistä huomaa, ettei aina osannut kohdistaa apua ja resursseja kaikkiin avun tarvitsijoihin. Tässä mielessä tuollaiset oppivat sovellukset olisivat todella tärkeitä.
Välittömästi tekoäly voisi esimerkiksi selata julkaistua tietomassaa (artikkeleja, kirjoja, webinareja, jne) ja referoida minulle valmiiksi minua kiinnostavat artikkelit. Tekoäly voisi tulkita (ja toki mm. Google näin jo tekee) tekemiäni tietohakuja ja tarjota automaattisesti samankaltaisia artikkeleja tai teoriaa tukevia ja kumoavia artikkeleja luotettavuusarvion kera. Tulevaisuudessa tekoäly voisi toimia yleisemminkin avusteisena älynä ja ”takapiruna” vinkaten paremmista vaihtoehdoista tai tarjoten muuta lisätietoa.
Hyödynnän tekoälyä jo nykyisin useiden eri palveluiden muodossa. Esimerkiksi, käytän Google-hakukonetta päivittäin ja tämän palvelun lisäksi hyödynnän myös muita hakukoneita, kuten Jyväskylän yliopiston JykDok-palvelua. Ilman näitä relavantin tiedon löytäminen Internetistä olisi lähestulkoon mahdotonta. Tiedon löytämisen lisäksi hyödynnän tekoälyä myös tiedon filtteröinnissä. Minulla on useita eri sähköpostitilejä ja jokainen näistä hyödyntää roskapostifilttereitä, jotka pyrkivät mainosten ja muun roskapostin poistamiseen.
Käsinkirjoitettujen harakanvarpaiden tulkinnassa ja muuntamisessa paremman luettavaksi yleiseksi fontiksi tekoäly voisi tukea niin opiskelijaa kuin opettajaa. Samoin tekoäly voisi suoraan sanelusta kirjoittaa tekstin ja korjata siitä kielioppi ja tyylivirheet.
Opiskelussa olisi hyödyllistä tehdä töitä mahdollisimman tehokkaasti, mutta ilman, että laatu kärsii. Ominaisuus, josta kokisin itselleni olevan hyötyä on sovellus, joka pystyisi tutkimaan ja kertomaan, minä kellon aikana työskentelen mahdollisimman tehokkaasti. Luulen, että olen tehokkain illalla, mutta välillä tuntuu, että työ valmistuu laadukkaimmin aamulla. Jotta tämä idea onnistuisi, pitäisi palautettavat tehtävät ja muut työt tehdä erillisessä sovelluksessa tai työpohjassa, joka tarkkailisi kellonaikaa ja samalla työskentelyn tehokkuutta. Mukaan voisi ottaa esimerkiksi web-kamerassa toimivat tunnistimen, joka tutkii silmän liikettä. Se voisi tutkia, miten usein silmä harhailee esimerkiksi kännykkään tai muille tehtävän kannalta epäoleellisille sivuille. Sovellus tutkisi myös, miten nopeasti tehtävä saadaan suoritettua, mutta myös, miten laadukasta työ on ollut. Esimerkiksi, jos essee tyyppinen vastaus on saatu tehtyä noin kahdessa tunnissa valmiiksi kello 18 alkaen, mutta sen arvosana on huono ja toinen essee on tehty kahdessa päivässä, mutta pääpaino on aamupäivällä, sovellus tallentaa erilaiset tiedot tietokantaan ja ajan saatossa saadaan dataa, joka kertoo, milloin tietylle henkilölle on opitimaalista tehdä tehtäviä.
Muutaman MOOC-kurssinkin olen suorittanut. Tosin oman kokemukseni mukaan tieto niissä on usein liian yleispätevää ja valmiiksi pureskeltua, jopa liian yksinkertaistettua, ehkäpä jotta kurssi sopisi mahdollisimman monelle. Esimerkiksi Helsingin yliopiston Elements of AI-kurssi, jonne ilmoittauduin ensimmäisten joukossa viime keväänä (voi olla, että kurssia on kehitetty!), sai minut suorastaan raivostumaan. Yhdessä kurssin tehtävässä piti tutustua ensin annettuun materiaaliin, muistaakseni muutama artikkeli, ja sitten vastata erilaisiin monivalintakysymyksiin ja aiheena oli etiikka! Ei tekoälyn etiikkaan liittyviin kysymyksiin voi vastata kyllä tai ei. Eettiset kysymykset ovat paljon monisyisempiä asioita, eikä niihin ikinä ole yhtä oikeaa vastausta. Kurssi jäi siihen.
Minulle opiskelu- ja työelämässä ilmeisimmin hyödyllisimmät tekoälysovellukset liittyvät tiedonhakuun ja sen lajitteluun. Muita hyödyllisiä tekoälyyn perustuvia teknologioita ovat kääntö- ja tulkkaustyökalut vieraille kielille, sekä kuvantunnistusteknologiat. Yhtenä esimerkkinä kuvantunnistuksesta on Mathpix OCR, joka generoi LaTeX-koodia kuvakaappauksista, tai jopa paperille käsinkirjoitetuista yhtälöistä.
Opiskeluissa voisin hyödyntää tekoälyä esimerkiksi niin, että Korpissa oleva tekoälyrobotti antaisi minulle joka lukukausi valmiin ehdotuksen kursseista, joita voisin ottaa kyseiselle lukukaudelle. Robotti pohjaisi valintansa aiemmin käymiini kursseihin, joiden avulla se muodostaisi kuvan millaisista kursseista pidän. Päätös pohjautuisi myös opintosuunnitelmani pakollisiin kursseihin, joita se myös valitsisi automaattisesti. Opiskeluihin liittyen tekoälyä voisi hyödyntää myös opiskelijaravintoloiden ja tietokoneluokkien vapaustilannetiedon saamisessa. Tekoälyrobotti voisi muodostaa kartan, jossa näkyisi kuinka paljon vapaita paikkoja missäkin ravintolassa ja tietokoneluokassa on, jolloin ei tarvitsisi mennä aina paikan päälle tarkastamaan, mahtuuko kyseiseen tilaan. Robotti voisi lisäksi muodostaa ajan kuluessa datasta tilastoja ja trendikaavioita, josta näkisi esimerkiksi kellonajan perusteella, milloin yleensä tila on tyhjimmillään ja milloin siellä on eniten ihmisiä.
Opiskelussa voisin mieluusti hyödyntää tekoälyä niin, että voisi kaapata video/audioluentoja ja transkriptoida ne tekstiksi vaikkapa epub-muotoon – varmasti melkeinpä mikä tahansa tiedostomuoto toimisi kunhan puheen saa kaapattua tekstiksi. Aina ei ole mahdollisuutta tai halua katsoa luentoa videolta – tekstiä voisi helposti lukea esimerkiksi junassa.
Olen tekemässä väitöskirjaa, metodina käytän grounded theorya. Grounded theoryssa käsitellään suurta tekstimassaa, minun materiaalissa on yli 150 venäjänkielistä asiakirjaa. Tekstiä käydään läpi rivi riviltä, ja kun löytyy tutkimuksen kannalta tärkeä termi/sana, sana koodataan ja koodatuista sanoista eli käsitteistä muodostetaan kategorioita. Kategorioista johdetaan teoria. Graduvaiheessa kävin tekstit läpi "käsin", merkitsemällä käsitteet erivärisillä yliviivauskynillä. Väitöskirjavaiheessa olen käyttänyt Atlas.ti- sovellusta. Tekstin läpikäynti ja koodaus on ollut äärimmäisen aikaa vievää toimintaa. Kyseinen tekstin läpikäynti tekoälypohjaisella tekstianalytiikalla säästäisi valtavasti aikaa ja myös standardisoisi koodausta. Ohjatussa oppimisessa tekstiä läpikäyvälle sovellukselle voisi opettaa tekstistä löytyvien tärkeiden sanojen koodaamista tyyliin "aina kun löydät tekstistä sanan informaatioinfrastruktuuri, merkitse se ja koodaa se kyberuhkan kohteeksi". Tekoälyllä voisi myös muodostaa käsitteistä kategeroita ja edelleen kategorioista teorian.
Opiskeluissa ja muillakin elämänalueilla on hyötyä esimerkiksi tekoälyllä toimivista kielenkääntäjistä kuten Google Translatesta. Vaikkapa vieraskielistä tutkimusartikkelia lukiessa voi turvautua kääntäjään tiedostaen kuitenkin mahdolliset virheet lauserakenteissa. Älypuhelimiin on myös olemassa kääntäjäsovelluksia, jotka pystyvät kamerakuvasta muuttamaan kuvatun tekstin esim. venäjän kielestä englanniksi. Opiskelussa voisi olla hyötyä myös mobiililaitteille kehitellyistä puheentunnistuspohjaisista IPA-sovelluksista (Intelligent Personal Assistant), jotka voivat suorittaa käyttäjän puolesta erilaisia tehtäviä kuten tiedonhakua tietystä aiheesta. Myös massiiviset avoimet MOCC-verkkokurssit kuulostavat mielenkiintoiselta ja helposti lähestyttäviltä tavalta kehittää osaamistaan ja opiskella uusia asioita, joten voisin kuvitella itsekin tulevaisuudessa osallistuvani jollekin tällaiselle kurssille.
Opintoneuvojana voisin hyödyntää tekoälyä siinä suhteessa, että voisin antaa syötteenä ohjelmalle tiedot siihen, mihin olen opinnoillani tähtäämässä ja lisäksi sille voitaisiin syöttää esimerkiksi tiedot aikaisemmin suorittamistani opinnoista, työhistoriasta jne., jolloin ohjelma pystyisi tekemään päätelmän, että mitä osaamisalueita pitää mahdollisesti vahvistaa tavoitteisiin nähden. Lisäksi opintoneuvoja voisi aikatauluttaa ja organisoida opinnot niin, että ne soveltuisivat käyttäjän tarpeisiin ja haluttuun valmistumisaikaan. Tietenkin perustietoina ohjelmalle annetaan tutkintoon vaadittavat opinnot ja pisterajat.
Olen hyödyntänyt omassa pian valmistumassa olevassa opinnäytetyössäni ohjattua koneoppimista uintitekniikoiden tunnistamiseksi. Menetelmä perustuu IMU -anturilla mitattuun liikkeeseen koehenkilön takaraivokyhmyn päältä uimalakin alla. Dataan yhdistetään tunnistetieto videokuvasta digitoitusta materiaalista.
Älykodit
Kotona tekoäly voisi huolehtia energiatehokkuudesta. Tyhjien huoneiden valot sammuisivat itsestään ja päälle jääneistä turhista sähkölaitteista katkaistaisiin virrat. Myös veden käyttöä tekoäly voisi säädellä optimaalisemmaksi.
Tekoäly voisi tunnistaa minut automaattisesti, jolloin lukkojen availu ja kaikki muu (tieto)turvallisuuteen liittyvä jäisi vähemmälle vapauttaen resursseja muuhun käyttöön.
Tulevaisuutta ajatellen tekoäly nähdään niin mahdollisuuten kuin uhkanakin. Tekoäly tulee kuitenkin varmasti kehittämään ja parantamaan ihmisten elämänlaatua. Se ilmoittaa sinulle mikä ruoka on pilaantumassa ja mitä ostaa lisää älyjääkaappiin.
Tekoäly arjessa
En pidä kotitaloustöistä. Tämä varmasti on hyvin tyypillistä. Siksi haluaisin valjastaa tekoälyn kotitontuksi, joka imuroisi, pesisi välillä lattiat, tiskaisi tiskit, pesisi pyykit, kuivaisi pyykit, vaihtaisi lakanat, puhdistaisi pihat lumesta, lehdistä sekä leikkaisi nurmikon. Tiedän, että nurmikon leikkaamiseen on ainakin jo robotteja olemassa ja olen sellaisia myös nähnyt. Bonuksena voisi olla vielä ikkunan pesu pari kolme kertaa vuodessa.
Itselleni olisi erityisen hyödyllinen sellainen tekoälyä hyödyntävä sovellus, joka lopettaisi tai ainakin vähentäisi jatkuvaa myöhästelyäni. Tätä mieleeni tullutta sovellusta voisi kuvailla Google kalenterin ja Google mapsin yhdistelmäksi. Sovellus olisi kykenevä seuraamaan kalenterini merkintöjä ja tunnistamaan missä nämä paikat sijaitsevat. Sovelluksen toiminnan perustana olisi, että sovellus ilmoittaisi esimerkiksi puhelimeeni tai tietokoneeseeni, että nyt on aika lähteä, jotta olen ajoissa seuraavassa sovitussa tapaamisessa tai luennolla. Olisi myös erittäin hyödyllistä, jos sovellus tunnistaisi aamulla millä kulkuvälineellä olen liikkeellä: kävellen, pyörällä vai autolla. Tekoälyn ja Big Datan hyödyntämisen ansiosta sovellus voisi tarkasti arvioida matkan vaatiman ajan ja todennäköisen ruuhkan vaatiman lisäajan tiettyyn vuorokaudenaikaan. Tämänkaltainen sovellus olisi varmasti mahdollista toteuttaa jo nykyisillä Google mapin ja kalenterin ominaisuuksilla. Sovellus poistaisi päänvaivan matkaan tarvittavien aikojen arvioinnista ja havahduttaisi käyttäjän lähtemään ajoissa.
Hyödyllinen tekoälyä hyödyntävä sovellus toimisi niin, että se osaisi arvioida kalenterini perusteella kuinka rankka päiväni on ollut fyysisesti ja henkisesti. Tämän perusteella sovellus arvioisi, kuinka paljon tarvitsen lepoa, jotta työtehoni ja jaksamiseni olisi palautunut seuraavaan päivään. Tämä mahdollistuisi sillä, että sovellus suosittelisi nukkumaanmenoaikani ja estäisi elektroniikkalaitteiden päällä olon esimerkiksi kaksi tuntia ennen tätä suositeltua aikaa. Sovellus voisi myös patjaan asetetun anturin avulla seurata nukkumistani ja täten osaisi arvioida kuinka palauttavaa uneni on ollut.
Personal trainerina että ruoka- ja unikoordinaattorina tekoäly olisi siitä hieno, että jos näille kehittettäisiin joku yleinen alusta, joka saisi käyttöönsä minun terveystietoni sekä henkilökohtaisen profiilini, jolla tarkoitan ikää, painoa, pituutta, sukupuolta jne., se voisi keräämänsä sekä siihen syötetyn tiedon pohjalta tuottaa käyttäjälle optimaalisen liikunta-aikataulun, varmistaa tarvittavien hivenaineiden jne. saannin ravinnosta ja ehdottaa oikeita aikoja nukkumaan menemiselle ja heräämiselle sekä rasituksesta palautumiselle.
Tekoäly myös mahdollistaa sääpalveluiden toiminnan ja sääennusteiden luomisen. Hyödynnän myös näitä palveluita päivittäin sään tarkkailuun. Tekoälyn suorittama tarkkailu kohdistuu kuitenkin myös minuun itseeni. Muun muassa Google pyrkii tarkastelemaan verkon käyttöäni ja hyödyntämään tätä tietoa mainosten kohdistamiseen. Pyrin kuitenkin suojaamaan itseäni tältä hyödyntämällä tekoälyyn pohjautuvia ohjelmia, jotka piilottavat mainokset verkkosivuilta sekä estävät verkkosivujen suorittamaa tarkkailua. Tekoälyn suorittama tarkkailu ei kuitenkaan nykyisin rajoitu vain nettiin. Esimerkiksi Valtatie 4:llä on nykyisin keskinopeutta tarkkailevia liikennekameroita, jotka tuovat tekoälyyn pohjautuvan tarkkailun myös ajoteille.
Muuten elämässä tekoälyä voisi käyttää esimerkiksi liikenneruuhkan tarkastelussa. Tekoälysovellus voisi aikaisemman sekä reaaliaikaisen datan avulla kertoa, mihin aikaan tiet ovat ruuhkaisimmillaan ja antaa sitten ajankohtaisia ruuhkahälytyksiä.
Itse koen kuitenkin tekoälyn hieman pelottavaksi ja asiaksi. Mielestäni sitä ei saisi liikaa kehittää ja tuoda ihan yleiseen käyttöön jokaisen ihmisen arkipäivään. Tekoälyn avulla on jo nyt luotu erilaisia hyvinvointisovelluksia, älykelloja jne., jotka osaltaan tukevat ihmisten hyvinvointia ja auttavat etenkin urheilijoita optimaalisessa harjoittelussa ja kehittymisessä. Kysymys on kuitenkin se, että unohdammeko kuinka kuunnella oman kehomme viestejä, jos ryhdymme täysin koneen orjaksi ja onko optimaalinen suorittaminen oikeasti aina se tärkein asia. Itselläni suorituksen ainainen mittaaminen pitkällä ajalla murentaa alkuperäistä syytä miksi jokaisen tulisi liikkua – liikunnan ilo ja nautinto. Monet asiat ovat siirtyneet numeroiksi, sekä sähköiseen muotoon ja sitä kautta ihmiselle tyypillinen luontainen liikkuminen on vähentynyt hurjasti. Tekoälyn avulla luodaan kuva toisesta todellisuudesta, jossa kaikki on paremmin ja hienompaa, mutta todellisuudessa sitä todellisuutta ei ole olemassa. Itse en halua tulevaisuudessa elää täysin virtuaalitodellisuudessa ja menettää normaaleja perusarjessa tarvittavia taitoja. Jatkuva tekoälyn hyödyntäminen vähentää varmasti omaa ajattelua ja itsensä haastamista.
Tekoälypohjainen uutisten aggregointipalvelu olisi kätevä. Uutisia julkaistaan valtavia määriä, joista osa on valeuutisia ja osa on eri uutislähteiden artikkeleita samasta aiheesta. Palvelu, joka pystyisi suodattamaan valeuutiset ja huomioimaan käyttäjän mieltymykset tekisi valtavan uutismassan käsittelystä helpompaa ja mielekkäämpää. Palvelu voisi esimerkiksi luokitella uutiset niiden sensaatiohakuisuuden/asiapitoisuuden mukaan. Esimerkiksi joku käyttäjä haluaa lukea kuivia asiapitoisia uutisia, kun taasen toinen käyttäjä tykkää enemmän provosoivasta mielipidekirjoituksesta. Lisäksi palvelu pyrkisi oppimaan, mistä aiheista käyttäjä on kiinnostunut, ja jakamaan uutisartikkelit erilaisiin ryhmiin. Ja vielä jos palvelu pystyisi tunnistamaan artikkelit joissa käsitellään samaa uutista ja näyttämään käyttäjälle niistä vain yhden, niin käyttäjän ei tarvitsisi selata kymmenen saman uutisen ohitse.
Matkoille avuksi tekoälyyn perustuva simultaanitulkkaussovellus. Liikenteessä: Älykäs sähköautojen lataus- ja navigointijärjestelmä, langaton lataus, ajonaikainen lataus ja latauksen optimoiva reitinsuunnittelu ja kuljettajan älykkäät apulaitteet.
Tekoäly eri ammattien apuna
Kirjastomaailmaankin tekoäly varmasti tulee vaikuttamaan. Juuri avattuun Helsingin keskustakirjasto Oodiin on tulossa robotteja hoitamaan kirjastoaineiston logistiikkaa, minkä lisäksi kirjastomaailmasta löytyy paljon muitakin tekoälyn sovelluskohteita. Asiakkaiden käyttämää verkkokirjastoa voi esimerkiksi kustomoida oppivan tekoälyn avulla siten, että kullakin käyttäjällä on hänelle räätälöity näkymä, uutta sisältöä ja aineistosuosituksia, jotka perustuvat käyttäjän aiemmin lainaamiin teoksiin.
Pelastustehtävissä hälytyksen syynä on usein automaattisen paloilmoittimen antama häly. Kun sitten paloautoinemme saavumme kohteeseen, esim. yöaikaan, ovat portit kiinni. Sitten alkaa etsiminen (fyysisesti tai selaamalla kohdekorttitiedostoja) mistä löytyy kohteen avaimet. Emme pääse alueelle emmekä kohteeseen sisälle jos portit ovat kiinni. Tekoäly voisi em. tapauksissa lukea kaikkien paloautojen rekisterinumerot ja sen perusteella antaa kulkuoikeuden alueelle. Näin pelastustoiminta nopeutuisi ja helpottuisi. Samaa tekniikkaa voi laajentaa ovien lukitukseen ja murtohälytysten blokkaamiseen (nyt aiheutamme hälyn kun menemme omilla avaimilla siään).
Poliisin työtehtäviin tekoälyä voisi hyödyntää monella tapaa. Tekoälyn avulla voisi analysoida rikosilmoituksista automaattisesti samankaltaisuuksia mm. ajallisesti,alueellisesti tai tekotavallisesti. Esimerkiksi tekoäly voisi huomata sen, että tietyllä alueella on alkanut tapahtua paljon vahingontekoja spraymaalaamalla tai vaikkapa asuntomurtoja tietynlaisella tekotavalla. Tekoäly voisi sarjoittaa rikosilmoituksia yhteen. Hyvin usein tietty tekijä tai tekijäryhmä tekee teot samanlaisesti ja jopa alueellisesti samalla alueella. Tällä hetkellä analyysityö on paljolti ihmisen tekemää. Analyysityön avulla voitaisiin sijoittaa poliisipartioita paremmin partioimaan tiettyjä alueita.
Ammattikääntäjän työssä aika näppärä saattaisi olla sellainen tekoälysovellus, joka olisi osana tekstinkäsittelyohjelmaa (kuten nytkin jo on) ja jolle voisi vain lukea suoraan ääneen kääntämänsä lauseen ja joka myös toimisi, toisin kuin nämä nykyiset. En siis kaipaa kielenkääntäjänä sitä, että kone kääntäisi puolestani – sillä ammattikääntäjä haluaa itse pohtia erilaisia sopivia käännöksiä kullekin lauseelle – mutta sellainen luotettava puheentunnistusohjelma, joka siirtäisi suoraan sanelun teksinkäsittelyohjelmaan täsmälleen niin kuin sen olisi kirjoittanut siihen. Lisäksi sovellukselta voisi kysellä sekä erilaisia sanojen käännösvaihtoehtoja että etenkin synonyymeja vaikka jollakin ääneen lausutulla koodilla.
Muusikkona tulee opeteltua pop-kappaleita keikkoja varten ja kiinnostaisi kokeilla neuroverkkosovellusta, joka osaisi tehdä niin sanotun "komppilapun" kappaleesta automaattisesti. Komppilappuun merkitään ylös mm. tahdit ja soinnut ja miksei joitakin melodioitakin. Käsittääkseni joku on yrittänyt joitakin tällaisia sovelluksia jo tehdä, mutta en ole vielä kokeillut sellaista.
Äänen ja kielen tunnistamiseen ja prosessointiin liittyvät sovellukset helpottavat työtä lähes joka alalla ja merkitys myös esimerkiksi sosiaalialalla on suuri, etenkin lastensuojelussa, jossa kirjaamiset pitäisi tehdä reaaliaikaisesti ja kentällä. Tekoälyä voisi hyödyntää myös erilaisten tilannearvioiden ja ennusteiden tekemisessä. Samoin prosessin simulointia voisi hyödyntää esimerkiksi oman työyhteisön toimintamallien kehittämisessä.
Työtehtävissäni käytetään ohjelmaa ennustamaan kauppojen myyntiä ja sitä kautta tuotekohtaista tilaustarvetta, jonka perusteella ohjelma automaattisesti lähettää tilaukset toimittajille. Myynnin ennustaminen tapahtuu kuitenkin ohjelmaan ennalta määritettyjen laskentamallien kautta ja välillä myyntiennusteet eivät osu kohdalleen. Täyteen 100 % ennustetarkkuuteen on toki vaikea päästä, sillä myynti riippuu yksittäisten ihmisten ostopäätöksistä. Kuitenkin ennustemalleja olisi mahdollista parantaa opettamalla laskenta-algoritmeja, sillä ohjelman on mahdollista saada palautetta ennusteilleen myöhemmin toteutuneista myynneistä. Jos tekoälyllä pystytään löytämään nykyistä paremmin myyntiin vaikuttavia tekijöitä (esim. sään vaikutus), voidaan laskentaa parantaa. Paremmalla laskennalla voidaan tehostaa toimitusketjuja ja saadaan oikea määrä tavaraa oikeaan paikkaan oikeaan aikaan. Erityisesti nopeasti pilaantuvien elintarvikkeiden osalta kyse on merkittävästä asiasta, kun hävikkiä ja turhaa tuotantoa voidaan pienentää.
Tekoälyn hyödyntäminen on keskeisessä roolissa nykyisessä työssäni. Työskentelen suomalaisessa mediatalossa ja tehtäviini kuuluu mm. verkkosivujen hallinnointi ja sosiaalisen median päivittäminen. Artikkelit valikoidaan verkkosivuille pääsääntöisesti niiden uutisarvon tai muun arvon perusteella. Tässä käytetään työstä itse opittua kokemusta. Artikkeleiden paikkaa ja ajallista pysymistä sivun taitossa seurataan tekoälyn tuottaman datan perusteella. Saan käyttööni reaaliaikaista dataa siitä, kuinka moni avaa artikkelin luettavaksi, miten kauan ja mihin asti artikkelia luetaan. Saan käyttööni myös dataa siitä, onko artikkelin suosio nousussa tai laskussa. Näitä tietoja yhdistelemällä voin tehdä päätöksiä siitä, pidänkö kyseistä juttua verkon taitossa tai onko sen paikkaa syytä muuttaa sivustolla. Käytössäni olevat sovellukset myös näyttävät, miten pitkään ja miten pitkälle eri laitteilla (älypuhelin, tabletti, pöytäkone) sivua selataan. Tämä auttaa suunnittelemaan sivun taittoa siten, että kohtiin, joissa lukija herkästi lopettaa sivun seuraamisen, on mahdollista taittaa kiinnostava artikkeli, joka saattaisi saada lukijan pysymään sivuilla.
Media-alalle on myös kehitetty sovelluksia, joissa robotti kirjoitaa artikkeleita. Robotin kirjoittamia uutisia on käytetty lähinnä urheilun ja vaalien tulosuutisoinneissa. Tämä hyödyttää toimittajakuntaa, sillä tulosuutisoinnin sijaan toimittajat voivat keskittyä ennemmän luovuutta vaativaan ja haasteellisempaan journalismiin.
Sosiaali- ja terveysala on yksi merkittävimmistä tämän hetken tekoälyn sovellutusaloista, mutta se on myös ala, jossa tekniikka ei voi koskaan täysin syrjäyttää ihmistä työntekijänä. Uskoisin, että vielä Suomessa melko harvinaiset ohjaus- ja seuranpitorobotit kuten “humanoidirobotti” Pepper- tai Paro-hylje tulevat yleistymään vanhustenhoidon parissa. Tietääkseni esimerkiksi Tampereen ikääntyneiden neuvontapisteestä, Kotitorista, löytyy jo hoivarobotti Zora. Itse haluaisin tulevaisuudessa päästä työpaikkaan, jossa hyödynnetään tekoälyn ja robotiikan mahdollisuuksia ikääntyneillä. Omalla työkentällä tekoälyä voisi hyödyntää muun muassa asiakkaan elintoimintojen mittaamisessa ennaltaehkäisevästi esimerkiksi puettavalla teknologialla, muistisairaiden asiakkaiden valvonnassa tai käytösoireiden seurannassa ja ennaltaehkäisyssä.
10.2 Hyödylliset ja mielenkiintoiset tekoälysovellukset
Luennon toisessa tehtävässä listattiin viisi hyödyllisintä/mielenkiintoisinta tekoälysovellysta. Vastauksissa esiintyi monia, sekä jo käytössä olevia että tulevaisuuden sovelluksia. Selvästi eniten mainintoja saivat itseajavat autot (lukuun on laskettu myös muutaman äänen saaneet lentokoneiden autopilotit) ja sairauksien diagnosointi tekoälyn avulla. Taulukkoon on kerätty 313 vastauksesta yli 10 mainintaa saaneet sovellukset.
| Tekoälysovellus | kpl |
|---|---|
| itseajavat autot (lentokoneiden autopilotit ja muut itseajavat ajoneuvot) | 104 |
| sairauksien diagnoosit | 102 |
| virtuaaliavustajat (esim. Siri, Alexa, Hound) | 61 |
| kääntäjät (esim. Google translate) | 58 |
| kasvojen tunnistus (kamerat, puhelimet, valvonta, maksaminen) | 47 |
| tiedonhaku hakukoneilla (esim. Google) | 46 |
| karttasovellukset, reittisovellukset, ruuhkatiedot (esim. Google Maps) | 41 |
| kommunikointi, puhe tekstiksi, teksti puheeksi | 39 |
| pelien tekoäly | 37 |
| chatbotit | 33 |
| (asiakas)palvelurobotiikka | 33 |
| roskapostin suodatus | 31 |
| syövän tunnistus ja hoito | 31 |
| musiikin/elokuvien/videoiden suosittelu (esim. Spotify, Netflix, Youtube) | 31 |
| kirurgia, leikkausrobotit | 30 |
| tekoäly tehtaissa (robotiikka, varastointi, logistiikka, laaduntarkkailu) | 30 |
| kohdennettu mainonta | 29 |
| uraohjaus, rekrytointi (esim. Mosaic) | 29 |
| sijoitusneuvonta, talousavustajat, lainananto, luottoarviot | 27 |
| tietoturvallisuuden sovellukset, kyberturvallisuus | 26 |
| lääkkeet (annostus, monilääkitys, lääkkeiden kehitys) | 25 |
| hoitorobotit ja sosiaaliset robotit | 23 |
| virtuaalilääkärit | 22 |
| oppimista tukevat sovellukset (esim. Luka-pöllö) | 22 |
| MOOC-verkkokurssit, tekoälyopettajat, oppimisympäristöt | 18 |
| tutkimus (esim. artikkeleiden/luentojen tiivistäminen) | 18 |
| virtuaalinen kunto-/ravintovalmennus | 15 |
| terveyden seuranta, potilaita monitoroivat laitteet | 14 |
| rekisterintunnistus esim. parkkihalleissa | 14 |
| hintavertailut (esim. Momondo) | 14 |
| terveydenhoitoon liittyvät tekoälyavustajat | 13 |
| älytalot | 12 |
| taidetta kuvista, soitetusta musiikista nuotittaminen, sävellys, näytelmät | 12 |
| uutisointi | 11 |
11. Tekoälyn toimijat Suomessa
(Pekka Neittaanmäki, Anniina Ojalainen)
Suomi on digitalisaation ja monipuolisten tietoliikenneyhteyksien kärkimaa. Suomen kansallinen tavoite on olla tekoälyn soveltamisessa maailman johtavien maiden kärkiryhmässä. Eri ministeriöt, CSC, Sitra, VTT, Suomen Akatemia, Business Finland ja useat säätiöt ovat edistäneet tekoälyn ja siihen liittyvien teknologioiden, kuten automaation, robotiikan, IoT-laitteiden, lohkoketjujen, 5G:n, virtuaalitodellisuuden, Big Datan ja kyberturvallisuuden kehittämistä ja soveltamista. Yliopistojen yhteistyö sekä yhteistyö yritysten ja julkisten organisaatioiden välillä on tiivistä. Digiparametrin mukaan vuonna 2017 Suomessa oli 348 liiketoiminnassaan tekoälyä hyödyntävää yritystä. Yritysten määrä nousee jatkuvasti tekoälyn käyttömahdollisuuksien kasvaessa ja kehittyessä yli alakohtaisten rajojen.
Seuraavaksi esitellään toimialoittain esimerkkejä Suomessa toimivista yrityksistä, jotka hyödyntävät toiminnoissaan tekoälyä tai ovat potentiaalisia tekoälyn hyödyntäjiä.
Biotalous:
Neste, Outotec, VAPO
Eläkerahastot ja vakuutukset:]
Elo, Fennia, Ilmarinen, Keva, Varma, Veritas Eläkevakuutus
Energiateollisuus:
Fingrid, Fortum, Gasum, Landis+Gyr, St1, Teboil, Vattenfall, Ydinvoimalaitokset, alueelliset energiayhtiöt
Finanssiala:
Aktia, Asiakastieto Group, Danske Bank, Mastercard, Nordea, OP ryhmä, Paytrail, Sampo, Sijoittaja Pro, S-Pankki, Sponda, Visa
ICT-ala:
3 Step It, Accountor Enterprise Solutions, Affecto, Aito, AJR Solutions, Artific Intelligence, Basware, Bittium, Bitwise, Boogie Software, CGI Suomi, Cinia, Comtiech, Culinar, Digia, Duranc, Eficode, Enfo, Fingersoft Oy, First Wave, Fonecta, Fujitsu Finland, Futurice, Gofore, Google, Herman IT, Hewlett-Packard, HP Finland, Husky Intelligence, IBM Finland, Innocode, Innofactor, Innofreaks, Istekki, Knowit, Kompozure, Lamia, Lekab, M-Files, Microsoft, Napa, Next Games, Nitor, Nordcloud Solutions, Nordomus, Opuscapita Group, Oracle, Protacon, Qvantel, Rakettitiede, RDVELHO, Reaktor Group, Reason, Remedy Entertainment, Round Zero, Rovio, Samlink, Sales Force, SAP Finland, Seriously Digital Entertainment, Siemens, Siili Solutions, Silo.AI, Small Giant Games, Sofor, Softability, Solinor, Solita Group, Starcut, Steamlane, Sulava, Suomen Mediatoimisto, Supercell, Symbio Finland, Teleste, The Curious AI Company, Tieto, Top Data Science, Tuntinetti, Unity Technologies Finland, Vainu, Vala Group, Valohai, Valossa Labs, Valuemotive, Visma Suomi, Wapice, Vincit
Kaupan ala:
Kesko, Lidl Suomi, S-ryhmä, Verkkokauppa.com
Konsultointi:
Accenture, Fourkind, Houston Inc, Invenco, KPMG, Louhia, Ramboll
Kuljetusala:
DHL Freight, Finavia, Finnair, Finnlines, Posti, Schenker, VR, Viking Line
Viestintä:
Alma Media, Helsingin Sanomat, Keskisuomalainen, MTV, Sanoma, Yleisradio
Rakentaminen ja kiinteistöhuolto:
Caverion, Lehto Group, NCC Suomi, Skanska, SRV yhtiöt, Tikkurila, Uponor, YIT
Teollisuusala:
ABB Group, Ahlstorm-Munksjö, Andritz, Aspo, Etteplan, Fiskars, Garcotec, Huhtamäki, John Deere Forestr, Kemira, KONE, Konecranes, Mercedes-Benz, Metso, Metsä Group, Meyer Turku, Moventas Gears, Nokia, Outokumpu, Patria, PKC Group, Ponsse, Raisio, Rolls Royce, Sandvik Mining and Construction, SSAB Stora Enso, UPM, VaisalaValmet, Wihuri, Wärtsilä
Terveysala: alueelliset sairaalat, Helsingin ja Uudenmaan sairaanhoitopiiri, Kela, Mehiläinen,
Oriola, Orion, Pihlajalinna, Planmeca, Tamro, Terveystalo
Tietoliikenne: DNA, Elisa, Huawei Technologies, Telia
Turvallisuusala: Airbus Defence and Space, F-Secure, Securitas, SSH Communications Security
Muut: Amer (urheiluvälineet), Atria (elintarvike), Houston Analytics Ltd (analytiikka),
Lingsoft (kielipalvelut), Marimekko (tekstiili- ja vaatetusala), Polar Electro (sykkeenmittaus), Valio (elintarviketeollisuus), Veikkaus (rahapelit)
12. Appendix A - Matematiikkaa
(Heli Tuominen)
Tässä luvussa käydään läpi neuroverkkojen matematiikkaa käsittelevässä luvussa ja yleisemminkin koneoppimisen taustalla olevaa matematiikkaa. Käsiteltäviä aiheita ovat funktioiden peruskäsitteet, osittaisderivaatat ja ääriarvojen etsiminen sekä lineaarialgebran perusteet. Asioiden esittelyn yhteydessä kerrataan niiden liitokset neuroverkkojen matemaattiseen teoriaan.
12.1 Analyysia
Tässä luvussa esitellään koneoppimisessa käytettävien menetelmien taustalla olevaa matemaattista analyysia ilman perinteistä "määritelmä, lause, todistus" -rakennetta. Aiheesta löytyy lisätietoa, esimerkkejä ja tehtäviä lukemattomista Calculus-nimisistä kirjoista.
Neuroverkkoja käsiteltäessä tarvitaan perustietoja funktioista ja niiden ominaisuuksista. Gradientteihin perustuvissa verkon opetusmenetelmissä kuten Luvussa käsiteltävässä vastavirta-algoritmissa tarvitaan esimerkiksi monen muuttujan funktioiden osittaisderivaattoja laskusääntöineen ja jonkin verran ääriarvoteoriaa.
12.1.1 Funktioista
Olkoot ja
joukkoja.
Funktio eli kuvaus joukosta
joukkoon
on sääntö, joka liittää jokaiseen joukon
alkioon
täsmälleen yhden joukon
alkion
.
Joukko on funktion
lähtöjoukokko (domain) ja joukko
maalijoukko (target set).
Alkiota sanotaan alkion
kuvaksi tai funktion
arvoksi pisteessä
.
Joukko on funktion
arvojoukko/kuvajoukko (range).
Jos , niin joukon
alkukuva (preimage) kuvauksessa
on joukko
Joukko on
-ulotteinen euklidinen avaruus. Sen alkiot ovat vektoreita
, missä
kaikilla
. Tutuimmat ulottuvuudet ovat
,
ja
;
on reaaliakseli,
taso ja
kolmiulotteinen avaruus.
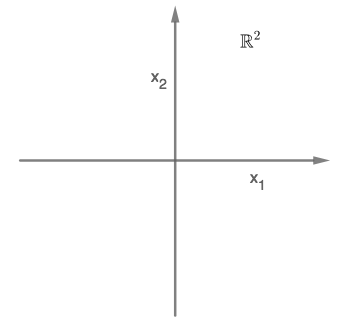
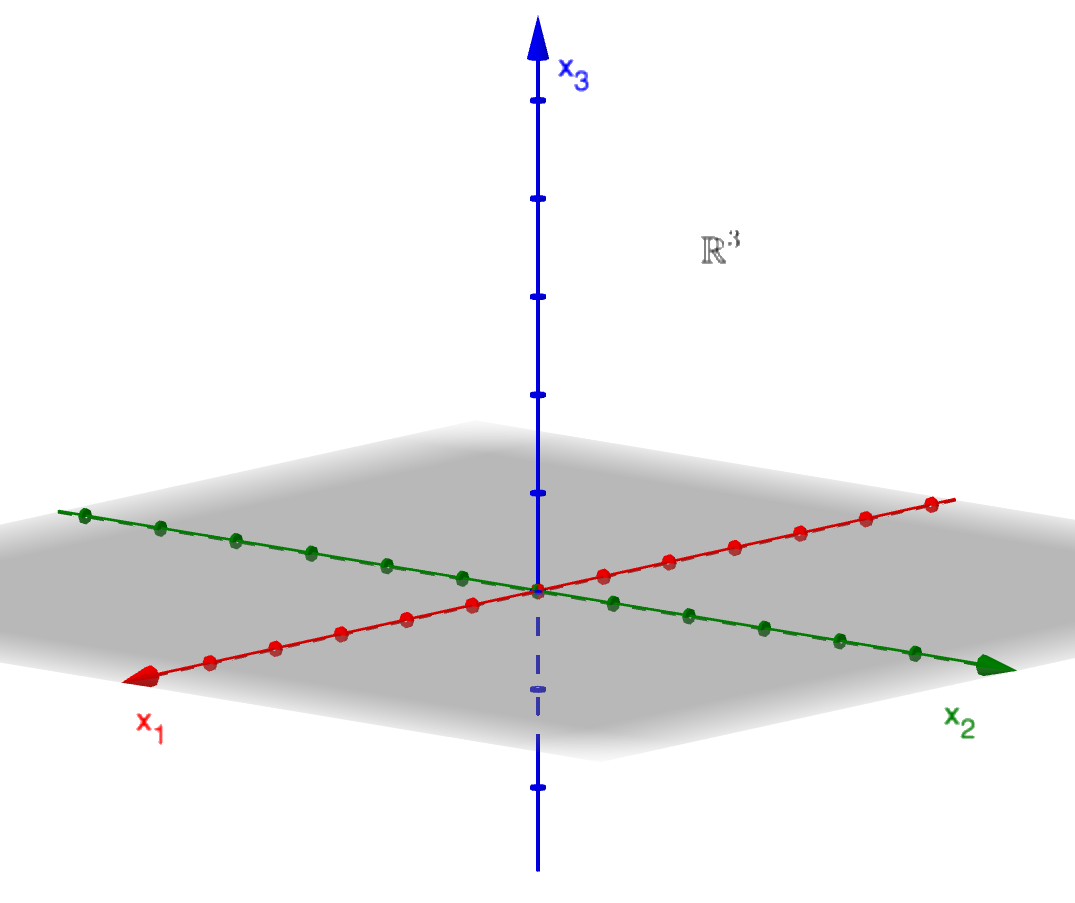
Euklidisen avaruuden väli (interval) on karteesinen tulo reaaliakselin väleistä ,
, missä väli
voi olla muotoa
(suljettu),
(avoin),
tai
Väli
on avoin/suljettu, jos kaikki välit
ovat avoimia/suljettuja. Jos
ja
kaikilla
, niin väli
on
.
Pisteiden ja
välistä etäisyyttä mitataan euklidisesta normista (norm)
saatavalla metriikalla (metric)
joka antaa luonnollisen etäisyyden; pisteiden välinen etäisyys on niiden välisen janan pituus.
Tässä liitteessä käsitellään pääasiassa funktioita , missä
on väli tai
,
kaikilla
, on äärellinen joukko.
Funktion kuvaaja eli graafi (graph) on joukko
ja reaalilukujen
alkukuvat
ovat funktion
tasa-arvojoukkoja (level set), joita tapauksessa
kutsutaan myös tasa-arvokäyriksi.
Yleisemmin, jos ja
ovat joukkoja ja
funktio, niin joukon
alkukuva kuvauksessa
on joukko
Huomaa, että jokaisella lähtöjoukon pisteellä on aina kuva mutta joukon alkukuva voi olla tyhjä.
Esimerkki
Olkoot ja
. Olkoon
funktio, jolle
Etsitään joukon
kuva ja maalijoukon alkioiden
ja
alkukuvat funktiolle
.
Joukon kuvajoukko on
.
Joukon alkioiden alkukuvat ovat
,
,
ja
.
Tasa-arvokäyriä käytetään funktion graafien piirtämiseen ja funktion kasvuvauhdin ja -suunnan tutkimiseen gradientin avulla. Topografisen kartan korkeuskäyrät ovat korkeusfunktion tasa-arvokäyriä. Tasa-arvokäyriä määritettäessä voi ensin piirtää käyrät kolmiulotteiseen tasoon. Nämä käyrät saadaan tasojen
ja funktion kuvaajan leikkauksina. Vastaavat tasa-arvokäyrät saadaan käyrien
projektioina
-tasoon.
Esimerkki
Olkoon ,
Funktion
kuvaaja on ylöspäin aukeava paraboloidi, jonka huippu on origossa. Kun
, niin tasa-arvokäyrät
ovat ympyröitä, joiden keskipiste on origo ja säde
. (Jos
, niin tasa-arvokäyrät ovat tyhjiä joukkoja sillä
kaikilla
.)
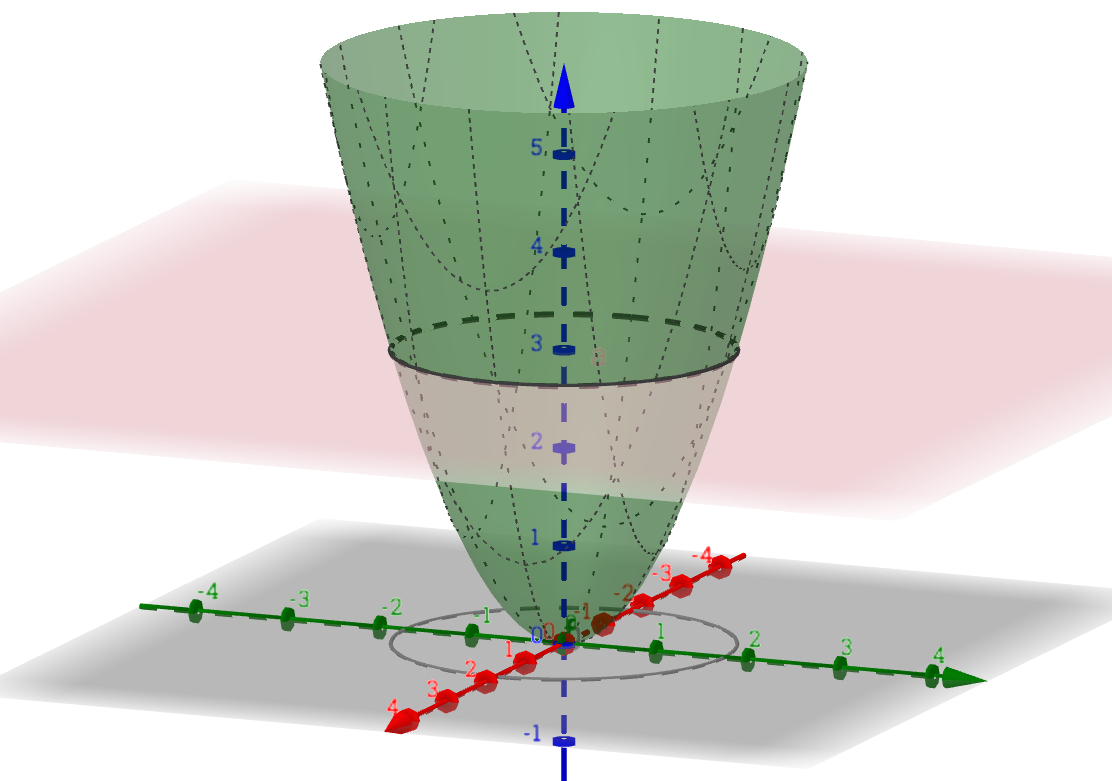
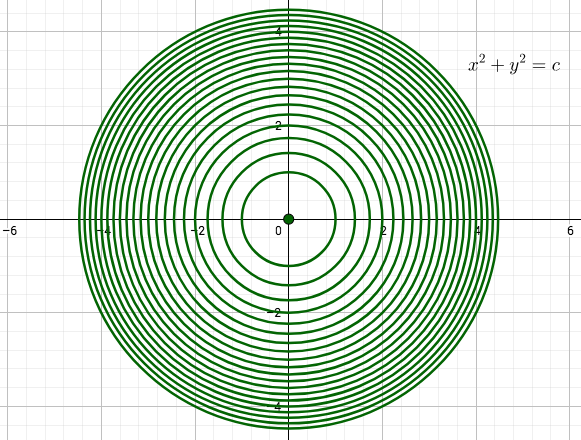
12.1.2 Harjoitustehtäviä
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Yhdistä funktioiden kuvaajat ja tasa-arvokäyrät.
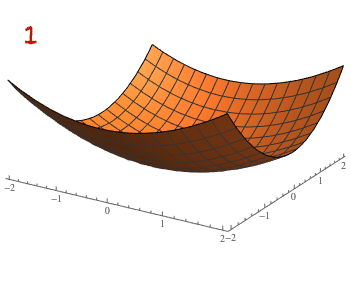
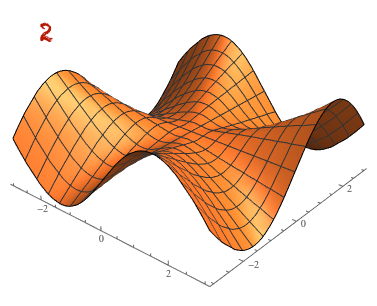
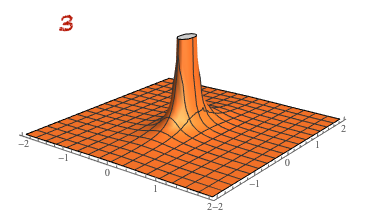
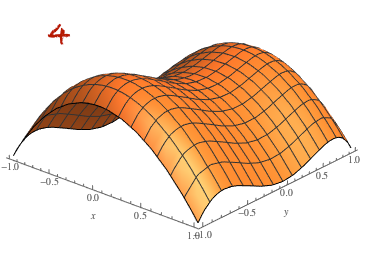
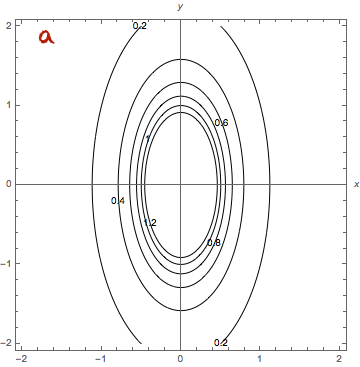
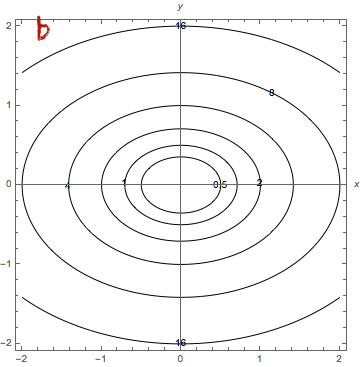
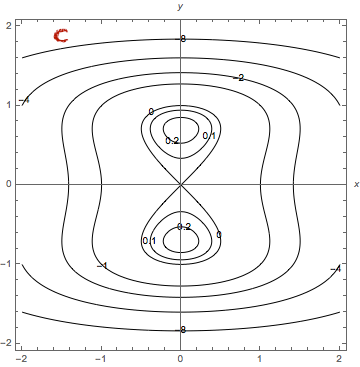
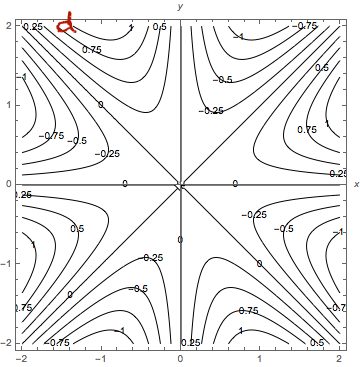
Affiini funktio
Neuroverkon piilo- ja ulostulokerroksen neuroneissa lasketaan edellisestä kerroksesta tulleiden syötteiden painotettu summa ja lisätään siihen vakiotermi. Jokaista neuronia vastaa siis affiini funktio, joka viedään aktivointifunktiolle.
Olkoon
-matriisi ja
. Funktio
,
missä
on matriisin
ja vektorin
tulo, on affiini funktio.
Affiini funktio voi kääntää, skaalata ja siirtää joukkoa. Se säilyttää joitakin geometrisia ominaisuuksia sillä se kuvaa suorat suoriksi, yhdensuuntaiset suorat yhdensuuntaisiksi ja säilyttää janojen osien suhteet. Kuvaus siis kuvaa pistejoukon uudelleen kääntäen, venyttäen, siirtäen joukon paikkaa tai skaalaten joukon kokoa.
Jos , niin affiini funktio on lineaarikuvaus. Jos
, niin
, joten kuvaus ei ole lineaarinen. Huomaa, että monissa lähteissä affiinia funktiota sanotaan virheellisesti lineaariseksi.
Esimerkki
Jos , niin affiinin funktion
,
kuvaaja on suora, jonka kulmakerroin on
ja joka leikkaa
-akselin pisteessä
.
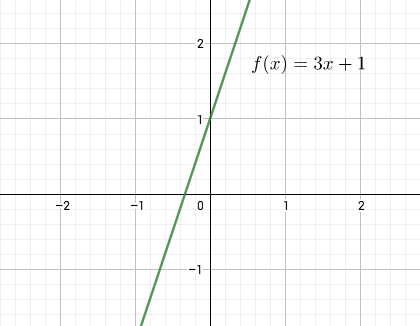
Kasvava ja vähenevä funktio
Olkoon väli ja olkoon
funktio. Jos
aina kun
, niin funktio
on kasvava (increasing). Jos
aina kun
, niin funktio
on vähenevä (decreasing).
Esimerkki
Funktio ,
on kasvava väleillä
ja
. Se on vähenevä välillä
.
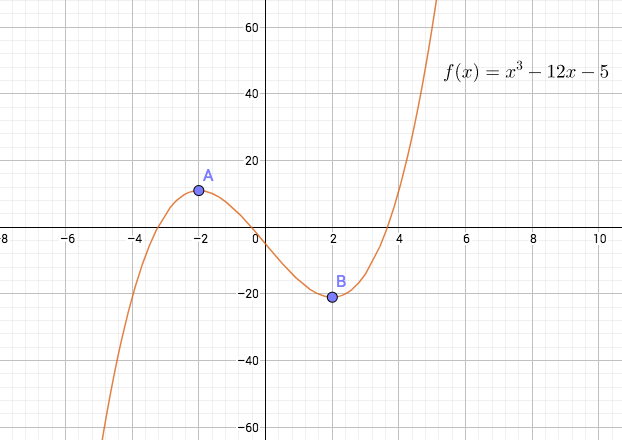
Yhdistetty funktio
Neuroverkkojen neuronin syöte seuraavalle kerrokselle saatiin laskemalla painotettu summa edellisen kerroksen syötteistä, lisäämällä siihen neuronin vakiotermi ja viemällä summa aktivointifunktiolle. Tässä on kyse yhdistetystä funktiosta: aktivointifunktion arvo lasketaan summafunktion antamassa pisteessä. Yleisesti yhdistetty funktio määritellään seuraavasti.
Olkoot ,
ja
joukkoja. Olkoot
ja
funktioita. Yhdistetty funktio (composite function) on funktio
,
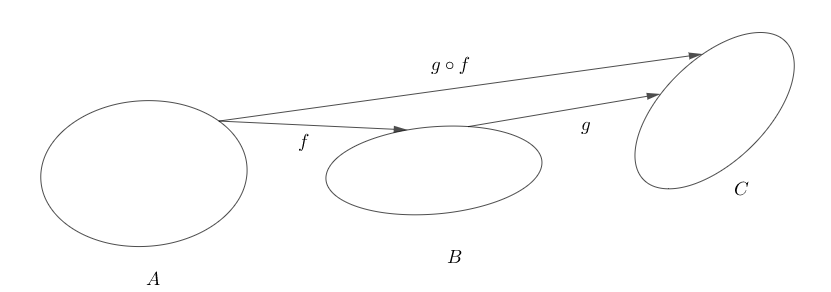
Esimerkki
Olkoot ,
ja
.
Näiden funktioiden yhdistetty funktio on ,
12.1.3 Derivaatta
Vastavirta-algoritmissa laskettavissa virhefunktion osittaisderivaatoissa tarvitaan aktivointifunktion derivaattaa ja derivoinnin ketjusääntöä. Verkon oppimisen tarkastelussa on hyvä olla käsitys siitä, mitä derivaatta kertoo funktiosta: lähellä nollaa oleva derivaatta kertoo, että funktion arvot muuttuvat hitaasti ja derivaatan suuri itseisarvo kertoo, että funktio muuttuu nopeasti.
Funktion derivaatta määritellään erotusosamäärien raja-arvona. Tarkastellaan, paljonko funktion arvo
muuttuu kun pistettä
siirretään vähän, pienen luvun
verran, joko oikealle tai vasemmalle. Muutosta tutkitaan keskimääräisenä muutoksena eli erotusosamääränä, jossa funktion arvojen erotus jaetaan siirtymällä
,
Geometrisesti tulkittuna erotusosamäärä kertoo pisteiden ja
kautta kulkevan suoran eli näiden pisteiden kautta kulkevan sekantin kulmakertoimen.
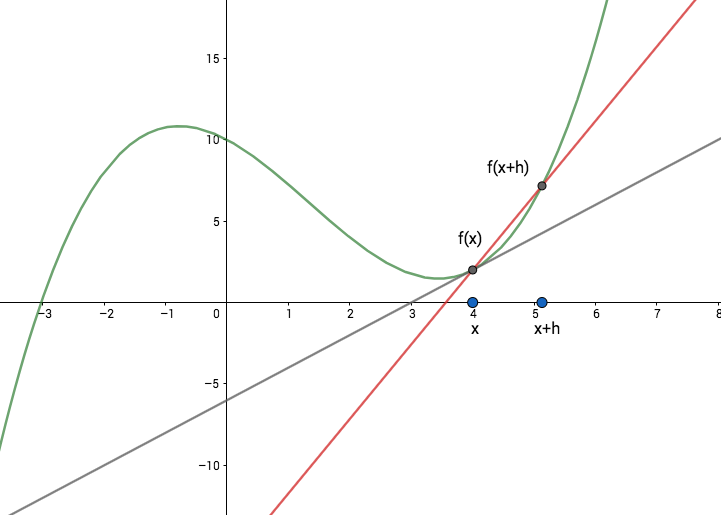
Jos tällä erotusosamäärällä on äärellinen raja-arvo kun muutos lähestyy nollaa, niin kyseinen raja-arvo on funktion
derivaatta (derivative)
pisteessä
,
Huomautus
Erotusosamäärässä siirtymä
voi olla myös negatiivinen.
Edellä määriteltiin derivaatta koko reaaliakselilla määritellyille funktioille. Jos
on määritelty avoimella välillä
, niin erotusosamäärää tutkittaessa otetaan mukaan pisteet
ja ne siirtymät, joille
.
Funktion
derivaatalle käytetään monesti derivointimuuttujan
sisältävää merkintää
tai
. Leibniziltä peräisin olevassa merkinnässä erotusosamäärää merkitään
ja derivaattaa
Tangenttitulkinta
Geometrisesti tulkittuna funktion derivoituvuus pisteessä kertoo, että funktion kuvaajalle voidaan piirtää pisteeseen
yksikäsitteinen tangentti, jolla on äärellinen kulmakerroin. Derivaatan arvo
on tangentin kulmakerroin ja tangentin yhtälö on
missä
.
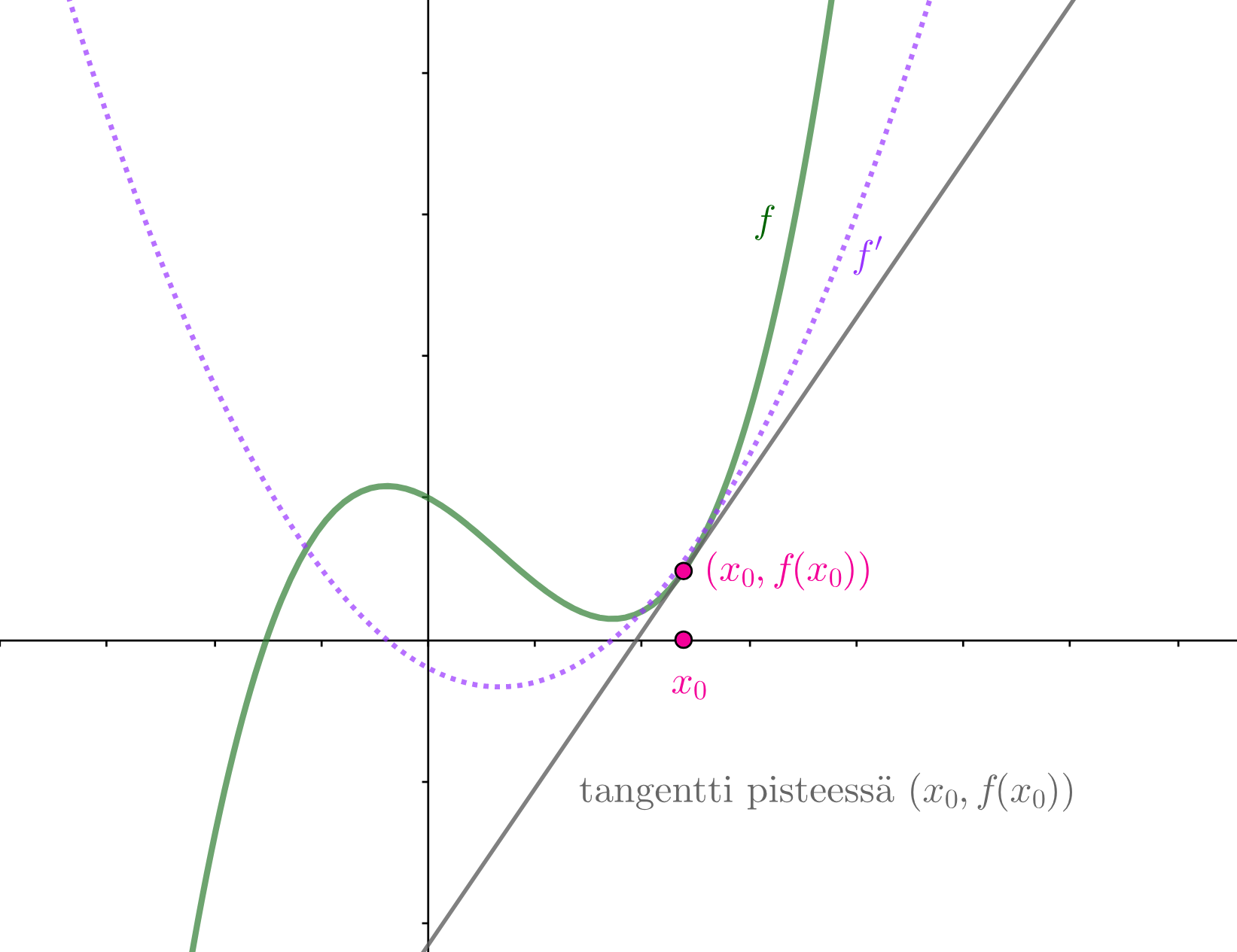
Pisteessä derivoituvalle funktiolle muutoksen
pienentyessä erotusosamääriä vastaavien sekanttien kulmakertoimien raja-arvo on siis tangentin kulmakerroin ja sekantit lähestyvät tangenttia. Mitä suurempi kulmakerroin on, sitä jyrkempi tangentti on. Positiivisilla kulmakertoimilla suora on nouseva ja negatiivisilla laskeva.
Tangenttitulkinnalla on helppo huomata, että pisteessä epäjatkuva funktio ei ole derivoituva. Sen kuvaajalle ei voi piirtää tangenttia epäjatkuvuuskohdassa. Jos tangentti on pystysuora, sillä ei ole äärellistä kulmakerrointa, eikä funktio ole derivoituva kyseisessä pisteessä.
Esimerkki
Tarkastellaan itseisarvofunktiota ,
Itseisarvofunktion kuvaajalla ei ole pisteessä
yksikäsitteistä tangenttia vaan niitä on äärettömän monta. Tangenttitulkinnan avulla voidaan päätellä, että
ei ole derivoituva pisteessä
. (Samaan tapaan voi yleisemminkin päätellä, että funktio, jonka kuvaajassa on kärki, ei ole derivoituva kärkeä vastaavassa pisteessä.)
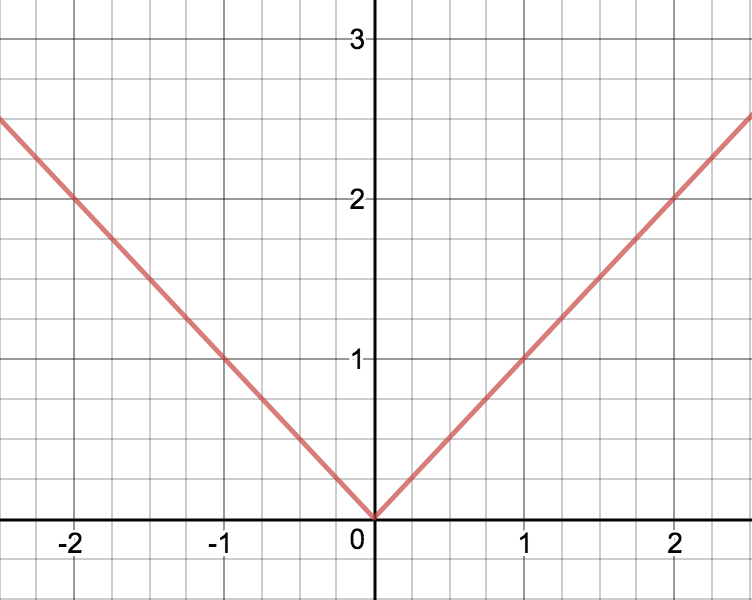
Erotusosamäärää tutkittaessa huomataan, että nollassa vasemman- ja oikeanpuoleiset raja-arvot ovat erisuuret eli raja-arvoa nollassa ei ole olemassa.
Kun , niin
ja kun
, niin
Siten
ei ole derivoituva nollassa.
Derivoituvien funktioiden ominaisuuksia
Derivoituvilla funktioilla on seuraavia hyviä ominaisuuksia, joita ei todisteta tässä.
Olkoot ja
derivoituvia funktioita ja
.
Funktiot
(summa),
(vakiolla kertominen),
(tulo) ja
(osamäärä) ovat derivoituvia ja
missä osamäärän derivaatta on olemassa niissä pisteissä, joissa
.
Jos
on derivoituva pisteessä
, niin se on jatkuva pisteessä
.
Joidenkin funktioiden derivaattoja
, kaikilla
,
,
,
ja
,
, kun
.
Leibnizin derivaattamerkintä on joskus kätevä yhdistetyn funktion derivaattojen yhteydessä. Merkitään ,
ja
. Funktioiden
ja
derivaatat Leibnizin merkinnöin ovat
ja
. Ketjusääntö tässä muodossa on
Esimerkki
Olkoon ,
Funktio
on yhdistetty funktio
kolmesta funktiosta
,
ja
. Ketjusääntöä kahteen kertaan käyttämällä saadaan
Derivaatta ja funktion käyttäytyminen
Derivaatan merkki ja suuruus kertovat paljon funktion käyttäytymisestä. Jos funktion derivaatta on positiivinen avoimella välillä, niin funktio on kasvava tällä välillä. Jos derivaatta on negatiivinen jollain avoimella välillä, niin funktio on vähenevä. Derivaatta on nolla jos tangentin kulmakerroin on nolla eli tangentti on -akselin suuntainen.
Jos funktio saavuttaa pisteessä suurimman tai pienimmän arvonsa, niin tässä pisteessä on
. Huomaa, että derivaatta voi olla nolla vaikka piste ei olisikaan funktion ääriarvopiste.
12.1.4 Harjoitustehtäviä
Olkoot
. Laske vakiofuntion
,
kaikilla
ja affinin funktion
,
kaikilla
, derivaatat erotusosamäärän avulla.
Todista joku derivaatan laskusääntö ominaisuuksia -kohdasta.
Reaalifunktion ääriarvoista
Funktion suurimman tai pienimmän arvon etsiminen on optimointitehtävä, jonka ratkaisemisessa hyödyllisiä työkaluja ovat derivaatta ja raja-arvot.
Olkoon väli ja olkoon
funktio. Olkoon
.
Jos
kaikilla
, niin
on funktion
maksimipiste ja
(globaali) maksimi eli suurin arvo.
Jos
kaikilla
, niin
on funktion
minimipiste ja
(globaali) minimi eli pienin arvo.
Suurinta ja pienintä arvoa kutsutaan yhteisellä nimellä globaalit ääriarvot. Globaalien ääriarvojen lisäksi voidaan tutkia funktion käyttäytymistä pisteen lähellä ja määritellä funktion
lokaalit eli paikalliset ääriarvot.
Jos on
, siten, että
kaikilla
, niin
on funktion
lokaali maksimipiste ja
lokaali maksimi eli suurin arvo.
Jos on
, siten, että
kaikilla
, niin
on funktion
lokaali minimipiste ja
lokaali minimi eli pienin arvo.
Huomaa, että funktiolla ei aina ole suurinta ja pienintä arvoa. Esimerkiksi funktio ,
, on rajoittamaton ja
ja
ja
kaikilla
. Siten funktiolla ei ole suurinta eikä pienintä arvoa. Suljetulla välillä määritellyille jatkuville funktioille ääriarvot ovat aina olemassa.
Ääriarvolause
Olkoon jatkuva funktio. Tällöin funktio
saavuttaa välillä
suurimman ja pienimmän arvonsa.
Funktion derivaatta, mikäli se on olemassa, on hyödyllinen työkalu ääriarvojen etsimisessä. Derivaatan määritelmän avulla on helppo näyttää, että jos funktiolla on lokaali ääriarvo pisteessä
ja
on derivoituva pisteessä
, niin
. Suljetulla välillä määritellyn funktion ääriarvoja etsittäessä riittää siis selvittää funktion arvo niissä pisteissä, joissa derivaatta on nolla, niissä pisteissä, joissa derivaattaa ei ole olemassa ja välin päätepisteissä. Derivaatan nollakohtia ja pisteitä, joissa derivaattaa ei ole olemassa, sanotaan kriittisiksi pisteiksi (critical points). Muulla kuin suljetulla välillä määritellylle funktiolle pitää tutkia funktion käyttäytymistä välin päätepisteissä esimerkiksi raja-arvojen avulla.
Esimerkki
Edellisen esimerkin funktion derivaatan nollakohdat antavat lokaalit ääriarvot. Nollakohdista
on lokaali maksimipiste ja
lokaali minimipiste. Koska
, niin funktiolla
ei ole globaaleja ääriarvoja.
Esimerkki
Derivaatta voi olla nolla, vaikka nollakohta ei olisikaan ääriarvopiste. Funktiolle on
ja funktio
ei ole derivoituva nollassa, joten
on molempien funktioiden kriittinen piste. Se ei kuitenkaan ole ääriarvopiste sillä
ja
kun
ja
ja
kun
. Funktioilla ei ole globaaleja ääriarvoja sillä
. Jos rajoitutaan suljetulle välille
, niin
on molempien funktioiden globaali minimipiste ja
globaali maksimipiste.
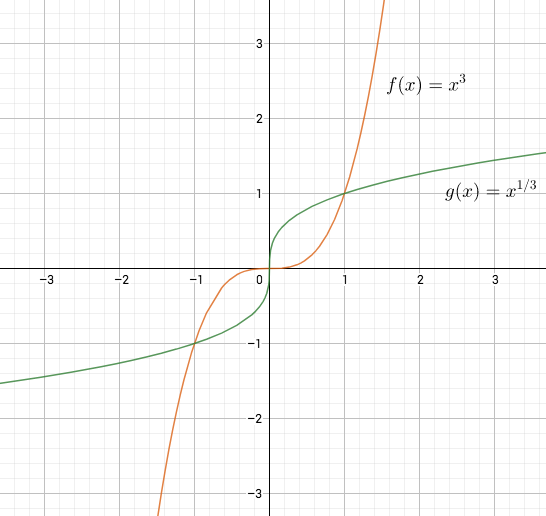
12.1.5 Harjoitustehtäviä
- Etsi funktion
,
ääriarvot. Etsi funktion
ääriarvot välillä
.
Lisätietoa derivaatoista
12.1.6 Osittaisderivaatat ja gradientti
Neuroverkkoa opetettaessa minimoidaan virhefunktiota, jonka arvo riippuu neuroverkon parametreista eli neuronien painoista ja vakiokertoimista. Virhefunktio on siis funktio useampiulotteisesta avaruudesta reaaliluvuille, , missä
on neuroverkon parametrien lukumäärä. Useammasta kuin yhdestä parametrista riippuvan funktion ääriarvojen etsiminen on yhden muuttujan funktion minimiointia/maksimointia haastavampi tehtävä. Ääriarvolausetta vastaava tulos on totta korkeampiulotteisessakin tilanteessa: kompaktissa (suljettu ja rajoitettu) joukossa jatkuva funktio saavuttaa suurimman ja pienimmän arvonsa.
Useamman muuttujan funktion osittaisderivaatta kertoo, miten funktio muuttuu yhden muuttujansa funktiona. Osittaisderivaatta saadaan pitämällä muita muuttujia vakiona ja laskemalla derivaatta tutkittavan muuttujan suhteen kuten tavallinen derivaatta kaavassa.
Osittaisderivaatta
Olkoon , olkoon
ja olkoon
. Jos erotusosamäärällä
on äärellinen raja-arvo, niin se on funktion
. osittaisderivaatta eli osittaisderivaatta muuttujan
suhteen pisteessä
,
Osittaisderivaattojen geometrinen tulkinta
Tarkastellaan osittaisderivaattojen geometrista tulkintaa kahden muuttujan funktiolle . Olkoon
. Pystysuoran tason
ja funktion kuvaajan muodostaman pinnan
leikkaus on käyrä
Tämä käyrä on funktion
kuvaaja tasossa
. Funktion
osittaisderivaatta muuttujan
suhteen pisteessä
on käyrän
tangentin kulmakerroin pisteessä
. Osittaisderivaatta
antaa siis funktion arvojen muutosvauhdin muuttujan
suhteen kun muuttuja
pidetään vakiona.
Esimerkki
Olkoon ,
. Funktion
osittaisderivaatat ovat
Kuva havainnollistaa osittaisderivaattaa
pisteessä
. Äskeisen tulkinnan taso
ja
ja tangentin kulmakerroin pisteessä
on
.
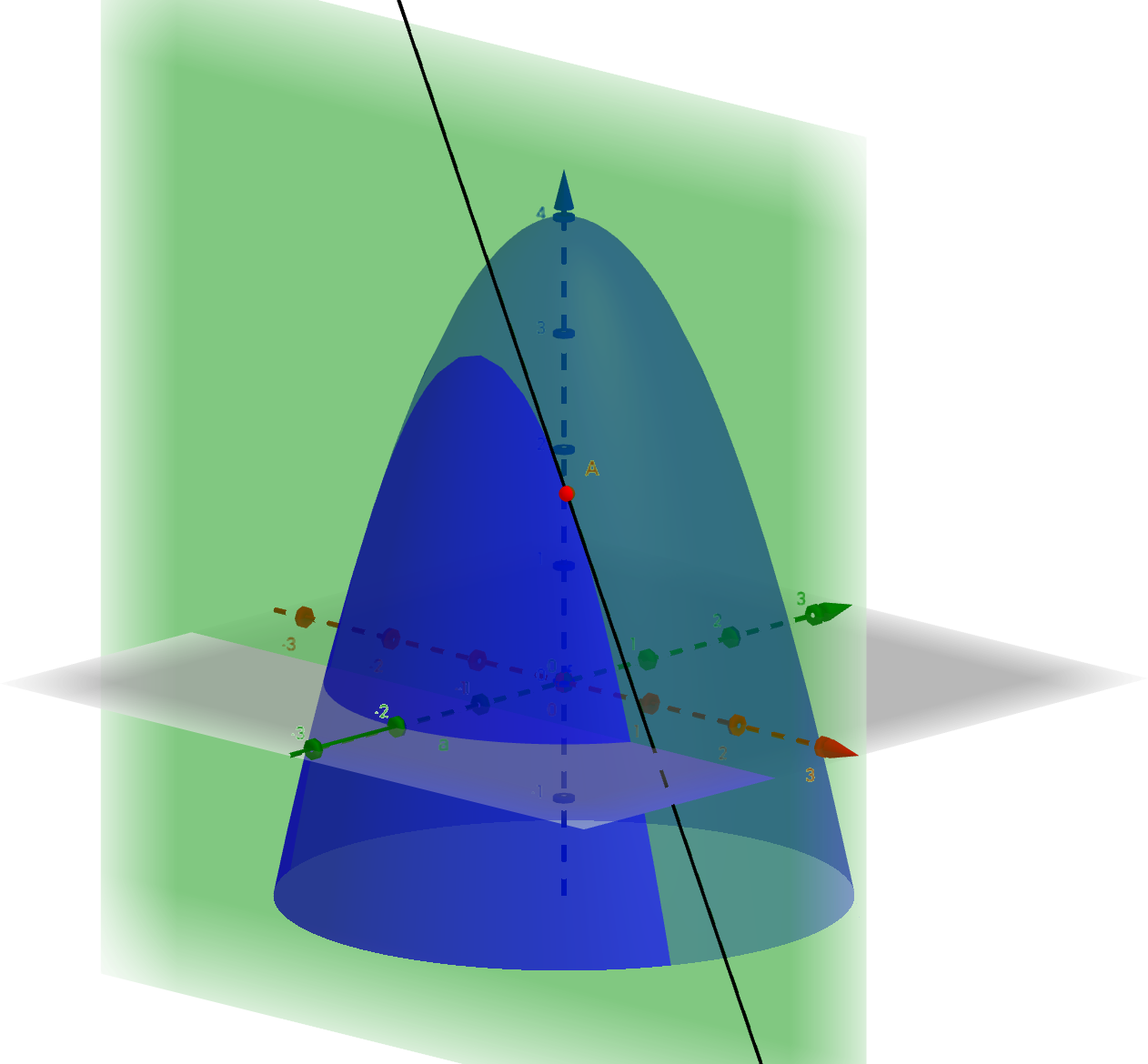
Yhden muuttujan funktiolle derivaatta on kuvaajan tangentin kulmakerroin. Tasossa määritellylle funktiolle osittaisderivaatat
ja
ovat kuvaajan tangenttitason kaltevuuskertoimia.
Tangenttitaso
Olkoon . Funktion
kuvaajan tangenttitaso pisteessä
saadaan yhtälöstä
Funktion kuvaajan tangenttitaso pisteessä
on taso, joka sisältää kaikki ne pisteen
kautta kulkevat suorat, jotka ovat tangentteja jollekin kuvaajalla sijaitsevalle pisteen
kautta kulkevalle käyrälle. Tangenttitaso sivuaa kuvaajaa pisteessä
ja kaikista pisteen
kautta kulkevista tasoista se on se, jolla on pisteessä
samat osittaisderivaatat kuin funktiolla
.
Esimerkki
Olkoon ,
Etsitään funktion
tangenttitaso pisteessä
(ja kerrataan trigonometrisia funktioita).
Nyt ,
joten
ja
Siten tangenttitaso pisteessä
saadaan yhtälöstä
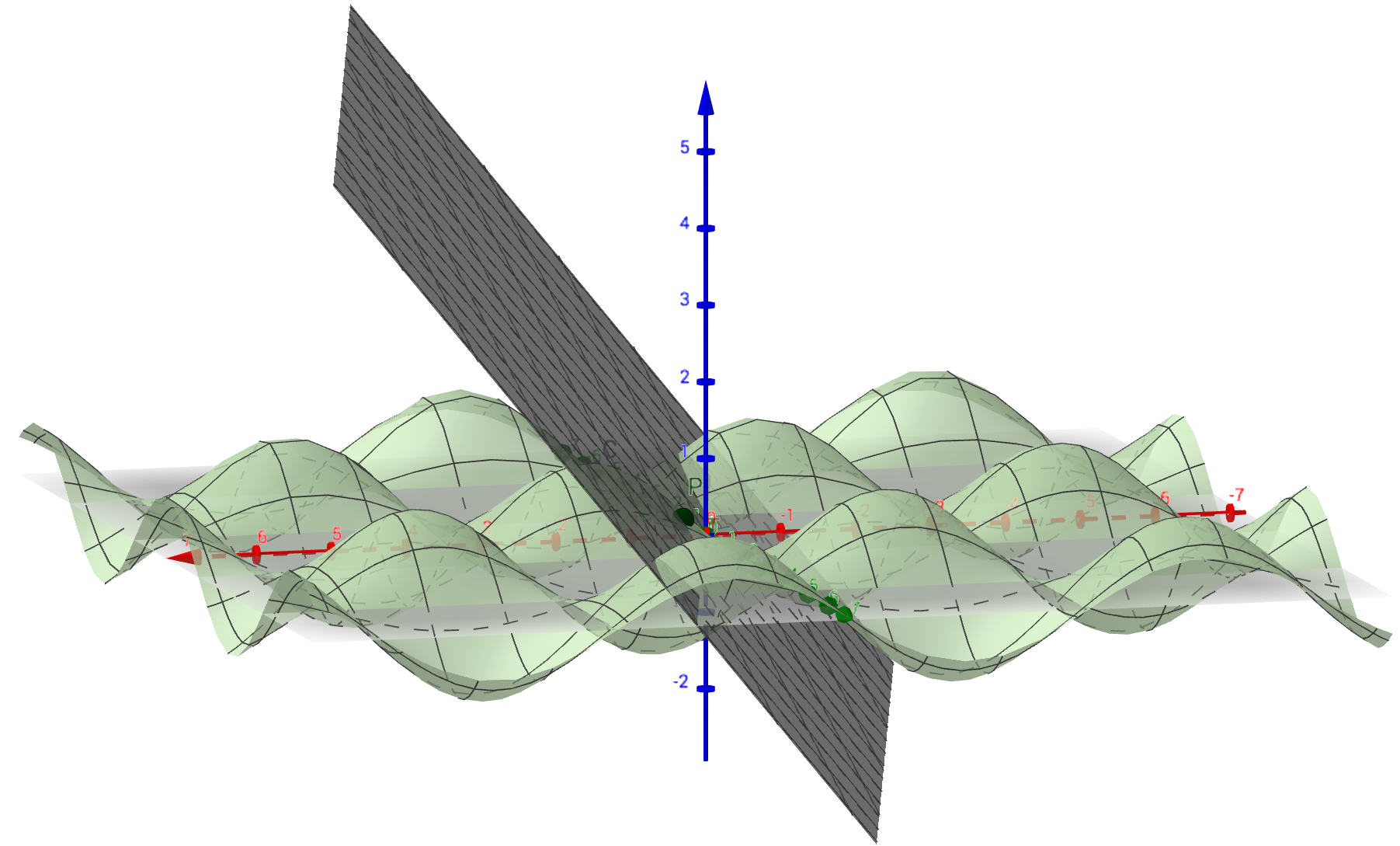
12.1.7 Harjoitustehtäviä
Olkoon
,
Laske funktion
osittaisderivaatat
ja
pisteessä
. Piirrä kuvia.
Olkoon
,
Laske funktion
osittaisderivaatat
ja
.
Olkoon
,
Määritä funktion
kuvaajan tangenttitaso pisteessä
.
Gradientti ja sen geometrinen tulkinta
Olkoon funktio, jolla on osittaisderivaatat kaikkien muuttujien
,
suhteen. Osittaisderivaatoista muodostettu vektori
on funktion
gradientti (gradient).
Funktion gradientti voidaan ajatella funktioksi
,
Tällaista funktiota voidaan havainnollistaa vektorikentällä, jossa jokaiseen tason pisteeseen piirretään vektori, jonka suunta ja pituus saadaan funktion arvosta kyseisessä pisteessä. Monesti pituus skaalataan tai ilmaistaan väreillä.
Esimerkki
Olkoon
,
. Funktion
gradientti on
Olkoon
,
. Funktion
gradientti on
Funktioiden ja
gradientteja voidaan havainnollistaa vektorikentillä.
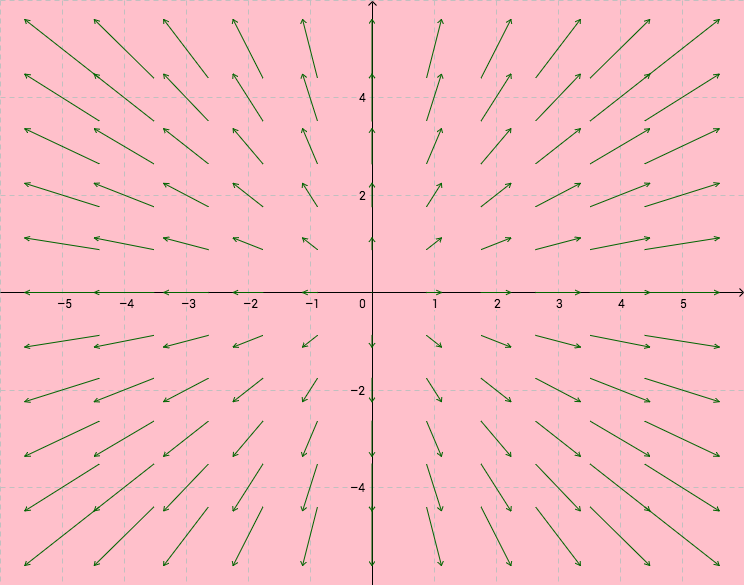
Osittaisderivaatat kertovat funktion kasvunopeuden koordinaattiakseleiden suuntiin ja funktion gradientti
pisteessä
kertoo suunnan, johon funktio
kasvaa nopeimmin. Gradientin pituus eli vektorin
normi
kertoo funktion kasvuvauhdin.
Se, että gradientti antaa nopeimman kasvun suunnan, todistetaan suuntaisderivaattojen avulla. (Ne määritellään samaan tapaan kuin osittaisderivaatat mutta erotusosamäärässä käytetään kantavektoreiden sijaan vektoria
, jonka suuntaan funktion kasvunopeus halutaan määrittää.)
Gradientin geometrisessa tulkinnassa käytetään vektorikentän lisäksi apuna tasa-arvokäyriä.
Esimerkki
Esimerkistä tutun funktion ,
tasa-arvokäyrät ja gradienttien
vektorikenttä piirrettynä samaan kuvaan.
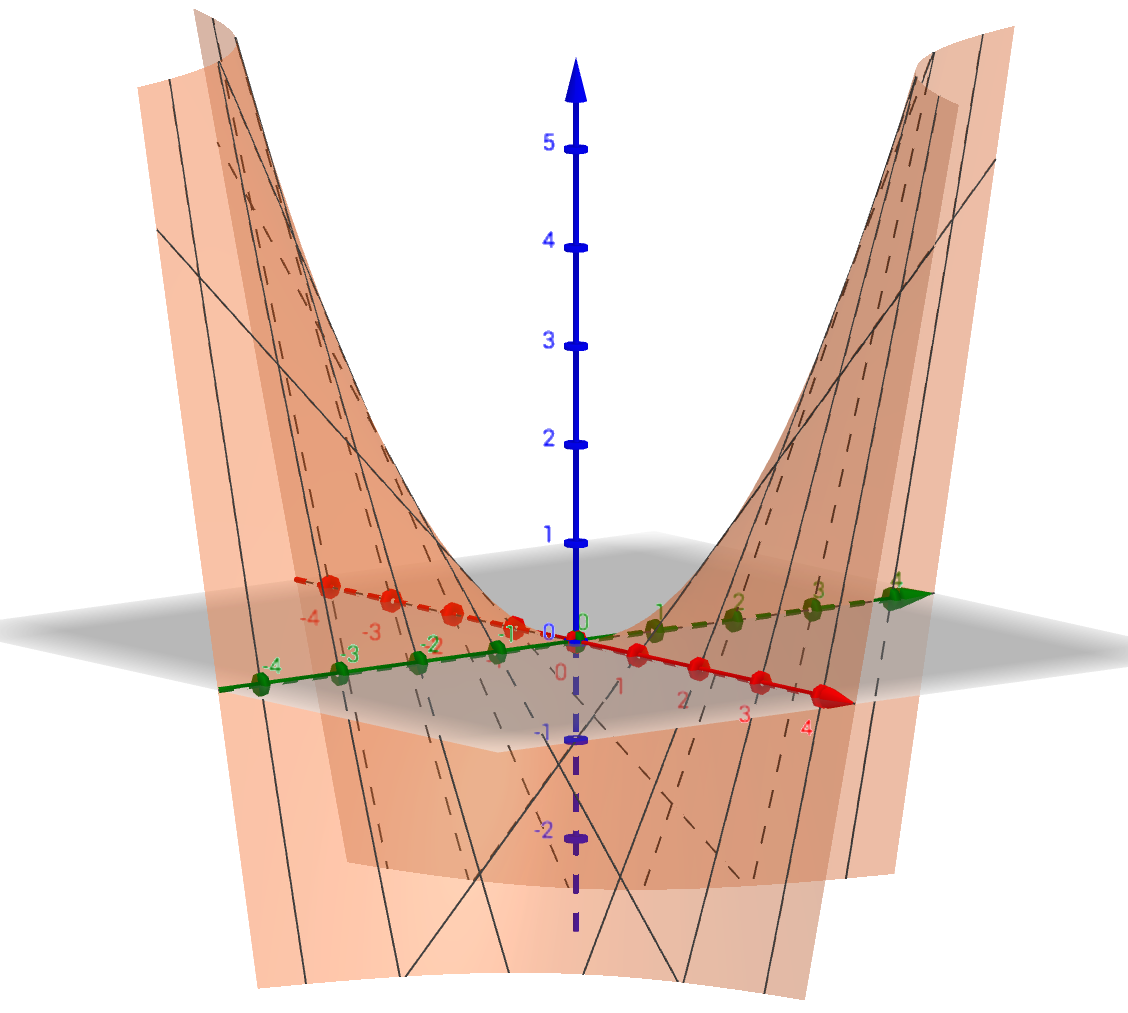
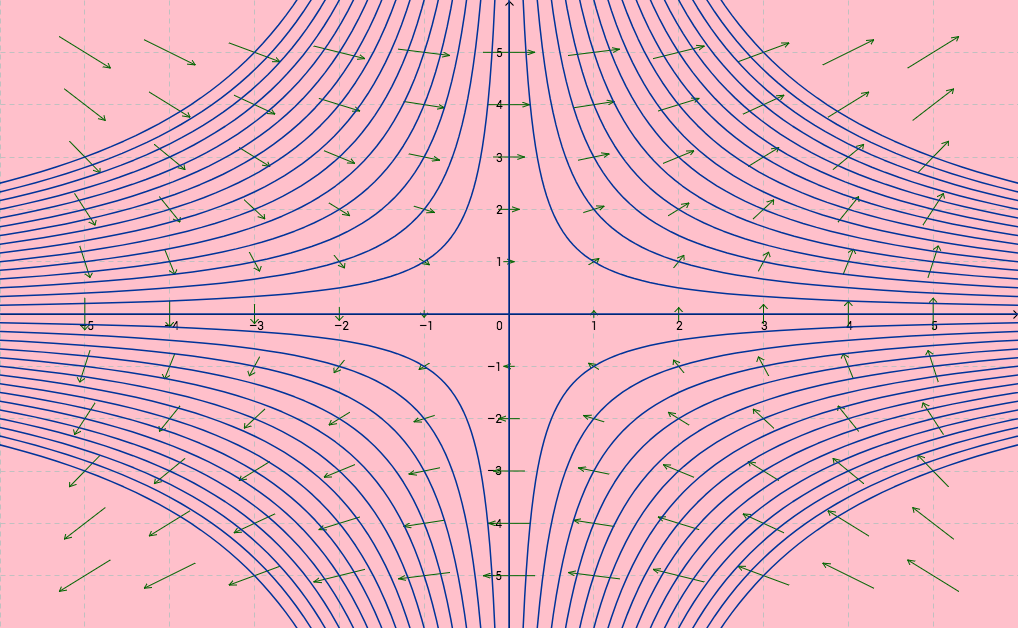
Esimerkin kuvassa funktion gradienttivektorit ovat kohtisuorassa tasa-arvokäyriä vastaan. Tämä ei ole sattumaa vaan gradienttivektorit ovat aina kohtisuorassa tasa-arvojoukkoja vastaan.
Funktioiden tapauksessa tätä ominaisuutta voi pohtia seuraavasti: olkoon
funktion
jokin tasa-arvokäyrä ja olkoon piste
tällä käyrällä. Halutaan, että funktion arvo kasvaa annetun määrän ja etsitään suuntaa, jossa tämä muutos saavutetaan siirtämällä pistettä
vähiten. Pienin siirto tulee siihen suuntaan, jossa isompia arvoja vastaavat tasa-arvokäyrät ovat tiheimmässä. Toisaalta gradientti osoittaa suurimman kasvunopeuden suuntaan. Pienessä mittakaavassa katsottuna eli pienellä arvon
lisäyksellä tasa-arvokäyrät ovat suoria ja kahden samansuuntaisen suoran välisen lyhimmän matkan antaa suora, joka on kohtisuorassa edellisiä suoria vastaan.
Ääriarvoista
Neuroverkkoa koulutettaessa halutaan minimoida monesta parametrista riippuvaa virhefunktiota. Yhden muuttujan funktioiden ääriarvojen etsiminen derivaatan nollakohtien avulla yleistyy useamman muuttujan funktion tilanteeseen niin, että mahdolliset ääriarvopisteet ovat ne pisteet, joissa kaikki osittaisderivaatat ovat nollia.
Olkoon väli.
Jos on
, siten, että
kaikilla
, joille
, niin
on funktion
lokaali maksimipiste ja
lokaali maksimi eli suurin arvo.
Jos on
, siten, että
kaikilla
, joille
, niin
on funktion
lokaali minimipiste ja
lokaali minimi eli pienin arvo.
Globaalit ääriarvot ja ääriarvopisteet määritellään kuten yhden muuttujan funktion tapauksessa.
Yhden muuttujan jatkuvan funktion ääriarvojen olemassaolotulos pätee myös yleisemmässä tapauksessa. (Tulos on totta yleisemmällekin määrittelyjoukolle kuin suljetuille väleille. Riittää, että joukko on kompakti eli suljettu ja rajoitettu.)
Ääriarvolause
Olkoon suljettu ja rajoitettu väli. Olkoon
jatkuva funktio. Tällöin funktio
saavuttaa välillä
suurimman ja pienimmän arvonsa.
Funktioiden kuvaajia katsottaessa on intuitiivisesti selvää, että funktion lokaaleissa ääriarvopisteissä tangettitaso on vaakasuorassa eli
-tason suuntainen. Tällaisten tasojen yhtälöt ovat muotoa
, joten tangenttitason yhtälön perusteella nähdään, että funktion osittaisderivaatat muuttujien
ja
suhteen ovat nollia ja että kuvaajan tangenttitason yhtälö pisteessä
on
.
Osittaisderivaattojen nolluus ääriarvopisteissä yleistyy myös useamman muuttujan funktioille. Derivaatan määritelmän ja yhden muuttujan funktion tulosten avulla on helppo näyttää, että jos funktiolla ,
, on lokaali ääriarvo pisteessä
ja funktiolla
on osittaisderivaatat pisteessä
, niin
kaikilla
eli
Suljetulla välillä määritellyn funktion ääriarvoja etsittäessä riittää siis selvittää funktion arvo niissä pisteissä, joissa gradientti on nolla, niissä pisteissä, joissa jotain osittaisderivaattaa ei ole olemassa ja välin reunapisteissä. Gradientin nollakohtia ja pisteitä, joissa jotain osittaisderivaattaa ei ole olemassa, sanotaan kriittisiksi pisteiksi (critical points). Muulla kuin suljetulla välillä määritellylle funktiolle pitää tutkia funktion käyttäytymistä välin reunapisteissä esimerkiksi raja-arvojen avulla.
Esimerkki
Olkoon ,
. Nyt
Yhtälöparin
ainoa ratkaisu on
, joten piste
on funktion
ainoa kriittinen piste ja funktion
kuvaajan tangenttitaso siinä pisteessä on
. Se, että
on funktion globaali maksimipiste selviää tutkimalla funktion
raja-arvoja kun
.
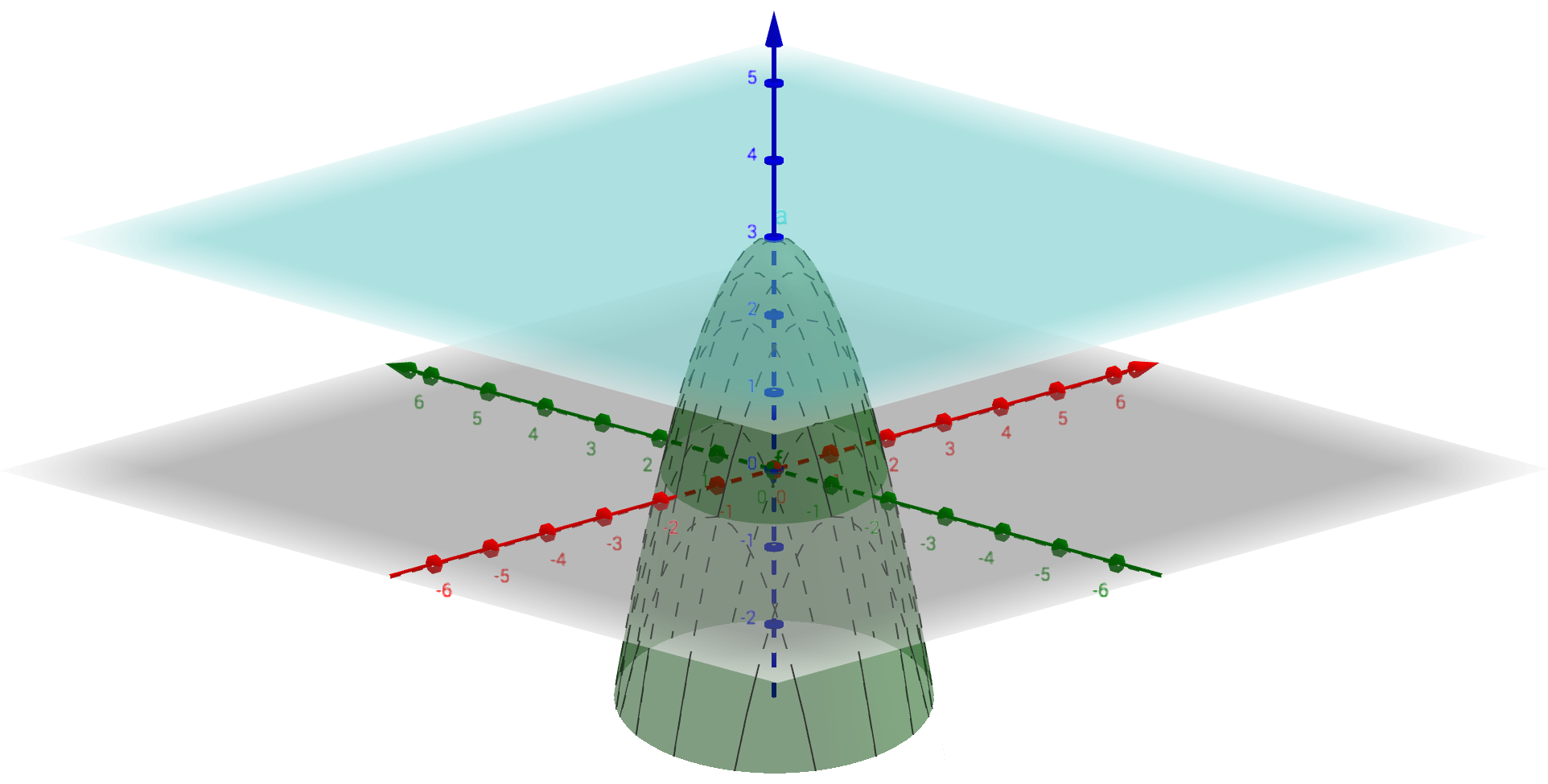
Esimerkki
Funktiolla ,
on useita maksimi- ja minimipisteitä. Sillä on globaali maksimi pisteessä
.
Esimerkki
Piste on funktioiden
,
satulapiste.
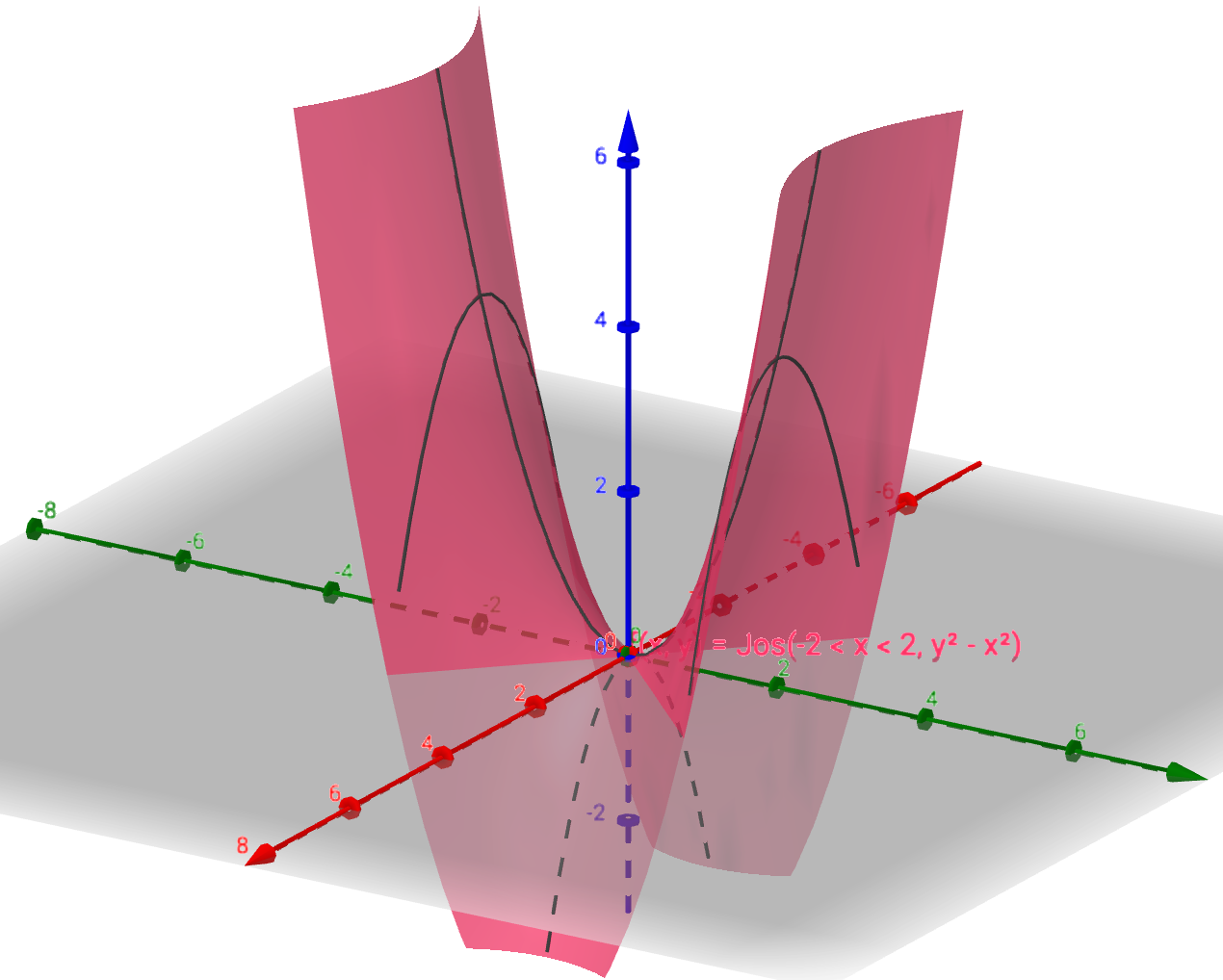
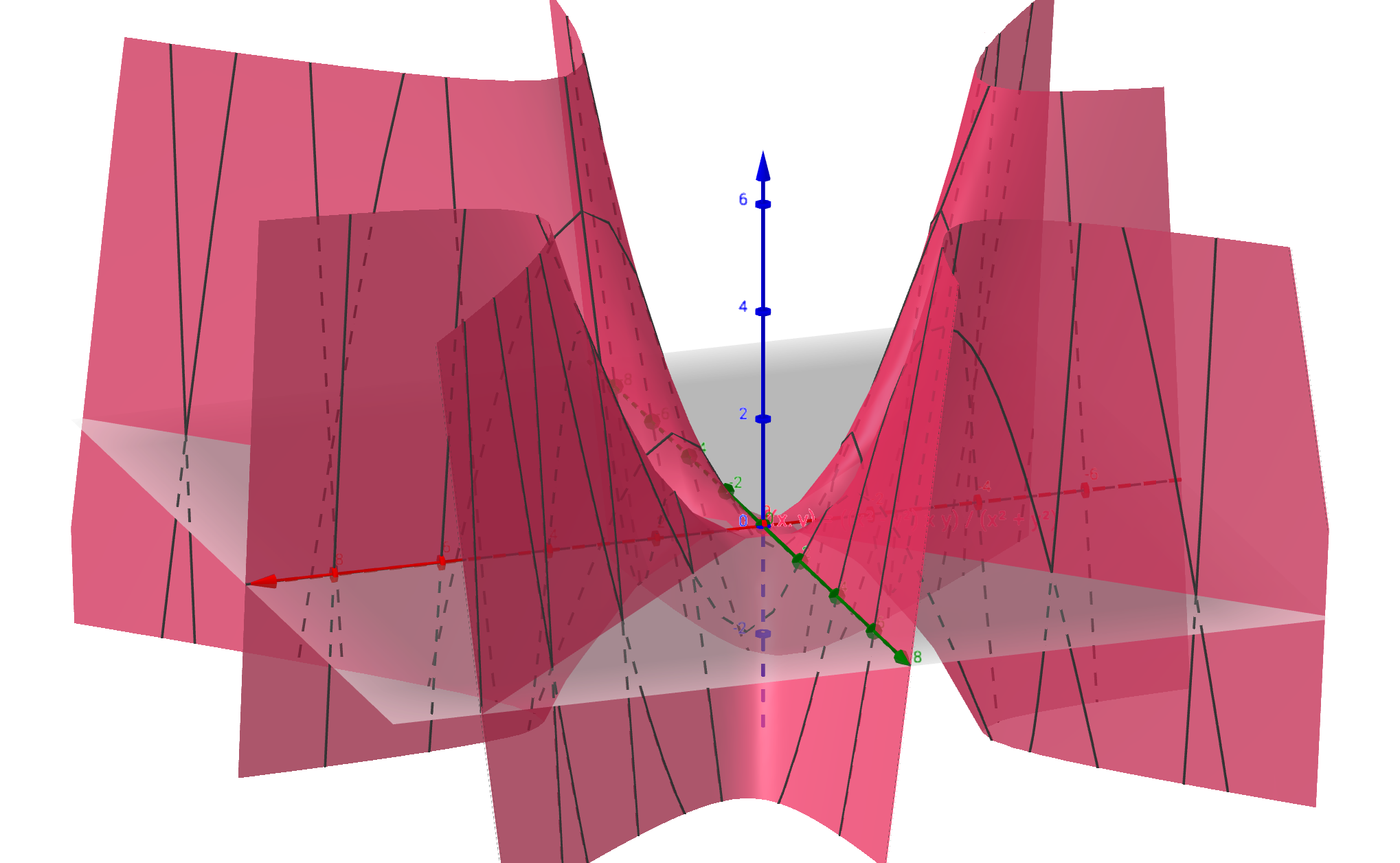
Osittaisderivaattojen ketjusääntö
Vastavirta-algoritmissa virhefunktion osittaisderivaattoja piilokerroksen painojen suhteen laskettaessa huomattiin, että muuttuja, jonka suhteen halutaan derivoida, riippuu neuroverkon edellisen kerroksen parametreista. Tämän takia tarvittiin osittaisderivaattojen ketjusääntöä.
Tarkastellaan ensin yksinkertaista tilannetta. Olkoon funktio, jonka parametrit
ja
ovat muuttujan
funktioita
. Funktioiden välistä yhteyttä voi havainnollistaa puumaisella kaaviolla. Funktion
osittaisderivaatan kaavan muuttujan
suhteen (tässä tapauksessa tavallisen derivaatan) voi muistaa siitä, että kuvassa edetään funktion
ja derivointimuuttujan
väli kaikkia reittejä pitkin, kerrotaan matkalla olevat osittaisderivaatat keskenään ja lasketaan eri reittien osittaisderivaattojen tulot yhteen.
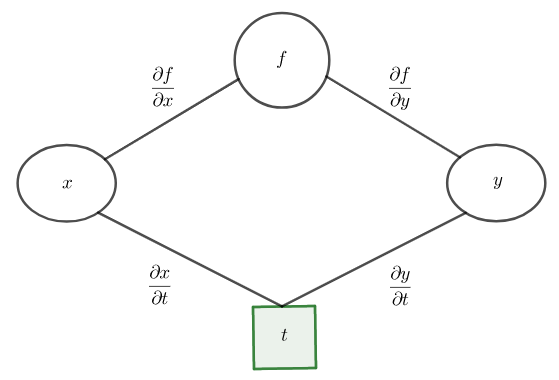
Jos funktiolla on jatkuvat osittaisderivaatat muuttujien
ja
suhteen ja funktiot
ja
ovat derivoituvia, niin funktion
derivaatta muuttujan
suhteen on
jonka Leibnizin merkinnöin kirjoitettu versio on
Esimerkki
Olkoot ,
ja
,
Lasketaan funktion
derivaatta muuttujan
suhteen.
Muuttujia on vain yksi ja osittaisderivaatta on funktion tavallinen derivaatta. Tässä tapauksessa derivaatta osattaisiin laskea ilman ketjusääntöäkin sijoittamalla funktioiden
ja
lausekkeet funktion
lausekkeeseen
joten
Osittaisderivaattojen ketjusääntöä käyttämällä saadaan
Laskettaessa osittaisderivaattaa muuttujan suhteen funktio
siis osittaisderivoidaan kaikkien muuttujiensa
suhteen ja muuttujat
muuttujan
suhteen. Nämä osittaisderivaatat kerrotaan keskenään ja lasketaan yhteen. Puukaavion lisäksi kaavan voi muistaa miettimällä, että muuttujan
muuttaminen vaikuttaa funktioiden
arvoihin ja siten muutos funktion
arvossa saadaan laskemalla nämä muutokset (osittaisderivaatat) yhteen.
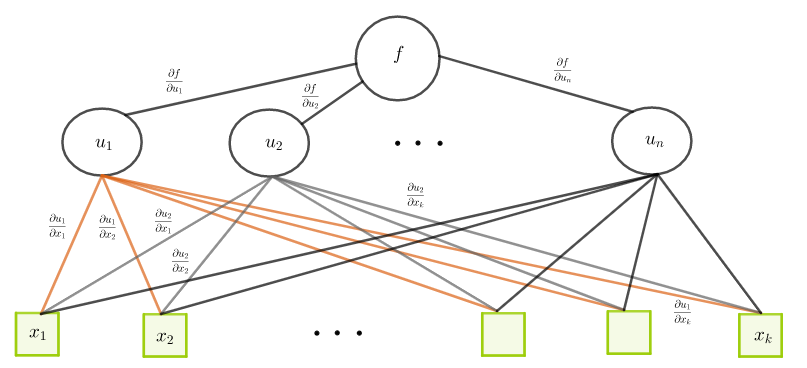
Esimerkki
Olkoot ,
Nyt
Funktion
osittaisderivaatat muuttujien
ja
suhteen ovat
ja
Halutut osittaisderivaatat voi laskea myös sijoittamalla funktioiden
ja
lausekkeet funktioon
ja osittaisderivoimalla muuttujien
ja
suhteen.
12.1.8 Harjoitustehtäviä
Olkoon
,
,
Laske funktion
derivaatta
sekä sijoittamalla funktioiden
ja
lausekkeet funktioon
että osittaisderivaattojen ketjusäännön avulla.
Olkoon
,
,
Laske funktion
osittaisderivaatat
ja
.
Lisätietoa osittaisderivaatoista
12.2 Lineaarialgebraa
Neuroverkon rakennetta esiteltäessä verkon parametreille ja niihin liittyville kaavoille annettiin myös vektori- ja matriisiesitykset. Ohjelmistokirjastoissa on paljon vektori- ja matriisilaskentaan sopivia paketteja, joiden avulla neuroverkon syötteiden tuloksen laskeminen ja parametreihin liittyvien laskujen tekeminen esimerkiksi virhefunktion minimoinnin yhteydessä on paljon nopeampaa kuin yksittäisten parametrien käsittely silmukoiden avulla.
Tässä luvussa käydään läpi vektoreihin ja matriiseihin liittyviä peruskäsitteitä, laskusääntöjä ja ominaisuuksia. Niihin liittyvää materiaalia löytyy Linear Algebra -nimisistä kirjoista. Motivointi lineaarialgebraan tehdään monesti lineaarisen yhtälöryhmän ratkaisemisen kautta.
12.2.1 Kahden lineaarisen yhtälön yhtälöryhmä
Tarkastellaan johdatuksena kahden muuttujan lineaarisista yhtälöistä muodostuvan yhtälöparin missä
kaikilla
, ratkaisemista. Paria
, joka toteuttaa yhtälöparin molemmat yhtälöt, sanotaan yhtälöparin ratkaisuksi (solution). Yhtälöparin ratkaisujen olemassaolo ja yksikäsitteisyys riippuu kertoimista
.
Esimerkki
Tutkitaan yhtälöpareja Yhtälöparista (a) saadaan laskemalla yhtälöt puolittain yhteen ja jakamalla kahdella että
. Sijoittamalla tämä toiseen yhtälöön saadaan
. Tästä seuraa, että
on yhtälöparin ainoa ratkaisu.
Yhtälöparin (b) toinen yhtälö on ensimmäinen yhtälö kerrottuna luvulla . Tämän yhtälön toteuttavat kaikki lukuparit
, joille
. Siten yhtälöparilla on äärettömän monta ratkaisua.
Kerrottaessa yhtälöparin (c) ensimmäinen yhtälö kahdella, saadaan yhtälöpari, jonka molempien yhtälöiden vasen puoli on . Koska oikeat puolet eivät ole samat, niin yhtälöparilla ei ole ratkaisua.
Yhtälöparien geometrinen tulkinta tehdään suorien avulla. Parien yhtälöt ovat suorien yhtälöitä tasossa. Ne pisteet, jotka ovat molemmilla suorilla, ovat yhtälöparin ratkaisuja. Kaksi suoraa ovat joko erisuuntaisia tai samansuuntaisia (eri tai sama kulmakerroin). Jos ne ovat erisuuntaisia, niin ne leikkaavat toisensa täsmälleen yhdessä pisteessä. Tapauksessa (a) yhtälöparin ratkaisu on yhtälöitä vastaavien suorien yksikäsitteinen leikkauspiste. Tapauksessa (b) suorat ovat samat eli kaikki suoran pisteet ovat leikkauspisteitä. Tapauksessa (c) suorat ovat samansuuntaisia eri suoria, joten ne eivät leikkaa toisiaan.
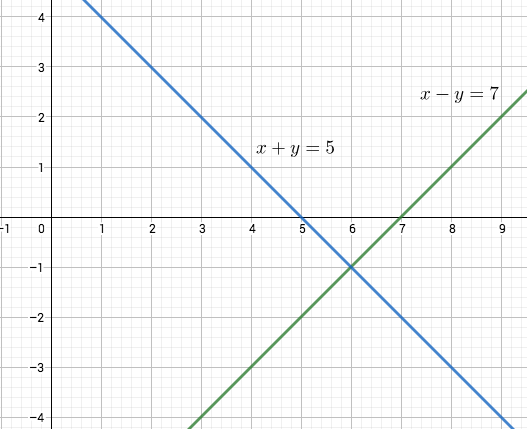
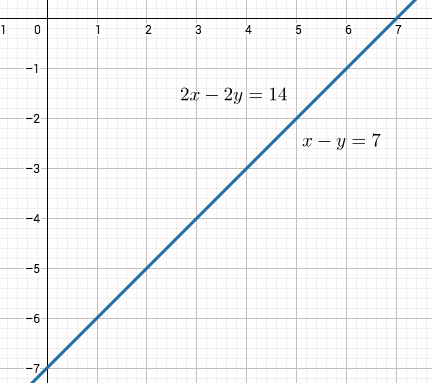
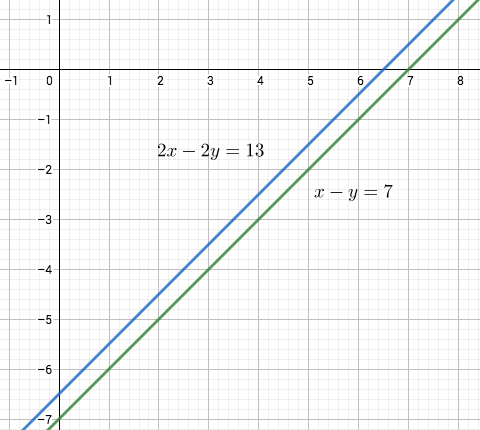
Kertomalla yhtälöparin ensimmäinen yhtälö puolittain luvulla ja toinen luvulla
ja vähentämällä yhtälöt toisistaan nähdään, että jos
, niin sijoittamalla luku
yhtälöpariin saadaan
ja ratkaisu
. Erotusta
sanotaan yhtälöparin determinantiksi (determinant).
Tämä liittyy yhtälöparin geometriseen tulkintaan sillä yhtälöparin ensimmäisen suoran kulmakerroin on ja toisen
. Yhtälöparilla on siis täsmälleen yksi ratkaisu jos ja vain jos sen determinantti ei ole nolla (erisuuret kulmakertoimet). Sillä ei ole ratkaisuja tai niitä on äärettömän monta jos ja vain jos determinantti on nolla (samat kulmakertoimet).
12.2.2 Yhtälöryhmä, jossa on  lineaarista yhtälöä ja
lineaarista yhtälöä ja  tuntematonta
tuntematonta
Yleisessä tapauksessa on yhtälöä ja
muuttujaa
missä
kaikilla
,
ja tavoitteena on löytää
luvun joukot
,
,
, jotka toteuttavat kaikki ryhmän
yhtälöä.
Tällaisen yhtälöryhmän ratkaisemisessa voidaan käyttää matriiseja. Tunnetussa Gauss-Jordan-menetelmässä yhtälöiden kertoimista muodostetaan kerroinmatriisi,
jota muunnetaan kerto-, yhteen- ja vähennyslaskuja sisältävillä rivioperaatioilla sellaiseen muotoon, josta ratkaisu (tai sen olemassaolemattomuus) saadaan helposti selville peräkkäisillä sijoituksilla.
12.2.3 Vektorit ja matriisit
Vektorit
Vektorit ja matriisit koostuvat järjestetyistä alkioista, jotka voivat olla mitä tahansa (reaalilukuja, vektoreita, funktioita). Keskitytään tässä tilanteeseen, jossa alkiot ovat reaalilukuja. Vektoreista tarvitaan sekä pysty- että vaakaversiot, jotta matriisien ja vektoreiden keskenäiset laskutoimitukset saadaan hoidettua muodollisesti oikein.
Olkoon . Olkoot
,
,
. Järjestetty joukko
on
-ulotteinen (rivi)vektori ((row) vector). Järjestetty joukko
on
-ulotteinen (sarake)vektori ((column) vector). Luvut
,
,
ovat vektorin komponentteja (component).
Vektoreiden samuus, vektorin kertominen vakiolla ja (samanulotteisten) vektoreiden yhteenlasku määritellään luonnollisella tavalla.
Olkoot ja
-vektoreita. Olkoon
.
jos ja vain jos
kaikilla
,
ja
Reaalilukujen laskusäännöistä seuraa, että vektoreiden yhteenlasku on vaihdannainen, liitännäinen ja distributiivinen (osittelulaki) eli jos ,
ja
ovat
-vektoreita ja
, niin
Jos
ja
, niin vektoreiden
ja
sisätulo/pistetulo on
Esimerkki
Olkoot ja
. Nyt
ja
Tehdään samat laskut Pythonin NumPy-kirjaston avulla:
Matriisit
Olkoot . Olkoot
kaikilla
ja
. Järjestetty taulukko
on
-matriisi, jossa on
riviä ja
saraketta.
Luvut ovat matrisin
alkioita/komponetteja, rivivektorit
,
, sen rivejä (row) ja sarakevektorit
, sen sarakkeita (column).
Jos , niin matriisi
on neliömatriisi (square matrix).
Huomaa, että rivivektori on
-matriisi ja
-komponentin sarakevektori on
-matriisi.
Matriisien yhtäsuuruus, vakiolla kertominen ja yhteenlasku määritellään samaan tapaan kuin vastaavat ominaisuudet vektoreille.
Olkoot ja
-matriiseja. Olkoon
.
- Matriisit
ja
ovat yhtäsuuret jos ja vain jos
kaikilla
ja
,
ja
.
Huomaa, että jos matriisit ja
ovat erikokoisia, niin niitä ei voi laskea yhteen.
Reaalilukujen ominaisuuksista ja matriisien summan ja vakiolla kertomisen määrittelystä seuraa, että matriisien laskutoimitukset käyttäytyvät seuraavasti.
Olkoot ,
ja
-matriiseja. Olkoon
. Olkoon
-matriisi, jonka kaikki alkiot ovat nollia. Tällöin
,
,
,
,
,
.
Esimerkki
Matriiseille on
Samat laskut Pythonin NumPy- ja SymPy-kirjastojen avulla:
12.2.4 Harjoitustehtäviä
Olkoot
ja
. Laske summa
ja sisätulo
.
Olkoot
,
ja
-vektoreita. Olkoon
-ulotteinen nollavektori. Olkoon
. Osoita, että
Olkoot
Laske matriisit
,
,
ja
.
Matriisitulo
Pikaisesti ajateltuna kahden matriisin tulo olisi matriisi, jossa tekijämatriisien saman indeksin alkiot kerrottaisiin keskenään samoin kuin ne lasketaan yhteen matriisien summassa. Tämän määritelmän antamalla tulolla ei ole riittävästi matriisien tulolta haluttavia ominaisuuksia. Sitä kuitenkin käytetään joissain yhteyksissä, esimerkiksi neuroverkon parametrien kaavoissa.
Olkoot ja
-matriiseja. Matriisien
ja
Hadamardin tulo/Schurin tulo on
Yleisemmin käytettävä matriisien tulo määritellään vektoreiden sisätulon avulla. Matriisien ja
tulon
. alkio on matriisin
. rivin ja matriisin
. sarakkeen vektoreiden sisätulo.
Olkoon
-matriisi ja olkoon
-matriisi. Matriisien
ja
tulo
on
-matriisi
, jolle
Matriisitulo on liitännäinen: jos on
- matriisi,
on
-matriisi ja
on
-matriisi, niin
ja tulo on
-matriisi. Osittelulaki (yhteen- ja kertolaskun suhteen oikean kokoisille) on myös voimassa eli
ja
Matriisitulo ei yleensä ole vaihdannainen eli
. Tulo ei ole edes määritelty paitsi jos sekä
että
ovat
-matriiseja jollain
.
Esimerkki
Olkoot ja
Koska on
-matriisi ja
on
-matriisi, niin tulo
on
-matriisi,
Sama lasku Pythonin NumPy-kirjaston avulla:
12.2.5 Harjoitustehtäviä
- Näytä, että matriisien Hadamard-tulo on vaihdannainen, liitännäinen ja distributiivinen: Jos
ja
ovat
-matriiseja, niin
- Olkoot
Laske tulot
ja
.
Erilaisia matriiseja
Olkoon
-matriisi.
on diagonaalimatriisi (diagonal matrix), jos
aina, kun
.
on yksikkömatriisi (identity matrix), jos se on diagonaalimatriisi ja
kaikilla
.
Matriisi on ylä(ala)kolmiomatriisi (upper(lower) diagonal matrix, jos kaikki komponentit diagonaalin ala(ylä)puolella ovat nollia.
Laskutoimitusten helpottamiseksi yleinen matriisi pyritään monesti esittämään kahden tai kolmen matriisin tulona, jossa tulon matriisit ovat diagonaali- tai kolmiomatriiseja.
Esimerkki
Olkoot Matriisit
ja
ovat diagonaalimatriiseja ja
on myös yksikkömatriisi. Matriisi
on yläkolmiomatriisi ja
on alakolmiomatriisi.
Samat matriisit Pythonin SymPy-kirjaston avulla:
Olkoot ja
-matriiseja. Jos
niin
on matriisin
käänteismatriisi (inverse of
), jota merkitään usein
. Tällöin sanotaan, että matriisi
on kääntyvä (invertible).
Käänteismatriisin käsin laskeminen on yleensä työlästä. Se onnistuu Gauss-Jordan menetelmällä, jossa kaavan oikean puolen vektori korvataan yksikkömatriisilla
. Jos
saadaan rivioperaatioilla muunnettua yksikkömatriisiksi, niin
on kääntyvä ja käänteismatriisi löytyy viivan oikealta puolelta. Käänteismatriisin etsinnässä riittää löytää
, jolle
Tällöin voidaan näyttää, että
.
Esimerkki
Olkoon Jos matriisilla
on käänteismatriisi
, niin
,
eli on oltava
Koska nyt myös
, niin
on itsensä käänteismatriisi.
Determinantti
Neliömatriisin kääntyvyyttä voidaan testata determinantin avulla. -matriisin
determinatti on reaaliluku
Esimerkki
Lasketaan matriisin käänteismatriisi kahdella tavalla.
Jos on matriisin
käänteismatriisi, niin on
Vastaavan yhtälöryhmä
hajoaa kahdeksi yhtälöryhmäksi
ja
jotka ratkaisemalla saadaan
,
,
,
.
Siten on .
Determinantin avulla käänteismatriisin laskeminen on helppoa. Koska , niin
Lasketaan käänteismatriisi ja determinantti myös Pythonin NumPy- ja SymPy-kirjastojen avulla.
Kun , niin determinantti määritellään alimatriisien determinanttien avulla.
-matriisille
on
Summassa on kolmen matriisin
alimatriisin determinantit: matriisi
saadaan poistamalla matriisista
. sarake ja
. rivi. Näiden matriisien determinantit kerrotaan matriisin
komponentilla
vaihtuvin etumerkein eli
Kun
, niin determinantti määritellään alimatriisien determinanttien avulla.
-matriisille
on
Yleiselle -matriisille
determinantti lasketaan samaan tapaan,
missä alimatriisi
saadaan poistamalla matriisista
. rivi ja
. sarake.
Determinantti voidaan laskea myös muun kuin ensimmäisen sarakkeen tai minkä tahansa rivin ja vastaavien alimatriisien avulla, Jos matriisin joku rivi tai sarake sisältää pelkkiä nollia, niin laskemalla determinantti tämän rivin tai sarakkeen avulla nähdään, että determinantti on nolla.
Jos on
ylä- tai alakolmiomatriisi, erityisesti siis jos se on diagonaalimatriisi, niin determinantti on diagonaalialkioiden tulo
Kääntyvyydellä ja determinantilla on yhteys yleisilläkin neliömatriiseilla: -matriisi
on kääntyvä jos ja vain jos
. Tällöin
Determinantin geometrinen tulkinta
Geometrisesti -matriisin
determinantti kertoo vektoreiden
ja
virittämän suunnikkaan pinta-alan ja vastaavasti
-matriisin
determinantti kertoo vektoreiden
,
ja
virittämän suuntaissärmiön tilavuuden.
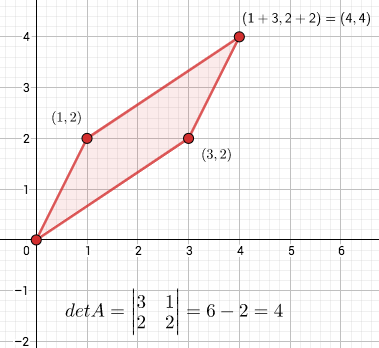
Esimerkki
Matriisin determinantti on
12.2.6 Harjoitustehtäviä
Todista kaava
.
Miksi käänteismatriisi määritellään vain neliömatriiseille?
Olkoon
kääntyvä neliömatriisi. Osoita, että käänteismatriisi on yksikäsitteinen. (Oleta, että matriisilla
oli kaksi käänteismatriisia
ja
ja näytä, että on
.)
Näytä, että kaava
antaa
-matriisin
käänteismatriisin.
Olkoon
. Onko
kääntyvä? Jos on, niin etsi
.
Olkoot
ja
. Laske matriisien
ja
determinantit.
Todista determinantin tulokaava
-matriiseille.
Symmetriset matriisit ja ortogonaaliset matriisit
Joissain tilanteissa tarvitaan matriisia, jossa alkuperäisen matriisin rivit vaihdetaan sarakkeiksi ja päinvastoin eli matriisi heijastetaan diagonaalinsa suhteen.
Olkoon
-matriisi. Matriisi
,
on matriisin
transpoosi (transpose).
Jos on neliömatriisi eli
ja
, niin
on symmetrinen (symmetric).
Esimerkki
Olkoot ja
.
Matriisin transpoosi on
ja
. Matriisi
on siis symmetrinen.
Lasketaan transpoosit myös Pythonin NumPy- ja SymPy-kirjastojen avulla.
Rivivektorin transpoosi on sarakevektori, jolla on samat komponentit. Vastaavasti sarakevektorin transpoosi on rivivektori, jolla on samat komponentit kuin alkuperäisellä sarakevektorilla. Vektoreiden transpooseja käytetään erityisesti siihen, että vektoreiden ja matriisien väliset laskutoimitukset saadaan muodollisesti oikeiksi.
Jos on
-matriisi ja
on
-matriisi, niin transpooseille pätee
Jos
, niin
Jos
, niin
Jos
on kääntyvä, niin myös
on kääntyvä ja
Symmetrisillä matriiseilla on hyödyllisiä ominaisuuksia. Siksi niitä pyritään käyttämään matriisihajotelmissa.
Olkoon
-matriisi. Matriisi
on ortogonaalinen (orthogonal), jos
on kääntyvä ja
Ortogonaaliselle matriisille siis . Matriisi
on ortogonaalinen jos ja vain jos sen sarakevektorit
,
, muodostavat ortonormaalin joukon.
Olkoot
-ulotteisia vektoreita. Joukko
on ortonormaali (orthonormal), jos
ja
(eli vektorit ovat kohtisuorassa toisiaan vastaan ja niiden pituus on
).
Koska vektoreiden ja
sisätulo on vektoreiden pituuden ja niiden välisen kulman
kosinin tulo,
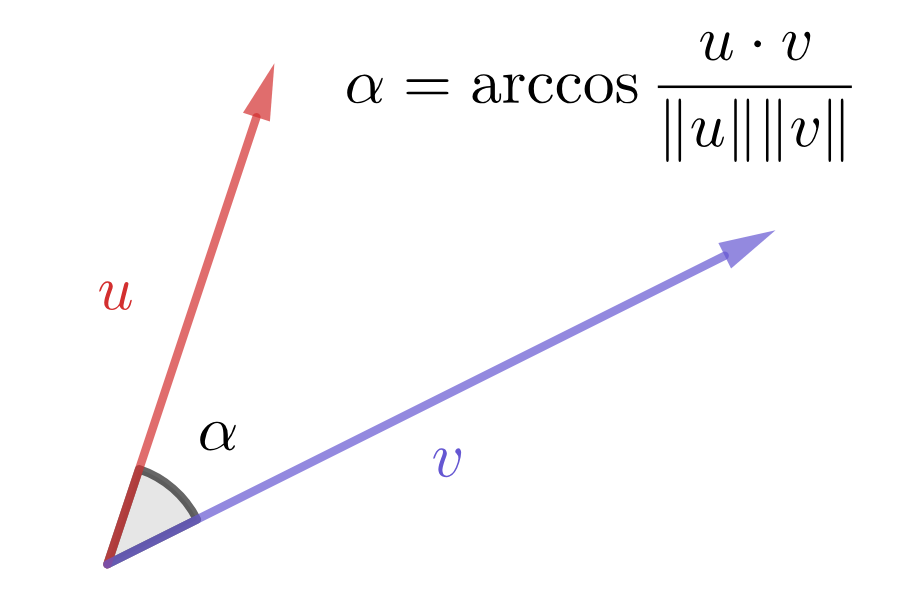
niin ortonormaalissa joukossa vektorit ovat kohtisuorassa toisiaan vastaan ja niiden pituus on .
12.2.7 Harjoitustehtäviä
Olkoot
Etsi matriisien
ja
ja tulon
transpoosit. Onko
tai
symmetrinen?
Olkoot
ja
. Miten sisätulo
voidaan esittää transpoosien avulla?
Olkoon
-matriisi. Osoita, että
on symmetrinen.
12.2.8 Matriisit ja lineaariset yhtälöryhmät
Jatketaan yhtälön ja
muuttujan yhtälöryhmän tarkastelua. Kun yhtälöiden kertoimista muodostetaan matriisi ja muuttujista ja yhtälöiden oikeista puolista vektorit,
niin yhtälöryhmä voidaan kirjoittaa muodossa
Jos yhtälöitä ja tuntemattomia on yhtä monta, kappaletta, niin
on neliömatriisi. Jos matriisi
on kääntyvä, niin yhtälöryhmän ratkaisu löydetään käänteismatriisin avulla. Käänteismatriisin ominaisuuksien perusteella on
eli yhtälöryhmällä
on yksikäsitteinen ratkaisu jos ja vain jos matriisi
on kääntyvä eli jos ja vain jos
.
Teoriassa yhtälöryhmän ratkaisu löydetään siis käänteismatriisin avulla mikäli se on olemassa. Käänteismatriisin laskeminen on kuitenkin raskasta, joten kääntämisen sijaan ratkaisussa käytetään erilaisia matriisihajotelmia.
Esimerkki
Yhtälöryhmää vastaava matriisiyhtälö on
, missä
Matriisi
on kääntyvä, joten
12.2.9 Harjoitustehtäviä
- Opiskele Gauss-Jordan menetelmä yhtälöryhmien ratkaisemiseksi.
12.2.10 Ominaisarvot ja ominaisvektorit
Olkoon
-matriisi. Luku
(reaali- tai kompleksiluku) on matriisin
ominaisarvo (eigenvalue), jos on
, joka ei ole nollavektori, jolle
Tällöin
on ominaisarvoa
vastaava ominaisvektori (eigenvector).
Ominaisarvon ja -vektorin määritelmistä nähdään, että on matriisin
ominaisarvo ja
vastaava ominaisvektori jos ja vain jos
. Tällä yhtälöllä on nollavektorista poikkeava ratkaisu
vain jos
Yhtälöä
sanotaan karakteristiseksi yhtälöksi (characteristic equation) ja sen vasenta puolta karakteristiseksi polynomiksi (characteristic polynomial).
Matriisin ominaisavot löydetään siis ratkaisemalla karakteristinen yhtälö. Algebran peruslause sanoo, että
. asteen polynomilla on
nollakohtaa kompleksilukujen joukossa. Siten karakteristisella polynomilla on
juurta ja matriisilla
ominaisarvoa, joista osa voi olla moninkertaisia.
Ominaisarvojen ja -vektoreiden etsiminen:
Muodosta karakteristinen yhtälö
.
Etsi ominaisarvot eli karakteristisen yhtälön juuret
.
Etsi ominaisarvoja
vastaavat ominaisvektorit ratkaisemalla yhtälöt
Jos matriisilla
on
eri ominaisarvoa
,
,
, niin vastaavat ominaisvektorit
,
,
ovat lineaarisesti riippumattomia (linearly independent).
Lineaarinen riippumattomuus tarkoittaa sitä, että jos on luvut ,
,
, joille
niin
kaikilla
. Tämä on yhtäpitävää sen kanssa, että vektoreista
muodostetun matriisin determinantti ei ole nolla.
12.2.11 Esimerkki
Olkoon Karakteristinen yhtälö on
Sen ratkaisut ovat
eli matriisin
ominaisarvot ovat
ja
.
Ominaisarvoa vastaava ominaisvektori toteuttaa yhtälön
eli
Ominaisvektoreita ovat siis vektorit
, joille
, esimerkiksi
.
Ominaisarvoa vastaava ominaisvektori toteuttaa yhtälön
eli
Ominaisvektoreita ovat siis vektorit
, joille
, esimerkiksi
.
Etsitään ominaisarvot ja -vektorit myös Pythonin SymPy-kirjaston avulla.
12.2.12 Harjoitustehtäviä
- Etsi matriisien
ja
ominaisarvot ja -vektorit.
LU-hajotelma
Matriisit pyritään monesti esittämään kahden tai kolmen matriisin tulona, jossa tulon matriisit ovat symmetrisiä tai diagonaali- tai kolmiomatriiseja. Esimerkiksi yhtälöryhmiä ratkaisevat ja käänteismatriiseja tai determinantteja laskevat algoritmit tehdään hajotelmien avulla.
LU-hajotelmassa neliömatriisi esitetään ala- ja yläkolmiomatriisien tulona missä alakolmiomatriisin
diagonaalialkiot ovat ykkösiä.
Jokaisella kääntyvällä matriisilla on LU-hajotelma mutta matriisille joudutaan joskus tekemään rivioperaatioita ennen hajotelmaa: Huomaa, että koska , niin jos
, niin joko
tai
. Koska kolmiomatriisin determinantti on diagonaalialkioden tulo, niin tästä seuraa, että joko
tai
. Siten olisi
. Kuitenkin kääntyvälle matriisille
on
mutta voi olla
.
Esimerkki
Etsitään matriisin LU-hajotelma eli matriisit
ja
, joille
Vastaava yhtälöryhmä on
ja sen ratkaisu
,
,
,
.
Siten Etsitään LU-hajotelma myös Pythonin SymPy-kirjaston avulla.
12.2.13 Harjoitustehtäviä
- Olkoon
. Etsi matriisin
-hajotelma.
Lisätietoa lineaarialgebrasta
Lineaarisen yhtälöryhmän ratkaiseminen (Approbatur 1 A, JYU)
Vectors, what even are they? | Essence of linear algebra, chapter 1, 3Blue1Brown
Linear combinations, span, and basis vectors | Essence of linear algebra, chapter 2, 3Blue1Brown
Linear transformations and matrices | Essence of linear algebra, chapter 3, 3Blue1Brown
Matrix multiplication as composition | Essence of linear algebra, chapter 4, 3Blue1Brown
The determinant | Essence of linear algebra, chapter 5, 3Blue1Brown
Inverse matrices, column space and null space | Essence of linear algebra, chapter 6, 3Blue1Brown
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10, 3Blue1Brown
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus, 3Blue1Brown
13. Appendix B - Sanasto
| activation function | aktivointifunktio |
| artificial intelligence (AI) | tekoäly |
| artificial neural network | (keinotekoinen) neuroverkko |
| augmented intelligence | laajennettu älykkyys |
| backpropagation | vastavirta(-algoritmi) |
| bias | kynnysarvo, vakiotermi |
| binary classification | luokittelu kahteen luokkaan |
| classification | luokittelu |
| cloud computing | pilvipalvelut, pilvilaskenta |
| clustering | klusterointi, ryhmittely |
| computer vision | tietokonenäkö |
| cost function | virhefunktio |
| cross-entropy | ristientropia |
| decision boundary | päätöspinta |
| decision tree | päätöspuu |
| gradient descent | gradienttimenetelmä |
| data mining | tiedonlouhinta |
| deep learning | syväoppiminen |
| feed forward network | eteenpäin kytketty verkko |
| hidden layer | piilokerros |
| image recognition | kuvantunnistus |
| input layer | syötekerros |
| learning rate | oppimisnopeus |
| logistic regression | logistinen regressio |
| loss function | tappiofunktio |
| machine learning | koneoppiminen |
| machine vision | konenäkö |
| mean squared error | keskineliösumma |
| multiclass classification | luokittelu moneen luokkaan |
| output layer | ulostulokerros |
| pattern recognition | hahmontunnistus |
| perceptron | perseptroni |
| regression | regressio |
| self-organizing map | itseorganisoituva kartta |
| speech recognition | puheentunnistus |
| superintelligence | supertekoäly |
| supervised learning | ohjattu oppiminen |
| support vector machine | tukivektorikone |
| test example | testiesimerkki |
| training example | opetusesimerkki |
| unsupervised learning | ohjaamaton oppiminen |
| validation example | vahvistusesimerkki |
| aktivointifunktio | activation function |
| eteenpäin kytketty verkko | feed forward network |
| gradienttimenetelmä | gradient descent |
| hahmontunnistus | pattern recognition |
| itseorganisoituva kartta | self-organizing map |
| keskineliösumma | mean squared error |
| klusterointi | clustering |
| konenäkö | machine vision |
| koneoppiminen | machine learning |
| kuvantunnistus | image recognition |
| laajennettu älykkyys | augmented intelligence |
| logistinen regressio | logistic regression |
| luokittelu | classification |
| luokittelu kahteen luokkaan | binary classification |
| luokittelu moneen luokkaan | multiclass classification |
| (keinotekoinen) neuroverkko | (artificial) neural network |
| ohjaamaton oppiminen | unsupervised learning |
| ohjattu oppiminen | supervised learning |
| opetusesimerkki | training example |
| oppimisnopeus | learning rate |
| perseptroni | perceptron |
| piilokerros | hidden layer |
| pilvipalvelut, pilvilaskenta | cloud computing |
| puheentunnistus | speech recognition |
| päätöspinta | decision boundary |
| päätöspuu | decision tree |
| regressio | regression |
| ristientropia | cross-entropy |
| ryhmittely | clustering |
| supertekoäly | superintelligence |
| syväoppiminen | deep learning |
| syötekerros | input layer |
| tappiofunktio | loss function |
| tekoäly | artificial intelligence (AI) |
| testiesimerkki | test example |
| tiedonlouhinta | data maining |
| tietokonenäkö | computer vision |
| tukivektorikone | support vector machine |
| ulostulokerros | output layer |
| vahvistusesimerkki | validation example |
| vakiotermi | bias |
| vastavirta(-algoritmi) | backpropagation (algorithm) |
| virhefunktio | cost function |
| assosiative | liitännäinen |
| bounded | rajoitettu |
| chain rule | ketjusääntö |
| characteristic polynomial | karakteristinen polynomi |
| characteristic equation | karakteristinen yhtälö |
| closed | suljettu |
| coefficient | kerroin |
| column | sarake |
| commutative | vaihdannainen |
| composite function | yhdistetty funktio |
| continuos | jatkuva |
| contour curve | korkeuskäyrä |
| curve | käyrä |
| decreasing | vähenevä |
| derivative | derivaatta |
| diagonal matrix | diagonaalimatriisi |
| differentiable | derivoituva, differentioituva |
| domain | lähtöjoukko |
| dot product, inner product, scalar product | sisätulo, pistetulo |
| eigenvalue | ominaisarvo |
| eigenvector | ominaisvektori |
| function | funktio |
| gradient | gradientti |
| graph | kuvaaja, graafi |
| identity matrix | yksikkömatriisi, identtinen matriisi |
| increasing | kasvava |
| interval | väli |
| inverse matrix | käänteismatriisi |
| invertible | kääntyvä |
| level curve, level set | tasa-arvokäyrä, tasa-arvojoukko |
| limit | raja-arvo |
| lower triangular matrix | alakolmiomatriisi |
| matrix | matriisi |
| partial derivative | osittaisderivaatta |
| plane | taso |
| preimage | alkukuva |
| range | arvojoukko, kuvajoukko |
| row | rivi |
| saddle point | satulapiste |
| solution | ratkaisu |
| tangent | tangentti |
| target set | maalijoukko |
| unbounded | rajoittamaton |
| upper triangular matrix | yläkolmiomatriisi |
| vector | vektori |
| vector field | vektorikenttä |
| alakolmiomatriisi | lower triangular matrix |
| alkukuva | preimage |
| arvojoukko, kuvajoukko | range |
| derivaatta | derivative |
| derivoituva, differentioituva | differentiable |
| diagonaalimatriisi | diagonal matrix |
| funktio | function |
| gradientti | gradient |
| jatkuva | continuos |
| karakteristinen polynomi | characteristic polynomial |
| karakteristinen yhtälö | characteristic equation |
| kasvava | increasing |
| kerroin | coefficient |
| ketjusääntö | chain rule |
| korkeuskäyrä | contour curve |
| kuvaaja, graafi | graph |
| käyrä | curve |
| käänteismatriisi | inverse matrix |
| kääntyvä | invertible |
| liitännäinen | assosiative |
| lähtöjoukko | domain |
| maalijoukko | target set |
| matriisi | matrix |
| ominaisarvo | eigenvalue |
| ominaisvektori | eigenvector |
| osittaisderivaatta | partial derivative |
| raja-arvo | limit |
| rajoitettu | bounded |
| rajoittamaton | unbounded |
| ratkaisu | solution |
| rivi | row |
| sarake | column |
| satulapiste | saddle point |
| sisätulo, pistetulo | dot product, inner product, scalar product |
| suljettu | closed |
| tangentti | tangent |
| tasa-arvojoukko | level set |
| tasa-arvokäyrä | level curve |
| taso | plane |
| vaihdannainen | commutative |
| vektori | vector |
| vektorikenttä | vector field |
| vähenevä | decreasing |
| väli | interval |
| yhdistetty funktio | composite function |
| yksikkömatriisi, identtinen matriisi | identity matrix |
| yläkolmiomatriisi | upper triangular matrix |
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.