Johdatus tekoälyn taustalla olevaan matematiikkaan (Heli Tuominen)
Yleistä tietoa kurssista ja luentokalvot löytyvät kurssin kotisivulta.
Kiinnostaako tekoäly? Miten koneet oppivat? Kurssilla tutustutaan koneoppimiseen, lähinnä neuroverkkoihin ja niiden toiminnan takana olevaan matematiikkaan. Neuroverkkojen opettamisessa käytetyn virhefunktion minimoinnissa tarvitaan differentiaalilaskentaa ja suurten datamäärien käsittelyssä matriisilaskentaa. Kurssilla opiskellaan näiden alojen perusasioita. Lisäksi kurssilla tutustutaan Python-kieleen.
| activation function | aktivointifunktio |
| artificial intelligence (AI) | tekoäly |
| artificial neural network (ANN) | (keinotekoinen) neuroverkko |
| backpropagation | vastavirta(-algoritmi) |
| bias | vakiotermi |
| binary classification | luokittelu kahteen luokkaan |
| classification | luokittelu |
| clustering | klusterointi, ryhmittely |
| cost function | virhefunktio |
| cross-entropy | ristientropia |
| decision tree | päätöspuu |
| gradient descent | gradienttimenetelmä |
| data maining | tiedonlouhinta |
| decision boundary | päätöspinta |
| deep learning | syväoppiminen |
| feed forward network | eteenpäin kytketty verkko |
| hidden layer | piilokerros |
| input layer | syötekerros |
| k-nearest neighbors algorithm (kNN) | k:n lähimmän naapurin menetelmä |
| learning rate | oppimisnopeus |
| logistic regression | logistinen regressio |
| loss function | tappiofunktio |
| machine learning | koneoppiminen |
| mean squared error | keskineliösumma |
| multiclass classification | luokittelu moneen luokkaan |
| output leyer | ulostulokerros |
| perceptron | perseptroni |
| regression | regressio |
| self-organizing Map | itseorganisoituva kartta |
| supervised learning | ohjattu oppiminen |
| support vector machine | tukivektorikone |
| test example | testiesimerkki |
| training example | opetusesimerkki |
| unsupervised learning | ohjaamaton oppiminen |
| validation example | vahvistusesimerkki |
| assosiative | liitännäinen |
| bounded | rajoitettu |
| chain rule | ketjusääntö |
| closed | suljettu |
| coefficient | kerroin |
| column | sarake |
| commutative | vaihdannainen |
| composite function | yhdistetty funktio |
| continuos | jatkuva |
| contour curve | korkeuskäyrä |
| curve | käyrä |
| decreasing | vähenevä |
| derivative | derivaatta |
| diagonal matrix | diagonaalimatriisi |
| differentiable | derivoituva, differentioituva |
| domain | lähtöjoukko |
| dot/inner/scalar product | sisätulo, pistetulo |
| eigenvalue | ominaisarvo |
| eigenvector | ominaisvektori |
| function | funktio |
| gradient | gradientti |
| graph | kuvaaja, graafi |
| identity matrix | yksikkömatriisi, identtinen matriisi |
| increasing | kasvava |
| interval | väli |
| inverse matrix | käänteismatriisi |
| invertible | kääntyvä |
| level curve, level set | tasa-arvokäyrä, tasa-arvojoukko |
| limit | raja-arvo |
| linearly separable | lineaarisesti erotettavat |
| lower triangular matrix | alakolmiomatriisi |
| matrix | matriisi |
| partial derivative | osittaisderivaatta |
| plane | taso |
| range | arvojoukko, kuvajoukko |
| row | rivi |
| saddle point | satulapiste |
| solution | ratkaisu |
| tangent | tangentti |
| target set | maalijoukko |
| unbounded | rajoittamaton |
| upper triangular matrix | yläkolmiomatriisi |
| vector | vektori |
| vector field | vektorikenttä |
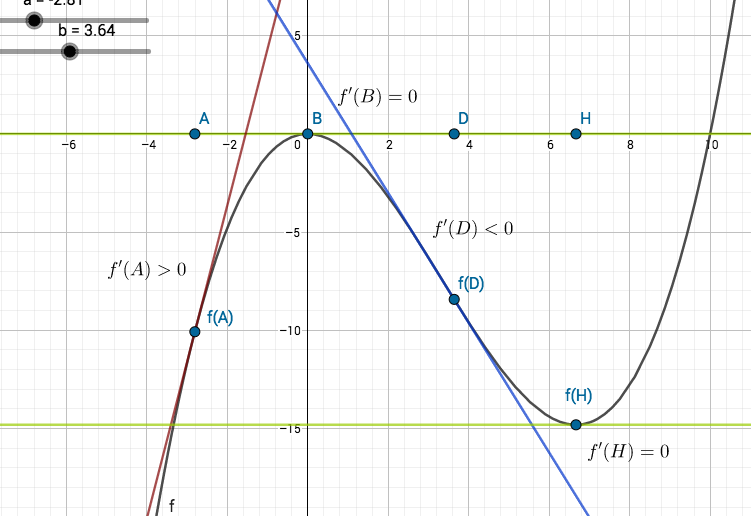
1. Koneoppiminen (Machine learning)
Koneoppiminen on tekoälyn osa-alue, jossa kone/ohjelma oppii pohjatiedon ja käyttäjän toiminnan perusteella. Kaikkia erilaisia tilanteita varten ei ole erillistä ohjetta vaan oppiminen tapahtuu kokemuksen avulla.
Mitchell 1997: A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P if its performance at tasks in T, as measured by P, improves with experience E.
Koneoppiminen voidaan jakaa kolmeen luokkaan oppimisen tyylin perusteella.
Ohjattu oppiminen: Konetta opetetaan luokitellun aineiston (syöte-tavoite-parit) avulla. Tavoitteena on, että kone osaa tehdä luokittelun samankaltaiselle aineistolle. Ohjattu oppiminen voidaan jakaa tavoitedatan luonteen perusteella kahteen luokkaan, luokittelu ja regressio. Jos syötteet voidaan luokitella erillisiin ryhmiin, niin kyse on luokittelusta, jos se on jatkuvaa, niin regressiosta. Esimerkki luokittelusta on käsinkirjoitettujen numeroiden tunnistus ja regressiosta jonkin tuotteen hinta.
Ohjaamaton oppiminen: Jäljittelee ihmisen oppimista. Opettamiseen käytetään raakadataa, josta kone pyrkii löytämään samankaltaisuuksia ja suhteita eri syötteiden välille. Syötteet pyritään ryhmittelemään niin, että yksittäisellä syötteellä on enemmän samanlaisia ominaisuuksia samaan ryhmään kuuluvien syötteiden kuin muihin ryhmiin kuuluvien syötteiden kanssa. Esimerkki ohjaamattomasta oppimisesta on akateemikko Teuvo Kohosen (1934) 1980-luvulla kehittämä itseorganisoituva kartta.
Vahvistettu oppiminen Kone oppii ympäristön antaman palautteen perusteella. Kone saa toiminnastaan dynaamisessa ympäristössä positiivista ja negatiivista palautetta ja oppii toimimaan niin, positiivisen palautteen määrä kasvaa ja negatiivisen vähenee. Esimerkkejä vahvistetusta oppimisesta ovat itseohjautuvat autot ja robotiikka.
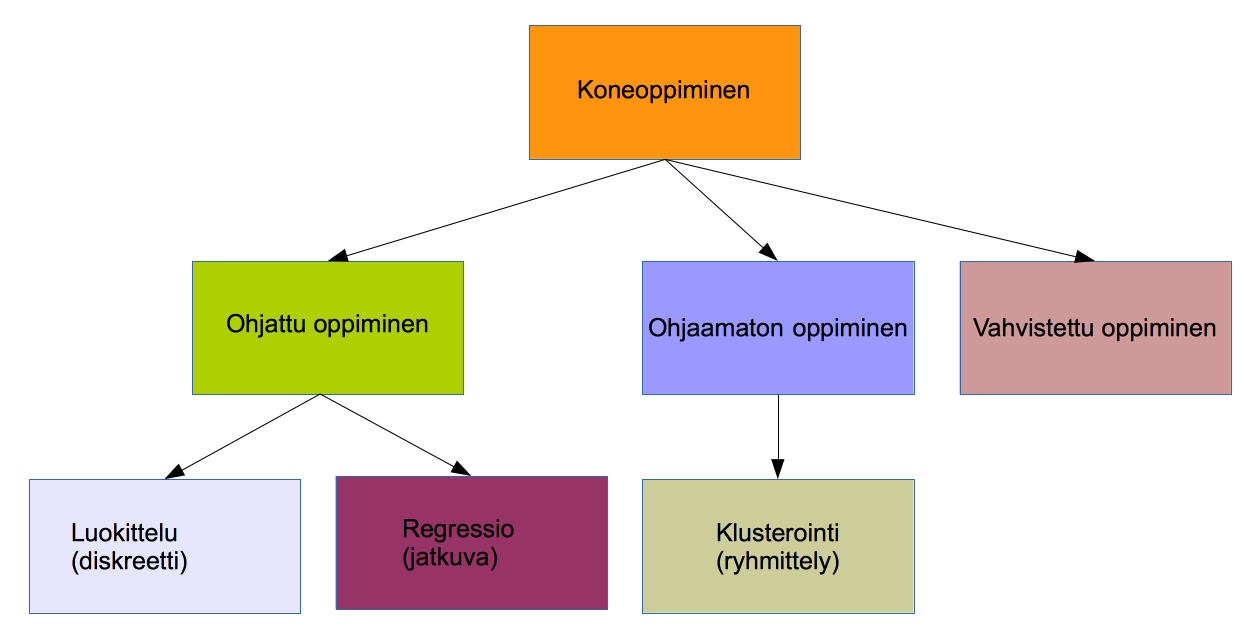
Kuhunkin oppimistyyliin sopivia algoritmeja on useita. Ratkaistavana olevaan ongelmaan sopivan algoritmin valinta riippuu oppimistyylin lisäksi esimerkiksi datan koosta ja tyypistä, algoritmin oppimisnopeudesta ja opetuksessa tarvittavasta tallennustilasta ja siitä, kuinka tehokasta tai yleistettävää ratkaisua ollaan etsimässä. Paras algoritmi ei välttämättä löydy ensimmäisellä kokeilulla.
Tällä kurssilla käsitellään pääasiassa ohjattua oppimista neuroverkkojen avulla. Ennen neuroverkkoihin siirtymistä tutustutaan hyvin lyhyesti muutamaan muuhun ohjatun oppimisen algoritmiin.
Ohjatun oppimisen luokittelu voi olla binääristä luokittelua tai luokittelua useampaan luokkaan. Binäärisessä luokittelussa mahdollisia luokkia, joihin yksittäinen datan alkio voi kuulua, on kaksi. Esimerkiksi sähköposti on roskapostia tai oikeaa postia ja vain kissojen ja koirien kuvia sisältävässä joukossa jokainen kuva on joko kissan tai koiran kuva, ei molempia. Jotkut algoritmit, kuten logistinen regressio, on suunniteltu erityisesti binääriseen luokitteluun ja ne ovat tehtävässään tehokkaita. Useampaan luokkaan luokittelu vaatii monimutkaisemman algoritmin.
Luokittelualgoritmeja
- Logistinen regressio: Sopii binääriseen luokitteluun. Malli kertoo, millä todennäköisyydellä datapiste kuuluu ongelmassa oleviin luokkiin. Se sopiii parhaiten tilanteisiin, jossa data voidaan erottaa lineaarisesti (suoralla, hypertasolla).
- k:n lähimmän naapurin menetelmä: K:n lähimmän naapurin menetelmässä datapisteet (opetusesimerkit) ovat pisteitä
-ulotteisessa avaruudessa. Jokaiselle datapisteelle etsitään euklidisen (tai muun) etäisyyden mielessä K lähintä pistettä ja datapiste luokitellaan naapureiden luokkien avulla käyttäen esimerkiksi keskiarvoa regression ja moodia luokittelun tapauksessa. Koko data on kerralla muistissa.
- Tukivektorikone: Tukivektorikoneen perusversiota käytetään binääriseen luokitteluun. Se luokittelee dataa etsimällä lineaarista päätöspintaa (hypertasoa), joka erottaa kahteen eri luokkaan kuuluvat datapisteet toisistaan. Jos data on lineaarisesti erotettava, niin paras erotteleva hypertaso on se, joka erottelee luokat toisistaan suurimmalla marginaalilla. Jos data ei ole lineaarisesti erotettava, niin väärällä puolella hypertasoa oleville pisteille käytetään virhefunktiota.
- Naiivi Bayes-luokittelija: Naiivi Bayes-luokittelija on yksinkertainen luokittelija, joka käsittelee alkioiden ominaisuuksia toisistaan riippumattomina. Luokittelu tehdään todennäköisyyksien avulla. Se on helppo toteuttaa ja hyvä menetelmä pienehkölle datalle, jossa on useita parametreja.
- Diskriminanttianalyysi Diskriminattianalyysi luokittelee dataa etsimällä sellaisia ominaisuuksien lineaarikombinaatioita, jotka joko karakterisoivat tai erottavat eri luokkiin kuuluvia datapisteitä. Diskriminantissa analyysissä oletetaan, että eri luokat noudattavat normaalijakaumaa. Opetettaessa etsitään normaalijakauman parametreja eri luokille ja niiden avulla etsitään luokkia erottavat lineaariset tai kvadraattiset funktiot.
- Päätöspuut Päätöspuu on helposti toteutettava ja vähän muistia käyttävä luokittelualgoritmi. Luokittelu tehdään valitsemalla luokiteltavan data-alkion ominaisuuksien perusteella binääripuun solmuissa vasen tai oikea haara. Datapiste viedään ensin juurisolmuun, josta se lopulta päätyy lehteen, joka kertoo luokan.
- Neuroverkot Ihmisen aivojen toimintaa jäljitteleviä oppivia verkkoja käsitellään seuraavissa luvuissa tarkemmin.
Lisätietoa koneoppimisesta
- T.Kohonen: MATLAB Implementations and Applications of the Self-Organizing Map
- R.S. Sutton ja A.G. Barto: Reinforcement Learning, An Introduction
- Y. Zhang: New Advances in Machine Learning
- Machine Learning Mastery: Your First Machine Learning Project in Python Step-By-Step
- Machine Learning Mastery: Machine Learning Algorithms
- H. Daumé: A Course in Machine Learning (University on Maryland)
- Decision Trees (Scikit learn)
- A Complete Tutorial on Tree Based Modeling from Scratch in R and Python
- Machine Learning Mastery: How To Implement The Decision Tree Algorithm From Scratch In Python
- Python and Machine Learning
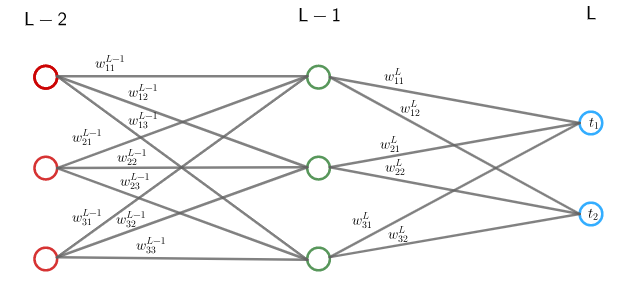
2. Keinotekoiset neuroverkot (Artificial neural networks)
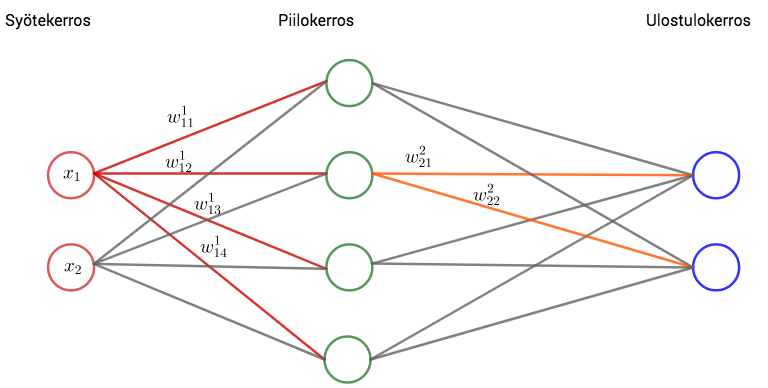
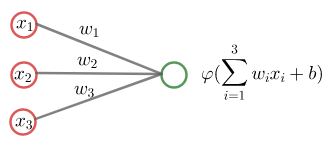
Keinotekoinen neuroverkko jäljittelee ihmisen aivoja. Se koostuu syöte- ja ulostulokerroksesta ja niiden välissä olevista piilokerroksista.
Neuroverkkoa voi ajatella funktiona ; syöte on
-ulotteinen vektori
, piilokerrokset hoitavat laskutehtävän ja funktion arvo
saadaan ulostulokerroksesta. Verkon käyttötarkoitus määrää, miten funktion arvo
tulkitaan.
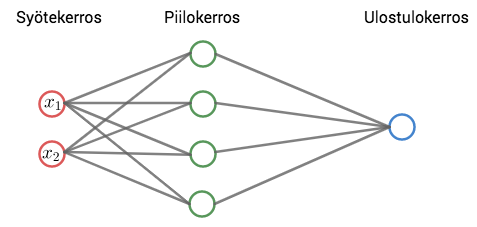
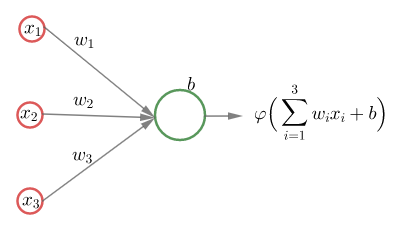
Piilokerroksien ja ulostulokerroksen jokaisessa neuronissa lasketaan syötekerroksesta tai piilokerroksesta tulleiden syötteiden painotettu summa ja siihen lisätään neuronin vakiotermi. Ennen neuronin tuloksen lähettämistä seuraavalle neuronille summa viedään aktivointifunktioon. Aktivointifunktiot muuttavat lineaarisen (affiinin eli ensimmäisen asteen polynomin) syötteen epälineaariseksi.
Esimerkki
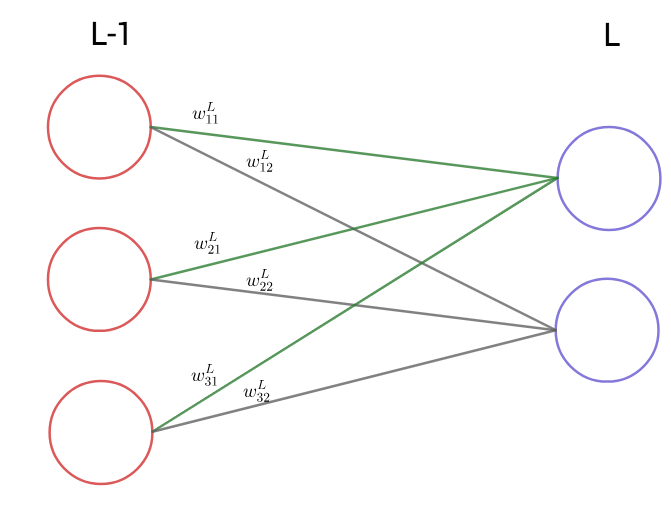
Verkossa on yksi piilokerros, jossa on neljä neuronia. Syöte on vektori . Ulostulokerroksessa on yksi neuroni.
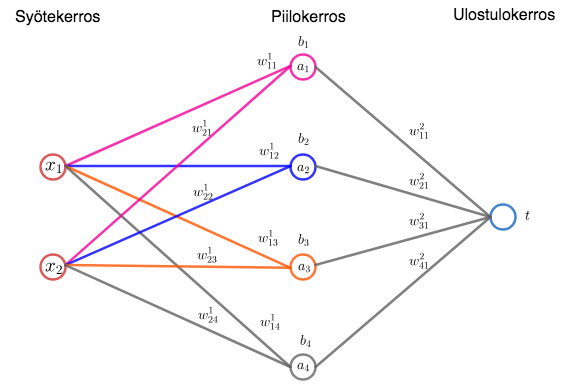 Syötevektorin komponentit kerrotaan piilokerroksen neuroneiden painoilla
Syötevektorin komponentit kerrotaan piilokerroksen neuroneiden painoilla , lasketaan yhteen ja summaan lisätään piilokerroksen neuronin
vakiotermi
:
Nämä summat viedään piilokerroksen aktivointifunktiolle, jolloin piilokerroksen neuronien antamat syötteet ulostulokerrokselle ovat
Verkon antama tulos saadaan käyttämällä piilokerroksen ja ulostulokerroksen välisiä painoja ja aktivointifunktiota (ulostulokerroksen vakiotermi on nolla):
2.1 Neuroverkkoihin liittyviä määritelmiä ja merkintöjä
Neuroneihin liittyvistä parametreistä käytetään seuraavia merkintöjä. Kerrosindeksi viittaa syötekerrokseen ja kerrosindeksi
ulostulokerrokseen:
kerroksen
neuronien lukumäärä,
kerroksen
neuronin
ja kerroksen
neuronin
välillä oleva paino,
kerroksen
neuronin
vakiotermi,
kerroksen
neuronia
vastaava summa
kerroksen
neuronin
tulos eli syöte seuraavaan kerrokseen
missä on aktivointifunktio (joka voi vaihdella kerroksesta toiseen).
Olisi kiva, jos tässä w:n indeksinä l käytettäisiin samaa indeksiä kuin edellisessä esimerkissä, tai päinvastoin.
—Neuroni
Piilokerroksen neuronit voidaan tulkita funktioiksi ,
,
missä
on yleensä edellisen kerroksen painotettu summa lisättynä vakiotermillä eli
ja
on kerroksen
aktivointifunktio. Ulostulokerroksen funktioille
arvojoukko on
.
Kaavat vektorimuodossa
Merkintöjen yksinkertaistamiseksi kaavat kirjoitetaan monesti vektori- ja matriisimuodossa, joilloin kerroksen vakiotermejä vastaa vektori
kerroksen
neuronien painotettuja summia vektori
ja kerroksen
neuronien tuloksia vektori
Kerroksen
painoja vastaa
-matriisi
jolloin
Huomaa, että jos vektorit
,
ja
määriteltäisiin pystyvektoreina, niin olisi
W, ensimmäinen sarake, toinen rivi, ensimmäinen alkio: tulisiko indeksi olla 21 eikä 12?
—Pitäisi. Kiitos.
—Huomautus
Joissain lähteissä painojen neuroni-indeksit
ja
ovat päinvastaisessa järjestyksessä. Tällöin vastaava matriisi
on
-matriisi ja
, missä
on vektorin
transpoosi.
2.1.1 Harjoitustehtäviä
- Tarkastellaan neuroverkkoa, jonka syöte on
, jossa on yksi neljän neuronin piilokerros, jonka ulostulokerroksessa on kaksi neuronia ja jonka aktivointifunktio sekä piilo- että ulostulokerroksessa on
. (Kuvassa vain osa painoista merkitty.)
Kirjoita verkkoon liittyvät neuronien painotetut summat ja neuronien tulokset
vektoreiden ja painomatriisien avulla.
2.2 Perseptroni (Perceptron)
Perseptroni on syötekerroksen ja yhden neuronin muodostama "minimaalinen neuroverkko", jonka syöte on ja tulos on
.
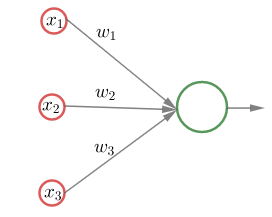 Perseptonia, jonka painojen muodostama vektori on
Perseptonia, jonka painojen muodostama vektori on , vakiotermi on
, ja aktivointifunktio on yksikköporrasfunktio (Heavisiden funktio)
,
vastaa funktio
,
missä
on vektoreiden
ja
sisätulo.
Kysymykseen, millaiset funktiot voidaan esittää perseptronilla, on yksinkertainen vastaus nollan ja ykkösen alkukuvien lineaarisen erotettavuuden avulla.
Joukot ja
ovat lineaarisesti erotettavat, jos on vakiot
ja
, joille
ja
Tasossa tämä tarkoittaa sitä, että joukoja
ja
vastaavat pisteet voidaan erottaa suoralla ja
:ssa sitä, että pistejoukot voidaan erottaa tasolla.
Lause
Funktio voidaan esittää perseptronilla jos ja vain jos alkukuvat
ja
ovat lineaarisesti erotettavat.
Esimerkki
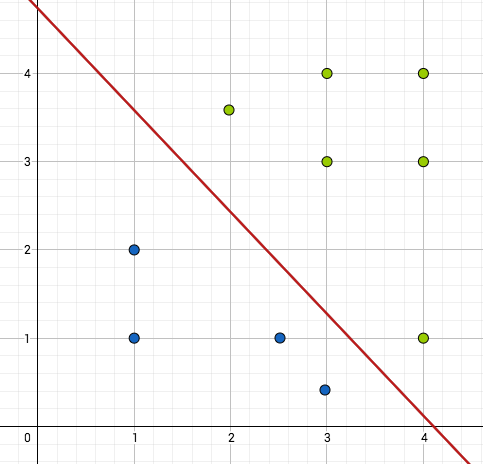
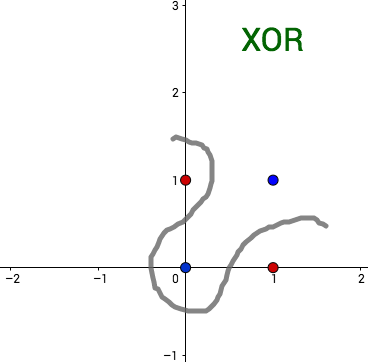
Ensimmäisen kuvan pistejoukko ei ole lineaarisesti erotettava, toisen kuvan on. Funktio, jonka arvot vihreitä palloja vastaavissa tason pisteissä on 1 ja sinisiä palloja vastaavissa pisteissä on 0, voidaan siis toisessa tapauksessa esittää perseptronilla, ensimmäisessä ei. 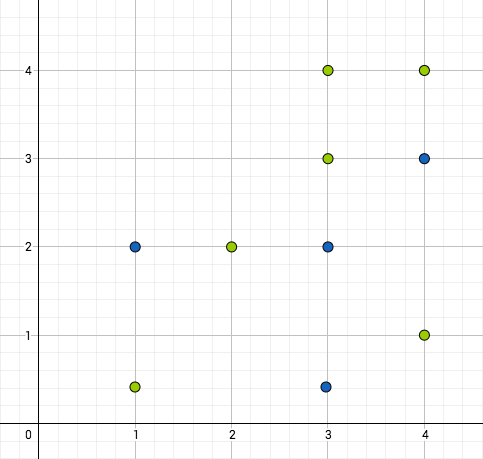
Esimerkki
Looginen konnektiivi AND (JA) voidaan esittää yhdellä perseptronilla mutta konnektiivia XOR (poissulkeva TAI) ei voi. Konnektiiveja vastaavat funktiot ovat ja
ja
Nollan ja ykkösen alkukuvat ovat siis
ja
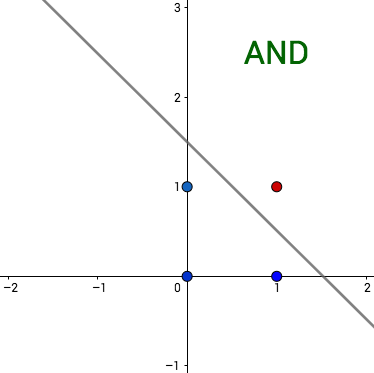
Edellisen esimerkin looginen konnektiivi AND saadaan perseptronilla 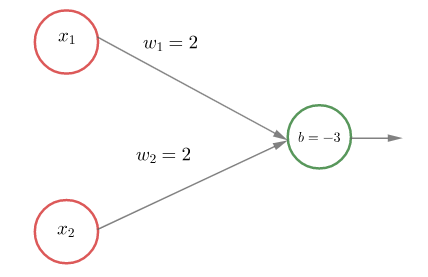 Muuttamalla painoiksi
Muuttamalla painoiksi ja vakiotermiksi
, saadaan AND-konnektiivin negaatio, NAND, jonka arvo parille
on
ja muille lukupareille
. NAND konnektiivin esityksen olemassaolosta seuraa, että perseptronien avulla voidaan rakentaa verkko, joka tekee minkä tahansa halutun loogisen päättelyn.
Perseptronin ongelma on se, että pienet muutokset painoissa tai syötteissä aiheuttavat ison muutoksen tuloksessa . Tämä on huono asia verkon opettamisen kannalta. Perseptronin yksikköporrasfunktion sijaan käytetäänkin yleensä verkon opettamiseen paremmin soveltuvia aktivointifunktioita.
2.2.1 Harjoitustehtäviä
- Loogista konnektiivia OR (TAI) vastaa funktio
,
- Määritä alkukuvat
ja
.
- Voidaanko OR esittää perseptronilla? Jos voidaan, niin etsi kertoimet
ja
ja perseptronin vakiotermi
.
(1,1)=1 OR
—Joo. Kiitos.
—2.3 Aktivointifunktiot (Activation functions)
Neuroverkon piilo- ja ulostulokerroksissa käytetään aktivointifunktioita. Ennen neuronin tuloksen lähettämistä seuraavalle neuronille tai ulostulokerroksesta ulos, edellisen kerroksen syötteistä laskettu painotettu summa viedään aktivointifunktioon . Aktivointifunktiot muuttavat lineaarisen (affiinin) syötteen epälineaariseksi ja niillä olisi toivottavaa olla seuraavia ominaisuuksia:
epälineaarisuus: Koska summa ja yhdistetty funktio lineaarisista funktioista on lineaarinen ja affiineista affiini ja neuroneiden summalausekkeet
ovat affiineja, niin lineaarisilla (tai affiineilla) aktivointifunktioilla saadaan affiini kuvaus.
(jatkuvasti) derivoituvuus: Vastavirta-algoritmissa ja muissa virhefunktion minimointitavoissa tarvitaan aktivointivointifunktion derivaattaa. Jos aktivointifunktio ei ole derivoituva, niin virhefunktion minimoinnissa pitää käyttää muita kuin gradienttiin perustuvia keinoja.
identtisen funktion approksimointi: Jos aktivointifunktio on lähellä identtistä funktiota nollan lähellä, niin neuroverkko oppii tehokkaasti kun painot alustetaan satunnaisluvuilla. Muussa tapauksessa painot pitää alustaa huolellisesti.
Se, onko aktivointifunktio rajoitettu vai ei, vaikuttaa verkon oppimisnopeuteen ja oppimisen vakauteen. Rajoitetuilla aktivointifunktioilla oppiminen on yleensä vakaata ja rajoittamattomilla monesti tehokasta. Rajoittamattomia aktivointifunktioita käytettäessä kannattaa käyttää pieniä oppimisnopeuksia.
Esimerkkejä aktivointifunktioista ovat sigmoid-funktio, hyperbolinen tangentti ja ReLu-funktio.
Sigmoid-funktio (logistinen funktio)
Sigmoid-funktiolla ,
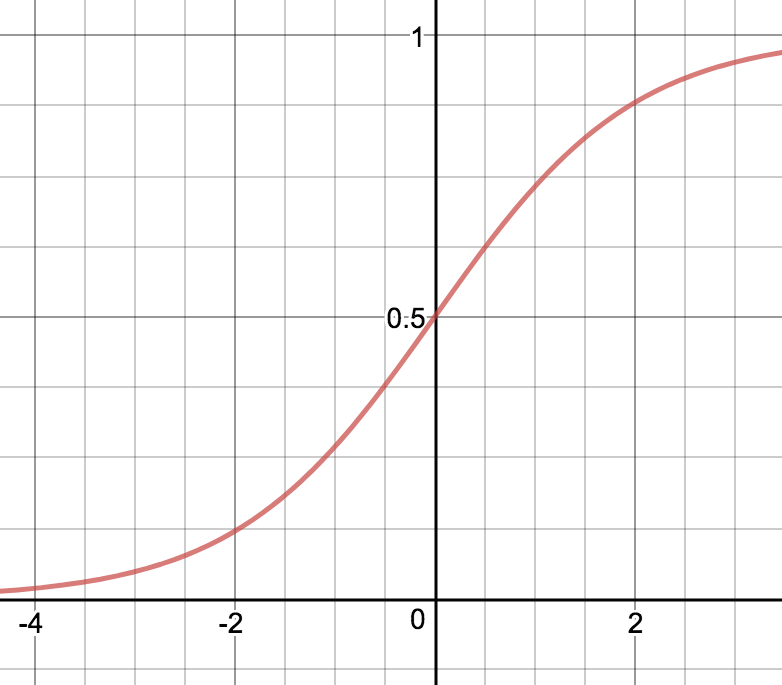
on seuraavat ominaisuudet:
rajoitettu, aidosti kasvava ja jatkuva
,
eli funktiolla
on kaikkien kertalukujen jatkuvat derivaatat ja
Sigmoid-funktio on (binäärisen) porrasfunktion (Heaviside step function) ,
kun
,
kun
, silotettu versio. Sigmoid-funktion huono ominaisuus on se, että se kasvaa hyvin hitaasti kun
kasvaa ja vähenee hyvin hitaasti kun
vähenee. Sen derivaatta on hyvin lähellä nollaa kun
on suuri tai pieni. Tästä seuraa ongelmia kun verkkoa opetetaan derivaattoihin perustuvilla menetelmillä. Vastavirta-algoritmia käsittelevässä luvussa nähdään, että virhefunktion osittaisderivaatat neuronin painojen ja vakiotermien suhteen riippuvat aktivointifunktion derivaatasta ja että painojen ja vakioiden muutoksen koulutettaessa ovat pieniä jos osittaisderivaatat ovat pieniä. Tällöin verkko oppii hitaasti. Toinen sigmoid-funktion huono puoli on se, että se ei ole symmetrinen nollan suhteen. Nykyisin sitä käytetään lähinnä ulostulokerroksessa varsinkin jos verkon tulokset ovat välillä
.
Hyperbolinen tangentti (tanh)
Hyperbolisella tangenttilla ,
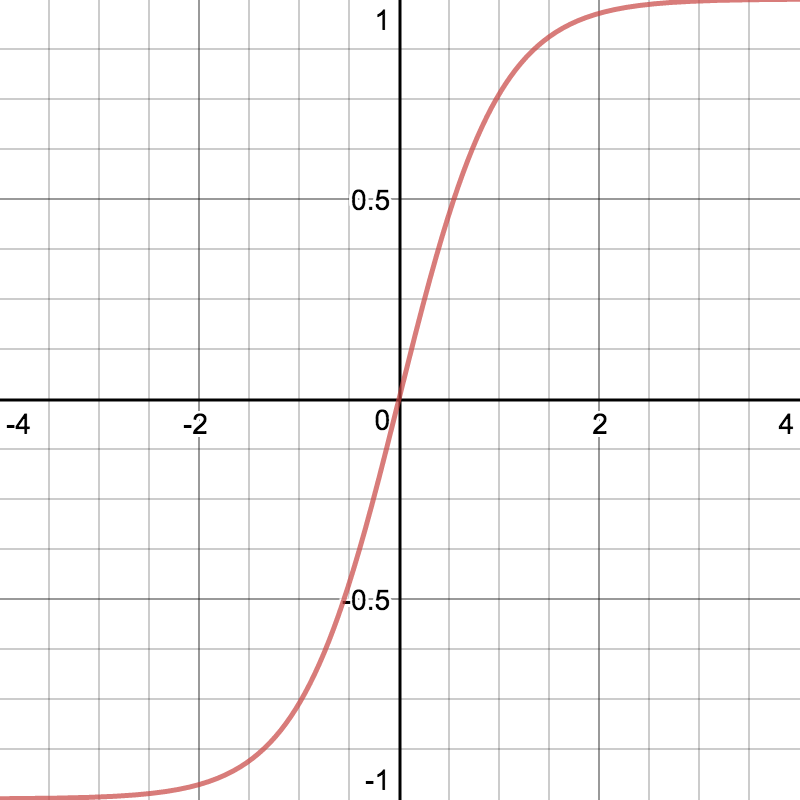 on monia samoja ominaisuuksia kuin sigmoid-funktiolla mutta se on symmetrinen nollan suhteen ja se kasvaa nopeammin nollan lähellä, jolloin sen derivaatta on suurempi. Hyperbolinen tangentti on
on monia samoja ominaisuuksia kuin sigmoid-funktiolla mutta se on symmetrinen nollan suhteen ja se kasvaa nopeammin nollan lähellä, jolloin sen derivaatta on suurempi. Hyperbolinen tangentti on
rajoitettu, aidosti kasvava ja jatkuva
,
ja
.
Gradientin pienuus isoilla ja pienillä arvoilla on myös hyperbolisen tangentin ominaisuus, joten sen käyttö aktivointifunktiona saattaa aiheuttaa verkon oppimisen hitautta.
Hyperbolinen tangentti on -listan toisessa kohdassa pitäisi varmaan puhua tanh:sta.
—Joo. Kiitos.
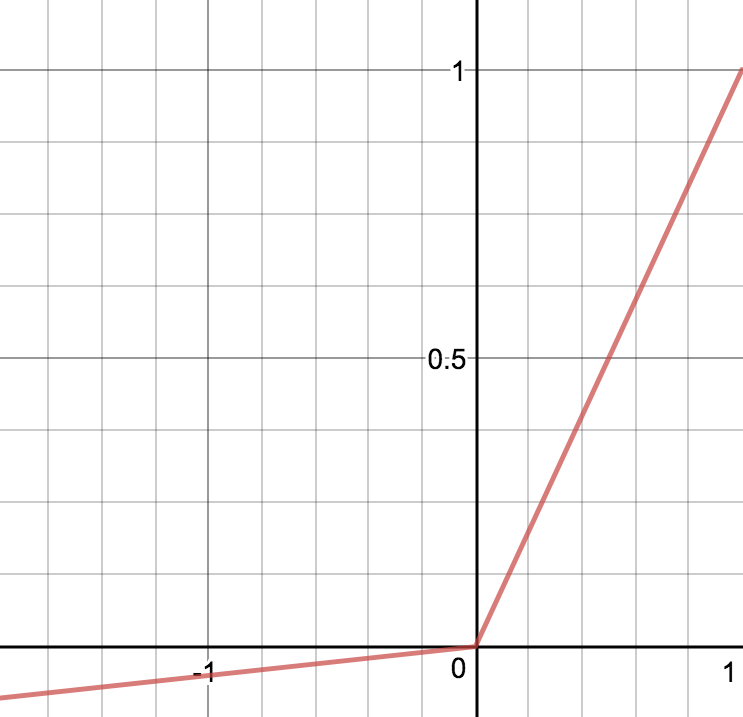
—ReLu (Rectified Linear Unit)
Neuroverkkojen piilokerroksissa paljon käytetty aktivointifunktio on ReLu-funktio ,
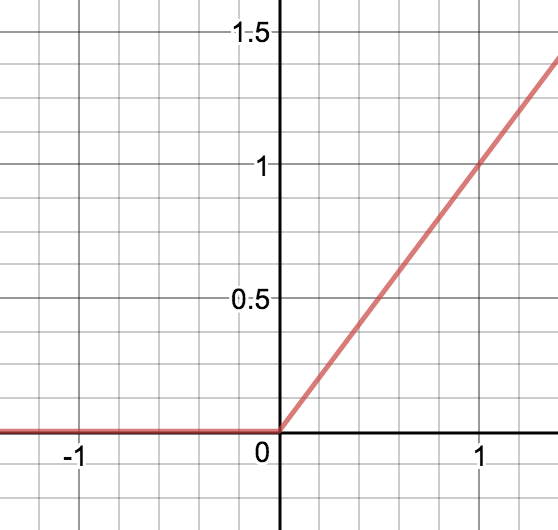
Jotta verkon toimintaan saadaan epälineaarisuutta, niin ulostulokerroksessa käytetään jotain epälineaarista aktivointifunktiota. ReLu-funktio ei ole derivoituva nollassa. Sen toinen huono ominaisuus on se, että se on nolla ja sen derivaatta on nolla negatiivisilla arvoilla. Tästä syystä joidenkin neuronien painot saattavat päivittyä oppimisen aikana nollaksi jolloin neuronit kuolevat. Neuronien kuoleentumisongelmaa pyritään välttämään muuttamalla aktivointifunktiota hieman. Yksi ReLun variantti on "Leaky ReLu", ,
Toimivimpien aktivointifunktioiden valinta riippuu siitä, mitä verkolla ollaan tekemässä eli mitä funktiota sillä approksimoidaan. Jos verkkoa vastaavalla funktiolla on samoja ominaisuuksia kuin aktivointifunktiolla, niin oppiminen on nopeampaa. Esimerkiksi sigmoid-funktiota kannattaa käyttää ulostulokerroksessa jos verkkoa käytetään luokitteluun .
Universaali approksimointilause
Funktionaalianalyysin keinoin voidaan todistaa neuroverkkojen universaali approksimointilause, joka sanoo, että jos aktivointifunktio on rajoitettu, kasvava ja jatkuva, niin mille tahansa :n kompaktin joukon jatkuvalle funktiolle on tätä aktivointifunktiota käyttävä neuroverkko, joka approksimoi haluttua funktiota hyvin. (Joukko on kompakti, jos se on suljettu ja rajoitettu.)
Lause
Olkoon rajoitettu, kasvava ja jatkuva funktio. Olkoon
kompakti joukko. Olkoon
ja olkoon
jatkuva funktio. Tällöin on
,
, ja
,
, siten, että
kaikilla
funktiolle
2.3.1 Harjoitustehtäviä
Näytä, että jos aktivointifunktiona käytetään affiinia funktiota
,
,
, niin neuroverkkoa vastaava kuvaus on affiini. Huomaa, että riittää todeta, että affiinien kuvausten summa ja yhdistetty kuvaus ovat affiineja.
Laske sigmoid-funktion ja hyperbolisen tangentin derivaatat osamäärän derivointisäännön ja ketjusäännön avulla. Muista, että eksponenttifunktiolle
,
on
kaikilla
. (Derivointia käsitellään luvussa Analyysia.)
2.4 Neuroverkon opettaminen
Ohjattua oppimista käytettäessä neuroverkkoa opetetaan syöte-tavoite-pareilla eli opetusesimerkeillä (training examples). Verkon syötteelle
antamaa tulosta
verrataan valitulla virhefunktiolla tavoitteeseen
. Opettamisen aikana yritetään minimoida virhefunktioita ja piilokerroksen parametreja muutetaan esimerkiksi vastavirta-algoritmin avulla. Kun verkko toimii halutulla tavalla opetusesimerkeille, sen toimintaa tarkastetaan testiesimerkeillä (test examples).
2.4.1 Vastavirta-algoritmi (backpropagation)
Eteenpäin kytketyssä neuroverkossa syötekerroksen syötteen komponentit kerrotaan ensimmäisen piilokerroksen neuroneita vastaavilla painoilla, jokaista ensimmäisen piilokerroksen neuronia vastaavat tulot lasketaan yhteen ja summaan lisätään neuronin vakiotermi (bias). Tämä summa syötetään aktivointifunktioon, joka antaa kyseisen neuronin syötteen seuraavalle kerrokselle. Tämä kerros käyttää omia painojaan, vakiotermejään ja aktivointifunktioitaan. Näin jatketaan kaikkien kerrosten läpi.
Syötteen (tai syötejoukon) antamaa tulosta verrataan tavoitteeseen ja lasketaan virhefunktion arvo. Tavoitteena on minimoida opetusesimerkkijoukkoa vastaava virhefunktio ja löytää minimointia vastaavat painot neuroneille. Monissa virhefunktion minimointikeinoissa, esimerkiksi gradienttimenetelmässä (gradient descent), tarvitaan virhefunktion osittaisderivaatat
ja
verkon kaikkien painojen
ja vakiotermien
suhteen. Osittaisderivaatat ja jokaisen neuronin vaikutus virheeseen lasketaan usein vastavirta-algoritmilla (backpropagation). Gradienttimenetelmässä neuroneille saadaan uudet painot ja vakiotermit muuttamalla edellisiä arvoja neuronien parametrien osittaisderivaatoista koostuvan gradientin vastavektorin suuntaan (eli virhefunktion nopeimman pienenemisen suuntaan).
Seuraavaksi lasketaan virhefunktion osittaisderivaatat
ja
verkon kaikkien painojen
ja vakiotermien
suhteen vastavirta-algoritmilla. Derivaatan ja osittaisderivaattojen määritelmät esimerkkeineen ja lukuvinkkeineen löytyvät luvusta Analyysia.
Virhefunktion osittaisderivaatat ulostulokerroksen parametrien suhteen
Ulostulokerroksen parametreihin liittyvät osittaisderivaatat on helppo laskea. Aloitetaan esimerkillä.
Esimerkki
Ulostulokerroksessa (. kerros) on kaksi ja viimeisessä piilokerroksessa (
kerros) kolme neuronia. Virhefunktio on
ja ulostulokerroksen neuronien tulokset ovat
Oletetaan, että aktivointifunktio on identtinen funktio ja että ulostulokerroksen vakiotermit ovat nollia. Tällöin
ja
.
Lasketaan virhefunktion osittaisderivaatat painojen
suhteen. Koska kaavan perusteella painot
,
ja
eivät vaikuta ulostuloon
, niin virhefunktion termi
on vakio osittaisderivoinneissa painojen
,
ja
suhteen. Siten derivoinnin ketjusäännön avulla nähdään, että kaikilla
on
Koska summan termit, joissa on kertoimena
,
, ovat muuttujan
suhteen vakiota, niin kaikilla
on
ja siten
Vastaavasti saadaan, että
ja
Palataan yleiseen tilanteeseen. Olkoon ulostulokerros verkon . kerros ja olkoon siinä
neuronia.
Osittaisderivaatat painojen  suhteen
suhteen
Koska virhefunktiossa termit ovat vakioita painon
suhteen kun
, niin derivoinnin ketjusääntöä käyttämällä saadaan
Huomaa, että syötteiden tulokset
ovat vakioita kaikkien painojen
suhteen ja siten niiden osittaisderivaatat ovat nollia. Siten kaikilla
saadaan ketjusäännön avulla
Koska
ja muut termit summassa paitsi
ovat vakioita painon
suhteen, niin
Yhdistämällä nämä laskut saadaan
Tämän kaavan indeksistä
riippuvaa osaa merkitään usein
Laskemalla huomataan, että
Siten on
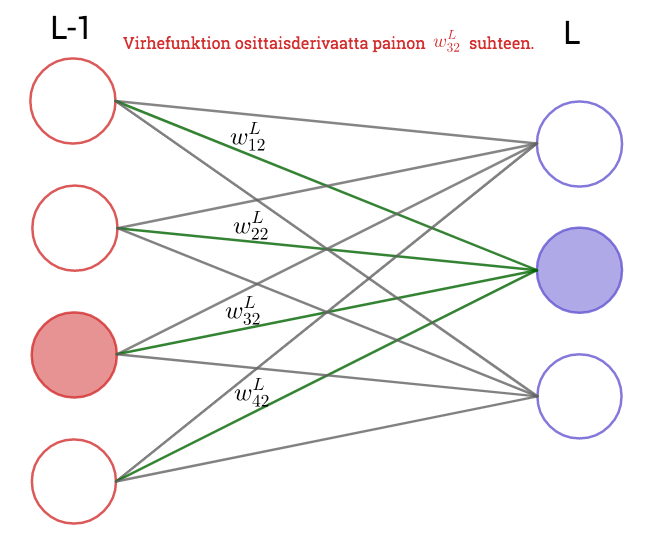
Osittaisderivaatat vakiotermien  suhteen
suhteen
Ulostulokerroksen osittaisderivaatat vakiotermien suhteen saadaan laskettua samaan tapaan kuin painojen suhteen. Virhefunktiossa termit ovat vakioita termin
suhteen kun
, joten ketjusääntöä käyttämällä saadaan
sillä viimeisessä osittaisderivoinnissa ainoastaan summan termi
vaikuttaa derivointiin ja sen osittaisderivaatta
:n suhteen on
. Siten saadaan
Huomautus
Ulostulokerroksen . neuroniin liittyvää virhettä
, ketjusääntöä ja
:n kaavaa käyttäen saadaan vastaavat kaavat myös muille virhefunktioille, joita merkitään tässä myös
:llä,
Seuraavaksi lasketaan virhefunktion osittaisderivaatat piilokerroksien painojen ja vakiotermien suhteen. Laskun avulla nähdään, että osittaisderivaatat kerroksen suhteen saadaan laskettua rekursiivisesti kun tiedetään yhtä ylemmän kerroksen osittaisderivaatat. Osittaisderivaattoja laskettaessa lähdetään siis liikkeelle ulostulokerroksen osittaisderivaatoista ja niitä käytetään ensimmäisen piilokerroksen derivaattojen laskemiseen. Osittaisderivaatat viimeisen piilokerroksen painojen ja vakioiden suhteen antavat vastaavat osittaisderivaatat viimeistä edelliselle piilokerrokselle. Näin jatketaan kunnes virhefunktion kaikki osittaisderivaatat saadaan laskettua. Nimi vastavirta-algoritmi tulee siitä, että osittaisderivaattoja lasketaan takaperoisesti ulostuloskerroksesta syöttökerrosta kohti "vastavirtaan".
Osittaisderivaatat piilokerroksen painojen  suhteen
suhteen
Lasketaan virhefuntion osittaisderivaatat piilokerroksen painojen suhteen Huomatuksen tyylillä. Lasku on teknisesti hieman haastavampi sillä paino, jonka suhteen osittaisderivoidaan, vaikuttaa virheeseen yhden tai useamman piilokerroksen kautta. Siksi laskussa tarvitaan tavallisen ketjusäännön lisäksi osittaisderivaattojen ketjusääntöä. Käytetään tässäkin merkintää kerroksen
neuroniin
liittyvälle virheelle.
Ketjusääntöä ja kaavaa käyttäen saadaan
Osittaisderivaattojen ketjusäännön, ketjusäännön ja kaavojen
ja
perusteella on
ja siten
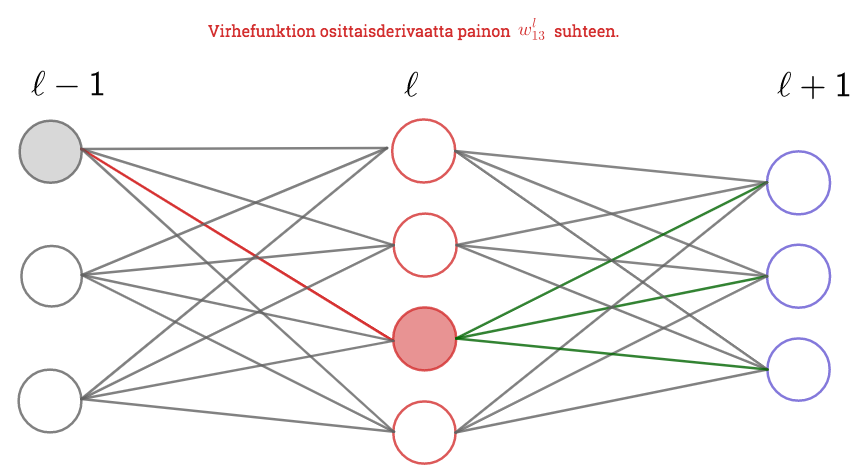
Osittaisderivaatat piilokerroksen vakiokertoimien  suhteen
suhteen
Samaan tapaan kuin painojen tapauksessa saadaan ja
Huomioita osittaisderivaattojen kaavoista
Kaavasta nähdään, että jos edellisen kerroksen syöte
on pieni, niin kerroksen
painoa vastaava virheen osittaisderivaatta
on pieni. Tällaiset painot muuttuvat vastavirta-algoritmin aikana vähän, monesti sanotaan, että ne oppivat hitaasti.
Kaavoista nähdään myös, että aktivointifunktion derivaatat vaikuttavat virheen osittaisderivaattoihin ja siten neuroneiden parametrien muutokseen. Jos derivaatta on hyvin pieni, niin parametrit muuttuvat vähän ja neuronit oppivat hitaasti. Tästä syystä verkon käyttötarkoitukseen sopivan virhefunktion valinta on tärkeää.
Verkon eri kerroksissa voidaan käyttää eri aktivointifunktioita. Jos näin on, niin äskeisissä laskuissa ja kaavoissa aktivointifunktioon lisätään verkon kerrosta vastaavat alaindeksit
.
2.4.2 Harjoitustehtäviä
Laske virhefunktion osittaisderivaatat piilokerroksen
painojen
suhteen samaan tapaan kuin ulostulokerroksen osittaisderivaatat. Mieti, mitkä painoista
vaikuttavat ulostuloon
.
Koodissa on kätevää ja nopeaa käyttää vastavirta-algoritmin kaavojen vektori- ja matriisiversioita. Lue näistä esimerkiksi linkkilistan lähteestä. Lähteessä pohditaan myös sitä, miksi vastavirta-algoritmi on paljon nopeampi tapa laskea tarvittavat osittaisderivaatat kuin osittaisderivaattojen erotusosamäärien raja-arvomääritelmään pohjautuva tapa.
Tarkastellaan neuroverkkoa, jonka syöte on
, jossa ei ole piilokerroksia, jonka ulostulokerroksessa on yksi neuroni ja jonka ulostulokerroksen aktivointifunktio on derivoituva funktio
. Käytetään syöte-tavoiteparin
ja verkon antaman tuloksen
vertailuun virhefunktiota
Laske virhefunktion osittaisderivaatat painojen
,
ja
suhteen.
Lisätietoa vastavirta-algoritmista
Vastavirta-algoritmista löytyy paljon monentasoista luettavaa, esimerkkejä ja koodia. Osassa selitetään matemaattinen tausta ja painojen muutoksen vaikutus verkon toimintaan hyvin, osan selitys on turhan monimutkaista. Kaavoissa indeksien käyttö on monesti epämatemaattista (osittaisderivaatan indeksit ja summausindeksit samoja).
2.4.3 Gradienttimenetelmä (gradient descent)
Tavoitteena on minimoida verkon parametreista riippuvaa virhefunktiota eli syötteiden ja verkon antamien tulosten välistä virhettä. Virhefunktio on monen muuttujan (kaikkien neuronien painojen ja vakiotermien) funktio, jolle etsitään pienintä arvoa.
Matemaattisen analyysin keinoin monen muuttujan funktion ääriarvoja etsitään riittävän siistille funktiolle gradientin nollakohdista ja niistä pisteistä, joissa funktiolla ei ole osittaisderivaattaa.
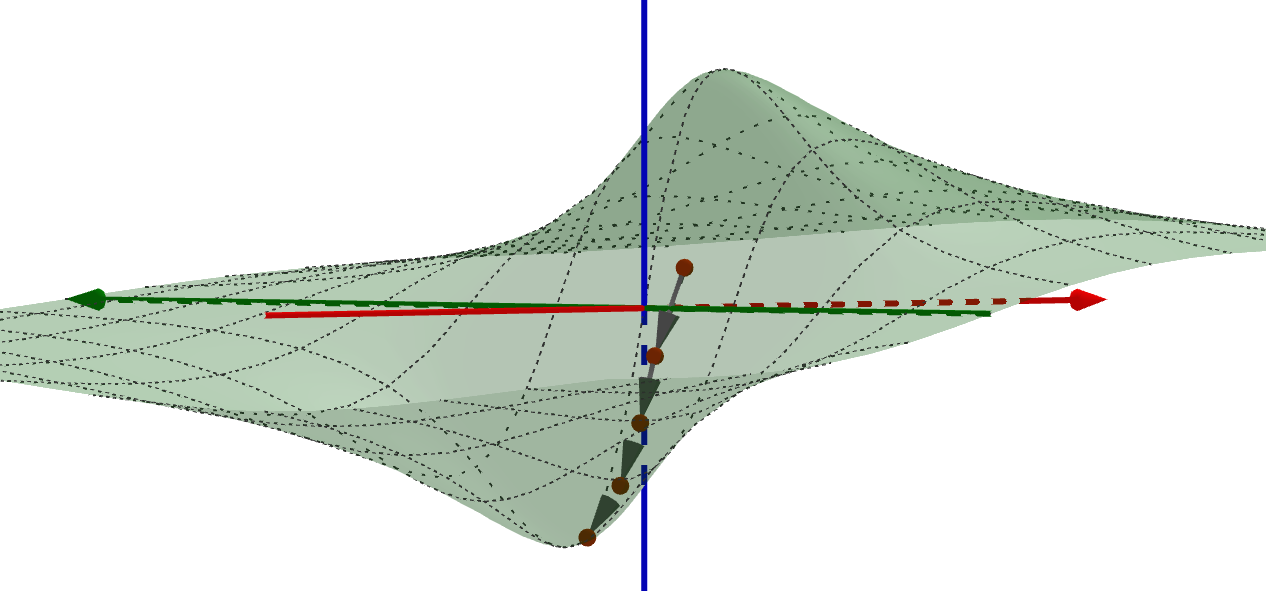
Gradientin nollakohtien etsimisen sijaan virhefunktion minimoinnissa käytetään erilaisia algoritmeja kuten gradienttimenetelmää. Siinä minimin etsiminen aloitetaan laskemalla tarkasteltavan funktion arvo aloitusparametreilla. Funktion gradientti kertoo nopeimman kasvun ja siten gradientin vastavektori nopeimman vähenemisen suunnan. Sopivilla askelilla nopeimman vähenemisen suuntaan siirtymällä löydetään (menetelmään sopiville funktioille) lokaali minimi.
Minimin etsimistä gradienttimenetelmällä havainnollistetaan usein yhden tai kahden muuttujan funktiolla. Kahden muuttujan tilanteessa funktion kuvaajan voi ajatella kumpuilevaksi maastoksi, missä rinteellä seisova ihminen haluaa mennä laakson pohjalle jyrkkyydestä välittämättä. Gradienttimenetelmän keinolla alas mennään vähän matkaa jyrkintä rinnettä (gradientin vastavektorin suuntaan), pysähdytään ja valitaan taas jyrkin suunta. Näin jatketaan, kunnes päästään laakson pohjalle. Huomaa, että jos maastossa on useita laaksoja, niin liian pitkä siirtymä yhteen suuntaan voi johtaa väärän laakson pohjalle.
Verkon opettamisen vaiheet
Vastavirta-algoritmia ja gradienttimenetelmää käytettäessä suoritetaan seuraavat tehtävät:
Syötetään opetusesimerkkijoukon
kaikki opetusesimerkit
verkolle.
Kaikille opetusesimerkeille
:
Lasketaan vastavirta-algoritmissa tarvittavat neuronikohtaiset summat
ja ulostulot
.
Lasketaan syötettä vastaavan virhefunktion osittaisderivaatat vastavirta-algoritmin avulla (ensin ulostulokerroksen painojen ja vakiotermien suhteen, sitten kerros kerrallaan alaspäin).
- Korjataan neuronien parametrit gradienttimenetelmän avulla. Matriisi- ja vektorimuodossa ilmoitettuna uudet parametrit ovat
missä
on verkon oppimisnopeus ja
opetusesimerkkijoukon
alkioiden lukumäärä.
Huomaa, että jos opetusesimerkkijoukko koostuu yhdestä syötteestä, niin yksittäisten neuronien uudet painot vastavirta-algoritmin jälkeen ovat
Gradienttimenetelmän eri versioita
(Satsi)gradienttimenetelmä (Gradient descent/ batch gradient descent/ vanilla gradient descent)
Perinteisessä gradienttimenetelmässä yksittäistä opetusesimerkkiä vastaava virhe
lasketaan jokaisen opetusesimerkin jälkeen ja minimoitavana virhefunktiona käytetään opetusesimerkkien virheiden summaa
missä
on opetusesimerkkijoukon alkioiden lukumäärä. Verkon parametrit päivitetään vasta, kun koko opetusesimerkkijoukko on käyty läpi. Jos parametrit laitetaan jonoon ja niistä muodostetaan vektori
, niin päivitetyt parametrit ovat
missä
on verkon oppimisnopeus ja virhefunktion osittaisderivaatat parametrien suhteen ovat gradientissa samassa järjestyksessä kuin parametrit vektorissa
.
Gradienttimenetelmässä koko opetusesimerkkijoukon tiedot ovat kerralla muistissa, ja verkko saattaa oppia hitaasti isoilla opetusesimerkkijoukoilla. Päivityksiä on vähän, joten menetelmä on virheen pienenemisen suhteen vakaa mutta se saattaa supeta liian aikaisin ja huonommilla parametreilla kuin stokastinen versio. Gradienttimenetelmällä löydetään globaali minimi konvekseille virhefunktioille (harvinainen tilanne) ja lokaali minimi ei-konvekseille virhefunktioille.
Stokastinen gradienttimenetelmä
Stokastisessa gradienttimenetelmässä virhe lasketaan ja neuronien parametrit päivitetään jokaisen opetusesimerkkijoukon syötteen jälkeen. Tällä menetelmällä saadaan nopea tieto verkon oppimisesta, sillä verkko oppii koko ajan. Menetelmä on helppo ymmärtää ja toteuttaa. Tiheä päivittäminen on kuitenkin hidasta, parametrien arvot saattavat heilua paljon päivittämisen aikana ja häiriöherkkyys voi hidastaa virhefunktion lokaalin minimin löytymistä. Joissain tilanteissa heiluminen on etu tavalliseen gradienttimenetelmään verrattuna - stokastinen versio saattaa päätyä pienempään lokaaliin minimiin.
Minisatsi gradienttimenetelmä (mini batch gradient descent)
Satsigradienttimenetelmä on perinteisen ja stokastisen gradienttimenetelmän välimuoto. Siinä opetusesimerkkijoukko jaetaan osajoukkoihin, jotka syötetään verkolle, lasketaan virhefunktio ja päivitetään parametrit. Tämä vähentää parametrien heiluntaa päivityksissä ja mahdollistaa paremman ja vakaamman suppenemisen lokaaliin minimiin kuin toisilla versioilla. Menetelmässä voidaan käyttää ohjelmakirjastojen tehokkaita lineaarialgebran laskurutiineja.
Lisätietoa gradienttimenetelmästä
Types of Optimization Algorithms used in Neural Networks and Ways to Optimize Gradient Descent
Ruder: An overview of gradient descent optimization algorithms
A Gentle Introduction to Mini-Batch Gradient Descent and How to Configure Batch Size
3Blue1Brown: Gradient descent, how neural networks learn | Deep learning, chapter 2
2.4.4 Virhefunktiot
Verkon oppimisen kannalta on tärkeää, että pieni muutos neuronin painossa aiheuttaa vain pienen muutoksen ulostulossa. Vastavirta-algoritmin vaiheita tutkiessa huomataan, että jos opetusesimerkkijoukon virhe saadaan keskiarvona yksittäisten opetusesimerkkien virheistä, niin opetusesimerkkijoukon virheen osittaisderivaatat saadaan laskettua opetusesimerkkien virheiden avulla.
Vastavirta-algoritmin yhteydessä käytettiin yksittäisen syötteen tuloksen
ja verkon antaman tuloksen
välisenä virheenä erotuksen euklidisen normin neliötä ja opetusesimerkkijoukon
virhefunktiona keskineliösummaa. Jos ulostulokerroksen arvot kuuluvat välille
, niin voidaan käyttää myös logistisen regression virhefunktiota (ristientropian virhefunktio, cross-entropy cost function),
missä vektorit
ovat syötteiden
tavoitteita ja vektorit
verkon antamia tuloksia ja
on opetusesimerkkijoukon koko.
Laskemalla nähdään, että Sigmoid-aktivointifunktiota käytettäessä tämän virhefunktion osittaisderivaatat neuroneiden painojen ja vakiotermien suhteen eivät riipu aktivointifunktion derivaatoista vaan pelkästään tavoitteiden ja tulosten erotuksista, ja
Siksi Sigmoid-funktion derivaatan pienuus suurilla ja pienillä arvoilla ei hidasta verkon oppimista niissä tapauksissa, joissa tavoitteet erovat paljon syötteistä.
Joissain lähteissä syöte-tavoite-parin välisistä virhefunktioista käytetään nimeä tappiofunktio (loss function) ja opetusesimerkkijoukon virhefunktiosta virhefunktio/maksufunktio (cost function).
Lisätietoa virhefunktioista
2.4.5 Yli- ja alisovittaminen (Overfitting/underfitting)
Neuroverkon ja yleisemmin koneoppimisen opettaminen suoritetaan opetusesimerkkien avulla, (toiminta varmistetaan ja oppimisnopeus- ja muita hyperparametreja säädetään vahvistusesimerkkijoukon (validation data) avulla) ja testataan testiesimerkkijoukolla. Tarkoitus on, että verkko osaa yleistää oppimansa ja toimii lopulta riittävän tarkasti tuntemattomalle datalle. Joskus käy niin, että verkko tuntuu oppivan hyvin mutta sitten tulee ongelmia:
- Opettamisen edetessä virhefunktion pieneneminen hidastuu tai tarkkuus huononee.
- Verkko toimii hyvin opetusesimerkeille mutta ei (opetusesimerkkien kaltaisille) vahvistus- tai testiesimerkeille.
Tätä ilmiötä sanotaan ylisovittamiseksi (overfitting). Siinä verkko on oppinut opetusesimerkkijoukon liian hyvin ja säätänyt parametrinsa sen erityisominaisuuksien ja häiriöiden mukaan. Ylisovittaminen on yleinen ongelma suurissa tuhansien parametrien neuroverkoissa joissa opetusesimerkkijoukko ei ole ole riittävän suuri suhteessa verkon kokoon.
Ylisovittamista voidaan estää seuraavilla tavoilla:
- opetusesimerkkijoukon kasvattaminen
- (verkon koon pienentäminen)
- opettamisen lopettaminen riittävän aikaisin (early stopping)
- neuroneiden osittainen poistaminen verkosta (dropout layer)
- painojen pienentämien L2- ja L1- säännöstelyllä (regularization)
Opetusesimerkkijoukon kasvattaminen
Opetusesimerkkijoukon koon kasvattaminen saattaa olla vaikeaa mutta joissain tilanteissa kokoa voi kasvattaa olemassaolevan datan avulla. Esimerkiksi uusia tunnistettavia kuvia saadaan helposti kiertojen, siirtojen ja skaalauksen avulla.
Aikainen lopettaminen
Verkon toimintaa testattaessa vahvistusesimerkkijoukolla opetusesimerkkijoukon jälkeen tarkastetaan tulosten tarkkuus jokaisen osajoukon jälkeen. Kun tarkkuus pienenee, lopetetaan.
Osittainen poistaminen
Yksi tapa pienentää ylisovittamista on neuroneiden hetkellinen poistaminen verkosta. Tässä tekniikassa osa piilokerrosten neuroneista poistetaan väliaikaisesti. Vajaaseen verkkoon syötetään opetusesimerkkejä, käytetään vastavirta-algoritmia ja päivitetään verkon parametrit. Tämän jälkeen poistetut neuronit palautetaan, poistetaan uusi neuronijoukko ja jatketaan opettamista. Menetelmässä jälkeen verkko on tavallaan keskiarvo monesta samaa tehtävää tekevästä verkosta. Koska neuroneiden lähellä olevat neuronit eivät välttämättä ole mukana jokaisella opetuskierroksella niin neuroneista tulee itsenäisempiä ja verkosta robustimpi. 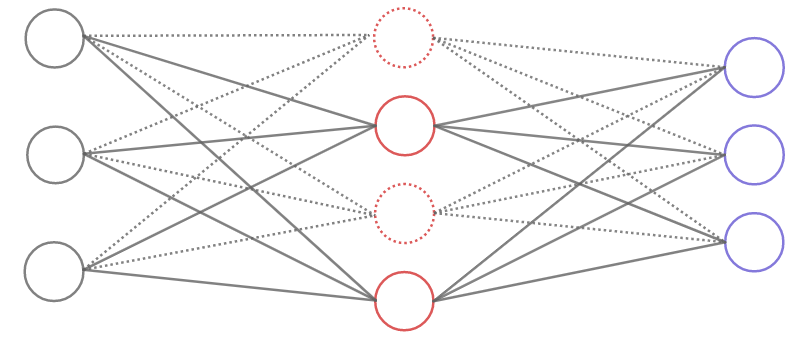
Säännöstely
Virhefunktion muuttaminen niin, että minimi löytyy pienillä painoilla perustuu siihen, että monesti verkot toimivat itseisarvoiltaan pienillä painoilla paremmin kuin suurilla. Säännöstelyssä virhefunktiota muutetaan niin, että minimi löytyy pienemmillä painoilla.
Jos verkossa on käytössä virhefunktio , niin L2-säännöstelyn virhefunktio on
missä
on opetusesimerkkijoukon koko,
ovat neuroneiden painot ja
on säännöstelyparametri. Neuroneiden vakiotermejä ei oteta mukaan säännöstelyosaan.
Virhefunktion jälkimmäinen osa on pieni kun painot ovat itseisarvoltaan pieniä. Minimoinnissa suuret painot ovat vain jos niillä saadaan alkuperäinen virhefunktio
hyvin pieneksi.
Virhefunktion osittaisderivaatat painojen
suhteen ovat
ja vakiotermien suhteen samat kuin alkuperäisellä virhefunktiolla
. Siten gradienttimenetelmän antamat uudet painot saadaan kaavalla
missä
on verkon oppimisnopeus.
Säännöstelyssä yritetään siis samanaikaisesti käyttää mahdollisimman pieniä painoja ja saada virhefunktio pieneksi.
L1-säännöstelyssä käytetään painojen neliöiden sijaan itseisarvoja. Virhefunktio on missä
on alkuperäinen virhefunktion,
on opetusesimerkkijoukon koko,
ovat neuroneiden painot ja
on säännöstelyparametri.
Virhefunktion osittaisderivaatat painojen
suhteen ovat
missä
, kun
,
, kun
ja nolla kun paino on nolla. Vakiotermien suhteen osittaisderivaatat ovat samat kuin alkuperäisellä virhefunktiolla
.
Gradienttimenetelmän antamat uudet painot saadaan kaavalla missä
on verkon oppimisnopeus.
L1-säännöstelyssä painot pienenevät askelilla, joiden pituus ei riipu painon koosta. L2-säännöstelyssä askeleen koko on paino kerrottuna vakiolla.
Alisovittamisessa verkon parametrit päivittyvät hyvin hitaasti ja verkko oppii huonosti.
Lisätietoa yli- ja alisovittamisesta
- A. Ng: Machine Learning, The Problem of Overfitting (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Regularization (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Why regularization reduces overfitting? (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Dropout Regularization (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Understanding Dropout (Coursera)
- A. Ng: Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization, Other regularization methods(Coursera)
- Chatbot's Life: Regularization in deep learning
- J. D. McCaffrey: Implementing Neural Network L2 Regularization
- J. D. McCaffrey: Neural Network L2 Regularization using Python, Visual Studio Magazine 09/2017
- M. Nielsen: Neural Networks and Deep learning, Chapter 3
2.4.6 Muita virhefunktion minimointikeinoja
Vastavirta-algoritmi ja muut osittaisderivaattoihin (gradientteihin) perustuvat menetelmät ovat monesti hitaita. Vastavirta-algoritmin tapauksessa hitaus johtuu paljosta laskemisesta: neuronien parametrien muutoksessa tarvittavia osittaisderivaattoja lasketaan koko ajan iteratiivisesti. Vastavirta-algoritmin erilaisilla muunnoksilla ja muilla verkon opetusmenetelmillä haetaan lisää nopeutta. Osassa menetelmiä käytettään ensimmäisen kertaluvun osittaisderivaattojen lisäksi toisen kertaluvun derivaattoja, joiden avulla saadaan tietoa ensimmäisen kertaluvun osittaisderivaattojen kasvusta.
3. Matematiikkaa
3.1 Analyysia
Tässä luvussa käydään läpi koneoppimisessa käytettävien menetelmien taustalla olevaa matemaattista analyysia ilman perinteistä määritelmä, lause, todistus-rakennetta. Aiheesta löytyy lisätietoa, esimerkkejä ja tehtäviä lukemattomista Calculus-nimisistä kirjoista.
Neuroverkkoja käsiteltäessä tarvitaan perustietoja funktioista ja niiden ominaisuuksista. Gradientteihin perustuvissa verkon opetusmenetelmissä kuten vastavirta-algoritmissa tarvitaan esimerkiksi monen muuttujan funktioiden osittaisderivaattoja laskusääntöineen ja jonkin verran ääriarvoteoriaa.
3.1.1 Funktio
Olkoot ja
joukkoja. Funktio eli kuvaus joukosta
joukkoon
on sääntö, joka liittää jokaiseen joukon
alkioon
täsmälleen yhden joukon
alkion
.
Joukkoa sanotaan funktion
lähtöjoukoksi (domain) ja joukkoa
maalijoukoksi (target set). Tällaista funktiota merkitään
Alkiota
sanotaan alkion
kuvaksi tai funktion
arvoksi pisteessä
. Joukko
on funktion
arvojoukko/kuvajoukko (range).
Jos , niin joukon
alkukuva kuvauksessa
on joukko
Joukko on
-ulotteinen euklidinen avaruus. Sen alkiot ovat vektoreita
, missä
kaikilla
.
Euklidisen avaruuden väli on karteesinen tulo reaaliakselin väleistä ,
, missä väli
voi olla muotoa
(suljettu),
(avoin),
tai
. Väli
on avoin/suljettu, jos kaikki välit
ovat avoimia/suljettuja. Jos
ja
kaikilla
, niin väli
on
.
Pisteiden ja
välistä etäisyyttä mitataan euklidisesta normista
saatavalla metriikalla
Tällä kurssilla käsitellään funktioita , missä
on väli.
Funktion kuvaaja eli graafi on joukko
ja reaalilukujen
alkukuvat
ovat funktion
tasa-arvojoukkoja, joita tapauksessa
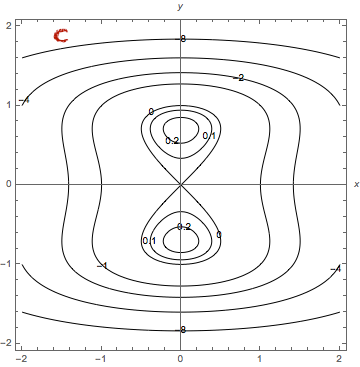
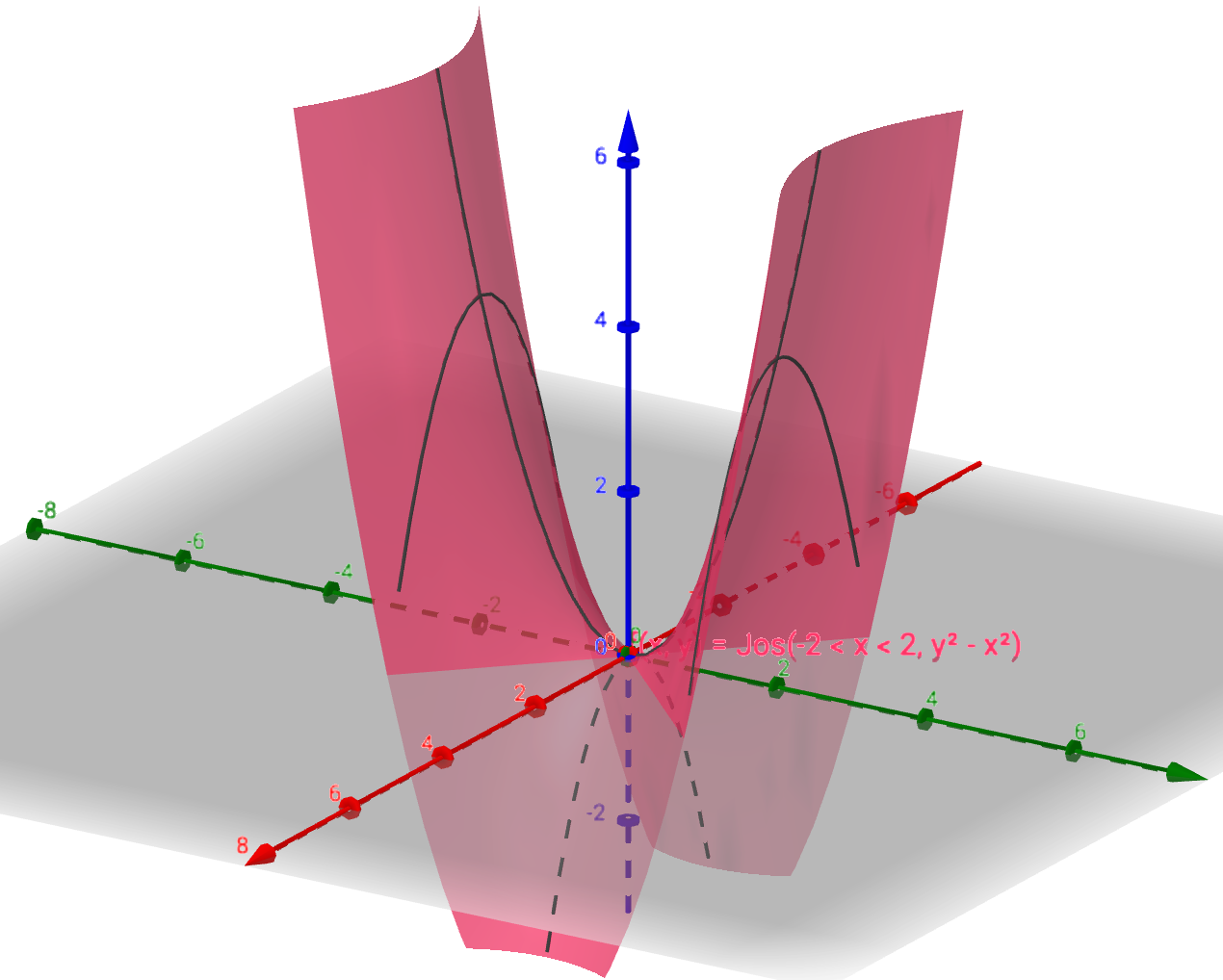
kutsutaan myös tasa-arvokäyriksi. Tasa-arvokäyriä käytetään funktion graafien piirtämiseen ja funktion kasvuvauhdin ja -suunnan tutkimiseen gradientin avulla. Topografisen kartan korkeuskäyrät ovat korkeusfunktion tasa-arvokäyriä. Tasa-arvokäyriä määritettäessä voi ensin piirtää käyrät
kolmiulotteiseen tasoon. Nämä käyrät saadaan tasojen
ja funktion kuvaajan leikkauksina. Vastaavat tasa-arvokäyrät saadaan käyrien
projektioina
-tasoon.
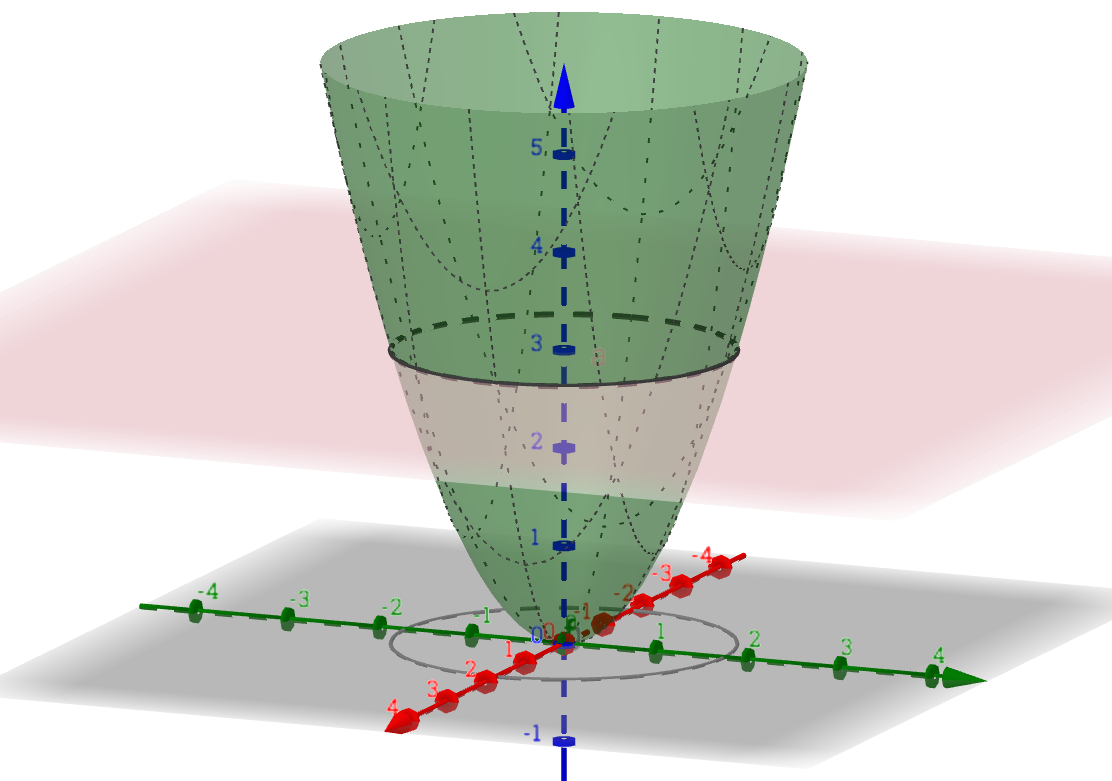
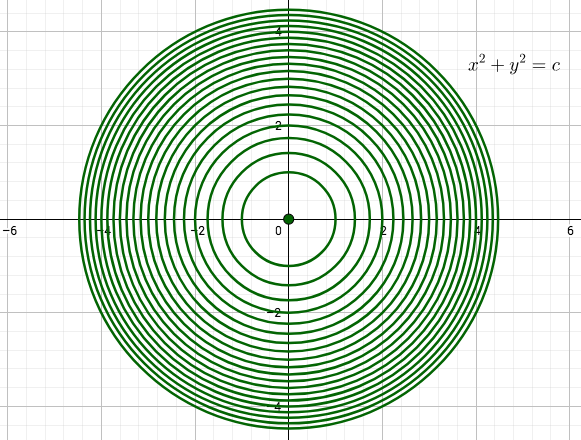
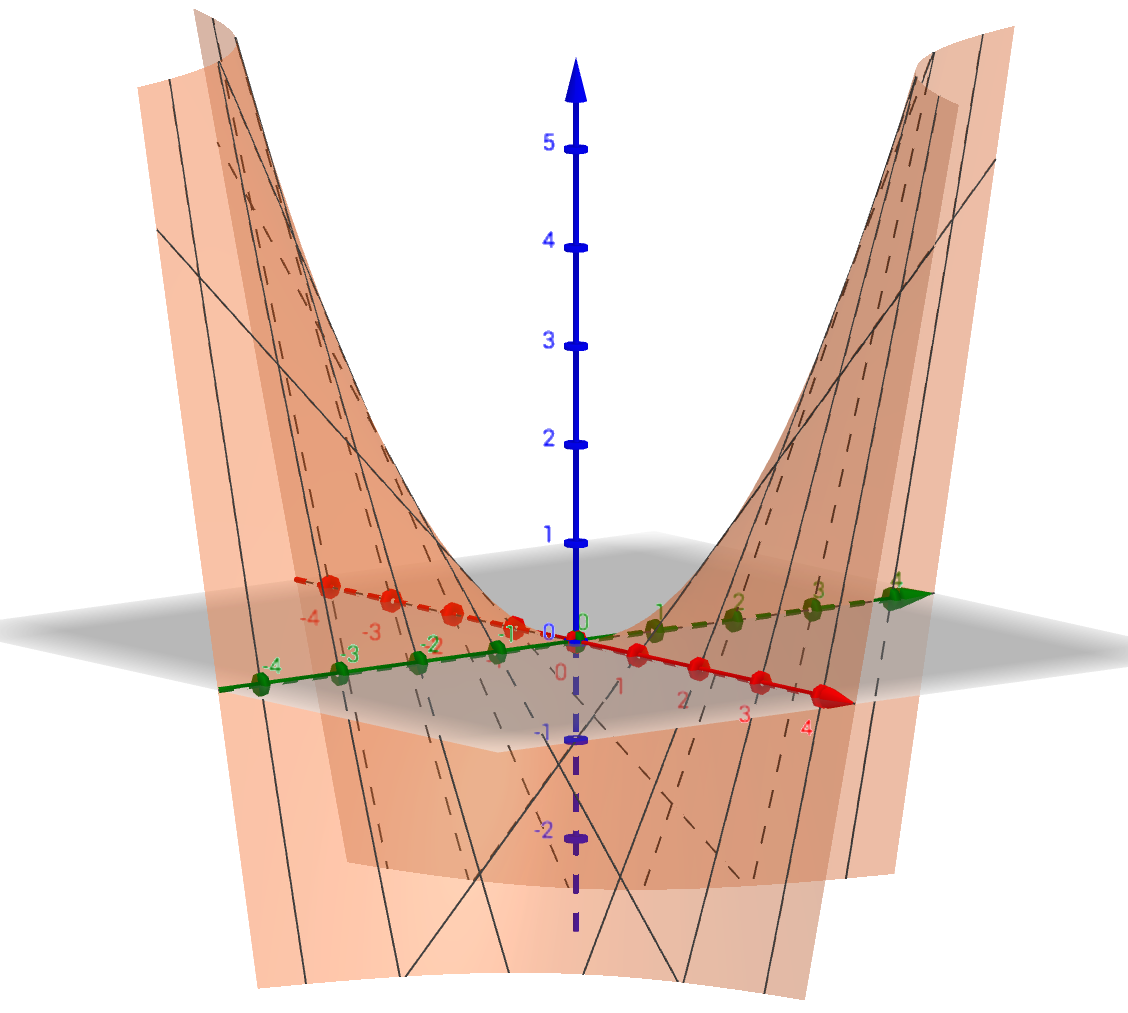
Esimerkki
Olkoon ,
. Funktion
kuvaaja on ylöspäin aukeava paraboloidi, jonka huippu on origossa. Kun
, niin tasa-arvokäyrät
ovat ympyröitä, joiden keskipiste on origo ja säde
. (Jos
, niin tasa-arvokäyrät ovat tyhjiä joukkoja sillä
kaikilla
.)
3.1.2 Harjoitustehtäviä
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Piirrä funktion
,
kuvaaja ja tasa-arvokäyrät.
Yhdistä funktioiden kuvaajat ja tasa-arvokäyrät.
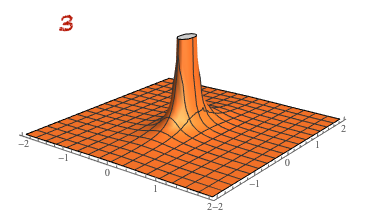
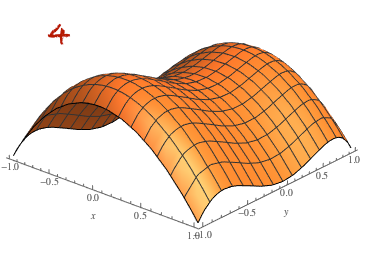
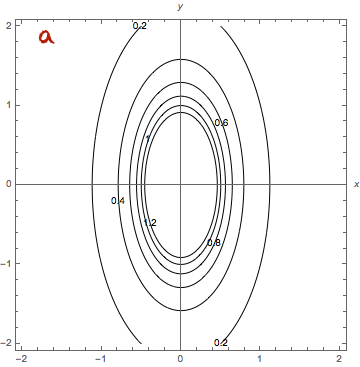
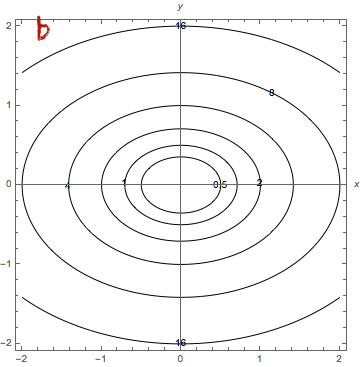
Affiini funktio
Neuroverkon piilo- ja ulostulokerroksen neuroneissa lasketaan edellisestä kerroksesta tulleiden syötteiden painotettu summa ja lisätään siihen vakiotermi. Jokaista neuronia vastaa siis affiini funktio, joka viedään aktivointifunktiolle.
Olkoon
-matriisi ja
. Funktio
,
missä
on matriisin
ja vektorin
tulo, on affiini funktio.
Affiini funktio voi kääntää, skaalata ja siirtää joukkoa. Se säilyttää joitakin geometrisia ominaisuuksia sillä se kuvaa suorat suoriksi, yhdensuuntaiset suorat yhdensuuntaisiksi ja säilyttää janojen osien suhteet. Kuvaus siis kuvaa pistejoukon uudelleen kääntäen, venyttäen, siirtäen joukon paikkaa tai skaalaten joukon kokoa. Jos , niin affiini funktio on lineaarikuvaus. Jos
, niin
, joten kuvaus ei ole lineaarinen. Huomaa, että monissa lähteissä affiinia funktiota sanotaan virheellisesti lineaariseksi.
Affiini funktio on yhdistetty funktio lineaarikuvauksesta
,
ja siirrosta
,
.
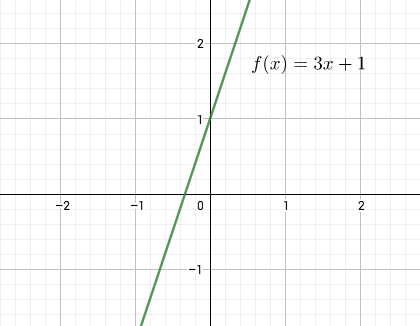
Esimerkki
Jos , niin affiinin funktion
,
kuvaaja on suora, jonka kulmakerroin on
ja joka leikkaa
-akselin pisteessä
.
Kasvava ja vähenevä funktio
Olkoon väli ja olkoon
funktio. Jos
aina kun
, niin funktio
on kasvava (increasing). Jos
aina kun
, niin funktio
on vähenevä (decreasing).
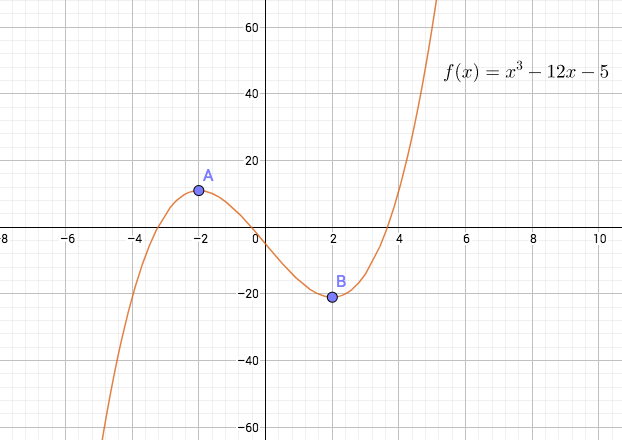
Esimerkki
Funktio ,
on kasvava väleillä
ja
. Se on vähenevä välillä
.
Yhdistetty funktio
Neuroverkkojen neuroninin syöte seuraavalle kerrokselle saatiin laskemalla painotettu summa edellisen kerroksen syötteistä, lisäämällä siihen neuronin vakiotermi ja viemällä summa aktivointifunktiolle . Tässä on kyse yhdistetystä funktiosta: aktivointifunktion arvo lasketaan summafunktion antamassa pisteessä. Yleisesti yhdistetty funktio määritellään seuraavasti.
Olkoot ,
ja
joukkoja. Olkoot
ja
funktioita. Yhdistetty funktio (composite function) on funktio
,
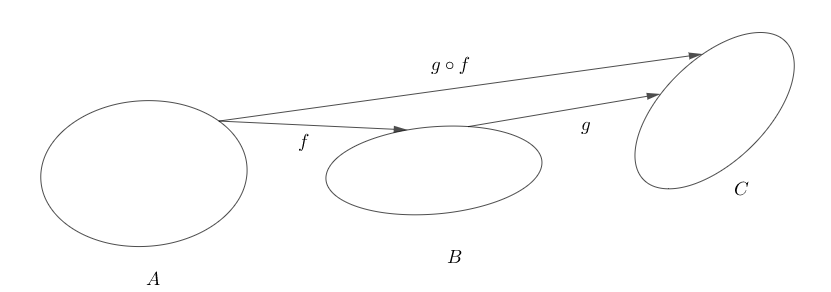
Esimerkki
Olkoot ,
ja
. Näiden funktioiden yhdistetty funktio on
,
3.1.3 Derivaatta
Vastavirta-algoritmissa laskettavissa virhefunktion osittaisderivaatoissa tarvitaan aktivointifunktion derivaattaa ja derivoinnin ketjusääntöä. Verkon oppimisen tarkastelussa on hyvä olla käsitys siitä, mitä derivaatta kertoo funktiosta: lähellä nollaa oleva derivaatta kertoo, että funktion arvot muuttuvat hitaasti ja derivaatan suuri itseisarvo kertoo, että funktio muuttuu nopeasti.
Funktion derivaatta määritellään erotusosamäärien raja-arvona. Tarkastellaan, paljonko funktion arvo
muuttuu kun pistettä
siirretään vähän, pienen luvun
verran, joko oikealle tai vasemmalle. Muutosta tutkitaan keskimääräisenä muutoksena eli erotusosamääränä, jossa funktion arvojen erotus jaetaan siirtymällä
,
Geometrisesti tulkittuna erotusosamäärä kertoo pisteiden ja
kautta kulkevan suoran eli näiden pisteiden kautta kulkevan sekantin kulmakertoimen.
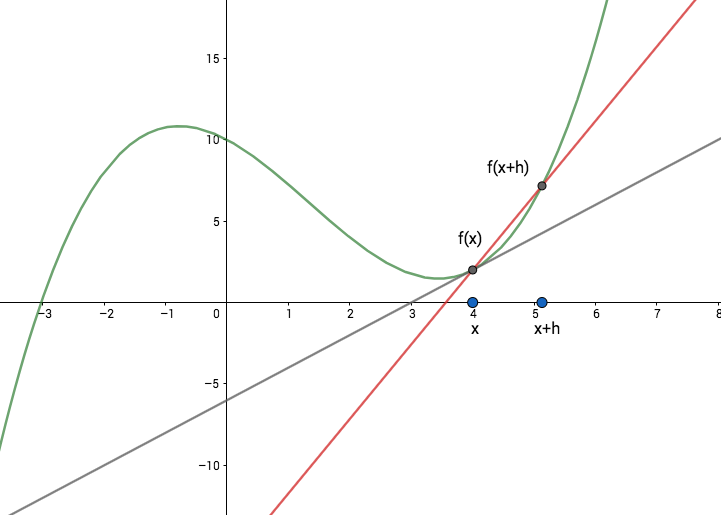
Jos tällä erotusosamäärällä on äärellinen raja-arvo kun muutos lähestyy nollaa, niin kyseinen raja-arvo on funktion
derivaatta (derivative)
pisteessä
,
Huomautus
Erotusosamäärässä siirtymä
voi olla myös negatiivinen.
Edellä määriteltiin derivaatta koko reaaliakselilla määritellyille funktioille. Jos
on määritelty avoimella välillä
, niin erotusosamäärää tutkittaessa otetaan mukaan pisteet
ja ne siirtymät, joille
.
Funktion
derivaatalle käytetään monesti derivointimuuttujan
sisältävää merkintää
tai
. Leibniziltä peräisin olevassa merkinnässä erotusosamäärää merkitään
ja derivaattaa
Tangenttitulkinta
Geometrisesti tulkittuna funktion derivoituvuus pisteessä kertoo, että funktion kuvaajalle voidaan piirtää pisteeseen
yksikäsitteinen tangentti, jolla on äärellinen kulmakerroin. Derivaatan arvo
on tangentin kulmakerroin ja tangentin yhtälö on
missä
.
Pisteessa derivoituvalle funktiolle muutoksen
pienentyessä erotusosamääriä vastaavien sekanttien kulmakertoimien raja-arvo on siis tangentin kulmakerroin ja sekantit lähestyvät tangenttia. Mitä suurempi kulmakerroin on, sitä jyrkempi tangentti on. Positiivisilla kulmakertoimilla suora on nouseva ja negatiivisilla laskeva.
Tangenttitulkinnalla on helppo huomata, että pisteessä epäjatkuva funktio ei ole derivoituva. Sen kuvaajalle ei voi piirtää tangenttia epäjatkuvuuskohdassa. Jos tangentti on pystysuora, sillä ei ole äärellistä kulmakerrointa, eikä funktio ole derivoituva kyseisessä pisteessä.
Esimerkki
Tarkastellaan itseisarvofunktiota ,
. Tangenttitulkinnan avulla voidaan päätellä, että
ei ole derivoituva pisteessä
. Itseisarvofunktion kuvaajalla ei ole pisteessä
yksikäisytteistä tangenttia vaan niitä on äärettömän monta. (Samaan tapaan voi päätellä, että funktio, jonka kuvaajassa on kärki, ei ole derivoituva kärkeä vastaavassa pisteessä.)
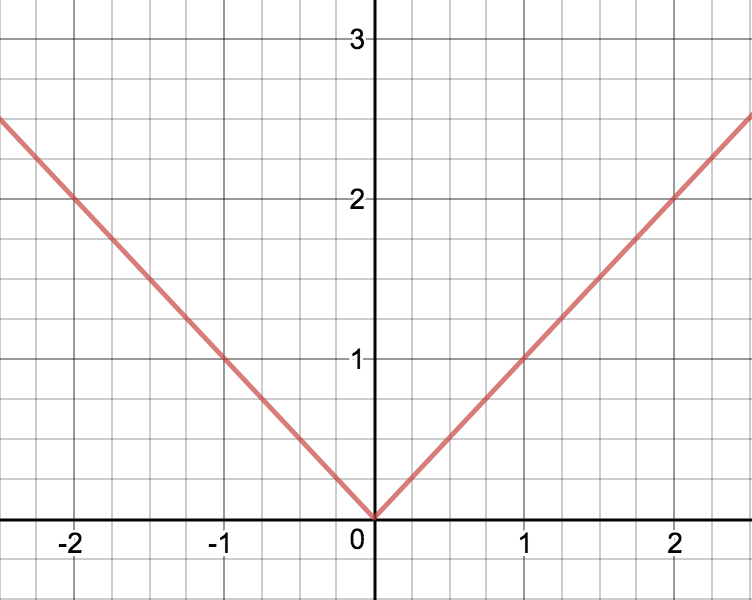
Erotusosamäärää tutkittaessa huomataan, että nollassa vasemman- ja oikeanpuoleinen raja-arvo ovat erisuuret eli raja-arvoa ei ole olemassa. Kun , niin
ja kun
, niin
Siten
ei ole derivoituva nollassa.
Derivoituvien funktioiden ominaisuuksia
Derivoituvilla funktioilla on seuraavia hyviä ominaisuuksia, joita ei todisteta tässä.
Olkoot ja
derivoituvia funktioita ja
.
Summa
, vakiolla kerrottu funktio
, tulo
ja osamäärä
ovat derivoituvia ja
missä osamäärän derivaatta on olemassa niissä pisteissä, joissa
.
Jos
on derivoituva pisteessä
, niin se on jatkuva pisteessä
.
Joidenkin funktioiden derivaattoja
, kaikilla
,
,
,
ja
,
, kun
.
Leibnizin derivaattamerkintä on joskus kätevä yhdistetyn funktion derivaattojen yhteydessä. Merkitään ,
ja
. Funktioiden
ja
derivaatat Leibnizin merkinnöin ovat
ja
. Ketjusääntö tässä muodossa on
Esimerkki
Olkoon ,
Funktio
on yhdistetty funktio
kolmesta funktiosta
,
ja
. Ketjusääntöä kahteen kertaan käyttämällä saadaan
Derivaatta ja funktion käyttäytyminen
Derivaatan merkki ja suuruus kertoo paljon funktion käyttäytymisestä. Jos funktion derivaatta on positiivinen avoimella välillä, niin funktio on kasvava tällä välillä. Jos derivaatta on negatiivinen jollain avoimella välillä, niin funktio on vähenevä. Derivaatta on nolla jos tangentin kulmakerroin on nolla eli tangentti on -akselin suuntainen.
Jos funktio saavuttaa pisteessä suurimman tai pienimmän arvonsa, niin tässä pisteessä on
. Huomaa, että derivaatta voi olla nolla vaikka piste ei olisikaan funktion ääriarvopiste.
3.1.4 Harjoitustehtäviä
Olkoot
. Laske vakiofuntion
,
kaikilla
ja affinin funktion
,
kaikilla
, derivaatat erotusosamäärän avulla.
Todista joku derivaatan laskusääntö ominaisuuksia -kohdasta.
Reaalifunktion ääriarvoista
Funktion suurimman tai pienimmän arvon etsiminen on optimointitehtävä, jonka ratkaisemisessa hyödyllisiä työkaluja ovat derivaatta ja raja-arvot.
Olkoon väli ja olkoon
funktio. Olkoon
.
Jos
kaikilla
, niin
on funktion
maksimipiste ja
(globaali) maksimi eli suurin arvo.
Jos
kaikilla
, niin
on funktion
minimipiste ja
(globaali) minimi eli pienin arvo.
Suurinta ja pienintä arvoa kutsutaan yhteisellä nimellä globaalit ääriarvot. Globaalien ääriarvojen lisäksi voidaan tutkia funktion käyttäytymistä pisteen lähellä ja määritellä funktion
lokaalit eli paikalliset ääriarvot.
Jos on
, siten, että
kaikilla
, niin
on funktion
lokaali maksimipiste ja
lokaali maksimi eli suurin arvo.
Jos on
, siten, että
kaikilla
, niin
on funktion
lokaali minimipiste ja
lokaali minimi eli pienin arvo.
Huomaa, että funktiolla ei aina ole suurinta ja pienintä arvoa. Esimerkiksi funktio ,
, on rajoittamaton ja
ja
ja
kaikilla
. Siten funktiolla ei ole suurinta eikä pienintä arvoa. Suljetulla välillä määritellyille jatkuville funktioille ääriarvot ovat aina olemassa.
Lause (Ääriarvolause)
Olkoon jatkuva funktio. Tällöin funktio
saavuttaa välillä
suurimman ja pienimmän arvonsa.
Funktion derivaatta, mikäli se on olemassa, on hyödyllinen työkalu ääriarvojen etsimisessä. Derivaatan määritelmän avulla on helppo näyttää, että jos funktiolla on lokaali ääriarvo pisteessä
ja
on derivoituva pisteessä
, niin
. Suljetulla välillä määritellyn funktion ääriarvoja etsittäessä riittää siis selvittää funktion arvo niissä pisteissä, joissa derivaatta on nolla, niissä pisteissä, joissa derivaattaa ei ole olemassa ja välin päätepisteissä. Derivaatan nollakohtia ja pisteitä, joissa derivaattaa ei ole olemassa, sanotaan kriittisiksi pisteiksi (critical points). Muulla kuin suljetulla välillä määritellylle funktiolle pitää tutkia funktion käyttäytymistä välin päätepisteissä esimerkiksi raja-arvojen avulla.
Esimerkki
Edellisen esimerkin funktion derivaatan nollakohdat antavat lokaalit ääriarvot. Nollakohdista
on lokaali maksimipiste ja
lokaali minimipiste. Koska
, niin funktiolla
ei ole globaaleja ääriarvoja.
Esimerkki
Derivaatta voi olla nolla, vaikka nollakohta ei olisikaan ääriarvopiste. Funktiolle on
ja funktio
ei ole derivoituva nollassa, joten
on molempien funktioiden kriittinen piste. Se ei kuitenkaan ole ääriarvopiste sillä
ja
kun
ja
ja
kun
. Funktioilla ei ole globaaleja ääriarvoja sillä
. Jos rajoitutaan suljetulle välille
, niin
on molempien funktioiden globaali minimipiste ja
globaali maksimipiste.
3.1.5 Harjoitustehtäviä
- Etsi funktion
,
ääriarvot. Etsi funktion
ääriarvot välillä
.
Lisätietoa derivaatoista
3.1.6 Osittaisderivaatat ja gradientti
Verkkoa opetettaessa minimoidaan virhefunktiota, jonka arvo riippuu verkon parametreista eli neuronien painoista ja vakiokertoimista. Virhefunktio on siis funktio useampiulotteisesta avaruudesta reaaliluvuille, , missä
on verkon parametrien lukumäärä. Useammasta kuin yhdestä parametrista riippuvan funktion ääriarvojen etsiminen on yhden muuttujan funktion minimiointia/maksimointia haastavampi tehtävä. Lausetta vastaava ääriarvolause on totta korkeampiulotteisessakin tilanteessa: kompaktissa (suljettu ja rajoitettu) joukossa jatkuva funktio saavuttaa suurimman ja pienimmän arvonsa.
Useamman muuttujan funktion osittaisderivaatta kertoo, miten funktio muuttuu yhden muuttujansa funktiona. Osittaisderivaatta saadaan pitämällä muita muuttujia vakiona ja laskemalla derivaatta tutkittavan muuttujan suhteen kuten tavallinen derivaatta kaavassa.
Osittaisderivaatta
Olkoon , olkoon
ja olkoon
. Jos erotusosamäärällä
on äärellinen raja-arvo, niin se on funktion
. osittaisderivaatta eli osittaisderivaatta muuttujan
suhteen pisteessä
,
Osittaisderivaattojen geometrinen tulkinta
Tarkastellaan osittaisderivaattojen geometrista tulkintaa kahden muuttujan funktiolle . Olkoon
. Pystysuoran tason
ja funktion kuvaajan muodostaman pinnan
leikkaus on käyrä
Tämä käyrä on funktion
kuvaaja tasossa
. Funktion
osittaisderivaatta muuttujan
suhteen pisteessä
on käyrän
tangentin kulmakerroin pisteessä
. Osittaisderivaatta
antaa siis funktion arvojen muutosvauhdin muuttujan
suhteen kun muuttuja
pidetään vakiona.
Esimerkki
Olkoon ,
. Funktion
osittaisderivaatat ovat
Kuva havainnollistaa osittaisderivaattaa
pisteessä
. Äskeisen tulkinnan taso
ja
ja tangentin kulmakerroin pisteessä
on
.
Yhden muuttujan funktiolle derivaatta on kuvaajan tangentin kulmakerroin. Tasossa määritellylle funktiolle osittaisderivaatat
ja
ovat kuvaajan tangenttitason kaltevuuskertoimia. Olkoon
. Funktion
kuvaajan tangenttitaso pisteessä
saadaan yhtälöstä
Funktion kuvaajan tangenttitaso pisteessä
on taso, joka sisältää kaikki ne pisteen
kautta kulkevat suorat, jotka ovat tangentteja jollekin kuvaajalla sijaitsevalle pisteen
kautta kulkevalle käyrälle. Tangenttitaso sivuaa kuvaajaa pisteessä
ja kaikista pisteen
kautta kulkevista tasoista se on se, jolla on pisteessä
samat osittaisderivaatat kuin funktiolla
.
Esimerkki
Olkoon ,
Etsitään funktion
tangenttitaso pisteessä
(ja kerrataan samalla trigonometrisia funktioita). Nyt
,
joten
ja
Siten tangenttitaso pisteessä
saadaan yhtälöstä
3.1.7 Harjoitustehtäviä
Olkoon
,
Laske funktion
osittaisderivaatat
ja
pisteessä
. Piirrä kuvia.
Olkoon
,
Laske funktion
osittaisderivaatat
ja
.
Olkoon
,
Määritä funktion
kuvaajan tangenttitaso pisteessä
.
Onko 3. tehtävän funktio f(x,y)=x cos (y-ye^x) vai f(x,y) = x cos (y) -ye^x ?
—siis mikä on olevinaan piste (0,0,f(0,0)) ?
—- tehtävässä ei ole sulkuja, joten jälkimmäinen vaihtoehto. f on kahden muuttujan funktio, jolle f(0,0)=0-0=0. Piste on siis (0,0,0).
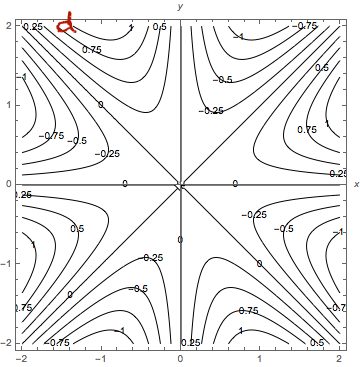
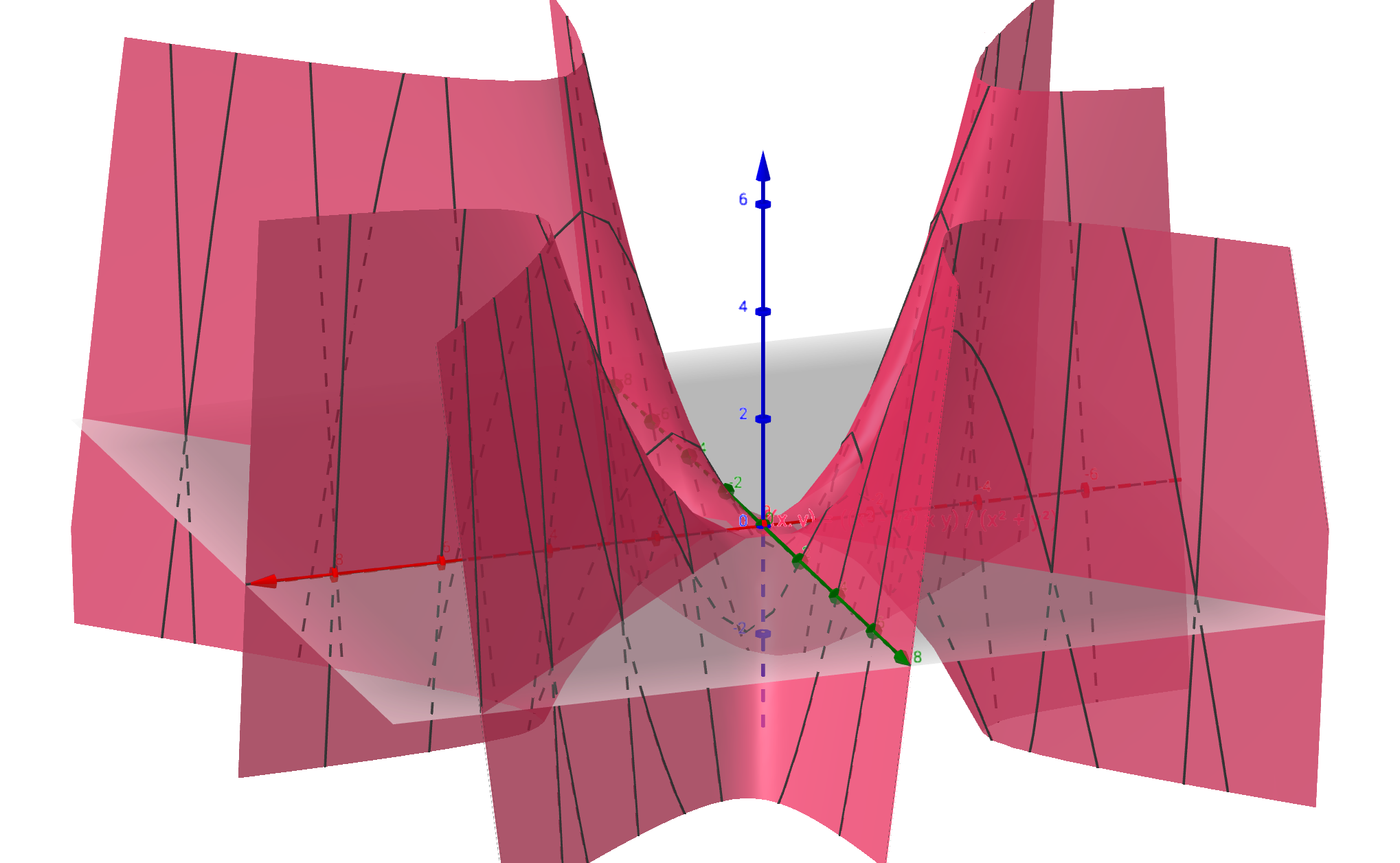
Gradientti ja sen geometrinen tulkinta
Olkoon funktio, jolla on osittaisderivaatat kaikkien muuttujien
,
suhteen. Osittaisderivaatoista muodostettu vektori
on funktion
gradientti.
Funktion gradientti voidaan ajatella funktioksi
,
Tällaista funktiota voidaan havainnollistaa vektorikentällä, jossa jokaiseen tason pisteeseen piirretään vektori, jonka suunta ja pituus saadaan funktion arvosta kyseisessä pisteessä. Monesti pituus skaalataan tai ilmaistaan väreillä.
Esimerkki
Olkoon
,
. Funktion
gradientti on
Olkoon
,
. Funktion
gradientti on
Funktioiden ja
gradientteja voidaan havainnollistaa vektorikentillä.
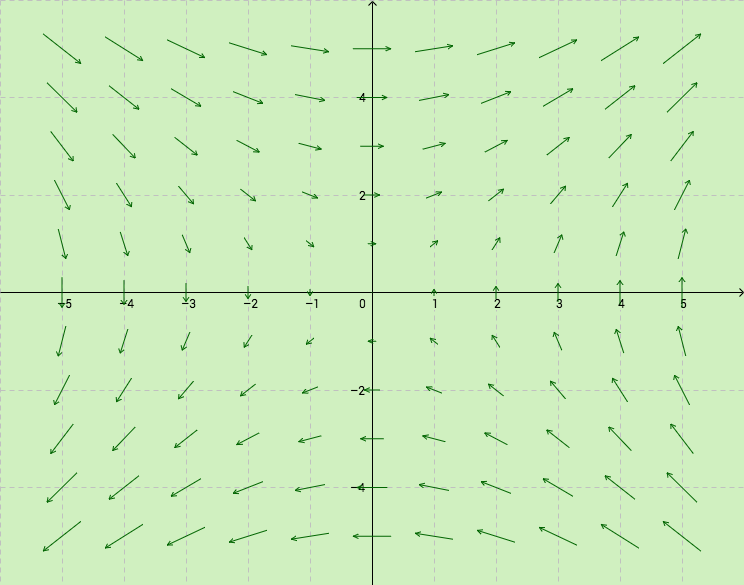
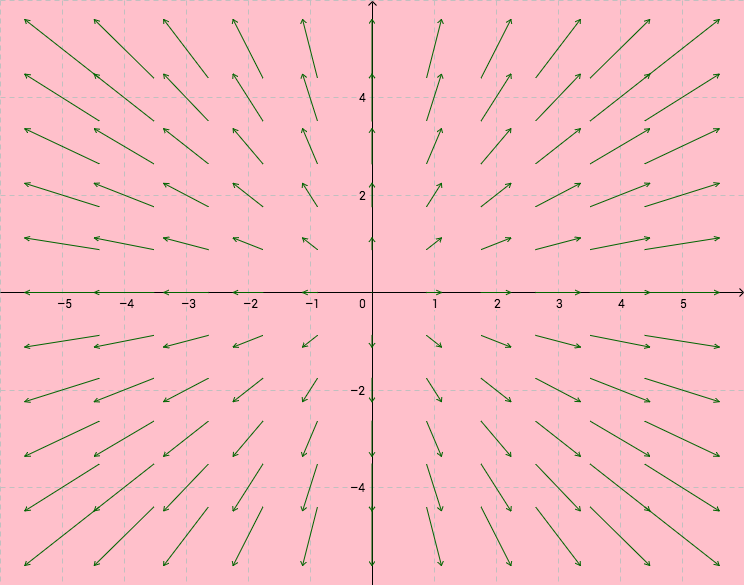
Osittaisderivaatat kertovat funktion kasvunopeuden koordinaattiakseleiden suuntiin ja funktion gradientti
pisteessä
kertoo suunnan, johon funktio
kasvaa nopeimmin. Gradientin pituus eli vektorin
normi kertoo funktion kasvuvauhdin. Se, että gradientti antaa nopeimman kasvun suunnan, todistetaan suuntaisderivaattojen avulla. (Ne määritellään samaan tapaan kuin osittaisderivaatat mutta erotusosamäärässä käytetään kantavektoreiden
sijaan vektoria
, jonka suuntaan funktion kasvunopeus halutaan määrittää.)
Gradientin geometrisessa tulkinnassa käytetään vektorikentän lisäksi apuna tasa-arvokäyriä.
Esimerkki
Esimerkistä tutun funktion ,
tasa-arvokäyrät ja gradienttien
vektorikenttä piirrettynä samaan kuvaan.
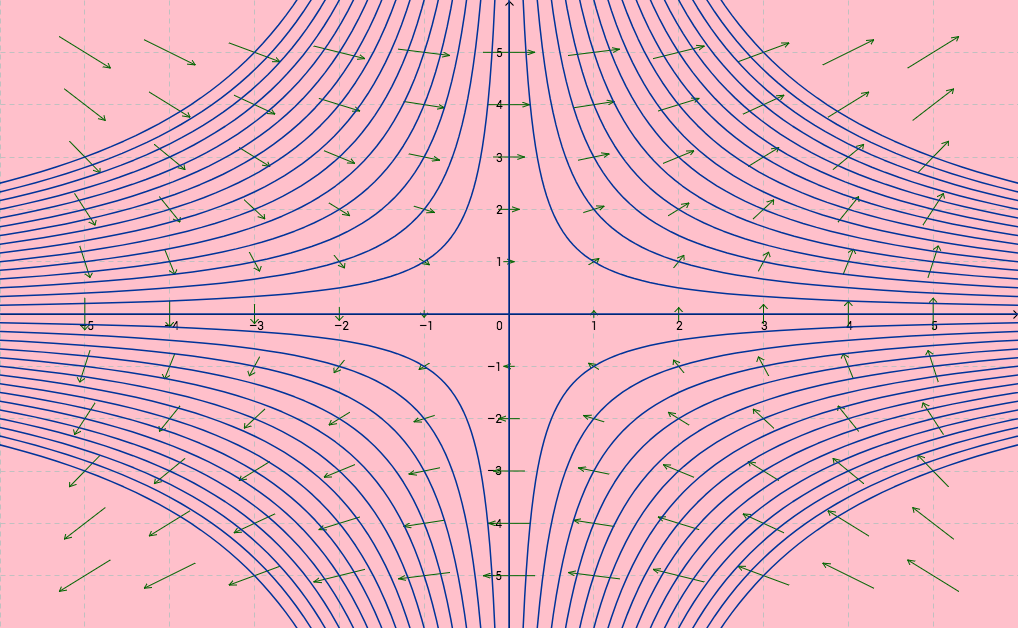
Esimerkin kuvassa funktion gradienttivektorit ovat kohtisuorassa tasa-arvokäyriä vastaan. Tämä ei ole sattumaa vaan gradienttivektorit ovat aina kohtisuorassa tasa-arvojoukkoja vastaan. Funktioiden tapauksessa tätä ominaisuutta voi pohtia seuraavasti: olkoon
funktion
jokin tasa-arvokäyrä ja olkoon piste
tällä käyrällä. Halutaan, että funktion arvo kasvaa annetun määrän ja etsitään suuntaa, jossa tämä muutos saavutetaan siirtämällä pistettä
vähiten. Pienin siirto tulee siihen suuntaan, jossa isompia arvoja vastaavat tasa-arvokäyrät ovat tiheimmässä. Toisaalta gradientti osoittaa suurimman kasvunopeuden suuntaan. Pienessä mittakaavassa katsottuna eli pienellä arvon
lisäyksellä tasa-arvokäyrät ovat suoria ja kahden samansuuntaisen suoran välisen lyhimmän matkan antaa suora, joka on kohtisuorassa edellisiä suoria vastaan.
Ääriarvoista
Neuroverkkoa koulutettaessa halutaan minimoida monesta parametrista riippuvaa virhefunktiota. Yhden muuttujan funktioiden ääriarvojen etsiminen derivaatan nollakohtien avulla yleistyy useamman muuttujan funktion tilanteeseen niin, että mahdolliset ääriarvopisteet ovat ne pisteet, joissa kaikki osittaisderivaatat ovat nollia.
Olkoon väli.
Jos on
, siten, että
kaikilla
, joille
, niin
on funktion
lokaali maksimipiste ja
lokaali maksimi eli suurin arvo.
Jos on
, siten, että
kaikilla
, joille
, niin
on funktion
lokaali minimipiste ja
lokaali minimi eli pienin arvo.
Globaalit ääriarvot ja ääriarvopisteet määritellään kuten yhden muuttujan funktion tapauksessa.
Yhden muuttujan jatkuvan funktion ääriarvojen olemassaolotulos pätee myös yleisemmässä tapauksessa. (Tulos on totta yleisemmällekin määrittelyjoukolle kuin suljetuille väleille. Riittää, että joukko on kompakti eli suljettu ja rajoitettu.)
Lause (Ääriarvolause)
Olkoon suljettu ja rajoitettu väli. Olkoon
jatkuva funktio. Tällöin funktio
saavuttaa välillä
suurimman ja pienimmän arvonsa.
Funktioiden kuvaajia katsottaessa on intuitiivisesti selvää, että funktion lokaaleissa ääriarvopisteissä tangettitaso on vaakasuorassa eli
-tason suuntainen. Tällaisten tasojen yhtälöt ovat muotoa
, joten tangenttitason yhtälön perusteella nähdään, että funktion osittaisderivaatat muuttujien
ja
suhteen ovat nollia ja että kuvaajan tangenttitason yhtälö pisteessä
on
.
Osittaisderivaattojen nolluus ääriarvopisteissä yleistyy myös useamman muuttujan funktioille. Derivaatan määritelmän ja yhden muuttujan funktion tulosten avulla on helppo näyttää, että jos funktiolla ,
, on lokaali ääriarvo pisteessä
ja funktiolla
on osittaisderivaatat pisteessä
, niin
kaikilla
eli
Suljetulla välillä määritellyn funktion ääriarvoja etsittäessä riittää siis selvittää funktion arvo niissä pisteissä, joissa gradientti on nolla, niissä pisteissä, joissa jotain osittaisderivaattaa ei ole olemassa ja välin reunapisteissä. Gradientin nollakohtia ja pisteitä, joissa jotain osittaisderivaattaa ei ole olemassa, sanotaan kriittisiksi pisteiksi (critical points). Muulla kuin suljetulla välillä määritellylle funktiolle pitää tutkia funktion käyttäytymistä välin reunapisteissä esimerkiksi raja-arvojen avulla.
Esimerkki
Olkoon ,
. Nyt
Yhtälöparin
ainoa ratkaisu on
, joten piste
on funktion
ainoa kriittinen piste ja funktion
kuvaajan tangenttitaso siinä pisteessä on
. Se, että
on funktion globaali maksimipiste selviää tutkimalla funktion
raja-arvoja kun
.
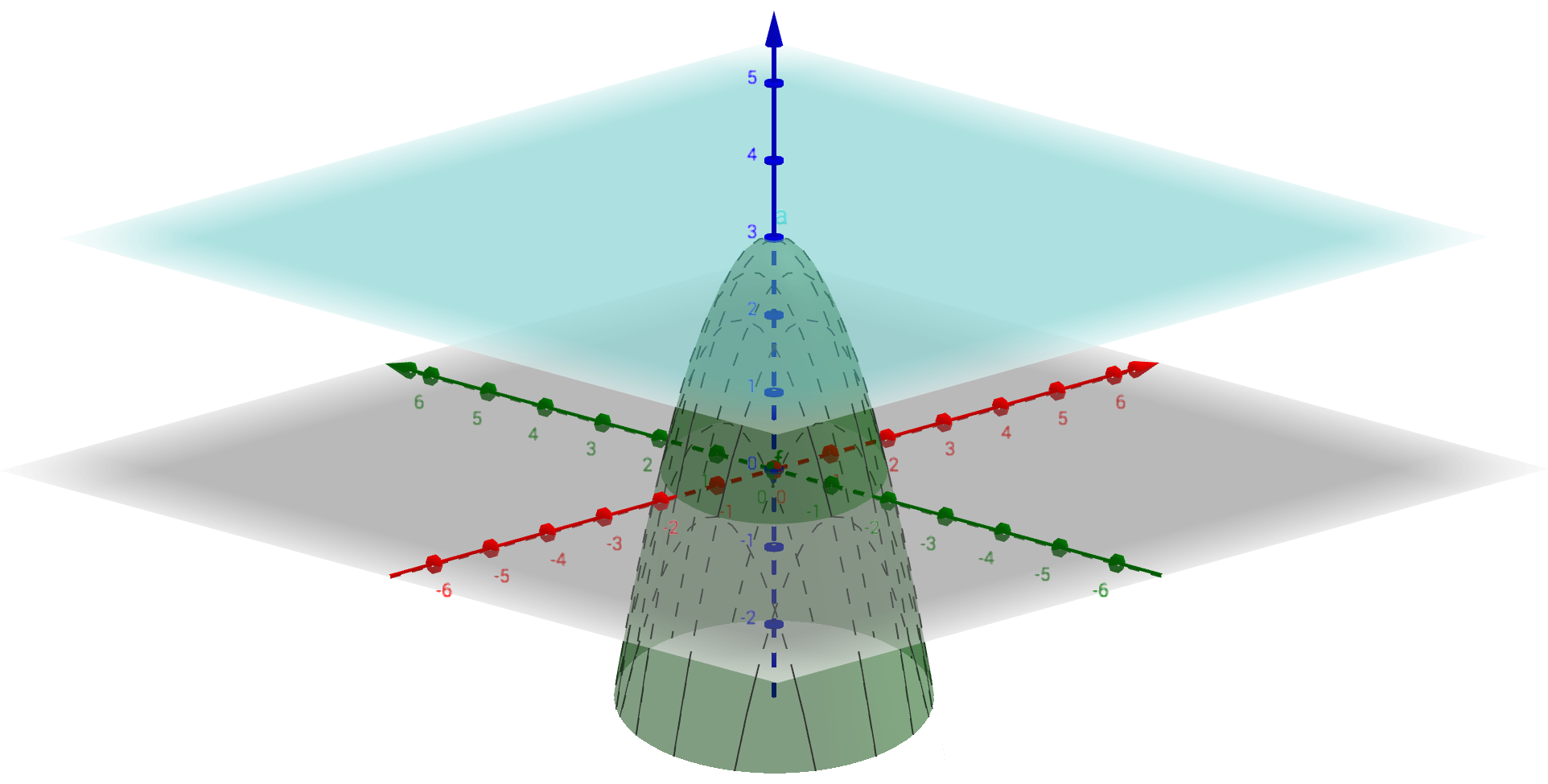
Esimerkki
Funktiolla ,
on useita maksimi- ja minimipisteitä. Sillä on globaali maksimi pisteessä
.
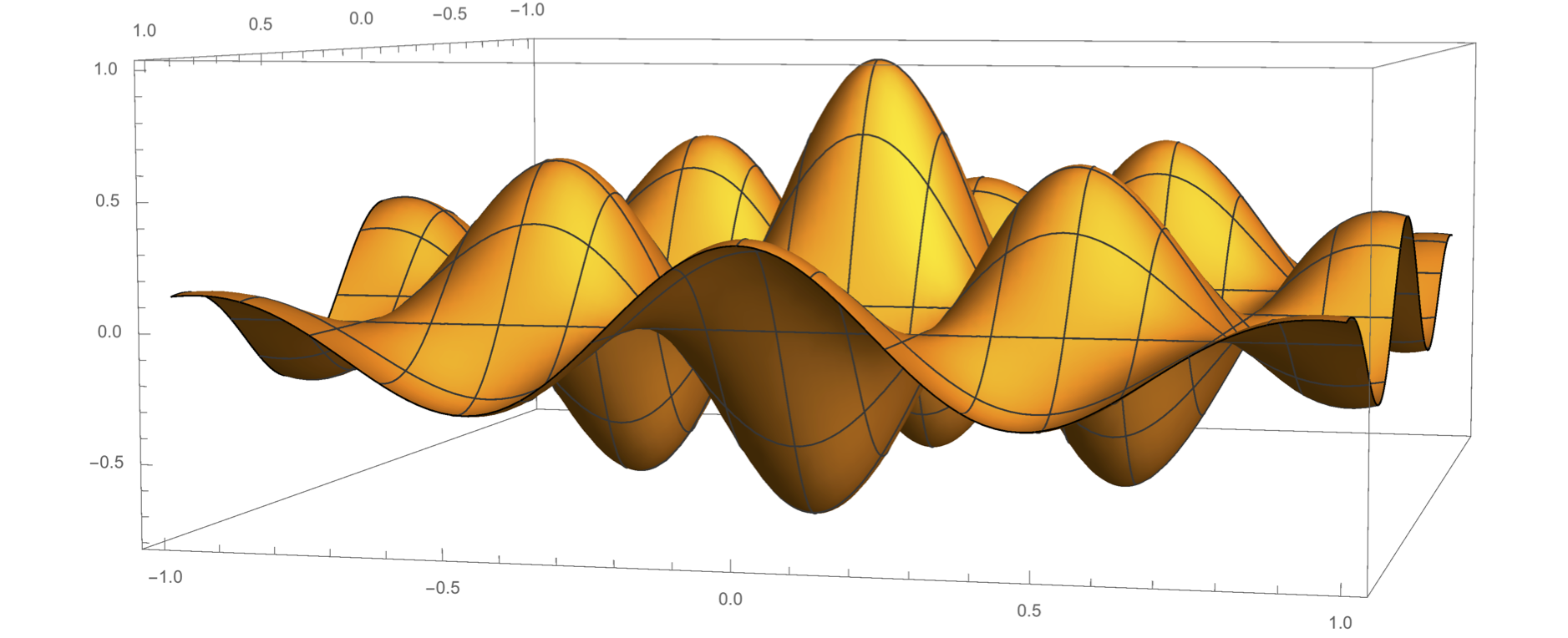
Ääriarvopisteissä funktion gradientti on nolla, mutta gradientin nolluus ei takaa sitä, että piste on funktion ääriarvopiste. Pistettä, jossa
mutta kaikilla
on piste
ja
, joille
,
,
ja
, sanotaan funktion
satulapisteeksi. Funktion kriittisten pisteiden laatua eli sitä, ovatko ne lokaaleja maksimi- tai minimipisteitä vai satulapisteitä voidaan tutkia esimerkiksi toisen kertaluvun osittaisderivaattojen merkin avulla.
Esimerkki
Piste on funktioiden
,
satulapiste.
Osittaisderivaattojen ketjusääntö
Vastavirta-algoritmissa virhefunktion osittaisderivaattoja piilokerroksen painojen suhteen laskettaessa huomattiin, että muuttuja, jonka suhteen halutaan derivoida, riippuu edellisen kerroksen parametreista. Tämän takia tarvittiin osittaisderivaattojen ketjusääntöä.
Tarkastellaan ensin yksinkertaista tilannetta. Olkoon funktio, jonka parametrit
ja
ovat muuttujan
funktioita
. Funktioiden välistä yhteyttä voi havainnollistaa puumaisella kaaviolla. Funktion
osittaisderivaatan kaavan muuttujan
suhteen (tässä tapauksessa tavallisen derivaatan) voi muistaa siitä, että kuvassa edetään funktion
ja derivointimuuttujan
väli kaikkia reittejä pitkin, kerrotaan matkalla olevat osittaisderivaatat keskenään ja lasketaan eri reittien osittaisderivaattojen tulot yhteen.
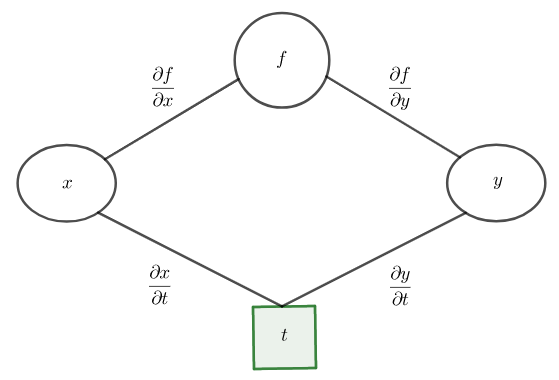
Jos funktiolla on jatkuvat osittaisderivaatat muuttujien
ja
suhteen ja funktiot
ja
ovat derivoituvia, niin funktion
derivaatta muuttujan
suhteen on
josta Leibnizin merkinnöin kirjoitettu versio on
Esimerkki
Olkoot ,
ja
,
Lasketaan funktion
derivaatta muuttujan
suhteen. Muuttujia on vain yksi ja osittaisderivaatta on funktion
tavallinen derivaatta. Tässä tapauksessa derivaatta osattaisiin laskea ilman ketjusääntöäkin sijoittamalla funktioiden
ja
lausekkeet funktion
lausekkeeseen
joten
Osittaisderivaattojen ketjusääntöä käyttämällä saadaan
Laskettaessa osittaisderivaattaa muuttujan suhteen funktio
siis osittaisderivoidaan kaikkien muuttujiensa
suhteen ja muuttujat
muuttujan
suhteen. Nämä osittaisderivaatat kerrotaan keskenään ja lasketaan yhteen. Puukaavion lisäksi kaavan voi muistaa miettimällä, että muuttujan
muuttaminen vaikuttaa funktioiden
arvoihin ja siten muutos funktion
arvossa saadaan laskemalla nämä muutokset (osittaisderivaatat) yhteen.
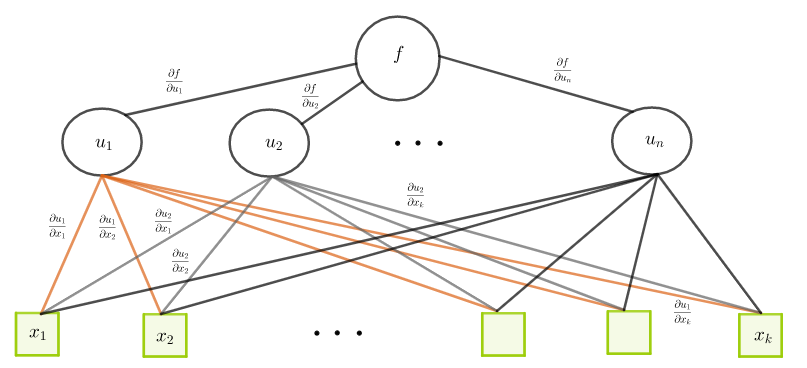
Esimerkki
Olkoot ,
Nyt
Funktion
osittaisderivaatat muuttujien
ja
suhteen ovat
ja
Halutut osittaisderivaatat voi laskea myös sijoittamalla funktioiden
ja
lausekkeet funktioon
ja osittaisderivoimalla muuttujien
ja
suhteen.
3.1.8 Harjoitustehtäviä
Olkoon
,
,
Laske funktion
derivaatta
sekä sijoittamalla funktioiden
ja
lausekkeet funktioon
että osittaisderivaattojen ketjusäännön avulla.
Olkoon
,
,
Laske funktion
osittaisderivaatat
ja
.
Lisätietoa osittaisderivaatoista
3.2 Lineaarialgebraa
Neuroverkon rakennetta esiteltäessä verkon parametreille ja niihin liittyville kaavoille annettiin myös vektori- ja matriisiesitykset. Ohjelmistokirjastoissa on paljon vektori- ja matriisilaskentaan sopivia paketteja, joiden avulla neuroverkon syötteiden tuloksen laskeminen ja parametreihin liittyvien laskujen tekeminen esimerkiksi virhefunktion minimoinnin yhteydessä on paljon nopeampaa kuin yksittäisten parametrien käsittely silmukoiden avulla.
Tässä luvussa käydään läpi vektoreihin ja matriiseihin liittyviä peruskäsitteitä, laskusääntöjä ja ominaisuuksia. Niihin liittyvää materiaalia löytyy Linear Algebra -nimisistä kirjoista. Motivointi lineaarialgebraan tehdään monesti lineaarisen yhtälöryhmän ratkaisemisen kautta.
3.2.1 Kahden lineaarisen yhtälön yhtälöryhmä
Tarkastellaan johdatuksena kahden muuttujan lineaarisista yhtälöistä muodostuvan yhtälöparin missä
kaikilla
, ratkaisemista. Paria
, joka toteuttaa yhtälöparin molemmat yhtälöt, sanotaan yhtälöparin ratkaisuksi. Yhtälöparin ratkaisujen olemassaolo ja yksikäsitteisyys riippuu kertoimista
.
Esimerkki
Tutkitaan yhtälöpareja Yhtälöparista (a) saadaan laskemalla yhtälöt puolittain yhteen ja jakamalla kahdella että
. Sijoittamalla tämä toiseen yhtälöön saadaan
. Tästä seuraa, että
on yhtälöparin ainoa ratkaisu.
Yhtälöparin (b) toinen yhtälö on ensimmäinen yhtälö kerrottuna luvulla . Tämän yhtälön toteuttavat kaikki lukuparit
, joille
. Siten yhtälöparilla on äärettömän monta ratkaisua.
Kerrottaessa yhtälöparin (c) ensimmäinen yhtälö kahdella, saadaan yhtälöpari, jonka molempien yhtälöiden vasen puoli on . Koska oikeat puolet eivät ole samat, niin yhtälöparilla ei ole ratkaisua.
Yhtälöparien geometrinen tulkinta tehdään suorien avulla. Parien yhtälöt ovat suorien yhtälöitä tasossa. Ne pisteet, jotka ovat molemmilla suorilla, ovat yhtälöparin ratkaisuja. Kaksi suoraa ovat joko erisuuntaisia tai samansuuntaisia (eri tai sama kulmakerroin). Jos ne ovat erisuuntaisia, niin ne leikkaavat toisensa täsmälleen yhdessä pisteessä. Tapauksessa (a) yhtälöparin ratkaisu on yhtälöitä vastaavien suorien yksikäsitteinen leikkauspiste. Tapauksessa (b) suorat ovat samat eli kaikki suoran pisteet ovat leikkauspisteitä. Tapauksessa (c) suorat ovat samansuuntaisia eri suoria, joten ne eivät leikkaa toisiaan.
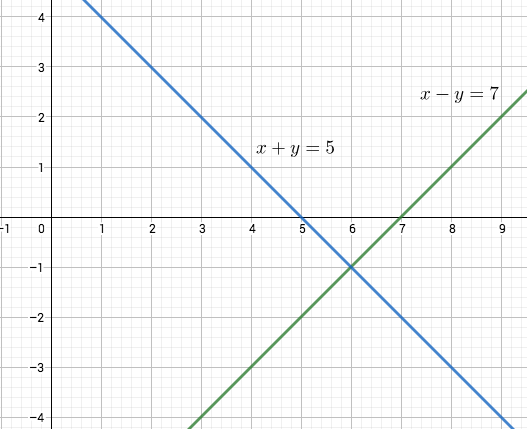
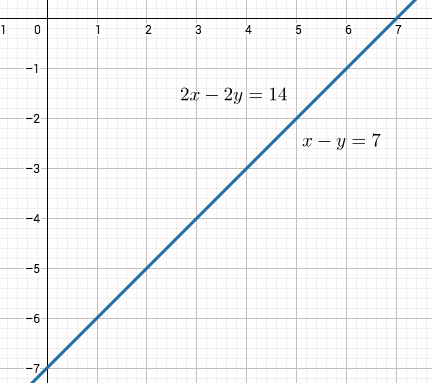
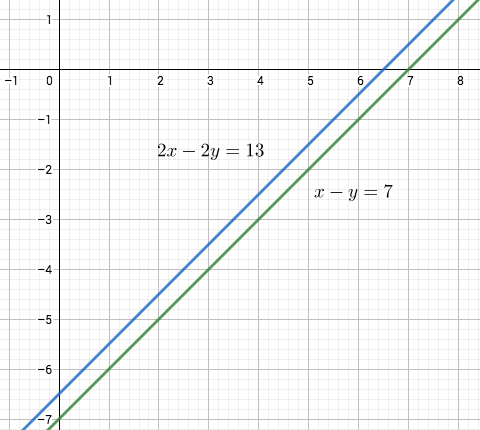
Kertomalla yhtälöparin ensimmäinen yhtälö puolittain luvulla ja toinen luvulla
ja vähentämällä yhtälöt toisistaan nähdään, että jos
, niin sijoittamalla luku
yhtälöpariin saadaan
ja ratkaisu
. Erotusta
sanotaan yhtälöparin determinantiksi.
Tämä liittyy yhtälöparin geometriseen tulkintaan sillä yhtälöparin ensimmäisen suoran kulmakerroin on ja toisen
. Yhtälöparilla on siis täsmälleen yksi ratkaisu jos ja vain jos sen determinantti ei ole nolla (erisuuret kulmakertoimet). Sillä ei ole ratkaisuja tai niitä on äärettömän monta jos ja vain jos determinantti on nolla (samat kulmakertoimet).
3.2.2 Yhtälöryhmä, jossa on  lineaarista yhtälöä ja
lineaarista yhtälöä ja  tuntematonta
tuntematonta
Yleisessä tapauksessa on yhtälöä ja
muuttujaa
missä
kaikilla
,
ja tavoitteena on löytää
luvun joukot
, jotka toteuttavat kaikki ryhmän
yhtälöä.
Tällaisen yhtälöryhmän ratkaisemisessa voidaan käyttää matriiseja. Tunnetussa Gauss-Jordan-menetelmässä yhtälöiden kertoimista muodostetaan kerroinmatriisi,
jota muunnetaan kerto-, yhteen- ja vähennyslaskuja sisältävillä rivioperaatioilla sellaiseen muotoon, josta ratkaisu (tai sen olemassaolemattomuus) saadaan helposti selville peräkkäisillä sijoituksilla.
3.2.3 Vektorit ja matriisit
Vektorit
Vektorit ja matriisit koostuvat järjestetyistä alkioista, jotka voivat olla mitä tahansa (reaalilukuja, vektoreita, funktioita). Keskitytään tässä tilanteeseen, jossa alkiot ovat reaalilukuja. Vektoreista tarvitaan sekä pysty- että vaakaversiot, jotta matriisien ja vektoreiden keskenäiset laskutoimitukset saadaan hoidettua muodollisesti oikein.
Olkoon . Olkoot
,
,
. Järjestetty joukko
on
-ulotteinen (rivi)vektori. Järjestetty joukko
on
-ulotteinen (sarake)vektori. Luvut
,
,
ovat vektorin komponentteja.
Vektoreiden samuus, vektorin kertominen vakiolla ja (samanulotteisten) vektoreiden yhteenlasku määritellään luonnollisella tavalla.
Olkoot ja
-vektoreita. Olkoon
. Nyt
jos ja vain jos
kaikilla
,
ja
Reaalilukujen laskusäännöistä seuraa, että vektoreiden yhteenlasku on vaihdannainen, liitännäinen ja distributiivinen (osittelulaki) eli jos ,
ja
ovat
-vektoreita ja
, niin
Jos
ja
, niin vektoreiden
ja
sisätulo/pistetulo on
Esimerkki
Olkoot ja
. Nyt
ja
ja samat laskut Pythonin NumPy-kirjaston avulla:
Matriisit
Olkoot . Olkoot
kaikilla
ja
. Järjestetty taulukko
on
-matriisi, jossa on
riviä ja
saraketta.
Luvut ovat matrisin
alkioita/komponetteja, rivivektorit
,
, sen rivejä (row) ja sarakevektorit
, sen sarakkeita (column).
Jos , niin matriisi
on neliömatriisi (square matrix).
Huomaa, että rivivektori on
-matriisi ja
-komponentin sarakevektori on
-matriisi.
Matriisien yhtäsuuruus, vakiolla kertominen ja yhteenlasku määritellään samaan tapaan kuin vastaavat ominaisuudet vektoreille.
Olkoot ja
-matriiseja. Olkoon
. Matriisit
ja
ovat yhtäsuuret jos ja vain jos
kaikilla
ja
,
ja
Huomaa, että jos matriisit ja
ovat erikokoisia, niin niitä ei voi laskea yhteen.
Reaalilukujen ominaisuuksista ja matriisien summan ja vakiolla kertomisen määrittelystä seuraa, että matriisien laskutoimitukset käyttäytyvät seuraavasti.
Olkoot ,
ja
-matriiseja. Olkoon
. Olkoon
-matriisi, jonka kaikki alkiot ovat nollia. Tällöin
,
,
,
,
,
.
Esimerkki
Matriiseille on
ja samat laskut Pythonin NumPy-kirjaston avulla:
3.2.4 Harjoitustehtäviä
Olkoot
ja
. Laske summa
ja sisätulo
.
Olkoot
,
ja
-vektoreita. Olkoon
-ulotteinen nollavektori. Olkoon
. Osoita, että
Olkoot
Laske matriisit
,
,
ja
.
Pitäisi varmaan olla (cu)dot v eikä (cvu)dot v tehtävässä 2
—Joo. Kiitos.
—Pikaisesti ajateltuna kahden matriisin tulo olisi matriisi, jossa tekijämatriisien saman indeksin alkiot kerrottaisiin keskenään samoin kuin ne lasketaan yhteen matriisien summassa. Tämän määritelmän antamalla tulolla ei ole riittävästi matriisien tulolta haluttavia ominaisuuksia. Sitä kuitenkin käytetään joissain yhteyksissä, esimerkiksi neuroverkon parametrien kaavoissa.
Olkoot ja
-matriiseja. Matriisien
ja
Hadamardin tulo/Schurin tulo on
Yleisemmin käytettävä matriisien tulo määritellään vektoreiden sisätulon avulla. Matriisien ja
tulon
. alkio on matriisin
. rivin ja matriisin
. sarakkeen vektoreiden sisätulo.
Olkoon
-matriisi ja
-matriisi. Matriisien
ja
tulo
on
-matriisi
, jolle
Matriisitulo on liitännäinen eli jos on
- matriisi,
on
-matriisi ja
on
-matriisi, niin
ja tulo on
-matriisi. Osittelulaki (yhteen- ja kertolaskun suhteen oikean kokoisille) on myös voimassa eli
ja
Matriisitulo ei yleensä ole vaihdannainen eli
. Tulo ei ole edes määritelty paitsi jos sekä
että
ovat
-matriiseja jollain
.
Esimerkki
Olkoot ja
Koska on
-matriisi ja
on
-matriisi, niin tulo
on
-matriisi,
3.2.5 Harjoitustehtäviä
Näytä, että matriisien Hadamard-tulo on vaihdannainen, liitännäinen ja distributiivinen: Jos
ja
ovat
-matriiseja, niin
,
ja
.
Olkoot
Laske tulot
ja
.
Olkoon
-matriisi.
on diagonaalimatriisi, jos
aina, kun
.
on yksikkömatriisi, jos se on diagonaalimatriisi ja
kaikilla
.
Matriisi on ylä(ala)kolmiomatriisi, jos kaikki komponentit diagonaalin ala(ylä)puolella ovat nollia.
Laskutoimitusten helpottamiseksi yleinen matriisi pyritään monesti esittämään kahden tai kolmen matriisin tulona, jossa tulon matriisit ovat diagonaali- tai kolmiomatriiseja.
Esimerkki
Olkoot Matriisit
ja
ovat diagonaalimatriiseja ja
on myös yksikkömatriisi. Matriisi
on yläkolmiomatriisi ja
on alakolmiomatriisi.
Olkoot ja
-matriiseja. Jos
niin
on matriisin
käänteismatriisi, jota merkitään usein
. Tällöin sanotaan, että matriisi
on kääntyvä.
Käänteismatriisin käsin laskeminen on yleensä työlästä. Se onnistuu Gauss-Jordan menetelmällä; kaavan oikean puolen vektori korvataan yksikkömatriisilla
. Jos
saadaan rivioperaatioilla muunnettua yksikkömatriisiksi, niin
on kääntyvä ja käänteismatriisi löytyy viivan oikealta puolelta. Käänteismatriisin etsinnässä riittää löytää
, jolle
tai
. Tällöin voidaan näyttää, että
.
Esimerkki
Olkoon Jos matriisilla
on käänteismatriisi
, niin
,
eli on oltava
Koska nyt myös
, niin
on itsensä käänteismatriisi.
Determinantti
Neliömatriisin kääntyvyyttä voidaan testata determinantin avulla. -matriisin
determinatti on reaaliluku
Esimerkki
Lasketaan matriisin käänteismatriisi kahdella tavalla.
Jos on matriisin
käänteismatriisi, niin on
Vastaavan yhtälöryhmä
hajoaa kahdeksi yhtälöryhmäksi
ja
jotka ratkaisemalla saadaan
,
,
,
.
Siten on .
Determinantin avulla käänteismatriisin laskeminen on helppoa. Koska , niin
Kun , niin determinantti määritellään alimatriisien determinanttien avulla.
-matriisille
on
Summassa on kolmen matriisin
alimatriisin determinantit: matriisi
saadaan poistamalla matriisista
. sarake ja
. rivi. Näiden matriisien determinantit kerrotaan matriisin
komponentilla
vaihtuvin etumerkein eli
Yleiselle -matriisille
determinantti lasketaan samaan tapaan,
missä alimatriisi
saadaan poistamalla matriisista
. rivi ja
. sarake.
Determinantti voidaan laskea myös muun kuin ensimmäisen sarakkeen tai minkä tahansa rivin ja vastaavien alimatriisien avulla, Jos matriisin joku rivi tai sarake sisältää pelkkiä nollia, niin laskemalla determinantti tämän rivin tai sarakkeen avulla nähdään, että determinantti on nolla.
Jos on
ylä- tai alakolmiomatriisi, erityisesti siis jos se on diagonaalimatriisi, niin determinantti on diagonaalialkioiden tulo
Kääntyvyydellä ja determinantilla on yhteys yleisilläkin neliömatriiseilla: -matriisi
on kääntyvä jos ja vain jos
. Tällöin
Geometrisesti -matriisin
determinantti kertoo vektoreiden
ja
virittämän suunnikkaan pinta-alan ja vastaavasti
-matriisin
determinantti kertoo vektoreiden
,
ja
virittämän suuntaissärmiön tilavuuden.
Esimerkki
Matriisin determinantti on
3.2.6 Harjoitustehtäviä
Todista kaava
.
Miksi käänteismatriisi määritellään vain neliömatriiseille?
Olkoon
kääntyvä neliömatriisi. Osoita, että käänteismatriisi on yksikäsitteinen. (Oleta, että matriisilla
oli kaksi käänteismatriisia
ja
ja näytä, että on
.)
Näytä, että kaava
antaa
-matriisin
käänteismatriisin.
Olkoon
. Onko
kääntyvä? Jos on, niin etsi
.
Olkoot
ja
. Laske matriisien
ja
determinantit.
Todista determinantin tulokaava
-matriiseille.
Symmetriset matriisit ja ortogonaaliset matriisit
Joissain tilanteissa tarvitaan matriisia, jossa alkuperäisen matriisin rivit vaihdetaan sarakkeiksi ja päinvastoin eli matriisi heijastetaan diagonaalinsa suhteen.
Olkoon
-matriisi. Matriisi
,
on matriisin
transpoosi.
Jos on neliömatriisi eli
ja
, niin
on symmetrinen.
Rivivektorin transpoosi on sarakevektori, jolla on samat komponentit. Vastaavasti sarakevektorin transpoosi on rivivektori, jolla on samat komponentit kuin alkuperäisellä sarakevektorilla. Vektoreiden transpooseja käytetään erityisesti siihen, että vektoreiden ja matriisien väliset laskutoimitukset saadaan muodollisesti oikeiksi.
Jos on
-matriisi ja
on
-matriisi, niin transpooseille pätee
Jos
, niin
Jos
, niin
Jos
on kääntyvä, niin myös
on kääntyvä ja
Myöhemmin nähdään, että symmetrisillä matriiseilla on hyödyllisiä ominaisuuksia. Siksi niitä pyritään käyttämään matriisihajotelmissa.
Olkoon
-matriisi. Matriisi
on ortogonaalinen, jos
on kääntyvä ja
Ortogonaaliselle matriisille siis . Matriisi
on ortogonaalinen jos ja vain jos sen sarakevektorit
,
, muodostavat ortonormaalin joukon.
Olkoot
-ulotteisia vektoreita. Joukko
on ortonormaali, jos
kaikilla
kun
ja
kaikilla
(eli vektorit ovat kohtisuorassa toisiaan vastaan ja niiden pituus on
.)
3.2.7 Harjoitustehtäviä
Olkoot
Etsi matriisien
ja
ja tulon
transpoosit. Onko
tai
symmetrinen?
Olkoot
ja
. Miten sisätulo
voidaan esittää transpoosien avulla?
Olkoon
-matriisi. Osoita, että
on symmetrinen.
Matriisit ja lineaariset yhtälöryhmät
Jatketaan yhtälön ja
muuttujan yhtälöryhmän tarkastelua. Kun yhtälöiden kertoimista muodostetaan matriisi ja muuttujista ja yhtälöiden oikeista puolista vektorit,
niin yhtälöryhmä voidaan kirjoittaa muodossa
Jos yhtälöitä ja tuntemattomia on yhtä monta, kappaletta, niin
on neliömatriisi. Jos matriisi
on kääntyvä, niin yhtälöryhmän ratkaisu löydetään käänteismatriisin avulla. Käänteismatriisin ominaisuuksien perusteella on
eli yhtälöryhmällä
on yksikäsitteinen ratkaisu jos ja vain jos matriisi
on kääntyvä eli jos ja vain jos
.
Teoriassa yhtälöryhmän ratkaisu löydetään siis käänteismatriisin avulla mikäli se on olemassa. Käänteismatriisin laskeminen on kuitenkin raskasta, joten kääntämisen sijaan ratkaisussa käytetään erilaisia matriisihajotelmia.
Esimerkki
Yhtälöryhmää vastaava matriisiyhtälö on
, missä
Matriisi
on kääntyvä, joten
3.2.8 Harjoitustehtäviä
- Opiskele Gauss-Jordan menetelmä yhtälöryhmien ratkaisemiseksi.
3.2.9 Ominaisarvot ja ominaisvektorit
Olkoon
-matriisi. Luku
(reaali- tai kompleksiluku) on matriisin
ominaisarvo, jos on
, joka ei ole nollavektori, jolle
Tällöin
on ominaisarvoa
vastaava ominaisvektori.
Ominaisarvon ja -vektorin määritelmistä nähdään, että on matriisin
ominaisarvo ja
vastaava ominaisvektori jos ja vain jos
. Tällä yhtälöllä on nollavektorista poikkeava ratkaisu jos ja vain jos
Yhtälöä
sanotaan karakteristisekssi yhtälöksi ja sen vasenta puolta karakteristiseksi polynomiksi.
Matriisin ominaisavot löydetään siis ratkaisemalla karakteristinen yhtälö. Algebran peruslause sanoo, että
. asteen polynomilla on
nollakohtaa kompleksilukujen joukossa. Siten karakteristisella polynomilla on
juurta ja matriisilla
ominaisarvoa, joista osa voi olla moninkertaisia.
Ominaisarvot ja -vektorit etsitään siis seuraavalla tavalla:
Muodosta karakteristinen yhtälö
=0.
Etsi ominaisarvot eli karakteristisen yhtälön juuret
.
Etsi ominaisarvoja
vastaavat ominaisvektorit ratkaisemalla yhtälöt
Jos matriisilla
on
eri ominaisarvoa
,
,
, niin vastaavat ominaisvektorit
,
,
ovat lineaarisesti riippumattomia.
Lineaarinen riippumattomuus tarkoittaa sitä, että jos on luvut ,
,
, joille
niin
kaikilla
. Tämä on yhtäpitävää sen kanssa, että vektoreista
muodostetun matriisin determinantti ei ole nolla.
Esimerkki
Olkoon Karakteristinen yhtälö on
Sen ratkaisut ovat
eli matriisin
ominaisarvot ovat
ja
.
Ominaisarvoa vastaava ominaisvektori toteuttaa yhtälön
eli
Ominaisvektoreita ovat siis vektorit
, joille
, esimerkiksi
.
Ominaisarvoa vastaava ominaisvektori toteuttaa yhtälön
eli
Ominaisvektoreita ovat siis vektorit
, joille
, esimerkiksi
.
3.2.10 Harjoitustehtäviä
- Etsi matriisien
ja
ominaisarvot ja -vektorit.
3.2.11 Matriisihajotelmia
Matriisit pyritään monesti esittämään kahden tai kolmen matriisin tulona, jossa tulon matriisit ovat symmetrisiä tai diagonaali- tai kolmiomatriiseja. Esimerkiksi yhtälöryhmiä ratkaisevat ja käänteismatriiseja tai determinantteja laskevat algoritmit tehdään hajotelmien avulla.
LU-hajotelma
LU-hajotelmassa neliömatriisi esitetään ala- ja yläkolmiomatriisien tulona , missä alakolmiomatriisin
diagonaalialkiot ovat ykkösiä.
"LU-hajotelmassa neliömatriisi esitetään ala- ja yläkolmiomatriisien tulona A=LUA=LUA=LU, missä alakolmiomatriisin LLL diagonaalialkiot ovat nollia." tulisi olla "LU-hajotelmassa neliömatriisi esitetään ala- ja yläkolmiomatriisien tulona A=LUA=LUA=LU, missä alakolmiomatriisin LLL diagonaalialkiot ovat ykkösiä. "
—Ykkösiä pitää olla. Kiitos.
—Jokaisella kääntyvällä matriisilla on LU-hajotelma mutta matriisille joudutaan joskus tekemään rivioperaatioita ennen hajotelmaa: Huomaa, että koska , niin jos
, niin joko
tai
. Koska kolmiomatriisin determinantti on diagonaalialkioden tulo, niin tästä seuraa, että joko
tai
. Siten olisi
. Kuitenkin kääntyvälle matriisille
on
mutta voi olla
.
Esimerkki
Etsitään matriisin LU-hajotelma eli matriisit
ja
, joille
Vastaava yhtälöryhmä on
ja sen ratkaisu
,
,
,
.
Siten
3.2.12 Harjoitustehtäviä
- Olkoon
. Etsi matriisin
-hajotelma.
Lisätietoa lineaarialgebrasta
Lineaarisen yhtälöryhmän ratkaiseminen (Approbatur 1 A, JYU)
Vectors, what even are they? | Essence of linear algebra, chapter 1, 3Blue1Brown
Linear combinations, span, and basis vectors | Essence of linear algebra, chapter 2, 3Blue1Brown
Linear transformations and matrices | Essence of linear algebra, chapter 3, 3Blue1Brown
Matrix multiplication as composition | Essence of linear algebra, chapter 4, 3Blue1Brown
The determinant | Essence of linear algebra, chapter 5, 3Blue1Brown
Inverse matrices, column space and null space | Essence of linear algebra, chapter 6, 3Blue1Brown
Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10, 3Blue1Brown
Visualizing the chain rule and product rule | Chapter 4, Essence of calculus, 3Blue1Brown
3.3 Harjoitustehtäviä Pythonilla
Kurssin yhteydessä tutustutaan myös Python-kieleen ja sen matematiikkaan liittyviin kirjastoihin.
Lineaarialgebraa NumPyn avulla
Käy läpi NumPy-kirjaston lineaarialgebran rutiineja.
Ota NumPy käyttöön komennolla
import numpy tai kaikki rutiinit komennolla
from numpy import *Edellisessä tapauksessa rutiineja käytettäessä rutiiniin nimen eteen pitää lisätä numpy. jälkimmäisessä riittää pelkkä rutiinin nimi. Esimerkiksi alla ensimmäisessä tehtävässä numpy.dot(u,v)tai dot(u,v).
Ota lineaarialgebrarutiinit käyttöön komennolla
from numpy import linalgJos haluat käyttää harjoituksissa lyhyempiä komentoja, joissa linalg-osan voi korvata haluamallaan kirjainyhdistelmällä, niin ota rutiinit käyttöön esimerkiksi komennolla
from numpy import linalg as lajolloin esimerkiksi 6. tehtävän komento on la.norm(v).
Ohjeita löytyy SciPy-sivulta.
Tehtävissä on tarkoituksella sellaiset matriisit ja vektorit, että tulokset on helppo laskea paperillakin. Kokeile eri toimintoihin suurempiakin matriiseja.
3.3.1 Harjoitustehtäviä
- Laske vektoreiden
ja
sisätulo.
numpy.dot(u,v) dot(u,v) - Laske matriisien
ja
tulo.
```
A=numpy.array([[1,2],[3,1]])
...
numpy.dot(A,B)
```- Laske edellisen tehtävän matriisin
kolmas potenssi.
```
linalg.matrix_power(A,3)
```- Etsi matriisin
käänteismatriisi ja determinantti.
```
linalg.inv(A)
linalg.det(A)
```Laske matriisin
transpoosi.
numpy.transpose(A)Laske vektorin
ja matriisin
normit. Ilman parametrja lasketaan standardinormi eli komponenttien itseisarvojen neliöiden summan neliöjuuri.
```
linalg.norm(v)
linalg.norm(A)
```
Parametreilla saadaan selville esimerkiksi vektorin itseisarvoltaan suurin
komponetti ja matriisin suurin rivien itseisarvojen summa.
```
linalg.norm(v,numpy.inf)
linalg.norm(A,numpy.inf)
```- Luo
nollamatriisi,
pelkkiä ykkösiä sisältävä matriisi,
pelkkiä ykkösiä kokonaislukuina sisältävä matriisi sekä
yksikkömatriisi.
```
numpy.zeros((3,4))
numpy.ones((5,4))
numpy.ones((4,5),dtype=numpy.int)
numpy.matlib.identity(5)
```Laske matriisin
ominaisarvot ja vastaavat ominaisvektorit.
linalg.eig(A)Ratkaise yhtälöryhmä
Yhtälöryhmää vastaava matriisiyhtälö on
, missä
ja
.
numpy.linalg.solve(A,b)Opiskele pienimmän neliösumman esimerkki ja etsi sitä muokkaamalla pienimmän neliösumman suora pistepareille
,
,
ja
Lineaarialgebraa SymPyn avulla
Käy läpi symbolisen matematiikan kirjaston SymPyn lineaarialgebran rutiineja. Ota SymPy käyttöön komennolla
import sympy tai kaikki rutiinit komennolla
from sympy import *Edellisessä tapauksessa rutiineja käytettäessä rutiiniin nimen eteen pitää lisätä numpy. jälkimmäisessä riittää pelkkä rutiinin nimi.
3.3.2 Harjoitustehtäviä
Luo matriisi
sekä riveittäin että rivi- ja sarakekokojen avulla.
Matrix([[1,2,3],[4,5,6]]) Matrix(2,3,[1,2,3,4,5,6])Luo
nollamatriisi,
vain ykkösiä sisältävä matriisi,
yksikkömatriisi ja diagonaalimatriisi, jonka diagonaalilla ovat luvut
.
```
zeros(2,3)
ones(5,4)
eye(5)
diag(1,2,3,4,5)
```Laske matriisien
ja
tulo.
A*BPyydä äskeisen tehtävän matriisin
rivejä ja sarakkeita (ensimmäinen 0, viimeinen -1).
A.row(0) A.col(0)Poista ja lisää edellisien tehtävien matriisista rivejä ja sarakkeita. Palauta alkuperäinen matriisi poistamisten jälkeen tai muuta tarvittaessa lisäystehtävien dimensioita. Huomaa, että lisäykset eivät muuta alkuperäistä matriisia.
```
A.row_del(0)
A.col_del(0)
A.row_insert(1,Matrix([[0,1,1]]))
A.col_insert(1,Matrix([[0],[1]]))
```- Laske matriisien
ja
tulo ja summa.
```
a,b,c,d,e,f,g,h=symbols('a b c d e f g h')
A=Matrix([[a,b],[c,d]])
```- Laske edellisen tehtävän matriisin
tulo itsensä kanssa, käänteismatriisi ja determinantti.
```
A**2
A**-1
A.det()
```Laske matriisin
transpoosi.
A.TMuunna matriisi
Gauss-Jordan menetelmässä tavoiteltuun muotoon (reduced row echelon form).
```
A.rref()
```- Laske matriisin
ominaisarvot ja niiden kertaluvut, ominaisvektorit ja karakteristinen polynomi.
```
A.charpoly()
A.eigenvals()
A.eigenvects()
lamda=symbols('lamda')
p=A.charpoly(lamda)
factor(p)
```- Diagonalisoi edellisen tehtävän matriisi
eli etsi diagonaalimatriisi
ja matriisi
, joille
. Muista matriisien
ja
yhteys ominaisarvoihin ja -vektoreihin.
```
P,D=A.diagonalize()
```Matrix(2,3[1,2,3,4,5,6]) on väärin, ei voi ottaa hakasulkeilla 3:sta mitään. Pitäisi olla Matrix(2,3,[1,2,3,4,5,6])
—Kiitos!
—Analyysia SymPyn avulla
Harjoittele SymPyn analyysiin liittyviä rutiineja. Kokeile rutiineja muihinkin kuin tehtävissä mainittuihin funktioihin ja yhtälöihin ja tutustu rutiineihin liittyvään dokumentaatioon. Ota SymPyn rutiinit käyttöön komennolla
from sympy import *SymPy-kirjastoa voi testata myös SymPy Liven avulla. Siinä SymPy toimii Google App Enginen avulla.
3.3.3 Harjoitustehtäviä
Symbolisen ja numeerisen laskennan ero: Vertaa Pythonin
math-kirjaston ja SymPyn neliöjuurifunktioiden toimintaa. Otamath-kirjasto käyttöön komennollaimport math. Testaa komentojamath.sqrt(8)jasympy.sqrt(8)symbols, *, expand, factor: Tarkastele SymPyn laskutoimituksia ja symbolisten lausekkeiden käsittelyä. Esittele symboliset muuttujat ja testaa laskuja ja tekijöihin jakoa.x,y,z=symbols('x y z') a=2*x+y-z a-y y*a ea=expand(y*a) ea factor(ea)simplify, exp, : Harjoittele lausekkeiden sieventämistä.simplify((x**2-x-2)/(x-2)) simplify((x-1)*(x+1)) simplify(exp(x)*exp(y))diff: Laske funktioiden,
ja
,
derivaatat.
h=exp(x**4) diff(h,x)Osittaisderivaatat: Laske esimerkin funktion
(osittais)derivaatta muuttujan
suhteen.
Osittaisderivaatat: Laske funktioiden
,
,
,
osittaisderivaatat muuttujien
,
ja
suhteen.
limit: Laske edellisen tehtävän funktioiden raja-arvoja, esimerkiksilimit(f,x,0)Huomaa, että ääretönkirjoitetaan kahdella pienellä o-kirjaimella "oo".
solveset: Harjoittele yhtälöitä algebrallista ratkaisemista. Ratkaise toisen asteen yhtälösekä yhtälöt
ja
.
solveset(x**2+x-2,x) solveset(exp(x)-1,x,domain=S.Reals)Huomaa, että oletuksena yhtälön oikea puoli on.
solveset(x**2+x-2,x)on sama kuinsolveset(Eq(x**2+x-2,0),x)Piirtäminen: Harjoittele 2- ja 3-ulotteisten funktioiden kuvaajien piirtämistä. Piirrä sigmoid-funktio ja funktiot
ja
. Testaa piirtämiseen liittyviä parametreja.
plot((1+exp(-x))**(-1),(x,-4,4),axis_center='center') plotting.plot3d(f,(x,-1,1),(y,-1,1)) plotting.plot3d(g,(x,-1,1),(y,-1,1)) plotting.plot3d(f,g,(x,-1,1),(y,-1,1))
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.