2-ulotteiset taulukot (matriisit)

Yksiulotteinen taulukko on kuin rivitalo: selvittääksemme tietyn henkilön asunnon meidän tarvitsee tietää vain asunnon (järjestys-)numero.

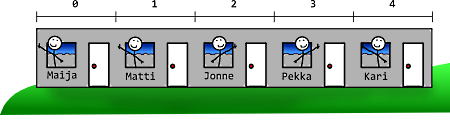
Voimme esimerkiksi sanoa, että Pekka asuu rivitalon asunnossa nro 3, ja Maija asunnossa 0. Huomaa, että indeksit eli taulukon alkioiden laskeminen alkaa aina nollasta.

Kaksiulotteinen taulukko sen sijaan on kuin kerrostalo. Kerrostalossa henkilön majapaikan selvittämiseksi tarvitaan ensin kerros, ja vielä asunnon numero siinä kerroksessa.

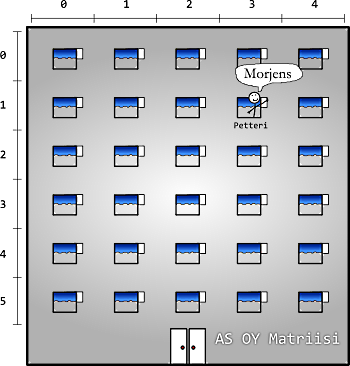
Petteri asuu kerrostalon kerroksessa 1, ja sen kerroksen asunnossa 3 -- siis "paikassa" (1, 3). Huomaa, että tässä kaksiulotteisessa tapauksessa "kerrosten", eli rivien, laskeminen tapahtuu ylhäältä alaspäin.

1. Käyttö

1.1 Taulukon alustaminen

Treenataan seuraavassa 2-ulotteisen taulukon indeksejä. Olkoon meillä taulukko:

    0  1  2  3  4
  ----------------
0 | 5  6  2  7  9|
1 |11 34 23  0 42|
2 |99  6  4 23 23|
3 |19 11  5 11 47|
4 |47  9  5 18 19|
5 |33 24 54 67 88|
  ----------------

C#:illa vastaava taulukko luotaisiin alustaen esim:

        int[,] mat = {
                        { 5, 6, 2, 7, 9},
                        {11,34,23, 0,42},
                        {99, 6, 4,23,23},
                        {19,11, 5,11,47},
                        {47, 9, 5,18,19},
                        {33,24,54,67,88}
                     };

tai tyhjäksi saman kokoiseksi, 0:ia täynnä olevaksi taulukoksi

        int[,] mat = new int[6, 5];

1.2 Taulukon indeksit

Esimerkkinä olevassa 2-ulotteisessa taulukossa on siis 6 riviä ja 5 saraketta. Indeksit alkavat 0:sta samoin kuin 1-ulotteisen taulukon tapauksessa.

Voisimme esimerkiksi sijoittaa taulukossa olevat 5:t paikoilleen lauseilla:

        mat[0, 0] = 5;
        mat[3, 2] = 5;
        mat[4, 2] = 5;

Vastaavasti voisimme tarkistaa onko meillä paikassa (2, 3) luku 23:

        if (mat[2,3] == 23) ...

tai ottaa paikassa (3, 4) olevan alkion:

        int luku = mat[3,4]; // esimerkin tapauksessa 47

2. Taulukon koon selvittäminen

Taulukon kunkin suunnan koko saadan selville GetLength(suunta) metodilla:

        int riveja = matriisi.GetLength(0);
        int sarakkeita = matriisi.GetLength(1);

3. Esimerkkialiohjelmia

3.1 for-silmukalla

for-silmukkaa, tai oikeastaan sisäkkäisiä for-silmukoita on käytettävä, mikäli läpikäynnin aikana on tiedettävä jotakin riveistä tai sarakkeista.

Tehdään esimerkkialiohjelma, joka laskisi monellako rivillä tietty luku esiintyy. Aliohjelmaa kutsuttaisiin seuraavasti:

        int lkm = MonellakoRivilla(mat,11);  // esimerkissä pitäisi palauttaa 2

Aliohjelma testeineen:

    /// <summary>
    /// Lasketaan monellako rivillä taulukossa esiintyy etsittävä luku.
    /// Jos luku on useasti samalla rivillä, rivi lasketaan yhden kerran.
    /// </summary>
    /// <param name="mat">matriisi, josta lukua etsitään</param>
    /// <param name="etsittava">luku jota etsitään</param>
    /// <returns>monellako rivillä etsittävä oli</returns>
    /// <example>
    /// <pre name="test">
    ///  int[,] t = {{2, 1, 2}, {3, 4, 2}, {1, 0, 1}, {1, 8, 9}};
    /// MonellakoRivilla(t, 2) === 2;
    /// MonellakoRivilla(t, 5) === 0;
    /// MonellakoRivilla(t, 0) === 1;
    /// MonellakoRivilla(t, 1) === 3;
    /// MonellakoRivilla(new int[0, 0], 1) === 0;
    /// </pre>
    /// </example>
    public static int MonellakoRivilla(int[,] mat, int etsittava)
    {
      int riveja = mat.GetLength(0);
      int sarakkeita = mat.GetLength(1);
      int lkm = 0;
      
      for (int iy = 0; iy < riveja; iy++)
        for (int ix = 0; ix < sarakkeita; ix++)
          if (mat[iy, ix] == etsittava)
          {
            lkm++;
            break;
          }
      return lkm;
    }

Tässä ei voida käyttää foreach-silmukkaa, koska silloin ei tiedetä mitään riveistä.

3.2 foreach-silmukka

foreach-silmukka käy kaikki matriisin alkiot samanarvoisesti lävitse. Esimerkiksi matriisin alkioiden summan laskemiseksi tämä kävisi:

        int s = Summa(mat);

ja silloin aliohjelman toteutus olisi:

    /// <summary>
    /// Lasketaan taulukon alkioiden summa
    /// </summary>
    /// <param name="mat">Taulukko jonka alkioiden summa lasketaan</param>
    /// <returns>Alkioiden summa</returns>
    /// <example>
    /// <pre name="test">
    ///  int[,] t = {{2, 1, 2}, {3, 4, 2}, {1, 0, 1}, {1, 8, 9}};
    ///  Summa(t) === 34;
    ///  Summa(new int[1, 1] {{5}}) === 5;
    ///  Summa(new int[0, 0]) === 0;
    /// </pre>
    /// </example>
    public static int Summa(int[,] mat)
    {
        int summa = 0;
        foreach (int luku in mat) summa += luku;
        return summa;
    }

foreach-silmukkaa ei voida käyttää tilanteissa joissa tarvitaan rivi- tai sarakeindeksejä, tai ylipäätään tietoa siitä, missä "kohtaa" taulukkoa ollaan menossa. Erityiseti tämä koskee tilannetta, jossa rivit ja sarakkeet täytyy erottaa toisistaan, kuten laivaupotuspeli tai edellisen esimerkin MonellakoRivilla.

4. Harjoituksia

Kirjoita kynällä paperille, missä kaikissa indekseissä mallitaulukossa on luku 11 esim tyyliin:

        if (mat[2,3] == 23) ...

entä missä 88
entä 9
kirjoita C#-lauseet, joilla sijoitat mallitaulukossa olevien lukujen 9 tilalle luvun 88
tee aliohjelma, joka laskee monessako sarakkeessa on tietty luku

5. Matriisi-aliohjelmien testaaminen

5.1 Parametrina matriisi

Jos aliohjelmalle annetaan parametrina taulukko, voi tämän taulukon luoda etukäteen (allaolevat kommentit ovat Comtest-testejä)

    ///  int[,] t = {{2,1,2},{3,4,2},{1,0,1},{1,8,9}};
    ///  Summa(t) === 34;

Taulukko voidaan luoda samalla kun aliohjelmaa kutsutaan

    ///  Summa(new int[0,0]) === 0;
    ///  Summa(new int[,]{{5}}) === 5;
    ///  Summa(new int[,]{{1,2},{3,4}}) === 10;

5.2 Tuloksena matriisi

Katso mieluummin uudempi tapa testata 2-ulotteisia taulukoita.

Mikäli tuloksena on matriisi, on helpointa tehdä oma Jonoksi funktio, joka muuttaa matriisin jonoksi (ja ehkä jopa aina desimaalit pisteeksi), jolloin testin voi kirjoittaa:

    /// <summary>
    /// Luodaan taulukko aloittaen x1:stä dx:n välein nx x ny kpl lukuja
    /// </summary>
    /// <param name="ny">montaka riviä tulee</param>
    /// <param name="nx">montaka saraketta tulee</param>
    /// <param name="x1">alkuarvo</param>
    /// <param name="dx">kasvatusaskel</param>
    /// <returns>taulukko jossa n reaalilukua</returns>
    /// <example>
    /// <pre name="test">
    ///    Jonoksi(Matriisit.Taulukko(0,0,0.1,0.1)) === "";
    ///    Jonoksi(Matriisit.Taulukko(1,1,0.2,0.1)) === "0.2";
    ///    Jonoksi(Matriisit.Taulukko(2,2,0.1,0.2)) === "0.1 0.3\n0.5 0.7";
    /// </pre>
    /// </example>
    public static double[,] Taulukko(int ny, int nx, double x1, double dx)
    {
        double[,] luvut = new double[ny,nx];
        double x = x1;
        for (int iy = 0; iy < ny; iy++)
            for (int ix = 0; ix < nx; ix++, x += dx)
                luvut[iy,ix] = x;
        return luvut;
    }

Edellä Jonoksi voisi olla esimerkiksi seuraavaa.

    /// <summary>
    /// Palauttaa taulukon merkkijonona niin, että alkioiden välissä on erotin.
    /// Alkioden formaatin voi valita itse, samoin mitä tulostetaan rivien väliin.
    /// Desimaalierotin on aina .
    /// </summary>
    /// <param name="luvut">Taulukko josta tehdään merkkijono</param>
    /// <param name="sarakeErotin">Jono, jolla rivin alkiot erotetaan toisistaan</param>
    /// <param name="sarakeformaatti"></param>
    /// <param name="rivierotin">Jono, jolla rivit erotetaan toisistaan</param>
    /// <param name="riviformaatti">C# tyylinen formaattijono, jolla yksi rivi käsitellään.
    /// Jos formaattijonossa ei ole lainkaan {-merkkiä, käytetään jonoa sellaisenaan rivien
    /// erottomina
    /// </param>
    /// <example>
    /// <pre name="test">
    ///  double[,] luvut = {{1,2.1,3},{4,5,6},{7,8,9}};
    ///  Jonoksi(luvut) === "1 2.1 3\n4 5 6\n7 8 9";
    ///  Jonoksi(luvut," ","{0}",",") === "1 2.1 3,4 5 6,7 8 9";
    ///  Jonoksi(luvut,":","{0:0.0}","|","[ {0} ]") === "[ 1.0:2.1:3.0 ]|[ 4.0:5.0:6.0 ]|[ 7.0:8.0:9.0 ]";
    ///  Jonoksi((double[,])null) === "null";
    ///  Jonoksi(new double[0,0]) === "";
    ///  Jonoksi(new double[1,0]) === "";
    ///  Jonoksi(new double[2,0]) === "\n";
    /// </pre>
    /// </example>
    public static string Jonoksi<T>(T[,] luvut, string sarakeErotin = " ",
                                 string sarakeformaatti = "{0}",
                                 string riviErotin = "\n",
                                 string riviformaatti = "{0}")
    {
        if (luvut == null) return "null";
        System.Globalization.CultureInfo ci = System.Globalization.CultureInfo.CreateSpecificCulture("en-US");
        StringBuilder tulos = new StringBuilder();
        string formaatti = riviformaatti;
        if (formaatti.IndexOf("{") < 0) formaatti = "{0}" + formaatti;
        string rivivali = "";
    
        for (int iy = 0; iy < luvut.GetLength(0); iy++)
        {
            string vali = "";
            StringBuilder rivi = new StringBuilder();
            for (int ix = 0; ix < luvut.GetLength(1); ix++)
            {
                rivi.Append(vali);
                rivi.Append(String.Format(ci, sarakeformaatti, luvut[iy, ix]));
                vali = sarakeErotin;
            }
            tulos.Append(rivivali + String.Format(formaatti, rivi));
            rivivali = riviErotin;
        }
        return tulos.ToString();
    }

6. Lisätietoa kiinnostuneille: Geneeriset tyypit

Tämä ei ole varsinaisesti Ohj1-kurssin asiaa, mutta esimerkki siitä, miten edellisen testin aliohjelmasta tehtäisiin geneerinen versio. Geneerisyys tarkoittaa sitä, ettei aliohjelmassa käytettyä tyyppiä sidota etukäteen mihinkään tiettyyn tyyppiin. Tämän ansiosta alla olevalla aliohjelmalla voidaan luoda taulukollinen minkätyyppisiä asioita vain, kunhan tyypille on mahdollista tehdä pluslaskuoperaatio.

    /// <summary>
    /// Luodaan taulukko aloittaen x1:stä dx:n välein nx x ny kpl lukuja
    /// </summary>
    /// <param name="ny">montaka riviä tulee</param>
    /// <param name="nx">montaka saraketta tulee</param>
    /// <param name="x1">alkuarvo</param>
    /// <param name="dx">kasvatusaskel</param>
    /// <returns>taulukko jossa n reaalilukua</returns>
    /// <example>
    /// <pre name="test">
    ///    Matriisit.Jonoksi(Matriisit.Taulukko(0,0,0.1,0.1)) === "";
    ///    Matriisit.Jonoksi(Matriisit.Taulukko(1,1,0.2,0.1)) === "0.2";
    ///    Matriisit.Jonoksi(Matriisit.Taulukko(2,2,0.1,0.2)) === "0.1 0.3\n0.5 0.7";
    ///    Matriisit.Jonoksi(Matriisit.Taulukko(1,1,4,1)) === "4";
    ///    Matriisit.Jonoksi(Matriisit.Taulukko(2,2,3,2)) === "3 5\n7 9";
    /// </pre>
    /// </example>
    public static T[,] Taulukko<T>(int ny, int nx, T x1, T dx) 
    {
        T[,] luvut = new T[ny,nx];
        dynamic x = x1;
        for (int iy = 0; iy < ny; iy++)
            for (int ix = 0; ix < nx; ix++, x += dx)
                luvut[iy,ix] = x;
        return luvut;
    }