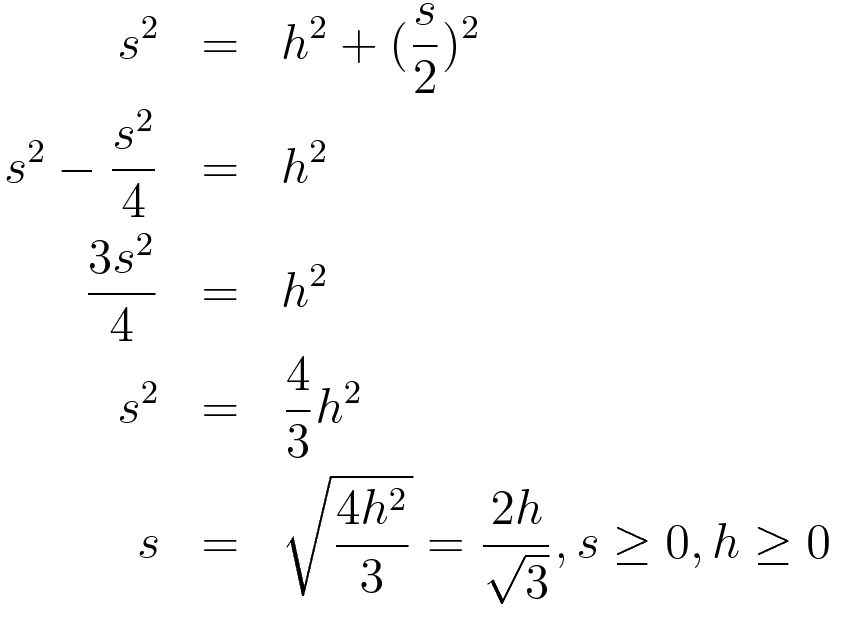avoin/avoin23

# avoin

Huom! TÄMÄ ON AVOIMEN YLIOPISTON SIVU.

Et voi suorittaa kurssia, ellet ole ilmoittautunut täällä.

Ohjelmointi 1, avoin 2023, luento 19

# L19

19. luento: ma 6.11.2023 klo 12:15-14:00: Rekursio

M: 22. Rekursio
Kertoma - esimerkki jossa määritelmä voidaan antaa itsensä avulla (=rekursiivinen määritelmä)
- Rekursion idea ja kertoma
- Rekursio.cs - luennon versio rekursiivisena ja iteratiivisena (silmukalla, ei saa laskea oikeasti muuten)
kuvioita rekursion avulla:
- Droste Effect (1, 2)
- Sierpinskin kolmio ja muut fraktaalit
- Mandelbrotin joukko, Kochin lumihiutale
- SierpinskiKolmio.cs - luentomonisteen versio
- SierpinskiKolmio2.cs - versio jossa kolmiot piirretään heti Jypelin olioilla
- SierpinskiKolmio3.cs - versio jossa kolmiot piirretään viivoina Canvakselle ja jossa voi animoida syntyä
- SierpinskiMatto.cs
- Wikipedia: Sierpinski triangle, kuva eräästä toteutuksesta
Haskell esimerkki rekursiosta
Luennolle tehdyt koodit versionhallinnassa
Luennon koodit versionhallinnassa
19. luento videona: Osa 1 MP4 alkuperäinen
luentoseinä

Tentti ja loput demot

tentti, ilmoittautuminen tulee TIMiin
demo 10 ja demo 11 saa tehdä niin monta tehtävää kuin haluaa (ei 8 ylärajaa)
erityisesti piirtotehtävä (tai tehtäviä) tulee tenttiin, eli harjoitelkaa demo 10:ssä. Varmaan lisätään esimerkki myös demo 11.
demo 11 on mallitentti, tentissä osattava myös itse tehdä testejä

# GLO_DemoN2

Kertausta

Sijoituksen suunta

# sijoitusblle

Kasvatusoperaattorit

# muuttujat1

# muuttujat2

# muuttujat3

Kysymyksiä

Rekursio

Kurssin aikana sinun on tarkoitus oppia seuraavia asioita (osaamisen taso sovelletulla Bloomin asteikolla: 1=muistaa, 2=ymmärtää, 3=osaa soveltaa, 4=osaa analysoida, 5=osaa arvioida, 6=osaa luoda)

Siirrä alla osaamisesi (punainen pallukka) aina sitä vastaavalle kohdalle. Keltainen ruutu on tavoite johon tulisi päästä kurssin lopuksi. Ruksaa ensin muokkaa.

# goaltable2

Please to interact with this component.

Osattava asia	1	2	3	4	6
Rakenteisen ohjelmoinnin perusajatus			o
Algoritminen ajattelu			o
C#-kielen perusteet			o
Peräkkäisyys				o
Muuttujat					o
Aliohjelmat ja funktiot					o
Parametrin välitys				o
Ehtolauseet				o
Silmukat				o
Taulukot			o
Tiedostot ohjelmasta käytettynä		o
Olioiden käyttö			o
Yksikkötestit (TDD)		o
Debuggerin käyttö			o
Lukujärjestelmät, ASCII-koodi		o
Rekursio	o
Dokumentointi ja sen lukeminen			o

Rekursiolla tarkoitetaan algoritmia, joka tarvitsee itseään ratkaistakseen ongelman.

M: Rekursio

hakemistopuu

# binaaripuu

# shell1

    public static void Rekursio(parametrit) 
    {
        if (lopetusehto) return;
        // toimenpiteitä ... 
        Rekursio(uudet parametrit);  // Itsensä kutsuminen
        // mahdollisesti lisää lauseita
    }

Kertoma

# rek

# kertoma

# ae_rekursioCS

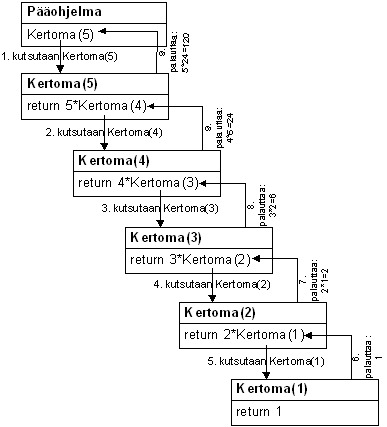
katso myös debuggerilla

# binomi

Tämän voi ajatella myös niin että 5 alkiota voidaan laittaa 5! eri järjestykseen. Kun niistä otetaan 2 ensimmäistä, niin laskussa 5! tuli laskettu liikaa kaikki näiden kahden erilaiset järjestykset. Toisaalta kussakin eri 5! järjestyksessä kahden alkion valinnan kannalta samoja ovat järjestykset, joissa jäljelle jääneet 3 ovat eri järjestyksissä.

$\binom {5}{2} = \frac {5!}{2! * (5-2)!} = \frac{1*2*3*4*5}{ 1*2 * 1*2*3} = \frac{4*5}{1*2} = 10$

demo 10

# nelioluku

Neliöluku

$K_{n} = \begin{cases} 0, & \mbox{kun } n < 1 \\ K_{n-1} + n, & \mbox{kun } n \geq 1 \\ \end{cases}$

# kolmioluku21

# neliolukutex

# neliolukufor

Mielenkiintoista sinällään, mutta neliöluvun voi esittää myös kolmiolukujen avulla:

$N_n = \begin{cases} K_n, & \mbox{kun } n < 1 \\ K_n + K_{n-1}, & \mbox{kun } n \geq 1 \\ \end{cases}$

Voit halutessasi kokeille tehdä tätäkin ohjelmaksi sekä rekursiolla että ilman.

Fraktaalit

Kochin lumihiutale

Sierpinskin kolmio

M: Sierpinskin kolmio

# k33

Kuva 33: Kolmion pisteiden laskeminen.

# k32_1

# k32_2

# Plugin1

SierpinskiKolmio.cs - luentomonisteen versio
SierpinskiKolmio2.cs - versio jossa kolmiot piirretään heti Jypelin olioilla
SierpinskiKolmio3.cs - versio jossa kolmiot piirretään viivoina Canvakselle ja jossa voi animoida syntyä
SierpinskiMatto.cs
Wikipedia: Sierpinski triangle, kuva eräästä toteutuksesta

Rekursio muilla ohjelmointikielillä

M: Rekursio muilla ohjelmointikielillä

Haskell:

sum []   = 0
sum (x:xs) = x + sum xs

# hellofs

# listfs

# listfs2

Fibonaccin luku

Wikipedia: Fibonaccin lukujono (fi), (en)

Linkkejä

Free CodeCamp: Understanding Recursion in Programming