Vektorilaskenta

Johdanto

Ohjelmoinnin peruskursseilla lähetään liikkeelle siitä, että dataa käsitellään yksittäisinä data-alkioina eli skalaareina (float, double, int, jne)
Skalaarimuuttujien väliset alkeisoperaatiot saattavat olla esimerkiksi yksinkertaisia aritmeettisia laskutoimituksia:

int a = 1;
int b = 55;
int c = -3;
int r = a * b + c

Oleellinen asia on se, että kukin alkeisoperaatio ottaa argumenttinaan joukon skalaarimuuttujia ja paluuarvo on myöskin skalaarimuuttuja

Sama pätee myöskin vertailuoperaatioiden tapauksessa:

if(r < 34) {
    ...
} else {
    ...
}

Vertailuoperaation osapuolet ovat skalaareja ja tulos on bool-tyyppinen skalaari eli voitaisiin kirjoittaa:

bool ret = r < 34; // false, koska c = 1 * 55 + (-3) = 52
if(ret) { ...

Vektorilaskennan ideana on käsitellä dataa skalaarien sijasta vektoreina
Matemaattisesti ajateltuna kyseessä on suure jolla on sekä suunta, että suuruus (pituus)
Ohjelmoinnin kannalta vektori voidaan ajatella muuttujaksi, joka sisältää indeksoidun joukon skalaareja
Vektorit eroavat taulukoista siinä, että taulukkojen tapauksessa alkiot käsitellään tyypillisesti erikseen skalaareina, mutta vektoreiden tapauksessa alkiot on tarkoitus käsitellä yhdessä

Vektorimuuttuja voisi sisältää esimerkiksi neljä kappaletta yksinkertaisen tarkkuuden liukulukuja:

float4 va = { 4.6f, 3.4f, -6.9f, 1.0f };
float4 vb = { 5.3f, -7.6f, 5.9f, 0.5f };

Yllä esitelty float4-tietotyyppi ei ole millään tavalla standardi vaan eri vektoriohjelmontirajapinnat määrittelevät tyypillisesti omat tietotyyppinsä ja alkeisoperaationsa

Useimman vektorilaskentaohjelmointirajapinnat tarjoavat mahdollisuuden käsitellä vektorimuuttujien alkioita yksittäisinä skalaarimuuttujina:

float d1 = va.s0; // = vektorimuuttujan va ensimmäinen alkio
float d2 = va.s1; // = vektorimuuttujan va toinen alkio
float d3 = d1 * d2 + vb.s3;
vb.s1 = d3; // vektorimuuttujan vb toinen alkio = d3

Vektorimuuttujia ei ole kuitenkaan järkevää käsitellä tällä tavalla vaan meidän tulisi pyrkiä käyttämään vektoroituja alkeisoperaatioita.
Lähdetään seuraavaksi tarkastelemaan esimerkkien kautta kuinka tämä olisi mahdollista.

Esimerkki

Oletetaan, että meillä on taulukollinen yksinkertaisen tarkkuuden liukulukuja \[ \left( x_1, x_2, \dots, x_{n-1}, x_n \right) \] ja haluamme muodostaa uuden taulukon \[ \left( f(x_1), f(x_2), \dots, f(x_{n-1}), f(x_n) \right), \] jossa \[ \begin{align} f : \mathbb{R} \to \mathbb{R}^+, \; f(x) = \begin{cases} |x|, & 1 \leq |x| \\ x^2, & |x| < 1. \end{cases} \end{align} \]

Skalaariversio

C-ohjelmointikielellä taulukon muodostaminen voitaisiin toteuttaa esimerkiksi seuraavasti:

void function(float *buff, int n) {
  
    for(int i = 0; i < n; i++) {
        float val = buff[i];
        float abs_val = fabs(val);
      
        float ret;
        if(abs_val < 1.0f)
            ret = val*val;
        else
            ret = abs_val;
 
        buff[i] = ret;
    }
}

Useimmissa tilanteissa kääntäjä tuottaa ohjelmakoodista skalaariversion, jossa ehtolause on toteutettu hyppykäskyllä.

Testiohjelman vektorointi-esimerkki/scalar.cpp tulostus tietokoneella, josta löytyy Intel Core i5 4690K -prosessori:

Time: 0.0583539 s
Flops: 0.666179 GFlops
Max error: 0

Advanced Vector Extensions

Lähdetään seuraavaksi tarkastelemaan, että miten algoritmi voitaisiin vektoroida manuaalisesti käyttäen moderneista x86-prosessoreista löytyvää AVX-käskykanta-laajennusta (Advanced Vector Extensions) ja siihen liittyvää C-kielen käärettä (wrapper).

Silmukan muokaaminen ja datan hakeminen muistista

AVX-käskykantalaajennuksen avulla 8 yksinkertaisen tarkkuuden liukulukua voidaan pakata samaan __m256-tyyppiseen vektorimuuttujaan.
Laajennus tukee myöskin kokonaislukujen ja kaksinkertaisen tarkkuuden liukulukujen käsittelyä.
Muokkaamme aluksi silmukkaa siten että siinä käsitellään 8 liukulukua yhdessä:

for(int i = 0; i < n; i += 8) {
    ...
}

Kaikki 8 liukulukua voidaan ladata buff-taulukosta _mm256_load_ps-aliohjelmakutsulla:

 __m256 val = _mm256_load_ps(buff+i); // vmovaps ymm, m256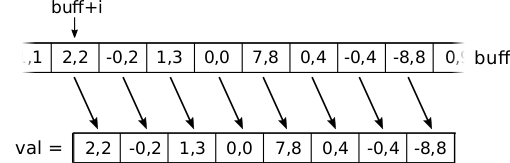

Tässä kohtaa oletataan, että n on jaollinen 8:lla ja, että osoitinmuuttujan buff arvo on jaollinen 32:lla sillä _mm256_load_ps-aliohjelma (vmovaps-käsky) heittää laitteistotason poikkeuksen mikäli sille annettu osoite ei jaollinen 32:lla.

Itseisarvon ja neliön laskeminen

Seuraavaksi haluamme laskea kaikille vektorin val komponenteille itseisarvot. Tätä varten olemme ennen silmukkaa määritelleet seuraavat muuttujat:

const unsigned int abs_coef = 0x7fffffff; 

// vbroadcastss ymm, m32
const __m256 abs_mask = _mm256_broadcast_ss((float*) &abs_coef);

Muuttuja abs_coef pitää sisällään bittimaskin, jonka avulla yksinkertaisen tarkkuuden liukuluvun merkkibitti voidaan nollata eli luvusta otetaan itseisarvo.
_mm256_broadcast_ss-aliohjelma palauttaa vektorin (abs_mask), jonka jokaisen komponentin arvoksi on asetettu argumenttina annetusta muistiosoitteesta löytyvä liukuluku.
Tässä tapauksessa emme kuitenkaan tallenna abs_mask-vektorin komponentteihin oikeaa liukulukua (0x7fffffff = NaN (Not a Number)) vaan käytämme vektorin binääriesitystä bittimaskina.

Nyt itseisarvot voidaan laskea ottamalla komponenteittainen bittitason ja-operaatio (logical AND) vektoreista val ja abs_mask:

__m256 abs_val = _mm256_and_ps(val, abs_mask); // vandps ymm, ymm, ymm

Seuraavaksi laskemme kaikille vektorin val komponenteille neliöt:

__m256 squ_val = _mm256_mul_ps(val, val); // vmulps ymm, ymm, ymm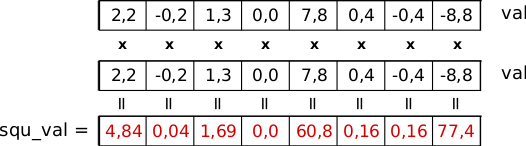

Vertailuoperaatio

Vertailuoperaatio voidaan toteuttaa vektoroidusti _mm256_cmp_ps-aliohjelmakutsulla.
Aliohjelma ottaa argumenttinaan vertailtavat vektorit ja vertailuoperaattorin. Aliohjelma palauttaa vektorin, jonka kukin komponentti pitää sisällään sitä vastaavan vertailuoperaation tuloksen eli tässä tapauksessa joko 0x00000000 tai 0xffffffff.

Kuten itseisarvon laskemisenkin yhteydessä, olemme etukäteen määritelleet seuraavat muuttujat:

const float one_coef = 1.0f;
const __m256 one_mask = _mm256_broadcast_ss(&one_coef);

Eli vektorin one_mask jokaisesta komponentista löytyy liukuluku 1.0f.

Nyt tarvitsemamme "pienempi kuin" -vertailu onnistuu esimerkiksi _CMP_LT_OS-vertailuoperaattorilla:

// vcmpps ymm, ymm, ymm, imm
__m256 pre = _mm256_cmp_ps(abs_val, one_mask, _CMP_LT_OS);

Lopullisen tuloksen muodostaminen "blend"-komennolla

Seuraavaksi muodostamme vastausvektorin valitsemalla abs_var ja squ_val vektoreista sopivat komponentit.
Yhdistäminen tapahtuu _mm256_blendv_ps-aliohjelmalla, joka ottaa argumentteinaan kaksi vektoria ja ohjausvektorin, joka määrittelee millä tavalla nämä kaksi vektoria tulisi yhdistää uudeksi vektoriksi.
Mikäli ohjausvektorin komponentti on nolla, valitaan uuden vektorin vastaavaksi komponentiksi ensimmäisen argumenttina annetun vektorin vastaava komponentti. Muissa tapauksissa valitaan toisen argumenttina annetun vektorin vastaava komponentti.

Tässä tapauksessa saamme muodotettua haluavamme vastausvektorin käyttämällä edellä muodostettua pre-vektoria ohjausvektorina:

// vblendvps ymm, ymm, ymm, ymm
_m256 ret = _mm256_blendv_ps(abs_val, squ_val, pre);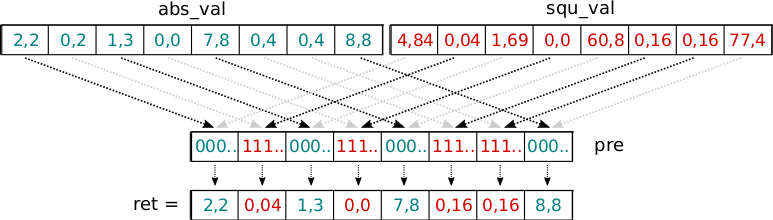

Viimeistely

Lopuksi tallennamme ret-vektorin takaisin buff taulukkoon:

_mm256_store_ps(buff+i, ret); // vmovaps m256, ymm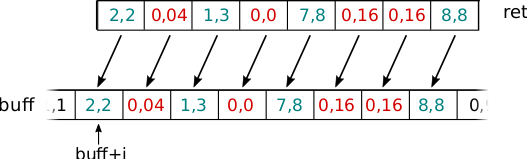

Lopullinen aliohjelma

Tässä vielä koko algoritmi kokonaisuudessaan:

const unsigned int abs_coef = 0x7fffffff;
const float one_coef = 1.0f;

void function(float *buff, int n) {
  
    const __m256 abs_mask = _mm256_broadcast_ss((float*) &abs_coef);
    const __m256 one_mask = _mm256_broadcast_ss(&one_coef);
    
    for(int i = 0; i < n; i += 8) {
        __m256 val = _mm256_load_ps(buff+i);
        __m256 abs_val = _mm256_and_ps(val, abs_mask);
        __m256 squ_val = _mm256_mul_ps(val, val);
        __m256 pre = _mm256_cmp_ps(abs_val, one_mask, _CMP_LT_OS);
        __m256 ret = _mm256_blendv_ps(abs_val, squ_val, pre);
        _mm256_store_ps(buff+i, ret);
    }
}

Testiohjelman vektorointi-esimerkki/vector.cpp tulostus tietokoneella, josta löytyy Intel Core i5 4690K -prosessori:

Time: 0.012953 s
Flops: 3.00116 GFlops (estimate)
Max error: 0

Vektoroitu ohjelmakoodi on siis noin 4,5 kertaa nopeampi kuin skalaariversio

Vertailuoperaation hyödyntäminen ehtolauseessa

Edellisen luvun esimerkissä silmukan sisällä ei esiintynyt yhtään ehtolausetta vaan kävimme läpi molemmat mahdollisuudet (\(|x_i| < 1\) ja \(1 \leq |x_i|\)) ja valitsimme sen jälkeen oikean vaihtoehdon "blend"-komennolla hyödyntäen pre-vertailuvektoria.
Voisimme kuitenkin lisätä ehtolauseen, jolloin välttyisimme neliön laskemiselta ja "blend"-komennolta niissä tilanteissa, joissa kaikki vektorin komponentit toteuttaisivat ehdon \(1 \leq |x_i|\).
Tämä onnistuu parhaiten _mm256_movemask_ps-aliohjelmalla, joka palauttaa int-tyyppisen muuttujan, jonka 8 vähiten merkitsevää bittiä määräytyvät argumenttina annetun vektorin komponenttien eniten merkitsevien bittien mukaan.

Tällöin voisimme antaa vertailuvektorin pre argumenttina kyseiselle aliohjelmalle ja käyttää paluuarvoa ehtolauseessa:

int cond = _mm256_movemask_ps(pre); // vmovmskps r32, ymm
if(cond) {
    __m256 squ_val = _mm256_mul_ps(val, val);
    __m256 ret = _mm256_blendv_ps(abs_val, squ_val, pre);
    _mm256_store_ps(buff+i, ret);
} else {
    _mm256_store_ps(buff+i, abs_val);
}

Seuraava kuva sisältä kaksi esimerkkitapausta _mm256_movemask_ps-aliohjelma käytöstä:

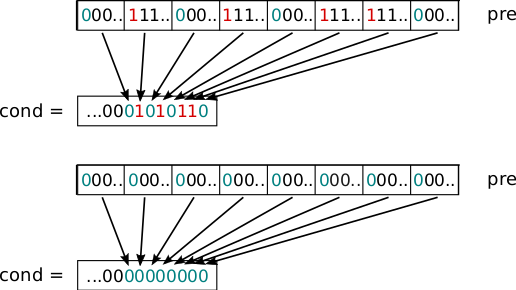
Ylemmän kaltaiseen tapaukseen törmätään silloin kun val-vektori sisältää komponentteja, joissa \(|x_i| < 1\) eli osa pre-vertailuvektorin komponenteista on saanut arvon 0xffffffff. Tällöin näitä elementtejä vastaavat bitit cond-muuttujassa saavat arvon 1 ja muuttujan cond totuusarvo vertailulauseessa on true.
Jälkimmäisessä tapauksessa kaikki vektorin val komponentit toteuttavat ehdon \(1 \leq |x_i|\), joten kaikki pre-vertailuvektorin komponentit ovat nollia ja siten cond-muuttuja saa arvon false.

Emme ota tässä kohtaa sen tarkemmin kantaa siihen, että onko ehtolauseen arvon palauttamisesta mitään oleellista hyötyä yleisessä tapauksessa.
Voidaan kuitenkin mainita sen verran, että mikäli yksittäinen vektorin komponentti toteuttaa ehdon \(|x_i| < 1\) todennäköisyydellä \(p\) niin tällöin ainakin yksi vektorin komponenteista toteuttaa ehdon todennäköisyydellä \(1-(1-p)^8\).

Suureen 1-(1-p)^8 käytös p:n funktiona — Suureen \(1-(1-p)^8\) käytös \(p\):n funktiona

Esimerkiksi tapaus, jossa pelkästään 1% luvuista kuuluu puoliavoimelle välille \((-1,1)\) johtaa tilanteeseen, jossa cond-muuttujalla on lähes 8% todennäköisyys saada nollasta eroava arvo. Yhdeksän prosentin todennäköisyys puolestaan johtaa jo lähes 53% todennäköisyyteen.
Kannattaa myöskin huomioida, että hyppykäskyillä on yleisesti ottaen negatiivinen vaikutus ohjelman suorituskykyyn sillä modernit prosessorit pyrkivät spekuloimaan ehtolauseiden lopputuloksilla jo etukäteen ja epäonnistunut ennuste johtaa pahimmillaan koko liukuhihnan mitätöimiseen.

Testiohjelman vektorointi-esimerkki/vector2.cpp tulostus tietokoneella, josta löytyy Intel Core i5 4690K -prosessori:

Time: 0.0164099 s
Flops: 2.36895 GFlops (estimate)
Max error: 0

Ehtolauseen lisääminen hidasti koodia kuten edellä spekulointiinkin

Vektorin komponenttien permutointi

Joissain tilanteissa saattaisimme haluta permutoida vektorin komponentit keskenään.
Lähdetään esimerkin vuoksi tarkastelemaan tapausta, jossa meille on annettu kaksi __m256-tyyppistä vektoria --- a ja b --- ja haluaisimme muodostaa uuden vektorin, joka sisältää ne vektoreiden a ja b komponentit, joiden indeksinumerot ovat parittomia.

Tätä varten määrittelemme ensiksi permutaatiovektorin, joka siirtää vektorin parittomasti indeksoidut komponentit vektorin alkuun ja parillisesti indeksoidut komponentit vektorin loppuun:

union perm_vector {
    __m256i m;
      __m256 f;
    int i[8];
};

const union perm_vector perm1 = { .i = { 1, 3, 5, 7, 0, 2, 4, 6 } };

Nyt voimme permutoida vektorin komponentit _mm256_permutevar8x32_ps-aliohjelmalla (vaatii AVX2-käskykantalaajennuksen), joka ottaa argumentteinaan permutoitavan vektorin ja __m256i-tyyppisen (8 etumerkillistä 32-bittistä kokonaislukua) permutaatiovektorin. Paluuarvona saadaan permutoitu vektori.
Permutaatiovektorin komponentti määrää sen permutoitavan vektorin komponentin, jonka arvo kopioidaan permutoidun vektorin vastaavaan komponenttiin.

Voimme nyt soveltaa perm1-permutaatiovektoria vektoriin a:

 __m256 aa = _mm256_permutevar8x32_ps(a, perm1.m);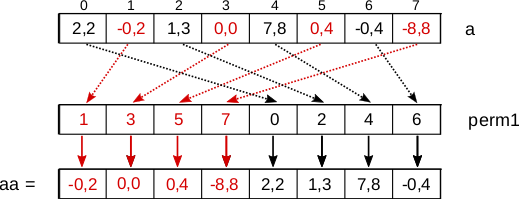

Samalla tavalla voimme määritellä permutaatiovektorin, joka siirtää vektorin parillisesti indeksoidut komponentit vektorin alkuun ja parittomasti indeksoidut komponentit vektorin loppuun.
Sen jälkeen voimme soveltaa kyseistä permutaatiovektoria vektoriin b:

const union perm_vector perm2 = { .i = { 0, 2, 4, 6, 1, 3, 5, 7 } };
__m256 bb = _mm256_permutevar8x32_ps(b, perm2.m);

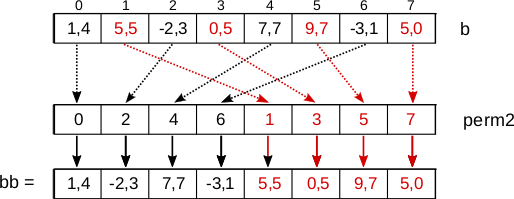
Lopuksi voimme yhdistää permutoidut vektorit aa ja bb siten että lopullisen vektorin neljä ensimmäistä komponenttia valitaan vektorin aa alusta ja neljä jälkimmäistä komponenttia vektorin bb lopusta. Tämä onnistuu tutulla _mm256_blendv_ps-aliohjelmalla:

const union perm_vector blend = { .i = { 0, 0, 0, 0, 1, 1, 1, 1 } };
return _mm256_blendv_ps(aa, bb, blend.f);

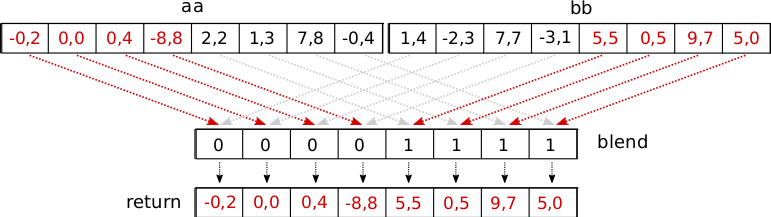
Lopuksi vielä koko ohjelmakoodi aliohjelman muodossa:

#include "immintrin.h"

union perm_vector {
    __m256i m;
      __m256 f;
    int i[8];
};

const union perm_vector perm1 = { .i = { 1, 3, 5, 7, 0, 2, 4, 6 } };
const union perm_vector perm2 = { .i = { 0, 2, 4, 6, 1, 3, 5, 7 } };
const union perm_vector blend = { .i = { 0, 0, 0, 0, 1, 1, 1, 1 } };

__m256 even_elements(__m256 a, __m256 b) {
    __m256 aa = _mm256_permutevar8x32_ps(a, perm1.m);
    __m256 bb = _mm256_permutevar8x32_ps(b, perm2.m);
    return _mm256_blendv_ps(aa, bb, blend.f);
}

Käänteisluvun laskeminen vektoroidusti

Luentomonisteen alussa esitetty esimerkkikoodi, jossa laskettiin lukujen käänteislukuja, voidaan myöskin vektoroida varsin helposti.
Tällä kertaa käytämme __m256d-tyyppisiä vektorimuuttujia, joihin voidaan tallentaa neljä kaksinkertaisen tarkkuuden liukulukua.
Sen lisäksi hyödynnämme _mm256_fmadd_pd-aliohjelmaa, joka ottaa argumenttinaan kolme vektoria ja laskee komponentittaisen fma-operaation (Fused multiply-add) eli ensimmäisen argumentin komponentti kerrotaan toisen argumentin vastaavalla komponentilla ja tulokseen lisätään kolmannen argumentin vastaava komponentti.

#include "immintrin.h"

void process(double *a, double *b, int n) {
  
    // Vektoriarvoiset vakiot alkuarvauksen ja Newtonin iteraation laskemiseen
    const __m256d coefA = { 48.0/17.0, 48.0/17.0, 48.0/17.0, 48.0/17.0 };
    const __m256d coefB = { 32.0/17.0, 32.0/17.0, 32.0/17.0, 32.0/17.0 };
    const __m256d coefC = { 1.0, 1.0, 1.0, 1.0 };

    // Muokattu silmukka
    for(int i = 0; i < n; i += 4) {

        __m256d md = - _mm256_load_pd(b+i);

        // Alkuarvaus, y_j = 32/17 * (md)_j + 48/17
        __m256d y = _mm256_fmadd_pd(coefB, md, coefA); 

        __m256d t;

        // Yksittainen Newtonin iteraatio on jaettu kahteen fma-operaatioon
        t = _mm256_fmadd_pd(md, y, coefC); // (t)_j = (md)_j * (y)_j + 1.0
        y = _mm256_fmadd_pd(y, t, y);      // (y)_j = (y)_j * (t)_j + (y)_j

        t = _mm256_fmadd_pd(md, y, coefC);
        y = _mm256_fmadd_pd(y, t, y);

        t = _mm256_fmadd_pd(md, y, coefC);
        y = _mm256_fmadd_pd(y, t, y);

        t = _mm256_fmadd_pd(md, y, coefC);
        y = _mm256_fmadd_pd(y, t, y);

        _mm256_store_pd(b+i, y);
    }
}