Twisted moire heterostructures

The slides of the fourth session are here

Lecture videos:

About these lecture notes

The lecture notes are provided a support to the lecture slides and the exercises. You do not need to read the lecture notes to do the hands-on exercises with pyqula, but they can provide a good support if you want to go deeper in the topic. The references at the end of the lecture notes for each session provide a more detailed discussion of the aspect discussed, and they would be very useful references to see a more in-depth discussion.

Learning goals

Understand the impact of superlattice modulations in a band structure
Understand the moire electronic structure in a twisted system
Rationalize the emergence of van Hove singularities in moire materials
Understand how moire effects can drive correlated states in twisted materials

Superpotentials and minibands

Although for the rest of this chapter we will consider periodic systems, it is interesting first to discuss a more general case: periodic systems subject to incommensurate potentials.

Different types of moire van der Waals materials

Quasicrystals are materials with atoms arranged in a non-periodic but ordered pattern. To describe their electronic properties, we consider hybridization of their valence electrons similar to what is done for periodic materials. Such a construction lends itself also to metamaterial structures, where waves interfere in the presence of a patterned medium. The longer-ranged quasiperiodic spatial arrangement of the "atoms" leads to splitting of the bands into infinitely-many mini-bands. Considering, for simplicity, the resulting tight-binding Hamiltonian description of the s-orbits hybridization along a \(1 \mathrm{D}\) quasiperiodic chain, we have \[ H_{s}=\sum_{n}\left\{\lambda^{\mathrm{d}} V_{n}^{\mathrm{d}} c_{n}^{\dagger} c_{n}+\sum_{m>0}\left[\left(t_{m}+\lambda_{m}^{\mathrm{od}} V_{n, m}^{\mathrm{od}}\right) c_{n}^{\dagger} c_{n+m}+h . c .\right]\right\}, \] where \(n, m\) are integers iterating over the atomic sites along the chain, \(c_{n}^{\dagger}\) is a second-quantized creation operator at site \(n, V_{n}^{\mathrm{d}}\) is an on-site quasiperiodic potential corresponding to the height of the potential-well at each site with modulation amplitude \(\lambda^{\mathrm{d}}\). The kinetic energy matrix elements are decomposed into hopping amplitudes \(t_{m}\) associated with the mean hybridization between orbits separated by \(m\) sites, on top of which a quasiperiodic function \(V_{n, m}^{\text {od }}\) of amplitude \(\lambda_{m}^{\text {od }}\) encodes the modulated inter-atomic distances. Note that generally we can also consider additional quasiperiodic potentials, e.g., spin-dependent and spin-orbit-dependent terms.

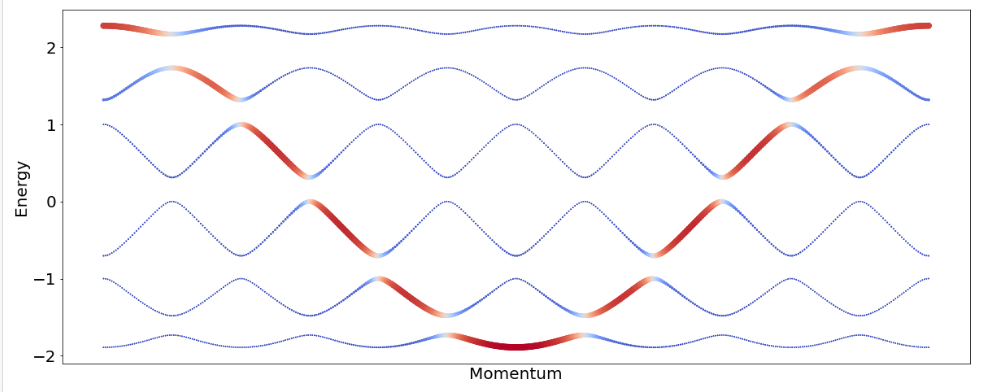
Emergence of minibands due to to a superlattice potential

The quasiperiodic 1D functions \(V_{n}^{\mathrm{d}}\) and \(V_{n, m}^{\mathrm{od}}\) can be constructed, for example, by primitive substitutions to iteratively generate a non-repeating sequence of discrete values. In the moire materials we will consider, such a potential somes directly from the structure of a twisted system

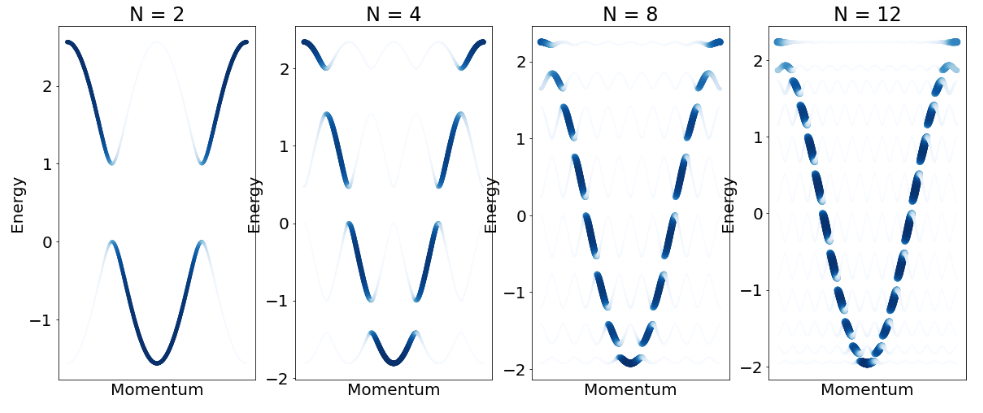
Mini-bands for different periodicities of a lattice of scattering potentials

Much research is pursued within the mathematical physics community, aiming to answer whether the spectrum has a well-defined structure with a countable number of bands and gaps, whether the eigenstates of the quasicrystals are spatially-extended or localized, and whether a topological classification of spectral bands of the quasicrystals is possible by harnessing K-theoretical tools. Sspecific quasiperiodic sequences fix the integrated density of states as a topological index that allows for labeling of spectral gaps of the material. Most importantly for this lecture, the emergence of energy gaps signals the appearence of a new electronic structure, potentially leading to new physical effects.

Electronic structure of a 1D chain as a function of the frequency of the modulation of a moire potential

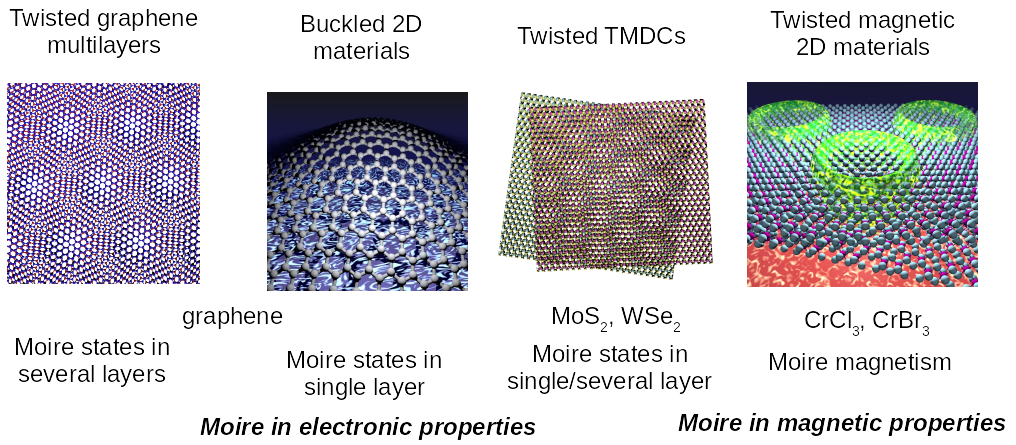
Structure of moire materials

When a \(2 {D}\) crystal is twisted relative to another, there is no guarantee of periodicity in the resulting atomic structure. The two crystal lattices 'beat' in space, giving rise to a 2D moiré pattern defined by the interference between the two layers' individual periodicities. For some special angles, a translational symmetry is retained, but its length scale is much larger than the original unit cells of the crystals. This is the case for a commensurate twist angle, and the retained symmetry defines the commensurate moiré supercell. When no such translational symmetry is retained, the system is incommensurate. Even in the incommensurate case, there is still a well-defined moiré length scale, \(\lambda_{ {m}}\), for the twisted bilayer. For twisted triangular lattices, the law of cosines yields \(\lambda_{ {m}}(\theta)=(a / 2) / \sin (\theta / 2)\), where \(a\) is the lattice constant of the constituent monolayer and \(\theta\) is the twist angle. This length scale can be interpreted as an approximate periodicity in the local arrangement between the layers' unit cells and is the distance between the light stacking spots of the twisted hexagonal bilayer. The case of materials with slight lattice mismatch is similar and is discussed when relevant. In those cases, \(\lambda_{ {m}}\) has a more complicated form and, generally, small lattice strain is required to create commensurate supercells. Given a lattice mismatch of \(\delta\), the moiré length is given by \[ \lambda_{ {m}}(\theta, \delta)=\frac{(1+\delta) a}{\sqrt{2(1+\delta)(1-\cos \theta)+\delta^{2}}} \] This expression is derived by considering the difference between the two layers' reciprocal lattice vectors.

Electronic structure folding of a triangular lattice, without including any superlattice potential

In real devices, the twist angle cannot be controlled as precisely as in simulations. Recent reports put the state-of-the-art experimental control of the angle near \(0.1^{\circ}\). The current stacking methods usually require breaking a monolayer into two parts and then placing one part on top of the other. This technique, named the tear-and-stack approach, can introduce huge amounts of mechanical strain and non-uniformity in the moiré heterostructure. As a result, sometimes the twist angle is often non-uniform in space.

More complicated structures with a single twist angle can also be considered, such as a three-sheet graphene system in which the top and botton sheets form one effective layer and the middle sheet another, with a relative twist angle between the two.

Moving the axis of rotation to a different point on the bilayer is equivalent to choosing a different initial in-plane displacement between the layers. After a rotation, the local displacement between the unit cells of each layer varies in space. Because the two lattices are no longer identical after twisting, there is always a spatial variation in this local stacking order. For a commensurate system, only a finite set of local stackings occur, but for an incommensurate system, all possible stackings occur, and each stacking has a one-to-one correspondence with a unique location in space. We will nonetheless focus on commensurate systems, as theoretical methologies are more easily understood in that case.

Local stackings that admit high-symmetry point groups often correspond to the critical points of stacking-dependent electronic properties. For graphene bilayers, \(A A\) and \(A B\) stacking refer to regions where two or one carbon atoms, respectively, are eclipsed by a carbon of the opposite layer in each unit cell, whereas the \(\{AB\}\) configuration is called Bernal stacking. In TMDCs, the \(\{AB\}\) and \(\{BA\}\) labels often refer to the orientation of the two layers rather than to their local stacking.

In a twisted system, the local configuration, \(d\), is a function of space, \(d(r)\). The electronic properties calculated from the untwisted reference stackings can be leveraged to approximate the twisted bilayer with a smoothly varying field over the moire pattern. This is the basis of most continuam descriptions of these systems.

The degree of control in moiré systems can be compared with that available in oeher artificial lattices, such as optical lattices, with moiré systems having a smaller length scale (nanometres instead of micrometres).

For moire systems with a single twist angle, it is useful to visualize the electronic Hamiltonian as divided into three parts: two periodic Hamiltonians, \(H_{1}\) and \(H_{1}\) and an interlayer coupling Hamiltonian, \(T\). The \(H_{j}\) have the periodicity of a conventional \(2 {D}\) lattice, of order angstrom, whereas \(T\) captures the periodicity of the superlattice. The length scale of this interlayer periodicity, \(\lambda_{\text {an }}\) is proportional to \(1 / \theta\). This provides an unprecedented amount of control on the moiré interface, allowing for the creation of systems with length scales anywhere between 1 and 100 nm.

Emergence of moire minibands in triangular lattice with a superlattice potential

The most direct way to model any crystalline system is to consider the local electronic environment near each atom. The starting point for most atomistic models is the construction of a moiré supercell. Atomistic models can only study commensurate systems but allow for the use of Bloch theory and conventional band-structure methods. The most common description of the supercell is with a pair of integers, \((M, N)\), such that one of the superlattice primitive vectors is given by \(N a_{1}+M a_{2}\), where \(a_{i}\) are the Bravais lattice vectors of one of the layers.

Emergent van Hove singularities due to a superlattice potential

The reciprocal lattice of the supercell, \(G\), can be derived from the supercell lattice vectors, \(A\), with the standard formula \(G=2 \pi\left(A^{ {T}}\right)^{-1}\). For \(2 {D}\) materials, \(G\) and \(A\) are \(2 \times 2\) matrices whose columns correspond to the 2D lattice vectors. The Brillouin zone of the supercell can also be understood in some cases by considering the Brillouin zone of the rotated monolayers.

Geometry of twisted bilayer graphene

Each graphene layer in the tBLG consists of two sublattices ( \(A 1, B 1\) in layer 1 , and \(A 2, B 2\) in layer 2). The positions of the carbon atoms in each sublattice in the bottom layer 1 are \[ \mathbf{r}_{\mathbf{n}}^{1 A} \equiv \mathbf{r}_{\mathbf{n}}=n \mathbf{a}_{1}+m \mathbf{a}_{2}, \quad \mathbf{r}_{\mathbf{n}}^{1 B}=\mathbf{r}_{\mathbf{n}}+\boldsymbol{\delta}_{1}, \] where \(\mathbf{n}=\{n, m\} \quad\left(n, m\right.\) are integers), \(\boldsymbol{\delta}_{1}=\left(\mathbf{a}_{1}+\mathbf{a}_{2}\right) / 3=\) \(a\{1 / \sqrt{3}, 0\}\), and \(\mathbf{a}_{1,2}\) are basis vectors of the graphene elementary unit cell, \[ \mathbf{a}_{1}=a\{\sqrt{3},-1\} / 2, \quad \mathbf{a}_{2}=a\{\sqrt{3}, 1\} / 2, \] with the lattice parameter \(a=2.46 \AA\). When the layers are not rotated \((\theta=0)\), the system is a perfect \(A B\) bilayer.

We will assume that the constituent graphene layers are perfectly flat, and separated by the distance \(d=3.35 \AA\) from each other. In a real tBLG sample the layers are not purely two dimensional. The interlayer distance varies depending on local arrangement of the atoms. The interlayer corrugation is quite small \((\sim 0.1 \AA)\), thus, it can be neglected.

Layer 2 is rotated with respect to layer 1 by the angle \(\theta\) around the axis connecting the atoms \(A 1\) and \(B 2\) with \(\mathbf{n}=0\). In this case the atoms of the top layer have the positions \[ \mathbf{r}_{\mathbf{n}}^{2 B} \equiv \mathbf{r}_{\mathbf{n}}^{\prime}=n \mathbf{a}_{1}^{\prime}+m \mathbf{a}_{2}^{\prime}, \quad \mathbf{r}_{\mathbf{n}}^{2 A}=\mathbf{r}_{\mathbf{n}}^{\prime}-\boldsymbol{\delta}_{2}, \] where \[ \mathbf{a}_{1,2}^{\prime}=\mathbf{a}_{1,2}\left(\cos \theta \mp \frac{\sin \theta}{\sqrt{3}}\right) \pm \mathbf{a}_{2,1} \frac{2 \sin \theta}{\sqrt{3}} \text {, } \] and \(\boldsymbol{\delta}_{2}=a\{\cos \theta, \sin \theta\} / \sqrt{3}\).

The structure of the tBLG is commensurate if \[ \cos \theta=\frac{3 m_{0}^{2}+3 m_{0} r+r^{2} / 2}{3 m_{0}^{2}+3 m_{0} r+r^{2}}, \] where \(m_{0}\) and \(r\) are coprime positive integers. The superlattice vectors, \(\mathbf{R}_{1,2}\), can be expressed via \(m_{0}, r\), and the single-layer graphene lattice vectors, \(\mathbf{a}_{1,2}\). These expressions are different when \(r\) is either nondivisible or divisible by 3 . In the former case, we have \[ \begin{aligned} &\mathbf{R}_{1}=m_{0} \mathbf{a}_{1}+\left(m_{0}+r\right) \mathbf{a}_{2} \\ &\mathbf{R}_{2}=-\left(m_{0}+r\right) \mathbf{a}_{1}+\left(2 m_{0}+r\right) \mathbf{a}_{2} \end{aligned} \quad(r \neq 3 n, n \in \mathcal{N}) . \] For \(r=3 n\), the superlattice vectors become \[ \begin{aligned} &\mathbf{R}_{1}=\left(m_{0}+n\right) \mathbf{a}_{1}+n \mathbf{a}_{2} \\ &\mathbf{R}_{2}=-n \mathbf{a}_{1}+\left(m_{0}+2 n\right) \mathbf{a}_{2} \end{aligned} \quad(r=3 n, n \in \mathcal{N}) . \] The number of sites in each supercell is \[ N\left(m_{0}, r\right)= \begin{cases}4\left(3 m_{0}^{2}+3 m_{0} r+r^{2}\right), & \text { if } r \neq 3 n, \\ 4\left(m_{0}^{2}+m_{0} r+r^{2} / 3\right), & \text { if } r=3 n .\end{cases} \] The linear size of the superlattice cell \(( {SC})\) is \[ L_{s c} \equiv\left|\mathbf{R}_{1,2}\right|=a \sqrt{N} / 2 . \] Besides \(L_{w}\), the tBLG has another characteristic length scale. The rotation of one graphene layer with respect to another one leads to the appearance of Moire pattems, which manifest themselves as altemating bright and dark regions in STM images. The Moiré period \(L\), is defined as the distance between centers of two neighboring bright (or dark) regions. It is related to the twist angle according to the following formula: \[ L=\frac{a}{2 \sin (\theta / 2)} . \] The Moiré pattern and the superstructure are two complementary concepts used to describe tBLG. The Moiré pattern depends smoothly on the twist angle. The pattern can be easily detected experimentally. However, working with the Moire theoretically may be challenging due to the fact that the pattem is strictly periodic only for a very limited discrete set of angles. For a generic value of \(\theta\), different Moiré cells in a pattern may look alike, but they are not exactly identical.

The superstructure, which is a periodic lattice of supercells, does not suffer from this shortcoming. Unfortunately, it has its own deficiencies. Namely, the superstructure is only defined for commensurate angles \(\theta\). The period \(L_{ {se}}\) is not a smooth function of \(\theta\) : two commensurate \(\theta\) and \(\theta^{\prime}, \theta \approx \theta^{\prime}\), may correspond to two very dissimilar \(L_{\text {se- }}\) As we will see below, such sensitivity to the twist angle may, in some situations, require additional efforts in interpreting theoretical results. One can easily demonstrate that the superstructure coincides with the Moiré pattern only when \(r=1\). For other superstructures, \(L_{k}\) is greater than \(L\). The supercells of these structures contain \(r^{2}\) (if \(r \neq 3 n\) ) or \(r^{2} / 3\) (if \(r=3 n\) ) Moiré cells, and the arrangements of atoms inside these Moiré cells are slightly different from each other. This means, in particular, that the structures with \(r>1\) can be considered as almost periodic repetitions of structures with \(r=1\). The basis vectors of the reciprocal superlattice can be written as \[ \begin{aligned} \mathbf{G}_{1} &=\frac{\left(2 m_{0}+r\right) \mathbf{b}_{1}+\left(m_{0}+r\right) \mathbf{b}_{2}}{3 m_{0}^{2}+3 m_{0} r+r^{2}} \\ \mathbf{G}_{2} &=\frac{-\left(m_{0}+r\right) \mathbf{b}_{1}+m_{0} \mathbf{b}_{2}}{3 m_{0}^{2}+3 m_{0}+r^{2}} \end{aligned} \]

if \(r \neq 3 n\), or \[ \begin{aligned} \mathbf{G}_{1} &=\frac{\left(m_{0}+2 n\right) \mathbf{b}_{1}+n \mathbf{b}_{2}}{m_{0}^{2}+m_{0} r+r^{2} / 3} \\ \mathbf{G}_{2} &=\frac{-n \mathbf{b}_{1}+\left(m_{0}+n\right) \mathbf{b}_{2}}{m_{0}^{2}+m_{0} r+r^{2} / 3} \end{aligned} \] if \(r=3 n\), where \[ \mathbf{b}_{1}=2 \pi\{1 / \sqrt{3},-1\} / a, \quad \mathbf{b}_{2}=2 \pi\{1 / \sqrt{3}, 1\} / a \]

Electronic structure of a twisted double bilayer graphene, without and with crystal field effects

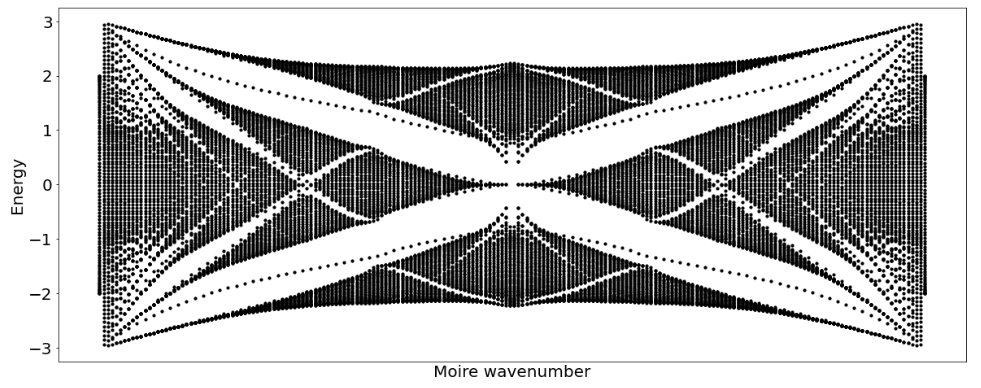
are the reciprocal-lattice vectors of the single-layer graphene. The first Brillouin zone of the superlattice has the shape of a hexagon with sides \(\left|\mathbf{G}_{2}-\mathbf{G}_{1}\right| / 3\). In the particular case of \(r=1\), this side is equal to \(\Delta K=\left|\mathbf{K}_{\theta}-\mathbf{K}\right|\), where \[ \mathbf{K}=\frac{4 \pi}{3}\{0,1\} \quad \text { and } \quad \mathbf{K}_{\theta}=\frac{4 \pi}{3}\{-\sin \theta, \cos \theta\} \] are the Dirac points of the bottom and top layers, respectively. As known from basic graphene tight-binding physics, in addition to the Dirac cone at the \(\mathbf{K}\) point, the bottom layer of the tBLG has another cone of opposite chirality at \(\mathbf{K}^{\prime}=-\mathbf{K}\). Likewise, the top layer has its second cone at \(\mathbf{K}_{\theta}^{\prime}=-\mathbf{K}_{\theta}\). It is important to determine where these two cones are located in the Brillouin zone of the superstructure. To find this out we express their coordinates in terms of reciprocal superlattice vectors. For \(r \neq 3 n\) we have \[ \begin{aligned} \mathbf{K} &=-\mathbf{K}^{\prime}=m_{0} \mathbf{G}_{2}+\frac{r}{3}\left(\mathbf{G}_{1}+2 \mathbf{G}_{2}\right) \\ \mathbf{K}_{\theta} &=-\mathbf{K}_{\theta}^{\prime}=m_{0} \mathbf{G}_{2}+\frac{r}{3}\left(\mathbf{G}_{2}-\mathbf{G}_{1}\right) \end{aligned} \] while for \(r=3 n\) we obtain \(\mathbf{K}=-\mathbf{K}^{\prime}=\frac{r}{3} \mathbf{G}_{2}+\frac{m_{0}}{3}\left(\mathbf{G}_{2}-\mathbf{G}_{1}\right)\), \(\mathbf{K}_{\theta}=-\mathbf{K}_{\theta}^{\prime}=-\frac{r}{3} \mathbf{G}_{1}+\frac{m_{0}}{3}\left(\mathbf{G}_{2}-\mathbf{G}_{1}\right) .\) It follows from these formulas that, if \(r \neq 3 n\), point \(\mathbf{K}^{\prime}\) is equivalent to \(\mathbf{K}_{\theta}\), and \(\mathbf{K}\) is equivalent to \(\mathbf{K}_{\theta}^{\prime}\) : for such a value of \(r\) the difference \(\mathbf{K}^{\prime}-\mathbf{K}_{9}\) is a reciprocal vector of the superlattice. When \(r=3 n\), the equivalent Dirac points are \(\mathbf{K} \sim \mathbf{K}_{\theta}\) and \(\mathbf{K}^{\prime} \sim \mathbf{K}_{9}^{r}\). Thus, for any commensurate angle we have two doubly degenerate nonequivalent Dirac points of the tBLG. It follows that inside the reciprocal cell of the superlattice, the two nonequivalent \(\mathrm{ABL}\) Dirac points are located at \[ \mathbf{K}_{1}=\frac{\mathbf{G}_{1}+2 \mathbf{G}_{2}}{3}, \quad \mathbf{K}_{2}=\frac{2 \mathbf{G}_{1}+\mathbf{G}_{2}}{3}, \] for any superstructure. As we will show below, this double degeneracy affects the electronic structure of the tBLG, leading to band splitting and band-gap formation. It is finally worth noting that this geometry can be systematically extended to other twisted graphene multilayers, including trilayers and double bilayers.

Atomistic model for twisted graphene bilayers

It is convenient to enumerate the sites in the sublattice in each layer using two integer-valued vectors \(\mathbf{j}=\{i, j\}\) and \(\mathbf{n}=\{n, m\}\), where \(\mathbf{j}\) labels the position of the supercell in the lattice, while \(\mathbf{n}\) enumerates the sites inside the supercell. Then, we can write down the tight-binding Hamiltonian of the \(\mathrm{BLG}\) in the form \(H=-t \sum_{\substack{i=j \mathrm{je} \\ \mathrm{se}}}\left(d_{\sin A \sigma}^{\dagger} d_{s \mathrm{jm} B \sigma}+\right.\) H.c. \()\) \(+\sum_{\substack{\mathbf{k} \mathbf{j o c} \\ \alpha \neq 0}}\left[t_{\perp}\left(\mathbf{R}_{\mathbf{i}}+\mathbf{r}_{\mathrm{n}}^{1 \alpha} ; \mathbf{R}_{\mathbf{j}}+\mathbf{r}_{\mathbf{m}}^{2 \hat{\beta}}\right) d_{1 \ln \alpha \sigma}^{\dagger} d_{2 j \mathbf{j} \hat{\beta} \sigma}+\right.\) H.c. \(]\), where \(\mathbf{R}_{\mathbf{j}}=i \mathbf{R}_{1}+j \mathbf{R}_{2}\), the symbol \(\langle\ldots\rangle\) stands for summation over the nearest neighbors within the same layer, \(d_{s j n a \sigma}^{\dagger}\) and \(d_{s j n a r s}\) are the creation and annihilation operators of an electron with the spin projection \(\sigma\) in the layer \(s(=1,2)\) on the sublattice \(\alpha(=A, B)\) in the supercell \(\mathbf{j}\) in the position \(\mathbf{n}\) (the position of this site is \(\mathbf{R}_{\mathbf{j}}+\mathbf{r}_{\mathbf{n}}^{s \alpha}\) ). The first term describes the inplane nearest-neighbor hopping with amplitude \(t=2.57 \mathrm{eV}\). The second term describes the interlayer hopping, with \(t_{\perp}\left(\mathbf{r} ; \mathbf{r}^{\prime}\right)\) being the hopping amplitude between sites in the positions \(\mathbf{r}\) and \(\mathbf{r}^{\prime}\).

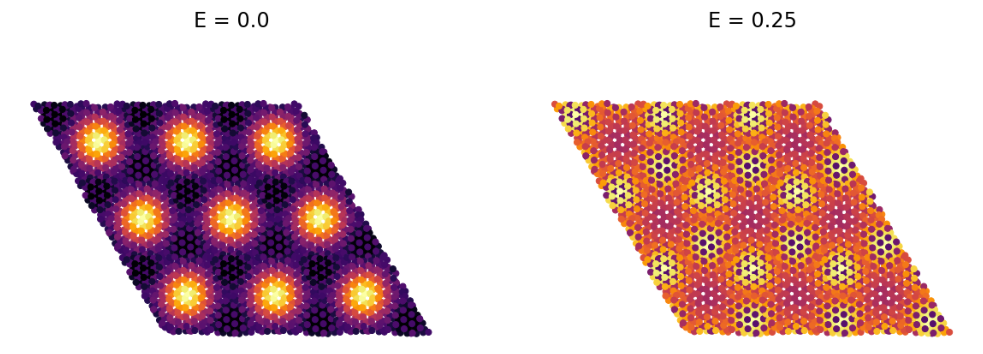
Spatial distribution of the moire states in a twisted graphene bilayer

This previous Hamiltonian is invariant with respect to translations by the superstructure vectors \(\mathbf{R}_{1,2}\). Performing the Fourier transform \(d_{s k n a \sigma}=\mathcal{N}_{s c}^{-1 / 2} \sum_{j} e^{-i \mathbf{k R}_{j}} d_{s j n \alpha \sigma}\), where \(\mathcal{N}_{s c}\) is the number of supercells in the bilayer, and using the relation \(t_{\perp}\left(\mathbf{R}_{\mathbf{j}}+\mathbf{r}^{-}, \mathbf{R}_{\mathbf{j}}+\mathbf{r}^{r}\right)=t_{\perp}\left(\mathbf{r} ; \mathbf{r}^{\prime}\right)\), we obtain \(H=\sum_{\substack{\operatorname{knm}}}\left[t_{\operatorname{mm}}^{s}(\mathbf{k}) d_{s k \operatorname{kn} A \sigma}^{\dagger} d_{s k \mathbf{m} B \sigma}+\right.\) H.c. \(]\) \(+\sum_{\substack{\mathbf{k a n} \\ \alpha \neq 0}}\left[t_{\perp \mathrm{mm}}^{\alpha \beta}(\mathbf{k}) d_{1 \mathbf{k n} \alpha \sigma}^{\dagger} d_{2 \mathbf{k m} \beta \sigma}+\right.\) H.c. \(]\), where \(\mathbf{k}\) runs over the first Brillouin zone of the superlattice. The vectors \[ \begin{gathered} t_{\mathbf{n m}}^{s}(\mathbf{k})=-t \sum_{j \delta} e^{-i \mathbf{k R}_{j} \delta_{\mathbf{N}_{j}+\mathbf{n}, \mathbf{m}-\delta},} \\ t_{\perp \mathrm{mm}}^{\alpha \hat{\beta}}(\mathbf{k})=\sum_{\mathrm{j}} e^{-i \mathbf{k R}_{j}} t_{\perp}\left(\mathbf{R}_{\mathrm{j}}+\mathbf{r}_{\mathbf{n}}^{1 \alpha} ; \mathbf{r}_{\mathbf{m}}^{2 \beta}\right), \end{gathered} \] take the values \(\{0,0\},\{1,0\},\{0,1\}\), and \[ \mathbf{N}_{\mathrm{j}}=\left\{m_{0} i-\left(m_{0}+r\right) j,\left(m_{0}+r\right) i+\left(2 m_{0}+r\right) j\right\} . \] With regards to the interlayer coupling, \(t_{\perp}\left(\mathbf{r} ; \mathbf{r}^{\prime}\right)\) in a real material would depend not only on the relative positions of the initial and final carbon atoms, but also on the positions of other atoms in the bilayer via the screening function \(S\left(\mathbf{r} ; \mathbf{r}^{\prime}\right)\). The closer some of the neighboring atoms are to the line connecting the sites \(\mathbf{r}\) and \(\mathbf{r}^{\prime}\), the stronger is the screening. For practical purposes, the electronic properties of twisted multilayers are qualitatively captured neglecting screening effects provided the hoppings are properly renormalized.

Twisted moire materials as correlated state emulators

Moiré heterostructures of van der Waals materials exploit quantum interference to quench the effective kinetic energy scales, which permits both driving the system at low energies to an interaction-dominated regime, and drastically enhancing anisotropies or reducing symmetries of the monolayer. Conceptually, the physical mechanism can be understood straightforwardly in analogy to classical moiré interference patterns. If two identical patterns with a discrete translation symmetry in two dimensions are superimposed at an angle, the combined motif retains a periodicity at much longer wavelengths for an infinite set of small rational angles.

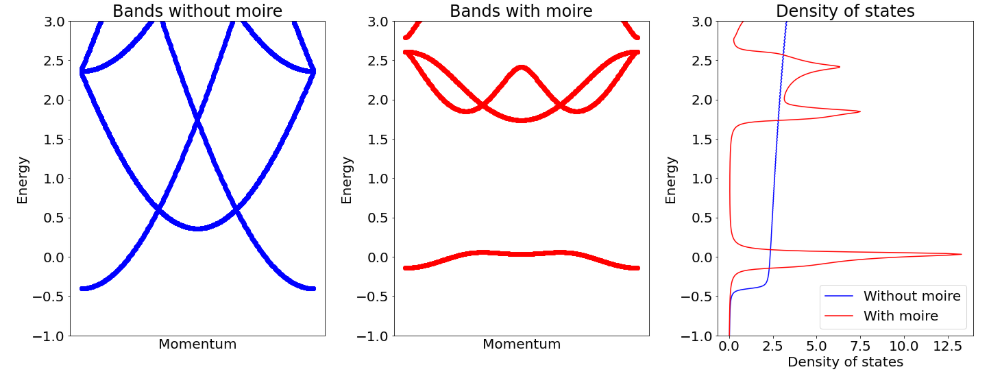
Electronic structure in the absence and presence of a moire, comparing their relatives density of states

Similarly, a heterostructure of two or more monolayers with commensurate lattice constants stacked at a twist retains spatial periodicity for small commensurate angles, albeit with a much larger moiré unit cell. This moiré superlattice can span many unit cells and defines a new crystal structure with a mini Brillouin zone. Within this moiré Brillouin zone, the folded bands lead to a multitude of crossings, which are subsequently split via interlayer hybridization. Crucially, lattice relaxation enhances these avoided crossings and typically segregates sets of almost-dispersionless bands on millielectronvolt energy scales, which can be addressed individually via gate-tuning the chemical potential. A complementary view of the physics of a moiré band follows from considering its real space description. A localized electron in a moiré band can be viewed as occupying a virtual 'moiré orbital' that can extend over hundreds of atoms, effectively spreading over the entire moiré unit cell. Importantly, the shape of moiré orbitals changes with the size of the moiré unit cell so that the electronic interactions become a function of the twist angle as well, decreasing at a slower rate than the kinetic energy scales for decreasing angle. This permits tuning a priori weakly interacting electronic systems into regimes dominated by electronic correlations in a controlled fashion.

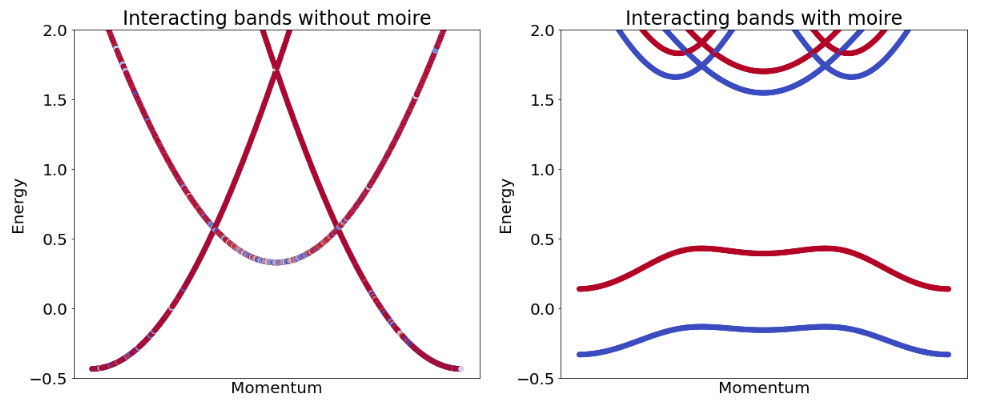
Electronic structure with interactions in the absence and presence of a moire, the latter showing a correlated state

A first demonstration of the above phenomenology was realized in materials with hexagonal structure and multiple atomic orbitals. The moiré band width for twisted bilayers of graphene does not behave monotonically as a function of twist angle but exhibits a series of 'magic' angles at which the moiré bands near charge neutrality become almost dispersionless over a large fraction of the moiré Brillouin zone. More broadly, as reductions of the electronic band width equivalently enhance the role of competing energy scales, this microscopic structural knob to selectively quench the kinetic energy scales in 2D materials opens up possibilities to selectively engineer heterostructures with properties that are dominated via many-body electronic interactions, ultrastrong spin-orbit interactions from heavier elements, electron-lattice interactions or electron-photon interactions, permitting realization of a wide range of correlated or topological phenomena.

Correlated honeycomb lattices

Twisted graphene bilayers provide a minimal platform for correlated honeycomb models. Due to destructive interference within the strongly asymmetric \(p_{x}-p_{y}\) Hubbard model itself (meaning that the two orbitals have very different hopping amplitudes), attached at the bottom and top of these flat bands one can find bands with even much lower dispersion. The asymmetric \(p_{x}-p_{y}\) Hubbard model is therefore another lattice Hamiltonian that can effectively be engineered in this solid-state framework, and also controlled by external parameters, such as strain or fields. This could provide interesting insights into highly degenerate systems and the interplay of magnetism with these types of band structure. Similar phenomena are expected to emerge in other twisted transition metal dichalcogenide (TMD) homobilayers, such as twisted bilayer \(\mathrm{MoSe}_{2}\) and \(\mathrm{WS}_{2}\).

Correlated triangular lattices

Triangular lattice structures can be engineered lattice structure by twisting two sheets of tungsten diselenide WSe\(_2\) or other TMD heterostructures. A superstructure emerges that effectively confines the low-energy physics onto a triangular lattice. In addition, the heavier transition metal elements in such TMD systems impose substantial spin-orbit coupling onto the low-energy degrees of freedom.

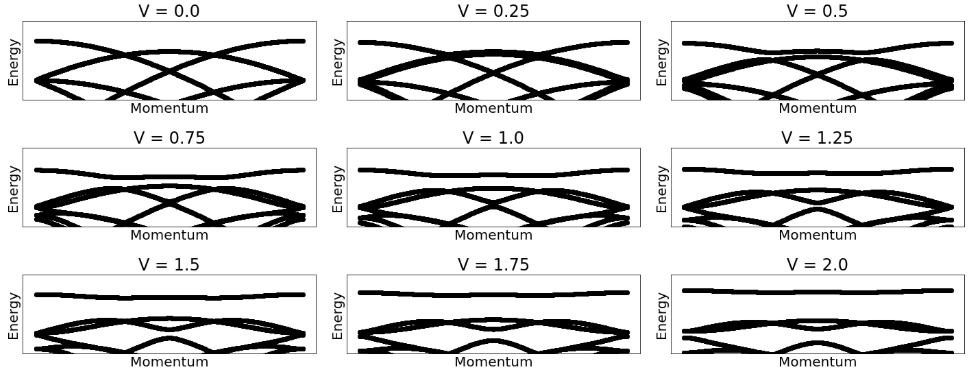
Emergence of flat bands featuring a triangular superlattice due to a moire potential

Fundamentally, triangular lattices are prototypical model systems to study the role of geometric frustration on electronic and magnetic orders. Using twisted materials one might thus simulate effectively the properties of these theoretically challenging models, relevant also for understanding many other condensed-matter systems. Among others, correlated states of matter that can be realized include \(120^{\circ}\) Neel ordered states, topological forms of superconductivity and quantum chiral spin liquids. In the case of TMD homobilayers, features consistent with superconducting phases have been seen in close proximity to the insulating phase. For these materials, angular precision is not as stringent as in graphene, so samples are easier to produce.

Emergence of Wannier states localized in a superlattice due to a moire potential

Emergent quantum states in twisted van der Waals multilayers

Artificial gauge fields

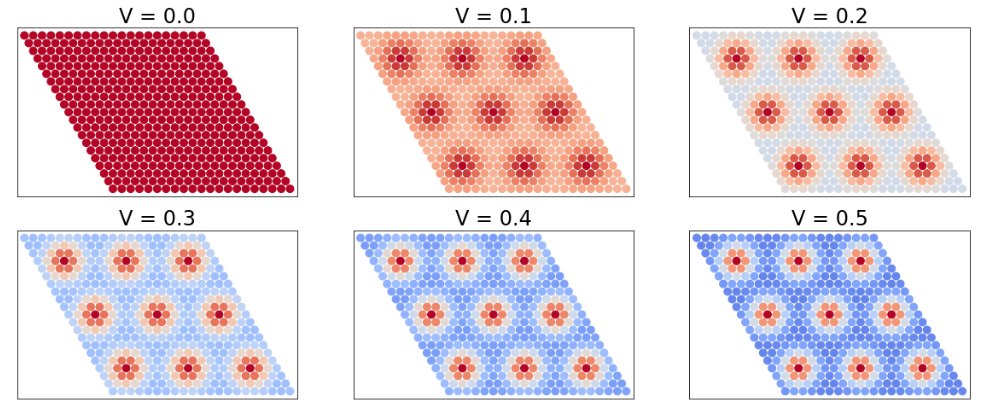
In twisted graphene bilayers, the effect of spatial modulations, such as those that arise upon shearing or twisting, give rise to elastic gauge fields, leading in turn to pseudo Landau levels. Their single-particle physics, characterized by charge accumulation and recurrent formation of zero-energy bands as the pattern period L increases, is governed by a non-Abelian gauge potential arising in the low-energy electronic theory due to the coupling between layers. Such gauge-type couplings give rise to a potential that, for certain discrete values of L, spatially confines states at zero energy in particular regions of the Moire patterns.

Topological networks

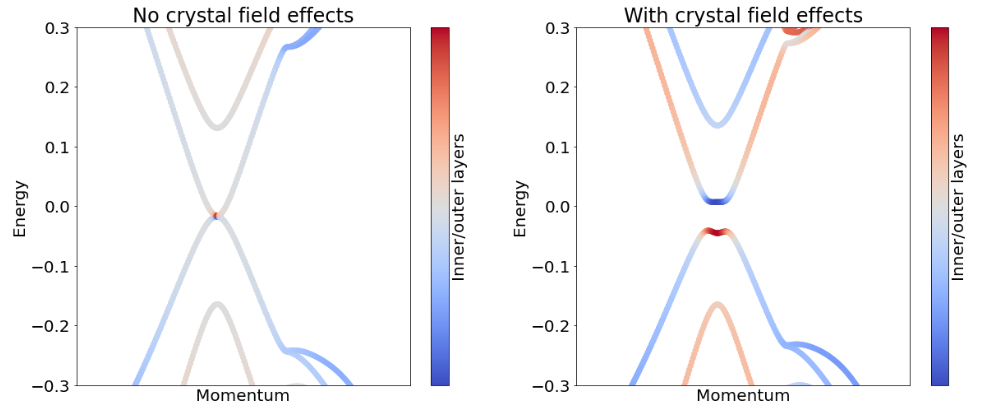
A twisted graphene bilayer exhibits a triangular Moiré pattern in the local stacking, that smoothly alternates between the three basic types AA', AB' and BA'. Under an interlayer bias U, the latter two types develop a spectral gap, characterised by opposite valley Chern numbers. For large enough Moiré periods and bias, these regions become depleted electronically, and topologically protected helical modes appear at their boundaries. This gives rise to a delocalised topological network of the Chalker-Coddington type, composed of valley current vortices. This network can be tailored by controlled deposition of valley-mixing adsorbates, which block transmission in selected links, thus opening the possibility of custom topological nanoelectronics.

Networks of helical channels offer several advantages for topologically protected quantum states. The two-dimensional nature of the network allows one to perform complex valleytronic operations and, as demonstrated in this work, stabilizes coherent bulk transport phenomena such, as Fabry-Perot oscillations, in magnetic field and against disorder. Furthermore, avoiding the physical edge leads to a better defined environment which improves topological protection. Our carbon-based system is flexible, making it an important building block for scalable and protected valleytronic devices.

Correlated insulators

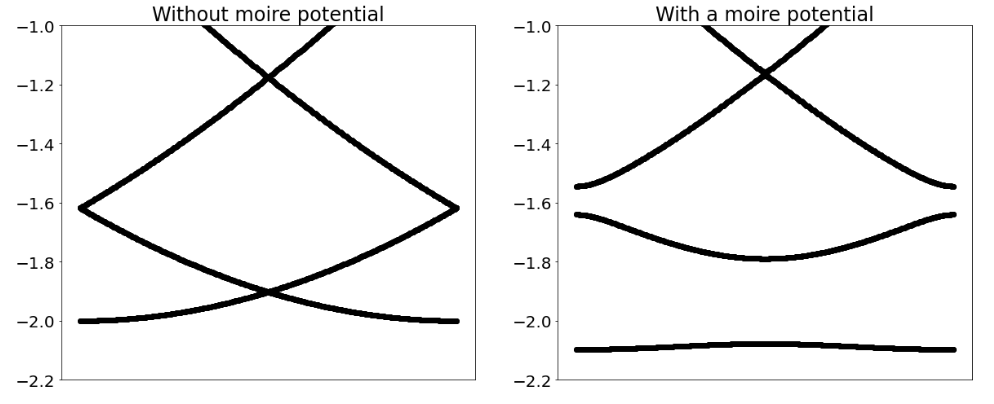
Exceptionally flat bands occur in tBLG for narrow ranges of \(\alpha \gtrsim 1\), which correspond to the magic angles. In addition to their flatness, the moiré bands possess incipient Berry curvature, arising from the original Dirac points of the graphene constituents. This feature allows topology to naturally enter tBLG physics. A variety of insulating correlated states have been observed in these regimes, yet understanding its microscopic origin remains an open challenge. Addressing the many-body ground states of tBLG in full generality is theoretically challenging. However, the extreme low density of electrons implies one simplification: Coulomb interactions conserve to an excellent approximation spin and charge of each valley separately, and also allow valley interchange via time-reversal symmetry. This emergent \(U(2) \times U(2) \times Z_{2}\) spin-valley symmetry has implications for symmetry breaking states and their excitations, similar to those studied in graphene quantum Hall ferromagnets. A Hartree-Fock approximation, which fills renormalized bands chosen to minimize the total energy, can explain insulating states at integer filling factors without enlarging the moiré unit cell.

Within Hartree-Fock theory, these correlated insulators must break some symmetry, in order that the band filling is consistent with a gap at the Fermi energy. At charge neutrality the only requirement is that the Dirac degeneracy of conduction and valence bands is removed. This may be minimally accomplished by breaking the \(\mathrm{C}_{2} T\) symmetry (time-reversal \(T\) combined with a two-fold rotation \(C_{2}\) around the axis normal to the bilayer) of ideal tBLG which locally protects Dirac points, but Dirac points may also be removed by pair annihilation via large \(C_{3}\)-breaking deformations ( \(C_{3}\) denotes three-fold rotation symmetry normal to the layers). In a practical experimental situation, the \(\mathrm{C}_{2} T\) symmetry is always broken explicitly to some degree by the layers of hexagonal boron nitride that encapsulate the tBLG. The more general case can be described in terms of the parameter \(\nu\), the filling, that labels how many of the moiré minibands are filled. At \(\nu=\pm 2\), in addition, the four-fold band degeneracy must be halved in a correlated insulator, most simply by breaking either spin or valley degeneracy. At \(\nu=\pm 1, \pm 3\), the filling constraints are most severe, and both spin and valley degeneracy must be lifted in a correlated insulator.

These filling constraints still allow a large number of possible symmetry breaking patterns, breaking spin and valley symmetries in different ways (for example, valley polarization versus inter-valley coherence) and interweaving them with space group operations (for example orbital-spin ferromagnetism versus antiferromagnetism or density waves and multipolar orders). The competition between different potential orders is keen and difficult to resolve unambiguously.

Disorder likely plays some role in sample variability, and small modifications to the single-particle structure are sufficient to tilt the balance between competing states. Variations like strain, alignment with a hexagonal boron nitride substrate, and twist angle can create or modify Chern bands and thereby change the ground state. The sensitivity to device details suggests that from the theory side an effective strategy is to address the set of insulators with competitive energy at a given filling factor, and to explain which perturbations favor which states within this set.

Superconductors

Whereas the correlated insulators are most easily understood as consequences of the Coulomb repulsion alone, superconductivity may arise from either an all-electronic mechanism or a more conventional, BCS-like phonon-mediated interaction. Identifying the underlying mechanism of superconductivity is, the major unsolved challenge in the field of unconventional superconductivity. Superconductivity in twisted bilayers can be observed broadly distributed across the entire lowest moiré band, it can appear in the absence of correlated insulators and even in the absence even of the \(\nu=\pm 4\).

Two-dimensional superconductors are not expected to show a detectable Meissner effect, making identification of superconductivity more challenging than in their three-dimensional counterparts. Moreover, high mobility devices can exhibit ballistic and phase coherent transport at low temperature \(^{6,51}\), providing a mechanism for observing zero resistance unrelated to superconductivity. In moiré systems superconductivity has generally been defined by the simultaneous observation of two characteristic transport signatures: a zero-resistance state that is rapidly suppressed with temperature and magnetic field, and measurement of a field-dependent critical current. In some devices, further evidence of superconductivity is provided by oscillations in the critical current versus magnetic field, interpreted as mesoscopic quantum interference arising from the presence of insulating or normal metal weak links related to spatial variations in the moiré pattern or charge disorder.

In some samples, a correlation between superconductors and correlated insulators suggests a direct relation between these phases. In this picture, Cooper pairing could be mediated by excitations of the correlated insulators, in an all-electronic mechanism similar to that proposed for unconventional superconductors like the cuprates. In other samples, superconductivity is decoupled from the appearance of the correlated insulators, suggestingg phonon-driven mechanisn as in typical metals. In this scenario, the correlated insulator and superconducting phases might not share a common microscopic mechanism, but rather compete. Coulomb interactions would drive the formation of the commensurate insulators while superconductivity might arise from a more conventional electron-phonon mechanism. Interestingly, the extreme sensitivity of electronic structure details also raises the possibility that the superconducting pairing mechanism may not be universal across all devices, or even across band fillings within

Quasicrystals

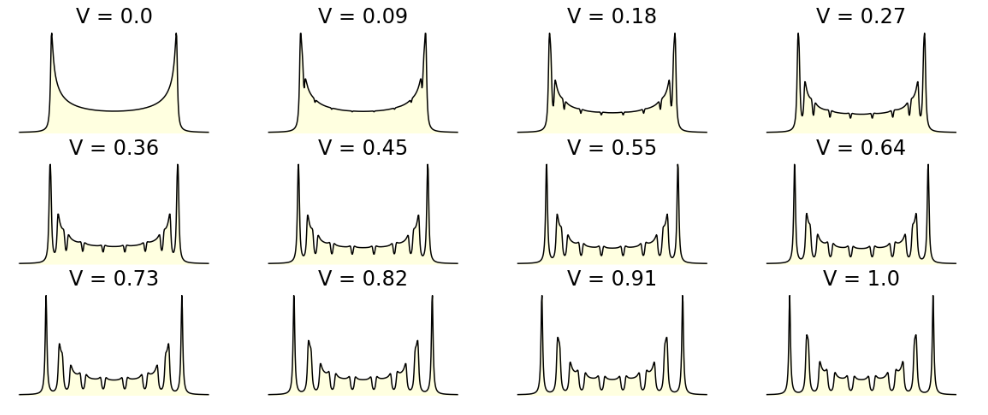
Quantum states of quasiparticles in solids are dictated by symmetry. Quantum states of Dirac electrons in a two-dimensional quasicrystal without translational symmetry can be realized by properly twisted two-layers of graphene, rotated exactly 30°. Multiple Dirac cones replicated with the 12-fold rotational symmetry can be observed in angle-resolved photoemission spectra, which revealed anomalous strong interlayer coupling with quasi-periodicity. These heterostructures provide a way to explore physical properties of relativistic fermions with controllable quasicrystalline orders.

In the previous regime, the electronic spectrum consists of resonant states labeled by 12-fold quantized angular momentum, together with the extended relativistic states. The resulting quasiband structure is composed of the nearly flat bands with spiky peaks in the density of states, where the wave functions exhibit characteristic patterns which fit to the fractal inflations of the quasicrystal tiling. The 12-fold resonant states appear as spatially localized states in a finite-size geometry, which is another hallmark of quasicrystals.

Chern insulating states

The quantum anomalous Hall (QAH) effect combines topology and magnetism to produce precisely quantized Hall resistance at zero magnetic field. QAH effect is realized in twisted bilayer graphene aligned to hexagonal boron nitride. The effect is driven by intrinsic strong interactions, which polarize the electrons into a valley-resolved moiré miniband with Chern number C = 1. In contrast to magnetically doped systems, the measured transport energy gap is larger than the Curie temperature for magnetic ordering, and quantization to within 0.1% of the von Klitzing constant persists to temperatures of several kelvin at zero magnetic field. Electrical currents as small as 1 nanoampere controllably switch the magnetic order between states of opposite polarization, forming an electrically rewritable magnetic memory. Such a Chern insulating state represents the starting point for the realization of fractional Chern insulators in twisted materials. Intuitivitively, such a Chern insulating state can be rationalized as symmetry broken state where a single pseudo-Landau level of the twisted bilayer is filled.

Proximal fractional Chern insulators

Fractional Chern insulators (FCIs) are lattice analogues of fractional quantum Hall states that may provide a new avenue towards manipulating non-Abelian excitations. Their existence in systems with flat Chern bands and highlighted the critical role of a particular quantum geometry. Magic-angle twisted bilayer graphene supports flat Chern bands at zero magnetic field, and therefore offers a promising route towards stabilizing zero-field FCIs. FCI states have been observed at low magnetic field in magic-angle twisted BLG enabled by high-resolution local compressibility measurements. The first of these states emerge at 5 T, and their appearance is accompanied by the simultaneous disappearance of nearby topologically trivial charge density wave states. The principal role of the weak field is merely to redistribute the Berry curvature of the native Chern bands and thereby realize a quantum geometry favourable for the emergence of FCIs. Ideally, an FCI could emerge in other twisted heterostructures provided the distribution of quantum geometry and Berry curvature is optimal.

Heavy-fermion Kondo insulators

Heavy-fermion systems represent one of the paradigmatic strongly correlated states of matter, featuring behavior ranging from quantum criticality and non-Fermi liquid behaviour to unconventional topological superconductivity. The heavy-fermion phenomenon arises from the exchange interaction between localized magnetic moments and conduction electrons leading to Kondo lattice physics. In a Kondo lattice, the exchange interaction gives rise to a band with heavy effective mass. A designer van der Waals heterostructure allows realizing artificial heavy fermions emerge from the Kondo coupling between a lattice of localized magnetic moments and itinerant electrons in a 1T/1H-TaS2 heterostructure. Such heterostructure using scanning tunnelling microscopy and spectroscopy, showing that depending on the stacking order of the monolayers, we can reveal either the localized magnetic moments and the associated Kondo effect, or the conduction electrons with a heavy-fermion hybridization gap. In such heterostructures, the twist angle control the Kondo exchange coupling, driving the system to different regions of a heavy fermion phase diagram.

Moire excitons

Semiconductor moiré superlattices represent a rapidly developing area of engineered photonic materials and a new platform to explore correlated electron states and quantum simulation. Experiments that identified new exciton resonances in transition metal dichalcogenide heterobilayers, featuring new optical selection rules. These states feature dynamics and diffusion properties of moiré excitons can be controlled via the twist angle. To interpret optical spectra, it is important to measure the energy modulation within a moiré supercell. Scanning tunnelling microscopy experiments allow measuring the moiré potential landscape directly. Applied excitonic optical spectroscopy to probe correlated electron phenomena in transition metal dichalcogenide moiré superlattices.

In van der Waals heterostructures formed by stacking two monolayer semiconductors, lattice mismatch or rotational misalignment introduces an in-plane moiré superlattice \({ }^{3}\). The moiré superlattice can modulate the electronic band structure of the material. Multiple interlayer exciton resonances have been observed with either positive or negative circularly polarized emission in a molybdenum diselenide/tungsten diselenide \(\left(\mathrm{MoSe}_{2} / \mathrm{WSe}_{2}\right)\) heterobilayer with a small twist angle. These resonances are attributed to excitonic ground and excited states confined within the moiré potential. This interpretation is supported by recombination dynamics and by the dependence of these interlayer exciton resonances on twist angle and temperature.

Twisted moire magnets

Exotic magnetic ordering fully driven by the twist between two van der Waals magnetic layers. Chromium triiodide (CrI3), shows a strong out-of-plane ferromagnetic ordering in the single-monolayer limit. In a twisted bilayer heterostructure, although each monolayer is ferromagnetic, the respective magnetic alignment between them can be either ferromagnetic or antiferromagnetic, depending on the local alignment. CrI3 is known to have a complex magnetic ordering associated with how its layers are stacked. In a nontwisted bilayer, a small lateral displacement between individual layers leads to switching from an aligned to the antialigned magnetic configuration between them. In a twisted bilayer, the local stacking between layers changes in space, only as a consequence of the relative rotation between the two crystals. As a result, whereas in certain regions the coupling between layers is ferromagnetic, in other regions it will be antiferromagnetic. The moiré pattern imprints a magnetic coupling in the twisted ferromagnet, leading to a whole new artificial magnetic system controlled by the twist. The emergent non-collinear magnetic structure can also lead to the emergence of a local ferroelectric polarization in the magnet.