Agenda for week 1: path integrals
Learning goals:
Main idea of posing the quantum mechanics axioms in terms of path integrals instead of the usual operator formalism
Path integrals for a single spinless particle moving in a one-dimensional system.
Harmonic oscillator propagator and the saddle point/semiclassical approximation
Reading assignment:
Notes for week 1: Path-integral formulation of the problem of one particle on a 1d potential, and the free-particle path integral
More details:
- Tuominen, Chapter 6
- Sakurai: Sec 2.5; Sakurai&Napolitano: Sec 2.6
Preliminary exercises
Do these during/after reading the assignment work. Will be discussed in class March 9th.
- We have a (single-particle) Hamiltonian
, where
. Let us find an estimate for the infinitesimal time propagator
in the limit
.
- You can take
. Why is this an approximation and why is it justified?
- Using this calculate
. Use the Gaussian integral result that is given. Do not worry about the convergence of the integrals. In your result identify the Lagrangian.
- You can take
- Using the classical action
, what is the equation satisfied by the path
that minimizes the action? If you use this path to find an approximative result for
what are the boundary conditions of this equation?
- Aharonov-Bohm effect: consider a vector potential
- Convince yourself that this corresponds to a magnetic field in the
-direction, confined into an infinitesimally small area in the
-plane:
. Draw a picture with the
and
field lines.
- How do you include the vector potential
in the path integral? How does this lead to the Aharonov-Bohm effect?
- Convince yourself that this corresponds to a magnetic field in the
Homework exercises, first week
Will be discussed in the tutorial session on Thursday March 11th. Return a scanned pdf with your solution by Friday March 12th, at 9 pm using the below form. Then check and grade your solution with the help of the model solutions and resubmit your graded solutions by Monday March 15th at 2 pm.
Starting from the discretized version of the path integral
compute the free particle propagator.
Derive the classical action
for the harmonic oscillator with boundary conditions
and
. You should obtain
Hint: You may do this via brute force and it does go through, but it may be helpful to do a partial integral over the kinetic energy term, to express it in terms of
...
Extract the energy levels
of the one-dimensional harmonic oscillator from the propagator. See Tuominen.
[Double points for this question] Calculate the determinant of
for a harmonic oscillator given in the lecture notes (leaving out some overall constants)
and show that it is
with
. One way to do this is a recursive algorithm, see e.g. See e.g. Sec 2.5 here, another possibility is to find the eigenvectors. Since this is a harmonic oscillator, the eigenfunctions are:
with the component
. As you know,
and
give you boundary conditions and the allowed values for
, from these you can calculate the eigenvalues. The determinant is the product of the eigenvalues. To calculate this product you need to write the eigenvalues in the right way so that you can take advantage of the limit
. You then need Eq.~(6.3.28) in Tuominen, and to get the normalization right also the magical identity
Solutions will come here.
Exercise points (filled by TA)
Please
Notes for week 1: Feynman path integrals
An alternative formulation of the dynamics in quantum mechanics is given by the path integrals. This formulation was developed by Richard Feynman and it is equivalent with the usual formulation of Schrödinger, Heisenberg et al. The path integral approach is particularly important and useful for quantum field theories, especially for non-Abelian gauge-field theories, such as quantum chromodynamics exhibiting strong interactions, and the unified electroweak theory in the Standard model of particle physics. However, it is also used in several other branches of physics and even beyond physics for example in econophysics. In statistical mechanics it allows for a practical approach for treating stochastic phenomena (Feynman-Vernon approach).
Some historical references on this approach are
R.P. Feynman: Space-time approach to Non-Relativistic Quantum Mechanics
R.P. Feynman and F.L. Vernon: The theory of a general quantum system interacting with a linear dissipative system
Prelude: Diffraction with infinitely many slits
Tuominen (Sec 6.1) has a nice justification for the path integral formalism in the form of an "infinite slit diffraction experiment". A brief version of the argument goes as follows:
- Start from the classical two-slit experiment. A free quantum mechanical particle starts at time
, going in the
-direction, and passing at time
through an infinite, opaque sheet at
, and is observed at
on a screen behind the sheet. We know that the probability distribution of particles on the screen displays an interference pattern, reflecting the wave-like nature of the particle.
- How does the interference happen in the formalism? We have a wave function
representing the state of the particle. In the case of two slits, the wave function on the screen is a superposition of waves that have passed through the different slits:
. We see an interference pattern on the screen, because the probability density
reflects the fact that the different slits have different functions
.
- Now consider the case of infinitely many holes in stead of slits. In the same way, our wavefunction is a superposition of infinitely many wavefunctions that have gone through different holes:
If the hole
lets through particles only at coordinate
, we can think of the infinite sum as an integral over the
plane
But in fact infinitely many holes is the same thing as not having a sheet at all, but just free propagation. Thus this integral just gives the wavefunction of a free particle.
- In addition to having infinitely many holes, the "no sheet at all" situation can have infinitely many sheets, that the particle passes through at a time
,
with
. Thus our wavefunction of a freely propagating particle an be represented as an infinite dimensional integral
This infinite-dimensional integral is the path integral. It expresses the wavefunction as an integral over all the possible positions of the particle at different times.
The quantity is the wave function (function of
) of a particle that passed through the coordinate
at a time
. To find what these functions are, we need to look at the time evolution of the wave function, which is given by the Hamiltonian of the system.
Terminology note In classical mechanics, electrodynamics etc. you have encountered things like ; integrals of some function or vector field over a line in 3d space. Such line integrals are sometimes called path integrals. The Feynman path integral is not the same thing. It is an infinite-dimensional integral over paths, i.e. integral over all the possible coordinates that the particle can have at different points in time, not the 1-dimensional integral of some function along a line in 3-dimensional space.
Propagator
Here, we limit the study to the perhaps simplest case of quantum mechanics of one spinless particle in a one-dimensional system. Let us start by reminding of the Schrödinger picture wave function, or the position representation of the state vector, It quantifies the probability amplitude for finding the particle at a certain location at a certain time. In what follows, we concentrate exclusively on the Schrödinger picture and therefore drop the subscript S.
The time evolution of a state in the Schrödinger picture can be written as Then
In other words,
where the Feynman kernel or the propagator is
From above, we see that the "propagation" of the wave function, or the states, from
to
is controlled by the function
.
Especially, if the particle is in an eigenstate of
(
) at the time
, the probability amplitude for finding the particle in a state
at time
is given by the propagator:
In the following, let us assume that
does not depend on time. Then, as we know,
and as a result,
In the exercises, we will compute the propagator of a free particle (). It reads
Below we see how propagators can be computed from the path integral.
Decomposition into time intervals
Now, let us develop the path integral formulation for the propagator. We start from a single step: Here we also inserted the resolution of unity
. Although the equation as such holds for any set of times, assume here that
.
The single propagator thus divides into two: The probability amplitude for finding the particle at a position at a time
, when it originally at time
was at a location
, is given by multiplying the probability amplitudes for the particle to first move from
to
and then from
to
, and summing (integrating) over all possible intermediate locations
.
This is known as the Markovian property: the probability of finding the particle at depends on its earlier location
and the propagator
, but not on any memory of what happened before
(other than the fact that whatever happened at
led to the particle being at
). This property is the basis of the path integral formulation.
Infinitesimal timesteps
Let us now repeat this procedure many times, so that the time interval gets split into
intervals of the same length
:
Thus,
, in which
and
.
The propagator now divides into pieces: Let us now insert a resolution of unity of the form
before each of the term of the form
,
. We get
or
where
,
,
, and
.
Graphically this looks as follows:

In other words, every possible path from to
is included!
Explicit form of the Hamiltonian
Now suppose that Then
Note that the operators
and
do not usually commute:
. Therefore, we have
where the "
" indicate higher-order commutators between
and
. Now, note that
when
. Thus, we can use
For the infinitesimal period
we thus have the propagator
From operators to coordinates and momenta
Our infinitesimal time evolution operator is still an operator. The path integral, on the other hand, is expressed in terms of integrals over classical variables. Thus we must get rid of the operators, by introducing complete sets of coordinate of momentum eigenstates. So we start with where we insert
It thus becomes Now the operators operate on their eigenstates so we may replace
by
and
by
. Now inserting
in front of the first exponential, and
in front of the other, we get
Now, using the representation of the plane wave states,
and the fact that the matrix elements
etc., we finally get this to the form
Note that this form contains no operators, so the Hamiltonian in the remaining expression is classical.
Substitute this to the equation for the propagator. It becomes Now use
so that we get
Note that in the limit
, the sum in the exponent becomes an integral.
We obtain This is the path integral representation of the propagator. The above formula also defines the sums over all path and momenta,
.
Integrating over momenta
In the above expansion, the whole phase space ( and
) is integrated over. We can actually still do the integrals over momenta. For example,
where
and
.
The exponent in the Gaussian integral is
Hence
The Gaussian integral can be found for example from https://en.wikipedia.org/wiki/Gaussian_integral.
Now you should be able to go back and do Question 1 in the preliminary exercises
Configuration space path integral, classical action
The infinitesimal propagator is thus Substituting again this back in Eq. [eq:prop1] gives
We hence get the a result for the propagator:
We write the right hand side with the notation
for the integration measure over all paths, including the normalization. Thus we get the
Feynman path integral representation of the propagator
Here the classical action is and the Lagrange function of the system is
We thus arrived in a configuration () space path integral form of the propagator of the system
The integration measure
is defined with the above formula.
Interpretation: classical and quantum
From here, we can see how quantum and classical mechanics differ in their behavior with respect to the path integral:
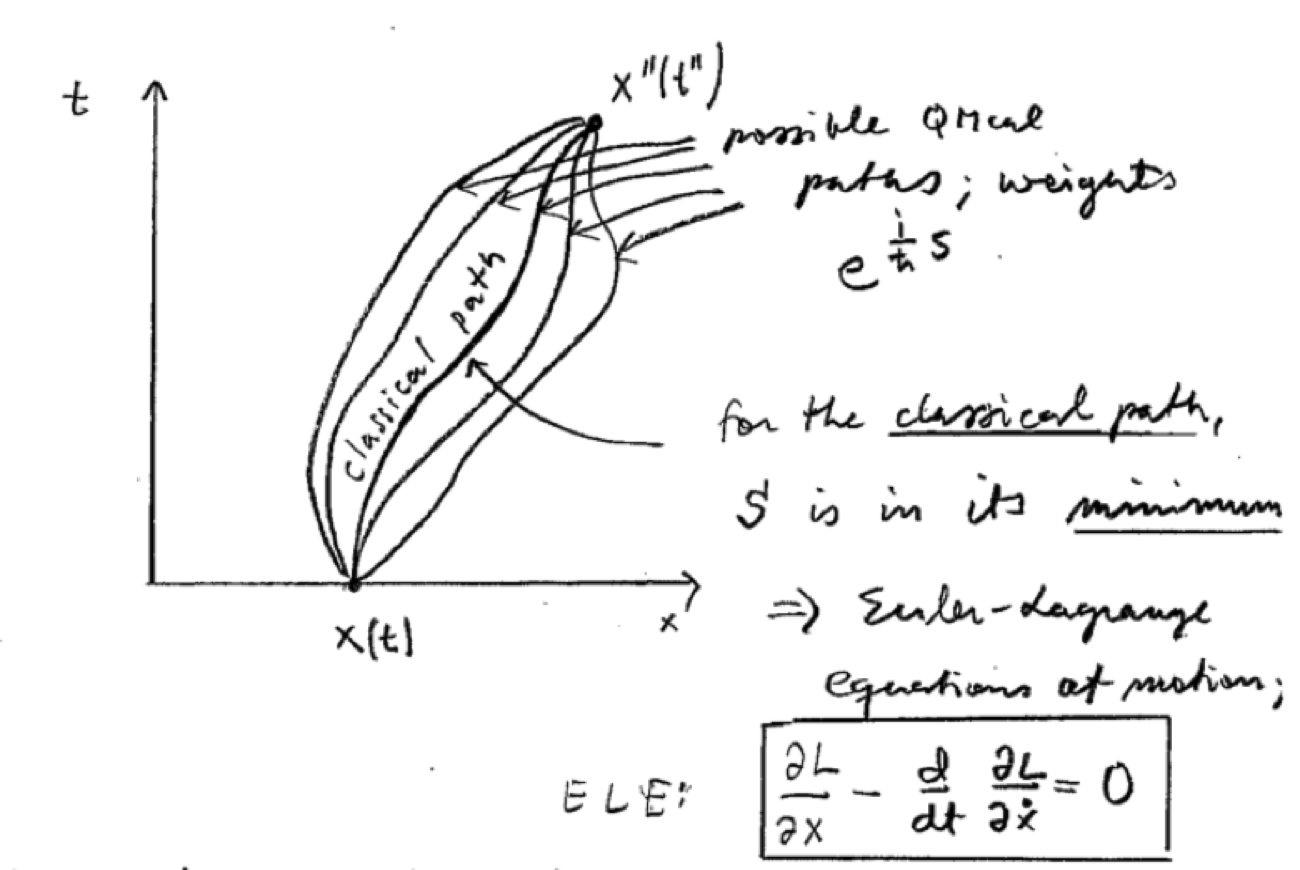
Let us look at the orders of magnitude, considering a classical free particle for which . Then
The Euler-Lagrange equation hence yields
Then the classical action is
Let us put in some numbers corresponding to a macroscopic system, say
kg,
m/s,
s. In this case
Now, if
is not at its minimum, the weight
oscillates rapidly. The contributions from such oscillations thus average out, and only the classical path corresponding to
is relevant in macroscopic systems.
For a quantum mechanical system, corresponding to different paths is not large (for example,
kg). Thus, in microscopic systems, many paths contribute, yielding quantum effects.
Now you should be able to go back and do Question 2 in the preliminary exercises
In the Feynman path integral formulation of the propagator, Eq. [eq:feynmanpropagator], we can make the following observations:
The constant
, but when computing physical quantities from the path integral, this constant cancels out. This means that the limit
should usually be done last.
Obviously, the whole path integral does not converge even when
. We hence need further definitions, which correspond to certain boundary conditions and convergence factors
.
Examples of calculable path integrals
Quite generally, you should think of the path integral as an infinitely many dimensional integral, where the integrand is of the form These forms are equivalent, because you can express the time derivative as a difference: thus a function of
becomes a function of just
at different timesteps, when time is discretized. Such integrals can be computed, when the function
is quadratic (i.e. a 2nd degree polynomial) in
, i.e. quadratic in
.
Particular calculable examples are
Free particle,
Harmonic oscillator,
Forced harmonic oscillator,
.
Multidimensional Gaussian integrals
To calculate the calculable path integrals explicitly, we need to take a little and learn how to do Gaussian integrals in many, many dimensions. Given a positive-definite matrix
(positive semidefinite meaning here that it is diagonalizable and all the eigenvalues have a positive real part), we want to calculate the
-dimensional integral
Here
is the vector
. Note that since
is symmetric, a possible antisymmetric part of
does not contribute, so we can assume that
is symmetric.
Since is real and symmetric, we know (linear algebra truth, not proven here), it can be diagonalized by an orthogonal transformation
:
where
are the eigenvalues of
. Then using
we get
Now, we want to take the components of the new, rotated vector as our integration variables to perform the Gaussian integral
Now we need to change the integration variable from
to
. The integration measure changes as
For this we need the Jacobi determinant
of the variable change. To calculate this we calculate the partial derivatives
Thus the Jacobi determinant is
Because
is an orthogonal transformation, the determinant is
and thus
. We hence get
The integrals to be done are simple Gaussian:
We can write this in a form that does not necessarily require diagonalizing the matrix (which could be difficult in the general case), by realizing that it involves the product of the eigenvalues of the matrix, i.e. its determinant: Thus the multidimensional integral is
Free-particle propagator
Let us first look at the free-particle propagator. Now the path integral is, using in Eq. [eq:feynmanpropagator]
Now the
-integrals are all Gaussian, and can therefore be straightforwardly done (see exercises). In the end, one should notice that
. As a result, no
appears in the final result, given by Eq. [eq:freeparticlepropagator]. We will go through the details of the calculation in the exercises.
Harmonic oscillator
The Lagrange function for the harmonic oscillator is
The discretized form of the action thus becomes (see Eq. [eq:feynmanpropagator]) Thus the discretized form of the path integral becomes
Here recall the definition of definition of from Eq. [eq:feynmanpropagator]. In particular note that the boundary conditions
are fixed. One is integrating over the intermediate points
.
In principle we could now proeed to straightforwardly evaluate the integral over . However, even if the exponent is purely quardatic in all the coordinates
, it is not purely quadratic in the integration variables, because the terms
in the sum have terms
and
that couple the integration variables to the (fixed) boundary conditions. Thus we cannot use the Gaussian integral directly, but would have to generalize it to calculate an integral of the form
This can indeed be done. However, let us do this by following an equivalent procedure that has a more transparent physical interpretation, that is discussed in a more general way in the section on the Semiclassical approximation
Instead, we perform a change of integration variables: where
is the classical path that satisfies the Euler-Lagrange equation of motion with the boundary conditions
. Thus the boundary conditions for the fluctuation around the classical path
are
(remember that we do not integrate over
, but the discretized time derivative couples
and
to these values).
For this manipulation it is easier to work in the continuum. With the Lagrangian and
we have
Expanding the squares and integrating over
we have three types of terms:
- The classical action
- The cross terms
Here we partially integrate and get
because the part in the [] brackets is the classical equation of motion.
- The quantum fluctuations around the classical action
Classical action part
We will calculate the classical action part for the harminic oscillator in the exercises. The result is
Quantum fluctuation part
We can again discretize the quantum fluctuation part as Note that this is exactly the same as the original action with
replaced by
, except that the boundary conditions are now
. Also note that
does not depend on the coordinates
and
at all, but only on
and
, i.e. on the total time interval
. Thus the cross term
and
are not present, and we can directly use the Gaussian integral
In order to write in the form
required by the Gaussian integral formula, we need to perform a few manipulations:
Now using the fact that
we note that the first two sums are equal, and all sums can be written to run from
to
. We thus get
where the latter form takes into account the fact that the product
involves a double sum.
We hence obtain from the required symmetric matrix
In order for this to be strictly speaking positive definite, some appropriate
needs to be introduced, we will not worry about this here.
We will calculate the determinant of this matrix also as a homework exercise. The result is
The result for the path integral now becomes, combining the definition in terms of the path integral, and the Gaussian integral
Finally, the full and exact propagator of the harmonic oscillator is
Point particle path integral in electromagnetic field
Let us add one more ingredient to the path integral description: a classical electromagnetic force. In chapter III we find that the electromagnetic force modifies the Lagrangian as where
is the Lagrangian without the electromagnetic field,
is the vector potential and
is the scalar potential. This thus changes the action to
The propagator is thus modified to
Including the electromagnetic field thus modifies the phase of each path in a way dependent on the field.
Aharonov-Bohm effect
Now consider describing the two-slit-type experiment in the presence of a magnetic field
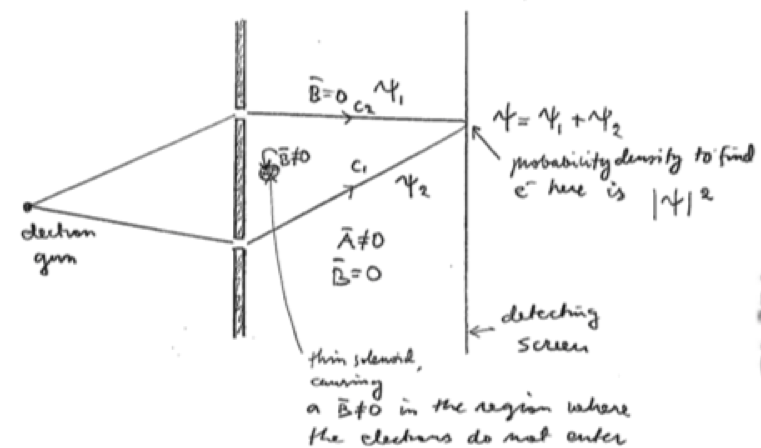
Assume there is no scalar potential, i.e., . We wish to find out the effect of the magnetic field on the interference pattern. The propagator in the presence of the background field is now is now
where
is the action without the gauge potential
.
The path integral is a sum over all paths, which must pass through either the slit or slit
. The wave function on the screen is just a superposition of two terms
which are given (apart from the initial wave function at
which is the same for both cases) by
Here the restricted measure
integrates only over paths that pass through one slit
or
.
The probability density for finding particles on the screen is . Thus the interference pattern is given by the relative phase of
and
, i.e. the phase of the product
. Let us calculate this product, denoting by
the coordinate of the particle on the paths going through slit 1, and by
the particles on path 2:
We can now change the direction of time on the path y to make it a path starting from
on the screen, back to the coordinate
of the particle source. This variable change
changes the sign of the exponent, and the limits of the path:
Now we can consider this double integration over paths going through slit 1 and paths
coming back through slit 2 as closed paths starting from
, going though slit 1 to
on the screen and then back through slit 2:
But now we recognize a familiar ingredient: for all closed paths C, by Stokes' theorem the integral is just the magnetic flux
inside the loop
. Thus the wave function product is modulated by a phase factor depending on the magnetic flux between the two sets of paths
This is thus of course nothing but the Aharonov-Bohm effect.
Now you should be able to go back and do Question 3 in the preliminary exercises
Let us consider one possible way to treat the path integral, [eq:feynmanpropagator], the semiclassical approximation or the Gaussian approximation. This is probably the most often used approach for solving path integrals. In essence, the semiclassical approximation linearizes the system dynamics around some (classical) fixed point. For any action which is quadratic, the Gaussian approximation is exact.
The basic idea here is to make an expansion with respect to the deviations from the classical paths .
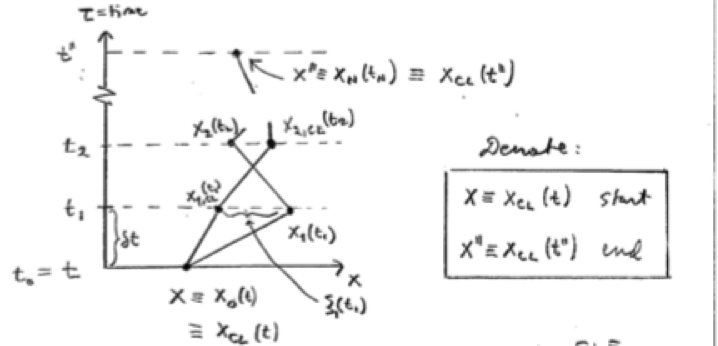
Let us hence write where
is a deviation from the classical path. Remember, in the path integral, the "path" denotes the positions
over which the integral in Eq. [eq:feynmanpropagator] is taken. In particular, the end points at
and
are fixed to
and
. In other words, the deviation satisfies at the end points
Now, let us make a change of variables over which we integrate in Eq. [eq:feynmanpropagator]: Thus
because the classical path is fixed. This means that the path integral measure over
is the same as the one over
:
and the propagator is
Now let us assume that the major contribution to the integral comes from the paths that are close to
, i.e., corresponding to small deviations
. This means that we can expand the exponent around
.
Let us start by expanding the Lagrange function to the second order in and
.
where we use a short-hand notation
For the action, this means Note that the linear terms in
vanish:
The first equality uses the Euler-Lagrange equation,
, and the second a partial integral to move the time derivative.
With this expansion, the action thus becomes and the path integral becomes
The above expression now expresses the main idea: the classical part
factorizes out of the path integral, and can thus be computed separately. For the remaining part, the path integral has to be performed using the discretized form in Eq. [eq:feynmanpropagator]. Our treatment of the harmonic oscillator was an example of this procedure. For the harmonic oscillator, as for any action that is quadratic (i.e. only terms
), the semiclassical approximation is exact. For other Lagrangians it is an approximation.
Some thoughts on the path integral philosophy
To conclude this section, let us think back what we have done:
In the first part of the course, we started from a formulation of quantum mechanics based on postulates. Two of these postulates are the canonical commutation relations of operators, e.g.
and the time dependence being given by the Schrödinger equation, using the Hamilton operator
. This Schrödinger equation describes the dynamics of the system.
We now introduced the propagator
of the system connecting the initial state wave function
to the final state wave function
. We can in principle obtain the propagator by solving the Schrödinger equation with a given Hamiltonian.
We then calculated an equivalent, exact, expression of
in terms of the path integral. Note, no operators appear in the path integral. Now quantum mechanics follows from the fact that many paths contribute (each with weight
) to the propagator, in contrast to classical mechanics where only one path corresponding to
is relevant.
In the calculation of the free-particle and harmonic-oscillator propagators above, we took the path integral as a starting point, without any knowledge of the Schrödinger equation or canonical commutation relations!
We also (partially) showed that we can compute the propagators from the path integrals. The results agree with the ones computed from
and the Schrödinger equation.
The above suggests that we could more generally replace the postulates of the commutation relations and Schrödinger equation by postulating the propagator of the system, whose form of classical we know, is given by the path integral. The dynamics of the quantum system then follows as we have seen above!
In quantum field theory one generalizes the single coordinate by the field
containing infinitely many coordinates (
to be integrated over describes thus the values of the field at each point
at each time t). When the path integrals are adapted as a starting point, the integral goes to
. The path integral is then of the form
In particular, the symmetries of the theory are easy to impose on the Lagrangian
. This path integral then yields the propagators and the Feynman rules for the theory.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.