# ii.-scattering-theory

Scattering theory

Learning goals for this week (check afterwards that you understand these concepts)

Understanding the concept of the scattering experiments
QM formulation of the scattering experiment
Cross section, differential cross section
Integral equation for scattering and the Green's function of the scattering problem
Complex integration; residue theorem; transforming an integral over a real axis to a closed complex line integral
Solving for the Green's function via complex integration
Born series solution of the integral equation; Born approximation

# ii.-1.-basic-concept-cross-section

Basic concept: cross section

The structure of matter is probed by doing

Spectroscopy: observe transitions between the different bound states at the system (atoms, molecules, $\dots$ ) - analyzed with the methods of the time-dependent perturbation theory, often with harmonic perturbations.
Scattering experiments: analyze the final states and deduce the properties of target and/or beam particles (for example the structure and properties of nuclei and elementary particles, or nature of electron transport inside solids)

A typical scattering experiment (with a fixed target) could look like this: 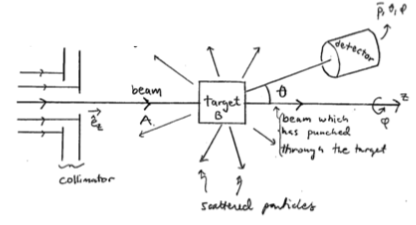$\begin{aligned} &{\mathbf p}_{\rm beam} || \hat e_z\\ &{\mathbf p}_{\rm target} = 0 \cong {\text{"fixed-target" experiment}}\\ &{\mathbf p}_{\rm target} \neq 0 \cong {\text{"colliding beams" experiment}}\end{aligned}$

It thus consists of two parts:

beam:
- consists of particles A (electrons, positrons, protons, neutrons, photons, phonons, $\dots$ )
- is nearly monoenergetic and well collimated: $\Delta p/p \ll 1$ (allows considering a given input energy/momentum)

target: (fixed target $\cong$ macroscopic sample)
- consists often of a large number of particles B (e.g., H-gas in a container, stack of lead plates, etc.)
- or an impurity potential in a solid (dislocations, vacancies, and other irregularities of the ion lattice)

One can generally separate the scattering to two categories:

Elastic scattering: $A + B \rightarrow A + B$ Same particles in the initial and final states, i.e., total kinetic energy is conserved
Inelastic scattering: final state particles $\neq$ initial state particles, or the structure of A,B can change.

For example: $\underset{\rm positron}{e^+} + \underset{\text{hydrogen in its ground state}}{H} \rightarrow \underset{\text{final state}}{X}$ could be for example

: elastic scattering
: excitation of
: ionization of
$p + 2 \gamma$ : annihilation
: positronium formation

(ii)-(v) are inelastic

The "final state" particles are taken to a detector, which can then measure for example the magnitude of their momentum (or their kinetic energy) $p=|{\mathbf p}|$ as a function of the angles $\theta$ , $\varphi$ . In addition, the detector can be sensitive to the polarization, spin, or some other internal property of the output beam.

A key quantity in scattering experiments is the cross section for scattering $A+B \rightarrow C+D + \cdots$ = number of these scattering events per unit time, per one target particle B, divided by the flux of incoming beam particles A

Let's illustrate it here:

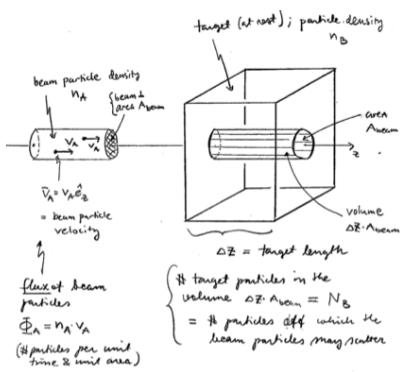
Let us assume that the detector observes the number n_S of scattering events in a unit time. Obviously, the more flux $\Phi_A$ and the larger N_B , the larger must n_S be: $\boxed{n_S=\sigma \Phi_A N_B}.$

# crosssection

We can therefore define the scattering cross section as $\boxed{\sigma = \frac{n_S}{\Phi_A N_B} = \frac{n_S}{n_A v_A n_B \Delta z A}}$

It depends on the scattering process considered, i.e., on the probability of scattering, i.e., on the strength and range of the interaction and the beam energy

Here $\sigma$ is an effective "cross section" which the beam particles see. It is also related to the probability for the scattering to happen. These have the physical units: $\begin{aligned} \text{Unit for }n_S &= 1/{\rm time}\\ [\Phi_A] &= 1/({\rm time} \cdot {\rm length}^2)\\ [N_B] &= 1\\ [\sigma] &= {\rm length}^2.\end{aligned}$

Units used in nuclear and particle physics: $[\sigma]=$ 1 b = 1 barn = 10 $^{-28}$ m = 100 fm.

Often, it is not easy to detect the particles scattered in all possible directions, or there is extra information in the precise angle to which the scattering takes place. Therefore, one often also considers the differential cross section $\frac{d \sigma}{d \Omega} = \frac{n_S(\theta,\varphi)}{\Phi_A N_B},$ where $dn_S=n_S(\theta,\varphi) d\Omega$ is the number of particles per unit time, scattered into the infinitesimal solid angle $d\Omega$ :

For example experimental figures on scattering cross sections in particle physics, see for example K. Nakamura, et al., Review of Particle Physics, J. Phys. G: Nucl. Part. Phys. 37, 075021 (2010).

You can get more information on particle physics measurements in the course FYSS4300 Particle Physics.

In this chapter,

We formulate the general 3d scattering problem, where the wave function far away from the scattering region satisfies $\psi({\mathbf r})=\underbrace{A e^{ikz}}_{\rm incoming} + \underbrace{f(\theta,\varphi) \frac{e^{ikr}}{r}}_{\rm outgoing}.$ The rest of the chapter deals with methods aiming to solve $f(\theta,\varphi)$ .
We use the Green's function technique to transform the Schrödinger equation to an integral equation. This is then solved with the Born approximation. It is especially useful for weak potentials, where the deviation of the particle's initial trajectory is small.
Another approach is the partial wave analysis, where the $\theta$ dependence is expanded in terms of the spherical harmonics. This method is useful especially for low-energy particles (compared to the potential strength), since for that case $f(\theta)$ is a weak function of $\theta.$

Alternatively to the lecture notes, you may also follow Ch. 11 in Griffiths' book.

# ii.2-formulation-of-the-3d-scattering-problem-boundary-conditions-of-the-wave-function-cross-section-optical-theorem

Formulation of the 3d scattering problem: boundary conditions of the wave function, cross section, optical theorem

We consider here the elastic scattering of two spinless, nonrelativistic particles. In laboratory frame, the incoming particles have a certain momentum and the target is at rest (sometimes referred to as the target rest frame). In the center-of-momentum (CMS) frame, the total momentum of an incoming particle and a target particle is zero: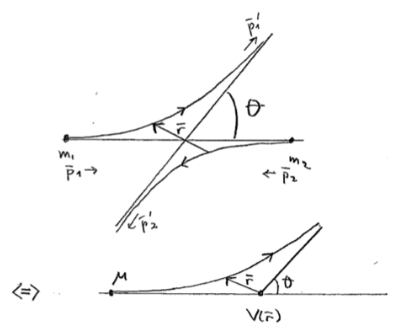

In the CMS frame the total momentum of the system vanishes, and hence ${\mathbf p}_1+{\mathbf p}_2={\mathbf p}_1' + {\mathbf p}_2'=0$ , the relevant energy is the relative kinetic energy between the particles, and the relevant position is the relative position, ${\mathbf r}={\mathbf r}_1-{\mathbf r}_2$ . This is equivalent to a scattering of a particle of a reduced mass $\mu=m_1 m_2/(m_1+m_2)$ of a potential $V({\mathbf r})$ .

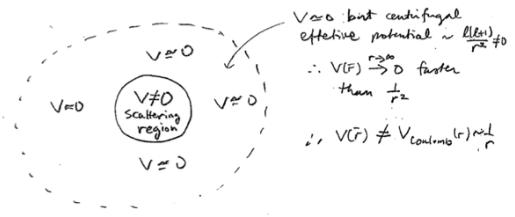
In order to be able to calculate the cross section, we must assume a finite-range, localized (and often spherically symmetric) potential $V=V({\mathbf r})$ ; $r^3 V({\mathbf r}) \xrightarrow{r\rightarrow \infty} 0$ :

We proceed analogously to what was done in QM I in the case of a 1D problem (Griffiths, Ch. II). Instead of using calculationally much more difficult wave packets and their time evolution to describe particles and their motion, we assume a stationary situation, i.e., that the beam has been "turned on" already for a while and that we thus have a steady flux of incoming and scattered particles. This "turning on" is described in more detail in the chapter on time-dependent phenomena. We thus consider the scattering problem within the following framework: 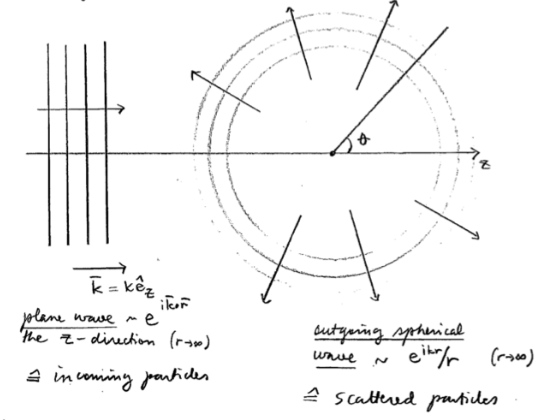That is, at $r \rightarrow \infty$ , the particles behave as free, $V(r \rightarrow \infty) \rightarrow 0$ .

Let us first specify the incoming plane wave in the 3d case, far away from the scattering center ${\mathbf r}=0$ . The stationary Schrödinger equation reads in the position representation $-\frac{\hbar^2}{2\mu} \nabla^2 \Psi({\mathbf r})= E \Psi({\mathbf r})$ This is solved with the plane wave solution (prefactor comes from the properties of Fourier transformation) $\boxed{\Psi({\mathbf r})=\frac{1}{(2\pi)^{3/2}} e^{i {\mathbf k}\cdot {\mathbf r}}, \quad k^2=\frac{2\mu E}{\hbar^2}}$ This is hence the form of the wave function for the beam of particles far away from the scattering center.

For a radially symmetric potential, we can make the separating Ansatz $\psi({\mathbf r})=R(r) Y_{lm}(\Omega)$ (see Griffiths, Ch. IV). There, R(r) satisfies the radial Schrödinger equation $\left[-\frac{\hbar^2}{2\mu} \frac{1}{r^2} \partial_r (r^2 \partial_r) + \underbrace{\frac{\hbar^2 l (l+1)}{2\mu r^2}}_{\text{This one remains}} + \underbrace{V(r)}_{\rightarrow 0 \text{ as } r\rightarrow \infty}\right] R(r) = E R(r),$ i.e., we assume V(r) to decay faster than the centrifugal term l (l+1)/r^2 at large . In other words, $\boxed{r^2 R''(r)+2r R'(r)+[(kr)^2-l(l+1)]R(r) = 0}$

The general solution to this can be specified in terms of spherical Bessel ( j_l(x) ) and Neumann (n_l(x)) functions: R(r)=A j_l(kr) + B n_l(kr) For large arguments, they have the asymptotic behavior $\begin{aligned} j_l(x) &\xrightarrow{x \gg l(l+1)/2} \frac{1}{x} \sin(x-l \pi/2) = \frac{1}{x} \frac{1}{2i} \left(e^{i(x-l \pi/2)} - e^{-i(x-l \pi/2)}\right)\\ n_l(x) &\xrightarrow{x \gg l(l+1)/2} -\frac{1}{x} \cos(x-l \pi/2) = -\frac{1}{x} \frac{1}{2} \left(e^{i(x-l \pi/2)} + e^{-i(x-l \pi/2)}\right)\end{aligned}$

# radialequationsolution

For a large , the solution to the radial equation can hence be written in terms of plane waves: $\boxed{R(r) \xrightarrow{kr \rightarrow \infty} \frac{1}{2kr}\left[\left(\frac{A}{i}-B\right) e^{-il \pi/2} \underbrace{e^{ikr}}_{\text{\parbox{1cm}{outgoing wave?}}} + \left(-\frac{A}{i}-B\right) e^{il \pi/2} \underbrace{e^{-ikr}}_{\text{\parbox{1cm}{incoming wave?}}}\right]}.$

Identification in terms of incoming and outgoing waves can be done by considering the probability flux, or probability current density $\boxed{{\mathbf j}=-\frac{i\hbar}{2\mu} \left[\Psi^*({\mathbf r}) \nabla \Psi({\mathbf r}) - (\nabla \Psi^*({\mathbf r})) \Psi({\mathbf r})\right] =\frac{\hbar}{\mu} {\rm Im}[\Psi^*({\mathbf r}) \nabla \Psi({\mathbf r})]}.$ This can be derived from the general continuity equation defining a relation between the probability density and probability current density.

QM expression for the current density obtained from the continuity equation

Generally in physics current densities can be defined in terms of the continuity equation relating the current density and the corresponding density $\rho$ (say, charge density, particle density, probability density, $\dots$ ) $\boxed{\frac{d \rho}{d t} + \nabla \cdot {\mathbf j} = 0}$ The continuity equation basically states that spatial variations in the current are accompanied by changes (in time) of the density, or in other words, time-dependent changes in density result into spatial dependence of the current.

Now consider the probability density in quantum mechanics, i.e., $\rho({\mathbf r})= |\Psi({\mathbf r})|^2,$ Its time derivative satisfies $\begin{aligned} \frac{d}{dt} |\Psi|^2 &= (\Psi \partial_t \Psi^* + \Psi^* \partial_t \Psi)\\ &=\frac{i}{\hbar} (\Psi H^* \Psi^*-\Psi^* H \Psi)\end{aligned}$ Now use the position representation of the Hamiltonian, $H=-\hbar^2 \nabla^2/(2m)+V({\mathbf r})$ . The potential commutes with $\rho({\mathbf r})$ and hence can be dropped. Moreover, we can use $\Psi \nabla^2 \Psi^* - \Psi^* \nabla^2 \Psi = \nabla \cdot (\Psi \nabla \Psi^* - \Psi^* \nabla \Psi).$

As a result, we get $\frac{d}{dt} |\Psi|^2 = -\frac{i\hbar}{2m}\nabla \cdot (\Psi \nabla \Psi^* - \Psi^* \nabla \Psi) \equiv -\nabla \cdot {\mathbf j}.$ We hence found an expression for the current density in terms of the wave function $\boxed{{\mathbf j}= \frac{i \hbar}{2m} (\Psi \nabla \Psi^* - \Psi^* \nabla \Psi) = \frac{\hbar}{m} {\rm Im}(\Psi^* \nabla \Psi).}$

For the plane wave solution describing the incoming wave, $\psi_{\rm in}=(2\pi)^{-3/2} e^{i{\mathbf k}\cdot {\mathbf r}}$ , we get $\begin{align*}\tag{1} \boxed{{\mathbf j}_{\rm in}=+ \frac{1}{(2\pi)^3} \frac{\hbar {\mathbf k}}{\mu}} \end{align*}$ In defining the cross section, we need the amount (per unit time) of scattered particles moving through a sphere surface at $r\rightarrow \infty$ : $n=\int \underbrace{{\mathbf dS}}_{r^2 d\Omega \hat e_r} \cdot {\mathbf j}_{\rm scatt} = r^2 \int d\Omega \underbrace{j_r}_{\text{radial component of flux}}.$ Recall the spherical-coordinates representation of gradient: $\nabla = \hat e_r \partial_r + \hat e_\theta \partial_\theta/r+\hat e_\varphi \partial_\varphi/(r \sin \theta)$ so that $j_r=\frac{\hbar}{\mu} {\rm Im}[\Psi^*({\mathbf r}) \nabla \Psi({\mathbf r})]_r = \frac{\hbar}{\mu} {\rm Im}[R^*(r) R'(r) Y_{lm}^*(\Omega) Y_{lm}(\Omega)].$

1=jin

Comparing to the generic solution to the radial equation we hence want to see what happens with $R(r)=C e^{\pm ikr}/r$ . Direct calculation gives $n=r^2 \frac{\hbar}{\mu} |C|^2 {\rm Im}\left[\frac{e^{\mp ikr}}{r} \cdot \frac{e^{\pm ikr}}{r}(\pm ik-\frac{1}{r}) \underbrace{\int d\Omega Y_{\rm lm}^*(\Omega) Y_{\rm lm}(\Omega)}_{=1}\right] = \pm |C|^2 \frac{\hbar k}{\mu}.$ The total particle flux is thus independent of the radial coordinate , which is desired because there are no sources or sinks of particles. Now we can identify what the signs mean:
"+" $\cong$ outgoing spherical wave
"-" $\cong$ incoming spherical wave
Moreover, we find that the proper asymptotic behavior of an outgoing spherical wave is $e^{ikr}/r$ .

Now we are in position of defining the quantum scattering problem:

# quantumscatteringproblem

Quantum scattering problem

With a potential $V=V({\mathbf r})$ decaying faster than 1/r^2 , find the solutions of the spherical Schrödinger equation $-\frac{\hbar^2}{2\mu} \nabla^2 \Psi({\mathbf r})+ V({\mathbf r}) \Psi({\mathbf r}) = E \Psi({\mathbf r})$ or $\boxed{(\nabla^2 + k^2) \Psi({\mathbf r}) = U({\mathbf r}) \Psi({\mathbf r}), \quad \text{ where } U({\mathbf r}) \equiv \frac{2\mu}{\hbar^2} V({\mathbf r})}$ fulfilling the boundary condition

# psifaraway

$\boxed{\Psi({\mathbf r}) \xrightarrow{r\rightarrow \infty} \frac{1}{(2\pi)^{3/2}} \left[\underbrace{e^{i{\mathbf k}\cdot {\mathbf r}}}_{\text{\parbox{1.5cm}{incoming particles}}} + \underbrace{\frac{e^{ikr}}{r} f_k(\theta,\varphi)}_{\text{\parbox{3cm}{spherical outgoing wave $\cong$ scattered particles}}}\right]}$ Here $\boxed{f_k(\theta,\varphi)=\text{ scattering amplitude}.}$

For the wave function modulus squared $|\Psi|^2$ to integrate (over all space) to probabilities (dimensionless number), the units of the wave function have to be $[\Psi]={\rm length}^{-3/2}$ . This unit is thus ''hidden'' in the normalization constant. The square bracket is dimensionless, so the scattering amplitude must have units ${\rm length}$ .

We have two remaining problems: What is $f_k(\theta,\varphi)$ if $V({\mathbf r})$ is known? What is the relation between $f_k(\theta,\varphi)$ and the scattering cross section $\sigma$ ?

Note that $f_k(\theta,\varphi)$ is a generalization of the transmission and reflection probability amplitudes from the one-dimensional scattering problem.

To answer the second question, let us check the particle fluxes for our Ansatz asymptotic wave function. The total flux is $\begin{aligned} {\mathbf j}=& \frac{\hbar}{\mu} {\rm Im}[\Psi^*({\mathbf r}) \nabla \Psi({\mathbf r})] = {\mathbf j}_{\rm in}+{\mathbf j}_{\rm scatt} + {\mathbf j}_{\rm int}\\ \overset{r \rightarrow \infty}{=}& \frac{\hbar}{\mu} {\rm Im}[\underbrace{\Psi_{\rm in}^*({\mathbf r}) \nabla \Psi_{\rm in}({\mathbf r})}_{\propto {\mathbf j}_{\rm in}}+\underbrace{\Psi_{\rm scatt}^*({\mathbf r}) \nabla \Psi_{\rm scatt}({\mathbf r})}_{\propto {\mathbf j}_{\rm scatt}} \\&+\underbrace{\Psi_{\rm in}^*({\mathbf r}) \nabla \Psi_{\rm scatt}({\mathbf r})+ \Psi_{\rm scatt}^*({\mathbf r}) \nabla \Psi_{\rm in}({\mathbf r})}_{\propto {\mathbf j}_{\rm int}}].\end{aligned}$

Therefore, we find that the total current consists of three parts. The first of these is nothing but the flux of incoming particles, denoted $\Phi_A$ above. To understand the second, let us consider the number of particles scattered into a solid angle $d\Omega$ in a unit time per target particle $\frac{dn_S}{N_B} = \frac{1}{N_B} n_S(\theta,\varphi) d\Omega \overset{r \rightarrow \infty}{=} {\mathbf dS} \cdot {\mathbf j}_{\rm scatt} = r^2 d\Omega (j_{\rm scatt})_r.$ Here ${\mathbf j}_{\rm scatt}=\frac{\hbar}{\mu} {\rm Im}[\Psi_{\rm scatt}^*({\mathbf r}) \nabla \Psi_{\rm scatt}({\mathbf r})]=\frac{1}{(2\pi)^3} \frac{\hbar}{\mu} {\rm Im}\left[\frac{e^{-ikr}}{r} f_k^*(\Omega) \nabla\left(\frac{e^{ikr}}{r}f_k(\Omega)\right)\right].$ In other words, $({\mathbf j}_{\rm scatt})_r = \frac{1}{(2\pi)^3} |f_k(\Omega)|^2 \frac{\hbar k}{\mu} \frac{1}{r^2}.$ and therefore $\frac{n_S}{N_B}=r^2 d\Omega ({\mathbf j}_{\rm scatt})_r = \frac{1}{(2\pi)^3} |f_k(\theta,\varphi)|^2 \frac{\hbar k}{\mu} d\Omega.$

Using $\Phi_A=j_{\rm in}$ from Eq. (1) we can hence define the cross section, $\sigma=\frac{n_S}{\Phi_A N_B}=\frac{1}{\Phi_A}\frac{\int n_S(\theta,\varphi) d\Omega}{N_B}$ yielding $\boxed{\sigma=\int d\Omega |f_k(\theta,\varphi)|^2} \quad \text{elastic cross section}$ and where $\boxed{\frac{d\sigma}{d\Omega} = |f_k(\theta,\varphi)|^2} \quad \text{differential cross section.}$ As the scattering amplitude has units ${\rm length}$ , it makes sense that |f|^2 has units of the (differential) cross section, i.e., ${\rm length}^2$ .

We have thus answered the second question above: finding the (absolute value of the) scattering amplitude $f_k(\theta,\varphi)$ amounts to calculating the differential cross section. In retrospect it is quite clear that the two quantities must contain the same information, because they are the only ingredients left open after specifying the scattering setup!

1=jin

Interference current and the optical theorem

Before proceeding to the methods to calculate $f_k(\theta,\varphi)$ , let us fix one loose end: what happens to the interference current term ${\mathbf j}_{\rm int}$ ? It is given by $\begin{aligned} {\mathbf j}_{\rm int}\overset{r\rightarrow \infty}{=}&\frac{\hbar}{\mu} {\rm Im}[\Psi_{\rm in}^* \nabla \Psi_{\rm scatt} + \Psi_{\rm scatt}^* \nabla \Psi_{\rm in}]\\ =&\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} {\rm Im}[e^{-i{\mathbf k}\cdot {\mathbf r}} \nabla(\frac{e^{ikr}}{r}f_k(\Omega))+\frac{e^{-ikr}}{r} f_k^*(\Omega) \nabla e^{i{\mathbf k}\cdot {\mathbf r}}].\end{aligned}$ Its radial component becomes $({\mathbf j}_{\rm int})_r=\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} {\rm Im}\left[e^{-ikr\cos(\theta)} f_k(\Omega) \underbrace{\partial_r \frac{e^{ikr}}{r}}_{\frac{e^{ikr}}{r}(ik-1/r)} + \frac{e^{-ikr}}{r} f_k^*(\Omega) \underbrace{\partial_r e^{ikr\cos(\theta)}}_{ik\cos(\theta) e^{ikr\cos(\theta)}}\right],$ where we defined the spherical angle $\theta$ by the relation ${\mathbf k}\cdot {\mathbf r}= kr \cos(\theta)$ .

Proceeding, we get $({\mathbf j}_{\rm int})_r \overset{r\rightarrow \infty}{=} \frac{\hbar}{\mu} \frac{1}{(2\pi)^3} {\rm Im}\left[\frac{ik}{r} (f_k(\theta,\varphi) e^{ikr(1-\cos(\theta))} + \text{complex conjugate}) + o\left(\frac{1}{r^2}\right)\right].$ Now, when $\theta \neq 0 \rightarrow 1-\cos(\theta) \neq 0$ , $e^{ikr(1-\cos \theta)}$ oscillates very rapidly when $r\rightarrow \infty$ .

So far we have assumed that the incoming beam is entirely monoenergetic, i.e., contains only a single wave vector. This certainty of momentum would correspond to a wave packet with an infinite spread in space. In reality, the beam is never monoenergetic, but contains some spread $\Delta k \ll k$ in the wave number. This spread is not very relevant for the incoming and outgoing currents, but it matters in the case of the very rapidly oscillating interference current. Therefore, let us average over this spread with some weight function g(k) . That means that when we compute the flux across a spherical surface at $r\rightarrow \infty$ , we should replace $\int {\mathbf dS} \cdot {\mathbf j}= r^2 \int d\Omega j_r(r,\theta,\varphi;k) \mapsto r^2 \int d\Omega \int dk g(k) j_r(r,\theta,\varphi;k),$ where g(k) is a smooth function of , with a spread $\Delta k$ around some maximal value of . Generally g(k) is set by the experiment in question.

This means that now we have integrals of the type $\lim_{r\rightarrow \infty} \int dk \underbrace{g(k) f_k}_{\text{smooth in k}} \exp(ikr\underbrace{(1-\cos \theta)}_{\neq 0}) = 0.$ Generally, these sort of arguments can be related to the Riemann-Lebesgue lemma.

Therefore, the oscillating terms appearing at $\theta \neq 0$ vanish. Let us include only the integration near $\theta \sim 0$ : $\begin{aligned} \int {\mathbf dS} \cdot {\mathbf j}_{\mathrm{int}}&\simeq \frac{\hbar}{\mu} \frac{1}{(2\pi)^3} r^2 \int_0^{2\pi} d\varphi \int_{1-\cos \delta\theta}^1 d(\cos\theta) {\rm Im}[\frac{ik}{r}(f_k(0) e^{ikr(1-\cos(\theta))} + \text{complex conj.}) + o(1/r^2)]\\ &=\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} 2\pi r^2 {\rm Im}[\frac{ik}{r}f_k(0)\frac{1}{-ikr} e^{-ikr(1-\cos(\theta))}|_{1-\cos \delta\theta}^1 + c.c. + o(1/r^2)]\\ &=\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} 2\pi r^2 {\rm Im}[\frac{i}{r^2} (if_k(0) \{1-e^{ikr \cos(\delta \theta)}\} + c.c.) + o(1/r^2)]\\ &=-\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} 2\pi {\rm Im}[f_k(0) -f_k^*(0) + o(1/r^2)]\\ &=-\frac{\hbar}{\mu} \frac{1}{(2\pi)^3} 4 \pi {\rm Im}[f_k(0)] + o(1/r^2).\end{aligned}$

So what is the consequence of this lengthy calculation? Recall the continuity equation $\partial_t \rho(t,{\mathbf r})+\nabla \cdot {\mathbf j}= 0,$ where $\rho$ is the (probability or particle) density. In the stationary case the first term vanishes, and the continuity equation is a statement of probability flux conservation. In other words, $\begin{aligned} 0 &= \underset{\text{\parbox{1.2cm}{sphere of radius $R$}}}{\int} d^3 {\mathbf r}\nabla \cdot {\mathbf j}\overset{\rm Gauss}{=} \underset{{\text{\parbox{1.3cm}{surface of $R$-sphere}}}}{\int} {\mathbf dS} \cdot {\mathbf j}= R^2 \int d\Omega \hat j_r\\ &=R^2 \int d\Omega [(j_{\rm in})_r+(j_{\rm scatt})_r+(j_{\rm int})_r].\end{aligned}$

The incoming current satisfies $(j_{\rm in})_r=(2\pi)^{-3} \hbar k/\mu (\hat e_z)_r=(2\pi)^{-3} \hbar k/\mu \cos(\theta)$ and therefore $\int d\Omega (j_{\rm in})_r \propto \int_{-1}^1 d(\cos(\theta)) \cos(\theta) =0.$ In other words, the incoming current brings in (say, from the left) equally much current as they take out (say, to the right). On the other hand, the scattered total current is $R^2 \int d\Omega (j_{\rm scatt})_r = \frac{1}{(2\pi)^3} \frac{\hbar k}{\mu} \underbrace{\int d\Omega |f_k(\Omega)|^2}_{\sigma_{\rm tot}}.$

# opticaltheorem

Combining the continuity equation and our result for the interference current, we get the optical theorem $\boxed{\sigma_{\rm tot} = \frac{4\pi}{k} {\rm Im}[f_k(\theta=0)]}$ According to the optical theorem, which we have now derived, the total cross section is related to the imaginary part of the forward scattering amplitude. Physically, this means that behind the target, at $\theta \rightarrow 0$ , the incoming wave and the scattered wave interfere destructively, so that the intensity of the beam which has passed the target decreases by an amount which is proportional to the total cross section.

# ii.-3.-integral-equation-for-potential-scattering

Integral equation for (potential) scattering

After having specified the scattering problem, we should try to solve it at least in some particular cases. In other words, we wish to solve the 3d differential equation

# 3ddiffeq

$(\nabla^2 + k^2) \Psi({\mathbf r})= U({\mathbf r}) \Psi({\mathbf r})$ with the asymptotic boundary condition $\Psi_{{\mathbf k}}({\mathbf r}) \xrightarrow{r\rightarrow \infty} \frac{1}{(2\pi)^{3/2}}\left(e^{i{\mathbf k}\cdot {\mathbf r}} + \frac{e^{ikr}}{r} f_k(\theta,\varphi)\right).$ Note that here the vector ${\mathbf k}$ , $k \equiv |{\mathbf k}|$ is some quantity specified for the problem. In particular, the direction of the vector ${\mathbf k}$ specifies a reference direction.

To solve the problem, let us first define

The solution $\phi_{\mathbf k}({\mathbf r})$ of the homogeneous () equation: $(\nabla^2 + k^2)\phi_{\mathbf k}({\mathbf r})=0;\quad \phi_{\mathbf k}({\mathbf r})=\frac{1}{(2\pi)^{3/2}} e^{i{\mathbf k}\cdot {\mathbf r}}$
Green's function $G_{\mathbf k}({\mathbf r},{\mathbf r}')$ satisfying $(\nabla^2 + k^2)G_{\mathbf k}({\mathbf r},{\mathbf r}')=\delta^{(3)}({\mathbf r}-{\mathbf r}').$

# integralequation

The differential equation can now be cast in the form of an integral equation: $\boxed{\Psi_{\mathbf k}({\mathbf r})=\phi_{\mathbf k}({\mathbf r})+\int d^3 {\mathbf r}' G_{\mathbf k}({\mathbf r},{\mathbf r}') U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}')}$ We wish to use this integral equation to help find a general scheme for solving the scattering problem. This is done below, but before we manage to do so, we need to discuss the Green's function in more detail.

$(\nabla^2 + k^2)\Psi_{\mathbf k}=\underbrace{(\nabla^2+k^2)\phi_{\mathbf k}}_{=0} + \int d^3 \mathbf r' \underbrace{(\nabla^2 + k^2)G_{\mathbf k}(\mathbf r, \mathbf r')}_{\delta^{(3)}(\mathbf r-\mathbf r')}U(\mathbf r')\Psi_{\mathbf k}(\mathbf r'))=U(\mathbf r) \Psi_{\mathbf k}(\mathbf r)$

Green's functions do not only depend on the differential equation, but also on the boundary conditions. Now, in order to fulfill the boundary conditions of the scattering problem, $\phi_{\mathbf k}({\mathbf r})$ has to be taken to be the incoming plane wave, and we have to define the Green's function suitably, so that $\int d^3 {\mathbf r}' G_{\mathbf k}({\mathbf r},{\mathbf r}') U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}') \xrightarrow{r\rightarrow \infty} \frac{e^{ikr}}{r} f_k(\theta,\phi),$ i.e., it should correspond to the outgoing spherical wave.

Let us make a Fourier expansion of $G_{\mathbf k}$ , by assuming that it only depends on the difference of its arguments: $G_{\mathbf k}({\mathbf r},{\mathbf r}')= G_{\mathbf k}({\mathbf r}-{\mathbf r}') = \int \frac{d^3 {\mathbf q}}{(2\pi)^3} e^{i{\mathbf q} \cdot ({\mathbf r}-{\mathbf r}')} g_{\mathbf k}({\mathbf q}).$ It satisfies $(\nabla^2+k^2) G_{\mathbf k}({\mathbf r}-{\mathbf r}')=\int \frac{d^3 {\mathbf q}}{(2\pi)^3} (k^2-q^2) e^{i{\mathbf q} \cdot ({\mathbf r}-{\mathbf r}')} g_{\mathbf k}({\mathbf q}) = \delta^{(3)}({\mathbf r}-{\mathbf r}') = \int \frac{d^3 {\mathbf q}}{(2\pi)^3} e^{i{\mathbf q}\cdot ({\mathbf r}-{\mathbf r}')}$ or $(k^2-q^2) g_{\mathbf k}({\mathbf q})=1.$

In order to compute $G_{\mathbf k}$ , we need to consider in the complex plane, $k \mapsto k+i\epsilon$ , and set $\epsilon \rightarrow 0$ at the end of the calculation. But how should it tend to 0, from positive or negative values? As a matter of fact, the choice of the sign of $\epsilon$ determines different Green's functions.

We hence have $g_{\mathbf k}({\mathbf q})=((k+i\epsilon)^2-q^2)^{-1}$ , and using the inverse Fourier transform

# GFequation

we get $G_{\mathbf k}({\mathbf r})=I_k(r)/(4\pi^2 ri)$ , where $I_k(r)=\int_{-\infty}^\infty dq \frac{q e^{iqr}}{(k+i\epsilon)^2-q^2}.$ This integral can be computed as an integral in the complex -plane, using the residue theorem. This means that we need to introduce some mathematical machinery that comes handy in various physics problems, but especially those dealing with Green's functions.

If you already know how to compute the integral via the residue theorem, you may skip directly to the discussion of that calculation.

# ii.3.1-functions-of-complex-variable-and-their-integration

Functions of complex variable and their integration

Let us start by the definition of a complex derivative $\boxed{f'(z) \equiv \lim_{h\rightarrow 0} \frac{f(z+h)-f(z)}{h}; f,z,h \in {\mathbb C}}$ This should be "isotropic", i.e., independent of the direction of : 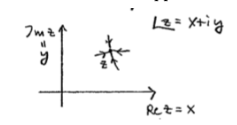In other words, $\begin{aligned} f'(z) &= \lim_{\Delta x \rightarrow 0} \frac{f(z+\Delta x)-f(z)}{\Delta x} = \frac{\partial f}{\partial x}\\ &=\lim_{i\Delta y \rightarrow 0} \frac{f(z+i\Delta y)-f(z)}{i\Delta y} = -i \frac{\partial f}{\partial y}.\end{aligned}$

Let us separate the real and imaginary parts of f(z)=u(z)+i v(z) , where $u,v \in {\mathbb R}$ , z=x+iy . Then $f'(z)=\frac{\partial f}{\partial x} = \frac{\partial u}{\partial x} + i \frac{\partial v}{\partial x}$ and $f'(z)=-i\frac{\partial f}{\partial y} = -i\frac{\partial u}{\partial y} + \frac{\partial v}{\partial y}.$

# cauchyriemann

Equating the real and imaginary parts separately yields $\boxed{\frac{\partial u}{\partial x}-\frac{\partial v}{\partial y} = 0 \text{ and } \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x} = 0}$ These are known as the Cauchy-Riemann equations.

# contour-integrals-viivaintegraalit

Contour integrals (viivaintegraalit)

Consider a closed path in the complex plane: 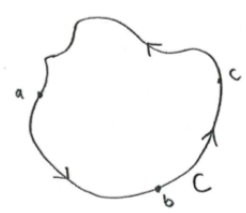Let us moreover define the winding direction to be counterclockwise (arrows in the figure). The contour integral along can be defined in parts, $\ointctrclockwise_C dz f(z) = \int_{C(a \rightarrow b)} f(z) + \int_{C(b \rightarrow c)} f(z) + \int_{C(c \rightarrow a)} f(z) = -\ointclockwise_C dz f(z).$ Let f(z) to be analytic on and within above. Consider the contour integral along : $\begin{aligned} \ointctrclockwise_C dz f(z) &= \ointctrclockwise_C (dx+idy) (u+iv) = \ointctrclockwise_C (u dx-vdy) + i\ointctrclockwise_C (vdx+u dy)\\ &=\ointctrclockwise \underbrace{(u \hat e_x-v \hat e_y)}_{\mathbf A} \cdot {\mathbf dx} + i \ointctrclockwise_C \underbrace{(v \hat e_x+u \hat e_y)}_{\mathbf B} \cdot {\mathbf dx}\\ &\overset{\text{\parbox{2cm}{Stokes\\theorem}}}{=} \int_{S_c} da \underbrace{\hat e_3 \cdot (\nabla \times {\mathbf A})}_{(\nabla \times {\mathbf A})_3} + i\int_{S_c} da \underbrace{\hat e_3 \cdot (\nabla \times {\mathbf B})}_{(\nabla \times {\mathbf B})_3}\\ &=\int_{S_c} da (-\partial_x v - \partial_y u) + i \int_{S_c} da (\partial_x u - \partial_y v) = 0.\end{aligned}$

The last result was obtained by using the Cauchy-Riemann equations: both integrands vanish. In other words, $\boxed{\ointctrclockwise dz f(z) = 0}$ This results allows us to state the

Cauchy's integral theorem

A contour integral of a complex function f(z) over a closed and simply connected (no holes) region vanishes if f(z) is analytic on and within its interior. In other words, f(z) has no singularities inside or on .

Now let us start transforming the contour. For example, take 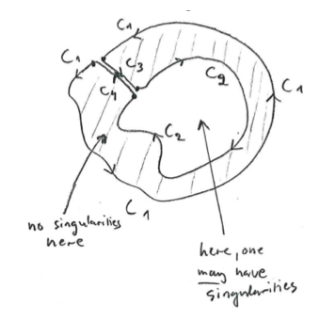C=C_1+C_3+C_2+C_4 : Assume that there are no holes or singularities within , i.e., the shaded region in the figure. Then, Cauchy's integral theorem states that $0 = \ointctrclockwise_C dz f(z) = \Bigg(\ointctrclockwise_{C_1} + \ointclockwise_{C_2} + \underbrace{\int_{C_3} + \int_{C_4}}_{\text{\parbox{2cm}{cancel, opposite directions}}}\Bigg)dz f(z) = \ointctrclockwise_{C_1} dz f(z) + \ointclockwise_{C_2} dz f(z).$ Changing the direction in C_2 this then yields $\ointctrclockwise_{C_1} dz f(z) = \ointctrclockwise_{C_2} dz f(z).$ In this way, we can "shrink" the contours. Note that the area spanned by C_2 is smaller than the one spanned by C_1 . However, the integrals are the same --- and not necessarily zero!

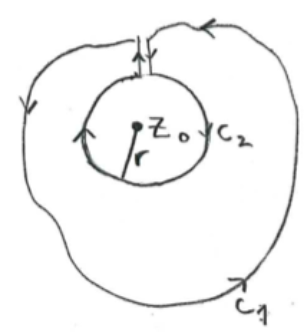
We can generalize this result to many loops, which may contain singularities at $z_1, z_2, \dots, z_n$ :
$\boxed{\ointctrclockwise_C dz f(z) = \sum_{n=1}^\infty \ointctrclockwise_{C_n} dz f(z)}$ Note that all contours run in the counterclockwise direction.

Suppose now that f(z) has an isolated singularity at z=z_0 . This means that f(z) is analytic in the area surrounding z_0 but not exactly at z=z_0 . By the definition of analyticity, f(z) cannot be written in terms of its Taylor series. Rather, we have to use the Laurent series of f(z) $f(z) = \sum_{n=-\infty}^\infty a_n (z-z_0)^n.$ Let us assume there is an $m \in {\mathbb Z}$ , m>0 so that $a_{n<-m}=0$ . Then $\begin{aligned} f(z) &= \underbrace{\frac{a_{-m}}{(z-z_0)^{m}} + \frac{a_{-m+1}}{(z-z_0)^{m+1}}+ \cdots +\frac{a_{-1}}{z-z_0}}_{\text{singular terms}}\\ &+\underbrace{a_0 + a_1(z-z_0) + a_2 (z-z_0)^2 + \cdots}_{\text{analytic}}.\end{aligned}$ Above, we call
z_0 a pole of order
$a_{-1}$ the residue of f(z) at z=z_0 $\boxed{a_{-1}= \underset{z=z_0}{\rm Res} f(z)}$ Let f(z) now have a pole of order at z=z_0 , $f(z)=\sum_{n=-m}^\infty a_n (z-z_0)^n.$

Take C_2 as a circle around z_0 : $\boxed{z-z_0=re^{i\varphi}}$ i.e., $dz=ir e^{i\varphi} d\varphi$ , $\varphi \in [0,2\pi]$ . The contour integral becomes $\begin{aligned} \ointctrclockwise_{C_1} dz f(z) &= \ointctrclockwise_{C_2} dz f(z) = \sum_{n=-m}^\infty a_n \ointctrclockwise_{C_2} dz \underbrace{(z-z_0)^n}_{r^n e^{in\phi}}\\ &=i \sum_{n=-m}^\infty a_n r^{n+1} \underbrace{\int_0^{2\pi} d\varphi e^{i(n+1) \varphi}}_{2\pi \delta_{n,-1}:\text{\parbox{3cm}{only $n=-1$ survives!}}}\\ &=2 \pi i a_{-1} = 2 \pi i \underset{z=z_0}{\rm Res} f(z).\end{aligned}$

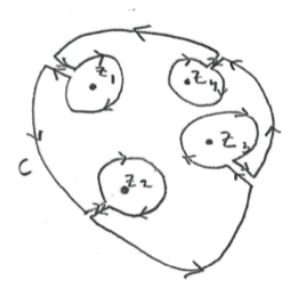
This result can be generalized to the case of many singularities at $z_1, z_2,\dots$ $\boxed{\ointctrclockwise_{C_1} dz f(z) = 2\pi i \sum_{j=1}^n \underset{z=z_j}{\rm Res} f(z)}$ We have derived the Residue theorem, a very important result.

The residues can be obtained from

Expanding as a Laurent series and taking the coefficient $a_{-1}$ or, more easily,
using a pocket formula for a pole of order (can be verified trivially) $\boxed{\underset{z=z_0}{\rm Res} f(z) = \underset{z\rightarrow z_0}{\lim} \frac{1}{(n-1)!} \left(\frac{d}{dz}\right)^{n-1} [(z-z_0)^n f(z)]}$

In the quite often encountered special case of a simple pole m=1 at z=z_0 we have $f(z)=\frac{a_{-1}}{(z-z_0)} + a_0 +\cdots$ and $\underset{z=z_0}{\rm Res} f(z) = \underset{z\rightarrow z_0}{\lim} (z-z_0) f(z).$ Let us now use these results for the evaluation of the Green's function.

# ii.3.2-evaluation-of-the-greens-function

Evaluation of the Green's function

We can finally come back to our initial problem of calculating the Green's function. We would like to calculate $I_k(r)=\int_{-\infty}^\infty dq \underbrace{\frac{q e^{iqr}}{(k+i\epsilon)^2-q^2}}_{f(q)}.$

Since $(k+i\epsilon)^2-q^2=(k+i\epsilon-q)(k+i\epsilon+q)$ , the poles of f(q) are at $k+i\epsilon-q=0$ and $k+i\epsilon+q=0$ , or $\boxed{q=k+i\epsilon \equiv q_+} \text{ and } \boxed{q=-k-i\epsilon \equiv q_-=-q_+}$ and since $f(q)=\frac{-q e^{iqr}}{(q-q_+)(q-q_-)} = -\frac{q e^{iqr}}{q_+-q_-} \left(\frac{1}{q-q_+} - \frac{1}{q-q_-}\right),$ the poles at $q=q_\pm$ are simple poles of order 1. Let us calculate the residues: $\begin{aligned} \underset{q=q_\pm}{\rm Res} f(q) &=\underset{q\rightarrow q_\pm}{\lim} \frac{(-q) e^{iqr}}{(q-q_+)(q-q_-)}=\frac{-q_{\pm} e^{iq_\pm r}}{\underbrace{q_{\pm}-q_{\mp}}_{=2q_\pm}}\\ &=-\frac{1}{2} e^{iq_\pm r}.\end{aligned}$ These are the residues of f(q) at $q=q_\pm$ .

Wait! We have a simple integral over real values of . Where is the contour? The trick is to consider the integral over the real axis as part of a closed contour that closes along the complex plane as shown in the following picture (where we have chosen $\epsilon>0$ ):

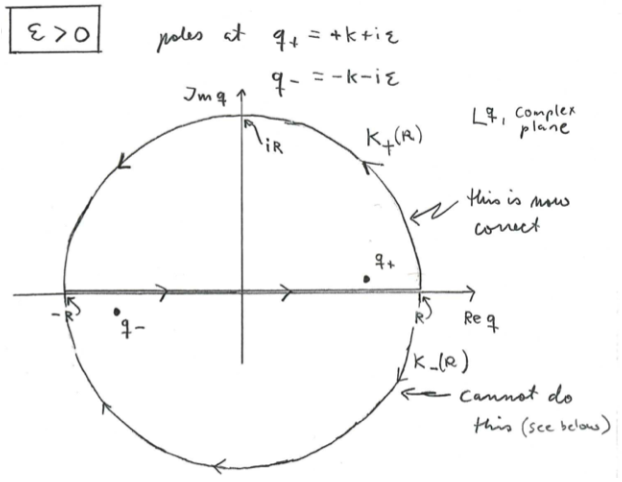
We should hence "close" the contour along the upper or lower complex half-plane. But which one should we use? This we see below. Either way, we can see that one of the poles is inside the contour , and the other one is outside. Anyway, the idea is the following: the residue theorem says $\begin{aligned} 2\pi i \underset{\underbrace{q=q_k}_{\text{poles inside $C$}}}{\rm Res} f(q) &= \ointctrclockwise_C dq f(q) \\&= \underset{R\rightarrow \infty}{\lim} \bigg[\int_{-R}^R dq f(q) + \underset{\text{\parbox{4cm}{$K_+(R)$ or $K_-(R)$\\semicircle at $|q|=R$}}}{\int dq f(q)}\mkern-54mu\bigg].\end{aligned}$

The first term inside the square brackets is the one we wish to compute. Now our aim is to choose the contour K_+(R) or K_-(R) so that the second integral vanishes. Let us choose first K_+(R) , i.e., close the contour in the upper half-plane:

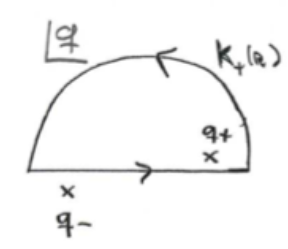
In this case, the pole q_+ is inside , and q_- is outside it. In other words, $\int_{-\infty}^\infty dq f(q) = 2\pi i \underset{q=q_+} {\rm Res} f(q) - \underset{R \rightarrow \infty}{\lim} \int_{K_+(R)} dq f(q).$

For $q \in K_+(R)$ , we can set $q=R e^{i\varphi}$ , $\varphi \in [0,\pi]$ . Let us show that the contour integral along K_+(R) vanishes as $R \rightarrow \infty$ . We have $\begin{aligned} f(q \in K_+(R)) &= \frac{-R e^{i\varphi} e^{iRr\cos(\varphi)} e^{-Rr \sin(\varphi)}}{R^2 e^{i2\varphi}-(k+i\epsilon)^2}\\ &=\frac{-e^{i(-\varphi+Rr\cos\varphi)}}{R(1-(q_+/R)^2 e^{-i2\varphi})} e^{-Rr \sin(\varphi)}.\end{aligned}$ Now take the limit $R \rightarrow \infty$ . The absolute value of $f(q=Re^{i\varphi})$ tends to $|f(q=Re^{i\varphi})|\xrightarrow{R\rightarrow \infty} \frac{1}{R} \exp[-\underbrace{Rr\sin \varphi}_{\text{\parbox{1.5cm}{$\ge 0$ since $\varphi \in [0,\pi]$}}}] \rightarrow 0.$

The integral along contour K_+(q) running along the upper half-plane therefore vanishes: note that the length of the contour is $\pi R$ , and hence increases linearly with an increasing . However, the integrand vanishes exponentially with an increasing . Exponential function wins a linear one, and thus the result vanishes. We can see why we have to close the contour through the upper half plane, as for K_-(R) we would have $q=R e^{-i\varphi}$ (again $\varphi \in [0,\pi]$ ) and $e^{iqr}\overset{q=Re^{-i\varphi}}=e^{iR r \cos \varphi} \exp[+\underbrace{Rr\sin \varphi}_{\text{\parbox{1.5cm}{$\ge 0$ since $\varphi \in [0,\pi]$}}}] \xrightarrow{R\rightarrow \infty} \infty!$ The integral along the lower half-plane would hence not vanish for $R\rightarrow \infty$ .

In general which half-plane to close the contour depends on the case. For exponential functions with poles in the upper half-plane, we can prove the

Jordan's lemma: If $|g(z)| \le M(R)$ , when |z|=R , ${\rm Im} z >0$ (upper half-plane), and $M(R) \overset{R\rightarrow \infty}{\rightarrow} 0$ , then $\lim_{R\rightarrow \infty} \int_{K_+(R)} g(z) e^{ikz}dz =0.$

Proof, using $z=Re^{i\varphi}$ and hence $dz=iR e^{i\varphi} d\varphi$ for a fixed : $\begin{aligned} &\int_{K_+(R)} g(z) e^{ikz} dz = \int_0^\varphi d\varphi i R e^{i\varphi} g(Re^{i\varphi}) e^{+ikR\cos \varphi} e^{-kR\sin \varphi}\\ &\Rightarrow |\int_{K_+(R)} g(z) e^{ikz}| \le \int_0^\pi d\varphi |iR e^{i\varphi} g(Re^{i\varphi}) \underbrace{e^{-ikR\cos \varphi}}_{\text{phase, }|.|=1} e^{-kR\sin(\varphi)}|\\ &=R\int_0^\varphi |g(Re^{i\varphi})| e^{-kR\sin(\varphi)}\\ &\overset{|g(z)| \le M(R)}{\le} R M(R) \int_0^\varphi d\varphi e^{-kR \sin \varphi} = 2 R M(R) \int_0^{\pi/2} d\varphi e^{-kR \sin \varphi}\\ &\overset{\sin \varphi \ge 2 \varphi/\pi}{\le} 2R M(R) \int_0^{\pi/2} d\varphi e^{-kR 2\varphi/\pi}\\ &=2RM(R) \frac{\pi}{2kR} (1-e^{-kR}) = \frac{\pi M(R)}{k} (1-e^{-kR}) \xrightarrow[M(R)\rightarrow 0]{R\rightarrow \infty} 0.\hfill _\square\end{aligned}$

Now let us apply Jordan's lemma to our problem: $f(q)=\underbrace{\frac{-q}{q^2-(k+i\epsilon)^2}}_{g(q)} e^{iqr},$ and we have that $|g(Re^{i\varphi})|=R^{-1}|1-(q/R)^2e^{-i2\varphi}|^{-1} \le 1/R=M(R) \rightarrow 0$ , so it fulfills the assumptions. This means that as $R\rightarrow \infty$ , the integral of f(q) of the contour K_+(R) over the upper half-plane vanishes. Moreover, from the equation for the Green's function we have for $\epsilon>0$ $I^{\epsilon>0}_k(r)=\int_{-\infty}^\infty dq f(q) = 2\pi i \underset{q=q_+}{\rm Res} f(q) = 2\pi i (-\frac{1}{2} e^{iq_+ r}) = -\pi i e^{i(k+i\epsilon)r}.$

In other words, the Green's function is $\boxed{G_{{\mathbf k}}^{\epsilon>0}({\mathbf r})=\frac{I_k^{\epsilon>0}}{4\pi^2 r i} = -\frac{1}{4\pi} \frac{e^{i(k+i\epsilon)r}}{r} \xrightarrow{\epsilon \rightarrow 0^+} -\frac{1}{4\pi} \frac{e^{ikr}}{r}}$ Let us quickly check what would happen with the choise $\epsilon < 0$ . In this case the pole at $q_+=k+i\epsilon=k-i|\epsilon|$ would be outside and the pole q_- inside it:

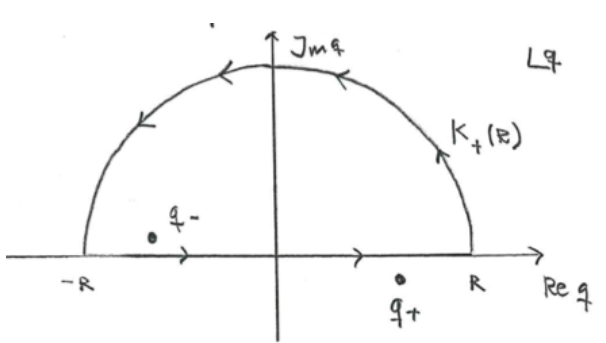
Now you should show that we get $I_{\mathbf k}^{\epsilon <0} = 2\pi i(-\frac{1}{2}e^{iq_- r})=-\pi i e^{-i(k+i\epsilon)r}$ and the corresponding Green's function would be $G_{\mathbf k}^{\epsilon<0}({\mathbf r})=-\frac{1}{4\pi} \frac{e^{-ikr}}{r}$ In other words, $G_{\mathbf k}^{\epsilon \rightarrow 0_\pm}({\mathbf r})=-\frac{1}{4\pi} \frac{e^{\pm ikr}}{r}.$ Next, we show that it is $+\epsilon$ that we want for the scattering problem, to describe an outgoing spherical wave.

# ii.3.3-integral-equation-for-potential-scattering-ieps

Integral equation for potential scattering (IEPS)

Now, finally, substitute the above Green's function back to the integral equation for scattering, still allowing for either sign of $\epsilon$ . We get

# IEPS

$\boxed{\Psi_{\mathbf k}({\mathbf r})=\phi_{\mathbf k}({\mathbf r})-\frac{1}{4\pi} \int d^{(3)} {\mathbf r}' \frac{e^{\pm ik|{\mathbf r}-{\mathbf r}'|}}{|{\mathbf r}-{\mathbf r}'|} U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}')}$

Here $U({\mathbf r}') \neq 0$ in some vicinity of ${\mathbf r}' \approx 0$ . We should check the boundary condition at $r \rightarrow \infty$ (not $r'\rightarrow \infty$ ) and choose the Green's function (+ or -) accordingly. Therefore, we should assume $r' \ll r \rightarrow \infty$ , and expand: $\begin{aligned} k|{\mathbf r}-{\mathbf r}'| &= k \sqrt{({\mathbf r}-{\mathbf r}')^2} = kr\sqrt{1-\frac{2{\mathbf r}\cdot {\mathbf r}'}{r^2}+\underbrace{\left(\frac{r'}{r}\right)^2}_{\rightarrow 0}}\\ &\approx kr\left(1-\frac{1}{2} 2 \underbrace{\frac{{\mathbf r}}{r}}_{\hat e_r} \cdot \frac{{\mathbf r}'}{r}+o\left(\left(\frac{r'}{r}\right)^2\right)\right)\\ &=kr-\underbrace{k\hat e_r}_{\equiv {\mathbf k}'} \cdot {\mathbf r}'.\end{aligned}$ Note that we identified (defined) here the wave vector of the scattered particle, ${\mathbf k}' \equiv k \hat e_r$ . As we are describing elastic scattering (energy of the incoming particle equals that of the outgoing particle), it has the same magnitude as the incoming particle, but a different direction.

Inserting this expansion into the integral equation for potential scattering yields in the lowest order $\Psi_{\mathbf k}({\mathbf r}) \overset{r\rightarrow \infty}{=}\phi_{\mathbf k}({\mathbf r})-\frac{e^{\pm ikr}}{r} \frac{1}{4\pi} \int d^3 {\mathbf r}' e^{\mp i{\mathbf k}' \cdot {\mathbf r}'} U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}').$ Comparing this to the desired form, we find that in order to get the proper behavior, we have to choose in the Green's function $\epsilon \rightarrow 0^+$ .

Now recall that $\phi_{\mathbf k}({\mathbf r})=\frac{1}{(2\pi)^{3/2}} e^{i{\mathbf k}\cdot {\mathbf r}}.$ Moreover, comparing to the boundary condition, we can find an expression for the scattering amplitude $f_k(\theta,\varphi)=-\frac{(2\pi)^{3/2}}{4 \pi} \int d^{(3)} {\mathbf r}' \underbrace{e^{-i{\mathbf k}' \cdot {\mathbf r}'}}_{(2\pi)^{3/2} \phi_{{\mathbf k}'}^*({\mathbf r}')} U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}')$ or $\boxed{f_k(\theta,\varphi)=-2 \pi^2\int d^{(3)} {\mathbf r}' \phi_{{\mathbf k}'}^*({\mathbf r}') U({\mathbf r}') \Psi_{\mathbf k}({\mathbf r}')}$ This we need for the calculation of the differential scattering cross section.

# ii.4.-solving-the-ieps-born-approximation

Solving the IEPS: Born approximation

Let us then solve the IEPS via an iteration method, using the fact that the integral equation contains $\Psi_{\mathbf k}({\mathbf r})$ on both sides of the equation. Let us hence substitute the left hand side to the right hand side. We get $\begin{aligned} \Psi_{\mathbf k}({\mathbf r})&=\phi_{\mathbf k}({\mathbf r})+\int d^{(3)}{\mathbf r}' G_{\mathbf k}({\mathbf r}-{\mathbf r}') U({\mathbf r}') \phi({\mathbf k}')\\ &+\int d^{(3)}{\mathbf r}' d^{(3)} {\mathbf r}'' G_{\mathbf k}({\mathbf r}-{\mathbf r}') U({\mathbf r}') G_{\mathbf k}({\mathbf r}'-{\mathbf r}'') U({\mathbf r}'') \Psi_{\mathbf k}({\mathbf r}'').\end{aligned}$

Substituting $\Psi_{\mathbf k}({\mathbf r})$ repeatedly to this equation hence generates the Born series of $\Psi_{\mathbf k}({\mathbf r})$ $\begin{aligned} \Psi_{\mathbf k}({\mathbf r})&=\phi_{\mathbf k}({\mathbf r})+\int d^{(3)}{\mathbf r}' G_{\mathbf k}({\mathbf r}-{\mathbf r}') U({\mathbf r}') \phi({\mathbf k}')\\ &+\int d^{(3)}{\mathbf r}' d^{(3)} {\mathbf r}'' G_{\mathbf k}({\mathbf r}-{\mathbf r}') U({\mathbf r}') G_{\mathbf k}({\mathbf r}'-{\mathbf r}'') U({\mathbf r}'') \phi_{\mathbf k}({\mathbf r}'') + \dots.\end{aligned}$ Note that each new term contains a higher-order power of $U=2 \mu V/(\hbar^2)$ . It is hence an expansion in .

Let us write the scattering amplitude in a similar series. For illustration, let us define the wave vector of the incoming particle or "initial state wave vector" by ${\mathbf k}_i \equiv {\mathbf k}=k \hat e_z$ and that of the outgoing particle or "final state wave vector" by ${\mathbf k}_f \equiv {\mathbf k}'=k \hat e_r$ . The Born series of the scattering amplitude is $\begin{aligned} f_k(\theta,\varphi)=&-2\pi^2 \int d^{(3)}{\mathbf r}_1 \phi_{{\mathbf k}_f}^*({\mathbf r}_1) U({\mathbf r}_1) \Psi_{{\mathbf k}_i}({\mathbf r}_1)\\ =&-2\pi^2 \int d^{(3)} {\mathbf r}_1 \phi_{{\mathbf k}_f}^*({\mathbf r}_1) U({\mathbf r}_1) \phi_{{\mathbf k}_i}({\mathbf r}_1)\\ &-2\pi^2 \int d^{(3)} {\mathbf r}_1 d^{(3)} {\mathbf r}_2 \phi_{{\mathbf k}_f}^*({\mathbf r}_2) U({\mathbf r}_2) G_{\mathbf k}({\mathbf r}_2-{\mathbf r}_1) U({\mathbf r}_1) \phi_{{\mathbf k}_i}({\mathbf r}_1)\\ &-2\pi^2 \int d^{(3)} {\mathbf r}_1 d^{(3)} {\mathbf r}_2 d^{(3)} {\mathbf r}_3 \phi_{{\mathbf k}_f}^*({\mathbf r}_3) U({\mathbf r}_3) G_{\mathbf k}({\mathbf r}_3-{\mathbf r}_2) U({\mathbf r}_2) G_{\mathbf k}({\mathbf r}_2-{\mathbf r}_1) U({\mathbf r}_1) \phi_{{\mathbf k}_i}({\mathbf r}_1) + o(U^4).\end{aligned}$ We can interpret this graphically and physically as follows:

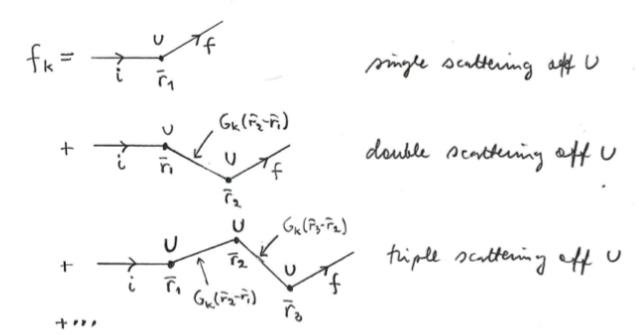
The Green's function $G_{\mathbf k}({\mathbf r}_i-{\mathbf r}_j)$ is also called the propagator, which describes the propagation of a free particle from ${\mathbf r}_j$ to ${\mathbf r}_i$ . The interpretation of the Born series is thus that f_k consists of a series of processes containing $n=1, 2, 3, \dots$ scattering events, where the incoming particle scatters off at ${\mathbf r}_1$ , after which it moves as a free particle to the point ${\mathbf r}_2$ , where it scatters off again, and so on. Obviously, if is very weak relative to the incident energy $E=\hbar^2 k^2/(2\mu)$ of the scattering particle(s), the contribution from multiple scatterings to the total scattering amplitude is small. In this case only the first term in the Born series is of relevance.

It can be shown that the Born series converges for all , if $U({\mathbf r})$ does not have bound states, i.e., $U({\mathbf r})$ is weak enough, and for (sufficiently) large , if $U(r) \xrightarrow{r\rightarrow \infty} 1/r^p$ , where p>3 and $U(r) \xrightarrow{r \rightarrow 0} 1/r^s$ , where s<2 . We can then define the

Born approximation = the first term in the Born series for $f_k(\Omega)$ $f_B(\theta,\varphi) = -2\pi^2 \int d^3 \mathbf r \phi^*_{\mathbf k_f}(\mathbf r)U(\mathbf r)\phi_{\mathbf k_i}(\mathbf r)=-\frac{1}{4\pi}\int d^3 {\mathbf r} e^{i(\mathbf k_i-\mathbf k_f)\cdot \mathbf r} U(\mathbf r).$

Let us examine this further by defining the momentum exchange vector $\boxed{\hbar {\mathbf q}= \hbar({\mathbf k}_f-{\mathbf k}_i)}$ By straightforward trigonometry (see the picture) one can show that $\frac{q}{2} = k \sin \frac{\theta}{2}$ Note that the momentum exchange vector depends on the angle $\theta$ . Using we can hence write the Born approximated form of the scattering amplitude in terms of the Fourier transform of the potential $\tilde U({\mathbf q}) \equiv {\cal F}[U({\mathbf r})] = \frac{1}{(2\pi)^{3/2}} \int d^3 \mathbf r e^{-i{\mathbf q}\cdot {\mathbf r}} U({\mathbf r})$ and hence $\boxed{f_B(\theta,\varphi) = -\frac{1}{4\pi} \int d^{(3)} {\mathbf r}e^{-i{\mathbf q}\cdot {\mathbf r}} U({\mathbf r}) = -\frac{(2\pi)^{3/2}}{4\pi}\tilde U({\mathbf q})}$

For a spherically symmetric potential, $V({\mathbf r})=V(r)$ we have $\begin{aligned} f_B(\theta,\varphi)&=-\frac{1}{4\pi} \frac{2\mu}{\hbar^2} \int \underbrace{d^{(3)} {\mathbf r}_1}_{d \cos \theta_1 d\varphi_1 r_1^2 dr_1} \exp(-i\underbrace{{\mathbf q}\cdot {\mathbf r}_1}_{qr_1\cos(\theta_1)})V(\mathbf{r}_1)\\ &=-\frac{1}{4\pi} \frac{2\mu}{\hbar^2} 4\pi \int_0^\infty dr_1 r_1^2 V(r_1) \frac{1}{qr_1} \sin(qr_1).\end{aligned}$

So, for a spherically symmetric potential we have $\boxed{f_B(\theta,\varphi) \overset{V({\mathbf r})=V(r)}=f_B(\theta) = -\frac{2\mu}{\hbar^2} \int_0^\infty dr r V(r) \frac{\sin(qr)}{q}}$ Remember that the $\theta$ -dependence is in $q=2k\sin \frac{\theta}{2}$ .

Example: Yukawa potential

Yukawa potential is $\boxed{V(r)=v_0 \frac{e^{-\kappa r}}{r}}$ The potential thus has a range $1/\kappa$ . It described a screened Coulomb potential, massive photons, or for example serves as a crude model for the nuclear binding force in an atomic nucleus. The benefit of it is that it leads to easy integrals using elementary functions. In the exercises you will show that for the Yukawa potential $f_B(\theta,\varphi)=-\frac{2\mu v_0}{\hbar^2} \frac{1}{q^2+\kappa^2} = -\frac{2\mu v_0}{\hbar^2} \frac{1}{4k^2 \sin^2 \frac{\theta}{2} + \kappa^2}.$ The differential cross section for elastic scattering off a Yukawa potential becomes in the Born approximation $\frac{d\sigma}{d\Omega} = |f_B(\theta,\varphi)|^2 = \frac{4\mu^2 v_0^2}{\hbar^4} \frac{1}{(4k^2 \sin^2\frac{\theta}{2}+\kappa^2)^2}.$ For curiosity, let us take the limit $\kappa \rightarrow 0$ , and set $v_0=q_1 q_2/(4\pi \epsilon_0)$ as in the Coulomb potential, recalling that $k^2=2\mu E/\hbar^2$ . We thus get $\frac{d\sigma}{d\Omega}|_{\kappa \rightarrow 0} = \left[\frac{q_1 q_2}{16\pi \epsilon_0 E \sin^2\frac{\theta}{2}}\right]^2 = \frac{d\sigma}{d\Omega}|_{\text{Rutherford}}$ Notice, however, that if we take the limit $\kappa \rightarrow 0$ , we are stepping outside the validity region of the above approach, since the range of $V_{\rm Coulomb}$ is infinite. In particular, integrating the above differential cross section over the angles yields $\sigma_{\rm Coulomb}=\infty$ . However, the above result for the differential cross section is nevertheless correct.

Phew! There are a lot of technical details in the above sections. What should you take along? Well, at least

Definition of the scattering problem, total and differential cross section
Quantum scattering problem and the scattering amplitude
Green's function and integral equation
Solving the scattering Green's function: small imaginary term into wave number; residue theorem (complex integration)
Using residue theorem to evaluate certain types of integrals
Once we have the Green's function, for "weak enough" potentials we can solve the scattering problem via Born series
Note how the Born approximated version couples to the scattering amplitude.

Partial wave expansion

Partial wave analysis

Another useful technique for calculating scattering amplitudes is the partial wave analysis, for the important special case of a rotation symmetric scattering potential. In this case, it is useful to project the angular dependence of the scattered wave amplitude (and thereby the differential cross section) into an orthonormal set of functions, the spherical harmonics.

Let us start by considering a spherically symmetric scattering potential V=V(r) , i.e., it only depends on the distance from the origin of the potential. The solutions of the Schrödinger equation for such a potential are of the form $\psi_{\mathbf k}(\mathbf r) = \sum_{l=0}^\infty \sum_{m=-l}^{l} a_{lm} R_l(r) Y_{lm}(\Omega),$ where we include only the scattering solutions, and thus ignore the bound states.

The scattering amplitude can then be obtained from $f_k(\theta,\varphi)=-\frac{(2\pi)^{3/2}}{4\pi} \int \overbrace{d^3 \mathbf r'}^{dr'r'^2 d\cos \theta' d\varphi'} e^{-i\overbrace{\mathbf k \cdot \mathbf r'}^{kr'\cos \theta'}} U(r) \psi_{\mathbf k}(\mathbf r').$ Substituting the above solution yields integrals over the angle $\varphi$ of the form $\int_0^{2\pi} d\varphi' \underbrace{Y_{lm}(\theta,\varphi)}_{\sim e^{-im\varphi}} = 0, \quad \text{if } m\neq 0.$

In other words, it is enough to take into account the Ansatz with m=0 : $\psi_\mathbf k(\mathbf r) = \sum_{l=0}^\infty a_l R_l(r) Y_{l0}(\theta).$ The problem has a rotation symmetry with respect to the axis parallel with the direction of the incoming beam, and thus there is no $\varphi$ dependence. Then also the scattering amplitude only depends on $\theta$ .

The radial Schrödinger equation reads $-\frac{\hbar^2}{2\mu} \left[\frac{1}{r^2} \frac{d}{dr} \left(r^2 \frac{d}{dr}\right)-\frac{l(l+1)}{r^2}\right]R_l(r)+V(r) R_l(r)=\epsilon R_l(r)$ For simplicity, denote again $U(r)=2\mu V(r)/\hbar^2$ and $k^2 = 2\mu E/\hbar^2$ . Then the radial equation goes to the form $\begin{aligned} r^2 R''(r) + 2r R'(r) + [(kr)^2-l(l+1)]R(r) -r^2 U(r) R(r)=0. \end{aligned}$

To solve the scattering problem, from the solutions to this equation we pick up the ones fulfilling the boundary condition at $r\rightarrow \infty$ . Outside the range of the potential U(r) , the solution to the radial equation can be specified in terms of spherical Bessel functions j_l(x) and n_l(x) : $\begin{aligned} R(r) = R_l(k,r) \overset{r \rightarrow \infty}{=} A(l,k) j_l(kr) + B(l,k) n_l(kr). \end{aligned}$ For small argument, the two spherical Bessel functions have different behavior, r^2 j_l(kr) staying regular at the origin, whereas r^2 n_l(kr) diverges as $r\rightarrow 0$ . In the absence of the scattering potential (free particle), we should hence have $B(l,k)\rightarrow 0$ . For non-zero U(r) , however, we need to include also this part, but the size of the coefficient B(l,k) measures the "strength" of scattering. In what follows, we quantify this strength with the scattering phase shift.

For a large argument, the two spherical Bessel functions behave as $\begin{aligned} j_l(kr) &\overset{kr \rightarrow \infty}{\rightarrow} \frac{1}{kr} \sin\left(kr-\frac{l\pi}{2}\right)\\ n_l(kr) &\overset{kr \rightarrow \infty}{\rightarrow} -\frac{1}{kr} \cos\left(kr-\frac{l\pi}{2}\right). \end{aligned}$

They hence are phase shifted by $\pi/2$ with respect to each other. Let us use this to define $\begin{aligned} R_l(k,r) \overset{r\rightarrow \infty} = A(l,k) \left[j_l(kr) + \frac{B(l,k)}{A(l,k)} n_l(kr)\right] = A(l,k)\left[j_l(kr) - \tan(\delta_l(k)) n_l(kr)\right], \end{aligned}$ where $\delta_l(k)$ is a phase shift determined by the scattering potential. For free particles, i.e., with U(r)=0 , B(l,k)=0 , and therefore $\delta_l=0$ . For a non-zero scattering potential we then get a non-zero $\delta_l$ . This allows writing $\begin{aligned} R_l(k,r) &\overset{r\rightarrow \infty}{=} \underbrace{\frac{A(l,k)}{\cos[\delta_l(k)]}}_{\equiv C(l,k)} \frac{1}{kr}\left[\sin\left(kr-\frac{l\pi}{2}\right)\cos \delta_l(k)+\cos\left(kr-\frac{l\pi}{2}\right)\sin \delta_l(k)\right]\\ &=C(l,k) \frac{1}{kr} \sin\left[kr-l\frac{\pi}{2} +\delta_l(k)\right]. \end{aligned}$

The whole wave function is hence of the form $\psi_{\mathbf k}(\mathbf r) = \sum_l R_l(r) Y_{l0}(r) \overset{r\rightarrow \infty}{=} \sum_{l=0}^\infty a_l C(l,k) \frac{\sin\left[kr-\frac{l\pi}{2}+\delta_l(k)\right]}{kr} Y_{l0}(\theta).$ The spherical harmonic functions are $Y_{l0}(\theta) = \sqrt{\frac{(2l+1)}{4\pi}} P_l(\cos \theta),$ where P_l(x) are Legendre polynomials. In other words, $\begin{aligned} \psi_{\mathbf k}(\mathbf r) \overset{r\rightarrow \infty}{=} \sum_{l=0}^\infty a(l,k) \frac{\sin[kr-l\pi/2+\delta_l(k)]}{kr} P_l(\cos \theta) \end{aligned}$ and $a(l,k)=a_l C(l,k) \sqrt{(2l+1)/4\pi}$ . Let us furthermore use $\sin(x)=(e^{ix}-e^{-ix})/(2i)$ to get $\begin{aligned} \psi_{\mathbf k}(\mathbf r) \overset{r\rightarrow \infty}{=} \sum_{l=0}^\infty a(l,k) \frac{1}{kr} \frac{1}{2i} \left[e^{ikr} \underbrace{e^{-il\pi/2}}_{(-i)^l} e^{i\delta_l(k)}-e^{-ikr} \underbrace{e^{il\pi/2}}_{i^l} e^{-i\delta_l(k)}\right]P_l(\cos \theta) \end{aligned}$ or

# asymptoticpsi

$\begin{aligned} \psi_{\mathbf k}(\mathbf r) \overset{r\rightarrow \infty}{=} & \frac{e^{ikr}}{r} \sum_{l=0}^\infty \left[\frac{a(l,k)}{2ik} (-i)^l e^{i\delta_l} P_l(\cos \theta)\right]\\ -& \frac{e^{-ikr}}{r} \sum_{l=0}^\infty \left[\frac{a(l,k)}{2ik} i^l e^{-i\delta_l} P_l(\cos \theta)\right]. \end{aligned}$ The asymptotic total wave function is hence a sum of outgoing and incoming spherical waves (first and second line).

Comparing to the asymptotic wave describing scattering, we see that the incoming plane wave term $e^{i\mathbf k \cdot \mathbf r}$ must contain a series of both outgoing and incoming spherical waves. This can be seen by the Legendre series of the plane wave (show this as an exercise): $\begin{aligned} e^{i\mathbf k \cdot \mathbf r} \underset{\mathbf k_i=k \hat e_z}{=}e^{ikr\cos \theta} =\sum_{l=0}^\infty (2l+1)i^lj_l(kr) P_l(\cos \theta) \end{aligned}$

Using the asymptotic form of j_l(x) at $x\rightarrow \infty$ again allows writing $\begin{aligned} e^{i\mathbf k \cdot \mathbf r} &\overset{kr \rightarrow \infty}{=} \sum_l (2l+1) i^l \frac{1}{kr} \sin(kr-l\pi/2)P_l(\cos \theta)\\ &=\frac{e^{ikr}}{r} \sum_{l=0}^\infty (2l+1)\frac{P_l(\cos \theta)}{2ik}-\frac{e^{-ikr}}{r} \sum_{l=0}^\infty i^{2l} (2l+1)\frac{P_l(\cos \theta)}{2ik}. \end{aligned}$ This allows writing the asymptotic scattering wave function as as $\begin{aligned} \psi_{\mathbf k}(\mathbf r) \overset{r \rightarrow \infty}{=} &\frac{e^{ikr}}{r} \left[\frac{1}{(2\pi)^{3/2}} f_k(\theta) + \frac{1}{(2\pi)^{3/2}} \sum_{l=0}^{\infty} \frac{2l+1}{2ik} P_l(\cos \theta)\right]\\ -& \frac{e^{-ikr}}{r} \frac{1}{(2\pi)^{3/2}} \sum_{l=0}^\infty \frac{(2l+1)i^{2l}}{2ik} P_l(\cos \theta) \end{aligned}$ This we can now compare to the general asymptotic solution of the Schrödinger equation. This comparison allows identifying the different coefficients for incoming and outgoing scattering waves.

Let us use the fact that the Legendre polynomials P_l(x) form an orthogonal basis. Their coefficients in the two expressions must therefore match. From the coefficients of the incoming waves ( $\sim e^{-ikr}/r$ ) we get $\boxed{a(l,k)=\frac{(2l+1)i^l}{(2\pi)^{3/2}} e^{i\delta_l(k)}}.$ On the other hand, the coefficients of the outgoing waves yield $\frac{1}{(2\pi)^{3/2}} f_k(\theta) + \frac{1}{(2\pi)^{3/2}} \sum_l \frac{2l+1}{2ik} P_l(\cos \theta) = \sum_l \frac{a(l,k)}{2ik} (-i)^l e^{i\delta_l} P_l(\cos \theta).$

# pwexpansionscatteringamplitude

Substituting a(l,k) from the boxed formula above and simplifying yields the partial wave expansion of the scattering amplitude $\begin{aligned} \boxed{f_k(\theta) = \frac{1}{k} \sum_{l=0}^\infty (2l+1) f_l(k) P_l(\cos \theta)} \end{aligned}$ with the partial wave amplitude $\begin{aligned} f_l(k) = e^{i\delta_l(k)} \sin \delta_l(k). \end{aligned}$

The differential cross section is then $\frac{\partial \sigma}{\partial \Omega} = |f_k(\Omega)|^2 =\frac{1}{k^2} \left\lvert\sum_{l=0}^\infty (2l+1)f_l(k) P_l(\cos \theta)\right\rvert^2$ Using the orthonormality relation for the Legendre polynomials, $\int_{-1}^{1} d \cos \theta P_l(\cos \theta) P_{l'}(\cos \theta) =\frac{2\delta_{ll'}}{2l+1},$

# pwexpcrosssection

we can express the total cross section in terms of the partial wave amplitudes or scattering phase shifts $\boxed{\sigma_{el}^{\rm tot} = \int d\Omega \frac{d\sigma}{d\Omega} = \sum_{l=0}^\infty \sigma_l = \frac{4\pi}{k^2} \sum_{l=0}^\infty (2l+1) |f_l(k)|^2 = \frac{4\pi}{k^2} \sum_{l=0}^\infty (2l+1)\sin^2 \delta_l(k).}$

In other words, we have expressed the scattering amplitude $f_k(\theta)$ and the cross section $\sigma$ in terms of partial waves, each of which carries a specific amount of angular momentum L^2(l) . The solutions of the radial Schrödinger equations are determined from the scattering potential V(r) , and thus it determines the scattering phase shifts $\delta_l(k)$ and the partial wave amplitude $f_l(k)=e^{i\delta_l(k)} \sin \delta_l(k)$ .

Such a partial wave expansion is a useful method for computing $f_k(\theta)$ and $\sigma$ when there are only a few relevant terms in the sum over . This is the case particularly when the energy (and thereby wave number ) of the incoming wave is small. Thinking classically: if the range of V(r) is , then $L_{\rm max} = pa = \hbar k a$ if $\epsilon \rightarrow 0$ i.e., $k\rightarrow 0$ . Then also $L_{\rm max} \rightarrow 0$ and the l=0 term is the most important.

Quantum mechanically, the potential showing up in the radial Schrödinger equation is 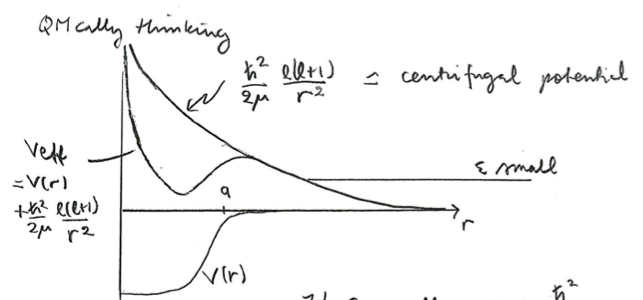Here shows the range of the potential. For small $\epsilon < \hbar^2/(\mu a)$ , the centrifugal barrier $\frac{\hbar^2}{2\mu} \frac{l(l+1)}{r}$ for $l\neq 0$ prevents the particle from entering the scattering region r<a . Therefore, scattering takes place only for l=0 .

Remember the nomenclature for the scattering to the different partial waves:

: "-wave" scattering
: "-wave" scattering
: "-wave" scattering $\dots$ and so on

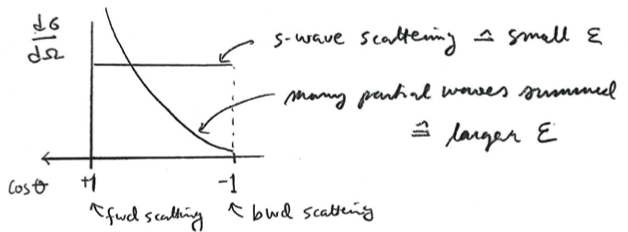
In the behaviour of $\frac{d\sigma}{d\cos \theta} = \underbrace{\int_0^{2\pi} \d\varphi}_{2\pi} \frac{d\sigma}{d\Omega} = 2 \pi \frac{d\sigma}{d\Omega},$ see the following qualitative difference between low-energy and high-energy scattering:

Small energy: -wave scattering only (). Thus $\frac{d \sigma}{d\Omega} = \frac{1}{k^2} \left\lvert (2\cdot 0+1) e^{i\delta_0(k)} \sin \delta_0(k) \underbrace{P_0(\cos \theta)}_{=1} \right\rvert^2 = \frac{sin^2 \delta_0(k)}{k^2}$ has no $\theta$ -dependence and is hence spherically symmetric.
Larger energy: more partial waves () involved. These now involve $P_l(\cos \theta)$ with . But $\begin{aligned} P_l(\cos \theta=1)&=1, \text{ for $\theta=0$, i.e., forward scattering}\\ P_l(\cos \theta=-1)&=(-1)^l, \text{ for $\theta=\pi$, i.e., backward scattering} \end{aligned}$ In other words, forward scattering is amplified with increasing energy. This also makes intuitively sense, right?

Optical theorem

Let us check the optical theorem from the partial wave expansion of the scattering amplitude. Taking its imaginary part and setting $\theta=0$ yields $\begin{aligned} {\rm Im} f_k(0) &= \frac{1}{k} \sum_{l=0}^\infty (2l+1) {\rm Im}\left[\underbrace{e^{i\delta_l(k)}}_{\cos \delta_l+i\sin \delta_l} \sin \delta_l(k)\right]\underbrace{P_l(1)}_{=1}\\ &=\frac{1}{k} \sum_{l=0}^\infty (2l+1) \sin^2 \delta_l(k). \end{aligned}$

Using the expression of the total cross section in terms of the partial waves we then get $\boxed{\sigma_{\rm el}^{\rm tot}(k) = \frac{4\pi}{k} {\rm Im} f_k(\theta=0)}$ similar to the result obtained above.

Example: hard sphere scattering

Consider a hard-sphere potential of the form $V(r) = \begin{cases} \infty, \quad r \le a\\ 0, \quad r>0. \end{cases}$ In the region r>a the solution of the radial Schrödinger equation is R_l(k,r)=A(l,k) j_l(kr) + B(l,k) n_l(kr) whereas in the region $r\le a$ it is R_l(k,r)=0 .

Requiring continuity at r=a we then get A(l,k) j_l(ka)+B(l,k) n_l(ka)=0 or $\frac{B(l,k)}{A(l,k)} = -\frac{j_l(ka)}{n_l(ka)} = -\tan \delta_l(k).$

The total cross section is hence $\begin{aligned} \sigma_{\rm el}^{\rm tot} &= \frac{4\pi}{k^2} \sum_{l=0}^\infty (2l+1) \underbrace{\sin^2 \delta_l(k)}_{\frac{\tan^2 \delta_l}{1+\tan^2 \delta_l}}\\ &=\frac{4\pi}{k^2} \sum_{l=0}^\infty (2l+1) \frac{j_l^2(ka)}{j_l^2(ka) + n_l^2(ka)}. \end{aligned}$

This is the general solution for the cross section and hence applies for any spherical harmonic and radius of the sphere. However, let us gain a bit more understanding to the result by considering the low-energy limit ( $k\rightarrow 0$ ). We need there small-argument expansions of the spherical harmonics, yielding $\begin{aligned} j_l(x) &= 2^l x^l \sum_{s=0}^\infty \frac{(-1)^s (s+l)! x^{2s}}{s! (2s+2l+1)!} \overset{x\rightarrow 0}{\rightarrow} \frac{2^l l!}{(2l+1)!} x^l\\ n_l(x) &= \frac{(-1)^{l+1}}{2^l x^{l+1}} \sum_{s=0}^\infty \frac{(-1)^s (s-l)!}{s!(2s-2l)!} x^{2s} \overset{x\rightarrow 0}{\rightarrow} \frac{-(2l)!}{2^l l!}x^{-(l+1)}. \end{aligned}$ Using these results for the expression in the total cross section then yields $\frac{j_l^2(ka)}{j_l^2(ka)+n_l^2(ka)} \approx \frac{j_l^2(ka)}{n_l^2(ka)} \approx \left(\frac{2^l l! 2^l l!}{(2l+1)!(2l)!} x^{l+l+1}\right)^2 = \frac{1}{(2l+1)^2} \left(\frac{2^l l!}{(2l)!}\right)^4 x^{4l+2}.$

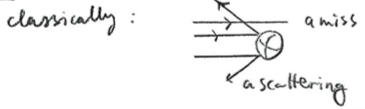
The total elastic cross section at low energies is hence $\sigma_{\rm el}^{\rm tot} \approx \frac{4\pi}{k^2} \sum_{l=0}^\infty \frac{1}{2l+1} \left(\frac{2^l l!}{(2l)!}\right)^4 \underbrace{(ka)^{4l+2}}_{\ll 1}.$ The largest term is l=0 , which yields $\boxed{\sigma_{\rm el}^{\rm tot} \overset{ka \ll 1}{=} 4\pi a^2.}$ In other words, the cross section is the total surface area of the sphere, not just the $\pi a^2$ "seen" by the beam coming from the left. The latter would be the "billiard ball" hard sphere scattering cross section for classical particles. In other words, the quantum mechanical particle waves "feel" their way around the whole hard sphere, whereas classical particles only would see the head-on cross section: