FY5 Pyöriminen ja gravitaatio
Tämän verkkomonisteen tarkoituksena on toimia lukion FY5-kurssin opetussuunnitelman mukaisena kattavana ja riittävänä opiskelumateriaalina.
Materiaali ei kuitenkaan ole kurssin keskeisin asia. Uuden oppiminen ja vanhojen tietojen vahvistaminen sen sijaan ovat. Siksi toivon ja pyydän, että jokainen kurssin opiskelija osallistuu kykyjensä mukaan materiaalin sisällön tekemiseen esim. tekstin, kuvien, kysymysten ja interaktiivisen sisällön muodossa. Myös virheet ja puutteet saa ja pitää korjata. Myös rakentavat kommentit vievät yhteistä oppimisasiaa eteenpäin.
Yksi tekijöistä
Henri Jaakkola
Minkä vuoden Ops?
2003 OPS
—1 Vaakasuora heittoliike
Kirjoitetaan tasaisen liikkeen mallit.
\[ v = \text{vakio} \qquad \text{ja} \qquad x = vt \]
Kirjoitetaan tasaisesti kiihtyvän liikkeen mallit.
\[ a = \text{vakio} \qquad \text{ja} \qquad v = v_0 + at \qquad \text{ja} \qquad x = v_0 t + \frac{1}{2}at^2 \]
Maan pinnan lähellä painovoiman vaikutuksesta tapahtuva liike on heittoliikettä, jossa vaaka- eli \(x\)-suuntainen ja pysty- eli \(y\)-suuntainen liike voidaan tarkastella erikseen toisistaan riippumattomina yksiulotteisina liikkeinä. Heittoliikkeen aiheuttajalla ei ole merkitystä.

Vaakasuoran heittoliikkeen vaakasuunnassa voidaan käyttää tasaisen liikkeen mallia, jos kappale on pistemäinen tai jos ilmanvastusta ei ole. Mallissa kappaleeseen ei siis vaikuta voimia vaakasuunnassa. Tällöin kappaleen liike on tasaista, ja sen kiihtyvyys \(a_x = 0\).
\[ \quad v_x = v_{0x} = \text{vakio} \qquad \text{ja} \qquad x(t) = v_{0x}t \]
Edellä \(x\)-akselin positiivinen suunta on vaakasuunnassa oikealle.
Vastaavasti vaakasuoran heittoliikkeen pystysuunnassa voidaan käyttää tasaisesti kiihtyvän liikkeen mallia, jos kappale on pistemäinen tai jos ilmanvastusta ei ole. Mallissa kappaleeseen vaikuttaa pystysuunnassa vain painovoima \(\overline{G}\), jonka suuruus voidaan ajatella vakioksi pienillä korkeuseroilla. Tällöin kappaleen liike on tasaisesti kiihtyvää, ja sen kiihtyvyys on putoamiskiihtyvyys \(\overline{g}\).
\[ v_{0y} = 0\,\frac{\text{m}}{\text{s}} \quad \text{joten} \quad v_y (t) = a_y t = -gt \quad \text{ja} \quad y(t) = \frac{1}{2}a_y t^2 = -\frac{1}{2}gt^2 \quad \text{pos. suunta ylös} \]
Edellä \(y\)-akselin positiivinen suunta on ylöspäin. Jos positiivinen suunta on alaspäin, on \(a_y = g\). Tällöin edellisten lausekkeiden etumerkit muuttuvat.
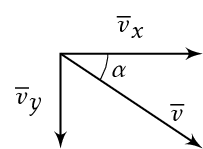
Kappaleen nopeus ajan \(t\) kuluttua on vaakasuoran ja pystysuoran nopeuden vektorisumma. Kirjoitetaan nopeuden suuruus ja suunta.
\[ v = \sqrt{v^2_x + v^2_y} \qquad \text{ja} \qquad \tan \alpha = \frac{v_y}{v_x} \]
ESIM. 1.
Lentokoneen vaakanopeus oikealle on 205 m/s. Koneesta pudotettu pieni punnus osuu maahan 11,2 sekunnissa. Ilmanvastusta ei tarvitse huomioida.
Laske punnuksen
a) pudotuskorkeus,
b) punnuksen vaakasuora lentomatka,
c) punnuksen nopeus ja sen suunta, kun se osuu maahan.
RATK.
\(v_0 = 205\,\frac{\text{m}}{\text{s}}, \quad t = 11,2\,\text{s}, \quad g = 9,81\,\frac{\text{m}}{\text{s}} \quad y = ?, \quad x = ? \quad \text{ja} \quad v = ?\)
Positiiviset suunnat ovat oikealle ja ylöspäin.
a) Lasketaan pudotuskorkeus.
Nollahetki on punnuksen irtoamishetki, ja origo on punnuksen irtoamiskohta.
Koneen lentosuunta on \(x\)-akseli, ja \(y\)-suunta on ylöspäin.
Koska ilmanvastusta ei ole, tarkastellaan putoamisliikettä pystysuunnassa tasaisesti kiihtyvänä liikkeenä.
\[a_y = -g = -9,81\,\frac{\text{m}}{\text{s}^2}\]
Punnuksen alkukorkeus lasketaan putoamisajan \(t\) avulla.
\[ y = -\frac{1}{2}gt^2 = -\frac{1}{2} \cdot 9,81\,\frac{\text{m}}{\text{s}^2} \cdot (11,2\,\text{s})^2 = -615,2832\,\text{m} \approx -620\,\text{m} \]
Tulos on maanpinnan \(y\)-koordinaatti, jonka itseisarvo on punnuksen alkukorkeus.
b) Lasketaan vaakasuora lentomatka.
Koska ilmanvastusta ei ole, tarkastellaan vaakasuoraa liikettä tasaisena liikkeenä. Lasketaan punnuksen vaakalentomatka.
\[ x = v_{0x}t = 205\,\frac{\text{m}}{\text{s}} \cdot 11,2\,\text{s} = 2296\,\text{m} \approx 2300\,\text{m} \]
c) Lasketaan punnuksen loppunopeus ja sen suunta.
Punnuksen vaakanopeus on \(v_x = v_{0x} = 205\,\frac{\text{m}}{\text{s}}\). Lasketaan pystysuuntainen \(y\)-nopeus lopussa.
\[ v_y = -gt = -9,81\,\frac{\text{m}}{\text{s}^2} \cdot 11,2\,\text{s} = -109,872\,\frac{\text{m}}{\text{s}} \]
Lasketaan loppunopeus Pythagoraan lauseella.
\[ v = \sqrt{v^2_x + v^2_y} = \sqrt{\left(205\,\frac{\text{m}}{\text{s}}\right)^2 + \left(-109,872\,\frac{\text{m}}{\text{s}}\right)^2} = 232,5873\,\frac{\text{m}}{\text{s}} \approx 233\,\frac{\text{m}}{\text{s}} \]
Lasketaan nopeusvektorille suunta vaakatasoon nähden.
\[ \tan \alpha = \frac{v_y}{v_x} = \frac{-109,872\,\frac{\text{m}}{\text{s}}}{205\,\frac{\text{m}}{\text{s}}} \qquad \Rightarrow \qquad\alpha = -28,1896^\circ \approx -28^\circ \]
VAST.
Punnuksen pudotuskorkeus on 620 m, vaakalentomatka on 2300 m ja nopeus on 233 m/s.
Vaakasuorassa heittoliikkeessä, kun ilmanvastusta ei ole, kappaleen
2 Vino heittoliike
Kuten vaakasuorassa heittoliikkeessä, myös vinossa heittoliikkeessä nopeus jaetaan komponentteihin, jotka ovat toisistaan riippumattomia. Liike on vaakasuunnassa tasaista liikettä ja pystysuunnassa tasaisesti kiihtyvää liikettä, jos kappale on pistemäinen tai jos ilmanvastusta ei ole.
Positiivinen suunta on vaakasuunnassa oikealle ja pystysuunnassa ylöspäin.
\[ v_x = v_{0x} = \text{vakio} \qquad \text{ja} \qquad v_y = v_{0y} - gt \]
Tutkitaan tilannetta, jossa kappaleen vinon heittoliikkeen alussa alkunopeus on \(\overline{v}_0\) ja kulma vaakatasosta ylöspäin on \(\alpha_0\). Positiivinen suunta on vaakasuunnassa oikealle ja pystysuunnassa ylöspäin. Kirjoitetaan alkunopeuden komponentit.
\[ v_{0x} = v_0 \cos \alpha_0 \qquad \text{ja} \qquad v_{0y} = v_0 \sin \alpha_0 \]
Vaakasuunnassa liike on tasaista. Pystysuunnassa liike on tasaisesti kiihtyvää kiihtyvyydellä \(a_y = -g\). Kirjoitetaan nopeudet ajan \(t\) kuluttua.
\[ v_x = v_{0x} = v_0 \cos \alpha_0 \qquad \text{ja} \qquad v_y = v_{0y} - gt = v_0 \sin \alpha_0 - gt \]
Kappaleen nopeus ajan \(t\) kuluttua on vaakasuoran ja pystysuoran nopeuden vektorisumma. Kirjoitetaan nopeuden suuruus ja suunta.
\[ v = \sqrt{v^2_x + v^2_y} \qquad \text{ja} \qquad \tan \alpha = \frac{v_y}{v_x} \]

Vaakasuunnasta ylöspäin liikkeelle saatetun kappaleen nousu- eli lakikorkeus \(h\) ratkaistaan nousuajan \(t_\text{n}\)avulla. Kun kappale on lakikorkeudessaan, on sen nopeus \(v_y = 0\).
\[ v_{0y} - gt_\text{n} = 0 \qquad \text{eli} \qquad t_\text{n} = \frac{v_{0y}}{g} = \frac{v_0 \sin \alpha_0}{g} \]
Kirjoitetaan kappaleen lakikorkeus.
\[ h = v_{0y}t_\text{n} - \frac{1}{2}gt^2_\text{n} \]
Jos kappaleen lähtökorkeus on sama kuin on sen maahanosumiskorkeus, on lentoaika \(t\) kaksinkertaa nousuaika \(t_\text{n}\). Kirjoitetaan kantama \(x\).
\[ x = v_{0x}t = v_0 \cos \alpha_0 t \]
ESIM. 2.
Pallo potkaistaan maanpinnasta 39,0 asteen kulmassa. Pallon alkunopeus on 14,1 m/s. Lopuksi pallo osuu maahan, eikä ilmanvastusta tarvitse huomioida.
Laske pallon lentoaika, pallon lakikorkeus ja pallon kantama.
RATK.
\(v_0 = 14,1\,\frac{\text{m}}{\text{s}}, \quad \alpha = 39,0^\circ, \quad t = ?, \quad h = ? \quad \text{ja} \quad x = ?\)
Lasketaan pallon lentoaika \(t\).
Valitaan nollahetkeksi pallon potkaisuhetki ja origoksi pallon potkaisuskohta. Valitaan \(x\)-akselin suunnaksi vaakasuunta eteenpäin ja \(y\)-akselin suunnaksi ylöspäin.
Kirjoitetaan alkunopeuden komponentit.
\[ v_{0x} = v_0 \cos \alpha_0 \quad \text{ja} \quad v_{0y} = v_0 \sin \alpha_0 \]
Käytetään tasaisen liikkeen mallia pallon liikkeelle vaakasuunnassa. Pystysuunnassa pallon liikettä muuttaa putoamiskiihtyvyys \(a_y = -g\).
Kirjoitetaan pallon nopeus ajan \(t\) kuluttua.
\[ v_x = v_{0x} = v_0 \cos \alpha_0 \quad \text{ja} \quad v_y = v_{0y} - gt = v_0 \sin \alpha_0 - gt \]
Kun pallo on lakipisteessä, on \(v_y = 0\,\frac{\text{m}}{\text{s}}\). Kirjoitetaan nousuajan \(t_\text{n}\) yhtälö.
\[ 0 = v_{0y} - gt_\text{n} \quad \text{eli} \quad t_\text{n} = \frac{v_{0y}}{g} = \frac{v_0 \sin \alpha_0}{g} \]
Lasketaan lentoaika \(t\), joka on kaksi kertaa nousuaika \(t_\text{n}\).
\[ t = 2t_\text{n} = \frac{2v_0 \sin \alpha_0}{g} = \frac{2 \cdot 14,1\,\frac{\text{m}}{\text{s}} \cdot \sin 39,0^\circ}{9,81\,\frac{\text{m}}{\text{s}^2}} = 1,8091\,\text{s} \approx 1,8\,\text{s} \]
Lakipisteen korkeus \(h\) saadaan tasaisesti kiihtyvän liikkeen mallin paikan yhtälöstä.
\[ h = y = v_{0y}t_\text{n} - \frac{1}{2}gt^2_\text{n} = v_0 \sin \alpha_0 t_\text{n} - \frac{1}{2}gt^2_\text{n} \]
Lasketaan lakipisteen korkeus \(h\), kun nousuaika \(t_\text{n}\) on puolet lentoajasta \(t\).
\[ h = 14,1\,\frac{\text{m}}{\text{s}} \cdot \sin 39,0^\circ \cdot 0,9045\,\text{s} - \frac{1}{2} \cdot 9,81\,\frac{\text{m}}{\text{s}^2} \cdot (0,9045\,\text{s})^2 = 4,0131\,\text{m} \approx 4,0\,\text{m} \]
Lasketaan pallon kantama \(x\) tasaisen liikkeen mallin avulla.
\[ x = v_{0x}t = v_0 \cos \alpha_0 \cdot t = 14,1\,\frac{\text{m}}{\text{s}} \cdot \cos 39,0^\circ \cdot 1,8091\,\text{s} = 19,8237\,\text{m} \approx 19,8\,\text{m} \]
VAST.
Pallon lentoaika on 1,8 s, pallon lakikorkeus on 4,0 m ja sen kantama on 19,8 m.
Vinossa heittoliikkeessä, kun ilmanvastusta ei ole, kappaleen
3 Ympyräliike tapahtuu tasossa
Liikkeessä nopeuden suuruus ja suunta voivat vaihdella. Kirjoitetaan nopeuden muutos.
\[ \Delta \overline{v} = \overline{v}_\text{l} - \overline{v}_\text{a} \]
Suoraviivaisessa liikkeessä nopeuden etumerkin muutos kertoo liikkeen suunnan muutoksesta.
Tasoliikkeessä keskikiihtyvyys on vektori.
\[ \overline{a}_\text{k} = \frac{\Delta \overline{v}}{\Delta t} = \frac{\overline{v}_2 - \overline{v}_1}{t_2 - t_1}. \]
Keskikiihtyvyyden suunta on nopeuden muutosvektorin suunta. Kirjoitetaan nopeuden muutos.
\[ \Delta \overline{v} = \overline{v}_2 - \overline{v}_1 = \overline{v}_2 + (-\overline{v}_1) \]
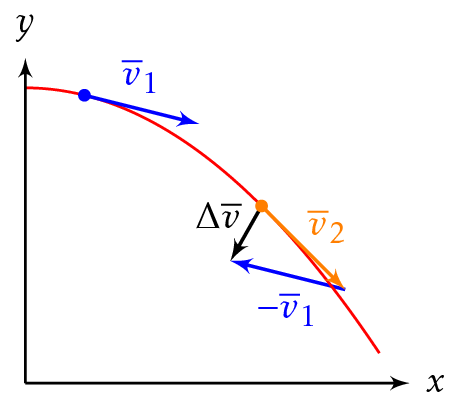
Nopeus on vektorisuure, jolla on suuruus ja suunta. Kappaleen liike on siksi kiihtyvää silloinkin, kun sen vauhti ei muutu, mutta nopeuden suunta muuttuu.
Ympyräliikkeessä kappaleen rata on ympyrä. Ympyräliike on kiihtyvää liikettä, koska kappale on kiihtyvässä liikkeessä aina silloin, kun sen nopeus muuttuu. Ympyräradalla liikkuva kappale on kiihtyvässä liikkeessä.
Heittoliike ja ympyräliike ovat tasoliikkeitä. Heittoliikettä voidaan tutkia erikseen vaaka- ja pystysuuntaisina suoraviivaisina liikkeinä. Ympyräradalla liikkuvan kappaleen kiihtyvyyden suunta muuttuu jatkuvasti.
Heittoliikkeessä kappaleen paikka kuvataan paikkakoordinaattien \(x\) ja \(y\) avulla. Ympyräliikkeessä kappaleen liike kuvataan kaarenpituuden \(s\) avulla. Kappaleen paikan muutosnopeus ympyräradalla on ratanopeus \(\overline{v}\).
Kappaleen kiihtyvyys ympyräliikkeessä on kohti ympyräradan keskipistettä. Kiihtyvyyttä tutkitaan normaalikiihtyvyyden \(\overline{a}_\text{n}\) eli rataa vastaan kohtisuoran komponentin ja tangenttikiihtyvyyden \(\overline{a}_\text{t}\) eli radan tangentin suuntaisen komponentin avulla.
Normaalikiihtyvyys on kohti ympyräradan keskipistettä ja kuvaa radan kaareutumisen eli nopeuden suunnan muutosnopeutta. Tangenttikiihtyvyys muuttaa kappaleen ratanopeutta.
Tasaisessa ympyräliikkeessä kappaleen tangenttikiihtyvyys on nolla. Ratanopeus on vakio, mutta nopeuden suunta muuttuu.
Koska tasaisessa ympyräliikkeessä kappaleen ratanopeus ei muutu, on kappaleen kiihtyvyys normaalikiihtyvyyttä \(a_\text{n}\). Kirjoitetaan yhtälö, kun ympyräradan säde on \(r\) ja kappaleen ratanopeus on \(v\).
\[ a_\text{n} = \frac{v^2}{r} \]
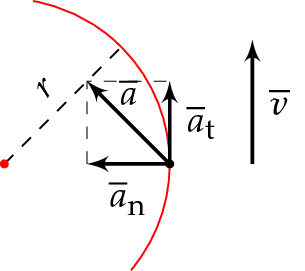
Kappaleen nopeuden suunta muuttuu ympyräradalla, joten se on kiihtyvässä liikkeessä. Kiihtyvyyden aiheuttaa Newtonin II lain mukaan kappaleeseen vaikuttava voima.
Tutkitaan vakiovauhdilla liikkuvan kappaleen liikettä ympyräradalla, kun on vain normaalikiihtyvyyttä. Ympyräradan kaarevuussäde on \(r\). Kappaleeseen vaikuttavat paino \(\overline{G}\), tukivoima \(\overline{N}\), vastusvoima \(\overline{F}_\text{v}\) ja lepokitka \(\overline{F}_\mu\), jonka komponentit ovat \(\overline{F}_{\mu\text{n}}\) ja \(\overline{F}_{\mu\text{t}}\).
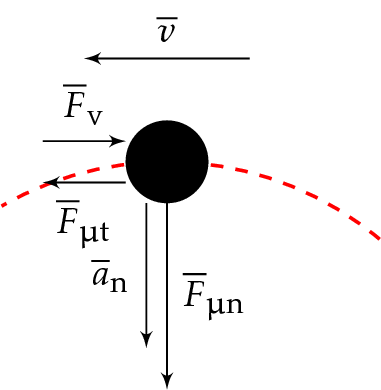
Kirjoitetaan dynamiikan peruslain mukainen yhtälö.
\[ \Sigma \overline{F} = m\overline{a} \qquad \text{ja} \qquad \overline{G} + \overline{N} + \overline{F}_\text{v} + \overline{F}_{\mu\text{n}} + \overline{F}_{\mu\text{t}} = m\overline{a} \]
Kappaleella ei ole kiihtyvyyttä pystysuunnassa. Paino \(\overline{G}\) ja tukivoima \(\overline{N}\) ovat yhtä suuria mutta vastakkaissuuntaisia.
\[ \overline{G} + \overline{N} = \overline{0} \]
Kappale liikkuu vakiovauhdilla. Voimat \(\overline{F}_{\mu\text{t}}\) ja \(\overline{F}_\text{v}\) ovat yhtä suuria mutta vastakkaissuuntaisia.
\[ \overline{F}_{\mu\text{t}} + \overline{F}_\text{v} = \overline{0} \]
Kappaleella ei ole kiihtyvyyttä nopeuden suuntaan. Kirjoitetaan kappaleeseen vaikuttava kokonaisvoima.
\[ \Sigma \overline{F} = \overline{G} + \overline{N} + \overline{F}_\text{v} + \overline{F}_{\mu\text{n}} + \overline{F}_{\mu\text{t}} = \overline{F}_{\mu\text{n}} \]
Ympyräliike johtuu kohtisuorassa liikesuuntaa vastaan ja radan keskipisteeseen päin olevasta lepokitkan komponentista \(\overline{F}_{\mu\text{n}}\).
Kappaleen kiihtyvyys on yhtä suuri kuin normaalikiihtyvyys.
\[ a_\text{n} = \frac{v^2}{r} \]
Dynamiikan peruslain mukainen liikeyhtälö \(\Sigma \overline{F} = m\overline{a}\) yksinkertaistuu.
\[ F_{\mu\text{n}} = ma = m\frac{v^2}{r} \]
Kirjoitetaan tasaisessa ympyräliikkeessä olevan kappaleen liikeyhtälö.
\[ \Sigma F = m\overline{a}_\text{n} \]
ESIM. 3.
Auto ajaa vakionopeudella (100 km/h) mutkassa, joka on vaakatasossa olevan ympyrän kaaren muotoinen ja jonka säde on 150 m.
a) Laske auton normaalikiihtyvyys.
b) Piirrä tilanteesta kuva.
RATK.
\(v_0 = 100\,\frac{\text{km}}{\text{h}}, \quad r = 150\,\text{m}, \quad a_\text{n} = ?\)
a) Lasketaan normaalikiihtyvyys.
\[ a_\text{n} = \frac{v^2}{r} = \frac{\left(\frac{100\,\text{m}}{3,6\,\text{s}}\right)^2}{150\,\text{m}} = 5,144033\,\frac{\text{m}}{\text{s}^2} \approx 5,1\,\frac{\text{m}}{\text{s}^2} \]
b) Piirretään tilannekuva. Nopeus on ympyrän tangentin suuntainen, ja kiihtyvyys on radan keskipistettä kohti.
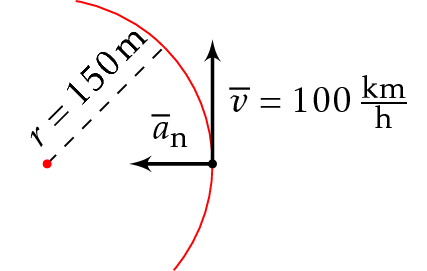
VAST.
a) Auton normaalikiihtyvyys on 5,1 m/s\(^2\).
ESIM. 4.
Auton massa on 1350 kg, ja sen vakiovauhti vaakasuoralla ympyräradalla on 90,0 km/h. Radan kaarevuussäde on 112 m. Laske tarvittava sivuttaissuuntainen kitkavoima.
RATK.
\(v = 90,0\,\frac{\text{km}}{\text{h}} = 25\,\frac{\text{m}}{\text{s}}, \quad m = 1350\,\text{kg}, \quad r = 112\,\text{m}, \quad F_{\mu\text{n}} = ?\)
Kirjoitetaan dynamiikan peruslain mukainen yhtälö, kun autoon vaikuttavat paino \(\overline{G}\), tukivoima \(\overline{N}\), vastusvoima \(\overline{F}_\text{v}\) ja lepokitka \(\overline{F}_\mu\), jonka komponentit ovat \(\overline{F}_{\mu\text{n}}\) ja \(\overline{F}_{\mu\text{t}}\).
\[ \Sigma \overline{F} = m\overline{a} \qquad \text{eli} \qquad \overline{G} + \overline{N} + \overline{F}_\text{v} + \overline{F}_{\mu\text{n}} + \overline{F}_{\mu\text{t}} = m\overline{a} \]
Autolla ei ole kiihtyvyyttä pystysuunnassa, ja sen vauhti on vakio.
\[ \overline{G} + \overline{N} = \overline{0} \qquad \text{ja} \qquad \overline{F}_\text{v} + \overline{F}_{\mu\text{t}} = \overline{0} \]
Ympyräliikkeen aiheuttaa siis lepokitkan komponentti \(\overline{F}_{\mu\text{n}}\).
\[ \Sigma \overline{F} = \overline{F}_{\mu\text{n}} \]
Lasketaan kitkavoima.
\[ F_{\mu\text{n}} = ma_\text{n} = m\frac{v^2}{r} = 1350\,\text{kg} \cdot \frac{(25,0\,\frac{\text{m}}{\text{s}})^2}{112\,\text{m}} = 7533,4821\,\text{N} \approx 7500\,\text{N} \]
VAST.
Tarvittavan lepokitkan suuruus on 7500 N.
Kun kappale etenee tasaista vauhtia ympyräradalla,
4 Muuttuvassa ympyräliikkeessä ratanopeus muuttuu
Muuttuvassa ympyräliikkeessä kappaleen nopeuden suuruus ja suunta muuttuvat.
Normaalikiihtyvyyden yhtälö pitää paikkansa tasaisen ympyräliikkeen lisäksi myös muuttuvassa ympyräliikkeessä siten, että nopeus on aina kulloinkin oleva hetkellinen ratanopeus.
\[ a_\text{n} = \frac{v^2}{r} \]
Muuttuvassa ympyräliikkeessä kappaleella on normaalikiihtyvyyden lisäksi myös tangenttikiihtyvyyttä \(\overline{a}_\text{t}\) eli ratakiihtyvyyttä. Se kertoo ratanopeuden muutoksen aikayksikössä.
\[ a_\text{t} = \frac{\Delta v}{\Delta t} \]
Liikkuvan kappaleen kiihtyvyys \(\overline{a}\) ympyräradalla on normaalikiihtyvyyden \(\overline{a}_\text{n}\) ja tangenttikiihtyvyyden \(\overline{a}_\text{t}\) komponenttien vektorisumma.
\[ \overline{a} = \overline{a}_\text{n} + \overline{a}_\text{t} \]
Kiihtyvyyden suuruus lasketaan Pythagoraan lauseen avulla.
\[ a = \sqrt{a^2_\text{n} + a^2_\text{t}} \]
Kiihtyvyyden suunta saadaan trigonometrian avulla, kun kulma \(\beta\) on ympyrän säteen ja kiihtyvyysvektorin välissä.
\[ \tan \beta = \frac{a_\text{t}}{a_\text{n}} \]
Kappaleen liikkeen suunta muuttuu, jos kokonaisvoimalla on normaalikomponentti \(\overline{F}_\text{n}\), joka on kohtisuorassa liikettä vastaan. Kappaleen ratanopeus muuttuu, jos kokonaisvoimalla on radan tangentin suuntainen tangenttikomponentti \(\overline{F}_\text{t}\).
Komponentit aiheuttavat normaalikiihtyvyyden \(\overline{a}_\text{n}\) ja ratakiihtyvyyden \(\overline{a}_\text{t}\).
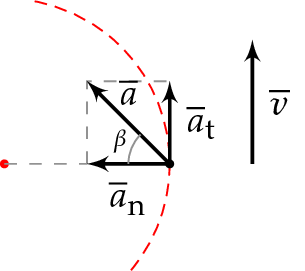
Muuttuvassa ympyräliikkeessä kappaleen kiihtyvyyden aiheuttaa siihen vaikuttava kokonaisvoima. Kiihtyvyyden suunta on aina kokonaisvoiman suunta.
\[ \Sigma \overline{F} = \overline{F}_\text{n} + \overline{F}_\text{t}. \]
Matemaattisessa eli ideaalisessa heilurissa on massaton ja venymätön lanka, josta riippuva punnus on pistemäinen. Heilurin liike on ympyräliikettä.

Punnukseen vaikuttavat paino \(\overline{G}\) ja langan jännitysvoima \(\overline{T}\). Kirjoitetaan punnuksen liikeyhtälö.
\[ \overline{T} + \overline{G} = m\overline{a} \]
Jaetaan liikeyhtälö ympyräradan normaalin ja tangentin suuntaisiin komponentteihin.
\[ T - G_\text{n} = ma_\text{n} \qquad \text{ja} \qquad G_\text{t} = ma_\text{t} \]
Langan ja pystysuunnan välinen kulma on \(\theta\).
\[ T - mg \cos \theta = ma_\text{n} \qquad \text{ja} \qquad mg \sin \theta = ma_\text{t} \]
Normaalikiihyvyys aiheutuu jännitysvoiman \(\overline{T}\) ja painon normaalikomponentin \(\overline{G}_\text{n}\) vektorisummasta. Tangenttikiihtyvyys aiheutuu ympyräradan tangentin suuntaisesta painon komponentista \(G_\text{t}\).
Kirjoitetaan kiihtyvyys tangentin suunnassa.
\[ mg \sin \theta = ma_\text{t} \qquad \text{eli} \qquad a_\text{t} = g \sin \theta \]
Ympyräradan alimmassa pisteessä paino \(\overline{G}\) ja tukivoima \(\overline{T}\) ovat yhdensuuntaisia ja kohtisuorassa nopeutta vastaan, jolloin tangenttikiihtyvyys on nolla.
\[ G_\text{t} = mg \sin \theta = 0 \qquad \text{ja} \qquad a_\text{t} = g \sin \theta = 0 \qquad \text{kun} \qquad \theta = 0^\circ \]
Vastaavasti tangenttikiihtyvyys saa suurimman arvonsa heilahtelun ääripisteessä, jossa punnus pysähtyy hetkellisesti ja vaihtaa suuntaansa.
Normaalikiihtyvyys on nolla heilahtelun ääripisteessä. Heilurin alimmassa asennossa punnuksella on suurin nopeus, jollon myös normaalikiihtyvyys saa suurimman arvonsa.
\[ a_\text{n} = \frac{v^2}{r} \]
Kiihtyvyys ei ole missään kohdassa nolla. Punnukseen vaikuttava kokonaisvoima ei ole missään kohdassa nolla.
ESIM. 5.
Pieni punnus on kiinnitetty ohuen langan päähän. Punnusta pyöritetään ympyräradalla, jonka säde on 94 cm. Punnuksen ratanopeus on 2,9 m/s ja tangenttikiihtyvyys on 0,12 m/s\(^2\). Laske punnuksen
a) normaalikiihtyvyys,
b) ja kokonaiskiihtyvyys.
RATK.
\(r = 0,94\,\text{m}, \quad v = 2,9\,\frac{\text{m}}{\text{s}}, \quad a_\text{t} = 0,12\,\frac{\text{m}}{\text{s}^2}, \quad a_\text{n} = ? \quad a = ?\)
a) Lasketaan normaalikiihtyvyys.
\[ a_\text{n} = \frac{v^2}{r} = \frac{(2,9\,\frac{\text{m}}{\text{s}})^2}{0,94\,\text{m}} = 8,9468\,\frac{\text{m}}{\text{s}^2} \approx 8,9\,\frac{\text{m}}{\text{s}^2}\]
b) Lasketaan kokonaiskiihtyvyys.
\[ a = \sqrt{a^2_\text{n} + a^2_\text{t}} = \sqrt{\left(8,9468\,\frac{\text{m}}{\text{s}^2}\right)^2 + \left(0,12\,\frac{\text{m}}{\text{s}^2}\right)^2} = 8,9476\,\frac{\text{m}}{\text{s}^2} \approx 8,9\,\frac{\text{m}}{\text{s}^2} \]
Lasketaan kiihtyvyyden suunta ympyräradan säteen ja kiihtyvyysvektorin välisen kulman tangentin avulla.
\[ \beta = \arctan{\left(\frac{0,12\,\frac{\text{m}}{\text{s}^2}}{8,9468\,\frac{\text{m}}{\text{s}^2}}\right)} = 0,7684^\circ \approx 0,77^\circ \]
VAST.
a) Normaalikiihtyvyys on 8,9 m/s\(^2\).
b) Kokonaiskiihtyvyys on 8,9 m/s\(^2\), ja radan säteen ja kiihtyvyysvektorin välinen kulma on 0,77\(^\circ\).
ESIM. 6.
Heilurin langan pituus on 2,0 m. Pistemäisen punnuksen massa on 35 grammaa. Heiluri päästetään levosta irti, kun sen langan ja pystysuunnan välinen kulma on 90\(^\circ\). Laske langan jännitysvoima, kun punnus on heilahduksen alimmassa paikassa. Ilmanvastusta ei ole.
RATK.
\(r = 2,0\,\text{m}, \quad m = 0,035\,\text{kg}, \quad g = 9,81\,\frac{\text{m}}{\text{s}^2}, \quad T = ?\)
Kirjoitetaan dynamiikan liikeyhtälö heilahduksen alimmassa paikassa.
\[ \Sigma \overline{F} = m\overline{a} \qquad \text{eli} \qquad \overline{T} + \overline{G} = m\overline{a} \]
Radan alimmassa paikassa punnukseen vaikuttaa vain radan säteen suuntaisia voimia, joten kiihtyvyys on normaalikiihtyvyyttä. Positiivinen suunta on ylöspäin.
\[ T - G = ma_\text{n} \qquad \text{eli} \qquad T = G + ma_\text{n} = m\left(g + \frac{v^2}{r}\right) \]
Koska ilmanvastusta ei ole, käytetään mekaanisen energian säilymislakia.
\[ E_\text{pa} + E_\text{ka} = E_\text{pl} + E_\text{kl} \]
Ratkaistaan nopeus, kun potentiaalienergian nollakohta on alin kohta ja alussa punnus on paikallaan.
\[ mgh = \frac{1}{2}mv^2 \qquad \text{eli} \qquad v = \sqrt{2gh} \]
Lasketaan jännitysvoima.
\[ T = m\left(g + \frac{2gh}{r}\right) = 0,035\;\text{kg} \cdot \left(9,81\;\frac{\text{m}}{\text{s}^2} + \frac{2 \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 2,0\;\text{m}}{2,0\;\text{m}}\right) = 1,0301\;\text{N} \approx 1,0\;\text{N} \]
VAST.
Narun jännitysvoima on 1,0 N.
Kun matemaattisen heilurin punnus
5 Gravitaatiovuorovaikutus välittyy gravitaatiokentän avulla
Gravitaatiovuorovaikutus vaikuttaa kahden kappaleen välillä. Se aiheuttaa niihin yhtä suuret mutta vastakkaissuuntaiset gravitaatiovoimat.
\[ F = \gamma\,\frac{m_1 m_2}{r^2} \]
Yhtälön termi \(\gamma\) on gravitaatiovakio, \(m_1\) ja \(m_2\) ovat kappaleiden massat ja \(r\) on kappaleiden keskipisteiden välinen etäisyys.
\[ \gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \]
Gravitaatiovuorovaikutuksen välittyminen kuvataan gravitaatiokentän avulla. Kentän voimakkuus on suoraan verrannollinen kappaleen massaan ja kääntäen verrannollinen etäisyyden neliöön.
Gravitaatiovoima vaikuttaa kaikkiin kappaleisiin
Gravitaatiovoima vaikuttaa kaikkiin kappaleisiin ja kaikkien kappaleiden välillä. Newtonin laeilla voidaan ennustaa kappaleiden liikkeet, kun kappaleiden massat, kappaleiden väliset vuorovaikutukset ja liikkeen alkutila on tiedossa. Gravitaatiovoiman kantama on ääretön, mutta voima heikkenee kääntäen verrannollisesti etäisyyden neliöön.
Yleisen vetovoimalain eli gravitaatiolain mukaan kappaleet vetävät toisiaan puoleensa voimalla, jonka suuruus riippuu kummankin kappaleen massasta ja niiden välisestä etäisyydestä.
Gravitaatiovoima välittyy avaruudessa
Gravitaatio on luonnonilmiö, joka saa kaikki massalliset kappaleet vetämään toisiaan puoleensa. Esimerkiksi Maan, Kuun ja Auringon muodostama systeemi kiertää yhteistä massakeskipistettä.
Gravitaatiovuorovaikutus selitetään kentän avulla
Gravitaatiovuorovaikutus selitetään kentän avulla. Kenttää havainnollistetaan kenttäviivoilla.
Cavendishin gravitaatiovaaka
Massallinen kappale voi synnyttää vetovoiman ja olla sen kohteena.
Maa ja Aurinko kiertävät yhteistä massakeskipistettä, minkä voimme helposti havaita. Pienen vetovoiman havaitseminen on sen sijaan vaikeaa. Emme esim. huomaa ihmisen ja pöydällä olevan pienen kappaleen välistä vetovoimaa.
Vetovoima on heikoin neljästä perusvuorovaikutuksesta. Näin ollen tarvitsemme erityisen laitteen demonstroimaan tätä heikko vuorovaikutusta.
Cavendishin gravitaatiovaa'assa on ohut narun varassa roikkuva tanko, jonka päissä on pienet punnukset. Samassa tasossa olevat suuret punnukset vetävät pieniä punnuksia puoleensa, jolloin naru kiertyy. Tämä mitataan valon säteellä peilin kautta. Punnusten välinen vetovoima voidaan laskea, kun langan kiertymä tiedetään.
ESIM. 7.
Riston massa on 80 kg ja Maijan massa on 71 kg. Heidän välinen etäisyys on 82 cm. Laske
a) gravitaatiovoiman suuruus,
b) pelkän gravitaatiovoiman aiheuttama kiihtyvyys Ristolle,
c) aika, jossa Risto lähenee Maijan alkuperäistä paikkaa yhden millimetrin vastuksettomassa tilanteessa.
RATK.
\(m_\text{R} = 81\,\text{kg}, \quad m_\text{M} = 71\,\text{kg}, \quad r = 0,82\,\text{m}, \quad \gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2}, \quad F = ?, \quad a = ?, \quad t = ?\)
a) Lasketaan gravitaatiolain mukainen kumpaankin henkilöön vaikuttava voima.
\[ F = \gamma\,\frac{m_\text{R} m_\text{M}}{r^2} = 6,6742 \cdot 10^{-11}\,\frac{\text{Nm}^2}{\text{kg}^2} \cdot \frac{81\,\text{kg} \cdot 71\,\text{kg}}{(0,82\,\text{m})^2} = 5,7084 \cdot 10^{-7}\,\text{N} \approx 5,7 \cdot 10^{-7}\,\text{N} \]
b) Lasketaan dynamiikan peruslain avulla Riston kiihtyvyys.
\[ a_\text{R} = \frac{F_\text{R}}{m_\text{R}} = \frac{5,7084 \cdot 10^{-7}\,\text{N}}{81\,\text{kg}} = 7,0474 \cdot 10^{-9}\,\frac{\text{m}}{\text{s}^2} \approx 7,0 \cdot 10^{-9}\,\frac{\text{m}}{\text{s}^2} \]
Huomaa, että kiihtyvyys kasvaa, koska gravitaatiovoima kasvaa etäisyyden pienentyessä.
c)
Lasketaan aika tasaisesti kiihtyvän liikkeen mallin avulla, kun gravitaatiovoima ajatellaan siirtymässä vakioksi.
\[ s_\text{R} = \frac{1}{2}a_\text{R}t^2 \qquad \text{eli} \qquad t_\text{R} = \sqrt{\frac{2s}{a_\text{R}}} = \sqrt{\frac{2 \cdot 0,001\,\text{m}}{7,0474 \cdot 10^{-9}\,\frac{\text{m}}{\text{s}^2}}} = 532,7219\,\text{s} \approx 530\,\text{s} \]
Huomaa, että myös Maija lähestyy, jolloin gravitaatiovoima kasvaa etäisyyden pienentyessä.
VAST.
a) Gravitaatiovoima on \(5,7 \cdot 10^{-7}\,\text{N}\).
b) Riston kiihtyvyys on \(7,0 \cdot 10^{-9}\,\frac{\text{m}}{\text{s}^2}\).
c) Millimetrin matkaan kuluu aikaa 530 sekuntia.
ESIM. 8.
Lasketaan gravitaatiolain mukainen putoamiskiihtyvyys Maan pinnassa.
RATK.
\(m_\text{Maa} = 5,974 \cdot 10^{24}\;\text{kg}, \quad r_\text{Maa} = 6\,370 \cdot 10^{24}\;\text{m}, \quad \gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \quad g = ?\)
Kirjoitetaan dynamiikan peruslaki.
\[ \Sigma \overline{F} = m\overline{a} \]
Yhdistetään edellinen gravitaatiolakiin.
\[ \gamma\,\frac{m_\text{Maa} m}{r^2_\text{Maa}} = ma \]
Lasketaan gravitaatiovoiman aiheuttama kiihtyvyys.
\[ a = \gamma\,\frac{m_\text{Maa}}{r^2_\text{Maa}} = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \cdot \frac{5,974 \cdot 10^{24}\;\text{kg}}{(6\,370 \cdot 10^{24}\;\text{m})^2} = 9,8262\;\frac{\text{m}}{\text{s}^2} \approx 9,83\;\frac{\text{m}}{\text{s}^2} \]
VAST.
Putoamiskiihtyvyys on 9,83 m/s\(^2\).
HUOM!
Ero opittuun putoamiskiihtyvyyden arvoon selittyy mm. Maan pyörimisliikkeellä ja sillä, ettei Maa ole täysin pyöreä. Lisäksi laskussa on oletettu Maa pistemäiseksi massalliseksi kappaleeksi.
ESIM. 9.
Lasketaan gravitaatiokentän voimakkuus Maan pinnalla.
RATK.
\(m_\text{Maa} = 5,974 \cdot 10^{24}\;\text{kg}, \quad r_\text{Maa} = 6\,370 \cdot 10^{24}\;\text{m}\)
\(\gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2}, \quad g(r_\text{Maa}) = ?\)
Lasketaan gravitaatiokentän voimakkuus.
\[ g(r_\text{Maa}) = \gamma\,\frac{m_\text{Maa}}{r^2_\text{Maa}} \approx 9,83\;\frac{\text{m}}{\text{s}^2} \]
VAST.
Gravitaatiokentän voimakkuus on 9,83 m/s\(^2\).
Kahden massallisen kappaleen välinen voima
6 Planeettojen ja satelliittien liike
Aurinkokuntamme planeetat (Merkurius, Venus, Maa, Mars, Jupiter, Saturnus, Uranus ja Neptunus) kiertävät Auringon ympäri ellipsiradoilla samaan suuntaan ja lähes samassa tasossa.
Kirjoitetaan satelliitin liikeyhtälö.
\[ \Sigma \overline{F} = m\overline{a} \]
Edellisessä yhtälössä
\[ \Sigma F = F = \gamma \frac{Mm}{r^2} \qquad \text{ja} \qquad a = a_\text{n} = \frac{v^2}{r} \]
Kirjoitetaan kokonaisenergia, kun kappale kiertää raskasta kappaletta.
\[ E = \frac{1}{2}mv^2 + \left(-\gamma \frac{Mm}{r}\right) = \text{vakio} \]
Gravitaatiovoima säätelee satelliittien liikettä
Maan gravitaatiovoima on ainoa satelliiteihin vaikuttava voima.
Dynamiikan peruslain \(\Sigma \overline{F} = m \overline{a}\) avulla voidaan kirjoittaa satelliitin liikeyhtälö.
\[ \gamma \frac{mM}{r^2} = m \frac{v^2}{r} \]
Planeetat kiertävät Aurinkoa
Kappaleen kiihtyvää liikettä systeemin massakeskipisteen ympäri kutsutaan myötäliikkeeksi.
Kaikki planeetat kiertävät Auringon ympäri samaan suuntaan ja lähes samassa tasossa pitkin ellipsiratoja.
Planeetan liike-energia on suurimmillaan ja potentiaalienergia pienimmillään, kun planeetta on lähimpänä Aurinkoa. Voidaan siis todeta, että kokonaisenergia määrää sen, miten kauas Auringosta planeetta voi etääntyä.
Avaruusalukset ja satelliitit
Satelliitti on taivaankappaletta kiertävä luotain, joka on viety radalleen. Se kiertää planeettaa ympyrä- tai ellipsiradalla. Satelliittien ratoihin kuuluu geosynkroninen rata, geostationäärinen rata sekä aurinkosynkroninen rata.
Avaruusaluksen siirtäminen kiertoradalle
Avaruuteen avaruusalukset siirretään joko sukkulalla tai kantoraketilla. Kun alus kiertää satelliittiradalla ja kun sen moottorit käynnistetään sopivassa kohdassa se siirtyy halutulle kiertoradalle. Nykyään on siirrytty käyttämään linkoratatekniikkaa. Alusta ei ohjata suoraan kohteeseen vievälle radalle, vaan käytetään toista planeettaa suuntaamaan rata tai antamaan lisävauhtia. Tämä säästää polttoainetta, joten alus voi olla pienempi ja kevyempi. Maassa aluksia siirretään rekka-autolla tai lentokoneella.
Satelliitit auttavat meitä
Satelliitti on taivaankappaletta kiertävä ihmisen tekemä luotain, jota käytetään muun muassa erinäisiin mittauksiin. GPS (Global Positioning System) määrittää laitteen sijainnin trigonometrian avulla. Laite vastaanottaa signaalin vähintään kolmesta GPS-satelliitista ja laskee signaalien välittämän datan perusteella sijainnin Maan pinnalla metrien tarkkuudella.
ESIM. 10.
Moottorittoman satelliitin kiertokorkeus Maan pinnasta on \(2\,200\) km. Laske nopeus.
RATK.
\(r = 6\,370\;\text{km} + 2\,200\;\text{km} = 8\,570\;\text{km}, \quad v = ?\)
Kirjoitetaan gravitaatiovuorovaikutuksen satelliittiin aiheuttaman voiman.
\[ F = \gamma \frac{Mm}{r^2} \]
Satelliitin liike ympyräradalla on tasaista. Satelliitin kiihtyvyys on normaalikiihtyvyyttä.
\[ a_\text{n} = \frac{v^2}{r} \]
Kirjoitetaan dynamiikan peruslaki.
\[ \Sigma \overline{F} = m\overline{a}_\text{n} \]
Yhdistetään edelliseen yhtälöön gravitaatiovoima ja tasaisen ympyräliikkeen normaalikiihtyvyys.
\[ \gamma \frac{Mm}{r^2} = m \frac{v^2}{r} \]
Ratkaistaan ja lasketaan nopeus \(v\).
\[ v = \sqrt{\gamma \frac{M}{r}} = \sqrt{6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \cdot \frac{5,974 \cdot 10^{24}\;\text{kg}}{8\,570 \cdot 10^3\;\text{m}}} = 6\,820,9019\;\frac{\text{m}}{\text{s}} \approx 6\,800\;\frac{\text{m}}{\text{s}} \]
VAST.
\(6\,800\) m/s
ESIM. 11.
Geostationaarinen satelliitti pysyy Maan pinnalta katsottuna paikallaan. Laske lentokorkeus, kun rata oletetaan ympyräradaksi.
RATK.
\(r = 6\,370\;\text{km}, \quad M = 5,974 \cdot 10^{24}\;\text{kg}, \quad T = 24\;\text{h}, \quad r = ?\)
Kirjoitetaan gravitaatiovuorovaikutuksen satelliittiin aiheuttaman voiman.
\[ F = \gamma \frac{Mm}{r^2} \]
Satelliitin liike ympyräradalla on tasaista. Satelliitin kiihtyvyys on normaalikiihtyvyyttä.
\[ a_\text{n} = \frac{v^2}{r} \]
Kirjoitetaan dynamiikan peruslaki.
\[ \Sigma \overline{F} = m\overline{a}_\text{n} \]
Kirjoitetaan ratanopeus.
\[ v = \frac{s}{t} = \frac{2 \pi r}{T} \]
Yhdistetään gravitaatiovoima, tasaisen ympyräliikkeen normaalikiihtyvyys ja ratanopeus.
\[ \gamma \frac{Mm}{r^2} = m \frac{\left(\frac{2 \pi r}{t}\right)^2}{r} \]
Ratkaistaan edellisestä säde \(r\).
\[ r = \sqrt[3]{\frac{T^2 \gamma M}{4 \pi^2}} \]
Sijoitetaan lukuarvot.
\[ r = \sqrt[3]{\frac{(24 \cdot 3\,600\;\text{s})^2 \cdot 6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \cdot 5,974 \cdot 10^{24}\;\text{kg}}{4 \pi^2}} \approx 42\,000\;\text{km} \]
Edellä laskettu korkeus tarkoittaa etäisyyttä Maan keskipisteestä.
VAST.
\(36\,000\) km
ESIM. 12.
Lasketaan gravitaatiokentän voimakkuus Maan pinnalla.
RATK.
\(m_\text{Maa} = 5,974 \cdot 10^{24}\;\text{kg}, \quad r_\text{Maa} = 6\,370 \cdot 10^{24}\;\text{m}, \quad \gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \quad g(r_\text{Maa}) = ?\)
Lasketaan gravitaatiokentän voimakkuus.
\[ g(r_\text{Maa}) = \gamma\,\frac{m_\text{Maa}}{r^2_\text{Maa}} \approx 9,83\;\frac{\text{m}}{\text{s}^2} \]
VAST.
Gravitaatiokentän voimakkuus on 9,83 m/s\(^2\).
Geostationaarinen satelliitti
7 Momentti kuvaa voiman vääntövaikutusta
Voima on mitattava ominaisuus eli suure, joka kuvaa vuorovaikutuksen suuruutta. Se voi muuttaa kappaleen etenemisliikettä ja pyörimisliikettä. Voimalla voi siis olla myös vääntövaikutus, ja momentti on suure, joka kuvaa voiman vääntövaikutusta.
Akseli on todellinen tai kuviteltu suora, jonka ympäri kappale pyörii. Voiman vaikutuspiste on se kappaleen kohta, johon voima vaikuttaa. Voimavektorin kanssa yhdensuuntainen suora, joka kulkee voiman vaikutuspisteen kautta, on voiman vaikutussuora. Voiman vaikutussuoran etäisyys pyörimisakselista on voiman varsi \(r\).
Voiman momentti on voiman ja voiman varren tulo akselin \(A\) suhteen.
\[ M_\text{A} = Fr \]
Kirjoitetaan momentin yksikkö.
\[ [M] = [F][r] = 1\;\text{Nm} = 1\;\frac{\text{kgm}^2}{\text{s}^2} \]
Huomaa, että momentin yksikkö ei ole sama asia kuin energian yksikkö joule. Työtä on esim. voiman ja voiman vaikutusmatkan tulo, ja tätä mitataan jouleina. Momentti lasketaan voiman ja voiman varren tulona, ja tätä mitataan newtonmetreinä. Jos voiman ja voiman varren tulon eli vääntömomentin annetaan kiertyä akselia ympäri, syntyy tehtyä työtä, jota mitataan jouleina.
Momentti voi olla positiivinen tai negatiivinen. Momentti on positiivinen, kun voima kiertää kappaletta valittuun positiiviseen kiertosuuntaan.
ESIM. 13.
Seinään on kiinnitetty saranalla ja jännitetyllä narulla hyllytaso, johon vaikuttavat kuvassa esitetyt voimat.
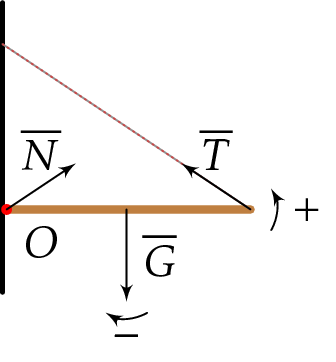
Tutki, mitkä momenteista ovat positiivisia ja mitkä negatiivisia saranan kautta kulkevan akselin \(O\) suhteen. Positiiviseksi kiertosuunnaksi on valittu suunta vastapäivään.
RATK.
Katsotaan kuvaa, johon on lisätty momenttien suuntanuolet.
Jännitysvoima \(\overline{T}\) vääntää tasoa vastapäivään, ja momentti on positiivinen.
Paino \(\overline{G}\) vääntää tasoa myötäpäivään, ja momentti on negatiivinen.
VAST.
Jännitysvoiman momentti on positiivinen ja painon negatiivinen.
ESIM. 14.
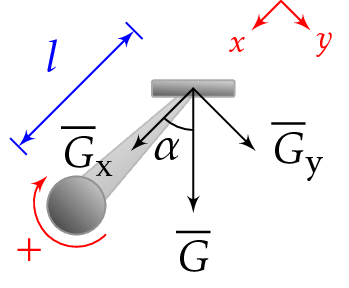
Pyöräilijä (64 kg) painaa poljinta 45 asteen kulmassa siten, että hän on noussut seisomaan koko painollaan yhdelle polkimelle. Laske pyörän napaan kohdistuva vääntömomentti, kun polkimen kammen pituus on 27 cm.
RATK.
\(m = 64\;\text{kg}, \quad \alpha = 45^\circ, \quad l = 27\;\text{h}, \quad g = 9,81\;\frac{\text{m}}{\text{s}^2}, \quad M = ?\)
Lasketaan pyöräilijän paino.
\[ G = mg = 64\;\text{kg} \cdot 9,81;\frac{\text{m}}{\text{s}^2} = 627,84\;\text{N} \]
Jaetaan paino \(\overline{G}\) kuvan mukaisesti kahteen komponenttiin, joista toinen \(\overline{G}_\text{x}\) on polkimen kammen suuntainen ja toinen \(\overline{G}_\text{y}\) on kohtisuorassa edellistä vastaan.

\[ G_\text{x} = G \cos \alpha \quad \text{ja} \quad G_\text{y} = G \sin \alpha \]
Vääntävän momentin aihettaa painon \(\overline{G}\) komponentti \(G_\text{y}\).
Lasketaan momentti.
\[ M = G_\text{y} l = 627,84\;\text{N} \cdot \sin 45^\circ \cdot 0,27\;\text{m} = 119,8665\;\text{Nm} \approx 120\;\text{Nm} \]
VAST.
120 Nm
Voiman momentti
8 Etenemisen ja pyörimisen tasapaino
Statiikka käsittelee kappaleiden tasapainotiloja. Se on mekaniikan osa-alue.
Tutkitaan aluksi tasapainoa etenemisen suhteen ja kirjoitetaan Newtonin II laki eli dynamiikan peruslaki.
\[ \Sigma \overline{F} = m \overline{a} \]
Kappaleeseen vaikuttavat voimat aiheuttavat kappaleen kiihtyvyyden. Staattisessa tasapainossa kappaleeseen vaikuttavien voimien summa on nolla. Tällöin kappale on etenemisen suhteen tasapainossa.
Jos voimien summa on nolla, on kappale paikallaan tai sen liike on tasaista. Statiikan tehtävissä kappale on yleensä aluksi ja lopuksi levossa, kun voimien summa nolla.
\[ \Sigma \overline{F} = \overline{F}_1 + \overline{F}_2 + \ldots = \overline{0} \]
Kappaleisiin vaikuttavista voimista osa voi aiheuttaa momentin. Näiden voimien momenttien kokonaisvaikutuksella on merkitystä kappaleen tasapainoon.
Tutkitaan vielä tasapainoa pyörimisen suhteen.
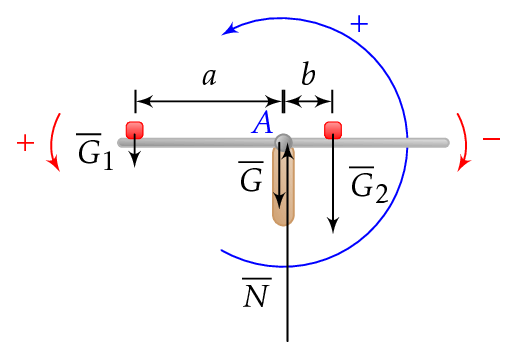
Voimat \(\overline{G}_1\) ja \(\overline{G}_2\) kohdistuvat jäykkään vaa'an orteen. Voimat ovat samassa tasossa ja kohtisuorassa suhteessa orren keskipisteen akseliin \(A\).
Olkoon positiivinen kiertosuunta vastapäivään akselin \(A\) suhteen. Paino \(\overline{G}\) ja tukivoima \(\overline{N}\) eivät aiheuta momenttia akselin \(A\) suhteen. Voima \(\overline{G}_1\) aiheuttaa väännön positiiviseen suuntaan, jolloin momentti \(M_1\) on positiivinen. Voima \(\overline{G}_2\) aiheuttaa väännön negatiiviseen suuntaan, ja momentti \(M_2\) on negatiivinen. Jotta kappale olisi tasapainossa pyörimisen suhteen, on momenttien oltava yhtä suuret akselin \(A\) suhteen. Momenttien summa on nolla.
\[ \Sigma M_\text{A} = 0 \quad \text{eli} \quad G_1 a - G_2 b = 0 \]
Jäykkä kappale on siis pyörimisen suhteen tasapainossa, kun kappaleeseen valitun pyörimisakselin \(A\) suhteen vaikuttavien voimien kokonaismomentti on nolla (\(\Sigma M_\text{A} = 0\)).
Momenttipiste on kohta, jossa todellinen pyörimisakseli lävistää kappaleen. Pyörimisakseli voi olla myös kuviteltu.
ESIM. 15.
Vaaka on tasapainossa ilman punnuksia. Vasemmalle lisätään punnus, jonka massa on \(m_1 = 17\;\text{g}\), ja oikealle punnus, jonka massa on \(m_1 = 51\;\text{g}\). Laske toisen punnuksen etäisyys vaa'an keskipisteestä, kun ensimmäisen etäisyys on \(a = 12\;\text{cm}\).
RATK.
\(m_1 = 0,017\;\text{kg}, \quad m_2 = 0,051\;\text{kg}, \quad a = 0,12\;\text{m}, \quad b = ?\)
Piirretään tilannekuva ja vaakaan vaikuttavat voimat.

Koska vaa'an orsi on tasapainossa ilman punnuksia, orren painon \(\overline{G}\) vektori kulkee tukipisteen eli pyörimisakselin kautta eikä se aiheuta momenttia. Myös tukivoiman \(\overline{N}\) vektori tekee samoin.
Positiivinen pyörimissuunta on vastapäivään akselin ympäri. Voiman \(\overline{G}_1\) momentti on positiivinen ja voiman \(\overline{G}_2\) momentti on negatiivinen. Orsi on tasapainossa, kun momenttien summa on nolla.
\[ \Sigma M_\text{A} = 0 \quad \text{eli} \quad G_1 a - G_2 b = 0 \quad \text{eli} \quad m_1 ga = m_2 gb \]
Ratkaistaan ja lasketan yhtälöstä voiman varsi \(b\).
\[ b = \frac{m_1 a}{m_2} = \frac{0,017\;\text{kg} \cdot 0,12\;\text{m}}{0,051\;\text{kg}} = 0,04\;\text{m} \]
VAST.
4 cm
ESIM. 16.
Kuvan tilanteessa tanko voi kääntyä kitkattomasti momenttipisteen \(O\) ympäri. Tanko ei voi liikkua sivusuunnassa. Punnusten massa on sama, ja ne on yhdistetty toisiinsa hyvin kevyellä ja kitkattomalla narulla. Aluksi systeemi on tasapainossa.
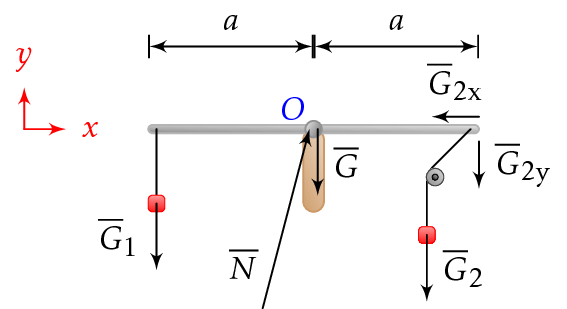
Kerro, mitä tapahtuu, kun tanko päästetään vapaasti liikkumaan.
RATK.
Punnusten massat ovat yhtä suuret. Vaikka tankoon vaikuttavat voimat ovat yhtä suuret, vaikuttavat voimat eri suuntiin.
Jaetaan voima \(\overline{G}_2\) komponentteihinsa.
Tangon oikeaan päähän vaikuttaa ainoastaan voima \(\overline{G}_\text{2y}\), joka vääntää tankoa.
Koska komponentti \(\overline{G}_\text{2y}\) on pienempi kuin \(\overline{G}_1\), ei tasapaino säily. Koska voimien varret ovat yhtä pitkät, eivät voimien momentit ole samat, ja tanko kääntyy vastapäivään.
VAST.
Näinhän siinä aina käy :(
Tasapainoehdot on otettava huomioon
9 Jäykän kappaleen tasapaino
Jäykän kappaleen muoto ei muutu, kun siihen kohdistuu voimia.
Voimaehto on tasapainoehto etenemisen suhteen. Kappaleeseen vaikuttavien voimien summa on nolla (\(\Sigma \overline{F} = \overline{0}\)). Tasossa voimaehto jakautuu kahdeksi yhtälöksi.
Momenttiehto on tasapainoehto pyörimisen suhteen. Kappaleeseen vaikuttavien momenttien summa on nolla (\(\Sigma M = 0\)) kaikkien akseleiden suhteen.
Jäykkä kappale on tasapainossa etenemisen ja pyörimisen suhteen, kun seuraavat ehdot ovat voimassa.
\[ \Sigma \overline{F}_\text{x} = \overline{0}, \qquad \Sigma \overline{F}_\text{y} = \overline{0} \qquad \text{ja} \qquad \Sigma M = 0 \]
Voimaehdoista ja momenttiehdosta saadaan kolme tasapainoyhtälöä, joista voidaan ratkaista kolme tuntematonta suuretta.
Kappale on ylituettu, jos se on tuettu useammalla voimalla kuin on tarpeen.
Tasapainotehtävässä on aina tutkittava tietyt vaiheet. Kappaleeseen vaikuttavia voimia ovat yleensä paino \(\overline{G}\) sekä erilaiset tuki- ja jännitysvoimat. Jos kappale ei pyöri minkään tietyn akselin suhteen, voidaan momenttipiste valita vapaasti.
Ratkaisun vaiheet
ESIM. 17.
Seinään on kiinnitetty saranalla ja jännitetyllä narulla hyllytaso, jonka massa on 1,4 kg ja leveys on 42 cm. Narun ja hyllyn välinen kulma on kuvan mukaisesti 33,7\(^\circ\). Laske narun jännitysvoima ja saranan tukivoima, kun hylly on tasapainossa.
RATK.
\(m = 1,4\;\text{kg}, \quad L = 0,42\;\text{m}, \quad \alpha = 33,7^\circ, \quad T = ?, \quad N = ?\)
Piirretään voimakuvio.
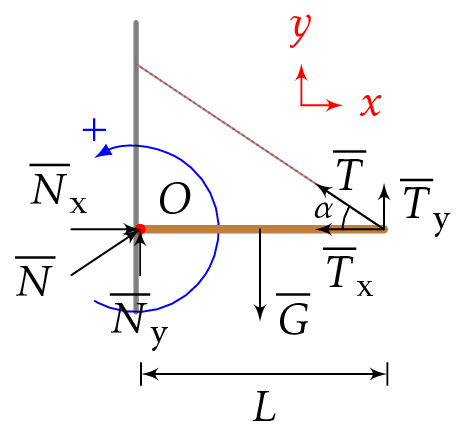
1.
Hyllyyn vaikuttavat paino \(\overline{G}\), narun jännitysvoima \(\overline{T}\) ja saranan tukivoima \(\overline{N}\), jonka komponentit ovat \(\overline{N}_\text{x}\) ja \(\overline{N}_\text{y}\).
Tukivoima \(\overline{N}\) ei ole kohtisuorassa seinää vastaan, koska hylly on kiinnitetty saranalla. Valitaan positiiviset suunnat.
2.
Todetaan tasapainoehto. Koska hylly on levossa, saadaan dynamiikan peruslain mukaisesti \(\Sigma \overline{F} = \overline{0}\).
3.
\[ \Sigma \overline{F}_\text{x} = \overline{0} \quad \text{ja} \quad \Sigma \overline{F}_\text{y} = \overline{0} \]
\[ \overline{N}_\text{x} + \overline{T}_\text{x} = \overline{0} \quad \text{ja} \quad \overline{G} + \overline{N}_\text{y} + \overline{T}_\text{y} = \overline{0} \]
Kirjoitetaan voimaehto skalaarimuodossa.
\[ N_\text{x} - T_\text{x} = 0 \quad \text{ja} \quad -G + N_\text{y} + T_\text{y} = 0 \]
4.
Hylly ei pyöri, joten voimien kokonaismomentti \(\Sigma M = 0\).
5.
Valitaan momenttipisteeksi saranapiste \(O\). Toinen tuntemattomista voimista vaikuttaa saranaan.
6.
Valitaan positiiviseksi pyörimisen suunnaksi vastapäivä. Vain voimalla \(\overline{G}\) ja tukivoiman \(\overline{T}_\text{y}\) komponentilla on momentti pisteen \(O\) suhteen. Muiden voimien vaikutussuorat kulkevat pisteen \(O\) kautta.
Kirjoitetaan yhtälö, kun hyllyn pituus on \(L\).
\[ \Sigma M = 0 \quad \text{eli} \quad -G \frac{L}{2} + T_\text{y} L = 0 \quad \text{eli} \quad T_\text{y} - \frac{G}{2} = 0 \quad \text{eli} \quad T_\text{y} = \frac{G}{2} \]
7.
Ratkaistaan yhtälöt, kun \(\sin \alpha = \frac{T_\text{y}}{T}\).
\[ T = \frac{T_\text{y}}{\sin \alpha} = \frac{G}{2 \sin \alpha} = \frac{1,4\;\text{kg} \cdot 9,18\;\frac{\text{m}}{\text{s}^2}}{2 \cdot \sin 33,7^\circ} = 12,3764\;\text{N} \]
Lasketaan saranan tukivoima. Voimaehdon mukaan \(N_\text{x} - T_\text{x} = 0\).
\[ N_\text{x} = T_\text{x} = T \cos \alpha = \frac{G}{2 \sin \alpha} \cdot \cos \alpha = \frac{G}{2 \tan \alpha} \]
Lasketaan tukivoiman suruus Pythagoraan lauseen avulla.
\[ N = \sqrt{N^2_\text{x} + N^2_\text{y}} = \sqrt{\left(\frac{G}{2 \tan \alpha}\right)^2 + \left(\frac{G}{2}\right)^2} = 12,3764\;\text{N} \]
Jännitysvoima \(\overline{T}\) ja tukivoima \(\overline{N}\) ovat yhtä suuret.
8.
VAST.
Molemmat voimat (12,4 N) ovat yhtä suuret.
ESIM. 18.
Laudan massa on 4,1 kg ja sen pituus on 6,2 metriä. Lauta on vaakatasossa kahden tuen varassa kuvan mukaisesti.
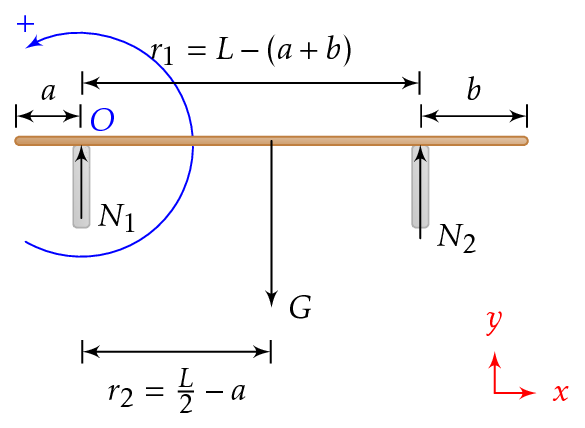
Laske lautaan kohdistuvat tukivoimat.
RATK.
\(m = 4,1\;\text{kg}, \quad L = 6,2\;\text{m}, \quad a = 0,8\;\text{m}, \quad b = 1,3\;\text{m}, \quad N_1 = ?, \quad N_2 = ?\)
Lautaan vaikuttavat paino \(\overline{G}\) ja tukivoimat \(\overline{N}_1\) ja \(\overline{N}_2\). Positiivinen suunta on kuvan mukainen.
Kirjoitetaan dynamiikan peruslain mukainen yhtälö.
\[ \Sigma \overline{F} = \overline{0} \quad \text{eli} \quad \overline{N}_1 + \overline{N}_2 + \overline{G} = \overline{0} \]
Kirjoitetaan edellinen skalaarimuodossa.
\[ N_1 + N_2 - G = 0 \]
Olkoon momenttipisteenä \(O\) vasemmanpuoleinen tukipiste ja kirjoitetaan momenttiyhtälö. Lauta on tasapainossa myös pyörimisen suhteen.
\[ \Sigma M_\text{O} = 0 \quad \text{eli} \quad N_2 r_1 - G r_2 = 0 \]
Kuvasta saadaan lausekkeet etäisyyksille \(r_1\) ja \(r_2\).
\[ r_1 = L - (a + b) \quad \text{ja} \quad r_2 = \frac{L}{2} - a \]
Sijoitetaan edellinen momenttiyhtälöön.
\[ N_2 (L - (a + b)) - G \left(\frac{L}{2} - a\right) = 0 \]
Ratkaistaan tukivoima \(N_2\).
\[ N_2 = \frac{mg\left(\frac{L}{2} - a\right)}{L - (a + b)} = \frac{4,1\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot \left(\frac{6,2\;\text{m}}{2} - 0,8\;\text{m}\right)}{6,2\;\text{m} - 2,1\;\text{m}} = 22,563\;\text{N} \approx 23\;\text{N} \]
Ratkaistaan toinen tukivoima voimayhtälöstä.
\[ N_1 = G - N_2 = 4,1\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} - 22,563\;\text{N} = 17,658\;\text{N} \approx 18\;\text{N} \]
VAST.
23 N ja 18 N
10 Painopiste määritetään momenttien avulla
Painopiste on ajateltu kappaleen painon vaikutuspiste.
Yksinkertaisessa koneessa kappaleeseen vaikuttavan voiman suuruutta ja suuntaa voidaan muuttaa. Yksinkertaiset koneet muodostavat kaltevan tason ryhmän ja vipuryhmän.
Tasapainolajit ovat vakaa eli stabiili, horjuva eli labiili ja epämääräinen eli indifferentti.
Paino vaikuttaa jäykän kappaleen painopisteeseen
Massallisen kappaleen jokaiseen pisteeseen vaikuttaa painovoima. Jäykän kappaleen paino voidaan kumota kappaleen painopisteeseen vaikuttavalla voimalla.
Kappaleen pistettä, jonka kautta sen painovoiman vektori kulkee aina kappaleen positiosta riippumatta kutsutaan painopisteeksi ja jos kappale tuetaan sen painopisteestä pysyy se tasapainossa kaikissa mahdollisissa asennoissa.
Kappaleen painopiste on painon ajateltu vaikutuspiste.
Painopisteen paikan laskeminen
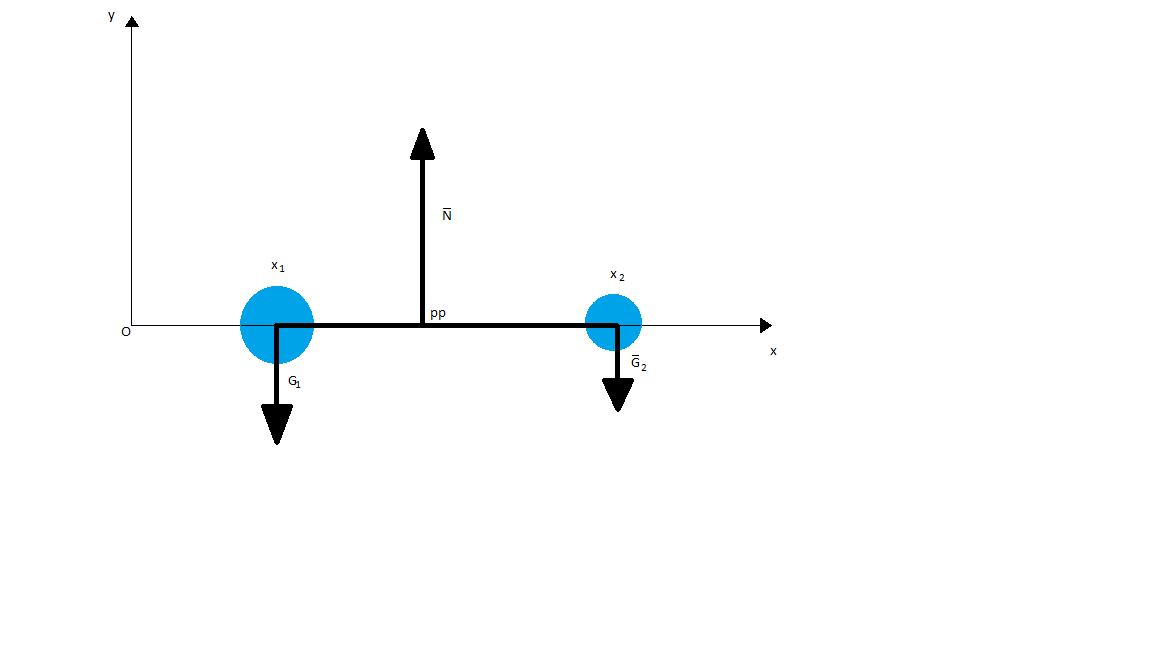
Kappaleen painopisteen paikan koordinaatistossa voi laskea, jos kappale koostuu erillisistä osista, joiden painopisteet tunnetaan.
\[ \text{x}_\text{pp} = \frac{\text{x}_1\text{m}_1 + \text{x}_2\text{m}_2+... + \text{x}_n\text{m}_n}{\text{m}_1 + \text{m}_2 + ... + \text{m}_n} \]
\[
\text{y}_\text{pp}
= \frac{\text{y}_1\text{m}_1 + \text{y}_2\text{m}_2+... + \text{y}_n\text{m}_n}{\text{m}_1 + \text{m}_2 + ... + \text{m}_n}
\] 
Kappaleen kaatuminen ja tasapainolajit
Esimerkiksi tuolissa jalat rajaavat tukipinnan, ja tuoli kaatuu jos, painopisteestä lähtevä luotisuora siirtyy tukipinnan ulkopuolelle.
On kolmenlaisia tasapainoja stabiili, indifferentti ja labiili
vakaa eli stabiili
kappale pysyy itsestään pystyssä, potentiaalienergia on pienin tasapainoasemassa
epämääräinen eli indifferentti
Esim. pallon tasapaino ei muutu vaikka sitä liikutetaan lattialla.
Potentiaalienergia ei muutu siirrettäessä.
horjuva eli labiili
kappale pysyy itsekseen pystyssä, mutta pienikin kosketus saa sen kaatumaan.
Kappaleen painopiste laskee, kun sitä poikkeutetaan tasapainoasemasta.
Potentiaalienergia pienenee kun se poistuu horjuvasta tasapainoasemasta.Yksinkertaiset koneet soveltavat tasapainoehtoja
Yksinkertaisella koneella kuvataan laitetta, jolla voidaan muuttaa kappaleeseen vaikuttavan voiman suuntaa ja suuruutta. Voimia siis sovelletaan esim. saksissa, ruuveissa ja kottikärryissä. Yksinkertaiset koneet jaetaan kaltevan tason ryhmään sekä vipuryhmään.
Koneen tasapainoehto saadaan voimien tekemän työn avulla
Yksinkertainen kone
Yksinkertaisen, eli ideaalisen koneen osat ovat jäykkiä, eikä energiaa muunnu koneen osien lämpöenergiaksi. Todellisessa koneessa tapahtuu kuitenkin aina energian muuntumista lämpöenergiaksi, joten koneeseen on tuotava enemmän energiaa kuin siitä siirtyy ulos.
Koneen tasapainoehto
Ideaalisen koneen syöttövoiman tekemä työ on yhtä suuri kuin kuormavoiman tekemä työ:
\(W_{s}=W_{k}\)
Eli
\(F_{s}x_{s}=F_{k}x_{k}\)
jossa
\(F_{s}=\)syöttövoima, \(F_{k}=\)kuormavoima,
\(x_{s}=\)syöttövoiman vaikutuspisteen siirtymä,
\(x_{k}=\)kuormavoiman vaikutuspisteen siirtymä,
\(W_{s}=\)syöttövoiman tekemä työ, \(W_{k}=\)kuormavoiman tekemä työ.
Kalteva taso helpottaa nostamista
Taakan nostamiseen kaltevaa tasoa pitkin tarvitaan vähemmän voimaa kuin suoraan ylöspäin nostaessa.
Työn määrä on vakio kummassakin tapauksessa.
Rautakanki on vipu
Rautakanki on oiva vipu, koska sillä voidaan sekä kääntää että vääntää. Käännettäessä kanki on yksivartinen vipu ja väännettäessä kaksivartinen vipu. Kuormittavan voiman momentti on yhtä suurin kuin on syöttövoiman momentti.
\[ F_\text{s} a = F_\text{k} b \]
Ihmisessä on runsaasti vipuja
Ihmisen luurangossa on monia niveliä, jotka ovat kiinnityspisteinä ja joiden ympäri luut pääsevät kääntymään. Luurangossa on sekä yksi-että kaksivartisia vipuja: Esim. sääri-ja kyynärvarsi ovat yksivartisia vipuja, kun taas kaksivartisia ovat pää ja nilkka. Ihmskehon kannalta tärkeämpiä ovat suuret liikeradat ja nopeus kuin suuri syttövoima.
Taljassa... Hynninen
TODO
ESIM. 19.
Sylinterin massa on 320 kg, ja se pitää vierittää 5,2 metrin korkeuteen. Laske tarvittavan kaltevan tason pituus, kun vierittämiseen käytettävä maksimivoima on 125 N.
RATK.
\(m = 320\;\text{kg}, \quad h = 5,2\;\text{m}, \quad F = 125\;\text{N}, \quad s = ?\)
Työntävän voiman tekemä työ \(W = Fs\) ja suorassa nostossa tarvittavan voiman tekemä työ \(W = Gh\) ovat yhtä suuret.
\[ Fs = Gh \]
Ratkaistaan ja lasketaan kaltevan tason pituus \(s\).
\[ s = \frac{Gh}{F} = \frac{mgh}{F} = \frac{320\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 5,2\;\text{m}}{125\;\text{N}} = 130,5907\;\text{m} \approx 130\;\text{m} \]
VAST.
130 m
ESIM. 20.
Laske tarvittava voima, kun kappale (210 kg) nostetaan tasaisella vauhdilla kuvan mukaisissa tilanteissa.
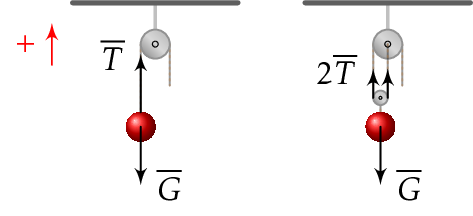
RATK.
\(m = 210\;\text{kg}, \quad F = ?\)
a)
Vasemmassa kuvassa on kiinteä väkipyörä, joka muuttaa vain voiman suuntaa. Narun jännitysvoima \(\overline{T}\) on sama kuin vetävä voima \(\overline{F}\).
Kirjoitetaan dynamiikan peruslain mukainen yhtälö.
\[ \Sigma \overline{F} = m \overline{a} \quad \text{eli} \quad \Sigma \overline{F} = \overline{T} + \overline{G} = \overline{0} \]
Kirjoitetaan edellinen yhtälö skalaarimuodossa.
\[ T - G = 0 \quad \text{eli} \quad T = G = 210\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} = 2\,060,1\;\text{N} \approx 2\,060\;\text{N} \]
Tarvittava voima \(F\) on siten 2060 N eli kappaleen paino.
b)
Oikeassa kuvassa on kannetteleva voima jakautuu kahdelle narulle.
Kirjoitetaan dynamiikan peruslain mukainen yhtälö.
\[ \Sigma \overline{F} = m \overline{a} \quad \text{eli} \quad \Sigma \overline{F} = \overline{T} + \overline{T} + \overline{G} = \overline{0} \]
Kirjoitetaan edellinen yhtälö skalaarimuodossa.
\[ T + T - G = 0 \quad \text{eli} \quad T = \frac{G}{2} \approx 1\,030\;\text{N} \]
Koska väkipyörä muuttaa voiman suuntaa, tarvittava voima \(\overline{F}\) on yhtä suuri kuin on narun jännitysvoima \(\overline{T}\) eli 1030 N.
VAST.
2060 N ja 1030 N
11 Kulmanopeus ja kulmakiihtyvyys kuvaavat pyörimisliikettä
Liikkeen perustyyppejä ovat etenemisliike, värähdysliike ja pyörimisliike.
Kiertokulma ilmoittaa kappaleen asennon. Pyörivän kappaleen pisteet liikkuvat ympyräradoilla, joiden keskipisteet ovat samalla konkreettisella tai teoreettisella pyörimisakselilla. Vapaan pyörivän kappaleen pyörimisakseli kulkee massakeskipisteestä.
Jäykän kappaleen koko ja muoto eivät muutu, vaikka asento muuttuu. Sen kaikkien osien paikka toisiinsa nähden on vakio. Kiertyvän sauvan jokainen osa liikkuu pitkin ympyrärataa, ja eri osat kulkevat eripituisen matkan eri nopeudella.

Kiertokulma eli kulman suuruus \(\varphi\) on kulmaa vastaavan kaaren \(s\) ja ympyrän säteen \(r\) suhde.
\[ \varphi = \frac{s}{r} \]
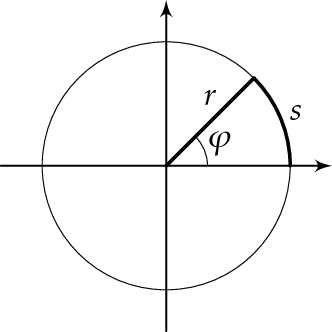
Kulman yksikkö radiaani on kaaren ja säteen yksikköjen suhde.
\[ [\varphi] = \frac{[s]}{[r]} = \frac{1\;\text{m}}{1\;\text{m}} = 1 = 1\;\text{rad} \]
Kiertymä on kiertokulman muutos \(\Delta \varphi\).
Kirjoitetaan asteiden ja radiaanien välinen suhde.
\[ 360^\circ = 2\pi\,\text{rad} \qquad \text{eli} \qquad 1^\circ = \frac{2\pi}{360}\;\text{rad} \qquad \text{eli} \qquad 1\;\text{rad} = \frac{360^\circ}{2\pi} \]
Pyörivän kappaleen positiivinen pyörimissuunta on yleensä vastapäivään.
Pyörimisnopeus eli kierrostaajuus \(n\) kertoo kierrosten \(N\) lukumäärän aikayksikössä \(\Delta t\).
\[ n = \frac{N}{\Delta t} \]
Kirjoitetaan pyörimisnopeuden yksikkö.
\[ [n] = \frac{[N]}{[\Delta t]} = 1\;\frac{1}{\text{s}} \]
Kulmanopeus kertoo kappaleen asennon muuttumisnopeuden.
Kirjoitetaan keskikulmanopeuden yhtälö, kun termit \(\varphi_1\) ja \(\varphi_2\) ovat kappaleen kiertokulmat hetkinä \(t_1\) ja \(t_2\).
\[ \omega_\text{k} = \frac{\Delta \varphi}{\Delta t} = \frac{\varphi_2 - \varphi_1}{t_2 - t_1} \]
Kirjoitetaan kulmanopeuden yksikkö.
\[ [\omega_\text{k}] = \frac{[\Delta \varphi]}{[\Delta t]} = 1\;\frac{\text{rad}}{\text{s}} = 1\;\frac{1}{\text{s}} \]
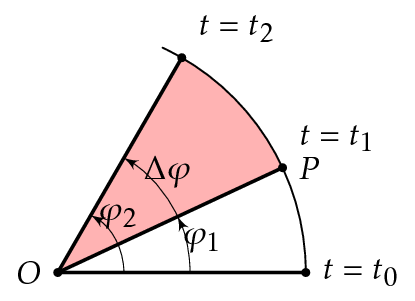
Kirjoitetaan ajanhetkien \(t_1\) ja \(t_2\) välinen keskikulmanopeus.
\[ \omega_\text{k} = \frac{\Delta \varphi}{\Delta t} = \frac{\varphi_2 - \varphi_1}{t_2 - t_1} \]
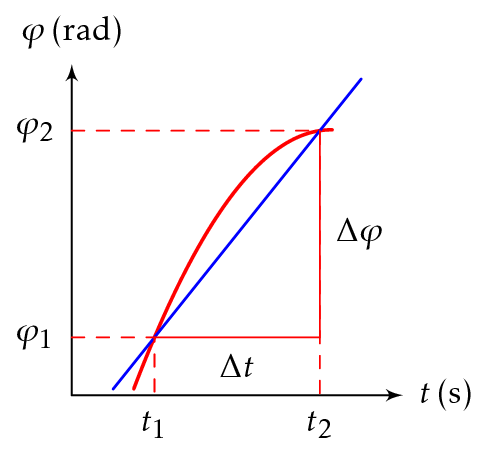
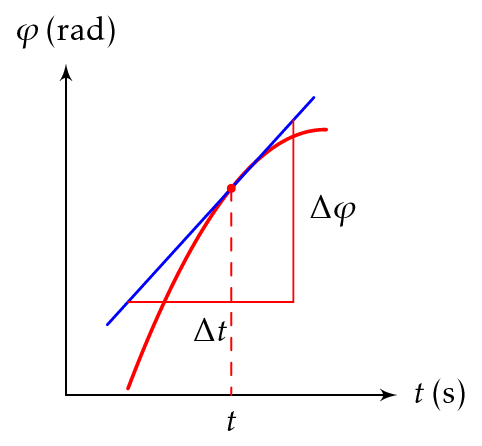
Hetkellinen kulmanopeus on kiertymän kuvaajaan hetkelle \(t\) piirretyn tangentin kulmakerroin.
\[ \omega = \frac{\Delta \varphi}{\Delta t} \]
Kirjoitetaan kulmanopeuden ja pyörimisnopeuden välinen yhteys, kun termi \(\omega\) on kappaleen hetkellinen kulmanopeus ja \(n\) on kappaleen hetkellinen pyörimisnopeus ilmaistuna yksikkönä 1/s.
\[ \omega = 2\pi n \]
Kulmakiihtyvyys on pyörimisliikkeen kulmanopeuden muutosnopeus.
Kirjoitetaan keskikulmakiihtyvyys, kun termit \(\omega_1\) ja \(\omega_2\) ovat kappaleen kulmanopeudet hetkinä \(t_1\) ja \(t_2\).
\[ \alpha_\text{k} = \frac{\Delta \omega}{\Delta t} = \frac{\omega_2 - \omega_1}{t_2 - t_1} \]
Kirjoitetaan kulmakiihtyvyyden yksikkö.
\[ [\alpha_\text{k}] = \frac{[\Delta \omega]}{[\Delta t]} = 1\;\frac{\frac{\text{rad}}{\text{s}}}{\text{s}} = 1\;\frac{\text{rad}}{\text{s}^2} \]
Kirjoitetaan ajanhetkien \(t_1\) ja \(t_2\) välinen keskikulmakiihtyvyys.
\[ \alpha_\text{k} = \frac{\Delta \omega}{\Delta t} = \frac{\omega_2 - \omega_1}{t_2 - t_1} \]
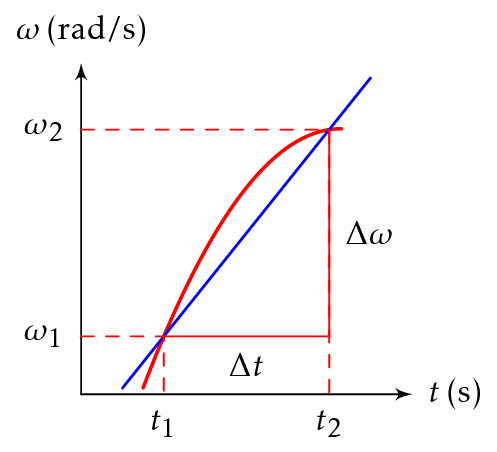
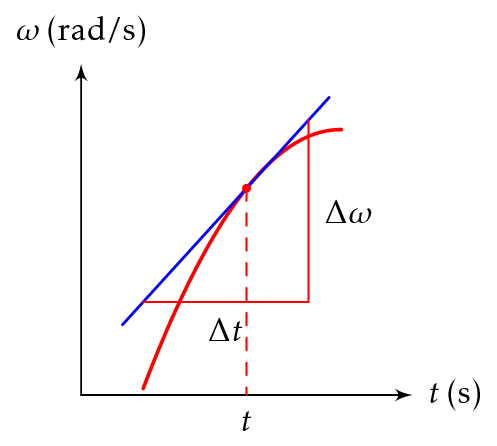
Hetkellinen kulmakiihtyvyys on kulmanopeuden kuvaajaan hetkelle \(t\) piirretyn tangentin kulmakerroin.
\[ \alpha = \frac{\Delta \omega}{\Delta t} \]
Ympyräradalla liikkuvan kappaleen liikettä kuvaavat etenemisliikkeen suureet paikka, nopeus ja kiihtyvyys sekä ympyräliikkeen suureet kulma, kulmanopeus ja kulmakiihtyvyys.
Kaaren pituuden \(s\) ja kiertokulman \(\varphi\) välillä on yhteys. Termi \(r\) on säde.
\[ s = r \varphi \]
Ratanopeuden \(v\) ja kulmanopeuden \(\omega\) välillä on yhteys. Termi \(r\) on säde.
\[ v = r \omega \]
Tasaisessa ympyräliikkeessä kappaleen ratanopeuden suuruus on vakio, mutta nopeuden suunta muuttuu. Normaalikiihtyvyys on kohti ympyräradan keskipistettä.
Kirjoitetaan normaalikiihtyvyys, kun termi \(v\) on kappaleen ratanopeus, \(r\) on ympyräradan säde ja \(\omega\) on kulmanopeus.
\[ a_\text{n} = \frac{v^2}{r} = r \omega^2 \]
Kirjoitetaan tangenttikiihtyvyys, kun termi \(\alpha\) on kappaleen kulmakiihtyvyys ja \(r\) on säde.
\[ a_\text{t} = r \alpha \]
ESIM. 21.
Muuta
a) 45\(^\circ\) radiaaneiksi,
b) 1 rad asteiksi.
RATK.
a)
\[ 45^\circ = \frac{45^\circ}{360^\circ} \cdot 2\pi \;\text{rad} = \frac{2\pi}{8}\;\text{rad} = \frac{\pi}{4}\;\text{rad} \]
b)
\[ 1\;\text{rad} = \frac{360^\circ}{2\pi} = 57,2958^\circ \approx 57,3^\circ \]
VAST.
\(\dfrac{\pi}{4}\;\text{rad}\) ja \(57,3^\circ\)
ESIM. 22.
Sauva (3,0 m) pyörähtää 2,0 rad. Laske kärjen kulkema matka.
RATK.
\(r = 3,0\;\text{m}, \quad \varphi = 2,0\;\text{rad}, \quad s = ?\)
Kaaren pituus lasketaan kulman määritelmästä. Lasketaan matka.
\[ s = r\varphi = 3,0\;\text{m} \cdot 2,0 = 6,0\;\text{m} \]
VAST.
6,0 m
ESIM. 23.
Auton moottorin pyörimisnopeus on \(1\,800\) RPM. Laske
a)
keskimääräinen pyörimisnopeus,
b)
moottorin keskikulmanopeus.
RATK.
\(N = 1\,800, \quad n = ?, \quad \omega_{\text{k}} = ?\)
a)
Lasketaan pyörimisnopeus.
\[ n = \frac{N}{\Delta t} = \frac{1\,800}{60\,\text{s}} = 30\,\frac{1}{\text{s}} \]
b)
Lasketaan kiertymä, kun yksi kierros on \(2 \pi\) rad.
\[ \Delta \varphi = 1\,800 \cdot 2\pi\;\text{rad} = 3\,600\pi\;\text{rad} \]
Lasketaan keskikulmanopeus.
\[ \omega_{\text{k}} = \frac{\Delta \varphi}{\Delta t} = \frac{3\,600\pi\;\text{rad}}{60\;\text{s}} = 60\pi\;\frac{\text{rad}}{\text{s}} \]
VAST.
\(30\;\dfrac{1}{\text{s}}\) ja \(60\pi\;\dfrac{\text{rad}}{\text{s}}\)
ESIM. 24.
Laske moottorin pyörimisnopeus, kun kulmanopeus on 320 rad/s.
RATK.
\(\omega = 320\;\frac{\text{rad}}{\text{s}}, \quad n = ?\)
Lasketaan pyörimisnopeus.
\[ n = \frac{\omega}{2\pi} = \frac{320\;\frac{\text{rad}}{\text{s}}}{2\pi} = 50,9296\;\frac{1}{\text{s}} \approx 51\;\frac{1}{\text{s}} \]
VAST.
\(51\;\frac{1}{\text{s}}\)
ESIM. 25.
Auton moottori saavuttaa yhdessä sekunnissa pyörimisnopeuden 900 RPM. Laske keskikulmakiihtyvyys.
RATK.
\(\Delta t = 1\;\text{s}, \quad \omega_0 = 0\;\frac{\text{rad}}{\text{s}}, \quad \omega = 900\;\frac{\text{rad}}{\text{s}}, \quad \alpha_{\text{k}} = ?\)
Lasketaan kulmanopeuden muutos.
\[ \Delta \omega = \omega - \omega_0 = 2\pi\;\text{rad} \cdot 900\;\frac{1}{\text{min}} - 0\;\frac{1}{\text{s}} = 2\pi\;\text{rad} \cdot 900\;\frac{1}{60\;\text{s}} - 0\;\frac{1}{\text{s}} = 94,2478\;\frac{\text{rad}}{\text{s}} \]
Lasketaan keskikulmakiihtyvyys.
\[ \alpha_{\text{k}} = \frac{\Delta \omega}{\Delta t} = \frac{94,2478\;\dfrac{\text{rad}}{\text{s}}}{1\,\text{s}} \approx 94\;\frac{\text{rad}}{\text{s}^2} \]
VAST.
94 rad/s\(^2\)
Täysi kulma on
12 Tasainen ja tasaisesti kiihtyvä pyörimisliike
Kappaleen kulmanopeus \(\omega\) on vakio tasaisessa pyörimisliikkeessä.
Kirjoitetaan kiertokulma, kun termi \(\varphi\) on kappaleen kiertokulma hetkellä \(t\), \(\varphi_0\) on kiertokulma hetkellä \(t = 0\,\text{s}\) ja \(\omega\) on kulmanopeus.
\[ \varphi = \varphi_0 + \omega t \]
Kuvaaja tasaisen pyörimisliikkeen kulmanopeudelle \(t\omega\)-koordinaatistossa on vaakasuora suora.
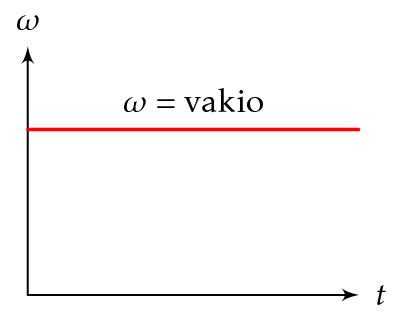
Kuvaaja tasaisen pyörimisliikkeen kiertokulmalle \(t\varphi\)-koordinaatistossa on nouseva tai laskeva suora.
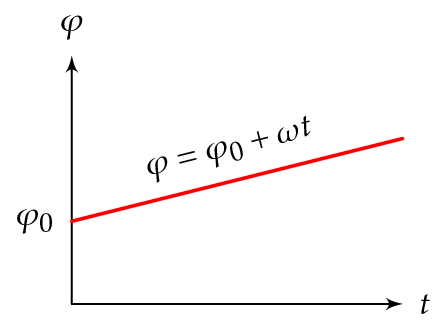
Kulmakiihtyvyys \(\alpha\) on vakio tasaisesti kiihtyvässä pyörimisliikkeessä.
Kuvaaja tasaisesti kiihtyvälle pyörimisliikkeelle \(t\alpha\)-koordinaatistossa on vaakasuora suora.
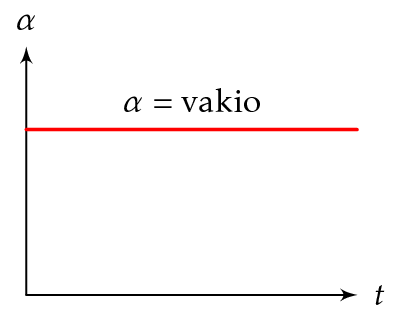
Kiertokulman muutos \(\Delta \varphi\) on \(t\omega\)-koordinaatistossa kulmanopeussuoran ja aika-akselin rajoittama pinta-ala.
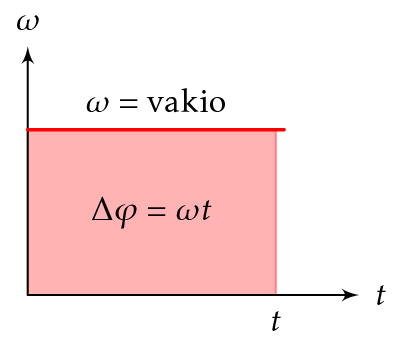
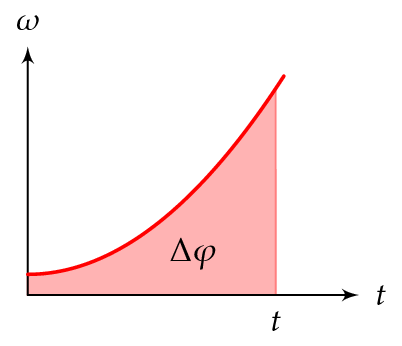
Tasaisesti kiihtyvässä pyörimisliikeessä, kun termi \(\alpha\) on kappaleen kulmakiihtyvyys, \(\omega\) on kulmanopeus hetkellä \(t\), \(\omega_0\) on kulmanopeus hetkellä \(t = 0\,\text{s}\), \(\varphi\) on kiertokulma hetkellä \(t\) ja \(\varphi_0\) on kiertokulma hetkellä \(t = 0\,\text{s}\),
- kulmakiihtyvyys
\[ \alpha = \text{vakio}, \]
- kulmanopeus
\[ \omega = \omega_0 + \alpha t, \]
- ja kiertokulma
\[ \varphi = \varphi_0 + \omega t + \frac{1}{2}\alpha t^2. \]
Kuvaaja tasaisesti kiihtyvälle pyörimisliikkeelle \(t\varphi\)-koordinaatistossa on paraabeli.
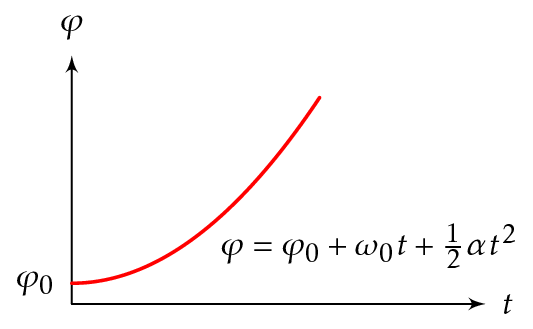
Etenemis- ja pyörimisliikkeiden yhtälöt vastaavat toisiaan.
| etenemisliike | pyörimisliike |
|---|---|
| paikka \(x\) | kiertokulma \(\varphi\) |
| nopeus \(v\) | kulmanopeus \(\omega\) |
| kiihtyvyys \(a\) | kulmakiihtyvyys \(\alpha\) |
| etenemisliike | pyörimisliike |
|---|---|
| tasainen liike \(v = \text{vakio}\) \(x = x_0 + vt\) |
tas. pyör.liike \(\omega = \text{vakio}\) \(\varphi = \varphi_0 + \omega t\) |
| tas. kiiht. liike \(a = \text{vakio}\) \(x = x_0 + v_0 t + \frac{1}{2}at^2\) \(v = v_0 + at\) |
tas. kiiht. pyör.liike \(\alpha = \text{vakio}\) \(\varphi = \varphi_0 + \omega_0 t + \frac{1}{2}\alpha t^2\) \(\omega = \omega_0 + \alpha t\) |
ESIM. 26.
Moottorin kulmanopeus on \(60\pi\;\frac{\text{rad}}{\text{s}}\). Laske kiertymä 0,2 sekunnissa.
RATK.
\(\omega = 60\pi\;\frac{\text{rad}}{\text{s}}, \quad t = 0,2\;\text{s}, \quad \Delta \varphi = ?\)
Lasketaan kiertymä.
\[ \Delta \varphi = \omega t = 60\pi\;\frac{\text{rad}}{\text{s}} \cdot 0,2\;\text{s} = 12\pi\;\text{rad} \]
VAST.
\(12\pi\,\text{rad}\)
ESIM. 27.
Auton moottorin pyörimisnopeus kasvaa tasaisesti kahdessa sekunnissa alkunopeudesta \(900\;\text{RPM}\) loppunopeuteen \(3\,600\;\text{RPM}\). Laske
a) kulmakiihtyvyys,
b) moottorin kulmanopeus yhden sekunnin kuluttua,
c) kierrosten lukumäärä kiihdytyksen aikana.
RATK.
\(\omega_0 = 900\;\text{RPM}, \quad \omega = 3\,600\;\text{RPM}, \quad \alpha = ?, \quad \omega = ?, \quad N = ?\)
a)
Lasketaan kulmakiihtyvyys yhtälöstä \(\omega = \omega_0 + \alpha t\).
\[ \alpha = \frac{\omega - \omega_0}{t} = \frac{3\,600 \cdot \dfrac{2\pi\;\text{rad}}{60\;\text{s}} - 900 \cdot \dfrac{2\pi\;\text{rad}}{60\;\text{s}}}{2,0\;\text{s}} = 141,3717\;\frac{\text{rad}}{\text{s}^2} \approx 140\;\frac{\text{rad}}{\text{s}^2} \]
b)
Kirjoitetaan moottorin kulmanopeus hetkellä \(t\).
\[ \omega = \omega_0 + \alpha t. \]
Lasketaan kulmanopeus.
\[ \omega = 900 \cdot \dfrac{2\pi\;\text{rad}}{60\;\text{s}} + 141,3717\;\frac{\text{rad}}{\text{s}^2} \cdot 1,0\;\text{s} = 235,6194\;\frac{\text{rad}}{\text{s}} \approx 240\;\frac{\text{rad}}{\text{s}} \]
c)
Kirjoitetaan moottorin kiertokulma hetkellä \(t\).
\[ \varphi = \varphi_0 + \omega_0 t + \frac{1}{2}\alpha t^2 \]
Lasketaan kiertymä, kun alkuhetkellä \(\varphi_0 = 0\).
\[ \Delta \varphi = 900 \cdot \frac{2\pi\;\text{rad}}{60\;\text{s}} \cdot 2\;\text{s} + \frac{1}{2} \cdot 141,3717\;\frac{\text{rad}}{\text{s}^2} \cdot (2\;\text{s})^2 = 471,2389\;\text{rad} \approx 470\;\text{rad} \]
Lasketaan kierrokset.
\[ N = \frac{\Delta \varphi}{2\pi} = \frac{471,2389\,\text{rad}}{2\pi\,\text{rad}} = 75,0000 \approx 75 \]
VAST. Kulmakiihtyvyys on 140 rad/s\(^2\), kulmanopeus on sekunnin kuluttua 240 rad/s ja kierroksia kertyy kiihdytyksen aikana 75.
ESIM. 28.
Lingon pyörimisnopeus hetkellä \(t\) on \(110\;\text{RPM}\) ja sen kulmakiihtyvyys on \(1\;\frac{\text{rad}}{\text{s}}\) Laske lingossa olevan kiven kokema kiihtyvyys, kun narun pituus on \(92\;\text{cm}\).
RATK.
\(n = 110\;\frac{1}{\text{min}}, \quad \alpha = 1\;\frac{\text{rad}}{\text{s}^2}, \quad r = 0,92\;\text{m}, \quad a = ?\)
Lasketaan normaalikiihtyvyys, kun \(\omega = 2 \pi n\).
\[ a_\text{n} = \frac{v^2}{r} = r \omega^2 = r \cdot 4\pi^2 \cdot n^2 = 0,92\;\text{m} \cdot 4\pi^2 \cdot \left(\frac{110}{60}\;\frac{1}{\text{s}}\right)^2 = 122,0706\;\frac{\text{m}}{\text{s}^2} \]
Lasketaan tangenttikiihtyvyys.
\[ a_\text{t} = r \alpha = 0,92\;\text{m} \cdot 1\;\frac{\text{rad}}{\text{s}^2} = 0,92\;\frac{\text{m}}{\text{s}^2} \]
Lasketaan kokonaiskiihtyvyys.
\[ a = \sqrt{a^2_\text{n} + a^2_\text{t}} = \sqrt{\left(122,0706\;\frac{\text{m}}{\text{s}^2}\right)^2 + \left(0,92\;\frac{\text{m}}{\text{s}^2}\right)^2} = 122,0741\;\frac{\text{m}}{\text{s}^2} \approx 120\;\frac{\text{m}}{\text{s}^2} \]
VAST.
\(120\;\frac{\text{m}}{\text{s}^2}\)
Etenemisliikkeen ja pyörimisliikkeen vastinparit ovat
13 Hitausmomentti kuvaa kappaleen pyörimishitautta
Hitausmomentti \(J\) kuvaa kappaleen kykyä vastustaa pyörimisliikkeen muutosta. Massa \(m\) kuvaa kappaleen kykyä vastustaa liiketilan muutosta etenemisliikkeessä.
Kappaleen hitausmomentti tietyn akselin suhteen on summa saman akselin suhteen laskettujen osien hitausmomenteista.
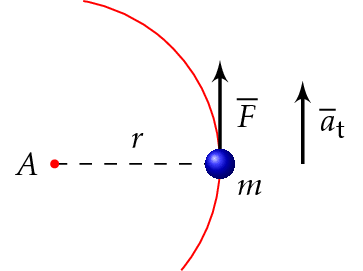
Kirjoitetaan yllä olevan kuvan kappaleen momentti.
\[ M = Fr = ma_\text{t}r = m \alpha r r = mr^2 \alpha = J \alpha \]
Edellisessä yhtälössä \(J = mr^2\) kuvaa pistemäisen kappaleen pyörimishitautta, jota kutsutaan kappaleen hitausmomentiksi.
Kirjoitetaan hitausmomentin yksikkö.
\[ [J] = [m][r^2] = 1\;\text{kgm}^2 \]
Pyörivän kappaleen pyörimisliike ei muutu, jos siihen ei vaikuta momenttia. Pyörimisliikkeelle pätee jatkuvuus samalla tavalla kuin on etenemisliikkeelle.
| Kappale | Hitausmomentti |
|---|---|
| pistemäinen kappale | \(J = mr^2\) |
| ohutseinäinen putki, putken akselin suhteen | \(J = mr^2\) |
| umpinainen sylinteri, sylinterin akselin suhteen | \(J = \frac{1}{2}mr^2\) |
| ympyrälevy, kp. kautta, levyä vast. kohtis. akselin suhteen | \(J = \frac{1}{2}mr^2\) |
| ympyrälevy, halkaisijan suhteen | \(J = \frac{1}{4}mr^2\) |
| ohut pallokuori, halkaisijan suhteen | \(J = \frac{2}{3}mr^2\) |
| umpinainen pallo, halkaisijan suhteen | \(J = \frac{2}{5}mr^2\) |
| sauva, kp. kautta, sauvaa vast. kohtis. akselin suhteen | \(J = \frac{1}{12}ml^2\) |
| sauva, toisen pään kautta, sauvaa vast. kohtis. akselin suhteen | \(J = \frac{1}{3}ml^2\) |
Huomaa edellisessä taulukossa, että esimerkiksi sylinterin pituus ei vaikuta sen hitausmomenttiin, jos massa ei muutu.
ESIM. 29.
Kuvan napakelkka muodostuu kahdesta erillisestä pistemäisestä kappaleesta, jotka on yhdistetty jäykällä varrella akseliin \(A\). Laske systeemin hitausmomentti akselin suhteen.
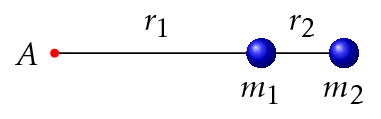
RATK.
\(m_1 = 54\;\text{kg}, \quad m_2 = 73\;\text{kg}, \quad r_1 = 2,5\;\text{m}, \quad r_2 = 1,0\;\text{m}\)
Pistemäisen kappaleen hitausmomentti \(J = mr^2\). Lasketaan systeemin hitausmomentti akselin \(A\) suhteen.
\[ J_\text{A} = \Sigma m_i r^2_i = 54\;\text{kg} \cdot (2,5\;\text{m})^2 + 73\;\text{kg} \cdot ((2,5 + 1,0)\;\text{m})^2 = 1\,231,75\;\text{kgm}^2 \approx 1\,230\;\text{kgm}^2 \]
VAST.
\(1\,230\;\text{kgm}^2\)
ESIM. 30.
Vauhtipyöräksi on kaksi vaihtoehtoa. Ensimmäinen on ohut ympyrävanne ja toinen on ohut umpinainen sylinteri. Laske molempien vaihtoehtojen hitausmomentti, kun niiden molempien massa on \(15,5\;\text{kg}\) ja kun säde on \(67\;\text{cm}\).
RATK.
\(m = 15,5\;\text{kg}, \quad r = 0,67\;\text{m}, \quad J_1 = ?, \quad J_2 = ?\)
Lasketaan ohuen ympyrävanteen hitausmomentti.
\[ J_1 = mr^2 = 15,5\;\text{kg} \cdot (0,67\;\text{m})^2 = 6,9580\;\text{kgm}^2 \approx 7,0\;\text{kgm}^2 \]
Lasketaan ohuen sylinterin hitausmomentti.
\[ J_2 = \frac{1}{2}mr^2 = \frac{1}{2} \cdot 15,5\;\text{kg} \cdot (0,67\;\text{m})^2 = 3,4790\;\text{kgm}^2 \approx 3,5\;\text{kgm}^2 \]
VAST.
\(7,0\;\text{kgm}^2\) ja \(3,5\;\text{kgm}^2\)
Hitausmomentti vastaa etenemisliikkeessä
14 Pyörimisen peruslaki ja pyörimismäärä
Kappaleen kulmakiihtyvyyden \(\alpha\) aiheuttaa siihen vaikuttava kokonaismomentti eli voimien momenttien summa akselin suhteen.
Kirjoitetaan pyörimisen peruslaki, jossa termi \(\Sigma M_\text{A}\) on kappaleeseen vaikuttava akselin \(A\) suhteen laskettu kokonaismomentti, \(J_\text{A}\) on hitausmomentti akselin \(A\) suhteen ja \(\alpha\) on kulmakiihtyvyys.
\[ \Sigma M_\text{A} = J_\text{A} \alpha \]
Pyörimisen peruslakia ja etenevän liikkeen dynamiikan peruslakia voidaan soveltaa samalla tavalla. Dynamiikan peruslain mukaan kappaleen kiihtyvyyden \(\overline{a}\) aiheuttaa siihen vaikuttava kokonaisvoima \(\overline{F}\).
\[ \Sigma \overline{F} = m \overline{a} \]
Pyörimisen peruslain avulla voidaan ratkaista kappaleen kiertymä, kulmanopeus tai kulmakiihtyvyys tietyllä hetkellä.
Kappale on helppo saada pyörimään tai sen pyöriminen on helppo pysäyttää, jos sen hitausmomentti on pieni. Pyörimisen hidastuvuuden aiheuttama momentti on kitkamomentti.
Pyörivän kappaleen pyörimismäärä eli liikemäärämomentti \(L\) riippuu kappaleen hitausmomentista \(J\) tarkasteluakselin suhteen ja kulmanopeudesta \(\omega\).
\[ L = J \omega \]
Kirjoitetaan pyörimismäärän yksikkö.
\[ [L] = [J][\omega] = 1\;\text{kgm}^2 \cdot 1\;\frac{\text{rad}}{\text{s}} = 1\;\text{kgm}^2 \frac{\text{rad}}{\text{s}} = 1\;\frac{\text{kgm}^2}{\text{s}} = 1\;\text{Nms} \]
Kappaleen hitausmomentti ja pyörimismäärä riippuvat siitä, minkä akselin suhteen ne lasketaan.
Muista, että kappaleen liikemäärä \(\overline{p}\) riippuu kappaleen massasta ja nopeudesta. Systeemin liikemäärä säilyy, jos siihen vaikuttavien ulkoisten voimien summa on nolla.
\[ \overline{p} = m \overline{v} \]
Pyörimismäärä \(L\) säilyy, jos ulkoinen kokonaismomentti on nolla, kappaleen hitausmomentti \(J\) ja sen kulmanopeus \(\omega\) ei muutu tai jos tulo \(L = J \omega\) on vakio. Termi \(J_1\) on kappaleen hitausmomentti alussa ja \(\omega_1\) on kulmanopeus alussa. Vastaavasti \(J_2\) ja \(\omega_2\) ovat loppuarvot.
\[ J_1 \omega_1 = J_2 \omega_2 \]
Pyörimismäärän säilymisestä seuraa, että
systeemin hitausmomentin muuttuessa sen kulmanopeus muuttuu,
systeemin jonkin osan pyöriessä myötäpäivään, sen loppuosa pyörii vastapäivään,
pyörimisakselin suunta säilyy.
ESIM. 31.
Rengas kiihdytetään levosta kulmanopeuteen 92 rad/s, ja sen hitausmomentti on 12,7 kgm\(^2\). Laske renkaan akseliin vaikuttava momentti, kun kiihdytysaika on puoli minuuttia.
RATK.
\(\Delta \omega = 92\;\frac{\text{rad}}{\text{s}}, \quad J = 12,7\;\text{kgm}^2, \quad \Delta t = 30\;\text{s}, \quad M = ?\)
Kirjoitetaan pyörimisen peruslain mukainen yhtälö.
\[ \Sigma M_\text{A} = J_\text{A} \alpha = J_\text{A} \frac{\Delta \omega}{\Delta t} \]
Lasketaan momentti.
\[ M = 12,7\;\text{kgm}^2 \cdot \frac{92\;\frac{1}{\text{s}}}{30\;\text{s}} = 38,9467\;\frac{\text{kgm}^2}{\text{s}^2} \approx 39\;\text{Nm} \]
VAST.
\(39\;\text{Nm}\)
ESIM. 32.
Viisi lasta leikkii karusellissa, jonka kulmanopeus on aluksi 1,3 rad/s. Lapsista kaksi kullannuppua siirtyy karusellissa kohti pyörimisen keskipistettä, jolloin kulmanopeus nousee arvoon 1,8 rad/s. Laske alkuperäisen systeemin hitausmomentin suhde lopputilanteen hitausmomenttiin. Kitkaa ja muita vastusvoimia ei tarvitse huomioida.
RATK.
\(\omega_1 = 1,3\;\frac{\text{rad}}{\text{s}}, \quad \omega_2 = 1,8\;\frac{\text{rad}}{\text{s}}\)
Olkoon kulmanopeudet ja hitausmomentit aluksi ja lopuksi \(\omega_1\), \(\omega_2\), \(J_1\) ja \(J_2\).
Pyörimismäärä säilyy.
\[ J_1 \omega_1 = J_2 \omega_2 \quad \text{eli} \quad J_2 = J_1 \frac{\omega_1}{\omega_2} = J_1 \frac{1,3\;\frac{\text{rad}}{\text{s}}}{1,8\;\frac{\text{rad}}{\text{s}}} = 0,7222 \cdot J_1 \approx 0,72 \cdot J_1 \]
VAST.
Hitausmomentti on 72 prosenttia alkuperäisestä.
Ratkaisun vaiheet
ESIM. 33.
Ohut sylinterivauhtipyörä pyörii kitkatta keskipisteestään kulkevan akselin ympäri. Pyörän massa on \(8,3\;\text{kg}\) ja sen säde on \(29\;\text{cm}\). Pyörää kiihdytetään kehän ympäri kiedotulla narulla 55 newtonin voimalla. Pyörä on pystyasennossa kuvan mukaisesti.
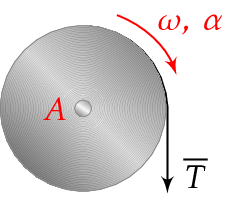
Laske
a)
pyörän kulmakiihtyvyys,
b)
akselin tukivoima pyörään.
RATK.
\(m = 8,3\;\text{kg}, \quad r = 0,29\;\text{m}, \quad T = 55\;\text{N}, \quad \alpha = ?, \quad N = ?\)
a)
1 Vauhtipyörään vaikuttavat paino \(\overline{G}\), akselin tukivoima \(\overline{N}\) ja narun jännitysvoima \(\overline{T}\). Kitkavoimia ei ole.
Vauhtipyörään sen akselin suhteen aiheuttaa momentin vain narun jännitysvoima, koska painon ja tukivoiman varret ovat nollia.
2 Piirretään voimakuvio.
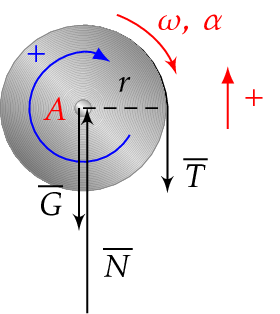
3 Kirjoitetaan momentti akselin \(A\) suhteen.
\[ \Sigma M_\text{A} = Tr \]
4 Kirjoitetaan ohuen sylinterin hitausmomentti akselin \(A\) suhteen.
\[ J_\text{A} = \frac{1}{2}mr^2 \]
5 Kirjoitetaan pyörimisen peruslain \(\Sigma M_\text{A} = J_\text{A} \alpha\) mukainen pyörän pyörimisen liikeyhtälö.
\[ Tr = \frac{1}{2}mr^2 \alpha \]
Ratkaistaan kulmakiihtyvyys.
\[ \alpha = \frac{Tr}{\frac{1}{2}mr^2} = \frac{T}{\frac{1}{2}mr} \]
Lasketaan kulmakiihtyvyys.
\[ \alpha = \frac{55\;\text{N}}{\frac{1}{2} \cdot 8,3\;\text{kg} \cdot 0,29\;\text{m}} = 45,7000\;\frac{1}{\text{s}^2} \approx 46\;\frac{\text{rad}}{\text{s}^2} \]
6 Saatu kulmakiihtyvyys vaikuttaa järkevältä ja sen suuruusluokka on oikea.
b)
Kirjoitetaan dynamiikan peruslain mukainen yhtälö.
\[ \Sigma \overline{F} = m \overline{a} \quad \text{eli} \quad \overline{N} + \overline{G} + \overline{T} = m \overline{a} \]
Vauhtipyörällä ei ole etenemisliikkeen kiihtyvyyttä.
\[ \overline{a} = \overline{0} \quad \text{ja} \quad \overline{N} + \overline{G} + \overline{T} = \overline{0} \]
Positiivinen suunta on ylöspäin. Kirjoitetaan yhtälö skalaarimuodossa ja lasketaan tukivoima.
\[ N - G - T = 0 \quad \text{eli} \quad N = G + T = 8,3\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} + 55\;\text{N} = 136,423\;\text{N} \approx 140\;\text{N} \]
VAST.
\(46\;\frac{\text{rad}}{\text{s}^2}\) ja \(140\;\text{N}\)
Pyörimismäärä säilyy, jos systeemin
15 Pyöriminen ja eteneminen on vierimistä
Kappaleen liikettä voidaan kuvata pelkkänä pyörimisenä, kun se pyörii liikkumattoman akselinsa ympäri. Kappale ei siis etene, mutta se pyörii akselinsa ympäri.
Kappaleen pyörimisenergia eli rotaatioenergia on mekaanista energiaa ja se riippuu kappaleen hitausmomentista \(J\) ja kulmanopeudesta \(\omega\).
\[ E_\text{r} = \frac{1}{2} J \omega^2 \]
Edellinen voidaan ymmärtää siten, että pyörivän kappaleen osat \(m_\text{i}\) liikkuvat ympyrärataa nopeudella \(v_\text{i}\) akselin ympäri kulmanopeudella \(\omega\). Tutkitaan osien yhteenlaskettua liike-energiaa, kun \(v_\text{i} = r_\text{i} \omega\).
\[ E_\text{k} = \frac{1}{2} m_1 v^2_1 + \frac{1}{2} m_2 v^2_2 +\ldots = \frac{1}{2} m_1 r^2_1 \omega^2 + \frac{1}{2} m_2 r^2_2 \omega^2 +\ldots = \frac{1}{2} (m_1 r^2_1 + m_2 r^2_2 +\ldots ) \omega^2 = \frac{1}{2} (\Sigma m_\text{i} r^2_\text{i}) \omega^2 = \frac{1}{2} J \omega^2 \]
Kappaleen etenemisliikkeen liike-energiaa voidaan kutsua myös translaatioenergiaksi.
Jos kappaleen massakeskipiste etenee nopeudella \(\overline{v}\), ja kappale pyörii samalla massakeskipisteen kautta kulkevan akselin ympäri kulmanopeudella \(\omega\), sen liike-energia on etenemisliikkeen energian \(E_\text{t}\) ja pyörimisliikkeen energian \(E_\text{r}\) summa.
\[ E_\text{k} = E_\text{t} + E_\text{r} = \frac{1}{2} mv^2 + \frac{1}{2} J_\text{p} \omega^2 \]
Edellisessä yhtälössä termi \(m\) on kappaleen massa, \(v\) on kappaleen massakeskipisteen nopeus, \(J_\text{p}\) on kappaleen hitausmomentti massakeskipisteen kautta kulkevan akselin suhteen ja \(\omega\) on kappaleen kulmanopeus massakeskipisteen kautta kulkevan akselin ympäri. Huomaa myös alaindeksit, jotka tarkoittavat siis translaatiota ja rotaatiota.
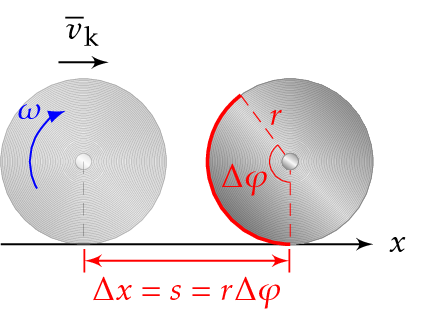
Kappale vierii, kun sen eteneminen alustalla on pyörimistä eikä liukumista. Kirjoitetaan vierimisehto.
\[ s = r \varphi, \quad v_\text{p} = r \omega \quad \text{ja} \quad a_\text{p} = r \alpha \]
Edellisessä yhtälössä termi \(v_\text{p}\) on vierivän kappaleen painopisteen etenemisnopeus ja \(a_\text{p}\) on kiihtyvyys.
ESIM. 34.
Laske umpinaisen pallon pyörimisenergia, kun sen massa on 425 kg, säde on 1,14 m ja sen kulmanopeus keskipisteen kautta kulkevan akselin ympäri on 0,75 rad/s.
Pallo pyörii etenemättä keskipisteen kautta kulkevan akselinsa ympäri.
RATK.
\(m = 425\;\text{kg}, \quad r =1,14\;\text{m}, \quad \omega = 0,75\;\frac{\text{rad}}{\text{s}}, \quad E_\text{r} = ?\)
Pallo pyörii etenemättä. Lasketaan pyörismisenergia.
\[ E_\text{r} = \frac{1}{2} J \omega^2 = \frac{1}{2} \cdot \frac{2}{5} m r^2 \omega^2 = \frac{1}{5} \cdot 425\;\text{kg} \cdot (1,14\;\text{m})^2 \cdot \left(0,75\;\frac{\text{rad}}{\text{s}}\right)^2 = 62,1371\;\text{J} \approx 62\;\text{J} \]
VAST.
\(62\;\text{J}\)
ESIM. 35.
Ohutseinäinen pallo vierii levosta lähtien pitkin kaltevaa tasoa. Laske pallon nopeus tason alapäässä, kun pallon massa on \(41\;\text{kg}\) ja tason muodostama korkeusero on \(3,4\;\text{m}\). Vastusvoimia ei ole.
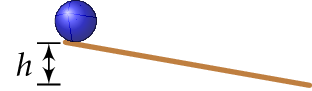
RATK.
\(m = 41\;\text{kg}, \quad h = 3,4\;\text{m}, \quad v = ?\)
Mekaaninen energia säilyy, koska vastusvoimia ei ole. Mekaaninen energia muodostuu pallon potentiaali- ja kokonaisliike-energioiden summasta.
\[ E_{\text{pa}} + E_{\text{ta}} + E_{\text{ra}} = E_{\text{pl}} + E_{\text{tl}} + E_{\text{rl}} \]
Koska mekaaninen energia säilyy, kappaleen potentiaalienergia muuntuu etenemisliikkeen ja pyörimisliikkeen energiaksi.
Olkoon potentiaalienergian nollataso kaltevan tason loppupää. Pallolla ei ole aluksi etenemisliikkeen energiaa eikä pyörimisliikkeen energiaa.
\[ mgh = \frac{1}{2}mv^2 + \frac{1}{2}J\omega^2 \]
Ratkaistaan nopeus \(v\), kun ohutseinäisen pallon hitausmomentti on \(J = \frac{2}{3}mr^2\) ja kulmanopeus on \(\omega = \frac{v}{r}\).
\[ mgh = \frac{1}{2}mv^2 + \frac{1}{2} \cdot \frac{2}{3}mr^2 \cdot \left(\frac{v}{r}\right)^2 \quad \text{eli} \quad gh = \frac{1}{2} v^2 + \frac{1}{3} v^2 = \frac{5}{6} v^2 \quad \text{eli} \quad v = \sqrt{\frac{6}{5}gh} \]
Lasketaan nopeus.
\[
v
= \sqrt{\frac{6}{5} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 3,4\;\text{m}}
= 6,3265\;\frac{\text{m}}{\text{s}}
\approx 6,3\;\frac{\text{m}}{\text{s}}
\]
VAST.
\(6,3\;\frac{\text{m}}{\text{s}}\)
Kappaleen pyörimisenergia eli rotaatioenergia riippuu
16 Työperiaate pyörimisliikkeessä
Voiman momentti tekee työn \(W\).
\[ W = Fs = Fr \Delta \varphi = M \Delta \varphi \]
Edellisessä yhtälössä termi \(F\) on kappaleeseen kohdistuva voima, \(r\) on säde, \(M\) on kappaletta vääntävä momentti ja \(\Delta \varphi\) on kappaleen kiertymä.
Kirjoitetaan momentin tekemän työn yksikkö.
\[ [W] = [M][\Delta \varphi] = 1\;\text{Nm} = 1\;\text{J} \]
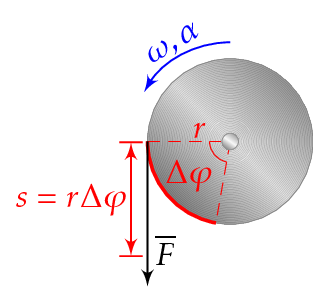
Kokonaismomentin \(\Sigma M\) tekemä työ \(W\) on yhtä suuri kuin kappaleen pyörimisenergian muutos \(\Delta E_\text{r}\). Kirjoitetaan pyörimisen työperiaate.
\[ W = \Sigma M \Delta \varphi = E_\text{rl} - E_\text{ra} = \frac{1}{2}J\omega^2 - \frac{1}{2}J\omega^2_0 \]
Edellisessä yhtälössä termi \(\Delta \varphi\) on kappaleen kokonaiskiertymä, \(J\) on kappaleen hitausmomentti, \(\omega\) on kappaleen loppukulmanopeus ja \(\omega_0\) on kappaleen alkukulmanopeus.
Kappaleen eteneminen ja pyöriminen eivät riipu toisistaan, sillä kappale voi liikkua millä tahansa nopeudella ja sillä voi olla mikä tahansa kulmanopeus.
Pyörimisliikkeen erikoistapaus on vierimisliike, jossa kappaleen eteneminen ja pyöriminen ovat yhteen kytkettyjä vierimisehdon mukaisesti. Vierimisliikkeessä ei tapahdu liukumista.
\[ v = r \omega \]
Jos kappale on sekä etenemis- että pyörimisliikkeessä, kappaleen
- etenemisen määrää dynamiikan peruslaki
\[ \Sigma \overline{F} = m \overline{a} \]
- pyörimisen määrää pyörimisen peruslaki
\[ \Sigma M = J \alpha \]

| Eteneminen | Vieriminen | ||
|---|---|---|---|
| paikka | \(x\) | kiertokulma | \(\varphi\) |
| siirtymä | \(\Delta x\) | kiertymä | \(\Delta \varphi\) |
| nopeus | \(\overline{v}\) | kulmanopeus, pyörimisnopeus \(n\) | \(\omega = 2\pi n\) |
| kiihtyvyys | \(\overline{a}\) | kulmakiihtyvyys | \(\alpha\) |
| massa | \(m\) | hitausmomentti | \(J\) |
| voima | \(\overline{F}\) | momentti | \(M\) |
| liikemäärä | \(\overline{p}=m\overline{v}\) | pyörimismäärä | \(\alpha\) |
| liike-energia | \(E_\text{t}=\frac{1}{2}mv^2\) | pyörimisenergia | \(E_\text{r}=\frac{1}{2}J\omega^2\) |
| työ | \(W=F\Delta x\) | työ | \(W=M\Delta\varphi\) |
| Massapiste | Jäykkä kappale |
|---|---|
| Liikeyhtälö \(\overline{F} = m\overline{a}\) |
Etenemisen liikeyhtälö \(\overline{F} = m\overline{a}\) Pyörimisen liikeyhtälö \(\Sigma M = J \alpha\) |
| Impulssiperiaate \(\overline{F}\Delta t=m\Delta\overline{v}=\Delta\overline{p}\) Työperiaate \(F\Delta x=\Delta(\frac{1}{2}mv^2)=\Delta E_\text{t}\) |
Etenemisen työperiaate \(F\Delta x=\Delta(\frac{1}{2}mv^2)\) Pyörimisen työperiaate \(M\Delta\varphi=\Delta(\frac{1}{2}J\omega^2)\) |
| Liikemäärä säilyminen \(\Delta\overline{p}=\Delta(m\overline{v})=0\) Mekaanisen energian säilyminen \(\Delta(E_\text{t}+E_\text{p}=0\) |
Pyörimismäärän säilyminen \(\Delta L=\Delta(J\omega)=0\) Mekaanisen energian säilyminen etenemisessä ja pyörimisessä \(\Delta(E_\text{t}+E_\text{r}+E_\text{p})=0\) |
ESIM. 36.
Vauhtipyörä pyörii kitkattomasti akselinsa ympäri. Pyörän säde on 0,31 m ja sen hitausmomentti on 2,4 kgm\(^2\). Laske pyörän saama kulmanopeus, kun sitä vedetään kehälle kiedotusta liukumattomasta narusta 5,0 newtonin voimalla 100,0 radiaanin kiertymän. Pyörä on aluksi levossa.
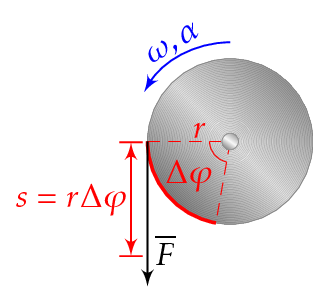
RATK.
\(r = 0,32\;\text{m}, \quad J = 2,4\;\text{kgm}^2 \quad F = 5,0\;\text{N}, \quad \Delta\varphi = 100,0\;\text{rad}, \quad \omega = ?\)
Ratkaisutapa 1.
Energiaperiaatteen mukaan kokonaismomentin tekemä työ on yhtä suuri kuin on pyörimisenergian muutos.
\[ W = \Sigma M \Delta\varphi = \frac{1}{2}J\omega^2 - \frac{1}{2}J\omega^2_0 \]
Vauhtipyörä on aluksi levossa, ja \(\Sigma M = Fr\).
\[ \Sigma M \Delta\varphi = Fr \Delta\varphi = \frac{1}{2}J\omega^2 \]
Ratkaistaan ja lasketaan kulmanopeus.
\[ \omega = \sqrt{\frac{2Fr\Delta\varphi}{J}} = \sqrt{\frac{2 \cdot 5,0\;\text{N} \cdot 0,32\;\text{m} \cdot 100,0\;\text{rad}}{2,4\;\text{kgm}^2}} = 11,5470\;\frac{\text{rad}}{\text{s}} \approx 12\;\frac{\text{rad}}{\text{s}} \]
Ratkaisutapa 2.
Vauhtipyörään vaikuttaa vakiomomentti. Kulmakiihtyvyys on vakio ja pyörimisliike on tasaisesti kiihtyvää.
Kirjoitetaan kulma \(\varphi\) hetkellä \(t\).
\[ \varphi = \varphi_0 + \omega_0 t + \frac{1}{2}\alpha t^2 \]
Pyörä on aluksi levossa, joten \(\varphi_0 = 0\) ja \(\omega_0 = 0\). Kirjoitetaan kulma \(\varphi\) hetkellä \(t\) uudestaan.
\[ \varphi = \frac{1}{2}\alpha t^2 \]
Ratkaistaan aika \(t\).
\[ t = \sqrt{\frac{2\varphi}{\alpha}} \]
Kirjoitetaan kulmanopeus hetkellä \(t\).
\[ \omega = \alpha t = \alpha \cdot \sqrt{\frac{2\varphi}{\alpha}} = \sqrt{2\varphi\alpha} \]
Kirjoitetaan pyörimisliikkeen peruslaki.
\[ \Sigma M = Fr = J\alpha \quad \text{eli} \quad \alpha = \frac{Fr}{J} \]
Ratkaistaan ja lasketaan kulmanopeus \(\omega\).
\[ \omega = \sqrt{2\varphi\alpha} = \sqrt{2\varphi \cdot \frac{Fr}{J}} = \sqrt{\frac{2 Fr \varphi}{J}} \approx 12\;\frac{\text{rad}}{\text{s}} \]
VAST.
\(12\;\frac{\text{rad}}{\text{s}}\)
ESIM. 37.
Kiekko on lappeellaan kitkattomalla alustalla. Sen massa on 4,7 kg ja sen säde on 16,8 cm. Kiekon ympärille on kiedottu erittäin pitkä, liukumaton ja massaton naru, josta vedetään 22 newtonin voimalla. Laske kiekon
a) kiihtyvyys,
b) kulmakiihtyvyys,
c) etenemisen liike-energia, kun narua on vedetty 88 cm,
d) liikkuma matka, kun narua on vedetty 88 cm.

RATK.
\(m = 4,7\;\text{kg}, \quad r = 0,168\;\text{m}, \quad F = 22\;\text{N}, \quad a = ?, \quad \alpha = ?, \quad E_\text{t} = ?, \quad x = ?\)
a) Kiekkoon vaikuttaa paino \(\overline{G}\), tukivoima \(\overline{N}\) ja narun jännistysvoima \(\overline{T}\). Vastusvoimia ei ole.
Kirjoitetaan dynamiikan peruslain mukainen liikeyhtälö.
\[ \Sigma \overline{F} = m\overline{a} \quad \text{eli} \quad \overline{G} + \overline{N} + \overline{T} = m\overline{a} \]
Paino ja tukivoima kumoavat toisensa.
\[ \overline{G} + \overline{N} = \overline{0} \]
Kiekkoa kiihdyttää narun jännitysvoima.
\[ \overline{T} = m\overline{a} \]
Lasketaan kiihtyvyys.
\[ T = ma \quad \text{eli} \quad a = \frac{T}{m} = \frac{22\;\text{N}}{4,7\;\text{kg}} = 4,6809\;\frac{\text{m}}{\text{s}^2} \approx 4,7\;\frac{\text{m}}{\text{s}^2} \]
b) Kirjoitetaan pyörimisen liikeyhtälö.
\[ \Sigma M = J\alpha \]
Kiekkoon aiheuttaa momentin vain narun jännitysvoima.
\[ \Sigma M = Tr \quad \text{ja} \quad \alpha = \frac{\Sigma M}{J} = \frac{Tr}{J} \]
Lasketaan kulmakiihtyvyys, kun \(J = \frac{1}{2}mr^2\).
\[ \alpha = \frac{Tr}{\frac{1}{2}mr^2} = \frac{2T}{mr} = \frac{2 \cdot 22\;\text{N}}{4,7\;\text{kg} \cdot 0,168\;\text{m}} = 55,7244\;\frac{\text{rad}}{\text{s}^2} \approx 56\;\frac{\text{rad}}{\text{s}^2} \]
c) Kirjoitetaan etenemisliikkeen translaatioenergia.
\[ E_\text{t} = \frac{1}{2}mv^2 \]
Kiekon kiertymä on \(\Delta\varphi = \frac{s}{r}\), kiertokulma on \(\varphi = \frac{1}{2}\alpha t^2\) ja kulmakiihtyvyys on \(\alpha = \frac{2T}{mr}\).
\[ \Delta\varphi = \frac{s}{r} = \frac{1}{2}\alpha t^2 = \frac{1}{2} \cdot \frac{2T}{mr} \cdot t^2 \quad \text{eli} \quad t = \sqrt{\frac{ms}{T}} \]
Ratkaistaan nopeus, kun tasaisesti kiihtyvässä liikkeessä nopeus \(v = at\).
\[ v = at = \frac{T}{m}\sqrt{\frac{ms}{T}} = \sqrt{\frac{Ts}{m}} \]
Lasketaan translaatioenergia.
\[ E_\text{t} = \frac{1}{2}mv^2 = \frac{1}{2}m\frac{Ts}{m} = \frac{Ts}{2} = \frac{22\;\text{N} \cdot 0,88\;\text{m}}{2} = 9,68\;\text{Nm} \approx 9,7\;\text{Nm} \]
d) Kirjoitetaan kiekon siirtymä.
\[ x = v_0 t + \frac{1}{2}at^2 \]
Lasketaan siirtymä, kun \(a = \frac{T}{m}\), \(t = \sqrt{\frac{ms}{T}}\) ja \(v_0 = 0\).
\[ x = \frac{1}{2} \cdot \frac{T}{m} \cdot \frac{ms}{T} = \frac{1}{2}s = \frac{1}{2} \cdot 0,88\;\text{m} = 0,44\;\text{m} \]
VAST.
a) \(4,7\;\frac{\text{m}}{\text{s}^2}\)
b) \(56\;\frac{\text{rad}}{\text{s}^2}\)
c) \(9,7\;\text{Nm}\)
d) \(0,44\;\text{m}\)
Vierivän kappaleen
Loppukokeesta
Lukion opetussuunnitelman mukaan kurssitavoitteena on, että opiskelija
syventää osaamistaan mekaniikassa sekä statiikkaan ja pyörimiseen liittyvien ilmiöiden laskennallista hallintaa
syventää tuntemustaan mekaniikan maailmankuvasta.
Suunnitelman keskeiset sisällöt ovat
momentti ja tasapaino pyörimisen suhteen
pyörimisliikkeen mallit, tasainen ja tasaisesti kiihtyvä pyörimisliike
pyörimisen liikeyhtälö
pyörimismäärän säilyminen
pyörimisliikkeen energia
ympyräliike ja ympyräliikkeen kiihtyvyys
gravitaatio ja gravitaation alainen liike
heittoliike ja planeettojen liike
satelliitit ja niiden käyttö
MAOL-taulukkokirjan tärkeät sivut ovat
- 126-127, hitausmomentit
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.