FY5 Harjoitustehtävien ratkaisut

Tältä sivulta löydät harjoitus- ja kotitehtävien ratkaisut.

Toivon ja pyydän tässäkin, että jokainen kurssin opiskelija osallistuu kykyjensä mukaan ratkaisujen tekemiseen esim. tekstin ja kuvien muodossa. Myös virheet ja puutteet saa ja pitää korjata. Myös rakentavat kommentit auttavat yhteistä oppimisasiaa.

Yksi tekijöistä
Henri Jaakkola

Tehtävä 11

RATK.

\(v_{0x} = 2,7\;\text{m}/\text{s} \quad y = -17,5\;\text{m} \quad \Delta y = 0,125\;\text{m}\)

a)

Lasketaan lentoaika ja loppunopeus tasaisesti kiihtyvän liikkeen mallista. Positiivinen \(y\)-suunta on ylöspäin.

\[ y = -\frac{1}{2} gt^2 \quad \text{eli} \quad t = \sqrt{\frac{-2y}{g}} = \sqrt{\frac{-2 \cdot (-17,5\;\text{m})}{9,81\;\frac{\text{m}}{\text{s}^2}}} = 1,8889\;\text{s} \]

\[ v_\text{y} = gt = 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 1,8889\;\text{s} = 18,5297\;\frac{\text{m}}{\text{s}} \]

Lasketaan loppunopeus Pythagoraan lauseella.

\[ v = \sqrt{v^2_\text{x} + v^2_\text{y}} = \sqrt{\left(2,7\;\frac{\text{m}}{\text{s}}\right)^2 + \left(18,5297\;\frac{\text{m}}{\text{s}}\right)^2} = 18,7254\;\frac{\text{m}}{\text{s}} \approx 19\;\frac{\text{m}}{\text{s}} \]

Lasketaan vielä kulma.

\[ \tan \alpha = \frac{v_\text{y}}{v_\text{x}} \]

\[ \alpha = \tan^{-1}{\left(\frac{v_\text{y}}{v_\text{x}}\right)} = \tan^{-1}{\left(\frac{18,5297\;\frac{\text{m}}{\text{s}}}{2,7\;\frac{\text{m}}{\text{s}}}\right)} = 81,7097^\circ \approx 82^\circ \]

b)

Lasketaan kantama tasaisen liikkeen mallin avulla.

\[ x = v_{0x} t = 2,7\;\frac{\text{m}}{\text{s}} \cdot 1,8889\;\text{s} = 5,1000\;\text{m} \approx 5,1\;\text{m} \]

c)

Lasketaan jarrutusaika tasaisen liikkeen mallin avulla.

\[ y_\text{jarrutus} = v_\text{k}t \quad \text{eli} \quad t = \frac{y_\text{jarrutus}}{v_\text{k}} = \frac{2 \cdot y_\text{jarrutus}}{v} = \frac{2 \cdot 0,125\;\text{m}}{18,7254\;\frac{\text{m}}{\text{s}}} = 0,0133\;\text{s} \]

Lasketaan vielä keskimääräinen hidastuvuus.

\[ y = \frac{1}{2}a_\text{k}t^2 \quad \text{eli} \quad a_\text{k} = \frac{2y}{t^2} = \frac{2 \cdot 0,125\;\text{m}}{(0,0133\;\text{s})^2} = 1\,413,3077\;\frac{\text{m}}{\text{s}^2} \approx 1\,400\;\frac{\text{m}}{\text{s}^2} \]

Huomioi, että kappale ajatellaan uppoavan hiekkaan siinä kulmassa, jossa se pintaan osuu. Tässä ei siis ole laskettu \(y\)-suuntaista uppoamista.

VAST.

a) 19 m/s ja 82\(^\circ\)

b) 5,1 m

c) 1400 m/s\(^2\)

Tehtävä 15

\(m_1 = 5,2\;\text{g}, \quad m_2 = 45\;\text{g}, \quad h = 78\;\text{cm}, \quad x = 1,7545\;\text{m}\)

Piirretään kuva. TODO!!!

Luodin ja puukappaleen törmäys on kimmoton, ja liikemäärä säilyy. Kirjoitetaan liikemäärää kuvaava yhtälö.

\[ m_1\overline{v}_1 = (m_1 + m_2)\overline{u} \]

Huomioidaan positiivinen suunta.

\[ m_1 v_1 = (m_1 + m_2)u \quad \text{eli} \quad v_1 = \frac{m_1 + m_2}{m_1}u \]

Ratkaistaan putoamisaika.

\[ y = \frac{1}{2}gt^2 \quad \text{eli} \quad t = \sqrt{\frac{2y}{g}} \]

Lentoaika ja -matka paljastavat toisiinsa takertuneiden kappaleiden yhteisen lähtönopeuden.

\[ u = v_\text{0x} = \frac{x}{t} = \frac{x}{\sqrt{\frac{2y}{g}}} = x \cdot \sqrt{\frac{g}{2y}} \]

Kirjoitetaan luodin alkunopeuden yhtälö.

\[ v_1 = \frac{m_1 + m_2}{m_1} \cdot x \cdot \sqrt{\frac{g}{2y}} \]

Lasketaan luodin alkunopeus. Massat voivat tässä olla aluksi grammoja. Ymmärrätkö miksi näin on?

\[ v_1 = \frac{5,2\;\text{g} + 45\;\text{g}}{5,2\;\text{g}} \cdot 1,75\;\text{m} \cdot \sqrt{\frac{9,81\;\frac{\text{m}}{\text{s}^2}}{2 \cdot 0,78\;\text{m}}} = 42,3653\;\frac{\text{m}}{\text{s}} \approx 150\;\frac{\text{km}}{\text{h}} \]

VAST.

150 km/h

Tehtävä 25

\(v_0 = 28\;\frac{\text{m}}{\text{s}}, \quad h = 4,2\;\text{m}\)

Piirretään kuva. TODO!!!

Tutkitaan kappaleen liikettä vain ja ainoastaan \(y\)-suunnassa.

Mekaaninen energia säilyy, kun vastusvoimia ei ole.

\[ E_\text{pa} + E_\text{ka} = E_\text{pl} + E_\text{kl} \]

Aluksi kappaleella on vain liike-energiaa ja lopuksi sillä on vain potentiaalienergiaa.

\[ \frac{1}{2}mv^2_\text{0y} = mgh \]

Kirjoitetaan nopeus.

\[ v_\text{0y} = \sqrt{2gh} \]

Kirjoitetaan kappaleen kokonaisnopeus millä tahansa ajanhetkellä.

\[ v = \sqrt{v^2_\text{x} + v^2_\text{y}} \]

Lasketaan \(x\)-suuntainen nopeus aluksi.

\[ v_\text{0x} = \sqrt{v^2_0 - v^2_\text{0y}} = \sqrt{\left(28\;\frac{\text{m}}{\text{s}}\right)^2 - 2 \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 4,2\;\text{m}} = 26,4877\;\frac{\text{m}}{\text{s}} \approx 26\;\frac{\text{m}}{\text{s}} \]

Jos vastusvoimia ei ole, on \(x\)-suuntainen nopeus koko ajan 26 m/s.

VAST.

26 m/s

Tehtävä 27

\[ \alpha = 30^\circ, \quad l = 4,0\;\text{m}, \quad h = 10,2\;\text{m}, \quad x = ? \]

Piirretään kuva. TODO!!!

Mekaaninen energia säilyy, kun vastusvoimia ei ole.

\[ E_\text{pa} + E_\text{ka} = E_\text{pl} + E_\text{kl} \]

Aluksi kappaleella on vain potentiaalienergiaa ja lopuksi sillä on vain liike-energiaa.

\[ mgh = \frac{1}{2}mv^2 \]

Kirjoitetaan nopeus.

\[ v = \sqrt{2gh} \]

Piirretään kuva nopeuden komponenteista. TODO!!!

Lasketaan \(x\) ja \(y\)-suuntaisen nopeudet.

\[ v_\text{x} = v \cdot \cos \alpha \approx 5,4250\;\frac{\text{m}}{\text{s}} \quad \text{ja} \quad v_\text{y} = v \cdot \sin \alpha 3,1321\;\frac{\text{m}}{\text{s}} \]

Lasketaan putoamisaika tasaisesti kiihtyvän liikkeen mallista. Huomioidaan positiiviset suunnat.

\[ -h = -v_\text{0y}t - \frac{1}{2}gt^2 \quad \text{eli} \quad \frac{1}{2}gt^2 + v_\text{0y}t - h = 0 \]

Kirjoitetaan toisen asteen yhtälön yleinen muoto.

\[ ax^2 + bx + c = 0 \]

Kirjoitetaan toisen asteen yhtälön ratkaisukaava.

\[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \]

Ratkaistaan aika toisen asteen ratkaisukaavalla.

\[ t = \frac{-v_\text{0y} \pm \sqrt{v^2_\text{0y} - 4 \cdot \frac{1}{2}g \cdot (-h)}}{2 \cdot \frac{1}{2}g} \]

Sijoitetaan arvot ja saadaan kaksi vastausta.

\[ t_1 = 1,1577\;\text{s} \quad \text{ja} \quad t_2 = -1,7962\;\text{s} \]

Jälkimmäinen arvoista ei ole järkevä.

Lasketaan kappaleen etenemä matka.

\[ x = v_\text{0x} t = 5,4250\;\frac{\text{m}}{\text{s}} \cdot 1,1577\;\text{s} = 6,2805\;\text{m} \approx 6,3\;\text{m} \]

VAST.

6,3 m.

Tehtävä 41

\(l = 15\;\text{m}, \quad m = 2\,100\;\text{kg}, \quad v = 7,6\;\frac{\text{m}}{\text{s}}\)

Piirretään kuva. TODO!!!

Kirjoitetaan dynamiikan peruslain mukainen yhtälö.

\[ \Sigma \overline{F} = m \overline{a} \qquad \text{eli} \qquad \overline{T} + \overline{G} = m \overline{a} \]

Huomioidaan positiivinen suunta.

\[ T - G = ma_\text{n} \quad \text{eli} \quad T = m\frac{v^2}{r} + mg \]

Lasketaan voima.

\[ T = 2\,100\;\text{kg} \cdot \frac{\left(7,6\;\frac{\text{m}}{\text{s}}\right)^2}{15\;\text{m}} + 2\,100\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} = 2\,8687,4\;\text{N} \approx 29\,000\;\text{N} \]

VAST.

29 kN

Tehtävä 45

RATK.

\(m = 7,3\;\text{kg} \quad r = 1,9\;\text{m} \quad v = 29\;\text{m}/\text{s}\)

Kirjoitetaan dynamiikan peruslain liikeyhtälö.

\[ \Sigma \overline{F} = m\overline{a} \]

Huomioidaan positiivinen suunta.

\[ T = ma_\text{n} = m\frac{v^2}{r} = 7,3\;\text{kg} \cdot \frac{(29\;\text{m}/\text{s})^2}{1,9\;\text{m}} = 3\,231,2105\;\text{N} \approx 3\,200\;\text{N} \]

VAST.

3,2 kN

Tehtävä 49

a) Ratanopeus ei muutu, koska levyn pyörintänopeus on vakio.

b) Tangenttikiihtyvyys on nolla, koska levyn pyörintänopeus on vakio.

c) Normaalikiihtyvyys on vakio ja sen suunta on kohti levyn keskipistettä, koska levyn pyörintänopeus on vakio.

d) Kokonaiskiihtyvyys on sama kuin on normaalikiihtyvyys.

Tehtävä 48

a) Normaalikiihtyvyys \(a_\text{n}\) tarkoittaa ympyräradalla liikkuvan kappaleen kiihtyvyyttä kohtisuoraan liikettä vastaan ja siis kohti ympyrän keskipistettä.

b) Tangenttikiihtyvyys \(a_\text{t}\) tarkoittaa ympyräradalla liikkuvan kappaleen nopeuden muutosta. Kappaleen ratanopeus voi kasvaa tai pienentyä. Tangenttikiihtyvyyden suunta on kohtisuorassa normaalikiihtyvyyttä vastaan.

c) Kokonaiskiihtyvyys \(a\) tarkoittaa ympyräradalla liikkuvan kappaleen normaalikiihtyvyyden ja tangenttikiihtyvyyden vektorisummaa.

\[ \overline{a} = \overline{a}_\text{n} + \overline{a}_\text{t} \]

Skalaarina normaalikiihtyvyys saadaan Pythagoraan lauseesta.

\[ a = \sqrt{a^2_\text{n} + a^2_\text{t}} \]

Tehtävä 51

\(r = 41\;\text{cm}, \quad g = 9,81\;\text{m}/\text{s}\)

Silmukan ylimmässä kohdassa auton liikeyhtälö on dynamiikan peruslain mukaan

\[ \Sigma \overline{F} = m\overline{a} \qquad \text{ja} \qquad \overline{N} + \overline{G} = m\overline{a} \]

Autoon vaikuttaa radan ylimmässä kohdassa vain radan säteen suuntaisia voimia. Kiihtyvyys on normaalikiihtyvyyttä.

Olkoon positiivinen suunta alaspäin.

\[ N + mg = m\frac{v^2}{r} \]

Radan ylimmässä kohdassa \(N = 0\).

\[ mg = m\frac{v^2}{r} \qquad \text{eli} \qquad g = \frac{v^2}{r} \qquad \text{eli} \qquad v = \sqrt{gr} \]

Lasketaan nopeus.

\[ v = \sqrt{gr} = \sqrt{9,81\;\frac{\text{m}}{\text{s}^2} \cdot 0,41\;\text{m}} = 2,0055\;\frac{\text{m}}{\text{s}} \approx 2,0055\;\frac{\text{m}}{\text{s}} \]

VAST.

2,0 m/s.

Tehtävä 52

\(r = 3,5\;\text{m}, \quad m = 0,32\;\text{kg}\)

a) Luetaan kuvaajasta kappaleen nopeus hetkettä \(t = 2,0\;\text{s}\).

\[ v = 1,8\,\text{m}/\text{s} \]

b) Lasketaan kappaleen normaalikiihtyvyys.

\[ a_\text{n} = \frac{v^2}{r} = \frac{\left(1,8\,\text{m}/\text{s}\right)^2}{3,5\;\text{m}} = 0,9257\;\frac{\text{m}}{\text{s}^2} \approx 0,93\;\frac{\text{m}}{\text{s}^2} \]

c) Lasketaan kappaleen tangenttikiihtyvyys kuvaajan avulla.

\[ a_\text{t} = \frac{\Delta v}{\Delta t} = \frac{2,5\;\frac{\text{m}}{\text{s}} - 0,5\;\frac{\text{m}}{\text{s}}}{3\;\text{s} - 0\;\text{s}} = 0,6667\;\frac{\text{m}}{\text{s}^2} \approx 0,67\;\frac{\text{m}}{\text{s}^2} \]

d) Lasketaan kappaleeseen kohdistuva voima.

Kappaleseen kohdistuva kokonaisvoima lasketaan kokonaiskiihtyvyyden avulla.

\[ F = m \cdot \sqrt{a^2_\text{n} + a^2_\text{t}} = 0,32\;\text{kg} \cdot \sqrt{\left(0,9257\;\frac{\text{m}}{\text{s}^2}\right)^2 + \left(0,6667\;\frac{\text{m}}{\text{s}^2}\right)^2} = 0,3651\;\text{N} \approx 0,37\;\text{N} \]

VAST.

a)

1,8 m/s

b)

0,93 m/s\(^2\)

c)

0,67 m/s\(^2\)

d)

0,37 N

Tehtävä 58

\(r = 75\;\text{cm}, \quad m = 150\;\text{g}, \quad h = 11\;\text{cm}\)

Heilurin punnus on radan alimmassa kohdassa. Kirjoitetaan dynamiikan peruslain mukainen yhtälö.

\[ \Sigma \overline{F} = m\overline{a} \quad \text{eli} \quad \overline{T} + \overline{G} = m\overline{a} \]

Radan alimmassa kohdassa on vain radan säteen suuntaisia voimia.

\[ T - G = ma \quad \text{eli} \quad T = mg + ma = mg + m\frac{v^2}{r} \]

Koska vastusvoimia ei ole, voidaan käyttää mekaanisen energian säilymislakia.

\[ E_{\text{pa}} + E_{\text{ka}} = E_{\text{pl}} + E_{\text{kl}} \]

Aluksi punnus on paikallaan korkeudella \(h\) ja lopuksi punnuksen nopeuden suuruus on \(v\). Ratkaistaan nopeus.

\[ mgh = \frac{1}{2}mv^2 \quad \text{eli} \quad v = \sqrt{2gh} \]

Sijoitetaan \(v\) jännitysvoiman yhtälöön ja lasketaan jännitysvoiman suuruus.

\[ T = mg + m\frac{2gh}{r} = 0,15\,\text{kg} \cdot 9,81\,\frac{\text{m}}{\text{s}^2} + 0,15\,\text{kg} \cdot \frac{2 \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 0,11\;\text{m}}{0,75\;\text{m}} = 1,9031\;\text{N} \approx 1,9\;\text{N} \]

VAST.

1,9 N

Tehtävä 60

\(r = 75\;\text{cm}, \quad m = 150\;\text{g}, \quad h = 11\;\text{cm}\)

a) Punnuksen nopeuden perusteet ja yhtälö saadaan tehtävästä 58.

\[ v = \sqrt{2gh} \]

Lasketaan normaalikiihtyvyys.

\[ a_\text{n} = \frac{v^2}{r} = \frac{2gh}{r} = \frac{2 \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 0,055\;\text{m}}{0,75\;\text{m}} = 1,4388\;\frac{\text{m}}{\text{s}^2} \approx 1,4\;\frac{\text{m}}{\text{s}^2} \]

b) Kirjoitetaan tangenttikiihtyvyyden yhtölö.

\[ a_\text{t} = g \cdot \sin \theta \]

TODO: SELVENTÄVÄ KUVA!

Lasketaan kulmat \(\alpha\) ja \(\theta\).

\[ \sin \alpha = \frac{0,695\;\text{m}}{0,75\;\text{m}} \quad \text{eli} \quad \theta = 90^\circ - \sin^{-1}\left(\frac{0,695\;\text{m}}{0,75\;\text{m}}\right) \approx 22,08^\circ \]

Lasketaan tangenttikiihtyvyys.

\[ a_\text{t} = 9,81\;\frac{\text{m}}{\text{s}^2} \cdot \sin (22,08^\circ) \approx 3,7\;\frac{\text{m}}{\text{s}^2} \]

c)

Lasketaan kokonaiskiihtyvyys Pythagoraan lauseen avulla.

\[ a = \sqrt{a^2_\text{t} + a^2_\text{n}} = \sqrt{\left(3,7\;\frac{\text{m}}{\text{s}^2}\right)^2 + \left(1,4\;\frac{\text{m}}{\text{s}^2}\right)} \approx 4,0\;\frac{\text{m}}{\text{s}^2} \]

Lasketaan vielä kulma.

\[ \beta = \tan^{-1}\left(\frac{a_\text{t}}{a_\text{n}}\right) \approx 69^\circ \]

Tehtävä 64

a) Tarkasti ottaen sekä Maa että laskuvarjohyppääjä liikkuvat toisiaan vastaan. Maan siirtymä on todellisuudessa häviävän pieni, sillä sen massa on suuri verrattuna hyppääjään.

b) Kahden massallisen kappaleen välillä on gravitaatiovuorovaikutuksesta johtuva gravitaatiovoima. Hyppääjät vetävät toisiaan puoleensa, mutta heidän välinen vetovoima on niin pieni, ettei sillä ole merkitystä lähentymisen kannalta hypyn aikana.

Tehtävä 65

Tarkasti ottaen Maa ja Kuu kiertävät yhteistä massakeskipistettä. Pisteen paikan voi laskea taulukkokirjan avulla, kun tietää kappaleiden välisen etäisyyden ja kappaleiden massat.

Tehtävä 66

\(m_1 = 1,2\;\text{kg}, \quad m_2 = 2,8\;\text{kg}, \quad r = 7,3\;\text{m}, \quad \gamma = 6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2}\)

a)

Kirjoitetaan kahden massallisen kappaleen välisen gravitaativoiman yhtälö.

\[ F = \gamma \frac{m_1 m_2}{r^2} \]

Lasketaan pallojen välisen gravitaatiovoiman suuruus.

\[ F = 6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \cdot \frac{1,2\;\text{kg} \cdot 2,8\;\text{kg}}{(7,3\;\text{m})^2} = 4,2082 \cdot 10^{-12}\;\text{N} \approx 4,2 \cdot 10^{-12}\;\text{N} \]

b)

Lasketaan kevyemmän pallon kiihtyvyys.

\[ a = \frac{F}{m_1} = \frac{4,2082 \cdot 10^{-12}\;\text{N}}{1,2\;\text{kg}} = 3,5068 \cdot 10^{-12}\;\frac{\text{m}}{\text{s}^2} \approx 3,5 \cdot 10^{-12}\;\frac{\text{m}}{\text{s}^2} \]

c)

Lasketaan siirtymäaika, jotta pallo siirtyisi yhden millimetrin. Oletetaan, ettei gravitaatiovoima ja siten myöskään kiihtyvyys muutu näin lyhyellä siirtymällä. Kirjoitetaan tasaisesti kiihtyvän liikkeen malli ja ratkaistaan aika.

\[ s = \frac{1}{2}at^2 \quad \text{eli} \quad t = \sqrt{\frac{2s}{a}} \]

Lasketaan aika.

\[ t = \sqrt{\frac{2 \cdot 0,001\;\text{m}}{3,5068 \cdot 10^{-12}\;\frac{\text{m}}{\text{s}^2}}} = 23881,3843\;\text{s} \approx 6\;\text{h}\;38\;\text{min} \]

VAST.

a) 4,2 pN

b) 3,5 pm/s\(^2\)

c) 6 h 38 min

Tehtävä 73

\(m = 78\,\text{kg}, \quad M = 5,974 \cdot 10^{24}\;\text{kg}, \quad r = 6\,370\,000\,\text{m}, \quad \gamma = 6,6724 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2}, \quad F = ?\)

a) Lasketaan gravitaatiolain mukainen kumpaankin kappaleeseen vaikuttava voima.

\[ F = \gamma\,\frac{mM}{r^2} = 6,6742 \cdot 10^{-11}\,\frac{\text{Nm}^2}{\text{kg}^2} \cdot \frac{78\,\text{kg} \cdot 5,974 \cdot 10^{24}\;\text{kg}}{(6\,370\,000\,\text{m})^2} = 766,4435\;\text{N} \approx 770\;\text{N} \]

VAST.

Jadda jadda

Tehtävä 75

\(F_\text{Maa} = 255\;\text{N}, \quad g_\text{Maa} = 9,81\;\text{m/s}^{2}, \quad g_\text{Kuu} = 1,622\;\text {m/s}^{2}, \quad r_\text{Maa} = 6\,370\,000\;\text{m},\)

\(\gamma = 6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2}, \quad m_\text{Maa} = 5,974 \cdot 10^{24}\;\text{kg}\)

a) Kirjoitetaan yhtälö, jolla selviää kuljetusastian massa.

\[ m = \frac{F_\text{Maa}}{g_\text{Maa}} = \frac{255\;\text{N}}{9,81\;\frac{\text{m}}{\text{s}^2}} = 25,9939\;\text{kg} \]

Nyt voidaan laskea astian paino kuussa.

\[ F_\text{Kuu} = m \cdot g_\text{kuu} = 25,9939\;\text{kg} \cdot 1,622\;\frac{\text{m}}{\text{s}^2} = 41,5902\;\text{N} \approx 42\;\text{N} \]

b) Kirjoitetaan yhtälö, jolla saadaan selville monta maan säteen etäisyyttä tarvitaan saavuttamaan 1,622 m/s\(^2\) gravitaatiokentän voimakkuus.

\[ r = \sqrt{\frac{\gamma \cdot m}{g_{\text{kuu}}}} \]

Saadaan

\[ r = \sqrt{\frac{6,6742 \cdot 10^{-11}\;\frac{\text{Nm}^2}{\text{kg}^2} \cdot 5,974 \cdot 10^{24}\;\text{kg}}{1,622\;\frac{\text{m}}{\text{s}^2}}} = 15\,678\,582,3896\;\text{m} \]

Jaetaan saatu \(r\) maan säteellä ja saadaan tulos

\[ \frac{15\,678\,582,3896\;\text{m}}{6\,370\,000\;\text{m}} = 2,4613 \approx 2,5 \]

VAST.

a) 42 N

b) 2,5 Maan sädettä

Tehtävä 78

\(r = 414 + 6\,370\;\text{km} = 6\,784\;\text{km}, \quad T = 91,69\;\text{min}\)

a)

Lasketaan ympyrän piiri.

\[ p = 2 \pi r = 2 \cdot \pi \cdot 6\,784\;\text{km} = 42\,625,1291\;\text{km} \approx 43\,000\;\text{km} \]

b)

Lasketaan ratanopeus.

\[ v = \frac{s}{t} = \frac{p}{T} = \frac{42\,625,1291\;\text{km}}{91,69 \cdot 60\;\text{s}} = 7,7481\;\frac{\text{km}}{\text{s}} \approx 7,7\;\frac{\text{km}}{\text{s}} \]

VAST.

a)

43 000 km

b)

7,7 km/s

Tehtävä 80

Geostationäärisellä kiertoradalla sateelliitin kiertoaika on sama kuin maan pyörähdysaika ja sen kiertorata kulkee maan päiväntasaajan kautta. Näin se pysyy aina samalla kohtaa taivaalla maasta katsottuna vuorokauden ajasta riippumatta.

Tehtävä 81

Dynamiikan peruslaki

\[ \Sigma \overline{F} = m \overline{a} \]

Normaalikiihtyvyys

\[ a_\text{n} = \frac{v^2}{r} \]

Gravitaatiolaki

\[ F = \gamma \frac{Mm}{r^2} \]

Eli

\[ \gamma \frac{Mm}{r^2} = m\frac{v^2}{r} \]

Eli

\[ r = \gamma \frac{M}{v^2} \]

Korkeus on siten

\[ h = r - 6\,370\;\text{km} = \gamma \frac{M}{v^2} - 6\,370\;\text{km} \]

Tehtävä 85

RATK.

\(r_{1} = 9379\;\text{km} \quad T_{1} = 0,319\text{d} \quad T_{2} = 1,26\text{d} \quad r_{2} = ?\)

Ratkaistaan gravitaatiolain avulla Deimoksen radan säde \(r_{2}\):

\[ \frac{T_{1}^2}{T_{2}^2} = \frac{r_{1}^3}{r_{2}^3} \]

\[ \frac{T_{1}^2}{T_{2}^2}r_{2}^3 = r_{1}^3 \]

\[ r_{2}^3 = \frac{r_{1}^3}{\frac{T_{1}^2}{T_{2}^2}} \]

\[ r_{2} = \sqrt[3]{\frac{r_{1}^3}{\frac{T_{1}^2}{T_{2}^2}}} \]

\[ = \sqrt[3]{\frac{9379\;\text{km}^3}{\frac{0,319\text{d}^2}{1,26\text{d}^2}}} \]

\[ = 23435,6\;\text{km} \approx 23400\;\text{km} \]

VAST.

\(23400\;\text{km}\)

Tehtävä 87

Ilmeisesti Maa ja asteroidi kiertävät Aurinkoa!

Käytetään tässä tehtävän ratkaisussa hyödyksi tehtävässä 85 ratkaistua radan säteen yhtälöä.

Verrataan asteroidin ja Maan säteitä toisiinsa.

\[ \frac{r_\text{ast}}{r_\text{Maa}} = \frac{\sqrt[3]{\frac{T^2_\text{ast} \cdot \gamma \cdot M}{4 \cdot \pi^2}}}{\sqrt[3]{\frac{T^2_\text{Maa} \cdot \gamma \cdot M}{4 \cdot \pi^2}}} = \frac{\sqrt[3]{T^2_\text{ast}}}{\sqrt[3]{T^2_\text{Maa}}} = \sqrt[3]{\frac{T^2_\text{ast}}{T^2_\text{Maa}}} = \sqrt[3]{\left(\frac{T_\text{ast}}{T_\text{Maa}}\right)^2} = \left(\frac{T_\text{ast}}{T_\text{Maa}}\right)^{\frac{2}{3}} \]

Lasketaan vielä säteiden suhde.

\[ \left(\frac{10,4\;\text{a}}{1\;\text{a}}\right)^{\frac{2}{3}} = 10,4^{\frac{2}{3}} = 4,7646 \approx 4,8 \]

VAST.

4,8

Tehtävä 95

\(r = 1,9\;\text{m}, \quad F = 85\;\text{N}\)

Lasketaan voiman momentti.

\[ M = Fr = 85\;\text{N} \cdot 1,9\;\text{m} = 161,5\;\text{Nm} \approx 160\;\text{Nm} \]

VAST.

160 Nm

Tehtävä 105

F = G = 49N, r = 0,55m

a) \[ M = Fr = 49N\cdot 0,55m = 26,95 \approx 27 N \]

Tehtävä 111

\(m = 50\;\text{g}, \quad \alpha = 45^\circ\)

Huomataan, että yhteen jousivaakaan kohdistuu vain puolet punnuksen aiheuttamasta painosta.

Lasketaan yhden jousivaa'an lukema trigonometrian avulla. Merkitään systeemin muodostaman suorakulmaisen kolmion hypotenuusaa \(F\)-kirjaimella.

\[ \cos \alpha = \frac{G}{F} = \frac{mg}{F} \]

Ratkaistaan hypotenuusan pituus.

\[ F = \frac{mg}{\cos\alpha} = \frac{0,05\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2}}{\cos 45^\circ} = 0,6937\;\text{N} \approx 0,69\;\text{N} \]

VAST.

0,69 N

Tehtävä 118

\(m = 250\;\text{g}, \quad l = 100\;\text{cm}\)

Systeemi on pyörimisen suhteen tasapainossa, jos tukipisteeseen kohdistuvien momenttien summa on nolla. Tässä tehtävässä systeemin tukipisteen vasemmalla ja oikealla puolella pyörimisen suhteen vastakkaissuuntaisen momentit kumoavat toisensa.

\[ M_\text{vasen} = M_\text{oikea} \]

Systeeminen vasemman puolen momentin aiheuttaa metallitanko, jonka pituus on 75 cm ja jonka massakeskipisteen etäisyys tukipisteestä on 37,5 cm. Vasemman puolen massa on \(0,75 \cdot 250\;\text{g} = 187,5\;\text{g}\).

Vastaavasti systeemin oikean puolen momentin aiheuttaa metallitanko, jonka pituus on 25 cm ja jonka massakeskipisteen etäisyys tukipisteestä on 12,5 cm. Oikean puolen massa on \(0,25 \cdot 250\;\text{g} = 62,5\;\text{g}\).

Lisäksi tangon oikealle puolelle ripustetaan 500 gramman lisäpaino. Ripustuskohdan etäisyys tukipisteestä pitää laskea.

Tasapainossa tilanne on kokonaismomentin suhteen seuraava.

\[ 0,75 \cdot 250\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2} \cdot 0,5 \cdot 75\;\text{cm} = 0,25 \cdot 250\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2} \cdot 0,5 \cdot 25\;\text{cm} + 500\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2} \cdot a \]

Ratkaistaan edellisestä yhtälöstä varren \(a\) pituus.

\[ a = \frac{0,75 \cdot 250\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2} \cdot 0,5 \cdot 75\;\text{cm} - 0,25 \cdot 250\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2} \cdot 0,5 \cdot 25\;\text{cm}}{500\;\text{g} \cdot 9.81\;\frac{\text{m}}{\text{s}^2}} = 12,5\;\text{cm} \]

VAST.

12,5 cm

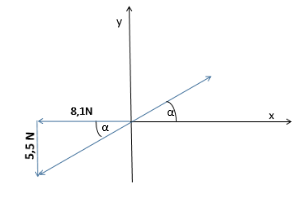
Tehtävä 110

Jaetaan voimat x- ja y-akselin suuntaisiin voimiin.

F_x = -8,1 N,     F_y = -5,5 N

Lasketaan voimista muodostuvan kolmion hypotenuusa.

Tehtävä 120

\(m = 100\;\text{g}, \quad \alpha_1 = 21^\circ, \quad \alpha_2 = 34^\circ\)

Piirretään kuva. TODO!!!

Kappale on tasapainossa etenemisen suhteen \(x\)-suunnassa, joten ko. voimat kumoavat toisensa. Kirjoitetaan skalaariyhtälö.

\[ F_\text{1x} = F_\text{2x} \quad \text{eli} \quad F_1 \cdot \sin \alpha_1 = F_2 \cdot \sin \alpha_2 \]

Ratkaistaan edellisestä yhtälöstä voimat \(F_1\) ja \(F_2\).

\[ F_1 = F_2 \cdot \frac{\sin \alpha_2}{\sin \alpha_1} \quad \text{ja} \quad F_2 = F_1 \cdot \frac{\sin \alpha_1}{\sin \alpha_2} \]

Kappale on tasapainossa etenemisen suhteen \(y\)-suunnassa. Kirjoitetaan skalaariyhtälö.

\[ F_\text{1y} + F_\text{2y} - G = 0 \quad \text{eli} \quad F_1 \cdot \cos \alpha_1 + F_2 \cdot \cos \alpha_2 - G = 0 \]

Sijoitetaan edelliseen yhtälöön \(F_1\).

\[ F_2 \cdot \frac{\sin \alpha_2}{\sin \alpha_1§} \cdot \cos \alpha_1 + F_2 \cdot \cos \alpha_2 = G \]

Ratkaistaan edellisestä yhtälöstä voima \(F_2\).

\[ F_2 = \frac{G}{\frac{\sin \alpha_2}{\sin \alpha_1§} \cdot \cos \alpha_1 + \cos \alpha_2} = \frac{0,1\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2}} {\frac{\sin 34^\circ}{\sin 21^\circ§} \cdot \cos 21^\circ + \cos 34^\circ} = 0,4292\;\text{N} \approx 0,43\;\text{N} \]

Vastaavasti ratkaistaan ja lasketaan myös voima \(F_1\).

VAST.

0,43 N ja 0,67 N

Tehtävä 126

\(m_\text{mies} = 91\;\text{kg}, \quad m_\text{hirsi} = 120\;\text{kg}, \quad L = 5,1\;\text{m}, \quad a = 1,2\;\text{m}\)

Piirretään kuva. TODO!!!

a)

Koska mies seisoo hirren keskipisteessä, voidaan tukivoimat ratkaista helposti.

\[ N_1 = N_2 = \frac{G_\text{mies} + G_\text{hirsi}}{2} = \frac{(91\;\text{kg} + 120\;\text{kg}) \cdot 9,81\;\frac{\text{m}}{\text{s}^2}}{2} = 1034,955\;\text{N} \approx 1030\;\text{N} \]

b)

Ratkaistaan tukivoimien suuruudet momenttiehdon avulla.

Olkoon positiivinen kiertosuunta vastapäivään. Olkoon hirren vasen pääty momenttipiste \(O\). Tällöin vasemman päädyn tukivoima ei aiheuta momenttia.

Kirjoitetaan momenttiehto, kun mies seisoo lähellä hirren vasenta päätä.

\[ \Sigma M_\text{O} = 0 \quad \text{eli} \quad -G_\text{hirsi} \cdot \frac{L}{2} - G_\text{mies} \cdot a + N_2 \cdot L = 0 \]

Ratkaistaan hirren oikean päädyn tukivoima.

\[ N_2 = \frac{G_\text{hirsi} \cdot \frac{L}{2} + G_\text{mies} \cdot a}{L} = \frac{120\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot \frac{5,1\;\text{m}}{2} + 91\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 1,2\;\text{m}}{5,1\;\text{m}} = 798,6497\;\text{N} \approx 800\;\text{N} \]

Hirren vasemman päädyn tukivoima voidaan ratkaista vastaavalla tavalla tai laskemalla se miehen ja hirren kokonaispainosta.

VAST.

a) 1030 N

b) 800 N ja 1270 N

Tehtävä 133

\(F_\text{max} = 52\,000\;\text{N}, \quad a = 6,0\;\text{m}, \quad b = 3,0\;\text{m}, \quad L = 7,0\;\text{m}, \quad m = 680\;\text{kg},\)

\(\alpha = 40^\circ, \quad \beta = 90^\circ - 70^\circ = 20^\circ, \quad \gamma = 70^\circ - (180^\circ - 90^\circ - 50^\circ) = 30^\circ\)

Piirretään kuva. TODO!!!

a)

Ratkaistaan maksimikuorma momenttiehdon avulla.

Olkoon positiivinen kiertosuunta vastapäivään. Olkoon nivelkohta \(A\) momenttipiste. Tällöin momenttipisteeseen kohdistuvat voimat eivät aiheuta momenttia.

Kirjoitetaan momenttiehto, kun vaijeriin kohdistuu maksimirasitus.

\[ \Sigma M_\text{A} = 0 \quad \text{eli} \quad -G_\text{puomi} \cdot b - G_\text{kuorma} \cdot L + F_\text{max} \cdot a = 0 \]

Huomioidaan suunnat.

\[ -G_\text{puomi} \cdot \cos \alpha \cdot b - G_\text{kuorma} \cdot \cos \alpha \cdot L + F_\text{max} \cdot \cos \beta \cdot a = 0 \]

Ratkaistaan maksimikuorma eli maksimivoima.

\[ G_\text{kuorma} = \frac{F_\text{max} \cdot \cos \beta \cdot a - G_\text{puomi} \cdot \cos \alpha \cdot b}{\cos \alpha \cdot L} \]

Lasketaan voima.

\[ G_\text{kuorma} = \frac{52\,000\;\text{N} \cdot \cos 20^\circ \cdot 6,0\;\text{m} - 680\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot \cos 40^\circ \cdot 3,0\;\text{m}}{\cos 40^\circ \cdot 7,0\;\text{m}} = 51\,816,0369\;\text{N} \approx 52\,000\;\text{N} \]

b)

Määritetään niveleen \(A\) vaikuttavat \(x\)- ja \(y\)-suuntaiset voimat erikseen.

Kirjoitetaan voimaehto.

\[ \Sigma \overline{F} = \overline{N} + \overline{F}_\text{max} + \overline{G}_\text{puomi} + \overline{G}_\text{kuorma} \]

Valitaan positiiviset suunnat ylös ja oikealle. Kirjoitetaan \(x\)- ja \(y\)-suunnan voimat skalaareina.

\[ N_\text{x} - F_\text{max, x} = 0 \quad \text{ja} \quad N_\text{y} + F_\text{max, y} - G_\text{puomi} - G_\text{kuorma} = 0 \]

Ratkaistaan ja lasketaan \(x\)-suuntainen tukivoima.

\[ N_\text{x} = F_\text{max, x} = F_\text{max} \cdot \cos \gamma = 52\,000\;\text{N} \cdot \cos 30^\circ = 45\,033,321\;\text{N} \]

Ratkaistaan \(y\)-suuntainan tukivoima.

\[ N_\text{y} = G_\text{puomi} + G_\text{kuorma} - F_\text{max, y} = G_\text{puomi} + G_\text{kuorma} - F_\text{max} \cdot \sin \gamma \]

Lasketaan \(y\)-suuntainan tukivoima.

\[ N_\text{y} = 680\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} + 52\,000\;\text{N} - 52\,000\;\text{N} \cdot \sin 30^\circ = 32\,670,8\;\text{N} \]

Lasketaan kokonaistukivoima Pythagoraan lauseella.

\[ N = \sqrt{N^2_\text{x} + N^2_\text{y}} = 55\,636,1499\;\text{N} \approx 56\,000\;\text{N} \]

Lasketaan tukivoiman suunta.

\[ \alpha = \tan^{-1}\left(\frac{N_\text{y}}{N_\text{x}}\right) = 35,9602^\circ \approx 36^\circ \]

VAST.

a) \(52\,000\,\text{N}\)

b) \(56\,000\,\text{N}\) ja \(36^\circ\)

Tehtävä 145

\(m = 151\;\text{kg}, \quad \mu = 0,18, \quad F = ?\)

a)

Laatikon liike on tasaista, joten siihen vaikuttava kokonaisvoima on nolla.

\[ \Sigma \overline{F} = \overline{0} \]

Olkoon positiiviset suunnat ylös ja oikealle. Pystysuunnassa laatikon paino \(\overline{G}\) ja pinnan tukivoima \(\overline{N}\) kumoavat toisensa.

\[ \overline{G} + \overline{N} = \overline{0} \]

Vaakasuunnassa vetävä voima \(F\) ja kitkavoima \(F_\mu\) kumoavat toisensa.

\[ \overline{F} + \overline{F_\mu} = \overline{0} \]

Kun väkipyörän kautta kulkevaa narua vedetään metrin verran, lähestyy laatikko seinää puoli metriä. Tarvittava voima siis puolittuu.

Lasketaan tarvittava vetävä voima, jos väkipyörää ei ole.

\[ F = F_\mu = \mu N = \mu G = \mu mg = 0,18 \cdot 151\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} = 266,6358\;\text{N} \]

Kirjoitetaan tarvittava voima, kun väkipyörä on apuna.

\[ F_\text{puoli} \approx 130\;\text{N} \]

b)

Tilanne muuttuu siten, että vetävän voiman suunta muuttuu. Tarvittava voima on edelleen 130 N.

VAST.

130 N

Tehtävä 150

a)

Katso tehtävän kuvaa. Origo on neliön vasemmassa alakulmassa.

Ratkaistaan tehtävä puuttuvan palan menetelmällä siten, että täydennetään levy neliöksi.

Täydennetyn neliön (pinta-ala \(A_1\)) painopiste \((x_1;y_1)\) on \((16,5\;\text{cm}; 16,5\;\text{cm})\) ja lisätyn pikkuneliön (pinta-ala \(A_2\)) painopiste \((x_2;y_2)\) on \((5,5\;\text{cm}; 16,5\;\text{cm})\)

Lasketaan pinta-alat.

\[ A_1 = 33\;\text{cm} \cdot 33\;\text{cm} = 1\,089\;\text{cm}^2 \quad \text{ja} \quad A_2 = 11\;\text{cm} \cdot 11\;\text{cm} = 121\;\text{cm}^2 \]

Kirjoitetaan painopisteet, kun lisätyn levyn pinta-ala huomioidaan negatiivisena.

\[ x_\text{pp} = \frac{x_1 A_1 - x_2 A_2}{A_1 - A_2}, \qquad y_\text{pp} = \frac{y_1 A_1 - y_2 A_2}{A_1 - A_2} \]

Sijoitetaan arvot ja lasketaan painopisteen \(x\)-koordinaatti.

\[ x_\text{pp} = \frac{16,5\;\text{cm} \cdot 1\,089\;\text{cm}^2 - 5,5\;\text{cm} \cdot 121\;\text{cm}^2}{1\,089\;\text{cm}^2 - 121\;\text{cm}^2} = 17,875\;\text{cm} \approx 17,9\;\text{cm} \]

Lasketaan vielä painopisteen \(y\)-koordinaatti.

\[ y_\text{pp} = \frac{16,5\;\text{cm} \cdot 1\,089\;\text{cm}^2 - 16,5\;\text{cm} \cdot 121\;\text{cm}^2}{1\,089\;\text{cm}^2 - 121\;\text{cm}^2} = 16,5\;\text{cm} \]

b)

Katso tehtävän kuvaa. Origo on sellaisen neliön vasemmassa alakulmassa siten, että ympyrä kuvitellaan neliön sisään.

Ratkaistaan tehtävä puuttuvan palan menetelmällä siten, että täydennetään levy ympyräksi.

Täydennetyn ympyrän (pinta-ala \(A_1\)) painopiste \((x_1;y_1)\) on \((15,0\;\text{cm}; 15,0\;\text{cm})\) ja lisätyn pikkuympyrän (pinta-ala \(A_2\)) painopiste \((x_2;y_2)\) on \((22,5\;\text{cm}; 15,0\;\text{cm})\)

Lasketaan pinta-alat.

\[ A_1 = \pi \cdot (15,0\;\text{cm})^2 = 706,8583\;\text{cm}^2 \quad \text{ja} \quad A_2 = pi \cdot (7,5\;\text{cm})^2 = 176,7146\;\text{cm}^2 \]

Kirjoitetaan painopisteet, kun lisätyn levyn pinta-ala huomioidaan negatiivisena.

\[ x_\text{pp} = \frac{x_1 A_1 - x_2 A_2}{A_1 - A_2}, \qquad y_\text{pp} = \frac{y_1 A_1 - y_2 A_2}{A_1 - A_2} \]

Sijoitetaan arvot ja lasketaan painopisteen \(x\)-koordinaatti.

\[ x_\text{pp} = \frac{15,0\;\text{cm} \cdot 706,8583\;\text{cm}^2 - 22,5\;\text{cm} \cdot 176,7146\;\text{cm}^2}{706,8583\;\text{cm}^2 - 176,7146\;\text{cm}^2} = 12,5000\;\text{cm} \approx 12,5\;\text{cm} \]

Lasketaan vielä painopisteen \(y\)-koordinaatti.

\[ y_\text{pp} = \frac{15,0\;\text{cm} \cdot 706,8583\;\text{cm}^2 - 15,0\;\text{cm} \cdot 176,7146\;\text{cm}^2}{706,8583\;\text{cm}^2 - 176,7146\;\text{cm}^2} = 15,0\;\text{cm} \]

VAST.

a)

\((17,9\;\text{cm}; 16,5\;\text{cm})\)

b)

\((12,5\;\text{cm}; 15,0\;\text{cm})\)

Tehtävä 155

Pyöriminen konkreettisen akselin ympäri: saranoitu ovi, karuselli,...

Pyöriminen kuvitteellisen akselin ympäri: jalkapallo, frisbee, bumerangi,...

Tehtävä 157

a)

\[ 33^\circ = \frac{33^\circ}{360^\circ} \cdot 2\pi\;\text{rad} = 0,5760\;\text{rad} \approx 0,58\;\text{rad} \]

b)

\[ 45^\circ = \frac{45^\circ}{360^\circ} \cdot 2\pi\;\text{rad} = 0,7854\;\text{rad} \approx 0,79\;\text{rad} \]

c)

\[ 0,1^\circ = \frac{0,1^\circ}{360^\circ} \cdot 2\pi\;\text{rad} = 0,001745\;\text{rad} \approx 0,0017\;\text{rad} \]

d)

\[ 1\,000^\circ = \frac{1\,000^\circ}{360^\circ} \cdot 2\pi\;\text{rad} = 17,4533\;\text{rad} \approx 17,5\;\text{rad} \]

Tehtävä 158

a)

\[ 3,0\;\text{rad} = \frac{3,0\;\text{rad}}{2 \pi\;\text{rad}} \cdot 360^\circ = 171,8873^\circ \approx 170^\circ \]

b)

\[ 0,50\;\text{rad} = \frac{0,50\;\text{rad}}{2 \pi\;\text{rad}} \cdot 360^\circ = 28,6479^\circ \approx 29^\circ \]

c)

\[ 10,0\;\text{rad} = \frac{10,0\;\text{rad}}{2 \pi\;\text{rad}} \cdot 360^\circ = 572,9578^\circ \approx 573^\circ \]

d)

\[ 1,50\;\text{rad} = \frac{1,50\;\text{rad}}{2 \pi\;\text{rad}} \cdot 360^\circ = 85,9437^\circ \approx 85,9^\circ \]

Tehtävä 159

\(\varphi = 130^\circ, \quad r = 0,40\;\text{m}\)

a)

\[ \varphi = 130^\circ = \frac{130^\circ}{360^\circ} \cdot 2 \pi\;\text{rad} = 2,2689\;\text{rad} \approx 2,27\;\text{rad} \]

b)

Lasketaan tangon pään kulkema matka.

\[ s = r \varphi = 0,40\;\text{m} \cdot 2,2689\;\text{rad} = 0,9076\;\text{m} \approx 0,91\;\text{m} \]

VAST.

2,27 rad ja 0,91 m

Tehtävä 161

\(r = 0,45\;\text{m}, \quad a_\text{n} = 40\,000\;g, \quad g = 9,81\;\frac{\text{m}}{\text{s}^2}\)

Normaalikiihtyvyyden suunta on kohti ympyräradan keskipistettä.

\[ a_\text{n} = \frac{v^2}{r} = r\omega^2 \quad \text{eli} \quad \omega = \sqrt{\frac{a_\text{n}}{r}} \]

Lasketaan kulmanopeus.

\[ \omega = \sqrt{\frac{40\,000 \cdot 9,81\;\frac{\text{m}}{\text{s}^2}}{0,45\;\text{m}}} = 933,8094\;\frac{\text{rad}}{\text{s}} \]

Lasketaan kierrosnopeus, kun \(\omega = 2 \pi n\).

\[ n = \frac{\omega}{2 \pi} = \frac{933,8094\;\frac{\text{rad}}{\text{s}}}{2 \pi \;\text{rad}} = 148,6204\;\frac{1}{\text{s}} \]

Lasketaan kierrosten määrä minuutissa.

\[ n = 148,6204\;\frac{1}{\text{s}} \cdot 60\;\frac{\text{s}}{\text{min}} = 8\,917,2229\;\frac{1}{\text{min}} \approx 8\,900\;\text{RPM} \]

VAST.

\(8\,900\;\text{RPM}\)

Tehtävä 171

\(r_1 = 32,0\;\text{cm}, \quad r_2 = 15,2\;\text{cm}, \quad \omega_1 = 2\,500\;\frac{\text{rad}}{\text{s}}, \quad \omega_1 = ?\)

Toisiinsa kytkettyjen pyörien kulmanopeudet ovat kääntäen verrannolliset niiden säteisiin.

Muodostetaan yhtälö.

\[ \omega_2 r_2 = \omega_1 r_1 \]

Ratkaistaan kulmanopeus.

\[ \omega_2 = \omega_1 \frac{r_1}{r_2} = 2\,500\;\frac{\text{rad}}{\text{s}} \cdot \frac{32,0\;\text{cm}}{15,2\;\text{cm}} = 5\,263,1579\;\frac{\text{rad}}{\text{s}} \approx 5\,300\;\frac{\text{rad}}{\text{s}} \]

Lasketaan vielä pyörimisnopeus.

\[ n = \frac{\omega}{2\pi} = \frac{5\,263,1579\;\frac{\text{rad}}{\text{s}}}{2 \pi \;\text{rad}} = 837,6576\;\frac{1}{\text{s}} \approx 840\;\frac{1}{\text{s}} \]

VAST.

\(5\,300\;\frac{\text{rad}}{\text{s}}\) ja \(840\;\frac{1}{\text{s}}\)

Tehtävä 174

\(n = 3\,600\;\frac{\text{r}}{\text{min}}\)

a)

Lasketaan kulmanopeus.

\[ \omega = 2 \pi n = 2 \pi \;\text{rad} \cdot \frac{3\,600\;\frac{\text{r}}{\text{min}}}{60\;\frac{\text{s}}{\text{min}}} = 120 \pi \;\frac{\text{rad}}{\text{s}} \]

b)

Lasketaan kiertymään kulunut aika.

\[ t = \frac{\varphi}{\omega} = \frac{1\,000\;\text{rad}}{120 \pi \;\frac{\text{rad}}{\text{s}}} = 2,652\;\text{s} \approx 2,7\;\text{s} \]

VAST.

\(120 \pi \;\text{rad}\) ja \(2,7\;\text{s}\)

Tehtävä 175

\(n = 12\;000\;\frac{1}{\text{min}}, \quad t = 270\;\text{s}\)

Koska kiihtyvyys on tasaista, voidaan tehtävä ratkaista keskimääräisen pyörimisnopeuden avulla.

Lasketaan kierrokset.

\[ N = n_\text{k} t = \frac{n}{2} t = \frac{12\;000\;\frac{1}{\text{min}}}{2 \cdot 60\;\frac{\text{s}}{\text{min}}} \cdot 270\;\text{s} = 27\,000 \]

VAST.

\(27\,000\)

Tehtävä 176

\(\omega_\text{A} = 375\;\frac{\text{rad}}{\text{s}}, \quad \omega_\text{B} = 542\;\frac{\text{rad}}{\text{s}}, \quad \Delta \varphi = 44,0\;\text{rad}\)

Koska kiihtyvyys on tasaista, voidaan tehtävä ratkaista keskimääräisen kulmanopeuden avulla.

Lasketaan kiihdytysaika.

\[ \Delta t = \frac{\Delta \varphi}{\omega_\text{k}} = \frac{44,0\;\text{rad}}{\frac{375\;\frac{\text{rad}}{\text{s}} + 542\;\frac{\text{rad}}{\text{s}}}{2}} = 0,09597\;\text{s} \]

Lasketaan kulmakiihtyvyys.

\[ \alpha = \frac{\Delta \omega}{\Delta t} = \frac{542\;\frac{\text{rad}}{\text{s}} - 375\;\frac{\text{rad}}{\text{s}}}{0,09597\;\text{s}} = 1\,740,1271\;\frac{\text{rad}}{\text{s}} \approx 1\,740\;\frac{\text{rad}}{\text{s}} \]

VAST.

\(1\,740\;\frac{\text{rad}}{\text{s}}\)

Tehtävä 180

\(n = 240\;\frac{1}{\text{min}}, \quad t_1 = 6,2\;\text{s}, \quad t_2 = 4,5\;\text{min}, \quad N = 2\,900\)

Lasketaan vauhtipyörän kierrokset kiihdytyksen ja jarrutuksen aikana.

Koska kiihtyvyys on tasaista, voidaan kierrosnopeus ajatella keskimääräiseksi.

Lasketaan kiihdytyksen kierrokset. \[ N_\text{kiihd.} = n_\text{k} t_1 = \frac{240}{2 \cdot 60\;\text{s}} \cdot 6,2\;\text{s} = 12,4 \]

Lasketaan jarrutukset kierrokset. \[ N_\text{jarr.} = n_\text{k} t_2 = \frac{240}{2 \cdot 60\;\text{s}} \cdot 4,5 \cdot 60\;\text{s} = 540 \]

Lasketaan käyntiajan kierrokset.

\[ N - N_\text{kiihd.} - N_\text{jarr.} = 2\,900 - 12,4 - 540 = 2\,347,6 \]

Lasketaan pyörimisaika.

\[ t = \frac{N}{n} = \frac{2\,347,6}{\frac{240}{60\;\text{s}}} = 586,9\;\text{s} \]

Lasketaan koko aika.

\[ t_\text{koko} = 586,9\;\text{s} + 6,2\;\text{s} + 4,5 \cdot 60\;\text{s} = 863,1\;\text{s} \approx 14,4\;\text{min} \]

VAST.

\(14,4\;\text{min}\)

Tehtävä 182

\(\omega_\text{0} = 1,88\;\frac{\text{rad}}{\text{s}}, \quad \varphi = 44,0\;\text{rad}, \quad t = 10,0\;\text{s}\)

Kiihtyvyys on tasaista.

\[ \varphi = \varphi_0 + \omega_0 t + \frac{1}{2}\alpha t^2. \]

Ratkaistaan kaavasta kulmakiihtyvyys, kun \(\varphi_0 = 0\).

\[ \alpha = \frac{\varphi - \omega_0 t}{\frac{1}{2}\alpha t^2} = \frac{44,0\;\text{rad} - 1,88\;\frac{\text{rad}}{\text{s}} \cdot 10,0\;\text{s}}{\frac{1}{2}\cdot (10,0\;\text{s})^2} = 0,504\;\frac{\text{rad}}{\text{s}^2} \approx 0,50\;\frac{\text{rad}}{\text{s}^2} \]

VAST.

\(0,50\;\frac{\text{rad}}{\text{s}^2}\)

Tehtävä 191

\(m = 1,2\;\text{kg}, \quad r = 0,15\;\text{m}\)

a)

\[ J = \frac{1}{2} \cdot 1,2\;\text{kg} \cdot (0,15\;\text{m})^2 = 0,0135\;\text{kgm}^2 \approx 0,014\;\text{kgm}^2 \]

b)

\[ J = \frac{2}{3} \cdot 1,2\;\text{kg} \cdot (0,15\;\text{m})^2 = 0,018\;\text{kgm}^2 \]

c)

\[ J = 1,2\;\text{kg} \cdot (0,15\;\text{m})^2 = 0,027\;\text{kgm}^2 \]

Tehtävä 197

\(m = 1,0\;\text{kg}, \quad a = 1,0\;\text{m}\)

a)

\[ J_\text{A} = \Sigma m_\text{i} r^2_\text{i} = 1,0\;\text{kg} \cdot (1,0\;\text{m})^2 = 1,0\;\text{kgm}^2 \]

b)

\[ J_\text{A} = \Sigma m_\text{i} r^2_\text{i} = 1,0\;\text{kg} \cdot (1,0\;\text{m})^2 + 1,0\;\text{kg} \cdot (2,0\;\text{m})^2 = 5,0\;\text{kgm}^2 \]

c)

\[ J_\text{A} = \Sigma m_\text{i} r^2_\text{i} = 1,0\;\text{kg} \cdot (1,0\;\text{m})^2 + 1,0\;\text{kg} \cdot (2,0\;\text{m})^2 + 1,0\;\text{kg} \cdot (3,0\;\text{m})^2 = 14,0\;\text{kgm}^2 \]

Tehtävä 201

a)

Jos kiekkoon vaikuttava kokonaismomentti on nolla, kiekon kulmanopeus ei muutu.

b)

Kiekkoon vaikuttava ulkoinen momentti on nolla. Kiekon akseliin vaikuttava kitkamomentti ei ole nolla. Kiekkoon vaikuttava kokonaismomentti ei ole nolla, ja kiekon kulmanopeus muuttuu.

Tehtävä 202

a)

Satelliittiin vaikuttavat voimat ovat yhtä suuria ja vastakkaissuuntaisia, joten sen etenemisliikkeen tila ei muutu. Nopeus ei siis muutu.

b)

Satelliittiin vaikuttavat voimat vaikuttavat kohtisuoraan suhteessa pyörimisakseliin eikä voiman varsi ole nolla. Satelliittiin kohdistuu momentti, joka saa sen pyörimisliikkeeseen.

Tehtävä 203

\(m = 2,4\;\text{kg}, \quad l = 1,7\;\text{m}\)

Lautaan vaikuttavat paino \(\overline{G}\) ja saranan tukivoima \(\overline{N}\).

Saranan tukivoima ei aiheuta momenttia. Momentti akselin \(A\) suhteen aiheutuu laudan keskipisteeseen vaikuttavasta painovoimasta.

\[ \Sigma M_\text{A} = G \cdot \frac{1}{2}l \]

Kirjoitetaan momentti akselin \(A\) suhteen.

\[ J_\text{A} = \frac{1}{3} ml^2 \]

Kirjoitetaan pyörimisen peruslain mukainen yhtälö.

\[ \Sigma M_\text{A} = J_\text{A} \alpha \quad \text{eli} \quad G \cdot \frac{1}{2}l = \frac{1}{3} ml^2 \alpha \quad \text{eli} \quad \alpha = \frac{3Gl}{2ml^2} = \frac{3G}{2ml} \]

Lasketaan kulmakiihtyvyys.

\[ \alpha = \frac{3 \cdot 2,4\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2}}{2 \cdot 2,4\;\text{kg} \cdot 1,7\;\text{m}} = 8,6559\;\frac{\text{rad}}{\text{s}^2} = 8,7\;\frac{\text{rad}}{\text{s}^2} \]

VAST.

\(8,7\;\frac{\text{rad}}{\text{s}^2}\)

Tehtävä 212

\(m = 8,3\;\text{kg}, \quad r = 0,29\;\text{m}, \quad T = 55\;\text{N}, \quad \alpha = ?, \quad N = ?\)

a)

1 Rullaan vaikuttavat paino \(\overline{G}\), akselin tukivoima \(\overline{N}\) ja paperin jännitysvoima \(\overline{T}\). Kitkavoimia ei ole.

Rullaan sen akselin suhteen aiheuttaa momentin vain paperin jännitysvoima, koska painon ja tukivoiman varret ovat nollia.

2 Piirretään voimakuvio.

TODO

3 Kirjoitetaan momentti akselin \(A\) suhteen.

\[ \Sigma M_\text{A} = Tr \]

4 Kirjoitetaan rullan hitausmomentti akselin \(A\) suhteen.

\[ J_\text{A} = \frac{1}{2}mr^2 \]

5 Kirjoitetaan pyörimisen peruslain \(\Sigma M_\text{A} = J_\text{A} \alpha\) mukainen rullan pyörimisen liikeyhtälö.

\[ Tr = \frac{1}{2}mr^2 \alpha \]

Ratkaistaan kulmakiihtyvyys.

\[ \alpha = \frac{Tr}{\frac{1}{2}mr^2} = \frac{T}{\frac{1}{2}mr} \]

Lasketaan kulmakiihtyvyys.

\[ \alpha = \frac{12\;\text{N}}{\frac{1}{2} \cdot 85\;\text{kg} \cdot 0,20\;\text{m}} = 1,4118\;\frac{1}{\text{s}^2} \]

Lasketaan kiihtyvyys.

\[ a = \alpha r = 1,4118\;\frac{1}{\text{s}^2} \cdot 0,20\;\text{m} = 0,2824\;\frac{\text{m}}{\text{s}^2} \approx 0,28\;\frac{\text{m}}{\text{s}^2} \]

6 Saatu kulmakiihtyvyys vaikuttaa järkevältä ja sen suuruusluokka on oikea.

b)

Kirjoitetaan dynamiikan peruslain mukainen yhtälö.

\[ \Sigma \overline{F} = m \overline{a} \quad \text{eli} \quad \overline{N} + \overline{G} + \overline{T} = m \overline{a} \]

Rullalla ei ole etenemisliikkeen kiihtyvyyttä.

\[ \overline{a} = \overline{0} \quad \text{ja} \quad \overline{N} + \overline{G} + \overline{T} = \overline{0} \]

Positiivinen suunta on ylöspäin ja oikealle. Kirjoitetaan yhtälö skalaarimuodossa.

\[ G_\text{x} = 0, \quad G_\text{y} = N_\text{y}, \quad T_\text{x} = N_\text{x}, \quad \text{ja} \quad T_\text{y} = 0 \]

Lasketaan tukivoima Pythagoraan lauseen avulla.

\[ N = \sqrt{G^2_\text{y} + T^2_\text{x}} = \sqrt{\left(85\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2}\right)^2 + (12\;\text{N})^2} = 833,9363\;\text{N} \approx 830\;\text{N} \]

Lasketaan vielä suunta.

\[ \alpha = \tan^{-1}\left(\frac{T_\text{x}}{G_\text{y}}\right) = \tan^{-1}\left(\frac{12\;\text{N}}{85\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2}}\right) = 0,8245^\circ \approx 0,82^\circ \]

VAST.

\(0,28\;\frac{\text{m}}{\text{s}}\) ja \(0,82^\circ\)

Tehtävä 214

\(m = 2 \cdot 5,0\;\text{kg}, \quad T_1 = 2,1\;\text{s}, \quad J_1 = 3,1\;\text{kgm}^2, \quad J_2 = 2,3\;\text{kgm}^2, \quad r = 0,80\;\text{m}\)

Paino ja tukivoima eivät aiheuta momenttia pyörimisakselin suhteen. Vastusvoimia ja -momenttia ei ole.

Pyörimismäärä säilyy, ja \(\omega = 2 \pi n\) ja \(n = \frac{1}{T}\).

\[ (J_1 + mr^2) \omega_1 = J_2 \omega_2 \quad \text{eli} \quad (J_1 + mr^2) \cdot 2 \pi \cdot \frac{1}{T_1} = J_2 \cdot 2 \pi \cdot \frac{1}{T_2} \]

Ratkaistaan ja lasketaan \(T_2\).

\[ T_2 = \frac{J_2 T_2}{J_1 + mr^2} = \frac{2,3\;\text{kgm}^2 \cdot 2,1\;\text{s}}{3,1\;\text{kgm}^2 + 2 \cdot 5,0\;\text{kg} \cdot (0,80\;\text{m})^2} = 0,5084\;\text{s} \]

Lasketaan vielä pyörimisnopeus.

\[ n_2 = \frac{1}{T_2} \cdot 60\;\frac{\text{s}}{\text{min}} = 118,0124\;\text{RPM} \approx 120\;\text{RPM} \]

VAST.

\(120\;\text{RPM}\)

Tehtävä 223

\(m_\text{s} = 0,53\;\text{kg}, \quad l_\text{s} = 0,60\;\text{m}, \quad m_\text{p} = 0,30\;\text{kg}\)

Sauvan massakeskipiste on sen painopisteessä eli sauvan puolivälissä. Pyörähtäessään sauvan painopiste laskee puolet sauvan pituudesta. Vastaavasti punnuksen painopiste laskee koko sauvan pituuden.

Koska vastusvoimia ei ole, mekaaninen energia säilyy.

\[ E_\text{pas} + E_\text{pap} + E_\text{ras} + E_\text{rap} = E_\text{pls} + E_\text{plp} + E_\text{rls} + E_\text{rlp} \]

Aluksi on vain potentiaalienergiaa ja lopuksi on vain rotaatioenergiaa.

\[ m_\text{s}g\frac{l}{2} + m_\text{p}gl = \frac{1}{2}J_\text{s}\omega^2 + \frac{1}{2}J_\text{p}\omega^2 \]

Sauvan hitausmomentti on \(J = \frac{1}{3}ml^2\) ja punnuksen hitausmomentti on \(J = mr^2\).

\[ m_\text{s}g\frac{l}{2} + m_\text{p}gl = \frac{1}{2} \cdot \frac{1}{3}m_\text{s}l^2 \cdot \omega^2 + \frac{1}{2} \cdot m_\text{p}l^2 \cdot \omega^2 \]

Ratkaistaan kulmanopeus \(\omega\).

\[ \omega = \sqrt{\frac{m_\text{s}g\frac{l}{2} + m_\text{p}gl}{\frac{1}{2}(\frac{1}{3}m_\text{s}l^2 + m_\text{p}l^2)}} \]

Lasketaan kulmanopeus.

\[ \omega = \sqrt{\frac{0,53\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot \frac{0,60\;\text{m}}{2} + 0,30\;\text{kg} \cdot 9,81\;\frac{\text{m}}{\text{s}^2} \cdot 0,60\;\text{m}} {\frac{1}{2}\left(\frac{1}{3} \cdot 0,53\;\text{kg} \cdot (0,60\;\text{m})^2 + 0,30\;\text{kg} \cdot (0,60\;\text{m})^2\right)}} = 6,2257\;\frac{\text{rad}}{\text{s}} \approx 6,2\;\frac{\text{rad}}{\text{s}} \]

Lasketaan vielä nopeus.

\[ v = l\omega = 0,60\;\text{m} \cdot 6,2257\;\frac{\text{rad}}{\text{s}} = 3,7354\;\frac{\text{m}}{\text{s}} \approx 3,7\;\frac{\text{m}}{\text{s}} \]

VAST.

6,2 rad/s ja 3,7 m/s

Tehtävä 226

\(m = 12,0\;\text{kg}, \quad v = 2,2\;\frac{\text{m}}{\text{s}}\)

a)

Lasketaan sylinterin translaatioenergia.

\[ E_{\text{t}} = \frac{1}{2} m v^2 = \frac{1}{2} \cdot 12,0\;\text{kg} \cdot \left(2,2\,\frac{\text{m}}{\text{s}}\right)^2 = 29,04\;\text{J} \approx 29\;\text{J} \]

b)

Umpinaisen sylinterin hitausmomentti on \(J = \frac{1}{2}mr^2\).

Ratkaistaan sylinterin kulmanopeus.

\[ \omega = \frac{v}{r} \]

Lasketaan sylinterin rotaatioenergia.

\[ E_{\text{r}} = \frac{1}{2} J \omega^2 = \frac{1}{2} \cdot \frac{1}{2} mr^2 \cdot \left(\frac{v}{r}\right)^2 = \frac{1}{4} \cdot mv^2 = \frac{1}{4} \cdot 12,0\;\text{kg} \cdot \left(2,2\,\frac{\text{m}}{\text{s}}\right)^2 = 14,52\;\text{J} \approx 15\;\text{J} \]

c)

Lasketaan sylinterin translaatio- ja rotaatioenergioiden summa.

\[ E_\text{k} = E_\text{t} + E_\text{r} = 29,04\;\text{J} + 14,52\;\text{J} = 43,56\;\text{J} \approx 44\;\text{J} \]

VAST.

29 J, 15 J ja 44 J

Tehtävä 238

\(F = 62\;\text{N}, \quad r = 0,65\;\text{m}, \quad \Delta \varphi = 2\pi\;\text{rad}\)

Lasketaan yhden kierroksen aikana tehty työ.

\[ W = Fs = Fr\Delta\varphi = 62\;\text{N} \cdot 0,65\;\text{m} \cdot 2\pi\;\text{rad} \approx 250\;\text{J} \]

VAST.

250 J

Tehtävä 239

\(v = 2,8\;\frac{\text{m}}{\text{s}}, \quad r = 0,50\;\text{m}, \quad m = 0,320\;\text{kg}\)

Tehty työ on sama kuin on vanteen translaatio- ja rotaatioenergian summa.

\[ W = E_\text{t} + E_\text{r} = \frac{1}{2}mv^2 + \frac{1}{2}J\omega^2 = \frac{1}{2}mv^2 + \frac{1}{2} \cdot mr^2 \cdot \left(\frac{v}{r}\right)^2 = \frac{1}{2}mv^2 + \frac{1}{2} \cdot mv^2 = mv^2 \]

Lasketaan työ.

\[ W = 0,320\;\text{kg} \cdot \left(2,8\;\frac{\text{m}}{\text{s}}\right)^2 \approx 2,5\;\text{J} \]

VAST.

2,5 J

Tehtävä 251

\(r = 60,0\;\text{m}, \quad a_\text{t} = 1,0\;\frac{\text{m}}{\text{s}^2}, \quad \mu = 0,50\)

Tehtävän huolellinen käsittely vaatisi...

Auto pysyy ympyräradalla.

\[ m\frac{v^2}{r} = \mu G \quad \text{eli} \quad \frac{v^2}{r} = \mu g \quad \text{eli} \quad v = \sqrt{\mu gr} \]

Nyt voidaan ratkaista...