Joukko-opista fraktaaleihin

Ohjeita käyttäjälle
Materiaali koostuu viidestä alaluvusta, jotka sisältävät tehtäviä, teoriaa sekä esimerkkejä liittyen joukko-oppiin ja fraktaaleihin. Löydät sisällysluettelon linkkeineen sivun vasemmasta reunasta.
Materiaali on pyritty suunnittelemaan niin, että sitä voidaan hyödyntää sekä oppitunneilla että itsenäisessä opiskelussa. Tehtäviä suositellaan tekemään annetussa järjestyksessä, sillä jokainen osio sisältää oman oppisisältönsä sekä mahdollisesti tärkeää taustatietoa seuraaviin tehtäviin.
Suurin osa tehtävistä on rakennettu siten, että vastaukset voi tallentaa tai
tarkistaa tehtävän yhteydessä. Tehtävät ovat tyypiltään sellaisia, että laskimeen ei tarvitse turvautua. Jos tehtävässä käsketään hyödyntämään vapaavalintaista ohjelmistoa, sen yhteyteen on lisätty kohta, johon voit ladata kuvakaappauksen tai vastaustiedoston, kun olet saanut tehtävän valmiiksi. Näin voit tallentaa kaikki vastaukset tälle sivulle. Jos teet tehtävän paperille, voit ottaa siitä kuvan ja ladata palautuskohtaan.
Ohjeita vastaamiseen:
- Osa tehtävistä avautuu kokonaiseksi vasta kun viet kursorin tehtävän päälle.
 -merkki tarkoittaa sulkeutuvaa aluetta, jota klikkaamalla saat näkyviin piilotetun sisällön, esim. vastausikkunan, kysymykset tai mallivastauksen.
-merkki tarkoittaa sulkeutuvaa aluetta, jota klikkaamalla saat näkyviin piilotetun sisällön, esim. vastausikkunan, kysymykset tai mallivastauksen.- Kaikista tehtävissä ei tule erillistä ilmoitusta, menikö vastaus oikein vai väärin. Etsi tällöin
Pointstehtävän yläreunasta:- Jos
Points: 0niin vastaus ei ole oikein. Alusta tehtävä ja kokeile uudelleen. Huom. joissain tehtävissä vastauskertojen määrä on rajoitettu. - Jos
Points: 1tai enemmän, vastaus meni oikein.
- Jos
- Tekstivastauksista ei tule automaattisesti pisteitä eikä oikein/väärin -ilmoitusta, mutta opettaja voi halutessaan pisteyttää nämä tehtävät.
Muita vinkkejä:
- Voit merkitä alueen luetuksi klikkaamalla sivun oikeassa reunassa näkyvää oranssia palkkia.
- Oikean reunan
 merkistä voit lisätä kyseiseen kohtaan julkisen kommentin tai tehdä muistiinpanoja, jotka näkyvät vain itsellesi (
merkistä voit lisätä kyseiseen kohtaan julkisen kommentin tai tehdä muistiinpanoja, jotka näkyvät vain itsellesi (Just me). - Jos reuna on keltainen, materiaaliin on tehty muutoksia sen jälkeen, kun olet lukenut sen.
- Materiaalin lopusta löytyy ylimääräisiä paikkoja vastaustiedostojen palauttamiselle.
- Aivan materiaalin lopusta löydät ylimääräisiä palautuspaikkoja vastaustiedostolle
1. Johdatus joukko-oppiin
1.1 Johdantotehtävä 1
1.2 Johdantotehtävä 2
Tässä tehtävässä tarvitset jotain ohjelmista, jolla voi piirtää. Esimerkiksi GeoGebran online-version voit avata alla olevasta pudotusvalikosta.
Seuraa tarkasti ohjeistusta, ja vastaa tämän jälkeen tehtäviin. Tehtävät löydät pudotusvalikoista hieman alempaa.
1. Piirrä GeoGebralla kolme erilaista ellipsiä siten, että voit liikuttaa niitä vapaasti raahaamalla.
2. Nimeä ellipsit seuraavasti:
3. Lajittele seuraavat luvut oikeisiin ellipseihin:
4. Ota kuvakaappaus tekemästäsi kuviosta ja palauta se alla olevaan palautuslaatikkoon.
2. Joukko-opin käsitteitä
Johdantotehtävässä 2 muodostamasi ympyrät tai ellipsit ovat esimerkkejä joukoista. Luvut, joita asetit ympyröiden sisälle, ovat nimeltään alkioita, eli joukon jäseniä. Joukossa voi olla ääretön tai äärellinen määrä alkioita.
Joukot ja alkiot
Olkoon joukko
Lukuja ,
,
, ja
kutsutaan joukon
alkioiksi.
Jos alkio kuuluu joukkoon
, merkitään
Jos alkio
ei kuulu joukkoon
, merkitään
Joukko voi olla myös tyhjä joukko, jolloin joukossa ei ole yhtään alkiota ja tällöin merkitään .
Kaksi joukkoa ovat samat, jos niillä on samat alkiot. Eli
2.1 Tehtävä: Joukot ja niiden alkiot
Kuvassa on hahmoteltu joukot ,
ja
, ja niihin sisältyvät alkiot. Valitse oikeat vastaus!
Joukon alkioista voidaan muodostaa myös pienempiä joukkoja. Tällöin kyseessä on osajoukoista. Jos vaikka joukko , sen osajoukkoja olisivat esimerkiksi
.
Osajoukot
Olkoon joukko Joukon
eräs osajoukko olisi joukko
Jos joukko on joukon
osajoukko, niin jokaisen joukon
alkio on oltava myös joukon
alkio. Tällöin merkitään
Jos joukko ei ole joukon
osajoukko, niin merkitään
Jokainen joukko on aina myös itsensä osajoukko, eli
Tyhjä joukko on jokaisen joukon osajoukko, eli jos joukko
on mikä tahansa joukko, niin aina
.
2.2 Tehtävä: Joukot ja niiden osajoukot
Olkoon joukot
2.3 Johdantotehtävä: Yhdiste, leikkaus ja erotus
Tutustutaan seuraavaksi joukko-opin käsitteisiin yhdiste, leikkaus ja erotus. Tee alla olevat tehtävät. Avaa GeoGebra-appi alla olevasta pudotusvalikosta ja hahmottele tehtävät kuvina!
Hahmottele GeoGebralla seuraava tilanne ja vastaa kysymyksiin.
- Piirrä joukko
, johon kuuluu alkiot
ja
.
- Piirrä joukko
, johon kuuluu alkiona joukko
ja myös alkiot
ja
.
- Piirrä joukko
, johon kuuluu alkiot
ja
.
- Kirjoita joukot käyttäen joukko-opin merkintöjä (
).
- Palauta alla olevaan palautuslaatikkoon kuvakaappaus piirroksestasi
Joukkojen yhdiste, leikkaus ja erotus
Olkoon joukot ja
.
Näiden kahden joukon yhdiste on sellainen joukko, joka sisältää molempien joukkojen alkiot. Yhdistettä merkitään :lla. Siis
Joukkojen ja
leikkaus sisältää kaikki ne alkiot, jotka löytyvät sekä joukosta
että joukosta
. Leikkausta merkitään
:lla. Siis
Joukkojen ja
erotus tarkoittaa, että joukon
alkioista poistetaan joukon
alkiot, ja luetellaan jäljelle jäänyt joukko. Joukkojen
ja
erotus merkitään
. Siis
2.4 Tehtävä: Yhdiste, leikkaus ja erotus
2.5 Tehtävä: Yhdisteet ja leikkaukset

3. Funktiot
3.1 Johdantotehtävä: Kahden alkion välinen yhteys
Tutustutaan seuraavaksi joukko-opin käsitteitä yhdiste, leikkaus ja erotus. Tee alla olevat tehtävät. Avaa GeoGebra-appi alla olevasta pudotusvalikosta ja hahmottele tehtävät kuvina!
Hahmottele GeoGebralla seuraava tilanne ja vastaa kysymyksiin.
- Piirrä joukko
, johon kuuluu alkiot
ja
.
- Piirrä joukko
, johon kuuluu alkiot
ja
.
- Onko näiden eri joukkojen alkioiden välillä jokin yhteys?
- Piirrä joukon
alkioista viiva niihin joukon
alkioihin, jotka mielestäsi liittyvät yhteen jollain säännöllä.
- Palauta alla olevaan palautuslaatikkoon kuvakaappaus piirroksestasi
- Vastaa alla oleviin kysymyksiin.
Tarkastellaan seuraavaksi funktioita joukko-opin näkökulmasta. Funktio liittää kahden eri joukon, määrittelyjoukon ja maalijoukon, alkiot toisiinsa. Tarkastellaan ensin, mitä nämä joukot ovat.
Funktio eli kuvaus
Funktio on sääntö, joka liittää jokaiseen määrittelyjoukon
alkioon yksikäsitteisesti jonkin maalijoukon
alkion. Maalijoukosta
voidaan erottaa erilleen arvojoukko, johon sisältyvät vain ne maalijoukon alkiot, joille funktio
kuvaa alkion
.
Jos on olemassa tälläinen sääntö, joka kuvaa yksikäsitteisesti jokaisen joukon alkion jollekin maalijoukon
alkiolle, niin sanotaan, että
on funktio eli kuvaus joukolta
joukkoon
. Tätä merkittäisiin
Jos funktio f liittää joukon alkion
joukon
alkioon
, niin merkitään
Sanotaan, että funktio kuvaa alkion
alkiolle
.
Kuvassa oleva sininen ympyrä kuvastaa funktion määrittelyjoukkoa. Funktio
kuvaa jokaisen määrittelyjoukon
alkion yksikäsitteisesti jollekin maalijoukon
alkiolle.
Funktion käsitteeseen liittyvät joukot
Määrittelyjoukoksi kutsutaan sitä joukkoa, jossa funktio on määritelty. Tämän joukon jokainen alkio on mahdollista kuvata funktion avulla jollekin toiselle alkiolle.
Esimerkiksi funktio on määritelty vain positiivisilla reaaliluvuilla, eli määrittelyjoukko on
.
Maalijoukoksi kutsutaan sitä joukkoa, johon kuuluvat määrittelyjoukon alkioiden kuvat. Kaikille maalijoukon alkioille ei välttämättä kuvaudu mikään määrittelyjoukon alkio. Esimerkiksi, jos tarkastellaan funktiota ja rajataan tarkastelussa määrittelyjoukoksi vain kokonaislukujen joukko
, tällöin funktion maalijoukko on myös ainoastaan kokonaislukujen joukko
. Tästä maalijoukosta voidaan vielä erottaa omaksi joukokseen arvojoukon.
Arvojoukko on se maalijoukon osa, jossa ovat ainoastaan ne alkiot, joihin funktio kuvasi määrittelyjoukon alkion. Esimekiksi funktion arvojoukko on kaikki parilliset kokonaisluvut
.
3.2 Tehtävä: Funktio eli kuvaus
a. Olkoon funktio . Yhdistä oikeat joukon
alkiot oikeisiin joukon
alkioihin.
Käänteisfunktio
Kaikilla funktioilla ei ole olemassa käänteisfunktiota. Käänteisfunktio on olemassa, jos jokaiselle maalijoukon alkiolle kuvautuu täsmälleen yksi määrittelyjoukon alkio.
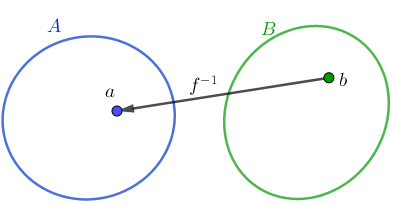 Tarkastellaan aiemmin käsiteltyä funktiota
Tarkastellaan aiemmin käsiteltyä funktiota . Oletetaan nyt, että
kuvaa maalijoukon jokaiselle alkiolle
täsmälleen yhden määrittelyjoukon alkion
. Silloin tämä funktio
liittää nyt jokaiseen alkioon
tietyn alkion
.
Sääntö, joka liittää jokaiseen joukon alkioon
yksikäsitteisesti jonkin joukon
alkion
, määrittelee käänteisfunktion
:
Käänteisfunktion määrityksestä
Käänteisfunktion määrittäminen tapahtuu käytännössä niin, että ratkaistaan esimerkiksi ensimmäisen asteen yhtälö (
) muuttujan
suhteen:
Ja tätä saatua lauseketta merkitään käänteisfunktiona
.
Koska olemme tottuneet käyttämään muuttujan paikalla kirjainta , niin vaihdetaan vielä saatuun käänteisfunktioon muuttujan paikalle
:
Osalle funktiosta voidaan määrittää helpostikin käänteisfunktio, mutta usein määritys on haastavaa ja työlästä.
3.3 Tehtävä: Käänteisfunktio
a.
Olkoon funktio nyt eri funktio kuin aiemmassa tehtävässä. Siirrä joukon
alkiot oikeisiin kohtiin. Mikä funktio
on?
b.
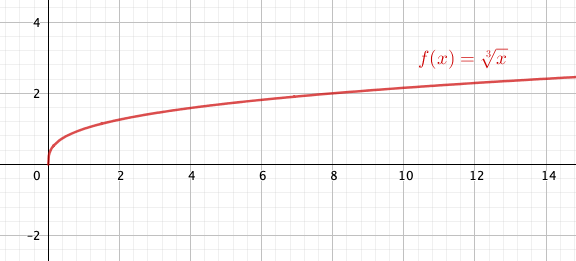
Kuvassa on funktio kun
. Tarkastele funktion kuvaajaa ja valitse oikeat vaihtoehdot.
c.
Miten käänteisfunktion arvo voidaan lukea funktion
kuvaajasta?
Seuraavaksi käsitellään fraktaalin käsite ja sen ominaisuuksia. Fraktaalit ovat itse asiassa joukkoja, joilla on tiettyjä ominaisuuksia.
4. Mitä ovat fraktaalit?

Fraktaalin määritteleminen tarkasti on melko haastavaa, mutta fraktaalina voidaan pitää sellaista kokonaisuutta, joka koostuu pienemmistä osista, jotka ovat kopioita tästä kokonaisuudesta. Fraktaalille tärkeimpiä ominaisuuksia on itsesimilaarisuus sekä fraktaalille ominainen Hausdorffin dimensio.
Yllä olevassa kuvassa Romanescu-kukkakaalissa voit huomata tämän toistuvan rakenteen: koko kaali näyttäisi koostuvan pienemmistä kaalin näköisistä osista.
Fraktaaligeometrian kehittäjänä pidetään Benoit Mandelbrotia, joka oli puolalaisyntyinen matemaatikko. Mandelbrot tutki kaaosteoriaa ja tutki niin kutsuttua luonnon uutta geometriaa.
Ensimmäistä fraktaaliteoriaa kehitettiin tarkoituksena ymmärtää matemaattista sisältöä käyrien jatkuvuudesta ja äärettömyydestä. Mandelbrot toi julki ajatuksen siitä, että fraktaalit ovat löydettävissä myös luonnosta.
Eräitä (jo nyt) klassisia fraktaaleja ovat Kochin lumihiutale, Sierpinskin kolmio sekä Mengerin pesusieni. Lisäksi on Cantorin joukko, Julian joukko sekä Mandelbrotin joukko. Näistä käsitellään tässä materiaalissa ensimmäiset kolme.

4.1 Johdantotehtävä: Mistä kaikkialta luonnosta fraktaaleja voi löytää?
Etsi internetistä tietoa siitä, mistä kaikkialta luonnosta voit löytää itsesimilaarisia rakenteita.
Tarkastellaan seuraavaksi Kochin lumihiutaletta. Eri fraktaalien rakentuminen sisältää paljon samanlaisia pääpiirteitä ja näin ollen myös Kochin lumihiutaleen vaiheet on paikannettavissa myös muiden fraktaalien rakentumisvaiheista.
Kochin lumihiutale
Kyseisen fraktaalin kehittäjä on nimensä mukaisesti Helge van Koch. Kuvion rakentaminen aloitetaan pohjajanasta.

Tämä pohjajana jaetaan kolmeen yhtä suureen osaan. Näistä keskimmäinen osa korvataan tasasivuisella kolmiolla.
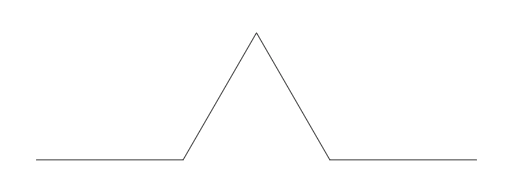
Edelleen nämä neljä janaa jaetaan jokainen kolmeen osaan. Näistä osista aina keskimmäinen korvataan tasasivuisella kolmiolla.
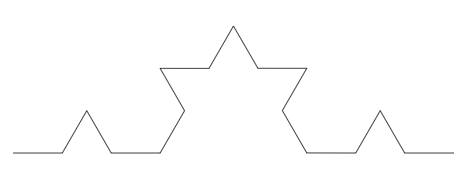
Tätä toistaen edetään, jolloin Kochin käyrä saa jo ominaisen muotonsa.
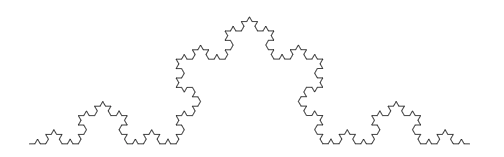
Jos jokaisella tasolla korvauksen ohessa uutta janaa myös käännetään °, muodostuu suljettu kuvio.

4.2 Tehtävä: Sierpinskin kolmio
a.

Järjestele kuviot oikeaan järjestykseen niin, että Sierpinksin kolmion ensimmäinen vaihe on vasemmalla ja viimeinen oikella.
Please
b.
4.3 Tehtävä: Mengerin pesusieni
a.
b.
4.4 Tehtävä: Muita fraktaaleja
Alla on kuvat Mandelbrotin joukosta sekä Julian fraktaaleista.
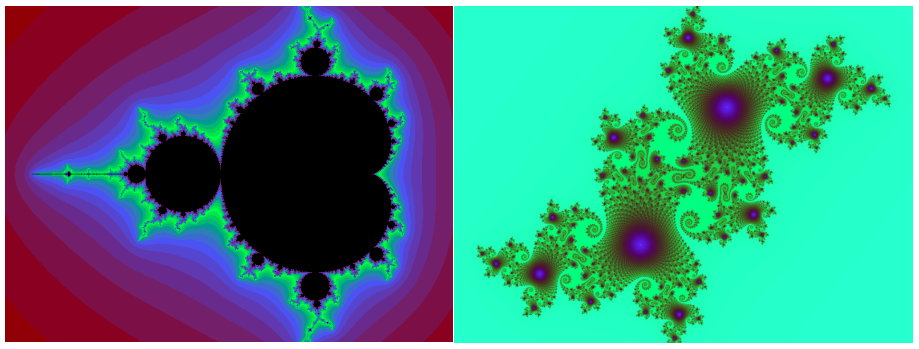
Mitä samanlaisia ja erilaisia piirteitä näillä kahdella fraktaalilla on? Kirjoita lyhyt pohdinta siitä, mitä kuvissa näet. Mandelbrotin ja Julian fraktaaleihin ei perehdytä tässä materiaalissa enempää, sillä ne ovat huomattavasti monimutkaisempia käsitellä.
5. Fraktaalien rakenne
Fraktaalien toistuvaa rakennetta kutsutaan itsesimilaarisuudeksi. Tämän similaarisuuden aiheuttaa similariteettikerroin, joka on jokaiselle fraktaalille ominainen. Lisäksi fraktaaleja käsiteltäessä usein törmätään Hausdorffin dimensioon, eli fraktaalin ulottuvuuteen. Tämä ulottuvuus poikkeaa niistä ulottuvuuksista, joita olemme yleisesti oppineet käyttämään, eli kokonaisluku-ulottuvuuksista.
Hausdorffin dimension määrittäminen
Fraktaalille pätee, että
jossa
ovat fraktaalin similariteetteja.
Nyt fraktaalille Hausdorffin dimensio
saadaan yhtälöstä, jossa
ovat similariteettien kertoimia.
Kerroin ilmaisee, mikä on kutistuksen suhde, eli paljonko osaa pienennetään.
5.1 Esimerkki: Hausdorffin dimension määrittäminen
Tarkastellaan Kochin lumihiutaleen Hausdorffin dimensiota. Tiedetään, että Kochin lumihiutale muotoutuu alkujanasta niin, että jana jaetaan aina pienempiin osiin ja korvataan keskimmäinen osa tasasivuisella kolmiolla. Lähtötietona tiedetään, että uuden osan kutistus tapahtuu kertoimella kolme.
Tarkastellaan nyt siirtymistä vaihesta kaksi vaiheeseen kolme, jossa jo alkuperäiseen janaan on jo liitetty tasasivuinen kolmio. Alla olevassa kuvassa yksi jana on jo jaettu kolmeen osaan ja siihen on liitetty tasasivuinen kolmio.
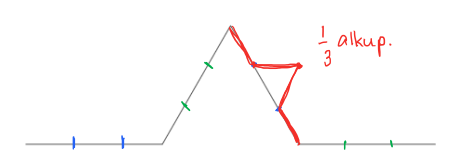
Tämä punainen kuvio on nyt pienennös alkuperäisestä kuviosta. Eli se on . Näitä korvauksia tehdään yhteensä neljä, eli molempiin kolmion sivuihin sekä vaakasuoriin janoihin.
Hyödynnetään nyt määritelmän laskukaavaa Hausdorffin dimension määrittämiselle: ja tässä esimerkissä
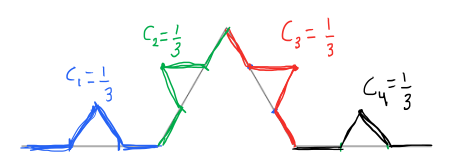
Kirjoitetaan yhtälö auki:
Kochin lumihiutaleen, jonka kutistuskerroin on , Hausdorffin dimensio
.
5.2 Tehtävä: Sierpinskin kolmion Hausdorffin dimensio
Määritä Sierpinskin kolmion Hausdorffin dimensio, kun tiedetään kutistuskertoimen olevan . Sierpinskin kolmion aloitustilanne on tasasivuinen kolmio, joka jaetaan neljään yhtä suureen kolmioon, joista keskimmäinen poistetaan.

Palauta vastaustiedosto tähän.
Tarkastele kahta ensimmäistä vaihetta. Kuinka monta varjostettua kolmiota syntyy yhdestä isosta varjostetusta kolmiosta? Montako eri kappaletta siis kutistetaan kertoimella ?
Uusien pienempien kolmioiden koko on alkuperäisestä, eli
.
Hyödynnetään nyt määritelmän laskukaavaa Hausdorffin dimension määrittämiselle: ja tässä tehtävässä
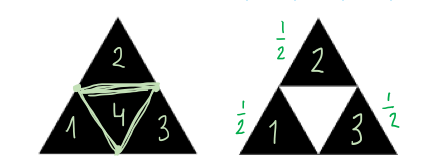
Kirjoitetaan yhtälö auki:
Sierpinskin kolmion, jonka kutistuskerroin on , Hausdorffin dimensio
.
5.3 Tehtävä: Mengerin pesusienen Hausdorffin dimensio
Määritä Mengerin pesusienen Hausdorffin dimensio, kun tiedetään kutistuskertoimen olevan . Mengerin pesusienen aloitustilanne on umpinainen kuutio, joka jaetaan
yhtä suureen kuutioon. Samoin kuin Sierpinskin kolmionkin tilanteessa aina keskimmäinen kuutio poistetaan.

Palauta vastaustiedosto tähän:
Tarkastele kahta ensimmäistä vaihetta. Yksi kuutio jaetaan aina yhtä suureen kuutioon, joista keskimmäiset poistetaan. Yhteensä siis poistetaan
kuutiota. Jäljelle jää
.
Uusien pienempien kolmioiden koko on alkuperäisestä, eli
.
Mengerin pesusieni aloitetaan umpinaisesta kuutiosta, joka jaetaan yhtä suureen pienempään kuutioon. Näistä kuutioista poistetaan aina keskimmäinen, eli yhteensä
kuutiota. Jäljelle jää tällöin
kuutiota, joiden koko on
alkuperäisestä.
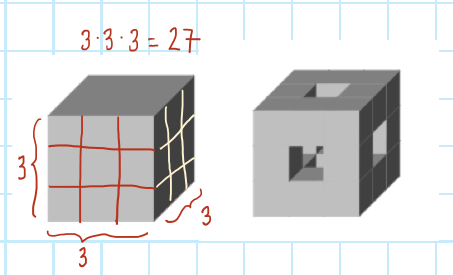
Hyödynnetään nyt määritelmän laskukaavaa Hausdorffin dimension määrittämiselle: ja tässä tehtävässä
Kirjoitetaan yhtälö auki:
Mengerin pesusienen, jonka kutistuskerroin on , Hausdorffin dimensio
.
6. Ylimääräisiä palautuspaikkoja vastaustiedostoille
Tähän voit tarvittaessa palauttaa tiedostoja, jos esimerkiksi tehtävän vastaus koostuu useammasta kuin yhdestä tiedostosta. Pyri kuitenkin palauttamaan vastaustiedosto vain yhtenä tiedostona itse tehtävän yhteyteen, jotta opettajan on helpompi löytää se.
These are the current permissions for this document; please modify if needed. You can always modify these permissions from the manage page.